Modeling and Exploration of Localized Wave Phenomena in Optical Fibers Using the Generalized Kundu–Eckhaus Equation for Femtosecond Pulse Transmission
Abstract
1. Introduction
2. Mathematical Analysis and Modeling
3. Multivariate Generalized Exponential Rational Integral Function Approach
- Step 01:
- When and then
- When and then
- When and then
- When and then
- When and then
- Step 02:
- Using the homogeneous balance principle, we may get the positive integer N by balancing the highest-order derivative and nonlinear variables in Equation (3).
- Step 03:
- After inserting Equations (11) and (12) in Equation (3) as a result of this substitution, we get a polynomial of with . Equivalently, setting all terms with the same power equal to zero. Then by solving this set of nonlinear algebraic systems with the help of Equation (12), the solutions of Equation (1) may be determined.
- Step 04:
3.1. Solutions by MGERIF Method
3.2. The Familiar Sin Description
- Case 1.1:
- Case 1.2:
- Case 1.3:
- Case 1.4:
3.3. The Familiar Cosine Description
- Case 1.1:
- Case 1.2:
- Case 1.3:
- Case 1.4:
3.4. The Familiar Exponential Description
- Case 1.1:
- Case 1.2:
- Case 1.3:
- Case 1.4:
3.5. The Familiar Cosine Hyperbolic Description
- Case 1.1:
- Case 1.2:
- Case 1.3:
- Case 1.4:
3.6. The Familiar Sin Hyperbolic Description
- Case 1.1:
- Case 1.2:
- Case 1.3:
- Case 1.4:
4. Expected Outcomes of the MGERIF Method
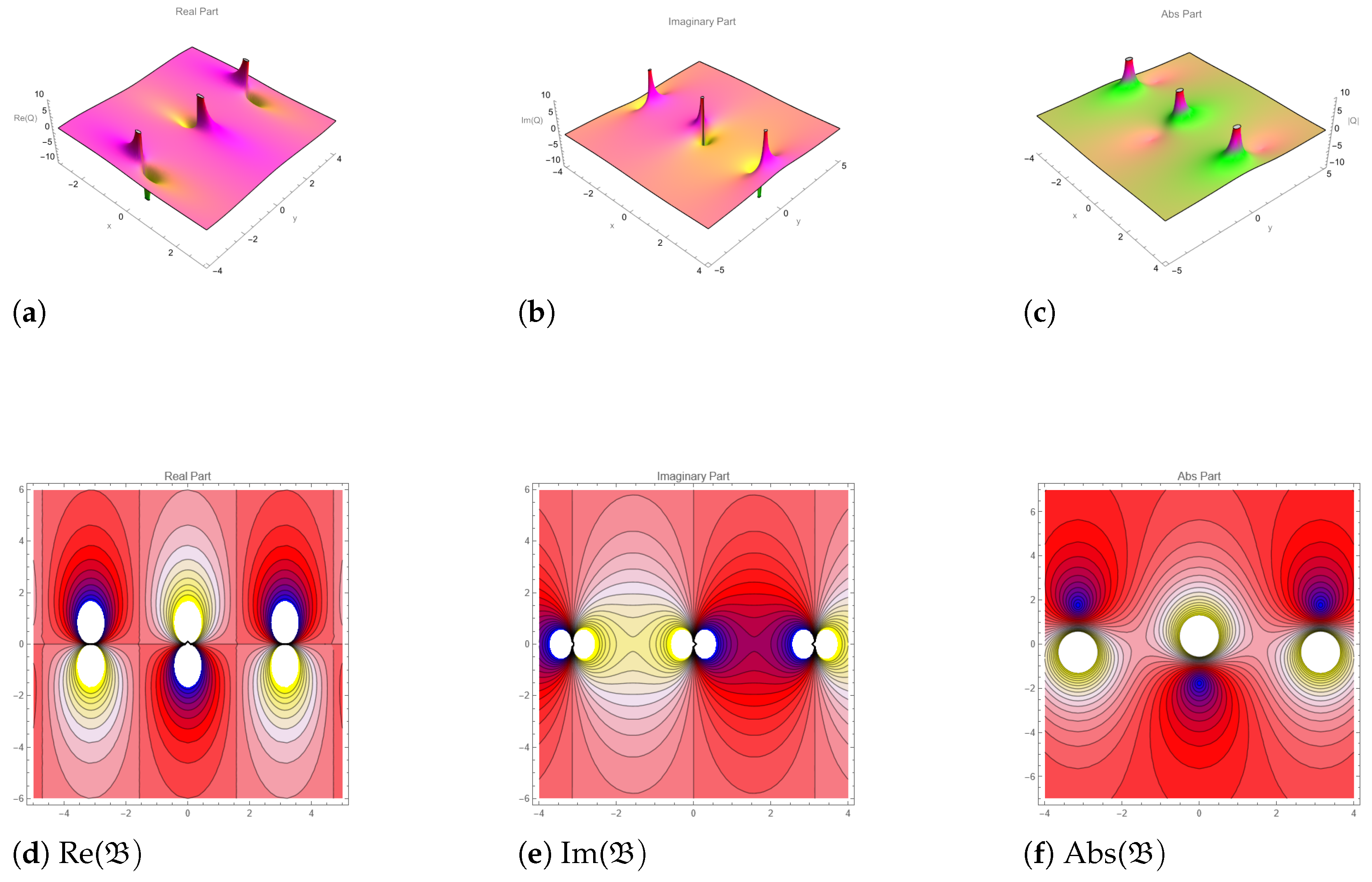
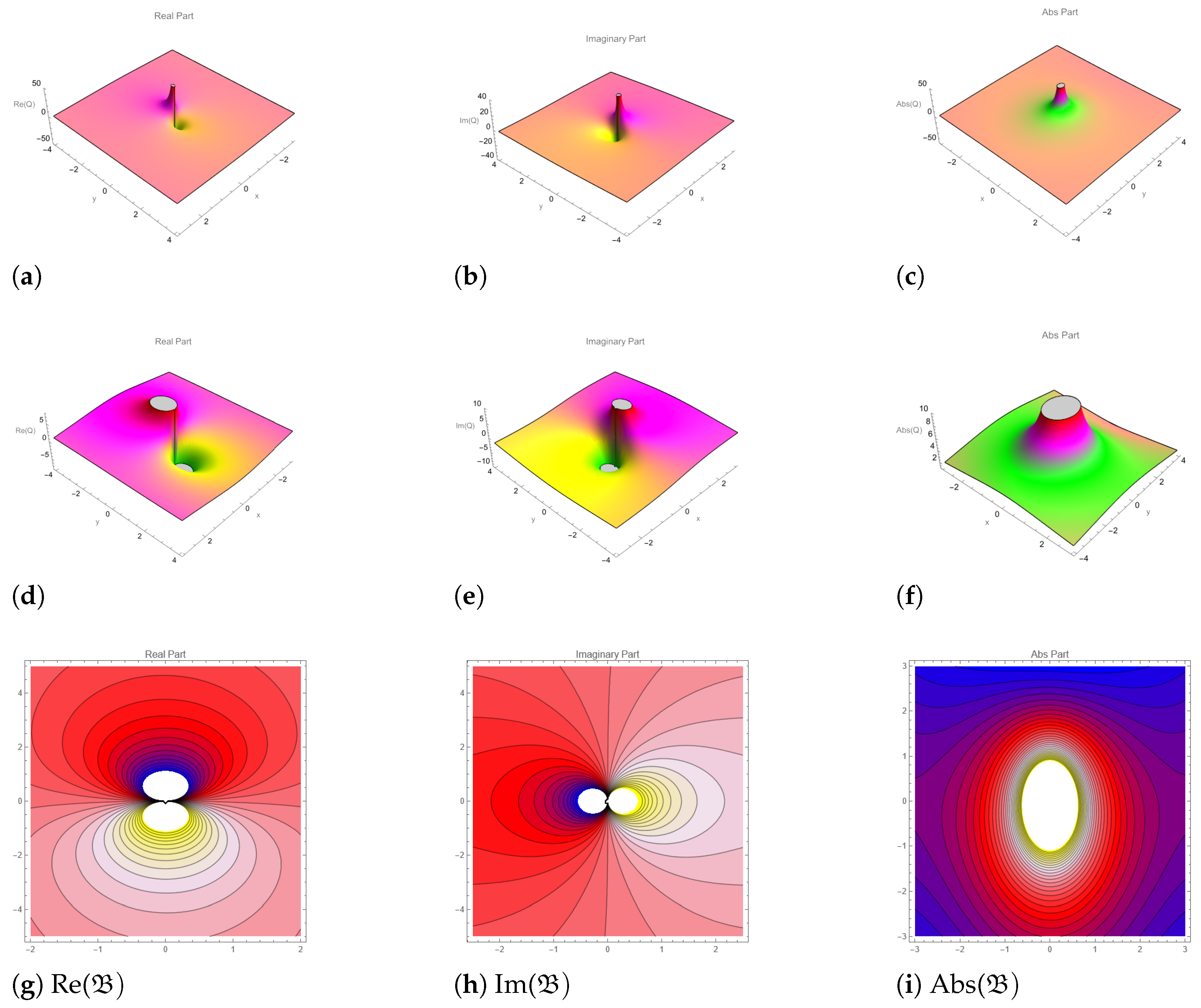
5. Graphical Representation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Description |
| t | Temporal variable |
| x | Spatial variables |
| Complex smooth envelop function | |
| A | Coefficient of weak dispersion |
| Third- and fourth-order extra dispersion coefficients | |
| G | Represents either self-focusing or self-defocusing polarized pulses |
| B | Represents cubic and quintic nonlinearity coefficients |
| K | Real fixed parameter that shows the frequency shift |
| Real fixed parameter that shows the wave number | |
| c | Stands for the phase constant |
| Real constant | |
| Represents the speed of the soliton |
References
- Sonmezoglu, A. Stationary optical solitons having Kudryashov’s quintuple power law nonlinearity by extended –expansion. Optik 2022, 253, 168521. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Davodi, A.G.; Gholami, D. Combined formal periodic wave-like and soliton-like solutions of the conformable Schrödinger-KdV equation using the -expansion technique. Result Phys. 2023, 47, 106352. [Google Scholar] [CrossRef]
- Wang, M.Y.; Biswas, A.; Yıldırım, Y.; Moraru, L.; Moldovanu, S.; Alshehri, H.M. Optical solitons for a concatenation model by Trial equation approach. Electronics 2023, 12, 19. [Google Scholar] [CrossRef]
- Ekici, M.; Sonmezoglu, A. Optical solitons with Biswas-Arshed equation by extended trial function method. Optik 2019, 177, 13–20. [Google Scholar] [CrossRef]
- Pandir, Y.; Gurefe, Y.; Misirli, E. The extended trial equation method for some time fractional differential equations. Discret. Dyn. Nat. Soc. 2013, 2013, 491359. [Google Scholar] [CrossRef]
- Zheng, B. The Riccati Sub-ODE method for fractional differential-difference equations. WSEAS Trans. Math. 2014, 13, 192–200. [Google Scholar]
- Akinyemi, L.; Mirzazadeh, M.; Amin, B.S.; Hosseini, K. Dynamical solitons for the perturbated Biswas–Milovic equation with Kudryashov’s law of refractive index using the first integral method. J. Mod. Opt 2022, 69, 172–182. [Google Scholar] [CrossRef]
- Ilie, M. An application of the first integral method for the time-fractional differential equation. J. Food Compos. Anal. 2022, 13, 32–44. [Google Scholar]
- Yao, S.W.; Manzoor, R.; Zafar, A.; Inc, M.; Abbagari, S.; Houwe, A. Exact soliton solutions to the Cahn–Allen equation and Predator–Prey model with truncated M-fractional derivative. Result Phys. 2022, 37, 105455. [Google Scholar] [CrossRef]
- Ibrahim, S.; Ashir, A.M.; Sabawi, Y.A.; Baleanu, D. Realization of optical solitons from nonlinear Schrödinger equation using modified Sardar sub-equation technique. Opt. Quantum Electron. 2023, 55, 617. [Google Scholar] [CrossRef]
- Cinar, M.; Secer, A.; Ozisik, M.; Bayram, M. Derivation of optical solitons of dimensionless Fokas-Lenells equation with perturbation term using Sardar sub-equation method. Opt. Quantum Electron. 2022, 54, 402. [Google Scholar] [CrossRef]
- Zayed, E.M.E. A note on the modified simple equation method applied to Sharma–Tasso–Olver equation. Appl. Math. Comput. 2011, 218, 3962–3964. [Google Scholar] [CrossRef]
- Kaplan, M.; Bekir, A.; Akbulut, A.; Aksoy, E. The modified simple equation method for nonlinear fractional differential equations. Rom. J. Phys. 2015, 60, 1374–1383. [Google Scholar]
- Ekici, M. Optical solitons with Kudryashov’s quintuple power–law coupled with the dual form of non–local law of refractive index with extended Jacobi’s elliptic function. Opt. Quantum Electron. 2022, 54, 279. [Google Scholar] [CrossRef]
- Khalil, T.A.; Badra, N.; Ahmed, H.M.; Rabie, W.B. Optical solitons and other solutions for coupled system of nonlinear Biswas–Milovic equation with Kudryashov’s law of refractive index by Jacobi elliptic function expansion method. Optik 2022, 253, 168540. [Google Scholar] [CrossRef]
- Ekici, M. Stationary optical solitons with Kudryashovs quintuple power law nonlinearity by extended Jacobi’s elliptic function expansion. J. Nonlinear Opt. Phys. Mater. 2023, 32, 2350008. [Google Scholar] [CrossRef]
- Mandal, U.K.; Malik, S.; Kumar, S.; Zhang, Y.; Das, A. Integrability aspects, rational type solutions and invariant solutions of an extended (3+ 1)-dimensional B-type Kadomtsev–Petviashvili equation. Chaos Solitons Fractals 2024, 181, 114689. [Google Scholar] [CrossRef]
- Malik, S.; Kumar, S.; Biswas, A.; Yıldırım, Y.; Moraru, L.; Moldovanu, S.; Iticescu, C.; Moshokoa, S.P.; Bibicu, D.; Alotaibi, A. Gap solitons in fiber Bragg gratings having polynomial law of nonlinear refractive index and cubic–quartic dispersive reflectivity by lie symmetry. Symmetry 2023, 15, 963. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Zaghrout, A.S.; Ahmed, H.M.; Arnous, A.H. Optical soliton perturbation of the Gerdjikov–Ivanov equation with spatio-temporal dispersion using a modified extended direct algebraic method. Optik 2022, 259, 168904. [Google Scholar] [CrossRef]
- Ghayad, M.S.; Badra, N.M.; Ahmed, H.M.; Rabie, W.B. Derivation of optical solitons and other solutions for nonlinear Schrödinger equation using modified extended direct algebraic method. Alex. Eng. J. 2023, 64, 801–811. [Google Scholar] [CrossRef]
- Zhang, X.; Ren, B. Resonance solitons, soliton molecules and hybrid solutions for a (2+1)-dimensional nonlinear wave equation arising in the shallow water wave. Nonlinear Dyn. 2024, 112, 4793–4802. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y.; Li, W. General high-order solitons and breathers with a periodic wave background in the nonlocal Hirota-Maccari equation. Nonlinear Dyn. 2024, 112, 4803–4813. [Google Scholar] [CrossRef]
- Wu, J. Riemann-Hilbert approach and soliton analysis of a novel nonlocal reverse-time nonlinear Schrödinger equation. Nonlinear Dyn. 2024, 112, 4749–4760. [Google Scholar] [CrossRef]
- Kumar, S.; Malik, S. The (3+ 1)-dimensional Benjamin–Ono equation: Painlevé analysis, rogue waves, breather waves and soliton solutions. Int. J. Mod. Phys. B 2022, 36, 2250119. [Google Scholar] [CrossRef]
- Shen, Y.; Tian, B.; Cheng, C.D.; Zhou, T.Y. N-soliton, M th-order breather, H th-order lump, and hybrid solutions of an extended (3+1)-dimensional Kadomtsev-Petviashvili equation. Nonlinear Dyn. 2023, 111, 10407–10424. [Google Scholar] [CrossRef]
- Rao, J.; Mihalache, D.; Cheng, Y.; He, J. Lump-soliton solutions to the Fokas system. Phys. Lett. A 2019, 383, 1138–1142. [Google Scholar] [CrossRef]
- Kumar, S.; Malik, S.; Rezazadeh, H.; Akinyemi, L. The integrable Boussinesq equation and it’s breather, lump and soliton solutions. Nonlinear Dyn. 2022, 107, 2703–2716. [Google Scholar] [CrossRef]
- Hussain, E.; Li, Z.; Shah, S.; Zo’bi, E.; Hussien, M. Dynamics study of stability analysis, sensitivity insights and precise soliton solutions of the nonlinear (STO)-Burger equation. Opt. Quantum Electron. 2023, 55, 1274. [Google Scholar] [CrossRef]
- Hussain, E.; Shah, S.A.A.; Bariq, A.; Li, Z.; Ahmad, M.R.; Ragab, A.E.; Az-Zo’bi, E.A. Solitonic solutions and stability analysis of Benjamin Bona Mahony Burger equation using two versatile techniques. Sci. Rep. 2024, 14, 13520. [Google Scholar] [CrossRef]
- Khater, M.M.A. Nonparaxial pulse propagation in a planar waveguide with Kerr–like and quintic nonlinearities; computational simulations. Chaos Soliton Fractals 2022, 157, 111970. [Google Scholar] [CrossRef]
- Xia, T.; Chen, X.; Chen, D. Darboux transformation and soliton-like solutions of nonlinear Schroedinger equations. Chaos Soliton Fractals 2005, 26, 889–896. [Google Scholar] [CrossRef]
- Jing, Z.; Yang, J.; Feng, W. Bifurcation and chaos in neural excitable system. Chaos Soliton Fractals 2006, 27, 197–215. [Google Scholar] [CrossRef]
- Li, Z.; Hussain, E. Qualitative analysis and optical solitons for the (1+ 1)-dimensional Biswas-Milovic equation with parabolic law and nonlocal nonlinearity. Results Phys. 2024, 56, 107304. [Google Scholar] [CrossRef]
- Beenish; Hussain, E.; Younas, U.; Tapdigoglu, R.; Garayev, M. Exploring Bifurcation, Quasi-Periodic Patterns, and Wave Dynamics in an Extended Calogero-Bogoyavlenskii-Schiff Model with Sensitivity Analysis. Int. J. Theor. Phys. 2025, 64, 146. [Google Scholar] [CrossRef]
- Li, Z.; Hussain, E. Qualitative analysis and traveling wave solutions of a (3+1)-dimensional generalized nonlinear Konopelchenko-Dubrovsky-Kaup-Kupershmidt system. Fractal Fract. 2025, 9, 285. [Google Scholar] [CrossRef]
- Beenish; Samreen, M. Bifurcation, Multistability, and Soliton Dynamics in the Stochastic Potential Korteweg-de Vries Equation. Int. J. Theor. Phys. 2025, 64, 1–22. [Google Scholar] [CrossRef]
- Yao, S.W.; Behera, S.; Inc, M.; Rezazadeh, H.; Virdi, J.P.S.; Mahmoud, W.; Arqub, O.A.; Osman, M.S. Analytical solutions of conformable Drinfeld–Sokolov–Wilson and Boiti Leon Pempinelli equations via sine–cosine method. Result Phys. 2022, 42, 105990. [Google Scholar] [CrossRef]
- Fendzi-Donfack, E.; Temgoua, G.W.K.; Djoufack, Z.I.; Kenfack-Jiotsa, A.; Nguenang, J.P.; Nana, L. Exotical solitons for an intrinsic fractional circuit using the sine-cosine method. Chaos Soliton Fractals 2022, 160, 112253. [Google Scholar] [CrossRef]
- Hussain, E.; Shah, S.A.A.; Rafiq, M.N.; Ragab, A.E.; Az-Zo’bi, E.A. Exact solutions and modulation instability analysis of a generalized Kundu-Eckhaus equation with extra-dispersion in optical fibers. Phys. Scr. 2024, 99, 055222. [Google Scholar] [CrossRef]
- Niwas, M.; Kumar, S.; Rajput, R.; Chadha, D. Exploring localized waves and different dynamics of solitons in (2+ 1)-dimensional Hirota bilinear equation: A multivariate generalized exponential rational integral function approach. Nonlinear Dyn. 2024, 1–14. [Google Scholar] [CrossRef]
- Younas, U.; Hussain, E.; Muhammad, J.; Sharaf, M.; Meligy, M.E. Chaotic Structure, Sensitivity Analysis and Dynamics of Solitons to the Nonlinear Fractional Longitudinal Wave Equation. Int. J. Theor. Phys. 2025, 64, 42. [Google Scholar] [CrossRef]
- Muhammad, J.; Younas, U.; Nasreen, N.; Khan, A.; Abdeljawad, T. Multicomponent nonlinear fractional Schrödinger equation: On the study of optical wave propagation in the fiber optics. Partial. Differ. Equ. Appl. Math. 2024, 11, 100805. [Google Scholar] [CrossRef]
- Ajmal, M.; Muhammad, J.; Younas, U.; Hussian, E.; El-Meligy, M.; Sharaf, M. Exploring the Gross-Pitaevskii Model in Bose-Einstein Condensates and Communication Systems: Features of Solitary Waves and Dynamical Analysis. Int. J. Theor. Phys. 2025, 64, 1–26. [Google Scholar] [CrossRef]
- Ahmed, K.K.; Badra, N.M.; Ahmed, H.M.; Rabie, W.B. Soliton solutions of generalized Kundu-Eckhaus equation with an extra-dispersion via improved modified extended tanh-function technique. Opt. Quantum Electron. 2023, 55, 299. [Google Scholar] [CrossRef]
- Hamza, A.E.; Suhail, M.; Alsulami, A.; Mustafa, A.; Aldwoah, K.; Saber, H. Exploring Soliton Solutions and Chaotic Dynamics in the (3+ 1)-Dimensional Wazwaz–Benjamin–Bona–Mahony Equation: A Generalized Rational Exponential Function Approach. Fractal Fract. 2024, 8, 592. [Google Scholar] [CrossRef]
- Asghari, Y.; Eslami, M.; Matinfar, M.; Rezazadeh, H. Novel soliton solution of discrete nonlinear Schrödinger system in nonlinear optical fiber. Alex. Eng. J. 2024, 90, 7–16. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, E.; Tedjani, A.H.; Farooq, K.; Beenish. Modeling and Exploration of Localized Wave Phenomena in Optical Fibers Using the Generalized Kundu–Eckhaus Equation for Femtosecond Pulse Transmission. Axioms 2025, 14, 513. https://doi.org/10.3390/axioms14070513
Hussain E, Tedjani AH, Farooq K, Beenish. Modeling and Exploration of Localized Wave Phenomena in Optical Fibers Using the Generalized Kundu–Eckhaus Equation for Femtosecond Pulse Transmission. Axioms. 2025; 14(7):513. https://doi.org/10.3390/axioms14070513
Chicago/Turabian StyleHussain, Ejaz, Ali H. Tedjani, Khizar Farooq, and Beenish. 2025. "Modeling and Exploration of Localized Wave Phenomena in Optical Fibers Using the Generalized Kundu–Eckhaus Equation for Femtosecond Pulse Transmission" Axioms 14, no. 7: 513. https://doi.org/10.3390/axioms14070513
APA StyleHussain, E., Tedjani, A. H., Farooq, K., & Beenish. (2025). Modeling and Exploration of Localized Wave Phenomena in Optical Fibers Using the Generalized Kundu–Eckhaus Equation for Femtosecond Pulse Transmission. Axioms, 14(7), 513. https://doi.org/10.3390/axioms14070513






