The (2+1)-Dimensional Chiral Nonlinear Schrödinger Equation: Extraction of Soliton Solutions and Sensitivity Analysis

Abstract

The objective of this manuscript is to investigate the (2+1)-dimensional Chiral nonlinear Schrödinger equation (CNLSE). We employ the traveling wave transformation to convert the nonlinear partial differential equation (NLPDE) into the nonlinear ordinary differential equation (NLODE). Utilizing the two new vital techniques to derive the solitary wave solutions, the generalized Arnous method and the Riccati equation method, we obtained various types of waves like bright solitons, dark solitons, and periodic wave solutions. Sensitivity analysis is also discussed using different initial conditions. Sensitivity analysis refers to the study of how the solutions of the equations respond to changes in the parameters or initial conditions. It involves assessing the impact of variations in these factors on the behavior and properties of the solutions. To better comprehend the physical consequences of these solutions, we showcase them through different visual depictions like 3D, 2D, and contour plots. The findings of this study are original and hold significant value for the future exploration of the equation, offering valuable directions for researchers to deepen knowledge on the subject.

1. Introduction

Real-world phenomena can be best modeled using partial differential equations (PDEs). The nonlinear terms are often seen in PDEs as real-world phenomena that exhibit nonlinear behavior. Nonlinear PDEs are integral to natural sciences such as biology, chemistry, and physics [1,2,3,4]. Furthermore, nonlinear PDEs have applications in emerging fields such as machine learning and microbiology. Conversely, certain complex phenomena can be effectively modeled using nonlinear PDEs. Finding the exact solution of NLPDEs is challenging compared to linear PDEs. There are several techniques to derive solutions for NLPDEs, such as the modified sub-equation method [5], extended $(G^{\prime }/G^2)$-expansion method [6], modified auxiliary equation method [7], Sardar sub-equation method [8], Darboux transformation method [9], Lie symmetry analysis [10], Hirota bilinear method [11], chaotic behavior and bifurcation analysis [12,13,14], and many more methods discussed in [15,16,17].

The nonlinear Schrödinger equation (NLSE) is one of modern science’s most prominent and ubiquitous nonlinear models, appearing in many physics and applied mathematics fields. The most notable solutions of the NLSE are solitary waves, or solitons, which manifest unique properties such as a localized waveform preserved upon interaction with other solitons, giving them a “particle-like” quality. The theory of NLSE solitons was first developed in 1971 by Zakharov and Shabat [18,19]. Following the novel techniques of Gardner et al. [20] and Lax [21,22], Zakharov and Shabat were the first to apply the inverse scattering transform (IST) method to this equation. This method was developed in the quantum scattering theory by Gel’fand et al. [23,24,25,26,27].

In recent decades, NLSE solitons have been experimentally verified across various branches of modern science and identified numerous soliton properties derivable from the IST theory. Hasegawa and Tappert [28] were the first to theoretically demonstrate that an optical pulse in a dielectric fiber forms a solitary wave as the wave envelope obeys the NLSE. The renowned experiment of Mollenauer et al. [29] was explicitly designed to authenticate the use of the prediction. Optical solitons are considered natural data bits and a favorable alternative for the following generation of ultrahigh-speed optical telecommunication systems [30]. Moreover, the theory of picosecond optical solitons, developed within the framework of the NLSE model, has shown remarkable agreement between theory and experiment [31].

In this article, our purpose lies in finding some exact solutions for the following $(2+1)$ CNLSE [32]

$$i{\displaystyle \frac{\partial \mathcal{U}}{\partial t}}+\beta \left({\displaystyle \frac{{\partial }^2\mathcal{U}}{\partial x^2}}+{\displaystyle \frac{{\partial }^2\mathcal{U}}{\partial y^2}}\right)+i\left[{\alpha }_1\left(\mathcal{U}{\displaystyle \frac{\partial {\mathcal{U}}^{\ast }}{\partial x}}-{\mathcal{U}}^{\ast }{\displaystyle \frac{\partial \mathcal{U}}{\partial x}}\right)+{\alpha }_2\left(\mathcal{U}{\displaystyle \frac{\partial {\mathcal{U}}^{\ast }}{\partial y}}-{\mathcal{U}}^{\ast }{\displaystyle \frac{\partial \mathcal{U}}{\partial y}}\right)\right]\mathcal{U}=0,$$

(1)

where $\mathcal{U}=\mathcal{U}(x,y,t)$ denotes a complex function, ${\mathcal{U}}^{\ast }$ is complex conjugate of $\mathcal{U}$, ${\alpha }_1$ and ${\alpha }_2$ are the coefficients of nonlinear coupling terms, and $\beta$ stands for the dispersion coefficient. The term $i{\displaystyle \frac{\partial \mathcal{U}}{\partial t}}$ is the evolution term. In the literature, several exact solutions of the Chiral stochastic NLSE have been derived using various methods such as the modified Khater and modified Jacobian expansion methods [33], the soliton ansatz method [32], the modified Jacobi elliptic expansion method [34], and the trial solution method [35]. This study aims to find solutions for the considered equation using the generalized Arnous technique and the Reccati equation method [36,37].

The paper provides a comprehensive overview of the proposed model and its analysis. In Section 2, the mathematical analysis of the model is described, wherein Equation (1) is transformed into a nonlinear ordinary differential Equation (ODE) using the traveling wave transformation. Section 3 outlines the methodologies employed, particularly focusing on the generalized Arnous method and its utilization to derive solitary wave solutions for Equation (1). In Section 4, the Riccati, equation method is introduced and applied to Equation (1). Section 5 addresses sensitivity analysis, examining various initial conditions. Finally, the conclusion is presented in Section 6.

2. Description of Proposed Model

Assume that the general form of the (NLPDE) is as follows:

$$\mathcal{M}\left(\mathcal{U},{\displaystyle \frac{\partial \mathcal{U}}{\partial t}},{\displaystyle \frac{\partial \mathcal{U}}{\partial x}},{\displaystyle \frac{\partial \mathcal{U}}{\partial y}},{\displaystyle \frac{{\partial }^2\mathcal{U}}{\partial x^2}},{\displaystyle \frac{{\partial }^2\mathcal{U}}{\partial y^2}},{\displaystyle \frac{{\partial }^2\mathcal{U}}{\partial t\partial x}},{\displaystyle \frac{{\partial }^2\mathcal{U}}{\partial t\partial y}},\dots \right)=0.$$

(2)

We can convert the NLPDEs into NLODES using the following traveling wave transformation [32,35]

$$\mathcal{U}(x,y,t)=\mathbb{M}\left(\xi \right)e^{\iota \theta },\xi =b_{1}x+b_{2}y-vt,\theta ={\lambda }_{1}x+{\lambda }_{2}y+\omega t+\phi ,$$

(3)

where $\omega$, $\varphi$, $vs.$, ${\lambda }_1$, ${\lambda }_2$, $b_1$, and $b_2$ are real constants. By inserting Equation (3) into Equation (2), we obtain the NLODE as

$$P({\mathbb{M}}^{\prime },{\mathbb{M}}^{″},{\mathbb{M}}^{‴},\dots )=0.$$

(4)

Plugging Equation (3) into Equation (1), we obtain the NLODE. The following equations can be derived after transformation from the imaginary and real parts, respectively:

$$(2\beta b_1{\lambda }_1+2\beta b_2{\lambda }_2-v){\displaystyle \frac{d}{d\xi }}\mathbb{M}\left(\xi \right)=0,$$

(5)

$$(2{\alpha }_1{\lambda }_1+2{\alpha }_2{\lambda }_2){\left(\mathbb{M}\left(\xi \right)\right)}^3+(-\beta {\lambda }_1^2-\beta {\lambda }_2^2-\omega )\mathbb{M}\left(\xi \right)+(\beta b_1^2+\beta b_2^2){\displaystyle \frac{d^2}{d{\xi }^2}}\mathbb{M}\left(\xi \right)=0.$$

(6)

From Equation (5), one may also obtain the following:

$$v=2\beta (b_1{\lambda }_1+b_2{\lambda }_2).$$

(7)

The following ODE is deduced from Equation (6):

$$2({\alpha }_1{\lambda }_1+{\alpha }_2{\lambda }_2){\mathbb{M}}^3\left(\xi \right)+(-\beta {\lambda }_1^2-\beta {\lambda }_2^2-\omega )\mathbb{M}\left(\xi \right)+(\beta b_1^2+\beta b_2^2){\mathbb{M}}^{″}\left(\xi \right)=0.$$

(8)

3. Mathematical Formulation for the Generalized Arnous Method

The main steps of the generalized Arnous (GA) method are given as follows [37]:

Step 1: The GA method provides the solution of Equation (4) as follows:

$$\mathbb{M}\left(\xi \right)={\gamma }_0+\sum _{k=1}^N{\displaystyle \frac{{\gamma }_K+{\eta }_k{Q}^{\prime }{\left(\xi \right)}^k}{Q{\left(\xi \right)}^k}},$$

(9)

where ${\gamma }_0,{\gamma }_k,$ and ${\eta }_k$ (for $k=1,2,\dots ,N$) are constants, and the function $Q\left(\xi \right)$ satisfies the relation

$${\left[Q^{\prime }\left(\xi \right)\right]}^2=[Q{\left(\xi \right)}^2-\rho ]\ln {\left(\delta \right)}^2,$$

(10)

with

$$Q^{\left(n\right)}\left(\xi \right)=\left\{\begin{array}{cc}Q\left(\xi \right)\ln {\left(\delta \right)}^n,\hfill & \mathrm{if}n\mathrm{is}\mathrm{even},\hfill \\ Q^{\prime }\left(\xi \right)\ln {\left(\delta \right)}^{n-1},\hfill & \mathrm{if}n\mathrm{is}\mathrm{odd},\hfill \end{array}\right.$$

(11)

where $\delta >0$, $\delta \ne 1$, and $n\ge 2$. Equation (10) has a solution of the form

$$Q(\xi )=A\ln (\delta ){\delta }^{\xi }+{\displaystyle \frac{\rho }{4A\ln (\delta ){\delta }^{\xi }}},$$

(12)

where A and $\rho$ are random parameters.

Step 2: By matching the nonlinear term with the highest-order derivative term in Equation (4), the value of N for Equation (9) is determined.

Step 3: After substituting Equations (10)–(12) into Equation (3) and $Q\left(\xi \right)\ne 0$, this results in a polynomial of ${\displaystyle \frac{1}{Q\left(\xi \right)}}$$\left({\displaystyle \frac{Q^{\prime }\left(\xi \right)}{Q\left(\xi \right)}}\right)$. Next, we collect all terms of the same power and set them equal to zero. Then, by solving the resulting nonlinear algebraic system, the solutions of Equation (2) can be derived.

Solution by Generalized Arnous Method

To find the exact solutions to Equation (8), first, we derive the value of N from Equation (8) by the homogeneous balance principle and then put it into Equation (9); then, Equation (9) can be written as follows:

$$\mathbb{M}\left(\xi \right)={\displaystyle \frac{{\gamma }_{0}Q\left(\xi \right)+{\gamma }_1+{\eta }_1{Q}^{\prime }\left(\xi \right)}{Q\left(\xi \right)}}.$$

(13)

By putting Equations (9)–(11) into Equation (8), we obtain a polynomial in terms of ${\displaystyle \frac{1}{Q\left(\xi \right)}}{\displaystyle \frac{Q^{\prime }\left(\xi \right)}{Q\left(\xi \right)}}$. This substitution gives a set of equations where all the terms of identical power are collected and set equal to zero as follows:

$$\begin{array}{cc}\begin{array}{c}0=6{\alpha }_1{\gamma }_0{\eta }_1^2{\lambda }_1{\ln }^2(\delta )+6{\alpha }_2{\gamma }_0{\eta }_1^2{\lambda }_2{\ln }^2(\delta )+2{\alpha }_1{\gamma }_0^3{\lambda }_1+2{\alpha }_2{\gamma }_0^3{\lambda }_2-\beta {\gamma }_0{\lambda }_1^2-\beta {\gamma }_0{\lambda }_2^2-{\gamma }_0\omega ,\hfill \\ 0=-6{\alpha }_1{\gamma }_1{\eta }_1^2{\lambda }_1\rho {\ln }^2(\delta )-6{\alpha }_2{\gamma }_1{\eta }_1^2{\lambda }_2\rho {\ln }^2(\delta )+2{\alpha }_1{\gamma }_1^3{\lambda }_1+2{\alpha }_2{\gamma }_1^3{\lambda }_2-2\beta b_1^2{\gamma }_1\rho {\ln }^2(\delta )-2\beta b_2^2{\gamma }_1\rho {\ln }^2(\delta ),\hfill \\ 0=-6{\alpha }_1{\gamma }_0{\eta }_1^2{\lambda }_1\rho {\ln }^2(\delta )-6{\alpha }_2{\gamma }_0{\eta }_1^2{\lambda }_2\rho {\ln }^2(\delta )+6{\alpha }_1{\gamma }_0{\gamma }_1^2{\lambda }_1+6{\alpha }_2{\gamma }_0{\gamma }_1^2{\lambda }_2,\hfill \\ 0=6{\alpha }_1{\gamma }_1{\eta }_1^2{\lambda }_1{\ln }^2(\delta )+6{\alpha }_2{\gamma }_1{\eta }_1^2{\lambda }_2{\ln }^2(\delta )+6{\alpha }_1{\gamma }_0^2{\gamma }_1{\lambda }_1+6{\alpha }_2{\gamma }_0^2{\gamma }_1{\lambda }_2+\beta b_1^2{\gamma }_1{\ln }^2(\delta )+\beta b_2^2{\gamma }_1{\ln }^2(\delta )-\beta {\gamma }_1{\lambda }_1^2-\beta {\gamma }_1{\lambda }_2^2-{\gamma }_1\omega ,\hfill \\ 0=6{\alpha }_1{\gamma }_1^2{\eta }_1{\lambda }_1+\left(\delta \right)+6{\alpha }_2{\gamma }_1^2{\eta }_1{\lambda }_2-2{\alpha }_1{\eta }_1^3{\lambda }_1\rho {\ln }^2(\delta )-2{\alpha }_2{\eta }_1^3{\lambda }_2\rho {\ln }^2(\delta )-2\beta b_1^2{\lambda }_1\rho {\ln }^2(\delta )-2\beta b_2^2{\lambda }_1\rho {\ln }^2\left(\delta \right),\hfill \\ 0=12{\alpha }_1{\gamma }_0{\gamma }_1{\eta }_1{\lambda }_1+12{\alpha }_2{\gamma }_0{\gamma }_1{\eta }_1{\lambda }_2,\hfill \\ 0=6{\alpha }_1{\gamma }_0^2{\eta }_1{\lambda }_1+6{\alpha }_2{\gamma }_0^2{\eta }_1{\lambda }_2+2{\alpha }_1{\eta }_1^3{\lambda }_1{\ln }^2(\delta )+2{\alpha }_2{\eta }_1^3{\lambda }_2{\ln }^2(\delta )-\beta {\eta }_1{\lambda }_1^2-\beta {\eta }_1{\lambda }_2^2-{\eta }_1\omega .\hfill \end{array}\hfill & \}\end{array}$$

(14)

Solving Equation (14) with the help of Maple, we obtain the following set of solutions:

• Result 1:

$$\begin{array}{cc}\hfill & {\gamma }_0=0,{\gamma }_1={\displaystyle \frac{\sqrt{-\beta \left(b_1^2+b_2^2\right)}\sqrt{\rho }\ln (\delta )}{\sqrt{-4{\alpha }_1{\lambda }_1-4{\alpha }_2{\lambda }_2}}},{\eta }_1={\displaystyle \frac{\sqrt{-\beta \left(b_1^2+b_2^2\right)}}{2\sqrt{{\alpha }_1{\lambda }_1+{\alpha }_2{\lambda }_2}}},\hfill \\ \hfill & \omega =-{\displaystyle \frac{1}{2}}\beta \left(b_1^2{\ln }^2(\delta )+b_2^2{\ln }^2(\delta )+2\left({\lambda }_1^2+{\lambda }_2^2\right)\right).\hfill \end{array}$$

(15)

By substituting Equations (15) and (13) into Equation (3), we obtain the solution for Equation (1) as follows

$$\begin{array}{cc}\hfill {\mathcal{U}}_1(x,y,t)=& \left({\displaystyle \frac{\sqrt{-\beta \left(b_1^2+b_2^2\right)}\left(A{\delta }^{\xi }{\ln }^2(\delta )-\frac{\rho {\delta }^{-\xi }}{4A}\right)}{2\sqrt{{\alpha }_1{\lambda }_1+{\alpha }_2{\lambda }_2}\left(\frac{\rho {\delta }^{-\xi }}{4A\ln \left(\delta \right)}+A{\delta }^{\xi }\ln (\delta )\right)}}+{\displaystyle \frac{i\sqrt{\beta }\sqrt{b_1^2+b_2^2}\sqrt{\rho }\ln (\delta )}{\sqrt{-4{\alpha }_1{\lambda }_1-4{\alpha }_2{\lambda }_2}\left(\frac{\rho {\delta }^{-\xi }}{4A\ln \left(\delta \right)}+A{\delta }^{\xi }\ln \left(\delta \right)\right)}}\right)\hfill \\ \hfill & \times e^{\iota \left({\lambda }_{1}x+{\lambda }_{2}y+\omega t+\phi \right)}.\hfill \end{array}$$

(16)

By taking the value of $\delta =e$ and $\rho =4A^2$, in Equation (16), we derive the bright soliton solution for Equation (1) as follows (Figure 1)

$${\mathcal{U}}_2(x,y,t)=\left({\displaystyle \frac{\sqrt{-\beta b_1^2-\beta b_2^2}tanh\left(\xi \right)}{2\sqrt{{\alpha }_1{\lambda }_1+{\alpha }_2{\lambda }_2}}}+{\displaystyle \frac{i\sqrt{A^2}\sqrt{\beta }\sqrt{b_1^2+b_2^2}\mathrm{sech}\left(\xi \right)}{A\sqrt{-4{\alpha }_1{\lambda }_1-4{\alpha }_2{\lambda }_2}}}\right)e^{\iota \left({\lambda }_{1}x+{\lambda }_{2}y+\omega t+\phi \right)}.$$

(17)

Similarly, when $\rho$ and $\delta$ are set to $-4A^2$ and e, respectively, in Equation (16), then it is reduced to following dark soliton solution (Figure 2)

$${\mathcal{U}}_3(x,y,t)=\left({\displaystyle \frac{\sqrt{-\beta b_1^2-\beta b_2^2}coth\left(\xi \right)}{2\sqrt{{\alpha }_1{\lambda }_1+{\alpha }_2{\lambda }_2}}}+{\displaystyle \frac{i\sqrt{-A^2}\sqrt{\beta }\sqrt{b_1^2+b_2^2}\mathrm{csch}\left(\xi \right)}{A\sqrt{-4{\alpha }_1{\lambda }_1-4{\alpha }_2{\lambda }_2}}}\right)e^{\iota \left({\lambda }_{1}x+{\lambda }_{2}y+\omega t+\phi \right)}.$$

(18)

• Result 2:

$${\gamma }_0=0,{\gamma }_1=0,{\eta }_1={\displaystyle \frac{\sqrt{-\beta \left(b_1^2+b_2^2\right)}}{\sqrt{{\alpha }_1{\lambda }_1+{\alpha }_2{\lambda }_2}}},\omega =-\beta \left(2b_1^2{\ln }^2(\delta )+2b_2^2{\ln }^2(\delta )+{\lambda }_1^2+{\lambda }_2^2\right).$$

(19)

By putting Equations (19) and (13) into Equation (3), we obtain the solution for Equation (1) as follows

$${\mathcal{U}}_4(x,y,t)={\displaystyle \frac{\sqrt{-\beta \left(b_1^2+b_2^2\right)}\left(A{\delta }^{\xi }{\ln }^2(\delta )-\frac{\rho {\delta }^{-\xi }}{4A}\right)}{\sqrt{{\alpha }_1{\lambda }_1+{\alpha }_2{\lambda }_2}\left(\frac{\rho {\delta }^{-\xi }}{4A\ln (\delta )}+A{\delta }^{\xi }\ln (\delta )\right)}}{e}^{\iota \left({\lambda }_{1}x+{\lambda }_{2}y+\omega t+\phi \right)}.$$

(20)

When the value of $\delta =e$ and $\rho =4A^2$, inserted into Equation (20), we obtain the dark soliton solution as follows (Figure 3)

$${\mathcal{U}}_5(x,y,t)={\displaystyle \frac{\sqrt{-\beta b_1^2-\beta b_2^2}tanh\left(\xi \right)}{\sqrt{{\alpha }_1{\lambda }_1+{\alpha }_2{\lambda }_2}}}{e}^{\iota \left({\lambda }_{1}x+{\lambda }_{2}y+\omega t+\phi \right)}.$$

(21)

Similarly, when we substitute the value of $\rho =-4A^2$ and $\delta =e$ in Equation (20), then Equation (20) transforms into a singular solution as

$${\mathcal{U}}_6(x,y,t)={\displaystyle \frac{\sqrt{-\beta b_1^2-\beta b_2^2}coth\left(\xi \right)}{\sqrt{{\alpha }_1{\lambda }_1+{\alpha }_2{\lambda }_2}}}{e}^{\iota \left({\lambda }_{1}x+{\lambda }_{2}y+\omega t+\phi \right)}.$$

(22)

• Result 3:

$${\gamma }_0=0,{\gamma }_1={\displaystyle \frac{i\sqrt{\beta }\sqrt{b_1^2+b_2^2}\sqrt{\rho }\ln (\delta )}{\sqrt{-{\alpha }_1{\lambda }_1-{\alpha }_2{\lambda }_2}}},{\eta }_1=0,\omega =\beta \left(b_1^2{\ln }^2\left(\delta \right)+b_2^2{\ln }^2(\delta )-{\lambda }_1^2-{\lambda }_2^2\right)\}.$$

(23)

Incorporating Equations (23) and (13) into Equation (3), the obtained solution for Equation (8) is given below

$$\begin{array}{cc}\hfill {\mathcal{U}}_7(x,y,t)=& {\displaystyle \frac{\sqrt{-{\beta }^{3/2}\left(b_1^2+b_2^2\right)\rho {\ln }^2(\delta )\left({\alpha }_2\sqrt{\beta }{\lambda }_2+{\alpha }_1\sqrt{\beta b_1^2{\ln }^2(\delta )+\beta b_2^2{\ln }^2(\delta )-\beta {\lambda }_2^2-\omega }\right)}}{\left(\frac{\rho {\delta }^{-\xi }}{4A\ln \left(\delta \right)}+A{\delta }^{\xi }\ln (\delta )\right)\sqrt{{\alpha }_1^2\left(\beta b_1^2{\ln }^2(\delta )+\beta b_2^2{\ln }^2(\delta )-\beta {\lambda }_2^2-\omega \right)-{\alpha }_2^2\beta {\lambda }_2^2}}}\hfill \\ \hfill & \times e^{\iota \left({\lambda }_{1}x+{\lambda }_{2}y+\omega t+\phi \right)}.\hfill \end{array}$$

(24)

By substituting the values of $\delta =e$ and $\rho =4A^2$, then Equation (24) turns into a bright soliton solution as (Figure 4)

$${\mathcal{U}}_8(x,y,t)={\displaystyle \frac{\mathrm{sech}\left(\xi \right)\sqrt{-A^2{\beta }^{3/2}\left(b_1^2+b_2^2\right)\left({\alpha }_2\sqrt{\beta }{\lambda }_2+{\alpha }_1\sqrt{\beta b_1^2+\beta b_2^2-\beta {\lambda }_2^2-\omega }\right)}}{A\sqrt{-{\alpha }_1^2\beta {\lambda }_2^2-{\alpha }_2^2\beta {\lambda }_2^2-{\alpha }_1^2\omega +{\alpha }_1^2\beta b_1^2+{\alpha }_1^2\beta b_2^2}}}{e}^{\iota \left({\lambda }_{1}x+{\lambda }_{2}y+\omega t+\phi \right)}.$$

(25)

Similarly, when $\rho =-4A^2$ and $\delta =e$, inserted into Equation (24), then Equation (24) attains a singular solution as

$${\mathcal{U}}_9(x,y,t)={\displaystyle \frac{\mathrm{csch}\left(\xi \right)\sqrt{A^2{\beta }^{3/2}\left(b_1^2+b_2^2\right)\left({\alpha }_2\sqrt{\beta }{\lambda }_2+{\alpha }_1\sqrt{\beta b_1^2+\beta b_2^2-\beta {\lambda }_2^2-\omega }\right)}}{A\sqrt{-{\alpha }_1^2\beta {\lambda }_2^2-{\alpha }_2^2\beta {\lambda }_2^2-{\alpha }_1^2\omega +{\alpha }_1^2\beta b_1^2+{\alpha }_1^2\beta b_2^2}}}{e}^{\iota \left({\lambda }_{1}x+{\lambda }_{2}y+\omega t+\phi \right)}.$$

(26)

4. Riccati Equation Method

The general solution of Equation (8), according to REM, has the following form [36]:

$$\mathbb{M}\left(\xi \right)=\sum _{i=0}^N{c}_i{Q}^i\left(\xi \right).$$

(27)

We apply the homogeneous balancing principle on Equation (8) and find the value of N. The function $Q\left(\xi \right)$ holds for the Riccati equation

$$Q^{\prime }\left(\xi \right)={\Theta }_2{Q}^2\left(\xi \right)+{\Theta }_{1}Q\left(\xi \right)+{\Theta }_0,{\Theta }_2\ne 0.\left(7\right)$$

(28)

with the constants ${\Theta }_2$, ${\Theta }_1$, ${\Theta }_0$. The solutions of Equation (28) are

$$Q\left(\xi \right)=\left\{\begin{array}{cc}-{\displaystyle \frac{{\Theta }_1}{2{\Theta }_2}}-{\displaystyle \frac{\sqrt{\mu }}{2{\Theta }_2}}tanh\left({\displaystyle \frac{\sqrt{\mu }}{2}}\xi +{\xi }_0\right),\hfill & \mu >0\hfill \\ \\ -{\displaystyle \frac{{\Theta }_1}{2{\Theta }_2}}-{\displaystyle \frac{\sqrt{\mu }}{2{\Theta }_2}}coth\left({\displaystyle \frac{\sqrt{\mu }}{2}}\xi +{\xi }_0\right),\hfill & \mu >0\hfill \\ \\ -{\displaystyle \frac{{\Theta }_1}{2{\Theta }_2}}+{\displaystyle \frac{\sqrt{-\mu }}{2{\Theta }_2}}tan\left({\displaystyle \frac{\sqrt{-\mu }}{2}}\xi +{\xi }_0\right),\hfill & \mu <0\hfill \\ \\ -{\displaystyle \frac{{\Theta }_1}{2{\Theta }_2}}-{\displaystyle \frac{\sqrt{-\mu }}{2{\Theta }_2}}cot\left({\displaystyle \frac{\sqrt{-\mu }}{2}}\xi +{\xi }_0\right),\hfill & \mu <0\hfill \\ \\ -{\displaystyle \frac{{\Theta }_1}{2{\Theta }_2}}-{\displaystyle \frac{1}{{\Theta }_2\xi }}+{\xi }_0,\hfill & \mu =0\hfill \end{array}\right.$$

(29)

where $\mu ={\Theta }_1^2-4{\Theta }_2{\Theta }_0$.

Solution by the Reccati Equation Method

The Reccati equation method indicates the solution of Equation (27) as follows:

$$\mathbb{M}\left(\xi \right)=c_0+c_{1}Q\left(\xi \right).$$

(30)

Putting Equation (30) into Equation (8) and setting the coefficients of different powers of $Q\left(\xi \right)=0$, we obtain the following set of equations:

$$\left.\begin{array}{c}Q{\left(\xi \right)}^0=\beta {\Theta }_0{\Theta }_1{b}_1^2{c}_1+\beta {\Theta }_0{\Theta }_1{b}_2^2{c}_1+2{\alpha }_1{\lambda }_1{c}_0^3+2{\alpha }_2{\lambda }_2{c}_0^3-\beta {\lambda }_1^2{c}_0-\beta {\lambda }_2^2{c}_0-\omega c_0=0,\hfill \\ \\ Q\left(\xi \right)=2\beta {\Theta }_0{\Theta }_2{b}_1^2{c}_1+2\beta {\Theta }_0{\Theta }_2{b}_2^2{c}_1+\beta {\Theta }_1^2{b}_1^2{c}_1+\beta {\Theta }_1^2{b}_2^2{c}_1+6{\alpha }_1{\lambda }_1{c}_0^2{c}_1\hfill \\ +6{\alpha }_2{\lambda }_2{c}_0^2{c}_1-\beta {\lambda }_1^2{c}_1-\beta {\lambda }_2^2{c}_1-\omega c_1=0,\hfill \\ \\ Q{\left(\xi \right)}^2=3\beta {\Theta }_1{\Theta }_2{b}_1^2{c}_1+3\beta {\Theta }_1{\Theta }_2{b}_2^2{c}_1+6{\alpha }_1{\lambda }_1{c}_0{c}_1^2+6{\alpha }_2{\lambda }_2{c}_0{c}_1^2=0,\hfill \\ \\ Q{\left(\xi \right)}^3=2\beta {\Theta }_2^2{b}_1^2{c}_1+2\beta {\Theta }_2^2{b}_2^2{c}_1+2{\alpha }_1{\lambda }_1{c}_1^3+2{\alpha }_2{\lambda }_2{c}_1^3=0.\hfill \\ \end{array}\right\}$$

(31)

The answer to the given set of equations is found by solving them simultaneously.

$$\begin{array}{cc}\hfill & \omega =2\beta {\Theta }_0{\Theta }_2{b}_1^2+2\beta {\Theta }_0{\Theta }_2{b}_2^2-{\displaystyle \frac{1}{2}}\beta {\Theta }_1^2{b}_1^2-{\displaystyle \frac{1}{2}}\beta {\Theta }_1^2{b}_2^2-\beta {\lambda }_1^2-\beta {\lambda }_2^2,\hfill \\ \hfill & c_0=\sqrt{-{\displaystyle \frac{\beta b_1^2+\beta b_2^2}{4{\alpha }_1{\lambda }_1+4{\alpha }_2{\lambda }_2}}}{\Theta }_1,c_1=2{\Theta }_2\sqrt{-{\displaystyle \frac{\beta b_1^2+\beta b_2^2}{4{\alpha }_1{\lambda }_1+4{\alpha }_2{\lambda }_2}}}.\hfill \end{array}$$

(32)

Corresponding to the above values, we derive the following cases:

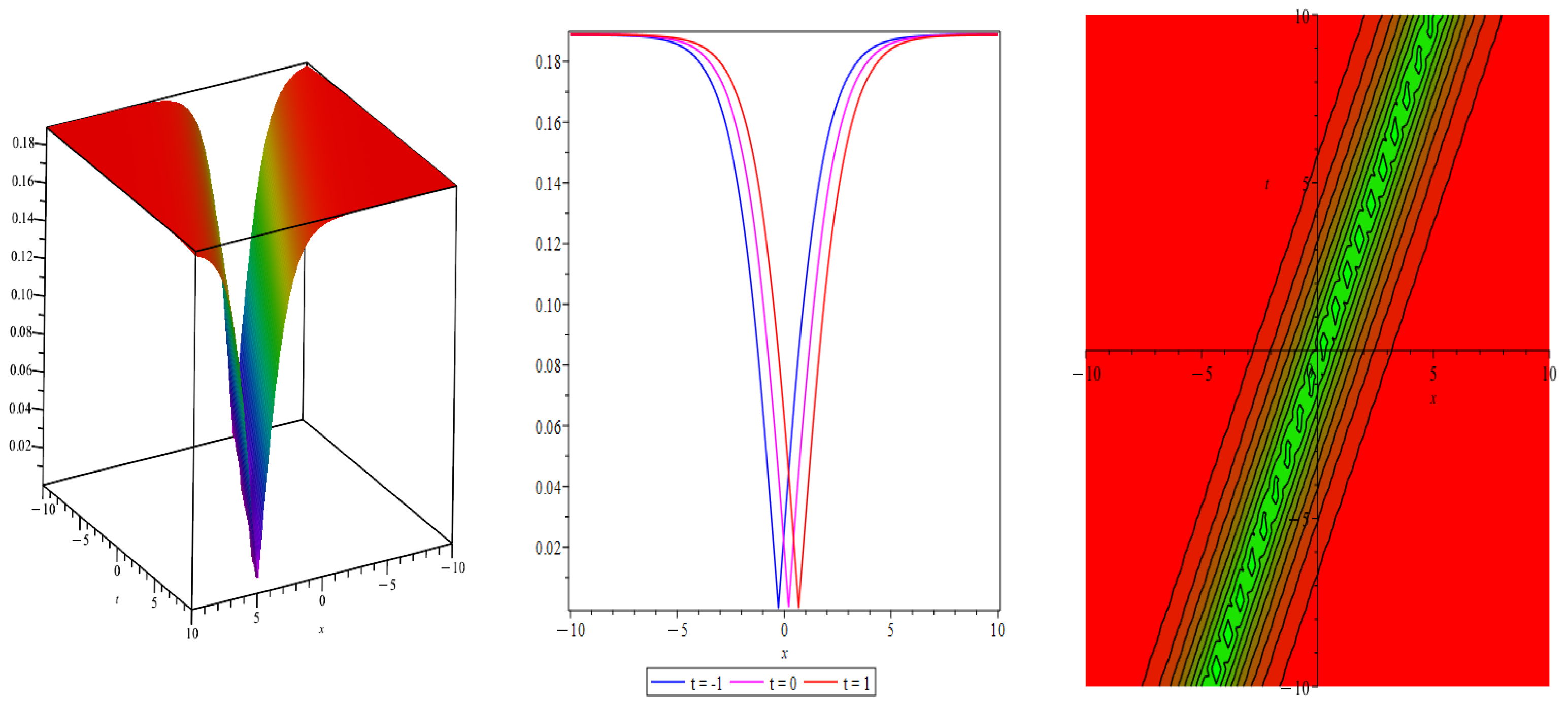
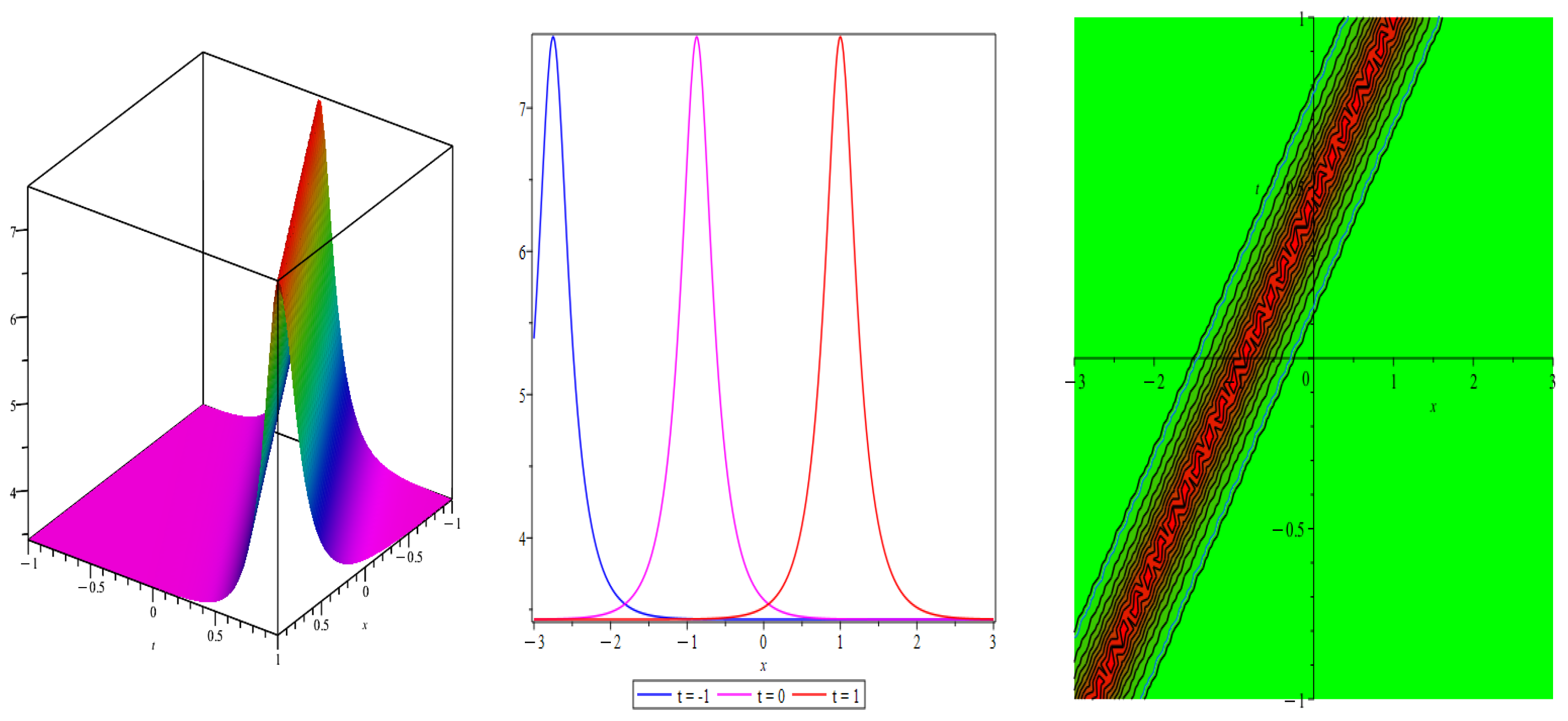
• Case 1: When $\mu >0$, then we obtain following dark soliton solution (Figure 5)

$$\begin{array}{cc}\hfill {\mathcal{U}}_{10}(x,y,t)=& -\sqrt{-{\displaystyle \frac{\beta \left(b_1^2+b_2^2\right)\left({\Theta }_1^2-4{\Theta }_0{\Theta }_2\right)}{4\left({\alpha }_1{\lambda }_1+{\alpha }_2{\lambda }_2\right)}}}tanh\left({\displaystyle \frac{\sqrt{{\Theta }_1^2-4{\Theta }_0{\Theta }_2}\left(b_{1}x+b_{2}y-vt\right)}{2}}+{\xi }_0\right)\hfill \\ \hfill & \times e^{\iota \left({\lambda }_{1}x+{\lambda }_{2}y+\omega t+\phi \right)}.\hfill \end{array}$$

(33)

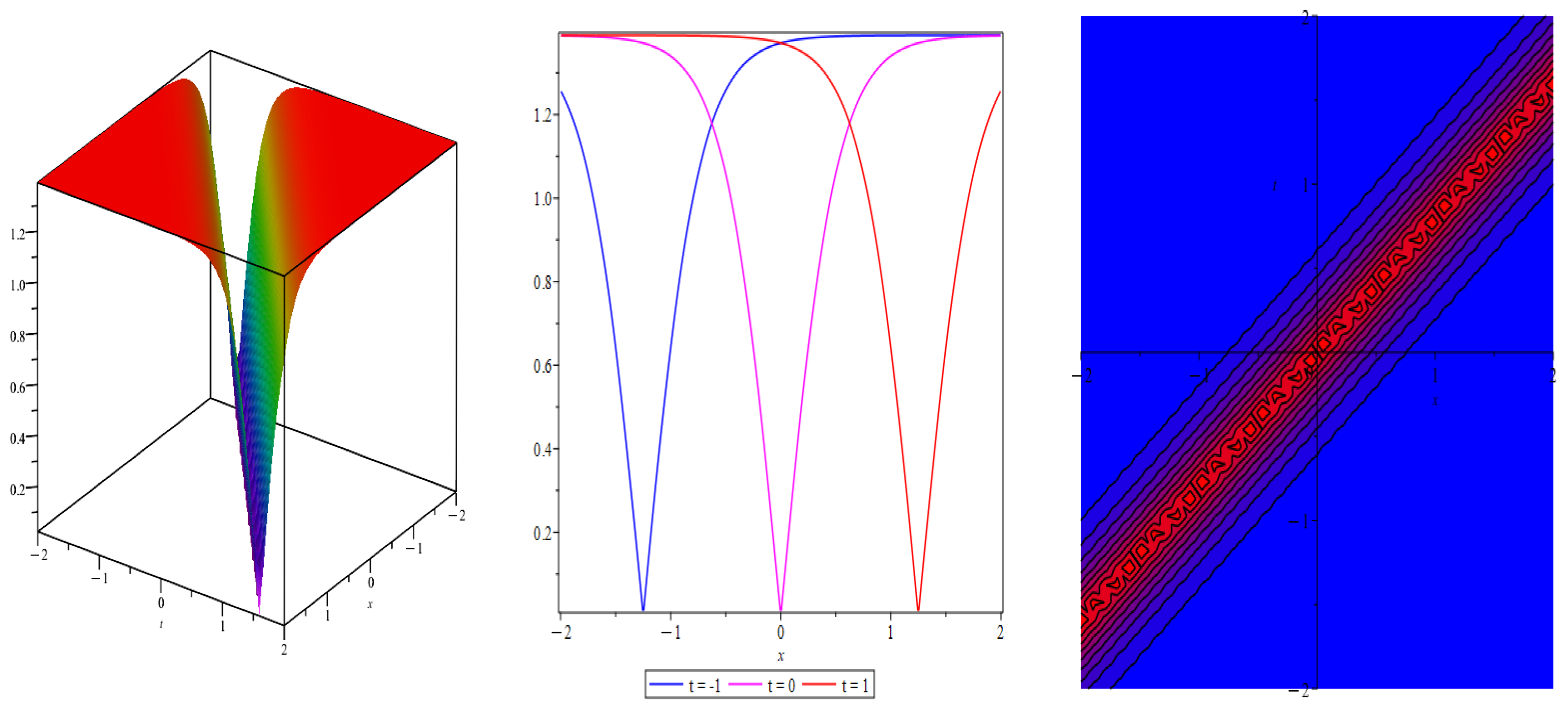
• Case 2: When $\mu >0$, then we derive the singular solution as (Figure 6)

$$\begin{array}{cc}\hfill {\mathcal{U}}_{11}(x,y,t)=& -\sqrt{-{\displaystyle \frac{\beta \left(b_1^2+b_2^2\right)\left({\Theta }_1^2-4{\Theta }_0{\Theta }_2\right)}{4\left({\alpha }_1{\lambda }_1+{\alpha }_2{\lambda }_2\right)}}}coth\left({\displaystyle \frac{\sqrt{{\Theta }_1^2-4{\Theta }_0{\Theta }_2}\left(b_{1}x+b_{2}y-vs.t\right)}{2}}+{\xi }_0\right)\hfill \\ \hfill & \times e^{\iota \left({\lambda }_{1}x+{\lambda }_{2}y+\omega t+\phi \right)}.\hfill \end{array}$$

(34)

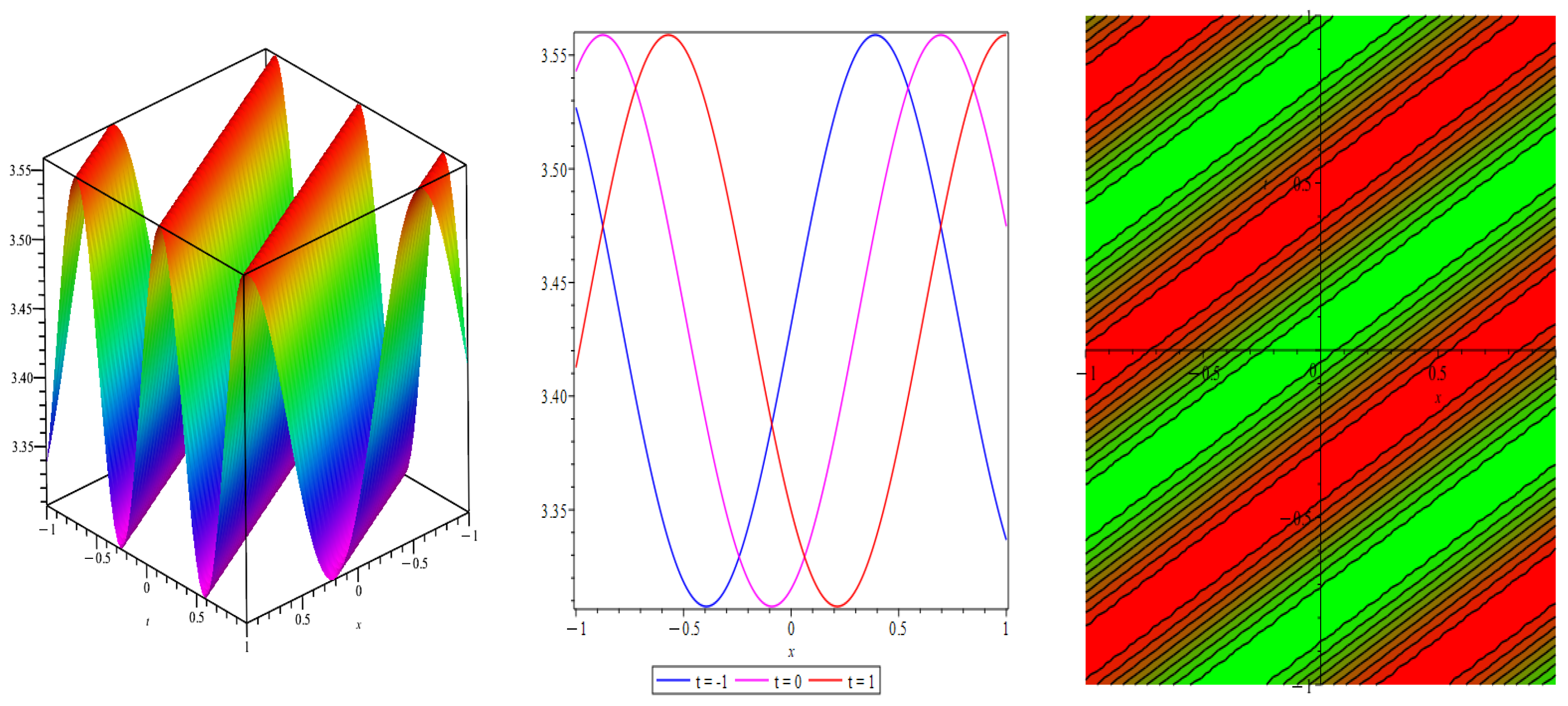
• Case 3: When $\mu <0$, then we obtain following periodic solution

$$\begin{array}{cc}\hfill {\mathcal{U}}_{12}(x,y,t)=& \sqrt{{\displaystyle \frac{\beta \left(b_1^2+b_2^2\right)\left({\Theta }_1^2-4{\Theta }_0{\Theta }_2\right)}{4\left({\alpha }_1{\lambda }_1+{\alpha }_2{\lambda }_2\right)}}}tan\left({\displaystyle \frac{\sqrt{4{\Theta }_0{\Theta }_2-{\Theta }_1^2}\left(b_{1}x+b_{2}y-vt\right)}{2}}+{\xi }_0\right)\hfill \\ \hfill & \times e^{\iota \left({\lambda }_{1}x+{\lambda }_{2}y+\omega t+\phi \right)}.\hfill \end{array}$$

(35)

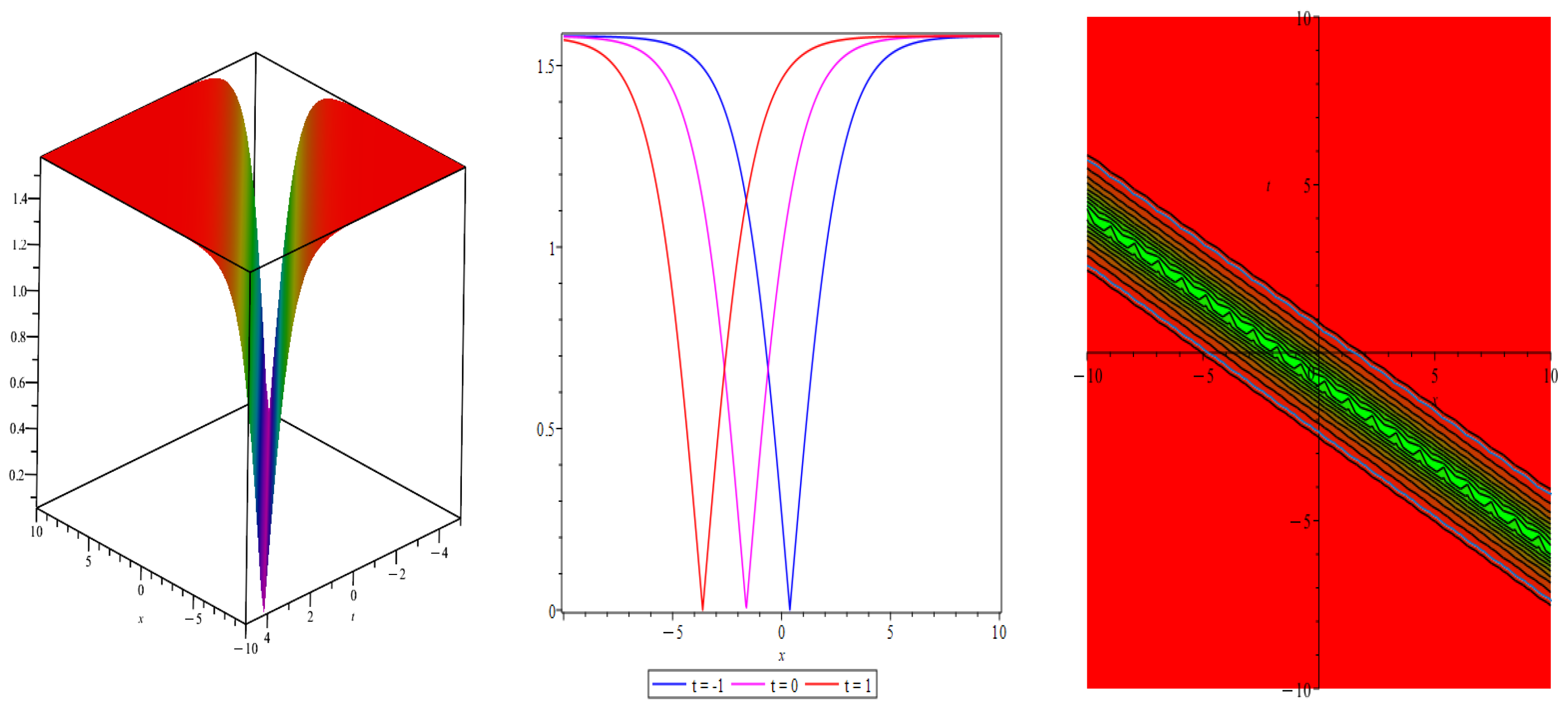
• Case 4: When $\mu <0$, then we derive following singular solutions (Figure 7)

$$\begin{array}{cc}\hfill {\mathcal{U}}_{13}(x,y,t)=& -\sqrt{{\displaystyle \frac{\beta \left(b_1^2+b_2^2\right)\left({\Theta }_1^2-4{\Theta }_0{\Theta }_2\right)}{4\left({\alpha }_1{\lambda }_1+{\alpha }_2{\lambda }_2\right)}}}cot\left({\displaystyle \frac{\sqrt{4{\Theta }_0{\Theta }_2-{\Theta }_1^2}\left(b_{1}x+b_{2}y-vt\right)}{2}}+{\xi }_0\right)\hfill \\ \hfill & \times e^{\iota \left({\lambda }_{1}x+{\lambda }_{2}y+\omega t+\phi \right)}.\hfill \end{array}$$

(36)

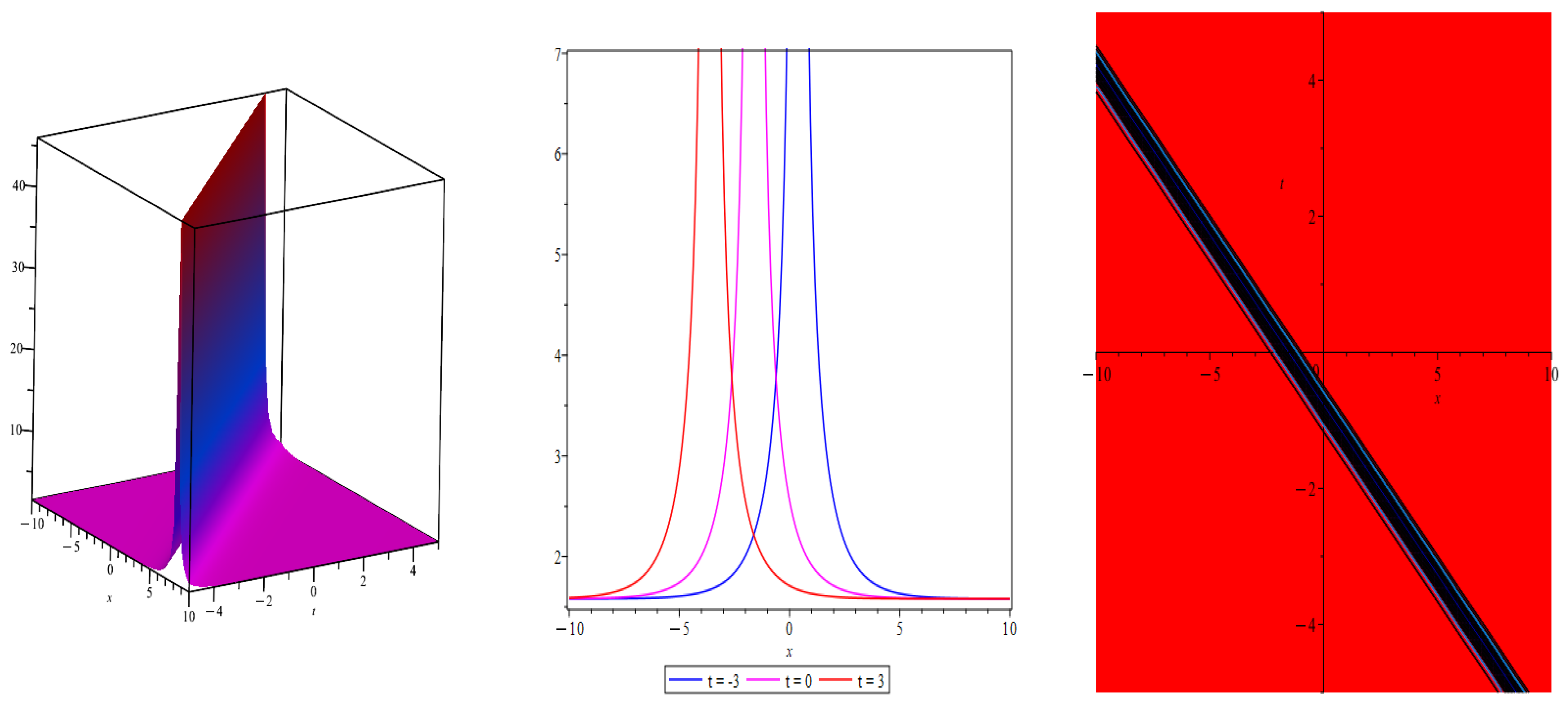
• Case 5: When $\mu =0$, then we obtain the following solution (Figure 8)

$${\mathcal{U}}_{14}(x,y,t)=-\sqrt{-{\displaystyle \frac{\beta \left(b_1^2+b_2^2\right)}{\left({\alpha }_1{\lambda }_1+{\alpha }_2{\lambda }_2\right)}}}{\displaystyle \frac{{\Theta }_2}{{\Theta }_2\left(b_{1}x+b_{2}y-vt\right)+{\xi }_0}}{e}^{\iota \left({\lambda }_{1}x+{\lambda }_{2}y+\omega t+\phi \right)}.$$

(37)

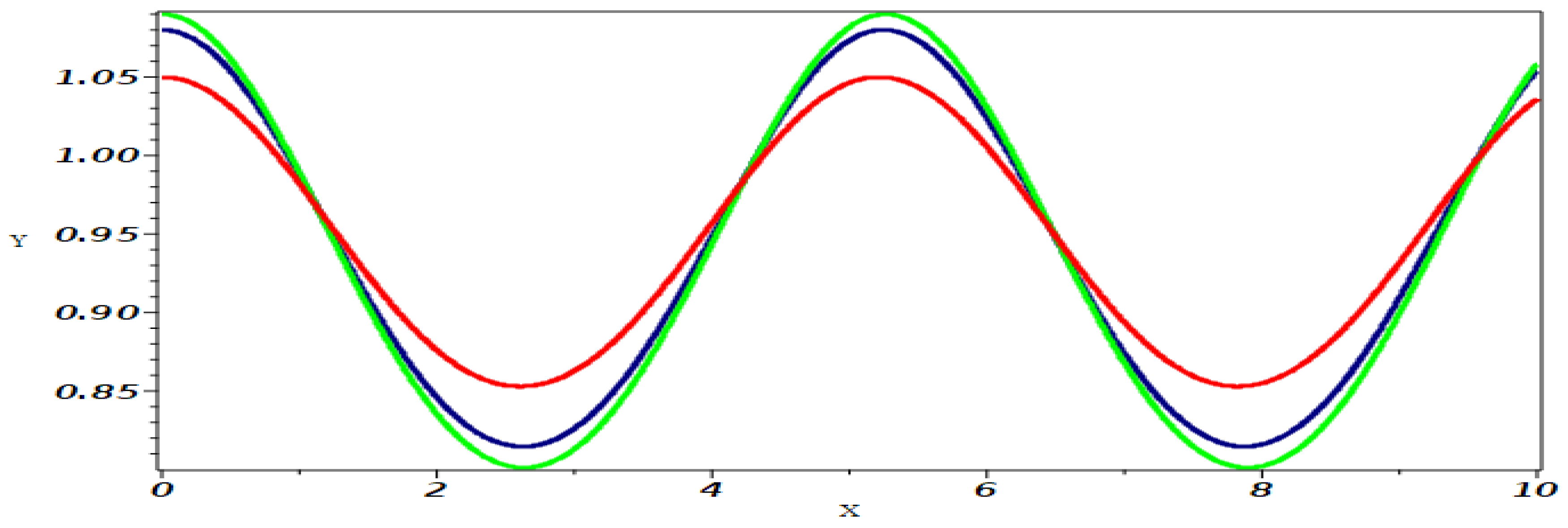
5. Sensitivity Analysis of Equation (1)

This section delves into the sensitivity analysis of the proposed model presented in Equation (8), which is conducted by applying the Runge–Kutta method, leveraging the provided initial conditions. Using the Galilean transformation, Equation (8) can be transformed into two distinct systems of equations. Assuming that ${\mathbb{M}}^{\prime }=R$, Equation (8) can subsequently be expressed in the following manner [38,39]:

$$\begin{array}{c}\hfill \left.\begin{array}{c}{\displaystyle \frac{d{\mathbb{M}}^{\prime }}{d\xi }}=R,\hfill \\ \\ {\displaystyle \frac{dR}{d\xi }}=-2A{\mathbb{M}}^3-B\mathbb{M},\hfill \end{array}\right\}\end{array}$$

(38)

where $A={\displaystyle \frac{{\alpha }_1{\lambda }_1+{\alpha }_2{\lambda }_2}{\beta b_1^2+\beta b_2^2}}$ and $B={\displaystyle \frac{-\beta {\lambda }_1^2-\beta {\lambda }_2^2-\omega }{\beta b_1^2+\beta b_2^2}}$.

The system Equation (38) is solved using the Runge–Kutta method by applying the suitable parameter values for ${\alpha }_1=1,{\alpha }_2=0.7,{\lambda }_1=0.5,{\lambda }_2=0.22,b_1=0.9,b_2=0.03,\omega =0.6,$ and $\beta =2$. Three solutions, red, navy blue, and green, indicated by $(R,\mathbb{M})=(0,1.05)$, $(R,\mathbb{M})=(0,1.08)$, and $(R,\mathbb{M})=(0,1.09)$, respectively, are shown in Figure 9. Upon observing the figures, it becomes evident that minor alterations in the initial conditions have a negligible impact on the stability of the solution.

6. Conclusions

In this manuscript, we investigated the (2+1)-dimensional CNLSE, a significant equation in nonlinear wave theory. Using the traveling wave transformation, we successfully converted the NLPDE into a solvable nonlinear ODE. Then, we employed two novel and effective methods as follows: the generalized Arnous method and the Riccati equation method. These methodologies enabled us to extract various solitary wave solutions, encompassing bright solitons, dark solitons, and periodic wave solutions. Each type of solution presents unique characteristics and behaviors that contribute to the broader understanding of wave dynamics governed by the CNLSE. An integral part of our study involved sensitivity analysis, wherein we examined how solutions respond to parameter variations or initial conditions. This analysis is crucial for assessing the robustness and stability of the obtained solutions. By altering different parameters and initial conditions, we observed and analyzed the resultant changes in the behavior and properties of the wave solutions.

To provide a comprehensive understanding of the physical implications of our findings, we visualized the solutions using various graphical representations, including 3D plots, 2D plots, and contour plots. These visualizations not only illustrate the theoretical results but also offer an intuitive grasp of the wave dynamics described by the CNLSE. The outcomes of this study are both original and significant, paving the way for future research endeavors. Our findings offer a solid foundation for the deeper exploration of the CNLSE and its applications in various scientific and engineering fields. This research contributes valuable insights and guidance for researchers aiming to advance the study of nonlinear wave equations and their diverse applications.