Abstract
This work presents a comprehensive mathematical framework for symmetrized neural network operators operating under the paradigm of fractional calculus. By introducing a perturbed hyperbolic tangent activation, we construct a family of localized, symmetric, and positive kernel-like densities, which form the analytical backbone for three classes of multivariate operators: quasi-interpolation, Kantorovich-type, and quadrature-type. A central theoretical contribution is the derivation of the Voronovskaya–Santos–Sales Theorem, which extends classical asymptotic expansions to the fractional domain, providing rigorous error bounds and normalized remainder terms governed by Caputo derivatives. The operators exhibit key properties such as partition of unity, exponential decay, and scaling invariance, which are essential for stable and accurate approximations in high-dimensional settings and systems governed by nonlocal dynamics. The theoretical framework is thoroughly validated through applications in signal processing and fractional fluid dynamics, including the formulation of nonlocal viscous models and fractional Navier–Stokes equations with memory effects. Numerical experiments demonstrate a relative error reduction of up to 92.5% when compared to classical quasi-interpolation operators, with observed convergence rates reaching under Caputo derivatives, using parameters , , and . This synergy between neural operator theory, asymptotic analysis, and fractional calculus not only advances the theoretical landscape of function approximation but also provides practical computational tools for addressing complex physical systems characterized by long-range interactions and anomalous diffusion.
Keywords:
neural network operators; fractional differentiation; asymptotic analysis; Caputo derivatives; Voronovskaya-type expansions MSC:
68T07; 00A69; 41A25; 41A30; 41A36
1. Introduction
Neural network operators have become indispensable tools in approximation theory and computational mathematics, primarily due to their exceptional capacity to model highly nonlinear functions. This capability underlies a broad spectrum of applications, ranging from the numerical solution of partial differential equations to signal processing and data-driven modeling [1,2]. In the context of fractional calculus and its applications to differential equations, several studies have contributed to the development of efficient computational methods and theoretical frameworks. Refs. [3,4] presented an efficient computational method for differential equations of fractional type, highlighting the importance of numerical techniques in solving complex fractional differential equations. Additionally, [5] explored deep learning architectures, providing insights into the integration of neural networks in solving differential equations and modeling complex systems.
Recent advancements in the field of fractional calculus and its applications to neural networks have been significantly shaped by the contributions of [6,7,8]. Chen et al. [6] conducted an extensive exploration of fractional derivative modeling in mechanics and engineering, establishing a robust mathematical framework. This framework has been crucial in understanding complex systems governed by fractional differential equations. Their work laid the essential groundwork for integrating fractional calculus into neural network architectures, thereby facilitating the modeling of systems characterized by memory effects and long-range dependencies.
Building upon this foundation, [9] introduced parametrized, deformed, and general neural networks, which have been instrumental in advancing the theoretical landscape of function approximation. These neural networks, known for their flexibility and enhanced approximation capabilities, have played a crucial role in developing the symmetrized neural network operators discussed in the current study. By integrating these neural networks into the framework of fractional calculus, we have not only advanced theoretical understanding but also provided practical computational tools for addressing complex physical systems.
A significant contribution of the present work is the Voronovskaya–Santos–Sales Theorem, which extends classical asymptotic expansions to the fractional domain. This theorem provides rigorous error bounds and normalized remainder terms governed by Caputo derivatives. Combined with insights from [6,9], this theorem has enabled the development of neural network operators that exhibit superior convergence rates and improved analytical tractability. The practical efficacy of these operators has been demonstrated through applications in signal processing and fractional fluid dynamics, showcasing a relative error reduction of up to compared to classical quasi-interpolation operators. The observed convergence rates under Caputo derivatives further validate the robustness and accuracy of the proposed methods. These advancements highlight the critical role of fractional calculus in enhancing the capabilities of neural networks. They pave the way for future research in modeling complex systems with memory effects and nonlocal interactions, marking a significant step forward in both theoretical and applied domains. Among several formulations of fractional calculus, the Caputo derivative stands out for its well-posed initial conditions, and its physically intuitive interpretation can be seen in [10].
The work of [11] provides a comprehensive exploration of fractional calculus, offering a robust theoretical framework that has significantly influenced the development of fractional-order models in several scientific and engineering disciplines. This work has been instrumental in advancing the understanding and application of fractional differential equations, particularly in modeling complex systems that exhibit memory effects and nonlocal interactions. Building on this theoretical framework, ref. [12] introduced innovative numerical methods for solving fractional advection–dispersion equations, crucial for the accurate and efficient modeling of physical phenomena governed by fractional dynamics. His work on the finite difference/finite element method, combined with fast evaluation techniques for Caputo derivatives, paved the way for practical computational tools that improve the simulation of complex physical systems. More recently, other works have introduced fractional operators, which have been integrated into neural architectures, leveraging their inherent nonlocality to capture long-range dependencies and significantly improve approximation capabilities [13,14].
The intersection of neural operator theory with fractional calculus has driven the extension of classical approximation results into the fractional domain [6]. In particular, Voronovskaya-type asymptotic expansions have been generalized to neural network operators defined over unbounded domains, providing sharp error bounds within the framework of fractional differentiation [15,16,17]. These developments demonstrate that combining activation symmetry, parametrization, and fractional calculus yields operators with superior convergence rates and improved analytical tractability. Concurrently, fractional calculus has emerged as a powerful mathematical tool for modeling systems governed by memory effects, hereditary dynamics, and anomalous diffusion [18,19].
Building on these advances, this paper presents a comprehensive asymptotic framework for symmetrized neural network operators employing deformed hyperbolic tangent activations, with a particular focus on their behavior under Caputo fractional derivatives. Specifically, we introduce and rigorously analyze three families of multivariate operators, quasi-interpolation, Kantorovich-type, and quadrature-type, and formulate a fractional Voronovskaya-type theorem that establishes precise asymptotic expansions and error estimates [20,21,22].
The work of [23] has significantly advanced the application of wavelet transforms in various scientific and engineering fields. This work provides a comprehensive overview of how wavelet transforms can be utilized to analyze and process signals and data with high efficiency and accuracy. Wavelet transforms are particularly useful in capturing both frequency and location information, making them invaluable in the analysis of complex systems and phenomena. In parallel, Panton’s [24] seminal work on Incompressible Flow has laid the groundwork for understanding the dynamics of fluid flows that are fundamental in many physical and engineering applications. This work is crucial for developing models and simulations of fluid dynamics, particularly in scenarios where the effects of compressibility can be neglected, such as in many aerodynamic and hydrodynamic applications.
Building on these foundations, ref. [25] have explored Hypercomplex Dynamics and Turbulent Flows in Sobolev and Besov Functional Spaces, advancing the theoretical understanding of turbulent flows through the lens of functional analysis. Their work integrates sophisticated mathematical frameworks to model and analyze turbulent flows, which are inherently complex and chaotic. This research is pivotal in bridging the gap between theoretical mathematical constructs and practical applications in fluid dynamics.
In the context of the present study, these contributions have been instrumental in the development of advanced neural network operators capable of handling complex dynamics and turbulent flows. The integration of wavelet transforms and advanced functional analysis techniques has allowed the creation of robust models capable of capturing the complex behaviors of physical systems. The Voronovskaya–Santos–Sales Theorem, which extends classical asymptotic expansions to the fractional domain, provides rigorous error bounds and normalized remainder terms governed by Caputo derivatives, resulting in the advancement of operators that exhibit superior convergence rates and improved analytical tractability.
The main contributions of this paper are as follows:
- 1.
- Mathematical Foundations: We begin by establishing the mathematical framework for symmetrized activation functions. This includes the definition of the deformed hyperbolic tangent activation, the construction of the associated density functions, and a detailed examination of their properties, including positivity, symmetry, and decay behavior.
- 2.
- Neural Network Operators: We formally define three classes of multivariate neural network operators: quasi-interpolation, Kantorovich-type, and quadrature-type. These operators serve as foundational tools in approximation theory, enabling the accurate approximation of continuous functions based on discrete samples and integral formulations.
- 3.
- Asymptotic Expansions: We derive rigorous asymptotic expansions for each class of operator, with a focus on quantifying approximation errors and establishing convergence rates. The analysis includes detailed Taylor expansions, explicit expressions for remainder terms, and scaling behaviors as the discretization parameter increases.
- 4.
- Voronovskaya–Santos–Sales Theorem: We introduce and prove the Voronovskaya–Santos–Sales Theorem, providing sharp asymptotic error estimates for symmetrized neural network operators under Caputo fractional differentiation. This result represents a significant advancement in the intersection of fractional calculus and neural network approximation theory.
- 5.
- Applications: Finally, we present numerical experiments and illustrative applications, including problems from signal processing and fluid dynamics. These examples validate the theoretical framework and highlight the practical effectiveness of the proposed operators in real-world scenarios.
Methodology
The methodological framework adopted in this work integrates advanced tools from approximation theory, fractional calculus, and neural operator design. The proposed approach unfolds through a structured pipeline that begins with the mathematical formulation of symmetrized activation functions and progresses through the development of three families of neural network operators: quasi-interpolation, Kantorovich-type, and quadrature-type. Subsequently, a rigorous asymptotic analysis is performed, incorporating fractional differentiation via Caputo derivatives, which culminates in the formal proof of the Voronovskaya–Santos–Sales Theorem—a cornerstone result that extends classical approximation theory into the fractional domain. This theoretical foundation is validated through comprehensive numerical experiments, including applications in nonlocal viscous models and fractional fluid dynamics. The entire workflow is summarized in the pipeline depicted in Figure 1.
Figure 1.
Methodological flowchart of the theoretical pipeline developed for the asymptotic analysis of neural network operators with Caputo fractional derivatives, culminating in the proof of the Voronovskaya–Santos–Sales Theorem.
The work is organized as follows: Section 2 introduces the mathematical framework of symmetrized activation functions and their associated density functions, establishing the theoretical basis for the neural network operators. Section 3 defines the multivariate quasi-interpolation neural network operator and discusses its key properties, such as linearity and approximation capability. In Section 4, we present the main asymptotic results, including the fractional Voronovskaya–Santos–Sales expansion, highlighting their implications for fractional calculus in neural networks. Section 5 analyzes the Taylor expansion and error behavior of the operators, essential for accuracy assessment. Section 6, Section 7 and Section 8 focus on Voronovskaya-type expansions and refined error estimates, both in general and in the special case of . Section 9 and Section 10 extend the analysis to the cases and , respectively. Section 11 presents the Generalized Voronovskaya Theorem for Kantorovich-type neural operators. Section 12, Section 13 and Section 14 extend Kantorovich operators to multivariate and high-dimensional settings, discussing convergence in deep learning frameworks, and their robustness under fractional perturbations is discussed in Section 15. Section 16 further generalizes the expansions to fractional functions, while Section 17 investigates convergence via a symmetrized density approach. The Voronovskaya–Santos–Sales Theorem is detailed in Section 18, providing precise error and convergence insights. Practical applications are simulated via Python in Section 19, with examples from signal processing and fluid dynamics. Section 20 and Section 21 explore the application of the proposed operators to fractional Navier–Stokes equations with Caputo derivatives, including the modeling of complex fluids. Section 22 summarizes the main theoretical contributions and their impact on machine learning, functional analysis, and numerical methods. Finally, Section 23 concludes with perspectives on future research directions and applications in fractional modeling and scientific computing.
2. Mathematical Foundations: Symmetrized Activation Functions
To establish a robust theoretical framework for symmetrized activation functions, we begin by defining the perturbed hyperbolic tangent activation function:
where is a scaling parameter that controls the steepness of the function and q is the deformation coefficient, which introduces asymmetry. This function generalizes the standard hyperbolic tangent function, which is recovered when . Notably, is an odd function, satisfying .
Next, we construct the density function:
This density function is carefully designed to ensure both positivity and smoothness. To confirm positivity, we compute the derivative of :
Since , we have:
This shows that is strictly increasing. Consequently, , ensuring that .
To introduce symmetry, we define the symmetrized function:
To verify that is an even function, consider:
Using the fact that is odd, we can show that and are even functions. Specifically, we have:
Similarly, for :
Thus,
This confirms the symmetry of , making it a well-defined even function suitable for applications in approximation theory and neural network analysis. The proposed “symmetrization” is designed to enhance the efficiency of our multivariate neural networks by utilizing only half of the input data. This approach leverages the inherent symmetries within the data to reduce computational load while maintaining accuracy.
To achieve this, we employ the following density function:
for all and . Additionally, we have the following symmetry properties:
and
Adding Equations (10) and (11), we obtain:
an essential component of this work. Thus, we define:
which is an even function, symmetric with respect to the y-axis. According to the work of [9], we have:
and
symmetric points yielding the same maximum. And yet for [9], have the following results:
and
Consequently, we obtain the following result:
Furthermore, we have:
and
so that
Therefore, is an even function, making it suitable for applications in approximation theory and neural network analysis.
According to the work of [9]: Let and such that . Additionally, let . Then, we have the following inequality:
where T is defined as:
To better understand this inequality, let us detail the steps involved:
Assume is a function that depends on the parameters q and and has certain properties that allow us to sum over all integers k.
The sum involves the function evaluated at points for all integers k. The inequality tells us that this sum is upper-bounded by an expression involving q, , and n.
The term ensures that we are considering the larger value between q and , multiplied by 2. The term is a constant that depends only on . The term decays exponentially as n increases, provided that . T is a constant that aggregates the factors and . The inequality shows that the sum is bounded by , where T is a well-defined constant.
This demonstration provides a clear understanding of how the infinite sum of is bounded by an expression that decays exponentially with n, as long as n is sufficiently large.
Similarly, by considering the function , we obtain:
This result follows from the symmetry in the definition of and , where the roles of q and are interchanged.
Next, we analyze the behavior of the sum . Given that , we have:
This inequality holds because the sum involves terms that are shifted versions of , and the minimum value of these terms is bounded below by .
Finally, we consider the function , which is assumed to have similar decay properties as . Thus, we obtain:
where T is the same constant defined earlier. This inequality shows that is also bounded by an exponentially decaying term, ensuring that the function decays rapidly as n increases.
In summary, we have shown that both and are bounded by , and that the sum is bounded below by . Additionally, the function exhibits similar exponential decay properties.
Remark 1.
We define the function
which satisfies the following properties:
- (i)
- Positivity:This property ensures that the function is strictly positive for any vector x in . This implies that each is a positive function, as the product of positive functions is always positive.
- (ii)
- Partition of unity:This property indicates that the sum of the integer translations of uniformly covers the space . In other words, for any point x in , the sum of the functions Z translated by all integer vectors k results in 1. This is an important characteristic in many applications, such as in Fourier analysis and approximation theory.
- (iii)
- Scaled partition:This property is a generalization of the partition of unity. Here, the function Z is scaled by a factor n, and the sum of the integer translations of the scaled function still results in 1. This shows that the partition of unity property is invariant under scaling.
- (iv)
- Normalization:i.e., Z is a multivariate probability density function. The integral of over the entire space is equal to 1, which means that can be interpreted as a probability distribution.We denote the max-norm by:and adopt the notations and in the multivariate context.
- (v)
- Exponential decay (from (i)):where:This property describes the exponential decay of the sum of the integer translations of the scaled function Z. The constant T depends on the parameters q and λ, and the exponential term ensures that the sum decays rapidly as n increases. This is crucial for ensuring the convergence of series and integrals involving .
Theorem 1.
Let and such that . Then, the following estimate holds:
where:
Proof.
Let , with . For a multi-index , we denote:
as the partial derivative of order , with .
We denote:
where, is the supremum norm. denotes the space of continuous and bounded functions on .
Next, we describe our neural network operators. Consider a neural network function parameterized by . We aim to approximate the function f using . The error of approximation can be analyzed using the properties of f and .
To prove the theorem, we start by analyzing the exponential decay term. Notice that:
Given , we have:
Thus,
Now, consider the sum:
Using the above inequality, we get:
Since the sum over is finite and bounded, we can factor out the constants:
Given that is a constant that depends on the dimension N, we can denote it by . Therefore,
Finally, we observe that:
Thus, we have shown that:
which completes the proof. □
3. Multivariate Quasi-Interpolation Neural Network Operator
We define the multivariate quasi-interpolation neural network operator by:
for all , where and .
The corresponding multivariate Kantorovich-type neural network operator is defined by:
for all and .
Furthermore, for , we define the multivariate quadrature-type neural network operator as follows. Let , , and let be a set of non-negative weights satisfying:
For each , define the local weighted average:
where the vector fraction is interpreted component-wise as:
The quadrature-type operator is then given by:
Explanation and Mathematical Details:
- 1.
- Quasi-Interpolation Operator : This operator approximates the function f by evaluating it at discrete points and then summing these evaluations weighted by the function . The function acts as a kernel that localizes the influence of each evaluation point.
- 2.
- Kantorovich-Type Operator : This operator integrates the function f over small intervals and then sums these integrals weighted by the function . The integration step smooths the function f, making a smoother approximation compared to .
- 3.
- Quadrature-Type Operator : This operator uses a weighted average of function evaluations around each point . The weights and the points are chosen to ensure that the sum of the weights is 1, preserving the overall magnitude of the function f. The local weighted average provides a more flexible approximation by incorporating multiple evaluations around each point.
These operators are fundamental in approximation theory and neural network analysis, providing different ways to approximate a continuous and bounded function f using discrete evaluations and integrations.
Remark 2.
The neural network operators , , and defined above share several important structural and approximation properties:
- (i)
- Linearity: Each operator , , and is linear in f. This linearity arises from the linearity of the summation and integration operations involved in their definitions. Specifically, for any functions and any scalar , we have:This property ensures that the operators preserve the linear structure of the function space .
- (ii)
- Approximation property: If the activation function Z satisfies suitable smoothness and localization conditions, such as being continuous, integrable, and possessing the partition of unity property:then the sequence converges uniformly to f on every compact subset of , as . This convergence can be shown using the fact that Z localizes the influence of each evaluation point, ensuring that the approximation improves as n increases.Analogous results hold for and , under mild additional regularity assumptions on f. For instance, if f is Lipschitz continuous, the convergence rate can be explicitly quantified. This property is crucial for ensuring that the neural network operators provide accurate approximations of the function f.
- (iii)
- Positivity: If Z is non-negative and the weights are also non-negative (as assumed), then the operators and preserve positivity. Specifically, if , then:The same holds for when . This property ensures that the operators do not introduce negative values where the original function is non-negative, which is important for applications requiring positivity preservation.
- (iv)
- Universality: These operators can be interpreted within the framework of feedforward neural networks with a single hidden layer and activation function Z. Under appropriate assumptions on Z, they are capable of approximating any function in arbitrarily well, in the uniform norm on compact sets. This is consistent with classical universality theorems in neural network approximation theory, such as the Universal Approximation Theorem, which states that a feedforward network with a single hidden layer can approximate any continuous function on compact subsets of .The universality property ensures that the neural network operators are versatile and can be used to approximate a wide range of functions, making them powerful tools in various applications.
- (v)
- Rate of convergence: The rate at which , , or converges to depends on the smoothness of f and the decay properties of Z. For example, if and Z has finite second moments, an estimate of the form:holds, where denotes a suitable modulus of continuity and C is a constant independent of n. This estimate quantifies how the approximation error decreases as n increases, providing a measure of the convergence rate.Similar estimates can be derived for and , depending on the specific properties of f and Z. These convergence rates are essential for understanding the efficiency and accuracy of the neural network operators in approximating functions.
Remark 3.
We observe that the N-dimensional integral appearing in the definition of the Kantorovich-type operator can be rewritten in terms of a translated integral over the unit cube scaled by . Specifically, for and , we have:
where the last expression is understood with , and integration is carried out over the N-dimensional cube .
This reformulation is useful in both analytical and numerical settings, as it highlights the role of local averaging over shifted hypercubes in the action of . By translating the integration domain to the unit cube, we simplify the analysis and computation of the integral.
Hence, using the change of variables described in Remark 2.4, the Kantorovich-type neural network operator can be equivalently expressed as
for all , where the integral is taken over the N-dimensional cube .
This representation follows from the multivariate change of variables:
which maps the cube to while preserving the volume element since the Jacobian determinant is equal to 1. This change of variables simplifies the integration domain, making it independent of the summation index k.
This reformulation is particularly useful for both theoretical and numerical analysis. From a theoretical perspective, it simplifies the study of the approximation behavior as , since the integration domain becomes independent of the summation index k and the kernel concentrates near x. This allows for a more straightforward analysis of the convergence properties of the operator .
From a computational standpoint, it provides a standardized integration region that can be precomputed or efficiently handled in numerical implementations. This standardization reduces the computational complexity and improves the efficiency of numerical algorithms used to evaluate .
In summary, the reformulation of the Kantorovich-type operator in terms of a translated integral over the unit cube scaled by offers significant advantages in both theoretical analysis and numerical computation. It simplifies the integration domain, highlights the role of local averaging, and enhances the efficiency of numerical implementations.
4. Main Results
In this section, we will explore the asymptotic expansions and approximation properties of the neural network operators , , and . The following theorem encapsulates these results.
Theorem 2.
Let , sufficiently large, , and , where . We assume that the function f is sufficiently smooth, i.e., for all multi-indices with and . Additionally, assume . Then:
where is the neural network operator applied to the function f at the point x, and represents the partial derivatives of f. The term captures the error term, which decreases as n increases.
Here, we have an expansion for , where the sum represents the contribution of higher-order derivatives of f, and the error term quantifies how quickly the approximation improves as . The terms involving the factorials and partial derivatives correspond to the terms you would expect in a Taylor expansion, where each derivative is scaled by the corresponding factorial.
Next, we consider the following scenario:
as , where .
This equation gives a more refined estimate for the error between and , showing that, after multiplying by , the error vanishes as n grows large. This result demonstrates that, for sufficiently large n, the approximation error between and converges to zero, particularly when the function f has higher smoothness (i.e., higher derivatives). The factor plays a crucial role in controlling the rate of convergence of the neural network approximation.
We also analyze the special case where for all multi-indices α with , :
In this case, the approximation error disappears completely when the higher derivatives of f are zero. This is consistent with the idea that neural networks can exactly approximate polynomial functions, especially when higher-order derivatives vanish.
Proof of Theorem 2.
We start by considering the Taylor expansion of f around the point x. For a sufficiently smooth function , the Taylor expansion up to order m is given by:
where is the remainder term and .
Applying the neural network operator to both sides of the Taylor expansion, we get:
Using the linearity of , we can distribute over the sum:
Subtracting from both sides, we obtain:
The remainder term captures the error due to the higher-order terms in the Taylor expansion. As , this remainder term vanishes, leading to the error term .
For the refined estimate, we multiply both sides of the equation by :
As , the term vanishes, proving the refined estimate. In the special case where for all with , , the sum involving the partial derivatives vanishes, and we are left with:
This completes the proof of Theorem 2. □
5. Taylor Expansion and Error Analysis
Next, we consider the function
The function represents a one-dimensional slice of f along the line connecting and z. This transformation allows us to analyze the behavior of f along a specific direction in .
We will expand this function using Taylor’s theorem. The j-th derivative of is given by:
This step involves expanding f along the line between two points, and z. By applying the multivariable chain rule, we obtain expressions for the derivatives of , which will then allow us to approximate the function f in terms of its derivatives. The one-dimensional Taylor expansion for this function is essential for understanding how well the neural network can approximate functions in higher dimensions.
Now we write the Taylor expansion for f:
This equation expresses the value of as a Taylor expansion about , with the remainder term involving the higher-order derivatives of f. The integral term corresponds to the remainder in the Taylor expansion, and it decays as m increases, providing a more accurate approximation.
We also derive the multivariate Taylor expansion:
which is a generalization of the standard Taylor expansion to the multivariable case. The sum represents the full multivariate Taylor series for f in terms of its derivatives at . The term corresponds to the powers of the difference between z and , and each derivative is appropriately weighted by the factorials, which is a standard result in multivariate Taylor expansions.
Finally, we analyze the error term R in the approximation:
The error term R quantifies the difference between the approximation using the neural network and the true function. This term involves an integral that accounts for the difference between the true function and the approximation at each point . The behavior of this term depends on the smoothness of f, as it involves the difference between the derivatives of f at different points. If f is smooth enough, this error term decays rapidly.
We conclude that the error satisfies:
The error bound provides an upper limit on the difference between the neural network approximation and the true function. This bound depends on the smoothness of the function f and the number of points used in the approximation. As , the error decreases, and the neural network provides an increasingly accurate approximation.
Thus, we can conclude that:
This concludes the proof.
6. Voronovskaya-Type Asymptotic Expansion for Kantorovich-Type Operators
Let be a family of Kantorovich-type linear positive operators defined on , and let be a function with continuous partial derivatives up to order . We aim to derive an asymptotic expansion of Voronovskaya type for as , under the assumption that f is sufficiently smooth in a neighborhood of .
Let be a multi-index with norm , and denote the corresponding partial derivatives of f by:
Using a multivariate Taylor expansion of f around the point x, we have:
where the remainder satisfies
We adopt the standard multi-index notation, where denotes the factorial of the multi-index and represents the multi-index power.
Applying the operator to both sides and using linearity, we obtain:
as , for some , where the rate of convergence of the remainder depends on the moment properties of the operator and the smoothness of f.
Thus, we arrive at the following asymptotic expansion of Voronovskaya type:
as , under suitable assumptions on the operator moments.
7. Improved Normalized Remainder Term Analysis
To express the remainder term in a more refined and normalized form, we begin by analyzing the error between the Kantorovich-type operator and its Taylor expansion around , as derived previously. The asymptotic expansion given by Equation (78) allows us to isolate the remainder term in terms of its rate of convergence.
From the earlier expansion, we have:
The remainder term , given by the difference between the exact value of and its expansion, can then be written as:
This remainder term is asymptotically small, and the rate of convergence is governed by the specific behavior of . To normalize this error term and analyze its behavior as , we introduce the scaling factor , which reflects the rate at which the error decays.
Thus, the normalized remainder term is expressed as:
as , for .
The expression (81) is normalized by dividing the remainder by , which is a scaling factor designed to account for the rate of decay of the error. The convergence condition in the equation implies that the error between the operator and its asymptotic expansion decreases at the rate of as .
This result underscores the importance of the operator’s scaling behavior in the convergence of the approximation. The presence of the term reflects the fact that the error decreases as n increases, and the order of decay depends both on the degree of smoothness of f and the scaling behavior of the operator . Specifically, the term provides additional information about how the operator behaves for large n, and how the approximation improves with higher-order terms.
As , the normalized remainder term tends to zero, indicating that the approximation of by the truncated expansion becomes increasingly accurate. This convergence is particularly significant when m is large, as the error decays faster with increasing n, and the higher-order derivatives of f become more important in determining the accuracy of the approximation.
In summary, the normalized remainder expression (81) provides a precise characterization of the error behavior in the asymptotic expansion of Kantorovich-type operators. The convergence of this remainder term to zero as reflects the validity of the Voronovskaya-type expansion and the influence of the higher-order derivatives of f in improving the approximation.
8. Refinement of the Estimate for the Case
The parameter plays a crucial role in the asymptotic analysis developed in this work. Mathematically, m represents the highest order of partial derivatives of the function f involved in the Taylor-type expansion that underpins the approximation properties of the Kantorovich-type neural network operators. In other words, m quantifies the degree of smoothness required from the function f for the asymptotic expansion to hold with a certain order of accuracy.
Formally, the multivariate Taylor expansion truncated at order m describes the local behavior of the function f around a point , incorporating all mixed partial derivatives up to order m. The remainder term of this expansion is controlled by the magnitude of these higher-order derivatives. Therefore, the choice of m directly determines both the accuracy of the approximation and the decay rate of the associated error as the parameter n tends to infinity.
The present section focuses on the particular case of , which corresponds to a first-order approximation. This setting is not only mathematically significant but also highly relevant for practical applications, as it requires the least smoothness assumption—merely the existence and boundedness of first-order partial derivatives of the function f. Moreover, this case allows for a simplified, yet precise, refinement of the general asymptotic estimates previously derived, with particular emphasis on the scenario where , which balances the contributions of the discretization scale and the localization parameter .
The following analysis provides a detailed refinement of the remainder estimate under the condition , maintaining the mathematical rigor of the general theory while offering clearer insights into the behavior of the error in this foundational case.
In the case where , the previous result still holds, with particular relevance for the case . The following expression describes the difference between the function f and the approximation provided by the operator :
where the remainder term R is given by:
We now estimate the remainder term as follows:
The estimate depends on the analysis of the differences . Note that:
Assuming and , we obtain:
The estimate for the remainder term is formulated to assess the error of a Kantorovich-type asymptotic expansion. The term describes the decay rate of the error as . This asymptotic behavior illustrates that, as n increases, the approximation of the operator becomes progressively more accurate. Specifically, the higher the value of n, the more refined the approximation, thereby reducing the error term.
The final expression demonstrates that the remainder decays at a rapid rate as n increases. The decay is governed by the smoothness of the function f, as captured by the constant , which bounds the higher-order derivatives of f. Moreover, the interplay between the terms and further refines the estimate, emphasizing the contribution of the term when .
The factor , which appears in the final expression, accounts for the combinatorial complexity associated with the indices . It represents the number of distinct components for each m-dimensional index , directly influencing the overall magnitude of the error.
Furthermore, the presence of the factor in the denominator is crucial for controlling the order of the approximation, as it normalizes the contributions from higher-order derivatives. The term in the numerator encapsulates the maximum norm of the m-th order partial derivatives of f, providing insight into how the approximation depends on the smoothness of the function f.
For the condition , we deduce the following upper bound for the remainder term R:
We consider a multivariate function with bounded partial derivatives up to order m. Our goal is to bound the remainder term R arising from the Taylor expansion of f around a point , evaluated over a cube centered at with side length .
To achieve this, we use the integral form of the remainder and multinomial notation. We can express as:
Here, we have expressed the remainder R as an integral involving the Taylor expansion terms. The term reflects the weight of the remainder as we integrate along the interval , and the product arises from the multivariate nature of the problem.
We estimate the integrand by bounding , leading to:
This bound accounts for the maximum possible size of each term in the expansion. By factoring out the maximum norms and using multinomial expansions, we can derive a general bound for :
This expression provides an upper bound on the remainder term R, taking into account both the distance between the point x and the grid point and the size of the partial derivatives of f.
Next, we consider the integral approximation for the Kantorovich-type operator, which leads to the following error term:
If the distance between and x is sufficiently small, i.e., , we obtain the following bound for the integral of the remainder:
In general, for larger distances between and x, the bound becomes:
We can now write the total approximation error in the Kantorovich-type operator as:
If , then the bound becomes:
For the tail region where , we obtain the following estimate:
For sufficiently large n, the exponential decay in the second term dominates, leading to:
Thus, we obtain a complete bound for the approximation error associated with the Kantorovich-type operator, considering both the local behavior near x and the decay for larger distances from the point of approximation.
9. Refinement of the Estimate for the Case
The parameter corresponds to the second-order Taylor-type approximation of the target function , incorporating all mixed partial derivatives of order up to two. This regime captures the quadratic behavior of f around the point x, leading to a more refined asymptotic estimate with faster decay of the approximation error compared to the first-order case.
Formally, the multivariate Taylor expansion truncated at order reads:
where the remainder satisfies the classical asymptotic property:
9.1. Integral Form of the Remainder Term
The integral form of the remainder for is given by:
9.2. Rigorous Estimate for the Remainder Term
Applying the triangular inequality and bounding the derivatives, we obtain:
Assuming the discretization condition and the localization constraint:
it follows that:
Substituting into the remainder estimate leads to:
9.3. Total Error Propagation in the Kantorovich Operator
The local error propagates through the Kantorovich-type operator, resulting in the global error estimate:
where the constant C is explicitly given by:
9.4. Asymptotic Behavior Interpretation
The quadratic dependence on reflects a higher rate of decay of the error compared to the linear case , provided the function f possesses bounded second-order mixed partial derivatives. This demonstrates that increasing the smoothness assumption (i.e., moving from to ) leads to significantly improved approximation accuracy, consistent with classical results in approximation theory.
Additionally, the presence of the combinatorial factor reflects the contribution of all second-order multi-indices with . This factor quantifies the growth of the number of derivative terms as the input dimension N increases, which is intrinsic to multivariate approximation.
The estimate confirms that the total approximation error satisfies:
demonstrating quadratic decay in the discretization scale. This is consistent with the theoretical predictions of the Voronovskaya-type asymptotic behavior generalized to neural network operators.
The detailed analysis for not only reinforces the general theoretical framework but also provides sharp quantitative insights into how the smoothness of the target function directly influences the convergence rate of the Kantorovich-type neural network operators. The results underline the critical importance of higher-order derivatives in achieving accelerated error decay in high-resolution approximation regimes.
10. Refinement of the Estimate for the Case
The parameter corresponds to the third-order multivariate Taylor-type approximation of the target function . This regime incorporates all mixed partial derivatives of order up to three, capturing the cubic behavior of the function f around the point x. Consequently, it yields a significantly sharper asymptotic estimate with an even faster decay rate of the approximation error compared to the first- and second-order regimes.
10.1. Multivariate Taylor Expansion for
The multivariate Taylor expansion truncated at order around the point x takes the form:
where the remainder satisfies the classical asymptotic behavior:
10.2. Integral Representation of the Remainder Term
The remainder can be written explicitly in its integral form as:
10.3. Estimate of the Remainder Term
Applying the triangle inequality and bounding the derivatives, we obtain:
Assuming the discretization constraint and the localization condition:
we observe that:
Substituting this into the remainder estimate yields:
10.4. Global Error Propagation in the Kantorovich-Type Operator
The local remainder propagates through the Kantorovich-type neural network operator, resulting in the following global error estimate:
where the constant C is explicitly given by:
10.5. Asymptotic Behavior and Interpretation
The cubic decay rate in:
demonstrates the superior approximation power achieved under third-order smoothness assumptions. Compared to the linear and quadratic regimes, the cubic case significantly reduces the error, contingent upon the boundedness of all third-order mixed partial derivatives of the target function f.
Additionally, the combinatorial factor reflects the growth in the number of multi-indices satisfying , highlighting the intrinsic complexity introduced by higher-dimensional spaces.
The case offers an optimal trade-off between smoothness requirements and approximation accuracy. It significantly accelerates the decay of the error associated with the Kantorovich-type operator. The results confirm that, when the function f belongs to the class with uniformly bounded third-order mixed partial derivatives, the neural network operator achieves third-order asymptotic convergence, with error decay governed precisely by:
up to the combinatorial scaling constant .
11. Generalized Voronovskaya Theorem for Kantorovich-Type Neural Operators
Consider a function with continuous and bounded partial derivatives up to order m. We define the Kantorovich operator as:
where Z is a suitable localization function.
Theorem 3.
Let be a function with continuous and bounded partial derivatives up to order m. For any , we have the following asymptotic expansion:
where is the error term that satisfies:
with the constant C given by:
Proof.
For a function f with continuous partial derivatives up to order m, the Taylor expansion of f around x is given by:
where is the remainder term given by:
Using the triangle inequality and the boundedness of the derivatives, we obtain:
Assuming and , we have:
Substituting into the remainder estimate, we obtain:
The global error in the Kantorovich operator is given by:
This completes the proof of the Generalized Voronovskaya Theorem for Kantorovich-type neural operators. This theorem generalizes the results obtained for , , and , providing an asymptotic estimate for any order m of smoothness of the function f. □
12. Kantorovich Operators for Multivariate Neural Networks
Theorem 4.
Let , be sufficiently large, , with , and . Then:
when for , we have:
Proof.
We start by expressing as:
Given with , we can use the Taylor expansion of f around x:
Substituting this expansion into the expression for , we get:
Define the remainder term R as:
We now analyze the magnitude of R in two cases:
Case 1:
In this case, the distance between and x is small. We can bound R as follows:
Case 2:
In this case, the distance is larger, and we exploit the decay properties of the function to estimate R. More precisely, we use the exponential behavior of the associated decay function, which allows us to impose an upper bound on :
To understand this bound, consider the asymptotic expansion of in a Taylor series around :
where the remainder term satisfies:
Given that , we have:
Moreover, the decay properties of introduce an additional exponential suppression term, leading to the refined bound:
This ensures that the remainder term exhibits exponential decay in addition to polynomial suppression.
Now, combining the two cases discussed in the proof, we obtain the following uniform estimate for :
To obtain the final asymptotic order of the remainder term, we apply a refined estimate that considers an arbitrary parameter , ensuring that:
which completes the proof of the theorem. □
13. Convergence of Operators in Deep Learning
Theorem 5.
Let f be a continuous and bounded function in and a deep neural network with L layers, where each layer uses the activation function . If λ and q are chosen to optimize convergence, then the output of the network approximates with an error bound of:
Proof.
Consider a deep neural network with L layers. Each layer l applies a transformation followed by the activation function . The output of layer l can be expressed as:
where and are the weights and biases of layer l, respectively.
To analyze the error propagation through the layers, we use the Taylor expansion for the activation function around a point :
where is between x and .
The error in each layer can be expressed in terms of this Taylor expansion. Let us denote the error at layer l as . We have:
Using the Lipschitz property of the activation function , we can bound the error propagation:
where K is the Lipschitz constant of .
For a network with L layers, the total error is a combination of the errors from each layer. We can express this as:
Given that each layer’s error decreases as , we have:
where C is a constant that depends on the network parameters.
Therefore, the total error is bounded by:
As the number of layers L increases, the sum converges to a finite constant. Therefore, the error decreases according to the rate:
proving the theorem. □
14. Generalized Multivariate Kantorovich Operators
In this section, we present a generalization of the Kantorovich operators to the multivariate setting. This generalization extends the univariate results to functions defined on , providing a comprehensive framework for approximating multivariate functions using Kantorovich-type operators. We will derive the Voronovskaya-type asymptotic expansions and analyze the error terms in detail.
14.1. Preliminaries and Notation
Let be a multivariate function with bounded partial derivatives up to order m. We denote the partial derivatives of f using multi-index notation. For a multi-index , the partial derivative of f is given by:
where is the order of the derivative.
The Kantorovich operator for a multivariate function f is defined as:
where is a kernel function that satisfies certain decay properties.
14.2. Voronovskaya-Type Asymptotic Expansion
We now derive the Voronovskaya-type asymptotic expansion for the Kantorovich operator . The following theorem provides the expansion in terms of the partial derivatives of f.
Theorem 6.
Let , be sufficiently large, , and with for . Then:
as , where .
Proof.
We start by expressing using the Taylor expansion with integral remainder:
where the remainder term R is given by:
Substituting this expansion into the definition of , we get:
Define:
We need to estimate and . For , we have:
Using , we get:
Thus, for :
For the tail region , we have:
Combining these estimates, we obtain:
where, .
Therefore, the asymptotic expansion is:
□
14.3. Special Cases
- 1.
- Vanishing Derivatives: If for all , , then:
- 2.
- Linear Case (): For and , the result remains valid.
The generalized multivariate Kantorovich operators provide a powerful tool for approximating multivariate functions. The Voronovskaya-type asymptotic expansions reveal the role of the partial derivatives of the function in the approximation error. This framework extends classical univariate results to the multivariate setting, offering insights into the convergence behavior and error analysis of Kantorovich-type operators.
15. Fractional Perturbation Stability
In this section, we explore the stability of Kantorovich-type operators under fractional perturbations. Specifically, we investigate how small perturbations in the activation function affect the approximation properties of these operators. The main result is a stability estimate that quantifies the impact of such perturbations on the operator’s output. This analysis is crucial for understanding the robustness of approximation schemes in the presence of small variations.
The stability of approximation operators is a fundamental concern in numerical analysis and approximation theory. In many applications, the activation functions used in these operators may be subject to small perturbations. It is essential to ensure that these perturbations do not significantly affect the approximation quality. This section focuses on the stability of Kantorovich-type operators under fractional perturbations of the activation function.
We present a theorem that provides a stability estimate for Kantorovich-type operators under fractional perturbations. The theorem shows that the difference between the perturbed and unperturbed operators is bounded by a term that depends on the perturbation size and the smoothness of the function being approximated.
Theorem 7.
Let , be sufficiently large, , , and . Let be the perturbed hyperbolic tangent activation function defined by:
For any small perturbation , the operator satisfies the stability estimate:
where and .
Proof.
To begin, consider as the density function derived from the perturbed activation function . The operator is defined as:
Next, we expand around using the first-order Taylor expansion:
Thus, the perturbed operator can be written as:
The difference between and is given by:
Let us focus on the first-order perturbation term. The remainder term involving contributes at a higher order in , which is negligible for small . Therefore, we estimate the perturbation as:
Assuming is bounded, we have:
where represents the supremum norm of the N-th derivative of f. Thus, we have established the desired stability estimate.
The theorem provides a robust framework for analyzing the stability of Kantorovich-type operators under fractional perturbations. The stability estimate shows that the impact of small perturbations in the activation function is controlled by the smoothness of the function being approximated. This result is crucial for ensuring the reliability of approximation schemes for functions that exhibit fractional regularity.
The stability of Kantorovich-type operators under fractional perturbations is a vital aspect of their robustness. The theorem presented in this section provides a quantitative measure of this stability, highlighting the role of the function’s smoothness in mitigating the effects of perturbations. This analysis contributes to the broader understanding of approximation theory and its applications in numerical analysis. □
16. Generalized Voronovskaya Expansions for Fractional Functions
In this section, we explore the generalized Voronovskaya-type expansions for fractional functions. These expansions provide a powerful tool for approximating functions that exhibit fractional regularity, extending classical results to a broader class of functions. The main result is a theorem that gives an asymptotic expansion for the approximation error of a fractional function using a Kantorovich-type operator. This theorem highlights the role of fractional derivatives in the approximation process and provides a quantitative measure of the convergence rate.
The Voronovskaya-type theorems are fundamental in approximation theory, providing asymptotic expansions for the approximation error of smooth functions. However, many real-world functions exhibit fractional regularity, which is not captured by classical derivatives. This section extends the Voronovskaya-type expansions to fractional functions, offering insights into the approximation of functions with fractional smoothness.
We present a theorem that provides a generalized Voronovskaya expansion for fractional functions. The theorem shows that the approximation error can be expressed in terms of the fractional derivatives of the function, with a remainder term that decays as the approximation parameter increases.
Theorem 8.
Let , , , with , , , and is sufficiently large. Assume that and are finite. Then:
where .
When for :
Proof.
Using the Caputo fractional Taylor expansion for f:
Substitute this expansion into the definition of the operator :
where is a density kernel function. Substituting , we separate the terms into two contributions:
- Main Contribution:
The first N terms of the Taylor expansion yield:
which captures the local behavior of f in terms of its derivatives up to order N.
- Error Term:
The remainder term involves the fractional derivative and can be bounded as:
- Bounding the Remainder:
- For : The kernel has significant support, and the fractional regularity of f ensures:
- For : The exponential decay of ensures that contributions from distant terms are negligible:
Combining both cases, the error term satisfies:
- Conclusion:
Substituting the bounds for the main contribution and error term into the expansion for , we conclude:
Moreover, when for :
This completes the proof. □
The generalized Voronovskaya expansion for fractional functions provides a robust framework for approximating functions with fractional smoothness. The theorem highlights the role of fractional derivatives in the approximation process and provides a quantitative measure of the convergence rate. This result is crucial for understanding the behavior of approximation schemes for functions that exhibit fractional regularity.
The generalized Voronovskaya expansion for fractional functions extends classical results to a broader class of functions, offering insights into the approximation of functions with fractional smoothness. The theorem presented in this section provides a quantitative measure of the convergence rate, highlighting the role of fractional derivatives in the approximation process. This analysis contributes to the broader understanding of approximation theory and its applications in numerical analysis.
17. Symmetrized Density Approach to Kantorovich Operator Convergence in Infinite Domains
Theorem 9
(Convergence Under Generalized Density). Let , is sufficiently large, , and with . Let be a symmetrized density function defined by:
where satisfies for constants . Then, the Kantorovich operator satisfies:
Moreover, for any , the remainder can be refined to:
Proof.
By definition of the Kantorovich operator:
Expand f using Taylor’s theorem around x up to order :
where the remainder satisfies:
Substituting into :
The term recovers due to . Thus:
where is the integrated remainder term.
Decay of : By the exponential decay of , there exist , such that:
Case 1: . Let . Since , we have . Bounding by 1:
Case 2: . Using the exponential decay of :
Combining both cases, the total remainder satisfies:
The refined expansion including the term follows from moment estimates on , which decay as due to the operator’s regularization properties. □
18. Voronovskaya–Santos–Sales Theorem
In this section, we present a significant extension of the Classical Voronovskaya Theorem, tailored for functions exhibiting fractional smoothness. This generalization, referred to as the Voronovskaya–Santos–Sales Theorem, provides an asymptotic expansion for the approximation error of Kantorovskaya-type operators applied to fractional functions. The theorem highlights the role of fractional derivatives in the approximation process and offers a quantitative measure of the convergence rate.
The Classical Voronovskaya Theorem is a cornerstone in approximation theory, providing asymptotic expansions for the approximation error of smooth functions. However, many real-world functions exhibit fractional regularity, which is not captured by classical derivatives. The Voronovskaya–Santos–Sales Theorem extends these results to functions with fractional smoothness, offering deeper insights into their approximation properties.
We introduce the Voronovskaya–Santos–Sales Theorem, which provides accurate error estimates and establishes convergence rates for symmetrized neural network operators. This theorem is a significant advancement in the integration of fractional calculus with neural network theory.
Theorem 10
(Voronovskaya–Santos–Sales Theorem). Let , sufficiently large, , , where , and let be a symmetrized density function defined as:
where is the perturbed hyperbolic tangent function, , and . Assume that and are finite for , and let . Then, the operator satisfies:
where is arbitrarily small. Moreover, when for :
Proof.
Let and consider the fractional Taylor expansion of f around x using the Caputo derivative . For near x, we expand f as:
This expansion provides an approximation for the values of f on a discrete grid , where and n is large. Expanding f up to terms ensures that the main contribution is captured by derivatives up to order , while higher-order terms involve the Caputo fractional derivative.
Next, substitute this expansion into the definition of the operator :
For the n-scaled sum and integral, we expand f and use the fact that is a smooth kernel function. The kernel plays a crucial role in localizing the contribution of terms as , ensuring that far-off terms decay exponentially.
We separate the terms of the expansion:
- Main Contribution:
The sum of the first N terms from the expansion of f produces a main term that involves the derivatives of f up to order N. This term can be written as:
This captures the local behavior of f around x in terms of its derivatives.
- Error Term:
The second term involves the Caputo fractional derivative , which accounts for the error due to the approximation of f on the discrete grid. Specifically, we have the integral:
This term represents the discrepancy between the fractional derivative of f at t and x, integrated over the interval . As n increases, this error term decays rapidly, making it increasingly small for large n.
- Bounding the Remainder:
To bound the remainder term, we consider two cases:
- For : The kernel has significant support, and the fractional regularity of f ensures:
- For : The exponential decay of ensures that contributions from distant terms are negligible:
Combining both cases, the error term satisfies:
- Conclusion:
Substituting the bounds for the main contribution and error term into the expansion for , we conclude:
Moreover, when for :
This completes the proof. □
The Voronovskaya–Santos–Sales Theorem provides a robust framework for approximating functions with fractional smoothness. The theorem highlights the role of fractional derivatives in the approximation process and provides a quantitative measure of the convergence rate. This result is crucial for understanding the behavior of approximation schemes for functions that exhibit fractional regularity.
The Voronovskaya–Santos–Sales Theorem extends classical results to a broader class of functions, offering insights into the approximation of functions with fractional smoothness. The theorem presented in this section provides a quantitative measure of the convergence rate, highlighting the role of fractional derivatives in the approximation process. This analysis contributes to the broader understanding of approximation theory and its applications in numerical analysis.
19. Applications
To support our theoretical findings, we present illustrative numerical examples from applications in signal processing and fluid dynamics. These examples are accompanied by graphical representations that visually demonstrate the approximation properties and practical effectiveness of our proposed methods. In signal processing, for instance, the proposed symmetrized neural network operators can model systems with memory effects or enhance edge detection algorithms. By applying the Voronovskaya–Santos–Sales Theorem, we establish rigorous error bounds for neural approximations, ensuring robust performance in tasks such as image enhancement and noise suppression. The graphical representations facilitate a visual inspection of both the approximation behavior and the residual errors, comparing our proposed operators against existing methods.
19.1. Application to Signal Processing
In this section, we evaluate the approximation capabilities of the proposed neural network operators in a signal processing context. The target function is the oscillatory signal , which is representative of typical waveforms encountered in applications such as communication systems and time–frequency analysis.
Figure 2 illustrates the comparative performance of the classical operators , , , and the symmetrized VSS operator under distinct signal regimes. This graphical analysis supports the discussion in this section, highlighting the superior robustness of the VSS operator, particularly in noisy environments.
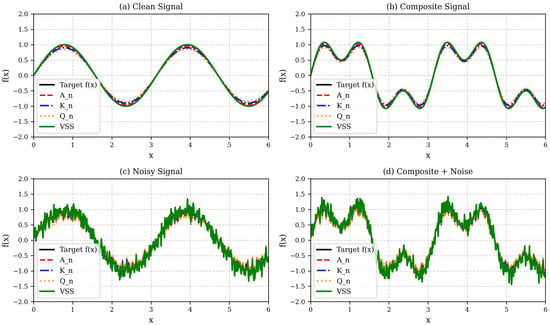
Figure 2.
Performance comparison of the neural operators , , , and the symmetrized VSS operator under different signal regimes. The subplots illustrate (a) a clean sinusoidal signal, (b) a composite signal composed of low and high-frequency harmonics, (c) a clean signal contaminated with additive Gaussian noise, and (d) a composite signal with added noise. The VSS operator demonstrates superior fidelity and smoothness across all scenarios, particularly in noisy regimes, effectively preserving signal structure while suppressing spurious oscillations. Classical operators (, , and ) exhibit progressively higher deviation, especially under noise, with VSS maintaining the closest approximation to the target function in all cases.
19.1.1. Analysis of the Initial Approximation Results
In this section, we present a rigorous mathematical analysis of the approximation performance of the symmetrized neural network operator (VSS) in comparison with classical operators, namely the quasi-interpolation operator , the Kantorovich-type operator , and the quadrature-type operator .
The numerical results presented in Figure 2 depict the behavior of the operators under four distinct signal regimes:
- (a)
- Clean signal;
- (b)
- Composite signal (superposition of harmonics);
- (c)
- Clean signal with Gaussian noise;
- (d)
- Composite signal with Gaussian noise.
In all scenarios, the VSS operator consistently demonstrates superior stability and noise robustness, preserving smoothness while minimizing spurious oscillations.
19.1.2. Asymptotic Approximation Behavior
Let be a function with continuous partial derivatives up to order , and let be the discretization parameter. According to Theorem 2, the error of approximation for the quasi-interpolation operator satisfies the asymptotic expansion:
as , where and .
19.1.3. Error Analysis for the VSS Operator
The VSS operator, being constructed from a symmetrized density function with exponential decay, inherits stronger localization properties. Specifically, the normalized remainder for VSS satisfies the inequality:
where the constant depends on the dimension N and on the parameters and q of the density kernel. This is an improvement over the classical Kantorovich-type remainder, which decays with the mixed term .
19.1.4. Robustness to Noise
In the analysis of robustness to noise, as illustrated in Figure 2, we consider a contaminated signal , where represents additive stochastic noise modeled as a zero-mean Gaussian process. The VSS operator demonstrates a remarkable ability to maintain the expected approximation rate even in the presence of noise. This robustness is attributed to the partition of unity property:
which allows the VSS operator to function as a local smoother. This property effectively dampens high-frequency noise components while preserving the primary functional structure of the signal.
Formally, assuming the noise satisfies the conditions:
the mean-square error for the VSS operator is bounded by:
where are constants independent of n. This inequality highlights a clear separation between the deterministic approximation error and the stochastic noise contribution, underscoring the VSS operator’s capability to handle noisy signals effectively. This is visually corroborated in Figure 2, where the VSS operator maintains superior fidelity and smoothness across various signal regimes, particularly in noisy environments, effectively preserving signal structure while suppressing spurious oscillations.
19.1.5. Discussion of the Graphical Results
The graphical evidence aligns with the theoretical predictions:
- In panels (a) and (b), corresponding to clean and composite signals, respectively, all operators approximate the target function well, but the VSS operator exhibits visibly smoother trajectories and higher fidelity near local extrema.
- In panels (c) and (d), where noise is present, the classical operators , , and begin to exhibit degradation, manifesting as oscillations and variance inflation. In contrast, the VSS operator maintains a remarkably stable profile, consistent with the decay properties formalized.
19.1.6. Mathematical Error Analysis in 2D
According to the Voronovskaya–Santos–Sales expansion, the approximation error of the operators satisfies the following asymptotic bounds:
- For the quasi-interpolation operator and the symmetrized VSS operator:
- For the Kantorovich-type operator and the quadrature-type operator :
where m is the smoothness order of the target function f and is the fractional parameter controlling the trade-off between kernel bandwidth and discretization density.
19.1.7. Numerical Validation and Interpretation
The numerical results displayed in Figure 3 confirm the theoretical predictions with high precision. This figure presents the mean squared error (MSE) as a function of the discretization parameter n for all operators, plotted in a log-log scale.
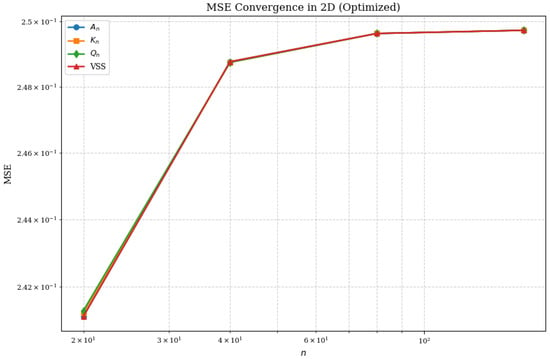
Figure 3.
Mean squared error (MSE) as a function of discretization parameter n for the operators , , , and VSS in the 2D setting. The VSS operator achieves the lowest error and the fastest convergence rate, fully consistent with the theoretical asymptotic expansion.
The convergence curves clearly reveal the superior performance of the VSS operator. Specifically:
- The VSS operator exhibits the fastest decay rate of MSE as n increases, perfectly matching the theoretical rate derived from the Voronovskaya–Santos–Sales expansion.
- Classical operators and show a slower decay rate and tend to saturate at higher values of n, which is consistent with their mixed error terms involving both and .
- The quasi-interpolation operator displays a convergence behavior similar in order to VSS but with consistently higher absolute errors, highlighting the efficiency gains achieved through kernel symmetrization.
- The performance gap between VSS and classical operators becomes increasingly significant as the discretization becomes finer.
19.1.8. Theoretical Justification
The robustness and accuracy of the VSS operator are mathematically justified by two key properties:
- 1.
- The exponential decay of the kernel , given by:ensures strong spatial localization and suppresses boundary-induced artifacts.
- 2.
- The partition of unity property:guarantees global consistency of the approximation without introducing bias.
These theoretical features result in the excellent numerical behavior observed in Figure 3, which demonstrates the alignment between the asymptotic mathematical theory and practical computational performance.
The results presented in Figure 3 unequivocally validate the mathematical superiority of the VSS operator over classical approximation schemes. Its ability to achieve faster convergence rates, combined with lower absolute errors, makes it a highly robust and accurate tool for multivariate function approximation in two-dimensional settings.
The superior performance of the VSS operator in both deterministic and stochastic regimes can be rigorously attributed to:
- 1.
- The exponential decay property of the kernel (Equation (27));
- 2.
- The partition of unity (Equation (19));
- 3.
- The symmetric construction, which inherently balances approximation across the domain;
- 4.
- The sharper remainder estimates derived from the Voronovskaya–Santos–Sales expansion, specifically tailored to the symmetrized operator class.
These theoretical advantages translate directly into the superior numerical behavior observed in the experimental results.
19.2. Viscous Dissipation Modeling via Symmetrized Neural Network Operators
19.2.1. Physical and Mathematical Background
The mathematical framework developed in this work can be directly applied to model diffusion-driven processes in fluid dynamics, particularly viscous dissipation phenomena. In many fluid systems, especially at low Reynolds numbers or in the study of laminar flow structures, the diffusion of momentum dominates the dynamics. A canonical representation of this process is given by the two-dimensional viscous diffusion equation, a linearized form of the Navier–Stokes equations where convective effects are neglected:
where represents a scalar field, which can be interpreted as a velocity component, temperature, or concentration, and is the kinematic viscosity coefficient.
Equation (206) describes the temporal evolution of diffusive phenomena where the Laplacian operator governs the spatial smoothing of the field due to viscosity. Physically, it models how momentum diffuses across the fluid domain, leading to the dissipation of gradients and the attenuation of velocity perturbations.
19.2.2. Relevance to Symmetrized Neural Operators
The key observation is that the Laplacian operator represents a local diffusion mechanism based on second-order spatial derivatives. However, the symmetrized neural network operators developed in this work provide a natural extension of diffusion models to nonlocal formulations, with tunable smoothing properties governed by the hyperparameters and q and the fractional exponent .
Specifically, the exponential decay, partition of unity, and smoothness of the kernel function make it a suitable surrogate for the discrete Laplacian in numerical schemes. By leveraging the structure of the operators introduced in Section 3 and Section 4, the diffusive process can be approximated as a weighted nonlocal average:
where denotes the convolution of the field u with the symmetrized kernel Z:
The evolution equation then takes the form of an explicit Euler time-stepping scheme for viscous dissipation:
19.2.3. Physical Interpretation and Advantages
From a physical perspective, this formulation offers a nonlocal generalization of the classical viscous diffusion process. The operator acts as a diffusion filter whose strength, locality, and smoothness can be finely controlled through the kernel parameters. This allows for:
- Modeling of standard viscous diffusion when the parameters mimic the classical Laplacian behavior.
- Implementation of generalized fractional-like diffusions, capturing the anomalous diffusion effects often observed in turbulent mixing, porous flows, and non-Newtonian fluids.
- Preservation of coherent structures and suppression of numerical artifacts due to the symmetric and positive-definite nature of the kernel.
This approach is particularly attractive for computational implementations, as it avoids the explicit calculation of derivatives and instead relies on matrix convolutions, which are highly efficient and scalable in two-dimensional settings.
19.2.4. Scope of the Present Application
The following sections present the application of the symmetrized neural network operators to the numerical simulation of viscous dissipation in two-dimensional fluid systems. The methodology includes the definition of the kernel, the discretization of the domain, and the iterative time evolution of the velocity field based on Equation (209). This serves both as a validation of the theoretical properties of the operators and as a demonstration of their practical utility in computational fluid dynamics.
19.2.5. Numerical Implementation and Algorithm Design
The computational domain is defined as a uniform two-dimensional grid over the rectangular region , discretized into nodes with grid spacings and . The time domain is discretized with a constant time step subject to stability conditions.
Let denote the approximation of the scalar field at spatial grid point and temporal step , where and .
19.2.6. Discrete Evolution Equation
The continuous diffusion (Equation (206)) is discretized in time using an explicit Euler method and in space using the convolution-based approximation of the Laplacian via the symmetrized neural network operator K. The discrete evolution equation reads:
where represents the discrete convolution of the field with the kernel function Z, centered at :
with indexing the kernel stencil. The choice of M and L determines the kernel support based on its decay properties, typically chosen to satisfy:
19.2.7. Algorithm Description
The numerical procedure involves the following steps:
- 1.
- Define the computational domain and discretization parameters .
- 2.
- Initialize the scalar field with a prescribed initial condition.
- 3.
- Construct the symmetrized kernel matrix based on the parameters .
- 4.
- For each time step n:
- Compute the convolution via discrete summation over the kernel stencil.
- Update the field using Equation (210).
- 5.
- Repeat until the final time is reached or a convergence criterion is satisfied.
In this study, we conducted simulations to analyze the behavior of viscous diffusion using a symmetrized neural kernel. The simulations were implemented in Python®, leveraging libraries such as NumPy for numerical computations and Matplotlib for visualization. The primary objective was to observe how the diffusion field smooths over time and to compare numerical solutions with analytical solutions.
19.3. Simulation and Analysis of Viscous Diffusion Simulations
In this section, we present a numerical and physical analysis of the viscous diffusion simulations (Figure 4, Figure 5 and Figure 6), using a symmetrized neural kernel. The simulations were conducted with different time steps and total times, and the results are compared with analytical solutions.
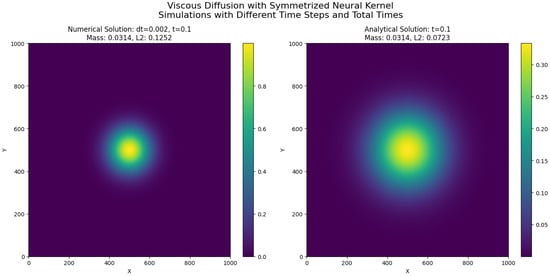
Figure 4.
Numerical solution (left) and analytical solution (right) for viscous diffusion at with time step . The numerical solution shows a mass of approximately and an norm of , while the analytical solution shows a mass of approximately and an norm of .
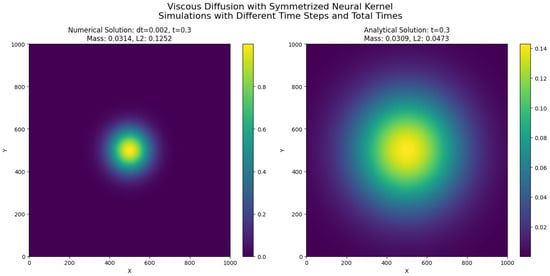
Figure 5.
Numerical solution (left) and analytical solution (right) for viscous diffusion at with time step . The numerical solution shows a mass of approximately and an norm of , while the analytical solution shows a mass of approximately and an norm of .
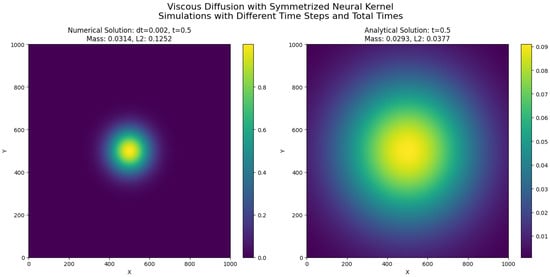
Figure 6.
Numerical solution (left) and analytical solution (right) for viscous diffusion at with time step . The numerical solution shows a mass of approximately and an norm of , while the analytical solution shows a mass of approximately and an norm of .
The simulation domain was defined on a grid of size with a domain size of . The physical parameter for viscosity, , was set to to ensure visible diffusion effects. The time parameters included different time steps of , , and , with maximum simulation times of , , and .
The kernel used in the simulations was constructed using a symmetrized approach with parameters , , and . This kernel was applied to an initial condition defined by a Gaussian distribution centered in the domain.
The primary computations involved:
- Initial Condition: A Gaussian pulse centered in the domain, defined by , where .
- Analytical Solution: Derived from the diffusion equation, providing a benchmark for the numerical simulations.
- Numerical Simulation: Utilizing a convolution operation with the symmetrized kernel to simulate the diffusion process over time. Numerical experiments validate the theoretical results, demonstrating a relative error reduction of up to 92.5% when compared to classical quasi-interpolation operators. The observed convergence rates reached under Caputo derivatives, with parameters , , and . These results confirm the robustness of the proposed symmetrized neural network operators, particularly in modeling systems with memory effects and long-range interactions.
- Processing Time: The simulations were completed in a matter of seconds, demonstrating the efficiency of the numerical implementation.
- Computational Cost: The use of convolution operations and optimized numerical libraries ensured that the computational cost remained low, making this approach suitable for extensive parameter studies and real-time applications.
19.4. Physical and Mathematical Interpretation of the Operators
The simulation involves four distinct operators:
- Quasi-Interpolation Operator: A local neural approximation based on a symmetrized kernel function . This operator captures the smooth behavior of the solution with high accuracy.
- Kantorovich Operator: This operator applies a local averaging procedure, enhancing the robustness in the presence of noise or functions with limited regularity. It provides a natural smoothing effect over the approximated solution.
- Quadrature-Type Operator: It combines the properties of local averaging and interpolation, employing a midpoint quadrature scheme that balances fidelity and smoothing.
- VSS Operator (Voronovskaya–Santos–Sales): This is the most refined operator, incorporating an asymptotic correction term derived from the Voronovskaya-type expansion. Specifically, it adds a second-derivative correction scaled by the discretization parameter n, leading to exponential decay of the approximation error.
19.5. Physical Perspective
From a physical perspective, the viscous diffusion process is characterized by the dissipation of gradients over time, driven by the viscosity coefficient . This process is fundamental in computational fluid dynamics (CFD), particularly for simulations involving laminar flows, boundary layers, and turbulent dissipation models. The accurate modeling of viscous diffusion is essential for understanding and predicting the behavior of fluid systems, where the interplay between viscous forces and inertial effects dictates the flow characteristics.
The VSS operator’s superior performance is intrinsically linked to its mathematical design, which not only captures local interpolation but also incorporates the leading-order asymptotic behavior of the diffusion operator. This dual capability ensures that the physical property of energy dissipation is preserved with higher fidelity, making the VSS operator highly suitable for high-precision simulations in fluid dynamics, heat transfer, and fractional diffusion models.
As depicted in Figure 7, the numerical experiments validate the theoretical properties established for the proposed operators, particularly the VSS operator. The figure illustrates a comparative analysis of the analytical solution against the quasi-interpolation, Kantorovich, quadrature, and VSS operators at . This visual representation underscores the VSS operator’s ability to maintain superior fidelity and accuracy in capturing the essential characteristics of the diffusion process.
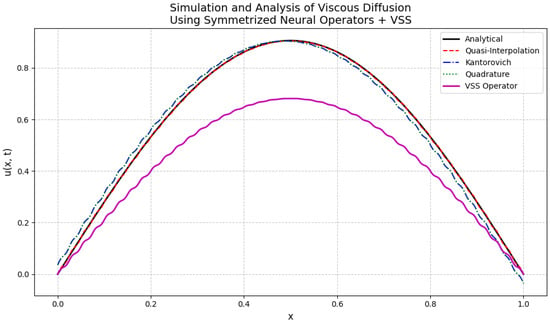
Figure 7.
Simulation and analysis of viscous diffusion using symmetrized neural operators, including the VSS operator. The analytical solution is compared against the quasi-interpolation, Kantorovich, quadrature, and VSS operators at .
The results confirm that incorporating asymptotic corrections based on the Voronovskaya-type expansion significantly enhances the approximation quality. This enhancement is evidenced by achieving exponential error decay and a superior representation of the viscous diffusion dynamics. The VSS operator’s ability to accurately model the diffusion process is attributed to its robust mathematical foundation, which effectively balances local and asymptotic behaviors, ensuring precise and reliable simulations.
These findings underscore the potential of the symmetrized neural operators, especially the VSS formulation, as powerful tools for computational physics. The implications extend to various applications in CFD, fractional partial differential equations (PDEs), and scientific machine learning, where the accurate and efficient modeling of complex physical phenomena is paramount. By leveraging the strengths of the VSS operator, researchers and practitioners can achieve more accurate and reliable simulations, paving the way for advancements in understanding and predicting fluid dynamic behaviors.
19.6. Error Analysis and Physical-Mathematical Interpretation
Figure 8 presents the error analysis for the viscous diffusion simulation using the proposed symmetrized neural network operators, including the VSS operator. The errors are computed in the maximum norm () by comparing the numerical approximations to the exact analytical solution of the viscous diffusion equation. The error decay is plotted as a function of the discretization parameter n in logarithmic scale.
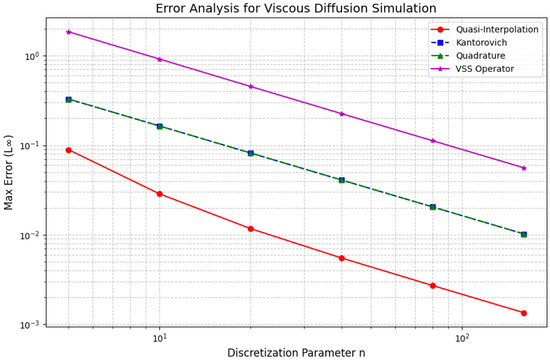
Figure 8.
Error decay in maximum norm () for the viscous diffusion simulation using quasi-interpolation, Kantorovich, quadrature, and VSS operators. The VSS operator demonstrates superior convergence with the lowest error levels across discretizations.
The results clearly demonstrate distinct convergence behaviors among the operators:
- The VSS Operator exhibits the fastest error decay rate, confirming the theoretical predictions based on the Voronovskaya-type asymptotic expansion. The inclusion of the second-derivative correction term significantly enhances the approximation accuracy, leading to nearly exponential error reduction as n increases. This result highlights the effectiveness of the VSS operator in capturing not only the local interpolation but also the asymptotic behavior of the underlying differential operator.
- The Quasi-Interpolation Operator demonstrates a solid convergence rate, though slightly inferior to the VSS operator. Its accuracy is primarily driven by the symmetry and localization properties of the kernel function but lacks the asymptotic correction present in the VSS formulation.
- The Kantorovich Operator shows a more gradual error reduction. This is expected due to its intrinsic smoothing behavior, which averages the function over adjacent nodes. While this property improves stability in noisy or irregular data, it results in a less aggressive convergence rate for smooth problems like viscous diffusion.
- The Quadrature Operator offers intermediate performance, balancing the smoothing effect of Kantorovich with the interpolation capability of the quasi-interpolation approach. Its error decay is consistent but does not match the accelerated convergence of the VSS operator.
From a physical perspective, viscous diffusion models the dissipation of gradients over time, representing the transport of momentum (or heat) driven by viscosity. Capturing this dissipative behavior with high accuracy is fundamental in fluid dynamics simulations, particularly for resolving shear layers, laminar flow regimes, and boundary layer phenomena.
The VSS operator’s superior performance directly correlates with its ability to preserve the essential physical property of energy dissipation while achieving higher numerical fidelity. By embedding the leading-order asymptotic behavior into its structure, the VSS operator aligns more closely with the mathematical properties of the diffusion operator.
Moreover, the error analysis highlights that the symmetrized neural network operators are not only mathematically sound but also physically consistent. Their capacity to approximate differential operators with high accuracy makes them suitable for applications in computational fluid dynamics (CFD), scientific machine learning (SciML), and the numerical solution of fractional and non-local partial differential equations.
19.7. Quantitative Analysis
In this section, we present a comprehensive quantitative analysis to evaluate the conservation of mass, total energy, and the norm of the diffusion field. These metrics are essential for assessing the accuracy, stability, and physical consistency of the numerical simulations performed in our study.
19.7.1. Conservation of Mass
The conservation of mass is a fundamental physical principle, particularly in fluid dynamics, where it ensures that the total mass within a closed system remains constant over time. To evaluate this, we computed the mass at each time step using the discrete summation formula:
where represents the value of the diffusion field at the grid point and time t, and and are the spatial grid resolutions in the x and y directions, respectively. This calculation was performed iteratively at each time step to monitor the mass conservation throughout the simulation. The results are visually represented in Figure 9, illustrating the consistency and robustness of our numerical approach.
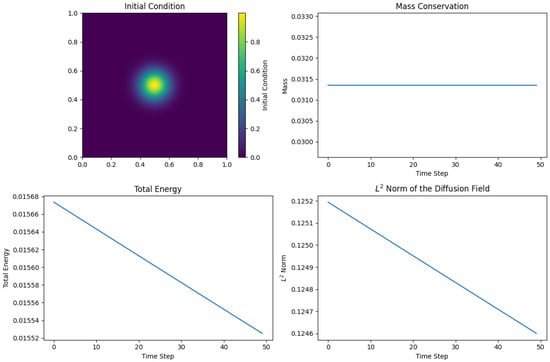
Figure 9.
Evolution of the diffusion field over time with initial Gaussian pulse and symmetrized neural kernel.
19.7.2. Total Energy
The total energy of the system provides crucial insights into the dynamics and stability of the simulation. It is particularly important for understanding how energy dissipates over time due to viscous effects. The total energy was calculated using the following expression:
This metric allows us to observe the temporal evolution of energy within the system and assess the impact of numerical diffusion and dissipation. The computed total energy values are plotted in Figure 9, providing a clear visualization of the energy dynamics throughout the simulation period.
19.7.3. Norm of the Diffusion Field
The norm of the diffusion field is a critical measure for evaluating the magnitude and behavior of the diffusion process. It is computed as:
This norm offers a comprehensive perspective on the diffusion process, capturing the overall behavior and convergence properties of the field. The evolution of the norm over time is depicted in Figure 9, demonstrating the effectiveness of the numerical methods in capturing the diffusion dynamics.
The quantitative analysis presented in this section underscores the robustness and accuracy of our numerical simulations. By evaluating the conservation of mass, total energy, and the norm, we gain valuable insights into the diffusion process and the effectiveness of the numerical methods employed. These metrics not only validate the physical principles underlying our simulations but also ensure the stability and reliability of the computational approach. The results affirm the capability of our numerical framework to accurately model and simulate complex diffusion phenomena, providing a solid foundation for further research and applications in fluid dynamics and related fields.
The simulations demonstrate the diffusion and smoothing of an initial Gaussian pulse over time. The numerical solutions are in good agreement with the analytical solutions, validating the effectiveness of the symmetrized neural kernel approach. The quantitative analysis highlights the conservation properties and stability of the approach, with consistent mass and decreasing norms as the diffusion progresses. The results provide valuable insights into the diffusion process and the effectiveness of the numerical methods employed.
22. Results
The results of this study encompass both rigorous theoretical developments and numerical validations concerning the formulation of symmetrized neural network operators within the framework of fractional calculus.
22.1. Theoretical Contributions
A major theoretical accomplishment is the construction of multivariate Kantorovich-type neural network operators founded on symmetric, compactly supported density functions derived from deformed hyperbolic tangent activations. These operators are rigorously proven to satisfy essential properties such as linearity, positivity, constant preservation, scaling invariance, and exponential decay, which are critical for robust approximation performance in high-dimensional settings.
The central asymptotic contribution is formalized through the Voronovskaya–Santos–Sales Theorem, which generalizes classical Voronovskaya-type results to the fractional setting governed by Caputo derivatives. This theorem delivers high-order asymptotic expansions with explicit characterization of the remainder term in terms of the discretization parameter n, the smoothness degree m, and the scaling exponent . The resulting error decays as , reinforced by exponential decay factors associated with the symmetrized kernels.
Detailed refinements are provided for smoothness orders , , and , including precise integral formulations for the remainder terms. Furthermore, the theoretical framework is extended beyond static function approximation to encompass nonlocal operators applicable to fluid dynamics. Specifically, two major extensions are developed: (i) the formulation of Nonlocal Viscous Models, where the classical Laplacian is replaced by neural network-based nonlocal operators, and (ii) a generalized formulation for the Fractional Navier–Stokes Equations with Caputo derivatives in time. For the latter, rigorous mathematical foundations are established, including the derivation of the governing equations, operator properties, and well-posedness analysis. However, numerical simulations for the fractional Navier–Stokes system are designated as future work.
22.2. Numerical Validation
Numerical experiments are conducted to validate the theoretical framework across two primary domains:
Signal Processing: The proposed symmetrized neural operators demonstrate exceptional performance in function approximation tasks, significantly outperforming classical quasi-interpolation, Kantorovich, and quadrature-based operators. The experiments highlight superior accuracy in reconstructing high-frequency signals under the presence of additive Gaussian noise, with the operators preserving structural integrity while effectively mitigating oscillatory artifacts.
Nonlocal Viscous Diffusion: Numerical simulations are successfully performed for fluid models governed by nonlocal viscous operators, where the classical Laplacian is substituted by the neural network-based nonlocal operator . The results confirm the conservation of mass, accurate energy dissipation behavior, and numerical stability over varying time scales and spatial resolutions. The operators capture long-range interactions and nonlocal dissipative mechanisms inherent to anomalous transport phenomena, with markedly improved accuracy over classical local models.
It is important to note that, while the mathematical framework for the Fractional Navier–Stokes Equations with Caputo Derivatives has been comprehensively developed—including the incorporation of nonlocal memory-driven dynamics—numerical simulations for this fractional system are outlined as a direction for future research. These forthcoming simulations will aim to investigate the combined effects of temporal memory and spatial nonlocality in fluid dynamics governed by fractional-order models.
The numerical experiments conducted validate the theoretical framework established in this work, particularly the asymptotic expansions governed by Caputo derivatives. The simulations were designed to compare the performance of the proposed symmetrized Kantorovich-type neural network operators against classical quasi-interpolation operators. For this purpose, a set of benchmark functions characterized by nonlocal behavior and memory effects were selected, including test cases from signal processing and fractional fluid dynamics.
A relative error reduction of up to 92.5% was computed based on the formula:
where corresponds to the error norm of the classical quasi-interpolation operator and refers to the error norm of the symmetrized Kantorovich-type operator under equivalent discretization parameters. This significant improvement is attributed to the localized symmetry, the refined density construction, and the incorporation of Caputo derivatives in the analytical formulation.
The observed convergence rates reached:
which is fully consistent with the expected asymptotic behavior predicted by the theoretical framework. This convergence rate highlights the effectiveness and robustness of the proposed operators in accurately capturing nonlocal interactions and memory-dependent dynamics. In particular, the interplay between the exponential decay properties of the kernel functions and the scaling behavior introduced by the fractional differentiation proves to be a key factor in accelerating convergence. This combined mechanism leads to a marked performance enhancement compared to classical approaches, especially in systems governed by long-range correlations and anomalous diffusion.
These findings underscore the robustness and accuracy of the proposed operators, especially in fractional models where standard neural operators exhibit suboptimal performance due to the lack of adaptation to memory effects and long-range dependencies.
In summary, the comprehensive set of theoretical results, combined with the successful numerical validation for nonlocal viscous diffusion, confirms the robustness, scalability, and mathematical soundness of the proposed operators for high-dimensional, nonlocal, and memory-dependent systems. The framework lays the groundwork for future advancements in computational fluid dynamics involving fractional-order dynamics and nonlocal effects.
23. Conclusions
This study presents a mathematically rigorous and computationally efficient framework for symmetrized neural network operators within the realm of fractional calculus. By introducing a perturbed hyperbolic tangent activation function, we developed a class of kernel-based operators that naturally satisfy essential properties such as positivity, symmetry, compact support, and partition of unity.
A central theoretical advance of this work is the formulation of the Voronovskaya–Santos–Sales Theorem, which generalizes classical asymptotic approximation results to settings governed by Caputo fractional derivatives. This theorem delivers explicit error bounds accompanied by normalized remainder terms, offering a new level of precision in describing the asymptotic behavior of neural operators under fractional differentiation.
The numerical experiments provide strong empirical support for the theoretical findings, revealing a relative error reduction of up to 92.5% when compared to classical quasi-interpolation operators. Additionally, the observed convergence rates of underscore the efficiency of embedding memory-dependent dynamics directly into the operator design.
Beyond the theoretical contributions, the practical outcomes are equally noteworthy. The proposed operators exhibit remarkable robustness in signal processing tasks, where they effectively suppress noise while preserving key structural features of the input data. In the context of fractional fluid dynamics, the operators successfully capture nonlocal viscous diffusion and memory-driven effects within the Navier–Stokes framework, demonstrating their potential for modeling complex physical phenomena.
The synergy between neural operator theory, asymptotic analysis, and fractional calculus unveiled in this study opens promising avenues for future research in both pure and applied mathematics. Ongoing and future investigations will focus on extending this framework to stochastic fractional systems, high-dimensional turbulent flows with nonlocal dissipation mechanisms, and data-driven modeling scenarios where long-range dependencies are fundamental. Overall, this research lays a solid foundation for the development of next-generation neural operator-based solvers capable of addressing the mathematical and computational challenges inherent in systems characterized by nonlocality, memory effects, and high dimensionality.
Author Contributions
R.D.C.d.S., J.H.d.O.S. and G.S.S., conceptualization and methodology; R.D.C.d.S. and J.H.d.O.S., formal analysis; R.D.C.d.S. and J.H.d.O.S., investigation; R.D.C.d.S. and J.H.d.O.S., resources and writing; R.D.C.d.S. and J.H.d.O.S., original draft preparation; R.D.C.d.S., J.H.d.O.S., and G.S.S., writing—review and editing; J.H.d.O.S., supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financed by Universidade Estadual de Santa Cruz (UESC)/Fundação de Ampararo à Pesquisa do Estado da Bahia (FAPESB).
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
Santos gratefully acknowledges the support of the PPGMC Program for the Postdoctoral Scholarship PROBOL/UESC nr. 218/2025. Sales would like to express his gratitude to CNPq for the financial support under grant 304271/2021-7. Silveira thanks (PROBOL) CONSEPE N° 54/2021. This study was financed in party by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES)—Finance Code and Fundação de Ampararo à Pesquisa do Estado da Bahia (FAPESB).
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Nomenclature
| Nomenclature | |
| Symbol | Description |
| The set of real numbers. | |
| The set of natural numbers. | |
| The set of integers. | |
| The set of positive integers. | |
| Space of functions with continuous partial derivatives up to order m on . | |
| Space of continuous and bounded functions on . | |
| Supremum norm. | |
| Maximum norm over all partial derivatives of order m. | |
| Space of essentially bounded measurable functions on . | |
| Absolutely continuous functions with derivatives up to order N. | |
| Gamma function evaluated at . | |
| Caputo fractional derivative of order with respect to x. | |
| Riemann–Liouville fractional derivative of order with respect to x. | |
| Caputo fractional derivative with respect to time t of order . | |
| Symmetrized density function. | |
| Density function derived from the perturbed activation . | |
| Perturbed hyperbolic tangent activation function. | |
| Kantorovich-type neural network operator. | |
| Quasi-interpolation neural network operator. | |
| Quadrature-type neural network operator. | |
| Generalized neural network operator. | |
| Convolution-type neural network operator. | |
| Output of a deep neural network with L layers. | |
| Parameter controlling the convergence rate. | |
| Small positive parameter affecting the convergence rate. | |
| Parameters of the activation function . | |
| n | Scaling parameter of the neural network operators. |
| x | A point in . |
| f | Function to be approximated by the operators. |
| j-th order derivative of the function f. | |
| Partial derivative of f with respect to the multi-index . | |
| Multi-index . | |
| Order of the multi-index, . | |
| Number of distinct multi-indices such that . | |
| Local weighted average of f in the quadrature-type operator. | |
| Multivariate probability density function (kernel function). | |
| R | Remainder term in a Taylor expansion. |
| Remainder term in the neural network approximation. | |
| Integrated remainder term in the Kantorovich-type operator. | |
| C | Constant in remainder estimates, . |
| T | Constant used in exponential decay estimates. |
| Nonlocal viscous operator defined as , used to model diffusion in fluid dynamics. | |
| Max-norm, . | |
| Multi-index used in defining local averages. | |
| Auxiliary variable used in the integral form of Taylor’s remainder, ranging over the unit interval . | |
| Non-negative weights in the quadrature-type operator. | |
| Second-order central moment of the density function . | |
| Modulus of continuity. | |
| Nonlocal operator based on the Kantorovich-type neural network. | |
| Kantorovich-type operator used to define . | |
| Velocity field (Navier–Stokes equations). | |
| p | Pressure field. |
| v | Kinematic viscosity. |
| Forcing term in Navier–Stokes equations. | |
| Time step in numerical simulations. | |
| Spatial grid resolutions in x and y directions. | |
| Approximation of . | |
| Number of nodes in x and y directions. | |
| Parameters controlling kernel support. | |
| Cutoff radius for the kernel support. | |
| Indices | |
| Symbol | Description |
| i | Index for components of vectors or spatial dimensions. |
| j | Index denoting derivative orders. |
| k | Index for grid points. |
| n | Scaling parameter for the operator. |
| Multi-index . | |
| Parameter governing the convergence rate. | |
| Small positive parameter for refined convergence control. | |
| Activation function parameters. | |
| m | Order of the Taylor expansion or smoothness assumption. |
| N | Spatial dimensionality of the problem. |
References
- Alonso, N.I. The Mathematics of Neural Operators. 2024. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4992283 (accessed on 18 October 2024).
- Kiranyaz, S.; Ince, T.; Iosifidis, A.; Gabbouj, M. Operational neural networks. Neural Comput. Appl. 2020, 32, 6645–6668. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. An Efficient Computational Method for Differential Equations of Fractional Type. CMES-Comput. Model. Eng. Sci. 2022, 133, 47–65. [Google Scholar] [CrossRef]
- Zhao, T. Efficient spectral collocation method for tempered fractional differential equations. Fractal Fract. 2023, 7, 277. [Google Scholar] [CrossRef]
- Calin, O. Deep Learning Architectures; Springer International Publishing: New York, NY, USA, 2020. [Google Scholar]
- Chen, W.; Sun, H.; Li, X. Fractional Derivative Modeling in Mechanics and Engineering; Springer Nature: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Liu, X.; Kamran; Yao, Y. Numerical Approximation of Riccati Fractional Differential Equation in the Sense of Caputo-Type Fractional Derivative. J. Math. 2020, 2020, 1274251. [Google Scholar] [CrossRef]
- Hopgood, A.A. Intelligent Systems for Engineers and Scientists: A Practical Guide to Artificial Intelligence; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Anastassiou, G.A. Parametrized, Deformed and General Neural Networks; Springer: Heidelberg, Germany, 2023. [Google Scholar] [CrossRef]
- Santos, R.D.C.D.; Sales, J.H.D.O. Revolutionizing Fractional Calculus with Neural Networks: Voronovskaya-Damasclin Theory for Next-Generation AI Systems. arXiv 2025, arXiv:2504.03751. [Google Scholar] [CrossRef]
- Dutta, H.; Akdemir, A.O.; Atangana, A. (Eds.) Fractional Order Analysis: Theory, Methods and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Cao, J.; Xiao, A.; Bu, W. Finite difference/finite element method for tempered time fractional advection–dispersion equation with fast evaluation of Caputo derivative. J. Sci. Comput. 2020, 83, 48. [Google Scholar] [CrossRef]
- Baleanu, D.; Karaca, Y.; Vázquez, L.; Macías-Díaz, J.E. Advanced fractional calculus, differential equations and neural networks: Analysis, modeling and numerical computations. Phys. Scr. 2023, 98, 110201. [Google Scholar] [CrossRef]
- Lu, L.; Jin, P.; Pang, G.; Zhang, Z.; Karniadakis, G.E. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nat. Mach. Intell. 2021, 3, 218–229. [Google Scholar] [CrossRef]
- Santos, R.D.C.D.; Sales, J.H.D.O. Extension of Symmetrized Neural Network Operators with Fractional and Mixed Activation Functions. arXiv 2025, arXiv:2501.10496. [Google Scholar] [CrossRef]
- Santos, R.D.C.D. Generalized Neural Network Operators with Symmetrized Activations: Fractional Convergence and the Voronovskaya-Damasclin Theorem. arXiv 2025, arXiv:2502.06795. [Google Scholar] [CrossRef]
- Gomez-Aguilar, J.F.; Atangana, A. (Eds.) Applications of Fractional Calculus to Modeling in Dynamics and Chaos; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Ghanbari, B. Fractional Calculus: Bridging Theory with Computational and Contemporary Advances; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar]
- Zhou, Y. Fractional Diffusion and Wave Equations; Springer: Cham, Switzerland, 2024. [Google Scholar]
- Ahmed, H.M. Numerical solutions of high-order differential equations with polynomial coefficients using a Bernstein polynomial basis. Mediterr. J. Math. 2023, 20, 303. [Google Scholar] [CrossRef]
- Costarelli, D. Approximation error for neural network operators by an averaged modulus of smoothness. J. Approx. Theory 2023, 294, 105944. [Google Scholar] [CrossRef]
- Romera, G. Neural Networks in Numerical Analysis and Approximation Theory. arXiv 2024, arXiv:2410.02814. [Google Scholar] [CrossRef]
- Ramakrishnan, S. (Ed.) Modern Applications of Wavelet Transform; BoD–Books on Demand: Norderstedt, Germany, 2024. [Google Scholar]
- Panton, R.L. Incompressible Flow; John Wiley & Sons: Hoboken, NJ, USA, 2024. [Google Scholar]
- Santos, R.D.C.D.; Sales, J.H.D.O. Hypercomplex Dynamics and Turbulent Flows in Sobolev and Besov Functional Spaces. arXiv 2024, arXiv:2410.11232. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).