Cloud Platform Selection Using Extended Multi-Attribute Decision-Making Methods with Interval Type-2 Fuzzy Sets

Abstract

The selection of an appropriate cloud platform represents a highly important strategic decision for any IT company. In pursuit of business optimization, cost reduction, improved reliability, and enhanced market competitiveness, selecting the most suitable cloud platform has become a major practical challenge. This paper proposes a novel two-stage multi-attribute decision-making (MADM) model, enhanced through the use of interval type-2 fuzzy sets (IT2FMADM). This was demonstrated through a case study in an IT company based in Serbia. In the first stage, three experts from the company were surveyed to assess the relative importance of the attributes, and their evaluations were aggregated using the fuzzy harmonic mean operator. As a result, unified fuzzy weight vectors were obtained. In the second stage, two MADM methods extended with interval type-2 fuzzy sets, namely COmplex PRoportional Assessment (IT2FCOPRAS) and Evaluation based on Distance from Average Solution (IT2FEDAS), were applied to support the selection of the most suitable cloud platform. Each platform was evaluated by decision-makers (DMs), who reached a consensus in their assessments, supported by data from company records. A comparative analysis of the results revealed that different methods may produce varying rankings of alternatives, particularly when the alternatives are objectively similar in their characteristics. Nevertheless, the proposed model can serve as a highly useful decision-support tool for company management.

1. Introduction

The advancement of modern information technology has caused significant changes in business processes, not just in the information technology (IT) industry but also in other economic sectors. Today, an increasing number of organizations use cloud technology, which has had a significant impact on how organizations plan and manage IT resources. In other words, cloud technology provides on-demand access to resources, including servers and data storage. This enables more efficient business operations through easier data access, improved support for remote collaboration, and facilitation of other aspects of modern business environments. In addition to these technical advantages, cloud solutions require minimal IT infrastructure, making them particularly attractive for small and medium-sized companies.

One of the most significant forms of cloud technology is cloud computing. In fact, cloud computing can be defined as a model for delivering services to end users over the internet, where users access these services on demand. Cloud computing allows businesses to save money by decreasing the need for initial hardware and software investments, as well as lowering maintenance and management costs. Unlike the conventional model, which requires enterprises to maintain their own infrastructure, cloud computing allows them to use resources on demand, paying only for what they need [1]. This is especially significant for IT managers, system architects, and end users since it increases flexibility and operational efficiency. Also, cloud computing has become a vital tool in the age of digital transformation and rapid advances in artificial intelligence, allowing organizations to improve their market competitiveness, drive innovation, and gain better agility [2].

The rapid development and widespread adoption of cloud computing have brought numerous opportunities to users but also many uncertainties. There are various cloud solutions on the market, i.e., cloud platforms, each with different features and capabilities. For a company to choose an appropriate cloud platform for its business, it is necessary to define the attributes on which the selection will be based, but first and foremost, it is essential to determine the relative importance of each considered attribute. However, given that such an assessment is very difficult and unreliable when using precise numerical values, as is the case with any other decision-making problem, it is most appropriate to apply fuzzy set theory [3].

The research trend indicates that the relative importance of attributes, as well as the estimated values of alternatives, in this case cloud platforms, can be more easily assessed when using linguistic terms instead of precise numbers. The development of mathematical theories, based on different types of fuzzy sets, has enabled linguistic variables to be quantitatively described in a sufficiently accurate manner. Accordingly, in the relevant literature, instead of assessments based on precise numbers [4], authors have used type-1 fuzzy sets [5,6,7], type-2 fuzzy sets [8,9,10], intuitionistic fuzzy sets [11,12,13], Pythagorean fuzzy sets [14,15,16], q-rung orthopair fuzzy sets [17,18,19], picture fuzzy sets [20,21], etc., for this purpose.

Each of the mentioned types has specific advantages and limitations, reflected in aspects such as computational complexity, interpretability, and underlying algebra. In this paper, pre-defined linguistic expressions modeled using type-2 sets [22] were used to describe uncertain and imprecise values. Type-2 fuzzy sets provide a higher degree of freedom and flexibility, allowing for better handling of uncertainty [23] and, consequently, yielding more accurate and robust results [24] compared to basic fuzzy sets (type-1) from which they originated.

Interval type-2 fuzzy numbers represent a special form of type-2 fuzzy sets, whose membership function is defined over a specific numerical scale. However, the drawback of this approach lies in the fact that the use of type-2 fuzzy numbers requires complex and extensive computational operations, which can be considered a disadvantage compared to basic fuzzy numbers. Although the basic type of fuzzy numbers is still used in the relevant literature [5,6,7], many authors suggest that modeling uncertainty and imprecision should be based on the use of interval type-2 fuzzy numbers. In numerous studies available in the relevant literature [8,9], uncertain data are modeled using interval type-2 trapezoidal fuzzy numbers (IT2TrFNs), which effectively capture the imprecision inherent in natural language expressions.

The evaluation of values using different fuzzy approaches serves only as input for the application of methods aimed at selecting the optimal solution, in this case, a cloud platform. For this purpose, multi-attribute decision-making (MADM) methods are used. In practice, finding the optimal solution to decision-making problems that exist in different economic domains almost always depends on multiple attributes. Therefore, the literature contains numerous studies proposing various MADM problems under an interval type-2 fuzzy environment (IT2FMADM) [25,26,27].

Since cloud platforms can be described by numerous attributes, in this study, the selection of the cloud platform that best supports a company’s business operations is formulated as a two-stage IT2FMADM problem. In the first stage, the attributes for evaluating cloud platforms are identified by decision-makers (DMs). Their assessments are based on experience as well as recommendations found in the relevant literature. The evaluation of the relative importance of attributes is formulated as a fuzzy group decision-making problem. A literature analysis reveals that many studies have employed subjective methods for determining the weight vector of the considered attributes [28,29,30,31,32,33,34,35,36,37]. In the second stage, the ranking of cloud platforms is determined using modified methods: (i) the COmplex PRoportional Assessment (COPRAS) [38] with interval type-2 fuzzy numbers (IT2FCOPRAS) as presented in [28,29,32,33], and (ii) the Evaluation based on Distance from Average Solution (EDAS) [39] method with interval type-2 fuzzy numbers (IT2FEDAS) as proposed in [30,31].

According to the classification of MADM methods presented in the paper [40], the COPRAS method belongs to the group of utility-based methods, while the EDAS method is classified as a distance-based method. This is one of the reasons why it was mathematically justified to compare the obtained results. For this purpose, the ranking similarity coefficient was used [41,42].

Accordingly, the broader aim of this study is to integrate the following components: (i) modeling existing uncertainties using IT2TrFNs, (ii) determining the relative importance of attributes used to evaluate cloud platforms through fuzzy group decision-making, with the aggregated weights of identified attributes obtained using the fuzzy harmonic mean, (iii) ranking cloud platforms using the proposed IT2FCOPRAS and IT2FEDAS methods, and (iv) determining the similarity coefficient of the ranking obtained by applying the proposed methods.

The rest of the paper is organized as follows: Section 2 presents a literature review of MADM methods extended with interval type-2 fuzzy numbers. Section 3 describes the proposed methodology. A case study is presented in Section 4, while Section 5 provides the conclusion.

2. Literature Review

2.1. Application of MADM Methods in Cloud Platform Selection

The application of MADM methods in the IT industry is not an unfamiliar approach. Many authors have used various MADM approaches to solve problems in this research domain [12,43,44]. However, the selection of a cloud platform has rarely been approached as an MADM problem in the literature, although some authors have proposed various approaches for selecting an appropriate cloud platform.

One of the primary goals of IT management is to increase customer satisfaction while lowering operating expenses over time. To accomplish this, IT resources must be allocated optimally, and the selection of an appropriate cloud platform is critical.

The problem of selection techniques for cloud service providers has been considered in a general sense in the study by [45]. This paper presents a comprehensive literature review on various approaches employed for this purpose while also explaining the broader scope of the problem.

In the study by [46], the author examined the selection of IoT (Internet of Things) cloud platforms based on key factors such as technical offerings, strategy, market presence, compliance, and recommendations. Each of the considered platforms was evaluated through pairwise comparisons. The platform that outperformed all others in direct comparisons the most times was selected as the best. Therefore, this approach cannot be classified as an MADM method.

A similar problem was addressed in the study by [47]. In this case, the authors selected IoT-based cloud platforms by applying the so-called Distance-Based Approach in combination with type-1 fuzzy numbers. The selection criteria were categorized into quality, technical, and economic factors.

Cloud service selection was the focus of the study by [48], where the authors employed multiple fuzzy MADM methods to compare the obtained results. Furthermore, an innovative hybrid fuzzy MADM approach was utilized in the study by [49], in which the authors conducted the selection of IoT cloud platforms.

Based on the reviewed literature, it is evident that cloud platform selection has been explored in relevant research, yet it remains insufficiently addressed. Notably, only a few studies have tackled this problem using an MADM approach [47,48,49]. Two of these studies employed the basic type of fuzzy numbers for modeling uncertainty [47,48]. Only in study [49] did the authors use one of the advanced approaches, namely neutrosophic fuzzy numbers. Another shortcoming of the proposed approaches lies in the fact that the authors used only a single MADM method for cloud platform selection. In this paper, IT2FCOPRAS and IT2FEDAS are applied in order to assess the robustness of the proposed solution.

When observing the attributes used for cloud platform selection, previous studies do not focus on the practical needs of companies. For example, in study [48], the authors consider criteria such as cloud syncing, file sharing, and productivity, which are more suitable for evaluating software functionalities rather than cloud infrastructure. Similarly, in study [47], the authors address practically relevant attributes only to a certain extent. Although they include qualitative indicators such as usability and maintainability, they omit crucial aspects such as cost and vendor reputation, which have a significant impact in real-world decision-making. Unlike the approaches proposed in previous studies, this paper employs a set of attributes oriented toward practical problem-solving, including performance and latency, unit price, security measures, additional services, management and monitoring costs, scalability, and platform reputation.

Although previous studies consider a larger number of cloud platforms than this paper, the justification for this lies in the practical applicability of the proposed methodology. In this study, an initial rough pre-selection of cloud platforms was carried out by the company under consideration. Taking into account budget constraints, technical specifications, and other relevant factors, the company eliminated alternatives that did not meet certain important practical requirements. Therefore, it can be concluded that the analysis conducted in this paper has a stronger practical orientation compared to purely theoretical models, as it does not rely solely on quantitative and theoretical data.

The proposed model consists of three main phases. Firstly, the proposed subjective method, extended with IT2TrFNs, is used to obtain the weight vectors of the identified attributes of cloud platforms. After that, the priority of the considered cloud platforms is determined using IT2FCOPRAS and IT2FEDAS, followed by a comparison, i.e., a sensitivity analysis of the obtained results.

2.2. Modeling of the Uncertain Data

In this section, studies in which existing uncertainties are described using linguistic variables modeled by interval type-2 fuzzy sets are reviewed [28,29,30,31,32], as in this study.

As is well known, the characteristics of fuzzy numbers are membership function, granularity, and domain. In the literature, there are no established rules or recommendations on how to determine the characteristics of fuzzy numbers. In all the analyzed studies [28,29,30,31,32], uncertainties in the relative importance and values of attributes are modeled by IT2TrFNs.

Some authors [29,31,32] describe the relative importance and values of attributes using seven pre-defined linguistic expressions, whose domains are defined within the interval (0–1). In paper [28], the authors also suggest that existing uncertainties can be described using five linguistic expressions. These authors defined the domains of IT2TrFNs, which model pre-defined linguistic terms, on the standard measurement scale (1–9) [50].

In paper [31], the authors consider that the relative importance of attributes can be described by seven linguistic expressions defined on the domain (0–1). The values in the fuzzy decision matrix are modeled by seven IT2TrFNs, whose domains are defined within the interval (0–10).

In this study, the description of the relative importance of attributes and their uncertain values is provided using seven linguistic expressions. The domains of IT2TrFNs, which model existing uncertainties, are defined on the measurement scale (1–10).

2.3. Ranking by Applying IT2FCOPRAS

Calculating the fuzzy maximizing and fuzzy minimizing indices is based on the procedure proposed in conventional COPRAS, combined with interval type-2 fuzzy algebra rules [28,29,32,33]. In this way, the values of the fuzzy maximizing and fuzzy minimizing indices are described using IT2TrFNs. The representative scalars of these fuzzy indices are obtained using different defuzzification procedures: (1) the procedure proposed by [51] in [29,32] and (2) the procedure by [52] in [28].

The ranking of alternatives is determined based on crisp values, as in conventional COPRAS. The relative significance values are calculated and described using IT2TrFNs in [33]. The ranking of alternatives is performed according to precise values obtained by applying the defuzzification procedure [52]. In this paper, the calculation of the relative significance value for each cloud platform, as well as the determination of their priority, is realized by analogy with [33].

2.4. Ranking by Applying IT2FEDAS

Determining the fuzzy positive distance and fuzzy negative distance from the mean values is based on the procedure proposed in conventional EDAS and interval type-2 fuzzy algebra rules in [30,31]. In this way, it is not possible to ensure that the obtained values are strictly positive IT2TrFNs.

Therefore, many authors in the literature suggest that the difference between two fuzzy numbers should be calculated as their distance. In this study, the difference between the values of the elements in the weighted normalized fuzzy decision matrix and the fuzzy averaging values is calculated as the distance between two IT2TrFNs [10]. This represents one of the main differences between the analyzed papers and this paper and can simultaneously be considered one of the key contributions of this study.

The normalized fuzzy positive distance and normalized fuzzy negative distance are determined using the linear Max normalization procedure [53], combined with interval type-2 fuzzy algebra rules [30,31].

In this study, the normalized fuzzy positive and fuzzy negative distances are obtained using a linear normalization procedure [54], which requires a lower computational burden and ensures that the obtained values are positive IT2TrFNs, which can be considered one of the contributions of this research.

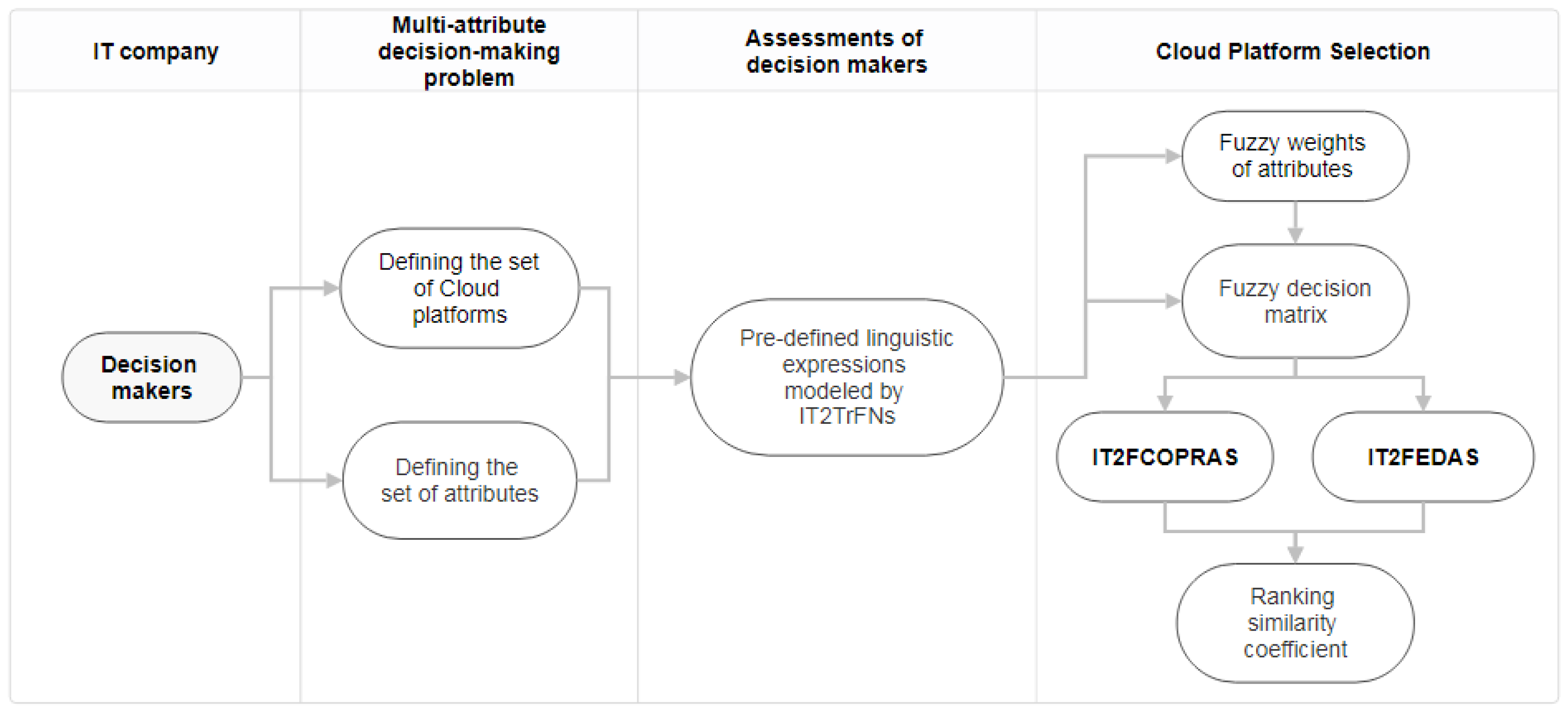
3. Methodology

In this section, the methodology used to solve the considered problem is briefly explained. In this paper, a two-stage fuzzy model is proposed. In the first stage, weight vectors of attributes for evaluating cloud platforms are determined. In the second stage, the ranking of the considered cloud platforms is established, allowing decision-makers to select the platform that best suits the specific type of IT company. A similarity analysis of the obtained rankings using IT2FCOPRAS and IT2FEDAS is conducted. The proposed methodology is presented in Figure 1.

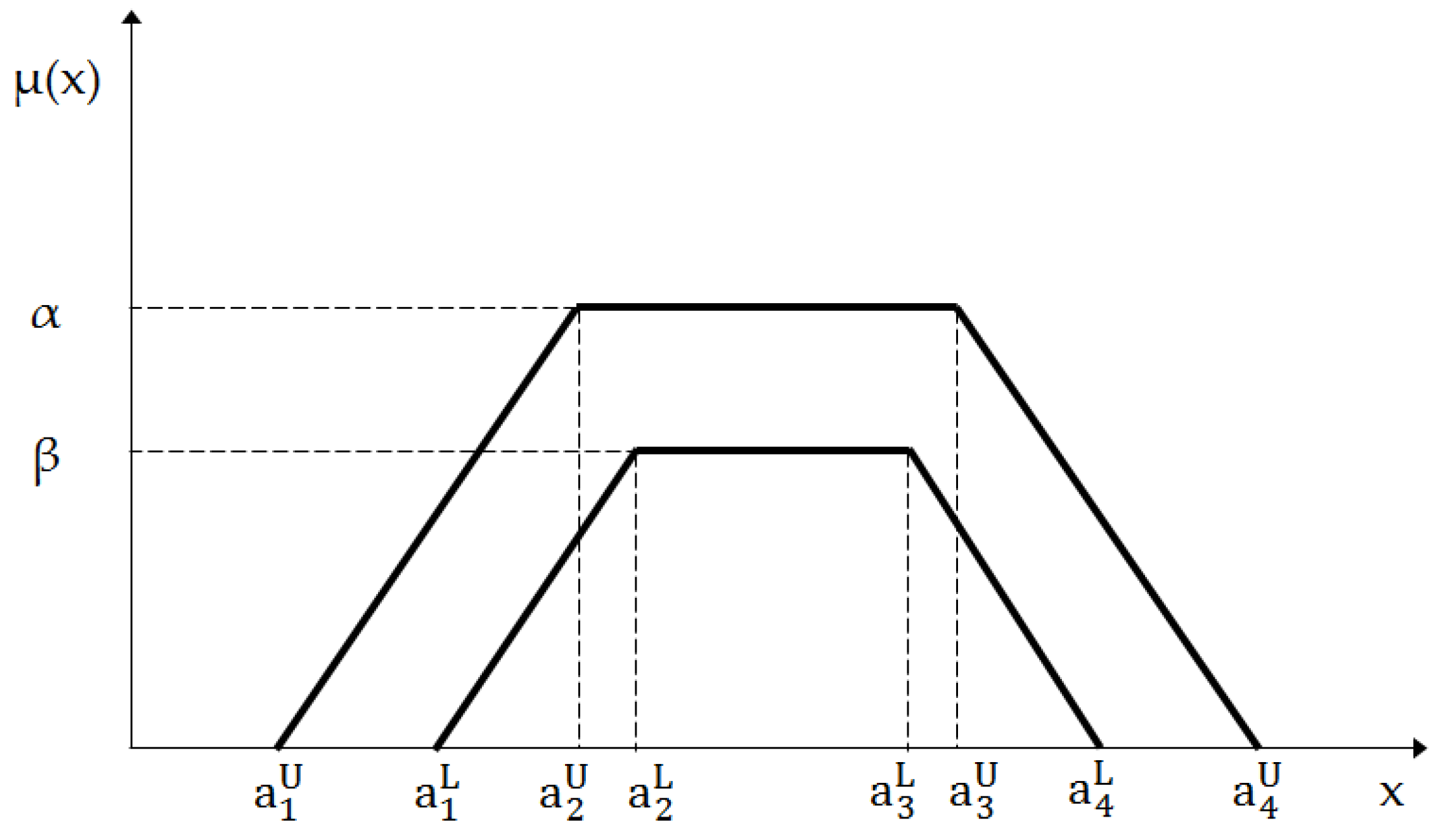
3.1. Preliminaries

In this section, fundamental definitions concerning the fuzzy algebra rules of IT2TrFNs are introduced [22].

Definition 1. 

A type-2 fuzzy set, $\widetilde{\stackrel{~}{A}}$ in the universe of discourse X can be represented by a type-2 membership function ${\mu }_{\widetilde{\stackrel{~}{A}}}$ shown as follows:

$$\widetilde{\stackrel{~}{\mathrm{A}}}=\left\{\left(\mathrm{x},\mathrm{u}\right),{\mathsf{\mu }}_{\widetilde{\stackrel{~}{\mathrm{A}}}}\left(\mathrm{x},\mathrm{u}\right)|\forall \mathrm{x}∊\mathrm{X},\forall \mathrm{u}∊{\mathrm{J}}_{\mathrm{x}}\subseteq \left(\mathrm{0,1}\right),0\le {\mathsf{\mu }}_{\widetilde{\stackrel{~}{\mathrm{A}}}}\left(\mathrm{x},\mathrm{u}\right)\le 1\right\}$$

(1)

Definition 2. 

If X is a set of real numbers, then a type-2 fuzzy set and an interval type-2 fuzzy set in X are called a type-2 fuzzy number and an interval type-2 fuzzy number, respectively.

Definition 3. 

If the upper membership function and lower membership function of  $\widetilde{\stackrel{~}{A}}$ are two trapezoidal type-1 fuzzy numbers, than  $\widetilde{\stackrel{~}{A}}$ is referred to as trapezoidal interval type-2 fuzzy number (IT2TrFNs), $\widetilde{\stackrel{~}{A}}=\left({\tilde{A}}^U,{\tilde{A}}^L\right)$ so that:

$$\widetilde{\stackrel{~}{\mathrm{A}}}=\left({\tilde{\mathrm{A}}}^{\mathrm{U}},{\tilde{\mathrm{A}}}^{\mathrm{L}}\right)=\left(\left({\mathrm{a}}_1^{\mathrm{U}},{\mathrm{a}}_2^{\mathrm{U}},{\mathrm{a}}_3^{\mathrm{U}},a_4^U;\alpha \right),\left({\mathrm{a}}_1^{\mathrm{L}},{\mathrm{a}}_2^{\mathrm{L}},{\mathrm{a}}_3^{\mathrm{L}},a_4^L;\mathsf{\beta }\right)\right)$$

(2)

where the lower and upper bound in the domain are denoted as  ${\mathrm{a}}_1^{\mathrm{U}},{\mathrm{a}}_3^{\mathrm{U}}$ , respectively, and  ${\mathrm{a}}_{1^{\prime }}^{\mathrm{L}},{\mathrm{a}}_3^{\mathrm{L}}$ respectively. The modal values are  ${\mathrm{a}}_2^{\mathrm{U}},$ respectively, and  ${\mathrm{a}}_2^{\mathrm{L}},$ respectively. The values of the membership function are defined as $(\alpha ,\mathsf{\beta })∊\left[\mathrm{0,1}\right]$. A graphical representation of the employed form of IT2TrFNs is given in Figure 2.

Definition 4. 

Let us two IT2TrFNs, $\widetilde{\stackrel{~}{A}}$, and  $\widetilde{\stackrel{~}{B}}$

$$\widetilde{\stackrel{~}{\mathrm{A}}}=\left(\left({\mathrm{a}}_1^{\mathrm{U}},{\mathrm{a}}_2^{\mathrm{U}},{\mathrm{a}}_3^{\mathrm{U}},a_4^U;{\alpha }_1\right),\left({\mathrm{a}}_1^{\mathrm{L}},{\mathrm{a}}_2^{\mathrm{L}},{\mathrm{a}}_3^{\mathrm{L}},a_4^L;{\beta }_1\right)\right)$$

(3)

$$\widetilde{\stackrel{~}{\mathrm{B}}}=\left(\left({\mathrm{b}}_1^{\mathrm{U}},{\mathrm{b}}_2^{\mathrm{U}},{\mathrm{b}}_3^{\mathrm{U}},b_4^U{;\alpha }_2\right),\left({\mathrm{b}}_1^{\mathrm{L}},{\mathrm{b}}_2^{\mathrm{L}},{\mathrm{b}}_3^{\mathrm{L}},b_4^L{;\beta }_2\right)\right)$$

(4)

The arithmetic operations are:

The addition operation, which is denoted as  $\widetilde{\stackrel{~}{\mathrm{A}}}+\widetilde{\stackrel{~}{\mathrm{B}}}$, can be defined as:

$$\widetilde{\stackrel{~}{\mathrm{A}}}+\widetilde{\stackrel{~}{\mathrm{B}}}=\left(\begin{array}{c}\left({\mathrm{a}}_1^{\mathrm{U}}+{\mathrm{b}}_1^{\mathrm{U}},{\mathrm{a}}_2^{\mathrm{U}}+{\mathrm{b}}_2^{\mathrm{U}},{\mathrm{a}}_3^{\mathrm{U}}+{\mathrm{b}}_3^{\mathrm{U}},{\mathrm{a}}_4^{\mathrm{U}}+{\mathrm{b}}_4^{\mathrm{U}};\min \left({\alpha }_1,{\alpha }_2\right),\min \left({\beta }_1,{\beta }_2\right)\right)\\ \left({\mathrm{a}}_1^{\mathrm{L}}+{\mathrm{b}}_1^{\mathrm{L}},{\mathrm{a}}_2^{\mathrm{L}}+{\mathrm{b}}_2^{\mathrm{L}},{\mathrm{a}}_3^{\mathrm{L}}+{\mathrm{b}}_3^{\mathrm{L}},{\mathrm{a}}_4^{\mathrm{L}}+{\mathrm{b}}_4^{\mathrm{L}};\min \left({\alpha }_1,{\alpha }_2\right),\min \left({\beta }_1,{\beta }_2\right)\right)\end{array}\right)$$

(5)

The subtraction operation, which is denoted as  $\widetilde{\stackrel{~}{\mathrm{A}}}-\widetilde{\stackrel{~}{\mathrm{B}}}$, can be defined as:

$$\widetilde{\stackrel{~}{\mathrm{A}}}-\widetilde{\stackrel{~}{\mathrm{B}}}=\left(\begin{array}{c}\left({\mathrm{a}}_1^{\mathrm{U}}-{\mathrm{b}}_4^{\mathrm{U}},{\mathrm{a}}_2^{\mathrm{U}}-{\mathrm{b}}_3^{\mathrm{U}},{\mathrm{a}}_3^{\mathrm{U}}-{\mathrm{b}}_2^{\mathrm{U}},{\mathrm{a}}_4^{\mathrm{U}}-{\mathrm{b}}_1^{\mathrm{U}};\min \left({\alpha }_1,{\alpha }_2\right),\min \left({\beta }_1,{\beta }_2\right)\right)\\ \left({\mathrm{a}}_1^{\mathrm{L}}-{\mathrm{b}}_4^{\mathrm{L}},{\mathrm{a}}_2^{\mathrm{L}}-{\mathrm{b}}_3^{\mathrm{L}},{\mathrm{a}}_3^{\mathrm{L}}-{\mathrm{b}}_2^{\mathrm{L}},{\mathrm{a}}_4^{\mathrm{L}}-{\mathrm{b}}_1^{\mathrm{L}};\min \left({\alpha }_1,{\alpha }_2\right),\min \left({\beta }_1,{\beta }_2\right)\right)\end{array}\right)$$

(6)

The multiplication operation, which is denoted as  $\widetilde{\stackrel{~}{\mathrm{A}}}·\widetilde{\stackrel{~}{\mathrm{B}}}$, can be defined as:

$$\widetilde{\stackrel{~}{\mathrm{A}}}·\widetilde{\stackrel{~}{\mathrm{B}}}=\left(\begin{array}{c}\left({\mathrm{a}}_1^{\mathrm{U}}·{\mathrm{b}}_1^{\mathrm{U}},{\mathrm{a}}_2^{\mathrm{U}}·{\mathrm{b}}_2^{\mathrm{U}},{\mathrm{a}}_3^{\mathrm{U}}·{\mathrm{b}}_3^{\mathrm{U}},{\mathrm{a}}_4^{\mathrm{U}}·{\mathrm{b}}_4^{\mathrm{U}};\min \left({\alpha }_1,{\alpha }_2\right),\min \left({\beta }_1,{\beta }_2\right)\right)\\ \left({\mathrm{a}}_1^{\mathrm{L}}·{\mathrm{b}}_1^{\mathrm{L}},{\mathrm{a}}_2^{\mathrm{L}}·{\mathrm{b}}_2^{\mathrm{L}},{\mathrm{a}}_3^{\mathrm{L}}·{\mathrm{b}}_3^{\mathrm{L}},{\mathrm{a}}_4^{\mathrm{L}}·{\mathrm{b}}_4^{\mathrm{L}};\min \left({\alpha }_1,{\alpha }_2\right),\min \left({\beta }_1,{\beta }_2\right)\right)\end{array}\right)$$

(7)

The division operation, which is denoted as $\widetilde{\stackrel{~}{\mathrm{A}}}:\widetilde{\stackrel{~}{\mathrm{B}}}$, can be defined as:

$$\widetilde{\stackrel{~}{\mathrm{A}}}:\widetilde{\stackrel{~}{\mathrm{B}}}=\left(\begin{array}{c}\left({\mathrm{a}}_1^{\mathrm{U}}:{\mathrm{b}}_4^{\mathrm{U}},{\mathrm{a}}_2^{\mathrm{U}}:{\mathrm{b}}_3^{\mathrm{U}},{\mathrm{a}}_3^{\mathrm{U}}:{\mathrm{b}}_2^{\mathrm{U}},{\mathrm{a}}_4^{\mathrm{U}}:{\mathrm{b}}_1^{\mathrm{U}};\min \left({\alpha }_1,{\alpha }_2\right),\min \left({\beta }_1,{\beta }_2\right)\right)\\ \left({\mathrm{a}}_1^{\mathrm{L}}:{\mathrm{b}}_4^{\mathrm{L}},{\mathrm{a}}_2^{\mathrm{L}}:{\mathrm{b}}_3^{\mathrm{L}},{\mathrm{a}}_3^{\mathrm{L}}:{\mathrm{b}}_2^{\mathrm{L}},{\mathrm{a}}_4^{\mathrm{L}}:{\mathrm{b}}_1^{\mathrm{L}};\min \left({\alpha }_1,{\alpha }_2\right),\min \left({\beta }_1,{\beta }_2\right)\right)\end{array}\right)$$

(8)

Definition 5. 

Let us discuss the triangular interval type-2 fuzzy number,  $\widetilde{\stackrel{~}{A}}$, and crisp value k:

$$\mathrm{k}·\widetilde{\stackrel{~}{\mathrm{A}}}=\widetilde{\stackrel{~}{\mathrm{A}}}=\left(\left(k·{\mathrm{a}}_1^{\mathrm{U}},{\mathrm{k}·\mathrm{a}}_2^{\mathrm{U}},{\mathrm{k}·\mathrm{a}}_3^{\mathrm{U}},{k·}_4^U;{\alpha }_1\right),\left({\mathrm{k}·\mathrm{a}}_1^{\mathrm{L}},{\mathrm{k}·\mathrm{a}}_2^{\mathrm{L}},{\mathrm{k}·\mathrm{a}}_3^{\mathrm{L}},{k·a}_4^L;{\beta }_1\right)\right)$$

(9)

$${\left(\widetilde{\stackrel{~}{\mathrm{A}}}\right)}^{-1}=\left(\left({\displaystyle \frac{1}{a_4^U}},{\displaystyle \frac{1}{a_3^U}},{\displaystyle \frac{1}{a_2^U}},{\displaystyle \frac{1}{a_1^U}};{\alpha }_1\right),\left({\displaystyle \frac{1}{a_4^L}},{\displaystyle \frac{1}{a_3^L}},{\displaystyle \frac{1}{a_2^L}},{\displaystyle \frac{1}{a_1^L}};{\beta }_1\right)\right)$$

(10)

Definition 6. 

The defuzzified trapezoidal interval type-2 fuzzy numbers approach (DTriT) is proposed [52]:

$$\begin{gathered} DTraT= \\ \begin{array}{c}{\displaystyle \frac{1}{2}}\{{\displaystyle \frac{\left({\mathrm{a}}_4^{\mathrm{U}}-{\mathrm{a}}_1^{\mathrm{U}}\right)+\left({\alpha }_1·a_2^U-{\mathrm{a}}_1^{\mathrm{U}}\right)+\left({\alpha }_1·a_3^U-{\mathrm{a}}_1^{\mathrm{U}}\right)}{4}}+{\mathrm{a}}_1^{\mathrm{U}}+\\ {\displaystyle \frac{\left({\mathrm{a}}_4^{\mathrm{L}}-{\mathrm{a}}_1^{\mathrm{L}}\right)+\left({\beta }_1·a_2^L-{\mathrm{a}}_1^{\mathrm{L}}\right)+\left({\beta }_1·a_3^L-{\mathrm{a}}_1^{\mathrm{L}}\right)}{4}}+{\mathrm{a}}_1^{\mathrm{L}}\}\end{array} \end{gathered}$$

(11)

Definition 7. 

The distance between two IT2TrFNs, $\widetilde{\stackrel{~}{A}}$ and  $\widetilde{\stackrel{~}{B}}$, can be adapted using the vertex method as follows [10]:

$$\begin{gathered} d_V\left(\widetilde{\stackrel{~}{A}},\widetilde{\stackrel{~}{B}}\right)= \\ \begin{array}{c}\{{{\displaystyle \frac{1}{8}}}^{[{\left(a_1^U-b_1^U\right)}^2+{\left(a_2^U-b_2^U\right)}^2+{\left(a_3^U-b_3^U\right)}^2+{\left(a_4^U-b_4^U\right)}^2+{\left(a_1^L-b_1^L\right)}^2}\\ +{\left(a_2^L-b_2^L\right)}^2+{\left(a_3^L-b_3^L\right)}^2+{\left(a_4^l-b_4^l\right)}^2+{\left({\alpha }_1-{\beta }_1\right)}^2\\ +{\left({\alpha }_2-{\beta }_2\right)}^2]{\}}^{{\displaystyle \frac{1}{2}}}\end{array} \end{gathered}$$

(12)

3.2. Defining the Set of Decision-Makers

The assessment of the relative importance of the attributes used to evaluate the considered cloud platforms, as well as the values of qualitative attributes, was conducted by multiple decision-makers. These decision-makers are formally represented by a set of indices $\left\{1,\dots ,e,\dots ,E\right\}$. The total number of decision-makers is denoted as E, and the index of a decision-maker is represented as e, where $e,e=1,\dots ,E$.

In this study, the decision-makers are the product owner $(e=1)$, the operations manager $(e=2)$, and the product development engineer $(e=3)$.

3.3. Defining the Set of Alternatives

In the general case, decision-makers may use different cloud platforms. The set of platforms is represented by the index set $\left\{1,\dots ,i,\dots ,I\right\}$. The total number of platforms is denoted as I, and the index of a platform is represented as i, where $i,i=1,\dots ,I$.

In this study, the following platforms are considered: AWS $(i=1)$, AZURE $(i=2)$, Google Cloud $(i=3)$, and Oracle $(i=4)$.

3.4. Defining the Set of Attributes

Each alternative can be evaluated based on multiple attributes. The set of attributes is represented by the index set $\{1,\dots ,k,\dots ,K\}$. The total number of attributes is denoted as $K$, and the index of an attribute is represented as $k$, where $k=1,\dots ,K$.

Determining the set of attributes for evaluating cloud platforms can be considered a problem in itself. In the considered research, the selection of attributes is determined by decision-makers based on their experience as well as the experiences of other companies from the IT sector. The selected attributes are:

• Performance and latency (the time period between sending a request for data retrieval and the moment when the data becomes available to a user or system) $(\mathrm{k}=1)$. This attribute depends on the server location;
• Unit price, measured per gigabyte on a monthly basis $(\mathrm{k}=2)$;
• Security measures (data encryption, authentication, protection against attacks) $(\mathrm{k}=3)$;
• Additional services (databases, analytics) $(\mathrm{k}=4)$;
• Management and monitoring costs $(\mathrm{k}=5)$;
• Scalability $(\mathrm{k}=6)$;
• Trust and platform reputation $(\mathrm{k}=7)$.

3.5. Defining a Set of Linguistic Variables for Describing Uncertain Data

In this study, the uncertain data, such as the relative importance of attributes and their values, can be adequately assessed by using a seven-point scale. Determining the weight vectors of attributes should be stated as a fuzzy group decision-making problem. These pre-defined linguistic expressions are modeled by IT2TrFNs:

• Very low importance/values (L1): $\left(\left(1,2,3,4;1\right),\left(1.5,2,3,3.5;0.9\right)\right)$
• Low importance/values (L2): $\left(\left(1.5,3,4,5.5;1\right),\left(2,3,4,5;0.9\right)\right)$
• Fairly medium-low importance/values (L3): $\left(\left(2.5,4,5,6.5;1\right),\left(3,4,5,6;0.9\right)\right)$
• Medium importance/values (L4): $\left(\left(3.5,5,6,7.5;1\right),\left(4,5,6,7;0.9\right)\right)$
• Fairly medium-low importance/values (L5): $\left(\left(4.5,6,7,8.5;1\right),\left(5,6,7,8;0.9\right)\right)$
• High importance/values (L6): $\left(\left(5.5,7,8,9.5;1\right),\left(6,7,8,9;0.9\right)\right)$
• Very high importance/values (L7): $\left(\left(7,8,9,10;1\right),\left(7.5,8,9,9.5;0.9\right)\right)$

The domain values of the IT2TrFNs are defined within the interval [1,2,3,4,5,6,7,8,9,10]. A value of 1 indicates that the relative importance of attributes, as well as their values, have an almost negligible influence, while a value of 10 denotes a significantly strong influence in the evaluation of cloud platforms.

3.6. Determining the Weight Vectors

In this study, the determination of the relative importance of attributes for cloud platform evaluation is formulated as a fuzzy group decision-making problem. It is assumed that the DMs have equal importance in assessing the relative importance of attributes. A graphical representation of the procedure for determining fuzzy weight vectors is shown in Figure 3.

The procedure for determining the fuzzy weight vectors is presented as follows:

Step 1. Each DM evaluates the relative importance of attribute $k,k=1,\dots ,K$ using one of the pre-defined linguistic expressions, ${\widetilde{\stackrel{~}{W}}}_k^e$.

Step 2. The aggregation of DMs’ assessments into a single evaluation at the level of each attribute, ${\widetilde{\stackrel{~}{W}}}_k$ is obtained by applying the fuzzy harmonic mean operator, so that:

$${\widetilde{\stackrel{~}{W}}}_k={\displaystyle \frac{E}{{\sum }_{e=1,\dots ,E}\left(\frac{1}{{\widetilde{\stackrel{~}{W}}}_k^e}\right)}}$$

(13)

Step 3. The normalized fuzzy weight vectors are given by applying a linear normalization procedure [55] combined with interval type-2 fuzzy algebra rules [22]:

$${\left[{\widetilde{\stackrel{~}{\omega }}}_k\right]}_{1xK}$$

(14)

where

$${\widetilde{\stackrel{~}{\omega }}}_k={\displaystyle \frac{{\widetilde{\stackrel{~}{W}}}_k}{{\sum }_{k=1,\dots ,K}{\widetilde{\stackrel{~}{W}}}_k}}$$

(15)

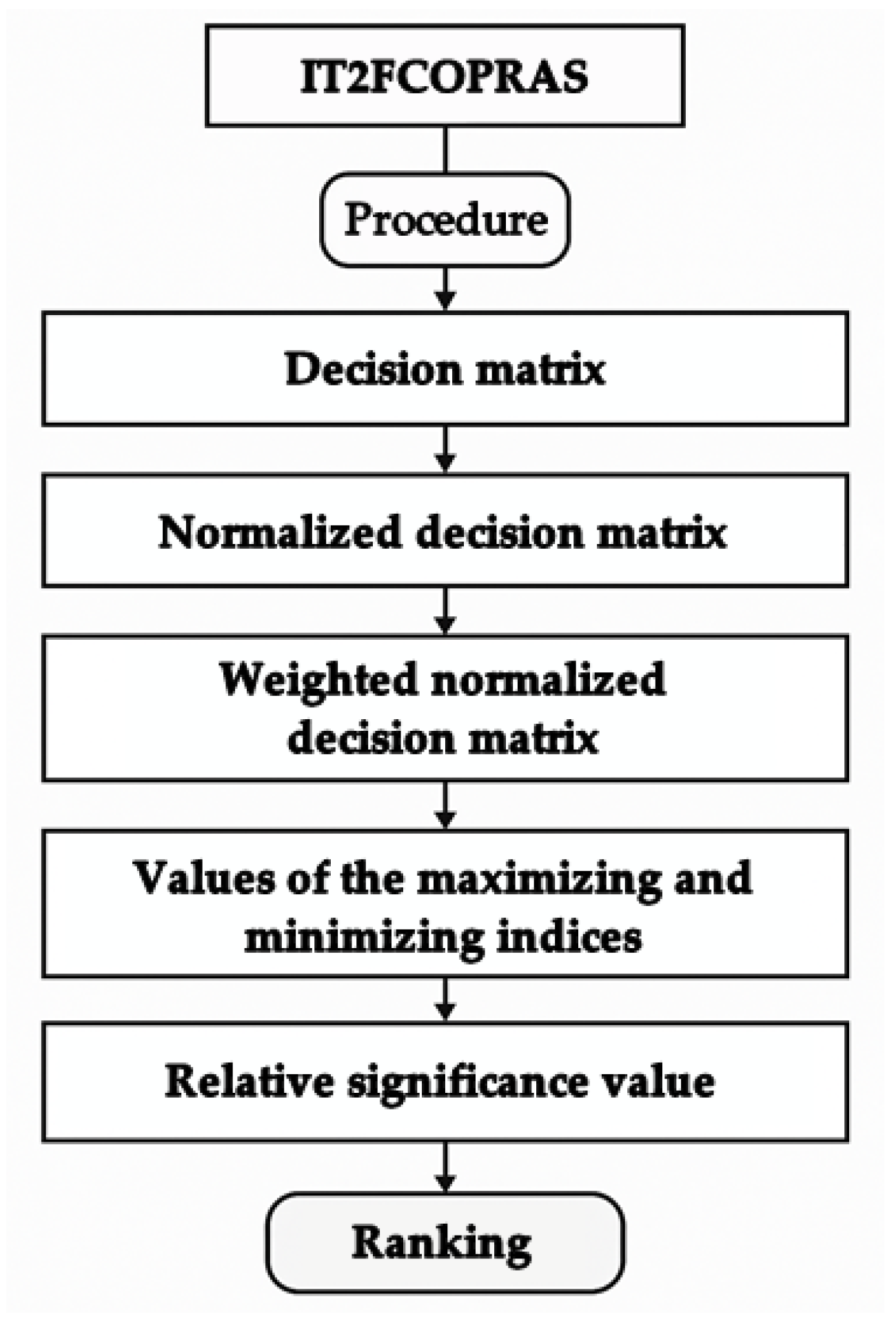
3.7. Determining the Rank of Cloud Platforms Using IT2FCOPRAS

Figure 4 presents the algorithm of the IT2FCOPRAS application, followed by a detailed explanation of the steps of the proposed model.

The algorithm of the proposed IT2FCOPRAS method is implemented through the following steps:

Step 1. Define the decision matrix:

$${\left[{\widetilde{\stackrel{~}{x}}}_{ik}\right]}_{IxK}$$

(16)

Step 2. The normalized decision matrix is obtained by applying the linear normalization procedure [55] combined with interval type-2 fuzzy algebra rules [22]:

$${\left[{\widetilde{\stackrel{~}{r}}}_{ik}\right]}_{IxK}$$

(17)

where

$${\widetilde{\stackrel{~}{r}}}_{ik}={\displaystyle \frac{{\widetilde{\stackrel{~}{x}}}_{ik}}{{\sum }_{i=1,\dots ,I}{\widetilde{\stackrel{~}{x}}}_{ik}}}$$

(18)

Step 3. Construct the weighted normalized decision matrix using the product procedure:

$${\left[{\widetilde{\stackrel{~}{z}}}_{ik}\right]}_{IxK}$$

(19)

where

$${\widetilde{\stackrel{~}{z}}}_{ik}={\widetilde{\stackrel{~}{\omega }}}_k·{\widetilde{\stackrel{~}{r}}}_{ik}$$

(20)

Step 4. Determine the values of the maximizing and minimizing indices:

$${\widetilde{\stackrel{~}{S}}}_i=\sum _{k\in \mathcal{B}}{\widetilde{\stackrel{~}{z}}}_{ik}$$

(21)

$${\widetilde{\stackrel{~}{R}}}_i=\sum _{k\in \mathcal{C}}{\widetilde{\stackrel{~}{z}}}_{ik}$$

(22)

Step 5. Determine the relative significance value:

$${\widetilde{\stackrel{~}{\zeta }}}_i={\widetilde{\stackrel{~}{S}}}_i+{\displaystyle \frac{{\widetilde{\stackrel{~}{R}}}^{min}·{\sum }_{k=1,\dots ,K}{\widetilde{\stackrel{~}{R}}}_i}{{\widetilde{\stackrel{~}{R}}}_i·{\sum }_{i=1,\dots ,I}\frac{1}{{\widetilde{\stackrel{~}{R}}}_i}}}$$

(23)

Step 6. The representative scalars of IT2TFNs ${\widetilde{\stackrel{~}{\zeta }}}_i$, ${\zeta }_i$, are obtained using the procedure described in [52].

Step 7. Sort the crisp values of the relative significance value in non-decreasing order. The cloud technology with the highest relative significance value is ranked first, while the one with the lowest value is ranked last.

3.8. Determining the Rank of Cloud Platforms Using IT2FEDAS

Figure 5 presents the algorithm of the IT2FEDAS application, followed by a detailed explanation of the steps of the proposed model.

The algorithm of the proposed FEDAS method is implemented through the following steps:

Step 1. Define the decision matrix:

$${\left[{\widetilde{\stackrel{~}{x}}}_{ik}\right]}_{IxK}$$

(24)

Step 2. The normalized decision matrix is obtained by applying the linear normalization procedure [55] combined with interval type-2 fuzzy algebra rules [22]:

$${\left[{\widetilde{\stackrel{~}{r}}}_{ik}\right]}_{IxK}$$

(25)

where

$${\widetilde{\stackrel{~}{r}}}_{ik}={\displaystyle \frac{{\widetilde{\stackrel{~}{x}}}_{ik}}{{\sum }_{i=1,\dots ,I}{\widetilde{\stackrel{~}{x}}}_{ik}}}$$

(26)

Step 3. Construct the weighted normalized decision matrix using the product procedure [56]:

$${\left[{\widetilde{\stackrel{~}{z}}}_{ik}\right]}_{IxK}$$

(27)

where

$${\widetilde{\stackrel{~}{z}}}_{ik}={\omega }_k·{\widetilde{\stackrel{~}{r}}}_{ik}$$

(28)

Step 4. Determine the positive distances from the mean values using the procedure proposed in conventional EDAS combined with fuzzy algebra rules [22]:

• benefit type

$${\widetilde{\stackrel{~}{PD}}}_{ik}=\begin{array}{ccc}{\displaystyle \frac{max\left(0,d\left({\widetilde{\stackrel{~}{z}}}_{ik},{\widetilde{\stackrel{~}{A}}}_k\right)\right)}{{\widetilde{\stackrel{~}{A}}}_k}}& if& {\widetilde{\stackrel{~}{z}}}_{ik}>{\widetilde{\stackrel{~}{A}}}_k\end{array}$$

(29)

• cost type

$${\widetilde{\stackrel{~}{PD}}}_{ik}=\begin{array}{ccc}{\displaystyle \frac{max\left(0,d\left({\widetilde{\stackrel{~}{A}}}_k,{\widetilde{\stackrel{~}{z}}}_{ik}\right)\right)}{{\widetilde{\stackrel{~}{A}}}_k}}& if& {\widetilde{\stackrel{~}{A}}}_k>{\widetilde{\stackrel{~}{z}}}_{ik}\end{array}$$

(30)

where

$${\widetilde{\stackrel{~}{A}}}_k={\displaystyle \frac{1}{I}}·{\sum }_{i=1,\dots ,I}{\widetilde{\stackrel{~}{z}}}_{ik}$$

(31)

Step 5. Determine the negative distances from the mean values using the procedure proposed in conventional EDAS combined with fuzzy algebra rules [22]:

• benefit type

$${\widetilde{\stackrel{~}{ND}}}_{ik}=\begin{array}{ccc}{\displaystyle \frac{max\left(0,d\left({\widetilde{\stackrel{~}{A}}}_k,{\widetilde{\stackrel{~}{z}}}_{ik}\right)\right)}{{\widetilde{\stackrel{~}{A}}}_k}}& if& {\widetilde{\stackrel{~}{A}}}_k>{\widetilde{\stackrel{~}{z}}}_{ik}\end{array}$$

(32)

• cost type

$${\widetilde{\stackrel{~}{ND}}}_{ik}=\begin{array}{ccc}{\displaystyle \frac{max\left(0,d\left({\widetilde{\stackrel{~}{z}}}_{ik},{\widetilde{\stackrel{~}{A}}}_k\right)\right)}{{\widetilde{\stackrel{~}{A}}}_k}}& if& {\widetilde{\stackrel{~}{z}}}_{ik}>{\widetilde{\stackrel{~}{A}}}_k\end{array}$$

(33)

Step 6. Determine the fuzzy positive and fuzzy negative distances:

$${\widetilde{\stackrel{~}{S}}}_i={\sum }_{k=1,\dots ,K}{\widetilde{\stackrel{~}{PD}}}_{ik}$$

(34)

$${\widetilde{\stackrel{~}{N}}}_i={\sum }_{k=1,\dots ,K}{\widetilde{\stackrel{~}{ND}}}_{ik}$$

(35)

Step 7. Determine the normalized fuzzy positive distance, ${\widetilde{\stackrel{~}{s}}}_i$ and the normalized fuzzy negative distance,${\widetilde{\stackrel{~}{n}}}_i$:

$${\widetilde{\stackrel{~}{s}}}_i=\left(\left({\displaystyle \frac{a_{1i}^U}{u^{*}}},{\displaystyle \frac{a_{2i}^U}{u^{*}}},{\displaystyle \frac{a_{3i}^U}{u^{*}}},{\displaystyle \frac{a_{4i}^U}{u^{*}}};\alpha \right),\left({\displaystyle \frac{a_{1i}^L}{u^{*}}},{\displaystyle \frac{a_{2i}^L}{u^{*}}},{\displaystyle \frac{a_{3i}^L}{u^{*}}},{\displaystyle \frac{a_{4i}^L}{u^{*}}};\beta \right)\right)$$

(36)

$${\widetilde{\stackrel{~}{n}}}_i=\left(\left({\displaystyle \frac{a^{*}}{a_{4i}^U}},{\displaystyle \frac{a^{*}}{a_{3i}^U}},{\displaystyle \frac{a^{*}}{a_{2i}^U}},{\displaystyle \frac{a^{*}}{a_{1i}^U}};\alpha \right),\left({\displaystyle \frac{a^{*}}{a_{4i}^L}},{\displaystyle \frac{a^{*}}{a_{3i}^L}},{\displaystyle \frac{a^{*}}{a_{2i}^L}},{\displaystyle \frac{a^{*}}{a_{1i}^L}};\beta \right)\right)$$

(37)

Step 8. Determine the appraisal score, ${\widetilde{\stackrel{~}{\zeta }}}_i$:

$${\widetilde{\stackrel{~}{\zeta }}}_i={\displaystyle \frac{1}{2}}·\left({\widetilde{\stackrel{~}{s}}}_i+{\widetilde{\stackrel{~}{n}}}_i\right)$$

(38)

Step 9. The representative scalars of IT2TFNs ${\widetilde{\stackrel{~}{\zeta }}}_i$, ${\zeta }_i$, are obtained using the procedure described in [52].

Step 10. Sort the crisp appraisal score values in non-decreasing order. The cloud technology with the highest EDAS index value is ranked first, while the one with the lowest value is ranked last.

3.9. Determining the Similarity Ranking Coefficient

The procedure for determining the similarity coefficient of the obtained ranking results, WS, was proposed in [41,42]. This coefficient is determined using the following expression:

$$WS=1-\sum _{i=1}^I{2}^{-R_{x_1}}·{\displaystyle \frac{\left|R_{x_1}-R_{x_2}\right|}{max\left\{\left|1-R_{x_1}\right|,\left|I-R_{x_1}\right|\right\}}}$$

(39)

where $I$ is the total number of alternatives; and $R_{x_1}$ and $R_{x_2}$ are the ranking positions for alternative $i,i=1,\dots ,I$.

The ranking similarity is determined based on the rules defined by [41,42]. According to these authors, if the coefficient value is below 0.234, it can be assumed that no ranking similarity exists. When the coefficient falls within the range [0.353–0.689], there is some similarity, but the correlation is not particularly strong. A coefficient value exceeding 0.808 indicates an absolute ranking similarity. Intermediate values represent transitions between low and moderate similarity, as well as between moderate and high similarity, forming a fuzzy boundary.

4. Case Study

The proposed model was tested on real data acquired from an IT company with a flat organizational structure. This style of organization has the following advantages: (1) employees have greater responsibility, (2) employees actively participate in decision-making, (3) management maintains a transparent working environment, (4) communication is more efficient and streamlined, and so on.

One of the most important factors in the effective operation of web applications in such a corporate environment is the selection of an appropriate cloud platform. An inadequate choice can result in the following issues:

• Excessive costs due to inefficient pricing or resource allocation.
• Limited scalability due to inflexibility or difficulty upgrading to larger resource capacity.
• Integration challenges due to platform incompatibility with existing applications and data processing processes.
• Insufficient data security might jeopardize safety and compliance with regulatory norms.
• Inefficient infrastructure management results in higher operational expenses and lost time.
• Insufficient data centers or geographical distance can lead to poor performance and negatively impact user experience.

The relative importance of the identified attributes was determined using an interview-based process that included assessments from the DMs (product owner, operations manager, and product development engineer). The DMs provided their assessments of attribute importance individually, and these evaluations were later aggregated using the proposed methodology. On the other hand, the evaluation of the considered cloud platforms with respect to each attribute was conducted through a 30-minute panel discussion, with the final conclusions reached by consensus. This approach was selected since not all decision-makers were familiar with every considered attribute. In this way, constructive discussion enabled the most objective possible assessments.

4.1. Determination of the Weight Vectors

The evaluations of each decision-maker, along with their aggregated and normalized values, are presented in

Table 1. The assessment of the relative importance of the considered attributes and their weights.

	$\mathit{e}=1$	$\mathit{e}=2$	$\mathit{e}=3$	The Normalized Weight Vectors
$k=1$	L6	L5	L6	${\widetilde{\stackrel{~}{\omega }}}_1=\left(\left(\mathrm{0.105,0.168,0.247,0.401};1\right),\left(\mathrm{0.142,0.168,0.247,0.330};0.9\right)\right)$
$k=2$	L2	L1	L3	${\widetilde{\stackrel{~}{\omega }}}_2=\left(\left(\mathrm{0.030,0.070,0.124,0.225};1\right),\left(\mathrm{0.050,0.070,0.124,0.175};0.9\right)\right)$
$k=3$	L7	L7	L7	${\widetilde{\stackrel{~}{\omega }}}_3=\left(\left(\mathrm{0.144,0.203,0.292,0.439};1\right),\left(\mathrm{0.189,0.203,0.292,0.381};0.9\right)\right)$
$k=4$	L4	L4	L5	${\widetilde{\stackrel{~}{\omega }}}_4=\left(\left(\mathrm{0.078,0.103,0.204,0.342};1\right),\left(\mathrm{0.102,0.103,0.204,0.278};0.9\right)\right)$
$k=5$	L1	L1	L2	${\widetilde{\stackrel{~}{\omega }}}_5=\left(\left(\mathrm{0.023,0.057,0.106,0.193};1\right),\left(\mathrm{0.041,0.057,0.106,0.148};0.9\right)\right)$
$k=6$	L3	L3	L3	${\widetilde{\stackrel{~}{\omega }}}_6=\left(\left(\mathrm{0.052,0.102,0.162,0.286};1\right),\left(\mathrm{0.076,0.102,0.162,0.229};0.9\right)\right)$
$k=7$	L4	L3	L1	${\widetilde{\stackrel{~}{\omega }}}_7=\left(\left(\mathrm{0.037,0.080,0.139,0.246};1\right),\left(\mathrm{0.060,0.080,0.139,0.192};0.9\right)\right)$

.

4.2. An Application of the Proposed IT2FCOPRAS

The evaluated attribute values are presented in

Table 2. Decision matrix.

	$\mathit{k}=1$	$\mathit{k}=2$	$\mathit{k}=3$	$\mathit{k}=4$	$\mathit{k}=5$	$\mathit{k}=6$	$\mathit{k}=7$
$i=1$	L3	0.023	L6	L5	L3	L6	L7
$i=2$	L3	0.018	L4	L3	L1	L3	L6
$i=3$	L4	0.020	L4	L2	L5	L3	L5
$i=4$	L6	0.025	L5	L5	L7	L4	L2

(Step 1).

By applying Step 3 of the proposed algorithm, the weighted normalized fuzzy decision matrix is obtained. Also, by applying Step 4 of the proposed algorithm, the values of the maximizing and minimizing indices are calculated. The values of the representative scalars of IT2TFNs ${\widetilde{\stackrel{~}{\zeta }}}_i$, ${\zeta }_i$ and the ranking of alternatives are calculated according to Steps 5 to 7 of the proposed algorithm (

Table 3. The ranking of cloud platforms using IT2FCOPRAS.

	${\widetilde{\stackrel{~}{\mathit{\zeta }}}}_{\mathit{i}}$	${\mathit{\zeta }}_{\mathit{i}}$	Rank
$i=1$	$\left(\left(\mathrm{0.056,0.166,0.602,7.533};1\right),\left(\mathrm{0.131,0.166,0.602,2.145};0.9\right)\right)$	1.416	2
$i=2$	$\left(\left(\mathrm{0.070,0.132,0.592,8.624};1\right),\left(\mathrm{0.106,0.132,0.592,2.310};0.9\right)\right)$	1.561	1
$i=3$	$\left(\left(\mathrm{0.065,0.114,0.478,6.150};1\right),\left(\mathrm{0.088,0.132,0.592,1.702};0.9\right)\right)$	1.156	3
$i=4$	$\left(\left(\mathrm{0.041,0.124,0.441,4.464};1\right),\left(\mathrm{0.068,0.124,0.441,1.366};0.9\right)\right)$	0.876	4

).

4.3. An Application of the Proposed IT2FEDAS

The first three steps of the proposed IT2FEDAS algorithm are identical to those of IT2FCOPRAS. By applying the proposed IT2FEDAS approach (step 4 to step 10 of the proposed algorithm), the ranking of alternatives was determined (

Table 4. The ranking of cloud platforms using IT2FEDAS.

	${\widetilde{\stackrel{~}{\mathit{\zeta }}}}_{\mathit{i}}$	${\mathit{\zeta }}_{\mathit{i}}$	Rank
$i=1$	$\left(\left(\mathrm{0.085,0.230,0.436,1};1\right),\left(\mathrm{0.150,0.230,0.436,0.683};0.9\right)\right)$	0.398	1
$i=2$	$\left(\left(\mathrm{0.024,0.065,0.158,0.543};1\right),\left(\mathrm{0.037,0.065,0.158,0.301};0.9\right)\right)$	0.166	2
$i=3$	$\left(\left(\mathrm{0.004,0.010,0.025,0.503};1\right),\left(\mathrm{0.006,0.010,0.025,0.045};0.9\right)\right)$	0.088	3
$i=4$	$\left(\left(\mathrm{0.006,0.020,0.051,0.124};1\right),\left(\mathrm{0.010,0.020,0.051,0.081};0.9\right)\right)$	0.044	4

).

Based on the obtained ranking, the company’s management should select the cloud platform that best supports the business operations of the enterprise. By applying IT2FCOPRAS, the top-ranked cloud platform is AZURE $(i=2)$, which can be considered the most suitable for the evaluated company. On the other hand, the ranking obtained using IT2FEDAS places AWS $(i=1)$ in the first position. Given the obtained ranking similarity coefficient of 0.708, it can be concluded that the correlation is quite strong. Based on these results, management can choose one of these two cloud platforms based on subjective assessment or conduct a more detailed analysis of these two platforms before making a final decision. In both proposed methods, Oracle $(i=4)$ ranked last. This cloud platform can be considered unsuitable for the evaluated type of IT company.

5. Conclusions

The selection of a cloud platform is one of the key challenges in operational management for companies operating in the information technology sector. Solving this issue directly contributes to meeting customer needs, which is one of the most important business objectives of the organization in question. The problem is formulated as a multi-attribute optimization task. In the first phase, the assessment of the relative importance of the attributes used to evaluate the identified cloud platforms is stated as a fuzzy group decision-making problem. The determination of the fuzzy weight vector of attributes is based on the application of the fuzzy harmonic mean.

In the second phase, the ranking of the identified cloud platforms is obtained by applying two proposed multi-attribute decision-making methods with IT2TrFNs: IT2FCOPRAS and IT2FEDAS. The similarity of the obtained results is determined. Based on the obtained ranking of cloud platforms, the operational management can make a decision on which cloud platform to select, aiming to enhance customer satisfaction while simultaneously reducing business costs.

The main contributions of this paper are: (1) the selection of a cloud platform for enterprises operating in the information technology sector–web applications, (2) the selection of attributes for cloud platform evaluation is based on the best IT practices in the IT sector, (3) the problem of determining weight vectors is formulated as a fuzzy group decision-making problem, (4) aggregation of assessments from decision-makers is conducted using the fuzzy harmonic mean, (5) the ranking of cloud platforms is determined precisely by applying the proposed IT2FCOPRAS and IT2FEDAS methods, and (6) the similarity of the obtained results is calculated.

When comparing the proposed model with those previously suggested in the literature for solving similar problems, it becomes evident that the proposed model adopts a more advanced approach for representing uncertain values. Furthermore, unlike prior studies that apply a single MADM method for cloud platform selection, this study employs two different methods. The results indicate that the two methods may produce different rankings of the alternatives, which supports the application of multiple parallel approaches. In addition, the attributes used for evaluating cloud platforms in this study were defined in collaboration with experts from the considered company, rather than being based solely on data from the literature. This ensures the practical relevance of the proposed model.

Although the proposed model offers clear scientific contributions and certain advantages over existing approaches in the literature, it is important to highlight several key limitations: (1) dependence on the experience, knowledge, and subjectivity of decision-makers; (2) a limited number of alternatives, which means the model cannot be easily applied in another company without prior adaptation; (3) the model is relatively complex for practitioners and may be difficult to apply without specialized software or the assistance of an expert in the field; and (4) the model relies on static input values.

The developed methodology is sufficiently flexible, allowing for easy incorporation of changes in the number and values of attributes, as well as modifications to their weights. Future research should focus on developing user-friendly software based on the proposed methodology.