Abstract
In this paper, we introduce a new distribution for modeling bimodal data supported on non-negative real numbers and particularly suited with an excess of very small values. This family of distributions is derived by multiplying the exponential distribution by a fourth-degree polynomial, resulting in a model that better fits the shape of the second mode of the empirical distribution of the data. We study the general density of this new family of distributions, along with its properties, moments, and skewness and kurtosis coefficients. A simulation study is performed to estimate parameters by the maximum likelihood method. Additionally, we present two applications to real-world datasets, demonstrating that the new distribution provides a better fit than the bimodal exponential distribution.
MSC:
62E15; 62F10; 62P99
1. Introduction
Weighted distributions frequently occur in research related to survival analysis, analysis of intervention data, ecology and biomedicine, and other areas. Fisher [1] and Rao [2] introduced the concept of weighted distributions to improve the fit of appropriate statistical models; this idea has been used to select an appropriate model for the data observed (see Rao [3]). A random variable Y follows the weighted distribution if its probability density function (pdf) is given by
where f is a density function, and w is a positive function. Analysis and applications using this methodology can be found in Patil and Ord [4], Patil and Rao [5], Gupta and Kirmani [6], Gupta and Tripathi [7], Gupta and Akman [8], Gupta and Kundu [9], Reyes et al. [10], Hassan and Hijazi [11], Gómez-Déniz et al. [12], Chesneau et al. [13], Alzaghal et al. [14], Cortés et al. [15], and others.
Reyes et al. [10] considered the exponential model, , and the weight function ; using (1) they constructed and study the bimodal exponential (BE) distribution, the pdf of which is given by
with and . It is denoted by . The BE distribution is bimodal and is an extension of the exponential distribution. Furthermore, it can be used to fit datasets containing zeroes and/or very small values. The motivation for studying these families of bimodal distributions stems from the lack of alternative models that can effectively replace mixture distributions, which—as is well known—present estimation problems when using classical approaches like Bayesian methods (see McLachan and Peel [16]; Marin et al. [17]).
The object of the present work is to modify the BE distribution considering a new function which increases the flexibility of the second mode. We thus obtain a modified bimodal exponential (MBE) distribution, which we denote by . We study its properties, estimating the parameters, and compare it with the BE distribution using a real dataset.
The work is organized as follows. In Section 2, we present the pdf of the MBE distribution and study some of its properties. In Section 3, we study the inferential statistics of the MBE distribution, in particular the moments estimators and maximum likelihood (ML) estimators, and present a simulation study. In Section 4, we present two applications to real-world datasets. Finally, Section 5 provides concluding remarks.
2. Density and Properties
In this section, we present the pdf of the MBE distribution and some of its properties.
Proposition 1.
Let . Then, the density function of Y is given by
with defining the rate parameter and defining the shape parameter.
Proof.
Considering , , and using (1), we obtain the result.
□
Below, we illustrate graphically the behavior of the density function of the MBE distribution, comparing it with the BE distribution.
Remark 1.
We observe that the MBE can be used to model datasets with an excess of zeroes or very small values, as its support includes zero, and it possesses a mode at zero. We likewise observe that when the parameter , the exponential distribution is obtained as a particular case.
Proposition 2.
Let . The solutions of
correspond to the anti-mode and the non-zero mode of the distribution of Y.
Proof.
This follows directly from analyzing the first derivative of (1) with respect to y. □
The quartic equation in (4) can be solved analytically using the Cardano–Ferrari formulas (for details, see Abramowitz and Stegun [18]). For numerical solutions, the WolframAlpha computational platform (https://www.wolframalpha.com/) provides an efficient alternative; for more details we refer the reader to Weisstein [19].
Let , and let . Table 1 shows the values of the modes for the BE and MBE distributions with the same parameter values as in Figure 1.

Table 1.
Values of the second modes of the BE and MBE distributions.
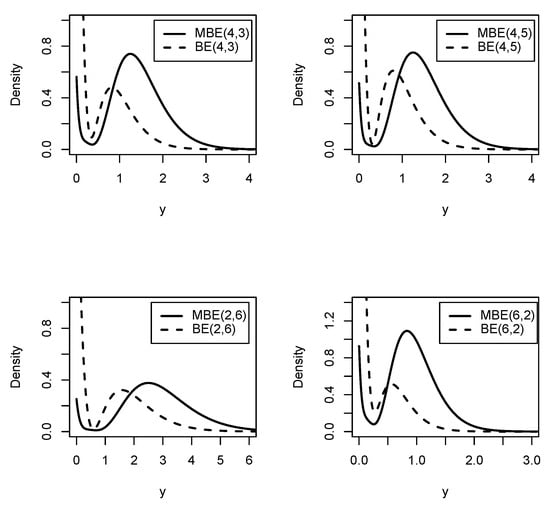
Figure 1.
Density function for the MBE and BE distributions for values of and q.
Proposition 3.
Let and . Then, the height of the second mode of Y is greater than the height of the second mode of Z for , where the second mode of Y is between and , and Z becomes .
Proof.
For , the second mode of Z is given by (see Reyes et al. [10]). The first derivative of is given by
Evaluating this at and yields
Thus, , which implies that the height of the second mode of Y is greater than . Furthermore, we calculate
The inequality holds for , as established by solving
Since , the proof is complete. □
Proposition 4.
Let . Then, the cumulative distribution function (cdf) of Y is given by
Proof.
Calculating directly from the definition of the cdf, we have
and the result is obtained by developing the integral. □
Remark 2.
The BE distribution has a unique mode at zero when (see Reyes et al. [10]); otherwise, like the MBE distribution, it has two modes, as shown in Figure 2. The MBE distribution always has two modes: one at zero and another at a point , with the latter having a greater height.
Below, we illustrate graphically the behavior of the pdf and cdf of the MBE distribution.
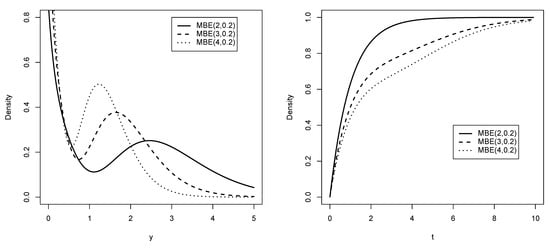
Figure 2.
Pdf and cdf for the MBE distribution for values of and q.
2.1. Order Statistics
Let be a random sample of the random variable ; let us denote by the order statistics .
Proposition 5.
The pdf of is
In particular, the pdf of the minimum, , is
and the pdf of the maximum, , is
2.2. The Reliability and Hazard Rate Functions
Two important reliability measures are the reliability function and the hazard (failure) rate function. The reliability function of a random variable Y is defined by , where denotes the cdf of Y. The hazard rate function is defined by . For the BE distribution, as a direct consequence of Proposition 1 and Proposition 2, both reliability measures can be expressed in closed form. The corresponding expressions are obtained in a straightforward manner.
Proposition 6.
Let . Then, the hazard function of Y is given by
Proof.
By definition of the hazard function, we have
and then by replacing and , the result is obtained. □
To prove the following proposition, we will use the theorem in Glaser [20], together with the idea that to study the behavior of the harzard function , we can examine the function defined by , where is the pdf given in (1).
Proposition 7.
Let . Then, the hazard function of T has a bathtub shape.
Proof.
Using item of Glaser’s Theorem [20], we define the functions
and the function . Their first derivatives are, respectively,
If , we obtain the following: in , , and for all when .
On the other hand, we observe that as , , and , which implies that as . Additionally, evaluating these functions at , we have
yielding . Since is a continuous function for all t, there exists such that . Consequently, ; by applying item of Glaser’s Theorem [20], the result follows.
If , is null at three points:
This is because
Since has a local minimum at , the hazard function also attains a local minimum at , resulting in a bathtub-shaped hazard function. □
Figure 3 presents the hazard rate function of the MBE distribution for various parameter configurations. Notably, the hazard function exhibits the characteristic bathtub shape, a feature frequently encountered in reliability and survival analysis.
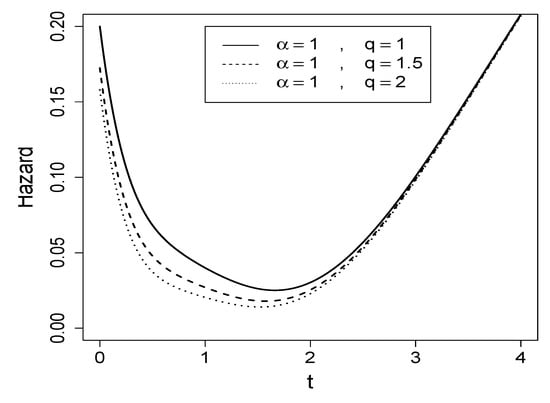
Figure 3.
The hazard rate functions for the MBE distribution.
2.3. Moments
The moments of a random variable with modified bimodal exponential distribution are given in the following proposition.
Proposition 8.
If , the r-th moment of Y is given by
Proof.
Calculating directly from the definition, we have
The result is obtained by developing the integral. □
Corollary 1.
Let ; then,
Proof.
This is an immediate consequence of the previous proposition. □
Corollary 2.
Let ; then, the expectation and the variance of Y are given by
Corollary 3.
Let ; then, the asymmetry coefficient () and the kurtosis coefficient () of Y are given by
respectively.
Proof.
Using the expressions obtained in the previous corollary and the following equations, the result is obtained as
and
respectively. □
Figure 4 shows the skewness and kurtosis coefficients as a function of the parameter q for the MBE model.
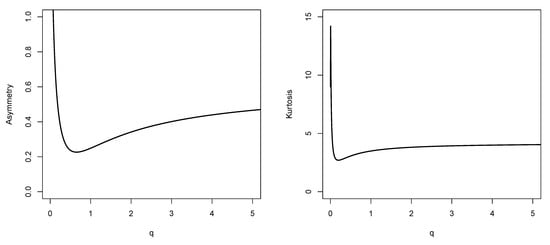
Figure 4.
Plots of the asymmetry (left) and kurtosis (right) coefficients of the MBE distribution.
Proposition 9.
Let . Then, the moment generating function for is given by
Proof.
Calculating directly from the definition, we have
and then, the result is obtained by calculating the integral for . □
3. Inference
In this section, we discuss statistical inferences from the moment estimators and maximum likelihood estimators.
3.1. Moment Estimators
Proposition 10.
Let be a random distributed sample defined as . Then, the moment estimators of are as follows:
where , the value of found is replaced in (8), and is obtained.
3.2. ML Estimation
We now discuss ML estimation. Given a random sample from the distribution of MBE(), the log likelihood function can be written as
and hence, the ML equations are given by
Solutions for Equations (11) and (12) can be obtained using numerical procedures such as the Newton–Raphson procedure. Alternatively, these estimates can be found by directly maximizing the log-likelihood surface given by (10) and using the optim subroutine in the R software (version 4.3.2) [21].
3.2.1. Regularity Conditions
To establish the consistency and asymptotic normality of the ML estimators of the parameters in the MBE distribution, it is necessary to verify a set of regularity conditions commonly used in likelihood theory (see [22]).
We verify the following regularity conditions:
- C1.
- Identifiability: The mapping is identifiable. That is, if for all , then . This holds because the parameters appear uniquely in both the exponential decay and the quartic polynomial term.
- C2.
- Parameter space: The parameter space is an open subset of .
- C3.
- Differentiability: The log-likelihood function is three times continuously differentiable with respect to both parameters in the interior of .
- C4.
- Dominated convergence: There exists an integrable function such that the partial derivatives of are uniformly dominated by in a neighborhood of the true parameter value . This condition ensures the validity of interchanging integration and differentiation—a key requirement for establishing consistency and asymptotic normality.The partial derivatives of the log-likelihood with respect to and q involve polynomial terms up to degree four in y multiplied by an exponentially decaying function. A suitable dominating function isfor some and . Sincethis function is integrable over , thus satisfying condition C4.
- C5.
- Fisher information: The Fisher information matrix is positive definite in a neighborhood of the true parameter values. This is supported empirically via simulations and numerically through the computation of the observed Fisher information matrix.
Given that conditions C1–C5 are satisfied, we conclude that the MLEs of are consistent and asymptotically normal:
Remark 3.
The fulfillment of these conditions was also supported empirically through simulation studies and real data applications, where profile log-likelihood plots confirmed the existence of a unique maximum for the likelihood function. Specifically, the profile likelihood plots for parameters α and q (presented in the Applications section) demonstrate the uniqueness of the MLE, thereby supporting the theoretical assumptions.
3.2.2. Fisher Information Matrix
Let random variable . For a single observation y, the log-likelihood function for is
The first derivatives of are
The second derivatives of are
It can be shown that the Fisher information matrix for the MBE distribution is given by
with the following elements:
where , for , must be computed numerically.
3.2.3. Simulation Study
We used the acceptance or rejection algorithm to generate random realizations of a variable with the MBE () distribution. The simulation results appear in Table 2, illustrating the behavior of the ML estimators for 1000 generated samples of sizes 50, 100, 150, and 200 from a population with MBE () distribution. For each sample generated, ML estimators were computed numerically using the Newton–Raphson procedure. The means of the estimations, the standard deviations (SDs), and the empirical coverage probabilities for 95%, C(·) (in percentages) are presented in Table 2. We observe that, in general, the standard deviation of the estimations diminished when the sample size was increased, suggesting that the ML estimators are consistent. The empirical coverage probabilities approached the nominal level of 95%. The results shown in Table 2 suggest that the ML estimators of and q show good behavior in small samples.

Table 2.
Simulation of 1000 iterations of the MBE () model.
3.2.4. Algorithm
To implement the algorithm for generating random values from the MBE (, q) distribution (presented in Algorithm 1), we first define the required parameters and random variables:
- n: Size of the output vector (i.e., number of values to be generated).
- Y: A random variable following the MBE (, q) distribution.
- : The probability density function (pdf) of the MBE distribution defined for .
- : The lower bound used to define the sampling interval for Y; must satisfy .
- : The upper bound for the pdf ; it must satisfy .
- : A uniform random variable on the interval used to propose candidate values for Y.
- : A uniform random variable on the interval , which is used in the acceptance/rejection step.
Given parameters and , we generate a vector of size n with values from the MBE (, q) distribution using the acceptance or rejection method.
| Algorithm 1: Random generation from MBE (, q) distribution |
 |
4. Applications
In this section, we analyze two real-world datasets, comparing the fit of the MBE and BE distributions.
4.1. Application to Vanadium Data
The dataset used was collected by the Mining Department of the University of Atacama, Chile, and represents the vanadium measured in 86 ore samples. The data are shown in Table 3.

Table 3.
Vanadium data.
The descriptive statistics of these data are shown in Table 4, where is the coefficient of asymmetry of the sample, and is the coefficient of kurtosis of the sample.

Table 4.
Descriptive statistics for vanadium data.
Using results from Section 3.1, the method of moments estimators was computed, leading to the following values: and ; these were used as initial estimates for the maximum likelihood approach.
Table 5 shows the ML estimates (with (SE) indicating standard error) for the parameter of the MBE and BE models, as well as the values of the AIC and BIC criteria for each model. For each model, we report the values the Akaike information criterion (AIC) introduced by Akaike [23] and the Bayesian information criterion (BIC) proposed by Schwarz [24].

Table 5.
Vanadium data: model, ML estimates, AIC values, and BIC values.
We observe that the smaller values of the AIC and BIC criteria correspond to the MBE model, indicating that the MBE model fits the data better than the BE model.
In Figure 5 (left), we present a histogram of the vanadium data, as well as the estimated pdfs of the MBE and BE distributions. We observe a good fit between the histogram of the vanadium data and the estimated pdf of the MBE distribution. Figure 5 (right) shows the empirical cdfs with the estimated cdfs of the MBE and BE distributions, which also indicated a good fit between the vanadium data and the BME model.
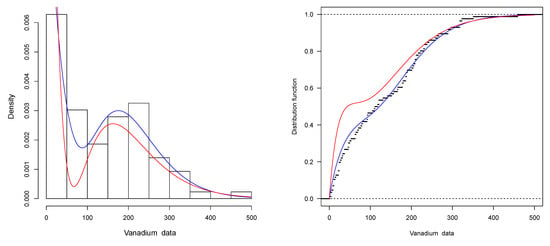
Figure 5.
Left: Histogram of the vanadium data, with estimated MBE pdf (blue) and estimated BE pdf (red). Right: Plots of the empirical cdf, with estimated MBE cdf (blue), estimated BE cdf (red), and empirical cdf (black).
In Figure 6, the log-likelihood profiles for and q show a single clear peak, indicating the uniqueness of the maximum likelihood estimator. The well-defined maxima suggest that the optimization converges to a unique solution. This supports the identifiability and stability of the parameter estimates.
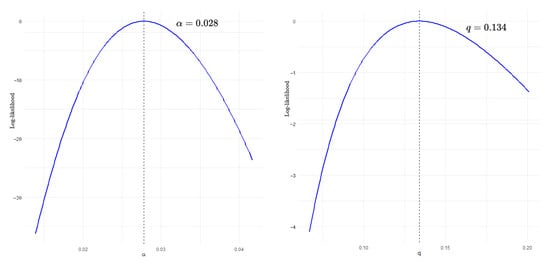
Figure 6.
Log-likelihood profiles with estimated parameter values (left) and q (right) for vanadium data.
We calculated the quantile residuals (QRs) for the MBE and BE distributions. If the model is appropriate for the data, the QR should be a sample of the standard normal model (see Dunn and Smyth [25]). This assumption can be validated with traditional normality tests, like the Anderson–Darling (AD), Cramér–von Mises (CVM), and Shapiro–Wilk (SW) tests. Figure 7 displays the quantile residuals (QRs) for each distribution. The associated p-values from the Anderson–Darling (AD), Cramér–von Mises (CVM), and Shapiro–Wilk (SW) normality tests are reported in parentheses to assess whether the QRs follow a standard normal distribution. As shown in the Figure 7, all three tests support the hypothesis that the QRs from the MBE distribution follow a standard normal distribution. In contrast, the CVM test rejects this hypothesis for the BE distribution, suggesting that the BE model does not provide an adequate fit to the vanadium data.
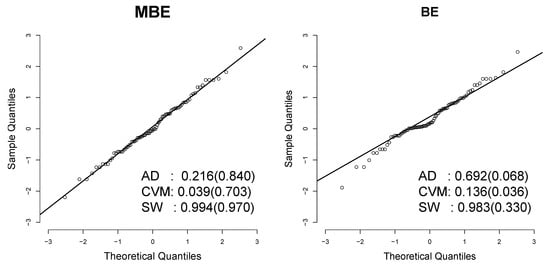
Figure 7.
Left: Q–Q plots of the QRs for MBE distribution. Right: Q–Q plots of the QRs for BE distribution.
4.2. Application to Exceedances of Flood Peaks Data
The data correspond to the exceedances of flood peaks (in /s) of the Wheaton River near Carcross in Yukon Territory, Canada. The data consist of 72 exceedances for the years 1958–1984, rounded to one decimal place, and are listed in Table 6. Table 7 presents descriptive statistics. In it, we compare the fit of the BE distribution with that of the MBE distribution.

Table 6.
Data on exceedances of Wheaton River floods.

Table 7.
Descriptive statistics for exceedances of flood peaks data.
Using results from Section 3.1, the method of moments estimators was computed, leading to the following values: and ; these were used as initial estimates for the maximum likelihood approach. Table 8 presents the ML estimates for the MBE and BE model parameters, along with their corresponding AIC and BIC values.

Table 8.
Exceedances of flood peaks data: model, ML estimates, AIC values, and BIC values.
The MBE model demonstrates superior fit to the data, as evidenced by its consistently lower AIC and BIC values compared to the BE model.
In Figure 8 (left), we plot the histogram of the flood peak exceedances data overlayed with the estimated pdfs of the MBE and BE distributions. We observe strong agreement between the histogram of flood peak exceedances and the estimated pdf of the MBE distribution. In Figure 8 (right), we plot the empirical cdf along with the estimated cdfs of the MBE and BE distributions, which further demonstrate the good fit between the MBE model and the flood peak exceedances data.
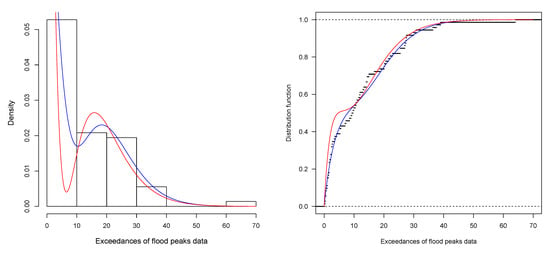
Figure 8.
Left side: histogram of the exceedances of flood peaks data with estimated MBE pdf (blue) and estimated BE pdf (red). Right side: plots of the empirical cdf with estimated MBE cdf (blue), estimated BE cdf (red) models, and empirical cdf (black).
Figure 9 and Figure 10 show the QRs for each distribution. The p-values for the normality tests (AD, CVM, and SW) are shown in parentheses to verify whether the QRs have a standard normal distribution. In Figure 9, we observe that all three tests indicate that the MBE distribution’s QRs follow a standard normal distribution. This is not the case for the BE distribution, as Figure 10 shows that all three tests reject the null hypothesis that the QRs come from a standard normal distribution, indicating that the BE distribution does not fit the flood peak exceedances data well.
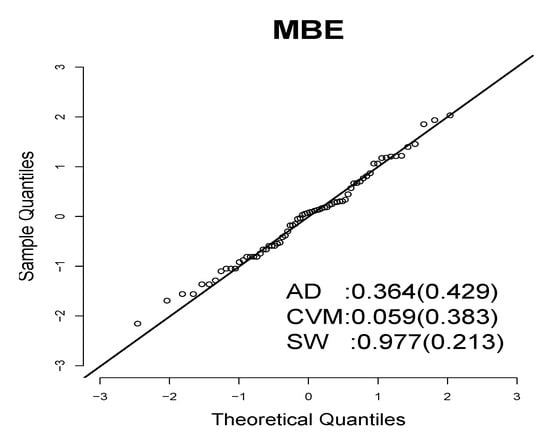
Figure 9.
Q–Q plots of the QRs for MBE distribution.
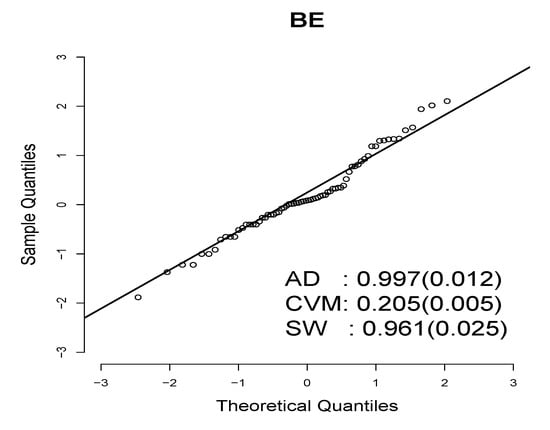
Figure 10.
Q–Q plots of the QRs for BE distribution.
Figure 11 demonstrates the ML estimates of and q, as evidenced by their log-likelihood profiles exhibiting a dominant, isolated peak. The absence of local optima or flat regions confirms that the numerical optimization procedure reliably attains a single, globally optimal solution. These results underscore both the statistical identifiability of the model parameters and the robustness of their estimation.
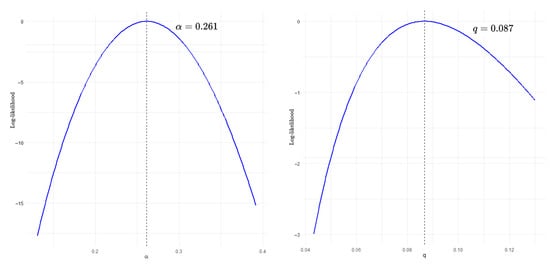
Figure 11.
The log-likelihood profiles with estimated parameter values (left) and q (right) for flood peak exceedance data.
5. Discussion
Using the methodology introduced by Reyes et al. [10] to generate bimodal distributions with positive support, we employed a new weight function to increase the height of the second mode. We retained the exponential distribution to enable comparison with the BE distribution. The key characteristics of the MBE distribution are as follows:
- The MBE distribution is an extension of the exponential distribution.
- The second mode of the MBE distribution is higher in height than that of the BE distribution.
- The cdf, survival function, hazard function, and moment-generating function are explicit and are represented by simple functions.
- The hazard function is bathtub-shaped.
- The simulation study shows that the ML estimators present good behavior with relatively small sample sizes.
- The two applications demonstrate that the MBE distribution possesses distinct characteristics, including a second mode that is both higher in height and more flexible than that of the BE distribution. Furthermore, the AIC and BIC selection criteria indicate that the MBE distribution provides a better fit for both datasets compared to the BE distribution. This conclusion was further confirmed through a comparison of the QRs of each distribution.
- Finally, exploring new models by substituting the exponential distribution with alternative distributions will be the aim of our future work.
Author Contributions
Conceptualization, J.R. and B.C.A.; methodology, Y.M.G. and H.W.G.; software, Y.M.G.; validation, J.R., Y.M.G. and B.C.A.; formal analysis, Y.M.G. and O.V.; investigation, O.V.; writing—original draft preparation, J.R. and Y.M.G.; writing—review and editing, O.V. and B.C.A.; funding acquisition, H.W.G. and O.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Fisher, R.A. The effects of methods of ascertainment upon the estimation of frequencies. Ann. Eugen. 1934, 6, 13–25. [Google Scholar] [CrossRef]
- Rao, C.R. On discrete distributions arising out of methods of ascertainment. In Classical and Contagious Discrete Distributions; Patil, G.P., Ed.; Calcutta Statist. Publ. Soc.: Calcutta, India, 1965; pp. 320–333, Reprinted in Sankhya A 27, 311–324. [Google Scholar]
- Rao, C.R. Weighted Distributions Arising Out of Methods of Ascertainment: What Population Does a Sample Represent? In A Celebration of Statistics; Atkinson, A.C., Fienberg, S.E., Eds.; Springer: New York, NY, USA, 1985. [Google Scholar]
- Patil, G.P.; Ord, J.K. On size biased sampling and related form invariant weighted distribution. Indian J. Stat. 1976, 39, 48–61. [Google Scholar]
- Patil, G.P.; Rao, C.R. Weighted distributions and size-biased sampling with applications to wildlife populations and human families. Biometrics 1978, 34, 179–189. [Google Scholar] [CrossRef]
- Gupta, R.C.; Kirmani, S.N. The role of weighted distributions in stochastic modeling. Commun. Stat. Theory Methods 1990, 19, 3147–3162. [Google Scholar] [CrossRef]
- Gupta, A.K.; Tripathi, R.C. Weighted bivariate logarithmic series distributions. Commun. Stat. Theory Methods 1996, 25, 1099–1117. [Google Scholar] [CrossRef]
- Gupta, R.C.; Akman, H.O. On the reliability studies of a weighted inverse Gaussian model. J. Stat. Plan. Inference 1998, 48, 69–83. [Google Scholar] [CrossRef]
- Gupta, R.D.; Kundu, D.A. New class of weighted exponential distribution. Statistics 2009, 43, 621–634. [Google Scholar] [CrossRef]
- Reyes, J.; Gómez-Déniz, E.; Gómez, H.W.; Calderín-Ojeda, E. A Bimodal Extension of the Exponential Distribution with Applications in Risk Theory. Symmetry 2021, 13, 679. [Google Scholar] [CrossRef]
- Hassan, M.Y.; Hijazi, R.H. A bimodal exponential power distribution. Pak. J. Stat. 2010, 26, 379–396. [Google Scholar]
- Gómez-Déniz, E.; Sarabia, J.M.; Calderín-Ojeda, E. Bimodal normal distribution: Extensions and applications. J. Comput. Appl. Math. 2021, 388, 113292. [Google Scholar] [CrossRef]
- Chesneau, C.; Kumar, V.; Khetan, M.; Arshad, M. On a Modified Weighted Exponential Distribution with Applications. Math. Comput. Appl. 2022, 27, 17. [Google Scholar] [CrossRef]
- Alzaghal, A.; Aldeni, M.; Al-Aqtash, R. A New Class of Exponentiated Exponential Distributions: Bimodality, Regression, and Application. J. Stat. Theory Pract. 2023, 52, 52. [Google Scholar] [CrossRef]
- Cortés, I.E.; Venegas, O.; Gómez, H.W. A Symmetric/Asymmetric Bimodal Extension Based on the Logistic Distribution: Properties, Simulation and Applications. Mathematics 2022, 10, 1968. [Google Scholar] [CrossRef]
- McLachan, G.; Peel, D. Mixture Models: Inference and Applications to Clustering; Marcel Dekker: New York, NY, USA, 2000. [Google Scholar]
- Marin, J.M.; Mengersen, K.; Robert, C. Bayesian modeling and inference on mixtures of distributions. Handb. Stat. 2005, 25, 459–503. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th ed.; National Bureau of Standards: Gaithersburg, MD, USA, 1968. [Google Scholar]
- Weisstein, E.W.; Quartic Equation. From MathWorld—A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/QuarticEquation.html (accessed on 8 June 2024).
- Glaser, R.E. Bathtub and Related Failure Rate Characterizations. J. Am. Stat. Assoc. 1980, 75, 667–672. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023; Available online: https://www.R-project.org/ (accessed on 28 June 2024).
- Casella, G.; Berger, R.L. Statistical Inference, 2nd ed.; Duxbury: North Scituate, MA, USA, 2002. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Dunn, P.K.; Smyth, G.K. Randomized Quantile Residuals. J. Comput. Graph. Stat. 1996, 5, 236–244. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).