Fixed Point Approximation for Enriched Suzuki Nonexpansive Mappings in Banach Spaces

Abstract

This paper investigates the approximation of fixed points for mappings that satisfy the enriched (C) condition using a modified iterative process in a Banach space framework. We first establish a weak convergence result and then derive strong convergence theorems under suitable assumptions. To illustrate the applicability of our findings, we present a numerical example involving mappings that satisfy the enriched (C) condition but not the standard (C) condition. Additionally, numerical computations and graphical representations demonstrate that the proposed iterative process achieves a faster convergence rate compared to several existing methods. As a practical application, we introduce a projection based an iterative process for solving split feasibility problems (SFPs) in a Hilbert space setting. Our findings contribute to the ongoing development of iterative processes for solving optimization and feasibility problems in mathematical and applied sciences.

1. Introduction

The theory of fixed points is a central theme in various domains of mathematics, finding applications in fields such as numerical analysis, differential equations, optimization, topology, geometry, mathematical physics, etc. Topological fixed point theorems, such as Brouwer’s [1] and Lefschetz’s [2] theorems, serve as foundational tools in algebraic topology. They are used to study continuous self-maps on compact manifolds, revealing crucial information about the underlying space’s structure. In algebraic geometry, fixed point theory plays a vital role in Higgs bundles and the Hitchin integrable system, where fixed points correspond to stable Higgs fields under natural flows or symmetries (cf. [3]). The study of the moduli spaces of principal bundles and Higgs pairs over smooth projective curves, where fixed points often encode geometric invariants relevant to deformation theory and gauge theory (cf. [4]). In quantum field theory and string theory, fixed points appear in the study of renormalization group flows, where a fixed point indicates scale-invariant behavior. Fixed point methods are instrumental in studying the solutions to nonlinear PDEs arising in general relativity, quantum mechanics, and gauge theories. Fixed point theorems provide powerful tools for proving the existence and uniqueness of solutions in diverse mathematical contexts (cf. [5,6,7]). Among the various classes of mappings, nonexpansive mappings have emerged as particularly significant due to their rich properties and wide applicability.

A mapping $P:V\to V$ defined on a convex subset V of a Banach space U was termed nonexpansive if it satisfied the following condition:

$$\parallel P\left(x\right)-P\left(y\right)\parallel \le \parallel x-y\parallel \forall x,y\in V.$$

This condition ensures that the mapping does not expand distances, which leads to important consequences regarding the convergence of iterative processes aimed at locating fixed points. Browder [8] and Göhde [9], each through distinct approaches, independently established the existence of fixed points for nonexpansive mappings on specific subsets of uniformly convex Banach spaces (UCBSs). The study of fixed points for nonexpansive operators is fundamental in many branches of applied sciences. As a result, efforts to generalize and extend these mappings to enhance their applicability have been a central theme in ongoing research. The pioneering work of Banach provides a fundamental framework for establishing fixed point results, while Suzuki extended these concepts further by considering specific classes of nonexpansive mappings endowed with additional structures that enhance their mathematical and computational properties.

Suzuki [10] proposed a specific condition, referred to as the (C) condition, for mappings in 2008. According to this, a mapping P defined on a subset V of a Banach space U satisfies the (C) condition if, for all $x,y\in V$, the following implication is true:

$${\displaystyle \frac{1}{2}}\parallel x-Px\parallel \le \parallel x-y\parallel \Rightarrow \parallel Px-Py\parallel \le \parallel x-y\parallel .$$

The class of mappings satisfying the (C) condition generalizes the class of nonexpansive mappings. Several authors have extended the concept of Suzuki generalized nonexpansive mapping from single-valued to multi-valued mappings and from Banach space to partial Hausdorff metric spaces (see [11]). In pursuit of broader generalizations, Berinde [12] introduced an extended class of nonexpansive mappings in 2019, referred to as enriched nonexpansive mappings. Both enriched nonexpansive mappings and those satisfying the $\left(C\right)$ condition represent important subclasses within the family of nonlinear mappings. It is worth noting that traditional nonexpansive mappings are special cases of enriched nonexpansive mappings when the parameter $b=0$ and they also meet the criteria of the $\left(C\right)$ condition. This natural inclusion motivates further investigation into the generalization of such mappings.

Recently, Ullah et al. [13] introduced the class of mappings with an enriched (C) condition. As demonstrated in [13], any mapping that satisfies the standard $\left(C\right)$ condition also meets the criteria of the enriched $\left(C\right)$ condition. Furthermore, there exist mappings that comply with the enriched $\left(C\right)$ condition but fail to satisfy the ordinary $\left(C\right)$ condition, highlighting the generality of the enriched version. This indicates that the class of mappings with the enriched (C) condition is broader than the class of mappings with the ordinary (C) condition and includes several other subclasses of nonlinear mappings. In their work, the authors also established results on the existence, weak convergence, and strong convergence for these mappings within the framework of Hilbert spaces. This paper aims to extend these results to a more general setting of Banach spaces.

Once the existence of a fixed point for a mapping is established, the next natural step is to develop methods for approximating the value of that fixed point. One of the earliest iterative techniques for this purpose was proposed by Picard [14], who focused on finding fixed points of certain nonlinear mappings. Later, Banach [15] demonstrated that Picard’s method is effective for contraction mappings. Over time, numerous researchers extended the applicability of Picard’s scheme to various classes of mappings, e.g., see [16,17,18,19,20,21,22] and references cited therein. Despite its simplicity, Picard’s iterative method has notable limitations when applied to nonexpansive mappings. For instance, consider a mapping $Px=-x$, which is nonexpansive and has a unique fixed point $x=0$. However, the Picard iteration for this mapping fails to converge to 0 unless the initial guess is exactly 0. Additionally, the convergence of Picard’s scheme is often slow, requiring a significant number of iterations to approximate the fixed point. To address these challenges, various generalizations of iterative schemes have been proposed by researchers, including Mann [21], Ishikawa [20], Noor [22], Agarwal [17], Abbas [16], etc. These methods not only improve the convergence rate, but also broaden the scope of mappings for which fixed point approximation is feasible.

For mappings satisfying the Zamfirescu conditions, Ali and Ali [23] introduced a three-step iterative process known as the F-iteration. They established stability and convergence results under specific assumptions and illustrated these results using an example of the Zamfirescu operator. Furthermore, they demonstrated numerically that the F-iteration outperforms the Thakur iterative method [24], two-step Agarwal iterative scheme [17], and the three-step M-iteration process in terms of convergence speed. In addition, Abdeljawad et al. [25] employed an enhanced iterative approach to approximate the fixed points of enriched nonlinear mappings.

This study is devoted to establishing the convergence of the F-iteration scheme for mappings that satisfy the enriched $\left(C\right)$ condition. In this context, we considered a self-mapping P defined on a subset V of a Banach space. Let $P_{\lambda }$ represent the averaged form of P, which is defined as

$$P_{\lambda }x=(1-\lambda )x+\lambda Px,$$

where $\lambda ={\displaystyle \frac{1}{b+1}}$ and $b\in [0,\infty )$. It is a well-established fact that the set of fixed points of $P_{\lambda }$ coincides with that of P. Using $P_{\lambda }$, the iterative processes can be expressed as follows:

Agarwal et al. [17] introduced the S-iteration scheme for sequences $\left\{a_n\right\},\left\{b_n\right\}\subset (0,1)$, which is defined as follows:

$$\left\{\begin{array}{c}{w}_0\in V,\hfill \\ w_{n+1}=(1-a_n)P_{\lambda }{w}_n+a_n{P}_{\lambda }{u}_n,\hfill \\ u_n=(1-b_n)w_n+b_n{P}_{\lambda }{w}_n,n=0,1,2,\dots \hfill \end{array}\right.$$

(1)

Gursoy et al. [26] proposed an enhancement known as the Picard-S iteration method, which refines the scheme introduced by Agarwal et al. [17]. For sequences $\left\{a_n\right\},\left\{b_n\right\}\subset (0,1)$, this method is described as follows:

$$\left\{\begin{array}{c}{w}_0\in V,\hfill \\ w_{n+1}=P_{\lambda }{u}_n,\hfill \\ u_n=(1-a_n)P_{\lambda }{x}_n+a_n{P}_{\lambda }{w}_n,\hfill \\ x_n=(1-b_n)w_n+b_n{P}_{\lambda }{w}_n,n=0,1,2,\dots \hfill \end{array}\right.$$

(2)

In 2016, Thakur et al. [24] introduced another iterative process for sequences $\left\{a_n\right\},\left\{b_n\right\}\subset (0,1)$, which is defined as follows:

$$\left\{\begin{array}{c}{w}_0\in V,\hfill \\ w_{n+1}=P_{\lambda }{u}_n,\hfill \\ u_n=P_{\lambda }\left((1-a_n)w_n+a_n{x}_n\right),\hfill \\ x_n=(1-b_n)w_n+b_n{P}_{\lambda }{w}_n,n=0,1,2,\dots \hfill \end{array}\right.$$

(3)

This method was shown to exhibit faster convergence for certain types of mappings in comparison to earlier methods, including those by Picard [14], Mann [21], Noor [22], Agarwal et al. [17], and Abbas and Nazir [16].

In 2020, Ali and Ali [27] proposed the F-iteration method, which demonstrated superior convergence properties compared to the methods introduced by Agarwal et al. [17], Gursoy et al. [26], Thakur et al. [24] and Ullah and Arshad [28]. This iteration, which is defined for $\left\{a_n\right\}\subset (0,1)$, is expressed as follows:

$$\left\{\begin{array}{c}{w}_0\in V,\hfill \\ w_{n+1}=P_{\lambda }{u}_n,\hfill \\ u_n=P_{\lambda }{x}_n,\hfill \\ x_n=P_{\lambda }\left((1-a_n)w_n+a_n{P}_{\lambda }{w}_n\right),n=0,1,2,\dots \hfill \end{array}\right.$$

(4)

This paper focused on the approximation of fixed points for mappings satisfying the enriched $\left(C\right)$ condition. The motivation stems from the limitations of existing iterative schemes, prompting the development of a modified iterative process to improve convergence behavior. We also explored how the enriched structure of these mappings can facilitate the development of efficient iterative algorithms for their approximation. The rest of this paper is organized as follows:

• Section 2 provides preliminary definitions, concepts, and necessary lemmas related to fixed point theory, nonexpansive mappings, and the enriched $\left(C\right)$ condition. These foundational results are essential for understanding the main contributions of this paper.
• Section 3 presents the main results on the weak and strong convergence of the proposed iterative scheme. Theorems and proofs are provided to establish the validity of the iterative process under certain conditions.
• Section 4 includes a numerical example demonstrating the behavior of mappings that satisfy the enriched $\left(C\right)$ condition but not the ordinary $\left(C\right)$ condition. This section also compares the convergence rates of different iterative schemes using graphical representations.
• Section 5 applies the main theoretical findings to the split feasibility problem (SFP). A new projection type iterative method is introduced, and its convergence properties are analyzed in the context of Hilbert spaces.
• Section 6 concludes this paper by summarizing the key contributions and suggesting potential directions for future research, including further extensions of the iterative scheme and applications in broader mathematical frameworks.

2. Preliminaries

In this section, we recall some foundational results and definitions from the literature that will be useful for proving our main results.

If there exists a point $x^{*}\in V$ such that $P{x}^{*}=x^{*}$, then $x^{*}$ is called a fixed point of P. Throughout this work, the set of fixed points of P is denoted as

$$F_P:=\{x^{*}\in V:P{x}^{*}=x^{*}\}.$$

Definition 1 

([29,30]). Let V be a nonempty closed convex subset of a uniformly convex Banach space (UCBS) U, and let $\left\{w_n\right\}$ be a bounded sequence in U. The asymptotic radius of $\left\{w_n\right\}$ with respect to V is defined as

$$r(V,\left\{w_n\right\})=inf\left\{\underset{n\to \infty }{lim\; sup}\parallel w_n-w\parallel :w\in V\right\}.$$

The asymptotic center of $\left\{w_n\right\}$ with respect to V is given by

$$A(V,\left\{w_n\right\})=\left\{w\in V:\underset{n\to \infty }{lim\; sup}\parallel w_n-w\parallel =r(V,\left\{w_n\right\})\right\}.$$

Moreover, the set $A(V,\left\{w_n\right\})$ contains exactly one element.

Definition 2 

([13]). A self-mapping P defined on a subset V is said to fulfill the enriched $\left(C\right)$ condition if there exists a constant $b\in [0,\infty )$ such that, for all $x,y\in V$, we have

$${\displaystyle \frac{1}{2}}\parallel x-Px\parallel \le (b+1)\parallel x-y\parallel \Rightarrow \parallel b(x-y)+Px-Py\parallel \le (b+1)\parallel x-y\parallel ,$$

(5)

for all $x,y\in V$.

The following example demonstrates that a mapping satisfying the enriched (C) condition may lack continuity on its entire domain.

Example 1 

([13]). Consider the mapping P, which is defined on $[0, 3]$ as follows:

$$Px=\left\{\begin{array}{cc}0,\hfill & \mathit{if}x\in [0, 3),\hfill \\ 1,\hfill & \mathit{if}x=3.\hfill \end{array}\right.$$

It is evident that P is neither nonexpansive nor enriched nonexpansive on V as P is not continuous at the point $x=3\in V$. Nonetheless, the mapping P satisfies the enriched (C) condition.

Definition 3 

([31]). A Banach space U is said to satisfy the Opial condition if, for any sequence $\left\{w_n\right\}$ in U that converges weakly to some $w\in U$, the inequality

$$\underset{n\to \infty }{lim\; sup}\parallel w_n-w\parallel <\underset{n\to \infty }{lim\; sup}\parallel w_n-w^{\prime }\parallel$$

holds for all $w^{\prime }\in U$ with $w^{\prime }\ne w$.

Definition 4 

([32]). Let V be a subset of a Banach space and let $P:V\to V$ be a self-mapping. The mapping P is said to satisfy condition (I) if there exists a nondecreasing function $h:[0,\infty )\to [0,\infty )$ satisfying the following:

• $h\left(0\right)=0$,
• $h\left(r\right)>0$ for all $r>0$,

such that for every $x\in V$, the inequality

$$d(x,Px)\ge h\left(d(x,F_P)\right)$$

holds, where $F_P$ denotes the set of fixed points of P and $d(x,F_P)=inf\{d(x,x^{*}):x^{*}\in F_P\}$.

Proposition 1 

([10]). Let U be a Banach space and $V\subseteq U$, and let $P:V\to V$.

1. 

If P satisfies the (C) condition, then, for all $x,y\in V$, the inequality

$$\parallel x-Py\parallel \le 3\parallel x-Px\parallel +\parallel x-y\parallel$$

holds.

2. 

Suppose P satisfies the Suzuki (C) condition and U satisfies Opial’s condition. If for any sequence $\left\{w_n\right\}$ that converges weakly to a point $x^{*}$, the condition

$$\underset{n\to \infty }{lim}\parallel w_n-P{w}_n\parallel =0$$

holds, then $P{x}^{*}=x^{*}$.

Lemma 1 

([33]). Let V be a closed convex subset of U, and let $P:V\to V$ be a mapping that satisfies the enriched $\left(C\right)$ condition with a constant $b\in [0,\infty )$. Then, the averaged mapping $P_{\lambda }$, which is defined by $P_{\lambda }w=(1-\lambda )w+\lambda Pw$ with $\lambda ={\displaystyle \frac{1}{b+1}}$, satisfies the Suzuki $\left(C\right)$ condition.

The next lemma, due to Schu [34], highlights a fundamental property of uniformly convex Banach spaces.

Lemma 2 

([34]). Let U be a uniformly convex Banach space [35]. Assume $0<i\le a_n\le j<1$ for all n, where $\left\{a_n\right\}$ is a sequence in $(0,1)$. Suppose there exists $z\ge 0$, such that, for any sequences $\left\{w_n\right\}$ and $\left\{u_n\right\}$ in U, the conditions ${lim\; sup}_{n\to \infty }\parallel w_n\parallel \le z$, ${lim\; sup}_{n\to \infty }\parallel u_n\parallel \le z$, and ${lim}_{n\to \infty }\parallel a_n{w}_n+(1-a_n)u_n\parallel =z$ hold. Then, it follows that ${lim}_{n\to \infty }\parallel w_n-u_n\parallel =0$.

3. Main Results

The objective of this section was to examine the iterative scheme (4) in the setting of mappings that fulfill the enriched $\left(C\right)$ condition (5). Prior to presenting our convergence results, we introduced a key preliminary lemma that is fundamental for our analysis.

Lemma 3. 

Let V be a closed convex subset of a uniformly convex Banach space (UCBS) U, and let $P:V\to V$ be a mapping satisfying the enriched $\left(C\right)$ condition with $F_P\ne \varnothing$. If the sequence $\left\{w_n\right\}$ is generated by the iterative scheme (4), then, for any fixed point $x^{*}\in F_P$, the limit ${lim}_{n\to \infty }\parallel w_n-x^{*}\parallel$ exists.

Proof. 

Let $x^{*}\in F_P$. It follows that $x^{*}\in F_{P_{\lambda }}$, where $P_{\lambda }$ is the averaged mapping defined by $P_{\lambda }w=(1-\lambda )w+\lambda Pw$ with $\lambda ={\displaystyle \frac{1}{b+1}}$. By Lemma 1, the mapping $P_{\lambda }$ satisfies the Suzuki $\left(C\right)$ condition. In particular, this implies that

$${\displaystyle \frac{1}{2}}\parallel x^{*}-P_{\lambda }{x}^{*}\parallel \le \parallel x^{*}-u\parallel \Rightarrow \parallel P_{\lambda }{x}^{*}-P_{\lambda }u\parallel \le \parallel x^{*}-u\parallel ,\forall u\in V.$$

Using this property, we estimate as follows:

$$\begin{array}{ccc}\hfill \parallel x_n-x^{*}\parallel & =& \parallel P_{\lambda }((1-a_n)w_n+a_n{P}_{\lambda }{w}_n)-x^{*}\parallel \hfill \\ & \le & \parallel (1-a_n)w_n+a_n{P}_{\lambda }{w}_n-x^{*}\parallel .\hfill \end{array}$$

By the triangle inequality and the convexity of the norm, we have

$$\begin{array}{ccc}\hfill \parallel x_n-x^{*}\parallel & \le & (1-a_n)\parallel w_n-x^{*}\parallel +a_n\parallel P_{\lambda }{w}_n-x^{*}\parallel \hfill \\ & \le & \parallel w_n-x^{*}\parallel .\hfill \end{array}$$

Similarly, we obtain the following inequality

$$\begin{array}{ccc}\hfill \parallel u_n-x^{*}\parallel & =& \parallel P_{\lambda }{x}_n-x^{*}\parallel \hfill \\ & \le & \parallel x_n-x^{*}\parallel \hfill \\ & \le & \parallel w_n-x^{*}\parallel .\hfill \end{array}$$

Finally, combining all these inequalities, we deduce that

$$\parallel w_{n+1}-x^{*}\parallel =\parallel P_{\lambda }{u}_n-x^{*}\parallel \le \parallel w_n-x^{*}\parallel ,$$

indicating that the sequence $\{\parallel w_n-x^{*}\parallel \}$ is nonincreasing. Since it is also bounded below by 0, it converges. Thus, we conclude that

$$\underset{n\to \infty }{lim}\parallel w_n-x^{*}\parallel \mathrm{exists}.$$

This completes the proof. □

Lemma 4. 

Let V be a closed and convex subset of a uniformly convex Banach space (UCBS) U, and let $P:V\to V$ be a mapping satisfying the enriched $\left(C\right)$ condition with $F_P\ne \varnothing$. If $\left\{w_n\right\}$ is generated by the iterative scheme (4), then $F_P\ne \varnothing \iff \left\{w_n\right\}$ is bounded in V and ${lim}_{n\to \infty }\parallel P_{\lambda }{w}_n-w_n\parallel =0$, where $\lambda ={\displaystyle \frac{1}{b+1}}$.

Proof. 

(Necessity): Assume $F_P\ne \varnothing$. By Lemma 3, for any $x^{*}\in F_P$, the sequence $\left\{w_n\right\}$ is bounded, and

$$\underset{n\to \infty }{lim}\parallel w_n-x^{*}\parallel \mathrm{exists}.$$

Let

$$z=\underset{n\to \infty }{lim}\parallel w_n-x^{*}\parallel .$$

From Lemma 3, we know

$$\parallel x_n-x^{*}\parallel \le \parallel w_n-x^{*}\parallel \mathrm{and}\parallel u_n-x^{*}\parallel \le \parallel x_n-x^{*}\parallel .$$

Thus, we have

$$\underset{n\to \infty }{lim\; sup}\parallel x_n-x^{*}\parallel \le \underset{n\to \infty }{lim\; sup}\parallel w_n-x^{*}\parallel =z.$$

Since $P_{\lambda }$ satisfies the Suzuki $\left(C\right)$ condition by Lemma 1, it follows that

$$\parallel P_{\lambda }{w}_n-x^{*}\parallel \le \parallel w_n-x^{*}\parallel \mathrm{and}\parallel u_n-x^{*}\parallel \le \parallel x_n-x^{*}\parallel .$$

Therefore, we obtain

$$\underset{n\to \infty }{lim\; sup}\parallel P_{\lambda }{w}_n-x^{*}\parallel \le \underset{n\to \infty }{lim\; sup}\parallel w_n-x^{*}\parallel =z.$$

By the definition of the iterative scheme, we have

$$w_{n+1}=P_{\lambda }{u}_n,u_n=P_{\lambda }{x}_n,x_n=P_{\lambda }\left((1-a_n)w_n+a_n{P}_{\lambda }{w}_n\right).$$

Hence,

$$\begin{array}{ccc}\hfill \parallel w_{n+1}-x^{*}\parallel & =& \parallel P_{\lambda }{u}_n-x^{*}\parallel \le \parallel u_n-x^{*}\parallel \le \parallel x_n-x^{*}\parallel \hfill \\ & =& \parallel P_{\lambda }\left((1-a_n)w_n+a_n{P}_{\lambda }{w}_n\right)-x^{*}\parallel \hfill \\ & \le & \parallel (1-a_n)(w_n-x^{*})+a_n(P_{\lambda }{w}_n-x^{*})\parallel \hfill \\ & \le & \parallel w_n-x^{*}\parallel .\hfill \end{array}$$

This implies that

$$\begin{array}{ccc}\hfill z=\underset{n\to \infty }{lim}\parallel w_{n+1}-x^{*}\parallel & \le & \underset{n\to \infty }{lim}\parallel x_n-x^{*}\parallel \hfill \\ & \le & \underset{n\to \infty }{lim}\parallel (1-a_n)(w_n-x^{*})+a_n(P_{\lambda }{w}_n-x^{*})\parallel \hfill \\ & \le & \underset{n\to \infty }{lim}\parallel w_n-x^{*}\parallel \le z.\hfill \end{array}$$

We conclude that

$$z=\underset{n\to \infty }{lim}\parallel (1-a_n)(w_n-x^{*})+a_n(P_{\lambda }{w}_n-x^{*})\parallel .$$

Using Lemma 2, we have

$$\underset{n\to \infty }{lim}\parallel P_{\lambda }{w}_n-w_n\parallel =0.$$

(Sufficiency): Conversely, assume that $\left\{w_n\right\}\subset V$ is bounded and ${lim}_{n\to \infty }\parallel P_{\lambda }{w}_n-w_n\parallel =0$. To prove $F_P\ne \varnothing$, it suffices to show that, for any $x^{*}\in A(V,\left\{w_n\right\})$, the point $P_{\lambda }{x}^{*}$ belongs to $A(V,\left\{w_n\right\})$, where $A(V,\left\{w_n\right\})$ denotes the asymptotic center of $\left\{w_n\right\}$ in V.

From Lemma 1, $P_{\lambda }$ satisfies the Suzuki $\left(C\right)$ condition. By Proposition 1, we have

$$r(P_{\lambda }{x}^{*},\left\{w_n\right\})=\underset{n\to \infty }{lim\; sup}\parallel w_n-P_{\lambda }{x}^{*}\parallel \le \underset{n\to \infty }{lim\; sup}\left(\parallel w_n-x^{*}\parallel +3\parallel w_n-P_{\lambda }{w}_n\parallel \right).$$

Since ${lim}_{n\to \infty }\parallel P_{\lambda }{w}_n-w_n\parallel =0$, it follows that

$$\parallel w_n-P_{\lambda }{x}^{*}\parallel \to r(x^{*},\left\{w_n\right\}).$$

Thus, $P_{\lambda }{x}^{*}\in A(V,\left\{w_n\right\})$. Since the asymptotic center $A(V,\left\{w_n\right\})$ contains exactly one element, we have $x^{*}=P_{\lambda }{x}^{*}$, which implies $x^{*}\in F_{P_{\lambda }}$. Since $F_{P_{\lambda }}=F_P$, we conclude $F_P\ne \varnothing$. □

Theorem 1. 

Let V be a closed and convex subset of a uniformly convex Banach space (UCBS) U, and let $P:V\to V$ be a mapping satisfying the enriched $\left(C\right)$ condition with $F_P\ne \varnothing$. If $\left\{w_n\right\}$ is generated by the iterative scheme (4), then $\left\{w_n\right\}$ converges weakly to a fixed point of P provided that U satisfies Opial’s condition.

Proof. 

Since U is a UCBS, it is reflexive. From Lemma 4, the sequence $\left\{w_n\right\}$ is bounded in V. By reflexivity, there exists a subsequence $\left\{w_{n_i}\right\}$ of $\left\{w_n\right\}$ that converges weakly to some point $w_1\in U$. We aim to show that $w_1$ is a weak limit of the entire sequence $\left\{w_n\right\}$ and a fixed point of P.

From Lemma 4, we know

$$\underset{n\to \infty }{lim}\parallel P_{\lambda }{w}_n-w_n\parallel =0,$$

where $\lambda ={\displaystyle \frac{1}{b+1}}$. Thus, for the subsequence $\left\{w_{n_i}\right\}$, we also have

$$\underset{i\to \infty }{lim}\parallel P_{\lambda }{w}_{n_i}-w_{n_i}\parallel =0.$$

Using Proposition 1, it follows that $w_1\in F_{P_{\lambda }}$. Since $F_{P_{\lambda }}=F_P$, we deduce that $w_1$ is a fixed point of P.

Next, we prove that $w_1$ is the weak limit of the entire sequence $\left\{w_n\right\}$. Assume that, to the contrary, $w_1$ is not the weak limit of $\left\{w_n\right\}$. Then, there exists another subsequence $\left\{w_{n_t}\right\}$ of $\left\{w_n\right\}$ that converges weakly to $w_2\in U$, with $w_2\ne w_1$. By a similar argument, we deduce that $w_2\in F_P$, making $w_1$ and $w_2$ distinct fixed points of P.

Since U satisfies Opial’s condition, we have

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}\parallel w_n-w_1\parallel & =& \underset{i\to \infty }{lim}\parallel w_{n_i}-w_1\parallel <\underset{i\to \infty }{lim}\parallel w_{n_i}-w_2\parallel =\underset{n\to \infty }{lim}\parallel w_n-w_2\parallel \hfill \\ & =& \underset{t\to \infty }{lim}\parallel w_{n_t}-w_2\parallel <\underset{t\to \infty }{lim}\parallel w_{n_t}-w_1\parallel =\underset{n\to \infty }{lim}\parallel w_n-w_1\parallel ,\hfill \end{array}$$

which is a contradiction. Therefore, $w_1$ is the unique weak limit of $\left\{w_n\right\}$, and the sequence $\left\{w_n\right\}$ converges weakly to $w_1$.

Since $w_1\in F_P$, it follows that $\left\{w_n\right\}$ converges weakly to a fixed point of P, completing the proof. □

Theorem 2. 

Let V be a convex subset of a uniformly convex Banach space (UCBS) U, and let $P:V\to V$ be a mapping satisfying the enriched $\left(C\right)$ condition with $F_P\ne \varnothing$. If $\left\{w_n\right\}$ is generated by the iterative scheme (4), then $\left\{w_n\right\}$ converges strongly to a fixed point of P provided that V is compact.

Proof. 

Since V is compact, the sequence $\left\{w_n\right\}$ is bounded and has a convergent subsequence. Let $\left\{w_{n_i}\right\}$ be a subsequence of $\left\{w_n\right\}$ such that

$$\underset{i\to \infty }{lim}\parallel w_{n_i}-w_0\parallel =0$$

for some $w_0\in V$.

From Lemma 4, we know that

$$\underset{n\to \infty }{lim}\parallel P_{\lambda }{w}_n-w_n\parallel =0,$$

where $\lambda ={\displaystyle \frac{1}{b+1}}$. In particular, for the subsequence $\left\{w_{n_i}\right\}$, we have

$$\underset{i\to \infty }{lim}\parallel P_{\lambda }{w}_{n_i}-w_{n_i}\parallel =0.$$

Using Lemma 1, $P_{\lambda }$ satisfies the $\left(C\right)$ condition. Hence, applying Proposition 1, we can estimate the following:

$$\parallel w_{n_i}-P_{\lambda }{w}_0\parallel \le 3\parallel w_{n_i}-P_{\lambda }{w}_{n_i}\parallel +\parallel w_{n_i}-w_0\parallel .$$

Taking the limit as $i\to \infty$ on both sides, we obtain

$$\underset{i\to \infty }{lim}\parallel w_{n_i}-P_{\lambda }{w}_0\parallel =0.$$

This implies that $w_{n_i}\to P_{\lambda }{w}_0$. Since $P_{\lambda }{w}_0\in V$ and $P_{\lambda }{w}_0=w_0$, it follows that $w_0$ is a fixed point of $P_{\lambda }$ and, thus, a fixed point of P (as $F_{P_{\lambda }}=F_P$).

Finally, from Lemma 3, we know that ${lim}_{n\to \infty }\parallel w_n-w_0\parallel$ exists. Since $\left\{w_n\right\}$ has a unique limit due to the compactness of V, it follows that $\left\{w_n\right\}$ converges strongly to $w_0$, which is a fixed point of P.

This completes the proof. □

Theorem 3. 

Let V be a convex and closed subset of a uniformly convex Banach space (UCBS) U, and let $P:V\to V$ be a mapping satisfying the enriched $\left(C\right)$ condition with $F_P\ne \varnothing$. If the sequence $\left\{w_n\right\}$ is generated by the iterative scheme (4), and if

$$\underset{n\to \infty }{lim\; inf}d(w_n,F_{P_{\lambda }})=0,$$

then $\left\{w_n\right\}$ converges strongly to a fixed point of P, where $d(w_n,F_{P_{\lambda }})=inf\{\parallel w_n-w_0\parallel :w_0\in F_{P_{\lambda }}\}.$

Proof. 

Assume that ${\displaystyle \underset{n\to \infty }{lim}infd(w_n,F_{P_{\lambda }})=0}$ and let $x^{*}\in F_{P_{\lambda }}=F_P$. By Lemma 3, the sequence $\{\parallel w_n-x^{*}\parallel \}$ converges for every $x^{*}\in F_P$ and, by assumption, we have ${\displaystyle \underset{n\to \infty }{lim}d(w_n,F_{P_{\lambda }})=0}$.

We now show that the sequence $\left\{w_n\right\}$ is Cauchy in V. Since ${\displaystyle \underset{n\to \infty }{lim}d(w_n,F_{P_{\lambda }})=0}$, for any $\epsilon >0$, there exists an index $n_0\in \mathbb{N}$ such that

$$d(w_n,F_{P_{\lambda }})<{\displaystyle \frac{\epsilon }{2}},\mathrm{for}\mathrm{all}n\ge n_0.$$

In particular, we have

$$inf\{\parallel w_{n_0}-x^{*}\parallel :x^{*}\in F_{P_{\lambda }}\}<{\displaystyle \frac{\epsilon }{2}}.$$

Hence, there exists $x^{*}\in F_{P_{\lambda }}$, such that

$$\parallel w_{n_0}-x^{*}\parallel <{\displaystyle \frac{\epsilon }{2}}.$$

Now, for any $m,n\ge n_0$, we estimate the following:

$$\parallel w_{n+m}-w_n\parallel \le \parallel w_{n+m}-x^{*}\parallel +\parallel w_n-x^{*}\parallel \le \parallel w_{n_0}-x^{*}\parallel +\parallel w_{n_0}-x^{*}\parallel =2\parallel w_{n_0}-x^{*}\parallel <\epsilon .$$

This shows that $\left\{w_n\right\}$ is a Cauchy sequence in V. Since V is closed and U is a Banach space, there exists a limit point $w_0\in V$ such that $w_n\to w_0$ as $n\to \infty$.

Finally, using the assumption ${\displaystyle \underset{n\to \infty }{lim}d(w_n,F_{P_{\lambda }})=0}$, we obtain the following:

$$d(w_0,F_{P_{\lambda }})=0\Rightarrow w_0\in F_{P_{\lambda }}=F_P.$$

This completes the proof. □

Theorem 4. 

Let V be a convex and closed subset of a uniformly convex Banach space (UCBS) U, and let $P:V\to V$ satisfy the enriched $\left(C\right)$ condition with $F_P\ne \varnothing$. Suppose $\left\{w_n\right\}$ is generated by the iterative scheme (4) and $P_{\lambda }$ satisfies condition $\left(I\right)$. Then, $\left\{w_n\right\}$ converges strongly to a fixed point of P.

Proof. 

From Lemma 4, we know that $\left\{w_n\right\}$ is bounded in V and

$$\underset{n\to \infty }{lim\; inf}\parallel w_n-P_{\lambda }{w}_n\parallel =0.$$

Since $P_{\lambda }$ satisfies condition $\left(I\right)$, there exists a function $\xi :[0,\infty )\to [0,\infty )$ such that

$$\parallel w-P_{\lambda }w\parallel \ge \xi \left(d(w,F_{P_{\lambda }})\right),$$

where $\xi \left(r\right)=0$ if $r=0$ and $\xi \left(r\right)>0$ for $r>0$. Substituting $w=w_n$, we obtain

$$\parallel w_n-P_{\lambda }{w}_n\parallel \ge \xi \left(d(w_n,F_{P_{\lambda }})\right).$$

Thus, ${lim\; inf}_{n\to \infty }\parallel w_n-P_{\lambda }{w}_n\parallel =0$ implies

$$\underset{n\to \infty }{lim\; inf}d(w_n,F_{P_{\lambda }})=0.$$

By Theorem 3, the condition

$$\underset{n\to \infty }{lim\; inf}d(w_n,F_{P_{\lambda }})=0$$

ensures that $\left\{w_n\right\}$ converges strongly to a fixed point of $P_{\lambda }$. Since $F_{P_{\lambda }}=F_P$ (as P satisfies the enriched $\left(C\right)$ condition), we conclude the following: $\left\{w_n\right\}$ converges strongly to a fixed point of P. This completes the proof. □

4. Numerical Results

Example 2. 

Consider the mapping $P:[0.2,3]\to [0.2,3]$ defined by

$$P\left(x\right)={\displaystyle \frac{2}{7x+1}}.$$

It can be easily seen that P is an enriched Suzuki nonexpansive mapping but not nonexpansive and that P has a fixed point $x^{*}=0.467845$.

Using this example, we constructed a comparative table. The results indicate that our proposed method converges to the fixed point of P for an initial value $w_0=1$. Furthermore, numerical comparisons demonstrate that our approach achieves better accuracy compared to other iterative schemes for initial value $w_0=1$ and control sequences $a_n={\displaystyle \frac{2n+1}{9n+3}},b_n={\displaystyle \frac{3n}{5n+1}}$. This is illustrated in

Table 1. Comparison of the convergence for different iterative schemes for Example 2.

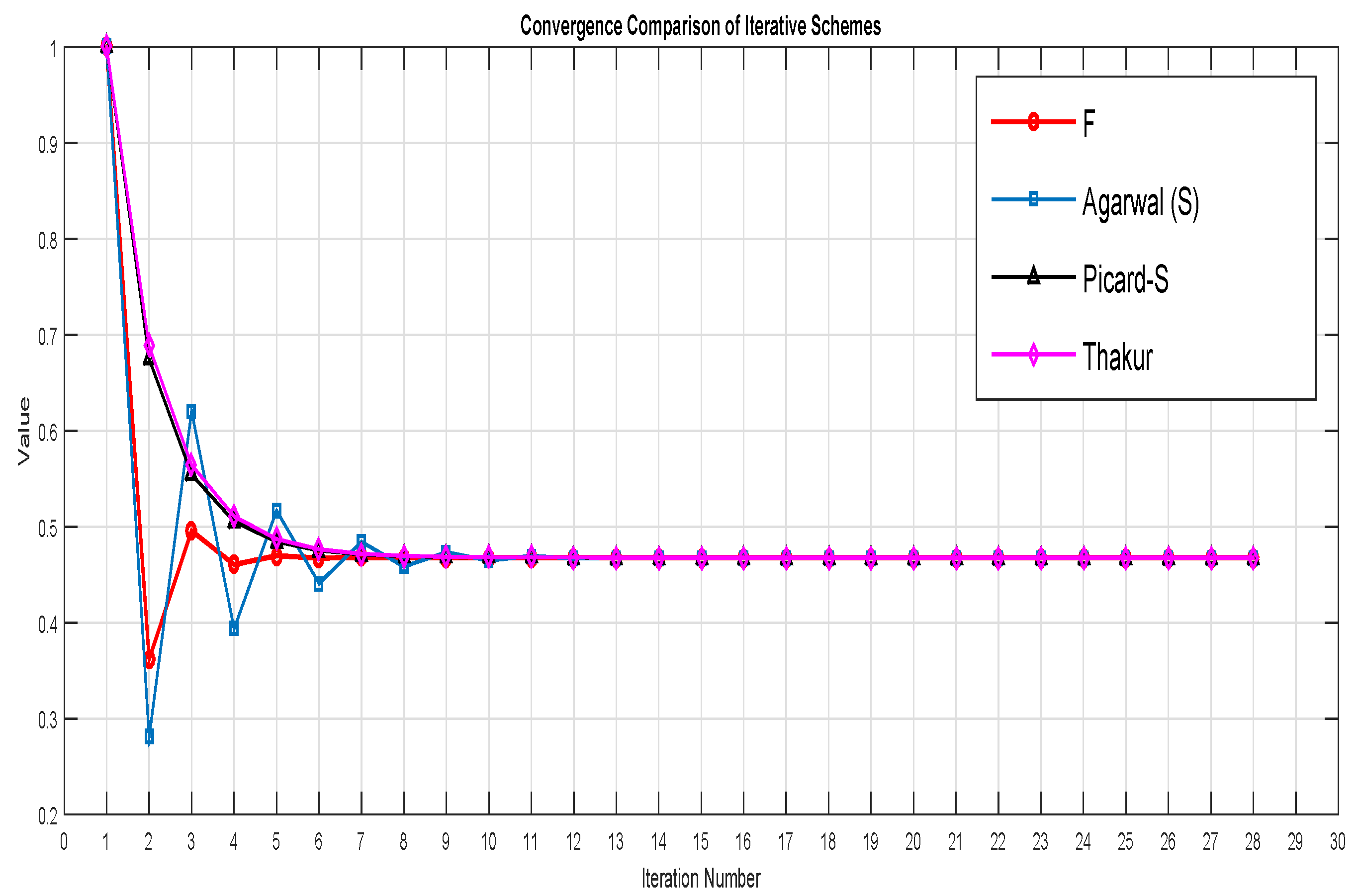
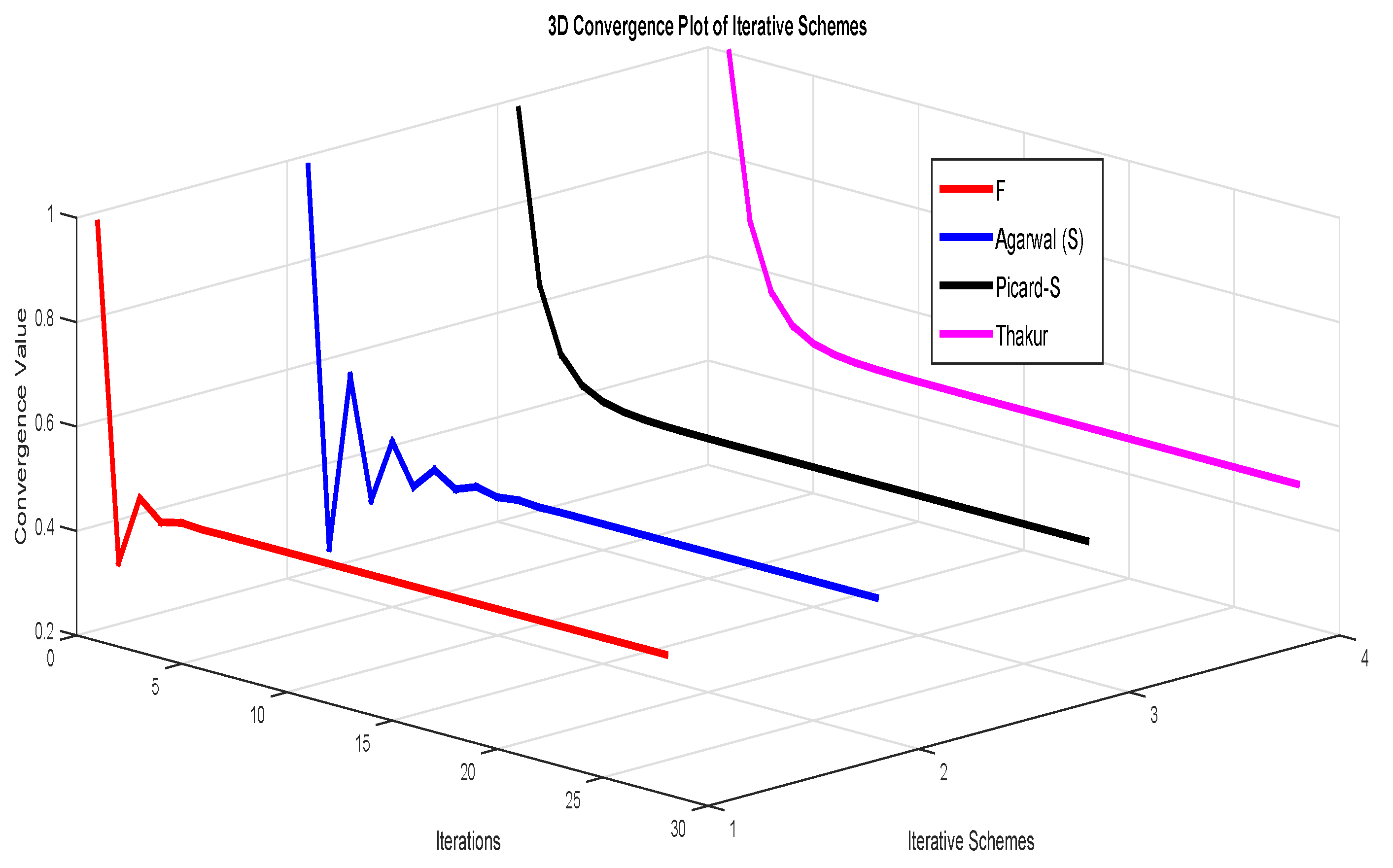
Sr. No.	F	Agarwal (S)	Picard-S	Thakur
1	1.000000	1.000000	1.000000	1.000000
2	0.361946	0.280523	0.674841	0.688141
3	0.495765	0.620713	0.554422	0.564395
4	0.460531	0.393557	0.505470	0.510906
5	0.469798	0.516776	0.484500	0.487153
6	0.467323	0.440975	0.475280	0.476516
7	0.467986	0.484251	0.471176	0.471741
8	0.467808	0.458440	0.469340	0.469596
9	0.467855	0.473438	0.468517	0.468632
10	0.467843	0.464592	0.468147	0.468199
11	0.467846	0.469762	0.467981	0.468004
12	0.467845	0.466725	0.467906	0.467917
⋮	⋮	⋮	⋮	⋮
20	0.467845	0.467830	0.467845	0.467845
⋮	⋮	⋮	⋮	⋮
28	0.467845	0.467845	0.467845	0.467845

and Figure 1 and Figure 2.

Remark 1. 

In the above figures, we can easily seen that all of the methods eventually converged to the same fixed point, which confirms the existence of the fixed point, thus aligning with the strong convergence results proved in the theoretical sections. The F iterative process defined in (4) exhibited significantly faster convergence, stabilizing at the fixed point in fewer steps, compared to all other classical schemes. The graphical results provide empirical validation for Theorems 3 and 4, which establish the strong convergence of the proposed iterative method under Suzuki’s enriched generalized nonexpansiveness.

Example 3. 

Let $U=\mathbb{R}$ be a uniformly convex Banach space and define a mapping $P:[0.1,2]\to [0.1,2]$ by

$$P\left(x\right)={\displaystyle \frac{1}{5x}}.$$

This mapping has a unique fixed point at

$$x^{*}=\sqrt{{\displaystyle \frac{1}{5}}}\approx 0.4472.$$

Let $P_{\lambda }\left(x\right)=(1-\lambda )x+\lambda P\left(x\right)$ with $\lambda ={\displaystyle \frac{1}{2}}$, and define the iterative process (4) with the control sequence $a_n=0.7$ and initial guess $w_0=1.2$ as follows:

$$\begin{array}{cc}\hfill x_n& =(1-a_n)w_n+a_n{P}_{\lambda }\left(w_n\right),\hfill \\ \hfill u_n& =P_{\lambda }\left(x_n\right),\hfill \\ \hfill v_n& =P_{\lambda }\left(u_n\right),\hfill \\ \hfill w_{n+1}& =P_{\lambda }\left(v_n\right),n\in \mathbb{N}.\hfill \end{array}$$

Then, the sequence $\left\{w_n\right\}$ converges to $x^{*}$.

Now, we compute the distance from $w_n$ to the fixed point set $F_{P_{\lambda }}=\left\{x^{*}\right\}$ as

$$d(w_n,F_{P_{\lambda }})=|w_n-x^{*}|.$$

We claim that

$$\underset{n\to \infty }{lim\; inf}d(w_n,F_{P_{\lambda }})=0.$$

Since the mapping P satisfies the enriched $\left(C\right)$ condition and the operator $P_{\lambda }$ is continuous, the sequence $\left\{w_n\right\}$ generated by the above iterative process is Fejér monotone with respect to $F_{P_{\lambda }}$, that is,

$$\parallel w_{n+1}-x^{*}\parallel \le \parallel w_n-x^{*}\parallel ,\forall n\in \mathbb{N}.$$

Hence, the sequence $\{\parallel w_n-x^{*}\parallel \}$ is non-increasing and bounded below by zero, so it converges as follows:

$$\underset{n\to \infty }{lim}\parallel w_n-x^{*}\parallel =\beta .$$

Since, by assumption ${lim\; inf}_{n\to \infty }d(w_n,F_{P_{\lambda }})=0$, we have

$$\beta =\underset{n\to \infty }{lim}\parallel w_n-x^{*}\parallel =0.$$

This confirms that

$$\underset{n\to \infty }{lim\; inf}d(w_n,F_{P_{\lambda }})=0.$$

Therefore, all the hypotheses of Theorem 3 are satisfied and we conclude that $\left\{w_n\right\}$ converges strongly to the fixed point $x^{*}$ of P.

Example 4. 

Let $U=\mathbb{R}$ be a uniformly convex Banach space and consider the closed convex subset $V=[0.5,2]\subset \mathbb{R}$. Define the mapping $P:V\to V$ by

$$P\left(x\right)={\displaystyle \frac{1}{2x}}.$$

The fixed point of P is obtained by solving $x={\displaystyle \frac{1}{2x}}\Rightarrow x^2={\displaystyle \frac{1}{2}}\Rightarrow x^{*}=\sqrt{{\displaystyle \frac{1}{2}}}\approx 0.7071$, so $F_P=\left\{x^{*}\right\}\ne \varnothing$.

Now, define the averaged mapping $P_{\lambda }\left(x\right)=(1-\lambda )x+\lambda P\left(x\right)$ and choose $\lambda =0.5$. Then,

$$P_{\lambda }\left(x\right)={\displaystyle \frac{1}{2}}x+{\displaystyle \frac{1}{2}}·{\displaystyle \frac{1}{2x}}={\displaystyle \frac{x}{2}}+{\displaystyle \frac{1}{4x}}.$$

Step 1: Verification of enriched $\left(C\right)$ condition. We show that there exists $b>0$, such that, for all $x,y\in V$, we have

$$\left|b(x-y)+P\left(x\right)-P\left(y\right)\right|\le (b+1)|x-y|.$$

Now,

$$P\left(x\right)-P\left(y\right)={\displaystyle \frac{1}{2x}}-{\displaystyle \frac{1}{2y}}={\displaystyle \frac{y-x}{2xy}},\mathit{and}\mathit{so}$$

$$\left|b(x-y)+{\displaystyle \frac{y-x}{2xy}}\right|=|x-y|·\left|b-{\displaystyle \frac{1}{2xy}}\right|\le (b+1)|x-y|$$

is satisfied for all $x,y\in V$ if $\left|b-{\displaystyle \frac{1}{2xy}}\right|\le b+1$. Since $x,y\in [0.5,2]\Rightarrow xy\in [0.25,4]$, so ${\displaystyle \frac{1}{2xy}}\in [0.125,2]$. In choosing $b=3$, we obtain

$$\left|3-{\displaystyle \frac{1}{2xy}}\right|\le 3-0.125=2.875<b+1=4,$$

and hence the enriched $\left(C\right)$ condition is satisfied.

Step 2: Verification of Condition $\left(I\right)$. We define the nondecreasing function $h:[0,\infty )\to [0,\infty )$ by $h\left(r\right)={\displaystyle \frac{r}{5}}$. Then, for any $x\in V$, we have

$$|x-P\left(x\right)|=\left|x-{\displaystyle \frac{1}{2x}}\right|=\left|{\displaystyle \frac{2x^2-1}{2x}}\right|.$$

We now show that $|x-P\left(x\right)|\ge h\left(\right|x-x^{*}\left|\right)$. Let us compute both for values near $x=1$ and $x^{*}\approx 0.7071$:

$|x-P(x\left)\right|=|1-0.5|=0.5$, $|1-x^{*}|\approx 0.2929$, $h\left(\right|1-x^{*}\left|\right)=0.2929/5\approx 0.0586$, and $0.5>0.0586$. Hence, $|x-P\left(x\right)|\ge h\left(\right|x-x^{*}\left|\right)$ holds for $h\left(r\right)=r/5$, verifying Condition $\left(I\right)$.

Step 3: Apply the Iterative Scheme (4). We generate the sequence $\left\{w_n\right\}$ using the following:

$$\begin{array}{cc}\hfill x_n& =(1-a_n)w_n+a_n{P}_{\lambda }\left(w_n\right),\hfill \\ \hfill u_n& =P_{\lambda }\left(x_n\right),\hfill \\ \hfill v_n& =P_{\lambda }\left(u_n\right),\hfill \\ \hfill w_{n+1}& =P_{\lambda }\left(v_n\right),\hfill \end{array}$$

with $a_n=0.5$ and $w_0=1.2\in V$. This defines an iterative scheme that converges strongly to $x^{*}\in F_P$, by Theorem 4, since P satisfies both the enriched $\left(C\right)$ condition and Condition $\left(I\right)$.

5. Application

In this section, we introduce an iterative scheme based on (4) for solving the split feasibility problem (SFP). Let $U_1$ and $U_2$ be two Hilbert spaces and let $S:U_1\to U_2$ be a linear and bounded operator. The SFP is given by the following formulation (see, e.g., [36] and others):

$$\mathrm{Find}{u}^{*}\in D\mathrm{such}\mathrm{that}S{p}^{*}\in E,$$

(6)

where $D\subseteq U_1$ and $E\subseteq U_2$ are compact, nonempty, and convex sets.

It is well known (see [33]) that various problems can be cast in the form of an SFP. We assume that (6) has at least one solution, and we denote the solution set by $P_S$. In [33], it was shown that $p^{*}\in D$ solves (6) if and only if it satisfies the following equation:

$$x=P_D\left(\mathrm{Id}-\nu S^{*}\left(\mathrm{Id}-P_E\right)S\right)x,$$

where $P_D$ and $P_E$ represent the nearest point projections onto D and E, respectively; $\nu >0$; and $S^{*}$ is the adjoint operator of S. Moreover, Byrne [37] demonstrated that, if $\eta$ is the spectral radius of $S^{*}S$ and $0<\nu <{\displaystyle \frac{2}{\eta }}$, then the operator

$$P=P_D\left(\mathrm{Id}-\nu S^{*}\left(\mathrm{Id}-P_E\right)S\right)$$

is nonexpansive. In this context, the iterative scheme

$$u_{n+1}=P_D\left(\mathrm{Id}-\nu S^{*}\left(\mathrm{Id}-P_E\right)S\right)u_n,n=0,1,2,\dots ,$$

is known to converge to a solution of (6).

In our approach, we focused on mappings satisfying the enriched $\left(C\right)$ condition, which may not necessarily be nonexpansive, as shown in Example 1. We propose the following modified iterative scheme based on (4).

Theorem 5. 

Suppose that the SFP (6) has a nonempty solution set $P_S$ and that $0<\nu <{\displaystyle \frac{2}{\eta }}$. Additionally, assume that $P_D\left(\mathit{Id}-\nu S^{*}\left(\mathit{Id}-P_E\right)S\right)$ satisfies the enriched $\left(C\right)$ condition. Let $\left\{a_n\right\}\subset (0,1)$ and consider the following iterative scheme:

$$\begin{array}{cc}\hfill w_0& \in D,\hfill \\ \hfill x_n& =(1-a_n)w_n+a_n{P}_D\left(\mathit{Id}-\nu S^{*}\left(\mathit{Id}-P_E\right)S\right)w_n,\hfill \\ \hfill u_n& =P_D\left(\mathit{Id}-\nu S^{*}\left(\mathit{Id}-P_E\right)S\right)x_n,\hfill \\ \hfill v_n& =P_D\left(\mathit{Id}-\nu S^{*}\left(\mathit{Id}-P_E\right)S\right)u_n,\hfill \\ \hfill w_{n+1}& =P_D\left(\mathit{Id}-\nu S^{*}\left(\mathit{Id}-P_E\right)S\right)v_n,n=0,1,2,\dots \hfill \end{array}$$

Thus, the sequence $\left\{w_n\right\}$ converges weakly to a fixed point $p^{*}\in P_S$, which provides a solution to the split feasibility problem (6).

Proof. 

Since every Hilbert space possesses the Opial property, we define

$$P=P_D\left(\mathrm{Id}-\nu S^{*}\left(\mathrm{Id}-P_E\right)S\right).$$

Under the assumption that $P_{\lambda }$ satisfies the enriched $\left(C\right)$ condition, it follows from Theorem 1 that the sequence $\left\{w_n\right\}$ converges weakly to a point in the fixed point set $F_P$. Since $F_P=P_S$, it follows that the sequence $\left\{w_n\right\}$ converges weakly to a solution $p^{*}\in P_S$ of the SFP (6). □

Theorem 6. 

Suppose that the SFP (6) has a nonempty solution set $P_S$ and that $0<\nu <{\displaystyle \frac{2}{\eta }}$. Additionally, assume that the operator $P_D\left(\mathit{Id}-\nu S^{*}\left(\mathit{Id}-P_E\right)S\right)$ satisfies the enriched $\left(C\right)$ condition. Let $\left\{a_n\right\}$ be a sequence in $(0,1)$ and consider the following iterative scheme:

$$\begin{array}{cc}\hfill w_0& \in D,\hfill \\ \hfill x_n& =(1-a_n)w_n+a_n{P}_D\left(\mathit{Id}-\nu S^{*}\left(\mathit{Id}-P_E\right)S\right)w_n,\hfill \\ \hfill u_n& =P_D\left(\mathit{Id}-\nu S^{*}\left(\mathit{Id}-P_E\right)S\right)x_n,\hfill \\ \hfill v_n& =P_D\left(\mathit{Id}-\nu S^{*}\left(\mathit{Id}-P_E\right)S\right)u_n,\hfill \\ \hfill w_{n+1}& =P_D\left(\mathit{Id}-\nu S^{*}\left(\mathit{Id}-P_E\right)S\right)v_n,n=0,1,2,\dots \hfill \end{array}$$

Then, the sequence $\left\{w_n\right\}$ converges strongly to a solution $p^{*}\in P_S$ of the SFP (6).

Proof. 

Let $P=P_D\left(\mathrm{Id}-\nu S^{*}\left(\mathrm{Id}-P_E\right)S\right)$. By assumption, $P_{\lambda }$ satisfies the enriched $\left(C\right)$ condition. Now, to establish strong convergence, we apply the condition that the set D is compact. From Theorem 2, we conclude that $\left\{w_n\right\}$ also converges strongly to the same limit $p^{*}$. Thus, the sequence $\left\{w_n\right\}$ converges strongly to a solution $p^{*}\in P_S$ of the SFP (6). □

6. Conclusions

In this paper, we propose and analyzed a new iterative method for solving the split feasibility problem (SFP) in the setting of uniformly convex Banach spaces (UCBSs). We established weak convergence of the proposed scheme under the assumption that the operator involved satisfies the enriched (C)-condition and that the underlying Banach space satisfies Opial’s condition. This result extends previous work where weak convergence was typically studied for similar iterative schemes.

Furthermore, we explored the strong convergence of the method, providing a detailed proof under the assumption that the operator involved satisfies the enriched (C)-condition and the sequence is generated with a suitable choice of step sizes. By leveraging known results for nonexpansive mappings and the geometry of Hilbert spaces, we established that the sequence converges strongly to a solution of the SFP, which is an important extension of the weak convergence result.

The results presented in this paper not only contribute to the theory of iterative methods for solving SFPs, but they also provide a framework for solving more general problems in optimization and applied mathematics, where such conditions are applicable. Our approach offers a reliable alternative to existing methods, with the added benefit of strong convergence under certain conditions, thus making it a promising tool for solving large-scale problems in computational mathematics.

Future work could focus on extending these results to more general classes of problems and developing practical algorithms for implementation in real-world scenarios.