A Linearized Conservative Finite Difference Scheme for the Rosenau–RLW Equation
Abstract
1. Introduction
2. Notations and Preliminaries
3. Finite Difference Scheme and Discrete Conservation Laws
4. Existence and Uniqueness of Numerical Solutions
5. Convergence and Stability of Numerical Solutions
6. Algorithm and Numerical Experiments
6.1. Algorithm
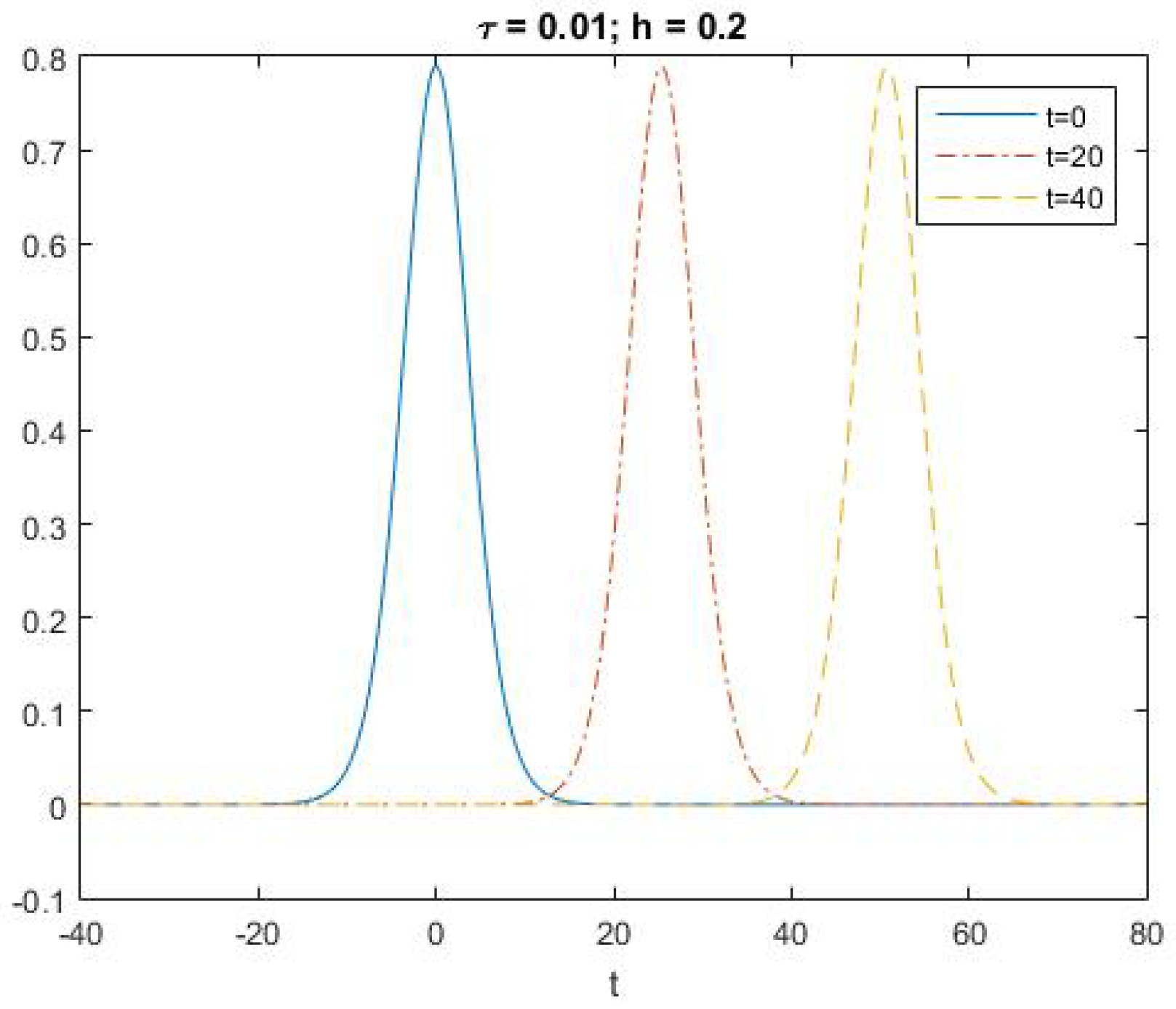
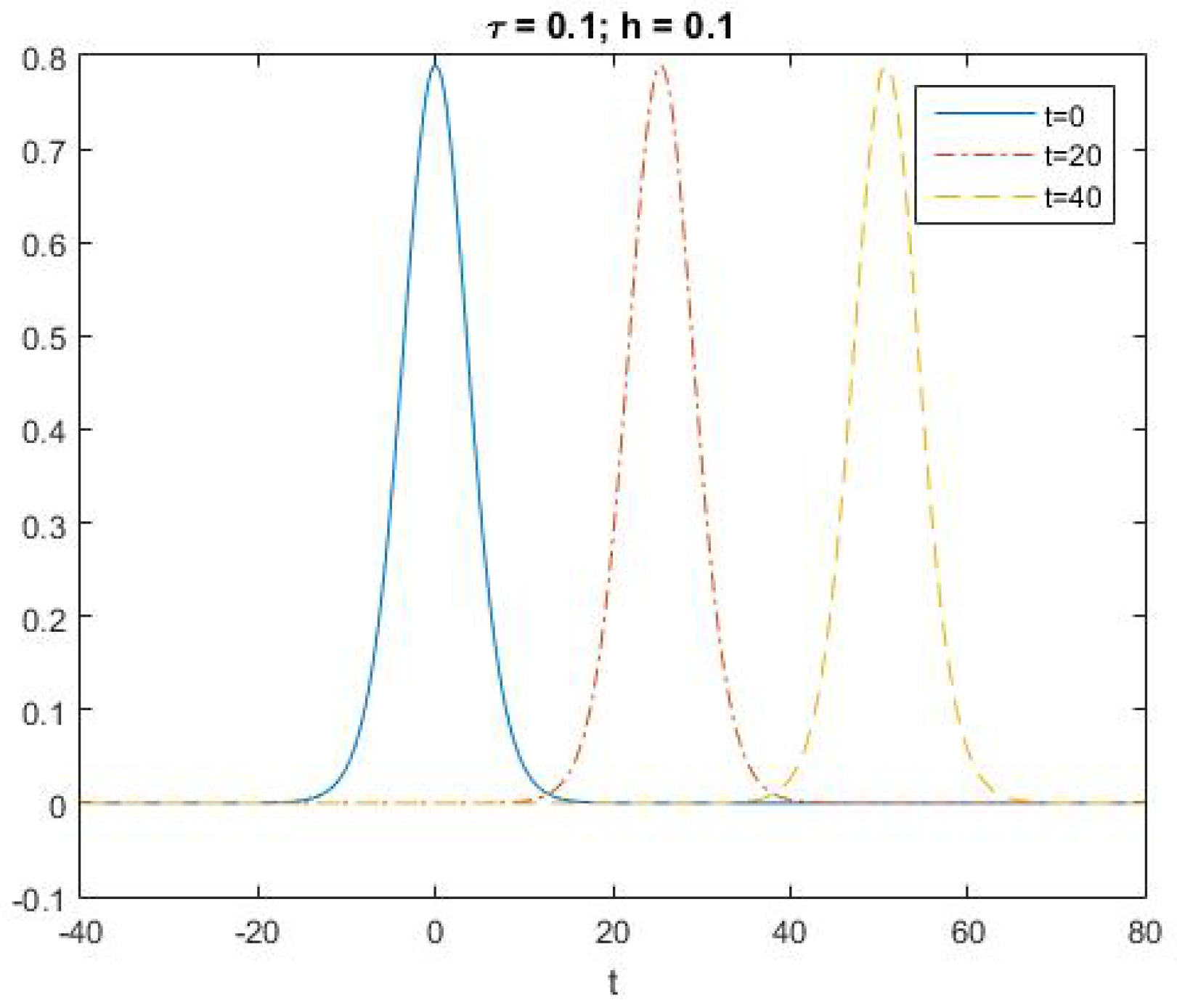
6.2. Numerical Experiments
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Rosenau–RLW | Rosenau–Regularized Long Wave. |
| KdV | Korteweg–de Vries. |
References
- Peregrine, D.H. Calculations of the development of an undular bore. J. Fluid Mech. 1966, 25, 321–330. [Google Scholar] [CrossRef]
- Peregrine, D.H. Long waves on a beach. J. Fluid Mech. 1967, 27, 815–827. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Analytic study on non-linear variants of the RLW and the PHI-Four equations. Commun. Nonlinear Sci. Numer. Simulat. 2007, 12, 314–327. [Google Scholar] [CrossRef]
- Mohammadi, M.; Mokhtari, R. Solving the generalized regularized long wave equation on the basis of a reproducing kernel space. J. Comput. Appl. Math. 2011, 235, 4003–4014. [Google Scholar] [CrossRef]
- Rosenau, P. A quasi-continuous description of a nonlinear transmission line. Phys. Scr. 1986, 34, 827–829. [Google Scholar] [CrossRef]
- Rosenau, P. Dynamics of dense discrete systems: High order effects. Prog. Theor. Phys. 1988, 79, 1028–1042. [Google Scholar] [CrossRef]
- Kim, Y.D.; Lee, H.Y. The convergence of finite element Galerkin solution for the Rosenau equation. Korean J. Comput. Appl. Math. 1998, 5, 171–180. [Google Scholar] [CrossRef]
- Chung, S.K.; Pani, A.K. Numerical methods for the Rosenau equation. Appl. Anal. 2001, 77, 351–369. [Google Scholar] [CrossRef]
- Hu, J.S.; Wang, Y.L. A high–accuracy linear conservative difference scheme for Rosenau–RLW equation. Math. Probl. Eng. 2013, 2013, 870291. [Google Scholar] [CrossRef][Green Version]
- Pan, X.T.; Zheng, K.L.; Zhang, L.M. Finite difference discretization of the Rosenau–RLW equation. Appl. Anal. 2013, 92, 2590–2601. [Google Scholar] [CrossRef]
- Zuo, J.M.; Zhang, Y.M.; Zhang, T.D.; Chang, F. A new conservative difference scheme for the general Rosenau-RLW equation. Bound. Value Probl. 2010, 2010, 516260. [Google Scholar] [CrossRef]
- Wang, H.; Li, S.G.; Wang, J. A conservative weighted finite difference scheme for the generalized Rosenau–RLW equation. Comput. Appl. Math. 2017, 3, 63–78. [Google Scholar] [CrossRef]
- Pan, X.T.; Zhang, L.M. On the convergence of a conservative numerical scheme for the usual Rosenau–RLW equation. Appl. Math. Model. 2012, 36, 3371–3378. [Google Scholar] [CrossRef]
- Wongsaijai, B.; Poochinapan, K. A three-level average implicit finite difference scheme to solve equation obtained by coupling the Rosenau–KdV equation and the Rosenau–RLW equation. Appl. Math. Comput. 2014, 245, 289–304. [Google Scholar] [CrossRef]
- Wongsaijai, B.; Mouktonglang, T.; Sukantamala, N.; Poochinapan, K. Compact structure-preserving approach to solitary wave in shallow water modeled by the Rosenau–RLW equation. Appl. Math. Comput. 2019, 340, 84–100. [Google Scholar] [CrossRef]
- Wongsaijai, B.; Poochinapan, K. Optimal decay rates of the dissipative shallow water waves modeled by coupling the Rosenau–RLW equation and the Rosenau–Burgers equation with power of nonlinearity. Appl. Math. Comput. 2021, 405, 126202. [Google Scholar] [CrossRef]
- Pan, X.T.; Wang, Y.J.; Zhang, L.M. Numerical analysis of a pseudo–compact C–N conservative scheme for the Rosenau–KdV equation coupling with the Rosenau–RLW equation. Bound. Value Probl. 2015, 2015, 65. [Google Scholar] [CrossRef]
- Ghiloufi, A.; Omrani, K. New conservative difference schemes with fourth–order accuracy for some model equation for nonlinear dispersive waves. Numer. Methods Partial. Differ. Equ. 2018, 34, 451–500. [Google Scholar] [CrossRef]
- Atouani, N.; Omrani, K. Galerkin finite element method for the Rosenau–RLW equation. Comput. Math. Appl. 2013, 66, 289–303. [Google Scholar] [CrossRef]
- Karakoc, S.B.G. A new numerical application of the generalized Rosenau–RLW equation. Sci. Iran. 2020, 27, 772–783. [Google Scholar] [CrossRef]
- Shi, D.; Jia, X. Superconvergence analysis of a mixed finite element approximation for the nonlinear fourth–order Rosenau–RLW equation. Comput. Math. Appl. 2021, 98, 169–180. [Google Scholar] [CrossRef]
- Kutluay, S.; Karta, M.; Uçar, Y. Strang time–splitting technique for the generalised Rosenau–RLW equation. PRAMANA-J. Phys. 2021, 95, 148. [Google Scholar] [CrossRef]
- Mustahsan, M.; Kiran, A.; Singh, J.; Nisar, K.S.; Kumar, D. Higher order B–spline differential quadrature rule to approximate generalized Rosenau–RLW equation. Math. Method. Appl. Sci. 2020, 43, 6812–6822. [Google Scholar] [CrossRef]
- Guo, C.; Li, F.; Zhang, W.; Luo, Y. A conservative numerical scheme for Rosenau–RLW equation based on multiple integral finite volume method. Bound. Value Probl. 2019, 2019, 168. [Google Scholar] [CrossRef]
- Ghiloufi, A.; Kadri, T. Analysis of new conservative difference scheme for two-dimensional Rosenau–RLW equation. Appl. Anal. 2017, 96, 1255–1267. [Google Scholar] [CrossRef]
- Li, S.G. Numerical analysis for fourth–order compact conservative difference scheme to solve the 3D Rosenau–RLW equation. Comput. Math. Appl. 2016, 72, 2388–2407. [Google Scholar] [CrossRef]
- Wang, X.F.; Dai, W.Z.; Yan, Y. Numerical analysis of a new conservative scheme for the 2D generalized Rosenau–RLW equation. Appl. Anal. 2021, 100, 2564–2580. [Google Scholar] [CrossRef]
- Tamang, N.; Wongsaijai, B.; Mouktonglang, T.; Poochinapan, K. Novel algorithm based on modification of Galerkin finite element method to general Rosenau–RLW equation in (2+1)–dimensions. Appl. Numer. Math. 2020, 148, 109–130. [Google Scholar] [CrossRef]
- Zhou, Y.L. Application of Discrete Functional Analysis to the Finite Difference Method; International Academic Publishers: Beijing, China, 1990. [Google Scholar]
- Zheng, K.L.; Hu, J.S. High–order conservative Crank–Nicolson scheme for regularized long wave equation. Adv. Differ. Equ. 2013, 2013, 287. [Google Scholar] [CrossRef]
- Fu, Y.Z.; Hu, B.; Zheng, M.B. Pseudo–compact Crank–Nicolson conservative difference scheme for Rosenau-RLW equations. J. Sichuan Univ. (Nat. Sci. Ed.) 2014, 51, 1143–1148. (In Chinese) [Google Scholar]
- Clainche, S.L.; Vega, J.M. Higher order dynamic mode decomposition. SIAM J. Appl. Dyn. Syst. 2017, 16, 882–925. [Google Scholar] [CrossRef]

| 6.7029 × | 1.6805 × | 4.2042 × | 2.6525 × | 6.6560 × | 1.6653 × | |
| 1.2440 × | 3.1213 × | 7.8109 × | 4.7213 × | 1.1855 × | 2.9670 × | |
| 1.7372 × | 4.3612 × | 1.0916 × | 6.3893× | 1.6058 × | 4.0197 × | |
| 2.1849 × | 5.4869 × | 1.3735 × | 7.8847 × | 1.9813 × | 4.9603 × | |
| – | 1.9959 | 1.9990 | – | 1.9946 | 1.9989 | |
| – | 1.9948 | 1.9986 | – | 1.9937 | 1.9984 | |
| – | 1.9940 | 1.9983 | – | 1.9924 | 1.9981 | |
| – | 1.9935 | 1.9981 | – | 1.9926 | 1.9979 | |
| 7.590639955020484 | 7.590639955020483 | 7.590639955020486 | |
| 7.590634665809471 | 7.590636068121576 | 7.590641816651537 | |
| 7.590634945172798 | 7.590637353103019 | 7.590647235368987 | |
| 7.590635182737761 | 7.590638486631225 | 7.590652070720461 | |
| 7.590657869703787 | 7.590752977258113 | 7.590646799689627 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Ren, L.; Hu, J.; Zheng, K. A Linearized Conservative Finite Difference Scheme for the Rosenau–RLW Equation. Axioms 2025, 14, 395. https://doi.org/10.3390/axioms14060395
Li Y, Ren L, Hu J, Zheng K. A Linearized Conservative Finite Difference Scheme for the Rosenau–RLW Equation. Axioms. 2025; 14(6):395. https://doi.org/10.3390/axioms14060395
Chicago/Turabian StyleLi, Yongzheng, Longcheng Ren, Jinsong Hu, and Kelong Zheng. 2025. "A Linearized Conservative Finite Difference Scheme for the Rosenau–RLW Equation" Axioms 14, no. 6: 395. https://doi.org/10.3390/axioms14060395
APA StyleLi, Y., Ren, L., Hu, J., & Zheng, K. (2025). A Linearized Conservative Finite Difference Scheme for the Rosenau–RLW Equation. Axioms, 14(6), 395. https://doi.org/10.3390/axioms14060395






