A Learning Path Recommendation Approach in a Fuzzy Competence Space

Abstract

This study proposes a learning path recommendation method based on fuzzy competence space theory. It is developed within the theoretical framework of knowledge space theory and fuzzy set theory, aiming to address the progressive nature of learners’ skill acquisition. The proposed method ensures that a learner can improve their knowledge state by increasing only one proficiency level of a skill at a time, thereby closely reflecting the incremental characteristics of real-world learning processes. Based on fuzzy skill mappings, this work systematically defines fuzzy competence states, fuzzy competence structures, and consistent fuzzy competence spaces. Then, given a consistent fuzzy competence space and a fuzzy skill mapping, the necessary and sufficient conditions for the existence of gradual and effective learning paths are proposed and proven under the disjunctive model. Finally, a gradual and effective learning path recommendation algorithm is designed, and its effectiveness is validated through simulation experiments. This method provides a theoretical foundation and algorithmic support for the development of adaptive learning systems and intelligent testing systems.

1. Introduction

Knowledge Space Theory (KST) is a mathematical framework for modeling and assessing an individual’s knowledge state, first introduced by Doignon and Falmagne [1]. Rooted in probabilistic measurement theory and mathematical psychology, KST evolved from foundational work in extensive measurement [2], multidimensional scaling [3,4,5], and conjoint measurement models [6,7]. Foundational contributions [1,8] established the theoretical basis for modeling knowledge structures based on logical dependencies among items. KST provides a formal mechanism to infer a person’s knowledge level in a specific domain based on their responses to a set of problems [9,10,11]. As the theory has evolved, KST has found applications in various domains—especially in educational psychology, artificial intelligence, and knowledge assessment—emerging as a powerful tool for evaluating individual knowledge states. Its successful applications include supporting learning, adaptive testing, and intelligent assessment systems [12,13,14,15].

During the evolution of KST, researchers gradually recognized that modeling a learner’s mastery solely based on a set of knowledge points has its limitations. Consequently, the incorporation of “competence” as an additional dimension has emerged as an important direction for extending KST [16,17,18]. Competence-based KST focuses on the holistic competence structures exhibited by learners in problem-solving, skill acquisition, and knowledge application, rather than simply judging responses as correct or incorrect [19]. This paradigm shift allows for a more nuanced representation of learner performance across varied tasks and contexts, enabling more targeted strategies for personalized instruction and assessment [20]. In terms of research methodology, many scholars have divided skills or competences into multiple dimensions or sub-skills, and employed hierarchical analyses based on cognitive process models or task structures to construct competence frameworks that more accurately reflect real-world learning scenarios [21]. Furthermore, several studies have explored multi-valued or multi-level competence states by modeling varying proficiency levels for the same skill, thereby enhancing the diagnostic and evaluative power of KST [22,23]. Competence-based KST not only more accurately captures the integrated mastery of knowledge and skills but also provides new perspectives and opportunities for personalized learning path planning, adaptive testing, and targeted instructional interventions [24,25,26,27,28].

To address the limitations of traditional KST in diagnostic precision and expressive diversity, researchers have integrated it with cognitive diagnosis theory, rough set theory, formal concept analysis, and fuzzy set theory, thereby enriching its representational capabilities from multiple perspectives [29,30,31,32]. In conjunction with cognitive diagnosis theory, research has focused on quantitatively evaluating learners’ fine-grained competencies by mapping item–attribute relationships, thereby improving the applicability of KST in individualized assessment [29]. In contrast, integrating rough set theory with KST addresses knowledge representation and reasoning under incomplete or uncertain information, offering more robust modeling approaches for learning states affected by noise or missing data [30]. Meanwhile, formal concept analysis, which depicts the lattice structures inherent in the associations among concepts, objects, and attributes, aligns well with the visualization and hierarchical characteristics of KST [33,34,35].

Among the extended approaches, integrating KST with fuzzy set theory has drawn particular attention. First introduced by Zadeh in 1965, fuzzy set theory provides a rigorous mathematical framework for representing and manipulating imprecise information [36]; it has since become a cornerstone technique in data science and artificial intelligence. Traditional KST typically adopts a dichotomous classification, labeling the learner’s mastery of a knowledge point or skill as either “mastered” or “not mastered”. However, in real learning scenarios, learners often exist in a fuzzy zone between full mastery and non-mastery. The integration of fuzzy set theory enables the representation of mastery levels through membership values, effectively overcoming the constraints of binary classifications [32]. Building on this foundation, researchers have proposed fuzzy skill maps to characterize the fuzzy relationships between skills and tasks or problems, enabling the construction of more flexible and accurate competence or knowledge structures [22,37,38]. Subsequent studies have explored the integration of fuzzy skill maps with graded proficiency levels to construct polytomous knowledge structures that more precisely capture the progressive mastery of learners at different stages [39]. These advancements lay a solid foundation for research on personalized learning path recommendation within fuzzy competence spaces, facilitating more nuanced diagnostic feedback and tailored instructional support.

Personalized learning path recommendation seeks to dynamically deliver suitable learning resources and task sequences tailored to learners’ diverse needs, current proficiency levels, and specific learning goals. These systems not only improve learning efficiency and alleviate the cognitive burden of information overload but also enhance learners’ engagement and motivation [40,41,42]. By leveraging big data and artificial intelligence, recent research has combined user profiling, knowledge graphs, and intelligent assessment techniques to design diverse learning path recommendation systems across various disciplines [43,44,45]. The incorporation of KST in this domain provides a logical and interpretable foundation for personalized recommendations by inferring learners’ knowledge states and prerequisite relationships. By identifying a learner’s current position within the knowledge structure, the system can predict the most appropriate next learning unit or assessment item [44,45,46]. Nevertheless, existing approaches primarily rely on binary or discretized evaluations of knowledge states, often neglecting the gradual and diverse nature of learners’ competence development. Consequently, such systems frequently fail to capture the dynamic progression from initial understanding to proficient mastery, which limits the precision and adaptability of personalized learning path recommendations.

As understanding of the learning process deepens, researchers have increasingly turned their attention to polytomous representations of knowledge and skills, culminating in the formalization of polytomous knowledge structures [46]. Compared to dichotomous knowledge structures, polytomous knowledge structures enable multi-level and continuous differentiation of the same knowledge point or skill, more accurately reflecting the gradual nature of learning [47]. Researchers have conducted systematic investigations into this concept, exploring aspects such as multi-level partitioning, structural closure, reachability, and their applications in assessment and instructional intervention [48,49]. These studies have yielded valuable insights for advancing personalized learning path recommendations.

Currently, most personalized learning path recommendation approaches based on KST primarily focus on “knowledge structures” by determining whether learners have mastered specific knowledge points or skills, while paying relatively little attention to the underlying competence structure—especially the application of fuzzy competence structures. This limitation results in recommendation systems that inadequately capture the gradual improvement in learners’ competence, making it difficult to fully represent the dynamic evolution from “initial mastery” to “proficient mastery”. To address these shortcomings, this paper proposes a learning path recommendation method based on fuzzy competence spaces. The proposed method ensures that learners can progressively improve their knowledge state by increasing only one proficiency level of a skill at a time, thereby closely mirroring real-world learning processes.

Specifically, this study formally defines fuzzy competence states, fuzzy competence structures, and consistent fuzzy competence spaces, laying a solid theoretical foundation. Moreover, it establishes and proves the necessary and sufficient conditions for the existence of gradual and effective learning paths under the disjunctive model. Furthermore, the study designs a learning path recommendation algorithm that respects the principle of single-skill incremental learning. The proposed approach is validated through rigorous simulation experiments, demonstrating its practical feasibility and applicability. Collectively, these contributions provide robust theoretical and algorithmic support for the development and implementation of intelligent assessment and adaptive learning systems.

The remainder of this paper is structured as follows. Section 2 introduces theoretical preliminaries. Section 3 presents the fuzzy competence framework. Section 4 describes the proposed learning path recommendation algorithm. Section 5 reports the results of simulation experiments. Section 6 concludes the paper and outlines potential directions for future research.

2. Preliminaries

This section briefly reviews the core concepts of knowledge space theory and fuzzy skills. Comprehensive treatments of these notions can be found in [1,22].

Definition 1

([1]). Let $Q$ be a nonempty finite set of problems. In an ideal state (i.e., free from distractions such as carelessness or guessing), the subset of $Q$ that an individual can correctly answer is called the individual’s knowledge state, denoted by $K$, where $K\subseteq Q$. Both $\varnothing$ and $Q$ can also be viewed as knowledge states. $\varnothing$ indicates that the individual cannot solve any problem in $Q$, while $Q$ indicates that the individual can solve all problems. We use the pair $\left(Q,\mathcal{K}\right)$ to denote the family of all such knowledge states, referred to as a knowledge structure. When there is no confusion, we simply use $\mathcal{K}$ to represent the knowledge structure $\left(Q,\mathcal{K}\right)$. If for any $K_1,K_2\in \mathcal{K}$ it holds that $K_1\cup K_2\in \mathcal{K}$, then $\left(Q,\mathcal{K}\right)$ is called a knowledge space.

When the knowledge structure is a knowledge space, it implies that individuals can learn from and collaborate with each other to solve problems that one cannot answer but the other can. In this way, both parties’ knowledge states are integrated and enhanced.

Definition 2

([22]). Let $Q$ be a nonempty finite set of problems and let $S$ be a nonempty finite set of skills related to solving problems in $Q$. $\mathcal{F}\left(S\right)$ is defined as follows:

$$\mathcal{F}\left(S\right)=\left\{T|T:S\to \left[0,1\right]\right\},$$

(1)

where $T:S\to \left[0,1\right]$ is a mapping from the skill set $S$ to the interval $\left[0,1\right]$. It can be written as follows:

$$T=\left\{\left(s,T\left(s\right)\right)|s\in S\right\},$$

(2)

with $T\left(s\right)\in \left[0,1\right]$ for all $s\in S$.

From the perspective of fuzzy sets, $T$ can be regarded as a fuzzy set, where $T\left(s\right)$ denotes the membership degree of element $s$ in the fuzzy set $T$. For any $T\in \mathcal{F}\left(S\right)$ and $s\in S$, $T$ represents the individuals’ potential competence state, referred to as a fuzzy competence state, and $T\left(s\right)$ indicates the individuals’ level of mastery of skill $s$.

Some operations defined on $\mathcal{F}\left(S\right)$ are as follows:

$$T_1\subseteq T_2\iff T_1\left(s\right)\le T_2\left(s\right), \forall s\in S;$$

(3)

$$\left(T_1\cup T_2\right)\left(s\right)=max\left\{T_1\left(s\right),T_2\left(s\right)\right\}, \forall s\in S;$$

(4)

$$\left(T_1\cap T_2\right)\left(s\right)=min\left\{T_1\left(s\right),T_2\left(s\right)\right\}, \forall s\in S.$$

(5)

Traditional competence states record only the skills that an individual has mastered and can be written as $T=\left\{s|s\in S\right\}$. By contrast, a fuzzy competence state specifies a degree of mastery for every skill, thereby capturing an individual’s competence more accurately.

Definition 3

([22]). The triple $\left(Q,S,\tau \right)$ is called a fuzzy skill mapping, where $Q$ and $S$ denote nonempty finite sets of problems and skills, respectively, and

$$T=\left\{\left(s,T\left(s\right)\right)|s\in S\right\}.$$

(6)

For any $q\in Q$, $\tau \left(q\right)$ indicates the minimum skill level required to solve $q$, denoted by ${\tau }_q$. If ${\tau }_q\left(s\right)=0$, it implies that skill $s$ is irrelevant to the solution of problem $q$.

Under the disjunctive model, for the individuals with a fuzzy competence state $T$, they can solve a problem $q$ as long as there exists a skill $s$ for which the individuals’ mastery level $T\left(s\right)$ is not lower than the minimum requirement ${\tau }_q\left(s\right)$ for that problem. Therefore, the knowledge state of the individuals with fuzzy competence state $T$ can be expressed as follows:

$$K=\left\{q\in Q|\exists s\in S,{0<\tau }_q\left(s\right)\le T\left(s\right)\right\}$$

(7)

Example 1.

Consider a fuzzy skill mapping $\left(Q,S,\tau \right)$, where $Q=\left\{q_1,q_2\right\}$, $S=\{\hspace{0.17em}{s}_1,s_2,s_3\}$, $\tau \left(q_1\right)=\{\hspace{0.17em}\left(s_1,0\right),\left(s_2,0.5\right),\left(s_3,0.5\right)\}$, and $\tau \left(q_2\right)=\{\hspace{0.17em}\left(s_1,0.5\right),\left(s_2,0.7\right),\left(s_3,0\right)\}$. Suppose an individual’s fuzzy competence state is $T_1=\{\hspace{0.17em}\left(s_1,0.3\right),\left(s_2,0\right),\left(s_3,0.3\right)\}$. Since solving $q_1$ does not require skill $s_1$, and the minimum mastery levels for $s_2$ and $s_3$ are both 0.5, this individual cannot solve$q_1$. Similarly, they cannot solve $q_2$, and thus their knowledge state is $\varnothing$. If another individual has a competence state $T_2=\{\hspace{0.17em}\left(s_1,0.5\right),\left(s_2,0.5\right),\left(s_3,0\right)\}$, they can solve both $q_1$ and $q_2$, and hence their knowledge state is $\{\hspace{0.17em}{q}_1,q_2\}$.

In practice, fuzzy skill mappings are usually defined by domain experts. Nevertheless, there is no consistent standard for specifying the exact values of $\tau \left(q\right)$, and the values of $T\left(s\right)$ are often determined retrospectively. In Example 1, if we consider another competence state $T$ such that $T\left(s_1\right)=T\left(s_3\right)=0$, but the individual can still solve $q_1$, it implies that there is a certain range constraint for $T\left(s_2\right)$ (for instance, $0.5\le T\left(s_2\right)<0.7$). If we change ${\tau }_{q_2}\left(s_2\right)$ from $0.7$ to $0.6$, this range-based judgment remains unaffected, indicating that small adjustments to certain skill thresholds do not alter the individual’s set of solvable problems.

3. Fuzzy Competence Space

In general, $T\in \mathcal{F}\left(S\right)$ is not necessarily a valid fuzzy competence state. For instance, consider an object-oriented programming context where skill $s_1$ represents “declaring a class” and skill $s_2$ represents “declaring a derived class”. If an individual’s competence state is $T=\{\left(s_1,0.95\right),\left(s_2,0\right)\}$, it indicates that the person has a solid grasp of “declaring a class” but has not begun learning “declaring a derived class”. In this example, it is clear that $T=\{\left(s_1,0\right),\left(s_2,0.95\right)\}$ cannot be a valid fuzzy competence state because it conflicts with the learning progression required in object-oriented programming, where “declaring a class” is fundamental to “declaring a derived class”. We next discuss the concept of a fuzzy competence structure.

Definition 4

([50]). Let $U$ be a nonempty finite set and denote

$$\mathcal{B}=\left\{B_i\subseteq U|i\in I\right\}.$$

(8)

Here $I$ is an index set. A subset $X \subseteq U$ is called a transversal of the family $\mathcal{B}$. If there exists a bijection $\phi :X\to I$ such that for every $x\in X$, it holds that $x\in B_{\phi \left(x\right)}$.

For example, let $U=\left\{u_1,u_2,u_3,u_4\right\}$ and $\mathcal{B}=\left\{B_1,B_2\right\}$, where $B_1=\left\{u_1,u_2\right\}$ and $B_2=\left\{u_3,u_4\right\}$. Suppose $X=\left\{u_1,u_3\right\}$ and there is a bijection $\phi :X\to I$ with $I=\left\{1,2\right\}$. Let $\phi \left(u_1\right)=1$ and $\phi \left(u_3\right)=2$. Then, $u_1\in B_{\phi \left(u_1\right)}$ and $u_3\in B_{\phi \left(u_3\right)}$, so $X$ is a transversal of $\mathcal{B}$. Similarly, $\left\{u_1,u_4\right\}$, $\left\{u_2,u_3\right\}$, and $\left\{u_2,u_4\right\}$ are also transversals of $\mathcal{B}$.

Given a skill set $S$, for each $s\in S$, let $\left(P_s,{\le }_s\right)$ be a nonempty finite set of numerical values, where $P_s$ represents all possible “response values” (or proficiencies) of skill $s$, with $1$ as the maximum element and $0$ as the minimum element. The relation ${\le }_s$ retains the usual ordering of real numbers. Define

$$S\times P_s={\bigcup }_{s\in S}\left\{s\right\}\times P_s,$$

(9)

which is the set of all pairs formed by each skill and its possible proficiency values. Let $\left\{\left\{s\right\}\times P_s:s\in S\right\}$ be the family of subsets built from each skill and its proficiency values. A transversal of this family is denoted by $T$, with the requirement that there exists a bijection $\phi :T\to S$ such that for any $\left(s,p_s\right)\in T$ we have $\phi \left(s,p_s\right)=s$, where $p_s\in P_s$.

Example 2.

Let $S=\left\{s_1,s_2\right\}$, with $P_{s_1}=\left\{0,0.5,1\right\}$ and $P_{s_2}=\left\{0,1\right\}$. Then

$$S\times P_s=\left\{\left(s_1,0\right),\left(s_1,0.5\right),\left(s_1,1\right),\left(s_2,0\right),\left(s_2,1\right)\right\} and$$

$$\left\{\left\{s\right\}\times P_s:s\in S\right\}=\left\{\left\{\left(s_1,0\right),\left(s_1,0.5\right),\left(s_1,1\right)\right\},\left\{\left(s_2,0\right),\left(s_2,1\right)\right\}\right\}.$$

Let $T$ be a transversal of $\left\{\left\{s\right\}\times P_s:s\in S\right\}$ and suppose there is a bijection $\phi :T\to S$ such that for any $\left(s,p_s\right)\in T$ we have $\phi \left(s,p_s\right)=s$. Denote by $P_s^S$ the family of all such transversals. Consequently, we obtain the following:

$$P_s^S=\left\{\left\{\left(s_1,0\right),\left(s_2,0\right)\right\},\left\{\left(s_1,0\right),\left(s_2,1\right)\right\},\left\{\left(s_1,0.5\right),\left(s_2,0\right)\right\},\left\{\left(s_1,0.5\right),\left(s_2,1\right)\right\},\left\{\left(s_1,1\right),\left(s_2,0\right)\right\},\left\{\left(s_1,1\right),\left(s_2,1\right)\right\}\right\}$$

Based on the above, we now introduce the definition of a fuzzy competence structure.

Definition 5.

Let $S$ be a nonempty finite set of skills and for each $s\in S$, let $\left(P_s,{\le }_s\right)$ be a finite set of numerical values whose minimum element is $0$ and maximum element is $1$. Let $P_s^S$ denote the family of all transversals of $\left\{\left\{s\right\}\times P_s|s\in S\right\}$. Suppose there exists a subset $\mathcal{C}\subseteq P_s^S$ satisfying $S\times \left\{0\right\}\in \mathcal{C}$, $S\times \left\{1\right\}\in \mathcal{C}$ and $\left\{\left(s,p_s\right)\in T|T\in \mathcal{C}\right\}=S\times P_s$. Then, the triple $\left(S,P_s,\mathcal{C}\right)$ is called a fuzzy competence structure and any $T\in \mathcal{C}$ is referred to as a fuzzy competence state.

Example 3.

Let $S=\left\{s_1,s_2,s_3\right\}$ with $P_{s_1}=P_{s_3}=\left\{0,0.5,1\right\}$ and $P_{s_2}=\left\{0,0.4,0.8,1\right\}$. Let $P_s^S$ be the family of all transversals of $\left\{\left\{s\right\}\times P_s|s\in S\right\}$. There are $36$ such transversals in total, and each corresponds to one state.

Table 1. A sample of fuzzy competence states.

$\mathit{T}$	Fuzzy Competence State	$\mathit{T}$	Fuzzy Competence State
$T_1$	$\left\{\left(s_1,0\right),\left(s_2,0\right),\left(s_3,0\right)\right\}$	$T_{13}$	$\left\{\left(s_1,1\right),\left(s_2,0.4\right),\left(s_3,0.5\right)\right\}$
$T_2$	$\left\{\left(s_1,0\right),\left(s_2,0\right),\left(s_3,0.5\right)\right\}$	$T_{14}$	$\left\{\left(s_1,1\right),\left(s_2,0.8\right),\left(s_3,0.5\right)\right\}$
$T_3$	$\left\{\left(s_1,0\right),\left(s_2,0\right),\left(s_3,1\right)\right\}$	$T_{15}$	$\left\{\left(s_1,1\right),\left(s_2,1\right),\left(s_3,0.5\right)\right\}$
$T_4$	$\left\{\left(s_1,0\right),\left(s_2,0.4\right),\left(s_3,0.5\right)\right\}$	$T_{16}$	$\left\{\left(s_1,0.5\right),\left(s_2,0\right),\left(s_3,1\right)\right\}$
$T_5$	$\left\{\left(s_1,0\right),\left(s_2,0.8\right),\left(s_3,0.5\right)\right\}$	$T_{17}$	$\left\{\left(s_1,0.5\right),\left(s_2,0.4\right),\left(s_3,1\right)\right\}$
$T_6$	$\left\{\left(s_1,0\right),\left(s_2,1\right),\left(s_3,0.5\right)\right\}$	$T_{18}$	$\left\{\left(s_1,0.5\right),\left(s_2,0.8\right),\left(s_3,1\right)\right\}$
$T_7$	$\left\{\left(s_1,0\right),\left(s_2,1\right),\left(s_3,1\right)\right\}$	$T_{19}$	$\left\{\left(s_1,0.5\right),\left(s_2,1\right),\left(s_3,1\right)\right\}$
$T_8$	$\left\{\left(s_1,0.5\right),\left(s_2,0\right),\left(s_3,0.5\right)\right\}$	$T_{20}$	$\left\{\left(s_1,1\right),\left(s_2,0\right),\left(s_3,1\right)\right\}$
$T_9$	$\left\{\left(s_1,0.5\right),\left(s_2,0.4\right),\left(s_3,0.5\right)\right\}$	$T_{21}$	$\left\{\left(s_1,1\right),\left(s_2,0.4\right),\left(s_3,1\right)\right\}$
$T_{10}$	$\left\{\left(s_1,0.5\right),\left(s_2,0.8\right),\left(s_3,0.5\right)\right\}$	$T_{22}$	$\left\{\left(s_1,1\right),\left(s_2,0.8\right),\left(s_3,1\right)\right\}$
$T_{11}$	$\left\{\left(s_1,0.5\right),\left(s_2,1\right),\left(s_3,0.5\right)\right\}$	$T_{23}$	$\left\{\left(s_1,1\right),\left(s_2,1\right),\left(s_3,1\right)\right\}$
$T_{12}$	$\left\{\left(s_1,1\right),\left(s_2,0\right),\left(s_3,0.5\right)\right\}$

lists $23$ of these states, denoted by $T_i\in P_s^S$ for $1\le i\le 23$. In particular, $T_1=S\times \left\{0\right\}$ and $T_{23}=S\times \left\{1\right\}$, and it holds that $\left\{\left(s,p_s\right)\in T_i|1\le i\le 23\right\}=S\times P_s$. By Definition 5, the family of these states forms a fuzzy competence structure $\left(S,P_s,\mathcal{C}\right)$. Any $T_i\in \mathcal{C}$ is regarded as a fuzzy competence state in $\left(S,P_s,\mathcal{C}\right)$.

Definition 6.

Let $\left(S,P_s,\mathcal{C}\right)$ be a fuzzy competence structure and let $\left(Q,S,\tau \right)$ be a given fuzzy skill mapping. For any $T\in \mathcal{C}$, under the disjunctive model, define the following:

$$K=\left\{q\in Q|\exists s\in S,{0<\tau }_q\left(s\right)\le T\left(s\right)\right\},$$

(10)

and denote $m\left(T\right)=K$. Then, $m$ is called the fuzzy disjunctive problem function corresponding to $\left(Q,S,\tau \right)$. Moreover, define the following:

$$\mathcal{K}=\left\{K|K=m\left(T\right),T\in \mathcal{C}\right\}$$

(11)

as the knowledge structure induced by $\left(S,P_s,\mathcal{C}\right)$ and $\left(Q,S,\tau \right)$ under the disjunctive model.

Proposition 1.

Let $\left(S,P_s,\mathcal{C}\right)$ be a fuzzy competence structure and let $\left(Q,S,\tau \right)$ be a fuzzy skill mapping. Suppose $m$ is the fuzzy disjunctive problem function corresponding to $\left(Q,S,\tau \right)$. Then, the following three properties hold:

(1) 

$m:\mathcal{C}\to \mathcal{K}$ is surjective;

(2) 

$m(S\times \left\{0\right\})=\varnothing$and $m(S\times \left\{1\right\})=Q$;

(3) 

if $T_1,T_2\in \mathcal{C}$ and $T_1\subseteq T_2$, then $m\left(T_1\right)\subseteq m\left(T_2\right)$.

Proof. 

(1) By Definition 6, $\mathcal{K}=\left\{K|K=m\left(T\right),T\in \mathcal{C}\right\}$. Hence, for every knowledge state $K\in \mathcal{K}$, there is at least one $T\in \mathcal{C}$ such that $m\left(T\right)=K$. Therefore, $m$ is surjective.

(2) When $T=S\times \left\{0\right\}$, for all $s\in S$, $T\left(s\right)=0.$ Thus, for all $q\in Q$, there is no $s\in S$ such that $0<{\tau }_q\left(s\right)\le T\left(s\right)$. Consequently, $m(S\times \left\{0\right\})=\varnothing$. When $T=S\times \left\{1\right\}$, for all $q\in Q$ and $s\in S$, ${\tau }_q\left(s\right)\le 1=T\left(s\right)$. Therefore, $m(S\times \left\{1\right\})=Q$.

(3) Suppose $T_1\subseteq T_2$. Then, $T_1\left(s\right)\le T_2\left(s\right)$ for all $s\in S$. If $q\in m\left(T_1\right)$, there exists some $s\in S$ such that ${\tau }_q\left(s\right)\le T_1\left(s\right)\le T_2\left(s\right)$. Hence, $q\in m\left(T_2\right)$, implying $m\left(T_1\right)\subseteq m\left(T_2\right)$. □

Example 4 (Continuation of Example 3).

Given $Q=\left\{q_1,q_2,q_3,q_4,q_5\right\}$, the fuzzy skill mapping is shown in

Table 2. Fuzzy skill mapping table.

$\mathit{Q}$	$\mathit{\tau }\left(\mathit{q}\right)$
$q_1$	$\left\{\left(s_1,0\right),\left(s_2,0\right),\left(s_3,0.5\right)\right\}$
$q_2$	$\left\{\left(s_1,0\right),\left(s_2,0\right),\left(s_3,0.7\right)\right\}$
$q_3$	$\left\{\left(s_1,0.3\right),\left(s_2,0.5\right),\left(s_3,0\right)\right\}$
$q_4$	$\left\{\left(s_1,0.7\right),\left(s_2,0.5\right),\left(s_3,0.5\right)\right\}$
$q_5$	$\left\{\left(s_1,0\right),\left(s_2,0.8\right),\left(s_3,0\right)\right\}$

, and the corresponding knowledge states and fuzzy competence states are presented in

Table 3. Fuzzy Competence States and Corresponding Knowledge States.

$\mathit{T}$	$\mathit{m}\left(\mathit{T}\right)$
$T_1$	$\varnothing$
$T_2,T_4$	$\left\{q_1\right\}$
$T_3$	$\left\{q_1,q_2\right\}$
$T_8,T_9$	$\left\{q_1,q_3\right\}$
$T_{12},T_{13}$	$\left\{q_1,q_3,q_4\right\}$
$T_{16},T_{17}$	$\left\{q_1,q_2,q_3\right\}$
$T_{20},T_{21}$	$\left\{q_1,q_2,q_3,q_4\right\}$
$T_5,T_6,T_{10},T_{11},T_{14},T_{15}$	$\left\{q_1,q_3,q_4,q_5\right\}$
$T_7,T_{18},T_{19},T_{22},T_{23}$	$Q$

. As shown in Table 2, solving problem $q_1$ is independent of skills $s_1$ and $s_2$ and requires at least a proficiency level of $0.5$ in skill $s_3$ to solve it. Therefore, individuals with fuzzy competence states $T_2$ and $T_4$ both have the knowledge state $\left\{q_1\right\}$. This case demonstrates that although individuals may have varying levels of proficiency in different skills, their knowledge state can be determined based on the fuzzy competence state. For instance, if an individual’s proficiency in skill $s_3$ is $0.5$ or higher, they are able to solve problem $q_1$, and no higher proficiency level is required.

The fuzzy competence structure is merely a pre-established evaluation criterion. For example, in the IELTS exam, some candidates achieve a score of 7 but do not reach 7.5. These candidates may have varying levels of English proficiency, but the IELTS exam cannot further differentiate their proficiency levels. Therefore, the form of the fuzzy competence structure and the specification of the fuzzy skill mapping are independent of each other. In Example 3, for an individual whose knowledge state is $\left\{q_1,q_2\right\}$, their fuzzy competence state will be determined as $T_3$. Naturally, since skill acquisition is a continuous process, a learner’s proficiency in skill $s_1$ could be $0.2$ or some other value; however, such granularity is not captured in this fuzzy competence structure.

Definition 7.

Given a fuzzy competence structure $\left(S,P_s,\mathcal{C}\right)$, if for any $T_1,T_2\in \mathcal{C}$, it holds that $T_1\cup T_2\in \mathcal{C}$, then $\left(S,P_s,\mathcal{C}\right)$ is called a fuzzy competence space.

Proposition 2.

Given a fuzzy competence structure$\left(S,P_s,\mathcal{C}\right)$ and a defined fuzzy skill mapping $\left(Q,S,\tau \right)$, the knowledge structure $\mathcal{K}$ induced by $\left(S,P_s,\mathcal{C}\right)$ and $\left(Q,S,\tau \right)$ is a knowledge space.

Proof. 

For any $K_1,K_2\in \mathcal{K}$, there exist $T_1,T_2\in \mathcal{C}$. From Proposition 1(3), we obtain $m\left(T_1\right)\subseteq m(T_1\cup T_2)$ and $m\left(T_2\right)\subseteq m(T_1\cup T_2)$, so $m\left(T_1\right)\cup m\left(T_2\right)\subseteq m(T_1\cup T_2)$ holds. For any $q\in m(T_1\cup T_2)$, there exists a skill $s\in S$ such that $0{<\tau }_q\left(s\right)\le (T_1\cup T_2)\left(s\right)=max\left\{T_1\left(s\right),T_2\left(s\right)\right\}$, thus ${0<\tau }_q\left(s\right)\le T_1\left(s\right)$ or $0{<\tau }_q\left(s\right)\le T_2\left(s\right)$. Therefore $q\in m\left(T_1\right)$ or $q\in m\left(T_2\right)$, so $m(T_1\cup T_2)\subseteq m\left(T_1\right)\cup m\left(T_2\right)$ holds. In conclusion, $K_1\cup K_2=m\left(T_1\right)\cup m\left(T_2\right)=m(T_1\cup T_2)\in \mathcal{K}$. By Definition 1, $\mathcal{K}$ is a knowledge space. □

Definition 8.

Given a fuzzy competence structure $\left(S,P_s,\mathcal{C}\right)$, we define the following operations and symbols:

(1) 

For any $T\in \mathcal{C}$, let

$$\left|T\right|=\left|\left\{s\in S|T\left(s\right)>0\right\}\right|,$$

(12)

where the absolute value symbol indicates the number of elements in the set.

(2) 

For any $T_1,T_2\in \mathcal{C}$, if $T_1\subseteq T_2$, define

$$T_2\setminus T_1=\left\{s\in S|T_2\left(s\right)-T_1\left(s\right)>0\right\};$$

(13)

(3) 

For any $P_s=\left\{p_1,p_2,\dots ,p_{\left|P_s\right|}\right\}$, where $0=p_1,p_2,\dots ,p_{\left|P_s\right|}=1$ for $1\le i<j\le \left|P_s\right|$, define

$$\Delta \left(p_i,p_j\right)=j-i;$$

(14)

(4) 

For any $T_1,T_2\in \mathcal{C}$, if $T_1\subseteq T_2$, define

$$\Delta \left(T_1,T_2\right)={\sum }_{s\in S}\Delta \left(T_1\left(s\right),T_2\left(s\right)\right).$$

(15)

In Example 3, a fuzzy competence state chain of the form $T_1\subseteq T_2\subseteq T_3\subseteq T_{16}\subseteq T_{20}\subseteq T_{21}\subseteq T_{22}\subseteq T_{23}$, adjacent fuzzy competence states $T_i\subseteq T_j$ satisfy $\left|T_j\setminus T_i\right|=1$, and $\Delta \left(T_i,T_j\right)=1$.

Definition 9.

Given a fuzzy competence structure $\left(S,P_s,\mathcal{C}\right)$, if $\mathcal{C}$ satisfies the following two properties, then $\left(S,P_s,\mathcal{C}\right)$ is called consistent:

(1) 

For any $T,T^{\prime }\in \mathcal{C}$, if $T\subseteq T^{\prime }$, there exist $T_0,T_1,\dots ,T_n\in \mathcal{C}$ such that $T$ = $T_0\subseteq T_1\subseteq \dots \subseteq T_n=T^{\prime }$, and $\left|T_i\setminus T_{i-1}\right|=1$, where $1\le i\le n$;

(2) 

For any $T,T^{\prime }\in \mathcal{C}$, if $T\subseteq T^{\prime }$, and $\left|T^{\prime }\setminus T\right|=1$, suppose $\left(T^{\prime }\setminus T\right)\left(s\right)>0$, then there exist $T_0,T_1,\dots ,T_n\in \mathcal{C}$ such that $T$ = $T_0\subseteq T_1\subseteq \dots \subseteq T_n=T^{\prime }$, and $\Delta \left(T_{i-1}\left(s\right),T_i\left(s\right)\right)=1$, where $1\le i\le n$.

Given a fuzzy competence structure $\left(S,P_s,\mathcal{C}\right)$, if it is consistent, then $\left(S,P_s,\mathcal{C}\right)$ is called a consistent fuzzy competence space.

A consistent fuzzy competence space has three educational learning principles similar to those of a knowledge space:

(1)

Closure under union of competences: this guarantees that individuals can interact and learn from one another, enabling their fuzzy competence states to merge and improve;

(2)

Gradualness of skill learning: for fuzzy competence states $T,T^{\prime }\in \mathcal{C}$, if $T\subseteq T^{\prime }$, there exists a chain of fuzzy competence states as described in Definition 8(1) and (2), meaning individuals can progressively learn skills;

(3)

Consistency of skill learning: an individual’s improvement in fuzzy competence states does not interfere with the learning of certain skills.

Proposition 3.

Given a fuzzy competence space $\left(S,P_s,\mathcal{C}\right)$ and $T,T^{\prime }\in \mathcal{C}$, where $T\subseteq T^{\prime }$, and $\left|T^{\prime }\setminus T\right|=1$. Suppose $\left(T^{\prime }\setminus T\right)\left(s_0\right)>0$. For any $T^{*}\in \mathcal{C}$, and $T\subseteq T^{*}$, if $T^{*}\left(s_0\right)<T^{\prime }\left(s_0\right)$, define $\widehat{T}\left(s\right)=\left\{\begin{array}{c}{T}^{*}\left(s\right) s\ne s_0\\ p s=s_0 \end{array}\right.$, where $T^{*}\left(s_0\right)\le p\le T^{\prime }\left(s_0\right)$, and $p\in P_{s_0}$, then $\widehat{T}\in \mathcal{C}$.

Proof. 

Since $T^{\ast }\in \mathcal{C}$ and $T^{\prime }\in \mathcal{C}$, and $\left(S,P_s,\mathcal{C}\right)$ is a fuzzy competence, it follows that $T^{\ast }\cup T^{\prime }\in \mathcal{C}$. For any $s\ne s_0$, we have $T^{\prime }\left(s\right)=T\left(s\right)\le T^{\ast }\left(s\right)$, so $\mathrm{m}\mathrm{a}\mathrm{x}\left\{T^{\ast }\left(s\right),T^{\prime }\left(s\right)\right\}=T^{\ast }\left(s\right)$. For $s=s_0$ we have $T^{\ast }\left(s\right)<T^{\prime }\left(s\right)$, so $\mathrm{m}\mathrm{a}\mathrm{x}\left\{T^{\ast }\left(s_0\right),T^{\prime }\left(s_0\right)\right\}=T^{\prime }\left(s_0\right)$. It follows that $\left|(T^{\prime }\cup T^{\ast }){\setminus T}^{\ast }\right|=1$, and hence $T^{\ast }\subseteq \widehat{T}\subseteq T^{\prime }\cup T^{\ast }$. By Definition 8(2), it follows that $\widehat{T}\in \mathcal{C}$. □

Remark 1.

Consider $T$ as the initial fuzzy competence state of an individual. Since $\left|T^{\prime }\setminus T\right|=1$ and $\left(T^{\prime }\setminus T\right)\left(s_0\right)>0$, the individual reaches fuzzy competence state $T^{\prime }$ by learning skill $s_0$. For another individual, whose fuzzy competence state is $T^{*}$, and $T\subseteq T^{*}$, this individual can also improve their fuzzy competence state by learning skill $s_0$, which shows that the improvement in competence does not interfere with the learning of skills.

4. Learning Paths of Fuzzy Skills

As shown in Example 3, the fuzzy disjunctive problem function $m:\mathcal{C}\to \mathcal{K}$ is not necessarily a bijection, meaning that the potential competence level of an individual cannot be uniquely inferred from their knowledge state. The following proposition provides a method for determining the upper bound of an individual’s potential competence level in a fuzzy competence space.

Proposition 4.

Given a fuzzy competence space $\left(S,P_s,\mathcal{C}\right)$ and fuzzy skill mapping $\left(Q,S,\tau \right)$, let $m$ be the fuzzy disjunctive problem function corresponding to $\left(Q,S,\tau \right)$. $\mathcal{K}=\left\{K|K=m\left(T\right),T\in \mathcal{C}\right\}$ is the knowledge space induced by $\left(S,P_s,\mathcal{C}\right)$ and $\left(Q,S,\tau \right)$ under the disjunctive model. For $K\in \mathcal{K}$, let ${\left[T\right]}_K=\left\{T\in \mathcal{C}|m\left(T\right)=K\right\}$, then the following two properties hold:

(1) 

$\bigcup {\left[T\right]}_K\in \mathcal{C}$, and $m\left(\bigcup {\left[T\right]}_K\right)=K$;

(2) 

For any $s\in S$, $\left(\bigcup {\left[T\right]}_K\right)\left(s\right)<{\bigcap }_{q\notin K}{\tau }_q\left(s\right)$.

Proof. 

(1) $\bigcup {\left[T\right]}_K$ represents the family of fuzzy competence states of all individuals with knowledge state $K$. Since $\left(S,P_s,\mathcal{C}\right)$ is a fuzzy competence space, $\bigcup {\left[T\right]}_K\in \mathcal{C}$ always holds. As in the proof of Proposition 2, we have $m\left(\bigcup {\left[T\right]}_K\right)={\bigcup }_{T\in {\left[T\right]}_K}m\left(T\right)=K$.

(2) If there exists $s_0\in S$ such that $\left(\bigcup {\left[T\right]}_K\right)\left(s_0\right)\ge {\bigcap }_{q\notin K}{\tau }_q\left(s_0\right)$, i.e., there exists $q_0\notin K$ such that $\left(\bigcup {\left[T\right]}_K\right)\left(s_0\right)\ge {\tau }_{q_0}\left(s_0\right)$, then there exists $T\in {\left[T\right]}_K$ such that $T\left(s_0\right)\ge {\tau }_{q_0}\left(s_0\right)$. This implies that $q_0\in m\left(T\right)=K$, which contradicts $q_0\notin K$. □

While consistent fuzzy competence spaces ensure gradual skill learning, they do not guarantee changes in knowledge states. For instance, in Example 4, although $T_8\subset T_9$, but $T_8,T_9\in {\left[T\right]}_{\left\{q_1,q_3\right\}}$, i.e., $m\left(T_8\right)=m\left(T_9\right)$. This indicates that an improvement in competence does not necessarily lead to an improvement in the knowledge state. The literature [24] refers to such a learning method or learning path as “ineffective”. The following proposition explores the existence of effective learning paths.

Proposition 5.

Given a consistent fuzzy competence space $\left(S,P_s,\mathcal{C}\right)$ and a fuzzy skill mapping $\left(Q,S,\tau \right)$, let $m$ be the fuzzy disjunctive problem function corresponding to $\left(Q,S,\tau \right)$. $\mathcal{K}$ is the knowledge space induced by $\left(S,P_s,\mathcal{C}\right)$ and $\left(Q,S,\tau \right)$ under the disjunctive model. Define $\widehat{\mathcal{C}}=\left\{\bigcup {\left[T\right]}_K|K\in \mathcal{K}\right\}$, and if $\left|\widehat{\mathcal{C}}\right|=\left|\mathcal{C}\right|$, the following two propositions hold:

(1) 

The fuzzy disjunctive problem function $m:\mathcal{C}\to \mathcal{K}$ is a bijection;

(2) 

Given $T\in \mathcal{C}$ and $m\left(T\right)=K$, for any knowledge state $K^{\prime }\in \mathcal{K}$ with $K\subset K^{\prime }$, there exist $T_0,T_1,\dots ,T_n\in \mathcal{C}$ such that $T$ = $T_0\subseteq T_1\subseteq \dots \subseteq T_n$, and $m\left(T_n\right)=K^{\prime }$, and the following conditions hold: $m\left(T_{i-1}\right)\subseteq m\left(T_i\right)$ and $\Delta \left(T_{i-1},T_i\right)=1$, where $1\le i\le n$.

Proof. 

(1) Since $\bigcup {\left[T\right]}_K\in \mathcal{C}$, and by Proposition 4(1), we know that $\bigcup {\left[T\right]}_K\in {\left[T\right]}_K$, and since $\left|\widehat{\mathcal{C}}\right|=\left|\mathcal{C}\right|$, for any $K\in \mathcal{K}$, we have $\left|{\left[T\right]}_K\right|=1$, so $m:\mathcal{C}\to \mathcal{K}$ is a bijection.

(2) Since $m:\mathcal{C}\to \mathcal{K}$ is a bijection, for any $K,K^{\prime }\in \mathcal{K}$, there exist $T,T^{\prime }\in \mathcal{C}$ such that $m\left(T\right)=K$ and $m\left(T^{\prime }\right)=K^{\prime }$. For any $K\in \mathcal{K}$, we have $\left|{\left[T\right]}_K\right|=1$, so $K\subset K^{\prime }\iff T\subset T^{\prime }$. This is consistent with the definition of a consistent fuzzy competence structure. Therefore, the proposition holds. □

If for any fuzzy competence state $T\in \mathcal{C}$, and any knowledge state $K^{\prime }\supset m\left(T\right)$, there exists a gradual and effective learning path as shown in Proposition 5(2), such a learning model benefits all learners. We call such a learning model “effective”. Proposition 5 provides a sufficient condition for the validity of the learning model, namely that $\left(S,P_s,\mathcal{C}\right)$ is a consistent fuzzy competence space and $\left|\widehat{\mathcal{C}}\right|=\left|\mathcal{C}\right|$. The following proposition provides a more general case.

Proposition 6.

Given a consistent fuzzy competence space $\left(S,P_s,\mathcal{C}\right)$ and a fuzzy skill mapping $\left(Q,S,\tau \right)$, let $m$ be the fuzzy disjunctive problem function corresponding to $\left(Q,S,\tau \right)$. $\mathcal{K}$ is the knowledge space induced by $\left(S,P_s,\mathcal{C}\right)$ and $\left(Q,S,\tau \right)$ under the disjunctive model. If the learning model is effective, then for any knowledge states $K,K^{\prime }\in \mathcal{K}$ with $K\subset K^{\prime }$, we have $\left|{\left[T\right]}_K\right|\le \left|{\left[T\right]}_{K^{\prime }}\right|$.

Proof. 

Assume there exist $K,K^{\prime }\in \mathcal{K}$, such that $K\subset K^{\prime }$, and $\left|{\left[T\right]}_K\right|>\left|{\left[T\right]}_{K^{\prime }}\right|$. Suppose $K^{\prime }$ is the smallest knowledge state containing $K$, i.e., there does not exist $K^{*}\in \mathcal{K}$ such that $K\subset K^{*}\subset K^{\prime }$. Let $\left|{\left[T\right]}_K\right|=m+n$, and $\left|{\left[T\right]}_{K^{\prime }}\right|=m$. Define ${\left[T\right]}_K=\left\{T_1,T_2,\dots ,T_{m+n}\right\}$ and ${\left[T\right]}_{K^{\prime }}=\left\{{T_1}^{\prime },{T_2}^{\prime },\dots ,{T_m}^{\prime }\right\}$. If the learning model is effective, there exist $T_1,T_2\in {\left[T\right]}_K$ and ${T_K}^{\prime }\in {\left[T\right]}_{K^{\prime }}$, such that $\Delta \left(T_i,{T_K}^{\prime }\right)=\Delta \left(T_j,{T_K}^{\prime }\right)=1$. Clearly, in this case, $T_i$ and $T_j$ do not have an inclusion relationship, so $T_i\cup T_j={T_K}^{\prime }$. Since $T_i\cup T_j\in {\left[T\right]}_K$, this contradicts the assumption. □

The preceding theoretical investigation establishes the foundation for a learning-path recommendation method within fuzzy competence spaces. Building on this foundation, Figure 1 presents the overall research framework of the proposed method. The upper-left quadrant contains the fundamental concepts used throughout the paper, namely the problem set $Q$, the skill set $S$, the fuzzy skill mapping $\left(Q,S,\tau \right)$, and the fuzzy competence structure $\left(S,P_s,\mathcal{C}\right)$. The lower-left quadrant provides the theoretical underpinning: The definition of a consistent fuzzy competence space given in Definition 9, and the necessary and sufficient conditions for the existence of gradual and effective learning paths stated in Propositions 5 and 6. The upper-right quadrant corresponds to the algorithmic layer, including the validation and construction of a consistent fuzzy competence space and the generation of gradual and effective learning paths. Finally, the lower-right quadrant covers simulation and discussion, comprising dataset construction, algorithm implementation, analysis of simulation results, and discussion of application scenarios. Arrows illustrate the dependencies among these components.

When the conditions of Proposition 5 are satisfied, every pair of knowledge states in the knowledge space induced by a consistent fuzzy competence space $\left(S,P_s,\mathcal{C}\right)$ and a fuzzy skill mapping $\left(Q,S,\tau \right)$ can be connected by a gradual and effective learning path. In practical learning environments, the path of greatest interest is the one that starts from the initial knowledge state $\varnothing$ and ends at the final knowledge state $Q$. Such a path upgrades exactly one skill-proficiency level at each step and guarantees a simultaneous improvement in the knowledge state until $Q$ is reached, thereby minimizing learning time and markedly enhancing learning efficiency.

According to Proposition 5, if $\left(S,P_s,\mathcal{C}\right)$ is a consistent fuzzy competence space and $\left|\widehat{\mathcal{C}}\right|=\left|\mathcal{C}\right|$, a gradual and effective learning path from $\varnothing$ to $Q$ is assured to exist; if $\left|\widehat{\mathcal{C}}\right|\ne \left|\mathcal{C}\right|$, the existence of such a path cannot be determined a priori. Algorithm 1 outlines the overall procedure for searching a gradual and effective learning path from $\varnothing$ to $Q$ given $\left(S,P_s,\mathcal{C}\right)$ and $\left(Q,S,\tau \right)$. Algorithm 2 refines Steps 1–2 of Algorithm 1 by deciding whether the given fuzzy competence structure is a consistent fuzzy competence space. Algorithm 3 refines Steps 3–5 by verifying whether the equality $\left|\widehat{\mathcal{C}}\right|=\left|\mathcal{C}\right|$ in Proposition 5 holds. Algorithm 4 further refines Step 6 and is responsible for finding the gradual and effective learning path. It is important to emphasize that Algorithm 4 is executed regardless of whether $\left|\widehat{\mathcal{C}}\right|=\left|\mathcal{C}\right|$ holds; if a gradual and effective learning path from $\varnothing$ to $Q$ is found, it is reported, otherwise an informative message is returned.

Algorithm 1 Learning path recommendation algorithm
Input: A fuzzy competence structure $\left(S,P_s,\mathcal{C}\right)$ and a fuzzy skill mapping $\left(Q,S,\tau \right)$.
Output: One of the following two outcomes: (1) A gradual and effective learning path from the initial knowledge state ∅ to Q. (2) A determination that no gradual and effective learning path exists from ∅ to Q.
1:	Check whether $\left(S,P_s,\mathcal{C}\right)$ is a fuzzy competence space. If yes, continue to Step 2; otherwise, $flag=\mathrm{F}\mathrm{A}\mathrm{L}\mathrm{S}\mathrm{E}$, go to Step 7.
2:	Check whether $\left(S,P_s,\mathcal{C}\right)$ is a consistent fuzzy competence space. If yes, proceed to Step 3; otherwise, $flag=\mathrm{F}\mathrm{A}\mathrm{L}\mathrm{S}\mathrm{E}$, go to Step 7.
3:	Compute the knowledge space $\mathcal{K}=\left\{K|K=m\left(T\right),T\in \mathcal{C}\right\}$ induced by the fuzzy competence space $\left(S,P_s,\mathcal{C}\right)$ and the fuzzy skill mapping $\left(Q,S,\tau \right)$.
4:	Compute $\widehat{\mathcal{C}}=\left\{\bigcup {\left[T\right]}_K|K\in \mathcal{K}\right\}$.
5:	Compute the set cardinalities of $\widehat{\mathcal{C}}$ and $\mathcal{C}$ denoted as $c1$ and $c2$.
6:	Finding and drawing the gradual and effective learning path.
7:	IF $flag=\mathrm{F}\mathrm{A}\mathrm{L}\mathrm{S}\mathrm{E}$ then Output “No gradual and effective learning path exists”.
8:	End.

Algorithm 2 Refines Steps 1–2 of Algorithm 1. Deciding whether the given fuzzy competence structure is a consistent fuzzy competence space.
Input: A fuzzy competence structure $\left(S,P_s,\mathcal{C}\right)$.
Output: TRUE if $\left(S,P_s,\mathcal{C}\right)$ is a consistent fuzzy competence space; FALSE otherwise
1:	for each pair $\left(T1,T2\right)$ in $\mathcal{C}\times \mathcal{C}$ do
2:	if $\left(T1\cup T2\right)\notin \mathcal{C}$ then
3:	return FALSE
4:	end if
5:	end for
6:	create empty directed graph $G=\left(\mathcal{C}, Adj\right)$
7:	for each pair $\left(T,U\right)$ in $\mathcal{C}\times \mathcal{C}$ with $T\subset U$ do
8:	$\mathrm{if} \left|diff\left(T,U\right)\right|=1$ then
9:	$\mathrm{add} \mathrm{edge} \left(T\to U\right)$  $\mathrm{to} Adj$
10:	end if
11:	end for
12:	for each pair $\left(T,U\right)$  $\mathrm{in} \mathcal{C}\times \mathcal{C}$  $\mathrm{with} T\subset U$
13:	if no path from $T$ $\mathrm{to} U$ $\mathrm{in} G$ then
14:	return FALSE
15:	end if
16:	end for
17:	for each pair$\left(T,U\right)$ in $\mathcal{C}\times \mathcal{C}$ with $T\subset U$ and $\left|diff\left(T,U\right)\right|=1$ do
18:	$\mathrm{let} s0\leftarrow$$\mathrm{the} \mathrm{unique} \mathrm{skill} \mathrm{in} diff\left(T,U\right)$
19:	$t0\leftarrow T\left(s0\right)$
20:	$U0\leftarrow U\left(s0\right)$
21:	$\mathrm{for} p$ $\mathrm{from} \mathrm{next} t0$ $\mathrm{to} U0$ $\mathrm{in} P_{s0}$ do
22:	$TP\leftarrow T$$, TP\left(s0\right)$$=p$
23:	$\mathrm{if} TP\notin \mathcal{C}$ then
24:	return FALSE
25:	end if
26:	end for
27:	end for
28:	return TRUE

Algorithm 3 Refines Steps 3–5 of Algorithm 1.
Input: A consistent fuzzy competence space $\left(S,P_s,\mathcal{C}\right)$ and a fuzzy skill mapping $\left(Q,S,\tau \right)$.
Output: $c1, c2,\mathcal{K},\widehat{\mathcal{C}}, Kmap$
1:	$n=\left|\mathcal{C}\right|$
2:	$CSET\leftarrow \mathcal{C}$
3:	create empty dictionary $Kmap$//key: knowledge state $K$
4:	$\mathrm{for} i=1$ to $n$ do
5:	$T\leftarrow CSET\left[i\right]$
6:	$K\leftarrow \varnothing$
7:	for each problem $q\in Q$ do
8:	for each skill $s\in S$ do
9:	if $\left({\tau }_q\left(s\right)>0 and {\tau }_q\left(s\right)<=T\left(s\right)\right)$ then
10:	$K\leftarrow K\cup \left\{q\right\}$; break
11:	end if
12:	end for
13:	$m\left(i\right)\leftarrow K$
14:	if $K$ not in $Kmap$ then
15:	$Kmap\left[K\right]\leftarrow$ empty list
16:	end if
17:	$\mathrm{append} i$  $\mathrm{to} Kmap\left[K\right]$
18:	end for
19:	end for
20:	$\mathcal{K}\leftarrow keys\left(Kmap\right)$
21:	$\widehat{\mathcal{C}}\leftarrow \varnothing$
22:	for each $K$ in $\mathcal{K}$ do
23:	$classIdx\leftarrow Kmap\left[K\right]$
24:	$U\leftarrow CSET\left[classIdx\left(1\right)\right]$
25:	for $j=2$ $\mathrm{to} \mathrm{l}\mathrm{e}\mathrm{n}\mathrm{g}\mathrm{t}\mathrm{h}\left(classIdx\right)$ do
26:	$U\leftarrow max\left(U,CSET\left[classIdx\left(j\right)\right]\right)$
27:	end for
28:	$\widehat{\mathcal{C}}\leftarrow \widehat{\mathcal{C}}\cup \left\{U\right\}$
29:	end for
30:	$c1\leftarrow \left|\widehat{\mathcal{C}}\right|$
31:	$c2\leftarrow n$
32:	$\mathrm{return} c1, c2,\mathcal{K},\widehat{\mathcal{C}}, Kmap$

Algorithm 4 Refines Step 6 of Algorithm 1. Finding and drawing the gradual and effective learning path.
Input: $c1, c2,\mathcal{K},\widehat{\mathcal{C}}, Kmap$
Output: $flag$
1:	$\mathrm{if} c1=c2$ then
2:	$flag\leftarrow \mathrm{T}\mathrm{R}\mathrm{U}\mathrm{E}$
3:	else
4:	$flag\leftarrow \mathrm{F}\mathrm{A}\mathrm{L}\mathrm{S}\mathrm{E}$
5:	end if
6:	$CS\leftarrow$$\mathrm{sort} \mathcal{C}$ by each skill’s proficiency in lexicographical order
7:	$KS\leftarrow \left\{\varnothing \right\}$
8:	$FP\leftarrow \left\{first\left(CS\right)\right\}$
9:	$KT\leftarrow \varnothing$
10:	$i\leftarrow 2$
11:	$\mathrm{while} i<=\left|CS\right|$ do
12:	$FTprev\leftarrow FP.last$
13:	$FTcur\leftarrow CS\left[i\right]$
14:	$\mathrm{if} \mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}\mathrm{S}\mathrm{k}\mathrm{i}\mathrm{l}\mathrm{l}\mathrm{C}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left(FTprev,FTcur\right)\ne 1$ then
15:	$i\leftarrow i+1$
16:	continue
17:	end if
18:	$Kcur\leftarrow induceKnowledge\left(FTcur,\tau \right)$
19:	$\mathrm{if} KT\subset Kcur$ then
20:	$append\left(KS,Kcur\right)$
21:	$append\left(FP,Fcur\right)$
22:	$KT\leftarrow Kcur$
23:	$\mathrm{if} KT=Q$ then
24:	break
25:	end if
26:	end if
27:	$i\leftarrow i+1$
28:	end while
29:	$\mathrm{if} KS.last=Q$
30:	$flag\leftarrow \mathrm{T}\mathrm{R}\mathrm{U}\mathrm{E}$
31:	$\mathrm{Output} FP,KS$
32:	$\mathrm{d}\mathrm{r}\mathrm{a}\mathrm{w}\mathrm{P}\mathrm{a}\mathrm{t}\mathrm{h}\mathrm{D}\mathrm{i}\mathrm{a}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{m}\left(FP,KS\right)$
33:	STOP
34:	end if
35:	$\mathrm{return} flag$

5. Simulation Experiments

To verify the effectiveness of Algorithm 1, we carried out a set of simulation experiments. The experiments were executed on an Intel^® Core™ i7-9700 CPU @ 3.00 GHz with 16 GB RAM under Windows 10, and the simulator that implements Algorithm 1 was written in Python 3.13.2.

First, we built ten datasets of different sizes, denoted d01–d10. Each dataset consists of three parts: (i) the skills together with their proficiency levels, (ii) the fuzzy competence states, and (iii) the fuzzy skill mapping; the basic statistics are listed in

Table 4. Basic information of the first group of 10 datasets.

ds	$\left|\mathit{S}\right|$	$\left|{\mathit{P}}_{\mathit{s}}\right|$	$\left|\mathit{Q}\right|$	$\left|\mathcal{C}\right|$
d01	2	3	4	9
d02	3	3	6	27
d03	3	3 or 4	9	36
d04	4	3 or 4	12	144
d05	5	3 or 4	15	432
d06	5	3 or 4 or 5	18	900
d07	6	3 or 4	20	1296
d08	6	3 or 4 or 5	23	1620
d09	7	3	25	2187
d10	8	3	28	6561

.

For every dataset, the fuzzy competence states comprise all possible states, which guarantees that the dataset forms a consistent fuzzy competence space and that a gradual and effective learning path from $\varnothing$ to $Q$ always exists.

All datasets are stored as Excel workbooks. The ps sheet stores the skills and their proficiency levels, the fcs sheet stores the fuzzy competence states, and the fsm sheet stores the fuzzy skill mapping. Taking dataset d03 as an example, the three sheets are shown in

Table 5. Dataset d03—ps worksheet.

s	p1	p2	p3	p4
s1	0	0.6	1
s2	0	0.6	1
s3	0	0.2	0.4	1

,

Table 6. Dataset d03—fcs worksheet.

T	s1	s2	s3	T	s1	s2	s3
T0	0	0	0	T18	0.6	0.6	0.4
T1	0	0	0.2	T19	0.6	0.6	1
T2	0	0	0.4	T20	0.6	1	0
T3	0	0	1	T21	0.6	1	0.2
T4	0	0.6	0	T22	0.6	1	0.4
T5	0	0.6	0.2	T23	0.6	1	1
T6	0	0.6	0.4	T24	1	0	0
T7	0	0.6	1	T25	1	0	0.2
T8	0	1	0	T26	1	0	0.4
T9	0	1	0.2	T27	1	0	1
T10	0	1	0.4	T28	1	0.6	0
T11	0	1	1	T29	1	0.6	0.2
T12	0.6	0	0	T30	1	0.6	0.4
T13	0.6	0	0.2	T31	1	0.6	1
T14	0.6	0	0.4	T32	1	1	0
T15	0.6	0	1	T33	1	1	0.2
T16	0.6	0.6	0	T34	1	1	0.4
T17	0.6	0.6	0.2	T35	1	1	1

and

Table 7. Dataset d03—fsm worksheet.

q	s1	s2	s3
q1	0	0	0.2
q2	0.6	0	0.2
q3	0	0	0.4
q4	0.6	0.6	0
q5	1	0.6	0.4
q6	0	1	0
q7	1	1	1
q8	0.6	0	0.4
q9	0.6	0	0

.

The simulator read the ten datasets and successfully located a gradual and effective learning path from $\varnothing$ to $Q$ for each of them, which confirms the validity of the algorithms proposed in Section 3 of this paper. Using dataset d03 as an example, the knowledge structure obtained by the simulation program is presented in

Table 8. Knowledge structure derived for dataset d03.

id	Knowledge State	Fuzzy Competence State
1	{}	[T0]
2	{q1,q2}	[T1]
3	{q1,q2,q3,q5,q8}	[T2]
4	{q1,q2,q3,q5,q7,q8}	[T3]
5	{q4,q5}	[T4]
6	{q1,q2,q4,q5}	[T5]
7	{q1,q2,q3,q4,q5,q8}	[T6]
8	{q1,q2,q3,q4,q5,q7,q8}	[T7]
9	{q4,q5,q6,q7}	[T8]
10	{q1,q2,q4,q5,q6,q7}	[T9]
11	{q1,q2,q3,q4,q5,q6,q7,q8}	[T10, T11]
12	{q2,q4,q8,q9}	[T12]
13	{q1,q2,q4,q8,q9}	[T13]
14	{q1,q2,q3,q4,q5,q8,q9}	[T14, T18]
15	{q1,q2,q3,q4,q5,q7,q8,q9}	[T15, T19, T26, T27, T30, T31]
16	{q2,q4,q5,q8,q9}	[T16]
17	{q1,q2,q4,q5,q8,q9}	[T17]
18	{q2,q4,q5,q6,q7,q8,q9}	[T20, T32]
19	{q1,q2,q4,q5,q6,q7,q8,q9}	[T21, T33]
20	{q1,q2,q3,q4,q5,q6,q7,q8,q9}	[T22, T23, T34, T35]
21	{q2,q4,q5,q7,q8,q9}	[T24, T28]
22	{q1,q2,q4,q5,q7,q8,q9}	[T25, T29]

. The gradual and effective learning path found from $\varnothing$ to $Q$ is depicted in Figure 2.

Table 9. Simulation results for the first dataset group.

ds	|Ĉ|	t_alg2 (s)	t_alg3 (s)	t_alg4 (s)	%A2	%A3	%A4	t_sum (s)
d01	8	0.0029588	0.0002256	0.0001866	87.772	6.692	5.535	0.003371
d02	12	0.0195838	0.0004235	0.0001666	97.075	2.099	0.826	0.0201739
d03	22	0.0338597	0.0005785	0.0002373	97.647	1.668	0.684	0.0346755
d04	72	0.468807	0.0020978	0.0005439	99.440	0.445	0.115	0.4714487
d05	168	3.9694118	0.0055021	0.0006219	99.846	0.138	0.016	3.9755358
d06	296	17.1784075	0.015804	0.0019423	99.897	0.092	0.011	17.1961538
d07	672	34.2429477	0.0176207	0.0025812	99.941	0.051	0.008	34.2631496
d08	427	53.6230973	0.0194081	0.0014302	99.961	0.036	0.003	53.6439356
d09	869	98.782046	0.0305387	0.0034947	99.966	0.031	0.004	98.8160794
d10	1991	889.9205651	0.0865662	0.0173953	99.988	0.010	0.002	890.0245266

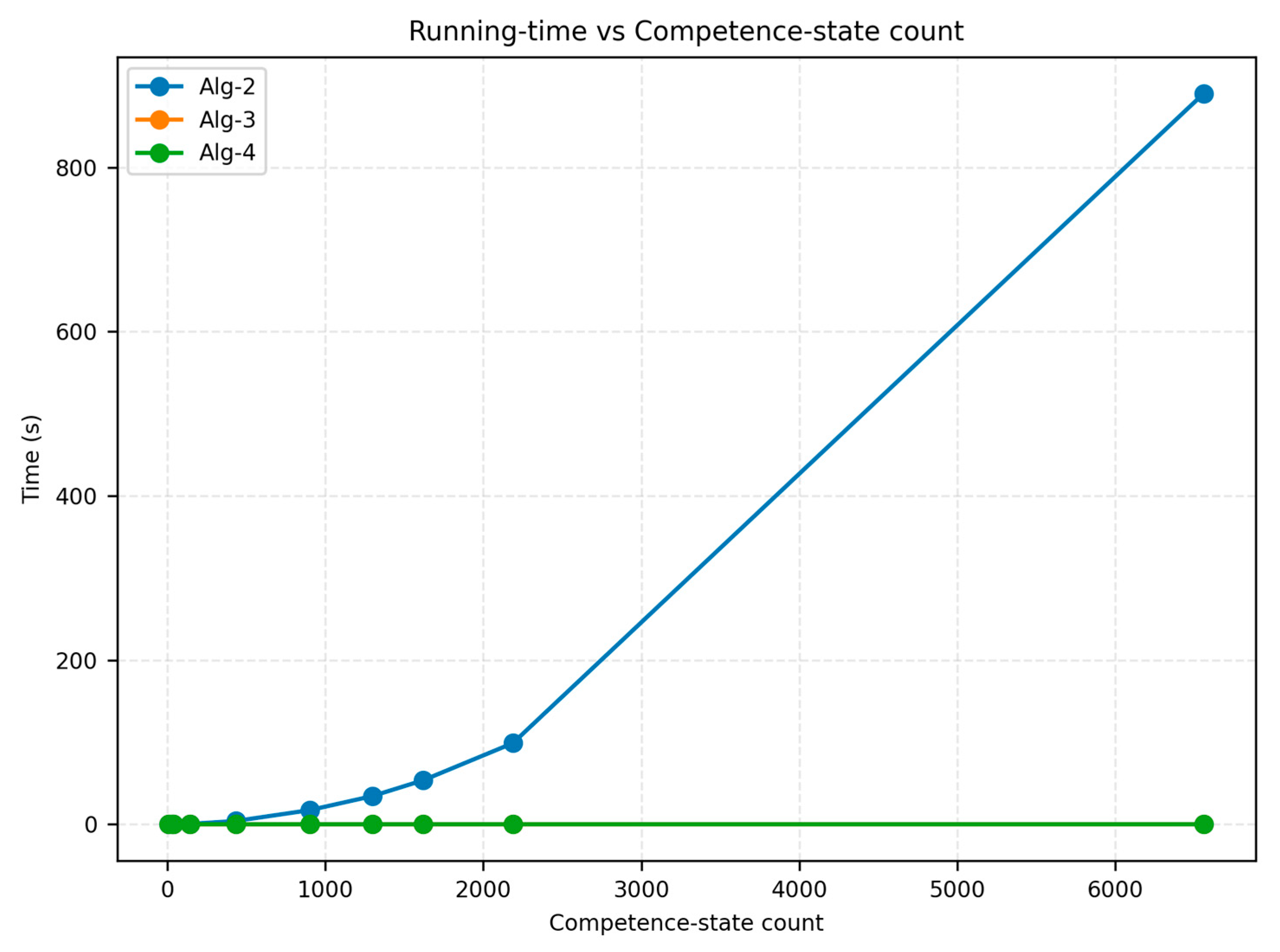
reports the simulation results for the first ten datasets; the column |Ĉ| gives the cardinality of $\widehat{\mathcal{C}}$, while columns t_alg2, t_alg3 and t_alg4 give, respectively, the execution time of Algorithms 2–4. columns %A2, %A3 and %A4 show their percentages of the total time given by column t_sum. It is clear that, as $\left|\mathcal{C}\right|$ grows, the total running time is dominated by Algorithm 2. The same trend can be seen in Figure 3, which plots the running time against the number of fuzzy competence states. It is worth noting that, as the number of fuzzy competence states grows, the running-time of Algorithm 2 is several orders of magnitude larger than those of Algorithms 3 and 4. Consequently, the curves for Algorithms 3 and 4 overlap and almost degenerate into a straight horizontal line; therefore, only the curve representing Algorithm 4 is visually discernible in Figure 3.

To study how the numbers of skills and problems affect the running time, we constructed another group of ten datasets with different skill and problem scales, as summarized in

Table 10. Basic information of the second group of 10 datasets.

ds	$\left|\mathit{S}\right|$	$\left|{\mathit{P}}_{\mathit{s}}\right|$	$\left|\mathit{Q}\right|$	$\left|\mathcal{C}\right|$
d01	3	3 or 4	8	9
d02	10	3 or 4 or 5	28	29
d03	20	3 or 4 or 5	63	64
d04	30	3 or 4	76	77
d05	40	3 or 4 or 5	130	131
d06	50	3 or 4 or 5	146	147
d07	55	3 or 4 or 5	166	167
d08	60	3 or 4 or 5	182	183
d09	65	3 or 4 or 5	202	203
d10	75	3 or 4 or 5	216	217

.

The simulation results of this second group are summarized in

Table 11. Simulation results for the second dataset group.

ds	|Ĉ|	t_alg2 (s)	t_alg3 (s)	t_alg4 (s)	%A2	%A3	%A4	t_sum (s)
d01	5	0.0025003	0.0002202	0.0001701	86.498	7.618	5.885	0.0028906
d02	20	0.0204677	0.0006195	0.000432	95.114	2.879	2.008	0.0215192
d03	35	0.0965181	0.0012357	0.0004883	98.245	1.258	0.497	0.0982421
d04	42	0.1401482	0.0015445	0.0005962	98.496	1.085	0.419	0.1422889
d05	74	0.3952275	0.003094	0.0004799	99.104	0.776	0.120	0.3988014
d06	81	0.5022423	0.0037556	0.0007904	99.103	0.741	0.156	0.5067883
d07	91	0.6776541	0.0046647	0.000595	99.230	0.683	0.087	0.6829138
d08	103	0.7992948	0.0051466	0.0009669	99.241	0.639	0.120	0.8054083
d09	112	0.975403	0.0062941	0.0007262	99.285	0.641	0.074	0.9824233
d10	127	1.1444909	0.0069527	0.0007232	99.334	0.603	0.063	1.1521668

.

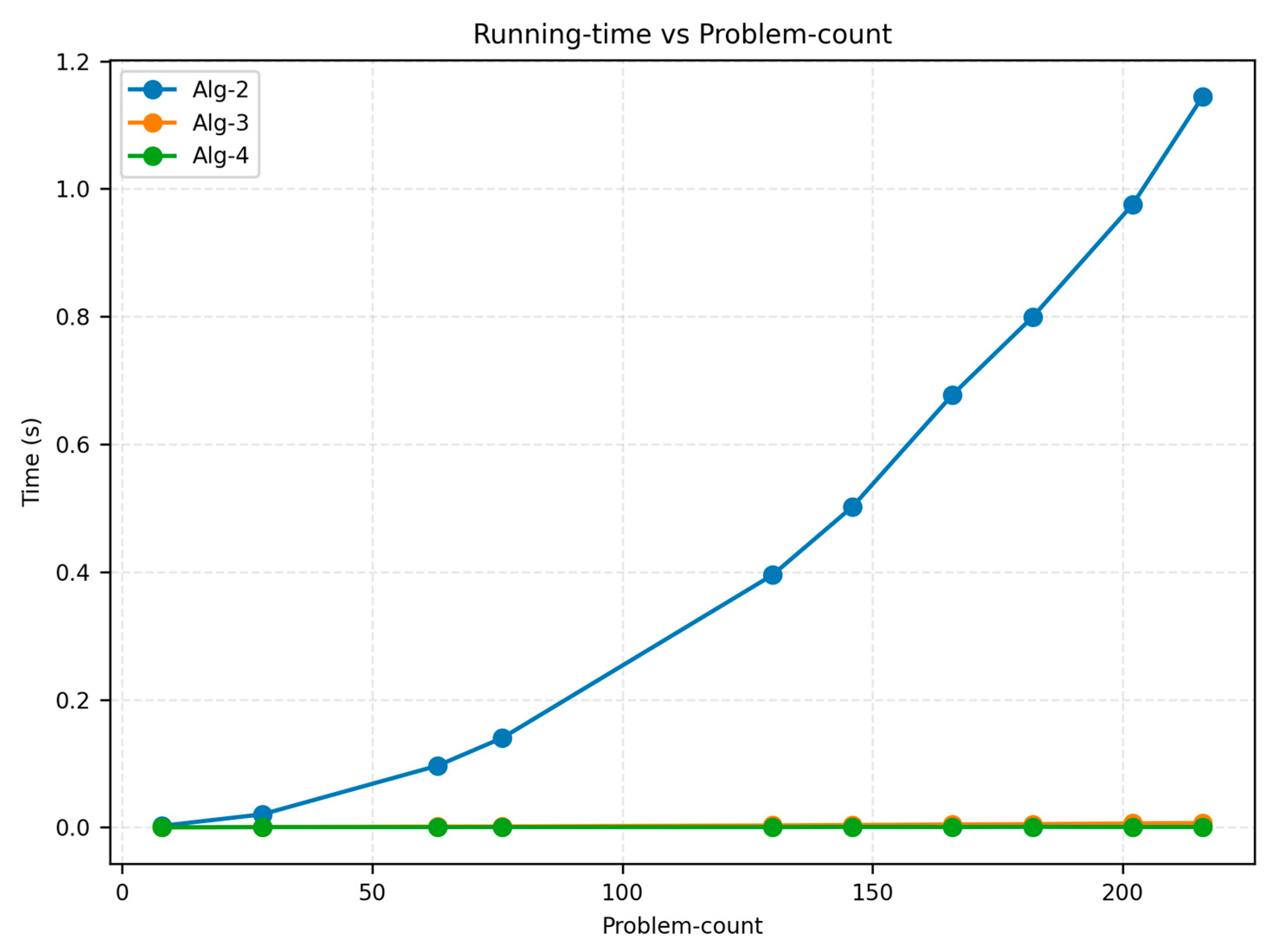
Figure 4 and Figure 5 plot the running time versus the number of skills and the number of problems, respectively.

From Table 11 and Figure 4 and Figure 5, we observe that the running time also increases with the numbers of skills and problems. Comparing the two groups of datasets, we conclude that $\left|\mathcal{C}\right|$ is the predominant factor that affects the overall running time of the algorithms. It is worth noting that the execution times of Algorithms 3 and 4 remain below 0.02 s for all test cases, which is negligible compared with Algorithm 2. Therefore, any optimization effort should mainly target Algorithm 2.

The simulation results show that when the number of fuzzy competence states is kept below 200, the overall running-time of the algorithms can be limited to less than one second. It should be noted that, in the second group of simulations, the fuzzy competence states of the ten datasets were randomly selected under the prerequisite that they form a consistent fuzzy competence space. The experimental outcomes reveal that, except for dataset d01, none of the remaining datasets possesses a gradual and effective learning path from the initial knowledge state $\varnothing$ to the target knowledge state $Q$.

In practical applications, the number of test items is usually no more than 100. Therefore, constructing a consistent fuzzy competence space with fewer than 200 fuzzy competence states—while guaranteeing, under the corresponding fuzzy skill mapping, the existence of a gradual and effective learning path from $\varnothing$ to $Q$—would be highly desirable. Therefore, beyond further optimizing Algorithm 2, an important avenue for future research is to devise ways to construct a consistent fuzzy competence space with as few competence states as possible while still guaranteeing that the associated fuzzy skill mapping admits a gradual and effective learning path from $\varnothing$ to $Q$.

6. Conclusions

Personalized, gradual, and effective learning paths have direct relevance to two major application domains.

(1)

Adaptive Learning Systems. In adaptive learning platforms, the recommended sequence of learning activities must accommodate fine-grained differences in learners’ mastery. Representing each learner’s state as a fuzzy competence state allows the system to assign membership degrees to every skill, so that content delivery, formative assessment and feedback can be aligned with the learner’s exact proficiency. The single-skill-increment principle ensures that the recommended path advances competence step-by-step without cognitive overload, thereby supporting mastery-based progression and just-in-time remediation.

(2)

Intelligent Testing Systems. In computerized adaptive testing or intelligent tutoring, the test-engine repeatedly selects the next item that is most informative with respect to the learner’s fuzzy knowledge state. A gradual and effective learning (or testing) path guarantees that item difficulty increases in tandem with skill levels, which safeguards measurement precision while avoiding abrupt jumps that may discourage test-takers.

Within this context, our study formulates personalized learning path recommendation inside the mathematical framework of fuzzy competence structures and consistent fuzzy competence spaces. By replacing the binary notion of mastery with fuzzy membership functions, the proposed approach captures incremental skill acquisition, and Algorithm 1—refined into Algorithms 2–4—systematically searches for a path that increases exactly one skill level at each step.

The current implementation handles small- and medium-scale datasets efficiently (≤200 competence states, total runtime < 1 s). Experimental results indicate that Algorithm 2—the consistency checker—accounts for the major share of computation as the number of competence states increases; when the state space reaches several thousand, runtime becomes prohibitive and limits immediate deployment in very-large-scale scenarios. Ongoing work therefore focuses on optimizing Algorithm 2 through parallel union-closure computation, incremental cover-graph construction, and heuristic state-selection strategies that keep the working set compact.

Future work will evaluate the method on large MOOC platforms by combining cognitive-diagnostic models with log-data analytics; incorporate learner traits such as preferences, metacognition and self-regulation into the fuzzy competence representation to achieve fully adaptive recommendation; extend the technique to cross-disciplinary curricula where skills have complex interdependencies; and investigate theoretical issues—including minimality, redundancy, and path pruning—under consistency constraints. Through these efforts, learning-path recommendation grounded in fuzzy competence space theory is expected to play an increasingly important role in next-generation adaptive learning and intelligent testing technologies.