Optimizing Parameter Estimation Precision in Open Quantum Systems
Abstract
1. Introduction
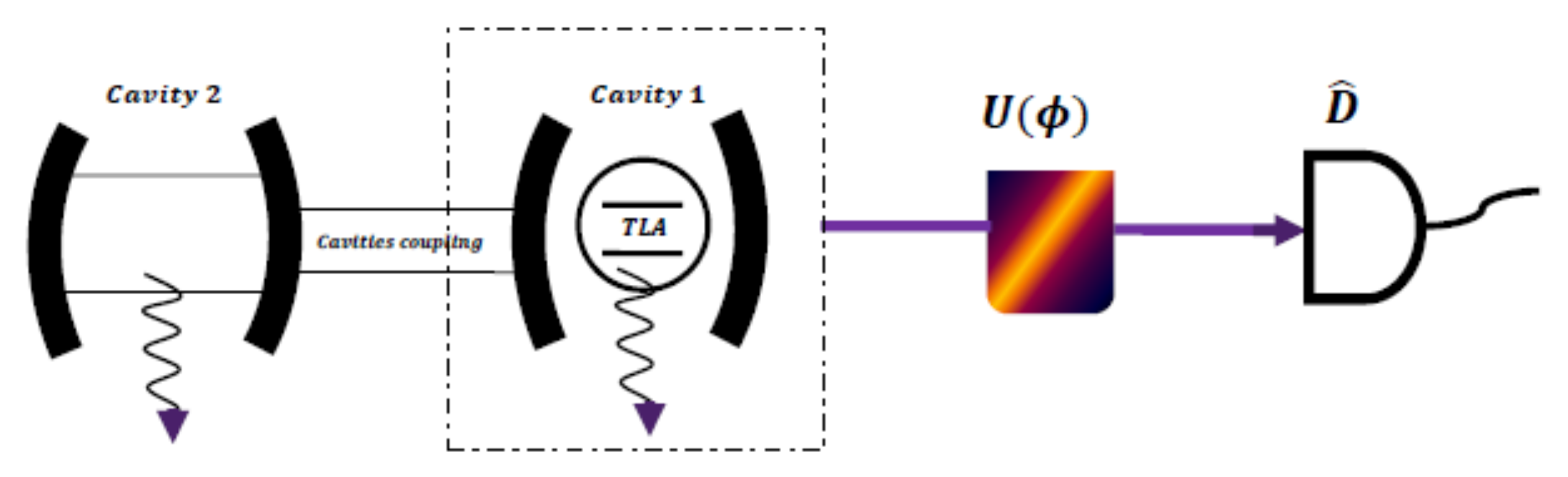
2. Physical Model and Measure of Parameter Estimation
3. Quantum Fisher Information
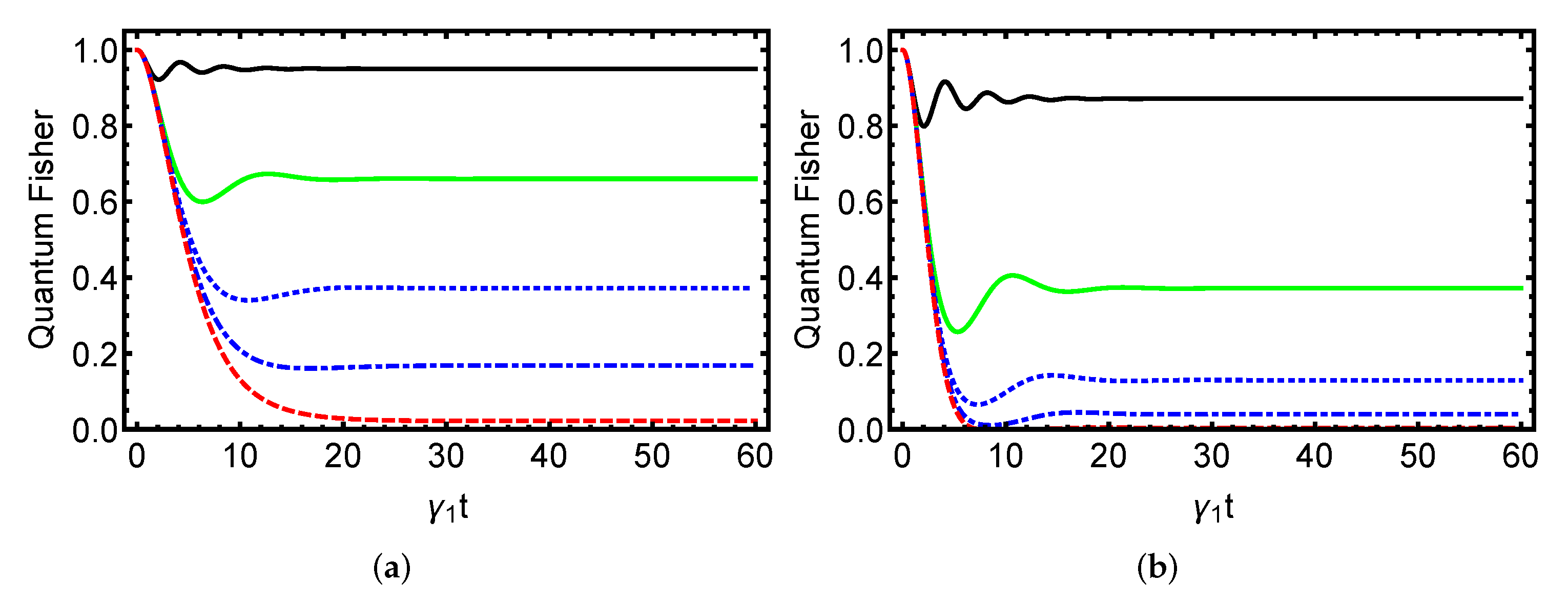
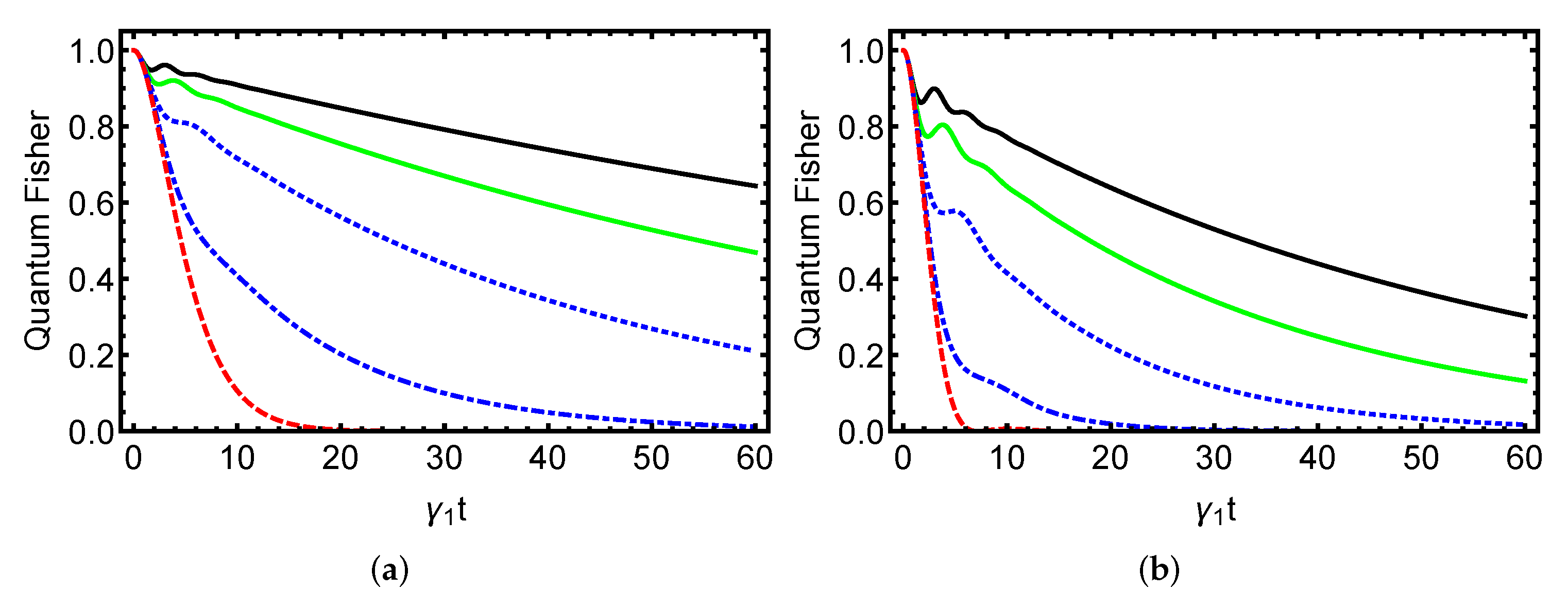
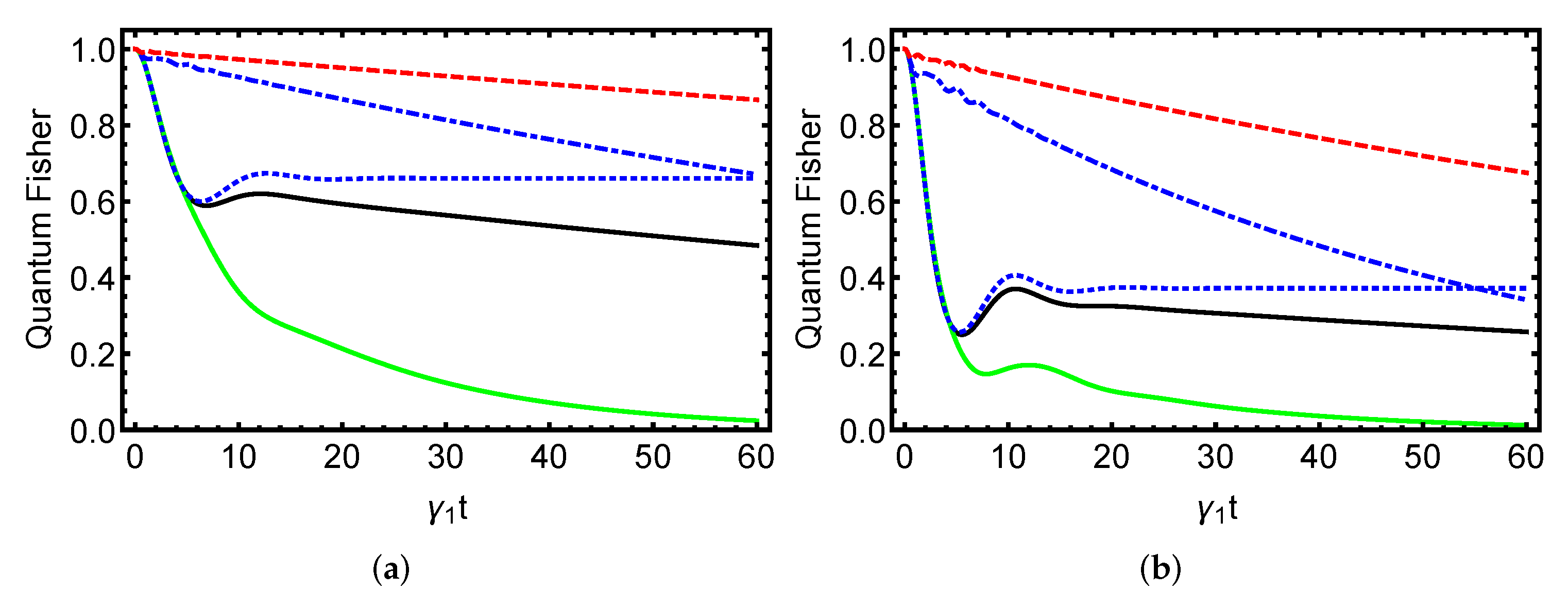
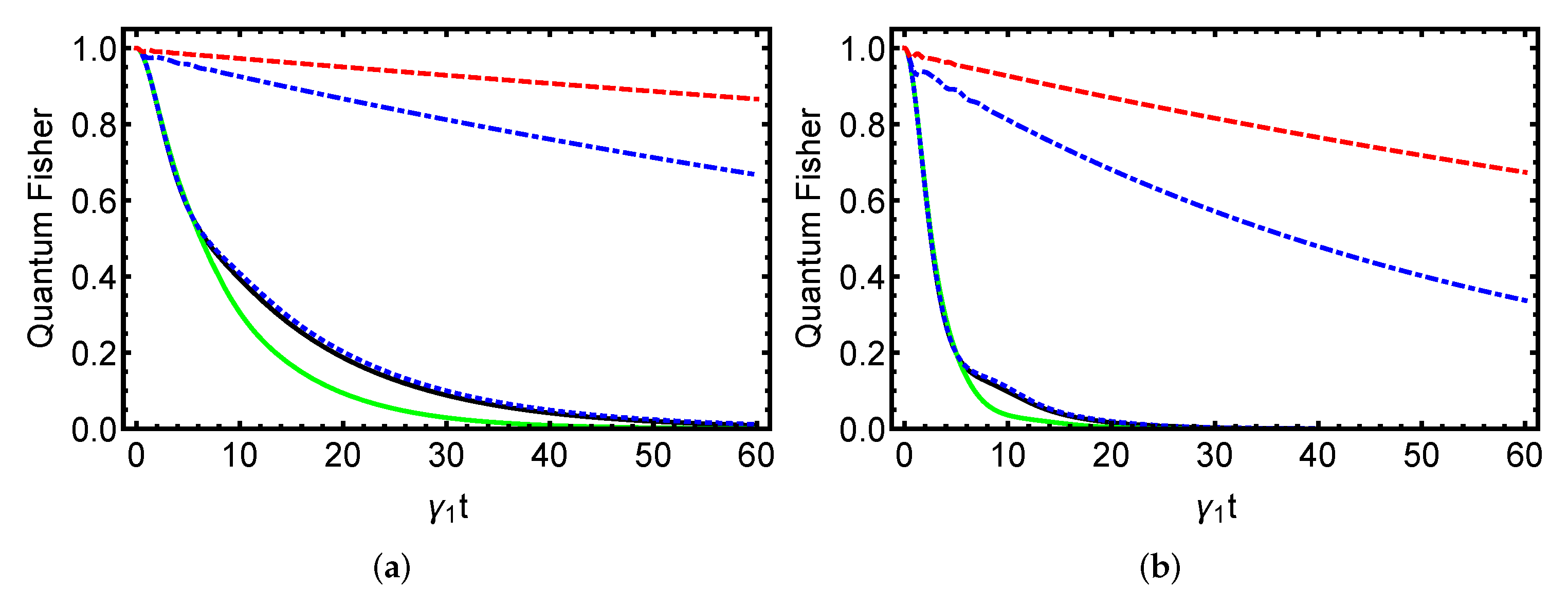
4. Numerical Findings and Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum-Enhanced Measurements: Beating the Standard Quantum Limit. Science 2004, 306, 1330. [Google Scholar] [CrossRef] [PubMed]
- Dowling, J. Quantum Optical Metrology—The Lowdown On High-N00N States. Contemp. Phys. 2008, 49, 125. [Google Scholar] [CrossRef]
- Jones, J.A.; Karlen, S.D.; Fitzsimons, J.; Ardavan, A.; Benjamin, S.C.; Briggs, G.A.D.; Morton, J.J.L. Magnetic Field Sensing Beyond the Standard Quantum Limit Using 10-Spin NOON States. Science 2009, 324, 1166. [Google Scholar] [CrossRef] [PubMed]
- Simmons, S.; Jones, J.A.; Karlen, S.D.; Ardavan, A.; Morton, J.J.L. Magnetic field sensors using 13-spin cat states. Phys. Rev. A 2010, 82, 022330. [Google Scholar] [CrossRef]
- Higgins, B.L.; Berry, D.W.; Bartlett, S.D.; Wiseman, H.M.; Pryde, G.J. Entanglement-free Heisenberg-limited phase estimation. Nature 2007, 450, 393. [Google Scholar] [CrossRef]
- Dorner, U.; Smith, B.J.; Lundeen, J.S.; Wasilewski, W.; Banaszek, K.; Walmsley, I.A. Quantum phase estimation with lossy interferometers. Phys. Rev. A 2009, 80, 013825. [Google Scholar]
- Fisher, R.A. Theory of Statistical Estimation. Math. Proc. Camb. Philos. Soc. 1925, 22, 700. [Google Scholar] [CrossRef]
- Cramer, H. Mathematical Methods of Statistics; Princeton University Press: Princeton, NJ, USA, 1946. [Google Scholar]
- Shukla, R.K.; Chotorlishvili, L.; Mishra, S.K.; Iemini, F. Prethermal Floquet time crystals in chiral multiferroic chains and applications as quantum sensors of AC fields. Phys. Rev. B 2025, 111, 024315. [Google Scholar] [CrossRef]
- Kurashvili, P.; Chotorlishvili, L.; Kouzakov, K.A.; Tevzadze, A.G.; Studenikin, A.I. Quantum witness and invasiveness of cosmic neutrino measurements. Phys. Rev. D 2021, 103, 036011. [Google Scholar] [CrossRef]
- Haikka, P.; Goold, J.; McEndoo, S.; Plastina, F.; Maniscalco, S. Non-Markovianity, Loschmidt echo, and criticality: A unified picture. Phys. Rev. A 2012, 85, 060101. [Google Scholar] [CrossRef]
- Laine, E.-M.; Breuer, H.-P.; Piilo, J.; Li, C.-F.; Guo, G.-C. Nonlocal Memory Effects in the Dynamics of Open Quantum Systems. Phys. Rev. Lett. 2012, 108, 210402. [Google Scholar] [CrossRef]
- Mazzola, L.; Rodríguez-Rosario, C.A.; Modi, K.; Paternostro, M. Dynamical role of system-environment correlations in non-Markovian dynamics. Phys. Rev. A 2012, 86, 010102. [Google Scholar] [CrossRef]
- Rodríguez-Rosario, C.A.; Modi, K.; Mazzola, L.; Aspuru-Guzik, A. Unification of witnessing initial system-environment correlations and witnessing non-Markovianity. Europhys. Lett. 2012, 99, 20010. [Google Scholar]
- Zhang, W.-M.; Lo, P.-Y.; Xiong, H.-N.; Tu, M.W.-Y.; Nori, F. General non-Markovian dynamics of open quantum systems. Phys. Rev. Lett. 2012, 109, 170402. [Google Scholar] [CrossRef] [PubMed]
- Apollaro, T.J.G.; Franco, C.D.; Plastina, F.; Paternostro, M. Memory-keeping effects and forgetfulness in the dynamics of a qubit coupled to a spin chain. Phys. Rev. A 2011, 83, 032103. [Google Scholar] [CrossRef]
- Žnidarič, M.; Pineda, C.; García-Mata, I. Non-Markovian Behavior of Small and Large Complex Quantum Systems. Phys. Rev. Lett. 2011, 107, 080404. [Google Scholar] [CrossRef] [PubMed]
- Breuer, H.-P.; Laine, E.-M.; Piilo, J. Measure for the Degree of Non-Markovian Behavior of Quantum Processes in Open Systems. Phys. Rev. Lett. 2009, 103, 210401. [Google Scholar] [CrossRef]
- Laine, E.-M.; Piilo, J.; Breuer, H.-P. Measure for the non-Markovianity of quantum processes. Phys. Rev. A 2010, 81, 062115. [Google Scholar] [CrossRef]
- Liu, B.H.; Li, L.; Huang, Y.-F.; Li, C.-F.; Guo, G.-C.; Laine, E.-M.; Breuer, H.-P.; Piilo, J. Experimental control of the transition from Markovian to non-Markovian dynamics of open quantum systems. Nat. Phys. 2011, 7, 931. [Google Scholar] [CrossRef]
- Smirne, A.; Mazzola, L.; Paternostro, M.; Vacchini, B. Interaction-induced correlations and non-Markovianity of quantum dynamics. arXiv 2013, arXiv:1302.2055v1. [Google Scholar] [CrossRef]
- Lu, X.-M.; Wang, X.; Sun, C.P. Quantum Fisher Information Flow in Non-Markovian Processes of Open Systems. Phys. Rev. A 2010, 82, 042103. [Google Scholar] [CrossRef]
- Rajagopal, A.K.; Devi, A.R.U.; Rendell, R.W. Kraus representation of quantum evolution and fidelity as manifestations of Markovian and non-Markovian avataras. Phys. Rev. A 2010, 82, 042107. [Google Scholar] [CrossRef]
- Aharonov, D.; Kitaev, A.; Preskill, J. Fault-Tolerant Quantum Computation with Long-Range Correlated Noise. Phys. Rev. Lett. 2006, 96, 050504. [Google Scholar] [CrossRef]
- Bellomo, B.; Franco, R.L.; Compagno, G. Non-Markovian Effects on the Dynamics of Entanglement. Phys. Rev. Lett. 2007, 99, 160502. [Google Scholar] [CrossRef]
- Zhong, W.; Sun, Z.; Ma, J.; Wang, X.; Nori, F. Fisher information under decoherence in Bloch representation. Phys. Rev. A 2013, 87, 022337. [Google Scholar] [CrossRef]
- Ma, J.; Huang, Y.; Wang, X.; Sun, C.P. Quantum Fisher information of the Greenberger-Horne-Zeilinger state in decoherence channels. Phys. Rev. A 2011, 84, 022302. [Google Scholar] [CrossRef]
- Sun, Z.; Ma, J.; Lu, X.; Wang, X. Fisher information in a quantum-critical environment. Phys. Rev. A 2010, 82, 022306. [Google Scholar] [CrossRef]
- Heng-Na, X.; Xiaoguang, W. Dynamical quantum Fisher information in the Ising model. Phys. A 2011, 390, 4719. [Google Scholar]
- Berrada, K. Non-Markovian effect on the precision of parameter estimation. Phys. Rev. A 2013, 88, 035806. [Google Scholar] [CrossRef]
- Breuer, H.-P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, NY, USA, 2002. [Google Scholar]
- Man, Z.-X.; Xia, Y.-J.; Franco, R.L. Cavity-based architecture to preserve quantum coherence and entanglement. Sci. Rep. 2015, 5, 13843. [Google Scholar] [CrossRef]
- Girolami, D.; Tufarelli, T.; Adesso, G. Characterizing Nonclassical Correlations via Local Quantum Uncertainty. Phys. Rev. Lett. 2013, 110, 240402. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berrada, K. Optimizing Parameter Estimation Precision in Open Quantum Systems. Axioms 2025, 14, 368. https://doi.org/10.3390/axioms14050368
Berrada K. Optimizing Parameter Estimation Precision in Open Quantum Systems. Axioms. 2025; 14(5):368. https://doi.org/10.3390/axioms14050368
Chicago/Turabian StyleBerrada, Kamal. 2025. "Optimizing Parameter Estimation Precision in Open Quantum Systems" Axioms 14, no. 5: 368. https://doi.org/10.3390/axioms14050368
APA StyleBerrada, K. (2025). Optimizing Parameter Estimation Precision in Open Quantum Systems. Axioms, 14(5), 368. https://doi.org/10.3390/axioms14050368




