Abstract
This manuscript addresses an application study by employing a mathematical model of a thermoelastic plate weakened by multi-curved holes under the effect of stress forces in the presence of heat conduction. When the initial heat flow is directed to the plate system, complex variable procedures are used to compute the basic Goursat functions, taking into account the time-dependent variables through conformal mapping, which transfers the domain to the exterior of a unit circle. The problem reduces to a general form of a contact problem in two dimensions, which is called an integrodifferential equation of the second type with the Cauchy kernel. Additionally, different hole shapes are generated using Maple 2023. Computational simulations are performed to determine the normal and shear stress components in the presence and absence of heat effects at various times. Furthermore, numerical calculations of Goursat functions are carried out and graphically displayed for some specific materials. This investigation provides valuable information about industries, such as those regarding ceramic tile, glass, rubber, paint, ceramic pigment, and metal alloys.
MSC:
74A15; 30C20; 45K05
1. Introduction
Thermoelasticity covers a broad spectrum of phenomena. It covers the theories of heat conduction, strain, and stress induced by heat flow when the temperature and strain fields are combined. Thermoelasticity allows us to identify the stresses created by a temperature field, as well as the temperature distribution caused by the actions of internal forces that change over time; see [1]. When external loads are applied to the plate’s structural components, the stress tends to concentrate in the area around the holes. Each component of the stress tensor is governed by a Poisson-type differential equation, and the boundary conditions and differential equations pertaining to the plane problem of thermoelectricity in stresses are examined; see [2]. Manickam et al. [3] attempted to use curvilinear fibers in a thermal setting to examine the nonlinear thermoelastic buckling characteristics of composite variable stiffness beams with several layers. Yuan et al. [4] used the method of fundamental solutions to study the stress fields of anti-plane finite elastic materials with holes that were susceptible to traction or displacement boundaries. An analytical solution for an elastic infinite plate with ellipse and circle holes that experiences internal traction along the holes as well as uniform stresses and shears at infinity was presented by Lu et al. [5]. For anisotropic elastic media with polygonal holes with rounded corners, Hsieh et al. [6] used the perturbation method with conformal mapping and the nonconformal mapping scheme to obtain two sets of solutions of Green’s functions. Savruk [7] undertook a survey of the findings from studies on the concentrations of stresses in elastic bodies that are weakened by nonsmoothly contoured notches and curvilinear holes. Using the Stroh formalism, Hsieh [8] derived a comprehensive solution for an infinite anisotropic plate featuring a hole deviating from an elliptical shape, which is subjected to uniform loading at infinity. Guo and Lu [9] presented a novel means of resolving the elastic–plastic fields along the major-axis line of the elliptical hole using the complex variable method. Boundary problems for infinite plates with holes have been covered by a number of authors [10,11]. Some of them used the Laurent theorem to show that the responses were power series. Applying Goursat functions is another method for handling complex variables. They integrate the characteristics of the circle or any mapped area of Cauchy integrals outside of a unit circle by using the general rational mapping function . Two complex functions are the result of their solution. Abdou et al. [11] used a limitless plate with two curved holes to deduce the first and second types using the Goursat functions in the complex variable technique. In order to tackle the basic issues of an infinite plate with a hole that is weakened by a strong pole of any kind, Abdou and Monaquel [12] used the Cauchy singular approach. The exterior conformal mapping of the inclusion provided Mattei and Lim [13] with a coordinate system, which they used to build a density basis function. Using the complex variable technique, Alhazmi et al. [14] considered an infinite elastic plate featuring two holes that compromise its integrity, aiming to develop a closed form of Goursat functions with varying time. Based on rational approximations for solving Dirichlet problems and least-squares fitting on the boundary, Trefethen [15] created novel techniques for numerical conformal mapping. Under certain conditions, Alharbi and Alhendi [16] used particular conformal mapping to represent the stress distributions of a thin endlessly flexible plate affected by many curvilinear apertures. A complex integrodifferential equation in the right half-plane was solved by Jann [17] using an infinite plate that was weakened by a curvilinear hole.
In this paper, we consider the conformal mapping
where , mapped the domain of the plate that maps the curvilinear hole into the domain outside the unit circle , and is a parameter constrained in such a way that it does not approach zero or reach infinity beyond the unit circle. The two complex analytic potential functions, Goursat functions and , at variable times are derived. Transferring the complex plane, which contains curvilinear holes, is the method’s concept. We employ a particular conformal mapping to achieve this. A method to easily look into shapes from the conformal map is shown, along with a way to compute the conformal map for the chosen bounds. By employing the complex variable technique with the Cauchy methodology, we solve the boundary value problem and obtain a closed version of the Goursat functions. We then simplify the problem using the second-type integrodifferential equation with a Cauchy kernel. We also identify the components of normal and shear stress. After explaining the different physical applications, we calculate and visualize the normal and shear stress components for each at the specified values using the Maple 2023 program. Finally, we discuss the main results of the work.
2. Formulation of the Problem
Take into consideration a thin infinite elastic plate with a thickness of h and weakened by closed and indefinite shape holes C; see Figure 1.
Figure 1.
Physical description of the problem.
Equation (1) is used to conformally transfer the points inside the holes to the unit circle.
Let q represent the constant temperature gradient, and let denote the heat equation that flows uniformly in the negative direction of the y-axis. The equation posits that the temperature increase is uniform throughout the thickness of the plate.
The following is satisfied by the heat equation in this case since C distributes the heat uniformly
The following formula can be used to express the thermoelastic potential (see Parkus [18])
where is a scalar indicating the thermal expansion coefficient and is the Poisson ratio. We assume that the plate’s faces are not subject to any loads. The thermoelastic plate satisfies both the first and second boundary criteria (see Parkus [18])
where is a specified free term and L is a constant that will be discussed. The affix of a point on the border is indicated by the variable .
In the plane theory of thermoelasticity, each of the two complex potential functions, and , with a single complex argument , are expressed as
Here, and represent the constituents of all external forces acting on the boundary; the resulting vectors are shown in Equation (5). At infinity, the stresses are Δ and Δ∗. Finally, the material’s thermal conductivity is denoted by .
In the case of the first fundamental boundary value problem, where , and are given the functions of stresses, and
whereas, for the second boundary value problem , and are referred to as the lame constants, where is a specified function of displacement such that
where u and v are the components of displacement, G is the shear modulus, and and are the components of the external forces specified on the boundary of the plane.
The components of stress are given by
where the heat transfer coefficient is shown by . When the heat is perpendicular to the plate, Equation (2) can be solved using the following (see [19])
In this case, Equation (1) defines the function z.
When Equation (3) is substituted with (9) and the result is integrated, the thermoelastic potential becomes
The values of and are now completely resolved from Equations (9) and (10).
As a result, Equation (8)’s stress components can be modified as follows:
Once the Goursat functions have been obtained, the stress components are determined in their entirety.
3. Conformal Mapping and Special Cases
The physical significance of mapping (1) depends on its ability to model various hole forms, as seen in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13, which include the following notations:
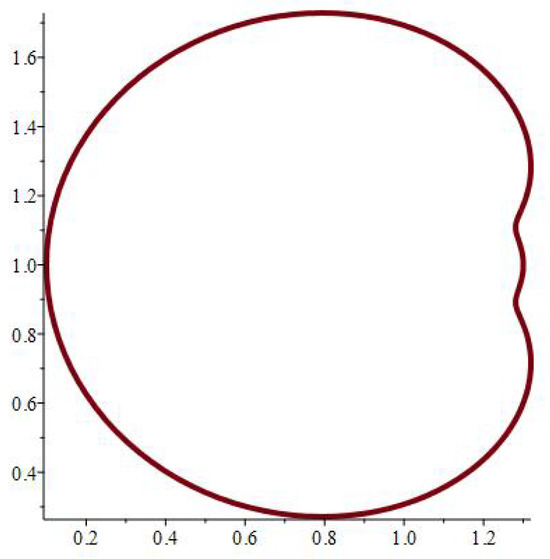
Figure 2.
.
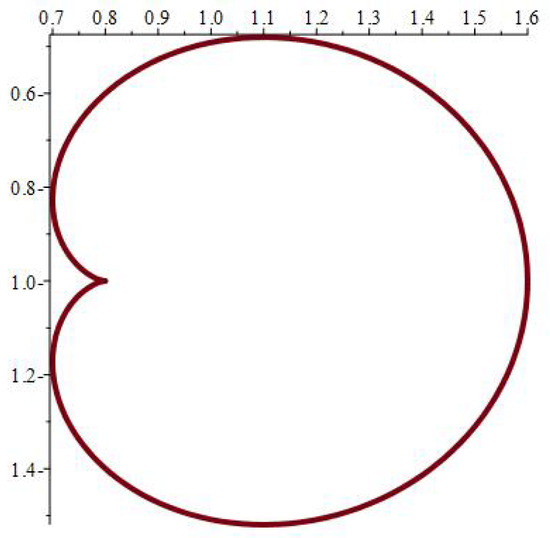
Figure 3.
.
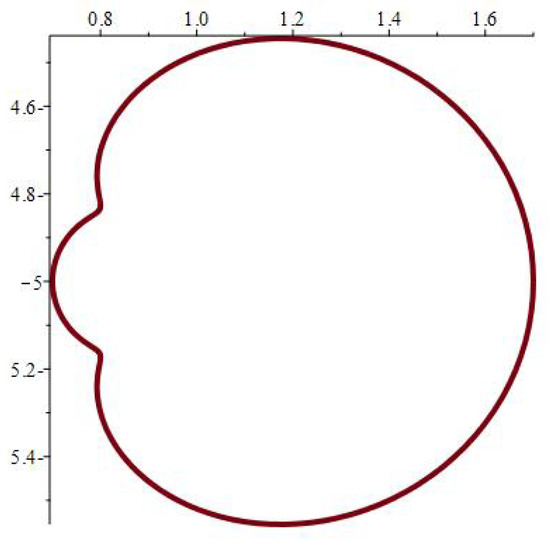
Figure 4.
.
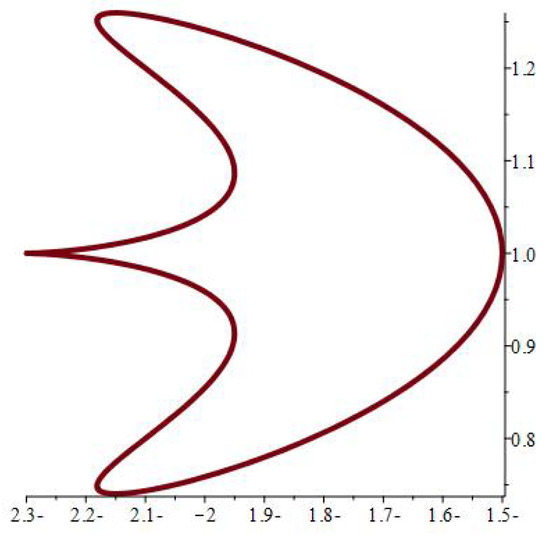
Figure 5.
.
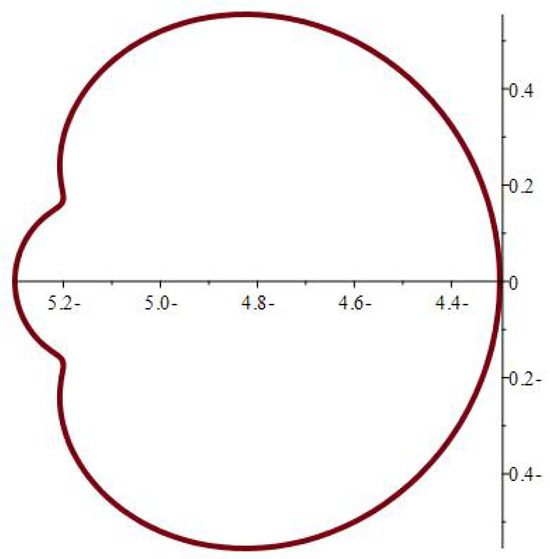
Figure 6.
.
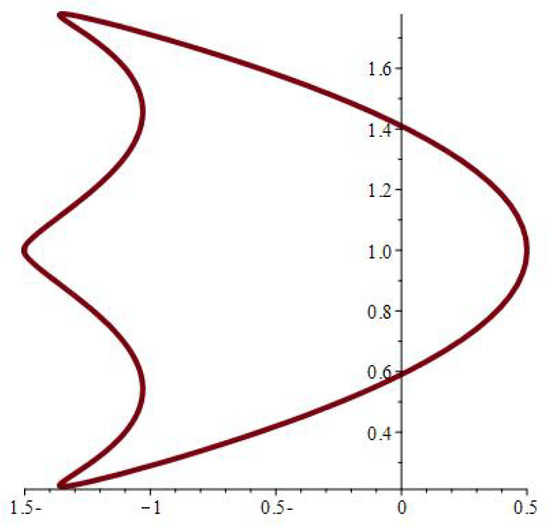
Figure 7.
.
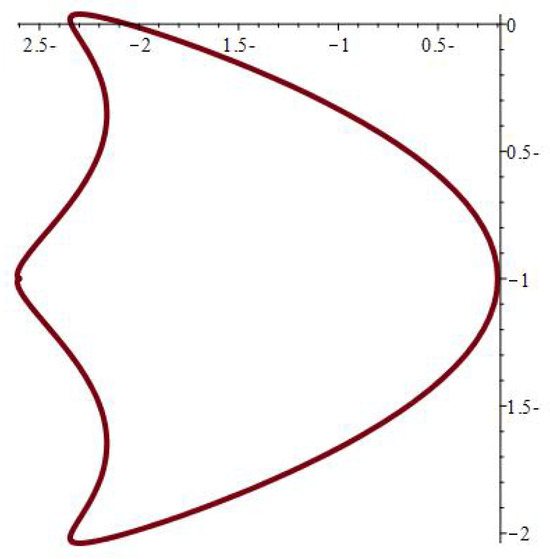
Figure 8.
.
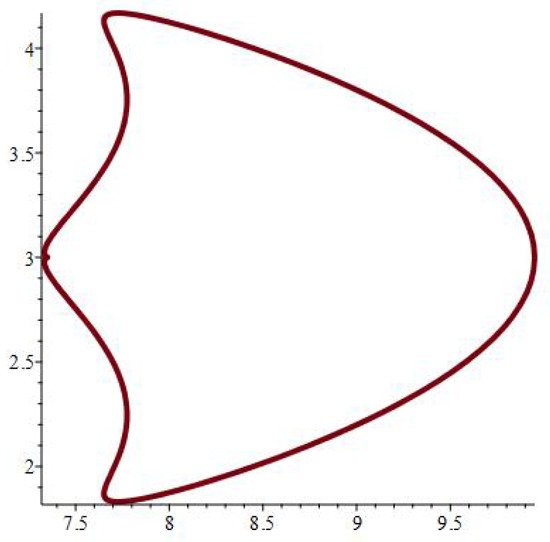
Figure 9.
.
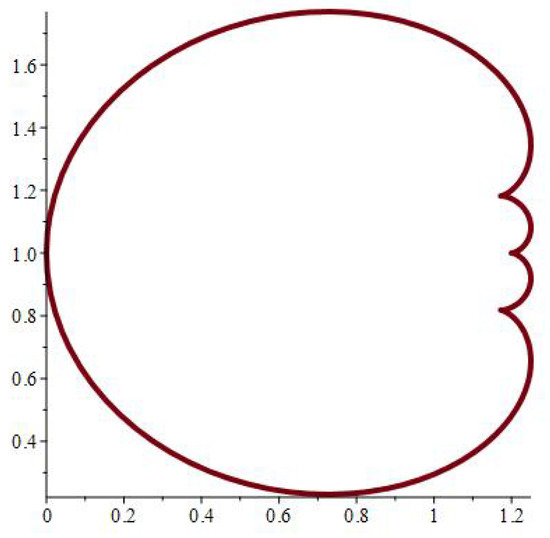
Figure 10.
.
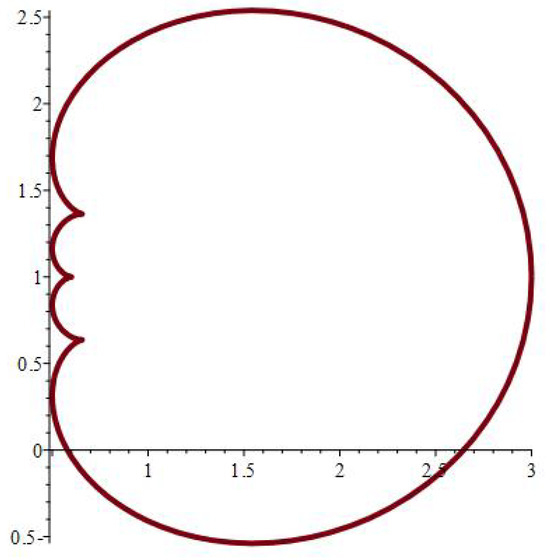
Figure 11.
.
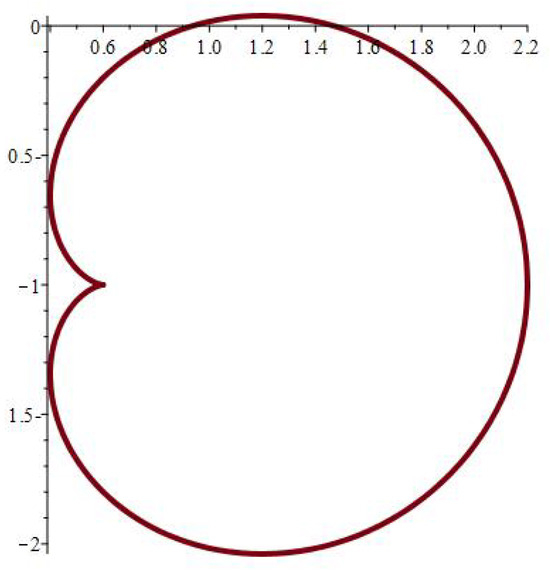
Figure 12.
.
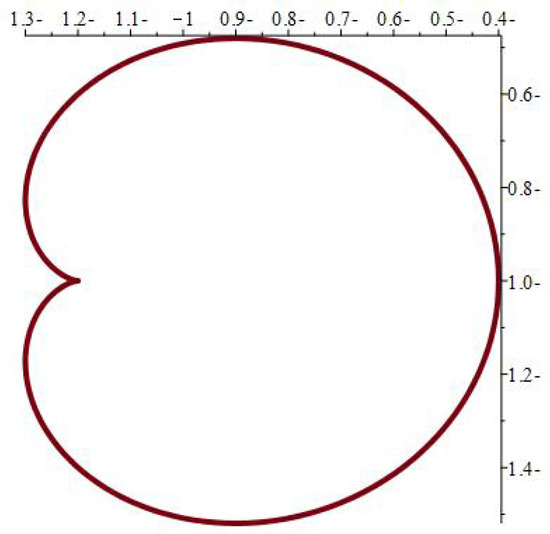
Figure 13.
.
4. Method of Solution
In this section, we use the transformation mapping (1) in the boundary condition (4). We apply the complex variable method with the residue theorem to obtain a closed expression for Goursat functions [20]. Therefore, the expression will be written in the form
where
and is a regular function for .
5. Applications
Application 1: Curvilinear Holes for an Infinite Plate Undergoing Uniform Tensile Stress
For , where and , a plate with infinite stretch is exposed to a uniform tensile stress with intensity , resulting in the formation of an angle with the x-axis. A curvilinear hole S, free of stresses, weakens the plate. The functions (20)–(22) take the following forms:
The figures of the two cases below demonstrate the graphical representation and large-form calculation of the three stress components , and :
For
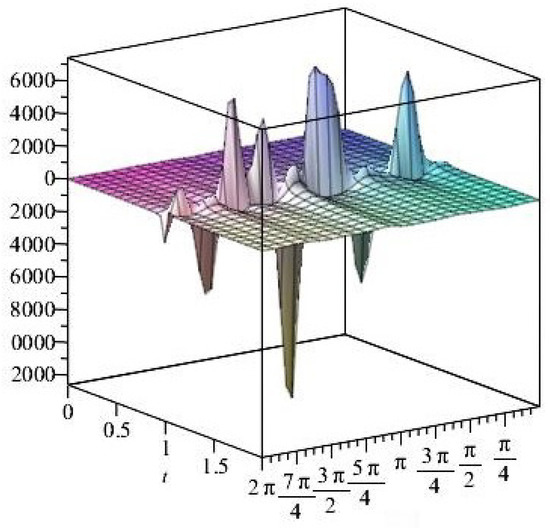
Figure 14.
The normal stress components versus the angle during variant times.
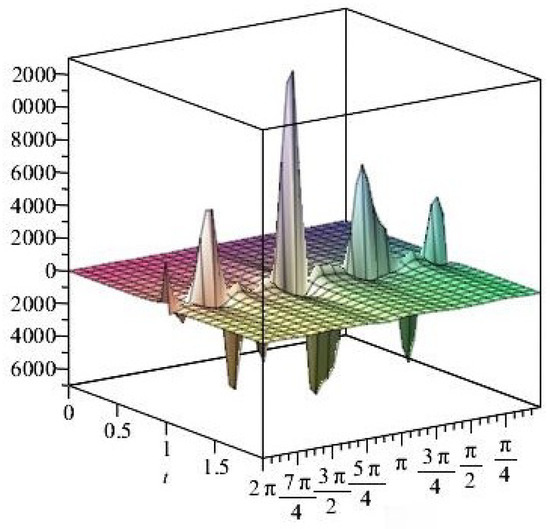
Figure 15.
The normal stress components versus the angle during variant times.
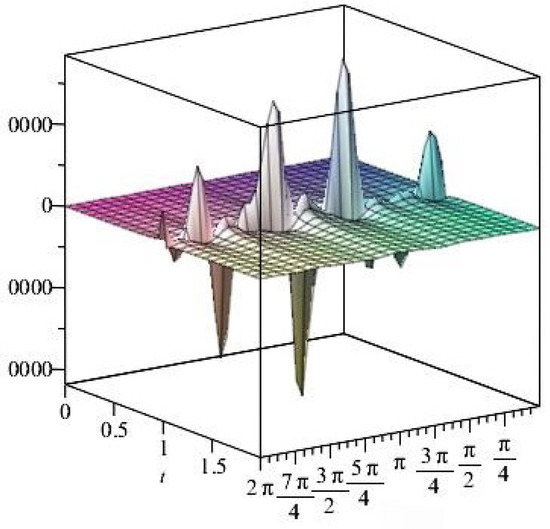
Figure 16.
The shear stress components versus the angle during variant times.
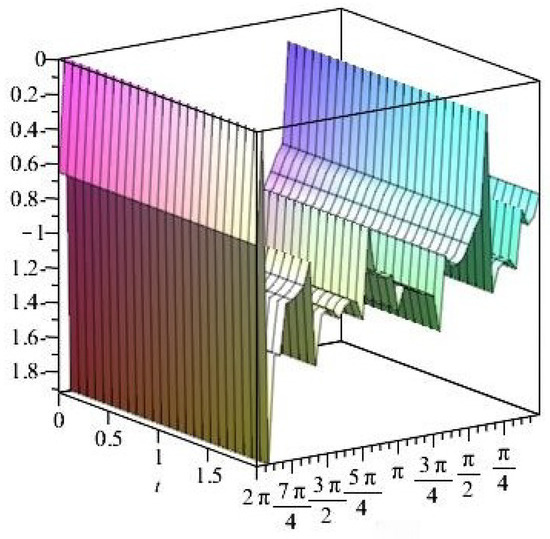
Figure 17.
Stress ratios .
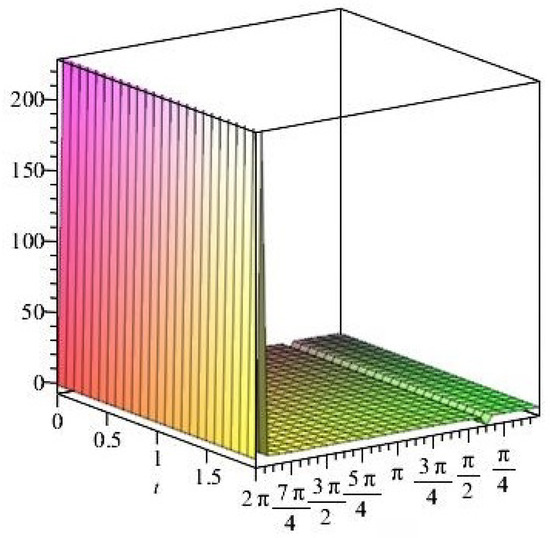
Figure 18.
Stress ratios .
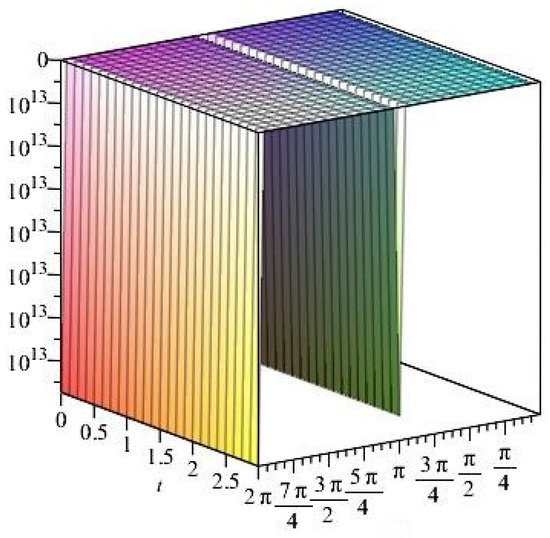
Figure 19.
The normal stress components versus the angle during variant times under heating flow effect.
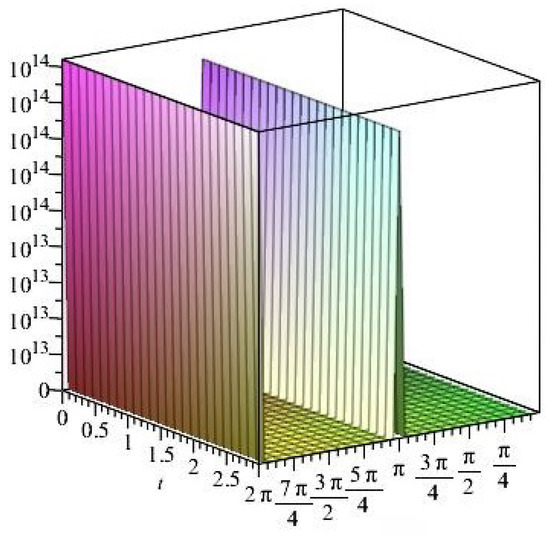
Figure 20.
The normal stress components versus the angle during variant times under heating flow effect.
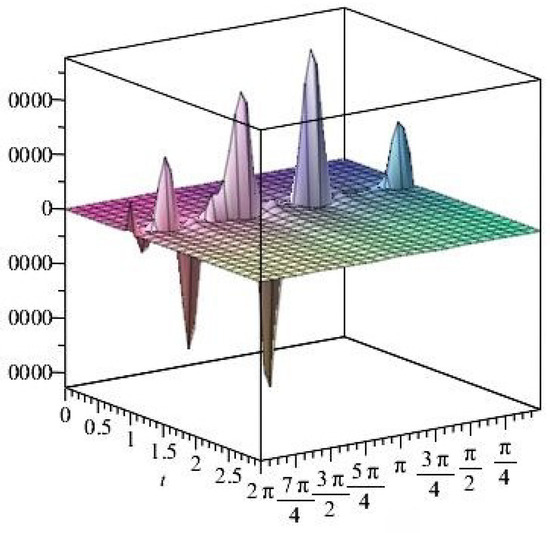
Figure 21.
The shear stress components versus the angle during variant times under heating flow effect.
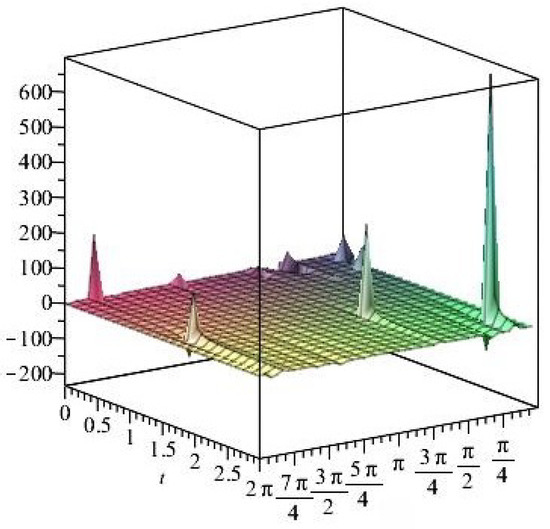
Figure 22.
Stress ratios .
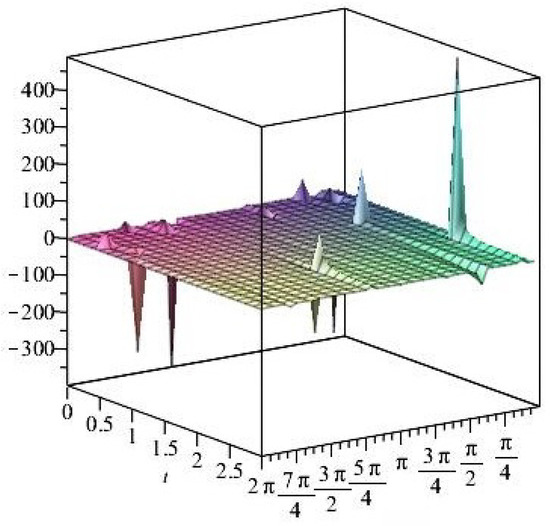
Figure 23.
Stress ratios .
Application 2: Uni-Directional Tension of an Infinite Plate with a Rigid Curvilinear Center
For , and , the two complex functions (20), (22) take the form
As a result, we obtain uni-directional tension on an infinite plate with a rigid curvilinear center. Considering the requirement that the total of the moments generated by the forces acting on the curvilinear center from all directions must equal zero, we can estimate the value of the constant , i.e.,
Hence,
where
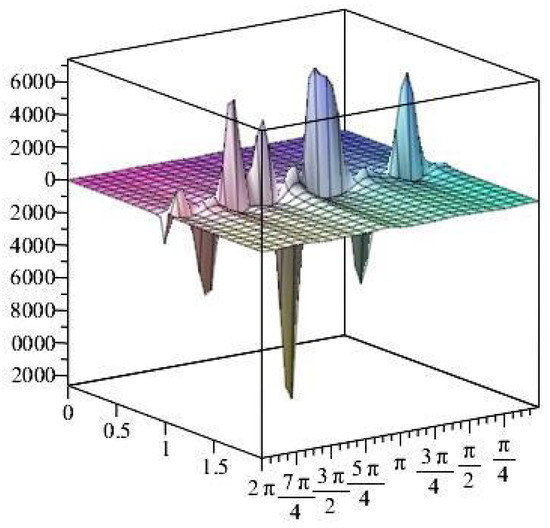
Figure 24.
The normal stress components versus the angle during variant times.
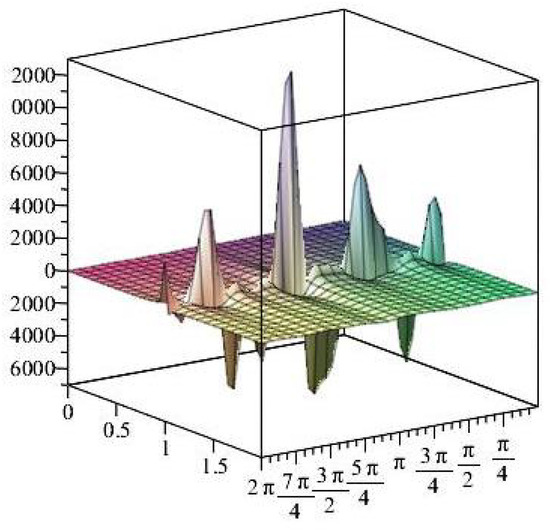
Figure 25.
The normal stress components versus the angle during variant times.
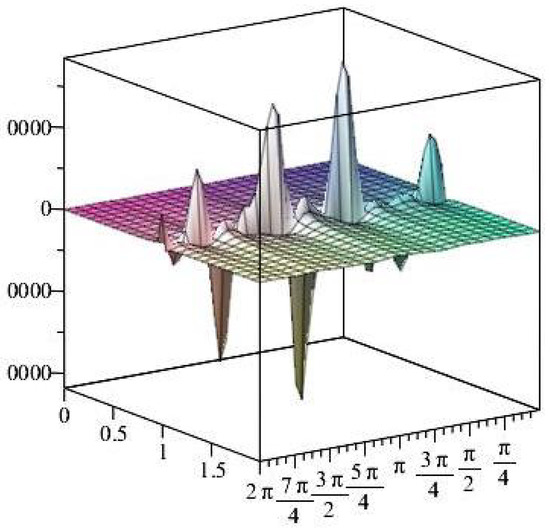
Figure 26.
The shear stress components versus the angle during variant times.
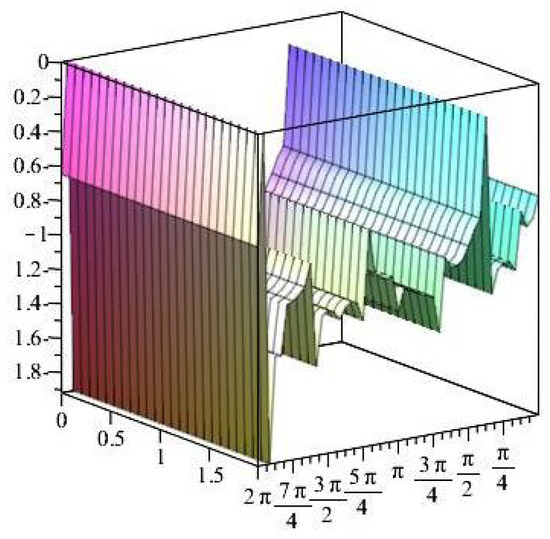
Figure 27.
Stress ratios .
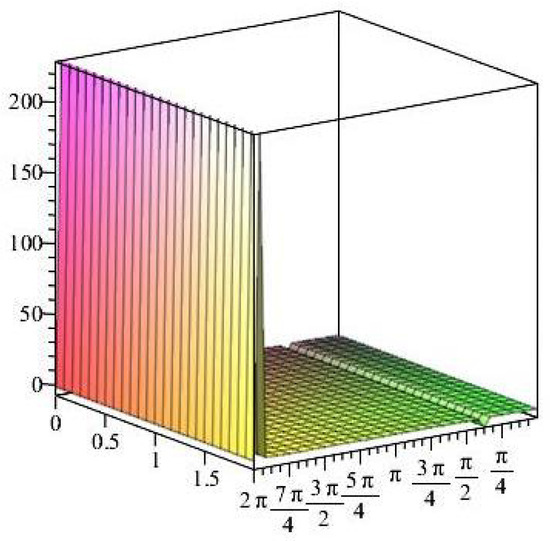
Figure 28.
Stress ratios .
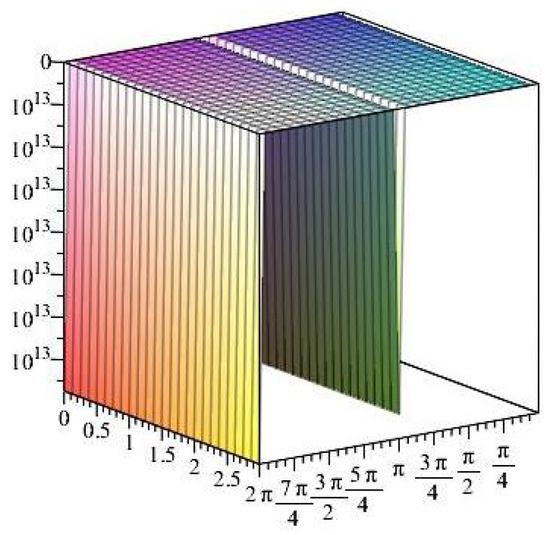
Figure 29.
The normal stress components versus the angle during variant times under heating flow effect.
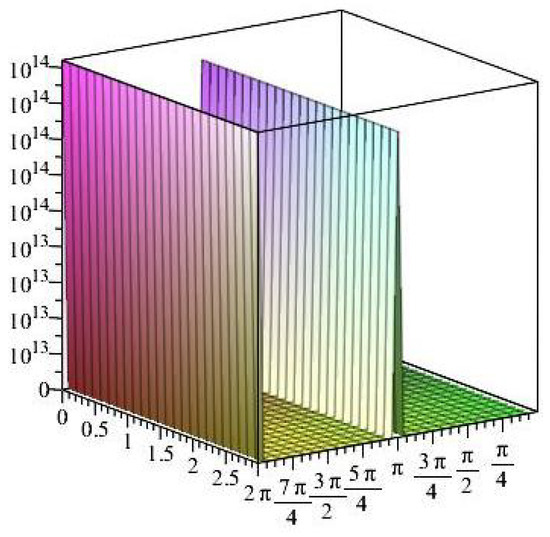
Figure 30.
The normal stress components versus the angle during variant times under heating flow effect.
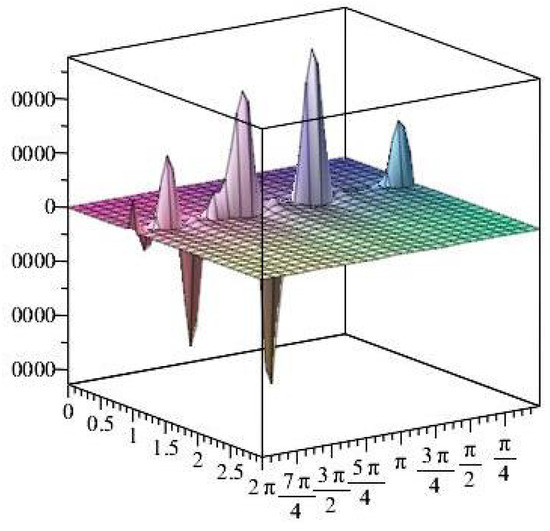
Figure 31.
The shear stress components versus the angle during variant times under heating flow effect.
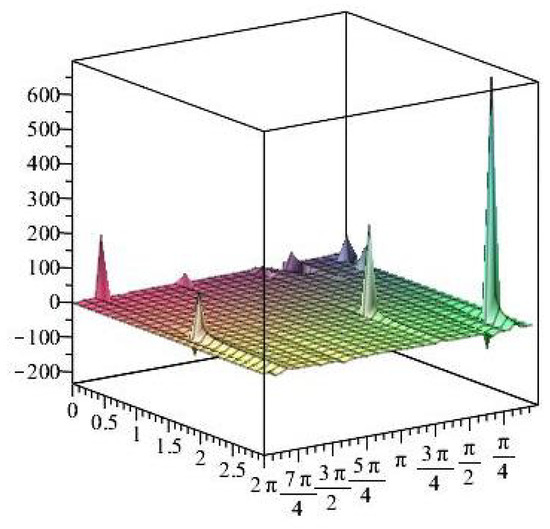
Figure 32.
Stress ratios .
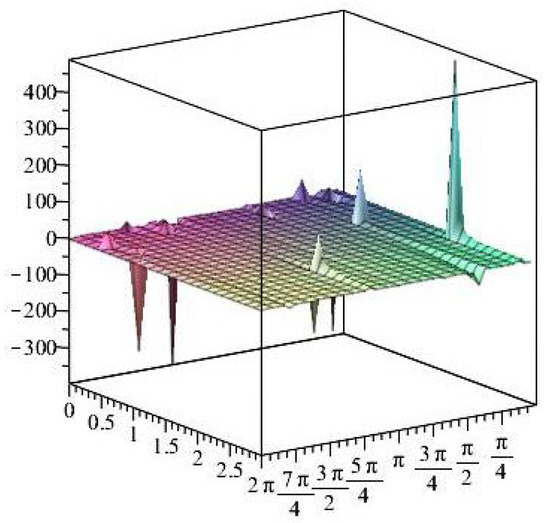
Figure 33.
Stress ratios .
- For
Taking nickel, copper, and silver, we calculate the absolute values of Goursat functions with time for these minerals. See Table 1, Table 2 and Table 3.

Table 1.
Values of and for nickel, where ( ).

Table 2.
Values of and for copper, where ( ).

Table 3.
Values of and for silver, where ( ).
Figure 34, Figure 35 and Figure 36 indicate the relationship between Goursat functions and different tenses.
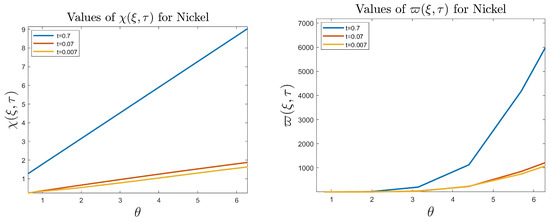
Figure 34.
Values of and f for nickel, where .
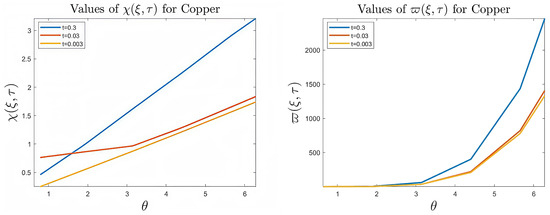
Figure 35.
Values of and f for copper, where .
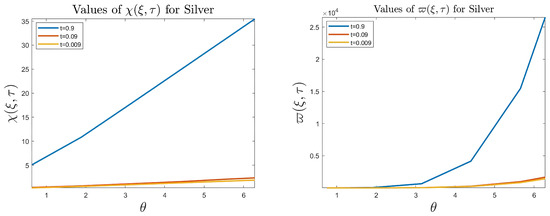
Figure 36.
Values of and f for silver, where .
Application 3: When the Center of the Curvilinear is Subjected to an External Force
For and , when the force is applied to the curvilinear kernel, we obtain the second boundary problem. It is hypothesized that stresses do not exist at limitless values, and it is readily apparent that the kernel does not undergo rotation.
In general, the kernal remains in the original position. The Goursat functions are
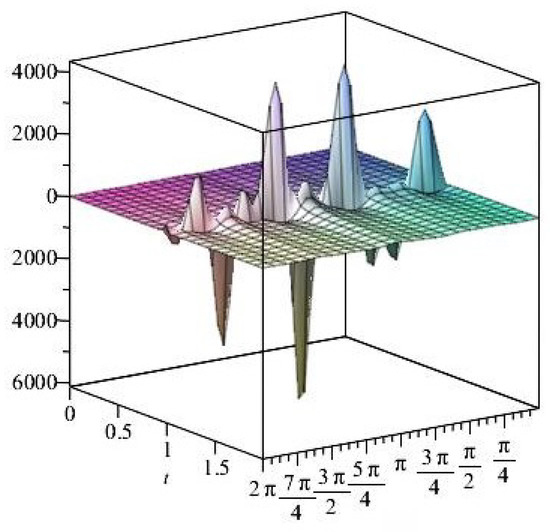 Figure 37. The normal stress components versus the angle during variant times.
Figure 37. The normal stress components versus the angle during variant times.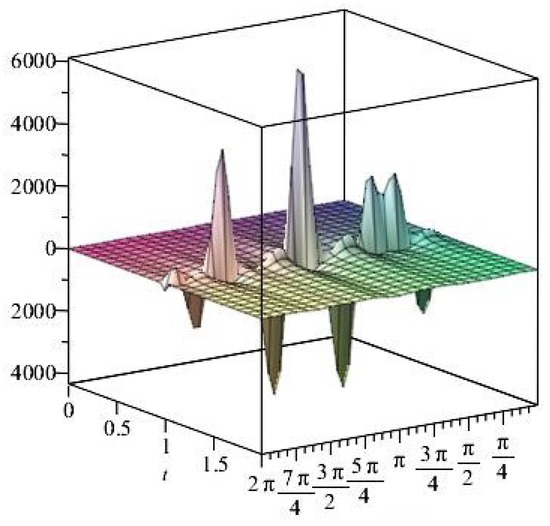 Figure 38. The normal stress components versus the angle during variant times.
Figure 38. The normal stress components versus the angle during variant times.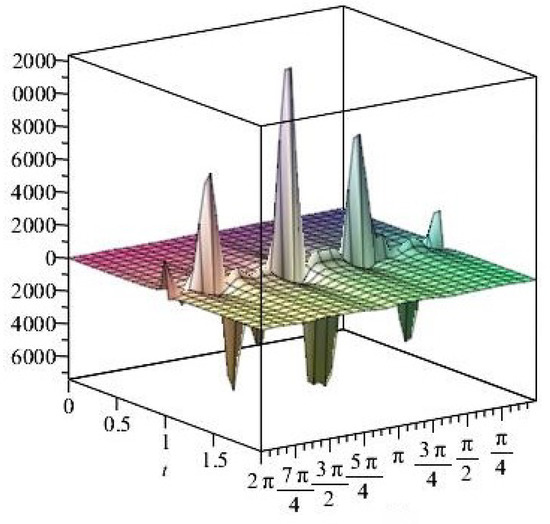 Figure 39. The shear stress components versus the angle during variant times.
Figure 39. The shear stress components versus the angle during variant times.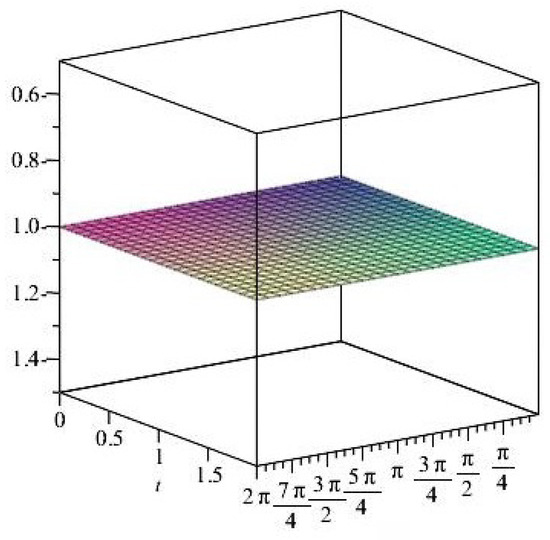 Figure 40. Stress ratios .
Figure 40. Stress ratios .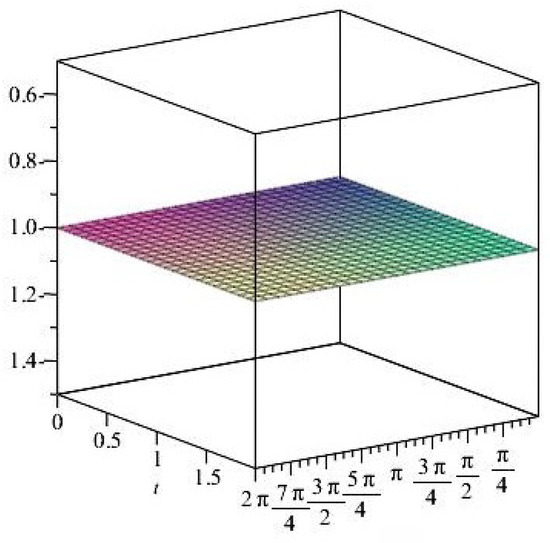 Figure 41. Stress ratios .
Figure 41. Stress ratios .- The stresses are calculated for the thermoelasticity plate using the following replacements: (see Figure 42, Figure 43, Figure 44, Figure 45 and Figure 46).
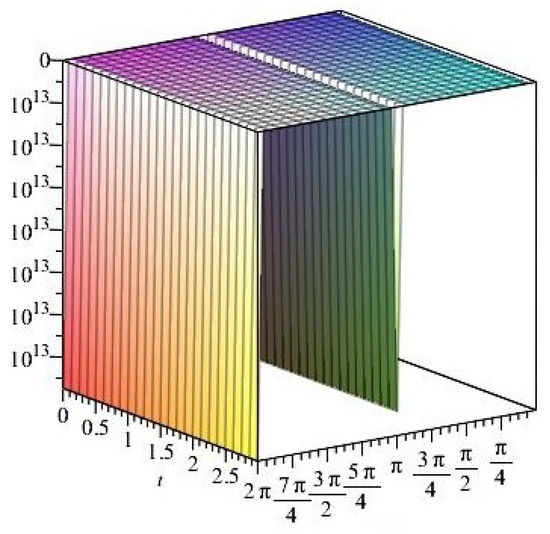 Figure 42. The normal stress components versus the angle during variant times under heating flow effect.
Figure 42. The normal stress components versus the angle during variant times under heating flow effect.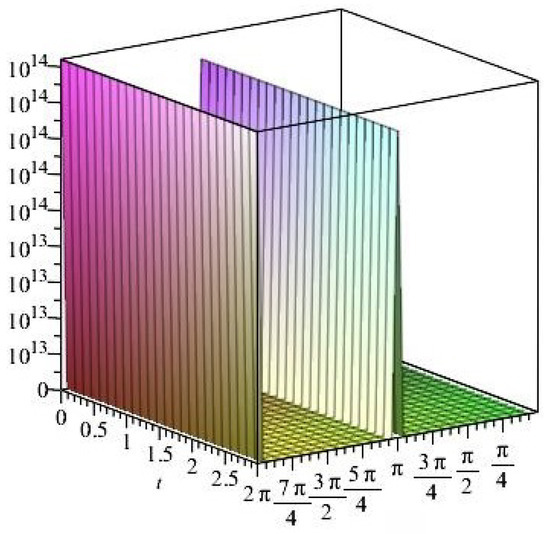 Figure 43. The normal stress components versus the angle during variant times under heating flow effect.
Figure 43. The normal stress components versus the angle during variant times under heating flow effect.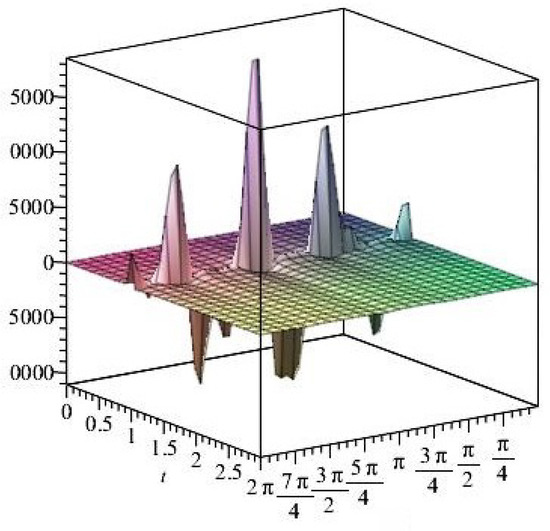 Figure 44. The shear stress components versus the angle during variant times under heating flow effect.
Figure 44. The shear stress components versus the angle during variant times under heating flow effect.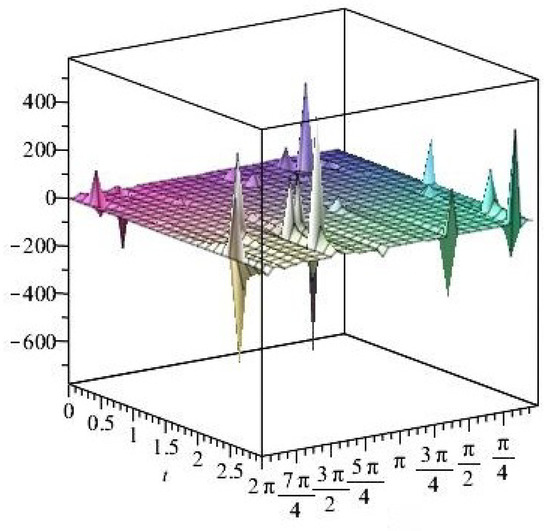 Figure 45. Stress ratios .
Figure 45. Stress ratios .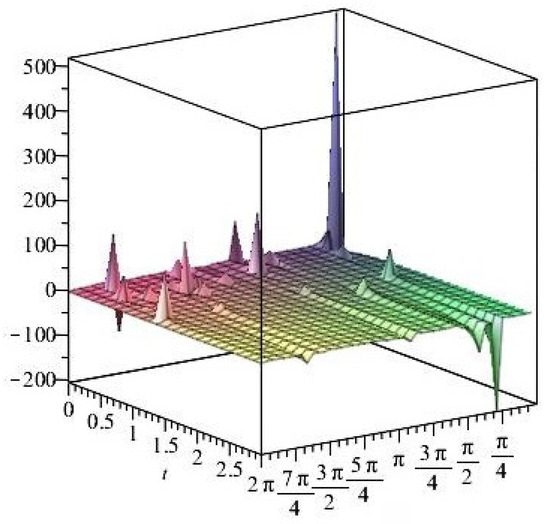 Figure 46. Stress ratios .
Figure 46. Stress ratios .
6. Discussion and Conclusions
In the current study, the physical model for an infinite elastic medium is presented, subjected to the uniform heat flow in the direction of a negative y-axis. In the context of thermoelastic theory under the effect of uniform stress forces, the medium weakens by multi-curvilinear holes. The complex variable method (Cauchy method) plays a main role to obtain the two Goursat functions at various times by projecting the infinite domain of the problem onto a unit circle. This technique is powerful to help deal with the infinite domain more efficiently, including the geometric interpretation and reducing the problem to a famous kind of contact problem that represents a second kind of integrodifferential equation with a discontinuous kernel (Cauchy kernel), ensuring the stability of the numerical approach. The investigations on the normal and shear stress components indicate an important area of the study. Then, the stress components and stress ratios for both the standard plate and the thermoelastic case were computed and displayed graphically in 3D for various physical applications. The theoretical knowledge and graphical results indicate that
- It is noticed from the resulting values of the stress ratios that the stress remains positive between the minimum and maximum tensile values; see Figure 17 and Figure 22, and, as a special case, when there is no stress change, then see Figure 40. Meanwhile, for a rigid curvilinear center, the stress ratios across a large surface domain are illustrated in Figure 27.
- The numerical results indicate that, besides the boundary conditions that restricted the domain of the problem, acting stress forces, and heat conduction at various times, the two Goursat functions provide increasing values with respect to increasing time (0,1). Therefore, a general visualization of the amplitude of waves or energy levels is determined. See Table 1, Table 2 and Table 3.
- The current model appears in more general physical phenomena. For example, in ceramic thermoelastic plates, the coupling of many curvilinear holes in a metallic ceramic plate under the effect of uniform stress forces in the presence of heat conduction necessitates a thorough examination of both thermal and mechanical stress factors. Numerical approaches, stress intensity factors, and fracture mechanics are crucial in forecasting material performance and failure. To optimize the design and reduce the danger of failure, special attention should be paid to the hole arrangement, thermal gradient, and material qualities.
Future Work:
- Study the physical model in the presence of a normal magnetic field.
- Expand the study to include the effect of the external forces near the edges of the plate.
Author Contributions
Conceptualization, F.M.A.; Methodology, F.M.A. and N.G.A.; Software, N.G.A.; Formal analysis, N.G.A.; Investigation, N.G.A.; Resources, F.M.A.; Writing—original draft, N.G.A.; Writing—review & editing, N.G.A.; Supervision, F.M.A.; Project administration, F.M.A.; Funding acquisition, F.M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nowacki, W. Thermoelasticity; Pergamon Press: Warsaw, Poland, 2013; Available online: https://shop.elsevier.com/books/thermoelasticity/nowacki/978-0-08-024767-0 (accessed on 22 October 2013).
- Khaldjigitov, A.; Tilovov, O.; Xasanova, Z. A new approach to problems of thermoelasticity in stresses. J. Therm. Stress. 2024, 47, 1228–1241. [Google Scholar] [CrossRef]
- Manickam, G.; Haboussi, M.; D’Ottavio, M.; Kulkarni, V.; Chettiar, A.; Gunasekaran, V. Nonlinear thermo-elastic stability of variable stiffness curvilinear fibres based layered composite beams by shear deformable trigonometric beam model coupled with modified constitutive equations. Int. J. Non-Linear Mech. 2023, 148, 104303. [Google Scholar] [CrossRef]
- Yuan, X.; Jiang, Q.; Zhou, Z.; Yang, F. Stress analysis of anti-plane finite elastic solids with hole by the method of fundamental solutions using conformal mapping technique. Arch. Appl. Mech. 2022, 92, 1823–1839. [Google Scholar] [CrossRef]
- Lu, A.Z.; Xu, Z.; Zhang, N. Stress analytical solution for an infinite plane containing two holes. Int. J. Mech. Sci. 2017, 128, 224–234. [Google Scholar] [CrossRef]
- Hsieh, M.L.; Hwu, C. Green’s functions for anisotropic elastic plates containing polygonal holes. Int. J. Mech. Sci. 2024, 276, 109396. [Google Scholar] [CrossRef]
- Savruk, M.P. Stress Concentration Near Curvilinear Holes and Notches with Nonsmooth Contours. Mater. Sci. 2021, 57, 331–343. [Google Scholar] [CrossRef]
- Hsieh, M.L.; Hwu, C. A full field solution for an anisotropic elastic plate with a hole perturbed from an ellipse. Eur. J. Mech. A/Solids 2023, 97, 104823. [Google Scholar] [CrossRef]
- Guo, J.; Lu, Z. Line field analysis and complex variable method for solving elastic-plastic fields around an anti-plane elliptic hole. Sci. China Phys. Mech. Astron. 2011, 54, 1495–1501. [Google Scholar] [CrossRef]
- Abdou, M.A. Fundamental problems for infinite plate with a curvilinear hole having finite poles. Appl. Math. Comput. 2002, 125, 79–91. [Google Scholar] [CrossRef]
- Abdou, M.A.; Ibrahim, E.; Basseem, M. The stress and strain components for a weakened elastic plate by two curvilinear holes in presence of heat. Curr. Sci. Int. 2022, 11, 199–216. Available online: https://www.curresweb.com/index.php/CSI1/article/view/81 (accessed on 30 May 2022).
- Abdou, M.A.; Monaquel, S.J. Integro Differential Equation and Fundamental Problems of an Infinite Plate with a Curvilinear Hole Having Strong Pole. Int. J. Contemp. Math. Sci. 2011, 6, 199–208. Available online: https://www.researchgate.net/profile/M-Abdou-3/publication/267677313_Integro_differential_equation_and_fundamental_problems_of_an_infinite_plate_with_a_curvilinear_hole_having_strong_pole/links/5523e5c80cf2c815e073650b/Integro-differential-equation-and-fundamental-problems-of-an-infinite-plate-with-a-curvilinear-hole-having-strong-pole.pdf (accessed on 1 January 2011).
- Mattei, O.; Lim, M. Explicit analytic solution for the plane elastostatic problem with a rigid inclusion of arbitrary shape subject to arbitrary far-field loadings. J. Elast. 2021, 144, 81–105. [Google Scholar] [CrossRef]
- Alhazmi, S.; Abdou, M.A.; Basseem, M. The stresses components in position and time of weakened plate with two holes conformally mapped into a unit circle by a conformal mapping with complex constant coefficients. AIMS Math. 2023, 8, 11095–11112. Available online: https://www.aimspress.com/aimspress-data/math/2023/5/PDF/math-08-05-562.pdf (accessed on 9 March 2023). [CrossRef]
- Trefethen, L.N. Numerical conformal mapping with rational functions. Comput. Methods Funct. Theory 2020, 20, 369–387. [Google Scholar] [CrossRef]
- Alharbi, F.M.; Alhendi, N.G. New Approach of Normal and Shear Stress Components for Multiple Curvilinear Holes Which Weakened a Flexible Plate. Symmetry 2024, 16, 360. [Google Scholar] [CrossRef]
- Jan, A.R. The solution of a complex integro differential equation in the right half-plane via an infinite plate weakened by a curvilinear hole. Appl. Math. 2024, 18, 493–503. [Google Scholar] [CrossRef]
- Parkus, H. Thermoelasticity; Springer: Berlin, Germany, 1976. [Google Scholar] [CrossRef]
- Abdou, M.A.; Basseem, M. Thermopotential function in position and time for a plate weakened by curvilinear hole. Arch. Appl. Mech. 2022, 92, 867–883. [Google Scholar] [CrossRef]
- Abdou, M.A.; Aseeri, S.A. Closed forms of Goursat functions in presence of heat for curvilinear holes. J. Therm. Stress. 2009, 32, 1126–1148. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).