Reliability Analysis and Numerical Simulation of Industrial Robot Drive System with Vacation
Abstract
:1. Introduction
2. Mathematical Modelling
3. Well-Posedness of the System (1)–(3)
 , where .
, where .4. Stability of the System
5. Some Indices of the System
5.1. Indices of Reliability of the System
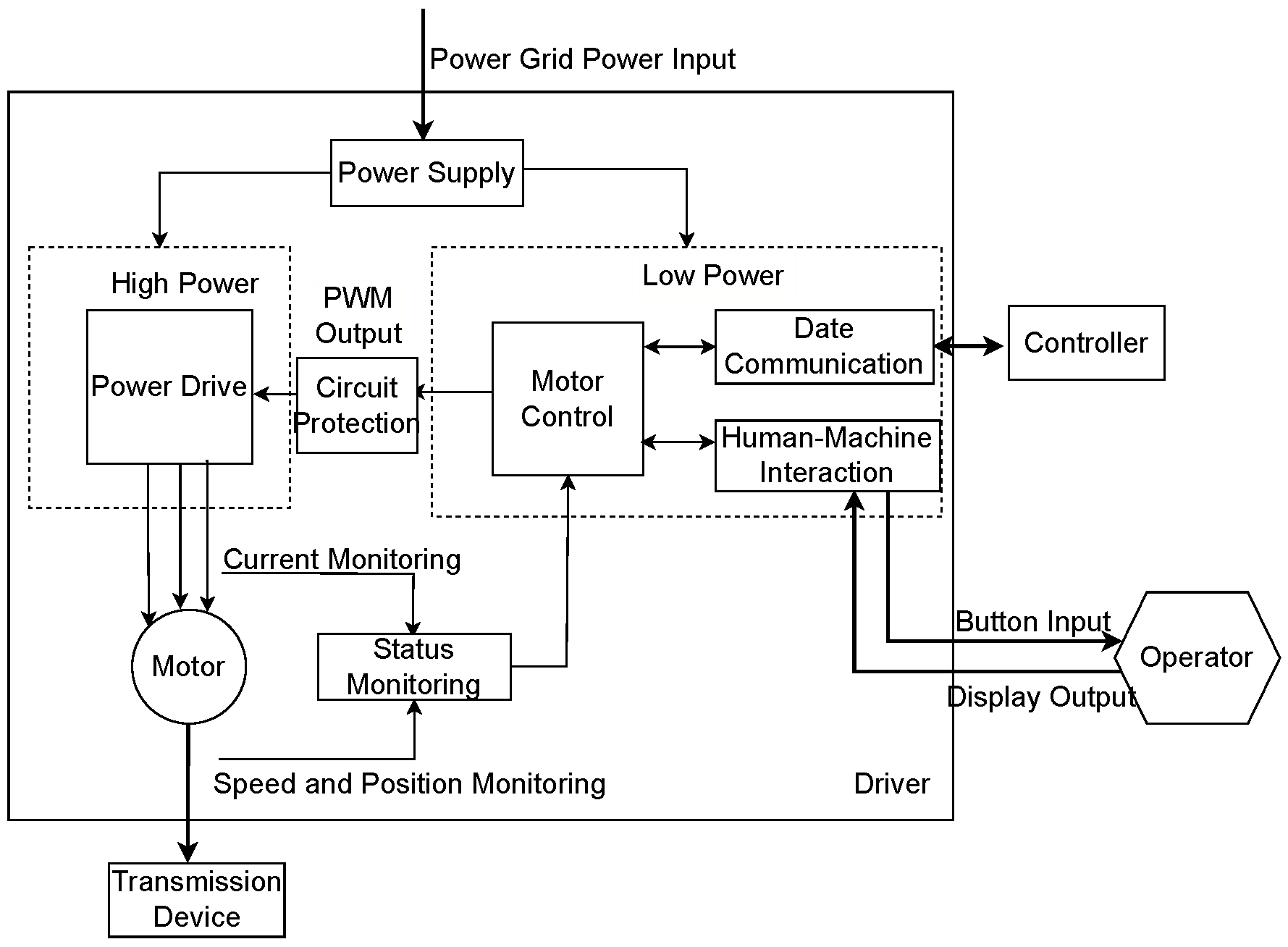
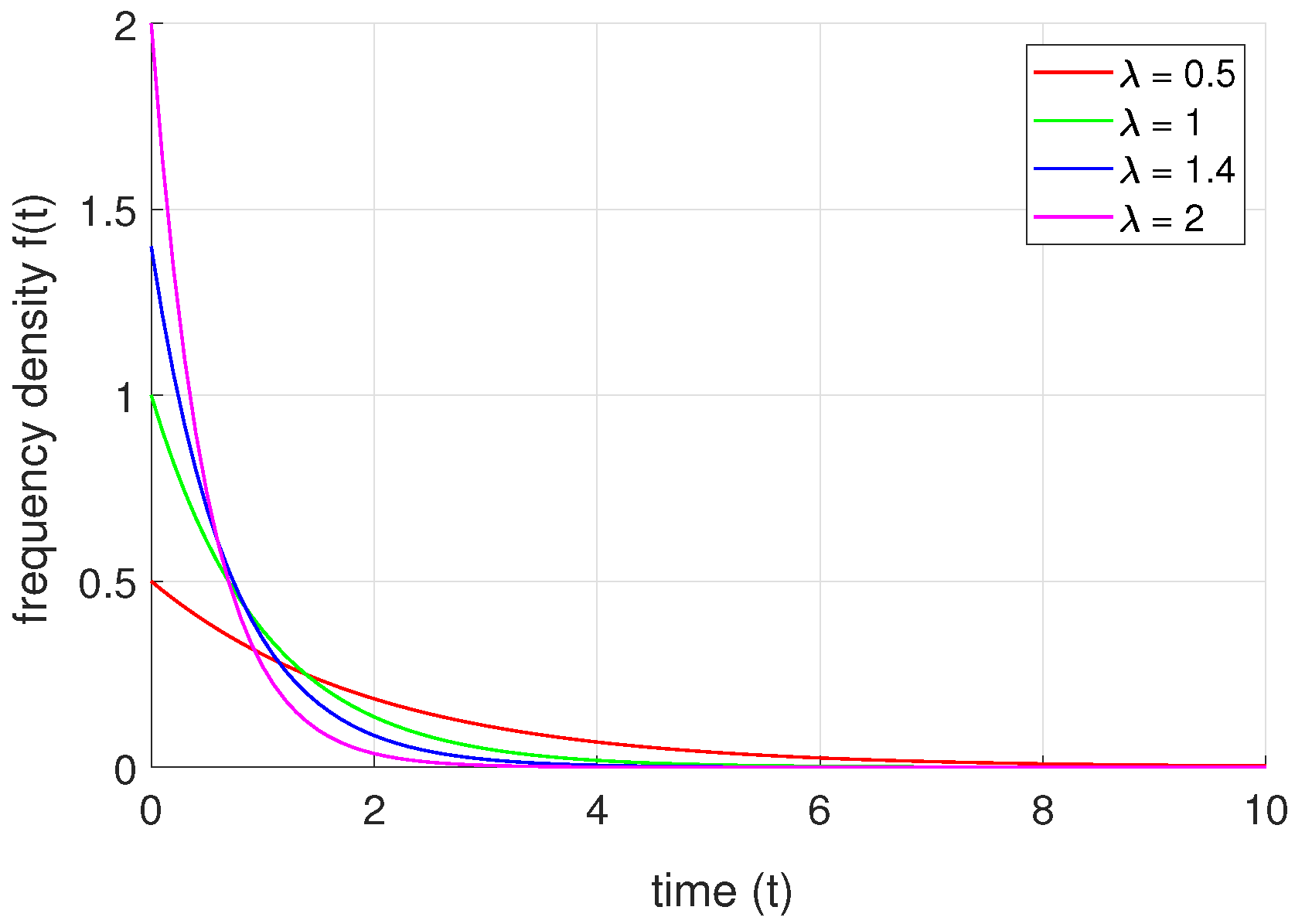
5.2. Numerical Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fazlollahtabar, H.; Niaki, S.T.A. Reliability Models of Complex Systems for Robots and Automation; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Cheng, J.; Tang, Y.H.; Yu, M.M. Reliability of unidirectional closed three-part series and parallel cold storage repairable system. Math. Appl. 2017, 30, 27–39. [Google Scholar]
- Li, Y.L.; Xu, G.Q. Analysis of two components parallel repairable system with vacation. Commun.-Stat.-Theory Methods 2021, 50, 2429–2450. [Google Scholar]
- Hu, L.M.; Yue, D.Q.; Ma, Z.Y. Availability analysis of a repairable series-parallel system with redundant dependency. Commun. -Stat.-Theory Methods 2018, 33, 446–460. [Google Scholar] [CrossRef]
- Qiao, X.; Feng, B.L.; Ma, D. Asymptotic Stability Analysis of Three Robot Safety System Models with Warning Function Analysis. Pract. Underst. Math. 2021, 51, 138–145. [Google Scholar]
- Qiao, X.; Ma, D.; Guo, S. Reliability Analysis and Numerical Simulation of the Five-Robot System with Early Warning Function. Axioms 2025, 14, 113. [Google Scholar] [CrossRef]
- Chen, W.L. System reliability analysis of retrial machine repair systems with warm standbys and a single server of working breakdown and recovery policy. Syst. Eng. 2018, 21, 59–69. [Google Scholar]
- Ke, J.C.; Liu, T.H.; Yang, D.Y. Modelling of Machine Interference Problem with Unreliable Repairman and Standbys Imperfect Switchover. Reliab. Eng. Syst. Saf. 2018, 174, 12–18. [Google Scholar]
- Guo, L.N.; Xu, H.B.; Gao, C. Stability analysis of a new kind n-unit series repairable system. Appl. Math. Model. 2011, 35, 202–217. [Google Scholar]
- Jau, C.; Dong, Y.Y.; Shey, H.S. Availability of a repairable retrial system with warm standby components. Int. J. Comput. Math. 2013, 11, 2279–2297. [Google Scholar]
- Wang, G.R.; Hu, L.M.; Hu, L.M. Reliability modeling for a repairable (k1, k2)-out-of-n: G system with phase-type vacation time. Appl. Math. Model. 2021, 91, 311–321. [Google Scholar] [CrossRef]
- Muhtar, M.; Haji, A.; Rozi, M. Semigroup method for a deteriorating system with multiple vacations of a repairman. Semigroup Forum 2021, 102, 477–494. [Google Scholar] [CrossRef]
- Wang, J.Y.; Ye, J.M.; Ma, Q.R. An extended geometric process repairable model with its repairman having vacation. Ann. Oper. Res. 2022, 311, 401–415. [Google Scholar]
- Qi, X.P.; Haji, A.; Muhtar, M. Dynamic Analysis of a Deteriorating System with Single Vacation of a Repairman. Acta Math. Appl. Appl.-Sin.-Engl. Ser. 2022, 38, 690–709. [Google Scholar]
- Muhtar, M.; Haji, A.; Rozi, M. Analysis of two components parallel repairable degenerate system with vacation. AIMS Math. 2022, 10, 10602–10619. [Google Scholar]
- Dong, Q.H.; Liu, P.; Jia, X.J. Reliability analysis of k-out-of-n: G repairable systems considering common cause failure and multi-level maintenance strategy. Microchim. Acta 2024, 238, 44–59. [Google Scholar]
- Wen, Y.Q.; Liu, B.L.; Zhang, Z.Q. Modeling and analysis for a repairable system with multi-state components under K-mixed redundancy strategy. Commun.-Stat.-Theory Methods 2024, 53, 748–764. [Google Scholar]
- Wang, W. Restoring ergodicity of stochastically reset anomalous-diffusion processes. Phys. Rev. Res. 2022, 4, 013161. [Google Scholar] [CrossRef]
- Zhang, W.Y.; Zhang, X.H.; He, S.G. Optimal condition-based maintenance policy for multi-component repairable systems with economic dependence in a finite-horizon. Reliab. Eng. Syst. Saf. 2024, 241, 748–764. [Google Scholar] [CrossRef]
- Pazy, A. Semigroup of Linear Operators and Application to Partial Differential Equations; Springer: New York, NY, USA, 1982. [Google Scholar]
- Nagel, R. One-Parameter Semigroup of Positive Operators. In Lecture Notes in Mathematics; Springer: New York, NY, USA, 1986. [Google Scholar]
- Guo, L.N.; Xu, H.B.; Gao, C.; Zhu, G.T. Stability analysis of a new kind series system. IMA J. Appl. Math. 2010, 75, 439–460. [Google Scholar] [CrossRef]


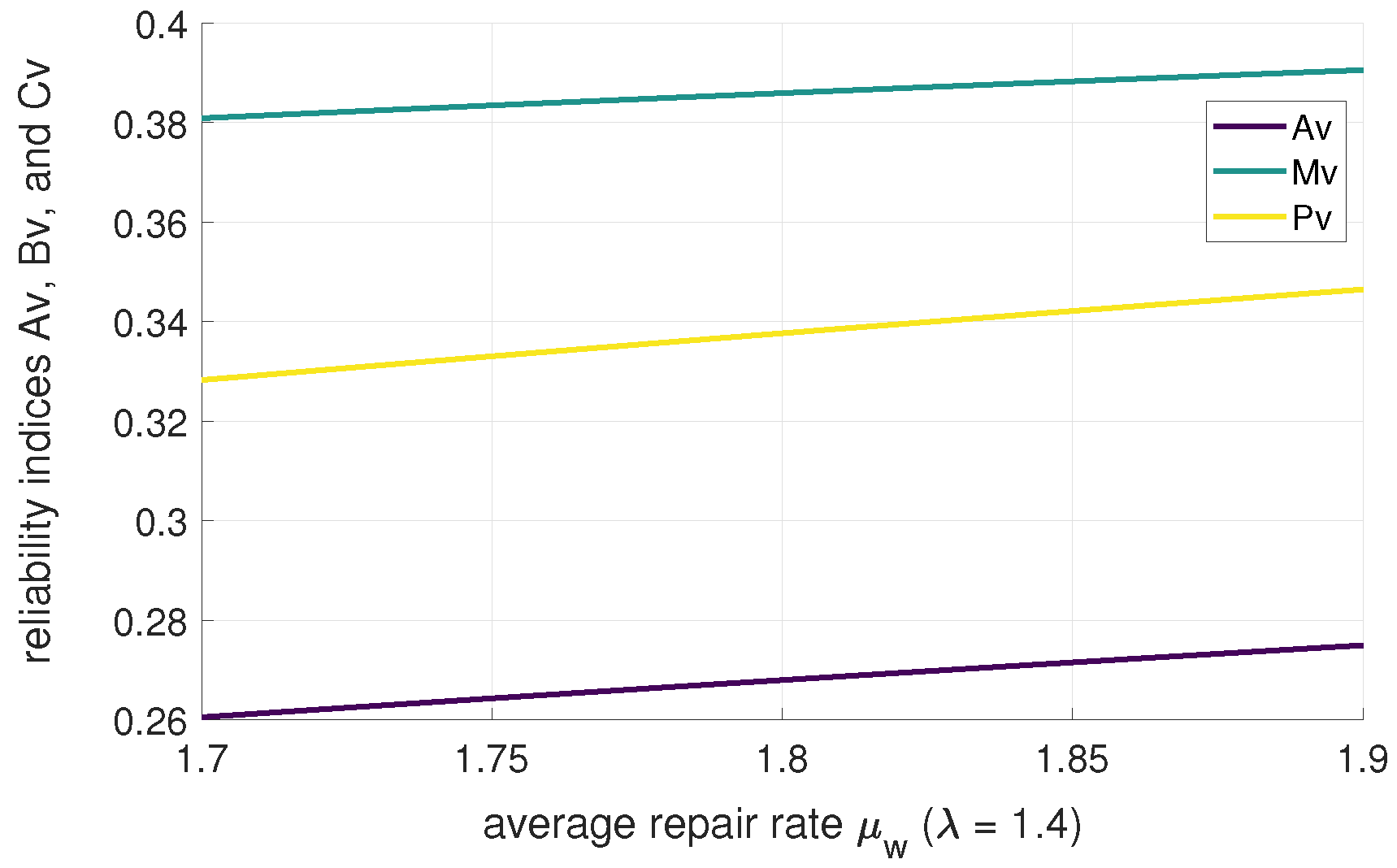
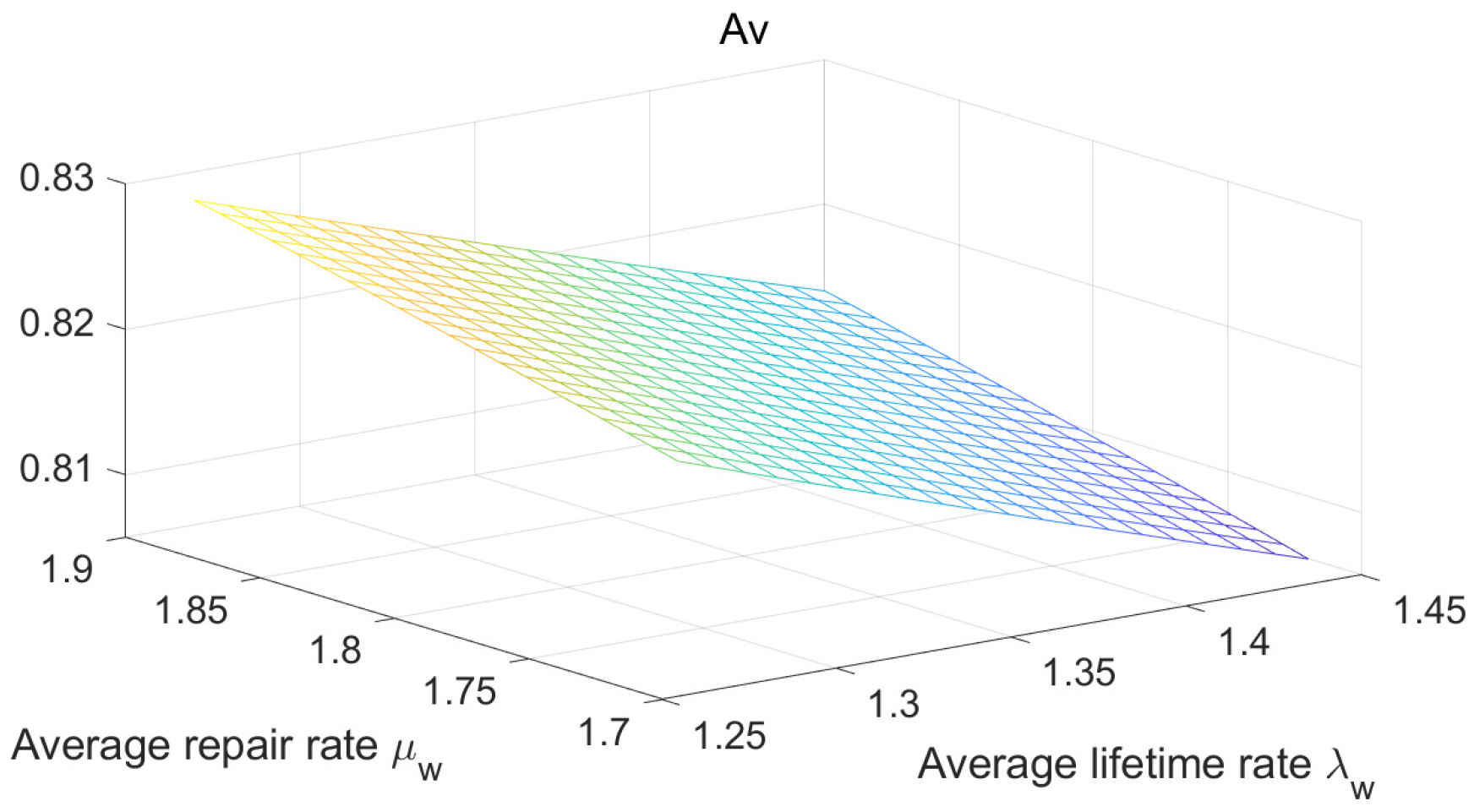
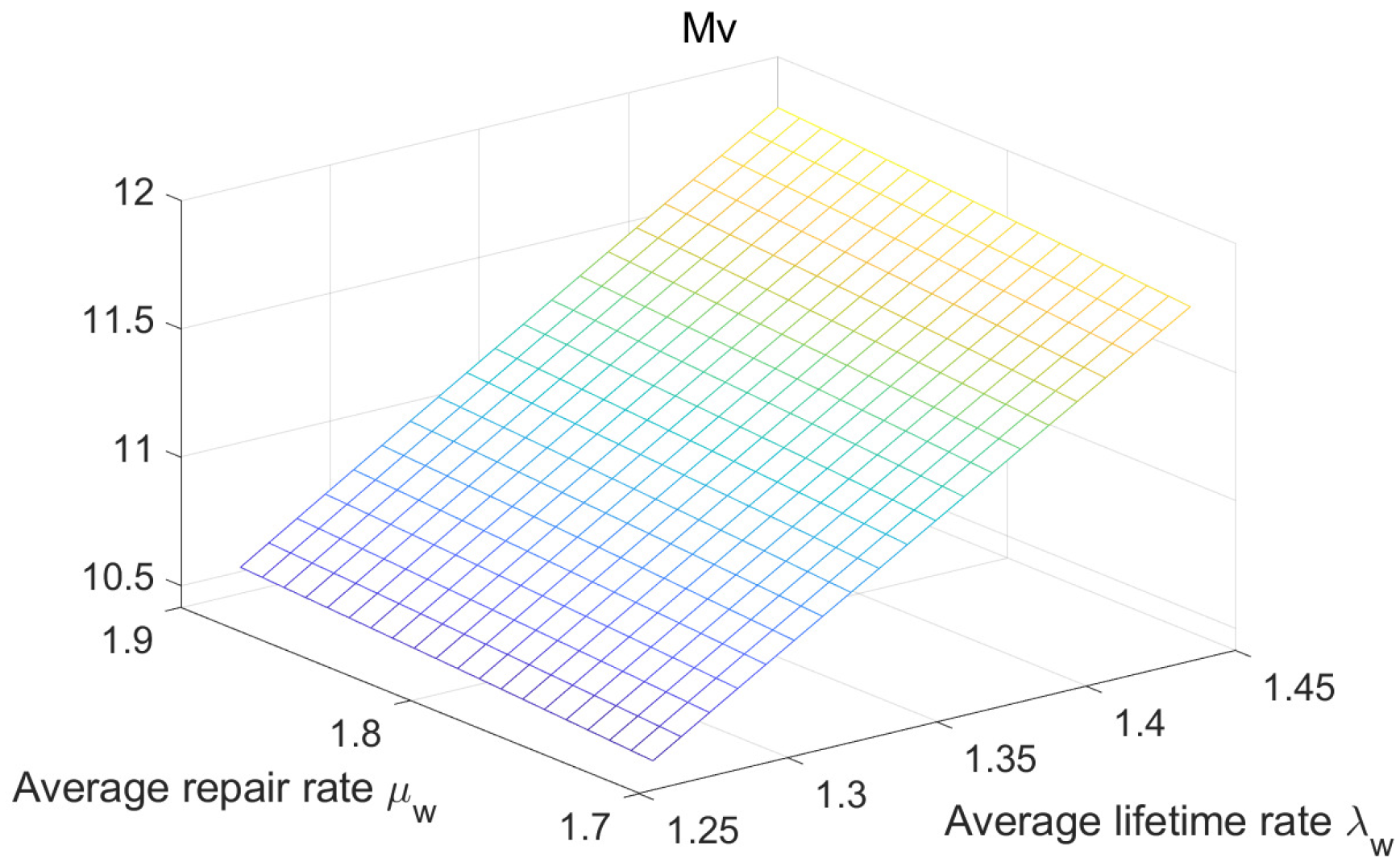
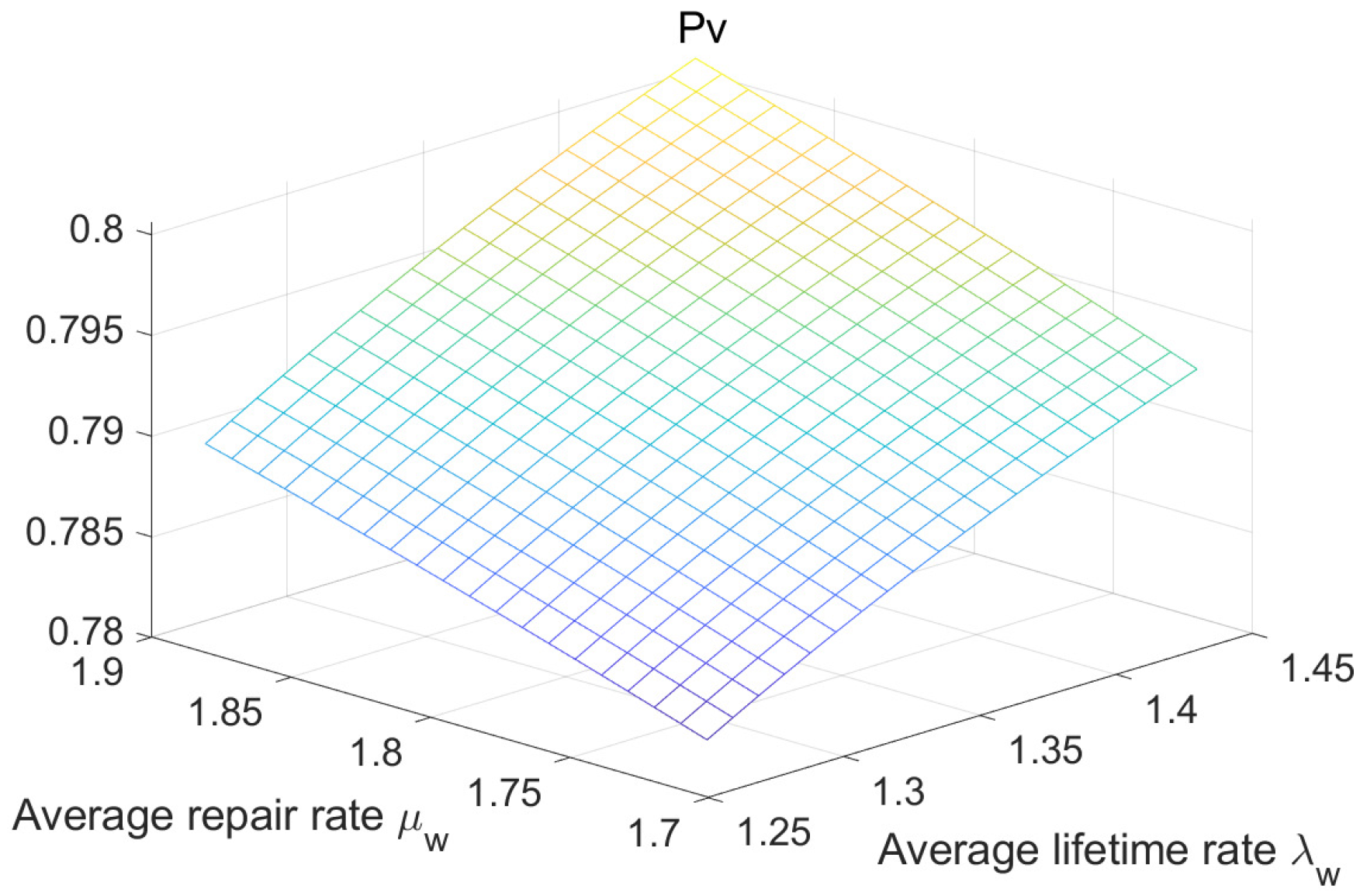
| 1.27 | 1.8 | 0.856 | 13.98 | 0.8185 | 1.37 | 1.8 | 0.839 | 13.70 | 0.8153 |
| 1.28 | 1.8 | 0.854 | 13.93 | 0.8180 | 1.38 | 1.8 | 0.836 | 13.65 | 0.8147 |
| 1.30 | 1.8 | 0.851 | 13.89 | 0.8175 | 1.40 | 1.8 | 0.834 | 13.61 | 0.8141 |
| 1.32 | 1.8 | 0.848 | 13.84 | 0.8169 | 1.42 | 1.8 | 0.831 | 13.56 | 0.8135 |
| 1.34 | 1.8 | 0.845 | 13.80 | 0.8164 | 1.43 | 1.8 | 0.828 | 13.51 | 0.8128 |
| 1.35 | 1.8 | 0.842 | 13.75 | 0.8158 | 1.45 | 1.8 | 0.825 | 13.46 | 0.8122 |
| 1.4 | 1.72 | 0.4094 | 0.5732 | 0.4777 | 1.4 | 1.81 | 0.4169 | 0.5837 | 0.4864 |
| 1.4 | 1.73 | 0.4107 | 0.5750 | 0.4792 | 1.4 | 1.83 | 0.4181 | 0.5854 | 0.4878 |
| 1.4 | 1.75 | 0.4120 | 0.5768 | 0.4807 | 1.4 | 1.85 | 0.4193 | 0.5871 | 0.4892 |
| 1.4 | 1.76 | 0.4132 | 0.5786 | 0.4821 | 1.4 | 1.86 | 0.4205 | 0.5887 | 0.4906 |
| 1.4 | 1.78 | 0.4145 | 0.5803 | 0.4836 | 1.4 | 1.88 | 0.4216 | 0.5903 | 0.4919 |
| 1.4 | 1.80 | 0.4157 | 0.5820 | 0.4850 | 1.4 | 1.90 | 0.4228 | 0.6919 | 0.4932 |
| 1.27 | 1.72 | 0.8537 | 13.93 | 0.8154 | 1.37 | 1.81 | 0.8406 | 13.71 | 0.8160 |
| 1.28 | 1.73 | 0.8515 | 13.89 | 0.8155 | 1.38 | 1.83 | 0.8383 | 13.68 | 0.8161 |
| 1.30 | 1.75 | 0.8493 | 13.86 | 0.8156 | 1.40 | 1.85 | 0.8361 | 13.64 | 0.8161 |
| 1.32 | 1.76 | 0.8472 | 13.82 | 0.8157 | 1.42 | 1.86 | 0.8339 | 13.61 | 0.8162 |
| 1.34 | 1.78 | 0.8450 | 13.79 | 0.8158 | 1.43 | 1.88 | 0.8317 | 13.57 | 0.8163 |
| 1.35 | 1.80 | 0.8428 | 13.75 | 0.8159 | 1.45 | 1.90 | 0.8294 | 13.53 | 0.8164 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Xu, G.; Wang, Y. Reliability Analysis and Numerical Simulation of Industrial Robot Drive System with Vacation. Axioms 2025, 14, 275. https://doi.org/10.3390/axioms14040275
Li Y, Xu G, Wang Y. Reliability Analysis and Numerical Simulation of Industrial Robot Drive System with Vacation. Axioms. 2025; 14(4):275. https://doi.org/10.3390/axioms14040275
Chicago/Turabian StyleLi, Yanling, Genqi Xu, and Yihui Wang. 2025. "Reliability Analysis and Numerical Simulation of Industrial Robot Drive System with Vacation" Axioms 14, no. 4: 275. https://doi.org/10.3390/axioms14040275
APA StyleLi, Y., Xu, G., & Wang, Y. (2025). Reliability Analysis and Numerical Simulation of Industrial Robot Drive System with Vacation. Axioms, 14(4), 275. https://doi.org/10.3390/axioms14040275





