Eigenvalue Spectra of Rabi Models with Infinite Matrix Representations
Abstract
1. Introduction
2. Solvable Infinite Matrix Generated by Semi-Classical Rabi Models
2.1. The Infinite Matrix
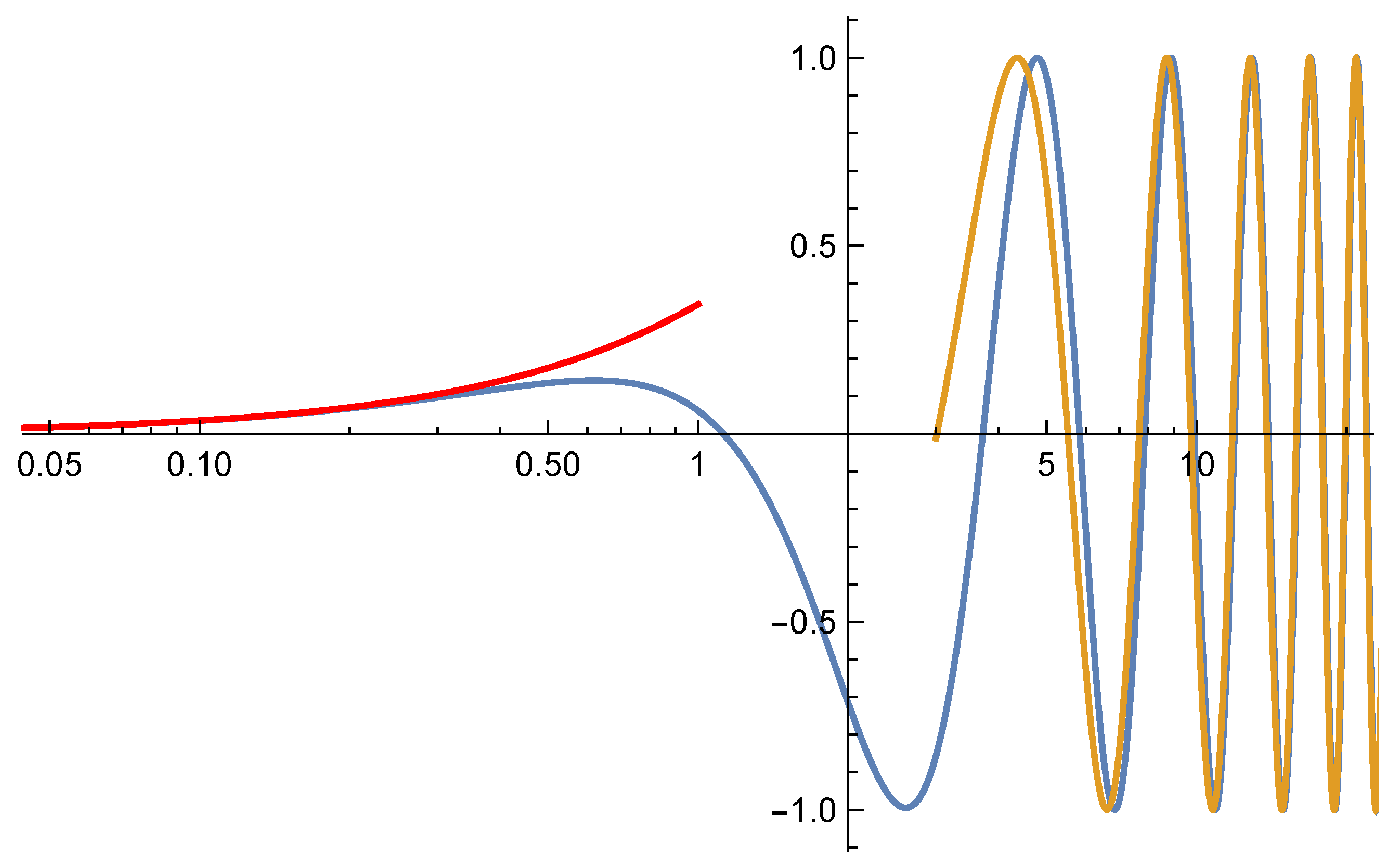
2.2. Solution to the Characteristic Exponent
2.3. Comparison with Previous Results
3. Solvable Infinite Matrix Generated by Quantum Rabi Models
3.1. The Quantum Rabi Model
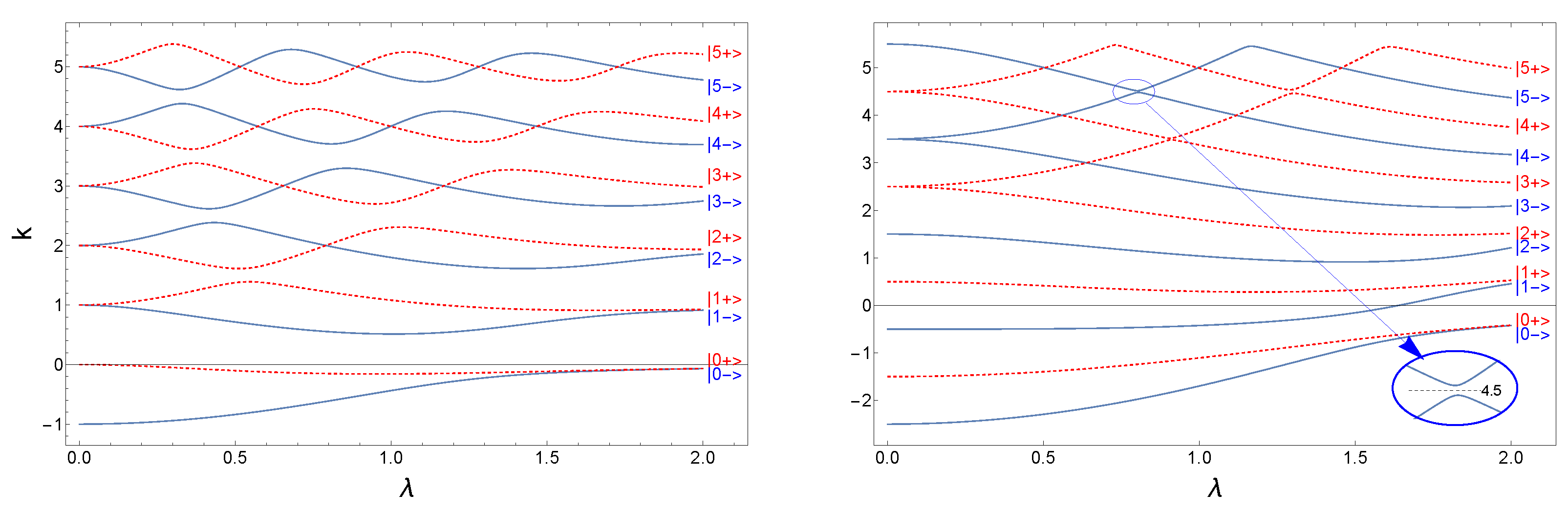
3.2. Conditions for Eigenvalues
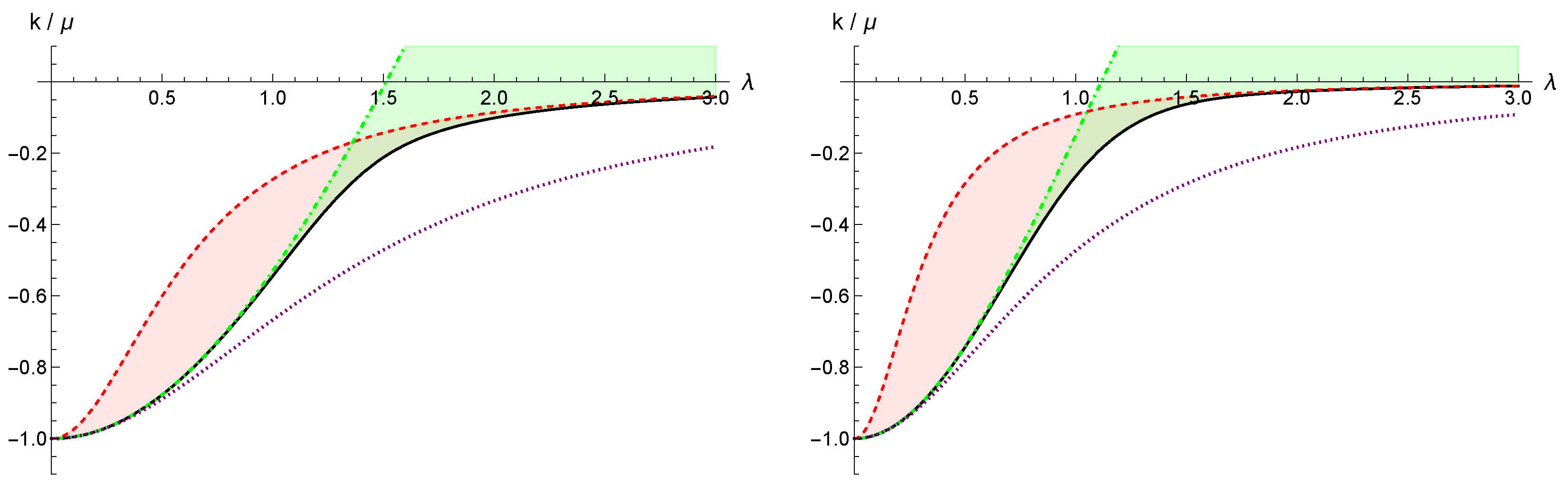
3.3. The Energy Spectrum of Quantum Rabi Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Notations in This Paper
Appendix B. Key Derivations in the Semi-Classical Rabi Model
Appendix C. Perturbation Theory for the Ground State Energy
References
- Rabi, I.I. On the Process of Space Quantization. Phys. Rev. 1936, 49, 324–328. [Google Scholar] [CrossRef]
- Rabi, I.I. Space Quantization in a Gyrating Magnetic Field. Phys. Rev. 1937, 51, 652–654. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University: Cambridge, UK, 2000. [Google Scholar]
- Bouwmeester, D.; Ekert, A.K.; Zeilinger, A. The Physics of Quantum Information: Quantum Cryptography, Quantum Teleportation, Quantum Computation; Springer: Berlin, Germany, 2000. [Google Scholar]
- Ashhab, S.; Johansson, J.R.; Zagoskin, A.M.; Nori, F. Two-level systems driven by large-amplitude fields. Phys. Rev. A 2007, 75, 063414. [Google Scholar] [CrossRef]
- Gerardot, B.D.; Öhberg, P. A Strongly Driven Spin. Science 2009, 326, 1489–1490. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, G.D.; Dobrovitski, V.V.; Toyli, D.M.; Heremans, F.J.; Awschalom, D.D. Gigahertz Dynamics of a Strongly Driven Single Quantum Spin. Science 2009, 326, 1520–1522. [Google Scholar] [CrossRef]
- Jaynes, E.; Cummings, F. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Milonni, P.W.; Ackerhalt, J.R.; Galbraith, H.W. Chaos in the SemiclassicalN-Atom Jaynes-Cummings Model: Failure of the Rotating-Wave Approximation. Phys. Rev. Lett. 1983, 50, 966–969. [Google Scholar] [CrossRef]
- Bonci, L.; Roncaglia, R.; West, B.J.; Grigolini, P. Quantum irreversibility and chaos. Phys. Rev. Lett. 1991, 67, 2593–2596. [Google Scholar] [CrossRef]
- Fukuo, T.; Ogawa, T.; Nakamura, K. Jaynes-Cummings model under continuous measurement: Weak chaos in a quantum system induced by unitarity collapse. Phys. Rev. A 1998, 58, 3293–3302. [Google Scholar] [CrossRef]
- Su, Y.; Wang, X. Parametrized protocol achieving the Heisenberg limit in the optical domain via dispersive atom–light interactions. Results Phys. 2021, 24, 104159. [Google Scholar] [CrossRef]
- Su, Y.; Lu, W.; Shi, H.L. Quantum metrology enhanced by the XY spin interaction in a generalized Tavis-Cummings model. Phys. Rev. A 2024, 109, 042614. [Google Scholar] [CrossRef]
- Braak, D.; Chen, Q.H.; Batchelor, M.T.; Solano, E. Semi-classical and quantum Rabi models: In celebration of 80 years. J. Phys. A 2016, 49, 300301. [Google Scholar] [CrossRef]
- Braak, D. Integrability of the Rabi Model. Phys. Rev. Lett. 2011, 107, 100401. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.H.; Wang, C.; He, S.; Liu, T.; Wang, K.L. Exact solvability of the quantum Rabi model using Bogoliubov operators. Phys. Rev. A 2012, 86, 023822. [Google Scholar] [CrossRef]
- Zhong, H.; Xie, Q.; Batchelor, M.T.; Lee, C. Analytical eigenstates for the quantum Rabi model. J. Phys. A Math. Theor. 2013, 46, 415302. [Google Scholar] [CrossRef]
- Maciejewski, A.J.; Przybylska, M.; Stachowiak, T. Full spectrum of the Rabi model. Phys. Lett. A 2014, 378, 16–20. [Google Scholar] [CrossRef]
- Xie, Q.; Zhong, H.; Batchelor, M.T.; Lee, C. The quantum Rabi model: Solution and dynamics. J. Phys. A Math. Theor. 2017, 50, 113001. [Google Scholar] [CrossRef]
- Kam, C.F.; Chen, Y. Analytical approximations for generalized quantum Rabi models. arXiv 2024, arXiv:2401.05615. [Google Scholar]
- Ma, T.; Li, S.M. Floquet system, Bloch oscillation, and Stark ladder. arXiv 2007, arXiv:0711.1458. [Google Scholar]
- Xie, Q.; Hai, W. Analytical results for a monochromatically driven two-level system. Phys. Rev. A 2010, 82, 032117. [Google Scholar] [CrossRef]
- Liang, H. Generating arbitrary analytically solvable two-level systems. J. Phys. A Math. Theor. 2024, 57, 095301. [Google Scholar] [CrossRef]
- Wang, G.; Li, C.; Cappellaro, P. Observation of Symmetry-Protected Selection Rules in Periodically Driven Quantum Systems. Phys. Rev. Lett. 2021, 127, 140604. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, H.J. The Floquet Theory of the Two-Level System Revisited. Z. für Naturforschung A 2018, 73, 705–731. [Google Scholar] [CrossRef]
- Lu, T.; Miao, X.; Metcalf, H. Bloch theorem on the Bloch sphere. Phys. Rev. A 2005, 71, 061405(R). [Google Scholar] [CrossRef]
- Creffield, C. Location of crossings in the Floquet spectrum of a driven two-level system. Phys. Rev. B 2003, 67, 165301. [Google Scholar] [CrossRef]
- Xie, Q. Floquet states and quasienergies of a periodically driven two-level system. J. Phys. B 2009, 42, 105501. [Google Scholar] [CrossRef]
- Shirley, J.H. Solution of the Schrödinger Equation with a Hamiltonian Periodic in Time. Phys. Rev. 1965, 138, B979–B987. [Google Scholar] [CrossRef]
- Ronveaux, A. Heun’s Differential Equations; Oxford University: Oxford, UK, 1995. [Google Scholar]
- Slavyanov, S.Y.; Lay, W. Special Functions: A Unified Theory Based on Singularities; Oxford University: Oxford, UK, 2000. [Google Scholar]
- Ishkhanyan, A.M.; Grigoryan, A.E. Fifteen classes of solutions of the quantum two-state problem in terms of the confluent Heun function. J. Phys. A 2014, 47, 465205. [Google Scholar] [CrossRef]
- Llorente, J.M.G.; Plata, J. Tunneling control in a two-level system. Phys. Rev. A 1992, 45, R6958–R6961. [Google Scholar] [CrossRef]
- Barata, J.C.A.; Wreszinski, W.F. Strong-Coupling Theory of Two-Level Atoms in Periodic Fields. Phys. Rev. Lett. 2000, 84, 2112–2115. [Google Scholar] [CrossRef]
- Angelo, R.M.; Wreszinski, W.F. Two-level quantum dynamics, integrability, and unitary NOT gates. Phys. Rev. A 2005, 72, 034105. [Google Scholar] [CrossRef]
- Frasca, M. Third-order correction to localization in a two-level driven system. Phys. Rev. B 2005, 71, 073301. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, X. Strong-Coupling Theory of Periodically Driven Two-Level Systems. Phys. Rev. Lett. 2007, 98, 013601. [Google Scholar] [CrossRef]
- Kayanuma, Y. Role of phase coherence in the transition dynamics of a periodically driven two-level system. Phys. Rev. A 1994, 50, 843–845. [Google Scholar] [CrossRef] [PubMed]
- Grossmann, F.; Dittrich, T.; Jung, P.; Hänggi, P. Coherent transport in a periodically driven bistable system. J. Statist. Phys. 1993, 70, 229–245. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, X.; Xiao, Y. Analytical Method for Yrast Line States in Interacting Bose-Einstein Condensates. Phys. Rev. Lett. 2001, 86, 2200–2203. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, X. Analytical results for energy spectrum and eigenstates of a Bose-Einstein condensate in a Mott insulator state. Phys. Rev. A 2003, 68, 013608. [Google Scholar] [CrossRef]
- Zhong, H.; Hai, W.; Lu, G.; Li, Z. Incoherent control in a non-Hermitian Bose-Hubbard dimer. Phys. Rev. A 2011, 84, 013410. [Google Scholar] [CrossRef]
- Takagi, T.; Wakayama, M.; Tanaka, K.; Kunihiro, N.; Kimoto, K.; Duong, D. Mathematical Modelling for Next-Generation Cryptography: CREST Crypto-Math Project; Mathematics for Industry; Springer Nature: Singapore, 2017. [Google Scholar]
- Li, Z.M.; Batchelor, M.T. Addendum to ‘Algebraic equations for the exceptional eigenspectrum of the generalized Rabi model’. J. Phys. A Math. Theor. 2016, 49, 369401. [Google Scholar] [CrossRef][Green Version]
- Li, Z.M.; Batchelor, M.T. Algebraic equations for the exceptional eigenspectrum of the generalized Rabi model. J. Phys. A Math. Theor. 2015, 48, 454005. [Google Scholar] [CrossRef]
- Judd, B.R. Exact solutions to a class of Jahn-Teller systems. J. Phys. C Solid State Phys. 1979, 12, 1685–1692. [Google Scholar] [CrossRef]
- Kimoto, K.; Reyes-Bustos, C.; Wakayama, M. Determinant Expressions of Constraint Polynomials and the Spectrum of the Asymmetric Quantum Rabi Model. Int. Math. Res. Not. 2020, 2021, 9458–9544. [Google Scholar] [CrossRef]
- Kuś, M. On the spectrum of a two-level system. J. Math. Phys. 1985, 26, 2792–2795. [Google Scholar] [CrossRef]
- Motygin, O.V. On evaluation of the confluent Heun functions. In Proceedings of the 2018 Days on Diffraction (DD), St. Petersburg, Russia, 4–8 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 223–229. [Google Scholar] [CrossRef]


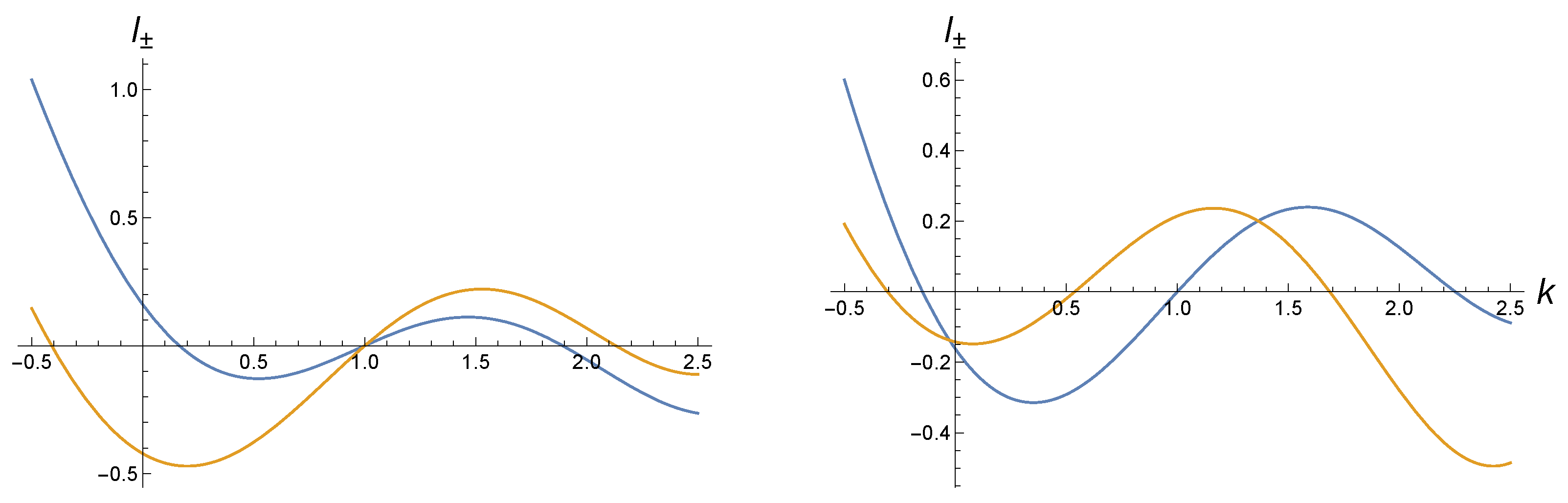
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, H.; Xia, S.; Chen, Y.; Su, Y.; Chen, J. Eigenvalue Spectra of Rabi Models with Infinite Matrix Representations. Axioms 2025, 14, 263. https://doi.org/10.3390/axioms14040263
Liang H, Xia S, Chen Y, Su Y, Chen J. Eigenvalue Spectra of Rabi Models with Infinite Matrix Representations. Axioms. 2025; 14(4):263. https://doi.org/10.3390/axioms14040263
Chicago/Turabian StyleLiang, Hongbin, Shucan Xia, Yixiang Chen, Yuguo Su, and Jie Chen. 2025. "Eigenvalue Spectra of Rabi Models with Infinite Matrix Representations" Axioms 14, no. 4: 263. https://doi.org/10.3390/axioms14040263
APA StyleLiang, H., Xia, S., Chen, Y., Su, Y., & Chen, J. (2025). Eigenvalue Spectra of Rabi Models with Infinite Matrix Representations. Axioms, 14(4), 263. https://doi.org/10.3390/axioms14040263






