Abstract
The primary objective of this study is to expand the application of analytical and numerical methods for solving nonlinear Systems of Fractional Differential Equations (SFDEs) with Caputo fractional derivatives (CFDs) under initial conditions. Our proposed approach, the Multistage Telescoping Decomposition Elzaki Method (MTDEM), integrates the advantages of the Elzaki transform with the Multistage Telescoping Decomposition Method (MTDM), significantly enhancing the efficiency of the solution process and improving the convergence rate. Additionally, it simplifies computational operations and reduces the computational complexity associated with solving these nonlinear systems. A comprehensive comparison is conducted to highlight the accuracy and computational advantages of our proposed method compared to existing techniques, including the exact solution and the Telescoping Decomposition Method (TDM), through numerical examples that demonstrate the effectiveness of the proposed approach. The flexibility of the MTDEM allows for its application in a wide range of nonlinear SFDEs, making it a valuable tool in various scientific and engineering fields. These systems are widely used in modeling numerous physical, biological, and economic phenomena, such as the dynamics of electrical systems, heat transfer, and population growth models, underscoring the importance of developing accurate and efficient computational methods for their solutions. Through this study, we present a novel contribution to enhancing numerical and analytical techniques, paving the way for broader applications in multiple domains that require precise and reliable solutions for complex fractional systems.
Keywords:
nonlinear system; numerical technique; Elzaki transform; fractional-order equations; Caputo derivatives MSC:
44A05; 26A33; 34K37; 34A08; 44A20
1. Introduction and Mathematical Preliminaries
Recently, fractional differential equations have attracted considerable attention, being studied and applied to various real-world phenomena across different fields. One reason for their limited popularity might be the existence of multiple, non-equivalent definitions of fractional derivatives. Additionally, their nonlocal nature makes it challenging to provide a clear geometric interpretation. However, over the recent years, scientists have increasingly focused on fractional calculus. Through the use of fractional derivatives, it has been discovered that numerous applications, particularly those spanning multiple disciplines, can be effectively described.
Various analytical and numerical techniques have emerged in recent years to tackle fractional differential equations; among the prominent techniques are the Adomian decomposition method (ADM) [1], the Homotopy perturbation method (HPM) [2,3], and the variational iteration method [4], which are frequently combined with integral transforms such as the Laplace transform [5,6,7,8], the Sumudu transform [4,9,10,11], the Elzaki transform (ET) [12,13,14,15,16,17], the ZZ transform (la transformation de Zain Ul Abadin Zafar [18,19,20,21,22,23,24]), the Aboodh transform [25], the ARA transform (Aliaa Burqan, Rania Saadeh, and Ahmad Qazza) [26,27], and the Double Kharrat–Toma transform [28] to improve their effectiveness. It is also worth noting that several modern techniques have explored the study of phenomena modeled by fractional-order equations, for example, [29,30,31].
The TDM was originally proposed in [19,21] as an analytical approach for resolving differential equations.
where is a compact subset of . Rooted in the principles of Taylor series expansion, this method constructs solutions in the form of polynomials. A notable advantage of TDM lies in its ability to circumvent the computation of Adomian polynomials, thereby offering a more streamlined a replacement for the TDM. Subsequent advancements in the field led to the development of the MTDM, as explored in [32], where it was applied to fractional differential equations. Further extending its applicability, the authors of [33] employed this approach to solve systems of nonlinear fractional differential equations.
The authors of [34] presented a new technique for addressing nonlinear fractional initial conditions problems, applying MTDM.
and the following initial condition:
where is the Caputo fractional derivative of the function , R is the linear differential operator of less order than represents the general nonlinear differential operator, and is the source term.
By integrating the MTDM with the ET, this method greatly improved computational efficiency and accuracy. Through a series of computational simulations, the recommended strategy was shown to be highly functional, trustworthy, and easy to apply, offering a solid structure for resolving complex fractional differential equations effectively.
This method is widely recognized for its precision and rapid convergence, making it particularly effective for solving intricate nonlinear equations. By decomposing the problem into successive stages, this method provides enhanced authority over the solution procedure and minimizes computational load. However, the method is not without its challenges, as it can encounter algorithmic complexity, needing a delicate equilibrium between precision and performance. Despite these challenges, it remains a powerful tool for addressing high-dimensional mathematical problems involving several variables.
This study uses the MTDEM to solve SFDEs using CFD with specified initial conditions. The following sections of this paper are structured as follows: The second section provides a comprehensive overview of the foundational concepts of fractional calculus, the ET, and the MTDEM. The third section describes how the algorithms are used, and their hybridization with the ET for solving SFDEs using Caputo derivatives, as well as analysis errors, convergence analysis, and its utilization in different examples. The fourth section evaluates the MTDEM by contrasting the results with those from previous studies to highlight its accuracy and efficiency. Finally, our conclusion and perspectives are presented.
2. Essential Definitions
This section provides essential background information on fractional calculus, specifically focusing on fractional derivatives, fractional integrals, and fundamental definitions and properties ET.
2.1. Fundamental Concepts and Key Properties
In this section, various key properties and basic definitions of fractional-order operators are introduced, which will be applied throughout the paper, including the most widely adopted definitions, defined in the context of Riemann–Liouville and Caputo, which are stated as follows.
Definition 1.
([35]). The Riemann–Liouville fractional-order integral generalizes the concept of integration by allowing for the integration of functions to non-integer orders. It is given by
The fractional-order derivative operators are defined accordingly within the framework of Riemann–Liouville and Caputo as follows:
where and .
Now, several important characteristics and properties of fractional-order operators are presented and demonstrated, which are crucial for understanding the core results of the present study.
Lemma 1
([35]). For , the Riemann–Liouville fractional integral of a power function is expressed as
Lemma 2
([35]). For , and , the CFD of a power function is expressed as
where denotes the integer part of ρ.
2.2. Basic Concepts of ET
The ET is an advanced integral transform constructed for functions of exponential order. It is particularly useful in solving fractional differential equations by simplifying their complexity [14]. The function space considered for this transform is
Definition 2.
Given a set of functions,
can be finite or infinite, and M is a real finite number. The ET of , , as
Next, the inverse of the ET is expressed as , then is called the inverse transform of Elzaki of , where is the operator of the inverse Elzaki transform.
When is a fractional number, there is
Definition 3.
([14]). The ET of CFD is given by
2.3. Investigation of MTDM
Consider generalized nonlinear fractional equation
Here, is a linear differential operator of higher order which is easily invertible, and signifies the nonlinear operators, while is the remaining linear part, f is a prescribed function, and x is the unknown function.
The fundamental concept of TDM [28] is used to represent the nonlinear term as an infinite series within the Banach space,
where is determined by
with
where is the solution of Equation (14) and the residual linear part is expressed as
Principle of the MTDM
The principle of the MTDM relies on dividing the time interval into subintervals, , such that and . The subintervals may be of uniform length , i.e., for .
3. Basic Idea of MTDEM
Assume a general SFDE of the form
where , and the initial conditions are
where are the CFD of the functions are the linear differential operator, stand for the general nonlinear differential operator, and are the source terms, end the solutions in the Banach space.
Theorem 1.
Proof.
Exploiting a property of the ET, from this, the following form can be derived
Performing the inverse ET on both sides of Equation (24).
With the initial conditions, (22) gives
where denotes the contributions from the nonhomogeneous terms and the given initial conditions.
On the other hand, the solutions are represented as follows:
and nonlinear terms can be decomposed:
where
By using (26) and (27), it can be rewritten (25) as
The two sides of Equation (29) are examined and compared, yielding the first term of the solution
By following the same method, the general recursive relation is obtained
Ultimately, the approximate solution is obtained through
□
3.1. Convergence Analysis
Theorem 2.
Proof.
Define a sequence such that represents the sequence of partial sums derived from the series solution .
Assume that and are Lipschitzian with and .
Let and be two arbitrary partial sums with . It will now be proven that is a Cauchy sequence in this Banach space.
Let ; then,
According to the triangle inequality, it can be show that
Since, and , then . As a result
However, and as , then , and hence forms a Cauchy sequence within this Banach space. So, the series converges, and this completes the proof. □
3.2. Error Analysis
For MTDEM, the maximum absolute truncated error of the series solution can be evaluated using the following theorem.
Theorem 3.
Proof.
From Theorem (37), it follows that equation But , and as , then , so
Thus, the upper bound of the absolute truncation error in the interval I is
Thus, the desired result follows. □
3.3. Demonstrative Example
This part employs the TDETM to resolve SFDEs. By analyzing this numerical example, readers will gain a clearer understanding of how the scheme can be implemented in SFDEs.
Example 1.
The first step, SFDEs, involves analyzing time-fractional derivatives.
By applying the ET on either side of Equation (36) and employing the differentiation property, it can be derived that
In the interval , the solution using the MTDEM method is given as
- For each interval
The initial conditions are
and
Now, the solution of the system (36) is provided in the piecewise form as
The recursive relations are given as follows.
- For
For
and for
The first few components of , and , are as follows:
and
for the third iteration
By continuing in the same way, the other components can be found. At last, the series solutions , and of Equation (36) are given by
4. Numerical Experiments and Discussion
All the computations presented in this section have been obtained using Maple software (Maple 2024, Waterloo Maple Inc., Waterloo, Ontario, Canada). The solution of this problem is obtained by applying the technique described in Equation (36).
Example 2.
In this part, an example is presented to demonstrate the method with exact solutions and other methods. This will help readers understand how to compare exact, numerical solutions. Let the system of FDEs be
By applying the ET for the SFDEs in Equation (49), it follows that
the initial conditions are
Since, , then .
- So,
Example 3.
Continuing the same steps explained in example 2, it follows that
4.1. TabularResults
Table 1 and Table 2 illustrate the comparison between the approximate solutions obtained using the proposed method, MFTDM, the exact solutions, and the solution of FTDM for each example, where . The tables clearly demonstrate a strong agreement between the exact solutions and those produced by the proposed method.

Table 1.
Comparison between the results from the exact solution, FTDM and MTDEM (), for Equation (49).

Table 2.
Comparison between the results from the exact solution, FTDM and MTDEM (), for Equation (53).
4.2. Graphical Analysis
The graphs in Examles 2 and 3 in Figure 1 and Figure 2, respectively, are given blow. The graph in Figure 1 shows the solutions of Example 2, and the graph in Figure 2 shows the solutions of Example 3. The X-axis is variable t, and the Y-axis is the solution .
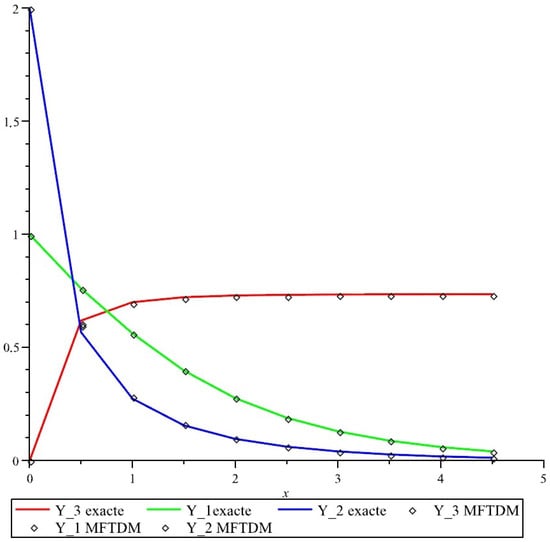
Figure 1.
The approximate solution for Example 2, using MFTEM (dashed line) and the exact solution (solid line).
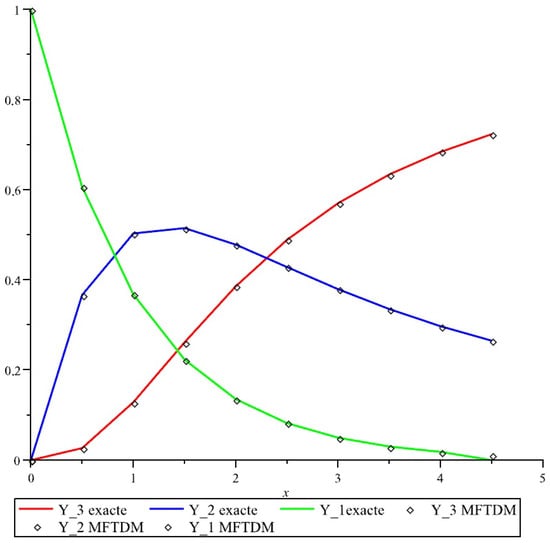
Figure 2.
The approximate solution for Example 3, using MFTEM (dashed line) and the exact solution (solid line).
The proposed method’s approximate solutions in Figure 1 and Figure 2 are compared with the exact solutions. Thus, these comparisons give us valuable information about how the approximate solutions converge in the exact solution. Based on these results, the MTDEM method is more accurate and comes closer to exact solutions along the domain .
5. Conclusions
We examine the key characteristics of the MTDEM, focusing on its application in solving various SFDEs. Additionally, graphs and tables demonstrate the accuracy and effectiveness of the proposed method by comparing it with exact solutions.
The findings confirm that the proposed approach is practical, reliable, and well suited for solving SFDEs with initial conditions. Consequently, this method can be effectively applied of SFDEs.
One of the notable advantages of the MTDEM is its ability to transform differential equations into algebraic equations, making them more comprehensible and easier to handle. This transformation significantly reduces the computational effort and time required to obtain exact solutions.
In the future, we hope we can use the MTDEM to solve the SFDEs with other types of derivatives. We could combine it with other numerical techniques to enhance its capabilities, which potentially could lead to more specialized solutions and broader applications across fields.
Author Contributions
Conceptualization, M.B., S.A., F.C. and M.E.E.; methodology, M.B., S.A. and F.C.; software, M.B. and F.C.; validation, S.A., M.E.E. and O.E.; formal analysis, F.C., S.A. and O.E.; investigation, M.B., F.C., S.A. and M.E.E.; writing—original draft preparation, M.B., F.C., S.A., M.E.E., O.E. and R.R.; writing—review and editing, O.E. and R.R.; visualization, M.B. and F.C.; supervision, O.E.; project administration, O.E. and R.R.; funding acquisition, O.E. and R.R. All authors have read and agreed to the published version of the manuscript.
Funding
This study is supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2025/R/1446).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare that they have no competing interests.
References
- Adomian, G. Solution of physical problems by decomposition. Comp. Math. Appl. 1994, 27, 145–154. [Google Scholar] [CrossRef]
- Ziane, D.; Belghaba, K.; Cherif, M.H. Fractional homotopy perturbation transform method for solving the time-fractional KdV, k(2,2) and Burgers equations. Int. J. Open Prob. Comput. Sci. Math. 2015, 8, 63–75. [Google Scholar]
- He, J.H. A coupling method of homotoping technique and perturbation technique for nonlinear problems. Int. J. Nonlinear Mech. 2000, 35, 37–43. [Google Scholar]
- Abel-Rady, A.S.; Rida, S.Z.; Arafa, A.A.M.; Abedi-Rahim, H.R. Variational iteration Sumudu transform method for solving fractional nonlinear gaz dynamics equation. Int. J. Res. Stud. Sci. Eng. Technol. 2014, 1, 82–90. [Google Scholar]
- Hilall, E.; Elzaki, M.T. Solution of nonlinear partial differential equations by new Laplace variational iteration method. J. Funct. Spaces 2014, 2014, 790714. [Google Scholar] [CrossRef]
- Elzaki, T.M.; Elzaki, S.M. On the connections between Laplace and Elzaki transforms. Adv. Theor. Appl. Math. 2014, 6, 1–10. [Google Scholar]
- Afshan, K.; Tauseef, M.S. Coupling of Laplace transform and correction functional for wave equations. Word J. Mod. Simul. 2013, 9, 173–180. [Google Scholar]
- Gul, N.; Noor, S.; Saeed, A.M.; Aldhabani, M.S.; Ullah, R. Analytical solution of the systems of nolinear fractional partial differential equations using conformale Laplace transform iterative method. Fractal Fract. 2025, 10, 1945–1966. [Google Scholar]
- Kumar, D.; Singh, J.; Rathore, S. Sumudu decomposition method for nonlinear equations. Int. Math. Forum 2012, 7, 515–521. [Google Scholar]
- Singh, J.; Kumar, D.; Sushila, D. Homotopy perturbation Sumudu transform method for nonlinear equations. Adv. Theor. Appl. Mach. 2011, 4, 165–175. [Google Scholar]
- Rathore, S.; Kumar, D.; Singh, J.; Gupta, S. Homotopy analysis Sumudu transform method for nonlinear equations. Int. J. Ind. Math. 2012, 4, 301–314. [Google Scholar]
- Elzaki, T.M. The new integral transform Elzaki transform. Glob. J. Pure Appl. Math. 2011, 7, 57–64. [Google Scholar]
- Elzaki, T.M.; Hilal, E.M.A. Homotopy perturbation and Elzaki transform for solving nonlinear partial differential equations. Math. Theor. Mod. 2012, 2, 33–42. [Google Scholar]
- Elzaki, T.M.; Elzaki, S.M.; Elnour, E.A. On the new integral transform “Elzaki Transform” fundamental properties investigations and applications. Glob. J. Math. Sci. 2012, 2, 1–13. [Google Scholar]
- Elzaki, T.M. On the Elzaki transform and ordinary differential equation with variable coefficients. Adv. Theor. Appl. Math. 2011, 6, 13–18. [Google Scholar]
- Elzaki, T.M.; Biazar, J. Homotopy perturbation method and Elzaki transform for solving system of nonlinear partial differential equatios. World Appl. Sci. 2013, 24, 944–948. [Google Scholar]
- Ige, O.E.; Oderinu, R.A.; Elzaki, T.M. Adomian polynomial and Elzaki transform method for solving Klein Gordon equations. Int. J. Appl. Math. 2019, 32, 451–468. [Google Scholar] [CrossRef]
- Riabi, L.; Belghaba, K.; Cherif, M.H.; Ziane, D. Homotopy perturbation method combined with ZZ transform to solve some nonlinear fractional differential equations. Int. J. Anal. Appl. 2019, 17, 406–419. [Google Scholar]
- Al-Refai, M.; Abu-Dalu, M.; Al-Rawashde, A. Telescoping decomposition method for solving first order nonlinear differential equations. In Proceedings of the International Multi-Conference of Engineers and Computer Scientists, (IMECS 2008), Kowloon, Hong Kong, 19–21 March 2008. [Google Scholar]
- Khalid, M.; Sultana, M.; Zaidi, F.; Arshad, U. An Elzaki transform decomposition algorithm applied to a class of non-linear differential equations. J. Nat. Sci. Res. 2015, 5, 48–55. [Google Scholar]
- Nibron, M.; Mishra, A.K.; Kabala, D. Telescoping decomposition method for solving second order nonlinear differential equations. Int. J. Eng. Res. Technol. 2014, 3, 590–595. [Google Scholar]
- Ige, O.E.; Heilio, M.; Oderinu, R.A.; Elzaki, T.M. Adomian polynomial and Elzaki transform method of solving third order Korteweg-De Vries equatios. Glob. J. Pure Appl. Math. 2019, 15, 261–277. [Google Scholar]
- Zafar, Z.U.A. ZZ transform method. Int. J. Adv. Eng. Glob. Technol. 2016, 4, 1605–1611. [Google Scholar]
- Zafar, Z.U.A. Application of ZZ transform method on some fractional differential equation. Int. J. Adv. Eng. Glob. Technol. 2016, 4, 1355–1363. [Google Scholar]
- Ziane, D. The combined of Homotopy analysis method with new transform for nonlinear partial differential equations. Malaya J. Math. 2018, 6, 34–40. [Google Scholar] [CrossRef]
- Saadeh, R.; Qazza, A.; Burqan, A. A new integral transform: ARA transform and its properties and applications. Symmetry 2020, 12, 925. [Google Scholar] [CrossRef]
- Raghavendar, K.; Pavani, K.; Aruna, K.; Okposo, N.I.; Inc, M. Application of Natural Transform Decomposition Method for Solution of Fractional Richards Equation. Contemp. Math. 2024, 5, 5881. [Google Scholar] [CrossRef]
- Kharrat, B.N. New Double Kharrat-Toma Transform and its Application in Partials Differential Equations. World Appl. Sci. J. 2024, 42, 30–36. [Google Scholar]
- Hui, J. Fixed-time fractional-order sliding mode controller with disturbance observer for U-tube steam generator. Renew. Sustain. Energy Rev. 2024, 205, 114829. [Google Scholar] [CrossRef]
- Hui, J.; Lee, Y.; Yuan, J. Load following control of a PWR with load-dependent parameters and perturbations via fixed-time fractional-order sliding mode and disturbance observer techniques. Renew. Sustain. Energy Rev. 2023, 184, 113550. [Google Scholar] [CrossRef]
- Hui, J.; Lee, Y.; Yuan, J. Fractional-order sliding mode load following control via disturbance observer for modular high-temperature gas-cooled reactor system with disturbances. Asian J. Control. 2023, 25, 3513–3523. [Google Scholar] [CrossRef]
- Bouhassoun, A. Multistage telescoping decomposition method for solving fractional differential equations. Int. J. Appl. Math. 2013, 43, 1–7. [Google Scholar]
- Chita, F.; Belghaba, K. Solving systems of nonlinear fractional differential equations using multistage telescoping decomposition method. Asian J. Math. Comput. 2016, 13, 203–214. [Google Scholar]
- Chita, F.; Ayadi, S.; Ege, M.; Ege, O.; Ramaswamy, R. A Novel Approach for Solving Fractional Differential Equations via a Multistage Telescoping Decomposition Method. Fractal Fract. 2025, 9, 65. [Google Scholar] [CrossRef]
- Diethelm, K. The Analysis Fractional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).