Superconvergence of Mixed Finite Element Method with Bernstein Polynomials for Stokes Problem
Abstract
1. Introduction
2. Review the Stokes Problem and Mixed FEM
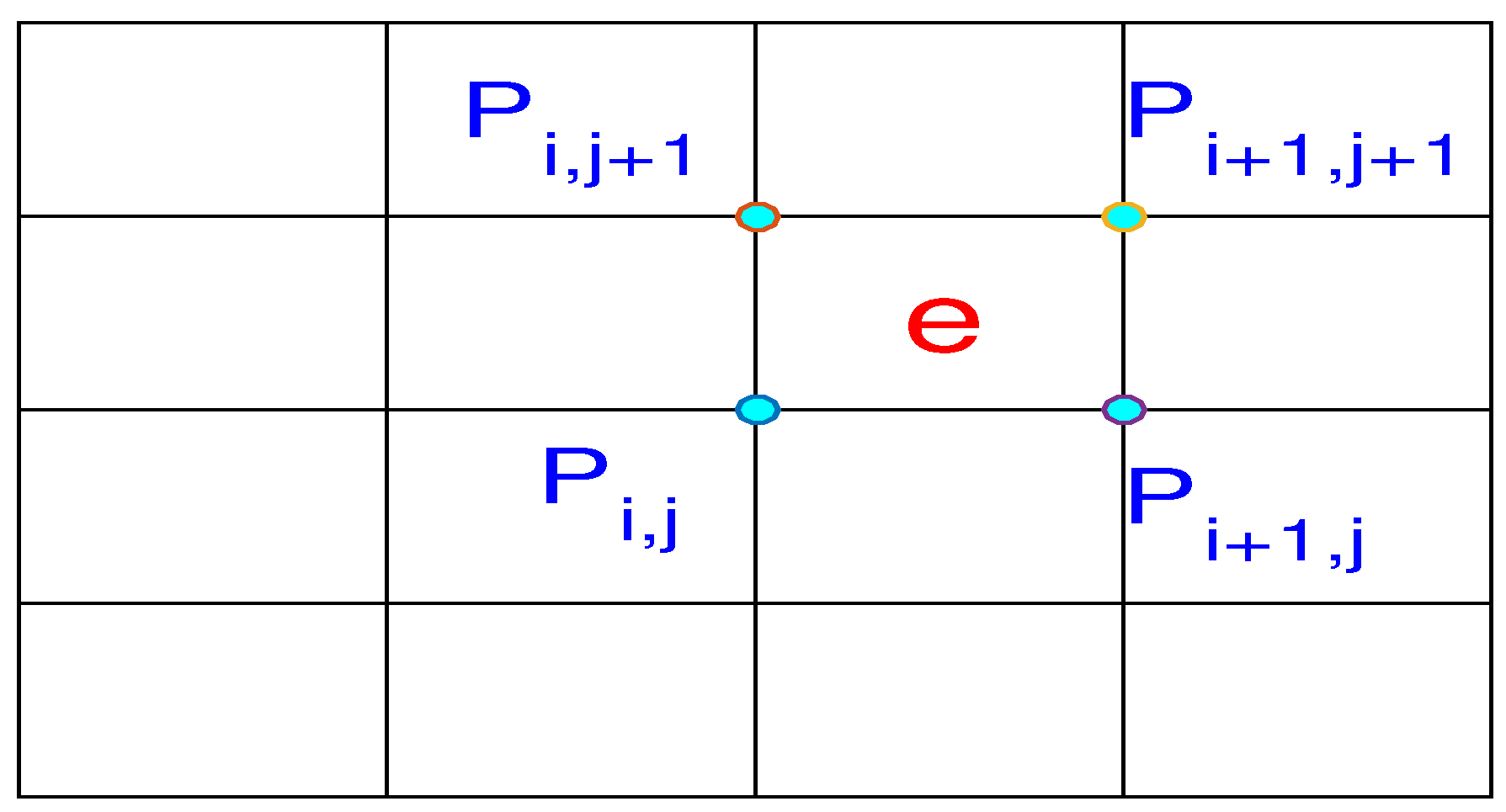
3. A General Framework for Superconvergence
4. Main Results of Superconvergence
5. Numerical Example
6. Conclusions and Further Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, M.; Shi, J.; Wang, L. A three-dimensional Petrov-Galerkin finite element interface method for solving inhomogeneous anisotropic Maxwell’s equations in irregular regions. Comput. Math. Appl. 2023, 152, 364–377. [Google Scholar] [CrossRef]
- Carrasco, S.; Caucao, S.; Gatica, G.N. New mixed finite element methods for the coupled convective Brinkman-Forchheimer and Double-Diffusion equations. J. Sci. Comput. 2023, 97, 1–81. [Google Scholar] [CrossRef]
- Wu, C.T.; Wu, S.W.; Niu, R.P.; Jiang, C.; Liu, G. The polygonal finite element method for solving heat conduction problems. Eng. Anal. Bound. Elem. 2023, 155, 935–947. [Google Scholar] [CrossRef]
- Zhao, W. Higher order weak Galerkin methods for the Navier–Stokes equations with large Reynolds number. Numer. Methods Partial. Differ. Equ. 2022, 38, 1967–1992. [Google Scholar] [CrossRef]
- Bochev, P.B.; Dohrmann, C.R.; Gunzburger, M.D. Stabilization of low-order mixed finite elements for the Stokes equations. SIAM J. Numer. Anal. 2006, 44, 82–101. [Google Scholar] [CrossRef]
- Gunzburger, M.D.; Zhao, W. Descriptions, Discretizations, and Comparisons of Time/Space Colored and White Noise Forcings of the Navier–Stokes Equations. SIAM J. Sci. Comput. 2019, 41, A2579–A2602. [Google Scholar] [CrossRef]
- Li, X. Element-free Galerkin analysis of Stokes problems using the reproducing kernel gradient smoothing integration. J. Sci. Comput. 2023, 96, 1–38. [Google Scholar] [CrossRef]
- Li, X. A weak Galerkin meshless method for incompressible Navier–Stokes equations. J. Comput. Appl. Math. 2024, 445, 1–21. [Google Scholar] [CrossRef]
- Wang, J.; Li, Q. Superconvergence analysis of a linearized three-step backward differential formula finite element method for nonlinear Sobolev equation. Math. Methods Appl. Sci. 2019, 42, 3359–3376. [Google Scholar] [CrossRef]
- Mandal, M.; Nelakanti, G. Superconvergence results of Legendre spectral projection methods for weakly singular Fredholm–Hammerstein integral equations. J. Comput. Appl. Math. 2019, 349, 114–131. [Google Scholar] [CrossRef]
- Zhang, G.; Dai, X. Superconvergence of discontinuous Galerkin method for neutral delay differential equations. Int. J. Comput. Math. 2021, 98, 1648–1662. [Google Scholar] [CrossRef]
- Guo, H.; Yang, X.; Zhang, Z. Superconvergence of partially penalized immersed finite element methods. IMA J. Numer. Anal. 2018, 38, 2123–2144. [Google Scholar] [CrossRef]
- Zhang, S.; Sun, S.; Yang, H. Optimal convergence of discontinuous Galerkin methods for continuum modeling of supply chain networks. Comput. Math. Appl. 2014, 68, 681–691. [Google Scholar] [CrossRef]
- Shi, D.; Wu, Y. Uniform superconvergent analysis of a new mixed finite element method for nonlinear Bi-wave singular perturbation problem. Appl. Math. Lett. 2019, 93, 131–138. [Google Scholar] [CrossRef]
- Anshelevich, M.; Wang, J.C.; Zhong, P. Local limit theorems for multiplicative free convolutions. J. Funct. Anal. 2014, 267, 3469–3499. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, S. Finite element derivative interpolation recovery technique and superconvergence. Appl. Math. 2011, 56, 513–531. [Google Scholar] [CrossRef]
- Schneider, M.; Wicht, D. Superconvergence of the effective Cauchy stress in computational homogenization of inelastic materials. Int. J. Numer. Methods Eng. 2023, 124, 959–978. [Google Scholar] [CrossRef]
- Huang, Y.; Li, J.; Wu, C. Averaging for superconvergence: Verification and application of 2D edge elements to Maxwell’s equations in metamaterials. Comput. Methods Appl. Mech. Eng. 2013, 255, 121–132. [Google Scholar] [CrossRef]
- Ren, J.; Long, X.; Mao, S.; Zhang, J. Superconvergence of finite element approximations for the fractional diffusion-wave equation. J. Sci. Comput. 2017, 72, 917–935. [Google Scholar] [CrossRef]
- Danielson, K.T. Barlow’s method of superconvergence for higher-order finite elements and for transverse stresses in structural elements. Finite Elem. Anal. Des. 2018, 141, 84–95. [Google Scholar] [CrossRef]
- Kim, N.I.; Choi, D.H. Super convergent shear deformable finite elements for stability analysis of composite beams. Compos. Part Eng. 2013, 44, 100–111. [Google Scholar] [CrossRef]
- Douglas, J.; Wang, J. Superconvergence of mixed finite element methods on rectangular domains. Calcolo 1989, 26, 121–133. [Google Scholar] [CrossRef]
- Durán, R. Superconvergence for rectangular mixed finite elements. Numer. Math. 1990, 58, 287–298. [Google Scholar] [CrossRef]
- Ewing, R.; Lazarov, R.; Wang, J. Superconvergence of the velocity along the Gauss lines in mixed finite element methods. SIAM J. Numer. Anal. 1991, 28, 1015–1029. [Google Scholar] [CrossRef]
- Wang, J.P. Superconvergence and extrapolation for mixed finite element methods on rectangular domains. Math. Comput. 1991, 56, 477–503. [Google Scholar] [CrossRef]
- Douglas, J.; Dupont, T. Superconvergence for Galerkin methods for the two point boundary problem via local projections. Numer. Math. 1973, 21, 270–278. [Google Scholar] [CrossRef]
- Douglas, J.J.; Milner, F.A. Interior and superconvergence estimates for mixed methods for second order elliptic problems. ESAIM Math. Model. Numer. Anal. 1985, 19, 397–428. [Google Scholar] [CrossRef]
- Ewing, R.E.; Liu, M.M.; Wang, J. Superconvergence of mixed finite element approximations over quadrilaterals. SIAM J. Numer. Anal. 1999, 36, 772–787. [Google Scholar] [CrossRef]
- Ewing, R.E.; Liu, M.; Wang, J. A new superconvergence for mixed finite element approximations. SIAM J. Numer. Anal. 2002, 40, 2133–2150. [Google Scholar] [CrossRef]
- Chen, Y.; Dai, Y. Superconvergence for optimal control problems governed by semi-linear elliptic equations. J. Sci. Comput. 2009, 39, 206–221. [Google Scholar] [CrossRef]
- Shi, D.; Ren, J.; Gong, W. Convergence and superconvergence analysis of a nonconforming finite element method for solving the Signorini problem. Nonlinear Anal. Theory, Methods Appl. 2012, 75, 3493–3502. [Google Scholar] [CrossRef]
- Shi, D.; Zhang, L. Superconvergence analysis of Galerkin finite element method for the nonlinear parabolic intergro-differential equation. J. Xinyang Norm. Univ. Nat. Sci. Ed. 2024, 37, 45–50. [Google Scholar]
- Bernstein, S. Démonstration du Théoréme de Weierstrass fonde sur le calcul des Probabilités. Commun. SociéTé MathéMatique Kharkov Ser. Xiii 1912, 13, 1–2. [Google Scholar]
- Ye, Z.; Long, X.; Zeng, X.M. Adjustment algorithms for Bézier curve and surface. In Proceedings of the 2010 5th International Conference on Computer Science & Education, Hefei, China, 24–27 August 2010; pp. 1712–1716. [Google Scholar]
- Cai, Q.; Lian, B.; Zhou, G. Approximation properties of λ-Bernstein operators. J. Inequalities Appl. 2018, 2018, 61. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Cao, H.; Qin, X. Construction of generalized developable Bézier surfaces with shape parameters. Math. Methods Appl. Sci. 2018, 41, 7804–7829. [Google Scholar] [CrossRef]
- Schurer, F. On Linear Positive Operators in Approximation Theory. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 1965. [Google Scholar]
- Yilmaz, O.; Bodur, M.; Aral, A. On approximation properties of Baskakov-Schurer-Szász operators preserving exponential functions. Filomat 2018, 32, 5433–5440. [Google Scholar] [CrossRef]
- Ayman-Mursaleen, M.; Rao, N.; Rani, M.; Kilicman, A.; Al-Abied, A.A.H.A.; Malik, P. A note on approximation of blending type Bernstein–Schurer–Kantorovich operators with shape parameter α. J. Math. 2023, 2023, 1–13. [Google Scholar] [CrossRef]
- Brenner, S.C.; Scott, L. The Mathematical Theory of Finite Element Methods; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Duran, R.; Muschietti, M.A.; Rodriguez, R. Asymptotically exact error estimators for rectangular finite elements. SIAM J. Numer. Anal. 1992, 29, 78–88. [Google Scholar] [CrossRef]
| h | ACPU(s) | Order | ACPU(s) | Order | ||
|---|---|---|---|---|---|---|
| − | − | |||||
| h | Order | Order | ||
|---|---|---|---|---|
| − | − | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Wen, S.; Dong, Z. Superconvergence of Mixed Finite Element Method with Bernstein Polynomials for Stokes Problem. Axioms 2025, 14, 168. https://doi.org/10.3390/axioms14030168
Sun L, Wen S, Dong Z. Superconvergence of Mixed Finite Element Method with Bernstein Polynomials for Stokes Problem. Axioms. 2025; 14(3):168. https://doi.org/10.3390/axioms14030168
Chicago/Turabian StyleSun, Lanyin, Siya Wen, and Ziwei Dong. 2025. "Superconvergence of Mixed Finite Element Method with Bernstein Polynomials for Stokes Problem" Axioms 14, no. 3: 168. https://doi.org/10.3390/axioms14030168
APA StyleSun, L., Wen, S., & Dong, Z. (2025). Superconvergence of Mixed Finite Element Method with Bernstein Polynomials for Stokes Problem. Axioms, 14(3), 168. https://doi.org/10.3390/axioms14030168





