Objective Posterior Analysis of kth Record Statistics in Gompertz Model
Abstract
1. Introduction and Motivation
- Generalized Gompertz distribution [6], which provides greater flexibility in modeling hazard functions with non-monotonic characteristics.
- Beta-Gompertz distribution [7], which incorporates additional shape parameters to better model diverse life phenomena.
- Gamma-Gompertz distribution [8], which extends the original model by incorporating a gamma-distributed heterogeneity component, making it useful in survival analysis.
- McDonald–Gompertz distribution [9], which introduces additional shape parameters for greater adaptability in real-world applications.
- We develop a comprehensive objective Bayesian framework for estimating the parameters of the Gompertz distribution using kth record values. This includes deriving and evaluating various objective priors such as Jeffreys’ prior, reference prior, maximal data information (MDI) prior, and probability matching priors.
- We rigorously establish the properness of the posterior distributions under these priors, ensuring the validity of the proposed approach.
- A detailed comparative analysis of the objective priors is performed through an extensive simulation study, highlighting their influence on Bayesian estimators in terms of mean squared error (MSE) and coverage probabilities (CPs).
- We address the computational challenges associated with maximum likelihood estimation (MLE) for kth record values and demonstrate the advantages of Bayesian methods, particularly under small sample settings, where MLE methods often struggle.
- The proposed methodology is applied to real-world record data, showcasing its practical relevance and robustness in modeling and inference.
2. Non-Informative Priors and Their Properties
2.1. Probability Matching Priors
2.2. Maximal Data Information Priors
- (a)
- The MDI prior for the parameters ( is selected as
- (b)
- The posterior distribution under is proper.
2.3. Reference Priors
2.4. Jeffrey’s Prior
3. Implementing the MCMC Algorithm
- Initialize the parameters and .
- Propose new candidate values and from the truncated normal distribution centered at the current values with variance matrix .
- Compute the acceptance probability
- Accept the candidate with probability A. If rejected, retain the current values.
- Repeat steps 2–4 for a pre-specified number of iterations.
4. Simulation Study
- The simulations reveal that larger sample sizes consistently reduced the MSE for all priors and improved the CPs of HPD intervals, with values converging to the nominal level of 0.95. This is readily apparent for instances and . In contrast, small sample sizes () exhibit higher variability and less reliable coverage probabilities, underscoring the challenges of record-based inference with limited data. For , the MSEs show similar trends to those observed with , highlighting the flexibility of Bayesian estimation under different record settings. In general, inference based on record values suffers from the low precision of estimators. This limitation is well recognized in the literature, where similar issues have been observed; see, for example, [19]. This only confirms the necessity of such an analysis.
- For the case when true values , the deviations have the highest values, while the CPs holds stable values, except for the case of the prior.
- The performance of the Bayesian estimators under the Jeffrey’s prior is generally superior to that under any other priors as indicated by both the MSEs and CPs. This is reasonable since is a second-order probability matching prior, in contrast to and . See Figure A2 and Figure A3 for a graphical presentation.
5. Data Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. The Problem on the Existence of MLE for α
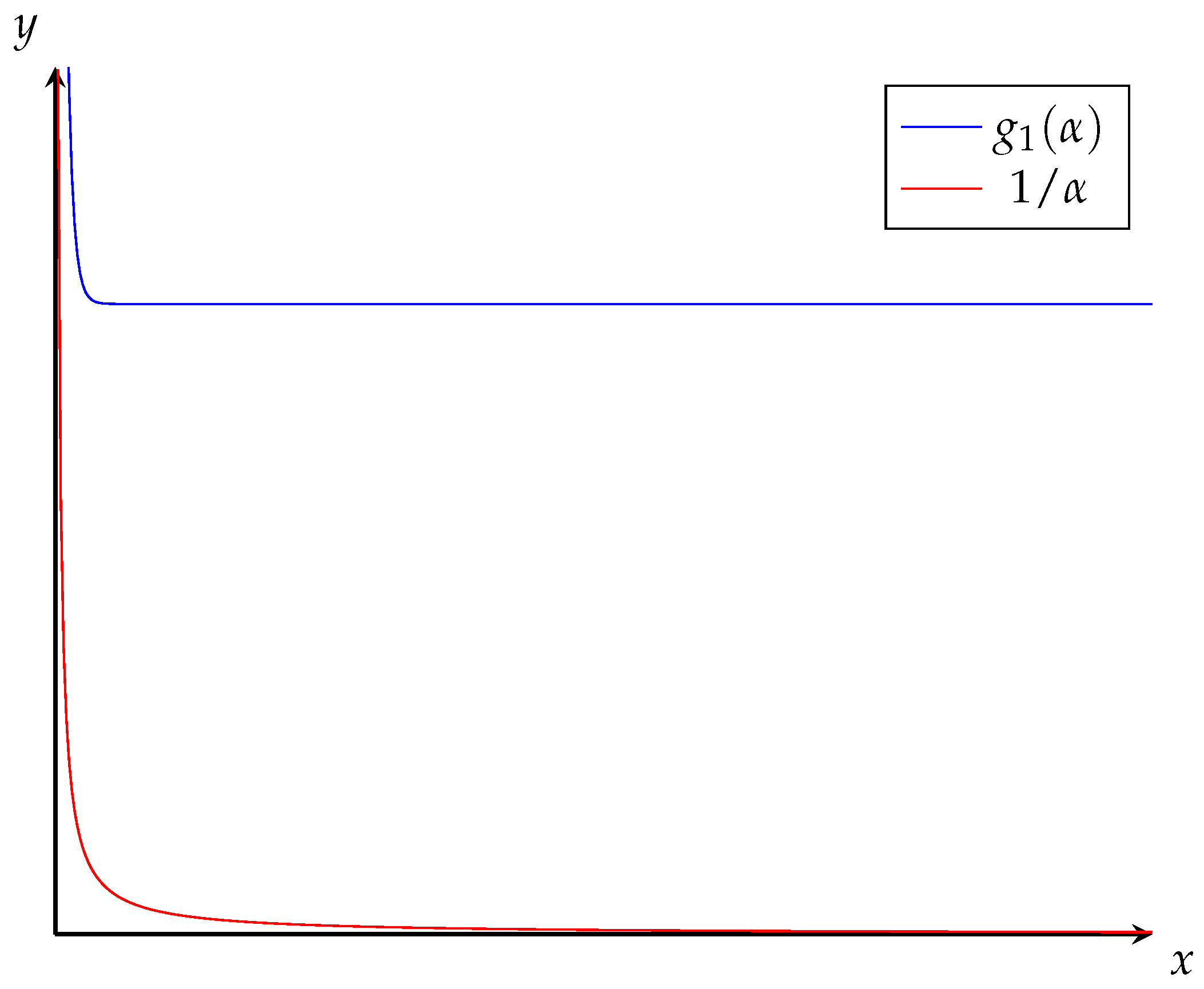
Appendix A.2. On the Properness of the Posterior
Appendix A.3. Proof of Theorem 1
Appendix A.4. Proof of Theorem 2
Appendix A.5. Proof of Theorem 3
Appendix A.6. Proof of Theorem 4
Appendix A.7. Conditional Posterior Distributions



| Prior | Parameter | ||||
|---|---|---|---|---|---|
| 1.7362 (0.932) | 1.2102 (0.932) | 1.0539 (0.902) | 0.7827 (0.924) | ||
| 1.6424 (0.978) | 1.9788 (0.974) | 1.925 (0.948) | 1.6002 (0.972) | ||
| 1.7592 (0.97) | 0.9793 (0.932) | 0.8322 (0.92) | 0.7636 (0.904) | ||
| 1.1298 (0.998) | 1.7745 (0.974) | 1.8069 (0.978) | 1.6755 (0.98) | ||
| 1.8439 (0.842) | 1.4707 (0.79) | 1.0848 (0.85) | 0.8439 (0.878) | ||
| 2.377 (0.964) | 2.785 (0.924) | 2.4906 (0.952) | 1.9889 (0.96) | ||
| 1.5546 (0.978) | 1.2402 (0.924) | 0.8938 (0.952) | 0.7753 (0.966) | ||
| 1.0959 (0.988) | 1.4218 (0.97) | 1.1956 (0.968) | 1.0505 (0.974) | ||
| 1.4957 (0.942) | 1.048 (0.886) | 0.8575 (0.884) | 0.7146 (0.894) | ||
| 1.3724 (0.978) | 2.146 (0.938) | 2.1382 (0.94) | 2.1277 (0.93) | ||
| 1.3398 (0.984) | 0.7242 (0.922) | 0.6621 (0.9) | 0.5555 (0.94) | ||
| 1.1552 (1) | 1.9265 (0.986) | 2.1219 (0.958) | 1.9719 (0.968) | ||
| 1.3055 (0.88) | 1.0662 (0.806) | 0.8812 (0.808) | 0.7455 (0.846) | ||
| 2.2305 (0.96) | 2.5247 (0.944) | 2.6387 (0.912) | 2.6454 (0.92) | ||
| 1.5645 (0.982) | 1.0097 (0.948) | 0.7429 (0.938) | 0.6122 (0.948) | ||
| 1.0612 (0.978) | 1.4921 (0.962) | 1.5654 (0.95) | 1.469 (0.946) | ||
| 0.9934 (0.972) | 0.8581 (0.9) | 0.6904 (0.892) | 0.5961 (0.91) | ||
| 1.5894 (0.972) | 1.9405 (0.958) | 2.1222 (0.948) | 2.1179 (0.93) | ||
| 1.8438 (0.984) | 0.5918 (0.956) | 0.5644 (0.882) | 0.4974 (0.89) | ||
| 1.0913 (0.996) | 1.8687 (0.996) | 2.3238 (0.952) | 2.1677 (0.96) | ||
| 0.8766 (0.944) | 0.844 (0.842) | 0.7265 (0.81) | 0.6344 (0.806) | ||
| 1.9598 (0.97) | 2.3987 (0.956) | 2.6637 (0.938) | 2.7873 (0.908) | ||
| 1.3672 (0.99) | 0.8012 (0.974) | 0.6592 (0.93) | 0.5548 (0.93) | ||
| 1.1989 (0.982) | 1.434 (0.968) | 1.7181 (0.94) | 1.6663 (0.934) | ||
| 2.4513 (0.962) | 1.049 (0.946) | 0.8486 (0.91) | 0.7696 (0.868) | ||
| 3.805 (0.94) | 2.8276 (0.956) | 3.6008 (0.934) | 3.7584 (0.918) | ||
| 12.7472 (0.706) | 1.4345 (0.968) | 0.6719 (0.962) | 0.5508 (0.958) | ||
| 3.2466 (0.754) | 2.276 (0.98) | 2.6135 (0.986) | 3.117 (0.97) | ||
| 1.192 (0.962) | 0.9704 (0.894) | 0.8767 (0.834) | 0.7855 (0.808) | ||
| 4.1568 (0.962) | 3.4359 (0.946) | 3.8024 (0.928) | 4.4419 (0.89) | ||
| 2.8096 (0.982) | 1.1815 (0.982) | 0.9151 (0.928) | 0.6964 (0.912) | ||
| 2.5463 (0.954) | 2.4604 (0.962) | 2.8278 (0.912) | 3.1741 (0.936) | ||
| 4.3602 (0.966) | 2.4604 (0.914) | 1.8525 (0.88) | 1.6201 (0.848) | ||
| 6.3537 (0.954) | 6.8124 (0.942) | 7.7799 (0.906) | 8.325 (0.916) | ||
| 44.3649 (0.126) | 6.8346 (0.656) | 2.2841 (0.898) | 1.4796 (0.926) | ||
| 9.6124 (0.058) | 6.4391 (0.69) | 4.9064 (0.886) | 4.8237 (0.92) | ||
| 2.5706 (0.952) | 1.9613 (0.89) | 1.7866 (0.826) | 1.6454 (0.79) | ||
| 7.178 (0.946) | 7.3819 (0.942) | 8.6658 (0.896) | 9.5319 (0.872) | ||
| 6.2331 (0.97) | 2.5782 (0.966) | 1.7945 (0.94) | 1.4292 (0.922) | ||
| 5.7429 (0.944) | 5.2623 (0.932) | 5.7694 (0.944) | 6.4812 (0.926) | ||
| Prior | Parameter | ||||
|---|---|---|---|---|---|
| 2.1334 (0.906) | 1.455 (0.904) | 1.1254 (0.912) | 0.9594 (0.91) | ||
| 1.2199 (0.96) | 1.5031 (0.978) | 1.5222 (0.956) | 1.3702 (0.964) | ||
| 3.0018 (0.944) | 1.0543 (0.958) | 0.8895 (0.936) | 0.7713 (0.942) | ||
| 0.6066 (0.988) | 1.0881 (0.994) | 1.1939 (0.978) | 1.2017 (0.98) | ||
| 1.9617 (0.858) | 1.6118 (0.816) | 1.2976 (0.844) | 1.0139 (0.87) | ||
| 1.6104 (0.966) | 1.8605 (0.946) | 1.9594 (0.94) | 1.6754 (0.954) | ||
| 2.6099 (0.974) | 1.3474 (0.936) | 1.0111 (0.946) | 0.8385 (0.942) | ||
| 0.7729 (0.99) | 1.0413 (0.966) | 1.1612 (0.962) | 1.0505 (0.952) | ||
| 1.4819 (0.97) | 1.1575 (0.9) | 1.0355 (0.862) | 0.8459 (0.88) | ||
| 1.1532 (0.976) | 1.4445 (0.948) | 1.7347 (0.898) | 1.6963 (0.922) | ||
| 6.8213 (0.892) | 0.9073 (0.972) | 0.7113 (0.94) | 0.6326 (0.914) | ||
| 0.7371 (0.962) | 1.183 (0.994) | 1.3923 (0.98) | 1.4029 (0.972) | ||
| 1.2328 (0.928) | 1.1683 (0.842) | 1.0485 (0.812) | 0.8664 (0.83) | ||
| 1.6365 (0.95) | 1.7396 (0.952) | 2.0795 (0.912) | 1.9476 (0.934) | ||
| 2.5595 (0.986) | 1.0307 (0.968) | 0.8997 (0.922) | 0.7498 (0.914) | ||
| 1.1424 (0.974) | 1.1226 (0.98) | 1.2761 (0.952) | 1.2239 (0.946) | ||
| 1.6862 (0.964) | 0.9628 (0.934) | 0.8384 (0.862) | 0.7328 (0.886) | ||
| 1.1864 (0.956) | 1.3059 (0.956) | 1.7547 (0.936) | 1.7597 (0.94) | ||
| 6.7843 (0.852) | 0.8998 (0.982) | 0.624 (0.958) | 0.5602 (0.928) | ||
| 1.0036 (0.946) | 1.1376 (0.988) | 1.3229 (0.994) | 1.5534 (0.962) | ||
| 0.869 (0.954) | 0.9311 (0.896) | 0.8535 (0.82) | 0.7681 (0.784) | ||
| 1.7139 (0.96) | 1.5577 (0.962) | 1.8474 (0.942) | 2.1392 (0.892) | ||
| 2.388 (0.988) | 0.9196 (0.984) | 0.8015 (0.95) | 0.6599 (0.922) | ||
| 1.0435 (0.972) | 1.0425 (0.976) | 1.3135 (0.952) | 1.3494 (0.946) | ||
| 2.9618 (0.97) | 1.3554 (0.952) | 0.9985 (0.936) | 0.9052 (0.906) | ||
| 2.8079 (0.93) | 2.3359 (0.94) | 2.2688 (0.97) | 2.7031 (0.94) | ||
| 33.0919 (0.262) | 3.2629 (0.816) | 1.2834 (0.954) | 0.7814 (0.97) | ||
| 4.4792 (0.214) | 2.3849 (0.878) | 1.9536 (0.952) | 2.0055 (0.968) | ||
| 1.614 (0.974) | 1.0475 (0.954) | 0.9707 (0.89) | 0.873 (0.878) | ||
| 3.6881 (0.97) | 2.5887 (0.958) | 2.5859 (0.948) | 3.0233 (0.932) | ||
| 4.3126 (0.994) | 1.5492 (0.986) | 1.0858 (0.986) | 0.8529 (0.956) | ||
| 2.611 (0.908) | 2.1368 (0.958) | 2.0915 (0.956) | 2.1985 (0.956) | ||
| 7.3097 (0.966) | 2.8326 (0.96) | 2.2558 (0.9) | 1.8764 (0.86) | ||
| 6.8628 (0.922) | 4.4389 (0.946) | 5.1001 (0.944) | 5.6842 (0.924) | ||
| 84.4238 (0.004) | 20.9314 (0.27) | 5.8657 (0.634) | 2.7898 (0.824) | ||
| 9.9741 (0) | 8.4092 (0.216) | 5.9635 (0.634) | 4.6369 (0.8) | ||
| 4.1755 (0.972) | 2.2731 (0.94) | 1.9344 (0.908) | 1.8518 (0.84) | ||
| 6.1125 (0.96) | 5.4758 (0.966) | 5.3633 (0.944) | 6.3066 (0.934) | ||
| 10.8352 (0.976) | 3.218 (0.988) | 2.1488 (0.964) | 1.7812 (0.946) | ||
| 5.7046 (0.88) | 4.1613 (0.952) | 4.3392 (0.952) | 4.5652 (0.94) | ||
References
- Troynikov, V.S.; Day, R.W.; Leorke, A.M. Estimation of seasonal growth parameters using a stochastic Gompertz model for tagging data. J. Shellfish Res. 1998, 17, 833–838. [Google Scholar]
- Moura, N.J.; Ribeiro, M.B. Evidence for the Gompertz curve in the income distribution of Brazil 1978–2005. Eur. Phys. J. B 2009, 67, 101–120. [Google Scholar] [CrossRef][Green Version]
- Pollard, J.H.; Valkovics, E.J. The Gompertz distribution and its applications. Genus 1992, 48, 15–28. [Google Scholar]
- Mueller, L.D.; Nusbaum, T.J.; Rose, M.R. The Gompertz equation as a predictive tool in demography. Exp. Gerontol. 1995, 30, 553–569. [Google Scholar] [CrossRef] [PubMed]
- Olshansky, S.J.; Carnes, B.A. Ever since Gompertz. Demography 1997, 34, 1–15. [Google Scholar] [CrossRef]
- El-Gohary, A.; Alshamrani, A.; Al-Otaibi, A.N. The generalized Gompertz distribution. Appl. Math. Model. 2013, 37, 13–24. [Google Scholar] [CrossRef]
- Jafari, A.A.; Tahmasebi, S.; Alizadeh, M. The beta-Gompertz distribution. Rev. Colomb. Estadística 2014, 37, 141–158. [Google Scholar] [CrossRef]
- Shama, M.S.; Dey, S.; Altun, E.; Afify, A.Z. The gamma–Gompertz distribution: Theory and applications. Math. Comput. Simul. 2022, 193, 689–712. [Google Scholar] [CrossRef]
- Roozegar, R.; Tahmasebi, S.; Jafari, A.A. The McDonald Gompertz distribution: Properties and applications. Commun. Stat. Simul. Comput. 2017, 46, 3341–3355. [Google Scholar] [CrossRef]
- Ahmadi, J.; Arghami, N.R. Comparing the Fisher information in record values and iid observations. Statistics 2003, 37, 435–441. [Google Scholar] [CrossRef]
- Chandler, K.N. The distribution and frequency of record values. J. R. Stat. Soc. Ser. B Methodol. 1952, 14, 220–228. [Google Scholar] [CrossRef]
- Berger, M.; Gulati, S. Record-breaking data: A parametric comparison of the inverse-sampling and the random-sampling schemes. J. Stat. Comput. Simul. 2001, 69, 225–238. [Google Scholar] [CrossRef]
- Glick, N. Breaking records and breaking boards. Am. Math. Mon. 1978, 85, 2–26. [Google Scholar] [CrossRef]
- Benestad, R.E. How often can we expect a record event? Clim. Res. 2003, 25, 3–13. [Google Scholar] [CrossRef]
- Kauffman, S.; Levin, S. Towards a general theory of adaptive walks on rugged landscapes. J. Theor. Biol. 1987, 128, 11–45. [Google Scholar] [CrossRef] [PubMed]
- Arnold, B.C.; Balakrishnan, N.; Nagaraja, H.N. Records; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 768. [Google Scholar]
- Nevzorov, V.B. Records: Mathematical Theory; Translations of Mathematical Monographs, AMS: Providence, RI, USA, 2000. [Google Scholar]
- Dziubdziela, W.; Kopociński, B. Limiting properties of the k-th record values. Appl. Math. 1976, 2, 187–190. [Google Scholar] [CrossRef]
- Vidović, Z. On MLEs of the parameters of a modified Weibull distribution based on record values. J. Appl. Stat. 2018, 46, 715–724. [Google Scholar] [CrossRef]
- Wang, L.; Shi, Y.; Yan, W. Inference for Gompertz distribution under records. J. Syst. Eng. Electron. 2016, 27, 271–278. [Google Scholar]
- Laji, M.; Chacko, M. Inference On Gompertz Distribution Based On Upper k-Record Values: Inference based on upper k-records. J. Kerala Stat. Assoc. 2019, 30, 47–63. [Google Scholar]
- Hemmati, A.; Khodadadi, Z.; Zare, K.; Jafarpour, H. Bayesian and Classical Estimation of Strength-Stress Reliability for Gompertz Distribution Based on Upper Record Values. J. Math. Ext. 2022, 16, 1–27. [Google Scholar]
- Tripathi, A.; Singh, U.; Kumar Singh, S. Estimation of P(X < Y) for Gompertz distribution based on upper records. Int. J. Model. Simul. 2022, 42, 388–399. [Google Scholar]
- El-Bassiouny, A.H.; Medhat, E.D.; Mustafa, A.; Eliwa, M.S. Characterization of the generalized Weibull-Gompertz distribution based on the upper record values. Int. J. Math. Its Appl. 2015, 3, 13–22. [Google Scholar]
- Kumar, D.; Wang, L.; Dey, S.; Salehi, M. Inference on generalized inverted exponential distribution based on record values and inter-record times. Afr. Mat. 2022, 33, 73. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, L.; Dey, S.; Liu, J. Estimation of stress-strength reliability from unit-Burr III distribution under records data. Math. Biosci. Eng. 2023, 20, 12360–12379. [Google Scholar] [CrossRef] [PubMed]
- Bashir, S.; Qureshİ, A. Gompertz-Exponential Distribution: Record Value Theory and Applications in Reliability. Istat. J. Turk. Stat. Assoc. 2022, 14, 27–37. [Google Scholar]
- Vidović, Z.; Nikolić, J.; Perić, Z. Properties of k-record posteriors for the Weibull model. Stat. Theory Relat. Fields 2024, 8, 152–162. [Google Scholar] [CrossRef]
- Jaheen, Z.F. A Bayesian analysis of record statistics from the Gompertz model. Appl. Math. Comput. 2003, 145, 307–320. [Google Scholar] [CrossRef]
- Tian, Q.; Lewis-Beck, C.; Niemi, J.B.; Meeker, W.Q. Specifying prior distributions in reliability applications. Appl. Stoch. Model. Bus. Ind. 2023, 40, 5–62. [Google Scholar] [CrossRef]
- Xu, A.; Fang, G.; Zhuang, L.; Gu, C. A multivariate student-t process model for dependent tail-weighted degradation data. IISE Trans. 2024. [Google Scholar] [CrossRef]
- Luo, F.; Hu, L.; Wang, Y.; Yu, X. Statistical inference of reliability for a K-out-of-N: G system with switching failure under Poisson shocks. Stat. Theory Relat. Fields 2024, 8, 195–210. [Google Scholar] [CrossRef]
- Gugushvili, S.; Spreij, P. Nonparametric Bayesian drift estimation for multidimensional stochastic differential equations. Lith. Math. J. 2014, 54, 127–141. [Google Scholar] [CrossRef]
- Kass, R.E.; Wasserman, L. The selection of prior distributions by formal rules. J. Am. Stat. Assoc. 1996, 91, 1343–1370. [Google Scholar] [CrossRef]
- Ramos, P.L.; Achcar, J.A.; Moala, F.A.; Ramos, E.; Louzada, F. Bayesian analysis of the generalized gamma distribution using non-informative priors. Statistics 2017, 51, 824–843. [Google Scholar] [CrossRef]
- Shakhatreh, M.K.; Dey, S.; Alodat, M.T. Objective Bayesian analysis for the differential entropy of the Weibull distribution. Appl. Math. Model. 2021, 89, 314–332. [Google Scholar] [CrossRef]
- Ramos, P.L.; Almeida, M.H.; Louzada, F.; Flores, E.; Moala, F.A. Objective Bayesian inference for the Capability index of the Weibull distribution and its generalization. Comput. Ind. Eng. 2022, 167, 108012. [Google Scholar] [CrossRef]
- Xu, A.; Fu, J.; Tang, Y.; Guan, Q. Bayesian analysis of constant-stress accelerated life test for the Weibull distribution using noninformative priors. Appl. Math. Model. 2015, 39, 6183–6195. [Google Scholar] [CrossRef]
- Kim, Y.; Seo, J.I. Objective Bayesian Prediction of Future Record Statistics Based on the Exponentiated Gumbel Distribution: Comparison with Time-Series Prediction. Symmetry 2020, 12, 1443. [Google Scholar] [CrossRef]
- Vidovic, Z.; Nikolić, J.; Perić, Z. Bayesian k-record analysis for the Lomax distribution using objective priors. J. Math. Ext. 2024, 18, 1–23. [Google Scholar]
- Consonni, G.; Fouskakis, D.; Liseo, B.; Ntzoufras, I. Prior distributions for objective Bayesian analysis. Bayesian Anal. 2018, 13, 627–679. [Google Scholar] [CrossRef]
- Datta, G.S.; Mukerjee, R. Probability Matching Priors: Higher Order Asymptotics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004; Volume 178. [Google Scholar]
- Lindley, D.V. On a measure of the information provided by an experiment. Ann. Math. Stat. 1956, 27, 986–1005. [Google Scholar] [CrossRef]
- Zellner, A. Maximal data information prior distributions. In New Developments in the Applications of Bayesian Methods; Elsevier: Amsterdam, The Netherlands, 1977; pp. 211–232. [Google Scholar]
- Berger, J.O.; Bernardo, J.M.; Sun, D. The formal definition of reference priors. arXiv 2009, arXiv:0904.0156. [Google Scholar] [CrossRef]
- Bernardo, J.M. Reference posterior distributions for Bayesian inference. J. R. Stat. Soc. Ser. B Methodol. 1979, 41, 113–128. [Google Scholar] [CrossRef]
- Berger, J.O.; Bernardo, J.M. Ordered group reference priors with application to the multinomial problem. Biometrika 1992, 79, 25–37. [Google Scholar] [CrossRef]
- Jeffreys, H. An invariant form for the prior probability in estimation problems. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1946, 186, 453–461. [Google Scholar]
- Gelman, A.; Gilks, W.R.; Roberts, G.O. Weak convergence and optimal scaling of random walk Metropolis algorithms. Ann. Appl. Probab. 1997, 7, 110–120. [Google Scholar] [CrossRef]
- Neal, P.; Roberts, G. Optimal scaling for random walk Metropolis on spherically constrained target densities. Methodol. Comput. Appl. Probab. 2008, 10, 277–297. [Google Scholar] [CrossRef]
- Empacher, C.; Kamps, U.; Volovskiy, G. Statistical Prediction of Future Sports Records Based on Record Values. Stats 2023, 6, 131–147. [Google Scholar] [CrossRef]
- Chen, M.H.; Shao, Q.M. Monte Carlo estimation of Bayesian credible and HPD intervals. J. Comput. Graph. Stat. 1999, 8, 69–92. [Google Scholar] [CrossRef]
- Hofmann, G.; Balakrishnan, N. Fisher information in k-records. Ann. Inst. Stat. Math. 2004, 56, 383–396. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2. [Google Scholar]
- Jolliffe, I.T. Principal component analysis. Technometrics 2003, 45, 276. [Google Scholar]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4. [Google Scholar]
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the number of clusters in a data set via the gap statistic. J. R. Stat. Soc. Ser. B Stat. Methodol. 2001, 63, 411–423. [Google Scholar] [CrossRef]
- Turkkan, N.; Pham-Gia, T. Computation of the highest posterior density interval in Bayesian analysis. J. Stat. Comput. Simul. 1993, 44, 243–250. [Google Scholar] [CrossRef]
- Ahsanullah, M. Record values of the Lomax distribution. Stat. Neerl. 1991, 45, 21–29. [Google Scholar] [CrossRef]
- Peers, H.W. On confidence points and Bayesian probability points in the case of several parameters. J. R. Stat. Soc. Ser. B Methodol. 1965, 27, 9–16. [Google Scholar] [CrossRef]

| Dataset I | 0.12528 | 0.21211 | 0.22784 | 0.26063 | 0.65258 |
| 0.66056 | 0.68255 | 0.79385 | 0.83778 | 0.92206 | |
| Dataset II | 4.85 | 18.79 | 20.44 | 22.00 | 27.47 |
| 33.44 |
| Dataset I | 1.483 | 5.572 |
| Dataset II | 0.0049 | 0.2659 |
| Prior | Parameter | Median | SD | 95% HDI | |
|---|---|---|---|---|---|
| Dataset I | |||||
| 0.6191 | 0.9874 | (0, 2.2369) | |||
| 7.2644 | 4.1427 | (1.3615, 14.5149) | |||
| 2.3136 | 1.6505 | (0, 5.1734) | |||
| 3.0662 | 3.5271 | (0.0473, 9.9768) | |||
| 0.4777 | 1.0322 | (0, 1.8967) | |||
| 8.2162 | 4.7862 | (2.1967, 15.9144) | |||
| 0.9855 | 0.9589 | (0.0002, 2.9002) | |||
| 6.1871 | 3.7258 | (0.627, 13.4511) | |||
| Dataset II | |||||
| 0.0235 | 0.0368 | (0, 0.0823) | |||
| 0.1041 | 0.1652 | (0.0062, 0.2482) | |||
| 0.0348 | 0.0565 | (0, 0.1319) | |||
| 0.0905 | 0.1838 | (0.0001, 0.3362) | |||
| 0.1967 | 0.0318 | (0, 0.0731) | |||
| 0.1193 | 0.1537 | (0.0124, 0.2693) | |||
| 0.0369 | 0.0518 | (0, 0.1097) | |||
| 0.0829 | 0.1835 | (0.0009, 0.2171) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vidović, Z.; Wang, L. Objective Posterior Analysis of kth Record Statistics in Gompertz Model. Axioms 2025, 14, 152. https://doi.org/10.3390/axioms14030152
Vidović Z, Wang L. Objective Posterior Analysis of kth Record Statistics in Gompertz Model. Axioms. 2025; 14(3):152. https://doi.org/10.3390/axioms14030152
Chicago/Turabian StyleVidović, Zoran, and Liang Wang. 2025. "Objective Posterior Analysis of kth Record Statistics in Gompertz Model" Axioms 14, no. 3: 152. https://doi.org/10.3390/axioms14030152
APA StyleVidović, Z., & Wang, L. (2025). Objective Posterior Analysis of kth Record Statistics in Gompertz Model. Axioms, 14(3), 152. https://doi.org/10.3390/axioms14030152






