Numerical Solution of Mathematical Model of Heat Conduction in Multi-Layered Nanoscale Solids
Abstract
1. Introduction
2. Finite Difference Approximation
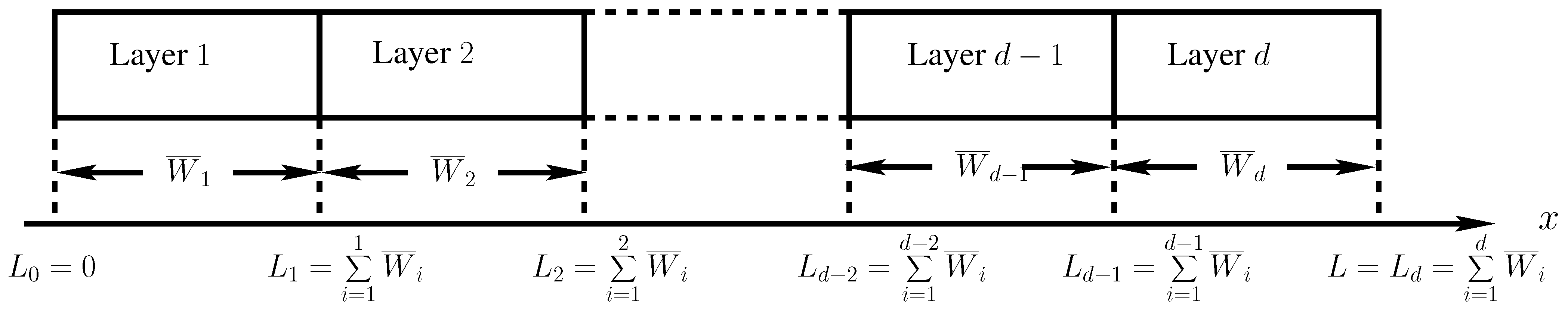
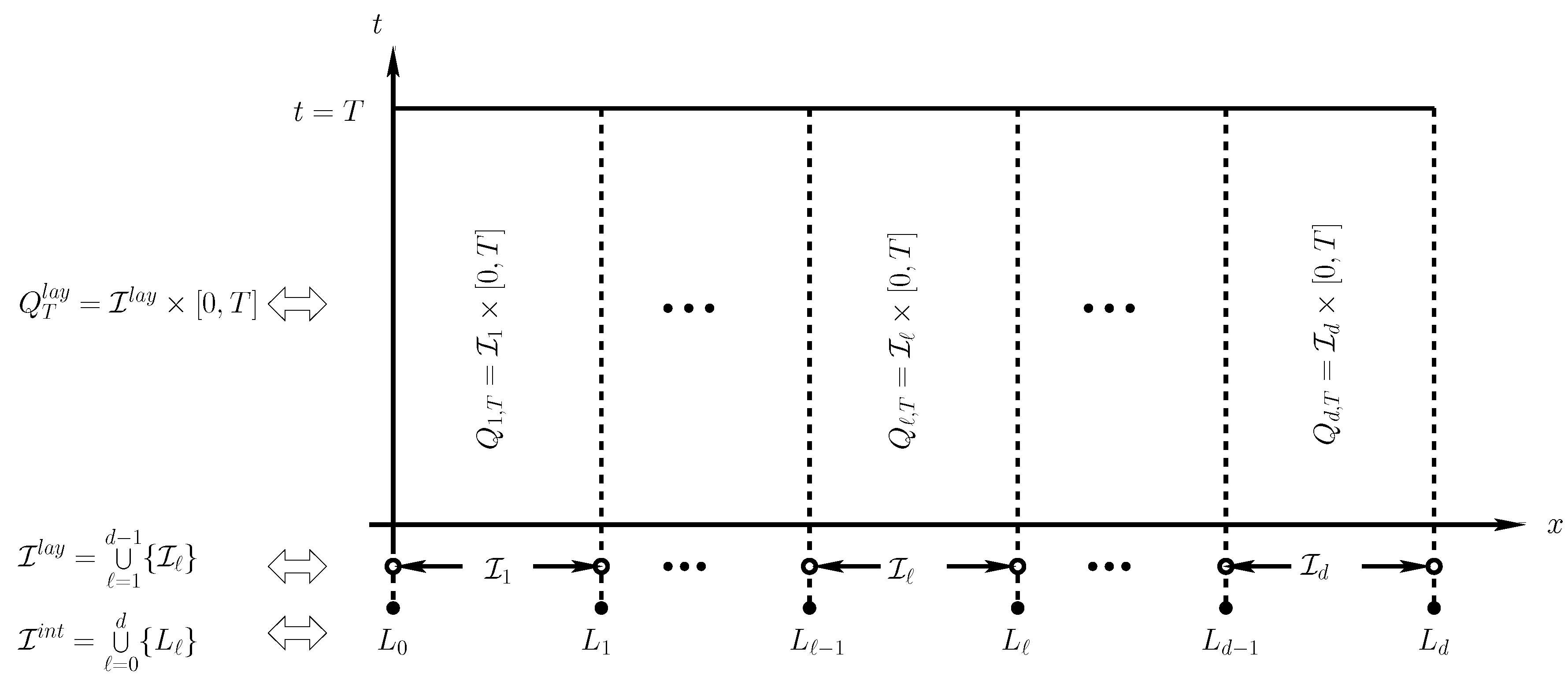
2.1. Discretization of the Domain
2.2. Semidiscrete Scheme Approximating the Rewritten System
2.3. Fully Discrete Finite Difference Scheme Approximating the Rewritten System
2.4. Finite Difference Scheme Approximating the Original System
3. Analytical and Numerical Analysis
3.1. Continuos Energy Estimation
3.2. Equivalence of Finite Difference Schemes for Rewritten and Original Systems
3.3. Discrete Energy Estimation
4. Numerical Examples
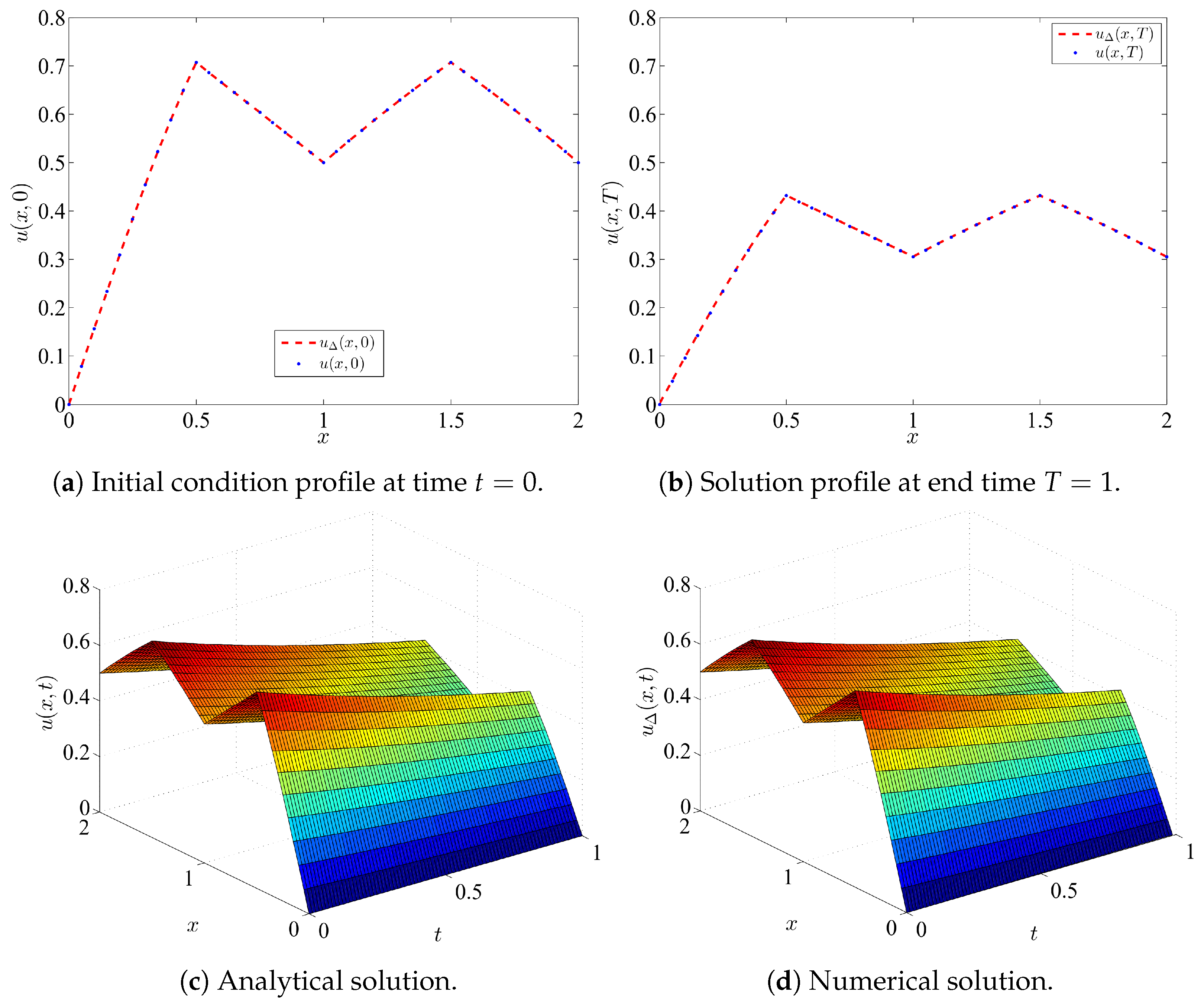
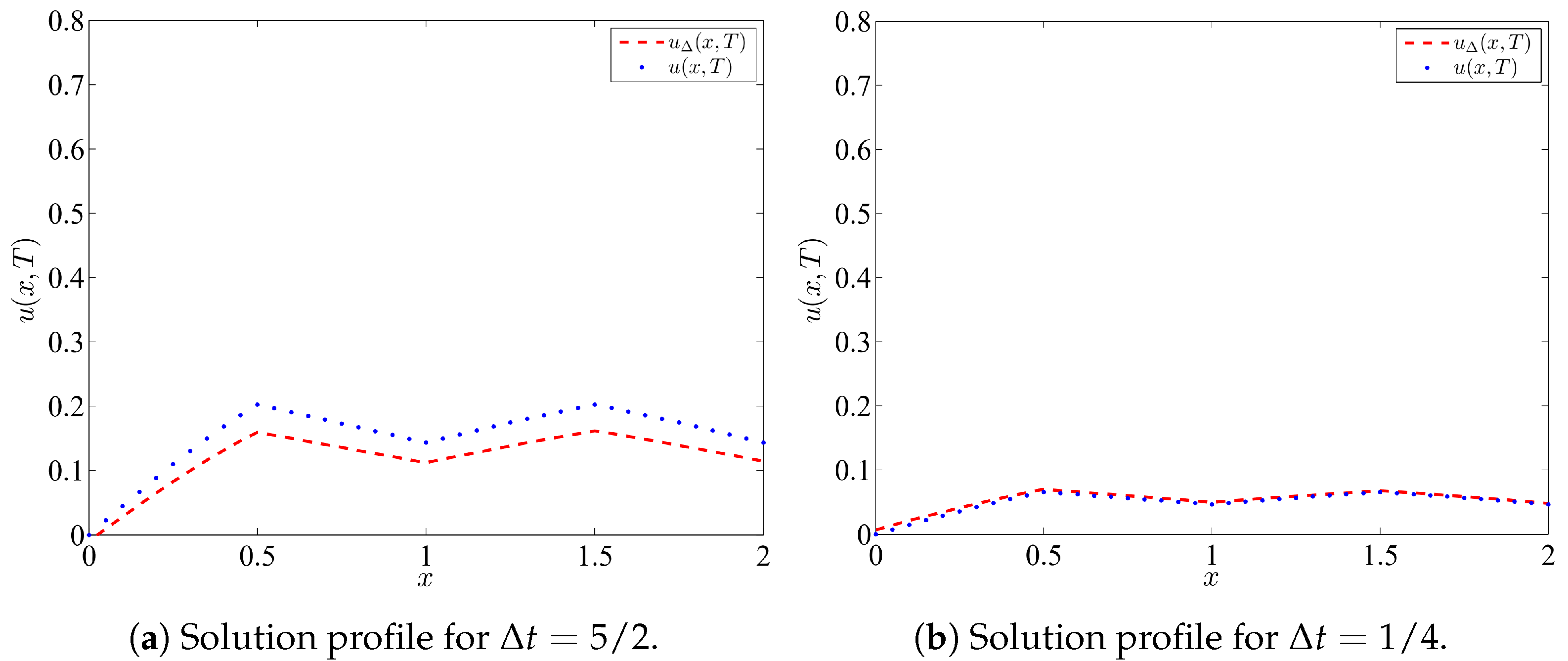
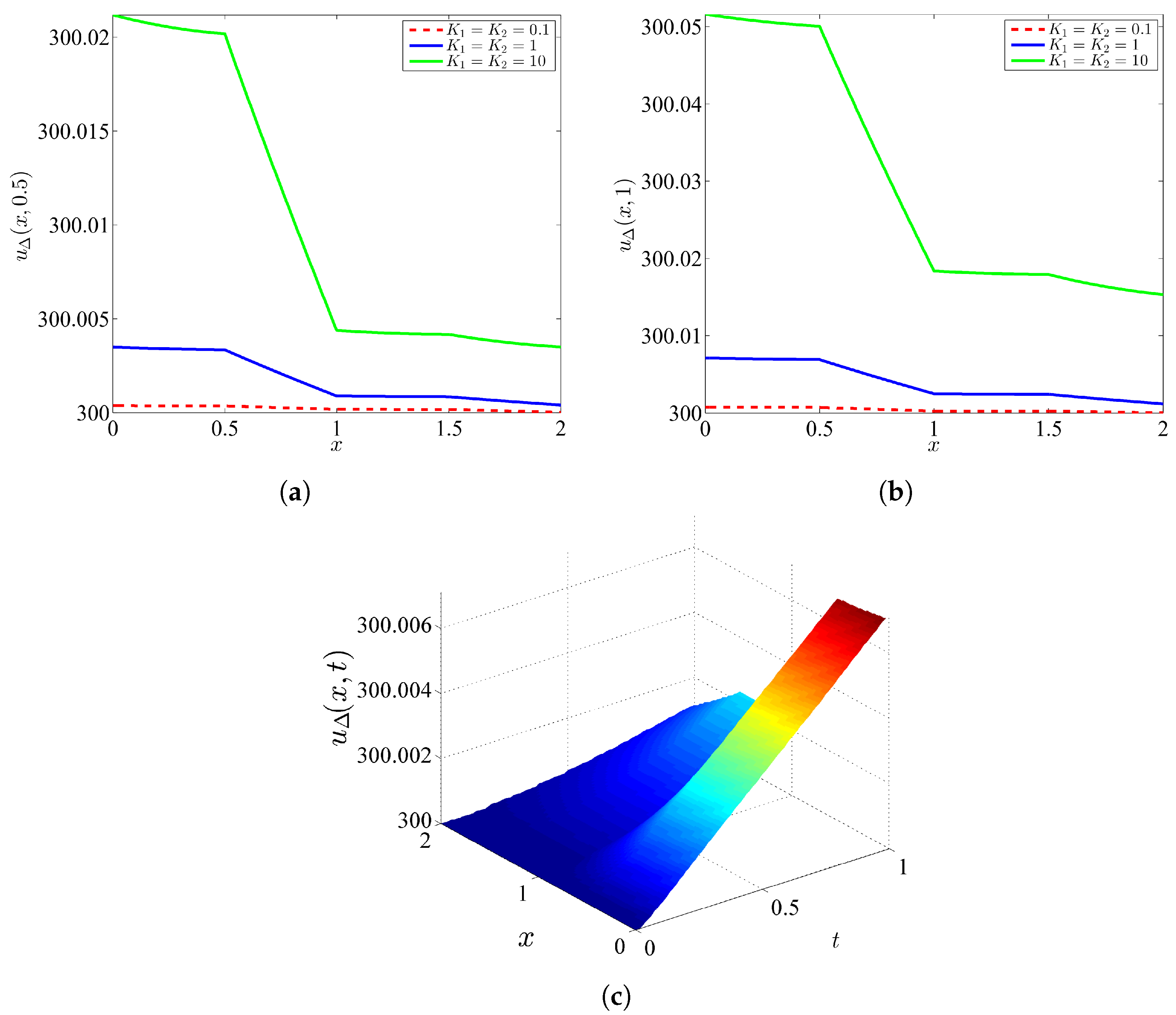
4.1. Example 1
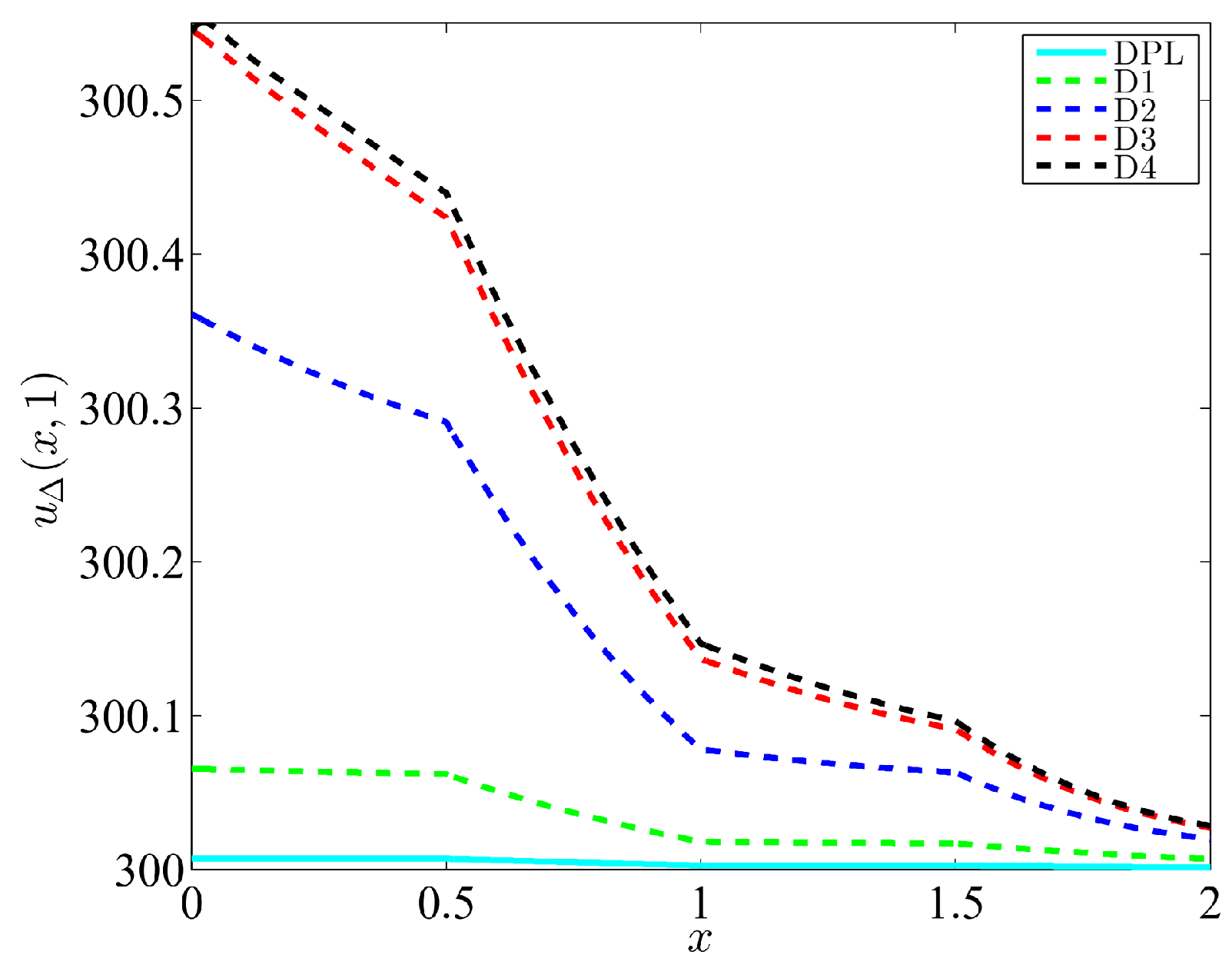
4.2. Example 2
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dorfman, A.; Renner, Z. Conjugate Problems in Convective Heat Transfer: Review. Math. Probl. Eng. 2009, 2009, 927350. [Google Scholar] [CrossRef]
- Zudin, Y.B. Theory of Periodic Conjugate Heat Transfer, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Kazemi-Kamyab, V.; van Zuijlen, A.H.; Bijl, H. A high order time-accurate loosely-coupled solution algorithm for unsteady conjugate heat transfer problems. Comput. Methods Appl. Mech. Eng. 2013, 264, 205–217. [Google Scholar] [CrossRef]
- Ooi, E.H.; van Popov, V. An efficient hybrid BEM–RBIE method for solving conjugate heat transfer problems. Comput. Math. Appl. 2014, 66, 2489–2503. [Google Scholar]
- Costa, R.; Nóbrega, J.M.; Clain, S.; Machado, G.J. Very high-order accurate polygonal mesh finite volume scheme for conjugate heat transfer problems with curved interfaces and imperfect contacts. Comput. Methods Appl. Mech. Eng. 2019, 357, 112560. [Google Scholar] [CrossRef]
- Pan, X.; Lee, C.; Choi, J.-I. Efficient monolithic projection method for time-dependent conjugate heat transfer problems. J. Comput. Phys. 2018, 369, 191–208. [Google Scholar] [CrossRef]
- Guo, S.; Feng, Y.; Tao, W.-Q. Deviation analysis of loosely coupled quasi-static method for fluid-thermal interaction in hypersonic flows. Comput. Fluids 2017, 149, 194–204. [Google Scholar] [CrossRef]
- Errera, M.-P.; Duchaine, F. Comparative study of coupling coefficients in Dirichlet-Robin procedure for fluid-structure aerothermal simulations. J. Comput. Phys. 2016, 312, 218–234. [Google Scholar] [CrossRef]
- Kazemi-Kamyab, V.; van Zuijlen, A.H.; Bijl, H. Analysis and application of high order implicit Runge-Kutta schemes for unsteady conjugate heat transfer: A strongly-coupled approach. J. Comput. Phys. 2014, 272, 471–486. [Google Scholar] [CrossRef]
- Dai, W.; Han, F.; Sun, Z. Accurate numerical method for solving dual-phase-lagging equation with temperature jump boundary condition in nano heat conduction. Int. J. Heat Mass Transf. 2013, 64, 966–975. [Google Scholar] [CrossRef]
- Tzou, D.Y. A unified field approach for heat conduction from macro-to micro-scale. ASME J. Heat Transf. 1995, 117, 8–16. [Google Scholar] [CrossRef]
- Tzou, D.Y. Macro to Microscale Heat Transfer. The Lagging Behaviour, 2nd ed.; Taylor & Francis: Washington, DC, USA, 2014. [Google Scholar]
- Borjalilou, V.; Asghari, M. Small-scale analysis of plates with thermoelastic damping based on the modified couple stress theory and the dual-phase-lag heat conduction model. Acta Mech. 2018, 229, 124720. [Google Scholar] [CrossRef]
- Sun, H.; Sun, Z.Z.; Dai, W. A second-order finite difference scheme for solving the dual-phase-lagging equation in a double-layered nano-scale thin film. Numer. Methods Partial. Differ. Equ. 2017, 33, 142–173. [Google Scholar] [CrossRef]
- Cattaneo, C. A Form of Heat Conduction Equation Which Eliminates the Paradox of Instantaneous Propagation. C. R. Acad. Sci. 1958, 247, 431–433. [Google Scholar]
- Quintanilla, R. Exponential stability in the dual-phase-lag heat conduction theory. Int. J. Heat Mass Transf. 2002, 27, 217–227. [Google Scholar] [CrossRef]
- Quintanilla, R.; Racke, R. A note on stability in dual-phase-lag heat conduction. Int. J. Heat Mass Transf. 2006, 49, 1209–1213. [Google Scholar] [CrossRef]
- Kumar, S.; Srivastava, A. Thermal analysis of laser-irradiated tissue phantoms using dual phase lag model coupled with transient radiative transfer equation. Int. J. Heat Mass Transf. 2015, 90, 466–479. [Google Scholar] [CrossRef]
- Poshti, A.G.T.; Khosravirad, A.; Ayani, M.B. Analyses of non-Fourier heat conduction in 1-D spherical biological tissue based on dual-phase-lag bio-heat model using the conservation element/solution element (CE/SE) method: A numerical study. Int. Commun. Heat Mass Transf. 2022, 132, 105881. [Google Scholar] [CrossRef]
- Ghazanfarian, J.; Abbassi, A. Effect of boundary phonon scattering on Dual-Phase-Lag model to simulate micro- and nano-scale heat conduction. Int. J. Heat Mass Transf. 2009, 52, 3706–3711. [Google Scholar] [CrossRef]
- Rapp, B. Microfluidics: Modeling, Mechanics and Mathematics; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Coronel, A.; Huancas, F.; Lozada, E.; Tello, A. A Numerical Method for a Heat Conduction Model in a Double-Pane Window. Axioms 2022, 11, 422. [Google Scholar] [CrossRef]
- Sun, Z.Z. Numerical Methods for Partial Differential Equations, 2nd ed.; Science Press: Beijing, China, 2012. [Google Scholar]
- Liao, H.L.; Sun, Z.Z. Maximum norm error estimates of efficient difference schemes for second-order wave equations. J. Comput. Appl. Math. 2011, 235, 2217–2233. [Google Scholar] [CrossRef]
- Coronel, A.; Lozada, E.; Berres, S.; Fernando, F.; Murúa, N. Mathematical modeling and numerical approximation of heat conduction in three-phase-lag solid. Energies 2024, 17, 2497. [Google Scholar] [CrossRef]
- Murúa, N.; Coronel, A.; Tello, A.; Berres, S.; Huancas, F. GPU Accelerating Algorithms for Three-Layered Heat Conduction Simulations. Mathematics 2024, 12, 3503. [Google Scholar] [CrossRef]
- Zhang, Y.; Tzou, D.Y.; Chen, J.K. Micro- and nanoscale heat transfer in femtosecond laser processing of metals. In High-Power and Femtosecond Lasers: Properties, Materials and Applications; Nova Science Publishers: Hauppauge, NY, USA, 2009; pp. 159–206. [Google Scholar]
- Liu, C.; Cao, W.; Song, X.; Wan, Y. A semi-analytical method of three-dimensional dual-phase-lagging heat conduction model. J. Heat Mass Transf. 2024, 218, 124720. [Google Scholar] [CrossRef]
| Example 1 | Example 2 | |||||||
|---|---|---|---|---|---|---|---|---|
| Layer 1 | Layer 2 | Layer 3 | Layer 4 | Layer 1 | Layer 2 | Layer 3 | Layer 4 | |
| 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | |
| 1 | 1 | 1 | 1 | 250 | 320 | 250 | 320 | |
| 1 | 1 | 1 | 1 | 8.5 | 0.136 | 8.5 | 0.136 | |
| 3 | 90 | 7.86 | 90 | 7.86 | ||||
| 315 | 93 | 315 | 93 | |||||
| m | Error | Order | |
|---|---|---|---|
| 5 | — | ||
| 10 | |||
| 20 | |||
| 40 | 1/80 | ||
| 80 |
| N | Error | Order | |
|---|---|---|---|
| 5 | — | ||
| 10 | |||
| 20 | |||
| 40 | |||
| 80 | |||
| 160 | |||
| 320 |
| Gold | Chromium | |||
|---|---|---|---|---|
| DPL | ||||
| D1 | ||||
| D2 | ||||
| D3 | ||||
| D4 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coronel, A.; Hess, I.; Huancas, F.; Chiroque, J. Numerical Solution of Mathematical Model of Heat Conduction in Multi-Layered Nanoscale Solids. Axioms 2025, 14, 105. https://doi.org/10.3390/axioms14020105
Coronel A, Hess I, Huancas F, Chiroque J. Numerical Solution of Mathematical Model of Heat Conduction in Multi-Layered Nanoscale Solids. Axioms. 2025; 14(2):105. https://doi.org/10.3390/axioms14020105
Chicago/Turabian StyleCoronel, Aníbal, Ian Hess, Fernando Huancas, and José Chiroque. 2025. "Numerical Solution of Mathematical Model of Heat Conduction in Multi-Layered Nanoscale Solids" Axioms 14, no. 2: 105. https://doi.org/10.3390/axioms14020105
APA StyleCoronel, A., Hess, I., Huancas, F., & Chiroque, J. (2025). Numerical Solution of Mathematical Model of Heat Conduction in Multi-Layered Nanoscale Solids. Axioms, 14(2), 105. https://doi.org/10.3390/axioms14020105






