Parallel Primal-Dual Method with Linearization for Structured Convex Optimization

Abstract

This paper presents the Parallel Primal-Dual (PPD3) algorithm, an innovative approach to solving optimization problems characterized by the minimization of the sum of three convex functions, including a Lipschitz continuous term. The proposed algorithm operates in a parallel framework, simultaneously updating primal and dual variables, and offers potential computational advantages. This parallelization can greatly accelerate computation, particularly when run on parallel computing platforms. By departing from traditional primal-dual methods that necessitate strict parameter constraints, the PPD3 algorithm removes reliance on the spectral norm of the linear operator, significantly reducing the computational burden associated with its evaluation. As the problem size grows, calculating the spectral norm, which is essential for many primal-dual methods, becomes progressively more expensive. In addition, adaptive step sizes are computed to accelerate the convergence process. In contrast to most primal-dual approaches that employ a fixed step size constrained by a global upper limit throughout all iterations, the adaptive step size is typically greater and may result in faster convergence. An O(1/k) ergodic convergence rate is proved theoretically. Applications in Fused LASSO and image inpainting demonstrate the method’s efficiency in computation time and convergence rate compared to state-of-the-art algorithms.

1. Introduction

In this paper, we focus on the structured nonlinear optimization problem below:

$$\begin{array}{c}\hfill \underset{x\in X}{min}f\left(x\right)+g\left(x\right)+h\left(Ax\right).\end{array}$$

(1)

Let $A\in {\mathbb{R}}^{m\times n}$, and let $X\subset {\mathbb{R}}^n$ and $Y\subset {\mathbb{R}}^m$ be closed convex sets. Consider three proper lower semi-continuous convex functions f, g, and h; the function f is differentiable, and its gradient is $\beta$-Lipschitz continuous, meaning that for all $x,y\in X$, we have

$$\parallel \nabla f\left(x\right)-\nabla f\left(y\right)\parallel \le {\beta \parallel x-y\parallel }^2.$$

This condition implies that the difference in function values of f at any two points in X is bounded by a constant $\beta$ times the Euclidean distance between those points.

It is crucial to understand that this original primal optimization problem embodies a primal-dual representation as follows:

$$\begin{array}{c}\hfill \underset{x\in X}{min}\underset{y\in Y}{max}f\left(x\right)+g\left(x\right)+y^{T}Ax-h^{\ast }\left(y\right),\end{array}$$

(2)

where $h^{\ast }$ denotes the conjugate of a convex function h, defined as

$$h^{\ast }\left(y\right)=\underset{x\in \mathrm{dom}\left(h\right)}{sup}\left(y^{T}x-h\left(x\right)\right).$$

The formulation in (1) encompasses a broad spectrum of applications, such as image restoration, machine and statistical learning, compressive sensing, and portfolio optimization. Several illustrative examples are provided below:

Elastic net [1]: The elastic net method incorporates both $l_1$ and $l_2$ regularization terms, leveraging the advantages of each. The elastic net estimator is defined as the solution to the following optimization problem:

$$\begin{array}{c}\hfill \underset{x\in X}{min}{\mu }_1{\parallel x\parallel }_1+{\mu }_2{\parallel x\parallel }_2^2+\ell (Ax-b),\end{array}$$

(3)

where $x\in {\mathbb{R}}^p$, $A\in {\mathbb{R}}^{n\times p}$, $b\in {\mathbb{R}}^n$, and ℓ is a loss function. The second term possesses a gradient that is Lipschitz continuous. When ${\mu }_2=0$, the elastic net reduces to LASSO regression. Conversely, when ${\mu }_1=0$, the elastic net simplifies to ridge regression.

Matrix completion [2]: Consider a matrix $Y\in {\mathbb{R}}^{m\times n}$ with entries confined to the interval $[l,u]$, where $l<u$ are positive real constants. The task is to recover a low-rank matrix, X, from the observed elements of Y. Let $\Omega$ be the set of $Y^{\prime }s$ non-zero elements, and let $P_{\Omega }$ be a linear operator that extracts the available entries of Y, leaving the missing entries as zeros. The problem, as defined in [2], is formulated as the following optimization problem:

$$\begin{array}{cc}\hfill \underset{X\in {\Re }^{m\times n}}{min}& {\mu \parallel X\parallel }_{\ast }+{\displaystyle \frac{1}{2}}{\parallel P_{\Omega }(X-Y)\parallel }_2^2\\ \hfill \mathrm{s}.\mathrm{t}.& l\le X\le u\end{array}$$

where $\mu >0$ is a regularization constant, and ${\parallel ·\parallel }_{\ast }$ denotes the nuclear norm. By applying the Lagrange multiplier method, the aforementioned optimization task can be restated in the form presented in (2).

Support vector machine classification [3]: The constrained quadratic optimization problem in ${\mathbb{R}}^d$ can likewise be reformulated as presented in (2).

$$\begin{array}{cc}\hfill \underset{x\in {\Re }^d}{min}& {\displaystyle \frac{1}{2}}{\parallel x\parallel }_Q^2+c^{T}x\\ \hfill \mathrm{s}.\mathrm{t}.& x\in C_1\cap C_2\end{array}$$

In the dual representation of the soft-margin kernelized support vector machine classifier, we encounter a situation involving a symmetric positive semi-definite matrix $Q\in {\mathbb{R}}^{d\times d}$, a vector $c\in {\mathbb{R}}^d$, and two sets of constraints, $C_1$ and $C_2$, within ${\mathbb{R}}^d$. In particular, $C_1$ represents a bounding constraint, and $C_2$ refers to a linear constraint.

Before introducing algorithms to solve (2), we begin by reviewing several established techniques for general saddle-point problems, particularly the case of (2), where f is not present. Three key splitting methods are typically used:

• The forward-backward-forward splitting method [4];
• The forward-backward splitting method [5];
• The Douglas-Rachford splitting method [6].

In recent years, several primal-dual splitting algorithms have emerged, grounded in three primary foundational techniques. The primal-dual hybrid gradient (PDHG) method, first introduced in [7], demonstrates significant numerical efficiency when applied to total variation (TV) minimization tasks. However, its convergence is highly sensitive to the choice of parameters. To mitigate this issue, Chambolle and Pock introduced the CP method in [8], which enhances the PDHG approach by adjusting the update rule for the dual variables. This adjustment improves both convergence rates and numerical efficiency. In [9], He and Yuan performed an extensive investigation of the CP approach, offering a comprehensive analysis via the Proximal Point Algorithm (PPA) and introducing a relaxation parameter within the PPA framework to expedite convergence (the HeYuan method). More recently, Goldstein et al. introduced the Adaptive Primal-Dual Splitting (APD) method in [10], which dynamically modifies the step-size parameters of the CP approach. In [11], O’Connor and Vandenberghe presented a primal-dual decomposition strategy based on Douglas-Rachford splitting, which is utilized for various primal-dual optimality condition decompositions. Additionally, the adaptive parallel primal-dual (APPD) method presented in [12] is an enhanced version of the primal-dual approach, designed with parallel computing capabilities to optimize performance.

A comprehensive framework outlining various well-known primal-dual methods tackles the saddle-point problem by following these steps:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}^{k+1}=\arg \underset{x\in X}{min}\{g\left(x\right)+x^T{A}^T{y}^k+{\displaystyle \frac{1}{2\tau }}\parallel x-x^k{\parallel }^2\},\hfill \\ \\ {\overline{x}}^k=x^{k+1}+\theta (x^{k+1}-x^k),\hfill \\ \\ y^{k+1}=\arg \underset{y\in Y}{min}\{h^{\ast }\left(y\right)-y^{T}A{\overline{x}}^k+{\displaystyle \frac{1}{2\sigma }}\parallel y-y^k{\parallel }^2\},\hfill \end{array}\right.\end{array}$$

(4)

As summarized in

Table 1. Comparison of algorithms with respect to $\theta$.

Algorithm	$\mathit{\theta }$	Correction Step Required
PDHG/Arrow-Hurwicz	0	No
CP	1	No
HeYuan	$[-1,1]$	Yes
APPD	$-1$	Yes

, different values of $\theta$ correspond to distinct methods under the framework described in Section 4. It is noteworthy that a straightforward correction step is necessary for both the HeYuan method and the APPD method.

In the context of (2), Condat and Vu proposed a primal-dual splitting framework, the CV scheme, in their studies [13,14]. This approach, based on forward-backward iteration, extends the Chambolle-Pock algorithm (CP) by linearizing the function f, though it operates with a narrower parameter range than CP. Later, the Asymmetric Forward-Backward-Adjoint (AFBA) splitting method, introduced in [15], generalizes the CV scheme. Additionally, the Primal-Dual Fixed-Point (PDFP) algorithm, proposed in [16], incorporates two proximal operations of g in each iteration. Other notable methods for solving (2) include the Primal-Dual Three-Operator splitting method (PD3O) from [17] and DavisYin’s three-operator splitting technique, known as PDDY, introduced in [18]. More recently, a modified primal-dual algorithm (MPD3O) was studied in [19], which combines the idea of the balanced augmented Lagrangian method (BALM) in [20] and PD3O. The parameter conditions are relaxed in [21] for the AFBA/PDDY method.

A similar overarching framework exists for algorithms addressing (2), analogous to the one in (4):

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}^{k+1}=\arg \underset{x\in X}{min}\{g\left(x\right)+x^T{A}^T{y}^k+{\displaystyle \frac{1}{2\tau }}\parallel x-x^k{\parallel }^2+x^T\nabla f\left(x^k\right)\},\hfill \\ \\ {\overline{x}}^k={\overline{x}}_{(x^k,x^{k+1})}^k,\hfill \\ \\ y^{k+1}=\arg \underset{y\in Y}{min}\{h^{\ast }\left(y\right)-y^{T}A{\overline{x}}^k+{\displaystyle \frac{1}{2\sigma }}\parallel y-y^k{\parallel }^2\}.\hfill \end{array}\right.\end{array}$$

(5)

The corresponding parameter restrictions for these methods are provided in

Table 2. Comparison of algorithms with respect to primal variable upgrade.

Algorithm	Primal Variable Upgrade
CV	${\overline{x}}^k=2x^{k+1}-x^k$
PDFP	${\overline{x}}^k={\mathrm{prox}}_{\tau g}(x^{k+1}-\tau \nabla f\left(x^{k+1}\right)-\tau A^{\top }{y}^k)$
PD3O	${\overline{x}}^k=2x^{k+1}-x^k+\tau \nabla f\left(x^k\right)-\tau \nabla f\left(x^{k+1}\right)$
AFBA/PDDY	$x^{k+1}={\overline{x}}^{k-1}-\tau A^{\top }(y^k-y^{k-1})$; ${\overline{x}}^{k+1}={\mathrm{prox}}_{\tau g}(x^{k+1}-\tau \nabla f\left(x^{k+1}\right)-\tau A^{\top }{y}^k)$

. The relationship between the aforementioned methods and the framework described in (5) is detailed in

Table 3. Comparison of algorithms with respect to parameter restrictions.

Algorithm	Parameter Restrictions
CV	$\tau \beta /2+\tau \sigma \parallel A^{T}A\parallel \le 1$
PDFP	$\tau \le {\displaystyle \frac{2}{\beta }},\tau \sigma \le {\displaystyle \frac{1}{\parallel A^{T}A\parallel }}$
PD3O	$\tau \le {\displaystyle \frac{2}{\beta }},\tau \sigma \le {\displaystyle \frac{1}{\parallel A^{T}A\parallel }}$
AFBA/PDDY	$\tau \le {\displaystyle \frac{2}{\beta }},\tau \sigma \le {\displaystyle \frac{1}{\parallel A^{T}A\parallel }}$

.

In the Discussion section of Chambolle’s work [8], a prominent challenge for existing primal-dual methods is emphasized: the handling of a linear operator, A, with a potentially large or unknown norm. Numerous methods, including the PDHG method described in [7], the CP algorithm presented in [8], the HeYuan method from [9], the CV scheme introduced in [13,14], the PDFP method proposed in [16], and the PD3O method outlined in [17], all necessitate the satisfaction of the condition $\tau \sigma \le 1/\parallel A^{T}A\parallel$ for convergence. Consequently, the norm of A must be computed prior to initializing the parameters. However, as the dimensionality of A escalates, computing this norm becomes increasingly costly, thereby introducing a substantial computational burden.

To tackle the aforementioned challenge, we introduce the PPD3 algorithm, aimed at minimizing the sum of three functions, one of which includes a Lipschitz continuous term. The method we propose consists of two separate phases. In the first phase, a parallel version of (5), where $\overline{x}$ is replaced by $x^k$, functions as a prediction step to produce an intermediate estimate. Subsequently, in the subsequent phase, the step length ${\alpha }_k$ is determined, after which a simple adjustment is applied to the predictor, ensuring the convergence of the PPD3 algorithm.

The key contributions presented in this paper are outlined as follows:

• In contrast to other primal-dual methods, which usually update the primal and dual variables alternately, the proposed approach computes both variables simultaneously and in parallel. This parallelization can greatly accelerate computation, particularly when run on parallel computing platforms.
• The proposed algorithm is independent of any prior knowledge about the linear operator A. The constraint $\tau \sigma \le 1/\parallel A^{T}A\parallel$ on the parameters is no longer required. In fact, as the problem size grows, calculating the spectral norm of A, which is essential for many primal-dual methods, becomes progressively more expensive.
• The step size ${\alpha }_k$ is adjusted dynamically at each iteration. This method tailors the step size for each specific iteration, in contrast to most primal-dual approaches that employ a fixed step size constrained by a global upper limit throughout all iterations. As a result, the adaptive step size, which is typically greater, may result in faster convergence.

The organization of this paper is structured as follows: In Section 2, we introduce the proposed algorithm. Section 3 presents a comprehensive convergence analysis of the algorithm, while Section 4 delves into an examination of its computational complexity. Section 5 reports the performance of the algorithm through diverse applications, accompanied by corresponding numerical results. Lastly, Section 6 summarizes the key conclusions and outlines potential directions for future research endeavors.

2. The Parallel Primal-Dual Algorithm

To facilitate understanding, we combine the primal and dual parameters and introduce them as follows:

$$u=\left(\begin{array}{c}x\\ y\end{array}\right),\theta \left(u\right)=g\left(x\right)+h^{\ast }\left(y\right),F\left(u\right)=\left(\begin{array}{c}{A}^{T}y+\nabla f\left(x\right)\\ -Ax\end{array}\right),\Omega =X\times Y.$$

The subsequent symbols are employed as well:

$$Q(x^k,{\tilde{x}}^k)=\left(\begin{array}{c}{\tau }^{-1}(x^k-{\tilde{x}}^k)-A^T(y^k-{\tilde{y}}^k)-(\nabla f\left(x^k\right)-\nabla f\left({\tilde{x}}^k\right))\\ A(x^k-{\tilde{x}}^k)+{\sigma }^{-1}(y^k-{\tilde{y}}^k)\end{array}\right),$$

$$H=\left(\begin{array}{cc}{\tau }^{-1}{I}_n& 0\\ 0& {\sigma }^{-1}{I}_m\end{array}\right),G=\left(\begin{array}{cc}({\tau }^{-1}-\beta )I_n& 0\\ 0& {\sigma }^{-1}{I}_m\end{array}\right),$$

and

$$M(x^k,{\tilde{x}}^k)=\left(\begin{array}{c}(x^k-{\tilde{x}}^k)-\tau A^T(y^k-{\tilde{y}}^k)-\tau (\nabla f\left(x^k\right)-\nabla f\left({\tilde{x}}^k\right))\\ \sigma A(x^k-{\tilde{x}}^k)+(y^k-{\tilde{y}}^k)\end{array}\right),$$

where $\tau >\beta$ and $\sigma >0$ represent positive parameters. It is clear that

$$M(x^k,{\tilde{x}}^k)=H^{-1}Q(x^k,{\tilde{x}}^k).$$

The concurrent primal-dual approach is described in Algorithm 1.

The loop in Algorithm 1 follows a pattern similar to the CV approach, with one key difference: the prediction step (6) utilizes $x^k$ rather than $\overline{x}$, as seen in (5). The incorporation of $x^k$ provides a notable benefit: it eliminates the requirement for any updated data related to x in the y-subproblem, thus enabling the parallel processing of both the x- and y-subproblems.

Subsequently, the residuals $p_k$ and $d_k$ are calculated as termination conditions. Once both residuals tend toward zero, we will show (in the subsequent section) that $\parallel Q(x^k,{\tilde{x}}^k)\parallel$ also approaches zero. Consequently, (1) converges to

$${\tilde{u}}^k\in \Omega ,\theta \left(u\right)-\theta \left({\tilde{u}}^k\right)+{(u-{\tilde{u}}^k)}^{T}F\left({\tilde{u}}^k\right)\ge 0,\forall u\in \Omega .$$

By contrasting this variational inequality with (3), it is evident that ${\tilde{u}}^k$ meets the criteria of the initial problem (2). Consequently, the convergence of the primal-dual algorithm can be assessed by analyzing the residuals’ norms (see also [10,22,23]).

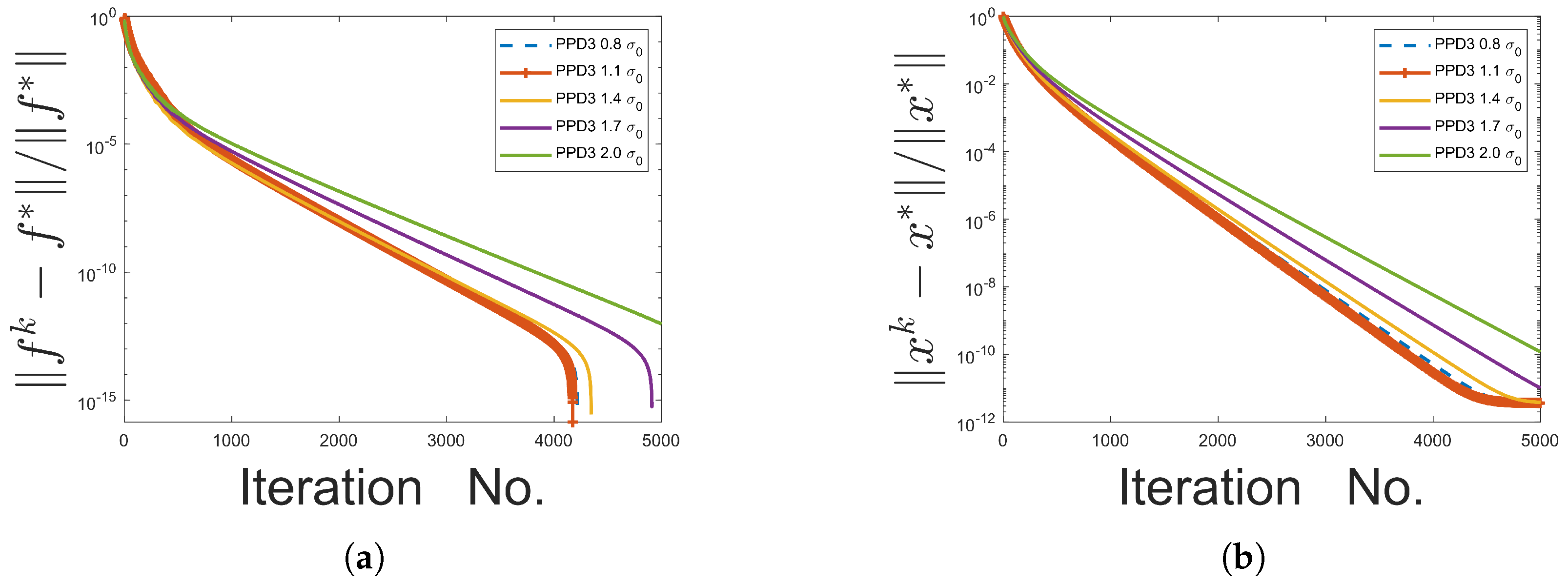
At each iteration, the step size ${\alpha }_k$ is computed, which addresses the challenge of setting a global upper bound for the step size across all iterations. In traditional primal-dual algorithms, this upper bound is usually constrained by the condition $\tau \sigma \le \parallel A^{T}A\parallel$. In contrast, our approach bypasses this limitation on the parameters $\tau$ and $\sigma$ by adaptively computing ${\alpha }_k$. Experimental observations indicate that, in certain cases, the step size in our method exceeds the upper bound $\parallel A^{T}A\parallel$, which has been found to accelerate the convergence process.

Ultimately, a straightforward adjustment procedure guarantees the algorithm’s convergence.

Algorithm 1: Parallel Primal-Dual Algorithm

Initialize $\tau <1/\beta$, $\sigma >0$, $x^0\in X$, $y^0\in Y$ While $p_k$, $d_k$> tolerance do Prediction $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\tilde{x}}^k=arg\underset{x\in X}{min}\left\{g\left(x\right)+x^T{A}^T{y}^k+{\displaystyle \frac{1}{2\tau }}{\parallel x-x^k\parallel }^2+x^T\nabla f\left(x^k\right)\right\},\hfill \\ {\tilde{y}}^k=arg\underset{y\in Y}{min}\left\{h^{\ast }\left(y\right)-y^{T}A{x}^k+{\displaystyle \frac{1}{2\sigma }}{\parallel y-y^k\parallel }^2\right\}.\hfill \end{array}\right.\end{array}$$ (6) Compute residual norms $$\begin{array}{c}\hfill \left\{\begin{array}{c}{p}_k=\parallel {\tau }^{-1}(x^k-{\tilde{x}}^k)-A^T(y^k-{\tilde{y}}^k)-(\nabla f\left(x^k\right)-\nabla f\left({\tilde{x}}^k\right))\parallel ,\hfill \\ d_k=\parallel {\sigma }^{-1}(y^k-{\tilde{y}}^k)+A(x^k-{\tilde{x}}^k)\parallel .\hfill \end{array}\right.\end{array}$$ (7) Calculate step-size $${\alpha }_k={\displaystyle \frac{{\tau }^{-1}\parallel x^k-{\tilde{x}}^k{\parallel }^2+{\sigma }^{-1}{\parallel y^k-{\tilde{y}}^k\parallel }^2-{(x^k-{\tilde{x}}^k)}^T(\nabla f\left(x^k\right)-\nabla f\left({\tilde{x}}^k\right))}{\tau p_k^2+\sigma d_k^2}}.$$ Correction $$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}^{k+1}=x^k-{\alpha }_k\left(x^k-{\tilde{x}}^k-\tau A^T(y^k-{\tilde{y}}^k)-\tau (\nabla f\left(x^k\right)-\nabla f\left({\tilde{x}}^k\right))\right),\hfill \\ y^{k+1}=y^k-{\alpha }_k\left(y^k-{\tilde{y}}^k+\sigma A(x^k-{\tilde{x}}^k)\right).\hfill \end{array}\right.\end{array}$$ (8) End while

The prediction stage in (6) is a special case of (5), where ${\overline{x}}^k=x^k$. Unlike other algorithms, such as the CV method, where ${\overline{x}}^k=2x^{k+1}-x^k$, our method uses the previous iterate $x^k$ as ${\overline{x}}^k$. When $f=0$, the prediction stage in (6) coincides with (4) when $\theta =-1$.

Note that our algorithm does not require the condition $\tau \sigma \le \parallel A^{T}A\parallel$ for theoretical analysis, and thus, no such constraint is necessary.

3. Convergence Analysis

We begin by providing the following reformulation of the variational inequality (VI) corresponding to (2):

Find $u^{\ast }=(x^{\ast },y^{\ast })$ such that

$$\mathrm{VI}(\Omega ,F,\theta ):u^{\ast }\in \Omega ,\theta \left(u\right)-\theta \left(u^{\ast }\right)+{(u-u^{\ast })}^{T}F\left(u^{\ast }\right)\ge 0,\forall u\in \Omega =X\times Y,$$

The mapping $F\left(u\right)$ is composed of the sum of an affine skew-symmetric matrix and a monotone operator, which ensures that $F\left(u\right)$ itself is monotone. Let ${\Omega }^{\ast }$ represent the solution set to the variational inequality VI($\Omega$, F, $\theta$); we assume that this solution set is non-empty.

Lemma 1.

For a given $u^k=\left(\begin{array}{c}{x}^k\\ y^k\end{array}\right)$, let ${\tilde{u}}^k$ be given by the expression in (6). Then,

$${\tilde{u}}^k\in \Omega ,\theta \left(u\right)-\theta \left({\tilde{u}}^k\right)+{(u-{\tilde{u}}^k)}^{T}F\left({\tilde{u}}^k\right)\ge {(u-{\tilde{u}}^k)}^{T}Q(u^k,{\tilde{u}}^k)\mathit{for}\mathit{all}u\in \Omega ,$$

Proof of Lemma 1.

By applying the optimality condition from (6), we derive

$$g\left(x\right)-g\left({\tilde{x}}^k\right)+{(x-{\tilde{x}}^k)}^T\{A^T{y}^k+{\tau }^{-1}({\tilde{x}}^k-x^k)+\nabla f\left(x^k\right)\}\ge 0,\forall x\in X,$$

and

$$h^{\ast }\left(y\right)-h^{\ast }\left({\tilde{y}}^k\right)+{(y-{\tilde{y}}^k)}^T\{-A{x}^k+{\sigma }^{-1}({\tilde{y}}^k-y^k)\}\ge 0,\forall y\in Y.$$

By combining the two inequalities above, it follows that ${\tilde{u}}^k=({\tilde{x}}^k,{\tilde{y}}^k)\in \Omega$, and

$$\begin{array}{cc}\hfill & \left[g\left(x\right)-g\left({\tilde{x}}^k\right)+h^{\ast }\left(y\right)-h^{\ast }\left({\tilde{y}}^k\right)\right]+{\left(\begin{array}{c}x-{\tilde{x}}^k\\ y-{\tilde{y}}^k\end{array}\right)}^T\hfill \\ \hfill & \left\{\left(\begin{array}{c}{A}^T{\tilde{y}}^k\\ -A{\tilde{x}}^k\end{array}\right)+\left(\begin{array}{cc}{\tau }^{-1}I& A^T\\ -A& {\sigma }^{-1}I\end{array}\right)\left(\begin{array}{c}{\tilde{x}}^k-x^k\\ {\tilde{y}}^k-y^k\end{array}\right)\right.\left.+\left(\begin{array}{c}\nabla f\left(x^k\right)-\nabla f\left({\tilde{x}}^k\right)\\ 0\end{array}\right)\right\}\ge 0,\hfill \end{array}$$

(9)

For every $u\in \Omega$, the assertion is established through the notation introduced in the preceding section. □

Lemma 2.

For a given $u^k=\left(\begin{array}{c}{x}^k\\ y^k\end{array}\right)$, let ${\tilde{u}}^k$ be defined by (6), then ${\tilde{u}}^k\in \Omega ,$

$$\begin{array}{cc}\hfill & {\alpha }_k(\theta \left(u\right)-\theta \left({\tilde{u}}^k\right)+{(u-{\tilde{u}}^k)}^{T}F\left({\tilde{u}}^k\right))\hfill \\ \hfill & \ge {\displaystyle \frac{1}{2}}\parallel u-u^{k+1}{\parallel }_H^2-{\displaystyle \frac{1}{2}}\parallel u-u^k{\parallel }_H^2+{\displaystyle \frac{{\alpha }_k}{2}}{\parallel u-{\tilde{u}}^k\parallel }_G^2\mathit{for}\mathit{all}u\in \Omega ,\hfill \end{array}$$

where ${\parallel ·\parallel }_H$,${\parallel ·\parallel }_G$ are semi-norm, defined as ${\parallel x\parallel }_H=x^{T}Hx$.

Proof of Lemma 2.

Step 5 and 6 in Algorithm 1 are equivalent to

$${\alpha }_k={(u^k-{\tilde{u}}^k)}^{T}Q(u^k,{\tilde{u}}^k)/{\parallel M(u^k,{\tilde{u}}^k)\parallel }_H^2\mathrm{and}$$

(10)

$$\begin{array}{c}\hfill u^{k+1}=u^k-{\alpha }_{k}M(u^k,{\tilde{u}}^k).\end{array}$$

(11)

By utilizing $Q(u^k,{\tilde{u}}^k)=HM(u^k,{\tilde{u}}^k)$ and the relation in (11), the right-hand side of (1) simplifies to ${(u-{\tilde{u}}^k)}^{T}H(u^k-u^{k+1})$, and therefore

$$\begin{array}{cc}\hfill & {\alpha }_k(\theta \left(u\right)-\theta \left({\tilde{u}}^k\right)+{(u-{\tilde{u}}^k)}^{T}F\left({\tilde{u}}^k\right))\hfill \\ \hfill & \ge {(u-{\tilde{u}}^k)}^{T}H(u^k-u^{k+1})\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\parallel u-u^{k+1}{\parallel }_H^2-{\displaystyle \frac{1}{2}}\parallel u-u^k{\parallel }_H^2+{\displaystyle \frac{1}{2}}\parallel u-{\tilde{u}}^k{\parallel }_H^2-{\displaystyle \frac{1}{2}}{\parallel u-{\tilde{u}}^{k+1}\parallel }_H^2\hfill \end{array}$$

For the last two terms, we have

$$\begin{array}{cc}& {\displaystyle \frac{1}{2}}\parallel u-{\tilde{u}}^k{\parallel }_H^2-{\displaystyle \frac{1}{2}}{\parallel u-{\tilde{u}}^{k+1}\parallel }_H^2\\ & ={\displaystyle \frac{1}{2}}[2{\alpha }_k{(u^k-{\tilde{u}}^k)}^{T}HM(u^k,{\tilde{u}}^k)-{\alpha }_k^2\parallel M(u^k,{\tilde{u}}^k){\parallel }_H^2]\\ & ={\displaystyle \frac{{\alpha }_k}{2}}{(u^k-{\tilde{u}}^k)}^{T}HM(u^k,{\tilde{u}}^k)\\ & ={\displaystyle \frac{{\alpha }_k}{2}}{\left(\begin{array}{c}x-{\tilde{x}}^k\\ y-{\tilde{y}}^k\end{array}\right)}^T\left[\left(\begin{array}{cc}{\tau }^{-1}I& A^T\\ -A& {\sigma }^{-1}I\end{array}\right)\left(\begin{array}{c}{x}^k-{\tilde{x}}^k\\ y^k-{\tilde{y}}^k\end{array}\right)+\left(\begin{array}{c}\nabla f\left(x^k\right)-\nabla f\left({\tilde{x}}^k\right)\\ 0\end{array}\right)\right]\\ & \ge {\displaystyle \frac{{\alpha }_k}{2}}\left({\tau }^{-1}\parallel x^k-{\tilde{x}}^k{\parallel }^2+{\sigma }^{-1}\parallel y^k-{\tilde{y}}^k{\parallel }^2-\beta {\parallel x^k-{\tilde{x}}^k\parallel }^2\right)\\ & ={\displaystyle \frac{{\alpha }_k}{2}}{\parallel u-{\tilde{u}}^k\parallel }_G^2,\end{array}$$

The proof of the assertion is, thus, complete. □

Lemma 3.

For a given $u^k=\left(\begin{array}{c}{x}^k\\ y^k\end{array}\right)$, let ${\tilde{u}}^k$ and $u^{k+1}$ be defined by (6) and (8), respectively. If ${\tau }^{-1}{\sigma }^{-1}\ge c{\parallel A\parallel }_2^2$, then there exists a positive constant ${\alpha }^{+}$ such that ${\alpha }^{+}\le {\alpha }_k$ for all $k>0$, and the following inequality is satisfied:

$$\begin{array}{c}\hfill \parallel u^{k+1}-u^{\ast }{\parallel }_H^2\le \parallel u^k-u^{\ast }{\parallel }_H^2-{\alpha }^{+}{\parallel u^k-{\tilde{u}}^k\parallel }_G^2,\forall u^{\ast }\in {\Omega }^{\ast }.\end{array}$$

(12)

Proof of Lemma 3.

By substituting $u=u^{\ast }$ into (10), we derive

$$\begin{array}{cc}\hfill & {\alpha }_k\left(\theta \left(u^{\ast }\right)-\theta \left({\tilde{u}}^k\right)+{(u^{\ast }-{\tilde{u}}^k)}^{T}F\left({\tilde{u}}^k\right)\right)\hfill \\ \hfill & \ge {\displaystyle \frac{1}{2}}\parallel u^{\ast }-u^{k+1}{\parallel }_H^2-{\displaystyle \frac{1}{2}}\parallel u^{\ast }-u^k{\parallel }_H^2+{\displaystyle \frac{{\alpha }_k}{2}}{\parallel u-{\tilde{u}}^k\parallel }_G^2,\forall u\in \Omega .\hfill \end{array}$$

(13)

Since

$${({\tilde{u}}^k-u^{\ast })}^{T}F\left({\tilde{u}}^k\right)\ge {({\tilde{u}}^k-u^{\ast })}^{T}F\left(u^{\ast }\right)$$

and

$$\theta \left({\tilde{u}}^k\right)-\theta \left(u^{\ast }\right)+{({\tilde{u}}^k-u^{\ast })}^{T}F\left(u^{\ast }\right)\ge 0,$$

these inequalities can be combined to yield:

$$\parallel u^{k+1}-u^{\ast }{\parallel }_H^2\le \parallel u^k-u^{\ast }{\parallel }_H^2-{\alpha }_k{\parallel u^k-{\tilde{u}}^k\parallel }_G^2,\forall u^{\ast }\in {\Omega }^{\ast }.$$

Next, let us recall the definition of ${\alpha }_k$:

$${\alpha }_k={\displaystyle \frac{{(u^k-{\tilde{u}}^k)}^{T}Q(u^k,{\tilde{u}}^k)}{\parallel M(u^k,{\tilde{u}}^k){\parallel }_H^2}}.$$

(14)

We proceed to compute the term ${(u^k-{\tilde{u}}^k)}^{T}Q(u^k,{\tilde{u}}^k)$:

$$\begin{array}{cc}\hfill {(u^k-{\tilde{u}}^k)}^{T}Q(u^k,{\tilde{u}}^k)& ={\left(\begin{array}{c}x-{\tilde{x}}^k\\ y-{\tilde{y}}^k\end{array}\right)}^T\left[\left(\begin{array}{cc}{\tau }^{-1}I& A^T\\ -A& {\sigma }^{-1}I\end{array}\right)\left(\begin{array}{c}{x}^k-{\tilde{x}}^k\\ y^k-{\tilde{y}}^k\end{array}\right)\right.\\ & \left.+\left(\begin{array}{c}\nabla f\left(x^k\right)-\nabla f\left({\tilde{x}}^k\right)\\ 0\end{array}\right)\right]\\ & \ge \left({\tau }^{-1}\parallel x^k-{\tilde{x}}^k{\parallel }^2+{\sigma }^{-1}\parallel y^k-{\tilde{y}}^k{\parallel }^2-\beta {\parallel x^k-{\tilde{x}}^k\parallel }^2\right)\\ & =(1-\tau \beta )\parallel u-{\tilde{u}}^k{\parallel }_H^2.\end{array}$$

Next, we examine the term $\parallel M(u^k,{\tilde{u}}^k){\parallel }_H^2$:

$$\begin{array}{cc}\hfill \parallel M(u^k,{\tilde{u}}^k){\parallel }_H^2& ={∥\left(\begin{array}{cc}I& \tau A^T\\ -\sigma A& I\end{array}\right)(u^k-{\tilde{u}}^k)+\tau \left(\begin{array}{c}\nabla f\left(x^k\right)-\nabla f\left({\tilde{x}}^k\right)\\ 0\end{array}\right)∥}_H^2\\ & \le 2{∥\left(\begin{array}{cc}I& \tau A^T\\ -\sigma A& I\end{array}\right)(u^k-{\tilde{u}}^k)∥}_H^2+2{\tau }^2{∥\left(\begin{array}{c}\nabla f\left(x^k\right)-\nabla f\left({\tilde{x}}^k\right)\\ 0\end{array}\right)∥}_H^2\\ & \le 2∥\left(\begin{array}{cc}I& \tau A^T\\ -\sigma A& I\end{array}\right)∥\parallel u^k-{\tilde{u}}^k{\parallel }_H^2+2{\tau }^2{\beta }^2{\parallel u^k-{\tilde{u}}^k\parallel }_H^2.\end{array}$$

(15)

Therefore, ${\alpha }_k$ is bounded below by a positive constant ${\alpha }^{+}$, and the conclusion follows directly. □

Theorem 1.

Given the sequence $u^k=(x^k,y^k)$, let ${\tilde{u}}^k$ and $u^{k+1}$ be defined by Equations (6) and (8), respectively. It follows that the sequence $\left\{u^k\right\}$ converges to a limit point $u^{\infty }\in {\Omega }^{\ast }$.

Proof of Theorem 1.

From Equation (12), it follows that the sequence $\left\{u^k\right\}$ is bounded, and consequently, we obtain

$$\underset{k\to \infty }{lim}\parallel u^k-{\tilde{u}}^k\parallel =0.$$

(16)

Thus, the sequence $\left\{{\tilde{u}}^k\right\}$ is also bounded. Let $u^{\infty }$ denote a cluster point of $\left\{{\tilde{u}}^k\right\}$, and assume that $\left\{{\tilde{u}}^{k_j}\right\}$ is a subsequence of $\left\{{\tilde{u}}^k\right\}$ that converges to $u^{\infty }$. Furthermore, let $\left\{u^k\right\}$ and $\left\{u^{k_j}\right\}$ represent the corresponding subsequences induced by $\left\{{\tilde{u}}^k\right\}$ and $\left\{{\tilde{u}}^{k_j}\right\}$, respectively. From Equation (1), it follows that

$${\tilde{u}}^{k_j}\in \Omega ,\theta \left(u\right)-\theta \left({\tilde{u}}^{k_j}\right)+{(u-{\tilde{u}}^{k_j})}^{T}F\left({\tilde{u}}^{k_j}\right)\ge {(u-u^{k_j})}^{T}Q(u^{k_j}-{\tilde{u}}^{k_j}),\forall u\in \Omega .$$

By utilizing the continuity of $\theta \left(u\right)$ and $F\left(u\right)$, we derive

$$w^{\infty }\in \Omega ,\theta \left(u\right)-\theta \left(u^{\infty }\right)+{(u-w^{\infty })}^{T}F\left(u^{\infty }\right)\ge 0,\forall w\in \Omega .$$

This variational inequality implies that $u^{\infty }$ satisfies the variational inequality VI($\Omega ,F$).

By applying Equation (16) and using the fact that ${lim}_{j\to \infty }{\tilde{u}}^{k_j}=u^{\infty }$, it follows that the subsequence $\left\{u^{k_j}\right\}$ converges to $u^{\infty }$. Moreover, from Equation (12), we obtain

$$\parallel u^{k+1}-u^{\infty }{\parallel }_H\le {\parallel u^k-u^{\infty }\parallel }_H,$$

This result demonstrates that the sequence $\left\{u^k\right\}$ approaches $u^{\infty }$, thus finalizing the proof. □

4. Computational Complexity

Lemma 4.

The solution set of the variational inequality VI$(\Omega ,F,\theta )$ is convex and can be described as

$${\Omega }^{\ast }=\bigcap _{u\in \Omega }\left\{\tilde{u}\in \Omega :\left(\theta \left(u\right)-\theta \left(\tilde{u}\right)\right)+{(u-\tilde{u})}^{T}F\left(u\right)\ge 0\right\}.$$

Proof of Lemma 4.

The proof can be derived as a natural extension of Theorem 2.3.5 in [24], or alternatively, one may consult the proof of Theorem 2.1 in [25] for a related approach. □

Lemma 4 demonstrates that $\tilde{u}\in \Omega$ constitutes an approximate solution to the variational inequality VI$(\Omega ,F,\theta )$, with an accuracy of $ϵ>0$, provided that it satisfies

$$\begin{array}{c}\hfill \theta \left(u\right)-\theta \left(\tilde{u}\right)+{(u-\tilde{u})}^{T}F\left(u\right)\ge -ϵ,\forall u\in \Omega \cap \mathcal{D}\left(\tilde{u}\right),\end{array}$$

(17)

where $\mathcal{D}\left(\tilde{u}\right)=\{u\mid \parallel u-\tilde{u}\parallel \le 1\}$ represents the neighborhood of $\tilde{u}$.

Theorem 2.

Algorithm 1 demonstrates convergence with an ergodic rate of $O(1/t)$. Specifically, let $\left\{u^k\right\}$ represent the sequence generated by Algorithm 1, starting from an arbitrary initial point $u^0$. For the sequence $\left\{{\overline{u}}^t\right\}$ defined by

$$\begin{array}{c}\hfill {\overline{u}}^t={\displaystyle \frac{1}{{\sum }_{k=0}^{t-1}{\alpha }_k}}\sum _{k=0}^{t-1}{\alpha }_k{\tilde{u}}^k,\end{array}$$

(18)

the subsequent convergence bound holds:

$$\begin{array}{c}\hfill \theta \left(u\right)-\theta \left({\overline{u}}^t\right)+{(u-{\overline{u}}^t)}^{T}F\left(u\right)\ge -{\displaystyle \frac{1}{2t{\alpha }^{+}}}{\parallel u-u^0\parallel }_H^2.\end{array}$$

(19)

Proof of Theorem 2.

By leveraging the monotonicity of F, we obtain

$$\begin{array}{c}\hfill \theta \left(u\right)-\theta \left({\tilde{u}}^k\right)+{(u-{\tilde{u}}^k)}^{T}F\left(u\right)\ge \theta \left(u\right)-\theta \left({\tilde{u}}^k\right)+(u-{\tilde{u}}^k)F\left(\tilde{u}\right).\end{array}$$

(20)

By substituting this into (12), we derive

$${\alpha }_k\left[\theta \left(u\right)-\theta \left({\tilde{u}}^k\right)+{(u-{\tilde{u}}^k)}^{T}F\left(u\right)\right]\ge {\displaystyle \frac{1}{2}}\parallel u-u^{k+1}{\parallel }_H^2-{\displaystyle \frac{1}{2}}{\parallel u-u^k\parallel }_H^2\forall u\in \Omega .$$

(21)

It is important to highlight that the above assertion holds when $G>0$.

By summing the inequality in (21) over $k=0,1,\cdots ,t-1$, we obtain

$$\begin{array}{c}\hfill \sum _{k=0}^{t-1}\left\{{\alpha }_k\left[\theta \left(u\right)-\theta \left({\tilde{u}}^k\right)+{(u-{\tilde{u}}^k)}^{T}F\left(u\right)\right]\right\}\ge -{\displaystyle \frac{1}{2}}{\parallel u-u^0\parallel }_H^2.\end{array}$$

(22)

By applying the definition of ${\overline{u}}^t$, this can be expressed as

$$\begin{array}{c}\hfill \left(\sum _{k=0}^{t-1}{\alpha }_k\right)\theta \left(u\right)-\sum _{k=0}^{t-1}{\alpha }_k\theta \left({\tilde{u}}^k\right)+\left(\sum _{k=0}^{t-1}{\alpha }_k\right){(u-{\overline{u}}^t)}^{T}F\left(u\right)\ge -{\displaystyle \frac{1}{2}}{\parallel u-u^0\parallel }_H^2.\end{array}$$

(23)

Given that $\theta \left(u\right)$ is convex, it follows that

$$\left(\sum _{k=0}^{t-1}{\alpha }_k\right)\theta \left({\tilde{u}}^t\right)\le \sum _{k=0}^{t-1}\left[{\alpha }_k\theta \left({\tilde{u}}^k\right)\right].$$

Substituting this into the preceding inequality yields

$$\begin{array}{c}\hfill \theta \left(u\right)-\theta \left({\overline{u}}^t\right)+{(u-{\overline{u}}^t)}^{T}F\left(u\right)\ge -{\displaystyle \frac{1}{2{\sum }_{k=0}^{t-1}{\alpha }_k}}\parallel u-u^0{\parallel }_H^2\ge -{\displaystyle \frac{1}{2t{\alpha }^{+}}}{\parallel u-u^0\parallel }_H^2.\end{array}$$

(24)

Therefore, the result has been established. □

5. Numerical Experiments

Algorithm 1 was applied to the Fused LASSO and image inpainting problem to show its numerical performance. We compare our method with Condat and Vu’s primal-dual splitting scheme (CV), Yan’s primal-dual three-operator splitting scheme (PD3O), and the Asymmetric Forward-Backward-Adjoint method (AFBA)/Davis and Yin’s three-operator splitting method (PDDY). All codes were written and implemented in Matlab $2024a$, and all experiments were carried out on a computer with a $1.20$ GHz Intel Core Ultra 5 125H processor and 32 GB of memory.

5.1. Fused LASSO

The formulation of Fused LASSO involves the following optimization problem:

$$\widehat{x}=argmin\left\{\sum _i{\left(b_i-\sum _j{a}_{ij}{x}_j\right)}^2\right\}$$

$$s.t.\sum _{j=1}^p|x_j|\le {\mu }_1\mathrm{and}\sum _{j=2}^p|x_j-x_{j-1}|\le {\mu }_2,$$

where ${\mu }_1$ and ${\mu }_2$ are tuning parameters that control the sparsity of the coefficients and the smoothness of their differences, respectively. This formulation captures both sparsity and smoothness, making it especially suited for high-dimensional settings where feature ordering is important. Examples of such problems include gene expression analysis and protein mass spectroscopy.

The optimization problem can be formulated as follows:

$$x^{\ast }=\underset{x}{argmin}\left({\displaystyle \frac{1}{2}}{\parallel Ax-b\parallel }_2^2+{\mu }_1{\parallel x\parallel }_1+{\mu }_2{\parallel Dx\parallel }_1\right),$$

where $x\in {\mathbb{R}}^p$, $A\in {\mathbb{R}}^{n\times p}$, and $b\in {\mathbb{R}}^n$. The matrix D captures the differences between consecutive coefficients, and the ${\ell }_1$-penalty on $Dx$ promotes smoothness. We let $f\left(x\right)={\displaystyle \frac{1}{2}}{\parallel Ax-b\parallel }^2$, $g\left(x\right)={\mu }_2{\parallel x\parallel }_1$, and $h\left(Dx\right)={\mu }_1{\parallel Dx\parallel }_1$. The problem can also be reformulated in a primal-dual form for efficient computation:

$$\underset{x\in {\mathbb{R}}^p}{min}\underset{y\in {\mathbb{R}}^{p-1}}{max}{\displaystyle \frac{1}{2}}{\parallel Ax-b\parallel }^2+{\mu }_2{\parallel x\parallel }_1+\langle Dx,y\rangle -{\mu }_1{I}_{B^{\infty }}\left({\displaystyle \frac{y}{{\mu }_1}}\right)$$

where $B^{\infty }$ is the closed unit ball in the $l\infty$ norm and $I_{B^{\infty }}$ is its indicator function. We used the same problem setting as in [21].

We set the initial parameter values ${\tau }_0=0.95/\beta =0.95/\parallel A^{T}A\parallel$ and ${\sigma }_0=1/(\tau \parallel D^{T}D\parallel )$, $\parallel D^{T}D\parallel \to 2(n\to \infty )$. Figure 1 shows that a larger primal step size produces a better convergence rate for PPD3; thus, we chose $\tau$ close to its upper bound for the PPD3 method in this subsection. Since PPD3 has no restriction of $\tau \sigma \le 1/\parallel D^{T}D\parallel$, we fixed the maximal primal step size at $\tau =1/\beta$ and chose a different dual step size $\sigma$ so as to find the optimal dual step size (Figure 2). We see that removing the restriction on the dual step size, indeed, provides more choice regarding the step size parameters and has the potential to speed up algorithmic convergence. We chose $\sigma =1.1/(\tau \parallel D^{T}D\parallel )$ for PPD3 to solve Fused LASSO, and the rest of the parameters are presented in

Table 4. Parameter settings for different algorithms.

Algorithm	Primal Stepsize ($\mathit{\tau }$)	Dual Stepsize ($\mathit{\sigma }$)	$\mathit{\sigma }·\mathit{\tau }$
CV	${\displaystyle \frac{1.9}{\parallel A^{T}A\parallel }}$	${\displaystyle \frac{0.095}{\tau \parallel D^{T}D\parallel }}$	$0.095·\parallel D^{T}D\parallel$
PD3O	${\displaystyle \frac{1.95}{\parallel A^{T}A\parallel }}$	${\displaystyle \frac{1}{\tau \parallel D^{T}D\parallel }}$	$1·\parallel D^{T}D\parallel$
AFBA/PDDY	${\displaystyle \frac{3.8}{\parallel A^{T}A\parallel }}$	${\displaystyle \frac{2}{3\tau \parallel D^{T}D\parallel }}$	${\displaystyle \frac{2}{3}}·\parallel D^{T}D\parallel$
PPD3	${\displaystyle \frac{0.95}{\parallel A^{T}A\parallel }}$	${\displaystyle \frac{1.1}{\tau \parallel D^{T}D\parallel }}$	$1.1·\parallel D^{T}D\parallel$

. All $\tau$ values take their upper bound as the same as the experiment in [21], drawing the conclusion that a larger $\tau$ leads to faster convergence in Fused LASSO. $\theta$ was 1.5 for improved parameter conditions in AFBA/PDDY, as in [21] (Figure 3, Figure 4 and Figure 5).

We compared PPD3 with other methods for Fused LASSO problems of different dimensions. The results are consistent with the dimension of the problem, showing that PPD3 converges faster among all methods. PPD3 and AFBA/PDDY have close performance and are significantly better than CV or PD3O.

5.2. Image Inpainting

The classical Rudin-Osher-Fatemi (ROF) model, which minimizes total variation (TV), serves as a foundational approach to image restoration. A generic model for image restoration can be derived from the classical ROF model (in the discrete setting) as

$$\underset{x\in X}{min}{\parallel \Phi x\parallel }_1+{\displaystyle \frac{\lambda }{2}}{\parallel x-f\parallel }_2^2,$$

(25)

where $\Phi$ is a linear transformation (e.g., wavelets and curvelets), and x represents the restored image. The first term enforces sparsity in the transformed domain, while the second term ensures the restored image is close to the observed image f, which is partially corrupted. $\lambda$ controls the trade-off between sparsity and fidelity.

Image inpainting is the process of reconstructing missing or corrupted parts of an image. We consider a simple modification of (25). Let $D=\left\{\right(i,j)\mid 1\le i\le M,1\le j\le N\}$ denote the set of indices of the image domain, and let $I\subset D$ denote the set of indices of the inpainting domain. The inpainting model can then be defined as

$$\underset{x\in X}{min}{\parallel \Phi x\parallel }_1+{\displaystyle \frac{\lambda }{2}}\sum _{i,j\in D\setminus I}{(x_{i,j}-f_{i,j})}^2,$$

(26)

This formulation minimizes the squared error between the reconstructed and observed image in non-missing regions. A large $\lambda$ focuses solely on inpainting, while a small $\lambda$ denoises the image. Here, we used a more compact form to present (26):

$$\begin{array}{c}\hfill \underset{l\le X\le u}{min}{\mu \parallel \nabla x\parallel }_1+{\displaystyle \frac{1}{2}}{\parallel Sx-f\parallel }_2^2,\end{array}$$

(27)

where ∇ is the discrete gradient operator, $S\in {\Re }^{N\times N}$ is the mask operator (i.e., a diagonal matrix where zero entries denote missed information and identity entries indicate observed information), and f is the observed image. We let $f\left(x\right)={\displaystyle \frac{1}{2}}{\parallel Sx-f\parallel }^2$, $g\left(x\right)=I_{[l,u]}\left(x\right)$, and $h(\nabla x)={\mu \parallel \nabla x\parallel }_1$. By rewriting (27), the primal-dual form

$$\begin{array}{c}\hfill \underset{x}{min}\underset{y}{max}{\displaystyle \frac{1}{2}}{\parallel Sx-f\parallel }_2^2+I_{[l,u]}\left(x\right)+\langle \nabla x,y\rangle -\mu I_{B\infty }\left({\displaystyle \frac{y}{\mu }}\right)\end{array}$$

(28)

was obtained, which fits the form (2). This formulation balances sparsity, fidelity, and structure for effective image reconstruction.

The tested images are $house.png(256\times 256)$, $lena.png(512\times 512)$, and $Peppers.png(512\times 512)$. The image of $house.png(256\times 256)$ is degraded by a character mask, where about 15% of the pixels are missing. The degraded $lena.png(512\times 512)$ retains one row of pixels in every eight rows, whereas the degraded Pepper.png (512 × 512) keeps one column of pixels in every eight columns, which means about 87% of the pixels are missing. For all images, a zero-mean Gaussian noise with a standard deviation of 0.02 was added. The original and degraded images are shown in Figure 6, Figure 7 and Figure 8.

Signal-to-Noise Ratio (SNR) is a measure used in science and engineering to quantify the level of a desired signal relative to the level of background noise. The formula for SNR in decibels (dB) is typically

$$\mathrm{SNR}\left(\mathrm{dB}\right)=10{log}_{10}\left({\displaystyle \frac{P_{\mathrm{signal}}}{P_{\mathrm{noise}}}}\right),$$

where $P_{\mathrm{signal}}$ is the power of the signal, and $P_{\mathrm{noise}}$ is the power of the noise. In the realm of image processing, it measures the clarity of images, especially in applications like medical imaging or low-light photography. Higher SNR values indicate a clearer, stronger signal relative to noise.

We set the initial parameter values as ${\tau }_0=0.95/\beta =0.95$, ${\sigma }_0=1/(\tau \parallel {\nabla }^T\nabla \parallel )$, and $\parallel {\nabla }^T\nabla \parallel \to 8(n\to \infty )$. SNR was plotted against iteration number for the masked house image inpainting problems in Figure 9 and Figure 10. As shown below in Figure 9, the step size parameter is less sensitive in image inpainting than in Fused LASSO. Figure 10 indicates that a larger primal step size always leads to better performance; hence, we chose $\tau =0.95/{\parallel S\parallel }^2,\sigma =1.5/\tau {\parallel \nabla \parallel }^2$ for PPD3, and we used the same settings listed in

Table 5. Parameter settings for image inpainting.

Algorithm	Primal Stepsize ($\mathit{\tau }$)	Dual Stepsize ($\mathit{\sigma }$)	$\mathit{\sigma }·\mathit{\tau }$
CV	${\displaystyle \frac{1.9}{\parallel S^{T}S\parallel }}$	${\displaystyle \frac{0.095}{\tau \parallel {\nabla }^T\nabla \parallel }}$	$0.095·\parallel {\nabla }^T\nabla \parallel$
PD3O	${\displaystyle \frac{1.95}{\parallel S^{T}S\parallel }}$	${\displaystyle \frac{1}{\tau \parallel {\nabla }^T\nabla \parallel }}$	$1·\parallel {\nabla }^T\nabla \parallel$
AFBA/PDDY	${\displaystyle \frac{3.8}{\parallel S^{T}S\parallel }}$	${\displaystyle \frac{2}{3\tau \parallel {\nabla }^T\nabla \parallel }}$	${\displaystyle \frac{2}{3}}·\parallel {\nabla }^T\nabla \parallel$
PPD3	${\displaystyle \frac{0.95}{\parallel S^{T}S\parallel }}$	${\displaystyle \frac{1.5}{\tau \parallel {\nabla }^T\nabla \parallel }}$	$1.5·\parallel {\nabla }^T\nabla \parallel$

for the rest of the parameters.

The recovered images are shown in Figure 11, Figure 12 and Figure 13, and the SNR was plotted against iteration number for all image inpainting in Figure 14.

The result in Figure 14 shows that in all three image inpainting missions, PPD3 is the best among the compared methods. The PPD3 and AFBA/PDDY methods are significantly better than the CV or PD3O methods.

5.3. Other Computational Advantages of PPD3

Beyond its rapid convergence in terms of iterations, the PPD3 method also demonstrates considerable computational efficiency in terms of time. By taking the image inpainting tasks of house.png ($256\times 256$) and pepper.png ($512\times 512$) as examples, the primary CPU time costs are detailed in

Table 6. CPU time for Pepper.png.

Algorithm	Total X-Update Time	Total Y-Update Time
CV	1.291	1.622
PD3O	1.283	1.62
PDDY	1.435	1.63
PPD3	1.475 (47.8% )	1.611

,

Table 7. CPU time for Pepper.png.

Method to Get Norm (${\mathit{A}}^{\mathit{T}}\mathit{A}$)	Time Cost	Value of Norm (${\mathit{A}}^{\mathit{T}}\mathit{A}$)
Norm(.)full	≥1000	7.9999
Normest(.)full	≥1000	7.8816
Svds(.)sparse	10.989552	7.9999
Normest(.)sparse	0.277960	7.8816

,

Table 8. CPU time for House.png.

Algorithm	Total X-Update Time	Total Y-Update Time
CV	0.400	0.557
PD3O	0.419	0.571
PDDY	0.487	0.609
PPD3	0.539 (46.6% )	0.618

and

Table 9. CPU Time for House.png.

Method to get Norm (${\mathit{A}}^{\mathit{T}}\mathit{A}$)	Time Cost	Value of Norm (${\mathit{A}}^{\mathit{T}}\mathit{A}$)
Norm(.)full	≥1000	7.9997
Normest(.)full	235.8755	7.8816
Svds(.)sparse	2.185456	7.9997
Normest(.)sparse	0.097847	7.8816

. In particular, the parallel implementation of PPD3 achieves theoretical time savings of up to $46.6\%$ and $47.8\%$, respectively, when communication overhead is ignored.

Furthermore, alternative methods typically require the computation of $\parallel A^{T}A\parallel$, an operation for which the time cost is non-trivial. Although the linear operators in both experiments happen to have theoretical values, this is not guaranteed in all situations. We report the computational times of various MATLAB commands for $\parallel A^{T}A\parallel$ under scenarios where A is either dense or sparse. If $\parallel A^{T}A\parallel$ is unknown, we observe that even the fastest estimation of $\parallel A^{T}A\parallel$ accounts for approximately $10\%$ of the total computation time. These results underscore that PPD3 is particularly advantageous as a solver, especially when the linear operator A is dense and of significant size. In practice, PPD3 can take $\tau$ to its upper bound and choose a relatively large $\sigma$ or a random one to avoid the calculation of $\parallel A^{T}A\parallel$.

6. Discussion

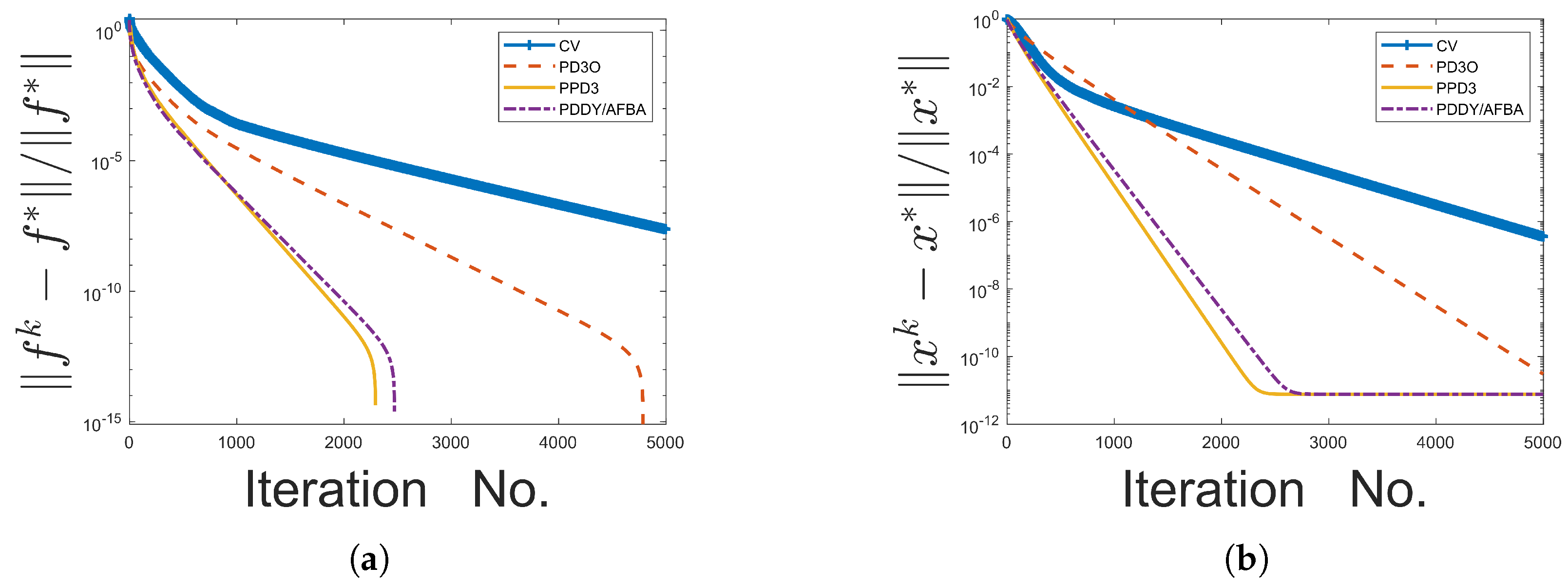
This paper introduces the Parallel Primal-Dual (PPD3) algorithm, a novel framework for solving optimization problems involving the minimization of the sum of three convex functions, including a Lipschitz continuous term. By leveraging parallel updates of primal and dual variables and removing stringent parameter dependencies, PPD3 addresses the computational inefficiencies inherent in existing methods. The algorithm’s adaptability to various problem settings and its ability to perform without reliance on the spectral norm of the linear operator mark notable progressions in the field of convex optimization.

In our algorithm, parallelization has the potential to accelerate computation, particularly when running on parallel computing platforms. The constraint $\tau \sigma \le {\displaystyle \frac{1}{\parallel A^{T}A\parallel }}$ on the parameters is removed, eliminating the need to compute the spectral norm of A, which is essential for most primal-dual methods. This also broadens the choice of parameters. Additionally, the step size is adjusted dynamically at each iteration rather than using a fixed global upper limit. As a result, our step size is typically larger, leading to faster convergence.

Through applications in image inpainting and Fused LASSO, PPD3 has demonstrated satisfactory performance in terms of computational efficiency and convergence speed. These results underscore its potential to handle complex, large-scale optimization challenges across a variety of domains.

For future work, we could explore extending the PPD3 framework to non-convex settings. Additionally, we may develop a stochastic version of PPD3. Furthermore, the parameters could be further investigated to determine whether they can be relaxed.