Dispersion-Governed Lump Waves in a Generalized Calogero–Bogoyavlenskii–Schiff-like Model with Spatially Symmetric Nonlinearity

Abstract

This study investigates lump wave structures that arise from the interplay of dispersion and nonlinearity in a generalized Calogero–Bogoyavlenskii–Schiff-like model with spatially symmetric nonlinearity in (2+1) dimensions. A generalized bilinear representation of the governing equation is formulated using extended bilinear derivatives of the fourth order, providing a convenient framework for analytic treatment. Through symbolic computation, we construct positive quadratic wave solutions, which give rise to rationally localized lump wave tructures that decay algebraically in all spatial directions at fixed time. Analysis shows that the critical points of these quadratic waves lie along a straight line in the spatial plane and propagate at a constant velocity. Along this characteristic trajectory, the amplitudes of the lump waves remain essentially unchanged, reflecting the stability of these coherent structures. The emergence of these lumps is primarily driven by the combined influence of five dispersive terms in the model, highlighting the crucial role of higher-order dispersion in balancing the nonlinear interactions and shaping the resulting localized waveforms.

1. Introduction

In soliton theory and the study of integrable models, solitons and lump waves receive a great deal of attention. These nonlinear wave phenomena are characterized by distinct dynamical features: solitons are stable, exponentially localized waves, while lump waves are rationally localized structures that decay to zero in all spatial directions. Such dispersive patterns arise from a delicate balance between nonlinearity and dispersion, and their analytical or numerical construction continues to play a central role in the study of nonlinear dispersive wave dynamics.

Hirota’s bilinear method [1] and the inverse scattering transform (IST) [2,3] are two cornerstone techniques for constructing the exact solutions described above. Hirota’s method provides a direct algebraic approach for systematically generating multi-soliton and rational solutions, especially in higher-dimensional systems [4,5,6,7,8,9]. In contrast, the IST offers a spectral framework for solving integrable PDEs through their associated Lax pairs of matrix spectral problems [10], enabling the analysis of soliton dynamics and the long-time behavior of dispersive waves [11].

Let P be a polynomal in M variables. In general, a Hirota bilinear equation can be written as

$$P(D_{x_1},D_{x_2},\cdots ,D_{x_M})f·f=0,$$

(1)

where $D_{x_i}$ denotes Hirota’s bilinear operator [1], defined by

$$D_{x_i}^{m}f·f={\left({\displaystyle \frac{\partial }{\partial x_i}}-{\displaystyle \frac{\partial }{\partial x_i^{\prime }}}\right)}^{m}f(x_1,x_2,\cdots ,x_M)f(x_1^{\prime },x_2^{\prime },\cdots ,x_M^{\prime }){|}_{x^{\prime }=x},$$

(2)

with $1\le i\le M$, $m\ge 0$, $x=(x_1,x_2,\cdots ,x_M)$, and $x^{\prime }=(x_1^{\prime },x_2^{\prime },\cdots ,x_M^{\prime })$. Within the bilinear framework, N-soliton solutions can be expressed as exponential superpositions (see, e.g., [4]):

$$f=\sum _{\nu =0,1}\exp (\sum _{i=1}^N{\nu }_i{\zeta }_i+\sum _{i<j}{\nu }_i{\nu }_j{d}_{ij}),$$

(3)

where the summation runs over all ${\nu }_i\in \{0,1\}$. The linear phases ${\zeta }_i$ and the phase shifts $d_{ij}$ are given by

$${\zeta }_i=k_{1,i}{x}_1+k_{2,i}{x}_2+\cdots +k_{M,i}{x}_M+{\zeta }_{i,0},\exp \left(d_{ij}\right)=-{\displaystyle \frac{P({\mathbf{k}}_i-{\mathbf{k}}_j)}{P({\mathbf{k}}_i+{\mathbf{k}}_j)}},1\le i<j\le N,$$

(4)

with the dispersion relations

$$P\left({\mathbf{k}}_i\right)=0,{\mathbf{k}}_i=(k_{1,i},k_{2,i},\cdots ,k_{M,i}),1\le i\le N.$$

(5)

Let f be defined by (3) and denote with $\widehat{\xi }$ that $\xi$ is omitted. Thus, one can obtain a recursive relation for computing the bilinear expression:

$$\begin{array}{ccc}& & P(D_{x_1},\cdots ,D_{x_M})f·f\hfill \\ & & {\displaystyle ={(-1)}^{\frac{1}{2}N(N-1)}\frac{H({\mathbf{k}}_1,{\mathbf{k}}_2,\cdots ,{\mathbf{k}}_N)}{{\prod }_{1\le i<j\le N}P({\mathbf{k}}_i+{\mathbf{k}}_j)}{\mathrm{e}}^{{\zeta }_1+{\zeta }_2+\cdots +{\zeta }_N}}\hfill \\ & & {\displaystyle +\sum _{n=1}^{N-1}{(-1)}^{\frac{1}{2}(N-n)(N-n-1)}\sum _{1\le i_1<\cdots <i_n\le N}\frac{H({\mathbf{k}}_1,\cdots ,{\widehat{\mathbf{k}}}_{i_1},\cdots ,{\widehat{\mathbf{k}}}_{i_n},\cdots ,{\mathbf{k}}_N)}{{\prod }_{\begin{array}{c}1\le i<j\le N\\ i,j\notin \{i_1,\cdots ,i_n\}\end{array}}P({\mathbf{k}}_i+{\mathbf{k}}_j)}}\hfill \\ & & {\displaystyle \times {\mathrm{e}}^{{\zeta }_1+\cdots +{\widehat{\zeta }}_{i_1}+\cdots +{\widehat{\zeta }}_{i_n}+\cdots +{\zeta }_N}}\hfill \\ & & {\displaystyle +\sum _{n=1}^{N-1}\sum _{1\le i_1<\cdots <i_n\le N}{\mathrm{e}}^{2({\zeta }_{i_1}+\cdots +{\zeta }_{i_n}+{\sum }_{1\le r<s\le n}{d}_{i_r{i}_s})}P(D_{x_1},\cdots ,D_{x_M})\tilde{f}·\tilde{f},}\hfill \end{array}$$

(6)

where

$$\tilde{f}={\tilde{f}}_{i_1\cdots i_n}=\sum _{{\tilde{\nu }}_{i_1\cdots i_n}=0,1}\exp (\sum _{\begin{array}{c}1\le i\le N\\ i\notin \{i_1,\cdots ,i_n\}\end{array}}{\nu }_i{\tilde{\zeta }}_i+\sum _{\begin{array}{c}1\le i<j\le N\\ i,j\notin \{i_1,\cdots ,i_n\}\end{array}}{d}_{ij}{\nu }_i{\nu }_j),$$

(7)

$${\tilde{\zeta }}_i={\zeta }_i+\sum _{r=1}^n{d}_{i{i}_r},{\tilde{\nu }}_{i_1\cdots i_n}=({\nu }_1,\cdots ,{\widehat{\nu }}_{i_1}\cdots ,{\widehat{\nu }}_{i_n},\cdots ,{\nu }_N),$$

(8)

with each ${\nu }_i$ in ${\tilde{\nu }}_{i_1\cdots i_n}$ belonging to $\{0,1\}$.

Based on the recursive relation (6), a Hirota bilinear equation admits an N-soliton solution if and only if all Hirota conditions are satisfied:

$$\begin{array}{c}{\displaystyle H({\mathbf{k}}_{i_1},\cdots ,{\mathbf{k}}_{i_n}):=\sum _{\sigma =\pm 1}P(\sum _{r=1}^n{\sigma }_r{\mathbf{k}}_{i_r})\prod _{1\le r<s\le n}P({\sigma }_r{\mathbf{k}}_{i_r}-{\sigma }_s{\mathbf{k}}_{i_s}){\sigma }_r{\sigma }_s=0,}\hfill \end{array}$$

(9)

for $1\le n\le N$ and $1\le i_1<\cdots <i_n\le N$, where $\sigma =({\sigma }_1,{\sigma }_2,\cdots ,{\sigma }_n)$ with ${\sigma }_r=\pm 1$. The case $n=1$ recovers the dispersion relations in (5).

For the (2+1)-dimensional case, let $x,y$ denote spatial variables and t time. A general Hirota bilinear equation in (2+1) dimensions can be expressed as

$$P(D_x,D_y,D_t)f·f=0,$$

(10)

where P is a polynomial in the three variables. Using Bell polynomial theory, nonlinear PDEs for a scalar field u can be derived from such bilinear forms via logarithmic derivative transformations. Typical transformations include

$$u=\beta {(lnf)}_{xx},u=\beta {(lnf)}_{yy},u=\beta {(lnf)}_{xy},u=\beta {(lnf)}_x,u=\beta {(lnf)}_y,$$

(11)

where $\beta \ne 0$ is a constant. A crucial step is to verify that f satisfies the bilinear equation and that the corresponding field u, defined through one of these logarithmic transformations, satisfies the associated nonlinear PDE. Systematic algorithms for performing this verification have been established for both (1+1)- and (2+1)-dimensional cases.

Another important class of explicit structures includes rogue waves and lump waves. Rogue waves are transient, large-amplitude localized structures that decay in all directions in both space and time. Lump waves, by contrast, are rationally localized, decaying algebraically in all spatial directions at fixed time [12]. For example, the KPI equation admits a variety of lump solutions, some of which arise as long-wave limits of multi-soliton configurations [6,13]. Lump-type solutions have also been observed in nonintegrable KP-, BKP-, and KP-Boussinesq-type systems (see, e.g., [14,15,16,17]) and even in linear higher-dimensional wave models through superposition principles.

The sum-of-squares ansatz, which inserts a positive quadratic function into a bilinear equation, has proven effective for constructing lump solutions [6]. When combined with logarithmic derivative transformations, this approach yields explicit lump solutions for a wide class of nonlinear PDEs.

In this work, we employ the sum-of-squares ansatz for a (2+1)-dimensional generalized Calogero–Bogoyavlenskii–Schiff-like (gCBS-like) model with spatially symmetric nonlinearity and five dispersion terms. The resulting lump wave structures emerge from the delicate interplay of these dispersive effects. Using symbolic computation, we derive explicit lump solutions and analyze the critical points of the associated quadratic forms, providing detailed insight into the wave dynamics. Examples with both 2D and 3D plots of the resulting lump waves are also presented.

2. A gCBS-like Model with Spatially Symmetric Nonlinearity

We employ generalized bilinear derivatives to formulate a gCBS-like model equation. A broad class of generalized bilinear differential operators was introduced in [18]. In the (2+1)-dimensional case with coordinates $(x,y,t)$, they are defined as

$$\begin{array}{ccc}& & D_{p,x}^m{D}_{p,y}^n{D}_{p,t}^{k}f·f\hfill \\ & & ={\left({\displaystyle \frac{\partial }{\partial x}}+{\alpha }_p{\displaystyle \frac{\partial }{\partial x^{\prime }}}\right)}^m{\left({\displaystyle \frac{\partial }{\partial y}}+{\alpha }_p{\displaystyle \frac{\partial }{\partial y^{\prime }}}\right)}^n{\left({\displaystyle \frac{\partial }{\partial t}}+{\alpha }_p{\displaystyle \frac{\partial }{\partial t^{\prime }}}\right)}^{k}f(x,y,t)f(x^{\prime },y^{\prime },t^{\prime }){|}_{x^{\prime }=x,y^{\prime }=y,t^{\prime }=t},\hfill \end{array}$$

(12)

where the coefficients ${\alpha }_p^k$ are given by

$${\alpha }_p^k={(-1)}^{r\left(k\right)}\mathrm{where}k\equiv r\left(k\right)\mathrm{mod}p,0\le r\left(k\right)<p.$$

(13)

For example, for $p=3$, the sequence of coefficients is

$${\alpha }_3=-1,{\alpha }_3^2={\alpha }_3^3=1,{\alpha }_3^4=-1,{\alpha }_3^5={\alpha }_3^6=1,\cdots ,$$

(14)

and for $p=5$, it is

$${\alpha }_5=-1,{\alpha }_5^2=1,{\alpha }_5^3=-1,{\alpha }_5^4={\alpha }_5^5=1,{\alpha }_5^6=-1,{\alpha }_5^7=1,{\alpha }_5^8=-1,{\alpha }_5^9={\alpha }_5^{10}=1,\cdots .$$

(15)

The coefficients for other values of p can be computed in a similar manner (see [18]). In summary, the sign sequences for $p=3,5,7$ are

$$-,+,+,-,+,+,-,+,+,\cdots (p=3),$$

(16)

$$-,+,-,+,+,-,+,-,+,+,-,+,-,+,+,\cdots (p=5),$$

(17)

$$-,+,-,+,-,+,+,-,+,-,+,-,+,+,-,+,-,+,-,+,+,\cdots (p=7).$$

(18)

Investigating the characteristic properties of these alternating sign sequences is an interesting endeavor.

2.1. Bilinear Form with Generalized Derivatives

For $p=3$, we propose the following gCBS-like model equation:

$$\begin{array}{ccc}& & P_{\mathrm{ssgCBS-like}}\left(f\right)\hfill \\ & & :=\left(D_{3,x}^3{D}_{3,y}+D_{3,x}{D}_{3,y}^3+{\gamma }_1{D}_{3,t}{D}_{3,x}+{\gamma }_2{D}_{3,t}{D}_{3,y}+{\gamma }_3{D}_{3,x}^2+{\gamma }_4{D}_{3,x}{D}_{3,y}+{\gamma }_5{D}_{3,y}^2\right)f·f\hfill \\ & & =2[3f_{xx}{f}_{xy}+3f_{yy}{f}_{xy}+{\gamma }_1(f_{tx}f-f_t{f}_x)+{\gamma }_2(f_{ty}f-f_t{f}_y)+{\gamma }_3(f_{xx}f-f_x^2)\hfill \\ & & +{\gamma }_4(f_{xy}f-f_x{f}_y)+{\gamma }_5(f_{yy}f-f_y^2)]=0,\hfill \end{array}$$

(19)

where $D_{3,x},D_{3,y}$, and $D_{3,t}$ are the generalized bilinear derivatives, and ${\gamma }_i$ for $1\le i\le 5$ denote arbitrary constants.

The fourth-order derivatives $D_{3,x}^3{D}_{3,y}$ and $D_{3,x}{D}_{3,y}^3$ appear in a partially symmetric form, generating the nonlinear terms in the corresponding nonlinear model. In contrast, the Bogoyavlensky–Konopelchenko-like equation, where the second fourth-order term is $D_{3,x}^4$ (see, e.g., ref. [19] for the $p=2$ case), leads to a different structure. Meanwhile, in the KP-like model, the nonlinearity involves only the fourth-order term $D_{3,x}^4$, without the mixed term $D_{3,x}^3{D}_{3,y}$.

This construction for $p=3$ produces a novel model capable of supporting lump wave solutions. We refer to this as a generalized model since it contains all second-order linear dispersion terms, whereas the original model only involves a single second-order term $D_{3,t}{D}_{3,x}$, which produces the linear dispersion.

2.2. Nonlinear Formulation

By redefining the dependent variables as

$$u=2{(lnf)}_{xy},v=2{(lnf)}_{xx},w=2{(lnf)}_{yy},r=2{(lnf)}_x,s=2{(lnf)}_y,$$

(20)

the gCBS-like model in its nonlinear form reads as follows:

$$\begin{array}{ccc}& & X_{\mathrm{ssgCBS-like}}(u,v,w,r,s)\hfill \\ & & :=K_{\mathrm{ssgCBS-like}}(u,v,w,r,s)+{\gamma }_1{u}_{tx}+{\gamma }_2{u}_{ty}+{\gamma }_3{u}_{xx}+{\gamma }_4{u}_{xy}+{\gamma }_5{u}_{yy}=0,\hfill \end{array}$$

(21)

where the nonlinear terms are given by

$$\begin{array}{ccc}& & K_{\mathrm{ssgCBS-like}}(u,v,w,r,s)={\displaystyle \frac{3}{4}}(u_{xx}+u_{yy})(2u+rs)+{\displaystyle \frac{3}{4}}{u}_{xy}(2v+2w+r^2+s^2)\hfill \\ & & +{\displaystyle \frac{3}{2}}{u}_x^2+{\displaystyle \frac{3}{2}}{u}_y^2+{\displaystyle \frac{3}{8}}{u}_x\left[4w_y+10ur+(4v+6w+3r^2+s^2)s\right]\hfill \\ & & +{\displaystyle \frac{3}{8}}{u}_y\left[4v_x+10us+(6v+4w+r^2+3s^2)r\right]+{\displaystyle \frac{3}{4}}{v}_x(us+wr)\hfill \\ & & +{\displaystyle \frac{3}{4}}{w}_y(ur+vs)+{\displaystyle \frac{9}{8}}(u^2+vw)(r^2+s^2)+{\displaystyle \frac{9}{4}}(v+w)(u^2+urs+{\displaystyle \frac{1}{3}}vw),\hfill \end{array}$$

(22)

provided the compatibility conditions hold:

$$u_x=v_y,u_y=w_x,r_y=s_x=u.$$

(23)

This equation incorporates a set of spatially symmetric nonlinear terms and five dispersive contributions. Despite its complexity, it admits lump wave solutions induced by the interplay of the dispersive terms.

Special reductions occur when only one pair of dispersion coefficients is nonzero. For example, if ${\gamma }_1=1$, ${\gamma }_5=\pm 1$, and the others vanish, the model Equation (21) reduces to

$$\begin{array}{ccc}& & K_{\mathrm{ssgCBS-like}}(u,v,w,r,s)+u_{tx}\pm u_{yy}=0.\hfill \end{array}$$

(24)

If ${\gamma }_2=1$, ${\gamma }_3=\pm 1$, and the others vanish, the model reduces to

$$\begin{array}{ccc}& & K_{\mathrm{ssgCBS-like}}(u,v,w,r,s)+u_{ty}\pm u_{xx}=0.\hfill \end{array}$$

(25)

In both cases, the compatibilty conditions (23) remain enforced. These reduced models still admit lump wave structures, regardless of the positive or negative signs in front of the dispersion terms $u_{xx}$ and $u_{yy}$.

2.3. Correspondence Between Bilinear and Nonlinear Forms

The bilinear form (19) and the nonlinear Equation (21) are related through

$$X_{\mathrm{ssgCBS-like}}(u,v,w,r,s)={\left[{\displaystyle \frac{P_{\mathrm{ssgCBS-like}}\left(f\right)}{f^2}}\right]}_{xy},$$

(26)

under the transformations in (20). Consequently, any solution f of the bilinear equation determines corresponding fields $u,v,w,r,s$, that satisfy the nonlinear model.

It can be readily verified that this model does not support a general class of N-soliton solutions. A natural question then arises: does it admit lump wave structures, which are often characteristic of integrable systems? In the following, we investigate lump wave solutions generated by the interplay of the five dispersive terms in the model.

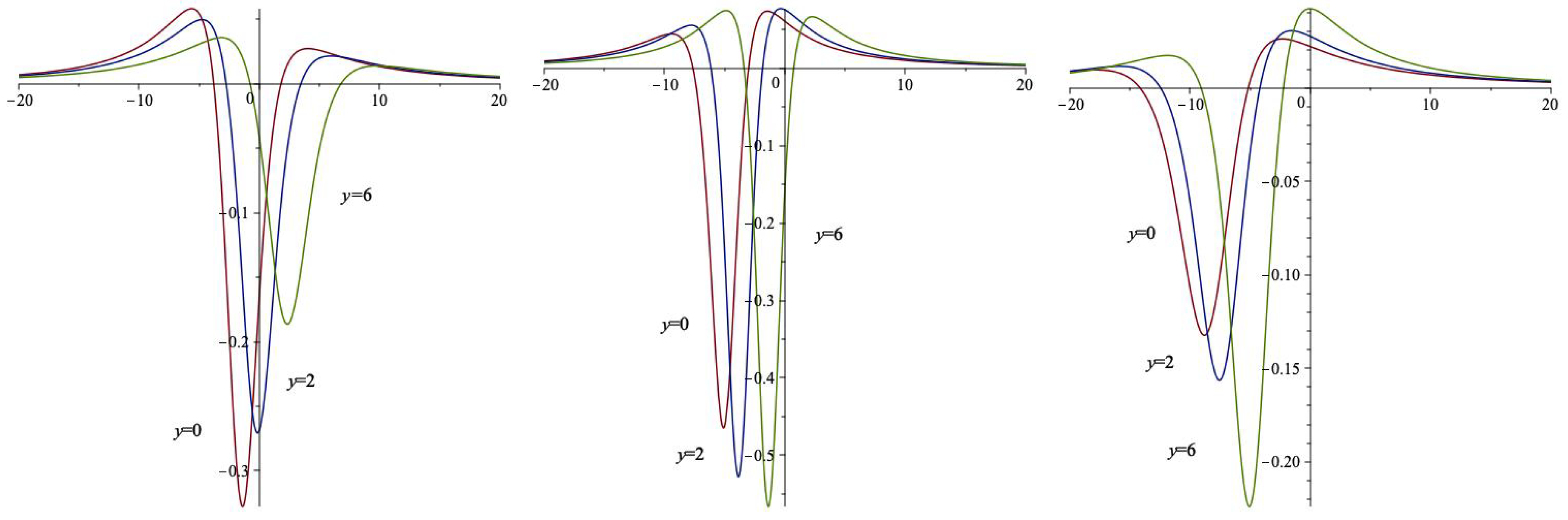
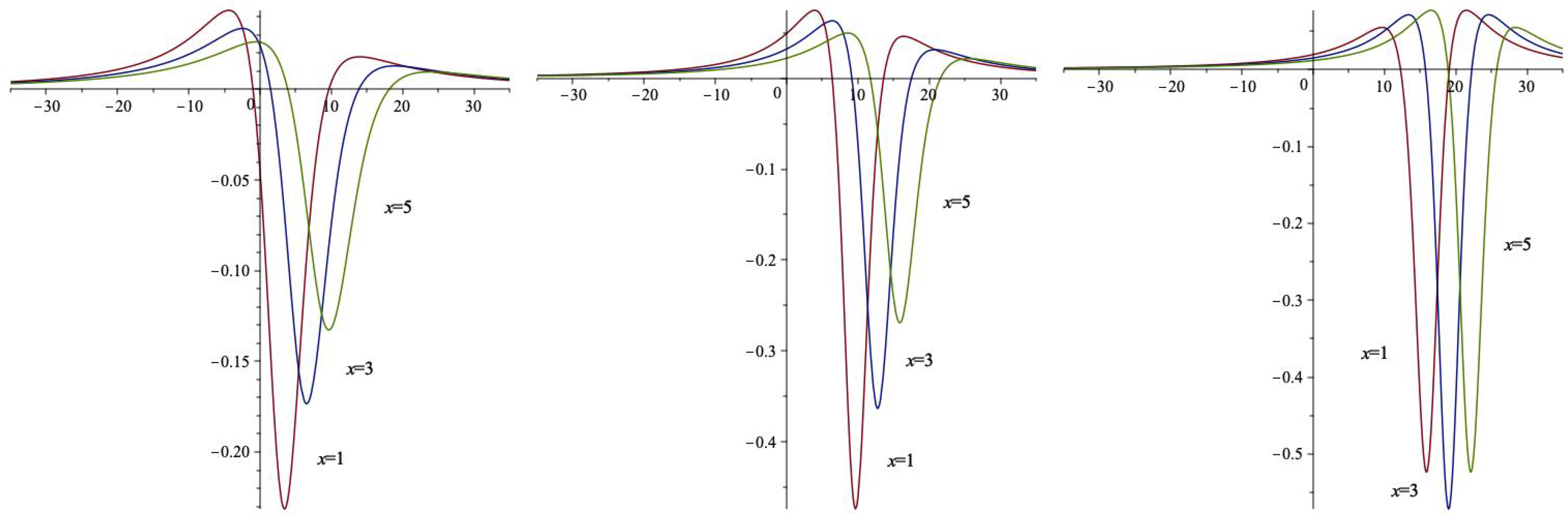
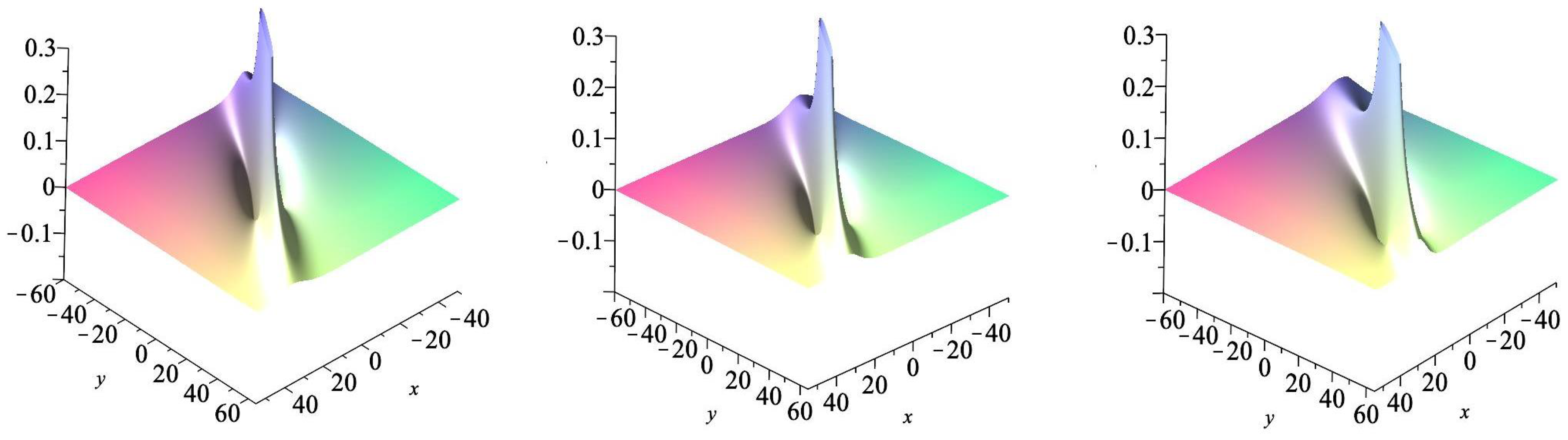
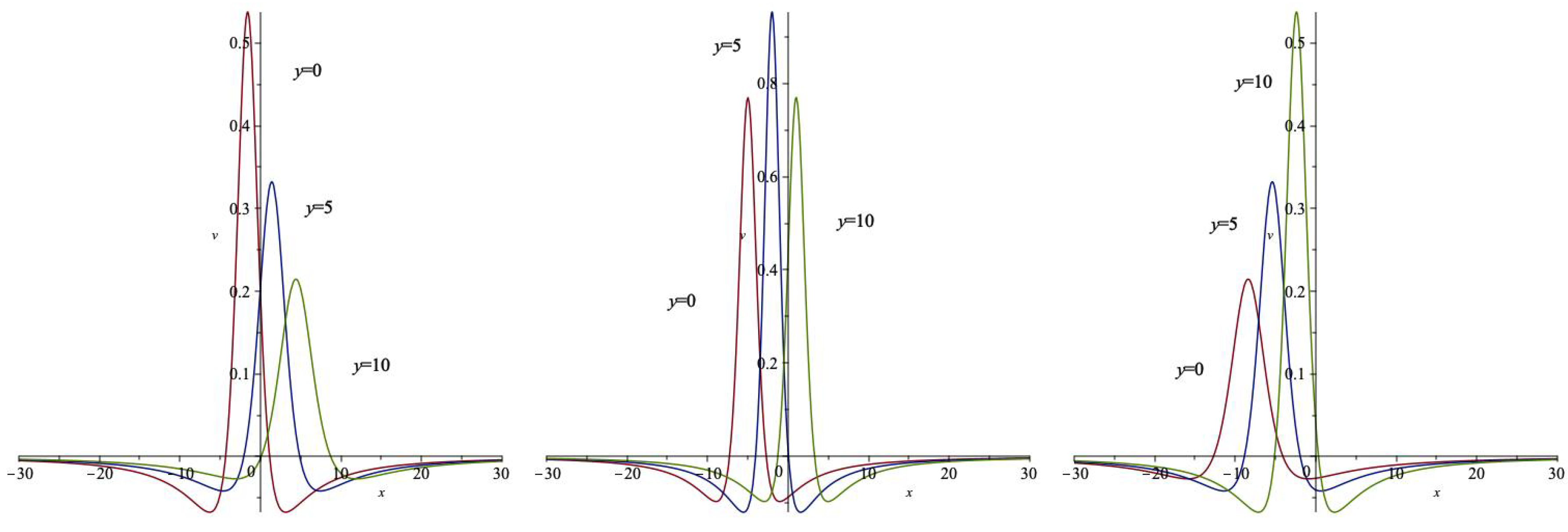
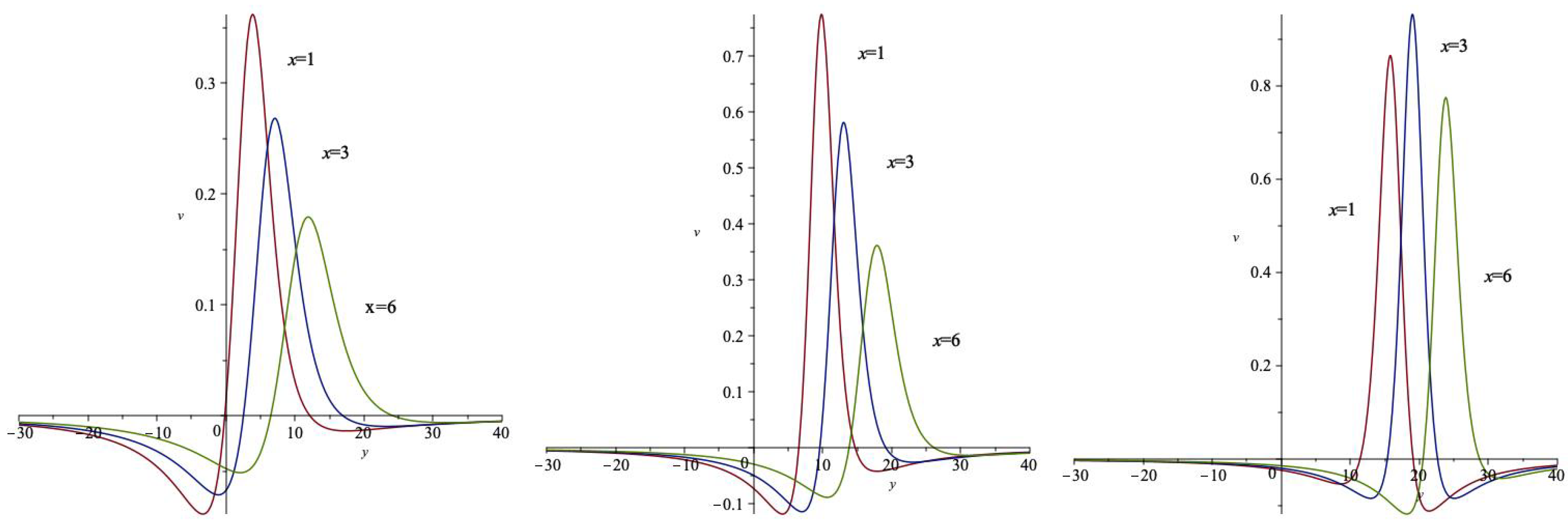
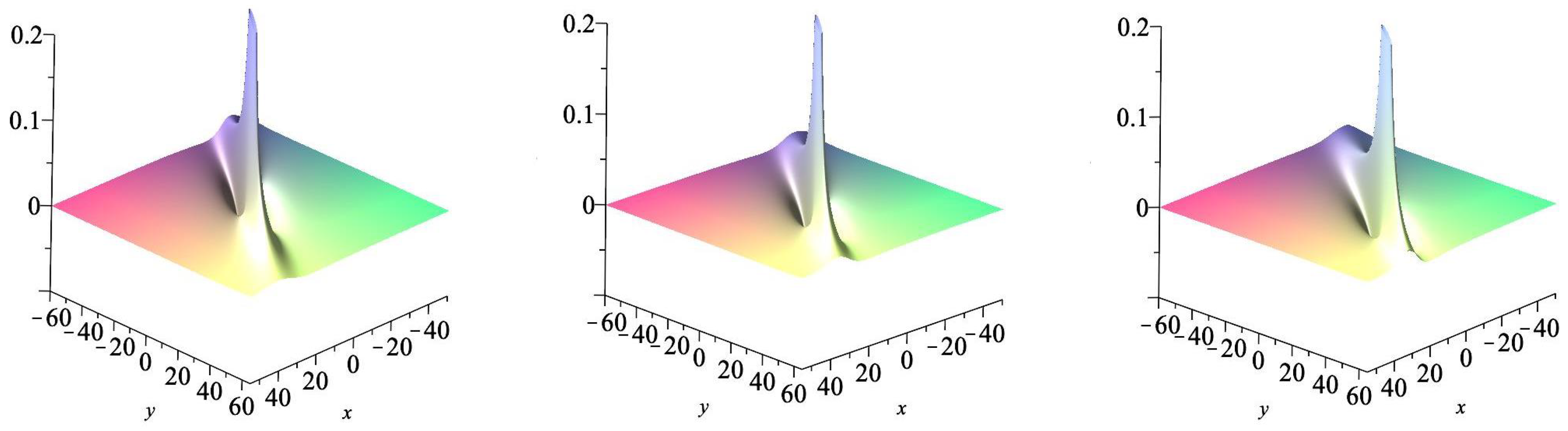
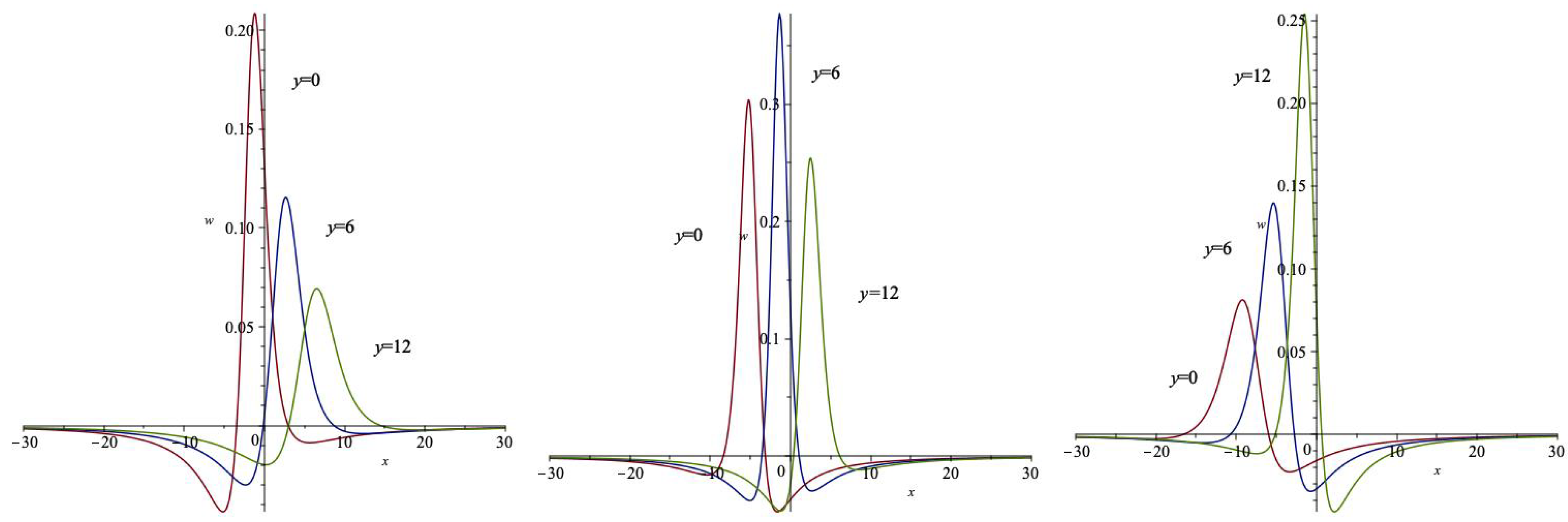
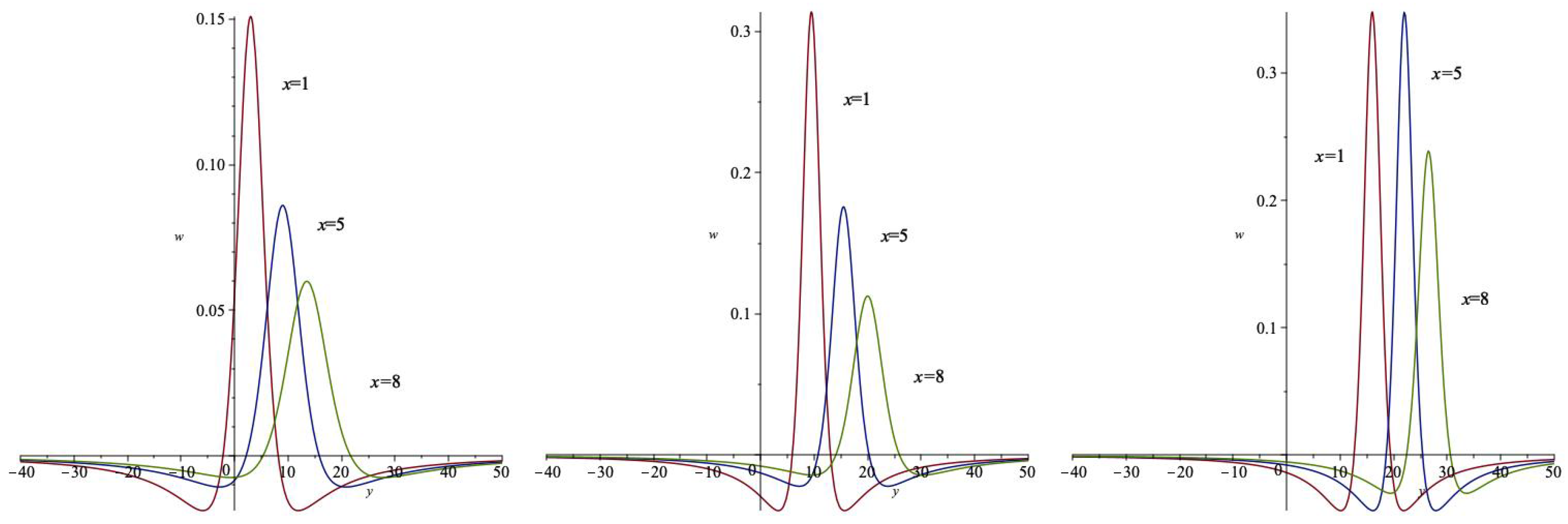
3. Formation of Lump Waves via Dispersion

We now focus on the explicit construction of lump wave solutions for the nonlinear model (21) by employing its generalized bilinear form (19) together with symbolic computation. Particular attention is given to the interplay of the five dispersive terms, which jointly give rise to the lump wave structures. Moreover, we examine the critical points of the corresponding quadratic function to gain insight into the localization and dynamical behavior of the resulting lump waves.

3.1. Sum-of-Squares Ansatz Approach

The sum-of-squares ansatz has become a standard approach for constructing lump solutions in higher-dimensional nonlinear evolution equations [6]. Its key idea is to express the dependent variable as logarithmic derivatives of a positive quadratic function f. In particular, we take

$$f={\theta }_1^2+{\theta }_2^2+a_9,{\theta }_1=a_{1}x+a_{2}y+a_{3}t+a_4,{\theta }_2=a_{5}x+a_{6}y+a_{7}t+a_8,$$

(27)

which can produce rational localization in all spatial directions in the $(x,y)$-plane. Substituting (27) into the generalized bilinear Equation (19) reduces the problem to an algebraic system for the parameters $a_i$.

Symbolic computation provides explicit expressions for $a_3$, $a_7$, and $a_9$ in terms of the other coefficients:

$$\begin{array}{ccc}& & a_3=-{\displaystyle \frac{1}{{(a_1{\gamma }_1+a_2{\gamma }_2)}^2+{(a_5{\gamma }_1+a_6{\gamma }_2)}^2}}[a_1(a_1^2+a_5^2){\gamma }_1{\gamma }_3+a_2(a_1^2+a_5^2){\gamma }_1{\gamma }_4\hfill \\ & & +(a_1{a}_2^2-a_1{a}_6^2+2a_2{a}_5{a}_6){\gamma }_1{\gamma }_5+(a_1^2{a}_2+2a_1{a}_5{a}_6-a_2{a}_5^2){\gamma }_2{\gamma }_3\hfill \\ & & +a_1(a_2^2+a_6^2){\gamma }_2{\gamma }_4+a_2(a_2^2+a_6^2){\gamma }_2{\gamma }_5],\hfill \end{array}$$

(28)

$$\begin{array}{ccc}& & a_7=-{\displaystyle \frac{1}{{(a_1{\gamma }_1+a_2{\gamma }_2)}^2+{(a_5{\gamma }_1+a_6{\gamma }_2)}^2}}[a_5(a_1^2+a_5^2){\gamma }_1{\gamma }_3+a_6(a_1^2+a_5^2){\gamma }_1{\gamma }_4\hfill \\ & & +(2a_1{a}_2{a}_6-a_2^2{a}_5+a_5{a}_6^2){\gamma }_1{\gamma }_5+(2a_1{a}_2{a}_5-a_1^2{a}_6+a_5^2{a}_6){\gamma }_2{\gamma }_3\hfill \\ & & +a_5(a_2^2+a_6^2){\gamma }_2{\gamma }_4+a_6(a_2^2+a_6^2){\gamma }_2{\gamma }_5],\hfill \end{array}$$

(29)

and

$$\begin{array}{ccc}& & a_9=-{\displaystyle \frac{3(a_1{a}_2+a_5{a}_6)(a_1^2+a_2^2+a_5^2+a_6^2)[{(a_1{\gamma }_1+a_2{\gamma }_2)}^2+{(a_5{\gamma }_1+a_6{\gamma }_2)}^2]}{{(a_1{a}_6-a_2{a}_5)}^2({\gamma }_1^2{\gamma }_5-{\gamma }_1{\gamma }_2{\gamma }_4+{\gamma }_2^2{\gamma }_3)}}.\hfill \end{array}$$

(30)

These expressions encode the dispersion relations and structural constraints for the lump waves. In particular, $a_3$ and $a_7$ determine the temporal frequencies associated with higher-order rational combinations of dispersion coefficients, while $a_9$ reflects a balance between the wave numbers and the dispersion parameters. Similar dispersion expressions appear in lump wave solutions of the second flow of the KP hierarchy and in generalized KP-type models (see, e.g., refs. [20,21,22]).

Well-posedness and spatial localization require two essential non-degeneracy conditions. First, the dispersion condition

$${\gamma }_1^2{\gamma }_5-{\gamma }_1{\gamma }_2{\gamma }_4+{\gamma }_2^2{\gamma }_3\ne 0,$$

(31)

ensures

$${\gamma }_1^2+{\gamma }_2^2\ne 0,$$

(32)

and, second, the determinant condition

$$a_1{a}_6-a_2{a}_5\ne 0,$$

(33)

guarantees

$$a_1^2+a_5^2\ne 0,a_2^2+a_6^2\ne 0,$$

(34)

ensuring that the solutions $u,v,w,r,s$ defined through the logarithmic derivative transformations in (20), decay to zero as $x^2+y^2\to \infty$, confirming spatial localization.

The positivity of f, and, hence, the analyticity of the resulting lump waves $u,v,w,r,s$, is ensured by the mixed necessary and sufficient condition involving the dispersion parameters and the wave numbers:

$$(a_1{a}_2+a_5{a}_6)\left({\gamma }_1^2{\gamma }_5-{\gamma }_1{\gamma }_2{\gamma }_4+{\gamma }_2^2{\gamma }_3\right)<0.$$

(35)

This requirement can be satisfied in either of the following two cases:

$${\gamma }_1^2{\gamma }_5-{\gamma }_1{\gamma }_2{\gamma }_4+{\gamma }_2^2{\gamma }_3<0,$$

(36)

with

$$a_1{a}_2+a_5{a}_6>0,$$

(37)

or

$${\gamma }_1^2{\gamma }_5-{\gamma }_1{\gamma }_2{\gamma }_4+{\gamma }_2^2{\gamma }_3>0,$$

(38)

with

$$a_1{a}_2+a_5{a}_6<0.$$

(39)

To satisfy the sufficient condition in (36), one may, for instance, choose

$${\gamma }_1\ne 0,{\gamma }_2=0,{\gamma }_5<0,\mathrm{or}{\gamma }_1=0,{\gamma }_2\ne 0,{\gamma }_3<0.$$

(40)

Similarly, to satisfy the sufficient condition in (38), one may assume

$${\gamma }_1\ne 0,{\gamma }_2=0,{\gamma }_5>0,\mathrm{or}{\gamma }_1=0,{\gamma }_2\ne 0,{\gamma }_3>0.$$

(41)

The dispersion coefficient ${\gamma }_4$ contributes only when both ${\gamma }_1$ and ${\gamma }_2$ are nonzero.

Condition (35) guarantees $a_9>0$ in (30), keeping f strictly positive and thus ensuring the analyticity of $u,v,w,r,s$ across the entire $(x,y,t)$-domain. The conditions in (36) and (38) essentially act as two dispersion-parameter constraints, emphasizing that the formation of lump waves stems from the linear dispersive terms. Interestingly, in either case, ${\gamma }_1\ne 0$ and ${\gamma }_2=0$ and ${\gamma }_1=0$ and ${\gamma }_2\ne 0$, the other dispersion coefficient ${\gamma }_5$ or ${\gamma }_3$ could be positive or negative, generating lump wave solutions.

In summary, the construction of lump wave solutions via the logarithmic derivative transformations requires two essential conditions: the determinant condition (33), which secures spatial localization, and the positivity condition (35), which guarantees the well-posedness of $u,v,w,r,$ and s across the spatial–temporal domain. The sufficient conditions (36) and (37) or (38) and (39) further establish the existence of lump waves. Under these constraints, the resulting $u,v,w,r,s$ indeed constitute valid lump wave solutions.

3.2. Trajectory of Critical Points

The dynamical behaviour of the lump waves can be further elucidated by analyzing the critical points of f. Setting $f_x=f_y=0$ leads to

$$a_1{\theta }_1+a_5{\theta }_2=0,a_2{\theta }_1+a_6{\theta }_2=0,$$

(42)

which, under the non-degeneracy condition (33), reduces to

$${\theta }_1=0,{\theta }_2=0,$$

(43)

with ${\theta }_1,{\theta }_2$ as defined in (27). Solving this system gives explicit linear trajectories $x\left(t\right)$ and $y\left(t\right)$, representing critical points of the quadratic function f:

$$\begin{array}{cc}\hfill & x\left(t\right)={\displaystyle \frac{[(a_1^2+a_5^2){\gamma }_3-(a_2^2+a_6^2){\gamma }_5]{\gamma }_1+[2(a_1{a}_2+a_5{a}_6){\gamma }_3+(a_2^2+a_6^2){\gamma }_4]{\gamma }_2}{{(a_1{\gamma }_1+a_2{\gamma }_2)}^2+{(a_5{\gamma }_1+a_6{\gamma }_2)}^2}}t+{\displaystyle \frac{a_2{a}_8-a_4{a}_6}{a_1{a}_6-a_2{a}_5}},\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill & y\left(t\right)={\displaystyle \frac{[(a_1^2+a_5^2){\gamma }_4+2(a_1{a}_2+a_5{a}_6){\gamma }_5]{\gamma }_1-[(a_1^2+a_5^2){\gamma }_3-(a_2^2+a_6^2){\gamma }_5]{\gamma }_2}{{(a_1{\gamma }_1+a_2{\gamma }_2)}^2+{(a_5{\gamma }_1+a_6{\gamma }_2)}^2}}t-{\displaystyle \frac{a_1{a}_8-a_4{a}_5}{a_1{a}_6-a_2{a}_5}}.\hfill \end{array}$$

(45)

These expressions describe straight-line trajectories in the $(x,y)$-plane, along which the lump waves remain stationary, while the solutions stay rationally localized in the surrounding region.

The Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 below provide 3D and 2D plots of the lump waves $u=2{(lnf)}_{xy}$, $v=2{(lnf)}_{xx}$, and $w=2{(lnf)}_{yy}$, computed for the parameter sets specified as follows:

$${\gamma }_1={\gamma }_2=-{\gamma }_3={\gamma }_4=-{\gamma }_5=-1,$$

and

$$a_1=1,a_2=-1,a_4=-2,a_5=2,a_6=-1,a_8=5.$$

4. Concluding Remarks

We formulated and analyzed a novel (2+1)-dimensional gCBS-like model with spatially symmetric nonlinearity and constructed its lump wave solutions using symbolic computation in computer algebra systems. These lump waves remain invariant along characteristic trajectories determined by the critical points of the corresponding quadratic function, illustrating the subtle interplay among the dispersive terms.

Lump waves arise in a wide range of physical and mathematical contexts, demonstrating both their versatility and the challenges associated with modeling nonlinear dispersive phenomena. They appear in linear models as well as in nonlinear and nonintegrable systems in (2+1) dimensions [23,24,25,26,27], (3+1) dimensions [20,28], and (4+1) dimensions [29]. Their explicit construction often relies on Hirota bilinear forms [1] and generalized bilinear techniques [18], providing a systematic framework for identifying spatially localized coherent structures.

Moreover, lump waves exhibit rich interactions with other coherent structures in (2+1)-dimensional integrable systems, including homoclinic and heteroclinic waves [30,31,32]. They can also be derived as long-wave or wave-number reductions from N-soliton solutions. At the same time, N-soliton solutions and integrability properties have been extensively studied in both local and nonlocal settings, for instance, via Riemann–Hilbert methods, bi-Hamiltonian formulations, and group reductions [33,34,35,36,37]. The existence, algebro-geometric structure, and dynamics of lump waves in (2+1)-dimensional extensions of integrable systems—whether scalar or multi-component, standard or generalized—remain active and compelling areas of research [38,39,40,41,42].

In summary, the study of lump waves deepens insight into nonlinear dispersive wave dynamics and may inform applications in physical and engineering contexts, where localized, coherent, energy-concentrated structures are important.