On Quadraticity of Linear Combinations of Two Essentially Cubic Matrices That Commute

Abstract

This work presents a complete and definitive characterization of all cases where every linear combination of two commuting essentially cubic matrices results in a quadratic matrix, thereby extending existing contributions in the literature. To facilitate a better understanding of the main results of this study, several numerical examples are provided at the end of the paper, and connections with the results in the literature are established.

1. Introduction and Preliminaries

This section begins with a brief overview of fundamental concepts and theorems, followed by a discussion of relevant studies in the literature.

A matrix $A\in {\mathbb{C}}_n$ is called $\{p,q\}$-quadratic if there exist $p,q\in \mathbb{C}$ such that

$$(A-p{I}_n)(A-q{I}_n)=\mathbf{0}$$

see, e.g., [1]. More generally, with respect to an idempotent matrix P, A is termed a generalized $\{p,q\}$-quadratic matrix when

$$(A-pP)(A-qP)=\mathbf{0}\mathrm{and}AP=PA=A,$$

which clearly reduces to the usual $\{p,q\}$-quadratic case when $P=I_n$ (see, e.g., [2,3]). Similarly, a matrix $A\in {\mathbb{C}}_n$ is referred to as $\{p,q,r\}$-cubic provided that there exist $p,q,r\in \mathbb{C}$ satisfying

$$(A-p{I}_n)(A-q{I}_n)(A-r{I}_n)=\mathbf{0}$$

see, e.g., [4,5,6]. The next three theorems are of considerable importance, since they offer complementary characterizations of the aforementioned classes of matrices.

Theorem 1 

([7]). Let $A\in {\mathbb{C}}_n$. The following statements are equivalent:

 (i) 

There exist $p,q\in \mathbb{C}$ with $p\ne q$ such that $(A-p{I}_n)(A-q{I}_n)=\mathbf{0}$;

 (ii)

A is diagonalizable and $\sigma \left(A\right)\subset \{p,q\}$;

 (iii)

There exist different $p,q\in \mathbb{C}$ and two idempotent matrices X and Y such that $A=pX+qY$, $X+Y=I_n$, and $XY=YX=\mathbf{0}$;

 (iv)

There exists an idempotent matrix X such that $A=(p-q)X+q{I}_n$ with $p\ne q$.

Theorem 2 

([8]). Let $A\in {\mathbb{C}}_n$. The following statements are equivalent:

 (i)

There exist $p,q\in \mathbb{C}$ with $p\ne q$, and an idempotent matrix P such that $(A-pP)(A-qP)=\mathbf{0}$ and $AP=PA=A$;

 (ii)

A is diagonalizable and $\sigma \left(A\right)\subset \{0,p,q\}$;

 (iii)

There exist different $p,q\in \mathbb{C}$ and two idempotent matrices X and Y such that $A=pX+qY$, $X+Y=P$, and $XY=YX=\mathbf{0}$;

 (iv)

There exists an idempotent matrix X such that $A=(p-q)X+qP$ and $XP=PX=X$ with $p\ne q$.

Theorem 3 

([4,6]). Let $A\in {\mathbb{C}}_n$. Then, the following statements are equivalent:

 (i)

There exist $p,q,r\in \mathbb{C}$ with $p\ne q$, $p\ne r$, and $q\ne r$ such that $(A-p{I}_n)(A-q{I}_n)(A-r{I}_n)=\mathbf{0}$;

 (ii)

A is diagonalizable and $\sigma \left(A\right)\subset \{p,q,r\}$;

 (iii)

There exist different $p,q,r\in \mathbb{C}$ and three idempotent matrices X, Y, and Z such that $A=pX+qY+rZ$, $X+Y+Z=I_n$, $XY=YX=\mathbf{0}$, $YZ=ZY=\mathbf{0}$, and $XZ=ZX=\mathbf{0}$;

 (iv)

There exist two idempotent matrices X and Y such that $A=(p-r)X+(q-r)Y+r{I}_n$ and $XY=YX=\mathbf{0}$ with $p\ne q$, $p\ne r$, and $q\ne r$.

The family of cubic matrices constitutes a broad and versatile class that encompasses several fundamental subclasses. Among these, tripotent matrices ($A^3=A$), quadratic matrices, and generalized quadratic matrices are particularly noteworthy, as they have been extensively studied in the literature due to their rich algebraic structures and diverse applications. By serving as a unifying framework that subsumes such well-investigated families, cubic matrices not only provide deeper insight into the interplay between polynomial identities and matrix theory but also extend the scope of classical results to a more general setting.

Now, we introduce the notion of an essentially $\{p,q,r\}$-cubic matrix. A $\{p,q,r\}$-cubic matrix A will be called essentially $\{p,q,r\}$-cubic if its spectrum is exactly equal to the set $\{p,q,r\}$. In particular, an essentially $\{p,q,r\}$-cubic matrix is neither a scalar matrix of the form $pI$, $qI$, or $rI$ nor a $\{p,q\}$-, $\{p,r\}$-, or $\{q,r\}$-quadratic matrix.

Since the early 2000s, the characterization of linear combinations of matrices with special algebraic structures has become a significant research topic (see, e.g., [5,6,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]). Initially, these studies focused on whether the linear combination of two commuting idempotent matrices remains idempotent, but over time they have expanded to encompass more complex structures, such as cubic matrices. Today, the question of whether the linear combinations of structured matrices preserve a particular algebraic property or give rise to a new one continues to attract considerable attention, not only in matrix theory but also in ring theory (see, e.g., [25,26]), operator theory (see, e.g., [27,28]), and quaternion algebra (see, e.g., [29]).

In this study, we focus on the problem of the quadraticity of linear combinations of two commuting essentially cubic matrices. To support the results presented here, we provide some numerical examples and establish connections with some well-known results in the literature.

2. Results

In this section, to achieve our goal, we first consider two commutative cubic matrices $A_1$ and $A_2$, and we express their linear combinations of the form $a_1{A}_1+a_2{A}_2$ as a linear combination of the generalized quadratic matrices $B_1$ and $B_2$ associated with $A_1$ and $A_2$. Then, by utilizing the structure of generalized quadratic matrices, we observe that the condition required for this linear combination to be quadratic is precisely the equality given in (8). Note that the equality (8) represents a combination of generalized quadratic matrices and idempotents.

After this point, we express the generalized quadratic and idempotent matrices involved in the combination by means of the block matrices given in (9)–(11), and (14). Consequently, the equality in (8) is decomposed into the equalities (20) and (21). At this stage, all of the matrices appearing in (20) and (21) are idempotent, and working with idempotent matrices is easier compared to quadratic, generalized quadratic, or cubic matrices.

By examining the equalities (20) and (21) in detail, we find that satisfying equality (21) depends on one of the eight conditions stated in Theorems 4 and 5. Similarly, satisfying equality (20) depends on one of the thirty-one conditions stated in Theorems 6 and 7. Therefore, the simultaneous satisfaction of (20) and (21) (which guarantees the equality in (8)) depends on one of the results of Theorem 4 or Theorem 5 being satisfied together with one of those of Theorem 6 or Theorem 7.

To achieve this, we analyze the theorems pairwise and obtain intersections related to the coefficients $c_k$, $k=1,\dots ,5$ in the equality (8). By substituting these intersections into the equality (8), taking into account the choices of submatrices within the blocks of the block matrices considered during the analysis, we derive the matrix equalities related to $B_1$ and $B_2$ stated in the main theorem. In many of the results obtained, we observe a role exchange among the coefficients and, consequently, express the results in a closed form using the indices i and j.

Now, let us examine in detail the procedural steps summarized above.

Let $A_1\in {\mathbb{C}}_n$ and $A_2\in {\mathbb{C}}_n$ be a $\{p_1,q_1,r_1\}$-essentially cubic matrix and a $\{p_2,q_2,r_2\}$-essentially cubic matrix, respectively, where $A_1{A}_2=A_2{A}_1$, $p_1\ne q_1$, $p_1\ne r_1$, $q_1\ne r_1$, $p_2\ne q_2$, $p_2\ne r_2$, and $q_2\ne r_2$. One has the following relations by Theorem 3:

$$A_1=(p_1-r_1)X_1+(q_1-r_1)Y_1+r_1{I}_n,{X_1}^2=X_1,{Y_1}^2=Y_1,X_1{Y}_1=Y_1{X}_1=\mathbf{0}$$

and

$$A_2=(p_2-r_2)X_2+(q_2-r_2)Y_2+r_2{I}_n,{X_2}^2=X_2,{Y_2}^2=Y_2,X_2{Y}_2=Y_2{X}_2=\mathbf{0}.$$

Let us denote $(p_1-r_1)X_1+(q_1-r_1)Y_1=B_1$, $X_1+Y_1=P_1$, $(p_2-r_2)X_2+(q_2-r_2)Y_2=B_2$, and $X_2+Y_2=P_2$. By Theorem 2, observe that the matrix $B_1$ is a $\{p_1-r_1,q_1-r_1\}$-generalized quadratic matrix with respect to the idempotent matrix $P_1$; similarly, the matrix $B_2$ is a $\{p_2-r_2,q_2-r_2\}$-generalized quadratic matrix with respect to the idempotent matrix $P_2$. Now, consider a linear combination $A_3=a_1{A}_1+a_2{A}_2$ with $a_1,a_2\in {\mathbb{C}}^{*}$. Since $A_1{A}_2=A_2{A}_1$, it is clear that $B_1{B}_2=B_2{B}_1$ by the hypotheses. So, the matrix $A_3$ can be written as

$$A_3=a_1{B}_1+a_2{B}_2+(a_1{r}_1+a_2{r}_2)I_n.$$

(1)

We aim to determine the conditions under which this combination becomes a $\{p_3,q_3\}$-quadratic matrix for some $p_3,q_3\in \mathbb{C}$. Equivalently, we look for the necessary and sufficient conditions ensuring that

$$(A_3-p_3{I}_n)(A_3-q_3{I}_n)=\mathbf{0}.$$

(2)

From (1) and (2), we get

$$(a_1{B}_1+a_2{B}_2+(a_3-p_3)I_n)(a_1{B}_1+a_2{B}_2+(a_3-q_3)I_n)=\mathbf{0}$$

(3)

with $a_3=a_1{r}_1+a_2{r}_2$. In view of the condition $B_1{B}_2=B_2{B}_1$, if Equation (3) is reorganized, then the following equation is obtained:

$$\begin{array}{c}{a}_1^2{B}_1^2+2a_1{a}_2{B}_1{B}_2+a_2^2{B}_2^2+a_1(2a_3-p_3-q_3)B_1+\hfill \\ a_2(2a_3-p_3-q_3)B_2+(a_3-p_3)(a_3-q_3)I_n=\mathbf{0}\hfill \end{array}$$

(4)

Since the matrix $B_1$ is a generalized $\{p_1-r_1,q_1-r_1\}$-quadratic matrix with respect to the idempotent matrix $P_1$, we have

$$B_1^2=(p_1-r_1+q_1-r_1)B_1-(p_1-r_1)(q_1-r_1)P_1,B_1{P}_1=P_1{B}_1=B_1.$$

(5)

Similarly, since the matrix $B_2$ is a generalized $\{p_2-r_2,q_2-r_2\}$-quadratic matrix with respect to the idempotent matrix $P_2$, one has

$$B_2^2=(p_2-r_2+q_2-r_2)B_2-(p_2-r_2)(q_2-r_2)P_2,B_2{P}_2=P_2{B}_2=B_2.$$

(6)

Substituting (5) and (6) into (4) yields

$$\begin{array}{cc}\hfill & \left(a_1^2(p_1+q_1-2r_1)+a_1(2a_3-p_3-q_3)\right)B_1\hfill \\ \hfill & +\left(a_2^2(p_2+q_2-2r_2)+a_2(2a_3-p_3-q_3)\right)B_2+2a_1{a}_2{B}_1{B}_2\hfill \\ \hfill & -a_1^2(p_1-r_1)(q_1-r_1)P_1-a_2^2(p_2-r_2)(q_2-r_2)P_2\hfill \\ \hfill & +(a_3-p_3)(a_3-q_3)I_n=\mathbf{0}.\hfill \end{array}$$

(7)

For the sake of simplicity, let us denote $c_1=a_1^2(p_1+q_1-2r_1)+a_1(2a_3-p_3-q_3)$, $c_2=a_2^2(p_2+q_2-2r_2)+a_2(2a_3-p_3-q_3)$, $c_3=-a_1^2(p_1-r_1)(q_1-r_1)\ne 0$, $c_4=-a_2^2(p_2-r_2)(q_2-r_2)\ne 0$, $c_5=(a_3-p_3)(a_3-q_3)$. Therefore, the equality (7) reduces to

$$c_1{B}_1+c_2{B}_2+2a_1{a}_2{B}_1{B}_2+c_3{P}_1+c_4{P}_2+c_5{I}_n=\mathbf{0}.$$

(8)

Note that $P_1$ (or $P_2$) is neither the zero matrix nor the identity matrix; otherwise, $A_1$ (or $A_2$) would not be essentially cubic. Therefore, there exists a nonsingular matrix S such that

$$P_1=S(I_r\oplus \mathbf{0})S^{-1},\mathrm{rank}\left(P_1\right)=r,1\le r<n.$$

(9)

In this block form, $B_1$ can be represented as

$$B_1=S\left(\begin{array}{cc}K& L\\ M& N\end{array}\right)S^{-1},$$

where $K,L,M,N$ are blocks of suitable sizes. If we use the condition $B_1{P}_1=P_1{B}_1=B_1$, then we get

$$B_1=S\left(\begin{array}{cc}K& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right)S^{-1}.$$

(10)

By definition, since $B_1$ is a generalized $\{p_1-r_1,q_1-r_1\}$-quadratic matrix with respect to the idempotent matrix $P_1$, it satisfies

$$(B_1-(p_1-r_1)P_1)(B_1-(q_1-r_1)P_1)=\mathbf{0}.$$

If we use (9) and (10) in the last equality, then we obtain $(K-(p_1-r_1)I_r)(K-(q_1-r_1)I_r)=\mathbf{0}$. This states that the matrix K is a $\{p_1-r_1,q_1-r_1\}$-quadratic matrix. It follows that K is nonsingular, because all of its eigenvalues are nonzero. Now, $B_2$ can be represented in block form as

$$B_2=S\left(\begin{array}{cc}X& Y\\ Z& T\end{array}\right)S^{-1},$$

where $X,Y,Z,T$ denote matrices of appropriate dimensions. Therefore, from the condition $B_1{B}_2=B_2{B}_1$, we get $XK=KX$, $KY=\mathbf{0}$, and $ZK=\mathbf{0}$. Since K is a nonsingular matrix, the equalities $KY=\mathbf{0}$ and $ZK=\mathbf{0}$ lead to $Y=\mathbf{0}$ and $Z=\mathbf{0}$. Thus, we have

$$B_2=S\left(\begin{array}{cc}X& \mathbf{0}\\ \mathbf{0}& T\end{array}\right)S^{-1}.$$

(11)

Next, $P_2$ can be expressed in block form as

$$P_2=S\left(\begin{array}{cc}{M}_1& M_2\\ M_3& M_4\end{array}\right)S^{-1},$$

(12)

with $M_1,M_2,M_3,M_4$ denoting matrices of appropriate dimensions. Substituting (9)–(12) into (8), we obtain

$$\begin{array}{cc}\hfill & c_1\left(\begin{array}{cc}K& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right)+c_2\left(\begin{array}{cc}X& \mathbf{0}\\ \mathbf{0}& T\end{array}\right)+2a_1{a}_2\left(\begin{array}{cc}KX& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right)+c_3\left(\begin{array}{cc}{I}_r& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right)\hfill \\ \hfill & +c_4\left(\begin{array}{cc}{M}_1& M_2\\ M_3& M_4\end{array}\right)+c_5\left(\begin{array}{cc}{I}_r& \mathbf{0}\\ \mathbf{0}& I_{n-r}\end{array}\right)=\left(\begin{array}{cc}\mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right).\hfill \end{array}$$

(13)

From blocks outside the diagonal in (13), one has $c_4{M}_2=\mathbf{0}$ and $c_4{M}_3=\mathbf{0}$. Therefore, it is obvious that $M_2=\mathbf{0}$ and $M_3=\mathbf{0}$ because $c_4\ne 0$. Thus, the matrix $P_2$ can be written as

$$P_2=S\left(\begin{array}{cc}{M}_1& \mathbf{0}\\ \mathbf{0}& M_4\end{array}\right)S^{-1}.$$

(14)

The idempotency of the matrix $P_2$ implies that both $M_1$ and $M_4$ are idempotents. Note that the matrices $M_1$ and $M_4$ cannot simultaneously coincide with either the zero matrix or the identity matrix; otherwise, $P_2$ becomes I or $\mathbf{0}$. From the upper-left block of (13), the equality

$$c_{1}K+c_{2}X+2a_1{a}_{2}KX+c_4{M}_1+(c_3+c_5)I_r=\mathbf{0}$$

(15)

is obtained. Moreover, since $B_2{P}_2=P_2{B}_2=B_2$, it follows from (11) and (14) that $X{M}_1=M_{1}X=X$ and $T{M}_4=M_{4}T=T$. On the other hand, the lower-right block of (13) yields

$$c_{2}T+c_4{M}_4+c_5{I}_{n-r}=\mathbf{0}.$$

(16)

Since the matrix $B_2$ is a generalized $\{p_2-r_2,q_2-r_2\}$-quadratic matrix with respect to the idempotent matrices $P_2$, the matrices X and T are generalized $\{p_2-r_2,q_2-r_2\}$-quadratic matrices with respect to the idempotent matrix $M_1$ and $M_4$, respectively. Thus, there exist idempotent matrices $Z_1$ and $Z_2$ such that

$$X=(p_2-q_2)Z_1+(q_2-r_2)M_1,Z_1{M}_1=M_1{Z}_1=Z_1$$

(17)

and

$$T=(p_2-q_2)Z_2+(q_2-r_2)M_4,Z_2{M}_4=M_4{Z}_2=Z_2.$$

(18)

Due to the $\{p_1-r_1,q_1-r_1\}$-quadraticity of the matrix K, there exists an idempotent matrix $Z_3$ such that

$$K=(p_1-q_1)Z_3+(q_1-r_1)I_r$$

(19)

by Theorem 1. Upon substituting the matrix X in (17) and the matrix K in (19) into (15), one obtains the equality

$$\begin{array}{cc}\hfill & (c_2(p_2-q_2)+2a_1{a}_2(q_1-r_1)(p_2-q_2))Z_1+(c_2(q_2-r_2)+2a_1{a}_2(q_1-r_1)(q_2-r_2)+c_4)M_1\hfill \\ \hfill & +c_1(p_1-q_1)Z_3+(c_1(q_1-r_1)+c_3+c_5)I_r+2a_1{a}_2(p_1-q_1)(p_2-q_2)Z_3{Z}_1\hfill \\ \hfill & +2a_1{a}_2(p_1-q_1)(q_2-r_2)Z_3{M}_1=\mathbf{0}.\hfill \end{array}$$

(20)

Similarly, if the matrix T in (18) is written in (16), then we get

$$c_2(p_2-q_2)Z_2+(c_2(q_2-r_2)+c_4)M_4+c_5{I}_{n-r}=\mathbf{0}.$$

(21)

Within the framework of the foregoing discussion, the necessary and sufficient condition for the linear combination in (1) to be $\{p_3,q_3\}$-quadratic, with $p_3,q_3\in \mathbb{C}$, is that the equalities (20) and (21) hold simultaneously, where $Z_1,Z_2,Z_3,M_1,M_4$ are the matrices defined in (17)–(19).

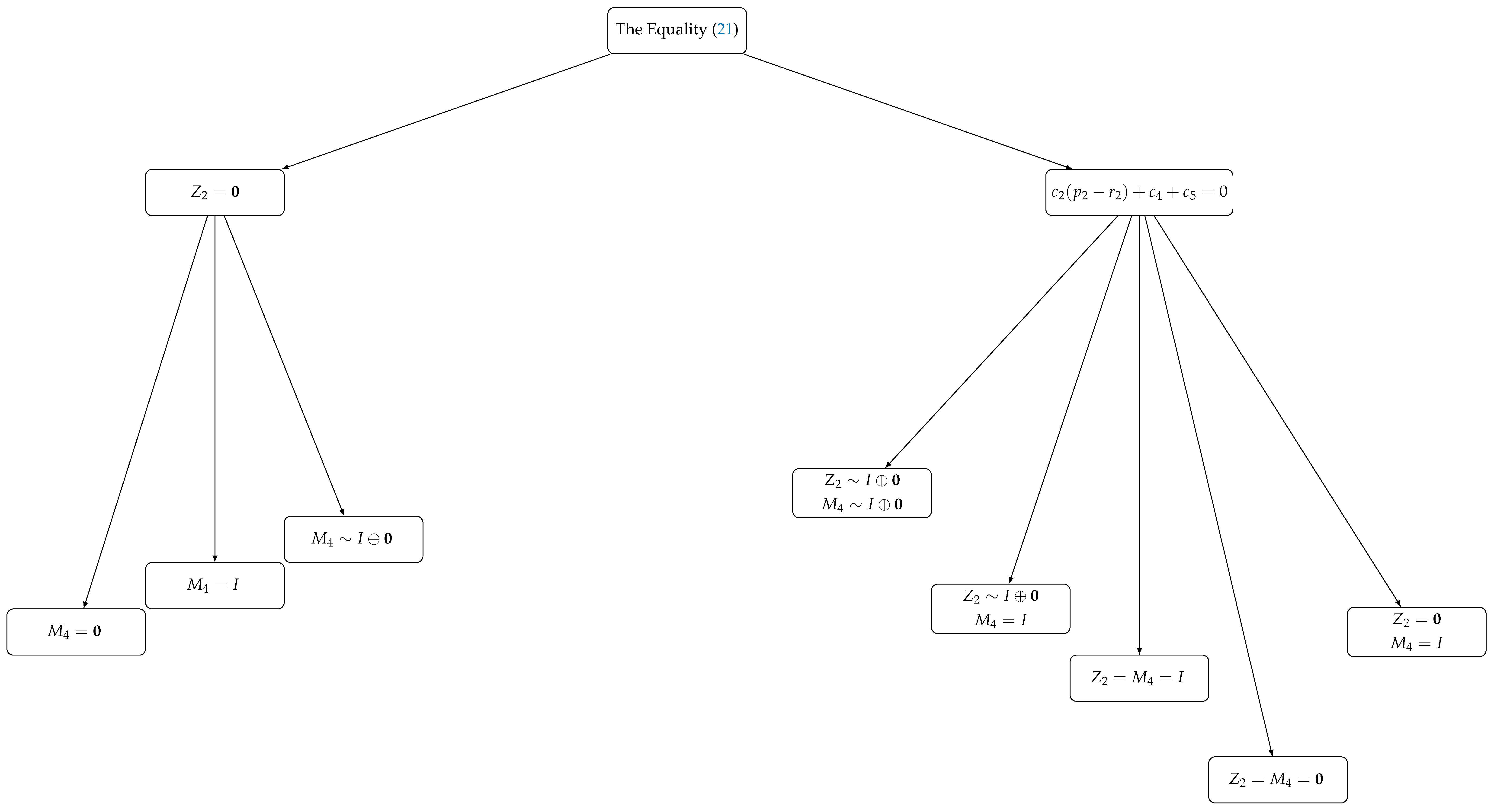
The conditions we use when examining the equality (21) can be summarized as in Figure 1. It is worth noting that these conditions naturally arise in the course of the proof; we do not start the proof by imposing them. The proof is constructed by taking possible cases into account.

Equation (21) will now be analyzed in detail.

If Equation (21) is multiplied by $Z_2$, recalling that $Z_2{M}_4=M_4{Z}_2=Z_2$ and $Z_2^2=Z_2$, then, after the necessary simplifications, one obtains

$$(c_2(p_2-r_2)+c_4+c_5)Z_2=\mathbf{0}.$$

From this, there are two situations:

• Case I. $Z_2=\mathbf{0}$.

Under this assumption, from the equality (21), we get

$$(c_2(q_2-r_2)+c_4)M_4+c_5{I}_{n-r}=\mathbf{0}.$$

(22)

Since $M_4$ is an idempotent matrix, $M_4=\mathbf{0}$ or $M_4=I$ or $M_4\sim I\oplus \mathbf{0}$. Therefore, there are three distinct possibilities for satisfying the equality in (22). It follows that the corresponding equalities are

$c_5=0$ or $c_2(q_2-r_2)+c_4+c_5=0$ or $c_2(q_2-r_2)+c_4=0$, $c_5=0$, respectively. Hence, we obtain the following theorem:

Theorem 4. 

The necessary and sufficient condition for the equality (21) to hold, provided that $Z_2=\mathbf{0}$, is that one of the following conditions is satisfied, where $M_4$ is the matrix in (18):

 (i)

$c_2(q_2-r_2)+c_4+c_5=0$, $M_4=I$;

 (ii)

$c_2(q_2-r_2)+c_4=0$, $c_5=0$, $M_4\sim I\oplus \mathbf{0}$;

 (iii)

$c_5=0$, $M_4=\mathbf{0}$.

• Case II. $c_2(p_2-r_2)+c_4+c_5=0$.

From (21), we obtain

$$c_2(p_2-q_2)Z_2+(c_2(q_2-r_2)+c_4)M_4+(-c_2(p_2-r_2)-c_4)I_{n-r}=\mathbf{0}.$$

(23)

Moreover, in view of the assumptions $c_4\ne 0$, $p_2\ne q_2$, and the relation $Z_2{M}_4=M_4{Z}_2=Z_2$, all admissible configurations of the matrices $Z_2$ and $M_4$ can be classified as follows:

$$\begin{array}{c}(Z_2\sim I\oplus \mathbf{0},M_4\sim I\oplus \mathbf{0}),(Z_2\sim I\oplus \mathbf{0},M_4=I),\hfill \\ (Z_2=I,M_4=I),(Z_2=\mathbf{0},M_4=\mathbf{0}),(Z_2=\mathbf{0},M_4=I).\hfill \end{array}$$

We next analyze these five cases in detail.

• Case II.I. $Z_2\sim I\oplus \mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$.

Under this assumption, Equation (23) yields $0=0,c_4=-c_2(p_2-r_2).$

• Case II.II. $Z_2\sim I\oplus \mathbf{0}$, $M_4=I$.

In this setting, from (23) it follows that $0=0,c_2=0.$

• Case II.III. $Z_2=I$, $M_4=I$.

Here, Equation (23) reduces to $0=0.$

• Case II.IV. $Z_2=\mathbf{0}$, $M_4=\mathbf{0}$.

In this scenario, Equation (23) yields $c_4=-c_2(p_2-r_2).$

• Case II.V. $Z_2=\mathbf{0}$, $M_4=I$.

Under these circumstances, from (23) it follows that $c_2=0.$

By combining the conclusions of the five subcases with the overarching hypothesis of Case II, we obtain the following theorem:

Theorem 5. 

The necessary and sufficient condition for the equality (21) to hold, provided that $c_2(p_2-r_2)+c_4+c_5=0$, is that one of the following conditions is satisfied, where $Z_2$ and $M_4$ are the matrices in (18):

 (iv)

$c_4=-c_2(p_2-r_2)$, $c_5=0$, $Z_2\sim I\oplus \mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$;

 (v)

$c_2=0$, $c_5=-c_4$, $Z_2\sim I\oplus \mathbf{0}$, $M_4=I$;

 (vi)

$c_5=-c_2(p_2-r_2)-c_4$, $Z_2=I$, $M_4=I$;

 (vii)

$c_4=-c_2(p_2-r_2)$, $c_5=0$, $Z_2=\mathbf{0}$, $M_4=\mathbf{0}$;

 (viii)

$c_2=0$, $c_5=-c_4$, $Z_2=\mathbf{0}$, $M_4=I$.

From the foregoing analysis, it follows that the equality in (21) holds if and only if one of the eight cases stated in Theorems 4 and 5 is satisfied.

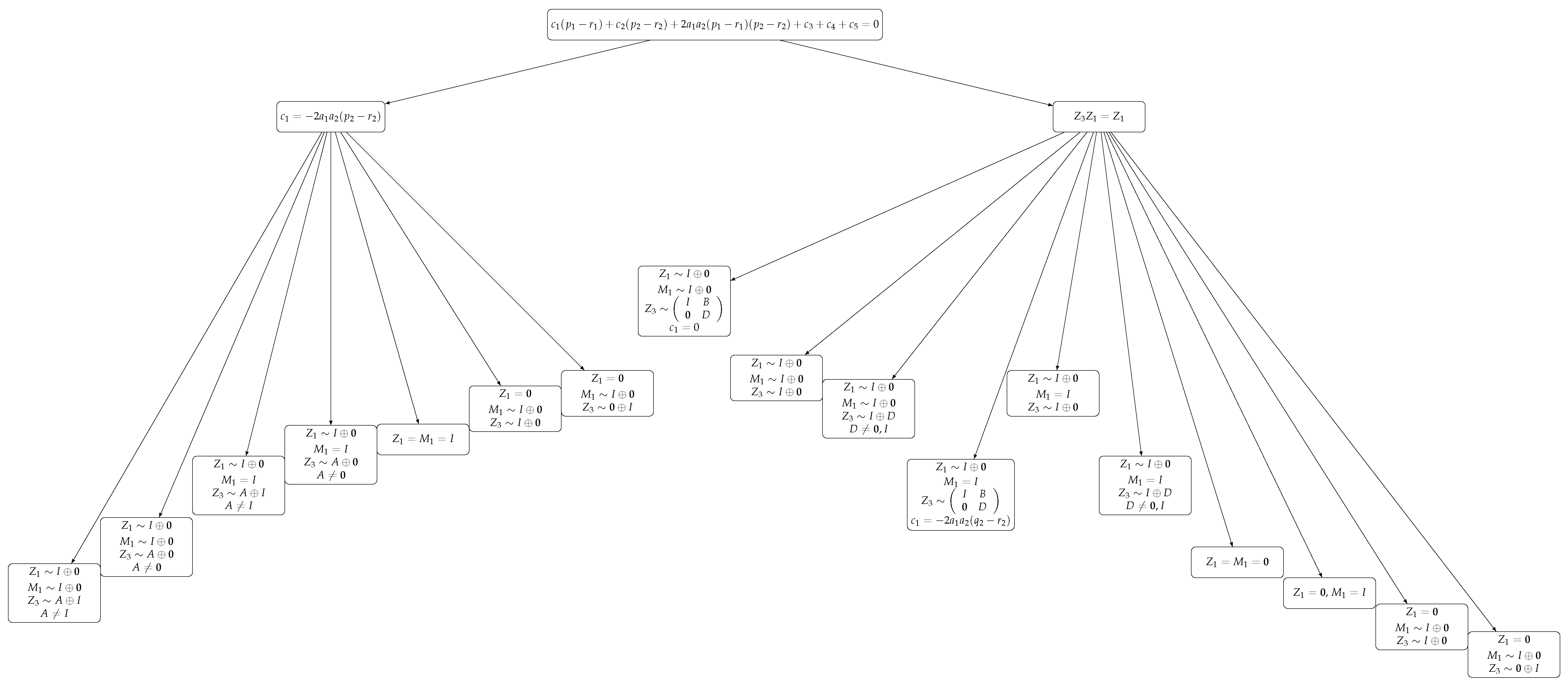
Now, similar to the diagram that we provided earlier for the equality (21), let us present a diagram for the equality (20). Since examining the equality (21) is more comprehensive than the equality (20), we will present the diagram in two parts.

The equality (20) is initially divided into two cases, as will be seen in the later parts of the proof:

$$c_1(p_1-r_1)+c_2(p_2-r_2)+2a_1{a}_2(p_1-r_1)(p_2-r_2)+c_3+c_4+c_5=0$$

and

$$Z_3{Z}_1=\mathbf{0}.$$

Each of these cases is further subdivided into subcases. Figure 2 and Figure 3 summarize this situation.

We now proceed to examine the equality (20) in detail.

Taking into account that $Z_1^2=Z_1$ and $Z_1{M}_1=M_1{Z}_1=Z_1$, and multiplying the equality (20) on the right by the matrix $Z_1$, after the necessary simplifications, one obtains

$$\begin{array}{cc}\hfill & (c_2(p_2-r_2)+2a_1{a}_2(q_1-r_1)(p_2-r_2)+c_1(q_1-r_1)+c_3+c_4+c_5)Z_1\hfill \\ \hfill & +(c_1(p_1-q_1)+2a_1{a}_2(p_1-q_1)(p_2-r_2))Z_3{Z}_1=\mathbf{0}.\hfill \end{array}$$

(24)

Subsequently, multiplying (24) on the left by the idempotent matrix $Z_3$ yields

$$(c_1(p_1-r_1)+c_2(p_2-r_2)+2a_1{a}_2(p_1-r_1)(p_2-r_2)+c_3+c_4+c_5)Z_3{Z}_1=\mathbf{0}.$$

(25)

There arise two possible situations:

• Case 1. $Z_3{Z}_1=\mathbf{0}$.

In this case, from (24), it follows that

$$(c_1(q_1-r_1)+c_2(p_2-r_2)+2a_1{a}_2(q_1-r_1)(p_2-r_2)+c_3+c_4+c_5)Z_1=\mathbf{0}.$$

Within this framework, two further subcases can be distinguished:

• Case 1.a. $Z_1=\mathbf{0}$.

From (20), it directly follows that

$$\begin{array}{cc}\hfill & (c_2(q_2-r_2)+2a_1{a}_2(q_1-r_1)(q_2-r_2)+c_4)M_1+c_1(p_1-q_1)Z_3\hfill \\ \hfill & +(c_1(q_1-r_1)+c_3+c_5)I+2a_1{a}_2(p_1-q_1)(q_2-r_2)Z_3{M}_1=\mathbf{0}.\hfill \end{array}$$

(26)

Furthermore, since $Z_1=\mathbf{0}$, we deduce from (17) that

$$X=(q_2-r_2)M_1.$$

From (19), we have

$$K=(p_1-q_1)Z_3+(q_1-r_1)I.$$

Combining the last two equalities with the relation $XK=KX$ and the assumptions $p_1\ne q_1$, $q_2\ne r_2$, we deduce that $M_1{Z}_3=Z_3{M}_1$. Since $M_1$ and $Z_3$ are commuting idempotent matrices, the following cases must therefore be considered:

$$\begin{array}{c}(M_1\sim I\oplus \mathbf{0},Z_3\sim I\oplus \mathbf{0}),(M_1\sim I\oplus \mathbf{0},Z_3\sim \mathbf{0}\oplus I),\hfill \\ (M_1=I,Z_3\sim I\oplus \mathbf{0}),(M_1=\mathbf{0},Z_3\sim I\oplus \mathbf{0}).\hfill \end{array}$$

It should be observed that $Z_3$ cannot be the zero matrix or the identity matrix, since in either case $A_1$ degenerates into a quadratic matrix, which contradicts its essentially cubic structure.

Next, we consider the aforementioned cases individually.

• Case 1.a.1. $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}$.

Under this configuration, from (26), we get

$$c_4=-c_1(p_1-q_1)-c_2(q_2-r_2)-2a_1{a}_2(p_1-r_1)(q_2-r_2),c_5=-c_1(q_1-r_1)-c_3.$$

• Case 1.a.2. $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim \mathbf{0}\oplus I$.

In this setting, the equality (26) gives

$$c_4=c_1(p_1-q_1)-c_2(q_2-r_2)-2a_1{a}_2(q_1-r_1)(q_2-r_2),c_5=-c_1(p_1-r_1)-c_3.$$

• Case 1.a.3. $M_1=I$, $Z_3\sim I\oplus \mathbf{0}$.

In this case, the equality (26) yields

$$c_1=-2a_1{a}_2(q_2-r_2),c_5=-c_2(q_2-r_2)-c_3-c_4.$$

• Case 1.a.4. $M_1=\mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}$.

With these assumptions, from the equality (26), one has

$$c_1=0,c_5=-c_3.$$

• Case 1.b. $c_1(q_1-r_1)+c_2(p_2-r_2)+2a_1{a}_2(q_1-r_1)(p_2-r_2)+c_3+c_4+c_5=0$.

Here, we have

$$c_3+c_4+c_5=-c_1(q_1-r_1)-c_2(p_2-r_2)-2a_1{a}_2(q_1-r_1)(p_2-r_2).$$

(27)

On the other hand, since $Z_3{Z}_1=\mathbf{0}$, from (20), it follows that

$$\begin{array}{cc}\hfill & (c_2(p_2-q_2)+2a_1{a}_2(q_1-r_1)(p_2-q_2))Z_1\hfill \\ \hfill & +(c_2(q_2-r_2)+2a_1{a}_2(q_1-r_1)(q_2-r_2)+c_4)M_1+c_1(p_1-q_1)Z_3\hfill \\ \hfill & +(c_1(q_1-r_1)+c_3+c_5)I+2a_1{a}_2(p_1-q_1)(q_2-r_2)Z_3{M}_1=\mathbf{0}.\hfill \end{array}$$

(28)

Next, we carry out the analysis according to the possible cases of $Z_1$ and $M_1$.

• Case 1.b.1. $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim \left(\begin{array}{cc}A& B\\ C& D\end{array}\right)$.

Since $Z_3{Z}_1=\mathbf{0}$, we have $A=\mathbf{0}$ and $C=\mathbf{0}$. Therefore, $Z_3\sim \left(\begin{array}{cc}\mathbf{0}& B\\ \mathbf{0}& D\end{array}\right)$. Because of the idempotency of $Z_3$, it is clear that $BD=B$ and $D^2=D$. If the matrices similar to $Z_1$, $M_1$, and $Z_3$ are substituted into the equality (28), we obtain

$$\begin{array}{c}{c}_1(q_1-r_1)+c_2(p_2-r_2)+2a_1{a}_2(q_1-r_1)(p_2-r_2)+c_3+c_4+c_5=0,\hfill \\ \mathrm{which}\mathrm{coincides}\mathrm{with}\left(27\right),\hfill \end{array}$$

$$c_1(p_1-q_1)B=\mathbf{0},$$

(29)

and

$$c_1(p_1-q_1)D+(c_1(q_1-r_1)+c_3+c_5)I=\mathbf{0}.$$

(30)

By the equality (29), there are two subcases:

• Case 1.b.1.1. $c_1=0.$

In this case, from (30), the equality

$$c_5=-c_3$$

(31)

is obtained. Thus, taking the equalities (27) and (31) into account yields the following set of results:

$$c_1=0,c_5=-c_3,c_4=-c_2(p_2-r_2)-2a_1{a}_2(q_1-r_1)(p_2-r_2).$$

• Case 1.b.1.2. $B=\mathbf{0}.$

In this case, $D\ne \mathbf{0}$; otherwise, $Z_3=\mathbf{0}$. Thus, without loss of generality, we may assume that $D=I$ or $D\sim I\oplus \mathbf{0}$.

• Case 1.b.1.2-1. $D=I.$

From (30), we get

$$c_1(p_1-r_1)+c_3+c_5=0.$$

(32)

Thus, by taking (27) and (32) together with the hypotheses of this case into account, we deduce that

$$\begin{array}{c}B=\mathbf{0},D=I,c_4=c_1(p_1-q_1)-c_2(p_2-r_2)-2a_1{a}_2(q_1-r_1)(p_2-r_2),\hfill \\ c_5=-c_1(p_1-r_1)-c_3.\hfill \end{array}$$

• Case 1.b.1.2-2. $D\sim I\oplus \mathbf{0}.$

Here, the equalities

$$c_1=0,c_3+c_5=0$$

(33)

are obtained from (30). If the hypotheses of this case and the equalities (27) and (33) are considered, then we arrive at

$$B=\mathbf{0},D\sim I\oplus \mathbf{0},c_1=0,c_5=-c_3,c_4=-c_2(p_2-r_2)-2a_1{a}_2(q_1-r_1)(p_2-r_2).$$

• Case 1.b.2. $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_3\sim \left(\begin{array}{cc}A& B\\ C& D\end{array}\right).$

The condition $Z_3{Z}_1=\mathbf{0}$ leads to $Z_3\sim \left(\begin{array}{cc}\mathbf{0}& B\\ \mathbf{0}& D\end{array}\right).$ Also, because of the idempotency of the matrix $Z_3$, we have $BD=B$ and $D^2=D$. Substituting the matrices similar to $Z_1$, $M_1$, and $Z_3$ into (28) yields

$$\begin{array}{c}{c}_1(q_1-r_1)+c_2(p_2-r_2)+2a_1{a}_2(q_1-r_1)(p_2-r_2)+c_3+c_4+c_5=0,\hfill \\ \mathrm{which}\mathrm{is}\mathrm{the}\mathrm{same}\mathrm{with}\left(27\right),\hfill \end{array}$$

$$(p_1-q_1)(c_1+2a_1{a}_2(q_2-r_2))B=\mathbf{0},$$

(34)

and

$$\begin{array}{cc}\hfill & (c_1(q_1-r_1)+c_2(q_2-r_2)+2a_1{a}_2(q_1-r_1)(q_2-r_2)+c_3+c_4+c_5)I\hfill \\ & +(c_1(p_1-q_1)+2a_1{a}_2(p_1-q_1)(q_2-r_2))D=\mathbf{0}.\hfill \end{array}$$

(35)

By (34), there are two subcases:

• Case 1.b.2.1. $c_1=-2a_1{a}_2(q_2-r_2).$

In this case, the equalities (27) and (35) yield

$$c_2(p_2-r_2)+2a_1{a}_2(q_1-r_1)(p_2-q_2)+c_3+c_4+c_5=0$$

(36)

and

$$c_2(q_2-r_2)+c_3+c_4+c_5=0,$$

(37)

respectively. If (37) is subtracted from (36), then we obtain

$$c_2=-2a_1{a}_2(q_1-r_1).$$

(38)

Thus, from (37), (38), and the hypothesis of this case, we obtain

$$c_1=-2a_1{a}_2(q_2-r_2),c_2=-2a_1{a}_2(q_1-r_1),c_5=-c_2(q_2-r_2)-c_3-c_4.$$

• Case 1.b.2.2. $B=\mathbf{0}.$

In this case, $D\ne \mathbf{0}$, since otherwise $Z_3=\mathbf{0}$. Consequently, one may conclude that $D=I$ or $D\sim I\oplus \mathbf{0}$.

• Case 1.b.2.2-1. The Case $D=I.$

In this case, from (35),

$$c_1(p_1-r_1)+c_2(q_2-r_2)+2a_1{a}_2(p_1-r_1)(q_2-r_2)+c_3+c_4+c_5=0$$

(39)

is obtained. Employing the equality (27) in (39), we obtain

$$(p_1-q_1)(c_1+2a_1{a}_1(q_2-r_2))+(q_2-p_2)(c_2+2a_1{a}_2(q_1-r_1))=0.$$

(40)

Thus, from (27) and (40), we conclude that

$$\begin{array}{c}\hfill c_5=-c_1(q_1-r_1)-c_2(p_2-r_2)-2a_1{a}_2(q_1-r_1)(p_2-r_2)-c_3-c_4,B=\mathbf{0},D=I,\\ \hfill -c_1(p_1-q_1)+c_2(p_2-q_2)=2a_1{a}_2[(q_2-r_2)(p_1-q_1)-(q_1-r_1)(p_2-q_2)]\end{array}$$

by the hypotheses of this case.

• Case 1.b.2.2-2. $D\sim I\oplus \mathbf{0}.$

From (35), we get

$$c_1(p_1-r_1)+c_2(q_2-r_2)+2a_1{a}_2(p_1-r_1)(q_2-r_2)+c_3+c_4+c_5=0$$

(41)

and

$$c_1(q_1-r_1)+c_2(q_2-r_2)+2a_1{a}_2(q_1-r_1)(q_2-r_2)+c_3+c_4+c_5=0.$$

(42)

If the equality (42) is subtracted from (41), then

$$c_1=-2a_1{a}_2(q_2-r_2)$$

(43)

is obtained. If the equalities (27) and (43) are considered together with the hypotheses of this case and the equality (41) (or (42)), then we arrive at

$$\begin{array}{c}B=\mathbf{0},D\sim I\oplus \mathbf{0},c_1=-2a_1{a}_2(q_2-r_2),c_2=-2a_1{a}_2(q_1-r_1),\hfill \\ c_3+c_4+c_5=2a_1{a}_2(q_1-r_1)(q_2-r_2).\hfill \end{array}$$

• Case 1.b.3. $Z_1=\mathbf{0}$, $M_1=\mathbf{0}.$

From (28), we have

$$c_1(p_1-q_1)Z_3+(c_1(q_1-r_1)+c_3+c_5)I=\mathbf{0}.$$

(44)

As $Z_3$ is neither the identity nor the zero matrix, it follows that, without loss of generality, $Z_3\sim I\oplus \mathbf{0}$. Thus, in this case, from (44) and (27), we get

$$c_1=0,c_5=-c_3,c_4=-c_2(p_2-r_2)-2a_1{a}_2(q_1-r_1)(p_2-r_2).$$

• Case 1.b.4. $Z_1=\mathbf{0}$, $M_1=I.$

Here, in view of (28), one obtains

$$\begin{array}{c}\hfill (c_1(q_1-r_1)+c_2(q_2-r_2)+2a_1{a}_2(q_1-r_1)(q_2-r_2)+c_3+c_4+c_5)I\\ \hfill +(c_1(p_1-q_1)+2a_1{a}_2(p_1-q_1)(q_2-r_2))Z_3=\mathbf{0}.\end{array}$$

(45)

Since $Z_3\sim I\oplus \mathbf{0}$, from (27) and (45), we conclude that

$$c_1=-2a_1{a}_2(q_2-r_2),c_2=-2a_1{a}_2(q_1-r_1),c_3+c_4+c_5=-c_2(q_2-r_2).$$

• Case 1.b.5. $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$.

Under this assumption, considering the cases $Z_3\sim I\oplus \mathbf{0}$ and $Z_3\sim \mathbf{0}\oplus I$, we obtain two distinct results. In the case $Z_3\sim I\oplus \mathbf{0}$, we get

$$\begin{array}{c}\hfill c_4=-c_2(p_2-r_2)-2a_1{a}_2(q_1-r_1)(p_2-r_2),c_5=-c_1(q_1-r_1)-c_3,\\ \hfill -c_1(p_1-q_1)+c_2(p_2-q_2)=2a_1{a}_2[(p_1-r_1)(q_2-r_2)-(p_2-r_2)(q_1-r_1)]\end{array}$$

by (27) and (28). Similarly, in the case $Z_3\sim \mathbf{0}\oplus I$, we obtain

$$c_2=-2a_1{a}_2(q_1-r_1),c_4=c_1(p_1-q_1),c_5=-c_1(p_1-r_1)-c_3$$

by (27) and (28).

Based on the foregoing analysis, the following theorem can be established:

Theorem 6. 

The necessary and sufficient condition the equality (20) to hold, provided that $Z_3{Z}_1=\mathbf{0}$, is that one of the following conditions is satisfied, where $Z_1,M_1,Z_3$ are the matrices in (17) and (19):

 (1)

$c_4=-c_1(p_1-q_1)-c_2(q_2-r_2)-2a_1{a}_2(p_1-r_1)(q_2-r_2),c_5=-c_1(q_1-r_1)-c_3$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}$.

 (2)

$c_4=c_1(p_1-q_1)-c_2(q_2-r_2)-2a_1{a}_2(q_1-r_1)(q_2-r_2),c_5=-c_1(p_1-r_1)-c_3$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim \mathbf{0}\oplus I$.

 (3)

$c_1=-2a_1{a}_2(q_2-r_2),c_5=-c_2(q_2-r_2)-c_3-c_4$, $Z_1=\mathbf{0}$, $M_1=I$, $Z_3\sim I\oplus \mathbf{0}$.

 (4)

$c_1=0,c_5=-c_3$, $Z_1=\mathbf{0}$, $M_1=\mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}$.

 (5)

$c_1=0,c_5=-c_3,c_4=-c_2(p_2-r_2)-2a_1{a}_2(q_1-r_1)(p_2-r_2)$,

$Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $\mathbf{0},I\ne Z_3\sim \left(\begin{array}{cc}\mathbf{0}& B\\ \mathbf{0}& D\end{array}\right)$.

 (6)

$c_4=c_1(p_1-q_1)-c_2(p_2-r_2)-2a_1{a}_2(q_1-r_1)(p_2-r_2),c_5=-c_1(p_1-r_1)-c_3$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim \mathbf{0}\oplus I.$

 (7)

$c_1=0,c_5=-c_3,c_4=-c_2(p_2-r_2)-2a_1{a}_2(q_1-r_1)(p_2-r_2)$,

$Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $\mathbf{0},I\ne Z_3\sim \mathbf{0}\oplus D$, $D\ne \mathbf{0},I$.

 (8)

$c_1=-2a_1{a}_2(q_2-r_2),c_2=-2a_1{a}_2(q_1-r_1),c_5=-c_2(q_2-r_2)-c_3-c_4$,

$Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $\mathbf{0},I\ne Z_3\sim \left(\begin{array}{cc}\mathbf{0}& B\\ \mathbf{0}& D\end{array}\right)$.

 (9)

$c_5=-c_1(q_1-r_1)-c_2(p_2-r_2)-2a_1{a}_2(q_1-r_1)(p_2-r_2)-c_3-c_4,-c_1(p_1-q_1)+c_2(p_2-q_2)=2a_1{a}_2[(q_2-r_2)(p_1-q_1)-(q_1-r_1)(p_2-q_2)]$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_3\sim \mathbf{0}\oplus I$.

 (10)

$c_1=-2a_1{a}_2(q_2-r_2),c_2=-2a_1{a}_2(q_1-r_1),c_3+c_4+c_5=2a_1{a}_2(q_1-r_1)(q_2-r_2)$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $\mathbf{0},I\ne Z_3\sim \mathbf{0}\oplus D$, $D\ne \mathbf{0},I$.

 (11)

$c_1=0,c_5=-c_3,c_4=-c_2(p_2-r_2)-2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $Z_1=\mathbf{0}$, $M_1=\mathbf{0}$, $Z_3\ne \mathbf{0},I$.

 (12)

$c_1=-2a_1{a}_2(q_2-r_2),c_2=-2a_1{a}_2(q_1-r_1),c_3+c_4+c_5=-c_2(q_2-r_2)$, $Z_1=\mathbf{0}$, $M_1=I$, $Z_3\ne \mathbf{0},I$.

 (13)

$c_4=-c_2(p_2-r_2)-2a_1{a}_2(q_1-r_1)(p_2-r_2),c_5=-c_1(q_1-r_1)-c_3,-c_1(p_1-q_1)+c_2(p_2-q_2)=2a_1{a}_2[(p_1-r_1)(q_2-r_2)-(p_2-r_2)(q_1-r_1)]$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}$.

 (14)

$c_2=-2a_1{a}_2(q_1-r_1),c_4=c_1(p_1-q_1),c_5=-c_1(p_1-r_1)-c_3$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim \mathbf{0}\oplus I$.

Next, we examine the second case:

• Case 2. $c_1(p_1-r_1)+c_2(p_2-r_2)+2a_1{a}_2(p_1-r_1)(p_2-r_2)+c_3+c_4+c_5=0.$

In this case,

$$-c_1(p_1-r_1)-c_2(p_2-r_2)-2a_1{a}_2(p_1-r_1)(p_2-r_2)=c_3+c_4+c_5$$

(46)

is obtained. Therefore, from (24) we get

$$(p_1-q_1)(c_1+2a_1{a}_2(p_2-r_2))(Z_3{Z}_1-Z_1)=\mathbf{0}.$$

Thus, there are two cases:

• Case 2.a. $c_1=-2a_1{a}_2(p_2-r_2).$

Under this assumption, the equality (46) leads to

$$c_3+c_4+c_5=-c_2(p_2-r_2).$$

(47)

Thus, from (47) and the hypothesis of this case, we have

$$c_1=-2a_1{a}_2(p_2-r_2),c_5=-c_2(p_2-r_2)-c_3-c_4.$$

(48)

Since $XK=KX$, it is obvious that

$$(p_2-q_2)(Z_1{Z}_3-Z_3{Z}_1)=(q_2-r_2)(Z_3{M}_1-M_1{Z}_3).$$

(49)

The following observations arise from the fact that $Z_1$ and $M_1$ are idempotent matrices with $Z_1{M}_1=M_1{Z}_1=Z_1$.

• Case 2.a.1. $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim \left(\begin{array}{cc}A& B\\ C& D\end{array}\right).$

If the matrices that are similar to $Z_1$, $M_1$, and $Z_3$ are substituted into (49), then we obtain $B=\mathbf{0}$ and $C=\mathbf{0}$. Therefore, we have $Z_3\sim \left(\begin{array}{cc}A& \mathbf{0}\\ \mathbf{0}& D\end{array}\right)$. In a similar manner, inserting the matrices similar to $Z_1$, $M_1$, and $Z_3$ into (20) results in

$$c_2(p_2-r_2)+c_3+c_4+c_5=0,\mathrm{which}\mathrm{is}\mathrm{the}\mathrm{same}\mathrm{with}\left(47\right)$$

and

$$-2a_1{a}_2(p_1-q_1)(p_2-r_2)D+(c_3+c_5-2a_1{a}_2(q_1-r_1)(p_2-r_2))I=\mathbf{0}.$$

(50)

• Case 2.a.1.1. $D=I.$

From (48) and (50), we arrive at the results

$$\begin{array}{c}D=I,c_1=-2a_1{a}_2(p_2-r_2),c_3+c_5=2a_1{a}_2(p_1-r_1)(p_2-r_2),\hfill \\ c_4=(p_2-r_2)(-c_2-2a_1{a}_2(p_1-r_1)).\hfill \end{array}$$

• Case 2.a.1.2. $D=\mathbf{0}.$

The equalities (48) and (50) yield

$$\begin{array}{c}D=\mathbf{0},c_1=-2a_1{a}_2(p_2-r_2),c_3+c_5=2a_1{a}_2(q_1-r_1)(p_2-r_2),\hfill \\ c_4=(p_2-r_2)(-c_2-2a_1{a}_2(q_1-r_1)).\hfill \end{array}$$

• Case 2.a.1.3. $D\sim I\oplus \mathbf{0}.$

In this case, the contradiction $p_1=q_1$ is obtained.

• Case 2.a.2. $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_3\sim \left(\begin{array}{cc}A& B\\ C& D\end{array}\right).$
• In this case, it is seen that $Z_3\sim \left(\begin{array}{cc}A& \mathbf{0}\\ \mathbf{0}& D\end{array}\right)$ by (49). Thus, from (20), we get

  $$(c_2+2a_1{a}_2(q_1-r_1))I+2a_1{a}_2(p_1-q_1)D=\mathbf{0}.$$

  (51)

• Case 2.a.2.1. $D=I.$

From (48) and (51), we obtain

$$D=I,c_1=-2a_1{a}_2(p_2-r_2),c_2=-2a_1{a}_2(p_1-r_1),c_3+c_4+c_5=-c_2(p_2-r_2).$$

• Case 2.a.2.2. $D=\mathbf{0}.$

In this case, the equalities (48) and (51) lead to

$$D=\mathbf{0},c_1=-2a_1{a}_2(p_2-r_2),c_2=-2a_1{a}_2(q_1-r_1),c_3+c_4+c_5=-c_2(p_2-r_2).$$

• Case 2.a.2.3. $D\sim I\oplus \mathbf{0}.$

The equality (51) yields the contradiction $p_1=q_1$.

• Case 2.a.3. $Z_1=I$, $M_1=I$.

In this case, the equality (20) is satisfied automatically. Thus, considering (48), we get

$$c_1=-2a_1{a}_2(p_2-r_2),c_3+c_4+c_5=-c_2(p_2-r_2).$$

• Case 2.a.4. $Z_1=\mathbf{0}$ and $M_1=\mathbf{0}.$

In this case, without loss of generality, we can write $Z_3\sim I\oplus \mathbf{0}$. On the other hand, from (20), we get

$$c_1(p_1-q_1)Z_3+(c_1(q_1-r_1)+c_3+c_5)I=\mathbf{0}.$$

(52)

Since $Z_3\sim I\oplus \mathbf{0}$, from (52) we obtain $c_1=0$ and $c_5=-c_3$. On the other hand, according to the hypothesis of Case 2.a, we have $c_1=-2a_1{a}_2(p_2-r_2)$. Hence, we arrive at the contradiction $p_2=r_2$ or $a_1=0$, or $a_2=0$.

• Case 2.a.5. $Z_1=\mathbf{0}$ and $M_1=I$.

Similar to the previous case, it is obvious that $Z_3\sim I\oplus \mathbf{0}$. The equalities (20) and (48) lead to

$$(c_2(q_2-p_2)+2a_1{a}_2(q_1-r_1)(q_2-p_2))I+2a_1{a}_2(p_1-q_1)(q_2-p_2)Z_3=\mathbf{0}.$$

(53)

Since $Z_3\sim I\oplus \mathbf{0}$, from (53), we obtain $c_2=-2a_1{a}_2(q_1-r_1)$ and $c_2=-2a_1{a}_2(p_1-r_1)$. Thus, we have the contradiction $p_1=q_1$ or $a_1=0$ or $a_2=0$ or $p_1=q_1=r_1$.

• Case 2.a.6. $Z_1=\mathbf{0}$ and $M_1\sim I\oplus \mathbf{0}$.

In this case, according to the matrix $Z_3$, there are two different cases:

• Case 2.a.6.1. $Z_3\sim I\oplus \mathbf{0}.$

In this case, from the equalities (20) and (48), we get

$$\begin{array}{cc}\hfill c_1& =-2a_1{a}_2(p_2-r_2),c_2=-2a_1{a}_2(p_1-r_1),\hfill \\ \hfill c_4& =2a_1{a}_2(p_2-r_2)(p_1-q_1),c_3+c_5=2a_1{a}_2(q_1-r_1)(p_2-r_2).\hfill \end{array}$$

• Case 2.a.6.2. $Z_3\sim \mathbf{0}\oplus I.$

Here, by the equalities (20) and (48), we obtain

$$\begin{array}{cc}\hfill c_1& =-2a_1{a}_2(p_2-r_2),c_2=-2a_1{a}_2(q_1-r_1),\hfill \\ \hfill c_4& =2a_1{a}_2(p_2-r_2)(q_1-p_1),c_3+c_5=2a_1{a}_2(p_1-r_1)(p_2-r_2).\hfill \end{array}$$

• Case 2.b. $Z_3{Z}_1=Z_1.$

In this case, from (25), we get

$$(c_1(p_1-r_1)+c_2(p_2-r_2)+2a_1{a}_2(p_1-r_1)(p_2-r_2)+c_3+c_4+c_5)Z_1=\mathbf{0}.$$

(54)

By (54), we have $Z_1=\mathbf{0}$ or $c_3+c_4+c_5=-c_1(p_1-r_1)-c_2(p_2-r_2)-2a_1{a}_2(p_1-r_1)(p_2-r_2)$, which is the same with (46). Now, we consider the following cases:

• Case 2.b.1. $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim \left(\begin{array}{cc}A& B\\ C& D\end{array}\right).$

Since $Z_3{Z}_1=Z_1$, we have $Z_3\sim \left(\begin{array}{cc}I& B\\ \mathbf{0}& D\end{array}\right).$ Thus, from (20),

$$c_1(p_1-r_1)+c_2(p_2-r_2)+2a_1{a}_2(p_1-r_1)(p_2-r_2)+c_3+c_4+c_5=0,\mathrm{which}\mathrm{is}\left(46\right)$$

$$c_1(p_1-q_1)B=\mathbf{0},$$

(55)

and

$$c_1(q_1-r_1)+c_3+c_5)I+c_1(p_1-q_1)D=\mathbf{0}$$

(56)

are obtained. By (55), there are two subcases:

• Case 2.b.1.1. $c_1=0.$

In this case, from (46) and (56), we get

$$c_3+c_4+c_5=-c_2(p_2-r_2)-2a_1{a}_2(p_1-r_1)(p_2-r_2)$$

and

$$c_5=-c_3,$$

respectively. Thus, in this case, we have

$$c_1=0,c_4=(p_2-r_2)(-c_2-2a_1{a}_2(p_1-r_1)),c_5=-c_3.$$

• Case 2.b.1.2. $B=\mathbf{0}.$

According to the matrix D, two different subcases will be considered:

• Case 2.b.1.2-1. $D=\mathbf{0}.$

In this case, from (56),

$$c_3+c_5=-c_1(q_1-r_1)$$

(57)

is obtained. If the equality (57) is substituted into (46), then we get

$$c_4=-c_1(p_1-q_1)-c_2(p_2-r_2)-2a_1{a}_2(p_1-r_1)(p_2-r_2).$$

(58)

Considering (57) and (58) together with the hypotheses of this case leads to

$$\begin{array}{c}B=\mathbf{0},D=\mathbf{0},c_4=-c_1(p_1-q_1)-c_2(p_2-r_2)-2a_1{a}_2(p_1-r_1)(p_2-r_2),\hfill \\ c_5=-c_1(q_1-r_1)-c_3.\hfill \end{array}$$

• Case 2.b.1.2-2. $D\sim I\oplus \mathbf{0}.$

The equality (56) gives

$$c_3+c_5=-c_1(p_1-r_1)=-c_1(q_1-r_1).$$

(59)

Since $p_1\ne q_1$, we have $c_1=0$. Thus, from (59), we get $c_5=-c_3$. Thus, we arrive at

$$c_1=0,c_5=-c_3,c_4=c_2(p_2-r_2)-2a_1{a}_2(p_1-r_1)(p_2-r_2)$$

in view of (46).

• Case 2.b.2. $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_3\sim \left(\begin{array}{cc}A& B\\ C& D\end{array}\right).$

It is clear that $Z_3\sim \left(\begin{array}{cc}I& B\\ \mathbf{0}& D\end{array}\right)$ because $Z_3{Z}_1=Z_1$. Thus, from (20), we get

$$c_1(p_1-r_1)+c_2(p_2-r_2)+2a_1{a}_2(p_1-r_1)(p_2-r_2)+c_3+c_4+c_5=0,\mathrm{which}\mathrm{is}\left(46\right)$$

(60)

$$(p_1-q_1)(c_1+2a_1{a}_2(q_2-r_2))B=\mathbf{0},$$

and

$$\begin{array}{cc}\hfill & (c_1(q_1-r_1)+c_2(q_2-r_2)+2a_1{a}_2(q_1-r_1)(q_2-r_2)+c_3+c_4+c_5)I\hfill \\ \hfill & +(c_1(p_1-q_1)+2a_1{a}_2(p_1-q_1)(q_2-r_2))D=\mathbf{0}.\hfill \end{array}$$

(61)

The subsequent analysis will be carried out by distinguishing cases based on the assumptions imposed on $c_1$ and B.

• Case 2.b.2.1. $c_1=-2a_1{a}_2(q_2-r_2)$.

In this case, from (60) and (61), we obtain

$$c_2(p_2-r_2)+2a_1{a}_2(p_1-r_1)(p_2-q_2)+c_3+c_4+c_5=0$$

(62)

and

$$c_2(q_2-r_2)+c_3+c_4+c_5=0,$$

(63)

respectively. By subtracting the equalities (62) and (63) side by side and performing the necessary simplifications, one obtains

$$c_2=-2a_1{a}_2(p_1-r_1).$$

(64)

The equalities (63) and (64), together with the hypothesis of this case, lead to

$$c_1=-2a_1{a}_2(q_2-r_2),c_2=-2a_1{a}_2(p_1-r_1),c_5=-c_2(q_2-r_2)-c_3-c_4.$$

• Case 2.b.2.2. $B=\mathbf{0}.$

A case-by-case analysis will be performed with respect to the matrix D.

• Case 2.b.2.2-1. $D=\mathbf{0}.$

In this case, from (61) and (60), we have

$$c_3+c_4+c_5=-c_1(q_1-r_1)-c_2(q_2-r_2)-2a_1{a}_2(q_1-r_1)(q_2-r_2)$$

(65)

and

$$c_3+c_4+c_5=-c_1(p_1-r_1)-c_2(p_2-r_2)-2a_1{a}_2(p_1-r_1)(p_2-r_2),$$

(66)

respectively. Thus, by considering the hypotheses of this case, from (65) and (66), we obtain

$$\begin{array}{cc}\hfill B& =\mathbf{0},D=\mathbf{0},\hfill \\ \hfill c_3+c_4+c_5& =-c_1(p_1-r_1)-c_2(p_2-r_2)-2a_1{a}_2(p_1-r_1)(p_2-r_2)\hfill \\ \hfill & =-c_1(q_1-r_1)-c_2(q_2-r_2)-2a_1{a}_2(q_1-r_1)(q_2-r_2).\hfill \end{array}$$

• Case 2.b.2.2-3. $D\sim I\oplus \mathbf{0}.$

From (61), the equalities

$$c_1(q_1-r_1)+c_2(q_2-r_2)+2a_1{a}_2(q_1-r_1)(q_2-r_2)+c_3+c_4+c_5=0$$

(67)

and

$$c_1(p_1-r_1)+c_2(q_2-r_2)+2a_1{a}_2(p_1-r_1)(q_2-r_2)+c_3+c_4+c_5=0$$

(68)

are obtained. Subtracting the equality (68) from the equality (67) yields the result

$$c_1=-2a_1{a}_2(q_2-r_2).$$

(69)

Thus, from (67), we get

$$c_3+c_4+c_5=-c_2(q_2-r_2).$$

(70)

On the other hand, from (60), one has

$$c_2=-2a_1{a}_2(p_1-r_1)$$

(71)

by considering the equality $c_1=-2a_1{a}_2(q_2-r_2)$ and the equality (70). Thus, from (69), (70), and (71), we have

$$B=\mathbf{0},D\sim I\oplus \mathbf{0},c_1=-2a_1{a}_2(q_2-r_2),c_2=-2a_1{a}_2(p_1-r_1),c_3+c_4+c_5=-c_2(q_2-r_2)$$

taking the hypotheses of this case into account.

• Case 2.b.3. $Z_1=\mathbf{0}$ and $M_1=\mathbf{0}$.

Here, the equality (52) is valid. Since $Z_3\sim I\oplus \mathbf{0}$, from (52), we obtain $c_1=0$ and $c_5=-c_3$. Therefore, we have

$$c_1=0,c_5=-c_3,c_4=(p_2-r_2)(-c_2-2a_1{a}_2(p_1-r_1))$$

taking into account (46).

• Case 2.b.4. $Z_1=\mathbf{0}$ and $M_1=I.$

In this case, from (20), we get

$$\begin{array}{cc}\hfill & \left(c_1(q_1-r_1)+c_2(q_2-r_2)+2a_1{a}_2(q_1-r_1)(q_2-r_2)+c_3+c_4+c_5\right)I\hfill \\ \hfill & +\left(c_1(p_1-q_1)+2a_1{a}_2(p_1-q_1)(q_2-r_2)\right)Z_3=\mathbf{0}.\hfill \end{array}$$

(72)

Since $Z_3\sim I\oplus \mathbf{0}$, from (72) we obtain

$$c_3+c_4+c_5=-c_1(p_1-r_1)-c_2(q_2-r_2)-2a_1{a}_2(p_1-r_1)(q_2-r_2)$$

(73)

and

$$c_3+c_4+c_5=-c_1(q_1-r_1)-c_2(q_2-r_2)-2a_1{a}_2(q_1-r_1)(q_2-r_2).$$

(74)

By subtracting the equality (74) from the equality (73), one obtains

$$c_1=-2a_1{a}_2(q_2-r_2).$$

(75)

If the equality (75) is substituted into the equality (73), then we get

$$c_3+c_4+c_5=-c_2(q_2-r_2).$$

(76)

Substituting the equalities (75) and (76) into (46) leads to

$$c_2=-2a_1{a}_2(p_1-r_1).$$

(77)

Thus, the equalities (75), (76), and (77) yield the result

$$c_1=-2a_1{a}_2(q_2-r_2),c_2=-2a_1{a}_2(p_1-r_1),c_3+c_4+c_5=-c_2(q_2-r_2).$$

• Case 2.b.5. $Z_1=\mathbf{0}$ and $M_1\sim I\oplus \mathbf{0}.$

In this case, according to the matrix $Z_3$, there are two cases:

• Case 2.b.5.1. $Z_3\sim I\oplus \mathbf{0}.$

From (20) and (46), we obtain

$$c_2=-2a_1{a}_2(p_1-r_1),c_4=-c_1(p_1-q_1),c_3+c_5=-c_1(q_1-r_1).$$

• Case 2.b.5.2. $Z_3\sim \mathbf{0}\oplus I.$

From (20) and (46), one obtains

$$\begin{array}{cc}\hfill c_1(p_1-q_1)+c_2(p_2-q_2)& =-2a_1{a}_2\left[(p_1-r_1)(p_2-r_2)-(q_1-r_1)(q_2-r_2)\right],\hfill \\ \hfill c_4& =c_1(p_1-q_1)-c_2(q_2-r_2)-2a_1{a}_2(q_1-r_1)(q_2-r_2),\hfill \\ \hfill c_3+c_5& =-c_1(p_1-r_1).\hfill \end{array}$$

Thus, we can give the following theorem:

Theorem 7. 

The necessary and sufficient condition for the equality (20) to hold, provided that $-c_1(p_1-r_1)-c_2(p_2-r_2)-2a_1{a}_2(p_1-r_1)(p_2-r_2)=c_3+c_4+c_5$, is that one of the following conditions is satisfied, where $Z_1,M_1,Z_3$ are the matrices in (17) and (19):

 (15)

$c_1=-2a_1{a}_2(p_2-r_2)$, $c_3+c_5=2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $c_4=(p_2-r_2)(-c_2-2a_1{a}_2(p_1-r_1))$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $\mathbf{0},I\ne Z_3\sim A\oplus I$.

 (16)

$c_1=-2a_1{a}_2(p_2-r_2)$, $c_3+c_5=2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $c_4=(p_2-r_2)(-c_2-2a_1{a}_2(q_1-r_1))$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $\mathbf{0},I\ne Z_3\sim A\oplus \mathbf{0}$.

 (17)

$c_1=-2a_1{a}_2(p_2-r_2)$, $c_2=-2a_1{a}_2(p_1-r_1)$, $c_3+c_4+c_5=-c_2(p_2-r_2)$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $\mathbf{0},I\ne Z_3\sim A\oplus I$.

 (18)

$c_1=-2a_1{a}_2(p_2-r_2)$, $c_2=-2a_1{a}_2(q_1-r_1)$, $c_3+c_4+c_5=-c_2(p_2-r_2)$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $\mathbf{0},I\ne Z_3\sim A\oplus \mathbf{0}$.

 (19)

$c_1=-2a_1{a}_2(p_2-r_2)$, $c_3+c_4+c_5=-c_2(p_2-r_2)$, $Z_1=I$, $M_1=I$, $Z_3\ne \mathbf{0},I$.

 (20)

$c_1=-2a_1{a}_2(p_2-r_2)$, $c_2=-2a_1{a}_2(p_1-r_1)$, $c_4=2a_1{a}_2(p_2-r_2)(p_1-q_1)$, $c_3+c_5=2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}$.

 (21)

$c_1=-2a_1{a}_2(p_2-r_2)$, $c_2=-2a_1{a}_2(q_1-r_1)$, $c_4=2a_1{a}_2(p_2-r_2)(q_1-p_1)$, $c_3+c_5=2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim \mathbf{0}\oplus I$.

 (22)

$c_1=0$, $c_4=(p_2-r_2)(-c_2-2a_1{a}_2(p_1-r_1))$, $c_5=-c_3$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $\mathbf{0},I\ne Z_3\sim \left(\begin{array}{cc}I& B\\ \mathbf{0}& D\end{array}\right)$.

 (23)

$c_4=-c_1(p_1-q_1)-c_2(p_2-r_2)-2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $c_5=-c_1(q_1-r_1)-c_3$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}$.

 (24)

$c_1=0$, $c_5=-c_3$, $c_4=(p_2-r_2)(c_2-2a_1{a}_2(p_1-r_1))$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $\mathbf{0},I\ne Z_3\sim I\oplus D$, $D\ne \mathbf{0},I$.

 (25)

$c_1=-2a_1{a}_2(q_2-r_2)$, $c_2=-2a_1{a}_2(p_1-r_1)$, $c_5=-c_2(q_2-r_2)-c_3-c_4$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $\mathbf{0},I\ne Z_3\sim \left(\begin{array}{cc}I& B\\ \mathbf{0}& D\end{array}\right)$.

 (26)

$c_3+c_4+c_5=-c_1(p_1-r_1)-c_2(p_2-r_2)-2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $-c_1(p_1-q_1)-c_2(p_2-q_2)=2a_1{a}_2[(p_1-r_1)(p_2-r_2)-(q_1-r_1)(q_2-r_2)]$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_3\sim I\oplus \mathbf{0}$.

 (27)

$c_1=-2a_1{a}_2(q_2-r_2),c_2=-2a_1{a}_2(p_1-r_1),c_3+c_4+c_5=-c_2(q_2-r_2)$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $\mathbf{0},I\ne Z_3\sim I\oplus D$, $D\ne I,\mathbf{0}$.

 (28)

$c_1=0,c_5=-c_3,c_4=(p_2-r_2)(-c_2-2a_1{a}_2(p_1-r_1))$, $Z_1=\mathbf{0}$, $M_1=\mathbf{0}$, $Z_3\ne \mathbf{0},I$.

 (29)

$c_1=-2a_1{a}_2(q_2-r_2),c_2=-2a_1{a}_2(p_1-r_1),c_3+c_4+c_5=-c_2(q_2-r_2)$, $Z_1=\mathbf{0}$, $M_1=I$, $Z_3\ne \mathbf{0},I$.

 (30)

$c_2=-2a_1{a}_2(p_1-r_1),c_4=-c_1(p_1-q_1),c_3+c_5=-c_1(q_1-r_1)$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}.$

 (31)

$c_1(p_1-q_1)+c_2(p_2-q_2)=-2a_1{a}_2[(p_1-r_1)(p_2-r_2)-(q_1-r_1)(q_2-r_2)],c_4=c_1(p_1-q_1)-(q_2-r_2)(c_2+2a_1{a}_2(q_1-r_1)),c_3+c_5=-c_1(p_1-r_1)$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim \mathbf{0}\oplus I.$

In summary, Theorems 4 and 5 provide a rigorous foundation for the validity of Equation (21), while Theorems 6 and 7 firmly establish Equation (20). The pivotal objective, however, is to demonstrate the simultaneous validity of both Equations (20) and (21), which constitutes a critical step toward consolidating the theoretical framework under consideration. To this end, a careful and systematic analysis of the interplay between the pairs (Theorem 4, Theorem 6), (Theorem 4, Theorem 7), (Theorem 5, Theorem 6), and (Theorem 5, Theorem 7) becomes indispensable. Each of these combinations not only strengthens the consistency of the overall argument but also highlights the structural necessity of examining the results in an integrated manner.

Note that it is not possible for $Z_1$ and $Z_2$ to simultaneously be the identity matrix or the zero matrix. Accordingly, when the theorems are considered in conjunction, the cases $Z_1=\mathbf{0},Z_2=\mathbf{0}$ and $Z_1=I,Z_2=I$ are omitted from consideration. The observation formulated in the context of $Z_1$ and $Z_2$ remains valid, mutatis mutandis, for the pair $M_1$ and $M_4$. Here, not only these cases but many others are excluded from consideration—for instance, the cases where $Z_1=\mathbf{0}$, $M_1=\mathbf{0}$, $Z_2=I$, $M_4=I$; $Z_1=I$, $M_1=I$, $Z_2=\mathbf{0}$, $M_4=\mathbf{0}$; or $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_2=\mathbf{0}$, $M_4=\mathbf{0}$; and similar situations. When disregarding such cases, our main consideration is that the matrices $S^{-1}{B}_{1}S$ and $S^{-1}{B}_{2}S$ must have exactly three distinct eigenvalues on their diagonals; otherwise, the matrices $A_1$ and $A_2$ would not be essentially cubic. Taking this into account, we construct the intersections accordingly. Note that some of the intersections that do not appear in the tables have also been disregarded because they contradict one of the hypotheses $a_1,a_2\ne 0$ and $p_i\ne q_i,p_i\ne r_i,q_i\ne r_i$ for $i=1,2$.

The following

Table 1. Theorems 4–6.

Cases	Intersections
(i)-(5)	$c_1=0,c_5=-c_3=c_2(p_2-q_2)+2a_1{a}_2(q_1-r_1)(p_1-r_2)$, $c_4=-(p_2-r_2)(c_2+2a_1{a}_2(q_1-r_1)$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_2=\mathbf{0}$, $M_4=I$, $\mathbf{0},I\ne Z_3\sim \left(\begin{array}{cc}\mathbf{0}& B\\ \mathbf{0}& D\end{array}\right).$
(i)-(6)	$c_3=-c_2(p_2-q_2)-(q_1-r_1)(c_1+2a_1{a}_2(p_2-r_2))$, $c_4=c_1(p_1-q_1)-(p_2-r_2)(c_2+2a_1{a}_2(q_1-r_1)),c_5=-c_1(p_1-q_1)+c_2(p_2-q_2)+2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim \mathbf{0}\oplus I$, $Z_2=\mathbf{0}$, $M_4=I$.
(i)-(7)	$c_1=0,c_5=-c_3=c_2(p_2-q_2)+2a_1{a}_2(q_1-r_1)(p_2-r_2)$,    $c_4=-(p_2-r_2)(c_2+2a_1{a}_2(q_1-r_1)$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $\mathbf{0},I\ne Z_3\sim \mathbf{0}\oplus D$, $D\ne \mathbf{0},I$, $Z_2=\mathbf{0}$, $M_4=I$.
(ii)-(6)	$c_3=-c_1(p_1-r_1)$, $c_4=-c_2(q_2-r_2)$, $c_1(p_1-q_1)-c_2(p_2-q_2)=2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $c_5=0$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim \mathbf{0}\oplus I$, $Z_2=\mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$.
(ii)-(9)	$c_3=-(p_1-r_1)(c_1+2a_1{a}_2(q_2-r_2))$, $c_4=-c_2(q_2-r_2)$, $c_5=0$, $-c_1(p_1-q_1)+c_2(p_2-q_2)=2a_1{a}_2[(q_2-r_2)(p_1-q_1)-(q_1-r_1)(p_2-q_2)]$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_3\sim \mathbf{0}\oplus I$, $Z_2=\mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$.
(iii)-(8)	$c_1=-2a_1{a}_2(q_2-r_2)$, $c_2=-2a_1{a}_2(q_1-r_1)$, $c_4=2a_1{a}_2(q_1-r_1)(q_2-r_2)-c_3$, $c_5=0$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_2=\mathbf{0}$, $M_4=\mathbf{0}$, $\mathbf{0},I\ne Z_3\sim \left(\begin{array}{cc}\mathbf{0}& B\\ \mathbf{0}& D\end{array}\right)$.
(iii)-(9)	$c_4=-(q_1-r_1)(c_1+2a_1{a}_2(p_2-r_2))-c_2(p_2-r_2)-c_3$, $-c_1(p_1-q_1)+c_2(p_2-q_2)=2a_1{a}_2[(q_2-r_2)(p_1-q_1)-(q_1-r_1)(p_2-q_2)]$, $c_5=0$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_3\sim \mathbf{0}\oplus I$, $Z_2=\mathbf{0}$, $M_4=\mathbf{0}$.
(iii)-(10)	$c_1=-2a_1{a}_2(q_2-r_2)$, $c_2=-2a_1{a}_2(q_1-r_1)$, $c_4=2a_1{a}_2(q_1-r_1)(q_2-r_2)-c_3$, $c_5=0$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_2=\mathbf{0}$, $M_4=\mathbf{0}$, $Z_3\sim \mathbf{0}\oplus D$, $D\ne \mathbf{0},I$.

,

Table 2. Theorems 4–7.

Cases	Intersections
(i)-(15)	$c_1=-2a_1{a}_2(p_2-r_2)$, $c_3=-c_2(p_2-q_2)$, $c_4=-(p_2-r_2)(c_2+2a_1{a}_2(p_1-r_1))$, $c_5=c_2(p_2-q_2)+2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_2=\mathbf{0}$, $M_4=I$, $\mathbf{0},I\ne Z_3\sim A\oplus I$.
(i)-(16)	$c_1=-2a_1{a}_2(p_2-r_2)$, $c_3=-c_2(p_2-q_2)$, $c_4=-(p_2-r_2)(c_2+2a_1{a}_2(q_1-r_1))$, $c_5=c_2(p_2-q_2)+2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_2=\mathbf{0}$, $M_4=I$, $\mathbf{0},I\ne Z_3\sim A\oplus \mathbf{0}$.
(i)-(22)	$c_1=0$, $c_4=-(p_2-r_2)(c_2+2a_1{a}_2(p_1-r_1))$, $c_3=-c_2(p_2-q_2)-2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $c_5=c_2(p_2-q_2)+2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_2=\mathbf{0}$, $M_4=I$, $\mathbf{0},I\ne Z_3\sim \left(\begin{array}{cc}I& B\\ \mathbf{0}& D\end{array}\right)$.
(i)-(23)	$c_3=-(p_1-r_1)(c_1+2a_1{a}_2(p_2-r_2))-c_2(p_2-q_2)$, $c_4=-c_1(p_1-q_1)-(p_2-r_2)(c_2+2a_1{a}_2(p_1-r_1))$, $c_5=c_1(p_1-q_1)+c_2(p_2-q_2)+2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}$, $Z_2=\mathbf{0}$, $M_4=I$.
(i)-(24)	$c_1=0$, $c_4=-(p_2-r_2)(c_2+2a_1{a}_2(p_1-r_1))$, $c_5=-c_3=c_2(p_2-q_2)+2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim I\oplus D$, $D\ne \mathbf{0},I$, $Z_2=\mathbf{0}$, $M_4=I$.
(ii)-(15)	$c_1=-2a_1{a}_2(p_2-r_2)$, $c_2(p_2-q_2)=-2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $c_3=2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $c_4=-c_2(q_2-r_2)$, $c_5=0$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_2=\mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$, $\mathbf{0},I\ne Z_3\sim A\oplus I$.
(ii)-(16)	$c_1=-2a_1{a}_2(p_2-r_2)$, $c_2(p_2-q_2)=-2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $c_3=2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $c_4=-c_2(q_2-r_2)$, $c_5=0$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_2=\mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$, $\mathbf{0},I\ne Z_3\sim A\oplus \mathbf{0}.$
(ii)-(17)	$c_1=-2a_1{a}_2(p_2-r_2)$, $c_2=-2a_1{a}_2(p_1-r_1)$, $c_5=0$, $c_3=2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $c_4=2a_1{a}_2(p_1-r_1)(q_2-r_2)$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_2=\mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$, $\mathbf{0},I\ne Z_3\sim A\oplus I$.
(ii)-(18)	$c_1=-2a_1{a}_2(p_2-r_2)$, $c_2=-2a_1{a}_2(q_1-r_1)$, $c_5=0$, $c_3=2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $c_4=2a_1{a}_2(q_1-r_1)(q_2-r_2)$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_2=\mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$, $\mathbf{0},I\ne Z_3\sim A\oplus \mathbf{0}.$
(ii)-(19)	$c_1=-2a_1{a}_2(p_2-r_2)$, $c_3=-c_2(p_2-q_2)$, $c_4=-c_2(q_2-r_2)$, $c_5=0$, $Z_1=I$, $M_1=I$, $Z_2=\mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$, $Z_3\ne I,\mathbf{0}$.
(ii)-(23)	$c_3=-c_1(q_1-r_1)$, $c_4=c_2(q_2-r_2)$, $c_1(p_1-q_1)+c_2(p_2-q_2)=-2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $c_5=0$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}$, $Z_2=\mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$.
(ii)-(26)	$c_3=-(q_1-r_1)(c_1+2a_1{a}_2(q_2-r_2))$, $c_4=-c_2(q_2-r_2)$, $c_5=0$, $-c_1(p_1-q_1)-c_2(p_2-q_2)=2a_1{a}_2[(p_1-r_1)(p_2-r_2)-(q_1-r_1)(q_2-r_2)]$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_3\sim I\oplus \mathbf{0}$, $Z_2=\mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$.
(iii)-(17)	$c_1=-2a_1{a}_2(p_2-r_2)$, $c_2=-2a_1{a}_2(p_1-r_1)$, $c_4=2a_1{a}_2(p_1-r_1)(p_2-r_2)-c_3$, $c_5=0$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_2=\mathbf{0}$, $M_4=\mathbf{0}$, $\mathbf{0},I\ne Z_3\sim A\oplus I$.
(iii)-(18)	$c_1=-2a_1{a}_2(p_2-r_2)$, $c_2=-2a_1{a}_2(q_1-r_1)$, $c_4=2a_1{a}_2(q_1-r_1)(p_2-r_2)-c_3$, $c_5=0$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_2=\mathbf{0}$, $M_4=\mathbf{0}$, $\mathbf{0},I\ne Z_3\sim A\oplus \mathbf{0}.$
(iii)-(25)	$c_1=-2a_1{a}_2(q_2-r_2)$, $c_2=-2a_1{a}_2(p_1-r_1)$, $c_4=2a_1{a}_2(p_1-r_1)(q_2-r_2)-c_3$, $c_5=0$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_2=\mathbf{0}$, $M_4=\mathbf{0}$, $\mathbf{0},I\ne Z_3\sim \left(\begin{array}{cc}I& B\\ \mathbf{0}& D\end{array}\right)$.
(iii)-(26)	$c_5=0$, $c_4=-(p_1-r_1)(c_1+2a_1{a}_2(p_2-r_2))-c_2(p_2-r_2)-c_3$, $-c_1(p_1-q_1)-c_2(p_2-q_2)=2a_1{a}_2[(p_1-r_1)(p_2-r_2)-(q_1-r_1)(q_2-r_2)]$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_3\sim I\oplus \mathbf{0}$, $Z_2=\mathbf{0}$, $M_4=\mathbf{0}$.
(iii)-(27)	$c_1=-2a_1{a}_2(q_2-r_2)$, $c_2=-2a_1{a}_2(p_1-r_1)$, $c_4=2a_1{a}_2(p_1-r_1)(q_2-r_2)-c_3$, $c_5=0$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $\mathbf{0},I\ne Z_3\sim I\oplus D$, $D\ne \mathbf{0},I$, $Z_2=\mathbf{0}$, $M_4=\mathbf{0}$.

,

Table 3. Theorems 5 and 6.

Cases	Intersections
(iv)-(1)	$c_3=-c_1(q_1-r_1)$, $c_4=-c_2(p_2-r_2)$, $c_5=0$, $-c_1(p_1-q_1)+c_2(p_2-q_2)=2a_1{a}_2(p_1-r_1)(q_2-r_2)$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_2\sim I\oplus \mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$.
(iv)-(2)	$c_3=-c_1(p_1-r_1)$, $c_4=-c_2(p_2-r_2)$, $c_5=0$, $c_1(p_1-q_1)+c_2(p_2-q_2)=2a_1{a}_2(q_1-r_1)(q_2-r_2)$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_2\sim I\oplus \mathbf{0}$, $Z_3\sim \mathbf{0}\oplus I$, $M_4\sim I\oplus \mathbf{0}$.
(iv)-(3)	$c_1=-2a_1{a}_2(q_2-r_2)$, $c_3=c_2(p_2-q_2)$, $c_4=-c_2(p_2-r_2)$, $c_5=0$, $Z_1=\mathbf{0}$, $M_1=I$, $Z_2\sim I\oplus \mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$.
(iv)-(8)	$c_1=-2a_1{a}_2(q_2-r_2)$, $c_2=-2a_1{a}_2(q_1-r_1)$, $c_5=0$, $c_3=-2a_1{a}_2(q_1-r_1)(p_2-q_2)$, $c_4=2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_2\sim I\oplus \mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$, $\mathbf{0},I\ne Z_3\sim \left(\begin{array}{cc}\mathbf{0}& B\\ \mathbf{0}& D\end{array}\right)$.
(iv)-(9)	$c_3=-(q_1-r_1)(c_1+2a_1{a}_2(p_2-r_2))$, $c_4=-c_2(p_2-r_2)$, $c_5=0$, $-c_1(p_1-q_1)+c_2(p_2-q_2)=2a_1{a}_2[(p_1-q_1)(q_2-r_2)-(q_1-r_1)(p_2-q_2)]$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_3\sim \mathbf{0}\oplus I$, $Z_2\sim I\oplus \mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$.
(iv)-(10)	$c_1=-2a_1{a}_2(q_2-r_2)$, $c_2=-2a_1{a}_2(q_1-r_1)$, $c_5=0$, $c_3=-2a_1{a}_2(q_1-r_1)(p_2-q_2)$, $c_4=2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_2\sim I\oplus \mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$, $\mathbf{0},I\ne Z_3\sim \mathbf{0}\oplus D$, $D\ne \mathbf{0},I$.
(iv)-(12)	$c_1=-2a_1{a}_2(q_2-r_2)$, $c_2=-2a_1{a}_2(q_1-r_1)$, $c_5=0$, $c_3=-2a_1{a}_2(q_1-r_1)(p_2-q_2)$, $c_4=2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $Z_1=\mathbf{0}$, $M_1=I$, $Z_3\sim I\oplus \mathbf{0}$, $Z_2\sim I\oplus \mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$.
(iv)-(14)	$c_2=-2a_1{a}_2(q_1-r_1)$, $c_3=-c_1(p_1-r_1)$, $c_4=2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $c_1(p_1-q_1)=2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $c_5=0$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim \mathbf{0}\oplus I$, $Z_2\sim I\oplus \mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$.
(v)-(1)	$c_2=0$, $c_3=-(p_1-r_1)(c_1+2a_1{a}_2(q_2-r_2))$, $c_4=-c_1(p_1-q_1)-2a_1{a}_2(p_1-r_1)(q_2-r_2)$, $c_5=-c_4=c_1(p_1-q_1)+2a_1{a}_2(p_1-r_1)(q_2-r_2)$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}$, $Z_2\sim I\oplus \mathbf{0}$, $M_4=I$.
(v)-(2)	$c_2=0$, $c_3=-(q_1-r_1)(c_1+2a_1{a}_2(q_2-r_2))$, $c_5=-c_4=-c_1(p_1-q_1)+2a_1{a}_2(q_1-r_1)(q_2-r_2)$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim \mathbf{0}\oplus I$, $Z_2\sim I\oplus \mathbf{0}$, $M_4=I$.
(v)-(4)	$c_1=c_2=0$, $c_5=-c_3=-c_4$, $Z_1=\mathbf{0}$, $M_1=\mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}$, $Z_2\sim I\oplus \mathbf{0}$, $M_4=I$.
(v)-(5)	$c_1=c_2=0$, $c_4=-2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $c_5=-c_3=-c_4$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_2\sim I\oplus \mathbf{0}$, $M_4=I$, $\mathbf{0},I\ne Z_3\sim \left(\begin{array}{cc}\mathbf{0}& B\\ \mathbf{0}& D\end{array}\right).$
(v)-(6)	$c_2=0$, $c_3=-(q_1-r_1)(c_1+2a_1{a}_2(p_2-r_2))$, $c_4=c_1(p_1-q_1)-2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $c_5=-c_4$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim \mathbf{0}\oplus I$, $Z_2\sim I\oplus \mathbf{0}$, $M_4=I$.
(v)-(7)	$c_1=c_2=0$, $c_4=-2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $c_5=-c_3=-c_4$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_2\sim I\oplus \mathbf{0}$, $M_4=I$, $\mathbf{0},I\ne Z_3\sim \mathbf{0}\oplus D$, $D\ne \mathbf{0},I$.
(v)-(11)	$c_1=c_2=0$, $c_4=-2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $c_5=-c_3=-c_4$, $Z_1=\mathbf{0}$, $M_1=\mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}$, $Z_2\sim I\oplus \mathbf{0}$, $M_4=I$.
(v)-(13)	$c_2=0$, $c_5=-c_4$, $c_3=-(p_1-r_1)(c_1+2a_1{a}_2(q_2-r_2))$, $c_4=-2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $c_1(p_1-q_1)=2a_1{a}_2[(q_1-r_1)(p_2-r_2)-(q_2-r_2)(p_1-r_1)]$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}$, $Z_2\sim I\oplus \mathbf{0}$, $M_4=I$.
(vi)-(1)	$c_3=-(p_1-r_1)(c_1+2a_1{a}_2(q_2-r_2))+c_2(p_2-q_2)$, $c_4=-c_1(p_1-q_1)-(q_2-r_2)(c_2+2a_1{a}_2(p_1-r_1))$, $c_5=c_1(p_1-q_1)-c_2(p_2-q_2)+2a_1{a}_2(p_1-r_1)(q_2-r_2)$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}$, $Z_2=I$, $M_4=I$.
(vi)-(2)	$c_3=-(q_1-r_1)(c_1+2a_1{a}_2(q_2-r_2))+c_2(p_2-q_2)$, $c_4=c_1(p_1-q_1)-(q_2-r_2)(c_2+2a_1{a}_2(q_1-r_1))$, $c_5=-c_1(p_1-q_1)-c_2(p_2-q_2)+2a_1{a}_2(q_1-r_1)(q_2-r_2)$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim \mathbf{0}\oplus I$, $Z_2=I$, $M_4=I$.
(vi)-(13)	$c_3=-(q_1-r_1)(c_1+2a_1{a}_2(p_2-r_2))$, $c_4=-(p_2-r_2)(c_2+2a_1{a}_2(q_1-r_1))$, $c_5=2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $-c_1(p_1-q_1)+c_2(p_2-q_2)=2a_1{a}_2[(p_1-r_1)(q_2-r_2)-(q_1-r_1)(p_2-r_2)]$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}$, $Z_2=I$, $M_4=I$.
(vi)-(14)	$c_2=-2a_1{a}_2(q_1-r_1)$, $c_4=c_1(p_1-q_1)$, $c_3=-(q_1-r_1)(c_1+2a_1{a}_2(p_2-r_2))$, $c_5=-c_1(p_1-q_1)+2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim \mathbf{0}\oplus I$, $Z_2=I$, $M_4=I$.
(vii)-(8)	$c_1=-2a_1{a}_2(q_2-r_2)$, $c_2=-2a_1{a}_2(q_1-r_1)$, $c_5=0$, $c_3=-2a_1{a}_2(q_1-r_1)(p_2-q_2)$, $c_4=2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_2=\mathbf{0}$, $M_4=\mathbf{0}$, $\mathbf{0},I\ne Z_3\sim \left(\begin{array}{cc}\mathbf{0}& B\\ \mathbf{0}& D\end{array}\right)$.
(vii)-(9)	$c_4=-c_2(p_2-r_2)$, $c_3=-(q_1-r_1)(c_1+2a_1{a}_2(p_2-r_2))$, $c_5=0$, $-c_1(p_1-q_1)+c_2(p_2-q_2)=2a_1{a}_2[(q_2-r_2)(p_1-q_1)-(q_1-r_1)(p_2-q_2)]$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_3\sim \mathbf{0}\oplus I$, $Z_2=\mathbf{0}$, $M_4=\mathbf{0}$.
(vii)-(10)	$c_1=-2a_1{a}_2(q_2-r_2)$, $c_2=-2a_1{a}_2(q_1-r_1)$, $c_5=0$, $c_3=-2a_1{a}_2(q_1-r_1)(p_2-q_2)$, $c_4=2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_2=\mathbf{0}$, $M_4=\mathbf{0}$, $\mathbf{0},I\ne Z_3\sim \mathbf{0}\oplus D$, $D\ne \mathbf{0},I.$
(viii)-(5)	$c_1=c_2=0$, $c_4=-2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $c_5=-c_3=-c_4$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_2=\mathbf{0}$, $M_4=I$, $\mathbf{0},I\ne Z_3\sim \left(\begin{array}{cc}\mathbf{0}& B\\ \mathbf{0}& D\end{array}\right).$
(viii)-(6)	$c_2=0$, $c_5=-c_4$, $c_3=-(q_1-r_1)(c_1+2a_1{a}_2(p_2-r_2))$, $c_4=c_1(p_1-q_1)-2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim \mathbf{0}\oplus I$, $Z_2=\mathbf{0}$, $M_4=I$,
(viii)-(7)	$c_1=c_2=0$, $c_4=-2a_1{a}_2(q_1-r_1)(p_2-r_2)$, $c_5=-c_3=-c_4$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_2=\mathbf{0}$, $M_4=I$, $\mathbf{0},I\ne Z_3\sim \mathbf{0}\oplus D$, $D\ne \mathbf{0},I$.

and

Table 4. Theorems 5–7.

Cases	Intersections
(iv)-(25)	$c_1=-2a_1{a}_2(q_2-r_2)$, $c_2=-2a_1{a}_2(p_1-r_1)$, $c_5=0$, $c_3=-2a_1{a}_2(p_1-r_1)(p_2-q_2)$, $c_4=2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_2\sim I\oplus \mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$, $\mathbf{0},I\ne Z_3\sim \left(\begin{array}{cc}I& B\\ \mathbf{0}& D\end{array}\right)\ne I$.
(iv)-(26)	$c_4=-c_2(p_2-r_2)$, $c_3=-(p_1-r_1)(c_1+2a_1{a}_2(p_2-r_2))$, $c_5=0$, $-c_1(p_1-q_1)-c_2(p_2-q_2)=2a_1{a}_2[(p_1-r_1)(p_2-r_2)-(q_1-r_1)(q_2-r_2)]$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_3\sim I\oplus \mathbf{0}$, $Z_2\sim I\oplus \mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$.
(iv)-(27)	$c_1=-2a_1{a}_2(q_2-r_2)$, $c_2=-2a_1{a}_2(p_1-r_1)$, $c_3=-2a_1{a}_2(p_1-r_1)(p_2-q_2)$, $c_4=2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $c_5=0$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_2\sim I\oplus \mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$, $\mathbf{0},I\ne Z_3\sim I\oplus D$, $D\ne \mathbf{0},I$.
(iv)-(29)	$c_1=-2a_1{a}_2(q_2-r_2)$, $c_2=-2a_1{a}_2(p_1-r_1)$, $c_3=-2a_1{a}_2(p_1-r_1)(p_2-q_2)$, $c_4=2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $c_5=0$, $Z_1=\mathbf{0}$, $M_1=I$, $Z_3\sim I\oplus \mathbf{0}$, $Z_2\sim I\oplus \mathbf{0}$, $M_4\sim I\oplus \mathbf{0}$
(iv)-(30)	$c_2=-2a_1{a}_2(p_1-r_1)$, $c_3=-c_1(q_1-r_1)$, $c_4=-c_2(p_2-r_2)$, $c_1(p_1-q_1)=-2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $c_5=0$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}$, $Z_2\sim I\oplus \mathbf{0}$, $M_4\sim I\oplus \mathbf{0}.$
(v)-(22)	$c_1=c_2=0$, $c_4=-2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $c_5=-c_3=-c_4$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_2\sim I\oplus \mathbf{0}$, $M_4=I$, $\mathbf{0},I\ne Z_3\sim \left(\begin{array}{cc}I& B\\ \mathbf{0}& D\end{array}\right)$.
(v)-(23)	$c_3=-(p_1-r_1)(c_1+2a_1{a}_2(p_2-r_2))$, $c_4=-c_1(p_1-q_1)-2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $c_2=0$, $c_5=-c_4$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_2\sim I\oplus \mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}$, $M_4=I$,
(v)-(24)	$c_1=c_2=0$, $c_4=-2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $c_5=-c_3=-c_4$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_2\sim I\oplus \mathbf{0}$, $M_4=I$, $\mathbf{0},I\ne Z_3\sim I\oplus D$, $D\ne \mathbf{0},I$.
(v)-(28)	$c_1=c_2=0$, $c_4=-2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $c_5=-c_3=-c_4$, $Z_1=\mathbf{0}$, $M_1=0$, $Z_3\sim I\oplus \mathbf{0}$, $Z_2\sim I\oplus \mathbf{0}$, $M_4=I.$
(v)-(31)	$c_2=0$, $c_5=-c_4$, $c_3=-(q_1-r_1)(c_1+2a_1{a}_2(q_2-r_2))$, $c_4=-2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $c_1(p_1-q_1)=2a_1{a}_2\left[(q_1-r_1)(q_2-r_2)-(p_1-r_1)(p_2-r_2)\right]$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim \mathbf{0}\oplus I$, $Z_2\sim I\oplus \mathbf{0}$, $M_4=I.$
(vi)-(30)	$c_2=-2a_1{a}_2(p_1-r_1)$, $c_3=-(p_1-r_1)(c_1+2a_1{a}_2(p_2-r_2))$, $c_4=-c_1(p_1-q_1)$, $c_5=c_1(p_1-q_1)+2a_1{a}_2(p_2-r_2)(p_1-r_1)$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}$, $Z_2=I$, $M_4=I.$
(vi)-(31)	$c_4=-(p_2-r_2)(c_2+2a_1{a}_2(p_1-r_1))$, $c_3=-(p_1-r_1)(c_1+2a_1{a}_2(p_2-r_2))$, $c_5=2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $-c_1(p_1-q_1)-c_2(p_2-q_2)=2a_1{a}_2[(p_1-r_1)(p_2-r_2)-(q_2-r_2)(q_1-r_1)]$, $Z_1=\mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim \mathbf{0}\oplus I$, $Z_2=I$, $M_4=I.$
(vii)-(25)	$c_1=-2a_1{a}_2(q_2-r_2)$, $c_2=-2a_1{a}_2(p_1-r_1)$, $c_5=0$, $c_3=-2a_1{q}_2(p_1-r_1)(p_2-q_2)$, $c_4=2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_2=\mathbf{0}$, $M_4=\mathbf{0}$, $\mathbf{0},I\ne Z_3\sim \left(\begin{array}{cc}I& B\\ \mathbf{0}& D\end{array}\right)$.
(vii)-(26)	$c_4=-c_2(p_2-r_2)$, $c_3=-(p_1-r_1)(c_1+2a_1{a}_2(p_2-r_2))$, $c_5=0$, $-c_1(p_1-q_1)-c_2(p_2-q_2)=2a_1{a}_2[(p_1-r_1)(p_2-r_2)-(q_1-r_1)(q_2-r_2)]$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_3\sim I\oplus \mathbf{0}$, $Z_2=\mathbf{0}$, $M_4=\mathbf{0}.$
(vii)-(27)	$c_1=-2a_1{a}_2(q_2-r_2)$, $c_2=-2a_1{a}_2(p_1-r_1)$, $c_3=-2a_1{a}_2(p_1-r_1)(p_2-q_2)$, $c_4=2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $c_5=0$, $Z_1\sim I\oplus \mathbf{0}$, $M_1=I$, $Z_2=\mathbf{0}$, $M_4=\mathbf{0}$, $\mathbf{0},I\ne Z_3\sim I\oplus D$, $D\ne I,\mathbf{0}$
(viii)-(22)	$c_1=c_2=0$, $c_4=-2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $c_5=-c_3=-c_4$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_2=\mathbf{0}$, $M_4=I$, $\mathbf{0},I\ne Z_3\sim \left(\begin{array}{cc}I& B\\ \mathbf{0}& D\end{array}\right)$.
(viii)-(23)	$c_2=0$, $c_4=-c_1(p_1-q_1)-2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $c_3=-(p_1-r_1)(c_1+2a_1{a}_2(p_2-r_2))$, $c_5=-c_4$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_3\sim I\oplus \mathbf{0}$, $Z_2=\mathbf{0}$, $M_4=I$
(viii)-(24)	$c_1=c_2=0$, $c_4=-2a_1{a}_2(p_1-r_1)(p_2-r_2)$, $c_5=-c_3=-c_4$, $Z_1\sim I\oplus \mathbf{0}$, $M_1\sim I\oplus \mathbf{0}$, $Z_2=\mathbf{0}$, $M_4=I$, $\mathbf{0},I\ne Z_3\sim I\oplus D$, $D\ne \mathbf{0},I.$

provide a comprehensive account of the detailed analysis arising from the aforementioned considerations:

Using the submatrices $Z_1$, $M_1$, $Z_2$, $M_4$, and $Z_3$ appearing in the rows of each table, the transformed forms of the matrices $B_1$, $B_2$, $P_1$, and $P_2$ are collectively presented in

Table 5. The structure of the matrices $B_1$, $B_2$, $P_1$, and $P_2$ according to the intersection cases presented in the previous tables.

Cases	Matrices
(i)-(5)	$B_1=S[(q_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $D\ne \mathbf{0}$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I]S^{-1}$,
(i)-(6)	$B_1=S[(q_1-r_1)I\oplus (p_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I]S^{-1}$,
(i)-(7)	$B_1=S[(q_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $D\ne \mathbf{0},I$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I]S^{-1}$,
(ii)-(6)	$B_1=S[(q_1-r_1)I\oplus (p_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I\oplus \mathbf{0}]S^{-1}$,
(ii)-(9)	$B_1=S[(q_1-r_1)I\oplus (p_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus I\oplus I\oplus \mathbf{0}]S^{-1}$,
(iii)-(8)	$B_1=S[(q_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $D\ne \mathbf{0}$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=P_2=S[I\oplus I\oplus \mathbf{0}]S^{-1}$,
(iii)-(9)	$B_1=S[(q_1-r_1)I\oplus (p_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=P_2=S[I\oplus I\oplus \mathbf{0}]S^{-1}$,
(iii)-(10)	$B_1=S[(q_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $D\ne \mathbf{0},I$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=P_2=S[I\oplus I\oplus \mathbf{0}]S^{-1}$,
(i)-(15)	$B_1=S[(p_1-q_1)A+(q_1-r_1)I\oplus (p_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $A\ne I$, $A^2=A$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I]S^{-1}$,
(i)-(16)	$B_1=S[(p_1-q_1)A+(q_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $A\ne \mathbf{0}$, $A^2=A$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I]S^{-1}$,
(i)-(22)	$B_1=S[(p_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $D\ne I$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I]S^{-1}$,
(i)-(23)	$B_1=S[(p_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I]S^{-1}$,
(i)-(24)	$B_1=S[(p_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I]S^{-1}$,
(ii)-(15)	$B_1=S[(p_1-q_1)A+(q_1-r_1)I\oplus (p_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $A\ne I$, $A^2=A$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I\oplus \mathbf{0}]S^{-1}$,
(ii)-(16)	$B_1=S[(p_1-q_1)A+(q_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $A\ne \mathbf{0}$, $A^2=A$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I\oplus \mathbf{0}]S^{-1}$,
(ii)-(17)	$B_1=S[(p_1-q_1)A+(q_1-r_1)I\oplus (p_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $A\ne I$, $A^2=A$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus I\oplus I\oplus \mathbf{0}]S^{-1}$,
(ii)-(18)	$B_1=S[(p_1-q_1)A+(q_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $A\ne \mathbf{0}$, $A^2=A$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus I\oplus I\oplus \mathbf{0}]S^{-1}$,
(ii)-(19)	$B_1=S[(p_1-q_1)Z_3+(q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $Z_3\ne \mathbf{0},I$, ${Z_3}^2=Z_3$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus I\oplus \mathbf{0}]S^{-1}$,
(ii)-(23)	$B_1=S[(p_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I\oplus \mathbf{0}]S^{-1}$,
(ii)-(26)	$B_1=S[(p_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus I\oplus I\oplus \mathbf{0}]S^{-1}$,
(iii)-(17)	$B_1=S[(p_1-q_1)A+(q_1-r_1)I\oplus (p_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $A\ne I$, $A^2=A$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=P_2=S[I\oplus I\oplus \mathbf{0}]S^{-1}$,
(iii)-(18)	$B_1=S[(p_1-q_1)A+(q_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $A\ne \mathbf{0}$, $A^2=A$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=P_2=S[I\oplus I\oplus \mathbf{0}]S^{-1}$,
(iii)-(25)	$B_1=S[(p_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $D\ne I$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=P_2=S[I\oplus I\oplus \mathbf{0}]S^{-1}$,
(iii)-(26)	$B_1=S[(p_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=P_2=S[I\oplus I\oplus \mathbf{0}]S^{-1}$,
(iii)-(27)	$B_1=S[(p_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $D\ne \mathbf{0},I$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=P_2=S[I\oplus I\oplus \mathbf{0}]S^{-1}$,
(iv)-(1)	$B_1=S[(p_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $B_2=S[(q_2-r_2)I\oplus \mathbf{0}\oplus (p_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I\oplus \mathbf{0}]S^{-1}$,
(iv)-(2)	$B_1=S[(q_1-r_1)I\oplus (p_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $B_2=S[(q_2-r_2)I\oplus \mathbf{0}\oplus (p_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I\oplus \mathbf{0}]S^{-1}$,
(iv)-(3)	$B_1=S[(p_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $B_2=S[(q_2-r_2)I\oplus (q_2-r_2)I\oplus (p_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus I\oplus I\oplus \mathbf{0}]S^{-1}$,
(iv)-(8)	$B_1=S[(q_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $D\ne \mathbf{0}$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus (p_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus I\oplus I\oplus \mathbf{0}]S^{-1}$,
(iv)-(9)	$B_1=S[(q_1-r_1)I\oplus (p_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus (p_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus I\oplus I\oplus \mathbf{0}]S^{-1}$,
(iv)-(10)	$B_1=S[(q_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $D\ne \mathbf{0},I$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus (p_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus I\oplus I\oplus \mathbf{0}]S^{-1}$,
(iv)-(12)	$B_1=S[(p_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $B_2=S[(q_2-r_2)I\oplus (q_2-r_2)I\oplus (p_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus I\oplus I\oplus \mathbf{0}]S^{-1}$,
(iv)-(14)	$B_1=S[(q_1-r_1)I\oplus (p_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $B_2=S[(q_2-r_2)I\oplus \mathbf{0}\oplus (p_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I\oplus \mathbf{0}]S^{-1}$,
(v)-(1)	$B_1=S[(p_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $B_2=S[(q_2-r_2)I\oplus \mathbf{0}\oplus (p_2-r_2)I\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I\oplus I]S^{-1}$,
(v)-(2)	$B_1=S[(q_1-r_1)I\oplus (p_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $B_2=S[(q_2-r_2)I\oplus \mathbf{0}\oplus (p_2-r_2)I\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I\oplus I]S^{-1}$,
(v)-(4)	$B_1=S[(p_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $B_2=S[\mathbf{0}\oplus \mathbf{0}\oplus (p_2-r_2)I\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[\mathbf{0}\oplus \mathbf{0}\oplus I\oplus I]S^{-1}$,
(v)-(5)	$B_1=S[(q_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $D\ne \mathbf{0}$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (p_2-r_2)I\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I\oplus I]S^{-1}$,
(v)-(6)	$B_1=S[(q_1-r_1)I\oplus (p_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (p_2-r_2)I\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I\oplus I]S^{-1}$,
(v)-(7)	$B_1=S[(q_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $D\ne \mathbf{0},I$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (p_2-r_2)I\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I\oplus I]S^{-1}$,
(v)-(11)	$B_1=S[(p_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $B_2=S[\mathbf{0}\oplus \mathbf{0}\oplus (p_2-r_2)I\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[\mathbf{0}\oplus \mathbf{0}\oplus I\oplus I]S^{-1}$,
(v)-(13)	$B_1=S[(p_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $B_2=S[(q_2-r_2)I\oplus \mathbf{0}\oplus (p_2-r_2)I\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I\oplus I]S^{-1}$,
(vi)-(1)	$B_1=S[(p_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $B_2=S[(q_2-r_2)I\oplus \mathbf{0}\oplus (p_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I]S^{-1}$,
(vi)-(2)	$B_1=S[(q_1-r_1)I\oplus (p_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $B_2=S[(q_2-r_2)I\oplus \mathbf{0}\oplus (p_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I]S^{-1}$,
(vi)-(13)	$B_1=S[(p_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $B_2=S[(q_2-r_2)I\oplus \mathbf{0}\oplus (p_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I]S^{-1}$,
(vi)-(14)	$B_1=S[(q_1-r_1)I\oplus (p_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $B_2=S[(q_2-r_2)I\oplus \mathbf{0}\oplus (p_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I]S^{-1}$,
(vii)-(8)	$B_1=S[(q_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $D\ne \mathbf{0}$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=P_2=S[I\oplus I\oplus \mathbf{0}]S^{-1}$,
(vii)-(9)	$B_1=S[(q_1-r_1)I\oplus (p_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=P_2=S[I\oplus I\oplus \mathbf{0}]S^{-1}$,
(vii)-(10)	$B_1=S[(q_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $D\ne \mathbf{0},I$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=P_2=S[I\oplus I\oplus \mathbf{0}]S^{-1}$,
(viii)-(5)	$B_1=S[(q_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $D\ne \mathbf{0}$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I]S^{-1}$,
(viii)-(6)	$B_1=S[(q_1-r_1)I\oplus (p_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I]S^{-1}$,
(viii)-(7)	$B_1=S[(q_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $D\ne \mathbf{0},I$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I]S^{-1}$,
(iv)-(25)	$B_1=S[(p_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $D\ne I$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus (p_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus I\oplus I\oplus \mathbf{0}]S^{-1}$,
(iv)-(26)	$B_1=S[(p_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus (p_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus I\oplus I\oplus \mathbf{0}]S^{-1}$,
(iv)-(27)	$B_1=S[(p_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $D\ne \mathbf{0},I$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus (p_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus I\oplus I\oplus \mathbf{0}]S^{-1}$,
(iv)-(29)	$B_1=S[(p_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $B_2=S[(q_2-r_2)I\oplus (q_2-r_2)I\oplus (p_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus I\oplus I\oplus \mathbf{0}]S^{-1}$,
(iv)-(30)	$B_1=S[(p_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $B_2=S[(q_2-r_2)I\oplus \mathbf{0}\oplus (p_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I\oplus \mathbf{0}]S^{-1}$,
(iv)-(31)	$B_1=S[(q_1-r_1)I\oplus (p_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $B_2=S[(q_2-r_2)I\oplus \mathbf{0}\oplus (p_2-r_2)I\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I\oplus I]S^{-1}$,
(v)-(22)	$B_1=S[(p_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $D\ne I$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (p_2-r_2)I\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I\oplus I]S^{-1}$,
(v)-(23)	$B_1=S[(p_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (p_2-r_2)I\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I\oplus I]S^{-1}$,
(v)-(24)	$B_1=S[(p_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $D\ne \mathbf{0},I$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (p_2-r_2)I\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I\oplus I]S^{-1}$,
(v)-(28)	$B_1=S[(p_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $B_2=S[\mathbf{0}\oplus (p_2-r_2)I\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}]S^{-1}$, $P_2=S[\mathbf{0}\oplus \mathbf{0}\oplus I]S^{-1}$,
(vi)-(30)	$B_1=S[(p_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $B_2=S[(q_2-r_2)I\oplus \mathbf{0}\oplus (p_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I]S^{-1}$,
(vi)-(31)	$B_1=S[(q_1-r_1)I\oplus (p_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $B_2=S[(q_2-r_2)I\oplus \mathbf{0}\oplus (p_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I]S^{-1}$,
(vii)-(25)	$B_1=S[(p_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $D\ne I$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=P_2=S[I\oplus I\oplus \mathbf{0}]S^{-1}$,
(vii)-(26)	$B_1=S[(p_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=P_2=S[I\oplus I\oplus \mathbf{0}]S^{-1}$,
(vii)-(27)	$B_1=S[(p_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $D\ne \mathbf{0},I$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus (q_2-r_2)I\oplus \mathbf{0}]S^{-1}$, $P_1=P_2=S[I\oplus I\oplus \mathbf{0}]S^{-1}$,
(viii)-(22)	$B_1=S[(p_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $D\ne I$, $D^2=D$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I]S^{-1}$,
(viii)-(23)	$B_1=S[(p_1-r_1)I\oplus (q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I]S^{-1}$,
(viii)-(24)	$B_1=S[(p_1-r_1)I\oplus (p_1-q_1)D+(q_1-r_1)I\oplus \mathbf{0}]S^{-1}$, $B_2=S[(p_2-r_2)I\oplus \mathbf{0}\oplus (q_2-r_2)I]S^{-1}$, $P_1=S[I\oplus I\oplus \mathbf{0}]S^{-1}$, $P_2=S[I\oplus \mathbf{0}\oplus I]S^{-1}$.

. This table allows us to easily derive the matrix equalities stated in the parts of the main theorem.

An examination of the above tables reveals that some rows coincide with others, differing only by an interchange in the roles of $p_1$ and $q_1$. Taking this into account, upon substituting the coefficient equalities and the submatrices from the tables into the equality (8), and after carrying out the necessary simplifications, we arrive at the following main theorem:

Here, to make the proof more comprehensible, let us demonstrate how one of the matrix equalities in the main theorem is obtained. All of the other matrix equalities are derived in a similar manner. For example, let us try to obtain the matrix equality corresponding to the intersection (i)–(5). The equalities related to the coefficients $c_k$, $k=1,\dots ,5$ in the corresponding intersection are as follows:

$$\begin{array}{c}{c}_1=0,c_5=-c_3=c_2(p_2-q_2)+2a_1{a}_2(q_1-r_1)(p_1-r_2),\hfill \\ c_4=-(p_2-r_2)(c_2+2a_1{a}_2(q_1-r_1))\hfill \end{array}$$

If we substitute these coefficients into (8), then we obtain

$$\begin{array}{c}{c}_2[B_2-(p_2-q_2)(P_1-I)-(p_2-r_2)P_2]+\hfill \\ 2a_1{a}_2[B_1{B}_2-(q_1-r_1)(p_2-r_2)(P_1+P_2-I)]=\mathbf{0}.\hfill \end{array}$$

(78)

Here, taking into account the forms of the matrices $B_1$, $B_2$, $P_1$, and $P_2$ in Table 5, it can be seen that

$$B_2=(p_2-q_2)(P_1-I)+(p_2-r_2)P_2,B_1{B}_2=(q_1-r_1)(p_2-r_2)(P_1+P_2-I).$$

It is clear that these matrix equalities verify the equality (78).

Similarly, let us consider the intersection (i)-(22). The equalities related to the coefficients $c_k$, $k=1,\dots ,5$ in the corresponding intersection are

$$\begin{array}{c}{c}_1=0,c_4=-(p_2-r_2)(c_2+2a_1{a}_2(p_1-r_1)),\hfill \\ c_5=-c_3=c_2(p_2-q_2)+2a_1{a}_2(p_1-r_1)(p_2-r_2).\hfill \end{array}$$

Substituting these equalities into (8) leads to

$$\begin{array}{c}{c}_2[B_2-(p_2-q_2)(P_1-I)-(p_2-r_2)P_2]+\hfill \\ 2a_1{a}_2[B_1{B}_2-(p_1-r_1)(p_2-r_2)(P_1+P_2-I)]=\mathbf{0}.\hfill \end{array}$$

(79)

The forms of the matrices $B_1$, $B_2$, $P_1$, and $P_2$ in Table 5 yield

$$B_2=(p_2-q_2)(P_1-I)+(p_2-r_2)P_2,B_1{B}_2=(p_1-r_1)(p_2-r_2)(P_1+P_2-I).$$

It is clear that these matrix equalities verify the equality (79).

Taking into account the coefficients $c_k$, $k=1,\dots ,5$ and the matrix equalities in the intersections (i)–(5) and (i)–(22), we observe that the coefficient $q_1$ in (i)–(5) has exchanged roles with the coefficient $p_1$ in (i)–(22). Therefore, when expressing the first item of the main theorem, the notation $(w_1,w_2)=(p_1,q_1)$ is used, and the coefficients $c_k$, $k=1,\dots ,5$ and the matrix equalities are written with the aid of the indices i and j. All of the remaining items of the main theorem are constructed following the same reasoning.

The notation $\kappa (p,q,r,B,P)$ will be used to denote the family of essentially $\{p,q,r\}$-cubic matrices associated with the matrix B, which is a generalized $\{p-r,q-r\}$-quadratic matrix with respect to the matrix P, under the condition $p\ne q,p\ne r,q\ne r$.

Theorem 8. 

Let

$$A_1\in \kappa (p_1,q_1,r_1,B_1,P_1),A_2\in \kappa (p_2,q_2,r_2,B_2,P_2),A_1,A_2\in {\mathbb{C}}_n,$$

and let $a_1$ and $a_2$ be nonzero complex numbers.

A necessary and sufficient condition for the linear combination

$$A_3=a_1{A}_1+a_2{A}_2$$

to be a $\{p_3,q_3\}$-quadratic matrix ($p_3,q_3\in \mathbb{C}$) is that one of the following holds, under the assumption $A_1{A}_2=A_2{A}_1$, where

$$a_3=a_1{r}_1+a_2{r}_2,(w_1,w_2)=(p_1,q_1),$$

$$c_1=a_1^2(p_1+q_1-2r_1)+a_1(2a_3-p_3-q_3),c_2=a_2^2(p_2+q_2-2r_2)+a_1(2a_3-p_3-q_3),$$

$$c_3=-a_1^2(p_1-r_1)(q_1-r_1)\ne 0,c_4=-a_2^2(p_2-r_2)(q_2-r_2)\ne 0,c_5=(a_3-p_3)(a_3-q_3).$$

Moreover, in the cases where only the index i appears, we have $i=1$ or $i=2$; and in the cases where both indices i and j appear, we have $(i,j)=(1,2)$ or $(i,j)=(2,1)$.

 1.

$$\begin{array}{cc}& c_1=0,c_3=-c_2(p_2-q_2)-2a_1{a}_2(w_i-r_1)(p_2-r_2),\hfill \\ & c_4=-(p_2-r_2)(c_2+2a_1{a}_2(w_i-r_1)),c_5=-c_3,\hfill \\ & B_2=(p_2-r_2)P_2+(p_2-q_2)(P_1-I),B_1{B}_2=(p_2-r_2)(w_i-r_1)(P_1+P_2-I),\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}i\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{5}\mathit{\right)}\mathit{,}\mathit{\left(}i\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{7}\mathit{\right)}\mathit{\left(}i\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{22}\mathit{\right)}\mathit{,}\mathit{\left(}i\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{24}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 2.

$$\begin{array}{cc}& c_3=-(w_j-r_1)(c_1+2a_1{a}_2(p_2-r_2))-c_2(p_2-q_2),\hfill \\ & c_4=c_1(w_i-w_j)-(p_2-r_2)(c_2+2a_1{a}_2(w_j-r_1)),\hfill \\ & c_5=-c_1(w_i-w_j)+c_2(p_2-q_2)+2a_1{a}_2(w_j-r_1)(p_2-r_2),\hfill \\ & B_1=(w_j-r_1)P_1+(w_i-w_j)(I-P_2),\hfill \\ & B_2=(p_2-r_2)P_2+(p_2-q_2)(P_1-I),P_1+P_2=I+P_1{P}_2,\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}i\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{6}\mathit{\right)}\mathit{and}\mathit{\left(}i\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{23}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 3.

$$\begin{array}{cc}& c_1=-2a_1{a}_2(p_2-r_2),c_4=-(p_2-r_2)(c_2+2a_1{a}_2(w_i-r_1)),\hfill \\ & c_5=c_2(p_2-q_2)+2a_1{a}_2(w_i-r_1)(p_2-r_2),c_3=-c_2(p_2-q_2),\hfill \\ & B_2=(p_2-q_2)(P_1-I)+(p_2-r_2)P_2,\hfill \\ & B_1{B}_2=(p_2-r_2)\left[B_1+(w_i-r_1)(P_2-I)\right],\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}i\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{15}\mathit{\right)}\mathit{and}\mathit{\left(}i\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{16}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 4.

$$\begin{array}{cc}& c_3=-c_1(w_i-r_1),c_4=-c_2(q_2-r_2),c_5=0,\hfill \\ & -c_1(w_i-w_j)+c_2(p_2-q_2)=-2a_1{a}_2(w_j-r_1)(p_2-r_2),\hfill \\ & (w_i-w_j)B_1{B}_2=-(w_j-r_1)(p_2-r_2)\left[B_1-(w_i-r_1)P_1\right],\hfill \\ & (p_2-q_2)B_1{B}_2=(w_j-r_1)(p_2-r_2)\left[B_2-(q_2-r_2)P_2\right],\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}\mathit{ii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{6}\mathit{\right)}\mathit{and}\mathit{\left(}\mathit{ii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{23}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 5.

$$\begin{array}{cc}& c_1=-2a_1{a}_2(p_2-r_2),c_3=-c_2(p_2-q_2),c_4=-c_2(q_2-r_2),c_5=0,\hfill \\ & B_2=(p_2-q_2)P_1+(q_2-r_2)P_2,B_1{B}_2=(p_2-r_2)B_1,\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersection}\mathit{\left(}\mathit{ii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{19}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 6.

$$\begin{array}{cc}& c_4=-c_2(q_2-r_2),c_5=0,c_3=-(w_i-r_1)(c_1+2a_1{a}_2(q_2-r_2)),\hfill \\ & c_1(w_i-w_j)-c_2(p_2-q_2)=2a_1{a}_2[(w_j-r_1)(p_2-r_2)-(w_i-r_1)(q_2-r_2)]\ne 0,\hfill \\ & (w_i-w_j)B_1{B}_2=\left[(w_i-r_1)(q_2-r_2)-(w_j-r_1)(p_2-r_2)\right]B_1\hfill \\ & +(p_1-r_1)(q_1-r_1)(p_2-q_2)P_1,\hfill \\ & (p_2-q_2)B_1{B}_2=(w_i-r_1)(q_2-r_2)(p_2-q_2)P_1\hfill \\ & +\left[(w_j-r_1)(p_2-r_2)-(w_i-r_1)(q_2-r_2)\right]\left[B_2-(q_2-r_2)P_2\right],\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}\mathit{ii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{9}\mathit{\right)}\mathit{and}\mathit{\left(}\mathit{ii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{26}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 7.

$$\begin{array}{cc}\hfill & c_3=-(w_i-r_1)\left(c_1+2a_1{a}_2(q_2-r_2)\right),\hfill \\ \hfill & c_4=-c_2(q_2-r_2),c_5=0,c_1(w_i-w_j)=c_2(p_2-q_2),\hfill \\ \hfill & (w_i-r_1)(q_2-r_2)=(w_j-r_1)(p_2-r_2),\hfill \\ \hfill & (p_2-q_2)\left[B_1-(w_i-r_1)P_1\right]+(w_i-w_j)\left[B_2-(q_2-r_2)P_2\right]=\mathbf{0},\hfill \\ \hfill & B_1{B}_2=(w_i-r_1)(q_2-r_2)P_1\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}\mathit{ii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{9}\mathit{\right)}\mathit{and}\mathit{\left(}\mathit{ii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{26}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 8.

$$\begin{array}{cc}& c_1=-2a_1{a}_2(p_2-r_2),c_3=2a_1{a}_2(p_2-r_2)(w_i-r_1),c_4=-c_2(q_2-r_2),\hfill \\ & c_2(p_2-q_2)=-2a_1{a}_2(w_i-r_1)(p_2-r_2),c_5=0,\hfill \\ & (p_2-q_2)B_1{B}_2=(p_2-r_2)(p_2-q_2)\left[B_1-(w_i-r_1)P_1\right]\hfill \\ & +(p_2-r_2)(w_i-r_1)\left[B_2-(q_2-r_2)P_2\right],\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}\mathit{ii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{15}\mathit{\right)}\mathit{and}\mathit{\left(}\mathit{ii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{16}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 9.

$$\begin{array}{cc}& c_1=-2a_1{a}_2(p_2-r_2),c_2=-2a_1{a}_2(w_i-r_1),\hfill \\ & c_3=2a_1{a}_2(p_2-r_2)(w_i-r_1),c_4=2a_1{a}_2(w_i-r_1)(q_2-r_2),c_5=0,\hfill \\ & B_1{B}_2=(p_2-r_2)B_1+(w_i-r_1)\left[B_2-(p_2-q_2)P_1-(q_2-r_2)P_2\right],\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}\mathit{ii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{17}\mathit{\right)}\mathit{and}\mathit{\left(}\mathit{ii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{18}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 10.

$$\begin{array}{cc}\hfill & c_1=-2a_1{a}_2(q_2-r_2),c_2=-2a_1{a}_2(w_i-r_1),c_5=0,\hfill \\ \hfill & c_4=2a_1{a}_2(w_i-r_1)(q_2-r_2)-c_3,\hfill \\ \hfill & B_1{B}_2=(w_i-r_1)B_2+(q_2-r_2)\left[B_1-(w_i-r_1)P_1\right],P_1=P_2,\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}\mathit{iii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{8}\mathit{\right)}\mathit{,}\mathit{\left(}\mathit{iii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{10}\mathit{\right)}\mathit{,}\mathit{\left(}\mathit{iii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{25}\mathit{\right)}\mathit{,}\mathit{\left(}\mathit{iii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{27}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 11.

$$\begin{array}{cc}& c_4=-(w_i-r_1)\left(c_1+2a_1{a}_2(p_2-r_2)\right)-c_2(p_2-r_2)-c_3,c_5=0,\hfill \\ & -c_1(w_i-w_j)-c_2(p_2-q_2)=2a_1{a}_2[(p_2-r_2)(w_i-r_1)-(w_j-r_1)(q_2-r_2)]\ne 0,\hfill \\ & (w_i-w_j)B_1{B}_2=(p_1-r_1)(q_1-r_1)(p_2-q_2)P_1+\left[(w_i-r_1)(q_2-r_2)-(p_2-r_2)(w_j-r_1)\right]B_1,\hfill \\ & (p_2-q_2)B_1{B}_2=(p_2-r_2)(q_2-r_2)(w_i-w_j)P_2+\left[(p_2-r_2)(w_j-r_1)-(w_i-r_1)(q_2-r_2)\right]B_2,\hfill \\ & P_1=P_2,\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}\mathit{iii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{9}\mathit{\right)}\mathit{and}\mathit{\left(}\mathit{iii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{26}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 12.

$$\begin{array}{cc}\hfill & c_5=0,c_4=-(w_i-r_1)\left(c_1+2a_1{a}_2(p_2-r_2)\right)-c_2(p_2-r_2)-c_3,\hfill \\ \hfill & c_1(w_j-w_i)=c_2(p_2-q_2),(w_i-r_1)(p_2-r_2)=(w_j-r_1)(q_2-r_2),\hfill \\ \hfill & B_1{B}_2=(w_i-r_1)(p_2-r_2)P_1,P_1=P_2,\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}\mathit{iii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{9}\mathit{\right)}\mathit{and}\mathit{\left(}\mathit{iii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{26}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 13.

$$\begin{array}{cc}\hfill & c_1=-2a_1{a}_2(p_2-r_2),c_2=-2a_1{a}_2(w_i-r_1),c_5=0,\hfill \\ \hfill & c_4=2a_1{a}_2(w_i-r_1)(p_2-r_2)-c_3,\hfill \\ \hfill & B_1{B}_2=(w_i-r_1)B_2+(p_2-r_2)\left[B_1-(w_i-r_1)P_1\right],P_1=P_2,\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}\mathit{iii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{17}\mathit{\right)}\mathit{and}\mathit{\left(}\mathit{iii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{18}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 14.

$$\begin{array}{cc}\hfill & c_3=-c_1(w_j-r_1),c_5=0,c_4=-c_2(p_2-r_2),\hfill \\ \hfill & -c_1(w_i-w_j)+c_2(p_2-q_2)=2a_1{a}_2(w_i-r_1)(q_2-r_2),\hfill \\ \hfill & (w_i-w_j)B_1{B}_2=(w_i-r_1)(q_2-r_2)\left[B_1-(w_j-r_1)P_1\right],\hfill \\ \hfill & (p_2-q_2)B_1{B}_2=-(w_i-r_1)(q_2-r_2)\left[B_2-(p_2-r_2)P_2\right],\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}\mathit{iv}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{1}\mathit{\right)}\mathit{and}\mathit{\left(}\mathit{iv}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{2}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 15.

$$\begin{array}{cc}\hfill & c_4=-c_2(p_2-r_2),c_1=-2a_1{a}_2(q_2-r_2),\hfill \\ \hfill & c_3=c_2(p_2-q_2),c_5=0,\hfill \\ \hfill & B_2=-(p_2-q_2)P_1+(p_2-r_2)P_2,B_1{B}_2=(q_2-r_2)B_1,\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersection}\mathit{\left(}\mathit{iv}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{3}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 16.

$$\begin{array}{cc}& c_1=-2a_1{a}_2(q_2-r_2),c_2=-2a_1{a}_2(w_i-r_1),c_3=-2a_1{a}_2(w_i-r_1)(p_2-q_2),\hfill \\ & c_4=2a_1{a}_2(w_i-r_1)(p_2-r_2),c_5=0,\hfill \\ & B_1{B}_2=(q_2-r_2)B_1+(w_i-r_1)\left[B_2-(p_2-r_2)P_2\right]+(w_i-r_1)(p_2-q_2)P_1,\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}\mathit{iv}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{8}\mathit{\right)}\mathit{,}\mathit{\left(}\mathit{iv}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{10}\mathit{\right)}\mathit{,}\mathit{\left(}\mathit{iv}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{25}\mathit{\right)}\mathit{,}\mathit{and}\mathit{\left(}\mathit{iv}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{27}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 17.

$$\begin{array}{cc}& c_4=-c_2(p_2-r_2),c_5=0,\hfill \\ & c_3=-(w_j-r_1)(c_1+2a_1{a}_2(p_2-r_2)),\hfill \\ & -c_1(w_i-w_j)+c_2(p_2-q_2)=2a_1{a}_2\left[(q_2-r_2)(w_i-r_1)-(w_j-r_1)(p_2-r_2)\right]\ne 0,\hfill \\ & (w_i-w_j)B_1{B}_2=\left[(w_i-r_1)(q_2-r_2)-(p_2-r_2)(w_j-r_1)\right]B_1+(p_1-r_1)(q_1-r_1)(p_2-q_2)P_1,\hfill \\ & (p_2-q_2)B_1{B}_2=(w_j-r_1)(p_2-q_2)(p_2-r_2)P_1\hfill \\ & +((w_j-r_1)(p_2-r_2)-(q_2-r_2)(w_i-r_1))\left[B_2-(p_2-r_2)P_2\right],\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersection}\mathit{\left(}\mathit{iv}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{9}\mathit{\right)}\mathit{and}\mathit{\left(}\mathit{iv}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{26}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 18.

$$\begin{array}{cc}\hfill & c_3=-(w_j-r_1)\left(c_1+2a_1{a}_2(p_2-r_2)\right),c_4=-c_2(p_2-r_2),c_5=0,\hfill \\ \hfill & c_1(w_i-w_j)=c_2(p_2-q_2),(w_j-r_1)(p_2-r_2)=(w_i-r_1)(q_2-r_2),\hfill \\ \hfill & (p_2-q_2)\left[B_1-(w_j-r_1)P_1\right]+(w_i-w_j)\left[B_2-(p_2-r_2)P_2\right]=\mathbf{0},\hfill \\ \hfill & B_1{B}_2=(w_j-r_1)(p_2-r_2)P_1,\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}\mathit{iv}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{9}\mathit{\right)}\mathit{and}\mathit{\left(}\mathit{iv}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{26}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 19.

$$\begin{array}{cc}\hfill & c_2=-2a_1{a}_2(w_j-r_1),c_3=-c_1(w_i-r_1),\hfill \\ \hfill & c_4=2a_1{a}_2(w_j-r_1)(p_2-r_2),\hfill \\ \hfill & c_1(w_i-w_j)=2a_1{a}_2(w_j-r_1)(p_2-r_2),c_5=0,\hfill \\ \hfill & (w_i-w_j)B_1{B}_2=(w_i-w_j)(w_j-r_1)\left[B_2-(p_2-r_2)P_2\right]\hfill \\ \hfill & -(w_j-r_1)(p_2-r_2)\left[B_1-(w_i-r_1)P_1\right],\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}\mathit{iv}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{14}\mathit{\right)}\mathit{and}\mathit{\left(}\mathit{iv}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{30}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 20.

$$\begin{array}{cc}\hfill & c_1=-2a_1{a}_2(q_2-r_2),c_2=-2a_1{a}_2(w_i-r_1),\hfill \\ \hfill & c_3=-2a_1{a}_2(w_i-r_1)(p_2-q_2),c_4=-2a_1{a}_2(w_i-r_1)(p_2-r_2),c_5=0,\hfill \\ \hfill & B_1{B}_2=(q_2-r_2)B_1+(w_i-r_1)\left[B_2+(p_2-q_2)P_1-(p_2-r_2)P_2\right],\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}\mathit{iv}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{12}\mathit{\right)}\mathit{and}\mathit{\left(}\mathit{iv}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{29}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 21.

$$\begin{array}{cc}\hfill & c_2=0,c_3=-(w_i-r_1)\left(c_1+2a_1{a}_2(q_2-r_2)\right),\hfill \\ \hfill & c_4=-c_1(w_i-w_j)-2a_1{a}_2(w_i-r_1)(q_2-r_2),\hfill \\ \hfill & c_5=c_1(w_i-w_j)+2a_1{a}_2(w_i-r_1)(q_2-r_2),\hfill \\ \hfill & B_1=(w_i-r_1)P_1+(w_i-w_j)\left[P_2-I\right],\hfill \\ \hfill & B_1{B}_2=(w_i-r_1)(q_2-r_2)\left[P_1+P_2-I\right],\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}v\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{1}\mathit{\right)}\mathit{and}\mathit{\left(}v\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{2}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 22.

$$\begin{array}{cc}\hfill & c_1=c_2=0,c_5=-c_3=-c_4,\hfill \\ \hfill & B_1{B}_2=\mathbf{0},P_1+P_2=I,\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersection}\mathit{\left(}v\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{4}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 23.

$$\begin{array}{cc}\hfill & c_1=c_2=0,c_4=-2a_1{a}_2(w_i-r_1)(p_2-r_2),c_5=-c_3=-c_4,\hfill \\ \hfill & B_1{B}_2=(w_i-r_1)(p_2-r_2)\left[P_1+P_2-I\right],\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}v\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{5}\mathit{\right)}\mathit{,}\mathit{\left(}v\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{7}\mathit{\right)}\mathit{,}\mathit{\left(}v\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{22}\mathit{\right)}\mathit{,}\hfill \\ & \mathit{\left(}v\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{24}\mathit{\right)}\mathit{,}\mathit{\left(}\mathit{viii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{5}\mathit{\right)}\mathit{,}\mathit{\left(}\mathit{viii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{7}\mathit{\right)}\mathit{,}\mathit{\left(}\mathit{viii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{22}\mathit{\right)}\mathit{,}\mathit{and}\mathit{\left(}\mathit{viii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{24}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 24.

$$\begin{array}{cc}\hfill & c_2=0,c_3=-(w_j-r_1)\left(c_1+2a_1{a}_2(p_2-r_2)\right),\hfill \\ \hfill & c_4=c_1(w_i-w_j)-2a_1{a}_2(w_j-r_1)(p_2-r_2),c_5=-c_4,\hfill \\ \hfill & B_1=(w_j-r_1)P_1-(w_i-w_j)\left[P_2-I\right],\hfill \\ \hfill & B_1{B}_2=(w_j-r_1)(p_2-r_2)\left[P_1+P_2-I\right],\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}v\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{6}\mathit{\right)}\mathit{and}\mathit{\left(}v\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{23}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 25.

$$\begin{array}{cc}\hfill & c_2=0,c_3=-(w_i-r_1)\left(c_1+2a_1{a}_2(q_2-r_2)\right),\hfill \\ \hfill & c_4=-2a_1{a}_2(w_j-r_1)(p_2-r_2),c_5=-c_4,\hfill \\ \hfill & c_1(w_i-w_j)=2a_1{a}_2[(w_j-r_1)(p_2-r_2)-(q_2-r_2)(w_i-r_i)]\ne 0,\hfill \\ \hfill & (w_i-w_j)B_1{B}_2=\left[(q_2-r_2)(w_i-r_1)-(w_j-r_1)(p_2-r_2)\right]B_1\hfill \\ \hfill & +(w_i-r_1)(w_j-r_1)(p_2-q_2)P_1\hfill \\ \hfill & +(w_i-w_j)(w_j-r_1)(p_2-r_2)\left[P_2-I\right],\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}v\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{13}\mathit{\right)}\mathit{and}\mathit{\left(}v\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{31}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 26.

$$\begin{array}{cc}\hfill & c_1=c_2=0,c_3=-2a_1{a}_2(w_i-r_1)(q_2-r_2),\hfill \\ \hfill & c_4=-2a_1{a}_2(w_j-r_1)(p_2-r_2),c_5=-c_4,\hfill \\ \hfill & (w_j-r_1)(p_2-r_2)=(q_2-r_2)(w_i-r_1),\hfill \\ \hfill & B_1{B}_2=(q_2-r_2)(w_i-r_1)\left[P_1+P_2-I\right],\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}v\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{13}\mathit{\right)}\mathit{and}\mathit{\left(}v\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{31}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 27.

$$\begin{array}{cc}\hfill & c_1=c_2=0,c_4=-2a_1{a}_2(w_i-r_1)(p_2-r_2),\hfill \\ \hfill & c_5=-c_4=-c_3,B_1{B}_2=\mathbf{0},P_1+P_2=I,\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}v\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{11}\mathit{\right)}\mathit{and}\mathit{\left(}v\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{28}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 28.

$$\begin{array}{cc}\hfill & c_3=-(w_i-r_1)\left(c_1+2a_1{a}_2(q_2-r_2)\right)+c_2(p_2-q_2),\hfill \\ \hfill & c_4=-c_1(w_i-w_j)-(q_2-r_2)(c_2+2a_1{a}_2(w_i-r_1)),\hfill \\ \hfill & c_5=c_1(w_i-w_j)-c_2(p_2-q_2)+2a_1{a}_2(w_i-r_1)(q_2-r_2),\hfill \\ \hfill & B_1=(w_i-r_1)P_1+(w_i-w_j)(P_2-I),\hfill \\ \hfill & B_2=(q_2-r_2)P_2-(p_2-q_2)(P_1-I),\hfill \\ \hfill & P_1+P_2=I+P_1{P}_2,\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}\mathit{vi}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{1}\mathit{\right)}\mathit{and}\mathit{\left(}\mathit{vi}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{2}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 29.

$$\begin{array}{cc}\hfill & c_3=-(w_j-r_1)\left(c_1+2a_1{a}_2(p_2-r_2)\right),\hfill \\ \hfill & c_4=-(p_2-r_2)\left(c_2+2a_1{a}_2(w_j-r_1)\right),\hfill \\ \hfill & c_5=2a_1{a}_2(w_j-r_1)(p_2-r_2),\hfill \\ \hfill & -c_1(w_i-w_j)+c_2(p_2-q_2)=2a_1{a}_2\left[(w_i-r_1)(q_2-r_2)-(p_2-r_2)(w_j-r_1)\right],\hfill \\ \hfill & B_1=(w_i-r_1)P_1+(w_i-w_j)(P_2-I),\hfill \\ \hfill & B_2=(q_2-r_2)P_2-(p_2-q_2)(P_1-I),\hfill \\ \hfill & P_1+P_2=I+P_1{P}_2,\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}\mathit{vi}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{13}\mathit{\right)}\mathit{and}\mathit{\left(}\mathit{vi}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{31}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 30.

$$\begin{array}{cc}\hfill & c_2=-2a_1{a}_2(w_j-r_1),c_3=-(w_j-r_1)\left(c_1+2a_1{a}_2(p_2-r_2)\right),\hfill \\ \hfill & c_4=c_1(w_i-w_j),c_5=-c_1(w_i-w_j)+2a_1{a}_2(w_j-r_1)(p_2-r_2),\hfill \\ \hfill & B_1=(w_j-r_1)P_1-(w_i-w_j)(P_2-I),\hfill \\ \hfill & B_1{B}_2=(w_j-r_1)\left[B_2-(p_2-r_2)(P_1-I)\right],\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}\mathit{vi}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{14}\mathit{\right)}\mathit{and}\mathit{\left(}\mathit{vi}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{30}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 31.

$$\begin{array}{cc}\hfill & c_3=-(w_j-r_1)\left(c_1+2a_1{a}_2(p_2-r_2)\right),\hfill \\ \hfill & c_4=-c_2(p_2-r_2),c_5=0,\hfill \\ \hfill & -c_1(w_i-w_j)+c_2(p_2-q_2)=2a_1{a}_2\left[(w_i-r_1)(q_2-r_2)-(w_j-r_1)(p_2-r_2)\right]\ne 0,\hfill \\ \hfill & (w_i-w_j)B_1{B}_2=\left[(w_i-r_1)(q_2-r_2)-(w_j-r_1)(p_2-r_2)\right]B_1\hfill \\ \hfill & +(p_1-r_1)(q_1-r_1)(p_2-q_2)P_1,\hfill \\ \hfill & (p_2-q_2)B_1{B}_2=\left[(w_j-r_1)(p_2-r_2)-(w_i-r_1)(q_2-r_2)\right]B_2\hfill \\ \hfill & +(w_i-w_j)(q_2-r_2)(p_2-r_2)P_2,\hfill \\ \hfill & P_1=P_2,\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}\mathit{vii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{9}\mathit{\right)}\mathit{and}\mathit{\left(}\mathit{vii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{26}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 32.

$$\begin{array}{cc}\hfill & c_3=-(w_j-r_1)\left(c_1+2a_1{a}_2(p_2-r_2)\right),\hfill \\ \hfill & c_4=-c_2(p_2-r_2),c_5=0,c_1(w_i-w_j)=c_2(p_2-q_2),\hfill \\ \hfill & (w_j-r_1)(p_2-r_2)=(w_i-r_1)(q_2-r_2),\hfill \\ \hfill & B_1{B}_2=(w_j-r_1)(p_2-r_2)P_1,P_1=P_2,\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}\mathit{vii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{9}\mathit{\right)}\mathit{and}\mathit{\left(}\mathit{vii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{26}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 33.

$$\begin{array}{cc}\hfill & c_1=-2a_1{a}_2(q_2-r_2),c_2=-2a_1{a}_2(w_i-r_1),c_5=0,\hfill \\ \hfill & c_3=-2a_1{a}_2(w_i-r_1)(p_2-q_2),c_4=2a_1{a}_2(w_i-r_1)(p_2-r_2),\hfill \\ \hfill & B_1{B}_2=(q_2-r_2)\left[B_1-(w_i-r_1)P_1\right]+(w_i-r_1)B_2,P_1=P_2,\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}\mathit{vii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{8}\mathit{\right)}\mathit{,}\mathit{\left(}\mathit{vii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{10}\mathit{\right)}\mathit{,}\hfill \\ & \mathit{\left(}\mathit{vii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{25}\mathit{\right)}\mathit{,}\mathit{and}\mathit{\left(}\mathit{vii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{27}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

 34.

$$\begin{array}{cc}\hfill & c_2=0,c_5=-c_4,c_3=-(w_j-r_1)\left(c_1+2a_1{a}_2(p_2-r_2)\right),\hfill \\ \hfill & c_4=c_1(w_i-w_j)-2a_1{a}_2(w_j-r_1)(p_2-r_2),\hfill \\ \hfill & B_1=(w_j-r_1)P_1-(w_i-w_j)(P_2-I),\hfill \\ \hfill & B_1{B}_2=(w_j-r_1)(p_2-r_2)(P_1+P_2-I),\hfill \\ & \mathit{This}\mathit{item}\mathit{corresponds}\mathit{to}\mathit{the}\mathit{intersections}\mathit{\left(}\mathit{viii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{6}\mathit{\right)}\mathit{and}\mathit{\left(}\mathit{viii}\mathit{\right)}\mathit{\text{-}}\mathit{\left(}\mathit{23}\mathit{\right)}\mathit{in}\mathit{the}\mathit{tables}\mathit{.}\hfill \end{array}$$

3. Numerical Examples

In this section, two numerical examples are given to exemplify the results.

Let us consider the cubic matrices $A_1=S[I\oplus -I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$ and $A_2=S[\mathbf{0}\oplus \mathbf{0}\oplus I\oplus -I]S^{-1}$. Let us take $p_1=1$, $q_1=-1$, $r_1=0$; $p_2=0$, $q_2=1$, $r_2=-1$. Let us investigate the necessary and sufficient conditions for the linear combination matrix $A_3=a_1{A}_1+a_2{A}_2$ ($a_1,a_2\in {\mathbb{C}}^{*}$) to be $\{1,-1\}$-quadratic—that is, involutive.

Since the matrix $A_3=a_1{A}_1+a_2{A}_2=S[a_{1}I\oplus -a_{1}I\oplus a_{2}I\oplus -a_{2}I]S^{-1}$ is involutive, its square must be the identity matrix. Therefore, the diagonal blocks of its square—namely, the matrices $a_1^{2}I$ and $a_2^{2}I$—must themselves be identity matrices. This implies $a_1^2=a_2^2=1$ and, hence, $a_1=\pm 1$ and $a_2=\pm 1$. Thus, we have $(a_1,a_2)\in \{(1,1),(1,-1),(-1,1),(-1,-1)\}$.

If $(a_1,a_2)=(1,1)$, then $A_3=A_1+A_2$. Therefore, $A_3^2=I$ if and only if $A_1^2+A_2^2=I$, because $A_1{A}_2=\mathbf{0}$. Similarly, it is natural to make the following observations:

If $(a_1,a_2)=(1,-1)$, then $A_3=A_1-A_2$. Therefore, $A_3^2=I$ if and only if $A_1^2+A_2^2=I$.

If $(a_1,a_2)=(-1,1)$, then $A_3=-A_1+A_2$. Therefore, $A_3^2=I$ if and only if $A_1^2+A_2^2=I$.

If $(a_1,a_2)=(-1,-1)$, then $A_3=-A_1-A_2$. Therefore, $A_3^2=I$ if and only if $A_1^2+A_2^2=I$. Thus, in each case, we arrive at the matrix identity $A_1^2+A_2^2=I$. Consequently, for the selected matrices $A_1$ and $A_2$, the necessary and sufficient condition for the linear combination matrix $A_3$ to be involutive is that $(a_1,a_2)\in \{(1,1),(1,-1),(-1,1),(-1,-1)\}$ and $A_1^2+A_2^2=I$.

Now, let us compare this observation with the item (v) of our main theorem.

Since $A_1=B_1+r_{1}I$ and $A_2=B_2+r_{2}I$, one obtains $A_1=B_1$ and $A_2=B_2-I$. So, the equality $A_1{A}_2=\mathbf{0}$ leads to

$$B_1{B}_2=B_1=(p_2-r_2)B_1.$$

(80)

Also, it is obvious that $B_1=A_1=S[I\oplus -I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$ and $B_2=A_2+I=S[I\oplus I\oplus 2I\oplus \mathbf{0}]S^{-1}$. Now, let us take $P_1=S[I\oplus I\oplus \mathbf{0}\oplus \mathbf{0}]S^{-1}$ and $P_2=S[I\oplus I\oplus I\oplus \mathbf{0}]S^{-1}$. Observe that $B_1{P}_1=P_1{B}_1=B_1$, $B_2{P}_2=P_2{B}_2=B_2$, $(B_1-(p_1-r_1)P_1)(B_1-(q_1-r_1)P_1)=\mathbf{0}$, and $(B_2-(p_2-r_2)P_2)(B_2-(q_2-r_2)P_2)=\mathbf{0}$. So, $A_1^2+A_2^2=I$ leads to $B_1^2+{(B_2-I)}^2=I$, that is

$$B_2=-P_1+2P_2=(p_2-q_2)P_1+(q_2-r_2)P_2.$$

(81)

On the other hand, considering the notations $c_1=a_1^2(p_1+q_1-2r_1)+a_1(2a_3-p_3-q_3)$, $c_2=a_2^2(p_2+q_2-2r_2)+a_2(2a_3-p_3-q_3)$, $c_3=-a_1^2(p_1-r_1)(q_1-r_1)$, $c_4=-a_2^2(p_2-r_2)(q_2-r_2)$, $c_5=(a_3-p_3)(a_3-q_3)$ together with the coefficient equalities $c_k$ appearing in item (v) of the main theorem, we obtain $(a_1,a_2)\in \{(1,1),(1,-1),(-1,1),(-1,-1)\}$.

Note that the matrix equalities appearing in Equations (80) and (81) are precisely the matrix equalities stated in the item (v) of the main theorem. Thus, we have obtained the necessary and sufficient conditions for the matrix $A_3$, which is the linear combination of the given matrices $A_1$ and $A_2$, to be involutive by a direct proof, and we have seen that this result is consistent with item (v) of the main theorem.

It should be noted that the results obtained from the example above are consistent with parts (a) and (b) of Theorem 2.3 in [21].

Now, let us give the second example. Consider the cubic matrices $A_1=S[-I\oplus I\oplus -I\oplus \mathbf{0}]S^{-1}$ and $A_2=S[-I\oplus I\oplus I\oplus \mathbf{0}]S^{-1}$. Let us take $p_1=1$, $q_1=-1$, $r_1=0$, $p_2=-1$, $q_2=0$, and $r_2=1$. Let us investigate the necessary and sufficient conditions for the linear combination matrix $A_3=a_1{A}_1+a_2{A}_2$ ($a_1,a_2\in {\mathbb{C}}^{*}$) to be $\{1,0\}$-quadratic—that is, idempotent.

Since the matrix $A_3=a_1{A}_1+a_2{A}_2=S[(-a_1-a_2)I\oplus (a_1+a_2)I\oplus (-a_1+a_2)I\oplus \mathbf{0}]S^{-1}$ is idempotent, its square must be equal to itself. Therefore, one has ${(-a_1-a_2)}^2=-(a_1+a_2)$, ${(a_1+a_2)}^2=a_1+a_2$, ${(-a_1+a_2)}^2=-a_1+a_2$. From this, $a_1=-{\displaystyle \frac{1}{2}}$ and $a_2={\displaystyle \frac{1}{2}}$ are obtained. Thus, we have $A_3=-{\displaystyle \frac{1}{2}}{A}_1+{\displaystyle \frac{1}{2}}{A}_2$. On the other hand, it is clear that $A_1^2=A_2^2$. Therefore, the condition $A_3^2=A_3$ leads to $-A_1+A_2+A_1{A}_2=A_1^2$. Thus, for the given matrices $A_1$ and $A_2$, the matrix $A_3$ is idempotent precisely when $(a_1,a_2)=\left(-\frac{1}{2},\frac{1}{2}\right)$ and the relation $-A_1+A_2+A_1{A}_2=A_1^2$ holds.

We now relate this result to item (i) of the main theorem in the case $i=2$.

Since $A_1=B_1+r_{1}I$ and $A_2=B_2+r_{2}I$, one obtains $A_1=B_1$ and $A_2=B_2+I$. Thus, we have $B_1=A_1=S[-I\oplus I\oplus -I\oplus \mathbf{0}]S^{-1}$ and $B_2=A_2-I=S[-2I\oplus \mathbf{0}\oplus \mathbf{0}\oplus -I]S^{-1}$. Now, let us take $P_1=S[I\oplus I\oplus I\oplus \mathbf{0}]S^{-1}$ and $P_2=S[I\oplus \mathbf{0}\oplus \mathbf{0}\oplus I]S^{-1}$. Observe that $B_1{P}_1=P_1{B}_1=B_1$, $B_2{P}_2=P_2{B}_2=B_2$, $(B_1-(p_1-r_1)P_1)(B_1-(q_1-r_1)P_1)=\mathbf{0}$, and $(B_2-(p_2-r_2)P_2)(B_2-(q_2-r_2)P_2)=\mathbf{0}$. Also, notice that $A_1^2=A_2^2=P_1$. The equality $A_2^2=P_1$ yields

$$B_2=-2P_2+I-P_1=(p_2-r_2)P_2+(p_2-q_2)(P_1-I).$$

(82)

Similarly, the equality $-A_1+A_2+A_1{A}_2=A_1^2$ together with (82) leads to

$$B_1{B}_2=2(P_1+P_2-I)=(p_2-r_2)(q_1-r_1)(P_1+P_2-I).$$

(83)

On the other hand, using the expressions $c_1=a_1^2(p_1+q_1-2r_1)+a_1(2a_3-p_3-q_3)$, $c_2=a_2^2(p_2+q_2-2r_2)+a_2(2a_3-p_3-q_3)$, $c_3=-a_1^2(p_1-r_1)(q_1-r_1)$, $c_4=-a_2^2(p_2-r_2)(q_2-r_2)$, $c_5=(a_3-p_3)(a_3-q_3)$ together with the coefficient relations $c_k$ stated in item (i) of the main theorem for $i=2$, it follows that the pair $(a_1,a_2)$ must be equal to $(-\frac{1}{2},\frac{1}{2})$.

Observe that the matrix identities in (82) and (83) coincide exactly with those presented in item (i) of the main theorem for the case $i=2$. Consequently, by employing a direct argument, we have derived the necessary and sufficient conditions for the matrix $A_3$, which is formed as a linear combination of $A_1$ and $A_2$, to be idempotent. Furthermore, this shows that our derivation is fully consistent with item (i) of the main theorem.

It is worth noting that the results derived from the above example align with part (a) of Theorem 2.2 in [19].

4. Conclusions and Discussion

In applications, when two cubic matrices $A_1$ and $A_2$ are given, the scalars $p_1,q_1,r_1$ and $p_2,q_2,r_2$ are already known. When addressing the problem of whether linear combinations of these two cubic matrices yield a $\{p_3,q_3\}$ quadratic matrix, the scalars $p_3$ and $q_3$ are likewise determined quantities. Accordingly, the unknown coefficients $a_1$ and $a_2$ of the linear combination can be readily obtained by substituting the known values into the above theorem. It should be noted that the cases of the theorem are expressed in terms of the matrices $B_1$ and $B_2$, rather than the matrices $A_1$ and $A_2$. However, since the matrices $B_1$ and $B_2$ differ from the matrices $A_1$ and $A_2$ only by a scalar multiple of the identity matrix, the cases of the theorem can also be formulated in terms of $A_1$ and $A_2$, if desired.

It may be asserted that Theorem 8 encompasses many results already established in the literature. For instance, if in Theorem 8 one takes $(p_1,q_1,r_1),(p_2,q_2,r_2)\in \{(1,-1,0),(-1,1,0),(1,0,-1),(-1,0,1),(0,1,-1),(0,-1,1)\}$ and $(p_3,q_3)\in \{(1,0),(0,1)\}$ (or $\in \left\{\right(1,-1),(-1,1\left)\right\}$), then the matrices $A_1$ and $A_2$ are tripotent, and the matrix $A_3$ is idempotent (or involutive). Thus, from the main theorem, the idempotency (or involutivity) of the linear combination of two tripotent matrices can be characterized, as these cases are already established in the literature. However, the main theorem not only deals with linear combinations of tripotent matrices but also covers a much broader class of cubic matrices whose eigenvalues are distinct and not necessarily limited to 1, $-1$, or 0. In the literature, apart from special matrices, linear combinations of such matrices have not been considered. Therefore, this study can be viewed as addressing this gap in the existing literature.

This study establishes a concrete link between cubic matrices and polynomial identities by determining the precise conditions under which a linear combination of two cubic matrices satisfies a quadratic identity. Indeed, the fact that the matrices $A_1$ and $A_2$ are cubic means that they satisfy polynomial identities of the form

$$A_i^3=(p_i+q_i+r_i)A_i^2-(p_i{q}_i+p_i{r}_i+q_i{r}_i)A_i+p_i{q}_i{r}_{i}I$$

which, in turn, determine the polynomials

$$x^3-(p_i+q_i+r_i)x^2+(p_i{q}_i+p_i{r}_i+q_i{r}_i)x-p_i{q}_i{r}_i$$

associated with each matrix. Since these polynomials govern not only the spectral structure of the matrices but also how their powers can be expressed, obtaining a quadratic identity of the form

$$A_3^2=(p_3+q_3)A_3-p_3{q}_{3}I$$

for the linear combination $A_3=a_1{A}_1+a_2{A}_2$ depends directly on the interaction between the coefficients of the two cubic polynomials. The algebraic conditions derived in this study identify precisely which relationships among the coefficients ensure that the square of $A_3$ can be expressed solely in terms of $A_3$ and I. Thus, the structural properties of the underlying cubic polynomials become the key factor that determines when the linear combination is quadratic, revealing how polynomial identities are transferred through matrix operations and reduced to lower-degree identities. Consequently, this study builds a direct bridge between the polynomials underlying cubic matrices and the quadratic nature of their linear combinations, thereby providing a new layer of connection within the theory of matrix polynomials.

It would be of interest to investigate whether the results of this study extend to the generalized families of cubic matrices discussed in [30], a question that seems to remain open.