Optimal Boundary-Flux Control of a Sharp Moving Interface in the Classical Two-Phase Stefan Problem

Abstract

In this paper, we study the optimal boundary control of solidification governed by the classical two-phase Stefan problem with a sharp moving interface. The main objective is to formulate an optimal control problem for interface motion using boundary heat-flux control. The control acts as a Neumann heat flux on a designated boundary segment and steers the interface through the Stefan condition. Using an enthalpy formulation, we prove well-posedness under boundary control and establish Lipschitz continuity of the control-to-state map and continuous dependence on the initial data. We then derive first-order necessary optimality conditions using a Lagrangian approach and propose a practical algorithm that couples a semismooth Newton method with Sequential Quadratic Programming (SQP) to compute the optimal boundary flux.

1. Introduction

The classical two-phase Stefan problem is a foundational model for melting and solidification in materials such as aluminum [1] and steel [2]. It is a free boundary problem where a sharp solid–liquid interface ${\Gamma }_t$ moves according to the Stefan condition, which balances heat fluxes across ${\Gamma }_t$ with latent heat release or absorption.

Although the sharp-interface formulation directly reflects the physical mechanism, it presents substantial analytical and numerical challenges, especially in higher dimensions. The shifted temperature variable $\theta :=T-T_m$ and the enthalpy formulation provide an alternative on a fixed domain, where temperature is expressed as a piecewise linear function of enthalpy and $\theta$ is used throughout, with the melting temperature corresponding to $\theta =0$. The latent-heat jump appears as a small regularized slope, and boundary heat fluxes enter naturally in weak form. This reformulation implicitly captures the moving interface as the set where $\theta =0$ and enthalpy lies in the latent-heat interval, which is advantageous for boundary-control analysis [3,4].

A primary challenge in controlling solidification processes is managing the moving interface. One avenue adopts a sharp-interface optimal-control formulation, treating the free boundary itself as an optimization variable and using boundary temperature to track a desired interface evolution, while explicitly enforcing the Stefan condition [5]. A second, classical approach formulates the Stefan problem as a variational inequality, which enables optimal control under mixed boundary conditions and accommodates elliptic degeneracy of the original formulation [6]. Complementing these open-loop and optimization-based methods, research has also focused on boundary feedback control through backstepping and energy-shaping designs, which guarantee exponential stabilization of the interface position at a desired setpoint in both one- and two-phase Stefan problems [7,8]. Taken together, these directions illustrate a clear evolution in methodology, where optimization-based formulations, sharp-interface methods, and variational-inequality approaches provide powerful tools for trajectory design and analysis, while feedback-based controllers supply real-time stabilization guarantees that are crucial under disturbances and modeling uncertainties. This complementarity shows that no single method dominates; rather, the strength of the field lies in the interplay between rigorous optimal-control formulations and stabilizing feedback strategies, offering a broad and adaptable set of methods for applications ranging from crystal growth to advanced thermal energy storage.

While optimal control of Stefan-type problems has been investigated in several works [5], most existing studies focus on distributed controls or adjustments of the initial state. In contrast, boundary control—directly relevant to practical applications—has not been examined with the same level of analytical detail. In particular, results establishing well-posedness under boundary heat-flux control, stability estimates such as Lipschitz continuity of the control-to-state mapping, and rigorous derivations of adjoint-based optimality conditions remain incomplete. Recent work on networked control systems has explored how asymmetric information and unreliable communication affect controller performance [9,10]. Studies on decentralized and remote–local control architectures under such constraints, though focused on finite-dimensional systems, provide insights on limited information exchange and robustness that are conceptually relevant to boundary control, where sensing and actuation may also be distributed or delayed.

This paper provides a rigorous analysis of the two-phase Stefan problem with boundary heat-flux control in the enthalpy formulation. We prove the well-posedness of the controlled state system and establish stability estimates, including Lipschitz continuity with respect to both control and initial conditions. Building on these results, we formulate a tracking-type optimal control problem for the solidification front and show the existence of optimal controls. We then derive first-order necessary conditions using a Lagrangian approach and analyze the associated adjoint system for this highly nonlinear and nonsmooth control problem. Finally, we introduce a numerical strategy based on semismooth Newton methods combined with Sequential Quadratic Programming (SQP), demonstrating how these theoretical conditions can be implemented computationally.

Our motivation is driven by both theoretical and applied considerations. Mathematically, the Stefan problem belongs to a class of nonlinear free boundary problems that raise fundamental questions about existence, stability, and solution sensitivity. From an applied perspective, solidification processes play a central role in metallurgy, crystal growth, and materials science, where microstructural properties such as grain size and porosity depend strongly on the evolution of the phase interface. The ability to guide these processes through boundary fluxes is of clear technological importance. The remainder of this paper is organized as follows: In Section 2, we establish well-posedness and continuity for the controlled enthalpy model. In Section 3, we formulate the optimal boundary control problem and derive adjoint-based first-order optimality conditions. In Section 4, we present the numerical discretization and algorithms, and we illustrate controlled solidification through computational experiments.

2. The Classical Two-Phase Stefan Problem

The heat equation is a parabolic partial differential equation that is central to thermodynamics and mathematical analysis. Originally formulated to describe heat’s diffusion through a medium, it has since become a cornerstone in both theoretical and applied mathematics.

The Stefan problem provides a moving-interface model for phase-change phenomena such as melting and solidification. The transition occurs within a mushy zone, called the interface, where liquid and solid phases coexist. This model has wide applications in natural sciences and industrial processes [11], as noted in the Introduction.

In the traditional temperature formulation of the two-phase Stefan problem, the location of the phase-change interface must be determined as part of the solution. This solid–liquid boundary is a free boundary whose position is unknown a priori, making the analysis particularly challenging in multiple dimensions. To avoid explicit interface tracking, the problem can be reformulated in terms of enthalpy (internal energy). In the enthalpy method, the heat equation is expressed in terms of internal energy, absorbing the Stefan condition (accounting for latent heat) into the material law rather than imposing it as a separate boundary condition. In what follows, we develop the enthalpy-based formulation for the two-phase Stefan problem.

2.1. Enthalpy Formulation of the Two-Phase Stefan Problem

Enthalpy (internal energy) represents the total heat content of a system, combining sensible heat (temperature variation) and latent heat (associated with phase transitions). For a single-phase medium with shifted temperature $\theta (x,t)$ and constant specific heats, the enthalpy is expressed as follows:

$$E\left(\theta \right)=\left\{\begin{array}{cc}\rho c_s\theta ,\hfill & \theta \le 0,\hfill \\ \rho c_{\mathsf{\ell }}\theta +\rho L,\hfill & \theta >0,\hfill \end{array}\right.$$

where $\rho \left(x\right)>0$ is the mass density, $c_s\left(\theta \right)$, $c_{\mathsf{\ell }}\left(\theta \right)$ are the specific heats of the solid and liquid phases, respectively, and L denotes the latent heat associated with the phase transition.

The specific heat c denotes the energy required to raise the temperature of one unit of mass by one degree. In the absence of phase change, E evolves in time according to heat diffusion. With a boundary heat-flux control g prescribed on a portion ${\Gamma }_c$ of the boundary, the standard heat conduction model takes the following form:

$$E_t=\kappa \Delta \theta ,\kappa {\partial }_{\nu }\theta =g,$$

(1)

where $\kappa >0$ is the thermal conductivity and ${\partial }_{\nu }$ denotes the outward normal derivative for the Neumann boundary condition. Equation (1) states that the time-rate of change in enthalpy E in a region equals the thermal diffusion of $\theta$, and the boundary flux $\kappa {\partial }_{\nu }\theta$ is controlled by g.

Now, consider a material that can exist in two phases (solid and liquid), with a phase change occurring at a constant melting (solidification)-shifted temperature $\theta =0$. In a two-phase (solid–liquid) scenario, the enthalpy as a function of $\theta$ exhibits a discontinuity at $\theta =0$ due to the absorption or release of latent heat L. As the material passes through $\theta =0$, an extra energy $\rho L$ (per unit volume) must be absorbed or released without a temperature change. This leads to a jump in the enthalpy–temperature relation, known as the Stefan condition. That is, enthalpy has a jump of magnitude $\rho L$ at $\theta =0$.

The two-phase Stefan problem describes heat diffusion in a medium undergoing a solid–liquid phase change, with a moving interface ${\Gamma }_t$ separating the two phases. We denote by ${\Omega }_t^{-}=\{x\in \Omega :\theta <0\}$ the solid region and by ${\Omega }_t^{+}=\{x\in \Omega :\theta >0\}$ the liquid region. Thus, ${\Gamma }_t$ is a moving free boundary, and we assume temperature continuity $\theta =0$ on ${\Gamma }_t$.

Within each phase, heat evolves according to Fourier’s law. The general heat equation is

$$\rho c{\displaystyle \frac{\partial \theta }{\partial t}}=\kappa \Delta \theta ,$$

(2)

Accordingly, the governing equations in the two phases are

$$\left\{\begin{array}{cc}{\rho }_s{c}_s{\displaystyle \frac{\partial {\theta }_s}{\partial t}}={\kappa }_s\Delta {\theta }_s,\hfill & x\in {\Omega }_t^{-},\hfill \\ {\rho }_{\mathsf{\ell }}{c}_{\mathsf{\ell }}{\displaystyle \frac{\partial {\theta }_{\mathsf{\ell }}}{\partial t}}={\kappa }_{\mathsf{\ell }}\Delta {\theta }_{\mathsf{\ell }},\hfill & x\in {\Omega }_t^{+},\hfill \end{array}\right.$$

together with the condition ${\theta }_s={\theta }_{\mathsf{\ell }}=0$ on ${\Gamma }_t$.

On a controlled portion ${\Gamma }_c\subset \partial \Omega$ of the external boundary, the normal heat flux is prescribed as a boundary control $g(t,x)$. The boundary condition is given by

$$\kappa {\partial }_{\nu }\theta =g,x\in {\Gamma }_c,$$

(3)

where we take $\kappa$ to be the thermal conductivity of the material in contact with $\partial \Omega$ at ${\Gamma }_c$. On the remaining boundary $\partial \Omega \setminus {\Gamma }_c$, we impose insulation: $\kappa {\partial }_{\nu }\theta =0$.

The interface ${\Gamma }_t=\{x\in \Omega :\theta (t,x)=0\}$ has unit normal $\nu$ and normal velocity $V(t,x)$.

Energy conservation across ${\Gamma }_t$ then implies that the latent heat absorbed or released by the moving boundary balances the jump in conductive heat flux between the two phases:

$$\rho LV(t,x)={\kappa }_{\mathsf{\ell }}{\partial }_{\nu }{\theta }_{\mathsf{\ell }}-{\kappa }_s{\partial }_{\nu }{\theta }_s,x\in {\Gamma }_t.$$

(4)

Here, $\nu$ points from solid to liquid, and V is the normal velocity in the direction of $\nu$.

Collecting the above, the strong form of the two-phase Stefan problem is

$$\left\{\begin{array}{cc}{\rho }_s{c}_s{\displaystyle \frac{\partial {\theta }_s}{\partial t}}={\kappa }_s\Delta {\theta }_s,\hfill & x\in {\Omega }_t^{-},{\theta }_s=0\mathrm{on}{\Gamma }_t,\hfill \\ {\rho }_{\mathsf{\ell }}{c}_{\mathsf{\ell }}{\displaystyle \frac{\partial {\theta }_{\mathsf{\ell }}}{\partial t}}={\kappa }_{\mathsf{\ell }}\Delta {\theta }_{\mathsf{\ell }},\hfill & x\in {\Omega }_t^{+},{\theta }_{\mathsf{\ell }}=0\mathrm{on}{\Gamma }_t,\hfill \\ \rho LV(t,x)={\kappa }_{\mathsf{\ell }}{\partial }_{\nu }{\theta }_{\mathsf{\ell }}-{\kappa }_s{\partial }_{\nu }{\theta }_s,\hfill & x\in {\Gamma }_t,\hfill \\ \kappa {\partial }_{\nu }\theta =g,\hfill & x\in {\Gamma }_c\subset \partial \Omega ,\hfill \\ \kappa {\partial }_{\nu }\theta =0,\hfill & x\in \partial \Omega \setminus {\Gamma }_c.\hfill \end{array}\right.$$

(5)

In System (5), the unknowns are the shifted temperature field $\theta (t,x)$ and the evolving interface ${\Gamma }_t$. Given an initial shifted temperature distribution and initial interface ${\Gamma }_0$, this system determines the coupled dynamics of the shifted temperature in each phase and the interface motion. Physically, the Stefan condition enforces that excess heat at the interface is consumed as latent heat to melt the solid, whereas a deficit of heat leads to solidification, thereby ensuring conservation of energy during the phase transition.

We define a set-valued enthalpy function $\gamma \left(\theta \right)$ to capture this behavior:

$$\gamma \left(\theta \right)=\left\{\begin{array}{cc}\rho c_{\mathsf{\ell }}\theta +\rho L,\hfill & \theta >0,\hfill \\ [0,\rho L],\hfill & \theta =0,\hfill \\ \rho c_s\theta ,\hfill & \theta <0,\hfill \end{array}\right.$$

(6)

This strong form is presented for physical clarity; our analysis and subsequent results are derived from the weak enthalpy formulation. Figure 1 illustrates the enthalpy graph [11,12,13], as defined in Equation (6).

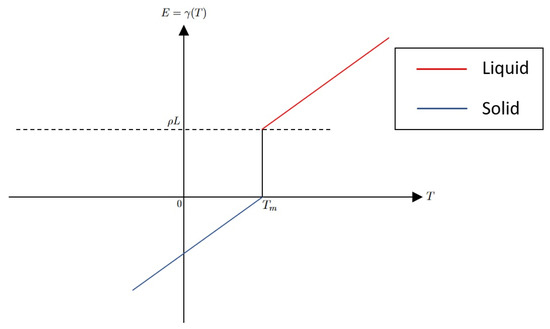
Figure 1. The enthalpy set-valued graph $\gamma \left(T\right)$.

Since $\gamma$ is multi-valued at $\theta =0$, its inverse $\beta$ is single-valued and continuous. Let $\beta \left(E\right)$ denote the inverse relation, giving the shifted temperature $\theta$ as a function of enthalpy E:

$$\beta \left(E\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{\rho c_{\mathsf{\ell }}}}(E-\rho L),\hfill & E>\rho L,\hfill \\ 0,\hfill & 0\le E\le \rho L,\hfill \\ {\displaystyle \frac{1}{\rho c_s}}E,\hfill & E<0.\hfill \end{array}\right.$$

(7)

Figure 2 shows the graph of the function $\beta \left(E\right)$. By construction, $\beta \left(E\right)$ is continuous and non-decreasing in E. In fact, $\beta$ is Lipschitz-continuous globally with the Lipschitz constant

$$L_{\beta }=max\left\{{\displaystyle \frac{1}{\rho c_s}},{\displaystyle \frac{1}{\rho c_{\mathsf{\ell }}}}\right\}.$$

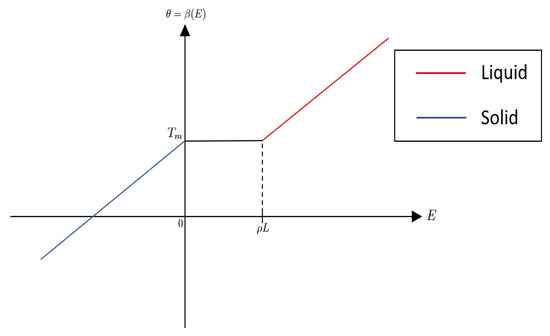
Figure 2. The inverse enthalpy graph $\beta \left(E\right)$.

Thus, $\beta$ is a continuous, monotone, Lipschitz function of enthalpy, and $\gamma$ is its (multi-valued) inverse, which is a monotone graph. Throughout, we write ${\beta }^{\prime }$ for the a.e. derivative, and identities involving ${\beta }^{\prime }$ are understood to hold almost everywhere. Physically, $\beta \left(E\right)$ shows that the shifted temperature $\theta$ remains constant at 0 while enthalpy changes within the latent heat interval $[0,\rho L]$.

Using the enthalpy–temperature relation above, we can reformulate the Stefan problem entirely in terms of enthalpy $E(x,t)$ on a fixed domain. Substituting $\theta =\beta \left(E\right)$ into the heat conduction law (1) gives the governing equation in enthalpy form:

$$E_t=\nabla ·\left(\kappa \nabla \left[\beta \right(E\left)\right]\right),\kappa {\partial }_{\nu }\left[\beta \left(E\right)\right]=g.$$

(8)

For simplicity, we take $\kappa$ to be constant in the enthalpy formulation; phase-dependent $\kappa$ can be handled with the same analysis (variable-coefficient elliptic operators).

If a solution $E(x,t)$ of (8) is known, the shifted temperature is recovered as $\theta (x,t)=\beta \left(E\right(x,t\left)\right)$. The solid–liquid interface at time $t>0$ is then the set of points

$${\Gamma }_t=\{x\in \Omega :\theta (x,t)=0\}=\{x\in \Omega :E(x,t)\in [0,\rho L]\}.$$

2.2. Weak Formulation and Time Discretization

We now establish the weak formulation of the enthalpy equation with boundary heat-flux control. Let $\Omega \subset {\mathbb{R}}^d$ be a fixed domain and ${\Gamma }_c\subseteq \partial \Omega$ the portion of the boundary where a Neumann control is prescribed. Multiplying the enthalpy equation by a test function $\varphi \in H^1(\Omega )$ and applying Green’s identity, we obtain

$${\int }_{\Omega }{E}_t\varphi dx={\int }_{{\Gamma }_c}g\varphi ds-{\int }_{\Omega }\kappa \nabla \beta \left(E\right)·\nabla \varphi dx.$$

(9)

Thus, in the weak form, the control g enters explicitly as a boundary Neumann term on ${\Gamma }_c$. Equivalently, we may write

$${(\kappa \Delta \beta \left(E\right),\varphi )}_{\Omega }=-{(\kappa \nabla \beta \left(E\right),\nabla \varphi )}_{\Omega }+{(g,\varphi )}_{{\Gamma }_c}.$$

(10)

The weak formulation implicitly encodes the global energy balance. The compatibility condition

$${\displaystyle \frac{d}{dt}}{\int }_{\Omega }E(t,x)dx={\int }_{{\Gamma }_c}g(t,s)ds,$$

expresses conservation of total enthalpy in the domain. Specifically, the rate of change in total enthalpy in the domain must equal the net heat flux through the controlled boundary.

To construct solutions, we discretize in time with step size $\Delta t>0$. The backward Euler scheme for the enthalpy formulation is

$${\displaystyle \frac{E^n-E^{n-1}}{\Delta t}}=\kappa \Delta \beta \left(E^n\right),\kappa {\partial }_{\nu }\beta \left(E^n\right)=g^n.$$

(11)

We introduce the convex functional $j:\mathbb{R}\to \mathbb{R}$, whose subdifferential $\partial j=\gamma$ characterizes the enthalpy–temperature relation:

$$j\left(\beta \right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{2}}\rho c_s{\beta }^2,\hfill & \beta <0,\hfill \\ {\displaystyle \frac{1}{2}}\rho c_{\mathsf{\ell }}{\beta }^2+\rho L\beta ,\hfill & \beta \ge 0,\hfill \end{array}\right.$$

(12)

Then, (11) is equivalent to the variational inclusion

$$\kappa \Delta t\Delta \beta \left(E^n\right)+E^{n-1}\in \partial j\left(\beta \left(E^n\right)\right),\kappa {\partial }_{\nu }\beta \left(E^n\right)=g^n.$$

(13)

The weak solution $\beta \left(E^n\right)$ is obtained as the unique minimizer of the convex functional

$$J_n\left(\beta \right)=\frac{1}{2}{\int }_{\Omega }\left({\kappa \Delta t|\nabla \beta |}^2+j\left(\beta \right)-E^{n-1}\left(x\right)\beta \right)dx-\Delta t{(g^n,\beta )}_{{\Gamma }_c}.$$

(14)

The functional $J_n$ is coercive and convex. While the Dirichlet energy term ensures convexity, we note that $j\left(\beta \right)$ is not strictly convex over the interval where $\beta \left(E\right)=0$ (the mushy region). Under the given Neumann boundary conditions, the constant nullspace of the Laplacian combined with the non-strict convexity of $j\left(\beta \right)$ in the mushy region means that uniqueness of the minimizer requires additional regularity conditions. We address this through regularization in Section 3, where we introduce a strictly convex approximation that guarantees both existence and uniqueness.

2.3. A Priori Bounds for the Finite-Difference Solution

We derive uniform a priori estimates for the finite-difference scheme, which are key for compactness and for passing to the continuous-time limit as $\Delta t\to 0$. Such estimates for enthalpy formulations of the Stefan problem go back to Crank [14], Damlamian [13], White [3], and Voller–Cross [4], with rigorous numerical error analysis by Elliott [15].

The main tool is the compactness result known as the Aubin–Lions compactness lemma. This result is significant in the theory of Sobolev spaces and the analysis of nonlinear evolution equations, as it provides a criterion for compact embedding into the space $L^2(0,T;X)$. In particular, it serves as a tool for establishing the existence of approximate solutions developed through the Galerkin method. The lemma is formally stated as follows:

Lemma 1 

(Aubin–Lions–Simon compactness lemma [16,17]). Let $X_0$, X, $X_1$ be Banach spaces with $X_0\subseteq X\subseteq X_1$, where $X_0$ is compactly embedded in X and X is continuously embedded in $X_1$. For $1\le p,q\le \infty$, set

$$W=\{u\in L^p(0,T;X_0):{\partial }_{t}u\in L^q(0,T;X_1)\}.$$

Then, if $p<\infty$, the embedding $W\hookrightarrow L^p(0,T;X)$ is compact, and if $p=\infty$ and $q>1$, the embedding $W\hookrightarrow C\left(\right[0,T];X)$ is compact.

While the original proof by Aubin required reflexivity of $X_0$ or $X_1$, Simon [18] later proved this relaxed version and extended the result without this assumption.

Theorem 1 

(Uniform bounds). Let $\Omega \subset {\mathbb{R}}^d$ be a bounded Lipschitz domain with ${\Gamma }_c\subset \partial \Omega$ measurable, and let $t_n=n\Delta t$ with $N\Delta t=T$. Assume that $\kappa >0$ and $E^0\in L^2(\Omega )$. Then, the discrete solution $(E^n,\beta \left(E^n\right))$ of (11) satisfies bounds independent of $\Delta t$:

(i) 

Assume that $g\in L^2(0,T;H^{-1/2}\left({\Gamma }_c\right))$. Then, the following energy bound holds:

$${\int }_{\Omega }\Phi \left(E^n\right)dx+\kappa \Delta t\sum _{k=1}^n\parallel \nabla \beta \left(E^k\right){\parallel }_{L^2(\Omega )}^2\le {\int }_{\Omega }\Phi \left(E^0\right)dx+C\sum _{k=1}^n\Delta t{\parallel g^k\parallel }_{H^{-1/2}\left({\Gamma }_c\right)}^2.$$

(15)

(ii) 

Assume in addition that $g\in L^1(0,T;L^1\left({\Gamma }_c\right))$. Then, the solution satisfies the following $L^1$ bound:

$${\int }_{\Omega }\left|E^n\right|dx\le M,{\int }_{\Omega }\left|\beta \left(E^n\right)\right|dx\le LM,$$

(16)

where M depends only on $\parallel E^0{\parallel }_{L^1(\Omega )}$ and ${\parallel g\parallel }_{L^1(0,T;L^1\left({\Gamma }_c\right))}$.

Proof. 

(i) Define the convex potential function

$$\Phi \left(E\right)={\int }_0^E\beta \left(z\right)dz=\left\{\begin{array}{cc}{\displaystyle \frac{1}{2\rho c_s}}{E}^2,\hfill & E<0,\hfill \\ 0,\hfill & 0\le E\le \rho L,\hfill \\ {\displaystyle \frac{1}{2\rho c_{\mathsf{\ell }}}}{(E-\rho L)}^2,\hfill & E>\rho L.\hfill \end{array}\right.$$

(17)

For a convex differentiable function f, we have

$$f\left(\widehat{x}\right)\ge f\left(x\right)+f^{\prime }\left(x\right)(\widehat{x}-x),\forall \widehat{x}.$$

(18)

Recall the discrete Equation (11); applying (18) with $f=\Phi$, $x=E^n$, $\widehat{x}=E^{n-1}$ yields

$$\Phi \left(E^{n-1}\right)-\Phi \left(E^n\right)\ge (\beta \left(E^n\right),E^{n-1}-E^n).$$

(19)

Using Green’s identity and substituting into (19) gives

$${\int }_{\Omega }\Phi \left(E^n\right)dx-{\int }_{\Omega }\Phi \left(E^{n-1}\right)dx+\kappa \Delta t{\parallel \nabla \beta \left(E^n\right)\parallel }_{L^2(\Omega )}^2\le \Delta t{(g^n,\beta \left(E^n\right))}_{{\Gamma }_c}.$$

(20)

Summing over $k=1,\dots ,n$ formally gives

$${\int }_{\Omega }\Phi \left(E^n\right)dx+\sum _{k=1}^n\kappa \Delta t\parallel \nabla \beta \left(E^k\right){\parallel }_{L^2(\Omega )}^2\le {\int }_{\Omega }\Phi \left(E^0\right)dx+\sum _{k=1}^n\Delta t{\parallel g^k\parallel }_{H^{-1/2}\left({\Gamma }_c\right)}^2,$$

(21)

once the boundary term is estimated as follows. By the trace inequality and Young’s inequality,

$$\Delta t{(g^n,\beta \left(E^n\right))}_{{\Gamma }_c}\le \Delta t\parallel g^n{\parallel }_{H^{-1/2}\left({\Gamma }_c\right)}\parallel \beta \left(E^n\right){\parallel }_{H^{1/2}\left({\Gamma }_c\right)}\le C_{\mathrm{tr}}\Delta t\parallel g^n{\parallel }_{H^{-1/2}\left({\Gamma }_c\right)}{\parallel \beta \left(E^n\right)\parallel }_{H^1(\Omega )}$$

$$\le \frac{\kappa }{2}\Delta t\parallel \nabla \beta \left(E^n\right){\parallel }_{L^2(\Omega )}^2+C\Delta t\parallel g^n{\parallel }_{H^{-1/2}\left({\Gamma }_c\right)}^2+C\Delta t{\parallel \beta \left(E^n\right)\parallel }_{L^2(\Omega )}^2.$$

Using the Lipschitz property of $\beta$,

$$\parallel \beta \left(E^n\right){\parallel }_{L^2(\Omega )}^2\le C_1\Phi \left(E^n\right)+C_2,$$

(22)

we substitute into the inequality above. After moving the gradient term to the left-hand side of (20), we arrive at the key recursive inequality:

$$(1-C\Delta t){\int }_{\Omega }\Phi \left(E^n\right)dx\le {\int }_{\Omega }\Phi \left(E^{n-1}\right)dx+C\Delta t{\parallel g^n\parallel }_{H^{-1/2}\left({\Gamma }_c\right)}^2+C\Delta t.$$

(23)

Applying the discrete Gronwall lemma to (23) yields the desired uniform estimate: there exists a constant $C>0$ independent of $\Delta t$ such that

$${\int }_{\Omega }\Phi \left(E^n\right)dx+{\displaystyle \frac{1}{2}}\sum _{k=1}^n\kappa \Delta t{\parallel \nabla \beta \left(E^k\right)\parallel }_{L^2(\Omega )}^2\le {\int }_{\Omega }\Phi \left(E^0\right)dx+C\sum _{k=1}^n\Delta t{\parallel g^k\parallel }_{H^{-1/2}\left({\Gamma }_c\right)}^2.$$

(24)

This proves (15).

(ii) For the $L^1$ bound, test (11) with

$$\varphi ={\rho }_{\epsilon }\left(\beta \left(E^n\right)\right),$$

where ${\rho }_{\epsilon }$ is a smooth regularization of sgn. Passing $\epsilon \to 0$ gives

$${\int }_{\Omega }|E^n|dx-{\int }_{\Omega }|E^{n-1}|dx\le \Delta t{\int }_{{\Gamma }_c}\left|g^n\right|ds.$$

(25)

Summing in n yields

$${\int }_{\Omega }\left|E^n\right|dx\le M,$$

(26)

for some constant M. Finally,

$${\int }_{\Omega }\beta \left(E^n\right)dx\le L{\int }_{\Omega }\left|E^n\right|dx\le LM,$$

(27)

where L is the Lipschitz constant of $\beta$. This proves (16).    □

Theorem 1 shows that $E^n$ is bounded in $L^{\infty }(0,T;L^1(\Omega ))$, $\beta \left(E^n\right)$ is bounded in $L^2(0,T;H^1(\Omega ))$, and $\left\{{\partial }_t{E}^n\right\}$ is bounded in $L^2(0,T;H^{-1}(\Omega ))$. By the Aubin–Lions compactness lemma, using the compact embedding $H^1(\Omega )\hookrightarrow L^2(\Omega )$ and the continuous embedding $L^2(\Omega )\hookrightarrow H^{-1}(\Omega )$, we can conclude that

$$\beta \left(E^n\right)\mathrm{is}\mathrm{relatively}\mathrm{compact}\mathrm{in}{L}^2(0,T;L^2(\Omega )),$$

which is the essential ingredient for passing to the limit $\Delta t\to 0$ and proving the existence of a weak solution.

Moreover, the estimate (24) shows that

$$\nabla \beta \left(E^n\right)\mathrm{is}\mathrm{uniformly}\mathrm{bounded}\mathrm{in}{L}^2\left((0,T)\times \Omega \right).$$

On any set where ${\beta }^{\prime }\left(s\right)\ge c_0>0$, this also controls $\nabla E^n$ in $L^2$; combined with the compactness of $\beta \left(E^n\right)$ and the local invertibility of $\beta$, this implies the strong convergence of $E^n$ on that set.

2.4. Convergence of Weak Solutions

We establish the existence of a weak solution to the enthalpy formulation (9) by passing to the limit $\Delta t\to 0$ in the discrete approximation. The compactness needed for this passage is provided by the Aubin–Lions compactness lemma.

Theorem 2 

(Existence of a weak solution). Let $\Omega \subset {\mathbb{R}}^d$ be a bounded Lipschitz domain with ${\Gamma }_c\subset \partial \Omega$. Assume that $E^0\in L^2(\Omega )$ and $g\in L^2(0,T;H^{-1/2}\left({\Gamma }_c\right))$. Then, there exists a pair $(E,\beta (E\left)\right)$ such that

$$E\in L^{\infty }(0,T;L^1(\Omega )),\beta \left(E\right)\in L^2(0,T;H^1(\Omega )),E_t\in L^2(0,T;H^{-1}(\Omega )),$$

and the weak formulation

$${\int }_0^T⟨E_t,\varphi ⟩dt+\kappa {\int }_0^T{\int }_{\Omega }\nabla \beta \left(E\right)·\nabla \varphi dxdt={\int }_0^T{⟨g,\varphi ⟩}_{{\Gamma }_c}dt$$

(28)

holds for all $\varphi \in L^2(0,T;H^1(\Omega ))$.

Proof. 

The continuous enthalpy formulation is given by

$$E_t=\kappa \Delta \beta \left(E\right),\kappa {\partial }_{\nu }\beta \left(E\right)=g.$$

(29)

Define the time interpolants from the discrete sequence $\left\{(E^n,\beta \left(E^n\right),g^n)\right\}$:

$${\overline{E}}_{\Delta t}\left(t\right):=E^n,{\overline{\beta \left(E\right)}}_{\Delta t}\left(t\right):=\beta \left(E^n\right),{\overline{g}}_{\Delta t}\left(t\right):=g^n,t\in (t_{n-1},t_n],$$

and the piecewise linear interpolant

$$E_{\Delta t}\left(t\right)=E^{n-1}+{\displaystyle \frac{E^n-E^{n-1}}{\Delta t}}(t-t_{n-1}),t\in [t_{n-1},t_n],$$

(30)

so that

$${\partial }_t{E}_{\Delta t}\left(t\right)={\displaystyle \frac{E^n-E^{n-1}}{\Delta t}},t\in (t_{n-1},t_n).$$

(31)

From the a priori estimates in Theorem 1, the following uniform bound holds

$$\underset{1\le n\le N}{sup}{\int }_{\Omega }\Phi \left(E^n\right)dx+\Delta t\sum _{n=1}^N{\parallel \nabla \beta \left(E^n\right)\parallel }_{L^2(\Omega )}^2\le C\left({\int }_{\Omega }\Phi \left(E^0\right)dx+{\parallel g\parallel }_{L^2(0,T;H^{-1/2}\left({\Gamma }_c\right))}^2\right).$$

(32)

Consequently,

$${\overline{E}}_{\Delta t}\mathrm{is}\mathrm{bounded}\mathrm{in}{L}^{\infty }(0,T;L^1(\Omega )),{\overline{\beta \left(E\right)}}_{\Delta t}\mathrm{is}\mathrm{bounded}\mathrm{in}{L}^2(0,T;H^1(\Omega )).$$

From the discrete weak form

$${(\kappa \nabla \beta \left(E^n\right),\nabla \varphi )}_{\Omega }-{(g^n,\varphi )}_{{\Gamma }_c}=\left({\displaystyle \frac{E^n-E^{n-1}}{\Delta t}},\varphi \right),\forall \varphi \in H^1(\Omega ),$$

(33)

we obtain

$$\left|⟨{\displaystyle \frac{E^n-E^{n-1}}{\Delta t}},\varphi ⟩\right|\le \kappa \parallel \nabla \beta \left(E^n\right){\parallel }_{L^2(\Omega )}{\parallel \nabla \varphi \parallel }_{L^2(\Omega )}+\parallel g^n{\parallel }_{H^{-1/2}\left({\Gamma }_c\right)}{\parallel \varphi \parallel }_{H^1(\Omega )}.$$

Hence,

$${\partial }_t{E}_{\Delta t}\mathrm{is}\mathrm{bounded}\mathrm{in}{L}^2(0,T;H^{-1}(\Omega )).$$

(34)

Using that ${\beta }^{\prime }\in L^{\infty }$, we obtain

$${\partial }_t{\overline{\beta \left(E\right)}}_{\Delta t}={\beta }^{\prime }\left({\overline{E}}_{\Delta t}\right){\partial }_t{E}_{\Delta t}\in L^2(0,T;H^{-1}(\Omega )),$$

with a uniform bound. By the Aubin–Lions compactness lemma with $X_0=H^1(\Omega )$, $X=L^2(\Omega )$, $X_1=H^{-1}(\Omega )$, there exists a subsequence such that

$$\begin{array}{c}\hfill {\overline{\beta \left(E\right)}}_{\Delta t}\to \beta \left(E\right)\mathrm{strongly}\mathrm{in}{L}^2(0,T;L^2(\Omega )),\end{array}$$

(35)

$$\begin{array}{c}\hfill {\overline{\beta \left(E\right)}}_{\Delta t}\rightharpoonup \beta \left(E\right)\mathrm{weakly}\mathrm{in}{L}^2(0,T;H^1(\Omega )).\end{array}$$

(36)

Moreover, since $\left\{{\overline{E}}_{\Delta t}\right\}$ is bounded in $L^{\infty }(0,T;L^1(\Omega ))$, it is weak-* relatively compact. Thus, up to a subsequence, ${\overline{E}}_{\Delta t}\rightharpoonup E$ weak-* in $L^{\infty }(0,T;L^1(\Omega ))$ for some $E\in L^{\infty }(0,T;L^1(\Omega ))$.

The discrete energy inequalities, derived in Theorem 1, are recalled here for the subsequent analysis. Testing the discrete weak form

$$\left({\displaystyle \frac{E^n-E^{n-1}}{\Delta t}},\varphi \right)=\kappa {(\nabla \beta \left(E^n\right),\nabla \varphi )}_{\Omega }-{(g^n,\varphi )}_{{\Gamma }_c},$$

(37)

with $\varphi =\beta \left(E^n\right)$ and using convexity of $\Phi$ yields

$${\int }_{\Omega }\left(\Phi \left(E^n\right)-\Phi \left(E^{n-1}\right)\right)dx+\kappa \Delta t{\parallel \nabla \beta \left(E^n\right)\parallel }_{L^2(\Omega )}^2\le \Delta t{(g^n,\beta \left(E^n\right))}_{{\Gamma }_c}.$$

(38)

Summing over $n=1,\dots ,m$ gives

$${\int }_{\Omega }\Phi \left(E^m\right)dx+\kappa \Delta t\sum _{n=1}^m{\parallel \nabla \beta \left(E^n\right)\parallel }_{L^2(\Omega )}^2\le {\int }_{\Omega }\Phi \left(E^0\right)dx+\Delta t\sum _{n=1}^m{(g^n,\beta \left(E^n\right))}_{{\Gamma }_c}.$$

(39)

Since $\beta$ is monotone, for any $\psi \in L^2(0,T;L^2(\Omega ))$,

$${\int }_0^T{\int }_{\Omega }\left({\overline{\beta \left(E\right)}}_{\Delta t}-\beta \left(\psi \right)\right)\left({\overline{E}}_{\Delta t}-\psi \right)dxdt\ge 0.$$

Passing to the limit using (35) and the weak convergence of ${\overline{E}}_{\Delta t}$ yields

$${\int }_0^T{\int }_{\Omega }\left(\beta \left(E\right)-\beta \left(\psi \right)\right)\left(E-\psi \right)dxdt\ge 0\forall \psi ,$$

which implies that $\beta \left(E\right)$ is the correct weak limit.

Finally, the interpolants satisfy the time-integrated discrete weak form

$${\int }_0^T⟨{\partial }_t{E}_{\Delta t},\varphi ⟩dt+\kappa {\int }_0^T{\int }_{\Omega }\nabla {\overline{\beta \left(E\right)}}_{\Delta t}·\nabla \varphi dxdt={\int }_0^T{⟨{\overline{g}}_{\Delta t},\varphi ⟩}_{{\Gamma }_c}dt.$$

Using the convergences ${\partial }_t{E}_{\Delta t}\rightharpoonup E_t$ in $L^2(0,T;H^{-1}(\Omega ))$ (by (34)), $\nabla {\overline{\beta \left(E\right)}}_{\Delta t}\rightharpoonup \nabla \beta \left(E\right)$ in $L^2(0,T;L^2(\Omega ))$ (by (35)), and ${\overline{g}}_{\Delta t}\to g$ in $L^2(0,T;H^{-1/2}\left({\Gamma }_c\right))$, we pass to the limit in each term and obtain (28).    □

2.5. Lipschitz Continuity of the Enthalpy Solution with Respect to Boundary Control

Let $\Omega \subset {\mathbb{R}}^d$ be a bounded Lipschitz domain, ${\Gamma }_c\subset \partial \Omega$ be a measurable subset, and define $V:=H^1(\Omega )$, $V^{*}:=H^{-1}(\Omega )$. We consider the enthalpy formulation

$$E_t-\kappa \Delta \beta \left(E\right)=0\mathrm{in}Q:=\Omega \times (0,T),$$

with boundary and initial conditions

$$\kappa {\partial }_{\nu }\beta \left(E\right)=g\mathrm{on}{\Sigma }_c:={\Gamma }_c\times (0,T),{\partial }_{\nu }\beta \left(E\right)=0\mathrm{on}(\partial \Omega \setminus {\Gamma }_c)\times (0,T),E\left(0\right)=E^0.$$

Throughout, we assume that $\beta :\mathbb{R}\to \mathbb{R}$ is strictly increasing and Lipschitz-continuous with inverse $\gamma ={\beta }^{-1}$. The natural control space is

$$\mathcal{G}:=L^2(0,T;H^{-1/2}\left({\Gamma }_c\right)).$$

This space is the most natural for the analysis in weak formulation, as it ensures that the boundary term is well defined. We note that the more regular space $L^2\left({\Gamma }_c\right)$ is continuously embedded in $H^{-1/2}\left({\Gamma }_c\right)$, a fact that we will use when formulating the optimal control problem.

Theorem 3 

(Dual-norm Lipschitz continuity). Let $g,\widehat{g}\in \mathcal{G}$ and let $E\left(g\right),E\left(\widehat{g}\right)$ be the corresponding enthalpy solutions with initial data $E^0,{\widehat{E}}^0\in V^{*}$. Then, the following stability estimate holds:

$$\parallel E\left(g\right)-E\left(\widehat{g}\right){\parallel }_{L^{\infty }(0,T;V^{*})}\le \parallel E^0-{\widehat{E}}^0{\parallel }_{V^{*}}+C_{\Omega }{\parallel g-\widehat{g}\parallel }_{L^2(0,T;H^{-1/2}\left({\Gamma }_c\right))},$$

(40)

where the constant $C_{\Omega }>0$ depends only on the domain Ω, the conductivity κ, and the constants associated with the trace theorem and Neumann map (in particular, it is independent of the final time T).

Proof. 

Let $\delta E:=E\left(g\right)-E\left(\widehat{g}\right)$, $\delta \beta :=\beta \left(E\left(g\right)\right)-\beta \left(E\left(\widehat{g}\right)\right)$, and $\delta g:=g-\widehat{g}$. The weak formulation of the enthalpy problem, tested with an arbitrary $\varphi \in V$, yields

$$⟨{\partial }_t\delta E,\varphi ⟩+\kappa {(\nabla \delta \beta ,\nabla \varphi )}_{\Omega }={⟨\delta g,\varphi {|}_{{\Gamma }_c}⟩}_{H^{-1/2},H^{1/2}}.$$

Let $\mathcal{N}:V^{*}\to V$ be the solution operator for the Neumann problem with zero mean. Specifically, for $f\in V^{*}$, $w=\mathcal{N}f\in V$ is the unique solution to

$${(\nabla w,\nabla \psi )}_{\Omega }={⟨f,\psi ⟩}_{V^{*},V}\forall \psi \in V,\mathrm{with}{\partial }_{\nu }w=0\mathrm{on}\partial \Omega .$$

Choosing $\varphi =\mathcal{N}\delta E$ gives

$$⟨{\partial }_t\delta E,\mathcal{N}\delta E⟩+\kappa {(\nabla \delta \beta ,\nabla \mathcal{N}\delta E)}_{\Omega }=⟨\delta g,\left(\mathcal{N}\delta E\right){|}_{{\Gamma }_c}⟩.$$

To establish the coercivity structure, we note that the dual norm satisfies

$${\parallel \delta E\parallel }_{V^{*}}^2={(\nabla \mathcal{N}\delta E,\nabla \mathcal{N}\delta E)}_{\Omega }.$$

Differentiating this identity with respect to time yields

$${\displaystyle \frac{d}{dt}}{\parallel \delta E\parallel }_{V^{*}}^2=2{(\nabla \mathcal{N}{\partial }_t\delta E,\nabla \mathcal{N}\delta E)}_{\Omega }.$$

However, by the definition of $\mathcal{N}$, we have ${(\nabla \mathcal{N}{\partial }_t\delta E,\nabla \mathcal{N}\delta E)}_{\Omega }=⟨{\partial }_t\delta E,\mathcal{N}\delta E⟩$, which establishes the key identity

$$⟨{\partial }_t\delta E,\mathcal{N}\delta E⟩={\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}{\parallel \delta E\parallel }_{V^{*}}^2.$$

Furthermore, by the trace theorem and the boundedness of $\mathcal{N}$, there exist constants $C_{\mathrm{tr}},C_N>0$ such that

$${\parallel \left(\mathcal{N}\delta E\right)|}_{{\Gamma }_c}{\parallel }_{H^{1/2}\left({\Gamma }_c\right)}\le C_{\mathrm{tr}}{\parallel \mathcal{N}\delta E\parallel }_{H^1(\Omega )}\le C_{\mathrm{tr}}{C}_N{\parallel \delta E\parallel }_{V^{*}}.$$

Using Cauchy’s inequality $ab\le \frac{1}{2}(ϵa^2+{ϵ}^{-1}{b}^2)$ and the previous bound, we obtain

$${\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}{\parallel \delta E\parallel }_{V^{*}}^2+\kappa {(\nabla \delta \beta ,\nabla \mathcal{N}\delta E)}_{\Omega }\le C_{\mathrm{tr}}{C}_N{\parallel \delta g\parallel }_{H^{-1/2}\left({\Gamma }_c\right)}{\parallel \delta E\parallel }_{V^{*}}.$$

The coercivity now follows from the monotonicity of $\beta$. Since $\beta$ is maximal monotone, we have

$$(\delta \beta ,\delta E)\ge 0.$$

By the definition of $\mathcal{N}$, this implies that

$${(\nabla \delta \beta ,\nabla \mathcal{N}\delta E)}_{\Omega }={⟨\delta E,\delta \beta ⟩}_{V^{*},V}\ge 0,$$

which provides the essential coercivity estimate. The positive term can be dropped, yielding

$${\displaystyle \frac{d}{dt}}{\parallel \delta E\parallel }_{V^{*}}\le C_{\Omega }{\parallel \delta g\parallel }_{H^{-1/2}\left({\Gamma }_c\right)},C_{\Omega }:=C_{\mathrm{tr}}{C}_N.$$

Integrating this inequality from 0 to t and applying Cauchy–Schwarz in time gives (40) and completes the proof.    □

If, in addition, $g,\widehat{g}\in L^1(0,T;L^1\left({\Gamma }_c\right))$ and $E^0,{\widehat{E}}^0\in L^1(\Omega )$, the standard discrete sign test argument yields the sharper $L^1$-estimate:

$$\parallel E\left(g\right)-E\left(\widehat{g}\right){\parallel }_{L^{\infty }(0,T;L^1(\Omega ))}\le \parallel E^0-{\widehat{E}}^0{\parallel }_{L^1(\Omega )}+{\parallel g-\widehat{g}\parallel }_{L^1\left({\Sigma }_c\right)}.$$

Define the set-valued nonlinear operator $A:L^1(\Omega )\rightrightarrows L^1(\Omega )$ with a homogeneous Neumann boundary condition by

$$D\left(A\right)=\left\{u\in L^1(\Omega ):\exists v\in H^1(\Omega )\mathrm{with}v\left(x\right)\in \gamma \left(u\left(x\right)\right)\mathrm{a}.\mathrm{e}.\mathrm{in}\Omega ,\Delta v\in L^1(\Omega ),{\partial }_{\nu }v=0\right\},$$

and, for $u\in D\left(A\right)$,

$$A\left(u\right)=\left\{-\Delta v\in L^1(\Omega ):v\in H^1(\Omega ),v\left(x\right)\in \gamma \left(u\left(x\right)\right)\mathrm{a}.\mathrm{e}.\mathrm{in}\Omega ,{\partial }_{\nu }v=0\right\}.$$

Then, A is m-accretive on $L^1(\Omega )$ and, thus, generates a nonlinear contraction semigroup. The boundary-controlled problem can be written abstractly as

$$E_t+A\left(E\right)\ni Bg\mathrm{in}{V}^{*},$$

where $B:H^{-1/2}\left({\Gamma }_c\right)\to V^{*}$ is the bounded linear operator mapping a boundary flux to the corresponding source term via the Neumann map. The accretivity of A combined with the boundedness of the control operator B directly implies the stability bound (40) and guarantees uniqueness in the natural $V^{*}$ topology; see, e.g., [19] for the analysis of evolution equations with boundary inputs.

We adopt controls $g\in L^2(0,T;L^2\left({\Gamma }_c\right))$, continuously embedded in $L^2(0,T;H^{-1/2}\left({\Gamma }_c\right))$ for the state equation; all boundary pairings are interpreted via the trace map.

For the natural control space $\mathcal{G}=L^2(0,T;H^{-1/2}\left({\Gamma }_c\right))$, the dual-norm estimate (40) is the sharp and natural stability result, directly implying continuous dependence and uniqueness. When boundary fluxes are more regular—that is, integrable on ${\Sigma }_c$—one recovers the classical $L^1$-contraction principle.

3. Optimal Control Problem for the Motion of the Interface of the Stefan Problem

In this section, we consider controlling the motion of the moving interface via a boundary heat-flux control $g(t,x)$ applied on a portion of the boundary ${\Gamma }_c$. The goal is to control the evolution of the interface toward a desired trajectory by appropriate heating or cooling at ${\Gamma }_c$. This leads to an optimal control problem where the state equations are the Stefan PDEs and the objective functional measures the deviation from a desired outcome together with the cost of applying control. We use the enthalpy formulation to describe the phase-change dynamics. Let $E(t,x)$ denote the enthalpy; the state system is given by

$$E_t=\nabla ·(\kappa \nabla \beta \left(E\right)),\kappa {\partial }_{\nu }\beta \left(E\right)=g\mathrm{on}{\Gamma }_c,$$

together with zero-flux conditions on $\partial \Omega \setminus {\Gamma }_c$ and initial condition $E(0,x)=E_0\left(x\right)$.

We introduce an enthalpy-tracking cost functional that measures the discrepancy between the state and a target while penalizing the control effort.

$$\underset{g}{min}J(E,g)={\displaystyle \frac{1}{2}}{\int }_0^T\parallel E-E_d{\parallel }_{L^2(\Omega )}^{2}dt+{\displaystyle \frac{\gamma }{2}}\parallel E\left(T\right)-E_T{\parallel }_{L^2(\Omega )}^2+{\displaystyle \frac{\alpha }{2}}{\int }_0^T{\parallel g\parallel }_{L^2\left({\Gamma }_c\right)}^{2}dt,$$

(41)

where $E_d\left(t\right)$ is the desired enthalpy trajectory and $E_T$ is the desired terminal enthalpy state, subject to the control constraint $\left|g\right|\le \delta$, while $\gamma >0$ weights the terminal tracking, and $\alpha >0$ penalizes control energy.

To define the moving-interface tracking criterion, let ${\overline{\Gamma }}_t$ be a desired interface, and let $\varphi (t,x)=\mathrm{dist}(x,{\overline{\Gamma }}_t)$ be the signed distance. Then,

$$\underset{g}{min}J(E,g)=\frac{1}{2}{\int }_0^T{\int }_{\Omega }{\left|\varphi (t,x)\right|}^2{\delta }_{\eta }\left(\beta \left(E\right(x,t\left)\right)\right)|\nabla \beta \left(E(x,t)\right)|dxdt+\frac{\alpha }{2}{\int }_0^T{\parallel g\parallel }_{L^2\left({\Gamma }_c\right)}^{2}dt.$$

(42)

In general, the cost functional may be summarized as

$$\underset{g}{min}J(E,g)={\int }_0^T{\int }_{\Omega }\Psi \left(E\right)dx+\gamma \Psi \left(E\left(T\right)\right)+{\displaystyle \frac{\alpha }{2}}{\int }_0^T{\parallel g\parallel }_{L^2\left({\Gamma }_c\right)}^{2}dt,$$

(43)

for some functional $\Psi$ that represents the tracking objective.

While the interface-tracking formulation provides the physical motivation for controlling the solidification front, the enthalpy-tracking formulation offers significant mathematical advantages for analysis and computation. The enthalpy tracking serves as a regularization of the interface-tracking objective, where guiding the full enthalpy field indirectly controls the interface position while avoiding the mathematical complexities of singular measures and geometric sensitivities. For the remainder of this work, we employ the enthalpy-tracking formulation to establish well-posedness and derive optimality conditions.

3.1. Existence of Optimal Control

We establish the existence of the optimal boundary control for the Stefan system via the direct method of the calculus of variations. Establishing existence is essential before one can pursue uniqueness, regularity, or numerical approximation results. The argument is based on the direct method in the calculus of variations, which provides a systematic methodology for proving existence by combining coercivity, compactness, and weak lower semicontinuity.

We show that the quadratic control cost enforces coercivity of the functional, while the control-to-state operator exhibits sufficient compactness properties to guarantee convergence of minimizing sequences. Together with the weak lower semicontinuity of the cost functional, these properties ensure the existence of an admissible control that minimizes the objective. Consequently, there exists an admissible boundary heat flux $g^{*}$ that optimally drives the solidification interface motion toward a desired target, while balancing accuracy against control effort. For related developments in free boundary optimal control, we refer to [5,20,21].

Theorem 4 

(Existence of an optimal control). Let $\alpha >0$. Define the admissible control set

$${\mathcal{U}}_{\mathrm{ad}}:=\left\{g\in L^2(0,T;L^2\left({\Gamma }_c\right)):\left|g(t,x)\right|\le \delta \mathit{for}\mathit{a}\mathit{.}\mathit{e}.(x,t)\in {\Gamma }_c\times (0,T)\right\}.$$

The optimal control problem (41), subject to the enthalpy formulation (8), admits at least one minimizer

$$g^{*}\in {\mathcal{U}}_{\mathrm{ad}},$$

with associated state $E^{*}=E\left(g^{*}\right)$.

Proof. 

Let $\tilde{J}\left(g\right):=J(E\left(g\right),g)$ be the reduced composite functional. By definition of J,

$$\tilde{J}\left(g\right)={\displaystyle \frac{1}{2}}{\int }_0^T\parallel E\left(g\right)-E_d{\parallel }_{L^2(\Omega )}^{2}dt+{\displaystyle \frac{\gamma }{2}}\parallel E\left(g\right)\left(T\right)-E_T{\parallel }_{L^2(\Omega )}^2+{\displaystyle \frac{\alpha }{2}}{\int }_0^T{\parallel g\parallel }_{L^2\left({\Gamma }_c\right)}^{2}dt$$

$$\ge {\displaystyle \frac{\alpha }{2}}{\parallel g\parallel }_{L^2(0,T;L^2\left({\Gamma }_c\right))}^2.$$

Thus, $\tilde{J}$ is coercive on $L^2(0,T;L^2\left({\Gamma }_c\right))$. Let $\left\{g^n\right\}\subset {\mathcal{U}}_{\mathrm{ad}}$ be a minimizing sequence. Since ${\mathcal{U}}_{\mathrm{ad}}$ is convex, closed, and bounded in the reflexive space $L^2(0,T;L^2\left({\Gamma }_c\right))$, it is weakly sequentially compact, up to a subsequence

$$g^n\rightharpoonup g^{*}\mathrm{in}{L}^2(0,T;L^2\left({\Gamma }_c\right)).$$

Let $E^n:=E\left(g^n\right)$ be the associated enthalpy solutions. From the well-posedness theory (Section 2) and $E^0\in L^2(\Omega )$, we have uniform bounds

$${\parallel E^n\parallel }_{L^{\infty }(0,T;L^2(\Omega ))}+\parallel \beta \left(E^n\right){\parallel }_{L^2(0,T;H^1(\Omega ))}+{\parallel E_t^n\parallel }_{L^2(0,T;H^{-1}(\Omega ))}\le C.$$

By the Aubin–Lions lemma, there exist $E^{*}$ and $\xi$ such that, up to a subsequence,

$$\begin{array}{cc}\hfill \beta \left(E^n\right)& \to \xi \mathrm{strongly}\mathrm{in}{L}^2(0,T;L^2(\Omega )),\hfill \\ \hfill \beta \left(E^n\right)& \rightharpoonup \xi \mathrm{in}{L}^2(0,T;H^1(\Omega )),\hfill \\ \hfill E^n& \rightharpoonup E^{*}\mathrm{in}{L}^2(0,T;L^2(\Omega )),\hfill \\ \hfill E_t^n& \rightharpoonup E_t^{*}\mathrm{in}{L}^2(0,T;H^{-1}(\Omega )).\hfill \end{array}$$

By the monotonicity of $\beta$ and the strong convergence of $\beta \left(E^n\right)$, we identify $\xi =\beta \left(E^{*}\right)$ a.e. For all $\varphi \in L^2(0,T;H^1(\Omega ))$, passing to the limit gives

$${\int }_0^T⟨E_t^n,\varphi ⟩dt+\kappa {\int }_0^T{(\nabla \beta \left(E^n\right),\nabla \varphi )}_{L^2(\Omega )}dt={\int }_0^T{(g^n,\varphi )}_{L^2\left({\Gamma }_c\right)}dt.$$

Using the convergences $E_t^n\rightharpoonup E_t^{*}$, $\nabla \beta \left(E^n\right)\rightharpoonup \nabla \beta \left(E^{*}\right)$ and $g^n\rightharpoonup g^{*}$, we obtain

$${\int }_0^T⟨E_t^{*},\varphi ⟩dt+\kappa {\int }_0^T{(\nabla \beta \left(E^{*}\right),\nabla \varphi )}_{L^2(\Omega )}dt={\int }_0^T{(g^{*},\varphi )}_{L^2\left({\Gamma }_c\right)}dt,$$

so $(E^{*},g^{*})$ satisfies the state system.

By weak convergence $E^n\rightharpoonup E^{*}$ in $L^2(0,T;L^2(\Omega ))$ and weak lower semicontinuity of the norm,

$${\int }_0^T\parallel E^{*}-E_d{\parallel }_{L^2(\Omega )}^{2}dt\le \underset{n\to \infty }{lim\; inf}{\int }_0^T{\parallel E^n-E_d\parallel }_{L^2(\Omega )}^{2}dt.$$

Similarly, by weak convergence $g^n\rightharpoonup g^{*}$ in $L^2(0,T;L^2\left({\Gamma }_c\right))$,

$${\int }_0^T\parallel g^{*}{\parallel }_{L^2\left({\Gamma }_c\right)}^{2}dt\le \underset{n\to \infty }{lim\; inf}{\int }_0^T{\parallel g^n\parallel }_{L^2\left({\Gamma }_c\right)}^{2}dt.$$

Finally, from the boundedness $E^n\in L^{\infty }(0,T;L^2(\Omega ))$ and $E_t^n\in L^2(0,T;H^{-1}(\Omega ))$, we have $E^n\left(T\right)\rightharpoonup E^{*}\left(T\right)$ weakly in $L^2(\Omega )$; hence,

$${\parallel E^{*}\left(T\right)-E_T\parallel }_{L^2(\Omega )}^2\le \underset{n\to \infty }{lim\; inf}{\parallel E^n\left(T\right)-E_T\parallel }_{L^2(\Omega )}^2.$$

Combining these inequalities,

$$\tilde{J}\left(g^{*}\right)\le \underset{n\to \infty }{lim\; inf}\tilde{J}\left(g^n\right)=\underset{g\in {\mathcal{U}}_{\mathrm{ad}}}{inf}\tilde{J}\left(g\right),$$

so $g^{*}$ is a minimizer.    □

3.2. Lagrangian Functional and Adjoint Equation

We derive the adjoint equation for the optimal control problem using a Lagrangian approach. The adjoint variable measures the sensitivity of the cost functional with respect to small perturbations in the state. This technique is classical in PDE-constrained optimization [21] and has been applied to Stefan-type problems in [5,20].

Theorem 5 

(Adjoint equation). For the regularized enthalpy function ${\beta }_{\epsilon }$ with ${\beta }_{\epsilon }^{\prime }>0$, the adjoint state p satisfies the backward parabolic equation

$$\begin{array}{cccc}\hfill -p_t& =\kappa \nabla ·\left({\beta }_{\epsilon }^{\prime }\left(E\right)\nabla p\right)-(E-E_d)\hfill & \hfill & \mathit{in}\Omega \times (0,T),\hfill \\ \hfill p\left(T\right)& =-\gamma (E\left(T\right)-E_T)\hfill & \hfill & \mathit{in}\Omega ,\hfill \\ \hfill {\partial }_{\nu }p& =0\hfill & \hfill & \mathit{on}\partial \Omega \times (0,T).\hfill \end{array}$$

(44)

Proof. 

The state equation in weak form is

$${\int }_0^T{(E_t,\varphi )}_{\Omega }dt+\kappa {\int }_0^T{(\nabla {\beta }_{\epsilon }\left(E\right),\nabla \varphi )}_{\Omega }dt-{\int }_0^T{(g,\varphi )}_{{\Gamma }_c}dt=0.$$

for all $\varphi \in L^2(0,T;H^1(\Omega ))$. Define the Lagrangian functional

$$\mathcal{L}(E,g,p)=J(E,g)+{\int }_0^T{(E_t,p)}_{\Omega }dt+\kappa {\int }_0^T{(\nabla {\beta }_{\epsilon }\left(E\right),\nabla p)}_{\Omega }dt-{\int }_0^T{(g,p)}_{{\Gamma }_c}dt.$$

(45)

Integration by parts in time gives

$${\int }_0^T{(E_t,p)}_{\Omega }dt=(E\left(T\right),p\left(T\right))-(E\left(0\right),p\left(0\right))-{\int }_0^T{(E,p_t)}_{\Omega }dt.$$

For a variation h in E,

$$\delta \left[{(\nabla {\beta }_{\epsilon }\left(E\right),\nabla p)}_{\Omega }\right]={({\beta }_{\epsilon }^{\prime }\left(E\right)\nabla h,\nabla p)}_{\Omega }.$$

The Lagrangian becomes

$$\begin{array}{cc}\hfill \mathcal{L}(E,g,p)& =J(E,g)-{\int }_0^T{(E,p_t)}_{\Omega }dt+\kappa {\int }_0^T{({\beta }_{\epsilon }^{\prime }\left(E\right)\nabla E,\nabla p)}_{\Omega }dt\hfill \\ \hfill & -{\int }_0^T{(g,p)}_{{\Gamma }_c}dt+(E\left(T\right),p\left(T\right))-(E\left(0\right),p\left(0\right)).\hfill \end{array}$$

The Gâteaux derivative in the direction h is given by

$$\begin{array}{cc}\hfill {\mathcal{L}}_E(E,g,p)\left[h\right]& ={\int }_0^T{(E-E_d,h)}_{\Omega }dt+\gamma (E\left(T\right)-E_T,h\left(T\right))\hfill \\ \hfill & -{\int }_0^T{(p_t,h)}_{\Omega }dt+\kappa {\int }_0^T{({\beta }_{\epsilon }^{\prime }\left(E\right)\nabla h,\nabla p)}_{\Omega }dt\hfill \\ \hfill & +\left(h\right(T),p(T\left)\right)-\left(h\right(0),p(0\left)\right).\hfill \end{array}$$

Integrating the spatial term by parts (using ${\partial }_{\nu }p=0$),

$$\kappa {\int }_0^T{({\beta }_{\epsilon }^{\prime }\left(E\right)\nabla h,\nabla p)}_{\Omega }dt=-\kappa {\int }_0^T{(\nabla ·({\beta }_{\epsilon }^{\prime }\left(E\right)\nabla p),h)}_{\Omega }dt.$$

Requiring ${\mathcal{L}}_E\left[h\right]=0$ for all admissible h with $h\left(0\right)=0$ yields the adjoint equation and terminal condition. The regularization parameter $\epsilon >0$ ensures that ${\beta }_{\epsilon }$ is differentiable and ${\beta }_{\epsilon }^{\prime }>0$, which is essential for the well-posedness of the adjoint equation.    □

We emphasize that the adjoint derivation is consistent with the weak formulation written in the enthalpy variable E, using the temperature–enthalpy relation. A similar scalar nonlinear diffusion structure is analyzed in [22], where the operator $-\nabla ·({\beta }^{\prime }\left(E\right)\nabla ·)$ arises naturally in the Gurtin–MacCamy-type equation. We follow this consistent formulation to ensure that the adjoint equation remains thermodynamically coherent.

Theorem 6 

(Discrete existence). Let ${\left\{t_n\right\}}_{n=0}^N$ be a uniform partition of $[0,T]$ with time step $\Delta t=T/N$, where $t_n=n\Delta t$ and $t_N=T$. Consider the regularized enthalpy function:

$${\beta }_{\epsilon }\left(s\right)={\displaystyle \frac{1}{2\epsilon }}{\int }_{s-\epsilon }^{s+\epsilon }\beta \left(z\right)dz,{\beta }_{\epsilon }^{\prime }\left(s\right)\ge \epsilon >0.$$

(46)

The backward Euler discretization of the adjoint equation (solved backward in time from $n=N$ to $n=0$) reads

$$-{\displaystyle \frac{p^n-p^{n-1}}{\Delta t}}=\kappa \nabla ·\left({\beta }_{\epsilon }^{\prime }\left(E^n\right)\nabla p^{n-1}\right)+(E^n-E_d^n),{\partial }_{\nu }{p}^{n-1}=0.$$

(47)

Here, $p^{n-1}$ is computed from $p^n$, with $p^N=\gamma (E^N-E_T)$. Then, for each n from N down to 1, given $p^n$, there exists a unique solution $p^{n-1}\in H^1(\Omega )$.

Proof. 

Equation (47) is equivalent to the elliptic problem for $p^{n-1}$:

$$-\kappa \nabla ·({\beta }_{\epsilon }^{\prime }\left(E^n\right)\nabla p^{n-1})+{\displaystyle \frac{1}{\Delta t}}{p}^{n-1}={\displaystyle \frac{1}{\Delta t}}{p}^n+(E^n-E_d^n).$$

The weak form seeks $p^{n-1}\in H^1(\Omega )$ such that, for all $\varphi \in H^1(\Omega )$,

$$a(p^{n-1},\varphi )=\mathsf{\ell }\left(\varphi \right),$$

where

$$\begin{array}{cc}\hfill a(u,\varphi )& :=\kappa {({\beta }_{\epsilon }^{\prime }\left(E^n\right)\nabla u,\nabla \varphi )}_{\Omega }+{\displaystyle \frac{1}{\Delta t}}{(u,\varphi )}_{\Omega },\hfill \\ \hfill \mathsf{\ell }\left(\varphi \right)& :={\displaystyle \frac{1}{\Delta t}}{(p^n,\varphi )}_{\Omega }+{((E^n-E_d^n),\varphi )}_{\Omega }.\hfill \end{array}$$

Since ${\beta }_{\epsilon }^{\prime }\left(E^n\right)\ge \epsilon >0$, the bilinear form $a(·,·)$ is coercive and continuous on $H^1(\Omega )$. The linear functional $\mathsf{\ell }(·)$ is continuous. By the Lax–Milgram theorem, there exists a unique solution $p^{n-1}\in H^1(\Omega )$.    □

To obtain stability estimates, we test (47) with $-\Delta p^{n-1}$ (formally, assuming sufficient regularity). This yields

$$\left({\displaystyle \frac{p^n-p^{n-1}}{\Delta t}},-\Delta p^{n-1}\right)=\kappa ({\beta }_{\epsilon }^{\prime }\left(E^n\right)\nabla p^{n-1},\nabla p^{n-1})+(E^n-E_d^n,-\Delta p^{n-1}).$$

Using the energy identity

$$(a-b,-\Delta b)=\frac{1}{2}\left({\parallel \nabla a\parallel }^2-{\parallel \nabla b\parallel }^2-{\parallel \nabla (a-b)\parallel }^2\right),$$

together with ${\partial }_{\nu }{p}^{n-1}=0$, the left-hand side becomes

$$\left({\displaystyle \frac{p^n-p^{n-1}}{\Delta t}},-\Delta p^{n-1}\right)={\displaystyle \frac{1}{2\Delta t}}\left(\parallel \nabla p^n{\parallel }_{L^2(\Omega )}^2-\parallel \nabla p^{n-1}{\parallel }_{L^2(\Omega )}^2-{\parallel \nabla (p^n-p^{n-1})\parallel }_{L^2(\Omega )}^2\right).$$

Applying Young’s inequality to the term $(E^n-E_d^n,-\Delta p^{n-1})$ and using ${\beta }_{\epsilon }^{\prime }\ge \epsilon$, we obtain the following for each step:

$${\displaystyle \frac{1}{2\Delta t}}\left(\parallel \nabla p^n{\parallel }_{L^2(\Omega )}^2-{\parallel \nabla p^{n-1}\parallel }_{L^2(\Omega )}^2\right)+\epsilon \kappa \parallel \Delta p^{n-1}{\parallel }_{L^2(\Omega )}^2\le {\displaystyle \frac{C}{\epsilon }}{\parallel E^n-E_d^n\parallel }_{L^2(\Omega )}^2.$$

Multiplying by $\Delta t$ and summing from $n=N$ down to 1 yields

$$\parallel \nabla p^0{\parallel }_{L^2(\Omega )}^2+2\epsilon \kappa \sum _{n=1}^N\Delta t\parallel \Delta p^{n-1}{\parallel }_{L^2(\Omega )}^2\le \parallel \nabla p^N{\parallel }_{L^2(\Omega )}^2+{\displaystyle \frac{C}{\epsilon }}\sum _{n=1}^N\Delta t{\parallel E^n-E_d^n\parallel }_{L^2(\Omega )}^2.$$

This provides uniform bounds for the discrete solutions, initialized with the given value of $\parallel \nabla p^N\parallel$. By weak compactness and consistency, the limit p (as $\Delta t\to 0$) satisfies

$$p\in L^{\infty }(0,T;H^1(\Omega ))\cap L^2(0,T;H^2(\Omega )),p_t\in L^2(0,T;L^2(\Omega )).$$

The adjoint state p propagates backward in time, reflecting the reversed causality of sensitivities: terminal perturbations influence the entire trajectory. In PDE-constrained optimization, the adjoint bridges state dynamics with the gradient of the cost functional with respect to the control. The regularization ${\beta }_{\epsilon }$ is essential for establishing well-posedness: without it, ${\beta }^{\prime }\left(E\right)$ may vanish or blow up, leading to degeneracy. The condition ${\beta }_{\epsilon }^{\prime }\left(E\right)\ge \epsilon >0$ restores uniform ellipticity, and the energy bound above guarantees the stability and regularity of solutions.

Corollary 1 

(Existence of the regularized adjoint). Let E be the enthalpy state associated with a given control g, and let ${\beta }_{\epsilon }$ be defined in (46) so that ${\beta }_{\epsilon }^{\prime }\ge \epsilon >0$. Then, the regularized adjoint equation

$$-p_t=\kappa \nabla ·\left({\beta }_{\epsilon }^{\prime }\left(E\right)\nabla p\right)+(E-E_d),{\partial }_{\nu }p=0\mathit{on}\partial \Omega ,p\left(T\right)=\gamma (E\left(T\right)-E_T),$$

admits a unique weak solution

$$p\in H^1\left(0,T;H^{-1}(\Omega )\right)\cap L^2\left(0,T;H^1(\Omega )\right).$$

Moreover, if Ω is $C^2$ and ${\beta }_{\epsilon }^{\prime }\left(E\right)\in W^{1,\infty }(\Omega \times (0,T))$, then

$$p_t\in L^2(0,T;L^2(\Omega ))\mathit{and}p\in L^{\infty }(0,T;H^1(\Omega )).$$

Proof. 

The backward Euler scheme (47) produces a sequence $\left\{p^n\right\}$ with the uniform estimate

$$\parallel \nabla p^0{\parallel }_{L^2}^2+2\epsilon \kappa \sum _{n=1}^N\Delta t\parallel \Delta p^{n-1}{\parallel }_{L^2}^2\le \parallel \nabla p^N{\parallel }_{L^2}^2+{\displaystyle \frac{C}{\epsilon }}\sum _{n=1}^N\Delta t{\parallel E^n-E_d^n\parallel }_{L^2}^2.$$

Using standard time-interpolants, this yields boundedness of the interpolated sequence in $L^{\infty }(0,T;H^1(\Omega ))$ and of the time differences in $L^2(0,T;L^2(\Omega ))$. By weak compactness (and Aubin–Lions), up to a subsequence, $p^{\Delta t}\rightharpoonup p$ weak-* in $L^{\infty }(0,T;H^1(\Omega ))$, and $p^{\Delta t}\to p$ strongly in $L^2(0,T;H^1(\Omega ))$.

Since ${\beta }_{\epsilon }^{\prime }$ is bounded and continuous, $E^n\to E$ a.e. implies ${\beta }_{\epsilon }^{\prime }\left(E^n\right)\to {\beta }_{\epsilon }^{\prime }\left(E\right)$ strongly in $L^q$ for any finite q (dominated convergence). Together with $\nabla p^{n-1}\rightharpoonup \nabla p$ in $L^2$, this yields ${\beta }_{\epsilon }^{\prime }\left(E^n\right)\nabla p^{n-1}\rightharpoonup {\beta }_{\epsilon }^{\prime }\left(E\right)\nabla p$ in $L^2$, so we can pass to the limit in (47) to obtain the weak form of the regularized adjoint. The terminal condition is inherited from the initialization $p^N=\gamma (E^N-E_T)$. Uniqueness follows by testing the homogeneous equation with the difference of two solutions and using ${\beta }_{\epsilon }^{\prime }\ge \epsilon$. The temporal regularity $p_t\in L^2(0,T;L^2(\Omega ))$ follows from the uniform bounds on the discrete time differences.    □

Remark 1. 

The regularization ${\beta }_{\epsilon }$ with ${\beta }_{\epsilon }^{\prime }\left(s\right)\ge \epsilon >0$ ensures that the corresponding functional $J_n^{\epsilon }\left(\beta \right)$ from Equation (14) becomes strictly convex. Since ${\beta }_{\epsilon }^{\prime }\left(s\right)\ge \epsilon >0$ everywhere, the convex potential associated with ${\beta }_{\epsilon }$ is strongly convex. Combined with the convex Dirichlet energy term and the linear terms, the functional $J_n^{\epsilon }\left(\beta \right)$ is strictly convex, guaranteeing both the existence and uniqueness of the minimizer.

3.3. Necessary Optimality Conditions

We derive the first-order necessary optimality conditions for the boundary control problem governed by the Stefan system. The method of Lagrange multipliers yields a coupled system of forward and backward PDEs characterizing local optima.

We define the control operator $B:L^2\left({\Gamma }_c\right)\to H^{-1}(\Omega )$ as the bounded linear operator given by $⟨Bg,\varphi ⟩={(g,\varphi )}_{{\Gamma }_c}$ for all $\varphi \in H^1(\Omega )$. Its adjoint $B^{\star }:H^1(\Omega )\to L^2\left({\Gamma }_c\right)$ is given by $B^{\star }{\varphi =\varphi |}_{{\Gamma }_c}$ when interpreted appropriately through the trace theorem.

Theorem 7. 

Let $(E^{*},g^{*})$ be a locally optimal pair for the control problem, and let p denote the associated adjoint state. Then, $(E^{*},g^{*},p)$ satisfies the following optimality system:

$$\left\{\begin{array}{cc}{\partial }_t{E}^{*}=\kappa \Delta \beta \left(E^{*}\right)\hfill & \mathit{in}\Omega \times (0,T),\hfill \\ \kappa {\partial }_{\nu }\beta \left(E^{*}\right)=g^{*}\hfill & \mathit{on}{\Gamma }_c\times (0,T),\hfill \\ -{\partial }_{t}p=\kappa \nabla ·({\beta }^{\prime }\left(E^{*}\right)\nabla p)-(E^{*}-E_d)\hfill & \mathit{in}\Omega \times (0,T),\hfill \\ {\partial }_{\nu }p=0\hfill & \mathit{on}\partial \Omega \times (0,T),\hfill \\ \alpha g^{*}-B^{\star }p=0\hfill & \mathit{on}{\Gamma }_c\times (0,T),\hfill \\ E^{*}\left(0\right)=E_0,p\left(T\right)=-\gamma (E^{*}\left(T\right)-E_T)\hfill & \mathit{in}\Omega .\hfill \end{array}\right.$$

(48)

Proof. 

The proof follows by taking first variations of the Lagrangian functional

$$\begin{array}{cc}\hfill \mathcal{L}(E,g,p)& =J(E,g)+{\int }_0^T\left[{(E_t,p)}_{\Omega }+\kappa {(\nabla \beta \left(E\right),\nabla p)}_{\Omega }-{(Bg,p)}_{\Omega }\right]dt,\hfill \\ \hfill J(E,g)& =\frac{1}{2}\parallel E-E_d{\parallel }_{L^2\left(Q\right)}^2+\frac{\alpha }{2}{\parallel g\parallel }_{L^2\left({\Sigma }_c\right)}^2+\frac{\gamma }{2}{\parallel E\left(T\right)-E_T\parallel }_{L^2(\Omega )}^2,\hfill \end{array}$$

(49)

with $Q=\Omega \times (0,T)$ and ${\Sigma }_c={\Gamma }_c\times (0,T)$.

For a variation $g^{*}+\epsilon w$, the first variation gives (for all $w\in L^2\left({\Sigma }_c\right)$)

$${\delta }_g\mathcal{L}(E,g,p)\left[w\right]=\alpha {(g,w)}_{{\Sigma }_c}-{(Bw,p)}_{\Omega }=\alpha {(g,w)}_{{\Sigma }_c}-{(w,B^{\star }p)}_{{\Sigma }_c}={\left(\alpha g-B^{\star }p,w\right)}_{{\Sigma }_c}=0.$$

Hence, the control condition

$$\alpha g^{*}-B^{\star }p=0\mathrm{on}{\Gamma }_c\times (0,T),$$

understood in the $L^2\left({\Sigma }_c\right)$ sense.

For a variation $E^{*}+\epsilon v$ with $v\left(0\right)=0$, we compute

$$\begin{array}{cc}\hfill ⟨{\displaystyle \frac{\partial \mathcal{L}}{\partial E}},v⟩& ={(E^{*}-E_d,v)}_Q+\gamma (E^{*}\left(T\right)-E_T,v\left(T\right))\hfill \\ \hfill & -{\int }_0^T{(p_t,v)}_{\Omega }dt+\kappa {\int }_0^T{(\nabla {\beta }^{\prime }\left(E^{*}\right)v,\nabla p)}_{\Omega }dt\hfill \\ \hfill & ={(E^{*}-E_d,v)}_Q+\gamma (E^{*}\left(T\right)-E_T,v\left(T\right))-{\int }_0^T{(p_t,v)}_{\Omega }dt\hfill \\ \hfill & -\kappa {\int }_0^T{(\nabla ·({\beta }^{\prime }\left(E^{*}\right)\nabla p),v)}_{\Omega }dt.\hfill \end{array}$$

Requiring $⟨{\mathcal{L}}_E(E^{*},g^{*},p),v⟩=0$ for all v yields the adjoint PDE

$$-p_t=\kappa \nabla ·({\beta }^{\prime }\left(E^{*}\right)\nabla p)-(E^{*}-E_d)\mathrm{in}\Omega \times (0,T),$$

with terminal condition $p\left(T\right)=-\gamma (E^{*}\left(T\right)-E_T)$ and ${\partial }_{\nu }p=0$ on $\partial \Omega$.

Variation with respect to p recovers the weak form of the state equation with boundary flux $g^{*}$.

Let $S:g\mapsto E\left(g\right)$ be the control-to-state map and define the reduced cost $\widehat{J}\left(g\right)=J(S\left(g\right),g)$. At a local optimum $g^{*}$, the first variation satisfies ${\widehat{J}}^{\prime }\left(g^{*}\right)h=0$ for all admissible $h\in L^2\left({\Sigma }_c\right)$. The adjoint construction above computes ${\widehat{J}}^{\prime }\left(g^{*}\right)$ and yields the optimality relation $\alpha g^{*}-B^{\star }p=0$ on ${\Sigma }_c$. Collecting the three stationarity conditions gives exactly the optimality system (48).    □

The optimality system (48) couples the forward enthalpy equation with the backward adjoint problem. The optimality condition $\alpha g^{*}=B^{\star }p$ shows that the optimal flux $g^{*}$ is determined by the boundary trace of the adjoint state through the adjoint operator $B^{\star }$. The backward adjoint dynamics transmit information from the final-time cost to earlier times, linking the desired terminal state to the boundary control strategy.

4. Numerical Methods for Enthalpy-Based Formulation of the Controlled Two-Phase Stefan Problem

Many optimal-control treatments of Stefan-type problems yield nonsymmetric linearized/adjoint operators, motivating Krylov solvers whose performance can be sensitive to non-normality. Prior work includes free boundary control in a level-set setting [5,20] with connections to classical level-set solvers [23] and enthalpy/phase-field formulations [3,4]. In contrast, our contribution enforces an SPD structure throughout: a temperature-linearized semismooth Newton step for the forward problem and a diagonal congruence for the discrete adjoint produce strictly SPD systems, enabling preconditioned CG within a reduced-space SQP algorithm.

We develop a numerically stable scheme for optimal boundary control of the two-phase Stefan problem in enthalpy formulation. The scheme integrates a cell-centered spatial discretization with homogeneous Neumann boundary conditions and a Kronecker-sum Laplacian, a temperature-linearized semismooth Newton method whose linear systems are strictly symmetric positive definite (SPD), an SPD-transformed discrete adjoint obtained via a diagonal congruence that enables efficient solution by Conjugate Gradients (CGs) for backward sweeps, and a reduced-space Sequential Quadratic Programming (SQP) algorithm that incorporates preconditioning, an Armijo line search, and checkpointing. In addition, the scheme provides expanded numerical validation, including convergence behavior, sensitivity to the interface slope, and performance comparisons.

We consider a unit square $\Omega ={[0,1]}^2$ discretized by a uniform Cartesian grid with $n\times n$ cells and spacing $\Delta x=1/n$. Shifted temperature is represented as $\beta \left(E\right)$ and evaluated at cell centers (the stored primary unknown is Eij).

Let I denote the $n\times n$ identity and h the standard one-dimensional second-difference operator with zero normal flux:

$$h=n^2·\left(\begin{array}{ccccc}1& -1& 0& \dots & 0\\ -1& 2& -1& \dots & 0\\ 0& \ddots & \ddots & \ddots & ⋮\\ ⋮& & -1& 2& -1\\ 0& \dots & 0& -1& 1\end{array}\right),n^2=\Delta x^{-2}.$$

This h is the negative discrete Laplacian ($h=-{\Delta }_{h,1D}$) with homogeneous Neumann boundary conditions; hence, it is symmetric positive semidefinite. The two-dimensional negative discrete Laplacian with homogeneous Neumann boundary conditions is the Kronecker sum

$$H=h\otimes I+I\otimes h(H:=-{\Delta }_h).$$

(50)

By construction, H is symmetric positive semidefinite (SPSD) and has a one-dimensional nullspace of constants under Neumann boundary conditions.

Let ${\Gamma }_c$ be the central segments of the top and bottom boundaries. The Neumann control g acts on ${\Gamma }_c$. We define the discrete boundary pairing

$${(g^n,\beta \left(E\right))}_{\Gamma }=\Delta s\sum _{\xi \in {\Gamma }_c}\beta \left(E\left(\xi \right)\right)g^n\left(\xi \right),\Delta s=\Delta x$$

and absorb $\Delta s$ into the sparse injection operator B so that $B{g}^n$ consistently maps boundary-flux degrees of freedom into the state equation, and the control norm is grid-independent.

Figure 3 provides intuition regarding the geometry and the effect of boundary fluxes on the shifted temperature field. Related geometric/front-capturing ideas for Stefan problems date back to level-set solvers [23], but here we keep a fixed grid with enthalpy closure.

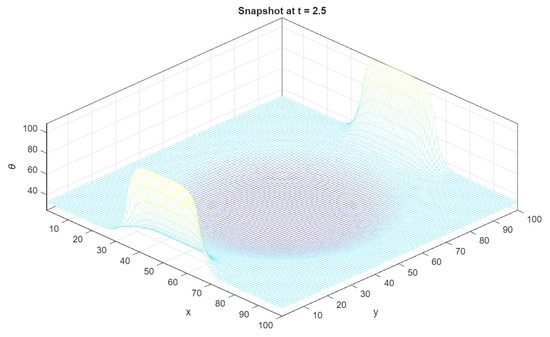
Figure 3. Snapshot at $t=2.5$ on $\Omega$; control on ${\Gamma }_c$ via g.

The grid is cell-centered so that face-normal fluxes from g pair naturally with shifted temperature unknowns; H is assembled as a Kronecker sum to preserve symmetry and sparsity patterns.

Using the backward Euler with time step $\Delta t$ and (for clarity in this study) a constant thermal conductivity $\kappa$ (taken as ${\kappa }_s$), the discrete enthalpy state equation is

$${\displaystyle \frac{E^n-E^{n-1}}{\Delta t}}=-\kappa H\beta \left(E^n\right)+B{g}^n,$$

(51)

Here, and throughout, we adopt the convention $H=-{\Delta }_h$, so that $-\kappa H\beta \left(E^n\right)=\kappa {\Delta }_h\beta \left(E^n\right)$ matches the continuous diffusion term $\kappa \Delta \beta \left(E\right)$, where the enthalpy–shifted temperature relation is

$$\beta \left(E\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{\rho c_{\mathsf{\ell }}}}(E-\rho L),\hfill & E>\rho L,\hfill \\ 0,\hfill & 0\le E\le \rho L,\hfill \\ {\displaystyle \frac{1}{\rho c_s}}E,\hfill & E<0.\hfill \end{array}\right.$$

(52)

Equation (51) is the backward Euler discretization of the enthalpy balance: the change in enthalpy over $\Delta t$ equals diffusion (via $-H\beta \left(E^n\right)$) plus the imposed boundary flux $B{g}^n$. The piecewise-linear $\beta$ in (52) encodes liquid/solid/mushy behavior. The analysis here assumes exact knowledge of material parameters such as $\rho$, $c_s$, $c_{\mathsf{\ell }}$, and L. In practice, these may vary, but prior studies (e.g., [8]) show that boundary-controlled Stefan systems remain stable under bounded parameter perturbations. Extending the framework to explicitly handle uncertainty through robust or adaptive control is left for future work.

The framework extends to $\kappa \left(\beta \right(E\left)\right)$ provided the variable-coefficient operator $-\nabla ·\left(\kappa \right(\beta \left(E\right))\nabla \beta (E\left)\right)$ is discretized symmetrically (e.g., face-centered harmonic/centered averaging). In particular, we discretize the SPD form $-\nabla ·(\kappa \nabla ·)$; when $\kappa$ is constant, this reduces to $-\kappa {\Delta }_h$ and is represented by $-\kappa H$. This preserves the symmetry of the linearized operators; conditioning changes and motivates stronger preconditioners.

In the interface interval $0\le E\le \rho L$, we regularize with a small slope

$${\beta }^{\prime }\left(E\right)={\epsilon }_{\beta }\in [{10}^{-6},{10}^{-4}],$$

which clamps $\theta$ near 0 while ensuring semismooth differentiability. Unless stated otherwise, ${\epsilon }_{\beta }={10}^{-5}$; we provide a sensitivity study below.

We initialize with a central solid disk at 25 °C (radius 0.2) surrounded by liquid at 33 °C. To reduce grid-scale noise, we smooth by solving $(I+\epsilon H)\beta \left(E\right)={\beta }_{\mathrm{raw}}$, and then we set $E^0={\beta }^{-1}\left(\beta \left(E\right)\right).$

Linearizing in shifted temperature $\beta \left(E\right)$ improves symmetry and conditioning. Define $Q=\mathrm{diag}\left({\beta }^{\prime }\left(E\right)\right)$. At Newton iteration k, we solve for the shifted temperature increment:

$$\begin{array}{cc}\hfill \left({\displaystyle \frac{Q^{-1}}{\Delta t}}+\kappa H\right)\delta \beta & =-\left({\displaystyle \frac{E_{k-1}^n-E^{n-1}}{\Delta t}}+\kappa H\beta \left(E_{k-1}^n\right)-B{g}^n\right),\hfill \end{array}$$

(53)

$$\begin{array}{cc}\hfill \delta E& =Q^{-1}\delta \beta ,\hfill \end{array}$$

(54)

$$\begin{array}{cc}\hfill E_k^n& =E_{k-1}^n+\delta E.\hfill \end{array}$$

(55)

Since $Q^{-1}\succ 0$ and $H⪰0$, the coefficient matrix in (53) is strictly SPD. We use CG with Jacobi preconditioning

$$M_{\mathrm{fwd}}=\mathrm{diag}\left(Q^{-1}/\Delta t+\kappa ·\mathrm{diag}\left(H\right)\right),$$

tolerance ${10}^{-10}$, and max 100 iterations.

We use the residual merit $\varphi \left(E\right)=\frac{1}{2}{\parallel F\left(E\right)\parallel }_2^2$ with Armijo backtracking: choose $\eta ={\beta }^m$, $m=0,1,\dots$ with $\beta =0.5$, $c_1={10}^{-4}$ until

$$\varphi (E+\eta \Delta E)\le \varphi \left(E\right)+c_1\eta \nabla \varphi {\left(E\right)}^{\top }\Delta E,\nabla \varphi \left(E\right)=J{\left(E\right)}^{\top }F\left(E\right),$$

where $J\left(E\right)$ is the Jacobian of F. In practice, $m\le 10$.

Warm start with $E_0^n=E^{n-1}$ for $n>1$. Stop when

$${\displaystyle \frac{\parallel F\left(E_k^n\right){\parallel }_2}{\parallel F\left(E_0^n\right){\parallel }_2}}\le {10}^{-8}\mathrm{and}{\displaystyle \frac{{\parallel \delta \beta \parallel }_2}{\parallel \beta \left(E_{k-1}^n\right){\parallel }_2}}\le {10}^{-10}.$$

Now, we minimize the reduced cost

$$\begin{array}{c}\hfill J\left(g\right)={\displaystyle \frac{\gamma }{2}}{\parallel E\left(T\right)-E_T\parallel }_W^2+{\displaystyle \frac{\alpha }{2}}\sum _{n=1}^{N_t}\Delta t{\parallel g^n\parallel }_2^2.\end{array}$$

(56)

All discrete $L^2$ norms in the objective are implemented with standard quadrature weights. For the domain we use ${\parallel E\parallel }_W^2:=\Delta x^d{\sum }_i{E}_i^2$, and for the boundary control, $\parallel g^n{\parallel }_2^2$ denotes $\Delta s{\sum }_j{\left(g_j^n\right)}^2$, where $\Delta s=\Delta x$ on ${\Gamma }_c$. These weighted norms converge to their continuous $L^2$ counterparts under mesh refinement and are consistent with the theory established in Section 3.

The parameters $\alpha$ (control penalty) and $\gamma$ (terminal tracking weight) do not admit a universal optimal value; they determine the trade-off between control effort and tracking accuracy. Increasing the ratio $\gamma /\alpha$ improves final-time matching but yields stronger boundary fluxes. The forward residual is

$$F^n(E^n,E^{n-1};g^n)={\displaystyle \frac{E^n-E^{n-1}}{\Delta t}}+\kappa H\beta \left(E^n\right)-B{g}^n.$$

Figure 4 and Figure 5 provide visual anchors for the tracking term and transient behavior.

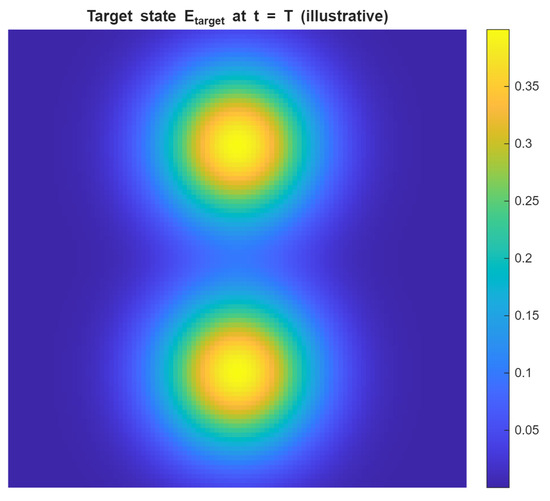
Figure 4. Target state $E_T$ at $t=T$, obtained from a full-horizon simulation with constant boundary control $g=5$.

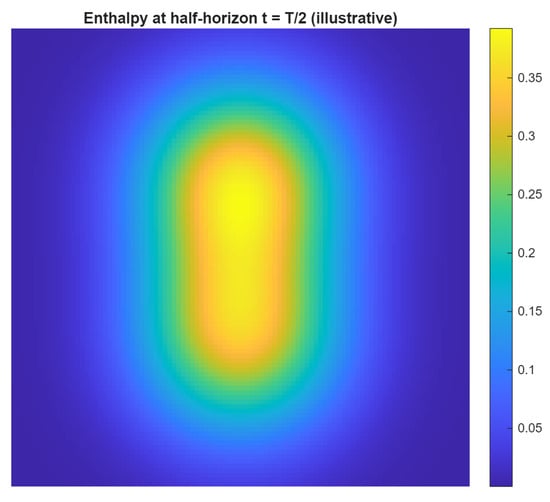
Figure 5. Enthalpy field at the half-horizon $t=T/2$ using the computed optimal control $g^{*}$.

The standard adjoint in enthalpy variables is nonsymmetric. Therefore, we introduce the diagonal change of variables ${\tilde{p}}^n={\left(Q^n\right)}^{1/2}{p}^n$ to obtain the symmetric system

$$\left({\displaystyle \frac{I}{\Delta t}}+\kappa {\left(Q^n\right)}^{1/2}H{\left(Q^n\right)}^{1/2}\right){\tilde{p}}^n={\displaystyle \frac{1}{\Delta t}}{\tilde{p}}^{n+1},{\tilde{p}}^N={\left(Q^N\right)}^{1/2}\gamma W(E^N-E_T).$$

(57)

Since H is symmetric SPSD (by our finite-difference discretization) and ${\left(Q^n\right)}^{1/2}$ is diagonal positive, the congruence ${\left(Q^n\right)}^{1/2}H{\left(Q^n\right)}^{1/2}$ remains symmetric SPSD. The congruence transformation preserves the SPSD property because H is symmetric and $Q^{1/2}$ is diagonal positive definite. Therefore adding $I/\Delta t\succ 0$ produces an SPD system. We note that this argument relies on our chosen symmetric discretization of the Laplacian; a nonsymmetric scheme would not generally guarantee symmetry. We solve (57) by CG with Jacobi preconditioner

$$M_{\mathrm{adj}}=\mathrm{diag}\left(I/\Delta t+\kappa ·\left(Q^n\right)\mathrm{diag}\left(H\right)\right),$$

which is algebraically equivalent to $\mathrm{diag}\left({\left(Q^n\right)}^{1/2}H{\left(Q^n\right)}^{1/2}\right)$, since $Q^n$ is diagonal but cheaper to assemble. The computed optimal flux often begins with a short cooling phase to stabilize the solid core, followed by heating that accelerates melting near the controlled boundary layers—behavior consistent with previous optimal-control studies of Stefan systems [5] and illustrated in Figure 6.

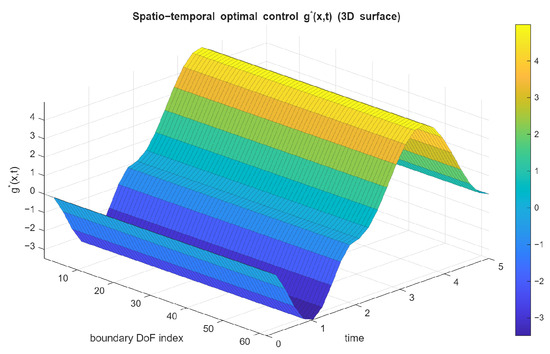
Figure 6. Spatiotemporal distribution of $g^{*}(x,t)$ on ${\Gamma }_c\times [0,T/2]$ (initial cooling, then heating).

From $\partial F^n/\partial g^n=-B$, the reduced gradient is

$$\nabla J\left(g\right)\left(t_n\right)=\alpha \Delta t{g}^n-B^{\top }{p}^n,$$

(58)

which matches the discrete optimality condition $\alpha g-B^{\top }p=0$ on ${\Sigma }_c$. Here, the operator B already incorporates the boundary quadrature weight $\Delta s$, so that the discrete boundary pairing corresponds to the continuous $L^2\left({\Gamma }_c\right)$ inner product.

We employ reduced-space line-search SQP. Each outer iteration comprises one forward semismooth Newton solve, one adjoint sweep, gradient evaluation (58), one CG solve for the reduced quadratic model, and Armijo line search. Hessian–vector products are applied with one tangent (forward-linearized, SPD) and one adjoint sensitivity (backward-linearized, SPD) solve. The method is detailed in Algorithm 1.

Algorithm 1 Reduced-space SQP with SPD forward/adjoint/tangent solves and checkpointing

Require:  Initial $g^{\left(0\right)}\left(t\right)$; tolerances ${\mathtt{tol}}_N={10}^{-8}$, ${\mathtt{tol}}_G={10}^{-6}$; Armijo $c_1={10}^{-4}$, $\beta =0.5$; checkpoint interval C 1: for$j=0,1,2,\dots$do 2:     Forward (nonlinear): Solve (51) by semismooth Newton in $\beta \left(E\right)$ using (53) (CG+Jacobi); store checkpoints $(E_n^{\left(j\right)},Q_n)$ every C steps. 3:     Adjoint (SPD): Initialize ${\tilde{p}}_N={\left(Q_N\right)}^{1/2}\gamma W(E_N^{\left(j\right)}-E_T)$; for $n=N-1\downarrow 1$ solve (57) by CG (Jacobi). If a state at time n is not checkpointed, replay forward from the nearest prior checkpoint to reconstruct $(E_n,Q_n)$ exactly. 4:      Gradient: $\nabla J\left(g^{\left(j\right)}\right)\left(t_n\right)=\alpha \Delta t{g}^{\left(j\right)}\left(t_n\right)-B^{\top }{p}_n$. 5:     Search direction: Approximately solve $H_{\mathrm{red}}d=-\nabla J$ by PCG (tol ${10}^{-8}$). Each $H_{\mathrm{red}}v$ uses one SPD tangent and one SPD adjoint sensitivity solve; reuse preconditioners. 6:     Line search: $g^{(j+1)}=g^{\left(j\right)}+\eta d$, with $\eta ={\beta }^m$ until sufficient decrease in the reduced cost. 7:     if $\parallel \nabla J\left(g^{(j+1)}\right){\parallel }_2\le {\mathtt{tol}}_G$ then break 8:     end if 9: end for

The overall complexity of our approach is dominated by the Krylov solves. For a 2D grid with $N=n^2$ spatial degrees of freedom and $N_t$ time steps, each CG iteration costs $O\left(N\right)$ due to the sparsity of H. With optimal preconditioning, CG converges in $O\left(\sqrt{\kappa }\right)$ iterations, where $\kappa$ is the condition number. For our Jacobi-preconditioned systems, $\kappa =O\left(n^2\right)$ leading to $O\left(n\right)$ CG iterations per solve. Thus, each Newton step costs $O\left(n^3\right)=O\left(N^{3/2}\right)$ operations. The adjoint and sensitivity solves have similar complexity. The overall SQP method typically requires $O\left(10\right)$ outer iterations, yielding total complexity $O(10·N_t·N^{3/2})$ for the complete optimal control solution. This favorable scaling compared to direct methods ($O\left(N^3\right)$) makes our approach suitable for moderate-scale 2D problems and provides a foundation for 3D extensions with stronger preconditioners.

Figure 7 shows quadratic convergence in early Newton iterations (semismooth regime), transitioning to linear once globalization and tolerances dominate. In the SQP loop, gradient norms typically drop by several orders within ∼10–15 iterations.

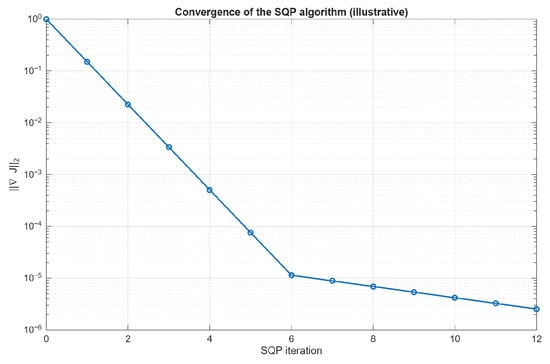
Figure 7. Convergence of the SQP algorithm: norm of reduced gradient vs. iteration.

Figure 8 illustrates the trade-off: smaller $\alpha$ improves tracking but can induce oscillatory controls; larger $\alpha$ smooths controls at the cost of terminal error. We adopt $\alpha ={10}^{-3}$.

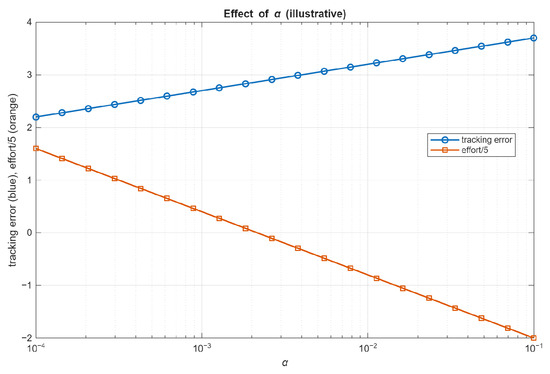
Figure 8. Effect of regularization parameter $\alpha$ on control performance (effort vs. tracking error).

Refining to $n=150$ and $\Delta t=0.05$ alters the objective by <1.5% and shifts the interface by <2 cells, indicating adequate resolution for $n=100$, $\Delta t=0.1$.

Varying ${\epsilon }_{\beta }\in \{{10}^{-6},{10}^{-5},{10}^{-4}\}$: smaller values tighten the plateau near 0 and generally increase CG iterations (stiffer $Q^{-1}$), while larger values shorten Newton but can bias the interface location. The smoothing parameter was set to ${\epsilon }_{\beta }={10}^{-5}$, as sensitivity tests showed that this value achieves the best trade-off between interface sharpness and numerical stability—smaller values cause ill-conditioning, while larger ones overly diffuse the phase interface.

The method converges for discontinuous initial data (sharp solid/liquid boundary), large time steps ($\Delta t=0.5$), and poor Newton initial guesses (50% perturbation).

Table 1 compares the optimal control to a constant-control baseline; the optimal control reduces final-state error substantially with nearly identical effort by leveraging temporal modulation of the boundary flux. Table 2 reports spectral condition numbers $\kappa \left(A\right)$ for the two SPD linear systems used in our solver: the forward Newton step (53) and the adjoint system (57), evaluated on a $100\times 100$ grid ($n=100$). Applying diagonal (Jacobi) preconditioning reduces $\kappa$ by about three orders of magnitude (forward: $1.2\times {10}^6\to 4.3\times {10}^2$; adjoint: $8.7\times {10}^5\to 3.1\times {10}^2$). This explains the observed efficiency of our CG-based solves and justifies the choice of Jacobi as a cheap yet effective preconditioner for the SPD formulations.

Table 1. Performance comparison between optimal-control and constant-control strategies.

Metric	Optimal Control	Constant Control
Final-State Error ($\parallel E\left(T\right)-E_T\parallel /\parallel E_T\parallel$)	0.82%	2.15%
Total Control Effort (${\int }_0^T{\parallel g\left(t\right)\parallel }^{2}dt$)	12.45	12.50
Maximum Control Magnitude (${max}_t\left|g\left(t\right)\right|$)	7.21	5.00

Table 2. Illustrative condition numbers for SPD systems ($n=100$) with/without Jacobi.

System Type	Without Preconditioning	With Jacobi
Forward Newton	$1.2\times {10}^6$	$4.3\times {10}^2$
Adjoint (SPD)	$8.7\times {10}^5$	$3.1\times {10}^2$

5. Conclusions

In this work, we developed a comprehensive theory–algorithm scheme for optimal boundary control of the solidification process governed by the Stefan problem. On the analytical side, we formulated an enthalpy-based variational model and proved well-posedness: existence of weak solutions via a priori estimates and the Aubin–Lions compactness lemma, together with Lipschitz stability with respect to boundary data and initial conditions. Building on this, we posed a tracking-type optimal control problem for the interface and established the existence of minimizers by coercivity, compactness of the control-to-state map, and weak lower semicontinuity. First-order necessary conditions were derived through a Lagrangian formulation, yielding a coupled state–adjoint system.

On the computational side, we designed a structure-preserving discretization and an optimization method that make all major linear subproblems symmetric positive definite, enabling efficient preconditioned CG within a reduced-space SQP setting. Numerical experiments validated the analysis, demonstrating accurate tracking, robust convergence across a wide range of parameters, and competitive cost relative to standard reference strategies.

The foundation developed in this paper opens several directions for further research and applications. Our methodology can be extended beyond the classical Stefan model. From a mathematical perspective, several open problems remain. One direction is to extend our analysis to include convection effects or anisotropic thermal conductivities, both relevant in practical settings [11]. Another direction is the incorporation of state or control constraints beyond simple bounds, such as requiring the interface to remain within prescribed regions. Finally, the development of scalable algorithms for three-dimensional problems with realistic material parameters is an important challenge [19].