The Fine-Structure Constant in the Bivector Standard Model
Abstract
1. Introduction
Scope and Goals
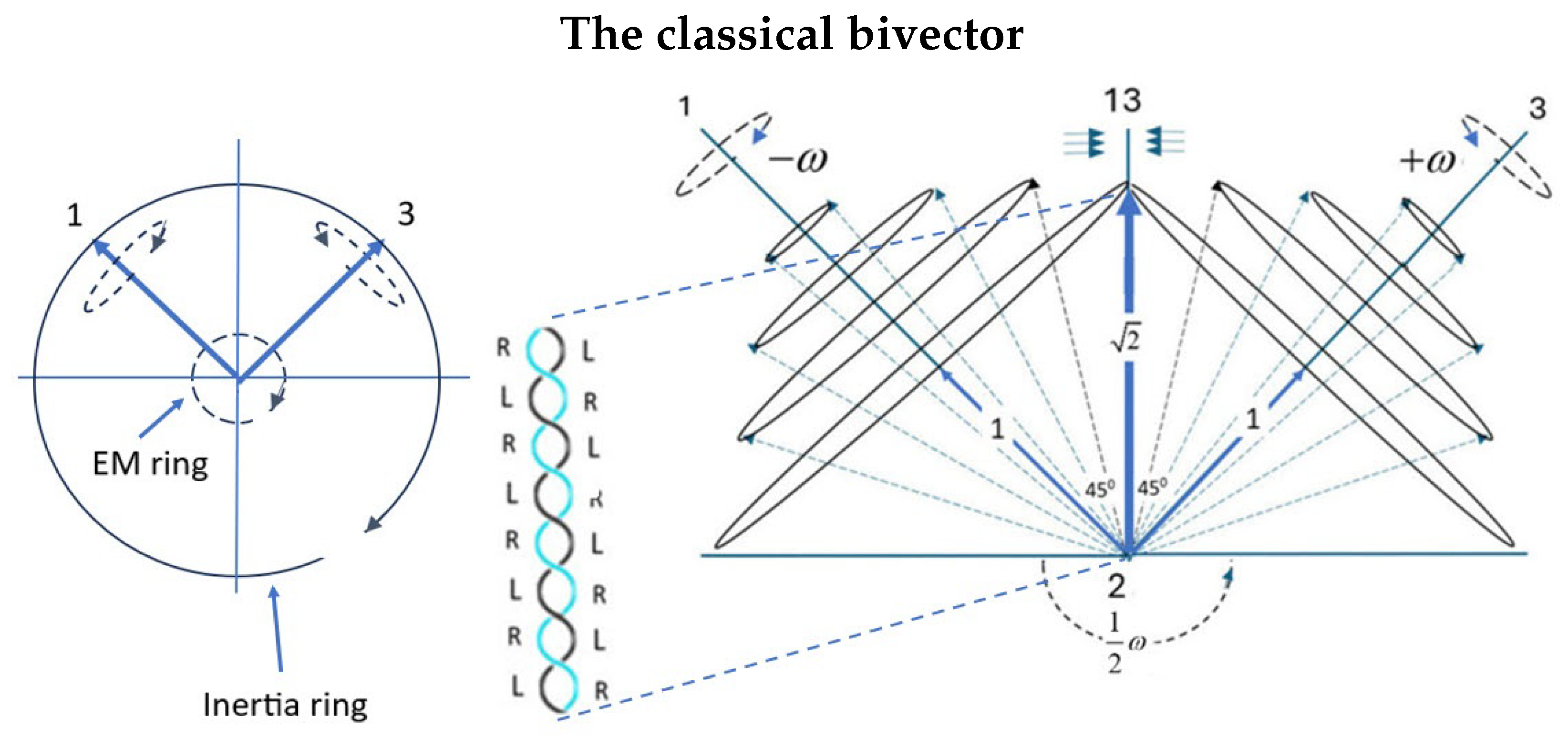
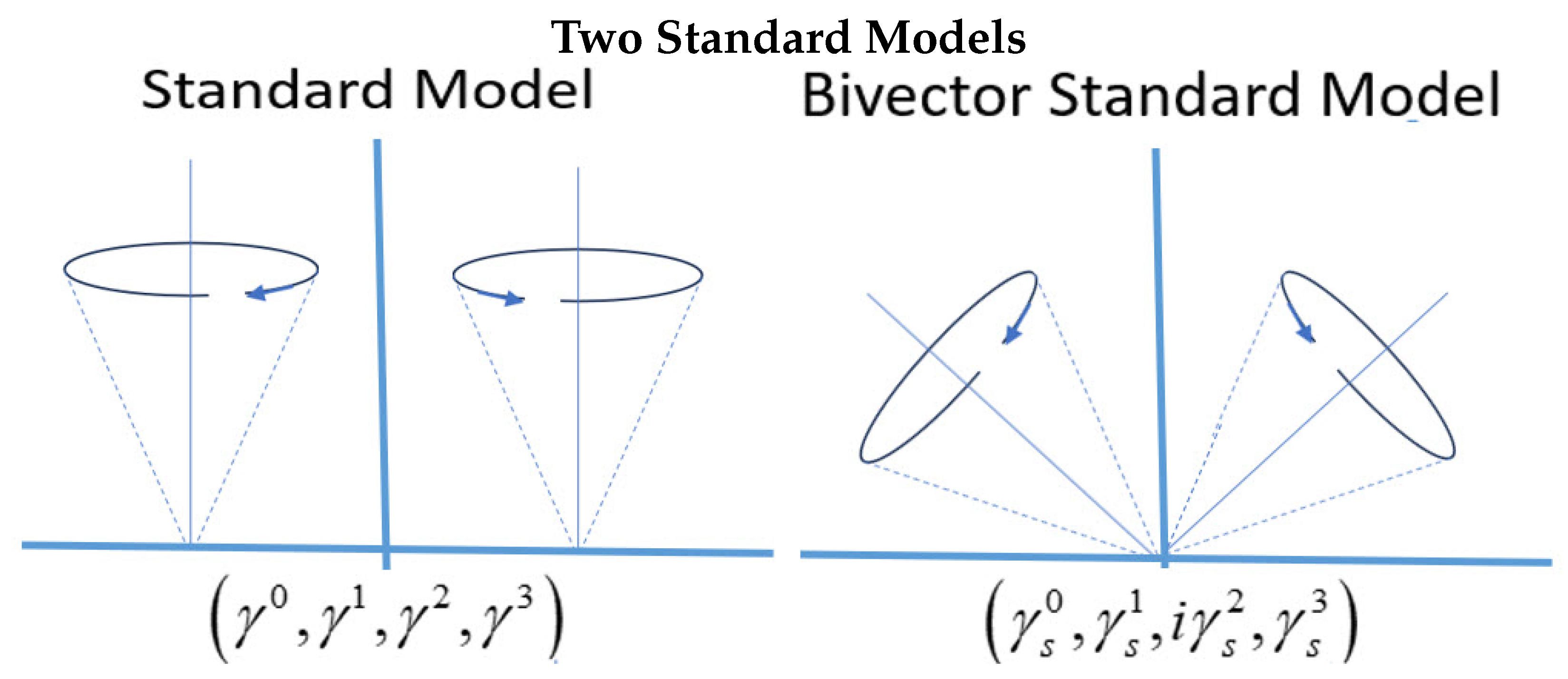
2. The Bivector Electron
Classical Rotor Lagrangian and FSC Partition
3. The Fine-Structure Constant
Thomson Scattering
4. Discussion
Note Added in Proof
Funding
Data Availability Statement
Conflicts of Interest
References
- Eddington, A.S.; Whittaker, E.T. Fundamental Theory; The University Press: Cambridge, UK, 1946. [Google Scholar]
- Dirac, P.A.M. A New Basis for Cosmology. Proc. R. Soc. A 1938, 165, 199–208. [Google Scholar] [CrossRef]
- Feynman, R.P. QED: The Strange Theory of Light and Matter; Princeton University Press: Princeton, NJ, USA, 1985. [Google Scholar]
- Feynman, R.P.; Leighton, R.B.; Sands, M. The Feynman Lectures on Physics; Addison-Wesley: Boston, MA, USA, 1964; Volume 1. [Google Scholar]
- Morel, L.; Yao, Z.; Cladé, P.; Khélifa, S.G. Determination of the fine-structure constant with an atom-interferometric measurement of the recoil velocity of rubidium. Nature 2020, 588, 61–65. [Google Scholar] [CrossRef] [PubMed]
- Parker, R.H.; Yu, C.; Zhong, W.; Estey, B.; Müller, H. Measurement of the fine-structure constant as a test of the Standard Model. Science 2018, 360, 191–195. [Google Scholar] [CrossRef] [PubMed]
- Cladé, P.; GuellatiKhélifa, S. The fine structure constant α and the ratio h/m. Comptes Rendus Phys. 2019, 20, 77–92. [Google Scholar] [CrossRef]
- Sanctuary, B. Quaternion Spin. Mathematics 2024, 12, 1962. [Google Scholar] [CrossRef]
- Sanctuary, B. The Classical Origin of Spin: Vectors Versus Bivectors. Axioms 2025, 14, 668. [Google Scholar] [CrossRef]
- Doran, C.; Lasenby, J. Geometric Algebra for Physicists; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Compton, A.H. A Quantum Theory of the Scattering of X-rays by Light Elements. Phys. Rev. 1923, 21, 483–502. [Google Scholar] [CrossRef]
- Hestenes, D. The zitterbewegung interpretation of quantum mechanics. Found. Phys. 1990, 20, 1213–1232. [Google Scholar] [CrossRef]
- Goldstein, H. Classical Mechanics; Addison-Wesley Publishing Compangy, Inc.: Reading, MA, USA, 1950; ISBN 0-201-02510-8. [Google Scholar]
- Carroll, S.M. Spacetime and Geometry; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Nakahara, M. Geometry, Topology and Physics, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar] [CrossRef]
- Wald, R.M. General Relativity; University of Chicago Press: Chicago, IL, USA, 2024. [Google Scholar]
- CODATA 2022 Recommended Values of the Fundamental Physical Constants, National Institute of Standards and Technology (NIST) Web Database. Available online: https://physics.nist.gov/cuu/Constants/ (accessed on 1 August 2025).
- Wilson, K.G. Renormalization group and critical phenomena. I. Renormalization group and the Kadanoff scaling picture. Phys. Rev. B 1971, 4, 3174. [Google Scholar] [CrossRef]
- Pauli, W.; Villars, F. On the invariant regularization in relativistic quantum theory. Rev. Mod. Phys. 1949, 21, 434. [Google Scholar] [CrossRef]
- Doplicher, S.; Fredenhagen, K.; Roberts, J.E. The quantum structure of spacetime at the Planck scale and quantum fields. Commun. Math. Phys. 1995, 172, 187–220. [Google Scholar] [CrossRef]
- Griffiths, D. Introduction to Elementary Particles; John Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 59–60. ISBN 978-3-527-40601-2. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; Wiley: Hoboken, NJ, USA, 1999; Sections 14–16. [Google Scholar]
- Damm, H.; Pasch, E.; Dinklage, A.; Baldzuhn, J.; Bozhenkov, S.A.; Brunner, K.J.; Winters, V. First results from an event synchronized—High repetition Thomson scattering system at Wendelstein 7-X. J. Instrum. 2019, 14, C09037. [Google Scholar] [CrossRef]
- Geltman, S. Topics in Atomic Collision Theory; Academic Press: Cambridge, MA, USA, 2013; Volume 30. [Google Scholar]
- Rybicki, G.B.; Lightman, A.P. Radiative Processes in Astrophysics; John Wiley & Sons: Hoboken, NJ, USA, 2024. [Google Scholar]
- Mohr, P.J.; Taylor, B.N. CODATA recommended values of the fundamental physical constants: 1998. J. Phys. Chem. Ref. Data 1999, 28, 1713–1852. [Google Scholar] [CrossRef]
- Heitler, W. The Quantum Theory of Radiation; Courier Corporation: North Chelmsford, MA, USA, 1984. [Google Scholar]
- Klein, O.; Nishina, Y. Über die Streuung von Strahlung durch freie Elektronen nach der neuen relativistischen Quantendynamik von Dirac. Z. Phys. 1929, 52, 853–868. [Google Scholar] [CrossRef]
- Egerton, R.F. Electron Energy-Loss Spectroscopy in the Electron Microscope, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Rehr, J.J.; Ankudinov, A.L. Progress in the theory and interpretation of X-ray spectra. Coord. Chem. Rev. 2005, 249, 131–140. [Google Scholar] [CrossRef]
- dos Santos, C.A.M.; Fleury, M.J.J. An electromagnetic model of the electron. Ann. Fond. Louis Broglie 2025, 49, 1–17. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanctuary, B. The Fine-Structure Constant in the Bivector Standard Model. Axioms 2025, 14, 841. https://doi.org/10.3390/axioms14110841
Sanctuary B. The Fine-Structure Constant in the Bivector Standard Model. Axioms. 2025; 14(11):841. https://doi.org/10.3390/axioms14110841
Chicago/Turabian StyleSanctuary, Bryan. 2025. "The Fine-Structure Constant in the Bivector Standard Model" Axioms 14, no. 11: 841. https://doi.org/10.3390/axioms14110841
APA StyleSanctuary, B. (2025). The Fine-Structure Constant in the Bivector Standard Model. Axioms, 14(11), 841. https://doi.org/10.3390/axioms14110841





