An Efficient Iteration Method for Fixed-Point Approximation and Its Application to Fractional Volterra–Fredholm Integro–Differential Equations

Abstract

This paper proposes an efficient iteration method for fixed-point approximation in Banach spaces. The method accelerates convergence by incorporating a squared operator term within the iteration process. Analytical proofs verify its convergence and stability. Comparative numerical tests show that it converges faster and more reliably than established Picard-type methods. Its application to fractional models involving the Gamma function highlights the method’s efficiency and potential for broader use in nonlinear and fractional systems.

1. Introduction

Fixed point theory is a central branch of mathematics that continues to expand, closely linked with areas such as functional analysis, topology, and nonlinear analysis. Its depth and adaptability make it indispensable in multiple disciplines, including optimization, economics, game theory, dynamical systems, and the analysis of differential and integral equations. A key aspect of the theory lies in its role within nonlinear operator theory, where contraction mapping results serve as fundamental tools. Due to their wide-ranging applications, many researchers have proposed refined versions and broader classes of contraction-type mappings in abstract settings, significantly enriching the theoretical landscape and strengthening its utility in practical computations.

Banach’s classical contraction principle [1] has long served as the cornerstone of fixed point theory and has inspired a variety of generalizations, including those by Agarwal et al. [2], Noor [3], and Alam et al. [4]. To compute fixed points of such mappings, a number of iteration methods have been devised, with the Picard [5], Mann [6], and Ishikawa [7] methods forming the traditional foundation. More recent research has focused on accelerating convergence and improving efficiency, giving rise to modified Picard-type iteration methods such as Picard-Mann, Picard-Noor, Picard-S*, Picard-SP, and Picard-CR, introduced respectively by Khan [8], Eke and Akewe [9], Lamba and Panwar [10], Nawaz et al. [11], and Nawaz et al. [12]. Complementing these developments, novel methods like the CR iteration of Chung et al. [13] and the three-step method of Daengsaen and Khempet [14] have further advanced the field.

Alam and Rohen [15] have recently contributed to iteration methods by establishing convergence in hyperbolic spaces for nonlinear integral equations with two delays, also Alam et al. [16] analyzed the Fibonacci–Ishikawa process for monotone asymptotically nonexpansive operators in uniformly convex Banach spaces. Over the years, these types of methods have attracted increasing research interest. For example, in 2018, Piri et al. [17] introduced an iterative method that outperformed the earlier method of Thakur et al. [18]. Later, the $D^{\ast \ast }$-iteration [19] was proposed, demonstrating faster convergence than several established approaches, including those of Agarwal et al. [2], Gürsoy and Karakaya [20], Noor [3], Piri et al. [17], and Thakur et al. [18]. More recently, Alam and Rohen [21] employed an improved version of their iteration method, surpassing the $D^{\ast \ast }$ method to effectively approximate solutions of a fractional Volterra–Fredholm integro-differential equation, thereby confirming its efficiency in applied problems.

Fixed point theory investigates essential issues such as how fixed points are constructed, whether they exist uniquely, and what properties they exhibit, with a strong emphasis on data dependence. This line of research examines the sensitivity of fixed points to small variations in the input data and has been a central theme for many years. Berinde [22] studied data dependence for the Picard iteration, while Soltuz [23,24] and Ali and Ali [25] extended the analysis to Mann and Ishikawa iterations involving contraction-type mappings. Illustrative results by Ćirić et al. [26] showed that the Noor scheme attains faster convergence compared to the Mann and Ishikawa processes. Later, Pheungrattana and Suantai [27] introduced the SP iteration and proved its superior convergence for monotone increasing functions. These contributions collectively demonstrate the steady advancement of iteration methods in the fixed point setting.

This paper proposes a refined iteration technique developed to enhance convergence efficiency for contraction mappings. Theoretical guarantees of stability are provided, while numerical testing and graphical evidence obtained through MATHEMATICA illustrate the method’s effectiveness. Comparative results indicate that the approach achieves faster and more precise convergence than several established schemes, including those proposed by Sainuan, Daengsaen, and Khempet, Chung et al., Nawaz et al., Lamba and Panwar, and Nawaz et al. Furthermore, a parameter-focused study highlights the scheme’s flexibility and dependability. To demonstrate practical applicability, the method is successfully implemented for solving a fractional Volterra-Fredholm integro-differential equation using the Gamma function.

The subsequent sections of this paper are organised as follows. Section 2 provides the development of the newly proposed iteration method. The convergence analysis of the newly proposed iteration method and its stability is discussed in Section 3. The comparative study of the proposed method compared to some existing methods is also discussed in this section through the numerical results. Section 4 deals with the application of our proposed method to a Fractional Volterra-Fredholm integro-differential equation with Gamma function. Finally, Section 5 presents the concluding remarks.

2. Preliminaries

In this study, let V denote a uniformly convex Banach space and $W\subseteq V$ a nonempty, closed, and convex subset. Recall that a Banach space V is said to be uniformly convex if, for every $ϵ>0$, there exists a $\delta >0$ such that whenever $a,b\in V$ with $\parallel a\parallel \le 1$, $\parallel b\parallel \le 1$, and $\parallel a-b\parallel \ge ϵ$, the inequality

$$\parallel a+b\parallel \le 2(1-\delta )$$

is satisfied. An equivalent characterization often used in the literature is the condition $\parallel a+b\parallel \le 2(1-\delta )$. This geometric property plays a fundamental role in guaranteeing the strong convergence of iteration sequences.

A mapping $L:W\to W$ is called a contraction if there exists a constant $\beta \in [0,1)$ such that

$$\parallel La-Lb\parallel \le \beta \parallel a-b\parallel , \forall a,b\in W.$$

Given the wide range of iteration schemes proposed for fixed-point approximation, a complete survey is beyond the scope of this work. Instead, this section presents essential preliminaries, including key definitions and lemmas, along with a concise overview of selected iteration processes. For example, Sainuan [28] introduced in 2015 the P-iteration process, defined for the sequences $\left\{s_n\right\},\left\{t_n\right\},\left\{u_n\right\}\subseteq (0,1)$ as follows:

$$\left\{\begin{array}{c}{a}_1\in W,\hfill \\ a_{n+1}=(1-s_n)L{a}_n+s_{n}L{b}_n,\hfill \\ b_n=(1-t_n)c_n+t_{n}L{c}_n,\hfill \\ c_n=(1-u_n)a_n+u_{n}L{a}_n,n\in \mathbb{N}.\hfill \end{array}\right.$$

(1)

In 2018, Daengsaen and Khempet [14] proposed the following D iteration process, defined as:

$$\left\{\begin{array}{c}{a}_1\in W,\hfill \\ a_{n+1}=(1-s_n)L{c}_n+s_{n}L{b}_n,\hfill \\ b_n=(1-t_n)L{a}_n+t_{n}L{c}_n,\hfill \\ c_n=(1-u_n)a_n+u_{n}L{a}_n,n\in \mathbb{N}.\hfill \end{array}\right.$$

(2)

Chung et al. [13] proposed the following CR iteration process for the sequences $\left\{s_n\right\},\left\{t_n\right\},\left\{u_n\right\}\subseteq (0,1)$ in 2012, defined as:

$$\left\{\begin{array}{c}{a}_1\in W,\hfill \\ a_{n+1}=(1-s_n)b_n+s_{n}L{b}_n,\hfill \\ b_n=(1-t_n)L{a}_n+t_{n}L{c}_n,\hfill \\ c_n=(1-u_n)a_n+u_{n}L{a}_n,n\in \mathbb{N}.\hfill \end{array}\right.$$

(3)

In 2024, Nawaz et al. [11] introduced the Picard-SP iteration process, which is defined as:

$$\left\{\begin{array}{c}{a}_1\in W,\hfill \\ a_{n+1}=L{b}_n,\hfill \\ b_n=(1-s_n)c_n+s_{n}L{c}_n,\hfill \\ c_n=(1-t_n)d_n+t_{n}L{d}_n,\hfill \\ d_n=(1-u_n)a_n+u_{n}L{a}_n,n\in \mathbb{N}.\hfill \end{array}\right.$$

(4)

Lamba and Panwar [10] proposed the following Picard-S* iteration process in 2021 which is defined as:

$$\left\{\begin{array}{c}{a}_1\in W,\hfill \\ a_{n+1}=L{b}_n,\hfill \\ b_n=(1-s_n)L{a}_n+s_{n}L{c}_n,\hfill \\ c_n=(1-t_n)L{a}_n+t_{n}L{d}_n,\hfill \\ d_n=(1-u_n)a_n+u_{n}L{a}_n,n\in \mathbb{N}.\hfill \end{array}\right.$$

(5)

Recently, in 2025, Nawaz et al. [12] proposed the following Picard-CR iteration process for the sequences $\left\{s_n\right\},\left\{t_n\right\},\left\{u_n\right\}\subseteq (0,1)$ as:

$$\left\{\begin{array}{c}{a}_1\in W,\hfill \\ a_{n+1}=L{b}_n,\hfill \\ b_n=(1-s_n)c_n+s_{n}L{c}_n,\hfill \\ c_n=(1-t_n)L{a}_n+t_{n}L{d}_n,\hfill \\ d_n=(1-u_n)a_n+u_{n}L{a}_n,n\in \mathbb{N}.\hfill \end{array}\right.$$

(6)

Motivated by these considerations, we propose a novel iteration scheme that exhibits a faster rate of convergence for contraction mappings compared with several existing methods, including those of Sainuan [28], Daengsaen and Khempet [14], Chung et al. [13], Nawaz et al. [11], Lamba and Panwar [10], Nawaz et al. [12], among others.

Our new iteration procedure is defined by:

$$\left\{\begin{array}{c}{a}_1\in W,\hfill \\ a_{n+1}=L^2{b}_n,\hfill \\ b_n=(1-s_n)L{c}_n+s_n{c}_n,\hfill \\ c_n=(1-t_n)L{a}_n+t_{n}L{d}_n,\hfill \\ d_n=(1-u_n)e_n+u_{n}L{e}_n,\hfill \\ e_n=(1-v_n)a_n+v_{n}L{a}_n,n\in \mathbb{N},\hfill \end{array}\right.$$

(7)

for sequences $\left\{s_n\right\},\left\{t_n\right\},\left\{u_n\right\},\left\{v_n\right\}\subseteq (0,1)$.

Remark 1.

Any iteration scheme $\left\{a_n\right\}$ initiated with $a_1\in W$ can be expressed in the general form

$$a_{n+1}=G(a_n,L),$$

where G denotes a suitably defined iteration function that depends on the previous iterate and the operator L. As a particular case, the iteration sequence $\left\{a_n\right\}$ presented in Equation (7) fits into this general framework.

$$\begin{array}{cc}\hfill a_{n+1}=& L^2((1-s_n)L((1-t_n)L{a}_n+t_{n}L((1-u_n)((1-v_n)a_n+v_{n}L{a}_n)+u_{n}L((1-v_n)a_n\hfill \\ & +v_{n}L{a}_n\left)\right))+s_n((1-t_n)L{a}_n+t_{n}L((1-u_n)((1-v_n)a_n+v_{n}L{a}_n)\hfill \\ & +u_{n}L((1-v_n)a_n+v_{n}L{a}_n)\left)\right)),\hfill \\ & =G(a_n,L),\forall n\in \mathbb{N}.\hfill \end{array}$$

Definition 1

([29]). Let V be a nonempty convex Banach space. An iteration process of the form

$$a_{n+1}=G(a_n,L),$$

which converges to a fixed point a, is said to be stable with respect to L (or simply L-stable) if

$$\begin{array}{c}\hfill \underset{n\to \infty }{\lim }\parallel {\zeta }_n-G({\zeta }_n,L)\parallel = 0 \iff \underset{n\to \infty }{\lim }{\zeta }_n=a\end{array}$$

for a given sequence $\left\{{\zeta }_n\right\}\subset V$.

Lemma 1

([30]). Let $\left\{{\zeta }_n\right\}$ and $\left\{{\delta }_n\right\}$ be two sequences of non-negative real numbers satisfying the recursive inequality

$${\zeta }_{n+1}\le (1-{\eta }_n){\zeta }_n+{\delta }_n, \mathit{for} \mathit{all} n\in \mathbb{N},$$

where $0<{\eta }_n<1$, ${\sum }_{n=0}^{\infty }{\eta }_n=\infty$, and ${\lim }_{n\to \infty }{\displaystyle \frac{{\delta }_n}{{\eta }_n}}=0$. Then, it follows that

$$\underset{n\to \infty }{\lim }{\zeta }_n=0.$$

Lemma 2

([25]). Let $\left\{{\zeta }_n\right\}$ and $\left\{{\delta }_n\right\}$ be two sequences of non-negative real numbers satisfying the recursive inequality

$${\zeta }_{n+1}\le (1-{\eta }_n){\zeta }_n+{\eta }_n{\delta }_n, \mathit{for} \mathit{all} n\in \mathbb{N},$$

where $0<{\eta }_n<1$, ${\sum }_{n=0}^{\infty }{\eta }_n=\infty$, and $\left\{{\delta }_n\right\}$ is a bounded sequence with ${\delta }_n\ge 0$. Then it holds that

$$0\le \underset{n\to \infty }{\mathrm{lim\; sup}}{\zeta }_n\le \underset{n\to \infty }{\mathrm{lim\; sup}}{\delta }_n.$$

Definition 2

([5]). Suppose two fixed point iteration sequences $\left\{a_n\right\}$ and $\left\{b_n\right\}$ both converge to the same point $a\in V$, and satisfy

$$\parallel a_n-a\parallel \le {\zeta }_n, \parallel b_n-a\parallel \le {\delta }_n, \forall n\in \mathbb{N},$$

where $\left\{{\zeta }_n\right\}$ and $\left\{{\delta }_n\right\}$ are two sequences of nonnegative real numbers. Then, $\left\{a_n\right\}$ is said to converge faster than $\left\{b_n\right\}$ if

$$\underset{n\to \infty }{\lim }{\displaystyle \frac{{\zeta }_n}{{\delta }_n}}=0.$$

3. Main Results

This section provides a rigorous analytical study of the convergence properties of the iteration sequence defined by Equation (7). In order to complement the theoretical findings, we also present numerical experiments which demonstrate that the convergence rates of the iteration schemes given in Equations (1)–(6) are slower in comparison with that of the proposed iteration in (7). We begin by establishing the existence and uniqueness of a fixed point of the contraction mapping, which serves as the limit of the iteration scheme in (7).

Theorem 1.

Let V be a Banach space and let $L:W\to W$ be a contraction mapping with contraction constant $\beta \in [0,1)$, where W is a nonempty, closed, and convex subset of V. Then, the iteration sequence $\left\{a_n\right\}$ generated by the scheme defined in (7) converges to the unique fixed point of L.

Proof. 

Let $L:W\to W$ be a contraction mapping with contraction constant $\beta \in [0,1)$, defined on a nonempty, closed, and convex subset W of a Banach space. The Banach Fixed Point Theorem [1] guarantees the existence of a unique fixed point $a\in W$ such that $La=a$.

From the iteration process defined in (7), we obtain the following five inequalities:

$$\begin{array}{cc}\hfill \parallel e_n-a\parallel & = \parallel (1-v_n)a_n+v_{n}L{a}_n-a\parallel \hfill \\ & \le (1-v_n)\parallel a_n-a\parallel +v_n\parallel L{a}_n-a\parallel \hfill \\ & =(1-v_n)\parallel a_n-a\parallel +v_n\parallel L{a}_n-La\parallel \hfill \\ & \le (1-v_n)\parallel a_n-a\parallel +\beta v_n\parallel a_n-a\parallel \hfill \\ & =(1+(\beta -1)v_n)\parallel a_n-a\parallel \hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill \parallel d_n-a\parallel & = \parallel (1-u_n)e_n+u_{n}L{e}_n-a\parallel \hfill \\ & \le (1-u_n)\parallel e_n-a\parallel +u_n\parallel L{e}_n-a\parallel \hfill \\ & =(1-u_n)\parallel e_n-a\parallel +u_n\parallel L{e}_n-La\parallel \hfill \\ & \le (1-u_n)\parallel e_n-a\parallel +\beta u_n\parallel e_n-a\parallel \hfill \\ & =(1+(\beta -1)u_n)\parallel e_n-a\parallel \hfill \end{array}$$

$$\begin{array}{cc}\hfill \parallel c_n-a\parallel & = \parallel (1-t_n)L{a}_n+t_{n}L{d}_n-a\parallel \hfill \\ & \le (1-t_n)\parallel L{a}_n-a\parallel +t_n\parallel L{d}_n-a\parallel \hfill \\ & =(1-t_n)\parallel L{a}_n-La\parallel +t_n\parallel L{d}_n-La\parallel \hfill \\ & \le (1-t_n)\beta \parallel a_n-a\parallel +t_n\beta \parallel d_n-a\parallel \hfill \\ & \le (1-t_n)\beta \parallel a_n-a\parallel +t_n\beta (1+(\beta -1)u_n)\parallel e_n-a\parallel \hfill \end{array}$$

from Equation (8), we have

$$\begin{array}{cc}\hfill \parallel c_n-a\parallel & \le (1-t_n)\beta \parallel a_n-a\parallel +t_n\beta (1+(\beta -1)u_n)(1+(\beta -1)v_n)\parallel a_n-a\parallel \hfill \\ & =\beta (1+\beta t_n{v}_n-t_n{v}_n+\beta t_n{u}_n+{\beta }^2{t}_n{u}_n{v}_n-2\beta t_n{u}_n{v}_n-t_n{u}_n+t_n{u}_n{v}_n)\parallel a_n-a\parallel \hfill \end{array}$$

$$\begin{array}{cc}\hfill \parallel b_n-a\parallel & = \parallel (1-s_n)L{c}_n+s_n{c}_n-a\parallel \hfill \\ & \le (1-s_n)\parallel L{c}_n-a\parallel +s_n\parallel c_n-a\parallel \hfill \\ & =(1-s_n)\parallel L{c}_n-La\parallel +s_n\parallel c_n-a\parallel \hfill \\ & \le (1-s_n)\beta \parallel c_n-a\parallel +s_n\parallel c_n-a\parallel \hfill \\ & =(\beta -s_n(\beta -1))\parallel c_n-a\parallel \hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \parallel a_{n+1}-a\parallel & = \parallel L^2{b}_n-a\parallel \hfill \\ & \le \beta \parallel L{b}_n-a\parallel \hfill \\ & \le {\beta }^2\parallel b_n-a\parallel \hfill \end{array}$$

Hence,

$$\begin{array}{cc}\hfill \parallel a_{n+1}-a\parallel & \le {\beta }^2(\beta -s_n(\beta -1))\parallel c_n-a\parallel \hfill \\ & \le {\beta }^3(\beta -s_n(\beta -1))\times \hfill \\ & (1+\beta t_n{v}_n-t_n{v}_n+\beta t_n{u}_n+{\beta }^2{t}_n{u}_n{v}_n-2\beta t_n{u}_n{v}_n-t_n{u}_n+t_n{u}_n{v}_n)\parallel a_n-a\parallel .\hfill \end{array}$$

Since

$$(\beta -s_n(\beta -1))(1+\beta t_n{v}_n-t_n{v}_n+\beta t_n{u}_n+{\beta }^2{t}_n{u}_n{v}_n-2\beta t_n{u}_n{v}_n-t_n{u}_n+t_n{u}_n{v}_n)<1$$

So,

$$\begin{array}{cc}\hfill \parallel a_{n+1}-a\parallel & \le {\beta }^3\parallel a_n-a\parallel \hfill \\ & \le {\beta }^6\parallel a_{n-1}-a\parallel \hfill \\ & \le {\beta }^{3n}\parallel a_1-a\parallel .\hfill \end{array}$$

Since $0\le \beta <1$, it follows that

$$\underset{n\to \infty }{\lim }\parallel a_{n+1}-a\parallel = 0.$$

Therefore, the iteration sequence $\left\{a_n\right\}$ defined in (7) converges to the unique fixed point a of the contraction mapping L. □

We now present the following theorem, which establishes the stability of the iteration process defined in (7).

Theorem 2.

In a Banach space V, let $L:W\to W$ be a contraction mapping with contraction constant $\beta \in [0,1)$, where W is a nonempty, closed, and convex subset of V. The iteration sequence $\left\{a_n\right\}$, defined in (7), is said to be stable with respect to L (or simply L–stable) if at least one of the sequences $\left\{s_n\right\}$, $\left\{t_n\right\}$, $\left\{u_n\right\}$, or $\left\{v_n\right\}$ remains bounded away from zero.

Proof. 

Assume that the iteration sequence $\left\{a_n\right\}$, defined in (7) by the recurrence

$$a_{n+1}=\mathit{G}(a_n+\mathit{L})$$

converges to a, the unique fixed point of the contraction mapping L. Now, consider an arbitrary sequence $\left\{p_n\right\}$. Then,

$$\begin{array}{c}\hfill \parallel p_{n+1}-a\parallel \le \parallel p_{n+1}-G(p_n,L)\parallel +\parallel G(p_b,L)-a\parallel ,\end{array}$$

where

$$\left\{\begin{array}{c}G(p_n,L)=L^2{b}_n,\hfill \\ b_n=(1-s_n)L{c}_n+s_n{c}_n,\hfill \\ c_n=(1-t_n)L{p}_n+t_{n}L{d}_n,\hfill \\ d_n=(1-u_n)e_n+u_{n}L{e}_n,\hfill \\ e_n=(1-v_n)p_n+v_{n}L{p}_n,n\in \mathbb{N}.\hfill \end{array}\right.$$

Proceeding similar to Theorem 1, we have

$$\begin{array}{cc}\hfill \parallel p_{n+1}-a\parallel & \le \parallel p_{n+1}-G(p_n,L)\parallel + {\beta }^3(\beta -s_n(\beta -1))\times \hfill \\ & (1+\beta t_n{v}_n-t_n{v}_n+\beta t_n{u}_n+{\beta }^2{t}_n{u}_n{v}_n-2\beta t_n{u}_n{v}_n-t_n{u}_n+t_n{u}_n{v}_n)\parallel p_n-a\parallel .\hfill \end{array}$$

Let

$${\delta }_n = \parallel p_{n+1}-G(p_n,L)\parallel , {\eta }_n=t_n{u}_n(1-\beta ), {\zeta }_n = \parallel p_n-a\parallel ,$$

if ${\lim }_{n\to \infty }\parallel p_{n+1}-G(p_n,L)\parallel = 0$, and the sequences $\left\{t_n\right\}$ and $\left\{u_n\right\}$ are nonnegative and bounded away from zero, then by Lemma 1 it follows that ${\lim }_{n\to \infty }{\zeta }_n=0$. That is,

$$\underset{n\to \infty }{\lim }\parallel p_n-a\parallel = 0,$$

which implies ${\lim }_{n\to \infty }{p}_n=a$.

Conversely, if ${\lim }_{n\to \infty }{p}_n=a$, i.e.,

$$\underset{n\to \infty }{\lim }\parallel p_n-a\parallel = 0 \mathrm{and} \underset{n\to \infty }{\lim }\parallel p_{n+1}-a\parallel = 0,$$

then,

$$\begin{array}{cc}\hfill \parallel p_{n+1}-G(p_n,L)\parallel & \le \parallel p_{n+1}-a\parallel + \parallel G(p_n,L)-a\parallel \hfill \\ & \le \parallel p_{n+1}-a\parallel +{\beta }^3(\beta -s_n(\beta -1))\times \hfill \\ & (1+\beta t_n{v}_n-t_n{v}_n+\beta t_n{u}_n+{\beta }^2{t}_n{u}_n{v}_n-2\beta t_n{u}_n{v}_n-t_n{u}_n+t_n{u}_n{v}_n)\parallel p_n-a\parallel .\hfill \end{array}$$

Which implies ${\lim }_{n\to \infty }\parallel p_{n+1}-G(p_n,L)\parallel = 0$. That is iteration procedure $\left\{a_n\right\}$ defined in (7) is stable with respect to L or $L-stable$. □

We now state the following corollary, which follows directly from the convergence analysis. For every fixed point a of the contraction mapping L, the iteration sequence $\left\{a_n\right\}$ defined by (7) satisfies

$$\underset{n\to \infty }{\lim }\parallel a_n-a\parallel$$

and therefore the distance between the iterates and the fixed point is well defined in the limit.

Corollary 1.

Let V be a Banach space, and let $L:W\to W$ be a contraction mapping on a nonempty, closed, and convex subset $W\subseteq V$. Then, for the iteration sequence $\left\{a_n\right\}$ defined in (7), the limit ${\lim }_{n\to \infty }\parallel a_n-a\parallel$ exists for every fixed point a of L.

Proof. 

Since $L:W\to W$ is a contraction mapping, then $\parallel La-Lb\parallel \le \parallel a-b\parallel$, $\forall a,b\in W$. Suppose $a\in W$ is a fixed point of L.

From the iteration procedure defined in (7), we obtain

$$\begin{array}{cc}\hfill \parallel e_n-a\parallel & = \parallel (\left(1v_n\right)a_n+v_{n}L{a}_n)-a\parallel \hfill \\ & \le (1-v_n)\parallel a_n-a\parallel +v_n\parallel L{a}_n-a\parallel \hfill \\ & =(1-v_n)\parallel a_n-a\parallel +v_n\parallel L{a}_n-La\parallel \hfill \\ & \le (1-v_n)\parallel a_n-a\parallel +v_n\parallel a_n-a\parallel \hfill \\ & = \parallel a_n-a\parallel ,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill \parallel d_n-a\parallel & = \parallel ((1-u_n)e_n+u_{n}L{e}_n)-a\parallel \hfill \\ & \le (1-u_n)\parallel e_n-a\parallel +u_n\parallel L{e}_n-a\parallel \hfill \\ & =(1-u_n)\parallel e_n-a\parallel +u_n\parallel L{e}_n-La\parallel \hfill \\ & \le (1-u_n)\parallel e_n-a\parallel +u_n\parallel e_n-a\parallel \hfill \\ & = \parallel e_n-a\parallel ,\hfill \end{array}$$

$$\begin{array}{cc}\hfill \parallel c_n-a\parallel & = \parallel ((1-t_n)L{a}_n+t_{n}L{d}_n)-a\parallel \hfill \\ & \le (1-t_n)\parallel L{a}_n-a\parallel +t_n\parallel L{d}_n-a\parallel \hfill \\ & =(1-t_n)\parallel L{a}_n-La\parallel +t_n\parallel L{d}_n-La\parallel \hfill \\ & \le (1-t_n)\parallel a_n-a\parallel +t_n\parallel d_n-a\parallel \hfill \\ & \le (1-t_n)\parallel a_n-a\parallel +t_n\parallel e_n-a\parallel \hfill \end{array}$$

from Equation (9), we have

$$\begin{array}{cc}\hfill \parallel c_n-a\parallel & \le (1-t_n)\parallel a_n-a\parallel +t_n\parallel a_n-a\parallel \hfill \\ & = \parallel a_n-a\parallel ,\hfill \end{array}$$

$$\begin{array}{cc}\hfill \parallel b_n-a\parallel & = \parallel ((1-s_n)L{c}_n+s_n{c}_n)-a\parallel \hfill \\ & \le (1-s_n)\parallel L{c}_n-a\parallel +s_n\parallel c_n-a\parallel \hfill \\ & =(1-s_n)\parallel L{c}_n-La\parallel +s_n\parallel c_n-a\parallel \hfill \\ & \le (1-s_n)\parallel c_n-a\parallel +s_n\parallel c_n-a\parallel \hfill \\ & = \parallel c_n-a\parallel ,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \parallel a_{n+1}-a\parallel & = \parallel L^2{b}_n-a\parallel \hfill \\ & \le \parallel L{b}_n-a\parallel \hfill \\ & \le \parallel b_n-a\parallel \hfill \\ & \le \parallel c_n-a\parallel \hfill \\ & \le \parallel a_n-a\parallel .\hfill \end{array}$$

It follows that the sequence $\{\parallel a_n-a\parallel \}$ is monotone non-increasing and bounded below. Therefore, it converges. Since a is an arbitrary fixed point of L, the limit ${\lim }_{n\to \infty }\parallel a_n-a\parallel$ exists for all fixed points of L, i.e., $a_n\to a$ as $n\to \infty$. □

To demonstrate the efficiency of the iteration scheme defined in (7), we establish that its rate of convergence is superior to that of the Picard-S* iteration introduced by Lamba and Panwar [10], as well as the Picard-CR process proposed by Nawaz et al. [12]. The following result provides the theoretical justification.

Theorem 3.

Let $L:W\to W$ be a contraction mapping with contraction constant $\beta \in [0,1)$, where W is a nonempty, closed, and convex subset of a Banach space. If the sequences $\left\{s_n\right\}$, $\left\{t_n\right\}$, $\left\{u_n\right\}$, and $\left\{v_n\right\}$ are bounded away from zero and lie strictly within the interval $(0, 1)$, then the iteration methods defined in (5) and (6) converge to the unique fixed point a of L, but their convergence is slower compared to the iteration scheme described in (7).

Proof. 

Since the sequences $\left\{s_n\right\}$, $\left\{t_n\right\}$, $\left\{u_n\right\}$, and $\left\{v_n\right\}$ are bounded away inside $(0,1)$, then, there exist $s^{\prime },s^{″},t^{\prime },t^{″},u^{\prime },u^{″},v^{\prime },v^{″}\in (0,1)$ so that $0<s^{\prime }\le s_n\le s^{″}<1$, $0<t^{\prime }\le t_n\le t^{″}<1$, $0<u^{\prime }\le u_n\le u^{″}<1$ and $0<v^{\prime }\le v_n\le v^{″}<1$.

For our iteration procedure (7), using the proof of Theorem 1, we obtain

$$\begin{array}{cc}\hfill \parallel a_{n+1}-a\parallel & \le {\beta }^3(\beta -s_n(\beta -1))\times \hfill \\ & (1+\beta t_n{v}_n-t_n{v}_n+\beta t_n{u}_n+{\beta }^2{t}_n{u}_n{v}_n-2\beta t_n{u}_n{v}_n-t_n{u}_n+t_n{u}_n{v}_n)\parallel a_n-a\parallel \hfill \\ & \le {\beta }^3(\beta -s^{\prime }(\beta -1))\times \hfill \\ & (1+\beta t^{\prime }{v}^{\prime }-t^{\prime }{v}^{\prime }+\beta t^{\prime }{u}^{\prime }+{\beta }^2{t}^{\prime }{u}^{\prime }{v}^{\prime }-2\beta t^{\prime }{u}^{\prime }{v}^{\prime }-t^{\prime }{u}^{\prime }+t^{\prime }{u}^{\prime }{v}^{\prime })\parallel a_n-a\parallel \hfill \\ & \le {\beta }^{3n}[(\beta -s^{\prime }(\beta -1))\times \hfill \\ & (1+\beta t^{\prime }{v}^{\prime }-t^{\prime }{v}^{\prime }+\beta t^{\prime }{u}^{\prime }+{\beta }^2{t}^{\prime }{u}^{\prime }{v}^{\prime }-2\beta t^{\prime }{u}^{\prime }{v}^{\prime }-t^{\prime }{u}^{\prime }+t^{\prime }{u}^{\prime }{v}^{\prime }){]}^n\parallel a_1-a\parallel .\hfill \end{array}$$

Proceeding similarly, for the iteration procedure (5), we get

$$\begin{array}{cc}\hfill \parallel a_{n+1}-a\parallel & \le {\beta }^2(1-u_n+\beta s_n-\beta s_n{t}_n{u}_n(1-\beta ))\parallel a_n-a\parallel \hfill \\ & \le {\beta }^2(1-u^{\prime }+\beta s^{\prime }-\beta s^{\prime }{t}^{\prime }{u}^{\prime }(1-\beta ))\parallel a_n-a\parallel \hfill \\ & \le {\beta }^{2n}{[1-u^{\prime }+\beta s^{\prime }-\beta s^{\prime }{t}^{\prime }{u}^{\prime }(1-\beta )]}^n\parallel a_1-a\parallel .\hfill \end{array}$$

Thus, on setting ${\zeta }_n={\beta }^{3n}{\left[(\beta -s^{\prime }(\beta -1))(1+\beta t^{\prime }{v}^{\prime }-t^{\prime }{v}^{\prime }+\beta t^{\prime }{u}^{\prime }+{\beta }^2{t}^{\prime }{u}^{\prime }{v}^{\prime }-2\beta t^{\prime }{u}^{\prime }{v}^{\prime }-t^{\prime }{u}^{\prime }+t^{\prime }{u}^{\prime }{v}^{\prime })\right]}^n$ and ${\delta }_n={\beta }^{2n}{[1-u^{\prime }+\beta s^{\prime }-\beta s^{\prime }{t}^{\prime }{u}^{\prime }(1-\beta )]}^n$, we get ${\displaystyle \frac{{\zeta }_n}{{\delta }_n}}={\left(\beta {\displaystyle \frac{(\beta -s^{\prime }(\beta -1))(1+\beta t^{\prime }{v}^{\prime }-t^{\prime }{v}^{\prime }+\beta t^{\prime }{u}^{\prime }+{\beta }^2{t}^{\prime }{u}^{\prime }{v}^{\prime }-2\beta t^{\prime }{u}^{\prime }{v}^{\prime }-t^{\prime }{u}^{\prime }+t^{\prime }{u}^{\prime }{v}^{\prime })}{(1-u^{\prime }+\beta s^{\prime }-\beta s^{\prime }{t}^{\prime }{u}^{\prime }(1-\beta ))}}\right)}^n$, where $\beta {\displaystyle \frac{(\beta -s^{\prime }(\beta -1))(1+\beta t^{\prime }{v}^{\prime }-t^{\prime }{v}^{\prime }+\beta t^{\prime }{u}^{\prime }+{\beta }^2{t}^{\prime }{u}^{\prime }{v}^{\prime }-2\beta t^{\prime }{u}^{\prime }{v}^{\prime }-t^{\prime }{u}^{\prime }+t^{\prime }{u}^{\prime }{v}^{\prime })}{(1-u^{\prime }+\beta s^{\prime }-\beta s^{\prime }{t}^{\prime }{u}^{\prime }(1-\beta ))}}<1$. That is, ${\lim }_{n\to \infty }{\displaystyle \frac{{\zeta }_n}{{\delta }_n}}=0$, proves that our iteration procedure (7) converges faster than the iteration procedure (5).

Again, for the iteration procedure (6), we get

$$\begin{array}{cc}\hfill \parallel a_{n+1}-a\parallel & \le {\beta }^2(1-s_n(1-\beta ))(1-t_n{u}_n(1-\beta ))\parallel a_n-a\parallel \hfill \\ & \le {\beta }^2(1-s^{\prime }(1-\beta ))(1-t^{\prime }{u}^{\prime }(1-\beta ))\parallel a_n-a\parallel \hfill \\ & \le {\beta }^{2n}{\left[(1-s^{\prime }(1-\beta ))(1-t^{\prime }{u}^{\prime }(1-\beta ))\right]}^n\parallel a_1-a\parallel .\hfill \end{array}$$

Thus, on setting ${\zeta }_n={\beta }^{3n}{\left[(\beta -s^{\prime }(\beta -1))(1+\beta t^{\prime }{v}^{\prime }-t^{\prime }{v}^{\prime }+\beta t^{\prime }{u}^{\prime }+{\beta }^2{t}^{\prime }{u}^{\prime }{v}^{\prime }-2\beta t^{\prime }{u}^{\prime }{v}^{\prime }-t^{\prime }{u}^{\prime }+t^{\prime }{u}^{\prime }{v}^{\prime })\right]}^n$ and ${\delta }_n={\beta }^{2n}{\left[(1-s^{\prime }(1-\beta ))(1-t^{\prime }{u}^{\prime }(1-\beta ))\right]}^n$, we get ${\displaystyle \frac{{\zeta }_n}{{\delta }_n}}={\left(\beta {\displaystyle \frac{(\beta -s^{\prime }(\beta -1))(1+\beta t^{\prime }{v}^{\prime }-t^{\prime }{v}^{\prime }+\beta t^{\prime }{u}^{\prime }+{\beta }^2{t}^{\prime }{u}^{\prime }{v}^{\prime }-2\beta t^{\prime }{u}^{\prime }{v}^{\prime }-t^{\prime }{u}^{\prime }+t^{\prime }{u}^{\prime }{v}^{\prime })}{(1-s^{\prime }(1-\beta ))(1-t^{\prime }{u}^{\prime }(1-\beta ))}}\right)}^n$, where $\beta {\displaystyle \frac{(\beta -s^{\prime }(\beta -1))(1+\beta t^{\prime }{v}^{\prime }-t^{\prime }{v}^{\prime }+\beta t^{\prime }{u}^{\prime }+{\beta }^2{t}^{\prime }{u}^{\prime }{v}^{\prime }-2\beta t^{\prime }{u}^{\prime }{v}^{\prime }-t^{\prime }{u}^{\prime }+t^{\prime }{u}^{\prime }{v}^{\prime })}{(1-s^{\prime }(1-\beta ))(1-t^{\prime }{u}^{\prime }(1-\beta ))}}<1$. That is, ${\lim }_{n\to \infty }{\displaystyle \frac{{\zeta }_n}{{\delta }_n}}=0$, proves that our iteration procedure (7) converges faster than the iteration procedure (6). □

Corollary 2.

Consider a Banach space in which $L:W\to W$ is a contraction mapping with contraction constant $\beta \in [0,1)$, defined on a nonempty, closed, and convex subset W. If the sequences $\left\{s_n\right\}$, $\left\{t_n\right\}$, $\left\{u_n\right\}$, and $\left\{v_n\right\}$ remain within the interval $(0,1)$ and are bounded away from zero, then the iteration methods described in (5) and (6) converge to the unique fixed point a of L, but their convergence rate is slower compared to the iteration process defined in (7).

Remark 2.

In the subsequent numerical experiments, the following procedure was adopted to approximate the values generated by the iteration sequence $\left\{a_n\right\}$ defined in (7):

• An initial approximation $a_1\in W$ is selected to start the iteration.
• Due to machine precision limitations and unavoidable round-off errors, the value $a_2=G(a_1,L)$ is not computed exactly; instead, we obtain an approximation $b_2$ such that $b_2\approx a_2$.
• Similarly, in evaluating $a_3=G(a_2,L)$, the numerical result is denoted by $b_3=G(a_2,L)$, which approximates $a_3$ and may differ slightly from the exact iterate because of computational inaccuracies.

In conclusion, the numerically generated sequence $\left\{b_n\right\}$ provides an approximation to the exact sequence $\left\{a_n\right\}$. The fixed-point iteration is said to be numerically stable if each approximation $b_n$ remains sufficiently close to its corresponding exact value $a_n$, and the sequence $\left\{b_n\right\}$ continues to converge to the same fixed point a of the operator L.

We now investigate the data dependence of operator approximations. An operator $L^{\prime }:W\to W$ is called an approximation of another operator $L:W\to W$ if there exists a constant $\rho >0$ such that

$$\parallel La-L^{\prime }a\parallel \le \rho , \forall a\in W.$$

Theorem 4.

Let $L,L^{\prime }:W\to W$ be contraction mappings with a common contraction constant $\beta \in [0,1)$, where W is a nonempty, closed, and convex subset of a Banach space V, and suppose that $L^{\prime }$ serves as an approximation to L. Assume that the sequence $\left\{a_n\right\}$ is generated by the iteration scheme (7) for the operator L. Correspondingly, let $\left\{a_n^{\prime }\right\}$ denote the sequence produced by applying the same iteration scheme to the operator $L^{\prime }$, defined as

$$\left\{\begin{array}{c}{a}_1^{\prime }\in W,\hfill \\ a_{n+1}^{\prime }=L^{\prime 2}{b}_n^{\prime },\hfill \\ b_n^{\prime }=(1-s_n)L^{\prime }{c}_n^{\prime }+s_n{c}_n^{\prime },\hfill \\ c_n^{\prime }=(1-t_n)L^{\prime }{a}_n^{\prime }+t_n{L}^{\prime }{d}_n^{\prime },\hfill \\ d_n^{\prime }=(1-u_n)a_n^{\prime }+u_n{L}^{\prime }{a}_n^{\prime },n\in \mathbb{N},\hfill \end{array}\right.$$

(10)

for sequences $\left\{s_n\right\},\left\{t_n\right\},\left\{u_n\right\},\left\{v_n\right\}\subseteq (0,1)$. If either of ${\sum }_{n=1}^{\infty }(1-s_n)=\infty$ and ${\sum }_{n=1}^{\infty }(1-t_n)=\infty$ and if $La=a$ and $L^{\prime }{a}^{\prime }=a^{\prime }$ such that ${\lim }_{n\to \infty }{a}_n^{\prime }=a^{\prime }$ and ${\lim }_{n\to \infty }{s}_n=s$, then $\parallel a-a^{\prime }\parallel \le {\displaystyle \frac{5\rho \left(1+\frac{s}{5}\right)}{(1-s)}}$.

Proof. 

From (7) and (10), we have

$$\begin{array}{cc}\hfill \parallel e_n^{\prime }-e_n\parallel & = \parallel ((1-v_n)a_n^{\prime }+v_n{L}^{\prime }{a}_n^{\prime })-((1-v_n)a_n+v_{n}L{a}_n)\parallel \hfill \\ & = \parallel (1-v_n)a_n^{\prime }+L^{\prime }{v}_n{a}_n^{\prime }-(1-v_n)a_n-L{v}_n{a}_n\parallel \hfill \\ & \le \parallel L{v}_n{a}_n-L^{\prime }{v}_n{a}_n^{\prime }\parallel + \parallel (1-v_n)a_n^{\prime }-(1-v_n)a_n\parallel \hfill \\ & \le \rho +(1-v_n)\parallel a_n^{\prime }-a_n\parallel ,\hfill \end{array}$$

$$\begin{array}{cc}\hfill \parallel d_n^{\prime }-d_n\parallel & = \parallel ((1-u_n)e_n^{\prime }+u_n{L}^{\prime }{e}_n^{\prime })-((1-u_n)e_n+u_{n}L{e}_n)\parallel \hfill \\ & = \parallel (1-u_n)e_n^{\prime }+L^{\prime }{u}_n{e}_n^{\prime }-(1-u_n)e_n-L{u}_n{e}_n\parallel \hfill \\ & \le \parallel L{u}_n{e}_n-L^{\prime }{u}_n{e}_n^{\prime }\parallel + \parallel (1-u_n)e_n^{\prime }-(1-u_n)e_n\parallel \hfill \\ & \le \rho +(1-u_n)\parallel e_n^{\prime }-e_n\parallel ,\hfill \end{array}$$

$$\begin{array}{cc}\hfill \parallel c_n^{\prime }-c_n\parallel & = \parallel ((1-t_n)L^{\prime }{a}_n^{\prime }+t_n{L}^{\prime }{d}_n^{\prime })-((1-t_n)L{a}_n+t_{n}L{d}_n)\parallel \hfill \\ & = \parallel (1-t_n)L^{\prime }{a}_n^{\prime }+L^{\prime }{t}_n{d}_n^{\prime }-(1-t_n)L{a}_n-L{t}_n{d}_n\parallel \hfill \\ & \le \parallel L{t}_n{d}_n-L^{\prime }{t}_n{d}_n^{\prime }\parallel +(1-t_n)\parallel L^{\prime }{a}_n^{\prime }-L{a}_n\parallel \hfill \\ & \le \rho +(1-t_n)\rho +(1-t_n)\beta \parallel a_n^{\prime }-a_n\parallel ,\hfill \end{array}$$

$$\begin{array}{cc}\hfill \parallel b_n^{\prime }-b_n\parallel & = \parallel ((1-s_n)L^{\prime }{c}_n^{\prime }+s_n{c}_n^{\prime })-((1-s_n)L{c}_n+s_n{c}_n)\parallel \hfill \\ & = \parallel (1-s_n)L^{\prime }{c}_n^{\prime }+s_n{c}_n^{\prime }-(1-s_n)L{c}_n-s_n{c}_n\parallel \hfill \\ & \le \parallel L{s}_n{c}_n-L^{\prime }{s}_n{c}_n^{\prime }\parallel +(1-s_n)\parallel L^{\prime }{c}_n^{\prime }-L{c}_n\parallel \hfill \\ & \le \rho +(1-s_n)\rho +(1-s_n)\beta \parallel c_n^{\prime }-c_n\parallel ,\hfill \end{array}$$

and so,

$$\begin{array}{cc}\hfill \parallel a_{n+1}^{\prime }-a_{n+1}\parallel & = \parallel L^{\prime 2}{b}_n^{\prime }-L^2{b}_n\parallel \hfill \\ & \le \parallel L^{\prime }\left(L^{\prime }{b}_n^{\prime }\right)-L\left(L^{\prime }{b}_n^{\prime }\right)\parallel + \parallel L\left(L^{\prime }{b}_n^{\prime }\right)-L\left(L{b}_n\right)\parallel \hfill \\ & \le \rho +\beta \parallel L^{\prime }{b}_n^{\prime }-L{b}_n\parallel \hfill \\ & =\rho +\beta \rho +{\beta }^2\parallel b_n^{\prime }-b_n\parallel \hfill \\ & \le \rho +\beta \rho +{\beta }^2(\rho +(1-s_n)\rho +(1-s_n)\beta \parallel c_n^{\prime }-c_n\parallel )\hfill \\ & =\rho +\beta \rho +{\beta }^2\rho +{\beta }^2\rho (1-s_n)+{\beta }^3(1-s_n)\parallel c_n^{\prime }-c_n\parallel \hfill \\ & \le \rho +\beta \rho +{\beta }^2\rho +{\beta }^2\rho (1-s_n)+{\beta }^3(1-s_n)(\rho +(1-t_n)\rho \hfill \\ & +(1-t_n)\beta \parallel a_n^{\prime }-a_n\parallel )\hfill \\ & =\rho +\beta \rho +{\beta }^2\rho +{\beta }^2\rho (1-s_n)+{\beta }^3\rho (1-s_n)+{\beta }^3\rho (1-s_n)(1-t_n)\hfill \\ & +{\beta }^4(1-s_n)(1-t_n)\parallel a_n^{\prime }-a_n\parallel .\hfill \end{array}$$

Since $\left\{s_n\right\},\left\{t_n\right\},\left\{u_n\right\},\left\{v_n\right\}\subseteq (0,1)$, $0\le \beta <1$ and suppose ${\sum }_{n=1}^{\infty }(1-s_n)=\infty$, on setting ${\zeta }_n=\parallel a_n^{\prime }-a_n\parallel$, ${\eta }_n=(1-s_n)$ and ${\delta }_n={\displaystyle \frac{5\rho \left(1+\frac{s_n}{5}\right)}{(1-s_n)}}$, we have

$$\begin{array}{cc}\hfill {\zeta }_{n+1}& \le 5\rho +\rho s_n+(1-s_n)\parallel a_n^{\prime }-a_n\parallel \hfill \\ & =5\rho \left(1+{\displaystyle \frac{s_n}{5}}\right)+(1-s_n)\parallel a_n^{\prime }-a_n\parallel \hfill \\ & \le 5\rho \left(1+{\displaystyle \frac{s_n}{5}}\right)+(1-s_n)\parallel a_n^{\prime }-a_n\parallel \hfill \\ & \le (1-s_n){\displaystyle \frac{5\rho \left(1+\frac{s_n}{5}\right)}{(1-s_n)}}+(1-(1-s_n))\parallel a_n^{\prime }-a_n\parallel \hfill \\ & ={\eta }_n{\delta }_n+(1-{\eta }_n){\zeta }_n.\hfill \end{array}$$

Hence, Lemma 2 implies

$$0\le {\mathrm{lim\; sup}}_{n\to \infty }{\zeta }_n\le {\mathrm{lim\; sup}}_{n\to \infty }{\delta }_n,$$

i.e.,

$$0\le \underset{n\to \infty }{\mathrm{lim\; sup}}\parallel a_n^{\prime }-a_n\parallel \le \underset{n\to \infty }{\mathrm{lim\; sup}}{\displaystyle \frac{5\rho \left(1+\frac{s_n}{5}\right)}{(1-s_n)}}.$$

(11)

As stated in Corollary 1, ${\lim }_{n\to \infty }\left\{a_n\right\}=a$. It is also given in the theorem that ${\lim }_{n\to \infty }\left\{a_n^{\prime }\right\}=a^{\prime }$. Using these results together with Equation (11), we obtain

$$\parallel a-a^{\prime }\parallel \le {\displaystyle \frac{5\rho \left(1+\frac{s}{5}\right)}{(1-s)}}.$$

□

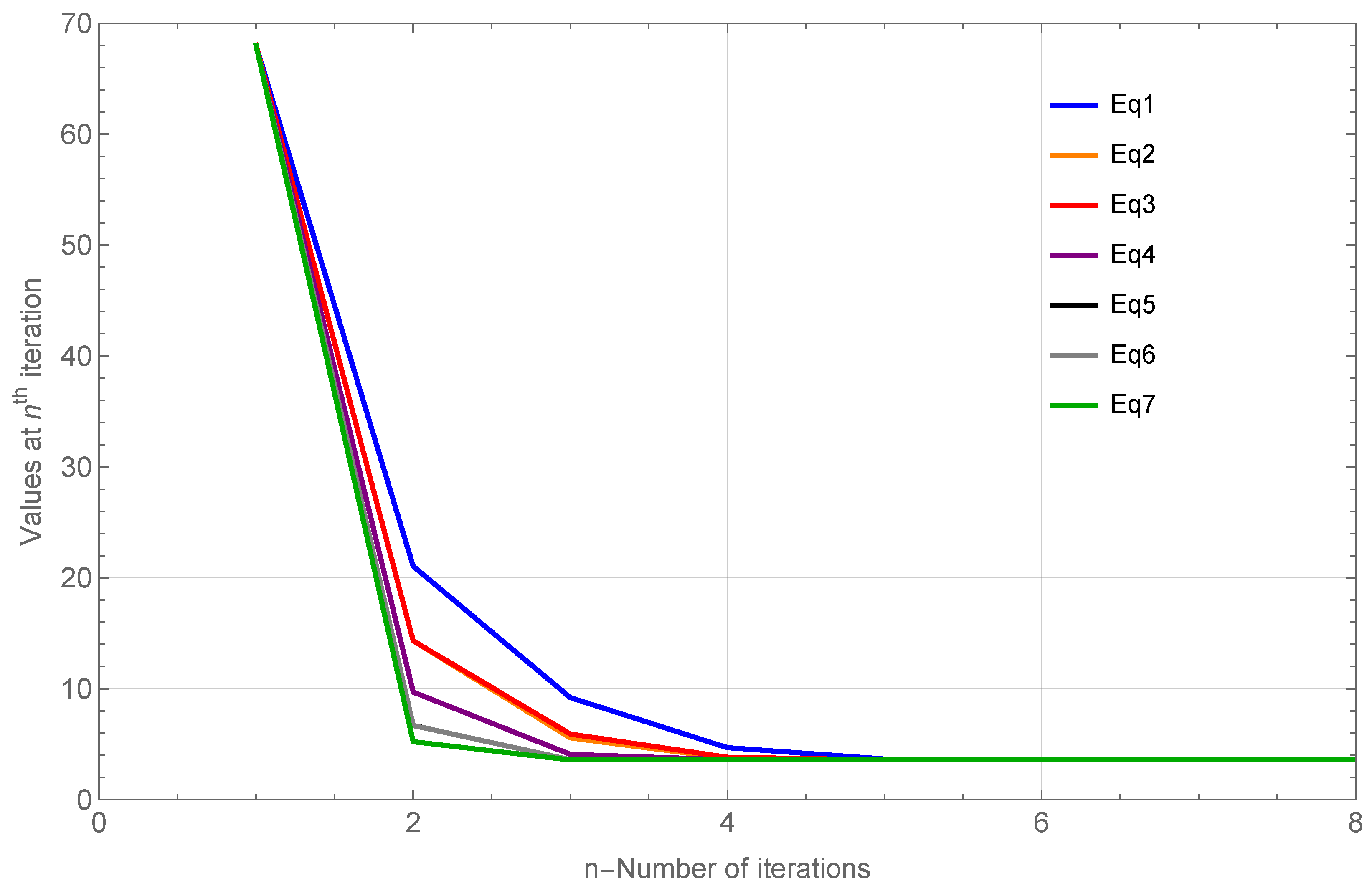
Example 1.

Let $L:W\to W$ be a contraction operator, defined as $La={\displaystyle \frac{1}{2}}\sqrt{a^2-6a+60},\forall a\in W,$ where $W=(-\infty ,\infty )$. Consider the sequences $\{s_n=\frac{1}{n^2}\},\{t_n=\frac{n}{n^3+1}\},\{u_n=\frac{n+1}{{(n+2)}^2}\},\{v_n=\frac{1}{n}\}\subseteq (0,1).$ Starting with the initial approximation $a_1=68$, the convergence of different iteration schemes are investigated. The numerical results, presented in Table 1, demonstrate the performance of the P-Iteration (Equation (1)), D-Iteration (Equation (2)), CR-Iteration (Equation (3)), Picard-SP-Iteration (Equation (4)), Picard-S*-Iteration (Equation (5)), Picard-CR-Iteration (Equation (6)), and our proposed Iteration Procedure (Equation (7)). Each of these schemes converges to the unique fixed point 3.5826 of L, under the stopping criterion $\parallel a_n-a\parallel <{10}^{-4}.$

Table 1. Comparisons Results for Example 1.

Steps	P	D	CR	Picard-SP	Picard-S*	Picard-CR	Our Iteration
1	68	68	68	68	68	68	68
2	$21.0440$	$14.3260$	$14.3260$	$9.7028$	$6.6947$	$6.6947$	$5.2290$
3	$9.2029$	$5.5737$	$5.9198$	$4.0881$	$3.6000$	$3.5989$	$3.5826$
4	$4.6903$	$3.7322$	$3.8229$	$3.6007$	$3.5826$	$3.5826$	$3.5826$
5	$3.6680$	$3.5881$	$3.5935$	$3.5831$	$3.5826$	$3.5826$	$3.5826$
6	$3.5863$	$3.5828$	$3.5830$	$3.5826$	$3.5826$	$3.5826$	$3.5826$
7	$3.5827$	$3.5826$	$3.5826$	$3.5826$	$3.5826$	$3.5826$	$3.5826$
8	$3.5826$	$3.5826$	$3.5826$	$3.5826$	$3.5826$	$3.5826$	$3.5826$

Also, Figure 1 confirms that, for Example 1, the newly proposed iteration method defined in Equation (7) converges more rapidly to the fixed point 3.5826 compared to the existing iteration methods given in Equations (1)–(6).

Figure 1. Convergence of Iterations for Example 1.

Example 2.

Starting with the initial approximation $a_1=12$, we consider the contraction operator $L:W\to W$ defined by $La=\frac{17}{21}a+\frac{12}{7}, \forall a\in W=(-\infty ,\infty )$, together with the sequences $\{s_n=\frac{n^2}{n^2+1}\}$, $\{t_n=\frac{1}{n^2+8}\}$, $\{u_n={\left(\frac{n+1}{n+2}\right)}^2\}$, $\{v_n=\frac{1}{n^2}\}$$\subseteq (0,1)$, and present in Table 2 the numerical results of the P-Iteration (Equation (1)), D-Iteration (Equation (2)), CR-Iteration (Equation (3)), Picard-SP-Iteration (Equation (4)), Picard-S*-Iteration (Equation (5)), Picard-CR-Iteration (Equation (6)), and our proposed Iteration Method (Equation (7)), all of which converge to the unique fixed point 9 of L under the stopping criterion $\parallel a_n-a \parallel <{10}^{-4}$.

Table 2. Comparisons Results for Example 2.

Steps	P	D	CR	Picard-SP	Picard-S*	Picard-CR	Our Iteration
1	12	12	12	12	12	12	12
2	$11.3020$	$11.0850$	$11.1770$	$10.9690$	$10.7710$	$10.7620$	$10.3990$
3	$10.6830$	$10.3850$	$10.4800$	$10.1870$	$9.9772$	$9.9700$	$9.7047$
4	$10.2010$	$9.9094$	$9.9857$	$9.6913$	$9.5272$	$9.5229$	$9.3637$
5	$9.8447$	$9.5954$	$9.6513$	$9.3954$	$9.2821$	$9.2797$	$9.1897$
6	$9.5886$	$9.3895$	$9.4288$	$9.2236$	$9.1504$	$9.1491$	$9.0994$
7	$9.4071$	$9.2548$	$9.2819$	$9.1254$	$9.0800$	$9.0793$	$9.0523$
8	$9.2801$	$9.1667$	$9.1851$	$9.0699$	$9.0426$	$9.0422$	$9.0276$
9	$9.1918$	$9.1091$	$9.1215$	$9.0388$	$9.0226$	$9.0224$	$9.0145$
10	$9.1308$	$9.0714$	$9.0797$	$9.0214$	$9.0120$	$9.0119$	$9.0077$
11	$9.0890$	$9.0467$	$9.0523$	$9.0118$	$9.0064$	$9.0063$	$9.0041$
12	$9.0603$	$9.0306$	$9.0343$	$9.0065$	$9.0034$	$9.0034$	$9.0021$
13	$9.0408$	$9.0200$	$9.0225$	$9.0036$	$9.0018$	$9.0018$	$9.0011$
14	$9.0276$	$9.0131$	$9.0147$	$9.0019$	$9.0010$	$9.0009$	$9.0006$
15	$9.0186$	$9.0086$	$9.0097$	$9.0011$	$9.0005$	$9.0005$	$9.0003$
16	$9.0125$	$9.0056$	$9.0063$	$9.0006$	$9.0003$	$9.0003$	$9.0002$
17	$9.0084$	$9.0037$	$9.0042$	$9.0003$	$9.0001$	$9.0001$	$9.0001$
18	$9.0056$	$9.0024$	$9.0027$	$9.0002$	$9.0001$	$9.0001$	9
19	$9.0038$	$9.0016$	$9.0018$	$9.0001$	9	9	9
20	$9.0025$	$9.0010$	$9.0012$	$9.0001$	9	9	9
21	$9.0017$	$9.0007$	$9.0008$	9	9	9	9
22	$9.0011$	$9.0004$	$9.0005$	9	9	9	9
23	$9.0008$	$9.0003$	$9.0003$	9	9	9	9
24	$9.0005$	$9.0002$	$9.0002$	9	9	9	9
25	$9.0003$	$9.0001$	$9.0001$	9	9	9	9
26	$9.0002$	$9.0001$	$9.0001$	9	9	9	9
27	$9.0001$	$9.0001$	$9.0001$	9	9	9	9
28	$9.0001$	9	9	9	9	9	9
29	$9.0001$	9	9	9	9	9	9
30	9	9	9	9	9	9	9

Also, Figure 2 confirms that, for Example 2, the newly proposed iteration method defined in Equation (7) converges more rapidly to the fixed point 9 compared to the existing iteration methods given in Equations (1)–(6).

Figure 2. Convergence of Iterations for Example 2.

From Table 3, it becomes apparent that the speed of convergence in our Iteration Procedure (7) depends strongly on how the parameters $s_n$, $t_n$, $u_n$, and $v_n$ are selected. Unlike other iteration methods, this scheme shows considerable variability with parameter choice, which emphasizes the necessity of parameter optimization for improved performance. Hence, any valid parameter setting can be used to validate the observations presented in Example 2.

Table 3. Effect of Parameters and Initial Conditions on Iteration Methods for Example 2.

Initial Points	0	61	174	432	1092	3451	6265
$s_n={\displaystyle \frac{1}{n}}$, $t_n={\displaystyle \frac{n}{n+1}}$, $u_n={\displaystyle \frac{2}{n^2+5}}$, $v_n={\displaystyle \frac{1}{n+2}}$
P	54	62	68	72	76	82	85
D	53	61	66	71	75	80	83
CR	53	61	66	71	75	81	83
Picard-SP	28	33	35	38	40	42	44
Picard-S*	27	31	34	36	38	41	42
Picard-CR	27	31	34	36	38	41	42
Our Iteration	$\mathbf{15}$	$\mathbf{17}$	$\mathbf{19}$	$\mathbf{20}$	$\mathbf{21}$	$\mathbf{22}$	$\mathbf{23}$
$s_n={\displaystyle \frac{n^2}{n^3+2}}$, $t_n={\displaystyle \frac{1}{n^2+4}}$, $u_n={\displaystyle \frac{5}{7}}$, $v_n={\displaystyle \frac{1}{n^3}}$
P	55	63	69	73	78	83	86
D	34	39	42	44	47	50	52
CR	54	62	67	72	76	82	84
Picard-SP	32	37	40	43	45	49	50
Picard-S*	28	32	34	37	39	42	43
Picard-CR	28	32	34	36	39	41	43
Our Iteration	$\mathbf{15}$	$\mathbf{17}$	$\mathbf{19}$	$\mathbf{20}$	$\mathbf{21}$	$\mathbf{22}$	$\mathbf{23}$
$s_n={\displaystyle \frac{51}{104}}$, $t_n={\displaystyle \frac{5}{17}}$, $u_n={\displaystyle \frac{7}{9}}$, $v_n={\displaystyle \frac{19}{21}}$
P	39	45	49	52	55	58	60
D	29	34	36	39	41	44	45
CR	35	40	43	46	48	51	53
Picard-SP	23	27	29	31	33	35	36
Picard-S*	23	26	28	30	32	34	35
Picard-CR	22	25	27	29	30	32	33
Our Iteration	$\mathbf{15}$	$\mathbf{17}$	$\mathbf{19}$	$\mathbf{20}$	$\mathbf{21}$	$\mathbf{22}$	$\mathbf{23}$
$s_n={\left({\displaystyle \frac{n}{n+1}}\right)}^2$, $t_n={\displaystyle \frac{n}{n^5+2}}$, $u_n={\displaystyle \frac{1}{n^3+1}}$, $v_n={\displaystyle \frac{1}{n}}$
P	57	66	71	76	80	86	88
D	32	36	39	41	44	46	48
CR	32	36	39	41	44	46	48
Picard-SP	32	36	39	41	43	46	48
Picard-S*	21	24	26	28	29	31	32
Picard-CR	21	24	26	27	29	31	32
Our Iteration	$\mathbf{18}$	$\mathbf{21}$	$\mathbf{23}$	$\mathbf{24}$	$\mathbf{25}$	$\mathbf{27}$	$\mathbf{28}$

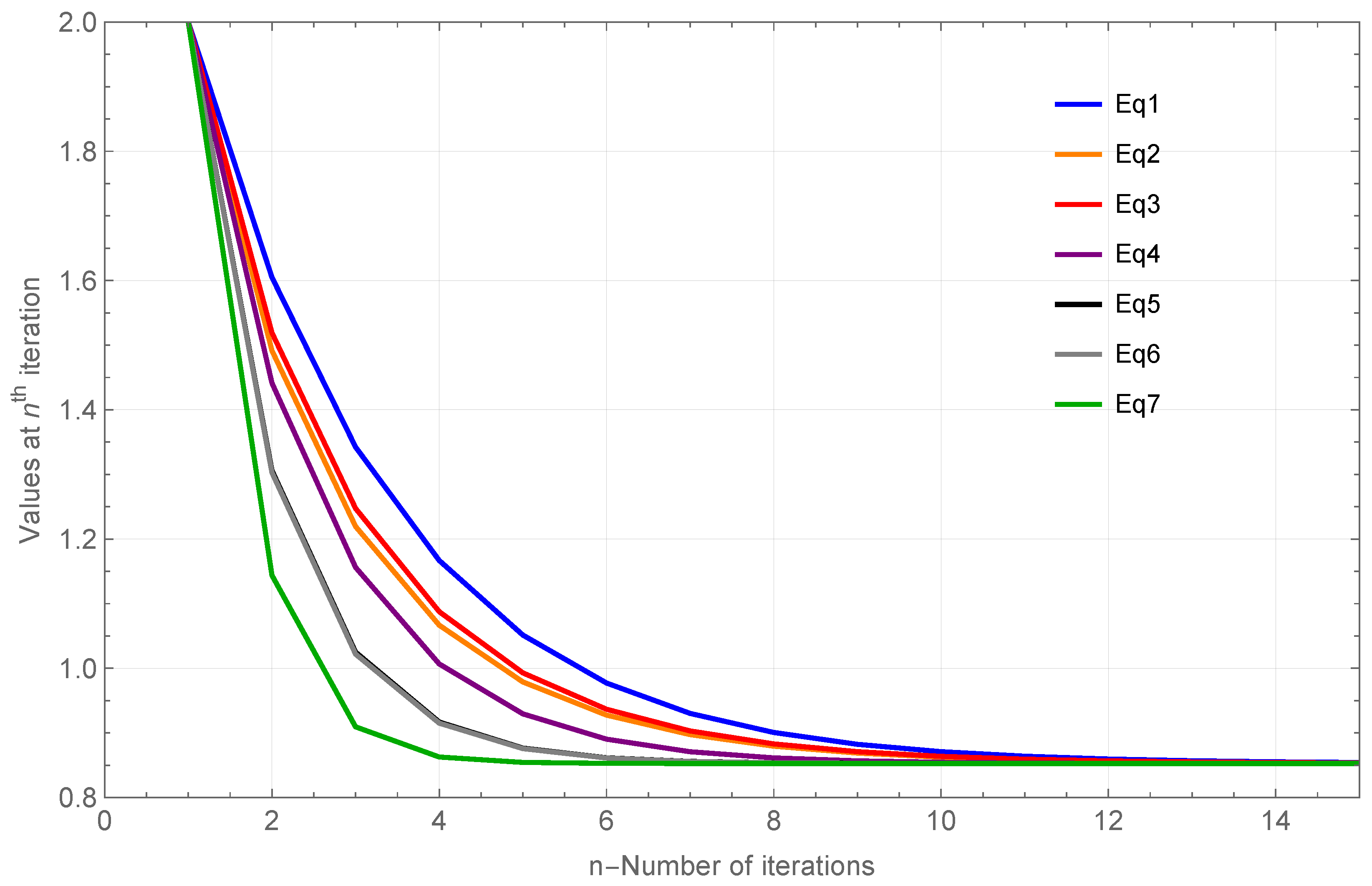
Example 3.

Let $L:W\to W$ be a contraction mapping, described as $La={\displaystyle \frac{2}{5}}{e}^{-a}+{\displaystyle \frac{4}{5}}a$, $\forall a\in W$, where $W=[0,\infty )$. Then for sequences $\{s_n={\displaystyle \frac{1}{n+1}}\}$, $\{t_n={\displaystyle \frac{n}{n+6}}\}$, $\{u_n={\displaystyle \frac{1}{n^2+3}}\}$, $\{v_n={\displaystyle \frac{n+2}{n^3+5}}\}$$\subseteq (0,1)$ and initial guess $a_1=2$, Table 4 below represent the P-Iteration (Equation (1)); D-Iteration (Equation (2)); CR-Iteration (Equation (3)); Picard-SP-Iteration (Equation (4)); Picard-S*-Iteration (Equation (5)); Picard-CR-Iteration (Equation (6)) and our Iteration Procedure (Equation (7)) converging to a unique fixed point $0.85261$ of L with the stop criterion $\parallel a_n-a\parallel <{10}^{-4}$.

Table 4. Comparisons Results for Example 3.

Steps	P	D	CR	Picard-SP	Picard-S*	Picard-CR	Our Iteration
1	2	2	2	2	2	2	2
2	$1.60490$	$1.49150$	$1.51910$	$1.44140$	$1.30610$	$1.30280$	$1.14380$
3	$1.34230$	$1.21940$	$1.24730$	$1.15610$	$1.02490$	$1.02190$	$0.90940$
4	$1.16680$	$1.06670$	$1.08760$	$1.00670$	$0.91679$	$0.91510$	$0.86270$
5	$1.05140$	$0.97884$	$0.99291$	$0.92946$	$0.87647$	$0.87567$	$0.85435$
6	$0.97718$	$0.92754$	$0.93659$	$0.89032$	$0.86152$	$0.86117$	$0.85290$
7	$0.93013$	$0.89734$	$0.90302$	$0.87086$	$0.85596$	$0.85581$	$0.85266$
8	$0.90065$	$0.87945$	$0.88297$	$0.86134$	$0.85387$	$0.85381$	$0.85261$
9	$0.88232$	$0.86878$	$0.87095$	$0.85675$	$0.85309$	$0.85306$	$0.85261$
10	$0.87096$	$0.86239$	$0.86373$	$0.85455$	$0.85279$	$0.85278$	$0.85261$
11	$0.86394$	$0.85854$	$0.85936$	$0.85351$	$0.85268$	$0.85267$	$0.85261$
12	$0.85961$	$0.85622$	$0.85672$	$0.85302$	$0.85263$	$0.85263$	$0.85261$
13	$0.85693$	$0.85481$	$0.85512$	$0.85280$	$0.85262$	$0.85262$	$0.85261$
14	$0.85528$	$0.85396$	$0.85415$	$0.85269$	$0.85261$	$0.85261$	$0.85261$
15	$0.85426$	$0.85343$	$0.85355$	$0.85265$	$0.85261$	$0.85261$	$0.85261$
16	$0.85363$	$0.85311$	$0.85319$	$0.85262$	$0.85261$	$0.85261$	$0.85261$
17	$0.85324$	$0.85292$	$0.85296$	$0.85261$	$0.85261$	$0.85261$	$0.85261$
18	$0.85300$	$0.85280$	$0.85283$	$0.85261$	$0.85261$	$0.85261$	$0.85261$
19	$0.85285$	$0.85272$	$0.85274$	$0.85261$	$0.85261$	$0.85261$	$0.85261$
20	$0.85276$	$0.85268$	$0.85269$	$0.85261$	$0.85261$	$0.85261$	$0.85261$
21	$0.85270$	$0.85265$	$0.85266$	$0.85261$	$0.85261$	$0.85261$	$0.85261$
22	$0.85266$	$0.85263$	$0.85264$	$0.85261$	$0.85261$	$0.85261$	$0.85261$
23	$0.85264$	$0.85262$	$0.85263$	$0.85261$	$0.85261$	$0.85261$	$0.85261$
24	$0.85263$	$0.85262$	$0.85262$	$0.85261$	$0.85261$	$0.85261$	$0.85261$
25	$0.85262$	$0.85261$	$0.85261$	$0.85261$	$0.85261$	$0.85261$	$0.85261$
26	$0.85261$	$0.85261$	$0.85261$	$0.85261$	$0.85261$	$0.85261$	$0.85261$

Also, Figure 3 confirms that, for Example 3, the newly proposed iteration method defined in Equation (7) converges more rapidly to the fixed point 0.85261 compared to the existing iteration methods given in Equations (1)–(6).

Figure 3. Convergence of Iterations for Example 3.

According to Table 5, the convergence behavior of our Iteration Procedure (7) is strongly affected by how the parameters $s_n$, $t_n$, $u_n$, and $v_n$ are chosen, with a greater dependency observed than in alternative iteration methods. This emphasizes that careful parameter selection plays a decisive role in enhancing the efficiency of the process. Thus, any valid configuration of these parameters may serve to support the conclusions presented in Example 3.

Table 5. Effect of Parameters and Initial Conditions on Iteration Methods for Example 3.

Initial Points	8	94	212	538	1169	3843	7271
$s_n={\displaystyle \frac{n^2}{n^3+4}}$, $t_n={\displaystyle \frac{1}{n^2+9}}$, $u_n={\displaystyle \frac{1}{n^2}}$, $v_n={\displaystyle \frac{n}{n+1}}$
P	33	44	47	51	55	60	63
D	29	40	43	47	51	56	59
CR	30	41	45	49	52	57	60
Picard-SP	29	39	43	47	50	55	58
Picard-S*	16	21	23	25	27	29	31
Picard-CR	16	21	23	25	27	29	31
Our Iteration	$\mathbf{9}$	$\mathbf{12}$	$\mathbf{13}$	$\mathbf{14}$	$\mathbf{15}$	$\mathbf{16}$	$\mathbf{17}$
$s_n={\left({\displaystyle \frac{n}{n^2+2}}\right)}^3$, $t_n={\displaystyle \frac{1}{n}}$, $u_n={\displaystyle \frac{1}{n^3+2}}$, $v_n={\displaystyle \frac{n+3}{n^2+7}}$
P	33	44	48	52	55	61	63
D	32	43	47	51	55	60	63
CR	32	43	47	51	55	60	63
Picard-SP	29	40	43	47	51	56	59
Picard-S*	17	22	24	26	28	30	32
Picard-CR	16	22	24	26	28	30	32
Our Iteration	$\mathbf{8}$	$\mathbf{11}$	$\mathbf{12}$	$\mathbf{13}$	$\mathbf{14}$	$\mathbf{15}$	$\mathbf{16}$
$s_n={\displaystyle \frac{n}{n^5+2}}$, $t_n={\displaystyle \frac{1}{n^3}}$, $u_n={\displaystyle \frac{1}{4}}$, $v_n={\displaystyle \frac{1}{n^2+3}}$
P	33	44	47	51	55	60	63
D	27	36	39	42	45	49	52
CR	32	43	47	51	55	60	63
Picard-SP	26	35	38	41	44	48	51
Picard-S*	16	22	24	26	28	30	32
Picard-CR	16	22	24	26	28	30	32
Our Iteration	$\mathbf{9}$	$\mathbf{11}$	$\mathbf{12}$	$\mathbf{13}$	$\mathbf{14}$	$\mathbf{16}$	$\mathbf{16}$
$s_n={\displaystyle \frac{17}{21}}$, $t_n={\displaystyle \frac{5}{9}}$, $u_n={\displaystyle \frac{19}{27}}$, $v_n={\displaystyle \frac{51}{57}}$
P	18	23	25	27	29	32	33
D	15	20	22	24	25	28	29
CR	16	21	23	25	26	29	30
Picard-SP	12	15	16	18	19	21	22
Picard-S*	11	15	16	17	18	20	21
Picard-CR	11	14	16	17	18	20	21
Our Iteration	$\mathbf{9}$	$\mathbf{12}$	$\mathbf{13}$	$\mathbf{14}$	$\mathbf{14}$	$\mathbf{16}$	$\mathbf{16}$

4. Application

Fractional Volterra–Fredholm integro-differential equations play a significant role in modeling complex processes in applied sciences and engineering. They are widely used in areas such as population dynamics, viscoelasticity, electrochemistry, financial mathematics, and signal analysis. These equations are particularly effective in describing systems that exhibit long-memory characteristics, hereditary effects, and non-local behaviours, thereby providing more realistic models than traditional differential equations. In population studies, they capture the influence of past states on current growth, while in financial markets, they explain persistent correlations and deviations from Markovian dynamics. The general structure of a fractional Volterra–Fredholm integro-differential equation is represented as:

$$\begin{array}{c}\hfill {}^{c}D_t^{o}a\left(t\right)=g(t,a\left(t\right))+{\int }_b^{t}F(t,l)a\left(l\right) dl.\end{array}$$

In this formulation, ${}^{c}D_t^o$ refers to the Caputo fractional derivative of order o with respect to t. The function $a\left(t\right)$ denotes the unknown solution, while $g(t,a(t\left)\right)$ is a prescribed function. The kernel of the integral is expressed as $F(t,l)$, and the integration extends from the lower bound b up to the present time t.

A variety of approaches are available for solving fractional Volterra–Fredholm integro-differential equations, ranging from analytical to computational techniques. Analytical methods, such as those based on fractional calculus, Laplace transforms, and fixed-point theory, provide exact results when the underlying conditions are favorable. Numerical schemes, including finite difference and finite element methods, approximate solutions by discretizing the problem. In addition, specialized methods like the Fractional Differential Transform Method (FDTM) and computational platforms such as the Fractional Differential Equation Toolbox offer efficient ways to handle fractional operators. Transform-based techniques, such as the fractional Fourier transform and the Mellin transform, are also useful in reducing the complexity of the equations. The selection of an appropriate method is influenced by factors such as the derivative order, kernel characteristics, and accuracy requirements, and often involves combining analytical and numerical procedures for reliable results.

In the Banach space $C\left(\right[0,I],\mathbb{R})$, endowed with the maximum norm $\parallel a_1-a_2{\parallel }_{\infty }={\max }_{t\in [0,1]}|a_1\left(t\right)-a_2\left(t\right)|$, we focus on the following nonlinear fractional Volterra–Fredholm integro-differential equation:

$$\begin{array}{c}\hfill {}^{c}D_t^{o}a\left(t\right)=g\left(t\right)a\left(t\right)+h\left(t\right)+{\int }_0^t{F}_1(t,l)G_1\left(a\left(l\right)\right) dl+{\int }_0^1{F}_2(t,l)G_2\left(a\left(l\right)\right) dl,\end{array}$$

(12)

with initial values

$$\begin{array}{c}\hfill a^j\left(0\right)={\theta }_j,j=0,1,\dots ,n-1 \mathrm{and} n\in {\mathbb{Z}}^{+}.\end{array}$$

(13)

In this setting, ${}^{c}D_t^o$ designates the Caputo fractional derivative of order o, subject to the condition $n-1<o<n$. The function $a:[0,1]\to \mathbb{R}$ is the unknown continuous solution. The functions $F_j:[0,1]\times [0,1]\to \mathbb{R}$ are continuous kernels, and $G_j:\mathbb{R}\to \mathbb{R}$ are Lipschitz continuous functions, for $j=1,2$.

Hamoud et al. [31], in 2018, derived the related integral equation for the problem (12) and confirmed the existence of a unique solution.

Lemma 3

([31]). For some $a_0\left(t\right)\in C([0,I],\mathbb{R})$, a solution $a\left(t\right)$ of the problem (12) must satisfy

$$\begin{array}{cc}\hfill a\left(t\right)=& a_0\left(t\right)+{\displaystyle \frac{1}{\Gamma \left(o\right)}}{\int }_0^t{(t-l)}^{o-1}g\left(l\right)a\left(l\right)dl+{\displaystyle \frac{1}{\Gamma \left(o\right)}}{\int }_0^t{(t-l)}^{o-1}h\left(l\right)dl\hfill \\ & +{\displaystyle \frac{1}{\Gamma \left(o\right)}}{\int }_0^t{(t-l)}^{o-1}\left({\int }_0^l{F}_1(l,k)G_1\left(a\left(k\right)\right)dk+{\int }_0^1{F}_2(l,k)G_2\left(a\left(k\right)\right)dk\right)dl.\hfill \end{array}$$

Theorem 5

([31]). Let us consider the following:

(C1) 

For any $a_1,a_2\in C([0,1],\mathbb{R})$, there are constants ${\alpha }_{G_1},{\alpha }_{G_2}>0$ so that

$$|G_1\left(a_1\left(t\right)\right)-G_1\left(a_2\left(t\right)\right)| \le {\alpha }_{G_1}|a_1-a_2|$$

and

$$|G_2\left(a_1\left(t\right)\right)-G_2\left(a_2\left(t\right)\right)| \le {\alpha }_{G_2}|a_1-a_2|.$$

(C2) 

There are two positive continuous functions ${\alpha }_{F_1}^{\ast }$ and ${\alpha }_{F_2}^{\ast }$ defined on $\{(x,y)\in {\mathbb{R}}^2:0\le y\le x\le 1\}$ so that

$${\alpha }_{F_1}^{\ast }=\underset{x,y\in [0,1]}{\max }{\int }_0^x\left|F_1(x,y)\right|dy<\infty$$

and

$${\alpha }_{F_2}^{\ast }=\underset{x,y\in [0,1]}{\max }{\int }_0^x\left|F_2(x,y)\right|dy<\infty .$$

(C3) 

The functions g and h are continuous.

(C4) 

Also the term ${\displaystyle \frac{{\parallel g\parallel }_{\infty }+{\alpha }_{G_1}{\alpha }_{F_1}^{\ast }+{\alpha }_{G_2}{\alpha }_{F_2}^{\ast }}{\Gamma (o+1)}}<1.$ Then the problem (12) possesses a unique solution.

Theorem 6.

In the Banach space $C\left(\right[0,1],\mathbb{R})$, let $L:C\left(\right[0,1],\mathbb{R})\to C\left(\right[0,I],\mathbb{R})$ be a mapping described as

$$\begin{array}{cc}\hfill La\left(t\right)=& a_0\left(t\right)+{\displaystyle \frac{1}{\Gamma \left(o\right)}}{\int }_0^t{(t-l)}^{o-1}g\left(l\right)a\left(l\right)dl+{\displaystyle \frac{1}{\Gamma \left(o\right)}}{\int }_0^t{(t-l)}^{o-1}h\left(l\right)dl\hfill \\ & +{\displaystyle \frac{1}{\Gamma \left(o\right)}}{\int }_0^t{(t-l)}^{o-1}\left({\int }_0^l{F}_1(l,k)G_1\left(a\left(k\right)\right)dk+{\int }_0^1{F}_2(l,k)G_2\left(a\left(k\right)\right)dk\right)dl,\hfill \end{array}$$

where $\left\{a_n\right\}=a_n\left(t\right)$ represents the iteration procedure provided by (7) with $a_0\left(t\right)={\sum }_{j=0}^{n-1}{a}^j\left(0\right){\displaystyle \frac{t^j}{j!}}$, for all $t\in [0,1]$ and the functions $g,h,F_1,F_2,G_1$ and $G_2$ satisfies $\left(C_1\right),\left(C_2\right),\left(C_3\right)$ and $\left(C_4\right)$. The iteration sequence $\left\{a_n\right\}$ is shown to converge to a single fixed point of the operator L. Hence, $\left\{a_n\right\}$ converges to the unique solution of the integro-differential problem (12).

Proof. 

Based on the given assumptions, problem (12) fulfills the conditions $\left(C_1\right),\left(C_2\right),\left(C_3\right)$, and $\left(C_4\right)$ of Theorem 5. Hence, it has a unique solution, which we denote by $a_{\ast }\left(t\right)$. Now,

$$\begin{array}{cc}\hfill |La\left(t\right)-L{a}_{\ast }\left(t\right)|& \le {\displaystyle \frac{1}{\Gamma \left(o\right)}}{\int }_0^t{(t-l)}^{o-1}\left|g\left(l\right)\right||a\left(l\right)-a_{\ast }\left(t\right)\left(l\right)|dl\hfill \\ & +{\displaystyle \frac{1}{\Gamma \left(o\right)}}{\int }_0^t{(t-l)}^{o-1}({\int }_0^l\left|F\right(l,k\left)\right||G_1\left(a\left(k\right)\right)-G_1\left(a_{\ast }\left(k\right)\right)|dk\hfill \\ & +{\int }_0^1|F_2(l,k)\left|\right|G_2\left(a\left(k\right)\right)-G_2\left(a_{\ast }\left(k\right)\right)|dk)dl,\hfill \\ & \le \left({\displaystyle \frac{{\parallel g\parallel }_{\infty }+{\alpha }_{G_1}{\alpha }_{F_1}^{\ast }+{\alpha }_{G_2}{\alpha }_{F_2}^{\ast }}{\Gamma (o+1)}}\right)|a\left(t\right)-a_{\ast }\left(t\right)|,\hfill \\ & =\alpha |a\left(t\right)-a_{\ast }\left(t\right)|.\hfill \end{array}$$

where $\alpha = {\displaystyle \frac{{\parallel g\parallel }_{\infty }+{\alpha }_{G_1}{\alpha }_{F_1}^{\ast }+{\alpha }_{G_2}{\alpha }_{F_2}^{\ast }}{\Gamma (o+1)}}<1$. It follows that L acts as a contraction mapping and hence meets the conditions of Theorem 1. Consequently, the sequence $\left\{a_n\right\}$ converges to the unique fixed point of L. Furthermore, according to Lemma 3, this iterative sequence converges to the unique solution of the integro-differential problem (12). □

5. Conclusions

This work proposes a new iteration method for approximating fixed points of contraction mappings in uniformly convex Banach spaces. The method’s stability is rigorously verified, and its effectiveness is illustrated through numerical experiments and graphical demonstrations. Comparative studies in MATHEMATICA show that the proposed method achieves faster and more accurate convergence compared to the iteration approaches developed by Sainuan, Daengsaen and Khempet; Chung et al.; Nawaz et al.; Lamba and Pawar; and Nawaz et al. The effect of varying parameters on convergence is also investigated, confirming the method’s robustness and flexibility. Furthermore, the method is applied to a fractional Volterra-Fredholm integro-differential equation using the Gamma function to demonstrate its practical relevance. Potential future research includes extending the approach to more general mappings and applying it to real-world problems to enhance fixed-point approximation techniques.