Weak Resolution Dimensions of Subcategories

Abstract

We investigate the relationships between the weak resolution dimensions of subcategories of module categories of Artinian algebras in the present paper. Let $\Lambda$ be an Artinian algebra, and $\mathcal{A}$, $\mathcal{B}$ and $\mathcal{X}$ subcategories of $\Lambda$-modules, such that each object X in $\mathcal{X}$ is given by an exact sequence $0\to A\to B\to X\to 0$ with $A\in Ob\mathcal{A}$ and $B\in Ob\mathcal{B}$. We prove that the weak resolution dimension of $\mathcal{X}$ is bounded above by the sum of the corresponding dimensions for $\mathcal{A}$ and $\mathcal{B}$ plus 1. As applications, we study weak resolution dimensions of Artinian algebras under left idealized extensions and conditions on special ideals.

1. Introduction

The representation dimension of an Artinian algebra was introduced by Auslander [1], who showed that an Artinian algebra is representation finite precisely when its representation dimension is no greater than 2. And Iyama later [2] showed that the representation dimensions of algebras are always finite. In [3], Oppermann introduced the concept of the weak resolution dimensions of Artinian algebras, proving it is bounded above by the representation dimension minus two. Therefore, this invariant, analogous to the representation dimension, serves as a measure of the algebra’s deviation from representation finite algebras.

The weak resolution dimension has since been linked to other homological dimensions, such as the finitistic dimension, the extension dimension, and so on. The weak resolution dimension of an algebra always lies between its extension dimension and its finitistic dimension (see [3,4,5] for details). And the Igusa–Todorov distance defined by Zhang and Zheng in [6] is equal to the weak resolution dimension of a particular subcategory of modules over Artinian algebras. Moreover, several important classes of Artinian algebras, such as Igusa–Todorov algebras, can be characterized in terms of their weak resolution dimensions (see [4,5,7,8] for details).

This study focuses on investigating the relationships between the weak resolution dimensions of subcategories of module categories of Artinian algebras. Our main theorem is the following:

Theorem A (Theorem 1) Suppose that $\mathcal{A}$, $\mathcal{B}$ and $\mathcal{X}$ are subcategories of $\mathrm{mod}\Lambda$, such that each object X in $\mathcal{X}$ is given by an exact sequence

$$0\to A\to B\to X\to 0$$

with $A\in Ob\mathcal{A}$, $B\in Ob\mathcal{B}$. Then,

$$O.w.resol.dim\mathcal{X}\le O.w.resol.dim\mathcal{A}+O.w.resol.dim\mathcal{B}+1$$

where $O.w.resol.dim\mathcal{X}, O.w.resol.dim\mathcal{A}, O.w.resol.dim\mathcal{B}$ stand for weak resolution dimensions of $\mathcal{X},\mathcal{A}$ and $\mathcal{B},$ respectively.

As applications, we establish relationships between the weak resolution dimensions of Artinian algebras linked by left idealized extensions.

Theorem B (Theorem 3) Let $\Lambda ={\Lambda }_0\subseteq {\Lambda }_1\subseteq \cdots \subseteq {\Lambda }_s=\Gamma$ be a chain of Artinian algebras, where ${\Lambda }_{i+1}$ is a left idealized extension of ${\Lambda }_i$, for all i. Then,

$$O.w.resol.dim\Lambda \le O.w.resol.dim\Gamma +s+1.$$

The organization of this paper begins with preliminaries in Section 2, followed by the proofs of Theorems A and B in Section 3.

2. Preliminaries

In this study, unless otherwise specified, all rings are Artinian algebras over a commutative Artinian ring R, and all modules are finitely generated left modules. Given an Artinian algebra $\Lambda$, $\mathrm{mod}\Lambda$ denotes the category formed by all finitely generated left $\Lambda$-modules. Let $\mathcal{C}$ be a subcategory of $\mathrm{mod}\Lambda$; we define ${\mathrm{add}}_{\Lambda }\mathcal{C}$ as its closure under finite direct sums and direct summands. In case of $\mathcal{C}=\left\{C\right\}$, we write ${\mathrm{add}}_{\Lambda }C$ instead of ${\mathrm{add}}_{\Lambda }\mathcal{C}$. A $\Lambda$-module X is said to be a generator-cogenerator for $\Lambda$-modules, provided that ${}_{\Lambda }\Lambda \in {\mathrm{add}}_{\Lambda }X$ and $\mathbf{D}\left({\Lambda }_{\Lambda }\right)\in {\mathrm{add}}_{\Lambda }X,$ where $\mathbf{D}(-)$ is the standard duality. An Artinian algebra $\Lambda$ is em representation finite, provided there exists a $\Lambda$-module X satisfying $\mathrm{mod}\Lambda ={\mathrm{add}}_{\Lambda }X$. The notation ${\mathrm{pd}}_{\Lambda }M$ will stand for the projective dimension of a $\Lambda$-module M.

The notions of weak resolution dimensions were introduced by Oppermann in ([3], Definition 2.4).

Definition 1

([3], Definition 2.4). Suppose that Λ is an Artinian algebra, and A is a Λ-module as follows:

(1)

We define the weak A-resolution dimension of a Λ-module Y as

$A-O.w.resol.dim\left(Y\right)=\min \left\{n\right|$; there exists an exact sequence$0\to A_n\to A_{n-1}\to \cdots \to A_1\to A_0\to Y\to 0$ with each $A_i\in \mathrm{add}A\}.$

(2)

For a subcategory $\mathcal{Y}$ of Λ-modules, the weak resolution dimension of $\mathcal{Y}$ is defined to be

$$A-O.w.resol.dim\left(\mathcal{Y}\right)=\mathrm{Sup}\{\mathrm{A}-O.w.resol.dim(\mathrm{Y}\left)\right|\mathrm{Y}\in \mathrm{Ob}\mathcal{Y}\}.$$

Furthermore, the weak resolution dimension of $\mathcal{Y}$ is defined as

$$O.w.resol.dim\left(\mathcal{Y}\right)=\inf \{A-O.w.resol.dim(\mathcal{Y}\left)\right|A\in \mathrm{mod}\Lambda \}.$$

Remark 1.

Iyama in [9], Definition 4.5(2) also introduced the concept of the weak resolution dimension. Let Λ be an Artinian algebra, and $M\in \mathrm{mod}\Lambda$. The weak M-resolution dimension of a module $X\in \mathrm{mod}\Lambda$ introduced by Iyama, denoted by I. w. resol. dim (X), is defined as $M-I.O.w.resol.dim\left(X\right)=\min \left\{n\right|$; there is an exact sequence $0\to M_n\to M_{n-1}\to \cdots \to M_1\to M_0\to X\oplus X^{\prime }\to 0$ with each $M_i\in \mathrm{add}M$ and $X^{\prime }\in \mathrm{mod}\Lambda$$\}.$ It is easy to see that $M-I.O.w.resol.dim\left(X\right)\le M-O.w.resol.dim\left(X\right)$ for Λ-modules M and X.

By the definition of the weak resolution dimension, the following result is directly applicable:

Lemma 1.

Let $\mathcal{C},\mathcal{D}$ be two subcategories of Λ-modules.

(1)

$O.w.resol.dim\mathcal{C}=0$ if and only if there is a Λ-module Y with $\mathcal{C}\subset {\mathrm{add}}_{\Lambda }Y$. This directly implies that Λ is finite representation precisely when $O.w.resol.dim\Lambda =0.$

(2)

$O.w.resol.dim\mathcal{C}\le O.w.resol.dim\mathcal{D}$, when $\mathcal{C}\subset \mathcal{D}$.

(3)

Let A and B be Λ-modules with $A\in {\mathrm{add}}_{\Lambda }B$, then

$$B-O.w.resol.dim\mathcal{C}\le A-O.w.resol.dim\mathcal{C}.$$

Proof. 

Points (1) and (2) are clear hold, we prove only Point (3).

(3) Assume that A-$O.w.resol.dim\mathcal{C}=m$. Then, for any $C\in \mathcal{C}$, we have a long exact sequence

$$0\to A_m\to A_{m-1}\to \cdots \to A_0\to C\to 0$$

with each $A_i\in \mathrm{add}A\subset \mathrm{add}B$. It means B-$O.w.resol.dim\mathcal{C}\le m$ as desired. □

For an Artinian algebra $\Lambda$, the finitistic dimension (fin.dim$\Lambda$) is the supremum of the projective dimensions of $\Lambda$-modules, while we recall from [1] that its representation dimension (rep.dim$\Lambda$) is the infimum of the global dimensions of the endomorphism algebras of generator-cogenerators.

Lemma 2.

Suppose that Λ is an Artinian algebra as follows:

(1)

$O.w.resol.dim\Lambda \le \mathrm{fin}.\dim \Lambda$.

(2)

If Λ is not semisimple, then $O.w.resol.dim\Lambda \le \mathrm{rep}.\dim \Lambda -2$.

Proof. 

(1) By the definition of the finitistic dimension of $\Lambda$, we have fin.dim$\Lambda$=${}_{\Lambda }\Lambda -O.w.resol.dim\Lambda$. The assertion follows:

Point (2) follows [3] (Remark 2.6). □

Let $\Lambda$ be an Artinian algebra, and let N be a $\Lambda$-module, and m a positive integer. Recall that a $\Lambda$-module X is said to be the m-th syzygy module of N, denoted by ${\Omega }^m\left(N\right)$, if there exists an exact sequence

$$0\to X\to Q_{m-1}\stackrel{h_{m-1}}{\to }{Q}_{m-2}\stackrel{h_{m-2}}{\to }\cdots \stackrel{h_2}{\to }{Q}_1\stackrel{h_1}{\to }{Q}_0\stackrel{h_0}{\to }N\to 0$$

with each $Q_i$ the projective cover of ${\mathrm{Imh}}_{\mathrm{i}}$. We used ${\Omega }^m\left(\mathcal{C}\right)$ to denote the subcategory of $\mathrm{mod}\Lambda$ whose objects are the m-th syzygies of modules in $\mathcal{C}$.

Lemma 3

([4], Lemma 2.8). Suppose that the sequence of Λ-module,

$$0\to D_n\to D_{n-1}\to \cdots \to D_1\to D_0\to 0$$

is exact. Then, for any $t\ge 1$, we have the following exact sequence:

$$0\to {\Omega }^t\left(D_n\right)\to {\Omega }^t\left(D_{n-1}\right)\oplus P_{n-1}\cdots \to {\Omega }^t\left(D_1\right)\oplus P_1\to {\Omega }^t\left(D_0\right)\to 0$$

in $\mathrm{mod}\Lambda$, where each $P_i$ is projective.

The following lemma from Lemma 3 applies directly:

Lemma 4.

Let $\mathcal{C}$ be a subcategory of modules over an Artinian algnbra Λ. Then, for any $n\ge 1$,

$$O.w.resol.dim{\Omega }^n\left(\mathcal{C}\right)\le O.w.resol.dim\mathcal{C}.$$

3. Main Results

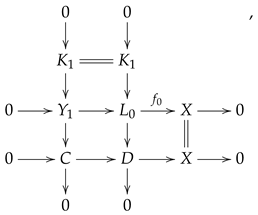
Proposition 1.

Assume that Λ is an Artinian algebra and $H,L\in \mathrm{mod}\Lambda$, and the sequence $0\to C\to D\to X\to 0$ is exact in modΛ. If there are exact sequences

$$0\to H_m\to H_{m-1}\to \cdots \to H_1\to H_0\to C\to 0$$

(1)

with each $H_i\in \mathrm{add}H$, and

$$0\to L_n\to L_{n-1}\to \cdots \to L_1\to L_0\to D\to 0$$

(2)

with each $L_j\in \mathrm{add}L$. Then, we have an exact sequence

$$0\to {\Omega }^n\left(H_m\right)\oplus Q_m\to {\Omega }^n\left(H_{m-1}\right)\oplus Q_{m-1}\to \cdots \to {\Omega }^n\left(H_0\right)\oplus Q_0$$

$$\to L_n\oplus P_n\to \cdots \to L_1\oplus P_1\to L_0\oplus P_0\to X\to 0,$$

where each $P_i,Q_j\in \mathrm{add}\Lambda$.

Proof. 

Set $K_i=\mathrm{Im}({\mathrm{L}}_{\mathrm{i}}\to {\mathrm{L}}_{\mathrm{i}-1})$, for any $i\ge 1.$ Then, $K_0=D$ and $K_n=L_n$. From the exact sequence (2), for each $1\le i\le n$, there exist short exact sequences

$$0\to K_i\to L_i\to K_{i-1}\to 0.$$

(3)

Consider the Pullback diagram

which is also a Pushout. We therefore derive a short exact sequence

$$0\to Y_1\to L_0\to X\to 0$$

(4)

and

$$0\to K_1\to Y_1\to C\to 0.$$

Let $P_1$ be the projective cover of C. The Pullback diagram

gives an exact sequence

$$0\to \Omega \left(C\right)\to K_1\oplus P_1\to Y_1\to 0$$

(5)

by the projective property of $P_1$.

From the exact sequence $0\to K_2\to L_1\to K_1\to 0,$ we derive another exact sequence

$$0\to K_2\to L_1\oplus P_1\to K_1\oplus P_1\to 0.$$

(6)

By Pullback, there is a commutative exact diagram

Thus, one obtains two exact sequences

$$0\to Y_2\to L_1\oplus P_1\to Y_1\to 0,$$

(7)

and

$$0\to K_2\to Y_2\to \Omega \left(C\right)\to 0.$$

(8)

The combination of the exact sequences (4) and (7) produces the following exact sequence:

$$0\to Y_2\to L_1\oplus P_1\to L_0\to X\to 0.$$

Proceeding inductively, we construct exact sequences

$$0\to Y_n\to L_{n-1}\oplus P_{n-1}\to \cdots \to L_1\oplus P_1\to L_0\to X\to 0$$

(9)

and $0\to L_n\to Y_n\to {\Omega }^{n-1}\left(C\right)\to 0.$

Let $P_n$ be the projective cover of ${\Omega }^{n-1}\left(C\right)$. By Pullback,

one obtains a long exact sequence

$$0\to {\Omega }^n\left(C\right)\to L_n\oplus P_n\to Y_n\to 0$$

(10)

since there is a $\Lambda$-module isomorphism $T_n\cong L_n\oplus P_n$ by the projective property of $P_n$.

Combining the exact sequences (9) and (10), we obtain a long exact sequence

$$0\to {\Omega }^n\left(C\right)\to L_n\oplus P_n\to \cdots \to L_1\oplus P_1\to L_0\to X\to 0.$$

Appealing to Lemma 3, one constructs the desired exact sequence. □

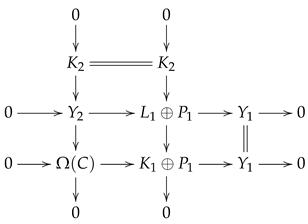
Theorem 1.

Suppose that $\mathcal{A}$, $\mathcal{B}$ and $\mathcal{X}$ are subcategories of $\mathrm{mod}\Lambda$, such that each object X in $\mathcal{X}$ is given by an exact sequence

$$0\to A\to B\to X\to 0$$

with $A\in Ob\mathcal{A}$, $B\in Ob\mathcal{B}$. Then,

$$O.w.resol.dim\mathcal{X}\le O.w.resol.dim\mathcal{A}+O.w.resol.dim\mathcal{B}+1.$$

Proof. 

Assume that, without loss of generality, $O.w.resol.dim\mathcal{A}=s$, and

$O.w.resol.dim\mathcal{B}=t$. Consequently, there exist $\Lambda$-modules U and L such that $U-O.w.resol.dim\mathcal{A}=s$ and $L-O.w.resol.dim\mathcal{B}=t.$

For any object X in $\mathcal{X}$, by assumption, one has a short exact sequence

$$0\to A\to B\to X\to 0$$

with $A\in Ob\mathcal{A}$ and $B\in Ob\mathcal{B}$. By assumption, one obtains two long exact sequences

$$0\to U_s\to U_{s-1}\to \cdots \to U_1\to U_0\to A\to 0$$

with each $U_i\in \mathrm{add}U$, and

$$0\to L_t\to L_{t-1}\to \cdots \to L_1\to L_0\to B\to 0$$

with each $L_j\in \mathrm{add}L$.

Applying Proposition 1 to these sequences yields a new exact sequence

$$0\to {\Omega }^t\left(U_s\right)\oplus Q_s\to {\Omega }^t\left(U_{s-1}\right)\oplus Q_{s-1}\to \cdots \to {\Omega }^t\left(U_0\right)\oplus Q_0$$

$$\to L_t\oplus P_t\to \cdots \to L_1\oplus P_1\to L_0\oplus P_0\to X\to 0,$$

where $P_i,Q_j$ are projective, for all $i,j.$

Taking $H={\Omega }^t\left(U\right)\oplus L\oplus \Lambda$, then, we have $H-O.w.resol.dim\mathcal{X}\le s+t+1.$ Thus, the ineqation $O.w.resol.dim\mathcal{X}\le O.w.resol.dim\mathcal{A}+O.w.resol.dim\mathcal{B}+1$ is proved by the above discussion. □

Remark 2.

Let Λ be an Artinain algebra. Take $\mathcal{A}={\mathrm{add}}_{\Lambda }\Lambda$, $\mathcal{B}=\Omega (\mathrm{mod}\Lambda )$ and $\mathcal{C}=\mathrm{mod}\Lambda$. Then $\mathcal{A}$, $\mathcal{B}$ and $\mathcal{C}$ satisfy the condition of Theorem 1. Moreover, suppose that Λ is a torsionless-finite algebra, that is, $\Omega (\mathrm{mod}\Lambda )$ is representation finite. Then $O.w.resol.dim\Lambda =1.$

Corollary 1.

Let $\mathcal{A}$, $\mathcal{B}$ and $\mathcal{C}$ be subcategories of $\mathrm{mod}\Lambda$, such that any object C in $\mathcal{C}$ is given by a long exact sequence

$$0\to A\to B_{s-1}\to \cdots \to B_1\to B_0\to C\to 0$$

where $A\in Ob\mathcal{A}$, and each $B_i\in Ob\mathcal{B}$. Then we have

$$O.w.resol.dim\mathcal{C}\le s(O.w.resol.dim\mathcal{B})+O.w.resol.dim\mathcal{A}+s.$$

In particular, if $\mathcal{B}$ is representation finite, then

$$O.w.resol.dim\mathcal{C}\le O.w.resol.dim\mathcal{A}+s.$$

Proof. 

Put ${\mathcal{C}}_0=\mathcal{A}$ and ${\mathcal{C}}_i=\left\{M\right|$ there exists an exact sequence $0\to A\to B\to M\to 0$, with $A\in {\mathcal{C}}_{i-1}$ and $B\in \mathcal{B}\}$, for any $1\le i\le s$. Then $\mathcal{C}\subseteq {\mathcal{C}}_n$. Through inductive application of Theorem 1, one gets $O.w.resol.dim{\mathcal{C}}_s\le O.w.resol.dim\mathcal{A}+s(O.w.resol.dim\mathcal{B})+s$. And the first part of this assertion is obtained by Lemma 1.

In particular, if $\mathcal{B}$ is representation finite. Due to Lemma 1, $O.w.resol.dim\mathcal{B}=0$. Thus, $O.w.resol.dim\mathcal{C}\le O.w.resol.dim\mathcal{A}+s.$ □

Corollary 2.

Let Λ be an Artinian algebra. For any positive integer s, we have

$$O.w.resol.dim(\Lambda )\le O.w.resol.dim{\Omega }^s(\mathrm{mod}\Lambda )+s.$$

Proof. 

The existence, for any $C\in \mathrm{mod}\Lambda$, of an exact sequence

$$0\to A\to P_{s-1}\to \cdots \to P_1\to P_0\to C\to 0$$

with each $P_i\in {\mathrm{add}}_{\Lambda }\Lambda$ ensures that $A\in {\Omega }^s(\mathrm{mod}\Lambda ).$ And the assertion follows from Corollary 1 in great detail. □

Let $\mathcal{A}$ and $\mathcal{B}$ be subcategories of $\mathrm{mod}\Lambda$. The class $\mathcal{A}*\mathcal{B}$ consists of those $X\in \mathrm{mod}\Lambda$ that admit an exact sequence $0\to A\to X\to B\to 0$, for some $A\in Ob\mathcal{A}$ and $B\in Ob\mathcal{B}$.

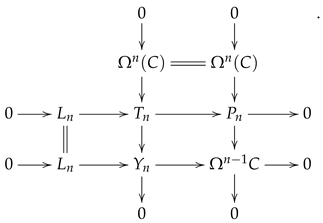
Theorem 2.

Let $\mathcal{A}$, $\mathcal{B}$ and $\mathcal{X}$ be subcategories of $\mathrm{mod}\Lambda$ with $\mathcal{X}\subseteq \mathcal{A}*\mathcal{B}$. Then

$$O.w.resol.dim\mathcal{X}\le O.w.resol.dim\mathcal{A}+O.w.resol.dim\mathcal{B}+1.$$

Proof. 

Assume that, without loss of generality, $O.w.resol.dim\mathcal{A}=s$ and

$O.w.resol.dim\mathcal{B}=t$.

For any object X in $\mathcal{X}$, by assumption, one obtains a short exact sequence

$$0\to A\to X\to B\to 0$$

where $A\in Ob\mathcal{A}$ and $B\in Ob\mathcal{B}$. Letting P be the projective cover of B, the construction of the pullback then yields the following commutative exact diagram.

This induces the following exact sequence

$$0\to \Omega B\to A\oplus P\to X\to 0$$

(11)

by the split property of the second row.

The assumption that $O.w.resol.dim\mathcal{A}=s$ guarantees the existence of a $\Lambda$-module U with U-$O.w.resol.dim\mathcal{A}=s$. Whence, A admits a resolution

$$0\to U_s\to U_{s-1}\to \cdots \to U_1\to U_0\to A\to 0$$

in which all $U_i\in \mathrm{add}U$. Combining this with the projective module P, we obtain an exact sequence

$$0\to U_s\to U_{s-1}\to \cdots \to U_1\to U_0\oplus P\to A\oplus P\to 0.$$

(12)

Noting that $O.w.resol.dim\mathcal{B}=t$, then, by Lemma 4, one has $O.w.resol.dim\Omega \left(\mathcal{B}\right)\le t$. Whence, there exists a $\Lambda$-module L satisfying L-$O.w.resol.dim\Omega \left(\mathcal{B}\right)\le t$, thereby providing an exact sequence in $\mathrm{mod}\Lambda$:

$$0\to L_t\to L_{t-1}\to \cdots \to L_1\to L_0\to \Omega \left(B\right)\to 0$$

(13)

in which each $L_j\in \mathrm{add}L$.

The application of Proposition 1 to exact sequences (11), (12), and (13) gives a long exact sequence

$$0\to {\Omega }^s\left(L_t\right)\oplus Q_t\to {\Omega }^s\left(L_{t-1}\right)\oplus Q_{t-1}\to \cdots \to {\Omega }^s\left(L_0\right)\oplus Q_0$$

$$\to U_s\oplus P_s\to \cdots \to U_1\oplus P_1\to U_0\oplus P_0\oplus P\to X\to 0$$

(14)

The terms ${\Omega }^s\left(L_k\right)\oplus Q_k\in {\mathrm{add}}_{\Lambda }({\Omega }^s\left(L\right)\oplus \Lambda )$ for all k, and $U_j\oplus P_j\in {\mathrm{add}}_{\Lambda }(U\oplus \Lambda )$ for all i. Since P is a projective $\Lambda$-module, all terms in sequence (14) belong to the additive subcategory ${\mathrm{add}}_{\Lambda }({\Omega }^s\left(L\right)\oplus U\oplus \Lambda )$.

Setting $H={\Omega }^s\left(L\right)\oplus U\oplus \Lambda$, the long exact sequence (14) is a resolution of X by modules in ${\mathrm{add}}_{\Lambda }H$. Therefore, we have $H-O.w.resol.dim\mathcal{X}\le s+t+1$. And the assertion follows. □

In the following, we give some application results above.

Let $\Lambda \to \Gamma$ be a homomorphism of Artinian algebras, then we have a restriction functor: $\mathrm{mod}\Gamma \to \mathrm{mod}\Lambda$. For any subcategory $\mathcal{H}$ of $\mathrm{mod}\Gamma$, ${}_{\Lambda }\mathcal{H}$ is defined as the image of ${}_{\Gamma }\mathcal{H}$ under the restricted functor. In particular, we use ${}_{\Lambda }(\mathrm{mod}\Gamma )$ to denote the image of $\mathrm{mod}\Gamma$ under the restricted functor.

Lemma 5.

Let $\Lambda \to \Gamma$ be a homomorphism of Artinian algebras. For any subcategory $\mathcal{H}$ of Γ-modules, we have

$$O.w.resol.{dim}_{\Lambda }\mathcal{H}\le O.w.resol.{dim}_{\Gamma }\mathcal{H}.$$

Proof. 

Assume that, without loss of generality, $O.w.resol.{dim}_{\Gamma }\mathcal{H}=m$. Then there exists $U\in \mathrm{mod}\Gamma$ with the property that for every $H\in {}_{\Gamma }\mathcal{H}$, there is an exact sequence in $\mathrm{mod}\Gamma$:

$$0\to U_m\to \cdots \to U_1\to U_0\to H\to 0,$$

in which each $U_i\in {\mathrm{add}}_{\Gamma }U$.

Applying the restrict functor (which is exact) to the above sequence, This yields, for each $H\in {}_{\Lambda }\mathcal{H}$, an exact sequence in $\mathrm{mod}\Lambda$:

$$0{\to }_{\Lambda }{U}_m\to \cdots {\to }_{\Lambda }{U}_1{\to }_{\Lambda }{U}_0{\to }_{\Lambda }H\to 0,$$

with ${}_{\Lambda }U_i\in {\mathrm{add}}_{\Lambda }U,i=1,2,\cdots ,m.$ This infers $O.w.resol.{dim}_{\Lambda }\mathcal{H}\le m.$ □

Let $\Lambda$ be a subalgebra of $\Gamma$ such that $\Lambda$ and $\Gamma$ have the same identity. Following [10], we say that $\Gamma$ is a left idealized extension of $\Lambda$ when rad $\Lambda$ is a left ideal of $\Gamma$. In the following, we will establish relationships between weak resolution dimensions of Artinian algebras linked by left idealized extensions. The following lemma is needed.

Lemma 6

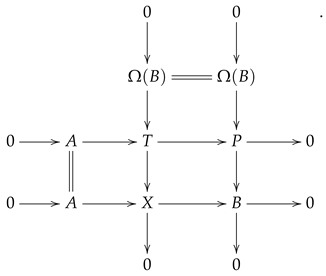
([11], Lemma 0.1 and Lemma 0.2). Let Γ be a left idealized extension of an Artinian algebra Λ. For a Λ-module X and an integer $i\ge 2$, then we have ${\Omega }_{\Lambda }^i\left(X\right)\in \mathrm{mod}\Gamma$ and a Γ-module isomorphism ${\Omega }_{\Lambda }^i\left(X\right)\cong {\Omega }_{\Gamma }\left(Y\right)\oplus Q$, where $Y\in \mathrm{mod}\Gamma$ and $Q\in {\mathrm{add}}_{\Gamma }\Gamma$.

Theorem 3.

Let $\Lambda ={\Lambda }_0\subseteq {\Lambda }_1\subseteq \cdots \subseteq {\Lambda }_s=\Gamma$ be a chain of Artinian algebras, where ${\Lambda }_{i+1}$ is a left idealized extension of ${\Lambda }_i$, for all i. Then

$$O.w.resol.dim\Lambda \le O.w.resol.dim\Gamma +s+1.$$

Proof. 

By assumption and by Lemma 6, for any $X_0\in \mathrm{mod}{\Lambda }_0$, we have ${\Omega }^2\left(X_0\right)\in \mathrm{mod}{\Lambda }_1$ and an ${\Lambda }_1$-module isomorphism ${\Omega }_{\Lambda }^2\left(X_0\right)\cong {\Omega }_{{\Lambda }_1}\left(X_1\right)\oplus Q_1$, for some projective ${\Lambda }_1$-module $Q_1$ and some ${\Lambda }_1$-module $X_1$.

Let $P_1^{\prime }$ be the projective cover of ${\Omega }_{{\Lambda }_1}\left(X_1\right)$ as a ${\Lambda }_1$-module. Then, there is an exact sequence in $\mathrm{mod}{\Lambda }_1$:

$$0\to {\Omega }_{{\Lambda }_1}^2\left(X_1\right)\to P_1^{\prime }\oplus Q_1\to {\Omega }_{\Lambda }^2\left(X_0\right)\to 0$$

which is also exact in $\mathrm{mod}\Lambda$.

Proceeding inductively, we are led to an exact sequence in $\mathrm{mod}\Lambda$:

$$0\to {\Omega }_{{\Lambda }_{s-1}}^2\left(X_{s-1}\right)\to P_{s-1}^{\prime }\oplus Q_{s-1}\to \cdots \to P_1^{\prime }\oplus Q_1\to {\Omega }_{\Lambda }^2\left(X_0\right)\to 0$$

(15)

with $X_{s-1}\in \mathrm{mod}{\Lambda }_{s-1}$ and each $P_i^{\prime }\oplus Q_i\in {\mathrm{add}}_{\Lambda }{\Lambda }_i$. By Lemma 6 again, ${\Omega }_{{\Lambda }_{s-1}}^2\left(X_{s-1}\right)\in \mathrm{mod}\Gamma$. So, ${}_{\Lambda }\left({\Omega }_{{\Lambda }_{s-1}}^2\left(X_{s-1}\right)\right)\in {}_{\Lambda }(\mathrm{mod}\Gamma )$. The definition of syzygy modules yields an exact sequence in $\mathrm{mod}\Lambda$:

$$0\to {\Omega }_{\Lambda }^2\left(X_0\right)\to P_1\to P_0\to X_0\to 0$$

(16)

where $P_1$ and $P_0$ are projective $\Lambda$-modules. Combining (15) and (16), one obtains a long exact sequence in $\mathrm{mod}\Lambda$

$$0\to {\Omega }_{{\Lambda }_{s-1}}^2\left(X_{s-1}\right)\to P_{s-1}^{\prime }\oplus Q_{s-1}\to \cdots \to P_1^{\prime }\oplus Q_1\to P_1\to P_0\to X\to 0.$$

On the other hand, let $\mathcal{D}={\mathrm{add}}_{\Lambda }({\Lambda }_0\oplus \cdots \oplus {\Lambda }_s)$. Then, by Lemma 1,

$O.w.resol.dim\mathcal{D}=0$. By Corollary 1 and Lemma 5, one has

$$O.w.resol.dim\Lambda \le O.w.resol.dim{(}_{\Lambda }(\mathrm{mod}\Gamma ))+s+1\le O.w.resol.dim\Gamma +s+1.$$

□

The left representation distance of an Artinian algebra $\Lambda$, denoted $lrep.dis(\Lambda )$, is defined as the smallest s for which one can construct a chain $\Lambda ={\Lambda }_0\subseteq \cdots \subseteq {\Lambda }_s$ by successively forming left idealized extensions (i.e., ${\Lambda }_{i+1}$ is a left idealized extension of ${\Lambda }_i$), until reaching a representation-finite algebra ${\Lambda }_s$. In the study of the finitistic dimension conjecture, Xi introduced the concept of left representation distances for Artinian algebras in [12], p. 341 and established their finiteness. Building on this, we provide a bound for the weak resolution dimension of an Artinian algebra by its left representation distances.

Corollary 3.

Assume that Λ is an Artinian algebra. Then,

$$O.w.resol.dim\Lambda \le \mathrm{lrep}.\mathrm{dis}(\Lambda )+1.$$

Proof. 

It follows from Theorem 3, combined with the fact that representation finite algebras have weak resolution dimension zero by Lemma 1.

□

We now present an example to illustrate Theorem 3.

Example 1.

Let F be an algebraically closed field, and let Λ be a finite-dimensional F-algebra defined by the quiver below:

$$\underset{5}{•}\stackrel{a}{⟵}\underset{2}{•}\stackrel{b}{⟵}\underset{3}{•}\stackrel{c}{⟵}\underset{1}{•}\stackrel{d}{⟵}\underset{4}{•}\stackrel{e}{⟵}\underset{6}{•}\stackrel{f_1}{⟵}\underset{7}{•}\stackrel{f_2}{⟵}\underset{8}{•\cdots }\stackrel{f_{s-6}}{⟵}\underset{s}{•}\stackrel{h_1}{⟵}\underset{s+1}{•}\stackrel{h_2}{⟵}\underset{s+2}{•\cdots }\stackrel{h_l}{⟵}\underset{s+l}{•}$$

with relations: $dcba=0=h_1{f}_{s-6},h_{i+1}{h}_i=0,1\le i<l$. And assume that $s\ge 7$ and $l>1$.

Let Γ be a finite-dimensional F-algebra defined by the quiver below:

with relations$dc=pd,cd=cp=a^2=ad=ap=pe=bd=bp=ea=edca=h_1{f}_{s-6}=0, h_{i+1}{h}_i=0,1\le i<l$.

Let Π be a finite-dimensional k-algebra given by the following quiver:

with relations $dc=p(e+b),cd=cp=a^2=ad=ap=(e+b)dca=0=f_1{h}_{s-6}, f_{i+1}{f}_i=0,1⩽i<l$.

By [5], Proposition 4.7, we obtain that Λ is representation finite and that $\Pi \subseteq \Gamma \subseteq \Lambda$ is a chain of left idealized extensions. It follows from Theorem 3 that $O.w.resol.dim(\Gamma )\le 2$ and $O.w.resol.dim(\Pi )\le 3.$

Theorem 4.

Suppose that I and J are two ideals of Artinian algebra Γ satisfying $IJrad\Gamma =0$ Then,

$$O.w.resol.dim\Gamma \le O.w.resol.dim(\Gamma /I)+O.w.resol.dim(\Gamma /J)+2.$$

Proof. 

Denote $\mathcal{C}={}_{\Gamma }\left(\mathrm{mod}(\Gamma /I)\right)$, and $\mathcal{D}={}_{\Gamma }\left(\mathrm{mod}(\Gamma /J)\right)$. We claim that $\Omega (\mathrm{mod}\Gamma )\subseteq \mathcal{C}\ast \mathcal{D}$. Indeed, for any $X\in \mathrm{mod}\Gamma$, we take P to be the projective cover of X. Then $\Omega \left(X\right)$$\subseteq {rad}_{\Gamma }P\subseteq \mathrm{add}{rad}_{\Gamma }\Gamma$. Take $X_1=J\Omega \left(X\right)$ and $X_2=\Omega \left(X\right)/J\Omega \left(X\right)$. We have an exact sequence in $\mathrm{mod}\Gamma$,

$$0\to X_1\to \Omega \left(X\right)\to X_2\to 0.$$

(17)

By assumption, $I{X}_1=IJ\Omega \left(X\right)\subseteq IJ{rad}_{\Gamma }P=0$. Then $X_1$ is a $\Gamma /I$-module. We have $X_1\in \mathcal{C}$. On the other hand, noting that $J{X}_2=0$, one has $X_2\in \mathrm{mod}(\Gamma /J)$. So, $X_2\in \mathcal{D}$. From the sequence (17), we have $\Omega \left(X\right)\in \mathcal{C}*\mathcal{D}$ and the claim is obtained.

Due to Theorem 2, it follows that $O.w.resol.dim\Omega (\mathrm{mod}\Gamma )\le O.w.resol.dim\left(\mathcal{C}\right)+O.w.resol.dim\left(\mathcal{D}\right)+1$. Therefore, by Corollary 2 and Lemma 5, one has $O.w.resol.dim\Gamma \le O.w.resol.dim\Omega (\mathrm{mod}\Gamma )+1\le O.w.resol.dim(\Gamma /I)+O.w.resol.dim(\Gamma /J)+2$ as regards. □

Proposition 2.

Assume that$0=J_0\subseteq J_1\subseteq \cdots \subseteq J_l$ are ideals of an Artinian algebra Γ such that $(J_{i+1}/J_i)rad(\Gamma /J_i)=0$, for each $0\le i\le l$. Then

$$O.w.resol.dim\Gamma \le O.w.resol.dim(\Gamma /J_l)+l.$$

Proof. 

Denote ${\Gamma }_i=\Gamma /J_i$, for each $0\le i\le l$, then ${\Gamma }_0=\Gamma$. For any $X_0\in \mathrm{mod}\Gamma$, we take the projective cover of $f:P_{X_0}\to X_0$ and denote $X_1={\Omega }_{{\Gamma }_0}\left(X_0\right)$. Then, one obtains an exact sequence in $\mathrm{mod}{\Gamma }_0$

$$0\to X_1\to P_{X_0}\to X_0\to 0.$$

Since $I_1{X}_1=I_1\Omega \left(X_0\right)\subseteq I_{1}rad\left(P_{X_0}\right)=0$, $X_1\in \mathrm{mod}{\Gamma }_1.$

Proceeding inductively, one has each $X_i\in \mathrm{mod}{\Gamma }_i$. Thus, we obtain the following exact sequence in $\mathrm{mod}\Gamma$:

$$0\to X_l\to P_{X_{l-1}}\to \cdots \to P_{X_0}\to X_0\to 0$$

with $X_l\in \mathrm{mod}{\Gamma }_l$ and each $P_{X_i}\in {\mathrm{add}}_{\Gamma }{\Gamma }_i$.

Denote $\mathcal{D}=\mathrm{add}\left({⨁}_{i=1}^{i=m}{}_{\Gamma }\Gamma _i\right)$ and $\mathcal{C}={}_{\Gamma }\left(\mathrm{mod}\left({\Gamma }_i\right)\right)$. Clearly, $\mathcal{D}$ is representative finite. By Lemma 5 and Corollary 1, we have $.resol.dim\Gamma \le .resol.dim{\Gamma }_l+l$ as regard. □

4. Conclusions

We mainly establish the relationships between the weak resolution dimensions of subcategories of module categories of Artinian algebras in the present paper. Our findings contribute to the study of Igusa–Todorov distances of Artinian algebras and the finitistic dimension conjecture. In future work, we will extend this study to weak resolution dimensions over general rings.