Fractional Error Bounds for Lobatto Quadrature: A Convexity Approach via Riemann–Liouville Integrals
Abstract
1. Introduction
2. Lobatto-Type Identity
3. Lobatto-Type Inequalities
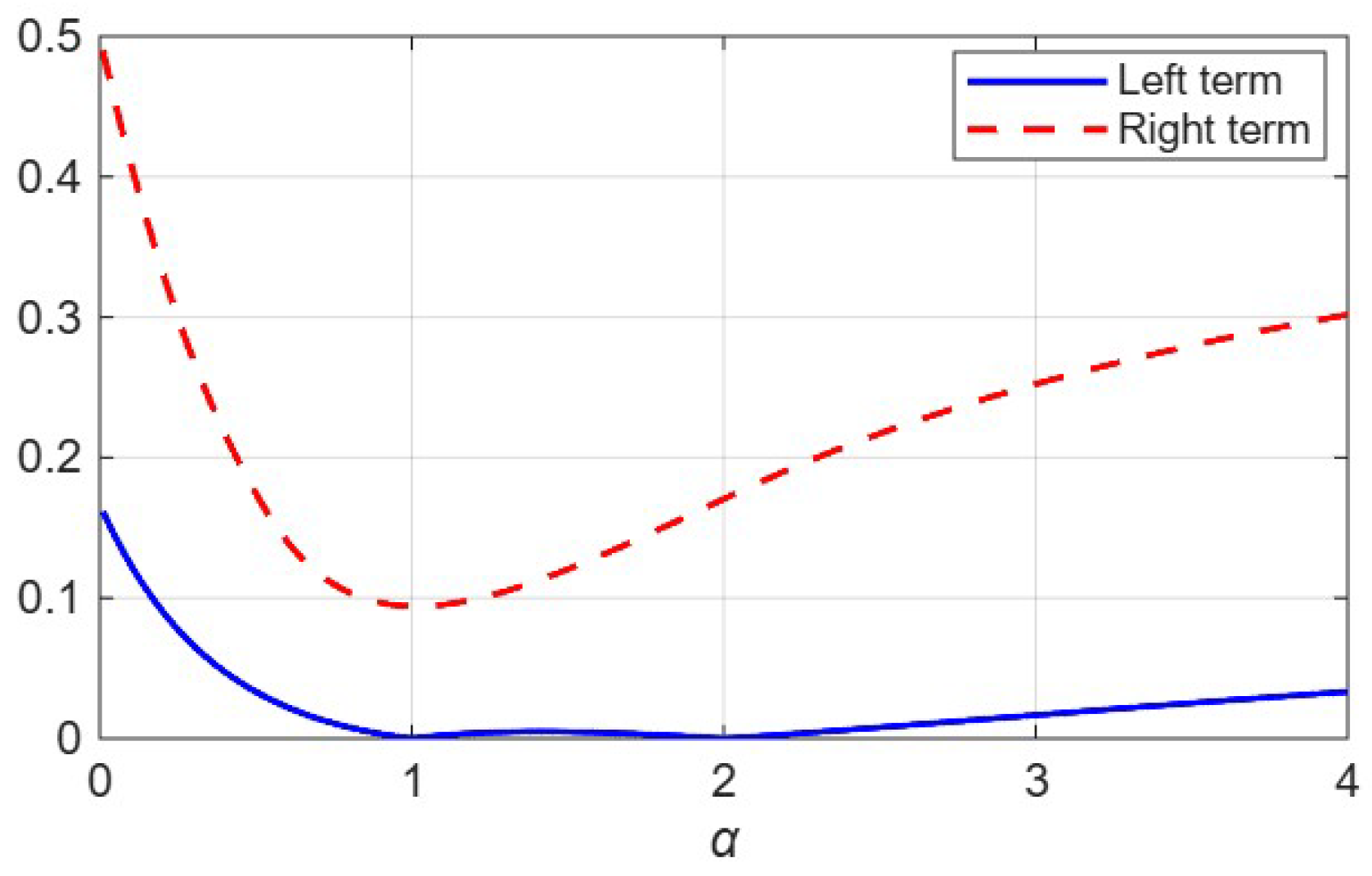
4. Numerical Validation and Graphical Illustration
5. Applications
6. Conclusions and Future Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ambati, H.; Eisenträger, S.; Kapuria, S. Cut spectral BFS plate element with Lobatto basis for wave propagation analysis. Comput. Mech. 2025, 76, 659–676. [Google Scholar]
- Atasoy, A.; Ghalehjoogh, M.B.; Demirkapi, A. A novel approach to linear and nonlinear time-history analysis of structures: Gauss–Lobatto–Hermite 4-point (GLH-4P) method. Arab. J. Sci. Eng. 2024, 49, 14205–14224. [Google Scholar]
- Shan, Y.; Liu, W. Space-time Legendre-Gauss-Lobatto collocation method for the two-dimensional Schrödinger equation. Numer. Algorithms 2025, 1–22. [Google Scholar] [CrossRef]
- Franjić, I.; Pečarić, J.; Perić, I.; Vukelić, A. Euler Integral Identity, Quadrature Formulae and Error Estimations (from the Point of View of Inequality Theory); Monographs in Inequalities; ELEMENT: Zagreb, Croatia, 2011; Volume 2. [Google Scholar]
- Niculescu, C.P.; Persson, L.-E. Convex Functions and Their Applications. A Contemporary Approach; CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC; Springer: New York, NY, USA, 2006; Volume 23. [Google Scholar]
- Nápoles Valdés, J.E.; Rabossi, F.; Samaniego, A.D. Convex functions: Ariadne’s thread or Charlotte’s Spiderweb? Adv. Math. Model. Appl. 2020, 5, 176–191. [Google Scholar]
- Aglić Aljinović, A.; Čivljak, A.; Kovačn, S.; Pečarić, J.; RibičiPenava, M. General Integral Identities and Related Inequalities; Monographs in Inequalities; ELEMENT: Zagreb, Croatia, 2013; Volume 5. [Google Scholar]
- Anderson, G.D.; Vamanamurthy, M.K.; Vuorinen, M. Generalized convexity and inequalities. J. Math. Anal. Appl. 2007, 335, 1294–1308. [Google Scholar] [CrossRef]
- Dragomir, S.S.; Agarwal, R.P. Two inequalities for differentiable mappings and applications to special means of real numbers and to trapezoidal formula. Appl. Math. Lett. 1998, 11, 91–95. [Google Scholar] [CrossRef]
- Kırmacı, U. Inequalities for differentiable mappings and applications to special means of real numbers and to midpoint formula. Appl. Math. Comput. 2004, 147, 137–146. [Google Scholar] [CrossRef]
- Toseef, M.; Mateen, A.; Aamir Ali, M.; Zhang, Z. A family of quadrature formulas with their error bounds for convex functions and applications. Math. Methods Appl. Sci. 2025, 48, 2766–2783. [Google Scholar] [CrossRef]
- Berkane, A.; Meftah, B.; Lakhdari, A. Right-Radau-type inequalities for multiplicative differentiable s-convex functions. J. Appl. Math. Inform. 2024, 42, 785–800. [Google Scholar]
- Bin-Mohsin, B.; Lakhdari, A.; Karabadji, N.E.I.; Awan, M.U.; Makhlouf, A.B.; Meftah, B.; Dragomir, S.S. An extension of left Radau type inequalities to fractal spaces and applications. Axioms 2024, 13, 653. [Google Scholar] [CrossRef]
- Liu, X.L.; Xu, H.; Shokri, A.; Lakhdari, A.; Meftah, B. Some error bounds for 2-point right Radau formula in the setting of fractional calculus via s-convexity. J. Math. 2024, 2024, 6709056. [Google Scholar] [CrossRef]
- Meftah, B.; Lakhdari, A.; Saleh, W. 2-point left Radau-type inequalities via s-convexity. J. Appl. Anal. 2023, 29, 341–346. [Google Scholar] [CrossRef]
- Aljurbua, S.F. Generalized existence results for solutions of nonlinear fractional differential equations with nonlocal boundary conditions. Ain Shams Eng. J. 2024, 15, 103035. [Google Scholar] [CrossRef]
- Aljurbua, S.F.; Hammad, H.A.; Almutairi, N.B. Existence of solutions to a new class of fractional differential equations with antiperiodic boundary conditions. Eur. J. Pure Appl. Math. 2025, 18, 5671. [Google Scholar] [CrossRef]
- Sadek, L.; Kashuri, A.; Sahoo, S.K.; Mishra, S. New perspective on Jensen type inequalities pertaining to local fractional derivatives. Filomat 2025, 39, 9651–9668. [Google Scholar]
- Ighachane, M.A.; Sadek, L.; Sababheh, M. Improved Jensen type inequalities for (p,h)-convex functions with applications. Kragujev. J. Math. 2023, 50, 71–89. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier Science B.V.: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Sarikaya, M.Z.; Yildirim, H. On Hermite-Hadamard type inequalities for Riemann-Liouville fractional integrals. Miskolc Math. Notes 2016, 17, 1049–1059. [Google Scholar] [CrossRef]
- Yuan, Z.; Du, T. Fractional integral approach to parameterized inequalities for (s,P)-preinvexity. J. Math. Inequal. 2025, 19, 387–419. [Google Scholar] [CrossRef]
- Butt, S.I.; Umar, M.; Khan, D.; Seol, Y.; Tipurić-Spužević, S. Hermite–Hadamard-type inequalities for harmonically convex functions via proportional Caputo-hybrid operators with applications. Fractal Fract. 2025, 9, 77. [Google Scholar] [CrossRef]
- Tunç, T.; Demir, İ. Some trapezoid-type inequalities for newly defined proportional Caputo-hybrid operator. J. Inequalities Math. Anal. 2025, 1, 65–78. [Google Scholar] [CrossRef]
- Long, Y.; Yuan, X.; Du, T. Simpson-like inequalities for functions whose third derivatives belong to s-convexity involving Atangana–Baleanu fractional integrals and their applications. Filomat 2024, 38, 9373–9397. [Google Scholar]
- Benaissa, B.; Azzouz, N. Hermite-Hadamard-Fejér type inequalities for h-convex functions involving Ψ-Hilfer operators. J. Inequalities Math. Anal. 2025, 1, 113–123. [Google Scholar]
- Fahad, A.; Ali, Z.; Furuichi, S.; Butt, S.I.; Wang, Y. New Inequalities for GA-h Convex Functions via Generalized Fractional Integral Operators with Applications to Entropy and Mean Inequalities. Fractal Fract. 2024, 8, 728. [Google Scholar]
| LHS | RHS | |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, L.; Lakhdari, A.; Awan, M.U.; Xu, H.; Meftah, B. Fractional Error Bounds for Lobatto Quadrature: A Convexity Approach via Riemann–Liouville Integrals. Axioms 2025, 14, 823. https://doi.org/10.3390/axioms14110823
Liao L, Lakhdari A, Awan MU, Xu H, Meftah B. Fractional Error Bounds for Lobatto Quadrature: A Convexity Approach via Riemann–Liouville Integrals. Axioms. 2025; 14(11):823. https://doi.org/10.3390/axioms14110823
Chicago/Turabian StyleLiao, Li, Abdelghani Lakhdari, Muhammad Uzair Awan, Hongyan Xu, and Badreddine Meftah. 2025. "Fractional Error Bounds for Lobatto Quadrature: A Convexity Approach via Riemann–Liouville Integrals" Axioms 14, no. 11: 823. https://doi.org/10.3390/axioms14110823
APA StyleLiao, L., Lakhdari, A., Awan, M. U., Xu, H., & Meftah, B. (2025). Fractional Error Bounds for Lobatto Quadrature: A Convexity Approach via Riemann–Liouville Integrals. Axioms, 14(11), 823. https://doi.org/10.3390/axioms14110823






