An Online Generalized Multiscale Method for Embedded Discrete Fracture Model
Abstract
1. Introduction
2. Embedded Discrete Fracture Model
2.1. Mathematical Formulation
2.2. Two-Point Flux-Approximation Scheme
3. Coarse-Grid Approximation
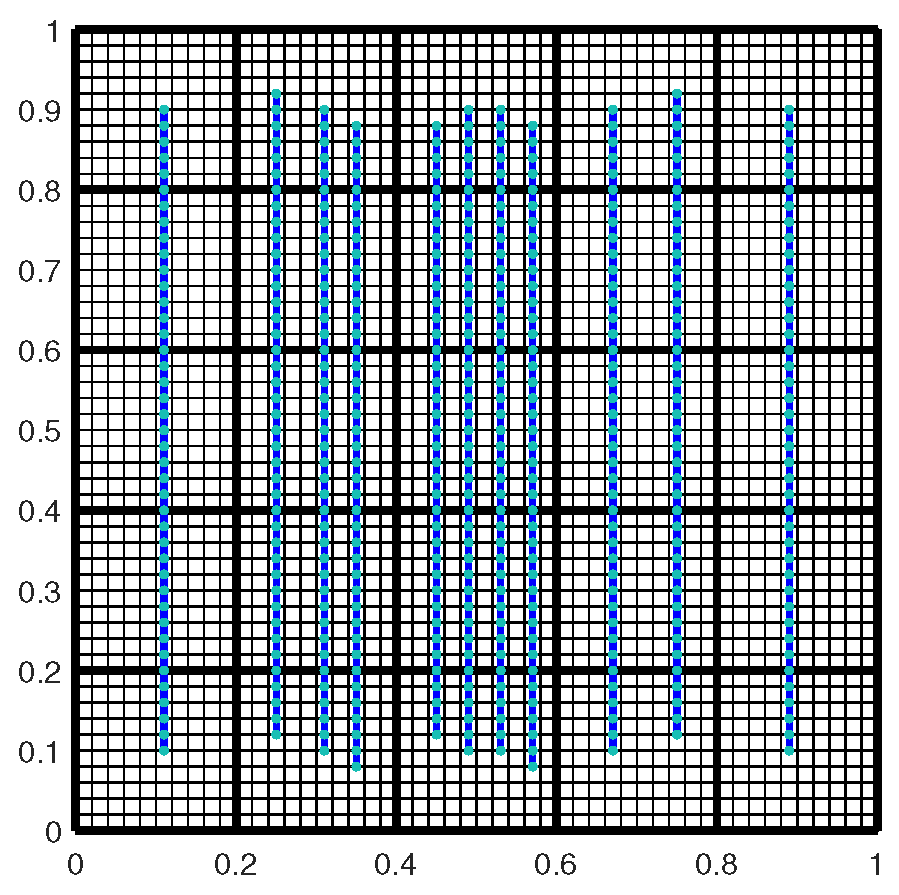
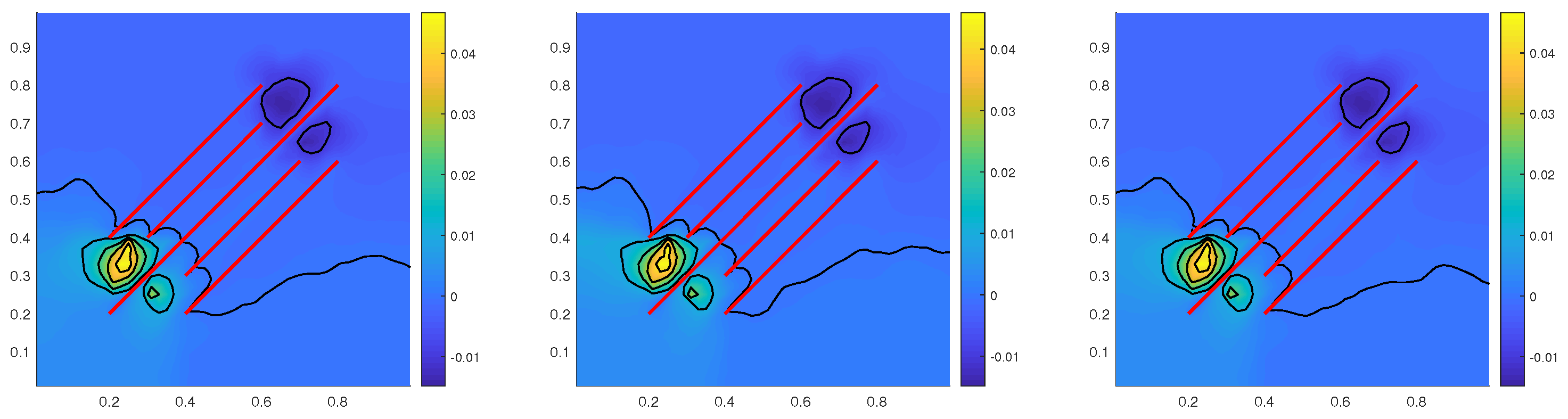
3.1. Snapshot Space
3.2. Offline Space
3.3. Online Enrichment
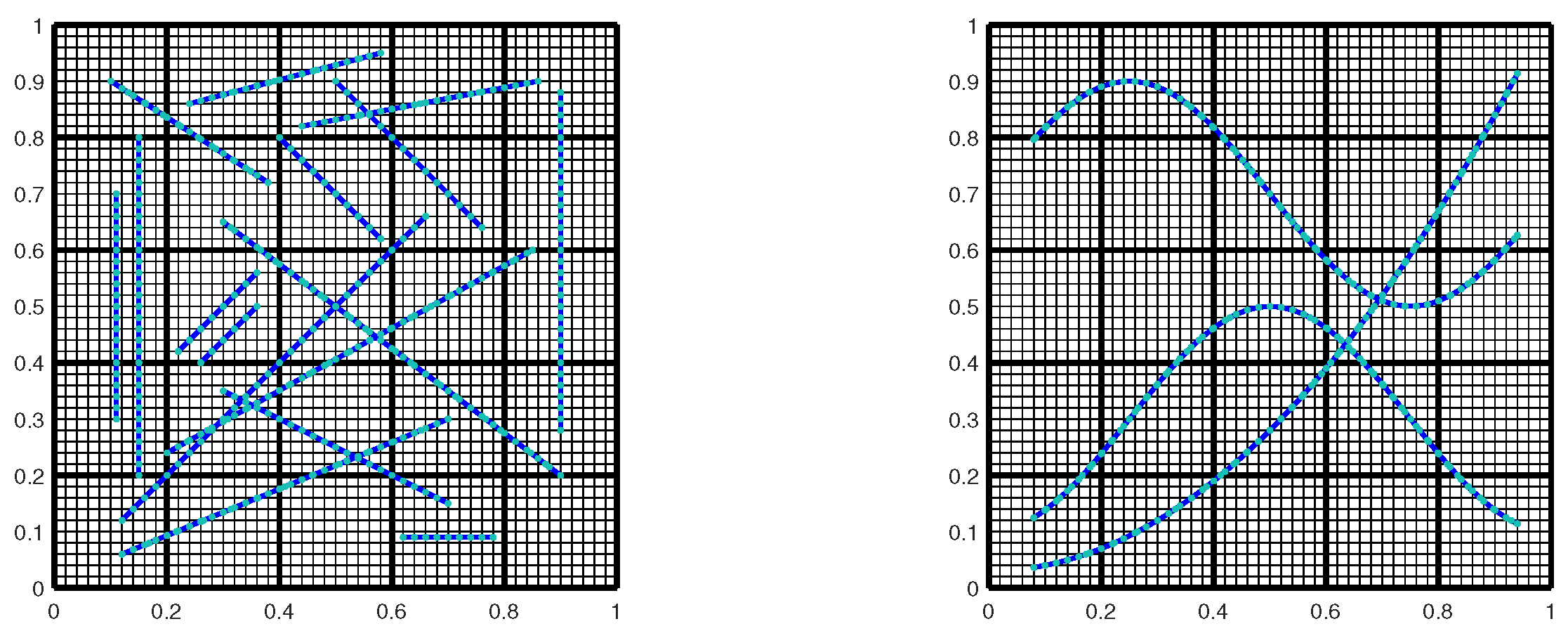
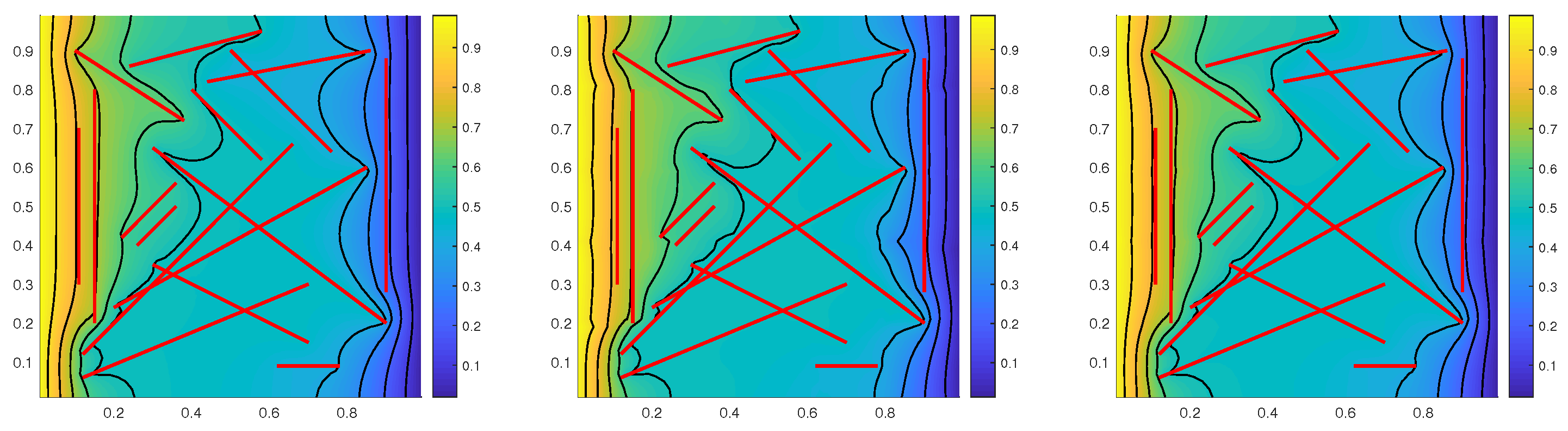
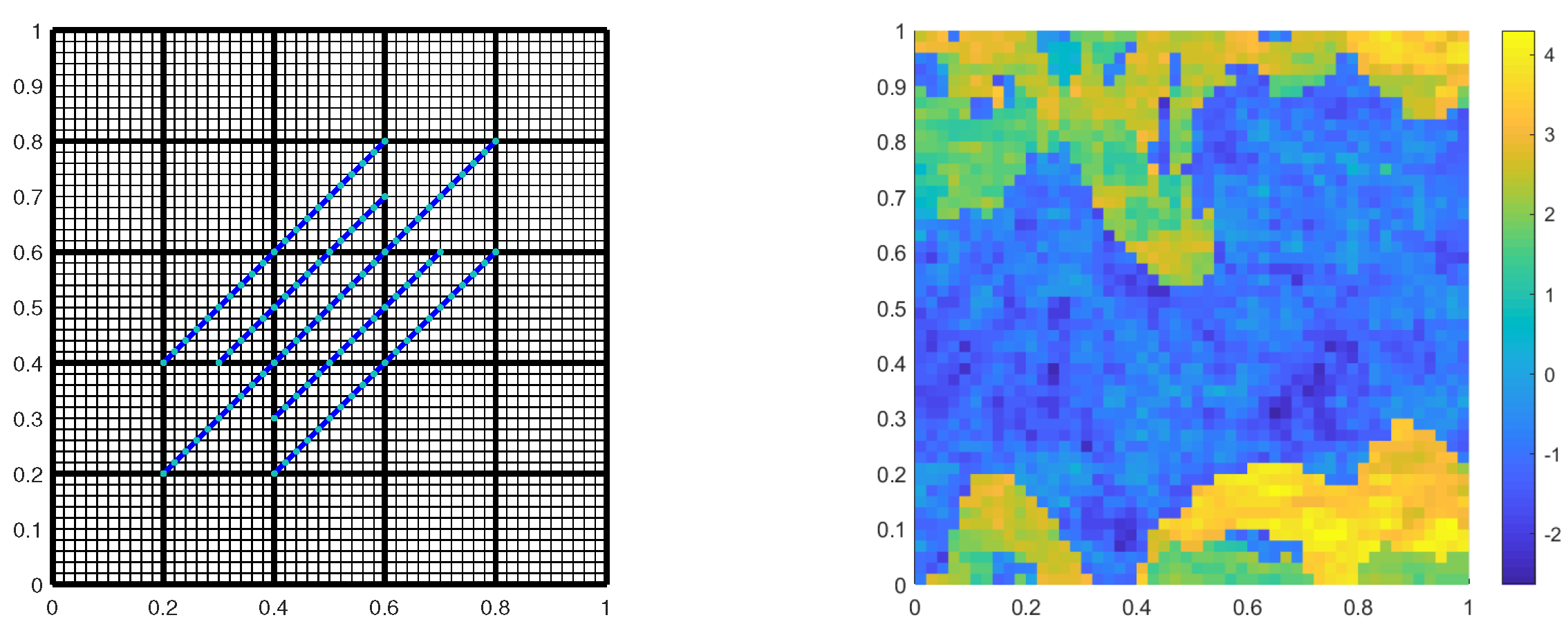
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Van Golf-Racht, T.D. Fundamentals of Fractured Reservoir Engineering; Elsevier: Amsterdam, The Netherlands, 1982; Volume 12. [Google Scholar]
- Berkowitz, B. Characterizing flow and transport in fractured geological media: A review. Adv. Water Resour. 2002, 25, 861–884. [Google Scholar] [CrossRef]
- He, Z.; Chen, H.; Chen, J.; Chen, Z. Generalized multiscale approximation of a mixed finite element method with velocity elimination for Darcy flow in fractured porous media. Comput. Methods Appl. Mech. Eng. 2021, 381, 113846. [Google Scholar] [CrossRef]
- Watanabe, S.; Sakai, T.; Jensen, C. A Physics-Based Coarsening Strategy in Multiscale Pressure Solver for Fractured Reservoir Simulation. In Proceedings of the SPE Reservoir Simulation Conference, Galveston, TX, USA, 25–27 March 2025; SPE: Galveston, TX, USA, 2025; p. D011S006R003. [Google Scholar]
- Karimi-Fard, M.; Firoozabadi, A. Numerical simulation of water injection in 2D fractured media using discrete-fracture model. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 30 September–3 October 2001; SPE: Galveston, TX, USA, 2001; p. SPE-71615. [Google Scholar]
- Karimi-Fard, M.; Durlofsky, L.J.; Aziz, K. An efficient discrete-fracture model applicable for general-purpose reservoir simulators. SPE J. 2004, 9, 227–236. [Google Scholar] [CrossRef]
- Ahmed, R.; Edwards, M.G.; Lamine, S.; Huisman, B.A.; Pal, M. Three-dimensional control-volume distributed multi-point flux approximation coupled with a lower-dimensional surface fracture model. J. Comput. Phys. 2015, 303, 470–497. [Google Scholar] [CrossRef]
- Martin, V.; Jaffré, J.; Roberts, J.E. Modeling fractures and barriers as interfaces for flow in porous media. SIAM J. Sci. Comput. 2005, 26, 1667–1691. [Google Scholar] [CrossRef]
- Chen, H.; Salama, A.; Sun, S. Adaptive mixed finite element methods for Darcy flow in fractured porous media. Water Resour. Res. 2016, 52, 7851–7868. [Google Scholar] [CrossRef]
- Chen, H.; Sun, S. A residual-based a posteriori error estimator for single-phase Darcy flow in fractured porous media. Numer. Math. 2017, 136, 805–839. [Google Scholar] [CrossRef]
- Lee, S.; Jensen, C.; Lough, M. Efficient finite-difference model for flow in a reservoir with multiple length-scale fractures. SPE J. 2000, 5, 268–275. [Google Scholar] [CrossRef]
- Lee, S.H.; Lough, M.; Jensen, C. Hierarchical modeling of flow in naturally fractured formations with multiple length scales. Water Resour. Res. 2001, 37, 443–455. [Google Scholar] [CrossRef]
- Li, L.; Lee, S.H. Efficient field-scale simulation of black oil in a naturally fractured reservoir through discrete fracture networks and homogenized media. SPE Reserv. Eval. Eng. 2008, 11, 750–758. [Google Scholar] [CrossRef]
- Moinfar, A.; Varavei, A.; Sepehrnoori, K.; Johns, R.T. Development of an efficient embedded discrete fracture model for 3D compositional reservoir simulation in fractured reservoirs. SPE J. 2014, 19, 289–303. [Google Scholar] [CrossRef]
- Jia, B.; Xian, C.G. Permeability measurement of the fracture-matrix system with 3D embedded discrete fracture model. Pet. Sci. 2022, 19, 1757–1765. [Google Scholar] [CrossRef]
- Wang, T.; Yao, J. An improved embedded discrete fracture model and domain connectivity algorithms on 3D unstructured grids. J. Comput. Phys. 2022, 459, 111142. [Google Scholar] [CrossRef]
- Zhou, B.; Chen, Z.; Song, Z.; Tang, Z.; Wang, B.; Olorode, O. A new analytically modified embedded discrete fracture model for pressure transient analysis in fluid flow. J. Hydrol. 2024, 636, 131330. [Google Scholar] [CrossRef]
- Hajibeygi, H.; Karvounis, D.; Jenny, P. A hierarchical fracture model for the iterative multiscale finite volume method. J. Comput. Phys. 2011, 230, 8729–8743. [Google Scholar] [CrossRef]
- Ţene, M.; Al Kobaisi, M.S.; Hajibeygi, H. Algebraic multiscale method for flow in heterogeneous porous media with embedded discrete fractures (F-AMS). J. Comput. Phys. 2016, 321, 819–845. [Google Scholar] [CrossRef]
- Shah, S.; Møyner, O.; Tene, M.; Lie, K.A.; Hajibeygi, H. The multiscale restriction smoothed basis method for fractured porous media (F-MsRSB). J. Comput. Phys. 2016, 318, 36–57. [Google Scholar] [CrossRef]
- Efendiev, Y.; Lee, S.; Li, G.; Yao, J.; Zhang, N. Hierarchical multiscale modeling for flows in fractured media using generalized multiscale finite element method. GEM-Int. J. Geomath. 2015, 6, 141–162. [Google Scholar] [CrossRef]
- Zhang, Q.; Huang, Z.; Yao, J.; Wang, Y.; Li, Y. Multiscale mimetic method for two-phase flow in fractured media using embedded discrete fracture model. Adv. Water Resour. 2017, 107, 180–190. [Google Scholar] [CrossRef]
- Efendiev, Y.; Galvis, J.; Hou, T.Y. Generalized multiscale finite element methods (GMsFEM). J. Comput. Phys. 2013, 251, 116–135. [Google Scholar] [CrossRef]
- Efendiev, Y.; Galvis, J.; Lazarov, R.; Moon, M.; Sarkis, M. Generalized multiscale finite element method. Symmetric interior penalty coupling. J. Comput. Phys. 2013, 255, 1–15. [Google Scholar] [CrossRef]
- Chung, E.T.; Efendiev, Y.; Leung, W.T. Constraint energy minimizing generalized multiscale finite element method. Comput. Methods Appl. Mech. Eng. 2018, 339, 298–319. [Google Scholar] [CrossRef]
- Chung, E.; Efendiev, Y.; Hou, T.Y. Multiscale Model Reduction: Multiscale Finite Element Methods and Their Generalizations; Springer Nature: Cham, Switzerland, 2023; Volume 212. [Google Scholar]
- Zhao, L.; Chung, E. Constraint energy minimizing generalized multiscale finite element method for convection diffusion equation. Multiscale Model. Simul. 2023, 21, 735–752. [Google Scholar] [CrossRef]
- Chung, E.T.; Efendiev, Y.; Leung, W.T. Residual-driven online generalized multiscale finite element methods. J. Comput. Phys. 2015, 302, 176–190. [Google Scholar] [CrossRef]
- Chung, E.; Efendiev, Y.; Hou, T.Y. Adaptive multiscale model reduction with generalized multiscale finite element methods. J. Comput. Phys. 2016, 320, 69–95. [Google Scholar] [CrossRef]
- Efendiev, Y.; Gildin, E.; Yang, Y. Online adaptive local-global model reduction for flows in heterogeneous porous media. Computation 2016, 4, 22. [Google Scholar] [CrossRef]
- Wang, Y.; Chung, E.; Fu, S.; Presho, M. Online conservative generalized multiscale finite element method for highly heterogeneous flow models. Comput. Geosci. 2021, 25, 1837–1853. [Google Scholar] [CrossRef]
- Spiridonov, D.; Vasilyeva, M.; Tyrylgin, A.; Chung, E.T. An online generalized multiscale finite element method for unsaturated filtration problem in fractured media. Mathematics 2021, 9, 1382. [Google Scholar] [CrossRef]
- Spiridonov, D.; Stepanov, S.; Vasiliy, V. An online generalized multiscale finite element method for heat and mass transfer problem with artificial ground freezing. J. Comput. Appl. Math. 2022, 417, 114561. [Google Scholar] [CrossRef]
- Chan, H.Y.; Chung, E.; Efendiev, Y. Adaptive mixed GMsFEM for flows in heterogeneous media. Numer. Math. Theory Methods Appl. 2016, 9, 497–527. [Google Scholar] [CrossRef]
- Yang, Y.; Fu, S.; Chung, E.T. Online mixed multiscale finite element method with oversampling and its applications. J. Sci. Comput. 2020, 82, 31. [Google Scholar] [CrossRef]
- Chung, E.T.; Efendiev, Y.; Leung, W.T. An online generalized multiscale discontinuous Galerkin method (GMsDGM) for flows in heterogeneous media. Commun. Comput. Phys. 2017, 21, 401–422. [Google Scholar] [CrossRef]
- Chung, E.T.; Efendiev, Y.; Leung, W.T. Fast online generalized multiscale finite element method using constraint energy minimization. J. Comput. Phys. 2018, 355, 450–463. [Google Scholar] [CrossRef]
- Chung, E.T.; Pun, S.M. Online adaptive basis enrichment for mixed CEM-GMsFEM. Multiscale Model. Simul. 2019, 17, 1103–1122. [Google Scholar] [CrossRef]
- He, Z.; Chung, E.T.; Chen, J.; Chen, Z. Adaptive generalized multiscale approximation of a mixed finite element method with velocity elimination. Comput. Geosci. 2021, 25, 1681–1708. [Google Scholar] [CrossRef]
- He, Z.; Chen, J.; Chen, Z.; Zhang, T. An online generalized multiscale approximation of the multipoint flux mixed finite element method. J. Comput. Appl. Math. 2024, 437, 115498. [Google Scholar] [CrossRef]
- He, Z.; Chung, E.T.; Chen, J.; Chen, Z. Generalized multiscale approximation of a multipoint flux mixed finite element method for Darcy–Forchheimer model. J. Comput. Appl. Math. 2021, 391, 113466. [Google Scholar] [CrossRef]
- Lie, K.A. An Introduction to Reservoir Simulation Using MATLAB/GNU Octave: User Guide for the MATLAB Reservoir Simulation Toolbox (MRST); Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Gunnar. dwarftools/LearnEDFM: V.1.1.; Zenodo: Geneva, Switzerland, 2016. [Google Scholar] [CrossRef]
- Eymard, R.; Gallouët, T.; Herbin, R. Optimal error bounds for the two-point flux approximation finite volume scheme. Math. Comput. 2025, 94, 2271–2298. [Google Scholar] [CrossRef]
- Chen, J.; Chung, E.T.; He, Z.; Sun, S. Generalized multiscale approximation of mixed finite elements with velocity elimination for subsurface flow. J. Comput. Phys. 2020, 404, 109133. [Google Scholar] [CrossRef]

| #Dofs | , | , | , | |||
|---|---|---|---|---|---|---|
| 25 | 0.0745 | 3.0000 | 0.0745 | 3.0000 | 0.0745 | 3.0000 |
| 50 | 0.0673 | 0.7300 | 0.0782 | 0.7819 | 0.0784 | 0.7826 |
| 75 | 0.0610 | 0.5252 | 0.0852 | 0.6512 | 0.0854 | 0.6525 |
| 100 | 0.0303 | 0.3270 | 0.0871 | 0.6155 | 0.0877 | 0.6182 |
| 125 | 0.0124 | 0.1619 | 0.0921 | 0.5880 | 0.0933 | 0.5917 |
| #Dofs | , | , | , | |||
|---|---|---|---|---|---|---|
| 50 | 0.1037 | 1.3101 | 0.1013 | 1.5461 | 0.2074 | 2.0073 |
| 75 | 0.0148 | 0.2534 | 0.0311 | 0.3569 | 0.0679 | 0.5138 |
| 100 | 0.0061 | 0.1126 | 0.0062 | 0.1245 | 0.0561 | 0.3616 |
| 125 | 0.0020 | 0.0358 | 0.0040 | 0.0657 | 0.0300 | 0.2527 |
| 150 | 7.9617 × 10−4 | 0.0151 | 0.0040 | 0.0565 | 0.0171 | 0.1812 |
| #Dofs | , | , | , | |||
|---|---|---|---|---|---|---|
| 75 | 0.0759 | 0.6927 | 0.0823 | 0.7418 | 0.1336 | 0.8385 |
| 100 | 0.0142 | 0.1958 | 0.0143 | 0.2007 | 0.0384 | 0.3188 |
| 125 | 0.0055 | 0.0735 | 0.0058 | 0.0760 | 0.0243 | 0.1923 |
| 150 | 0.0020 | 0.0257 | 0.0039 | 0.0515 | 0.0097 | 0.1099 |
| 175 | 8.2117 × 10−4 | 0.0112 | 0.0033 | 0.0469 | 0.0040 | 0.0633 |
| #Dofs | , | , | , | |||
|---|---|---|---|---|---|---|
| 100 | 0.0616 | 0.5955 | 0.0720 | 0.5902 | 0.0722 | 0.5907 |
| 125 | 0.0145 | 0.2025 | 0.0115 | 0.1922 | 0.0115 | 0.1925 |
| 150 | 0.0047 | 0.0688 | 0.0027 | 0.0520 | 0.0027 | 0.0520 |
| 175 | 0.0017 | 0.0214 | 8.0132 × 10−4 | 0.0132 | 8.0084 × 10−4 | 0.0132 |
| 200 | 4.4674 × 10−4 | 0.0071 | 1.5293 × 10−4 | 0.0033 | 1.4898 × 10−4 | 0.0032 |
| #Dofs | Fracture 2 | Fracture 3 | ||
|---|---|---|---|---|
| 75 | 0.1156 | 0.7277 | 0.1098 | 0.7177 |
| 100 | 0.0175 | 0.1812 | 0.0141 | 0.1989 |
| 125 | 0.0027 | 0.0529 | 0.0028 | 0.0401 |
| 150 | 3.9197 × 10−4 | 0.0108 | 8.4589 × 10−4 | 0.0108 |
| 175 | 7.2413 × 10−5 | 0.0027 | 1.8707 × 10−4 | 0.0032 |
| #Dofs | ||
|---|---|---|
| 75 | 0.3127 | 0.4936 |
| 100 | 0.1025 | 0.1079 |
| 125 | 0.0445 | 0.0451 |
| 150 | 0.0159 | 0.0145 |
| 175 | 0.0032 | 0.0037 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Wu, B. An Online Generalized Multiscale Method for Embedded Discrete Fracture Model. Axioms 2025, 14, 820. https://doi.org/10.3390/axioms14110820
He Z, Wu B. An Online Generalized Multiscale Method for Embedded Discrete Fracture Model. Axioms. 2025; 14(11):820. https://doi.org/10.3390/axioms14110820
Chicago/Turabian StyleHe, Zhengkang, and Bangmin Wu. 2025. "An Online Generalized Multiscale Method for Embedded Discrete Fracture Model" Axioms 14, no. 11: 820. https://doi.org/10.3390/axioms14110820
APA StyleHe, Z., & Wu, B. (2025). An Online Generalized Multiscale Method for Embedded Discrete Fracture Model. Axioms, 14(11), 820. https://doi.org/10.3390/axioms14110820






