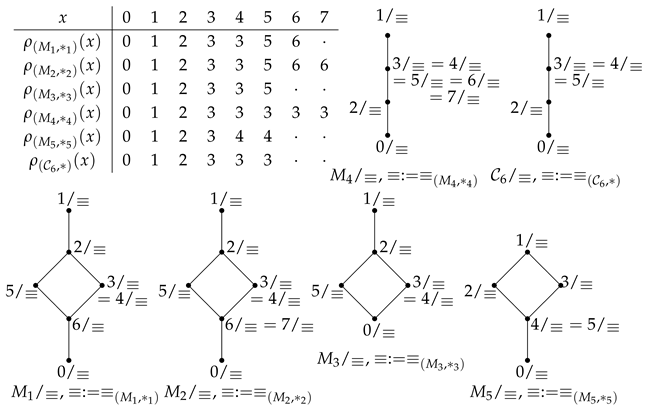
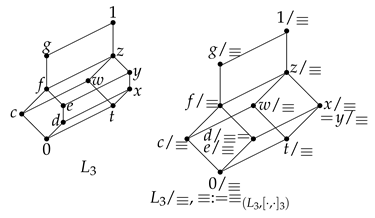
4. The Minimal Prime Spectrum
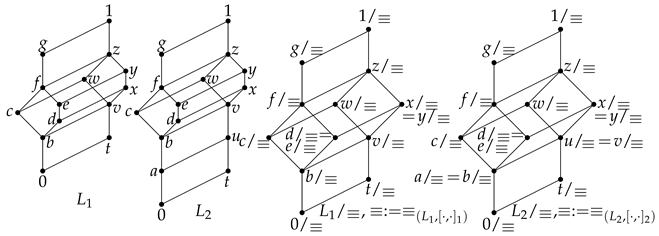
Throughout this section, will be an arbitrary commutator lattice and we will denote , , and by →, ⊥, and ≡, respectively.
Let be a nonempty totally ordered family of prime elements of and . Then and .
Let such that , thus , and, for each , , hence or since is prime.
If for all , then , hence .
If there exists such that , then let and , so that and . Since is totally ordered, we have , hence . We have for all , therefore for all , thus , hence .
Therefore , hence by Lemma 2. (3).
Thus is inductively ordered and clearly the same holds for for any , therefore, by Zorn’s Lemma:
for any , there exists an such that , hence ;
moreover, for any and any , there exists an such that , hence:
Remark 12. For any , we have:
;
if and only if if and only if if and only if if and only if if and only if if and only if ;
if and only if ;
if and only if , which holds if ; recall that, if and , then , so: if and only if ;
clearly, implies ; the converse implication holds if and only if if and only if is an antichain.
Indeed, is an antichain if and only if , case in which .
Now, if implies , then let us assume by absurdum that , that is , so that there exists a . But then , while since ; a contradiction.
4.1. Two Conditions on Commutator Lattices
Let us consider the following conditions on as an arbitrary commutator lattice:
Condition 1. L is algebraic, is closed with respect to the commutator, and .
If L is compact and , then clearly satisfies Condition 1.
As mentioned in
Section 3, by [
10] (Lemma 5.7), if
L is algebraic,
is closed with respect to the commutator,
and
, then
L satisfies Condition 1.
Thus if L is compact and , then satisfies Condition 1.
Condition 2. All principal ideals of generated by minimal prime elements are minimal prime ideals, that is: for any , we have .
As we’ve mentioned in [
6], in any lattice, a principal ideal is prime if and only if its generator is meet–prime, hence any minimal prime principal ideal is generated by a minimal meet–prime element. So the converse of the implication in Condition 2 always holds, thus Condition 2 is equivalent to:
Note that satisfies Condition 2 if all prime ideals of are principal, in particular if all ideals of are principal, that is if is compact, which means that , in particular if , in particular if , that is if L is compact. Thus satisfies Conditions 1 and 2 if L is compact and , in particular if L is compact and .
4.2. m–systems
A subset S of is called an m–system in if and only if, for any , there exists a such that . For instance, if , then S is an m–system; also, if and , then is an m–system in .
Lemma 6. ([
11] (Lemma
))
. If L is algebraic and , then: if and only if is an m–system in . Lemma 7. Let S be a nonempty m–system in and let such that .
- (1)
If L is algebraic, then , in particular, for the case , .
- (2)
If , then the set is nonempty, in particular the set is nonempty.
Proof. (1) This is [
11] (Proposition
).
(2) Let be a nonempty chain in such that for every . Then and . Indeed, assuming by absurdum that there exists some , it follows that and , hence there exist and such that for some . Thus , a contradiction.
Hence the subset of L is inductively ordered, thus it has maximal elements by Zorn’s lemma. □
Proposition 4. If L is algebraic and , then, for any and any , the following are equivalent:
- (1)
;
- (2)
is a maximal element of the set of m–systems of which are disjoint from .
Proof. Since and , that is and , we have , so , and, by Lemma 6, is an m–system.
Note that, since any m–system S is included in , S is disjoint from if and only if .
(1)⇒(2): By Zorn’s Lemma, there exists a maximal element M of the set of m–systems of which include and are disjoint from , so and clearly M is a maximal element of the set of m–systems of which are disjoint from .
By Lemma 7. (1) & (2), there is , so that and , thus , hence , therefore , thus, since L is algebraic, , hence , so , thus , therefore , so is a maximal element of the set of m–systems of which are disjoint from .
(2)⇒(1): Let with .
By Lemma 6, is an m–system, disjoint from since , and . By the hypothesis of this implication, it follows that , that is , therefore , thus, since L is algebraic, . □
Corollary 1. If L is algebraic and , then, for any , the following are equivalent:
;
is a maximal element of the set of m–systems of which do not contain 0.
Proof. By Proposition 4 for . □
4.3. Preparatives for Characterizing Minimal Primes
We will need the following characterization of minimal prime ideals in bounded distributive lattices.
Lemma 8. ([
33])
. For any bounded distributive lattice D and any , the following are equivalent:;
for any , .
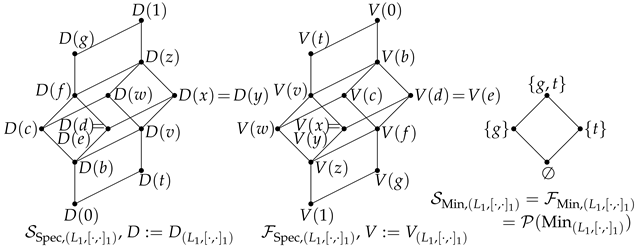
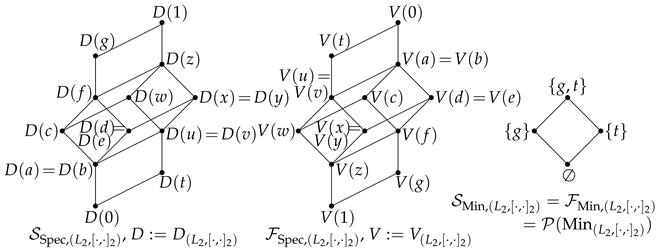
For what follows, recall from Lemma 2. (3) that the prime elements of are the meet–irreducible radical elements in and that all annihilators in are principal lattice ideals of L. Since is a frame, in particular distributive, the prime elements of the commutator lattice are exactly its meet–irreducible elements.
Lemma 9. If , then:
- (1)
for any , ;
- (2)
;
- (3)
for all , and ;
- (4)
is an order isomorphism from to ;
- (5)
is an order isomorphism from to .
Proof. (1) By [
10] (Lemma
).
(2) By [
10] (Proposition
).
(3) By [
10] (Remark
).
(4) By (2), (3) and the fact that and .
(5) By (2) and the definition of radical elements, . Moreover, by (3), for any : if and only if . □
We will follow the reasoning from [
5].
Since and thus for all , it follows that, for any subset S of L which is closed with respect to the join and the commutator operation, is a sublattice of and thus is a distributive lattice.
Hence, if is closed with respect to the commutator operation, then is a sublattice of and thus a distributive lattice with 0, since . So, if and is closed with respect to the commutator operation, then is a bounded sublattice of and thus a bounded distributive lattice.
Let us consider the maps:
, for all , ;
, for all , .
Remark 13. The maps and are order–preserving, since, for all and all :
implies , thus , so ;
implies that , thus .
If is closed with respect to the commutator, then the restriction will be denoted by , as well. Note that, in this case, for every , .
Remark 14. Let . Then since, for any , implies . Thus .
Lemma 10. If is closed with respect to the commutator, then:
for any , ;
for any , .
Proof. Since , we have , so is nonempty.
Let , so that and for some . Then , thus .
Now let and such that . Then and for some and . Hence since and , so .
Therefore .
By Remark 14, since , which is a sublattice of .
Now let , so that for some such that . Then since and , so . Thus . □
If is closed with respect to the commutator, then the corestriction will be denoted by , as well.
Lemma 11. Let and .
If , then .
If S is nonempty and closed with respect to the join and to lower bounds, then if and only if .
In particular, if is closed with respect to the commutator and , then if and only if .
Proof. If , then , thus .
Now assume that S is nonempty and closed with respect to the join and to lower bounds and that . Since , it follows that there exist and such that and . Then , hence . □
Lemma 12. (1) If L is algebraic, then and for all and .
- (2)
If is nonempty and closed with respect to the join and to lower bounds, then . In particular, if is closed with respect to the commutator and , then .
Proof. (1) Let and .
For any , , thus by Lemma 11. Since L is algebraic, it follows that .
Since , we have , thus , hence since L is algebraic.
(2) By Lemma 11, for any , we have: if and only if if and only if for some if and only if for some with if and only if for some with if and only if . Therefore . □
Proposition 5. If Cp(L) is closed with respect to the commutator, then:
- (1)
the map is injective;
- (2)
the map is surjective.
Proof. Assume that Cp(L) is closed with respect to the commutator.
(1) Let such that . By Lemma 12. (2), it follows that .
(2) Let and denote . Again by Lemma 12. (2), it follows that . □
Recall that, if and , then .
Remark 15. If , then, clearly:
Now assume that is closed with respect to the commutator and . If , in particular if , then, for any , we have: I is a proper ideal of if and only if .
Indeed, by Lemma 11: if and only if if and only if if and only if .
Lemma 13. Assume that L is algebraic, is closed with respect to the commutator and . Then:
- (1)
for any , we have ;
- (2)
if , that is if L satisfies Condition 1, then, for any , we have .
Proof. (1) Let , so that is a proper ideal of by Lemma 11 and Remark 15.
Now let such that . Then and for some , so that by the assumption in the enunciation, and , thus by Lemma 11 and Lemma 12. (1). Since p is a prime element of , it follows that or , thus or , again by Lemma 11 and Lemma 12. (1). Hence is a prime ideal of .
(2) Assume that and let , so that P is a proper ideal of and thus by Remark 15.
Let such that , so that and, by Lemma 11 and Lemma 12. (2), . Since P is a prime ideal of the lattice , it follows that or , hence or by Lemma 11. By Lemma 1, it follows that is a prime element of the commutator lattice . □
Proposition 6. If L satisfies Condition 1, then the restrictions and are mutually inverse order isomorphisms.
Proof. By Lemma 13, these maps are well defined.
By (1) and (2) from Lemma 12, we have for any and for any , respectively. Hence these maps are mutually inverse bijections and thus order isomorphisms by Remark 13. □
Lemma 14. Assume that is closed with respect to the commutator and let and .
- (1)
If , then .
- (2)
If , and , then: if and only if .
Proof. Recall that, for any , and, if , then , so if and only if . Thus:
, so, if , then ;
, so, if , then .
(1) Assume that , that is for any which satisfies for all .
Now let such that . Then, for all , , thus . Hence and thus by Lemma 11.
Therefore .
(2) Assume that , and . By (1), we only have to prove the converse implication, so assume that . Then by Lemma 11, so .
Since , according to Lemma 10, thus . □
4.4. Characterizations for Minimal Primes
Remark 16. For any and any , if , then .
Indeed, since and p is a prime element of , we have or , hence the implication above.
Proposition 7. Assume that , let and let us consider the following statements:
- (1)
;
- (2)
for any , implies ;
- (3)
for any , if and only if ;
- (4)
for any , implies ;
- (5)
for any , if and only if .
If L satisfies Condition 1, then statements (1), (2) and (3) are equivalent.
If L satisfies Condition 2, then statements (1), (4) and (5) are equivalent.
Thus, if L satisfies Conditions 1 and 2, in particular if L is compact and , then statements (1), (2), (3), (4) and (5) are equivalent.
Proof. By Remark 16, (2) is equivalent to (3), while (4) is equivalent to (5).
The mutually inverse order isomorphisms between and from Proposition 6 restrict to mutually inverse order isomorphisms between and . Hence: if and only if .
By Lemmas 8 and 10 and Lemma 14. (2), the latter is equivalent to the fact that:
for any , ,
that is, for any , ,
which means that, for any , ,
that is, for any , ,
which is equivalent to the fact that, for any , ,
that is, for any , if , then .
if and only if if and only if ;
if and only if , which is equivalent to by Condition 2.
According to Lemma 8, Remark 6, Lemma 9. (1) and Lemma 3, the latter is equivalent to the fact that:
for any , ,
that is, for any , if , then ,
which means that, for any , if , then ,
that is, for any , if , then ,
which means that, for any , if , then ,
that is, for any , if , then ,
that is, for any , if , then ,
which means that, for any , if , then ,
which is equivalent to the fact that, for any , if , then . □
Recall from [
6] (Example 1) that the equivalence between (1), (4) and (5) in Proposition 7 does not hold for any commutator lattice that satisfies Condition 1 and
.
Remark 17. • , hence .
For any and any , implies .
If and is such that:
for any , implies ,
then: for any such that , implies .
Indeed, since , we have and thus by Remark 9. Hence the equality of the minimal prime spectra.
Now let and , so that and . By Remark 8, Hencethus, if , then , so . Now let such that any satisfies the implication: implies . Let such that and .
Since , it follows that and hence by the assumption on S. By the above, , hence .
satisfies Condition 1 if and only if is algebraic, is closed with respect to , and .
Note that:
if L is algebraic, then is algebraic;
if , then .
Thus, if L satisfies Condition 1, then satisfies Condition 1.
Corollary 2. Let and let us consider the following statements:
- (1)
;
- (2)
for any , implies ;
- (3)
for any , if and only if ;
- (4)
for any , implies ;
- (5)
for any , if and only if ;
- (6)
for any , implies ;
- (7)
for any , if and only if ;
- (8)
for any , implies ;
- (9)
for any , if and only if .
If satisfies Condition 1, in particular if L satisfies Condition 1, then statements (1), (2), (3), (4) and (5) are equivalent.
If satisfies Condition 2, then statements (1), (6), (7), (8) and (9) are equivalent.
Thus, if satisfies Conditions 1 and 2, in particular if is compact and , in particular if L is compact and , then all nine statements above are equivalent.
Proof. By Remark 17, and we have the equivalence: if and only if .
Recall that, for any , .
By Remark 9, and .
By Remark 10, every satisfies , hence, according to Remark 17, properties (2), (3), (4) and (5) are equivalent.
Again by Remark 17, conditions (6), (7), (8) and (9) are equivalent.
From Proposition 7 applied to the quotient commutator lattice we get the rest of the equivalences in the enunciation. □
Corollary 3. Assume that L is algebraic, , is closed with respect to the commmutator and, for all , , and let . Then the following are equivalent:
;
for any , implies ;
for any , if and only if .
Proof. Recall from Remark 17 that, for any , implies .
Since and , we have and thus L satisfies Condition 1.
By Lemma 11, . By Corollary 2 it follows that: if and only if, for any , .
But , so , thus any satisfies: . By Lemma 4. (2), for any , . Hence the equivalences in the enunciation. □
6. (Min–)Admissible Maps
Throughout this section, and will be commutator lattices and will be a map that preserves arbitrary joins.
Then
h is order–preserving and, according to [
32],
h has a unique right adjoint
, that is a map
satisfying:
,
namely: for all , .
Note that preserves arbitrary meets, so it is also order–preserving and, for every and , we have: and .
We consider the direct image of . We call the map h:
admissible if and only if ;
–admissible if and only if .
If h is admissible, respectively –admissible, then we will consider its restriction and corestriction , respectively .
We say that h preserves compactness if and only if .
We also consider two members A and B of a variety of similar algebras whose term–condition commutators are commutative and distributive with respect to arbitrary joins, along with a morphism in .
We denote by the map defined by for all , where denotes the congruence of B generated by Y for any . We denote by : the inverse image of restricted to and corestricted to .
Then
and
are algebraic commutator lattices,
preserves arbitrary joins and the right adjoint of
is
:
. Also,
preserves compactness, because
for any
[
6,
36,
37].
Following [
6], we call the morphism
f:
We use the following notations from [
6]:
,
and
.
Remark 26. For any and , we have: , that is:hence also: . Therefore:
if h is admissible and , then:
and
;
if h is –admissible and , then:
and
.
Thus:
if h is admissible, then:
, so ,
and , so ;
if h is –admissible, then:
,
so ,
and ,
so .
Let us consider the following condition on h:
Condition 3. For any , .
Remark 27. If L and M are algebraic and h preserves compactness and satisfies Condition 3, then: for any , .
Indeed, then, for any , since the commutator is distributive with respect to arbitrary joins and h preserves arbitrary joins, along with the fact that h preserves compactness and the lattice order, we have:
.
Similarly if we replace in Condition 3 the set with any join–dense subset S of L such that is join–dense in M.
By [
4] (Lemma
), if
is congruence–modular, then
satisfies Condition 3. Note that Condition 3 on
or congruence–modularity for
needs to be enforced in Propositions 10–19, Corollaries 3–8, Remark 3 and Theorems 3–7 in [
6].
Remark 28. By [32] (Theorem 1), if for all and for all , then the following are equivalent: h is admissible;
for all , .
Thus, if h is admissible, for all and for all , then:
for all such that , we have, by Proposition 1. (2): ;
thus, if , in particular if , in particular if M is algebraic and , then h satisfies Condition 3.
Remark 29. By [32] (Lemma 7), if L and M are algebraic, for all , for all and h preserves compactness, then . Remark 30. Trivially, the commutator lattice automorphism has , hence is admissible and –admissible. Trivially, preserves compactness and satisfies Condition 3.
Now let , , and be commutator lattices, and , and let us consider the direct product map . Then, clearly:
preserves arbitrary joins if and only if and preserve arbitrary joins;
preserves compactness if and only if and preserve compactness;
satisfies Condition 3 if and only if and satisfy Condition 3.
For all and , , thus .
Consequently, if , and 1 is a neutral element with respect to the commutator in each of , , and , then, by Remark 25:
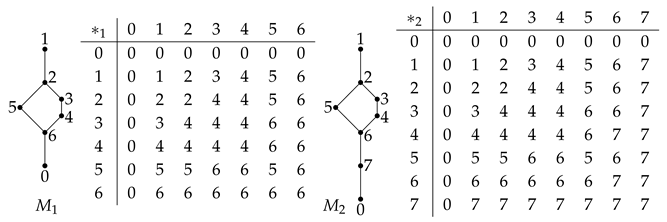
Example 2. Let us consider the commutator lattices in Example 1. Since they are finite and thus compact, trivially any join–preserving map between two of these lattices preserves arbitrary joins and compactness.
Let be the map defined by: and for all , and let , so that , and for all . Note that k and are surjective (bounded) lattice morphisms, while and are, of course, bounded lattice embeddings.
For any , , thus: and for all . For any , , thus: , and for all , which could also have been obtained from the definition of and Remark 30. and are surjective (bounded) lattice morphisms, as well, so we may calculate their right adjoints.
For any , and , thus . Now we can apply Remark 30 or make the direct verification: for any , and , thus .
Notice that none of the maps , , , , k and is a commutator lattice morphism. k and satisfy Condition 3, while fails Condition 3, so, as expected from Remark 30, and satisfy Condition 3, while fails Condition 3.
and , thus and , hence k, , and are admissible and –admissible. Of course, the (–)admissibility of the first two is equivalent to that of the last two, by Remark 30.
and , thus and , hence and are admissible and –admissible. Again, the (–)admissibility of the former is equivalent to that of the latter, by Remark 30.
Note that is a join–semilattice morphism, but not a lattice morphism and it does not preserve the commutator, but it satisfies Condition 3, thus the same holds for . Let us also consider the surjective commutator lattice morphisms , defined by and for all , and ; since they preserve the commutator, in particular they satisfy Condition 3. We will apply Remark 30.
For all , , thus , hence .
For all , , so and for all , hence is a lattice morphism, but not a bounded lattice morphism, thus clearly so is .
For all , , so , thus .
, but , thus l is admissible, but not –admissible, hence is admissible, but not –admissible.
and , thus and are neither admissible, nor –admissible, hence and are neither admissible, nor –admissible.
Finally, let us consider the bounded lattice embeddings
and
, along with the neither injective, nor surjective bounded lattice morphism
, neither of which satisfy Condition 3, in particular neither preserves the commutators:
| s | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 1 | 5 | 6 | 4 | 2 | · |
| 0 | 1 | 2 | 3 | 5 | 4 | · |
| 0 | 1 | 3 | 2 | 2 | 3 | 2 |
We have
and
, defined by:
and
for any
. Also,
,
for all
. So these maps are given by the following tables, which show that
and
are not join–preserving, but
is a bounded lattice morphism, so we may calculate
,
for all
. We obtain the following definition, which shows that
does not preserve the join.
| s | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 1 | 5 | 3 | 4 | 2 | 3 | 4 |
| 0 | 1 | 2 | 3 | 5 | 4 | 5 | 5 |
| 0 | 1 | 3 | 2 | 3 | 3 | · | · |
| 0 | 1 | 3 | 4 | 0 | 0 | 0 | · |
and , while and , thus j and n are admissible and –admissible;
and , while and , hence i and are –admissible, but not admissible.
Lemma 19. If h preserves compactness and satisfies Condition 3, then, for any m–system S in , is an m–system in .
Proof. Since h preserves compactness, .
Let , so that and for some . Since S is an m–system in , there exists such that . Then and, since h is order–preserving and satisfies Condition 3, . □
Lemma 20. Assume that L and M are algebraic, and h preserves compactness and satisfies Condition 3.
If h is admissible, then .
If h is –admissible, then .
Proof. Assume that h is admissible or –admissible, so that .
Let , thus . Since L is algebraic, it follows that is an m–system in , hence is an m–system in by Lemmas 6 and 19.
By Lemma 7, there exists a , so and , thus there exists an with and hence , that is , so each satisfies:
if , then ,
that is: if , then ,
otherwise written: if , then ,
therefore, since L is algebraic: .
Since and , it follows that .
Hence . If h is –admissible, then the converse inclusion holds, as well. □
Lemma 21. If L and M are algebraic, , h is –admissible, preserves compactness and satisfies Condition 3, then, for any :
;
;
;
.
Proof. Let . By Lemma 20, there exists an such that . By Remark 26:
if and only if ;
if and only if .
Therefore:
,
,
,
.
By Remark 26, the converse inclusions hold, as well. □
Lemma 22. Assume that L and M are algebraic, , h is –admissible, preserves compactness and satisfies Condition 3 and let .
- (1)
If and either satisfies Condition 2 or and satisfies Condition 1, then:
;
;
;
.
- (2)
If and either satisfies Condition 2 or (in particular if ) and satisfies Condition 1, then:
;
;
;
.
- (3)
If , and either and satisfy Condition 2 or and and satisfy Condition 1, then:
;
;
;
.
Proof. By Lemma 21 and Proposition 8. □
Theorem 3. If L and M are algebraic, , h is –admissible, preserves compactness and satisfies Condition 3, then:
- (1)
is continuous with respect to the Stone topologies and the flat topologies;
if one of the following holds:
and satisfies one of the Conditions 1 and 2,
and satisfies one of the Conditions 1 and 2,
then is continuous;
if and satisfies one of the Conditions 1 and 2, then:
if , in particular if is closed with respect to the polar, then is continuous;
if and satisfies one of the Conditions 1 and 2, then:
if , in particular if is closed with respect to the polar, then is continuous;
- (2)
if is injective, then:
if , then is a homeomorphism with respect to the Stone topologies;
if , then is a homeomorphism with respect to the flat topologies;
if one of the following holds:
, satisfies one of the Conditions 1 and 2, and is closed with respect to the polar,
, satisfies one of the Conditions 1 and 2 and ,
, satisfies one of the Conditions 1 and 2 and ,
then is a homeomorphism;
if one of the following holds:
, satisfies one of the Conditions 1 and 2 and ,
, satisfies one of the Conditions 1 and 2 and ,
, satisfies Condition 2 and ,
, satisfies one of the Conditions 1 and 2 and ,
, satisfies Condition 2 and ,
then is a homeomorphism.
Proof. Assume that L and M are algebraic, , h is –admissible, preserves compactness and satisfies Condition 3.
(1) By Lemma 21:
for any , , therefore is continuous with respect to the Stone topologies;
for any , and , thus is continuous with respect to the flat topologies.
By Lemma 22. (1), if and satisfies Condition 1, respectively Condition 2, then, for any , respectively any :
, thus is continuous;
, thus, if , in particular if is closed with respect to the polar (in view of the fact that h preserves compactness), then is continuous.
By Lemma 22. (2), if and satisfies Condition 1, respectively Condition 2, then, for any , respectively any :
, thus is continuous;
, thus, if , in particular if is closed with respect to the polar (in view of the fact that h preserves compactness), then is continuous.
(2) Now assume, furthermore, that is injective. By Lemma 20, it is also surjective, thus it is bijective.
By Lemma 21, for any :
, thus, if , then is open with respect to the Stone topologies, thus it is a homeomorphism with respect to the Stone topologies by (2);
, thus, if , then is open with respect to the flat topologies, thus it is a homeomorphism with respect to the flat topologies by (2).
By Lemma 22. (1), if and satisfies Condition 1, respectively Condition 2, then, for any , respectively any :
, thus, if and is closed with respect to the polar, then is open, thus it is a homeomorphism by (1);
, thus, if , then is open, thus it is a homeomorphism by (1);
, thus, if , then is open, thus it is a homeomorphism by (1);
, thus, if either or fulfills Condition 2 and , then is open, thus it is a homeomorphism by (1).
By Lemma 22. (2), if and satisfies Condition 1, respectively Condition 2, then, for any such that (in particular any ), respectively any :
, thus, if , then is open, thus it is a homeomorphism by (1);
, thus, if either or satisfies Condition 2 and , then is open, thus it is a homeomorphism by (1). □
Corollary. 5 If , f is –admissible and satisfies Condition 3, then:
- (1)
is continuous with respect to the Stone and the flat topologies;
if one of the following holds:
A is semiprime and satisfies one of the Conditions 1 and 2,
B is semiprime and satisfies one of the Conditions 1 and 2,
then is continuous;
if A is semiprime and satisfies one of the Conditions 1 and 2, then:
if , in particular if is closed with respect to the polar, then is continuous;
if B is semiprime and satisfies one of the Conditions 1 and 2, then:
if , in particular if is closed with respect to the polar, then is continuous;
- (2)
if is injective, then:
if , then is a homeomorphism with respect to the Stone topologies;
if , then is a homeomorphism with respect to the flat topologies;
if one of the following holds:
A is semiprime, satisfies one of the Conditions 1 and 2, and is closed with respect to the polar,
A is semiprime, satisfies one of the Conditions 1 and 2 and ,
B is semiprime, satisfies one of the Conditions 1 and 2 and ,
then is a homeomorphism;
if one of the following holds:
A is semiprime, satisfies one of the Conditions 1 and 2 and ,
A is semiprime, satisfies one of the Conditions 1 and 2 and ,
A is semiprime, satisfies Condition 2 and ,
B is semiprime, satisfies one of the Conditions 1 and 2 and ,
B is semiprime, satisfies Condition 2 and ,
then is a homeomorphism.
Remark 31. Note, in Theorem 3, that, whenever is continuous with respect to two of these topologies, its direct image is a complete morphism of join–semilattices between them as bounded sublattices of the power sets of the minimal prime spectra. Clearly, when it is a homeomorphism, its direct image is a lattice isomorphism.
In view of the definition of , in Corollary 5, whenever is continuous with respect to two of these topologies, its direct image is a complete lattice morphism between them as bounded sublattices of the power sets of the minimal prime spectra of congruences. Of course, again, when it is a homeomorphism, its direct image is a lattice isomorphism.