Enhancing Classification Results of Slope Entropy Using Downsampling Schemes

Abstract

Entropy calculation provides meaningful insight into the dynamics and complexity of temporal signals, playing a crucial role in classification tasks. These measures are able to describe intrinsic characteristics of temporal series, such as regularity, complexity or predictability. Depending on the characteristics of the signal under study, the performance of entropy as a feature for classification may vary, and not any kind of entropy calculation technique may be suitable for that specific signal. Therefore, we aim to increase entropy’s classification accuracy performance, specially in the case of Slope Entropy (SlpEn), by enhancing the information content of the patterns present in the data before calculating the entropy, with downsampling techniques. More specifically, we will be using both uniform downsampling (UDS) and non-uniform downsampling techniques. In the case of non-uniform downsapling, the technique used is known as Trace Segmentation (TS), which is a non-uniform downsampling scheme that is able to enhance the most prominent patterns present in a temporal series while discarding the less relevant ones. SlpEn is a novel method recently proposed in the field of time series entropy estimation that in general outperforms other methods in classification tasks. We will combine it both with TS or UDS. In addition, since both techniques reduce the number of samples that the entropy will be calculated on, it can significantly decrease the computation time. In this work, we apply TS or UDS to the data before calculating SlpEn to assess how downsampling can impact the behaviour of SlpEn in terms of performance and computational cost, experimenting on different kinds of datasets. In addition, we carry out a comparison between SlpEn and one of the most commonly used entropy calculation methods: Permutation Entropy (PE). Results show that both uniform and non-uniform downsampling are able to enhance the performance of both SlpEn and PE when used as the only features in classification tasks, gaining up to 13% and 22% in terms of accuracy, respectively, when using TS and up to 10% and 21% when using UDS. In addition, when downsampling to 50% of the original data, we obtain a speedup around ×2 with individual entropy calculations, while, when incorporating the downsampling algorithms into time count, speedups with UDS are between ×1.2 and ×1.7, depending on the dataset. With TS, these speedups are above ×2, while maintaining accuracy levels similar to those obtained when using the 100% of the original data. Our findings suggest that most temporal series, specially medical ones, have been measured using a sampling frequency above the optimal threshold, thus obtaining unnecessary information for classification tasks, which is then discarded when performing downsampling. Downsampling techniques are potentially beneficial to any kind of entropy calculation technique, not only those used in the paper. It is able to enhance entropy’s performance in classification tasks while reducing its computation time, thus resulting in a win-win situation. We recommend to downsample to percentages between 20% and 45% of the original data to obtain the best results in terms of accuracy in classification tasks.

1. Introduction

The concept of entropy originates in information theory and statistical mechanics as a quantitative measure of uncertainty or information content in a system. Given a discrete probability function $P=p_1,p_2,\dots ,p_N$, the Shannon Entropy [1] is defined as:

$$H\left(P\right)=-\sum _{i=1}^N{p}_i\log p_i$$

(1)

where $p_i\ge 0$ and ${\displaystyle \sum _{i=1}^N}{p}_i=1$. Entropy reaches its maximum when all outcomes are equally likely ($p_i={\displaystyle \frac{1}{N}}$), and its minimum when one outcome has its probability equal to 1 (i.e., full determinism). In the context of time series analysis, entropy-based methods quantify the degree of regularity, complexity, or predictability of a temporal signal ${x_t}_{t=1}^T$. A low entropy value indicates highly regular or deterministic dynamics, while high entropy suggests complex, stochastic, or chaotic behavior. Most entropy methods rely on computing its value with the mentioned Shannon expression, but there are many variations where the estimator uses Rényi Entropy [2] (Equation (2)) or Tsallis Entropy [3] (Equation (3)). These frameworks underpin the mathematical foundation of entropy as measures of uncertainty, diversity, or disorder, concepts that Slope Entropy adapts to geometric and temporal features of real-world time series.

$$H_{\alpha }\left(P\right)={\displaystyle \frac{1}{1-\alpha }}\log \left(\sum _i{p}_i^{\alpha }\right);\alpha >0,\alpha \ne 1$$

(2)

$$H_q\left(P\right)={\displaystyle \frac{1}{q-1}}(1-\sum _i{p}_i^q)$$

(3)

The patterns that entropy-based methods identify correspond to recurring motifs or dynamical signatures within the time series. Mathematically, entropy quantifies the dispersion or uniformity of the pattern distribution in the reconstructed state space. Let $\Omega$ denote the set of all admissible patterns, and let $p\left(\omega \right)$ be the empirical probability of observing pattern $\omega \in \Omega$. The entropy measures the heterogeneity of $p\left(\omega \right)$:

$$\begin{array}{c}\hfill H\left(p\right)=0\iff \exists {\omega }_0:p\left({\omega }_0\right)=1,\\ \hfill H\left(p\right)=\log |\Omega |\iff p\left(\omega \right)={\displaystyle \frac{1}{|\Omega |}}\forall \omega \end{array}$$

(4)

Thus, entropy-based analysis detects whether the system’s evolution is dominated by a few deterministic configurations or explores the available pattern space uniformly: it is a hallmark of stochastic or chaotic dynamics.

Entropy analysis for time series has been playing a crucial role in many scientific domains, such as economy and finances [4,5,6,7], biology and medicine [8,9,10,11] and engineering [12,13,14,15], among others. One of its main applications is using it as a feature for signal classification [16,17,18,19,20], since entropy calculation is able to provide very valuable insights into the predictability, dynamics and complexity of the studied signals. Nowadays there are many different entropy estimation methods, but the recently proposed Slope Entropy (SlpEn) shows promise in the field of signal classification, since it is able to capture the different intricacies of the patterns found in a signal, taking advantage of both the amplitude of the analysed temporal series and the symbolic representation of its intrinsic patterns.

SlpEn was introduced in 2019 by Cuesta-Frau [21]. It takes advantage of the slope between two data samples to estimate entropy in a Shannon entropy-fashion. Making use of two different thresholds, $\delta$ and $\gamma$, as well as the basic subsequence length m, it is able to transform the original time series into a symbolic representation of data subsequences (patterns) according to the differences between consecutive time series samples. The specifics will be described later in Section 2.2. Making use of the three mentioned parameters, as well as the slope between two data samples, SlpEn is allowed to be more customizable and refined when analyzing temporal series, although it requires more input parameters compared to other of the most commonly used entropy calculation methods, such as Permutation Entropy (PE) [22] (see Section 2.3 for further details).

The original SlpEn paper gives some guidelines regarding the selection of values for both $\delta$ and $\gamma$, proving it is well behaved under many different conditions. It has been successfully applied in other works, such as [23,24,25], achieving in most cases better results than other most commonly used entropy calculation methods like Permutation, Approximate or Sample Entropy [26]. In addition, there has been some research to study how to improve SlpEn’s performance by removing $\delta$ from its parameters [27] or taking an asymmetric approach with respect to the values of $\gamma$ [28]. SlpEn has also been successfully applied in combination with other entropy calculation methods [29], signal decomposition methods like VMD or CEEMDAN [30,31], optimization algorithms for choosing the best SlpEn parameters, like the snake optimizer [32], and also using different time scales [33].

In this paper, we aim to further improve SlpEn classification capabilities by combining it with downsampling techniques, such as Trace Segmentation (TS), which is a non-uniform downsampling scheme [34,35,36], but also with uniform downsampling (UDS). TS (detailed in Section 2.4) allows to reduce the size or length of the input temporal series, choosing the samples of the original series where the greatest variation between them occurs, thus enhancing the peaks of the signal at the cost of discarding less significant values. TS has already been successfully applied in combination with Sample Entropy [37], showing great results and inquiring in many advantages, including shorter computation time and better accuracy results in most cases. We hypothesize that these benefits can be applied to any entropy calculation method, not only to Sample Entropy. Additionally, in the case of SlpEn, we expect that the enhancement of obtained results will be higher than those obtained with other entropy calculation methods, since SlpEn bases its calculation on the differences between samples and TS is able to downsample a sequence choosing the samples where the biggest difference occurs, thus increasing differences among them.

Additionally, we also implemented UDS (Section 2.5), which allows us to downsample the series uniformly, as its name suggests, up to the desired number of samples. Since non-uniform downsampling has already been applied successfully to entropy-based classification methods, we will try to reproduce similar results with the uniform method, since it is highly correlated to effectively using temporal scales in entropy calculation [38]: using entropy with $\tau =2$ is equivalent to downsample to 50%, with $\tau =3$, to downsampling to 33%, and so on.

Our main hypothesis for applying downsampling is that most features present in datasets and that are considered key in classification tasks belong in certain frequency bands that are below the sampling frequency, thus noise and confounding data is added to the temporal record and classification accuracy is hindered. To support it, we have chosen a comprehensive benchmark that is comprised of seven different datasets from different fields that belong to different domains. For further details on each one of the datasets that comprise our benchmark, refer to Section 2.1. In EEG recordings, as it is the case of the Bonn EEG and Bern-Barcelona datasets we use in the present work, the data is divided into bands, mainly five: Delta, Theta, Alpha, Beta and Gamma. Then, from these bands, one can extract components to perform classification tasks. Four of these bands (Delta, Theta, Alpha and Beta) are below 30 Hz, whereas the sampling frequencies for Bonn EEG and Bern-Barcelona are 173.61 Hz and 512 Hz respectively, which is way above 30 Hz, or even 60 Hz, which would be the minimal sampling frequency to capture all information from these bands while avoiding loss, according to the Nyquist-Shannon sampling theorem [39,40]. Only using such low frequency bands, classification tasks for different applications, such as epileptic seizures, can be performed with relative ease, such as demonstrated in the works [41,42,43,44]. With the Fantasia RR database, which is comprised of ECGs, something similar happens. The database is sampled at 250 Hz, but the main HRV frequency bands are the Low-Frequency (LF) band (0.04–0.15 Hz) and High-Frequency (HF) band (0.15–0.4 Hz) [45,46], even some references going up to approximately 0.9 Hz with respiration signals [47]. With the Paroxysmal Atrial Fibrillation (PAF) prediction dataset, which is also a ECG-comprised database, the exact same thing happens, its sampling rate is 128 Hz, way more than double of the minimum needed, which would be around 30 Hz if the HRV signal is band-pass filtered between 5 Hz and 15 Hz [48,49].

Outside the medical field, we have three more datasets. First, we have the House Twenty database, which contains electricity consumptions, sampled at 8-s interval, which would be a frequency of 0.125 Hz. Next, the Worms Two-Class dataset. This one contains recordings of mutant and non-mutant worms movements. These were sampled at 30 Hz. Finally we have the Ford A dataset, which measures engine noise. Up to our knowledge, there is no reference as how the noise data was captured nor any sampling rate, it is only said that it is “engine noise”, and that the dataset was used for a competition in a 2008 IEEE World Congress on Computational Intelligence. Note that, in these cases, we do not know the ideal frequency components to perform classification tasks, so we do not know the ideal sampling rate for each case neither. Regardless, we are interested to see if, what we think is applicable to medical EEG and ECG datasets, it is also feasible to non-medical datasets.

We have applied TS or UDS as a data processing technique before performing entropy calculation. Since these techniques allow to reduce the temporal sequence in size as much as we want, we have applied downsampling to obtain sequences downsampled from $10\%$ to $70\%$ in $1\%$ steps. Then, we calculate SlpEn on the downsampled sequences, comparing the results, in terms of classification accuracy, with the ones achieved with no downsampling or, in other words, the original time series without applying TS nor UDS. Such comprehensive experiment will allow to see if there is some specific percentage of downsampling more appropriate to improve classification accuracy. In addition, the same experiment has been performed with one of the most commonly used entropy calculation methods: Permutation Entropy. Comparing the results achieved by the two different entropies will show how each entropy, as well as TS and UDS, behave under different conditions. The experiments are explained in more detail in Section 3.1. In order to carry them out, we will make used of the benchmark mentioned previously. As it has many varied datasets, it will make it possible to evaluate the effectiveness of each method.

The main contribution of this paper is to show how downsampling techniques can be applied effectively in combination with not only SlpEn, but with any entropy calculation methodology in order to improve results in terms of classification accuracy. In addition, in most cases applying downsampling before calculating the entropy value of a temporal series will lead to faster computation times: calculating the downsampled series and then obtaining its entropy value is much cheaper, in terms of computational cost, than calculating the entropy value of the original non-downsampled sequence. To sum up: using downsampling will not only allow to enhance the results in classification tasks, but also to obtain them faster.

The organization of the paper is the following: Section 2, Materials and Methods, presents a comprehensive review of both the benchmark used in the experiments, having a look into each individual dataset, and the specifics of the four different methods used in the experiments: SlpEn, PE, TS and UDS. Next, in Section 3, the specifics of how the experiments have been executed are explained, while also presenting the results, paying attention to how TS and UDS affect the accuracy results achieved by both SlpEn and PE. In addition, the time of execution will also be taken into account to show the benefits gained in timing after applying downsampling. A discussion of the results will take place in Section 4, where the results are evaluated, as well as the implications of using downsampling to enhance the discriminating power of entropy when used as a feature for classification. Finally, the paper concludes in Section 5, where we summarize the main contributions of this paper and highlight potential future research directions which can enhance SlpEn’s capabilities, or other entropy techniques, in different contexts.

2. Materials and Methods

This section presents the benchmark utilized in the experiments, as well as the methodologies and techniques used. The benchmark is comprised of a total of seven different datasets, coming each one from a different background and captured for different purposes, although in this case all of them have been used in classification tasks. All of them are publicly available, and have been used in many different studies, making them very reputed representatives time series for analysis, allowing for easy comparison between the obtained results and previous ones in different studies. In addition, the specific datasets have been carefully selected so that they are diverse in their intrinsic characteristics, such as length, number of samples, background, etc., ensuring that the results have high potential for generalization and mitigating any possible bias, both in interpretation or regarding the values of the time series themselves.

Apart from the benchmark, this section will also focus on the insights of the techniques used in the experiments: entropy calculation methods, mainly Slope Entropy and Permutation Entropy, and the downsampling techniques, Trace Segmentation (TS) and Uniform Downsampling (UDS). We will review how both entropies work, as well as explaining how TS and UDS perform their downsampling. Combining TS or UDS with both types of entropy, and then comparing results with different levels of downsampling will be the main point of the experiments that have been carried out and that will be presented, along with the results, in Section 3.

2.1. Benchmark

As previously stated, in order to assess both the resilience and efficacy of the proposed combination of downsampling with SlpEn, it is imperative to conduct experiments on diverse datasets that exhibit several variations in many time series characteristics, such as level of ties, length or regularity. Thus, the specific datasets contained in the benchmark used in this present work are:

• Bonn EEG dataset [50,51]. This dataset comprises 4097 electroencephalograms (EEGs), each with a duration of 23.6 s. The instances are categorized into five distinct classes (A, B, C, D, and E), representing different neural activity scenarios. Classes A and B correspond to healthy subjects with eyes open and closed respectively. Classes C, D, and E pertain to different classifications of epileptic subjects (see further details in [50]). For the specific experiments in the present paper, we focused only on classes D and E, with 50 records from each class. Class D corresponds to seizure-free periods at the epileptogenic zone, whilst seizure activity from the hippocampal focus pertains to class E. This dataset has been extensively used in numerous scientific works, being [10,52,53] examples of such research.
• Bern–Barcelona EEG database [54]. This dataset includes both non-focal and focal time series extracted from seizure-free recordings of patients with pharmacoresistant focal-onset epilepsy. The classes have 427 and 433 records each, each record being sampled at a sampling frequency of 512 Hz and being comprised of 272 data points. It has been used in other classification studies, including the works [55,56,57], which reviewed the results achieved using time series from this database.
• Fantasia RR database [58]. It showcases a carefully selected collection consisting of 40 distinct time series, divided into two groups of 20 records each, where one of these two groups corresponds to youthful subjects, whereas the other is comprised of data from mature subjects. All subjects were initially in good health, thus eliminating potential health-related variables. The monitoring duration lasted 120 min, and the sampling frequency was set at 250 Hz. This database has been utilized in various studies, including [59,60].
• Ford A dataset [61]. It is a collection of data extracted from a specific automotive subsystem. The primary purpose of its creation was to empirically evaluate the effectiveness of classification schemes on the acoustic characteristics of engine noise. From this experimental project, a set of 40 distinct records was carefully chosen and utilized for analysis from each individual class. Examples of research where this dataset has been used are [62,63].
• House Twenty dataset [64,65]. This dataset consists of temporal sequences originating from 40 different households as part of the Personalised Retrofit Decision Support Tools for UK Homes using Smart Home Technology (REFIT) project. This dataset includes two classes with 20 recordings in each, thus having the dataset data from 40 different households. One of the classes represents overall electricity consumption, while specific electrical consumption of washing machines and dryers is represented on the other. This dataset belongs to the UCR archive [66,67].
• PAF (Paroxysmal Atrial Fibrillation) prediction dataset [68]. This dataset comprises discrete 5-min temporal recordings from patients diagnosed with PAF. The recordings are classified into two categories: one preceding the onset of a PAF episode and the other representing instances distant from any PAF manifestation. A total of 25 distinct files is included in each category. This dataset is widely known and used in many and varied scientific research [69,70,71].
• Worms two-class dataset [72,73]. It is comprised of time series data from a certain species of worm. More specifically, it refers to locomotive patterns, which are used in behavioral genetics research. The records are selected from two classes: non-mutant and mutant worms. The first class consists of 76 records, while the second class has 105 records. Both classes share the time series length, which is 1800 samples. Similar to the other datasets, this one has been utilized in various scientific works [74,75].

2.2. Slope Entropy

SlpEn [21] is a method for calculating entropy by extracting symbolic subsequences through the application of thresholds to amplitude differences between consecutive samples of a time series. The resulting histogram of relative frequencies is then subjected to a Shannon entropy-like expression, allowing to obtain the final result, which is the SlpEn value. This method operates on an input time series $\mathbf{x}$ with input parameters N, m, $\gamma$ and $\delta$, aiming to compute SlpEn$(N,m,\gamma ,\delta )$.

The input time series $\mathbf{x}$ is considered as an N-length vector which contains the samples $x_i$, and it is then defined as $\mathbf{x}=\{x_0,x_1,x_2,\dots ,x_{N-1}\}$, $x_i\in \mathbb{R}$, $0\le i<N$. The time series is divided iteratively into overlapping data epochs of length m, denoted as ${\mathbf{x}}_j=\{x_{j+0},x_{j+1},\dots ,x_{j+m-1}\}$, $0\le j<N-m+1$, with j incremented after each iteration as $j\to j+1$.

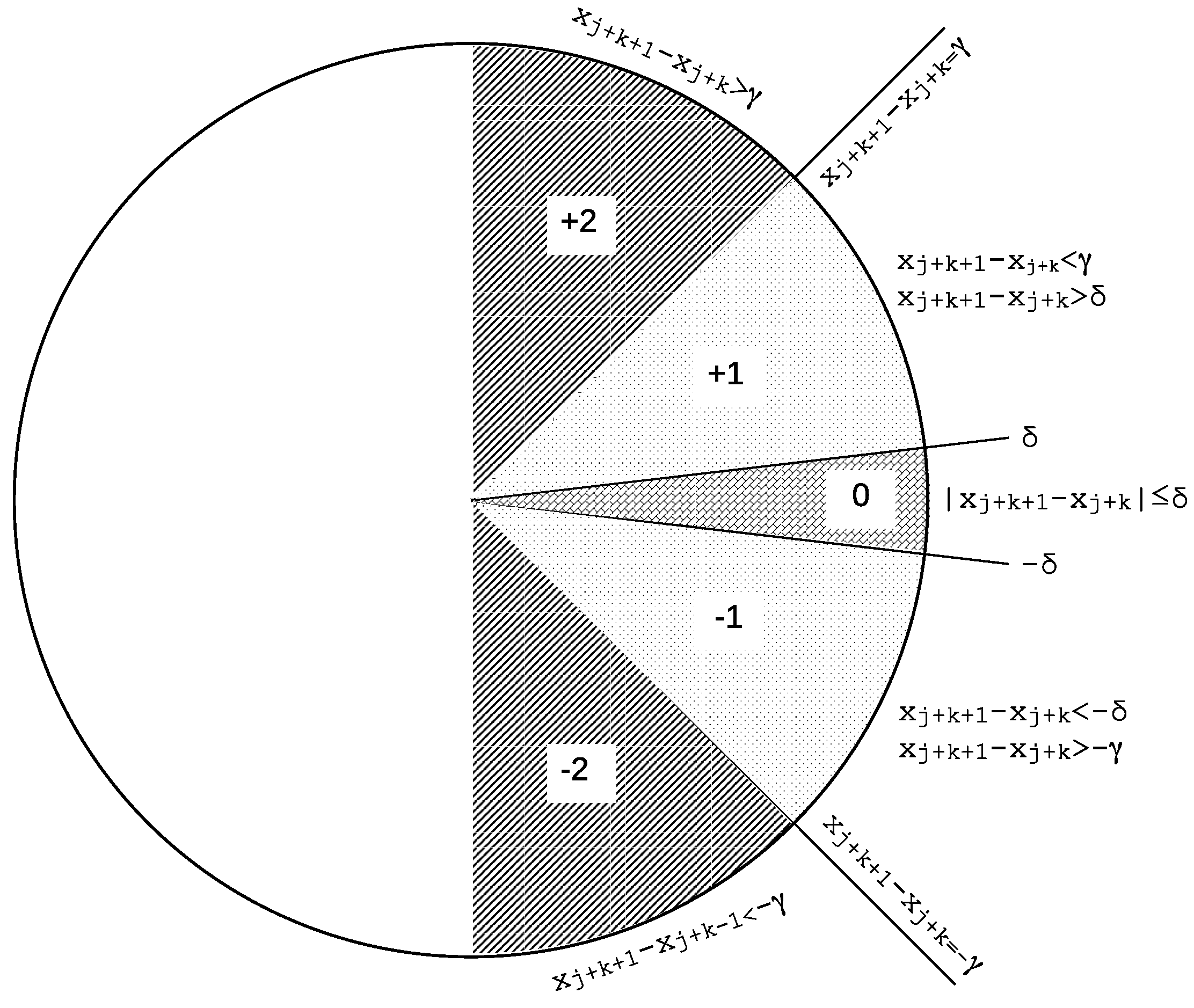
For each subsequence, a symbolic pattern is generated, ${\mathbf{x}}_j\to {\psi }_j$, where ${\psi }_j=\{{\psi }_0=f(x_{j+1}-x_{j+0}),{\psi }_1=f(x_{j+2}-x_{j+1}),\dots ,{\psi }_{m-2}=f(x_{j+m-1}-x_{j+m-2})\}$. The symbols used in the pattern are selected from a set $S=\{+2,+1,0,-1,-2\}$, based on a thresholding function f. The function relies on two different thresholds, $\delta$ and $\gamma$. These two thresholds can take any positive real value with the restriction $\delta <\gamma$, and the following rules (that apply for $0\le k<m-1$):

• If $x_i>x_{i-1}+\gamma$, +2 (or just 2) is the symbol be assigned to the current active symbolic string position, ${\psi }_j={\psi }_j+\{+2\}$.
• If $x_i>x_{i-1}+\delta$ and $x_i\le x_{i-1}+\gamma$, +1 (or just 1) is the symbol to be assigned to the current active symbolic string position, ${\psi }_j={\psi }_j+\{+1\}$.
• If $|x_i-x_{i-1}|\le \delta$, 0 is the symbol to be assigned to the current active symbolic string position, ${\psi }_j={\psi }_j+\left\{0\right\}$. This is the case when, depending on threshold $\delta$, two consecutive values are very similar, which could be the case for ties [76].
• If $x_i<x_{i-1}-\delta$ and $x_i\ge x_{i-1}-\gamma ,-$ 1 is the symbol to be assigned to the current active symbolic string position, ${\psi }_j={\psi }_j+\{-1\}$.
• If $x_i<x_{i-1}-\gamma$, −2 is the symbol to be assigned to the current active symbolic string position, ${\psi }_j={\psi }_j+\{-2\}$.

Possible ties are handled with the use of the threshold $\delta$ [21]. It also tries to avoid incorrect conclusions [77]. On the other hand, $\gamma$ is used to differentiate between low and high consecutive sample gradients. In the standard configuration described in the SlpEn seminal paper [21], $\delta$ is recommended to take a small value, 0.001, while $\gamma$ is typically a constant value close to 1.0, depending on the normalization of the input time series. These thresholds are applied to both negative and positive gradients just by changing the sign. This symmetrical baseline scheme has achieved very good results in classification tasks performed in many works, such as [24,29,78,79,80].

Figure 1 is a visual representation of how the regions defined by the two thresholds described above. This representation follows the standard symmetric SlpEn approach described in its original paper [21] and utilized in previous scientific studies, as well as in the experiments described in this paper.

After computing all the symbolic patterns, the histogram bin height is calculated by counting the total number of occurrences for each pattern, and it is then normalized by the number of unique different patterns found. These normalized values are referred to as $p_k$. Finally, a Shannon entropy expression is used to obtain the SlpEn value for the temporal series $\mathbf{x}$ using the input parameters m, $\delta$ and $\gamma$:

$$\mathrm{SlpEn}(\mathbf{x},m,\gamma ,\delta )=-\sum _{\forall k}{p}_k\log p_k$$

(5)

All the steps needed to compute SlpEn are shown in Algorithm 1. Note that, contrary to the basic algorithm presented in [21], this one is optimized so that the patterns from the last subsequence are reused in the current one, instead of computing them all each time.

Algorithm 1 Slope Entropy (SlpEn) Algorithm

Input:  Time series $\mathbf{x}$, embedded dimension $m>2$, length $N>m+1$, $\delta$, $\gamma >\delta$ Initialisation:  $SlpEn=0$, slope pattern counter vector $\mathbf{c}\leftarrow \{\varnothing \}$, slope patterns relative frequency vector $\mathbf{p}\leftarrow \{\varnothing \}$, list of slope patterns found ${\Psi }^{\mathbf{m}}\leftarrow \{\varnothing \}$ for  $i=1,\dots ,m-1$ do     if $(x_i-x_{i-1})\in [-\delta ,\delta ]$ then ${\psi }^0\leftarrow 0$ end if     if $(x_i-x_{i-1})\in ]\delta ,\gamma ]$ then ${\psi }^0\leftarrow 1$ end if     if $(x_i-x_{i-1})\in ]\gamma ,\infty [$ then ${\psi }^0\leftarrow 2$ end if     if $(x_i-x_{i-1})\in [-\gamma ,-\delta [$ then ${\psi }^0\leftarrow -1$ end if     if $(x_i-x_{i-1})\in ]-\infty ,\gamma [$ then ${\psi }^0\leftarrow -2$ end if end for ${\Psi }^{\mathbf{m}}\leftarrow {\psi }^0$ $\mathbf{c}\leftarrow 1$ for  $j=1,\dots ,n-m$  do     for $i=1,\dots ,m-1$ do         ${\psi }^j\leftarrow {\psi }_i^{j-1}$     end for     if $(x_i-x_{i-1})\in [-\delta ,\delta ]$ then ${\psi }^j\leftarrow 0$ end if     if $(x_i-x_{i-1})\in ]\delta ,\gamma ]$ then ${\psi }^j\leftarrow 1$ end if     if $(x_i-x_{i-1})\in ]\gamma ,\infty [$ then ${\psi }^j\leftarrow 2$ end if     if $(x_i-x_{i-1})\in [-\gamma ,-\delta [$ then ${\psi }^j\leftarrow -1$ end if     if $(x_i-x_{i-1})\in ]-\infty ,\gamma [$ then ${\psi }^j\leftarrow -2$ end if     $bFound=False$     for $i=0,\dots ,sizeOf\left({\Psi }^m\right)-1$ do         if ${\psi }^j={\Psi }_i^m$ then            $c_i=c_i+1$            $bFound=True$            break         end if     end for     if not $bFound$ then         ${\Psi }^{\mathbf{m}}\leftarrow {\psi }^j$         $\mathbf{c}\leftarrow 1$     end if end for for  $i=0,\dots ,sizeOf\left({\Psi }^{\mathbf{m}}\right)-1$  do     $p_i={\displaystyle \frac{c_i}{sizeOf\left({\Psi }^{\mathbf{m}}\right)}}$     $\mathbf{p}\leftarrow p_i$     $SlpEn=SlpEn+(-p_i\ast log{p}_i)$ end for return  $SlpEn$

2.3. Permutation Entropy

PE [22] is an entropy calculation method based on deriving an ordinal symbolic representation based on the amplitude of the input time series and the application of the Shannon entropy expression to their relative frequencies. It is one of the most popular methods for calculating entropy, along with its many variations, mainly for its simplicity, low computation time and excellent performance in classification applications [81,82,83,84,85]. In this study, this method has been included for comparison purposes, as well as to prove that TS is well suited for any kind of entropy, not only to SlpEn.

This procedure divides a time series $\mathbf{x}$ of length N into overlapping subsequences of length m. An ordering procedure of the samples, generally in ascending order, is performed for each sample position j of length m, ${\mathbf{x}}_j^m$.

As a result from ordering the indices of the samples in ${\mathbf{x}}_j^m$, which by default were ordered as $\{0,1,\dots ,m-1\}$, a new symbolic pattern is obtained with the indices of each sample at their corresponding ordered position. This symbolic vector is represented as ${\pi }_j^m=\{{\pi }_0,{\pi }_1,\dots ,{\pi }_{m-1}\}$, where ${\pi }_0$ is the original index of the sample which is the smallest of ${\mathbf{x}}_j^m$, ${\pi }_1$ the index of the next sample in ascending order, and so on. To put it in another way, the samples in ${\mathbf{x}}_j^m$ satisfy $x_{j+{\pi }_0}\le x_{j+{\pi }_1}\le x_{j+{\pi }_2}\le \dots \le x_{j+{\pi }_{m-1}}$.

Once all the patterns have been obtained, a histogram is calculated using all the patterns that have been found as bins and the number of times they have appeared as their value or height. Then, their relative frequencies, $p_j$, are extracted using the number of occurrences of each found pattern and the total number of possible ordinal patterns $m!$. Finally, these relative frequencies are used to obtain their Shannon entropy, corresponding in this case to their PE:

$$\mathrm{PE}(\mathbf{x},m)=-\sum _{k=0}^{m!-1}{p}_k\log p_k,\forall p_k>0$$

(6)

The basic steps for computing Permutation Entropy are detailed in Algorithm 2.

2.4. Trace Segmentation

TS is a non-uniform downsampling scheme that samples the input signal at the points where the greatest variation occurs. This technique has been successfully used in other research, such as [76,86,87].

Mathematically, TS works in the following way. Given an input time series $\mathbf{x}=\{x_0,x_1,x_2,\dots ,x_{N-1}\}$, an accumulative derivative is obtained as:

$${\mathrm{TS}}_k=\sum _{j=1}^k|x_j-x_{j-1}|$$

(7)

where $k\in [1,N-1]$ and ${\mathrm{TS}}_0=0$. The last point, ${\mathrm{TS}}_{N-1}$, corresponds to the maximum value of the accumulative derivative, and one can obtain the sampling intervals’ amplitude $\Delta$ as $\Delta ={\displaystyle \frac{{\mathrm{TS}}_{N-1}}{N^{\prime }-1}}$, being $N^{\prime }$ the number of desired output samples, with $N^{\prime }<N$. Each sampling point for the output signal ${\mathbf{x}}^{\prime }$ is provided by the minimum index i of $\mathbf{x}$ for which ${\mathrm{TS}}_i$ exceeds an integer multiple q of $\Delta$:

$$x_q^{\prime }=x_i|i=\underset{1\le q\le N^{\prime }}{\mathrm{argmax}}({\mathrm{TS}}_i\le q\Delta )$$

(8)

with $x_0^{\prime }=x_0$. The main objective of using TS is to reinforce the presence of peaks in a non-linear way. This may result to be very beneficial in the case of SlpEn, since it takes advantage of the difference between samples and TS transforms the input signal to keep only the most prominent patterns. Algorithm 3 shows how to compute TS.

Algorithm 2 Permutation Entropy (PE) Algorithm

Input:  Time series $\mathbf{x}$, embedded dimension $m>2$, length $N>m+1$ Initialisation:  $PE=0$, ordinal pattern counter vector $\mathbf{c}\leftarrow \{\varnothing \}$, ordinal patterns relative frequency vector $\mathbf{p}\leftarrow \{\varnothing \}$, list of ordinal patterns found ${\Pi }^{\mathbf{m}}\leftarrow \{\varnothing \}$ for  $j=1,\dots ,n-m$  do     for $i=0,\dots ,m-1$ do         $y^j\leftarrow x_{j+i}$         ${\pi }^j\leftarrow i$     end for     $bSorted=False$     while $bSorted=False$ do         $bSorted=True$         for $i=0,\dots ,m-2$ do            if $y_i^j>y_{i+1}^j$ then                $swap(y_i^j,y_{i+1}^j)$                $swap({\pi }_i^j,{\pi }_{i+1}^j)$                $bSorted=False$            end if         end for     end while     $bFound=Frue$     for $i=0,\dots ,sizeOf\left({\Pi }^m\right)-1$ do         if ${\pi }^j={\Pi }_i^m$ then            $c_i=c_i+1$            $bFound=True$            break         end if     end for     if not $bFound$ then         ${\Pi }^{\mathbf{m}}\leftarrow {\pi }^j$         $\mathbf{c}\leftarrow 1$     end if end for for  $i=0,\dots ,sizeOf\left({\Pi }^{\mathbf{m}}\right)-1$  do     $p_i={\displaystyle \frac{c_i}{N-m+1}}$     $\mathbf{p}\leftarrow p_i$     $PE=PE+(-p_i\ast log{p}_i)$ end for return  $PE$

Algorithm 3 Trace Segmentation (TS) Algorithm

Input:  Time series $\mathbf{x}$, length N, desired number of samples $N^{\prime }<N$ Initialisation:  ${\mathbf{x}}^{\prime }\leftarrow \{\varnothing \}$ $k=0$ for  $i=1,\dots ,N-1$  do     $k=k+|x_i-x_{i-1}|$ end for $\Delta ={\displaystyle \frac{k}{N^{\prime }-1}}$ ${\mathbf{x}}^{\prime }\leftarrow x_0$ $k=0$ $j=1$ for  $i=1,\dots ,N-1$  do     $k=k+|x_i-x_{i-1}|$     if $k\ge \Delta \ast j$ then         ${\mathbf{x}}^{\prime }\leftarrow x_i$         $j=j+1$     end if end for ${\mathbf{x}}^{\prime }\leftarrow x_{N-1}$ return  ${\mathbf{x}}^{\prime }$

2.5. Uniform Downsampling

UDS is a basic uniform downsampling technique that allows to reduce the number of samples up to the desired number, removing elements in a uniform way. That is, in the case we want to remove half of the samples, we remove 1 out of 2 consecutive samples (we are using a downsampling factor of 2), removing values across all the series. If we wanted to remove 1/3 of the samples (downsampling to 67% or, said in other words, use a downsampling factor of 1.5 since we are keeping 2/3 of the samples), we would remove 1 out of 3 consecutive samples, removing always the sample in the same position if no overlapping window is used. As an example, with the sequence (3, 9, −7, 0, −34, 5), if we wanted to downsample to 67%, we would remove the pairs of numbers 3 and 0, 9 and −34 or −7 and 5. Note that these examples remove elements in the position of the chosen integer number, M. This is commonly known as integer decimation. Equation (9) depicts how the elements for integer decimation are chosen:

$$x_i^{\prime }=x_{i}M$$

(9)

where $i=0,1,2,\dots ,{\displaystyle \frac{N-1}{M}}$, so that the inequality $iM\le N-1$ is satisfied.

In the uniform downsampling performed on the experiments in this work, we are downsampling up to a desired number of samples, which is always smaller to the original sequence size, and then translating this to a percentage. This makes it fundamentally different to previously mentioned integer decimation using integer M, since most percentages won’t be equivalent to just keeping the Mth sample of a given temporal series, they will be fractional numbers. It is worh noting the integer decimation is a special case of the UDS we have used and implemented. Equation (10) depicts how the indices are chosen in this case:

$$x_i^{\prime }=x_{⌊i\ast {\displaystyle \frac{N-1}{N^{\prime }-1}}⌋}$$

(10)

where $i=0,1,2,\dots ,N^{\prime }-1$.

To implement how we will be choosing each sample, we will be using an accumulator. This accumulator, c, will be adding to itself the fraction of samples we want to keep, $N^{\prime }$, with respect to the series size N: $p={\displaystyle \frac{N^{\prime }}{N}}$. This addition, $c=c+p$, will take place each time we evaluate whether a certain sample is to be added to the resulting sequence of not. Whenever the accumulator exceeds 1, we will keep this sample, and then reset it by removing 1 from the accumulator, thus keeping the excess for the next iteration where we pick the next sample. Algorithm 4 depicts the algorithm used to perform UDS:

Algorithm 4 Uniform Downsampling (UDS) Algorithm

Input:  Time series $\mathbf{x}$, length N, desired number of samples $N^{\prime }<N$ Initialisation:  ${\mathbf{x}}^{\prime }\leftarrow \{\varnothing \}$ $p={\displaystyle \frac{N^{\prime }}{N}}$ $c=0$ ${\mathbf{x}}^{\prime }\leftarrow x_0$ for  $i=1,\dots ,N-1$  do     $c=c+p$     if $c>1$ then         ${\mathbf{x}}^{\prime }\leftarrow x_i$         $c=c-1$     end if end for ${\mathbf{x}}^{\prime }\leftarrow x_{N-1}$ return  ${\mathbf{x}}^{\prime }$

Note that the downsampling factor ($DF$) can be inferred from the algorithm, mainly by dividing the desired number of samples N by the total number of samples $N^{\prime }$: $DF={\displaystyle \frac{N}{N^{\prime }}}$. In this work, instead of specifying certain downsampling factors, we say we “are downsampling to $X\%$”, that is, we are keeping $X\%$ of the samples. To obtain the downsampling factor, one must simply divide 1 by the percentage of kept samples and multiply by 100: $(1/X)\ast 100$.

3. Experiments and Results

This section is divided into two parts. The first one will present all the experiments that have been carried out, going into detail about what has been recorded and under which conditions. In addition, the second part will focus on the results obtained from experimentation, briefly commenting them. These results will be further discussed in Section 4.

3.1. Experiments

The experiments were devised to assess how SlpEn can benefit in terms of accuracy in classification tasks from the pattern reinforcement provided by processing the temporal series under analysis with TS. In addition, the same experiments carried out for SlpEn have also been implemented with PE, not only for comparison purposes, but also to show that TS can be beneficial for any kind of entropy whenever used in classification tasks. Figure 2 depicts a flow diagram of the conducted experiments, detailing step by step how they have been executed. Moreover, we performed again the experiments substituting TS with UDS in order to asses how uniform dowsampling performs in combination with entropy calculation.

In favour of finding the best combination of parameters for SlpEn and PE, we conducted a grid search. For SlpEn, three parameters must be explored: m, $\delta$ and $\gamma$. In order to meet the temporal demands of the experiments, we opted for omitting $\delta$ from the grid search, keeping its value fixed in 0.001, as suggested by SlpEn’s seminal paper [21]. Regarding the other two parameters, m has taken values between 3 and 9 (with a step of 1), and $\gamma$ has been explored between 0.1 and 1 with steps of 0.1. In the case of PE, the only required parameter is m, so the grid search only explored that parameter, making it vary from 3 to 9 once again. To keep the experiments simple, and to avoid taking downsampling even further, we discarded using multiple temporal scales, thus maintaining $\tau =1$ in both entropy calculations.

In addition, the downsampling schemes have also been searched in a grid search manner. Since both techniques allow to downsample up to whatever value the user needs, we have performed downsampling ranging from 10% of the original input data up to 70%, in 1% steps. We have chosen these two boundaries (10% and 70%) mainly for two reasons. The first and most important one, is to try as many relevant combinations as we can. We chose 10% as the lower bound because percentages lower than this one might output a time series with too few samples, thus making it unrepresentative of reality. The upper bound, 70%, was chosen as such to avoid making it too high, since we would lose one of the main benefits of downsampling, which is reducing computation time. Finally, we chose to perform 1% steps to try as many percentages as we could, without using decimal steps to keep things simple. In addition, we have also a second reason, which involves the time consumption of the experiment. We are performing a grid search to find the optimal combination of parameters both for TS/UDS and SlpEn/PE, so it will be quite time consuming.

Then, both TS/UDS and SlpEn, and TS/UDS and PE are combined: first TS or UDS are applied with a certain downsampling percentage and then the grid search for parameter optimization of the corresponding entropy is conducted. This is repeated until all the possible combinations are explored, recording all the results in terms of accuracy, as well as recording how long it takes to calculate, in seconds, for each combination to finish.

Finally, both SlpEn and PE are calculated directly over the original sequences, or, said in other words, with no downsampling. Its purpose is twofold: first, demonstrate that downsampling enhances accuracy results, and second to show the calculation speed improvements allowed by the use of these techniques.

Classification accuracy is the main measure used to assess the performance of the methods tested. Additionally, we also used speed improvements, as mentioned previously. That accuracy corresponds to the percentage of correctly classified time series based on TS/UDS+SlpEn, SlpEn, TS/UDS+PE or PE as features individually, for each one of the seven experimental datasets found in the benchmark [28,88].

3.2. Results

The data shown in

Table 1. Classification accuracy achieved with SlpEn using TS. Results achieved with SlpEn with no TS are also reported for comparison, as well as the gain in accuracy terms (difference between not using TS and using TS) and the TS% used to maximise results.

Dataset	SlpEn Without TS	SlpEn with TS	Enhancement	TS%
Bonn EEG	95%	93%	−2%	45%
Bern–Barcelona	81%	85%	4%	13%
Fantasia	85%	98%	13%	27%
Ford Machinery A	85%	81%	−4%	48%
House Twenty	95%	95%	0%	64%
PAF prediction	76%	82%	6%	43%
Worms	71%	77%	6%	26%

,

Table 2. Classification accuracy achieved with PE using TS. Results achieved with PE with no TS are also reported for comparison, as well as the gain in accuracy terms (difference between not using TS and using TS) and the TS% used to maximise results.

Dataset	PE Without TS	PE with TS	Enhancement	TS%
Bonn EEG	92%	78%	−14%	70%
Bern–Barcelona	63%	81%	18%	10%
Fantasia	68%	90%	22%	18%
Ford Machinery A	75%	74%	−1%	56%
House Twenty	68%	83%	15%	10%
PAF prediction	82%	88%	6%	31%
Worms	69%	77%	8%	22%

and

Table 3. Parameters used to maximise the classification accuracy results shown in Table 1 and Table 2.

Dataset	SlpEn Without TS	SlpEn with TS	PE Without TS	PE with TS
Bonn EEG	$m=4,\gamma =0.1$	$m=6,\gamma =0.2$	$m=3$	$m=3$
Bern–Barcelona	$m=6,\gamma =1.0$	$m=7,\gamma =0.1$	$m=9$	$m=6$
Fantasia	$m=5,\gamma =0.5$	$m=6,\gamma =0.3$	$m=4$	$m=6$
Ford Machinery A	$m=9,\gamma =0.3$	$m=9,\gamma =1.0$	$m=5$	$m=4$
House Twenty	$m=3,\gamma =0.1$	$m=4,\gamma =0.1$	$m=9$	$m=6$
PAF prediction	$m=3,\gamma =0.1$	$m=8,\gamma =0.1$	$m=3$	$m=4$
Worms	$m=5,\gamma =0.2$	$m=6,\gamma =0.6$	$m=7$	$m=6$

corresponds to the best results achieved using the grid search approach for parameter optimization mentioned previously. Table 1 and Table 2 show classification accuracy and the gain (or enhancement) obtained when using TS compared to the case where no TS is applied, for SlpEn and PE respectively. This enhancement can be obtained by the difference between the accuracy obtained when the entropy methods (PE or SlpEn) is used by itself and the accuracy obtained when the entropy is used in combination of any downsampling methods (TS or UDS) (Enhancement = SlpEn/PE without TS/UDS − SlpEn/PE with TS/UDS). They also show the percentage of the downsampling needed using TS to achieve those numbers. As an example, if TS% is 5%, it means that only 5% of the total amount of samples provided by the original sequence were used to calculate its corresponding entropy value. In the case of a draw, that is, the accuracy achieved is the same for two or more different TS%, the lowest one is the one that has been reported. Additionally, Table 3 shows the optimal parameter configuration which has achieved the results shown in the previous tables.

Table 4. Classification accuracy achieved with SlpEn using UDS. Results achieved with SlpEn with no UDS are also reported for comparison, as well as the gain in accuracy terms (difference between not using UDS and using UDS) and the UDS% used to maximise results.

Dataset	SlpEn Without UDS	SlpEn with UDS	Enhancement	UDS%
Bonn EEG	95%	95%	0%	70%
Bern–Barcelona	81%	87%	6%	11%
Fantasia	85%	95%	10%	18%
Ford Machinery A	85%	90%	5%	55%
House Twenty	95%	100%	5%	61%
PAF prediction	76%	84%	8%	36%
Worms	71%	79%	8%	46%

,

Table 5. Classification accuracy achieved with PE using UDS. Results achieved with PE with no UDS are also reported for comparison, as well as the gain in accuracy terms (difference between not using UDS and using UDS) and the UDS% used to maximise results.

Dataset	PE Without UDS	PE with UDS	Enhancement	UDS%
Bonn EEG	92%	83%	−9%	70%
Bern–Barcelona	63%	84%	21%	18%
Fantasia	68%	88%	20%	19%
Ford Machinery A	75%	75%	0%	11%
House Twenty	68%	85%	17%	30%
PAF prediction	82%	90%	8%	35%
Worms	69%	77%	8%	29%

and

Table 6. Parameters used to maximise the classification accuracy results shown in Table 4 and Table 5.

Dataset	SlpEn Without UDS	SlpEn with UDS	PE Without UDS	PE with UDS
Bonn EEG	$m=4,\gamma =0.1$	$m=7,\gamma =0.1$	$m=3$	$m=4$
Bern–Barcelona	$m=6,\gamma =1.0$	$m=4,\gamma =0.1$	$m=9$	$m=8$
Fantasia	$m=5,\gamma =0.5$	$m=7,\gamma =0.3$	$m=4$	$m=3$
Ford Machinery A	$m=9,\gamma =0.3$	$m=5,\gamma =0.4$	$m=5$	$m=6$
House Twenty	$m=3,\gamma =0.1$	$m=5,\gamma =0.1$	$m=9$	$m=4$
PAF prediction	$m=3,\gamma =0.1$	$m=4,\gamma =0.4$	$m=3$	$m=3$
Worms	$m=5,\gamma =0.2$	$m=6,\gamma =0.4$	$m=7$	$m=9$

show the same results, but using UDS instead of TS.

Table 7. Time reported in seconds for each dataset and representative percentages obtained with TS and UDS. The values correspond to the whole optimization grid search for m and $\gamma$ of SlpEn.

Dataset	100%	70% (TS/UDS)	50% (TS/UDS)	25% (TS/UDS)	10% (TS/UDS)
Bonn EEG	232.73	143.26/203.25	101.67/144.39	59.94/73.67	16.99/17.58
Bern–Barcelona	180.09	152.68/234.09	126.87/212.44	79.82/121.37	34.37/38.74
Fantasia	336.00	207.14/223.51	127.60/131.98	43.29/47.00	9.29/9.85
Ford Machinery A	4.19	3.25/3.93	2.55/2.86	1.52/1.55	0.63/0.63
House Twenty	13.44	6.74/7.97	4.48/4.56	1.82/1.73	0.60/0.60
PAF prediction	4.80	2.66/2.88	1.71/1.79	0.80/0.81	0.34/0.34
Worms	27.17	15.66/17.70	10.52/11.42	5.02/5.37	2.29/2.41

(SlpEn) and

Table 8. Time reported in seconds for each dataset and representative percentages obtained with TS and UDS. The values correspond to the whole optimization grid search for m of PE.

Dataset	100%	70% (TS/UDS)	50% (TS/UDS)	25% (TS/UDS)	10% (TS/UDS)
Bonn EEG	30.81	19.85/23.96	14.10/18.43	8.30/9.64	2.85/2.90
Bern–Barcelona	49.65	35.33/50.03	25.79/40.62	13.49/17.54	4.94/5.08
Fantasia	47.70	29.61/29.82	17.73/17.67	5.78/5.72	1.37/1.36
Ford Machinery A	0.89	0.66/0.70	0.50/0.52	0.27/0.28	0.11/0.11
House Twenty	2.03	1.05/1.26	0.72/0.80	0.31/0.32	0.11/0.11
PAF prediction	0.76	0.47/0.48	0.32/0.32	0.15/0.15	0.06/0.06
Worms	5.68	3.40/3.47	2.27/2.29	1.05/1.08	0.44/0.44

(PE) show the computation time when using TS and UDS, compared again to the case where no downsampling is applied. In this case, they refer to the total time dedicated to perform the grid search to optimize the parameters, using the indicated percentage of samples (100% corresponds to no downsampling). It’s important to highlight that it takes much longer to perform the search for SlpEn than PE. The reason for this is that it has two parameters to optimize, m and $\gamma$, whereas PE only has m. In addition, the differences between each dataset, specifically the number of samples and the length of each one, will also impact the time it takes to execute. Note that the numbers are only for reference, since they are directly impacted by the specifics of the machine and the programming language used. In this case, they have been executed with the programming language Python, in a MacBook Air 2024 with macOS Sequoia 15.6.1 as operative system, Apple M3 with 8 cores and 8 GB of RAM.

Table 9. Time reported in seconds for the Bonn EEG dataset, accounting for different values of m and representative percentages obtained with TS and UDS. The values correspond to individual SlpEn calculations, keeping $\gamma$ fixed at 1.0 and $\delta$ to 0.001.

m	100%	70%	50%	25%	10%
3	0.84	0.60	0.42	0.22	0.09
4	0.88	0.62	0.44	0.25	0.12
5	0.99	0.69	0.49	0.31	0.19
6	1.19	0.81	0.55	0.45	0.28
7	1.62	0.94	0.68	0.69	0.35
8	2.36	1.26	1.11	0.94	0.40
9	3.66	1.75	1.56	1.31	0.42

and

Table 10. Time reported in seconds for the Bonn EEG dataset, accounting for different values of m and representative percentages obtained with TS and UDS. The values correspond to individual PE calculations.

m	100%	70%	50%	25%	10%
3	1.22	0.88	0.62	0.31	0.13
4	1.59	1.10	0.79	0.41	0.17
5	2.06	1.47	1.05	0.57	0.26
6	2.88	1.99	1.45	0.85	0.41
7	4.48	2.91	2.15	1.33	0.55
8	7.16	4.53	3.25	1.96	0.63
9	11.41	6.96	4.79	2.86	0.69

correspond to the time it takes to obtain individual values of entropy, for SlpEn and PE respectively. The purpose of these tables is to show the impact TS or UDS have when calculating entropy values with different values of m. As one would expect, with higher m values, the higher the computing time required. The values are representative of the Bonn EEG dataset. In the case of the other datasets, we have included them in Appendix A.1 for the case of SlpEn and in Appendix A.2 for PE. We did not diferentiate between UDS and TS in this tables, since their execution time is not included in the individual entropy calculations.

Figure 3 and Figure 4 illustrate the maximum values of accuracy attained in each downsampling percentage (TS% and UDS%), comparing the curves given by SlpEn and PE for each different dataset. It includes values for all the different downsampling percentages that have been applied in the grid search, that is, the percentage of samples of the original sequence that have been used in the calculation of the entropy values. The last value of the plot, 100%, refers to the case where there is no downsampling or, in other words, the best value obtained by using just the entropy methods without applying any downsampling method.

Finally, Figure 5, Figure 6 and Figure 7 show heatmaps that represent the accuracy of SlpEn combined with TS and PE combined with UDS for all the downsampling percentages tested, that is, from 10% to 70%. Again, the instance where no downsampling is applied (100, bottom row) is also included. Representations for each dataset are shown. The first two images correspond to SlpEn, comparing the TS% against different m and $\gamma$ values, respectively. The third figure shows PE’s accuracy results, confronting the values of UDS% and m. The cases where PE and TS and SlpEn and UDS are combined show similar results, they have been included in Appendix B. In order to elaborate the heatmaps, we haven chosen three variables for each: accuracy, m or $\gamma$ and the downsampling percentage. We have represented these variables in three dimensions, where the third dimension, which corresponds to the accuracy, is then colored according to how high the accuracy has been achieved with the combination of the other two parameters.

4. Discussion

The original SlpEn method [21] by itself already has a very high performance in classification tasks. Its main drawback is the optimization of its parameters: m, $\delta$ and $\gamma$. Since it has three, when performing a grid search, it can be quite slow, specially compared to other methods such as PE, that only has m to optimize. In this work we have explored the possibility of combining SlpEn with downsampling techniques, such as TS and UDS, not only to try to reduce its computation time by downsampling the temporal series under study, but also to enhance its performance by maximizing the most prominent patterns present in the sequences in the case of TS, while working in different temporal scales and removing noise when using UDS. In addition, downsampling can also be applied to other entropy calculation techniques, as the results have shown with the case of PE and the work [37] with Sample Entropy with TS, and also with temporal scales, which are specific cases of UDS [38,89,90,91].

It is evident from Table 1 and Table 2 that using TS to downsample the original sequence is quite beneficial, since the accuracy both in SlpEn and PE increases in four out of seven of cases and five out of seven, respectively. For SlpEn, depending on the dataset, the results are enhanced between 4% and 13%. In datasets where results are not enhanced, they only worsen by 4% at maximum, which may be worth it when compared to the time we gain thanks to downsampling. On the other hand, PE seems to benefit more from using TS, since it increases its accuracy results up to 22%, except in the case of the Bonn EEG dataset, where the results worsen considerably by 14%. Comparing the two of them, it appears that PE has its highest increase in performance in the datasets that initially had the worst results (Bern-Barcelona, Fantasia and House Twenty) compared to the initial results of SlpEn. On the other hand, the performance enhancement is less prominent, under 10%, in the datasets where both SlpEn and PE have similar results when TS is not applied.

Regarding the downsampling percentages, for SlpEn, most of them are between 25% and 50% (5 out of 7). In the case of PE, the range varies greatly, being between 10% and 31%, with two datasets with the lowest downsampling percentage tested (10%). From this results we can extract that downsampling below 50% of the data can be highly beneficial, since, both for PE and SlpEn, 11 out of 14 datasets increase their accuracy. Ranges of less than 25% are also quite promising in the case of PE (4 out of 7), whereas SlpEn tends to benefit more for percentages closer to 50% (3 datasets within the vicinity of 40% to 50%). Additionally, it is extremely important to highlight that, depending on the number of available samples, specially if this number is not high, the performance might be hindered because the temporal series result of the downsampling may end up being too short.

In the case of UDS, we can extract similar conclusions from Table 4 and Table 5. Classification results for both SlpEn and PE highly benefit from UDS, even more than with combined with TS. With UDS combined with SlpEn, the maximum gain is a bit more conservative (up to 10% in the Fantasia dataset compared to the 13% obtained with TS), but there is no instance where the performance worsens, only with the Bonn EEG dataset it is has no improvement and maintains its accuracy compared when no downsampling is applied. Once again, when UDS is used with PE, the results are similar: in the case where the accuracy levels decrease, they do so in a smaller scale (−9% compared to the −14% obtained in the Bonn EEG dataset).

Results from these tables, both when TS and UDS are used accompanying SlpEn and PE, seem to confirm our initial hypothesis. That is, data which is sampled at a much higher rate than needed is adding a lot of possible confounding data to the sequence. Performing downsampling, we are enhancing the main patterns and reducing this unnecessary data, thus keeping key features that will be used to enhance classification performance. Moreover, it seems performance increases more in cases where the sampling rate in Hz is higher, as it is the case with both the ECG and EEG datasets. In the case of ECG, the Fantasia RR database (sampled at 250 Hz), compared to the PAF dataset (sampled at 128 Hz), has a much higher increase in classification accuracy when used downsampling, with a maximum of 20% when UDS is used with PE, compared to a maximum of 8% with the same settings. Very similar behaviour exhibit the EEG datasets: Bern-Barcelona (sampled at 512 Hz) benefits much more from downsampling than the Bonn EEG dataset (sampled at 173.61 Hz). In this case, the first one increases its accuracy by 21% with UDS and PE, whereas the second datasets sees its performance not increased in the best case, where UDS and SlpEn are combined, and hindered in the remaining cases. Regarding the three non-medical datasets, they depend on the dataset. Both House Twenty and Worms datasets seem to benefit from both techniques of downsampling, specially in the case of House Twenty. Finally, in the case of Ford Machinery A, downsampling seems to be a hinderance, but we do not know the exact sampling rate for these temporal series.

From Table 7 we can extract another major advantage from using downsampling: the computation time is reduced a lot. Downsampling the original sequences leads to less than half the time used (with TS) when reducing the samples to 50%, both for SlpEn and PE. With UDS, the algorithm is a bit slower, so they the execution times do not halve, but are close to. Of course, the more the number of data in the sequence is reduced by downsampling, the faster the results are calculated. Since those two tables refer to the whole grid search explained in the previous section, the gain in seconds is huge, specially in the case of SlpEn, since it has more combinations to check. It is worth noting that, in the case of our implementations of TS and UDS, UDS is slower, so it leads to slower times, which in any case are by no means negligible. In addition, with smaller downsampling percentages, times for both TS and UDS converge, as one would expect.

Table 8 illustrates similar information, but in this case they focus on individual entropy calculations for different m values. It is clear that, on an individual basis, SlpEn is faster to calculate than PE, and the speedups are very similar between the two entropies, being a bit higher in the case of PE. This is more noticeable in the cases where m is 8 and 9, and also in the last column, where the percentage of samples used is only 10. In this case, in terms of physical seconds, the difference is higher for PE, making it much faster when using downsampling compared to the case with no downsampling. Furthermore, there are many instances (at least 3 out of 7), both with SlpEn and PE, where the maximum accuracy has beet attained using high m values ($m\ge 6$) as it can be observed in Table 3 and Table 6, thus implying great potential for improvement in execution time. It is also worth noting that the downsampling algorithm used to obtain these execution times is not relevant, since they only take into account the time it takes to perform entropy calculations, excluding the time it takes to downsample.

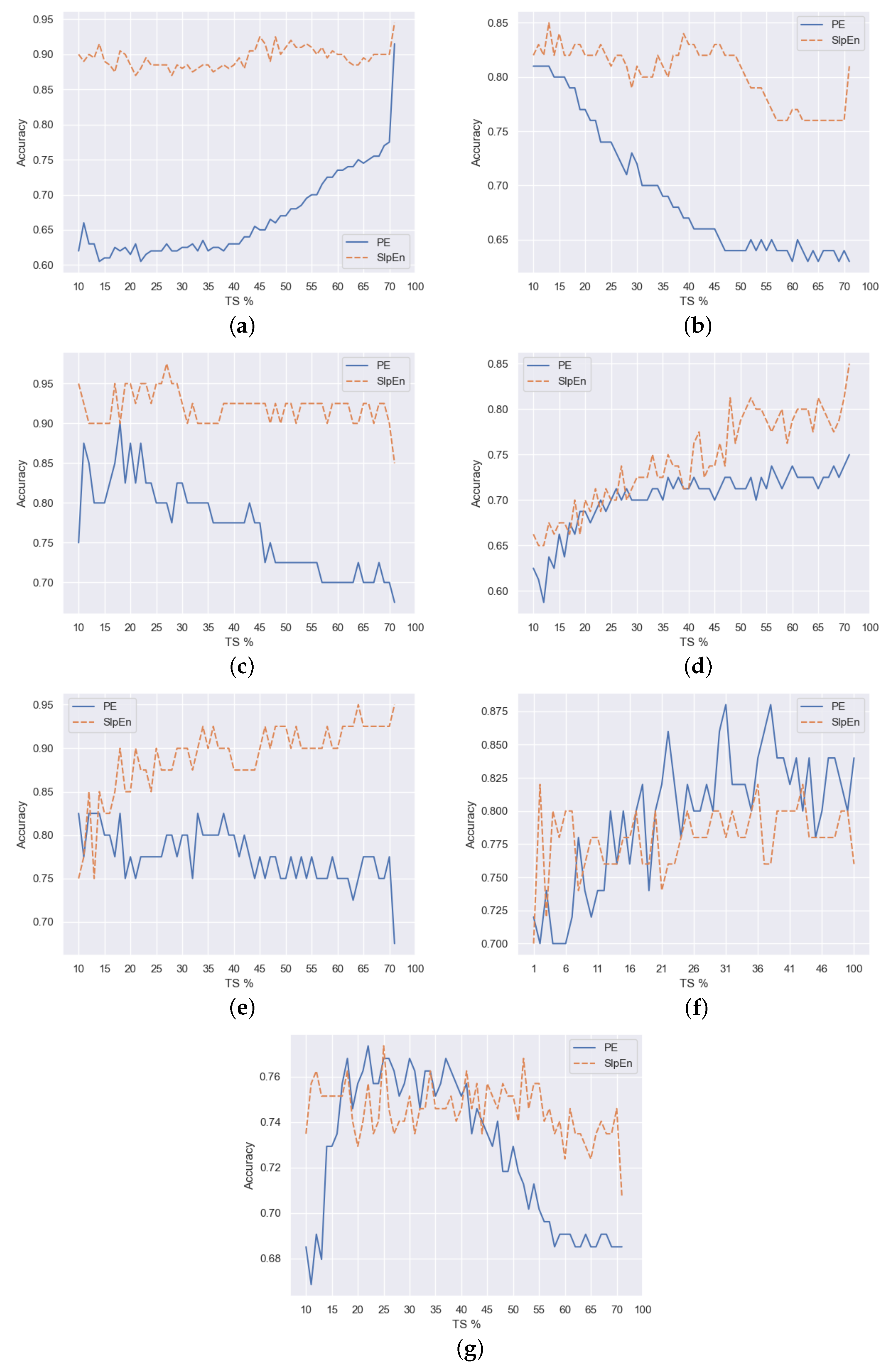
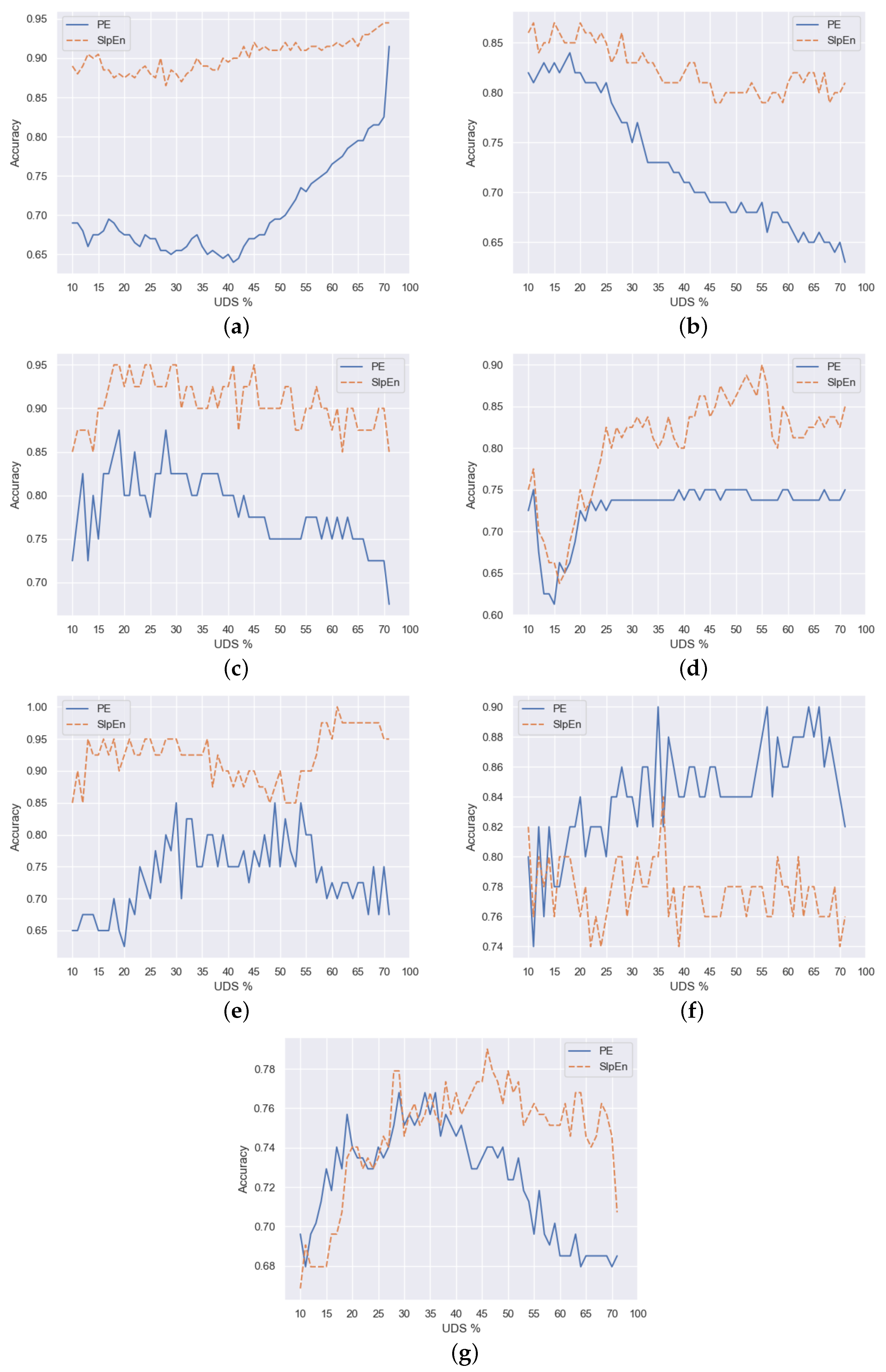
Figure 3 and Figure 4 show graphs that represent the maximum accuracy achieved for each percentage of downsampling, including also the case without it, which corresponds to the rightmost value of the curves. In general, SlpEn outperforms PE. We can arguably say so in 5 out of 7 datasets (Bonn EEG, Bern-Barcelona, Fantasia, Ford A, House Twenty), regardless of the downsampling technique used. It is also noticeable that in most cases, both for SlpEn and PE, there are many values of downsampling that outperform the accuracy level obtained without using any downsampling technique, which can help to reduce testing to find out any downsampling percentage that is better than just calculating the entropy.

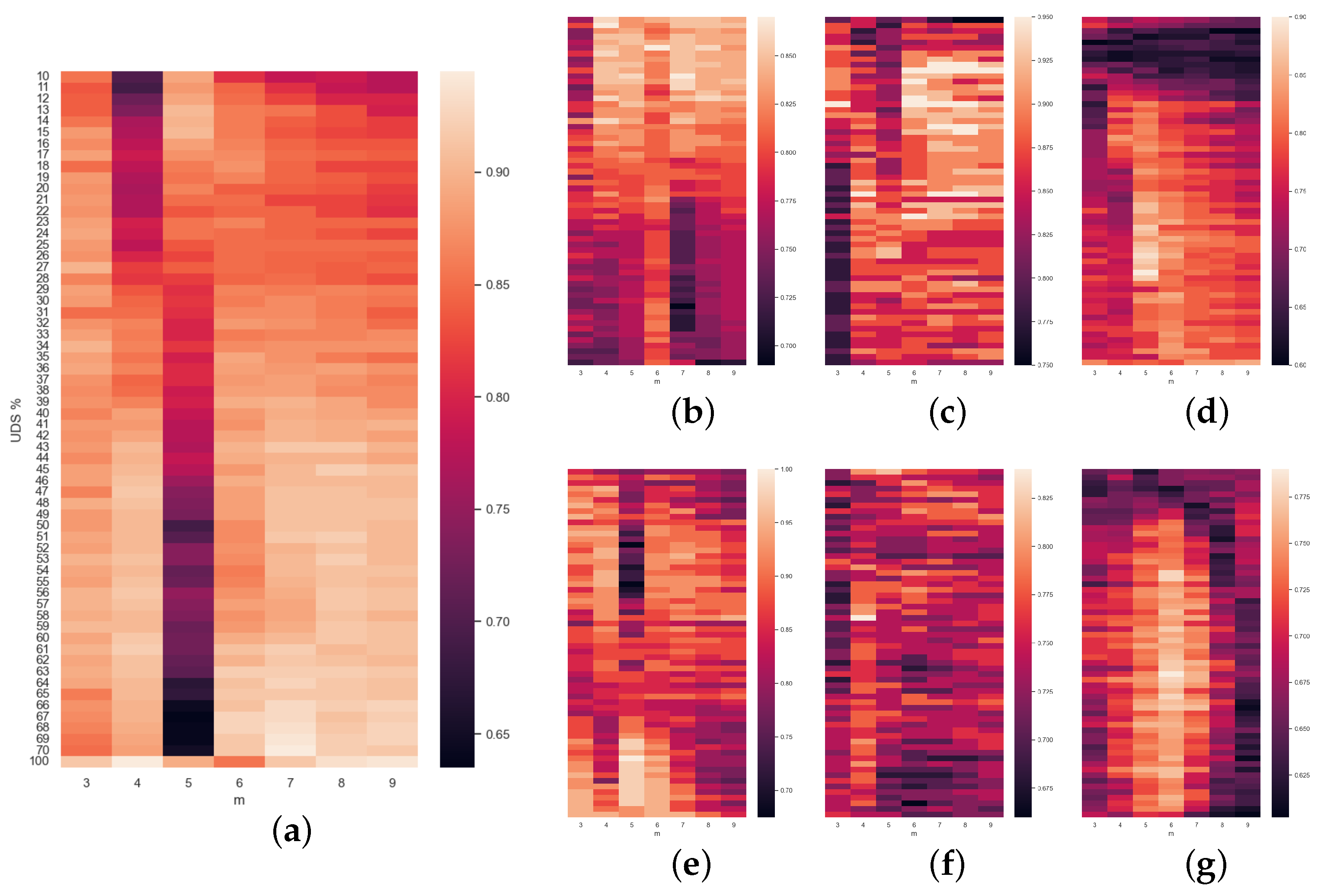
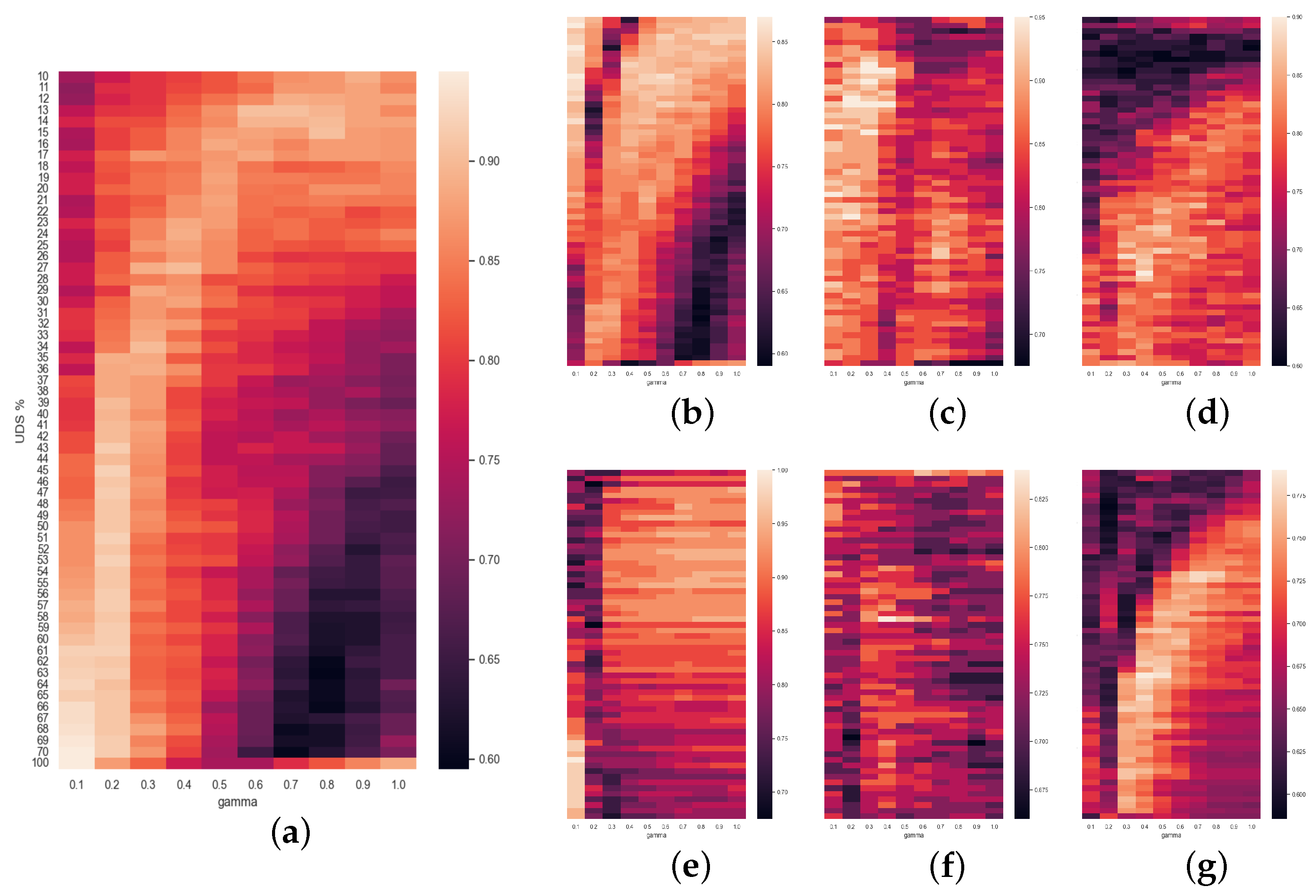
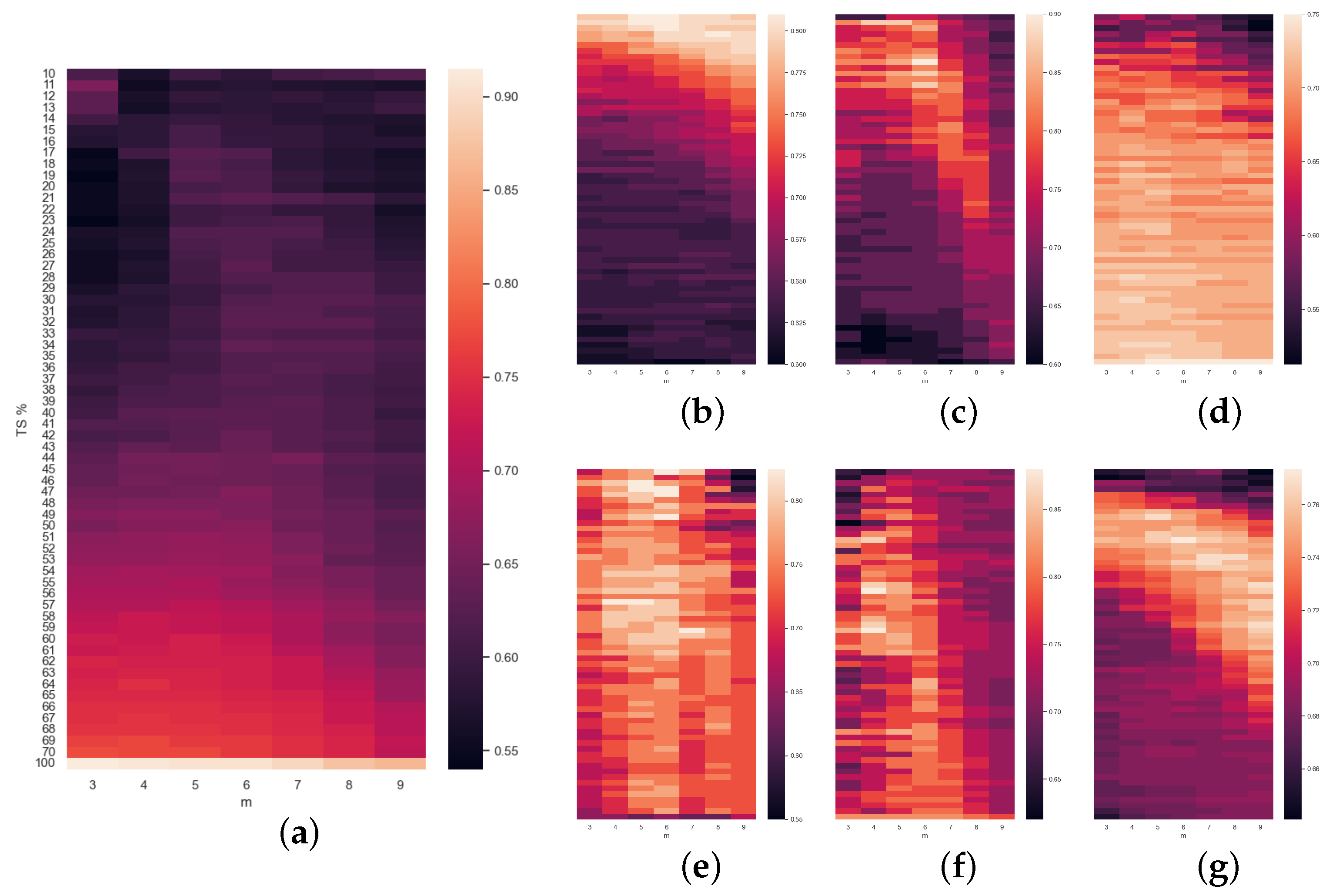
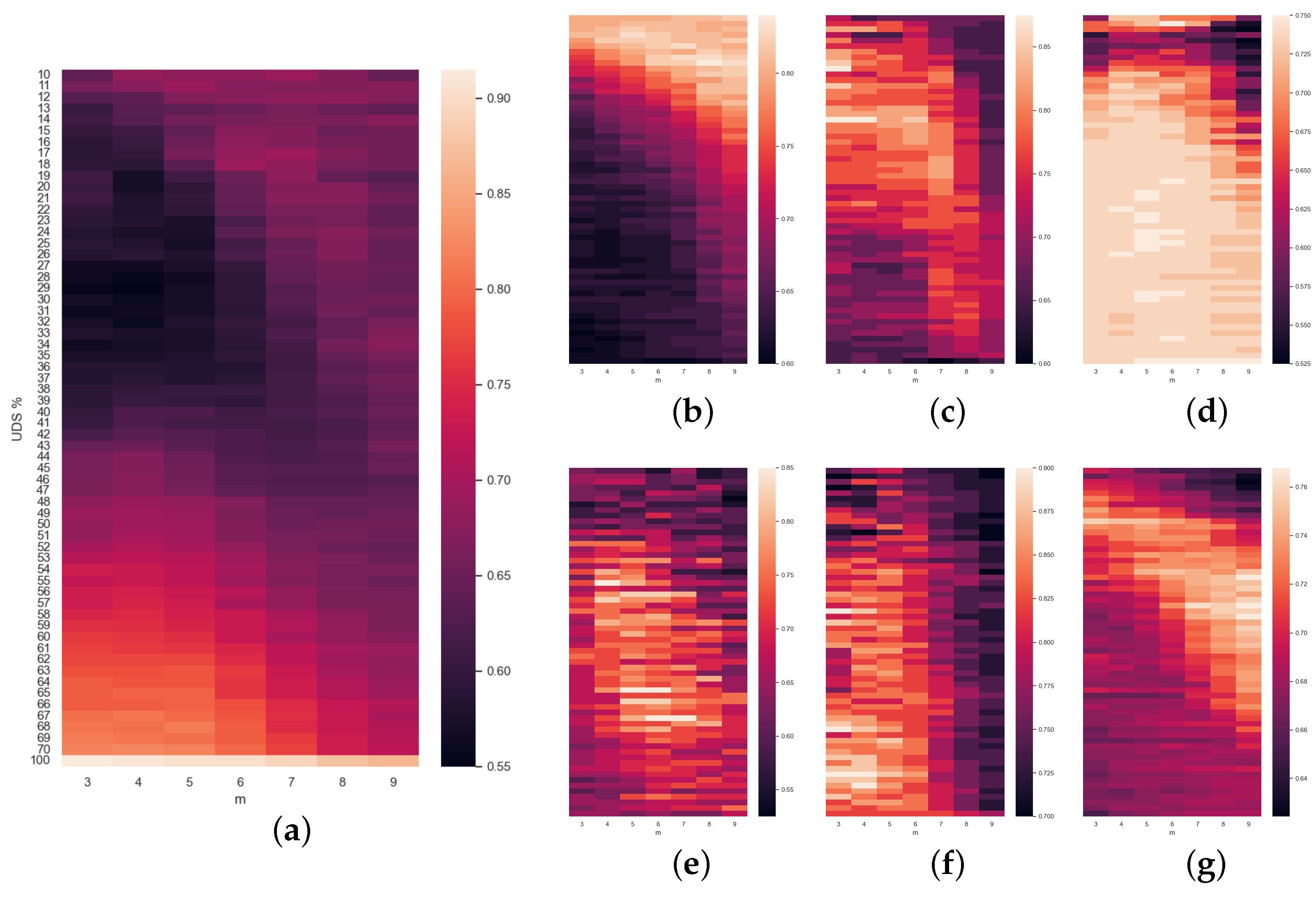
Finally, the rest of the Figure 5, Figure 6 and Figure 7 are a compendium of heatmaps that represent the whole result of the grid search in terms of accuracy. They confront the level of downsampling used (TS% or UDS%) to m (and also to $\gamma$ in the case of Figure 6). For SlpEn, comparing the last row (no downsampling) to the rest, we can observe that there are many instances (both in the same column and in other columns) where the accuracy is higher than the one achieved without TS. There are some cases where, for the same value of m, the best accuracy is obtained using the whole data series with no downsampling. Having said that, even though the accuracy is not as high, it can be compensated by the execution speed gain, since with just 50% of the samples the speedup is 2, and the accuracy loss is almost minimal. Moreover, these maps show that high accuracy normally gathers up in some kind of shape: curves, circles, etc., which can be useful to optimize the search and avoid using grid search as an optimization method, which in theory is much more costly. For example, we could use heuristic methods that look for local or absolute maximums. The same thing can be said of Figure 7, where PE is compared against UDS%. Heatmaps reporting SlpEn combined with UDS and PE with TS have not been reported since they are very similar to the ones presented in this work, thus we can extract very similar conclusions, if not the same.

Overall, the outcomes of the experiments highlight the high potential that downsampling offers: it is easy to implement, cheap in terms of computational resources and in most cases it is able to not only reduce computation time, but also to enhance classification results in terms of accuracy. However, the search for the right downsampling percentage might increment the computational cost, in the case one wants to maximise performance. In other cases, we recommend the use of TS, performing downsampling in the interval between 25% and 50% for SlpEn and between 10% and 30% for PE, which normally outputs the best results. In addition, we believe percentages below 50% might be a good start for any kind of entropy, not just for SlpEn or PE, specially values in between 20% and 45%. In case such results are not satisfactory, one could try to calculate them with no downsampling to compare and help to decide, since the improvements in reduction of the execution time will always be there, regardless of how well it performs in classification tasks. Moreover, it would seem the best case scenario would be to sample data at the minimum rate necessary, if possible, thus avoiding adding extra data which may lead classification algorithms to lower performance.

5. Conclusions

This study addressed the combination of SlpEn and downsampling, mainly TS and UDS, aimed at enhancing time series classification accuracy, as well as reducing computation time. In addition, our work also has as a secondary objective proving that downsampling can keep its advantages when being used in combination with any other entropy calculation method, as suggested by [37] with Sample Entropy and TS, many cases where UDS is applied indirectly in the form of temporal scales [38,89] and our experiments with both SlpEn and PE with TS and UDS. Our experimentation highlights the benefits of combining downsampling with entropy in classification tasks, showing great improvements both in accuracy results and in computation time.

In general, our results suggest that using TS as a downsampling technique that amplifies the most prominent patterns present in a temporal sequence is beneficial and very helpful when computing its entropy to use as a feature in classification tasks. In most cases, the accuracy levels achieved outperform those of the instances where downsampling has not been applied, both for SlpEn and PE. Of course, this is not true in all scenarios, specially when the resulting sequences have too few samples, so one must apply the downsampling technique carefully to avoid such cases. Notably, the results specially benefit instances where the initial classification accuracy is not very high and leaves room for improvements. Regarding UDS as a technique to reduce noise and focus at different temporal scales when using specific downsampling percentages, we obtain similar results to those obtained with TS. Both PE and SlpEn benefit from UDS in most of the datasets used, having more room for improvement in cases where classification accuracy is initially low, just like it is the case with TS. Moreover, our experiments lead us to believe that sampling rates above the minimum required one might have a negative impact in classification tasks since confounding data is added to the temporal series and the key features less apparent, thus making it harder to classify easily or reliably.

Additionally, both downsampling techniques are very good options in optimization of computational cost. It is able to reduce computation time consistently and independently of the data being treated, providing speedups of approximately 50% when downsampling the original sequence to half of its samples. That is specially notable when the computation times are the slowest, since the amount of time in seconds that downsampling is able to reduce is much higher compared to instances where computation times are faster, even though they have a similar speedup. That can happen when the embedding values (m) are quite high, as it is in many of our results, thus making the computation times slower. Moreover, according to [92], high embedding dimension values can have higher performance in many cases, even if the generally accepted inequality $m!<<N$ (where N is the length of the sequence under study) suggests otherwise. In such cases, downsampling would become very useful to reduce computation times.

Other optimization techniques might include making use of more powerful computing hardware, faster programming languages, refining entropy algorithms or parallel processing, but those are not as simple as the downsampling schemes used in this paper. Furthermore, using heuristic techniques when optimizing entropy parameters and downsampling levels instead of our “brute-force” grid-search approach could significantly contribute in the reduction of computational cost in terms of timing and could be beneficial not only to the approach suggested in this work, but to any other research in the field.

As a summary, we encourage the use of downsampling to process the data present in temporal sequences before calculating its entropy: it is able not only to enhance classification results, but also to reduce computational cost. Of course, one must find a good compromise between speedup and classification results, since not in all cases downsampling will help entropy to outperform itself when using the entire series of data. As an initial recommendation, we would choose the interval [25%, 50%] to perform downsampling using TS, being another possibility [10%, 30%] when using UDS, although this will always depend on the intrinsic characteristics of the dataset under study.