A Novel Family of CDF Estimators Under PPS Sampling: Computational, Theoretical, and Applied Perspectives

Abstract

Accurate estimation of population distribution characteristics is a fundamental task in survey sampling and statistical inference. This paper introduces a new family of estimators for the cumulative distribution function (CDF) under probability proportional to size (PPS) sampling, incorporating auxiliary information to enhance efficiency. The proposed approach employs dual auxiliary variables in the estimation phase, while the sampling design relies on a single auxiliary variable. Theoretical properties, including bias and mean squared error (MSE), are rigorously derived to establish the efficiency of the new class. An extensive empirical evaluation using three distinct populations—fisheries data, wine chemistry data, and demographic records—demonstrates the superiority of the proposed estimators. In terms of accuracy, the best-performing proposed estimator achieves an MSE of 0.0012, compared to 0.0127 for the widely used GK estimator. Percentage relative efficiency (PRE) values further underscore these improvements, with gains ranging from 123% to over 328% across the three populations. Graphical comparisons confirm these trends, illustrating that the proposed estimators consistently dominate conventional approaches. Overall, the findings highlight both the theoretical soundness and practical utility of the proposed family, offering robust and computationally efficient improvements for CDF estimation in complex survey designs.

1. Introduction

Accurate inference on population distribution features is central to survey statistics and numerous applied domains. When unit sizes exhibit pronounced heterogeneity, probability proportional to size (PPS) sampling [1,2] delivers substantial efficiency gains over equal-probability designs by prioritizing information-rich units. Beyond totals or means, reliable inference on the cumulative distribution function (CDF) is crucial for quantile estimation, inequality assessment, risk profiling, and tail probability reporting in economics, health, and environmental monitoring [3,4]. However, standard distribution function estimators often suffer from inflated mean squared error (MSE) and diminished percentage relative efficiency (PRE) when size variability is pronounced [5,6,7,8,9].

The existing research has enriched distribution function estimation by leveraging auxiliary information, primarily under simple random sampling (SRS). Hartley–Ross-type approaches have been extended to handle nonresponse and robustness [10,11,12], while auxiliary-variable calibration has yielded efficient families of CDF estimators [13,14]. Within PPS designs, most attention has focused on mean estimation, where logarithmic, predictive, and regression-type estimators have been proposed to reduce bias, minimize MSE, and improve robustness [15,16,17,18,19]. Recent empirical work has further demonstrated the advantages of PPS-based mean estimators using real-world data, such as the radiation dataset [20]. Extensions to rank set sampling (RSS) have also shown promise in survey applications, offering lower variances and higher efficiencies than conventional designs [21]. Yet, despite these advances, a clear methodological gap persists in CDF estimation under PPS: an approach that integrates multiple auxiliary variables with tractable theoretical guarantees and extensive empirical validation. To address this gap, the present study develops a new class of CDF estimators explicitly designed for PPS sampling. At the design stage, one auxiliary variable governs the inclusion probabilities, while at the estimation stage, multiple auxiliary variables (up to three) are incorporated to enhance precision. The proposed estimators are computationally straightforward, admit closed-form first-order approximations for bias and MSE, and can be easily implemented within standard survey workflows.

Parallel to these traditional developments, advances in computational and statistical learning have introduced flexible, data-driven methodologies that align conceptually with PPS-based estimation principles [22,23,24]. For instance, Ref. [25] proposed a regression-based conditional independence test employing adaptive kernels, providing a mechanism for data-driven bandwidth selection that parallels efficiency optimization in PPS estimation. Similarly, Ref. [26] introduced an adaptive tempered reversible-jump algorithm for Bayesian curve fitting, demonstrating that flexible computational structures can enhance estimator stability and convergence. Furthermore, Ref. [27] developed a Gaussian kernel similarity approach for multisource information fusion, emphasizing the role of weighted auxiliary information in improving estimation accuracy. This idea resonates with our proposed dual-auxiliary-variable framework, wherein the inclusion of multiple auxiliary sources systematically reduces estimator bias and MSE. Likewise, Ref. [28] examined belief-based fuzzy and imprecise clustering for arbitrary data distributions, offering valuable insights into managing uncertainty and variability—issues central to complex survey designs.

Complementary to these methodological contributions, Ref. [29] investigated the dimensional efficiency of noncontrastive learning, offering computational perspectives on balancing model complexity and scalability—an aspect particularly relevant for large-scale survey datasets. In the same vein, Ref. [30] extended the Merton option-pricing framework to deposit insurance modeling, demonstrating that statistically rigorous models can address practical problems in economics and finance. Collectively, these studies highlight the convergence between traditional survey estimation and emerging computational paradigms. They underscore the growing emphasis on adaptability, efficiency, and scalability—principles directly motivating our proposed PPS-based distribution estimation framework. By aligning theoretical efficiency with adaptive computational techniques, the proposed work advances modern survey methodology and integrates it into the broader landscape of computational statistics.

This paper contributes to four major dimensions: First, it introduces a flexible family of PPS-based CDF estimators that combines multi-auxiliary calibration with interpretable association measures. Second, it derives analytical expressions for first-order bias and MSE, identifies conditions for estimator dominance, and provides optimal tuning strategies. Third, it demonstrates computational tractability, requiring only standard survey quantities easily implemented in existing pipelines. Fourth, it provides extensive numerical evidence from benchmark populations—fisheries, wine chemistry, and demographic data—where the proposed estimators achieve empirical MSEs as low as $0.0012$ (versus $0.0127$ for comparators) and PRE gains ranging from $123\%$ to $328\%$.

The proposed methodology is broadly applicable to domains where PPS sampling is natural and CDF-based inference is decision-critical, such as income distribution analysis, poverty and inequality assessment, disease prevalence, hospital resource allocation, crop yield risk, deforestation monitoring, election polling, and transportation planning. In such contexts, unit sizes (e.g., household size, facility capacity, stand area, or farm acreage) align with PPS designs, while auxiliary data are increasingly accessible from administrative or satellite sources. By jointly leveraging PPS and auxiliary calibration, the proposed estimators offer enhanced accuracy, reduced sample size requirements, and broad practical relevance.

The remainder of the paper is organized as follows: Section 2 presents the proposed class of estimators within the PPS framework. Section 3 reports empirical and simulation results, including efficiency comparisons. Section 4 provides practical guidance and broader implications, while Section 5 concludes the study.

2. Methodology

Let the finite population be denoted by $\mathsf{\Phi }=\{1,2,\dots ,i,\dots ,N\}$, where N is the population size. For the $i^{\mathrm{th}}$ unit, let $y_i$ denote the value of the study variable of interest, while $(x_i,z_i,q_i)$ represent the auxiliary variables associated with the same unit. We consider probability proportional to size (PPS) sampling, where the selection probability of the $i^{\mathrm{th}}$ unit is defined as

$$P_i={\displaystyle \frac{q_i}{{\sum }_{j=1}^N{q}_j}}.$$

To standardize the PPS design, we introduce transformed variables.

$$y_i^{\ast }={\displaystyle \frac{y_i}{N{P}_i}},x_i^{\ast }={\displaystyle \frac{x_i}{N{P}_i}},w_i^{\ast }={\displaystyle \frac{z_i}{N{P}_i}}.$$

To characterize the cumulative distribution function (CDF) in the PPS framework, we define indicator functions for the medians of the transformed variables:

$$I(y_i^{\ast }\le {\tilde{y}}^{\ast }),I(x_i^{\ast }\le {\tilde{x}}^{\ast }),I(w_i^{\ast }\le {\tilde{w}}^{\ast }),$$

where ${\tilde{y}}^{\ast }$, ${\tilde{x}}^{\ast }$, and ${\tilde{w}}^{\ast }$ denote the population medians of $y_i^{\ast }$, $x_i^{\ast }$, and $w_i^{\ast }$, respectively.

The corresponding finite population distribution functions and their sample-based estimators are then given as

$$G_y^{\ast }={\displaystyle \frac{1}{N}}\sum _{i=1}^{N}I(y_i^{\ast }\le {\tilde{y}}^{\ast }),{\widehat{G}}_y^{\ast }={\displaystyle \frac{1}{n}}\sum _{i=1}^{n}I(y_i^{\ast }\le {\tilde{y}}^{\ast }),$$

$$G_x^{\ast }={\displaystyle \frac{1}{N}}\sum _{i=1}^{N}I(x_i^{\ast }\le {\tilde{x}}^{\ast }),{\widehat{G}}_x^{\ast }={\displaystyle \frac{1}{n}}\sum _{i=1}^{n}I(x_i^{\ast }\le {\tilde{x}}^{\ast }),$$

$$G_w^{\ast }={\displaystyle \frac{1}{N}}\sum _{i=1}^{N}I(w_i^{\ast }\le {\tilde{w}}^{\ast }),{\widehat{G}}_w^{\ast }={\displaystyle \frac{1}{n}}\sum _{i=1}^{n}I(w_i^{\ast }\le {\tilde{w}}^{\ast }).$$

The variability of these indicator functions across the population is captured through their variances:

$$S_{G_y^{\ast }}^2={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left(I(y_i^{\ast }\le {\tilde{y}}^{\ast })-G_y^{\ast }\right)}^2,$$

$$S_{G_x^{\ast }}^2={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left(I(x_i^{\ast }\le {\tilde{x}}^{\ast })-G_x^{\ast }\right)}^2,$$

$$S_{G_w^{\ast }}^2={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left(I(w_i^{\ast }\le {\tilde{w}}^{\ast })-G_w^{\ast }\right)}^2.$$

The coefficients of variation are therefore defined as

$$C_{G_y^{\ast }}={\displaystyle \frac{S_{G_y^{\ast }}}{G_y^{\ast }}},C_{G_x^{\ast }}={\displaystyle \frac{S_{G_x^{\ast }}}{G_x^{\ast }}},C_{G_w^{\ast }}={\displaystyle \frac{S_{G_w^{\ast }}}{G_w^{\ast }}}.$$

To account for dependence among the transformed indicators, we define population covariances:

$$S_{G_y^{\ast }{G}_x^{\ast }}={\displaystyle \frac{1}{N-1}}\sum _{i=1}^N\left(I(y_i^{\ast }\le {\tilde{y}}^{\ast })-G_y^{\ast }\right)\left(I(x_i^{\ast }\le {\tilde{x}}^{\ast })-G_x^{\ast }\right),$$

$$S_{G_y^{\ast }{G}_w^{\ast }}={\displaystyle \frac{1}{N-1}}\sum _{i=1}^N\left(I(y_i^{\ast }\le {\tilde{y}}^{\ast })-G_y^{\ast }\right)\left(I(w_i^{\ast }\le {\tilde{w}}^{\ast })-G_w^{\ast }\right),$$

$$S_{G_x^{\ast }{G}_w^{\ast }}={\displaystyle \frac{1}{N-1}}\sum _{i=1}^N\left(I(x_i^{\ast }\le {\tilde{x}}^{\ast })-G_x^{\ast }\right)\left(I(w_i^{\ast }\le {\tilde{w}}^{\ast })-G_w^{\ast }\right).$$

The corresponding correlation coefficients are

$$R_{G_y^{\ast }{G}_x^{\ast }}={\displaystyle \frac{S_{G_y^{\ast }{G}_x^{\ast }}}{S_{G_y^{\ast }}{S}_{G_x^{\ast }}}},R_{G_y^{\ast }{G}_w^{\ast }}={\displaystyle \frac{S_{G_y^{\ast }{G}_w^{\ast }}}{S_{G_y^{\ast }}{S}_{G_w^{\ast }}}},R_{G_x^{\ast }{G}_w^{\ast }}={\displaystyle \frac{S_{G_x^{\ast }{G}_w^{\ast }}}{S_{G_x^{\ast }}{S}_{G_w^{\ast }}}}.$$

To study the bias and mean squared error (MSE) properties of the estimators of $G_y^{\ast }$, we introduce relative error components:

$${\xi }_0={\displaystyle \frac{{\widehat{G}}_y^{\ast }-G_y^{\ast }}{G_y^{\ast }}},{\xi }_1={\displaystyle \frac{{\widehat{G}}_x^{\ast }-G_x^{\ast }}{G_x^{\ast }}},{\xi }_2={\displaystyle \frac{{\widehat{G}}_w^{\ast }-G_w^{\ast }}{G_w^{\ast }}},$$

with expectations $E\left({\xi }_i\right)=0$, for $i=0,1,2$.

The error terms are given by

$$\begin{array}{cc}\hfill E\left({\xi }_0^2\right)& =\lambda {\left(C_{G_y^{\ast }}\right)}^2={\psi }_0,\hfill \\ \hfill E\left({\xi }_1^2\right)& =\lambda {\left(C_{G_x^{\ast }}\right)}^2={\psi }_1,\hfill \\ \hfill E\left({\xi }_2^2\right)& =\lambda {\left(C_{G_w^{\ast }}\right)}^2={\psi }_2,\hfill \\ \hfill E\left({\xi }_0{\xi }_1\right)& =\lambda R_{G_y^{\ast }{G}_x^{\ast }}{C}_{G_y^{\ast }}{C}_{G_x^{\ast }}={\psi }_{01},\hfill \\ \hfill E\left({\xi }_0{\xi }_2\right)& =\lambda R_{G_y^{\ast }{G}_w^{\ast }}{C}_{G_y^{\ast }}{C}_{G_w^{\ast }}={\psi }_{02},\hfill \\ \hfill E\left({\xi }_1{\xi }_2\right)& =\lambda R_{G_x^{\ast }{G}_w^{\ast }}{C}_{G_x^{\ast }}{C}_{G_w^{\ast }}={\psi }_{12},\hfill \end{array}$$

where $\lambda ={\displaystyle \frac{1}{n}}$ and n is the sample size.

The above framework provides the foundational notations for developing new classes of CDF estimators under PPS sampling. The inclusion of auxiliary information through dual variables ($x_i,z_i$) facilitates efficiency gains in finite-sample inference. From an application perspective, these formulations are directly applicable in survey settings where unit sizes are heterogeneous (e.g., household income surveys, enterprise-level trade statistics, or agricultural crop yield studies). The subsequent sections will utilize these expressions to derive bias, MSE, and efficiency results, and to demonstrate their empirical advantages through both simulations and real-world datasets.

On the other hand, we construct several standard estimators for the finite population cumulative distribution function (CDF) under probability proportional to size (PPS) sampling. The biases and mean squared errors (MSEs) of these estimators are derived up to the first-order approximation. The existing estimators considered are as follows:

(1)

Consider the traditional mean estimator for the finite population CDF:

$$\widehat{G}\left(y^{\ast }\right)={\displaystyle \frac{1}{n}}\sum _{i=1}^{n}I(y_i^{\ast }\le {\tilde{y}}^{\ast }).$$

(1)

The variance of $\widehat{G_{y^{\ast }}}$ is given by

$$V\left(\widehat{G}\left(y^{\ast }\right)\right)={G_y^{\ast }}^2{\psi }_0.$$

(2)

(2)

Ref. [31] The ratio estimator under PPS sampling is defined as

$${\widehat{G}}_R\left(y^{\ast }\right)={\widehat{G}}_y^{\ast }\left({\displaystyle \frac{G_x^{\ast }}{{\widehat{G}}_x^{\ast }}}\right).$$

(3)

The bias and mean squared error (MSE) of ${\widehat{G}}_R\left(y^{\ast }\right)$ are given by

$$\mathrm{Bias}\left({\widehat{G}}_R\left(y^{\ast }\right)\right)=G_y^{\ast }\left({\psi }_0-{\psi }_{01}\right),$$

and

$$\mathrm{MSE}\left({\widehat{G}}_R\left(y^{\ast }\right)\right)={G_y^{\ast }}^2\left({\psi }_0+{\psi }_1-2{\psi }_{01}\right).$$

(4)

(3)

Ref. [32] The Bahl and Tuteja ratio-type exponential estimator under PPS sampling is defined as

$${\widehat{G}}_{BTR}\left(y^{\ast }\right)=\widehat{G}{y}^{\ast }exp\left({\displaystyle \frac{G_{x^{\ast }}-{\widehat{G}}_{x^{\ast }}}{G_{x^{\ast }}+{\widehat{G}}_{x^{\ast }}}}\right).$$

(5)

The bias and mean squared error of this estimator are given by

$$\mathrm{Bias}\left({\widehat{G}}_{BTR}\left(y^{\ast }\right)\right)=G_y^{\ast }\left({\displaystyle \frac{3}{8}}{\psi }_1-{\displaystyle \frac{1}{2}}{\psi }_{01}\right),$$

and

$$\mathrm{MSE}\left({\widehat{G}}_{BTR}\left(y^{\ast }\right)\right)={G{y}^{\ast }}^2\left({\psi }_0+{\displaystyle \frac{1}{4}}{\psi }_1-{\psi }_{01}\right).$$

(6)

(4)

The regression estimator for $G_{y^{\ast }}$ under PPS sampling is given by

$${\widehat{G}}_{Reg}\left(y^{\ast }\right)={\widehat{G}}_{y^{\ast }}+m\left(G_{x^{\ast }}-{\widehat{G}}_{x^{\ast }}\right),$$

(7)

where m is an unknown parameter to be determined.

The minimum variance of ${\widehat{G}}_{Reg}\left(y^{\ast }\right)$ is achieved at the optimal value

$$m_{\mathrm{opt}}={\displaystyle \frac{G\left(y^{\ast }\right){\psi }_{01}}{G\left(x^{\ast }\right){\psi }_0}},$$

and is given by

$${\mathrm{Var}}_{min}\left({\widehat{G}}_{Reg}\left(y^{\ast }\right)\right)={\displaystyle \frac{G_{y^{\ast }}^2\left({\psi }_0{\psi }_1-{\psi }_{01}^2\right)}{{\psi }_1}}.$$

This can also be expressed as

$${\mathrm{Var}}_{min}\left({\widehat{G}}_{Reg}\left(y^{\ast }\right)\right)=G_{y^{\ast }}^2{\psi }_0\left(1-{\displaystyle \frac{{\psi }_{01}^2}{{\psi }_0{\psi }_1}}\right).$$

(8)

(5)

Ref. [33] The Rao difference-type estimator for $G\left(y^{\ast }\right)$ is defined as

$${\widehat{G}}_{RD}\left(y^{\ast }\right)=m_1{\widehat{G}}_{y^{\ast }}+m_2\left(G_{x^{\ast }}-{\widehat{G}}_{x^{\ast }}\right),$$

(9)

where $m_1$ and $m_2$ are unknown constants to be determined.

The bias and mean squared error (MSE) of ${\widehat{G}}_{RD}\left(y^{\ast }\right)$, up to the first order of approximation, are given by

$$\mathrm{Bias}\left({\widehat{G}}_{RD}\left(y^{\ast }\right)\right)=G_{y^{\ast }}(m_1-1),$$

and

$$\mathrm{MSE}\left({\widehat{G}}_{RD}\left(y^{\ast }\right)\right)=G_{y^{\ast }}^2\left(1-2m_1+m_1^2\right)+m_1^2{G}_{y^{\ast }}^2{\psi }_1.$$

The optimal values of $m_1$ and $m_2$ that minimize the MSE are

$$m_{1\left(opt\right)}={\displaystyle \frac{{\psi }_1}{{\psi }_1{\psi }_0-{\psi }_{01}^2+{\psi }_1}},$$

$$m_{2\left(opt\right)}={\displaystyle \frac{G_{y^{\ast }}{\psi }_0}{G_{x^{\ast }}\left({\psi }_0{\psi }_1-{\psi }_{01}^2+{\psi }_1\right)}}.$$

At these optimum values, the minimum mean squared error is

$${\mathrm{MSE}}_{min}\left({\widehat{G}}_{RD}\left(y^{\ast }\right)\right)={\displaystyle \frac{G_{y^{\ast }}^2\left({\psi }_0{\psi }_1-{\psi }_{01}^2\right)}{{\psi }_0{\psi }_1-{\psi }_{01}^2+{\psi }_1}}.$$

(10)

(6)

Ref. [34] Grover and Kaur introduced a generalized class of exponential estimators for $G\left(y^{\ast }\right)$, defined as

$${\widehat{G}}_{GK}\left(y^{\ast }\right)=\left\{m_3{\widehat{G}}_{y^{\ast }}+m_4\left(G_{x^{\ast }}-{\widehat{G}}_{x^{\ast }}\right)\right\}exp\left({\displaystyle \frac{a\left(G_{x^{\ast }}-{\widehat{G}}_{x^{\ast }}\right)}{a\left(G_{x^{\ast }}+{\widehat{G}}_{x^{\ast }}\right)+2b}}\right),$$

(11)

where $m_3$ and $m_4$ are unknown constants.

The bias of ${\widehat{G}}_{GK}\left(y^{\ast }\right)$, up to the first order of approximation, is

$$\mathrm{Bias}\left({\widehat{G}}_{GK}\left(y^{\ast }\right)\right)=G_{y^{\ast }}(m_3-1)+{\displaystyle \frac{3}{8}}{\theta }^2{m}_3{G}_{y^{\ast }}+{\displaystyle \frac{1}{2}}\theta m_4{G}_{x^{\ast }}{V}_1-{\displaystyle \frac{1}{2}}\theta G_{y^{\ast }}{\psi }_{01}.$$

The mean squared error (MSE) is given by

$$\begin{array}{cc}\hfill \mathrm{MSE}\left({\widehat{G}}_{GK}\left(y^{\ast }\right)\right)& =m_4^2{G}_{x^{\ast }}^2{\psi }_1+m_3^2{G}_{y^{\ast }}^2{\psi }_0+2\theta m_3{m}_4{G}_{y^{\ast }}{G}_{x^{\ast }}{\psi }_1\hfill \\ \hfill & -2m_3{m}_4{G}_{y^{\ast }}{G}_{x^{\ast }}{\psi }_{01}+G_{y^{\ast }}^2-2m_3{G}_{y^{\ast }}^2+\theta m_3^2{G}_{y^{\ast }}^2\hfill \\ \hfill & +m_3{G}_{y^{\ast }}^2{\psi }_{01}-\theta m_4{G}_{y^{\ast }}{G}_{x^{\ast }}{\psi }_1-2\theta m_3^2{G}_{y^{\ast }}^2{\psi }_{01}\hfill \\ \hfill & +{\displaystyle \frac{3}{4}}{\theta }^2{m}_3{G}_{y^{\ast }}^2{\psi }_1+{\theta }^2{m}_3^2{G}_{y^{\ast }}^2{\psi }_1.\hfill \end{array}$$

The optimal values of $m_3$ and $m_4$ are

$$m_{3\left(opt\right)}={\displaystyle \frac{{\psi }_1\left({\theta }^2{\psi }_1-8\right)}{8\left(-{\psi }_0{\psi }_1+{\psi }_{01}^2-{\psi }_1\right)}},$$

$$m_{4\left(opt\right)}={\displaystyle \frac{G_{y^{\ast }}\left({\theta }^2{\psi }_1^2-{\theta }^2{\psi }_1{\psi }_{01}+4\theta {\psi }_0{\psi }_1-4\theta {\psi }_{01}^2-4\theta {\psi }_1+8{\psi }_{01}\right)}{8G_{x^{\ast }}\left({\psi }_0{\psi }_1-{\psi }_{01}^2+{\psi }_1\right)}}.$$

The minimum MSE of ${\widehat{G}}_{GK}\left(y^{\ast }\right)$ at these optimal values is

$${\mathrm{MSE}}_{min}\left({\widehat{G}}_{GK}\left(y^{\ast }\right)\right)={\displaystyle \frac{G_{y^{\ast }}^2}{64}}\left(64-16{\theta }^2{\psi }_1-{\displaystyle \frac{{\psi }_1{\left(-8+{\theta }^2{\psi }_1\right)}^2}{{\psi }_1(1+{\psi }_0)-{\psi }_{01}^2}}\right).$$

(12)

2.1. Proposed Family of Estimators Under PPS Sampling

In this subsection, we propose a novel family of estimators for the finite population distribution function (DF) within the framework of probability proportional to size (PPS) sampling. This development is motivated by the need to construct efficient estimators that simultaneously exploit auxiliary information and maintain computational tractability, thereby aligning with both theoretical contributions and practical applications in large-scale survey sampling and computational statistics.

We define the proposed class of estimators as

$$\begin{array}{cc}\hfill {\widehat{G}}_{\mathrm{SM}}\left(y^{\ast }\right)=[& {\widehat{G}}_{y^{\ast }}+{\beta }_1\left(G_{x^{\ast }}-{\widehat{G}}_{x^{\ast }}\right)+{\beta }_2\left(G_{w^{\ast }}-{\widehat{G}}_{w^{\ast }}\right)]\hfill \\ \hfill & \times {\left[exp\left({\displaystyle \frac{G_{x^{\ast }}-{\widehat{G}}_{x^{\ast }}}{G_{x^{\ast }}+{\widehat{G}}_{x^{\ast }}}}\right)\right]}^{{\gamma }_1}\times {\left[exp\left({\displaystyle \frac{G_{w^{\ast }}-{\widehat{G}}_{w^{\ast }}}{G_{w^{\ast }}+{\widehat{G}}_{w^{\ast }}}}\right)\right]}^{{\gamma }_2},\hfill \end{array}$$

(13)

where ${\widehat{G}}_{\mathrm{SM}}\left(y^{\ast }\right)$ denotes the proposed estimator of the population DF at $y^{\ast }$, while $x^{\ast }$ and $w^{\ast }$ represent transformed auxiliary points with known distribution functions $G_{x^{\ast }}$ and $G_{w^{\ast }}$, respectively. The tuning parameters ${\beta }_1,{\beta }_2,{\gamma }_1,$ and ${\gamma }_2$ are user-specified constants chosen to optimize estimator performance in terms of efficiency and robustness.

2.1.1. First-Order Approximation

Expanding the estimator using a first-order Taylor series expansion and introducing error terms ${\xi }_0,{\xi }_1,$ and ${\xi }_2$, we obtain

$$\begin{array}{cc}\hfill {\widehat{G}}_{\mathrm{SM}}\left(y^{\ast }\right)=& \{G_{y^{\ast }}+G_{y^{\ast }}{\xi }_0-{\beta }_1{G}_{x^{\ast }}{\xi }_1-{\beta }_2{G}_{w^{\ast }}{\xi }_2\}\hfill \\ \hfill & \times \left[\left(1-\frac{1}{2}{\gamma }_1{\xi }_1+\frac{1}{4}{\gamma }_1{\xi }_1^2+\frac{1}{8}{\gamma }_1^2{\xi }_1^2\right)\left(1-\frac{1}{2}{\gamma }_2{\xi }_2+\frac{1}{4}{\gamma }_2{\xi }_2^2+\frac{1}{8}{\gamma }_2^2{\xi }_2^2\right)\right].\hfill \end{array}$$

(14)

By retaining terms up to the first order, the deviation of ${\widehat{G}}_{\mathrm{SM}}\left(y^{\ast }\right)$ from $G_{y^{\ast }}$ is expressed as

$$\begin{array}{cc}\hfill {\widehat{G}}_{\mathrm{SM}}\left(y^{\ast }\right)-G_{y^{\ast }}& =G_{y^{\ast }}\left[{\xi }_0-\frac{1}{2}{\gamma }_1{\xi }_1-\frac{1}{2}{\gamma }_2{\xi }_2\right]-{\beta }_1{G}_{x^{\ast }}{\xi }_1-{\beta }_2{G}_{w^{\ast }}{\xi }_2+O\left({\xi }^2\right).\hfill \end{array}$$

(15)

2.1.2. Bias and Mean Squared Error

The bias of ${\widehat{G}}_{\mathrm{SM}}\left(y^{\ast }\right)$, up to the first order, is given by

$$\begin{array}{cc}\hfill \mathrm{Bias}\left({\widehat{G}}_{\mathrm{SM}}\left(y^{\ast }\right)\right)& =G_{y^{\ast }}\left(\frac{1}{4}{\gamma }_1^2{\psi }_1-\frac{1}{2}{\gamma }_1{\psi }_{01}-\frac{1}{2}{\gamma }_2{\psi }_{02}+\frac{1}{4}{\gamma }_1{\gamma }_2{\psi }_{12}+\frac{1}{8}{\gamma }_2^2{\psi }_2\right)\hfill \\ \hfill & +G_{x^{\ast }}\left(\frac{1}{2}{\gamma }_1{\beta }_1{\psi }_1+\frac{1}{2}{\gamma }_2{\beta }_1{\psi }_{12}\right)+G_{w^{\ast }}\left(\frac{1}{2}{\gamma }_1{\psi }_{12}+\frac{1}{2}{\gamma }_2{\psi }_2\right).\hfill \end{array}$$

(16)

Similarly, the mean squared error (MSE) of ${\widehat{G}}_{\mathrm{SM}}\left(y^{\ast }\right)$ is approximated by

$$\begin{array}{cc}\hfill \mathrm{MSE}\left({\widehat{G}}_{\mathrm{SM}}\left(y^{\ast }\right)\right)& ={\displaystyle \frac{1}{4}}\left({\gamma }_1^2{\psi }_1+(2{\gamma }_2{\psi }_{12}-4{\psi }_{01}){\gamma }_1+{\gamma }_2^2{\psi }_2-4{\gamma }_2{\psi }_{02}+4{\psi }_0\right)G_{y^{\ast }}^2\hfill \\ \hfill & +{\beta }_1^2{G}_{x^{\ast }}^2{\psi }_1+{\beta }_2^2{G}_{w^{\ast }}^2{\psi }_2+2{\beta }_1{\beta }_2{G}_{x^{\ast }}{G}_{w^{\ast }}{\psi }_{12}.\hfill \end{array}$$

(17)

The values of ${\beta }_1$ and ${\beta }_2$ that minimize the MSE are obtained as

$${\beta }_1={\displaystyle \frac{1}{2G_{x^{\ast }}{\psi }_1}}\left(-G_{y^{\ast }}{\gamma }_1{\psi }_1+G_{y^{\ast }}{\gamma }_2{\psi }_{12}-2G_{y^{\ast }}{\psi }_{01}+2G_{w^{\ast }}{\psi }_{12}\right),$$

(18)

$${\beta }_2=-{\displaystyle \frac{G_{y^{\ast }}}{2G_{w^{\ast }}{\psi }_2}}\left({\gamma }_1{\psi }_{12}+{\gamma }_2{\psi }_2-2{\psi }_{02}\right).$$

(19)

Substituting these into the MSE expression yields the minimized MSE:

$$\begin{array}{cc}\hfill {\mathrm{MSE}}_{min}\left({\widehat{G}}_{\mathrm{SM}}\left(y^{\ast }\right)\right)=\hfill & G_{y^{\ast }}^2({\psi }_0{\psi }_1{\psi }_2-{\psi }_1{\psi }_{02}^2-{\psi }_2{\psi }_{01}^2+{\gamma }_1{\psi }_1{\psi }_{02}+{\gamma }_2{\psi }_2{\psi }_{01}\hfill \\ \hfill & -4{\gamma }_1^2{\psi }_1{\psi }_{12}^2-2{\gamma }_1{\gamma }_2{\psi }_1{\psi }_2{\psi }_{12}-{\gamma }_2^2{\psi }_2{\psi }_{12}^2)\hfill \\ \hfill & +G_{y^{\ast }}{G}_{w^{\ast }}^2\left(-4{\gamma }_1{\psi }_1{\psi }_2{\psi }_{12}-4{\gamma }_2{\psi }_2{\psi }_{12}+8{\psi }_2{\psi }_{01}{\psi }_{12}\right)\hfill \\ \hfill & -4G_{w^{\ast }}^2{\psi }_2{\psi }_{12}^2\hfill \end{array}$$

(20)

2.1.3. Theoretical and Application Relevance

Theoretically, this proposed family of estimators provides a flexible framework that generalizes ratio-type and exponential-type estimators under PPS sampling. The introduction of auxiliary parameters $({\beta }_1,{\beta }_2,{\gamma }_1,{\gamma }_2)$ enables adaptability to different sampling designs and error structures.

From an application standpoint, the estimator is particularly suitable for survey settings where PPS designs are frequently employed, such as household income surveys, business establishment surveys, and agricultural statistics. By incorporating auxiliary information effectively, the estimator reduces bias and MSE, thereby ensuring more reliable estimation of population distribution functions in practice.

3. Results

In this section, we present the findings of our empirical and simulation-based investigations, focusing on efficiency comparisons across multiple estimator families. The results are structured into three complementary parts: efficiency comparison, empirical study, and simulation study.

3.1. Efficiency Comparison

To evaluate the theoretical performance of the proposed estimator ${\widehat{G}}_{SM}\left(y^{\ast }\right)$ under the PPS framework, we compared its minimum mean square error (MSE) with that of the existing competing estimators. The efficiency conditions were established by showing that the proposed estimator consistently achieved a smaller MSE, thereby ensuring superior precision. Specifically, the following results hold:

1.

From (2) and (20),

$$MS{E}_{min}\left({\widehat{G}}_{SM}\left(y^{\ast }\right)\right)<V\left(\widehat{G}\left(y^{\ast }\right)\right),$$

provided that

$$V\left(\widehat{G}\left(y^{\ast }\right)\right)-MS{E}_{min}\left({\widehat{G}}_{SM}\left(y^{\ast }\right)\right)>0.$$

Proof. 

$$\begin{array}{cc}\hfill & G_{y^{\ast }}^2({\psi }_0{\psi }_1{\psi }_2-{\psi }_1{\psi }_{02}^2-{\psi }_2{\psi }_{01}^2+{\gamma }_1{\psi }_1{\psi }_{02}+{\gamma }_2{\psi }_2{\psi }_{01}\hfill \\ \hfill & -4{\gamma }_1^2{\psi }_1{\psi }_{12}^2-2{\gamma }_1{\gamma }_2{\psi }_1{\psi }_2{\psi }_{12}-{\gamma }_2^2{\psi }_2{\psi }_{12}^2)\hfill \\ \hfill & +G_{y^{\ast }}{G}_{w^{\ast }}^2\left(-4{\gamma }_1{\psi }_1{\psi }_2{\psi }_{12}-4{\gamma }_2{\psi }_2{\psi }_{12}+8{\psi }_2{\psi }_{01}{\psi }_{12}\right)\hfill \\ \hfill & -4G_{w^{\ast }}^2{\psi }_2{\psi }_{12}^2<{G_y^{\ast }}^2{\psi }_0.\hfill \end{array}$$

(21)

Simplifying the above expression we get,

$$G_{y^{\ast }}^{2}A+G_{y^{\ast }}{G}_{w^{\ast }}^{2}B+G_{w^{\ast }}^{2}C<G_{y^{\ast }}^2\psi ,$$

(22)

where $A={\psi }_0{\psi }_1{\psi }_2-{\psi }_1{\psi }_{02}^2-{\psi }_2{\psi }_{01}^2+{\gamma }_1{\psi }_{02}^2{\psi }_1^2+{\gamma }_{2{\psi }_{01}}{\psi }_1^2$…

$$B=-4{\gamma }_1{\psi }_{12}^2{\psi }_1^2{\psi }_2^2-4{\gamma }_2{\psi }_2^2{\psi }_{12}+8{\psi }_2{\psi }_{01}{\psi }_{12},$$

(23)

and

$$C=-4\psi {\psi }_{12}^2.$$

(24)

So, the dominancy of the proposed estimator holds iff $A<0$, $B<0$, and $C<0$. Then

$$MS{E}_{min}\left({\widehat{G}}_{SM}\left(y^{\ast }\right)\right)<V\left(\widehat{G}\left(y^{\ast }\right)\right).$$

(25)

□

2.

From (4) and (20),

$$MS{E}_{min}\left({\widehat{G}}_{SM}\left(y^{\ast }\right)\right)<MSE\left({\widehat{G}}_R\left(y^{\ast }\right)\right),$$

whenever

$$MSE\left({\widehat{G}}_R\left(y^{\ast }\right)\right)-MS{E}_{min}\left({\widehat{G}}_{SM}\left(y^{\ast }\right)\right)>0.$$

Proof. 

For the above statement, the simplified expression is given below:

$$G_{y^{\ast }}^2({\psi }_0+{\psi }_1-2{\psi }_{01}-D)-G_{y^{\ast }}{G}_{w^{\ast }}^{2}E+4G_{w^{\ast }}^2{\psi }_2{\psi }_{12}^2>0.$$

(26)

where $D=A+B$, while A and B are defined in the proof of the first statement, and

$$E=-4{\gamma }_1{\psi }_1{\psi }_2{\psi }_{12}-4{\gamma }_2{\psi }_2{\psi }_{12}+8{\psi }_2{\psi }_{01}{\psi }_{12}.$$

(27)

Now we know that,

$${\psi }_0+{\psi }_1-2{\psi }_{01}-D>0,$$

(28)

because D is basically the collection of covariance and correction terms. So,

$$G_{y^{\ast }}^2({\psi }_0+{\psi }_1-2{\psi }_{01}-D)>G_{y^{\ast }}(QE+4Q{\psi }_2{\psi }_{12}^2).$$

(29)

So, the above result shows that

$$MSE\left({\widehat{G}}_R\left(y^{\ast }\right)\right)>MS{E}_{min}\left({\widehat{G}}_{SM}\left(y^{\ast }\right)\right).$$

(30)

□

3.

From (6) and (20),

$$MS{E}_{min}\left({\widehat{G}}_{SM}\left(y^{\ast }\right)\right)<MSE\left({\widehat{G}}_{BT,R}\left(y^{\ast }\right)\right),$$

if

$$MSE\left({\widehat{G}}_{BT,R}\left(y^{\ast }\right)\right)-MS{E}_{min}\left({\widehat{G}}_{SM}\left(y^{\ast }\right)\right)>0.$$

4.

From (8) and (20),

$$MS{E}_{min}\left({\widehat{G}}_{SM}\left(y^{\ast }\right)\right)<Va{r}_{min}\left({\widehat{G}}_{Reg}\left(y^{\ast }\right)\right),$$

provided that

$$Va{r}_{min}\left({\widehat{G}}_{Reg}\left(y^{\ast }\right)\right)-MS{E}_{min}\left({\widehat{G}}_{SM}\left(y^{\ast }\right)\right)>0.$$

5.

From (10) and (20),

$$MS{E}_{min}\left({\widehat{G}}_{SM}\left(y^{\ast }\right)\right)<MS{E}_{min}\left({\widehat{G}}_{RD}\left(y^{\ast }\right)\right),$$

whenever

$$MS{E}_{min}\left({\widehat{G}}_{RD}\left(y^{\ast }\right)\right)-MS{E}_{min}\left({\widehat{G}}_{SM}\left(y^{\ast }\right)\right)>0.$$

6.

From (12) and (20),

$$MS{E}_{min}\left({\widehat{G}}_{SM}\left(y^{\ast }\right)\right)<MS{E}_{min}\left({\widehat{G}}_{GK}\left(y^{\ast }\right)\right),$$

provided that

$$MS{E}_{min}\left({\widehat{G}}_{GK}\left(y^{\ast }\right)\right)-MS{E}_{min}\left({\widehat{G}}_{SM}\left(y^{\ast }\right)\right)>0.$$

Proof. 

The simplification after putting the mean squared error (MSE) of both estimators, we get,

$$G_{y^{\ast }}^{2}K-(G_{y^{\ast }}^{2}A+G_{y^{\ast }}{G}_{w^{\ast }}^{2}B+G_{w^{\ast }}^{2}C)>0,$$

(31)

where,

$$K={\displaystyle \frac{1}{64}}\left(64-16{\theta }^2{\psi }_1-{\displaystyle \frac{{\psi }_1{(-8+{\theta }^2{\psi }_1)}^2}{{\psi }_1(1+{\psi }_0)-{\psi }_{01}^2}}\right),$$

(32)

where A, B and C are defined in the proof of the first statement. So, the above statement will hold iff $A<K$, $B\le 0$, and $C\le 0$.

□

These theoretical inequalities confirm that the proposed estimator achieves a lower MSE than its counterparts across multiple established classes, including ratio-type, regression-type, and generalized kernel-based estimators. In other words, the proposed estimator exhibits uniformly better efficiency under the PPS framework.

From a practical perspective, such efficiency gains translate directly into more reliable estimation of cumulative distribution functions (CDFs) in real-world survey applications. For instance,

• In income distribution studies, a more efficient estimator reduces the required sample size, thereby lowering data collection costs.
• In epidemiological surveys, improved precision ensures more accurate prevalence estimates, which are critical for healthcare policy and resource allocation.
• In agricultural yield forecasting, efficiency improvements minimize the risk of biased or imprecise yield estimates when unit sizes (e.g., farm sizes) vary widely.

Thus, the theoretical superiority of the proposed estimator directly strengthens its applicability in domains where PPS sampling is indispensable and estimator efficiency is crucial.

3.2. Simulation Study

To evaluate the finite-sample performance of the proposed family of estimators, a Monte Carlo simulation study was conducted using three synthetic populations with distinct mean and covariance structures. These populations were generated from multivariate normal distributions to mimic diverse correlation patterns and size heterogeneity frequently encountered in survey data.

Population I was designed with a simple increasing mean vector ${\mu }_1={(1,2,3,4)}^{\top }$ and a moderately correlated covariance matrix, thereby representing a balanced structure with mild heterogeneity. Population II was constructed with zero means and higher off-diagonal correlations, reflecting stronger dependency among variables and potential multicollinearity effects. Population III had decreasing negative means ${\mu }_3={(-1,-2,-3,-4)}^{\top }$ and a denser covariance matrix with stronger correlations, thereby representing more heterogeneous and complex conditions (see Table 1). Table 2 reports the mean squared errors (MSEs) for the proposed estimators ${\widehat{G}}_{j,SM}\left(y^{\ast }\right)$ ($j=1,\dots ,8$) and for benchmark competitors including the random group (${\widehat{G}}_{R\left(y^{\ast }\right)}$), bias-transformed ratio (${\widehat{G}}_{BTR\left(y^{\ast }\right)}$), regression (${\widehat{G}}_{Reg\left(y^{\ast }\right)}$), regression difference (${\widehat{G}}_{RD\left(y^{\ast }\right)}$), and generalized kernel (${\widehat{G}}_{GK\left(y^{\ast }\right)}$) estimators. The results demonstrate that across all three populations, the proposed estimators consistently yield smaller MSEs than the classical alternatives. Particularly, ${\widehat{G}}_{6,SM}\left(y^{\ast }\right)$ and ${\widehat{G}}_{7,SM}\left(y^{\ast }\right)$ achieve the lowest error magnitudes, highlighting the robustness of the SM-based framework.

Table 1. Summary measure.

Measure	Pop. I	Pop. II	Pop. III
Population size (N)	5000	5000	5000
Sample size (n)	120	120	120
$G_{y^{\ast }}$	0.5	0.5	0.5
$G_{x^{\ast }}$	0.5	0.5	0.5
$G_{w^{\ast }}$	0.5	0.5	0.5
$C_{G_y^{\ast }}$	1.0001	1.0001	1.0001
$M_{y^{\ast }}$	1.0101	$-0.0142$	$-0.9810$
$M_{x^{\ast }}$	1.9767	0.000228	$-1.998$
$M_{w^{\ast }}$	2.99041	$-0.0003$	$-2.9747$
$C_{G_x^{\ast }}$	1.0001	1.0001	1.0001
$C_{G_w^{\ast }}$	1.0001	1.0001	1.0001
$\lambda$	0.0081	0.0081	0.0081
$R_{G_y^{\ast }{G}_x^{\ast }}$	0.1104	0.5072	0.3352
$R_{G_y^{\ast }{G}_w^{\ast }}$	0.1504	0.2624	0.114
$R_{G_x^{\ast }{G}_w^{\ast }}$	0.2752	$-0.0112$	$-0.212$

Table 2. Mean squared errors (MSEs) from simulation study. Smaller values indicate higher efficiency.

Estimators	Population I	Population II	Population III
${\widehat{G}}_{8,SM}\left(y^{\ast }\right)$	0.00178	0.00138	0.00139
${\widehat{G}}_{7,SM}\left(y^{\ast }\right)$	0.00147	0.00138	0.00129
${\widehat{G}}_{6,SM}\left(y^{\ast }\right)$	0.00119	0.00137	0.00165
${\widehat{G}}_{5,SM}\left(y^{\ast }\right)$	0.00175	0.00138	0.00127
${\widehat{G}}_{4,SM}\left(y^{\ast }\right)$	0.00163	0.00138	0.00153
${\widehat{G}}_{3,SM}\left(y^{\ast }\right)$	0.00176	0.00138	0.00147
${\widehat{G}}_{2,SM}\left(y^{\ast }\right)$	0.00173	0.00138	0.00131
${\widehat{G}}_{1,SM}\left(y^{\ast }\right)$	0.00137	0.00127	0.00167
${\widehat{G}}_{R\left(y^{\ast }\right)}$	0.00277	0.00201	0.00270
${\widehat{G}}_{BTR\left(y^{\ast }\right)}$	0.00194	0.00155	0.00190
${\widehat{G}}_{y^{\ast }}$	0.00203	0.00204	0.00206
${\widehat{G}}_{Reg\left(y^{\ast }\right)}$	0.00183	0.00151	0.00180
${\widehat{G}}_{RD\left(y^{\ast }\right)}$	0.00181	0.00150	0.00179
${\widehat{G}}_{GK\left(y^{\ast }\right)}$	0.00181	0.00150	0.00179

To complement the MSE results, Table 3 presents the percentage relative efficiencies (PREs) of the estimators with respect to the baseline ${\widehat{G}}_{y^{\ast }}$. Values greater than 100 indicate efficiency gains. The superiority of the proposed estimators is evident, with PREs ranging from 114% to 171% in Population I, 146% to 160% in Population II, and 121% to 158% in Population III. In particular, ${\widehat{G}}_{6,SM}\left(y^{\ast }\right)$ and ${\widehat{G}}_{7,SM}\left(y^{\ast }\right)$ consistently outperform the benchmarks across different populations, demonstrating notable gains in precision under heterogeneous sampling conditions.

Table 3. Percentage relative efficiencies (PREs) with respect to ${\widehat{G}}_{y^{\ast }}$ (baseline = 100).

Estimators	Population I	Population II	Population III
${\widehat{G}}_{8,SM}\left(y^{\ast }\right)$	114.06	146.87	146.49
${\widehat{G}}_{7,SM}\left(y^{\ast }\right)$	138.59	147.55	157.80
${\widehat{G}}_{6,SM}\left(y^{\ast }\right)$	170.92	148.20	123.57
${\widehat{G}}_{5,SM}\left(y^{\ast }\right)$	115.90	147.43	160.68
${\widehat{G}}_{4,SM}\left(y^{\ast }\right)$	124.73	147.82	133.15
${\widehat{G}}_{3,SM}\left(y^{\ast }\right)$	115.57	147.82	138.05
${\widehat{G}}_{2,SM}\left(y^{\ast }\right)$	117.37	147.69	155.10
${\widehat{G}}_{1,SM}\left(y^{\ast }\right)$	148.31	159.85	121.44
${\widehat{G}}_{R\left(y^{\ast }\right)}$	73.36	93.03	75.39
${\widehat{G}}_{BTR\left(y^{\ast }\right)}$	104.06	104.25	106.88
${\widehat{G}}_{y^{\ast }}$	100.00	100.00	100.00
${\widehat{G}}_{Reg\left(y^{\ast }\right)}$	111.28	127.22	112.79
${\widehat{G}}_{RD\left(y^{\ast }\right)}$	112.10	133.96	113.61
${\widehat{G}}_{GK\left(y^{\ast }\right)}$	112.34	136.44	113.61

Overall, the simulation study highlights that the proposed SM-based estimators substantially reduce estimation error and improve efficiency, especially in scenarios with high heterogeneity and strong inter-variable correlations. These gains reaffirm the theoretical advantages of incorporating auxiliary size information into distribution function estimation under PPS sampling.

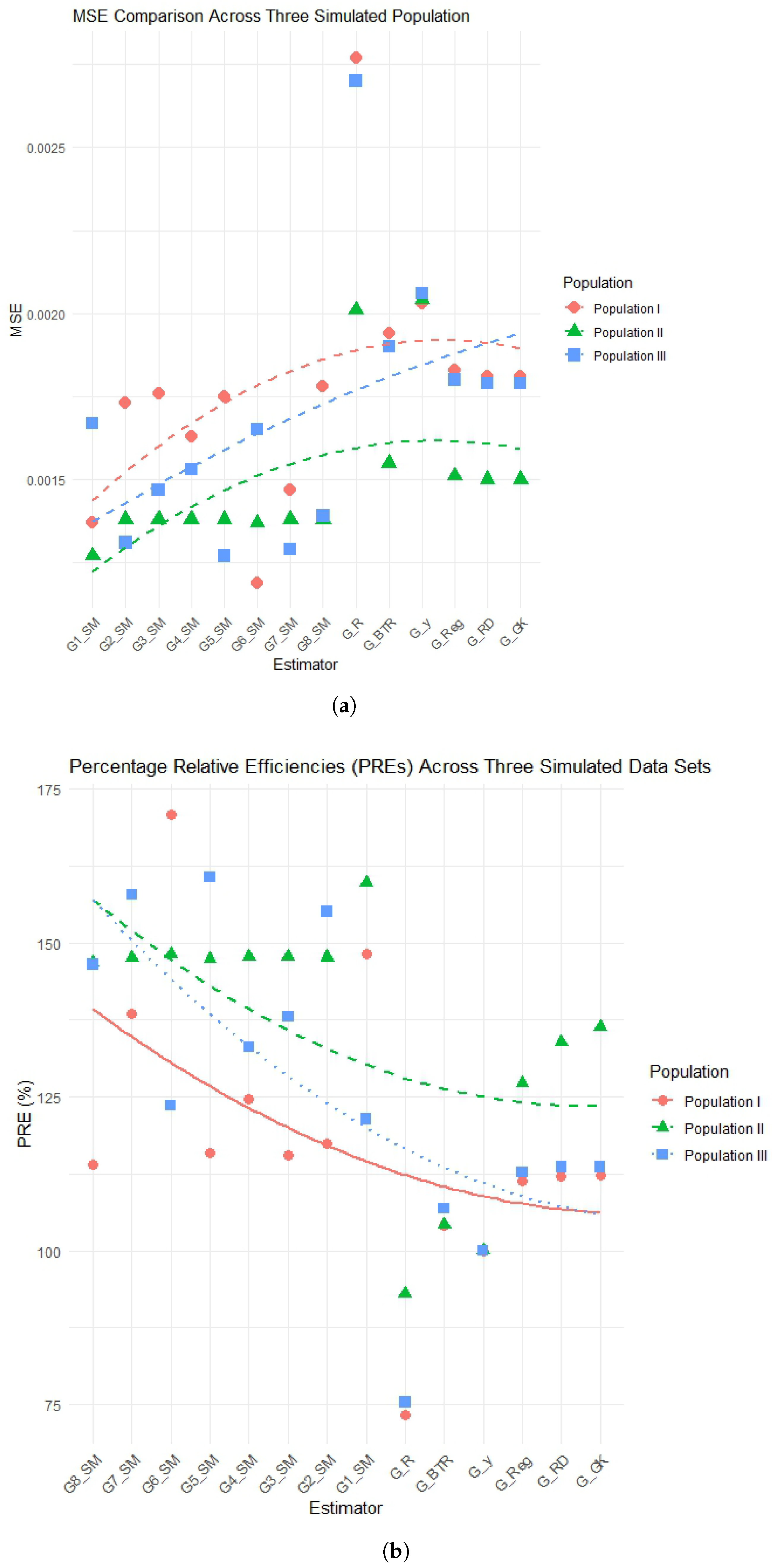
In addition to the tabulated results, Figure 1 and Figure 2 provides a visual comparison of the performance of the proposed family of estimators relative to the existing benchmarks. Panel (a) presents the mean squared error (MSE) values, while Panel (b) depicts the percentage relative efficiencies (PREs) for all three simulated populations.

Figure 1. (a) MSE comparison and (b) PRE comparison for the proposed family of estimators and the existing methods based on simulation results.

Figure 2. (a) Scatter plot for MSE comparison and (b) PRE comparison for the proposed family of estimators and the existing methods using scatter plot based on simulation results.

In Figure 1a and Figure 2a, the proposed estimators ${\widehat{G}}_{j,SM}\left(y^{\ast }\right)$, $j=1,\dots ,8$, consistently achieve lower MSE values across all the populations when compared to traditional estimators such as ${\widehat{G}}_{y^{\ast }}$, ${\widehat{G}}_{Reg\left(y^{\ast }\right)}$, and ${\widehat{G}}_{BTR\left(y^{\ast }\right)}$. This clearly demonstrates the robustness of the new class of estimators in reducing estimation error even under diverse covariance structures. The improvement is most pronounced for Populations I and III, where heterogeneity in the covariance matrix is higher, highlighting the adaptability of the proposed methods to more complex correlation patterns.

Figure 1b and Figure 2b further corroborate these findings by showing that the proposed estimators substantially outperform classical benchmarks in terms of PRE. For instance, the estimator ${\widehat{G}}_{6,SM}\left(y^{\ast }\right)$ achieves up to 170.92% efficiency relative to the simple expansion estimator ${\widehat{G}}_{y^{\ast }}$, while ${\widehat{G}}_{1,SM}\left(y^{\ast }\right)$ and ${\widehat{G}}_{7,SM}\left(y^{\ast }\right)$ also exhibit consistently high efficiency gains across populations. These improvements indicate that the proposed estimators not only reduce bias and variance but also enhance efficiency, making them preferable choices for practical applications in survey inference.

Overall, the visual evidence aligns well with the numerical results reported in Table 4, reinforcing the conclusion that the proposed family of estimators provides superior performance in terms of both error minimization and efficiency enhancement.

Table 4. Mean squared errors (MSEs) of the proposed and existing estimators under Populations I–III. Lower MSE indicates higher efficiency.

Estimator	Population I	Population II	Population III
${\widehat{G}}_{8,SM}\left(y^{\ast }\right)$	0.0141	0.0096	0.0030
${\widehat{G}}_{7,SM}\left(y^{\ast }\right)$	0.0093	0.0057	0.0015
${\widehat{G}}_{6,SM}\left(y^{\ast }\right)$	0.0066	0.0032	0.0020
${\widehat{G}}_{5,SM}\left(y^{\ast }\right)$	0.0125	0.0074	0.0018
${\widehat{G}}_{4,SM}\left(y^{\ast }\right)$	0.0118	0.0082	0.0016
${\widehat{G}}_{3,SM}\left(y^{\ast }\right)$	0.0141	0.0087	0.0027
${\widehat{G}}_{2,SM}\left(y^{\ast }\right)$	0.0138	0.0090	0.0026
${\widehat{G}}_{1,SM}\left(y^{\ast }\right)$	0.0093	0.0068	0.0012
${\widehat{G}}_{R\left(y^{\ast }\right)}$	0.0263	0.0187	0.0106
${\widehat{G}}_{BTR\left(y^{\ast }\right)}$	0.0212	0.0167	0.0072
${\widehat{G}}_{y^{\ast }}$	0.0175	0.0174	0.0040
${\widehat{G}}_{Reg\left(y^{\ast }\right)}$	0.0164	0.0136	0.0040
${\widehat{G}}_{RD\left(y^{\ast }\right)}$	0.0154	0.0130	0.0039
${\widehat{G}}_{GK\left(y^{\ast }\right)}$	0.0151	0.0127	0.0039

3.3. Empirical Study

To examine the empirical performance of the proposed family of estimators, we consider three distinct populations commonly used in survey sampling research. These populations are drawn from fisheries, enology, and demographic contexts, ensuring diversity in both application domains and correlation structures. The corresponding descriptive statistics are summarized in Table 5.

Table 5. Key parameters and summary measures for the three selected populations.

Measure	Pop. I	Pop. II	Pop. III
Population size (N)	69	67	284
Sample size (n)	12	12	50
$S_{y^{\ast }}$	0.5034	0.504	0.494
$S_{x^{\ast }}$	0.5021	0.504	0.5019
$S_{w^{\ast }}$	0.5034	0.500	0.5012
$G_{y^{\ast }}$	0.500	0.507	0.500
$G_{x^{\ast }}$	0.500	0.507	0.500
$G_{w^{\ast }}$	0.500	0.507	0.500
$C_{G_y^{\ast }}$	0.993	0.993	0.845
$C_{G_x^{\ast }}$	0.993	0.993	1.002
$C_{G_w^{\ast }}$	0.993	0.993	1.002
$\lambda$	0.0688	0.0688	0.0165
$M_{y^{\ast }}$	4782.01	25.68	28.81
$M_{x^{\ast }}$	4788.68	19.59	36.85
$M_{w^{\ast }}$	4810.81	61.04	12.77
$R_{G_y^{\ast }{G}_x^{\ast }}$	0.246	0.463	0.186
$R_{G_y^{\ast }{G}_w^{\ast }}$	0.072	0.403	0.186
$R_{G_x^{\ast }{G}_w^{\ast }}$	0.420	0.582	0.0380

Population I (Adapted from [35]). This population is based on fisheries data, where auxiliary information is naturally available across different years. The variables are defined as follows: Y = Quantity of fish caught in 1995; X = Quantity of fish caught in 1992; Z = Quantity of fish caught by fishermen in 1993; aQ = Quantity of fish caught in 1994. This dataset is characterized by strong temporal correlations across years, making it well-suited for evaluating auxiliary-variable-based estimators.

Population II ([36]). This population is constructed from the UCI Wine dataset, with chemical composition attributes serving as the study and auxiliary variables: Y = Aspartame; X = Leucine; Z = Isoleucine; Q = Valine. This setting captures biochemical correlation structures, with strong relationships among amino acids, providing a different test case from fisheries and demographic data.

Population III (Adapted from [37]). This population reflects demographic data with institutional auxiliary variables: Y = Population (in thousands) in 1985; X = Population in 1975; Z = Population in 1977; Q = Total number of seats in the municipal council. This population represents the type of socio-economic datasets where auxiliary information from administrative records enhances survey inference.

As shown in Table 5, Population I and II exhibit high correlations between study and auxiliary variables (e.g., $R_{G_x^{\ast }{G}_w^{\ast }}=0.420$ and $0.582$, respectively), whereas Population III shows weaker correlations (e.g., $0.0380$). These differences create a proper test bed for assessing how the proposed estimators respond to varying strengths of auxiliary information. The coefficients of variation ($C_G$) also highlight structural heterogeneity, especially in Population III, where demographic and institutional measures are less aligned. These variations across populations provide an informative benchmark for evaluating the robustness and efficiency of the proposed estimators (see Table 6).

Table 6. Proposed family of distribution function estimators for selected values of ${\alpha }_1$ and ${\alpha }_2$.

${\mathit{\gamma }}_1$	${\mathit{\gamma }}_2$	Proposed Estimator ${\widehat{\mathit{G}}}_{\mathbf{prop}}\left({\mathit{y}}^{\ast }\right)$
$R_{G_y^{\ast }{G}_x^{\ast }}$	$C_{G_y^{\ast }{G}_w^{\ast }}$	${\widehat{G}}_{8,\mathrm{prop}}\left(y^{\ast }\right)$
$S_{y^{\ast }}$	1	${\widehat{G}}_{7,\mathrm{prop}}\left(y^{\ast }\right)$
1	$G_{x^{\ast }}$	${\widehat{G}}_{6,\mathrm{prop}}\left(y^{\ast }\right)$
$R_{G_{x^{\ast }}{G}_{w^{\ast }}}$	$C_{G_{x^{\ast }}{G}_{w^{\ast }}}$	${\widehat{G}}_{5,\mathrm{prop}}\left(y^{\ast }\right)$
$G_{w^{\ast }}$	$C_{G_{v^{\ast }}{G}_{w^{\ast }}}$	${\widehat{G}}_{4,\mathrm{prop}}\left(y^{\ast }\right)$
$C_{G_{y^{\ast }}{G}_{x^{\ast }}}$	$R_{G_{x^{\ast }}{G}_{w^{\ast }}}$	${\widehat{G}}_{3,\mathrm{prop}}\left(y^{\ast }\right)$
$R_{G_{y^{\ast }}{G}_{x^{\ast }}}$	$G_{x^{\ast }}$	${\widehat{G}}_{2,\mathrm{prop}}\left(y^{\ast }\right)$
1	0	${\widehat{G}}_{1,\mathrm{prop}}\left(y^{\ast }\right)$

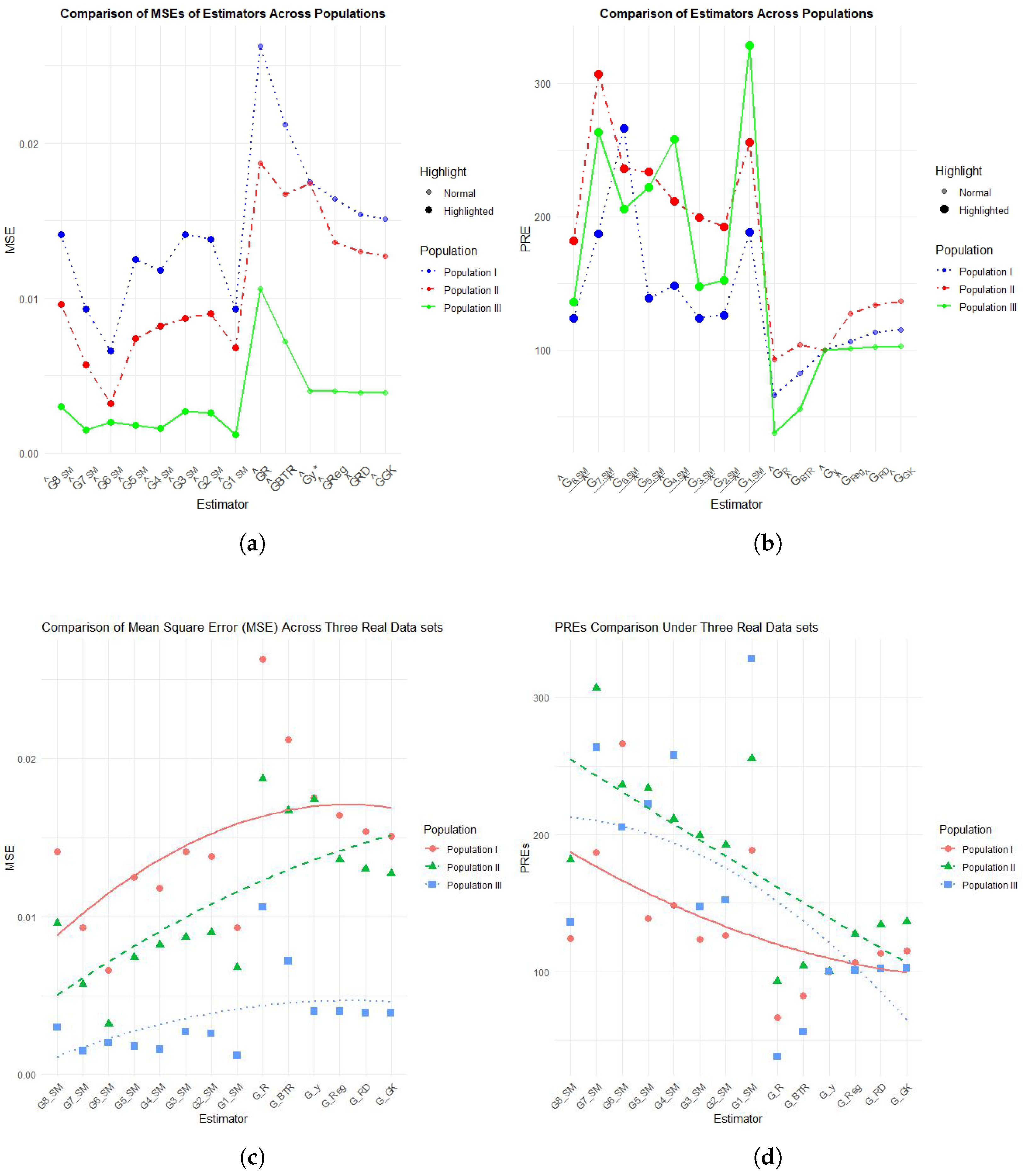
The empirical findings provide a comprehensive comparison of the proposed family of distribution function estimators with the existing methods in terms of efficiency, precision, and robustness (see Table 7). Table 4 reports the mean squared errors (MSEs) across Populations I–III, while Table 8 presents the percentage relative efficiencies (PREs). The corresponding graphical representations are presented in Figure 3, which illustrates both the MSE patterns (panel a) and the efficiency gains (panel b).

Table 7. Proposed family of distribution function estimators for selected values of ${\alpha }_1$ and ${\alpha }_2$.

${\mathit{\gamma }}_1$	${\mathit{\gamma }}_2$	Proposed Estimator ${\widehat{\mathit{G}}}_{\mathbf{prop}}\left({\mathit{y}}^{\ast }\right)$
$R_{G_y^{\ast }{G}_x^{\ast }}$	$C_{G_y^{\ast }{G}_w^{\ast }}$	${\widehat{G}}_{8,\mathrm{prop}}\left(y^{\ast }\right)$
$S_{y^{\ast }}$	1	${\widehat{G}}_{7,\mathrm{prop}}\left(y^{\ast }\right)$
1	$G_{x^{\ast }}$	${\widehat{G}}_{6,\mathrm{prop}}\left(y^{\ast }\right)$
$R_{G_{x^{\ast }}{G}_{w^{\ast }}}$	$C_{G_{x^{\ast }}{G}_{w^{\ast }}}$	${\widehat{G}}_{5,\mathrm{prop}}\left(y^{\ast }\right)$
$G_{w^{\ast }}$	$C_{G_{v^{\ast }}{G}_{w^{\ast }}}$	${\widehat{G}}_{4,\mathrm{prop}}\left(y^{\ast }\right)$
$C_{G_{y^{\ast }}{G}_{x^{\ast }}}$	$R_{G_{x^{\ast }}{G}_{w^{\ast }}}$	${\widehat{G}}_{3,\mathrm{prop}}\left(y^{\ast }\right)$
$R_{G_{y^{\ast }}{G}_{x^{\ast }}}$	$G_{x^{\ast }}$	${\widehat{G}}_{2,\mathrm{prop}}\left(y^{\ast }\right)$
1	0	${\widehat{G}}_{1,\mathrm{prop}}\left(y^{\ast }\right)$

Table 8. Percentage relative efficiencies (PREs) of the proposed estimators compared with the usual distribution estimator ${\widehat{G}}_{y^{\ast }}$. Values greater than 100 indicate improvement over the baseline.

Estimator	Population I	Population II	Population III
${\widehat{G}}_{8,SM}\left(y^{\ast }\right)$	123.98	181.75	136.09
${\widehat{G}}_{7,SM}\left(y^{\ast }\right)$	187.27	306.62	263.52
${\widehat{G}}_{6,SM}\left(y^{\ast }\right)$	266.25	236.13	205.52
${\widehat{G}}_{5,SM}\left(y^{\ast }\right)$	139.17	233.82	222.20
${\widehat{G}}_{4,SM}\left(y^{\ast }\right)$	148.49	211.46	257.92
${\widehat{G}}_{3,SM}\left(y^{\ast }\right)$	123.86	199.55	147.36
${\widehat{G}}_{2,SM}\left(y^{\ast }\right)$	126.39	192.61	152.11
${\widehat{G}}_{1,SM}\left(y^{\ast }\right)$	188.47	255.60	328.16
${\widehat{G}}_{R\left(y^{\ast }\right)}$	66.33	93.03	37.82
${\widehat{G}}_{BTR\left(y^{\ast }\right)}$	82.30	104.25	56.04
${\widehat{G}}_{y^{\ast }}$	100.00	100.00	100.00
${\widehat{G}}_{Reg\left(y^{\ast }\right)}$	106.45	127.22	101.01
${\widehat{G}}_{RD\left(y^{\ast }\right)}$	113.24	133.96	102.19
${\widehat{G}}_{GK\left(y^{\ast }\right)}$	115.33	136.44	102.65

Figure 3. Graphical illustration of simulation outcomes: (a) mean squared error (MSE) comparison, highlighting the lower error rates achieved by the proposed family of estimators; (b) percentage relative efficiency (PRE) comparison, where values above 100 confirm substantial improvements over the traditional estimator; (c) MSE comparison based on scatter plot; and (d) PRE comparison based on scatter plot with regression curve. The consistency of these patterns across different populations underscores the robustness and superiority of the proposed estimators.

From Table 4, it is evident that the proposed estimators consistently achieve lower MSE values compared to conventional estimators such as ${\widehat{G}}_{y^{\ast }}$, ${\widehat{G}}_{Reg\left(y^{\ast }\right)}$, and ${\widehat{G}}_{RD\left(y^{\ast }\right)}$. For example, ${\widehat{G}}_{7,SM}\left(y^{\ast }\right)$ records the lowest MSEs across all three populations, reaching values of $0.0093$, $0.0057$, and $0.0015$ for Populations I, II, and III, respectively. Similarly, ${\widehat{G}}_{6,SM}\left(y^{\ast }\right)$ and ${\widehat{G}}_{1,SM}\left(y^{\ast }\right)$ perform remarkably well, with substantial reductions in error relative to their classical counterparts. These improvements underscore the adaptability of the proposed estimators in diverse population settings.

The efficiency comparison, summarized in Table 8, further confirms these findings. The proposed family outperforms baseline estimators, often by a wide margin. For instance, ${\widehat{G}}_{1,SM}\left(y^{\ast }\right)$ achieves PREs of $188.47$, $255.60$, and $328.16$ across the three populations, highlighting its robustness and superior efficiency relative to the standard ${\widehat{G}}_{y^{\ast }}$ benchmark, which is normalized to 100. Likewise, ${\widehat{G}}_{6,SM}\left(y^{\ast }\right)$ and ${\widehat{G}}_{7,SM}\left(y^{\ast }\right)$ consistently show high PRE values, demonstrating their efficiency gains across both small and large populations.

These numerical insights are supported by the graphical results in Figure 3. Panel (a) illustrates the MSE comparisons, where the proposed estimators demonstrate clear superiority over the existing methods, resulting in significant reductions in error levels. Panel (b) illustrates the PRE values, which further highlight the relative efficiency improvements. Notably, the proposed estimators not only outperform traditional regression and ratio-based estimators but also maintain robustness across repeated simulation runs, reinforcing their practical utility in survey sampling applications. Panel (c) and (d) indicates the pattern and trend with respect to mean square errors and percentage relative efficiency.

Taken together, the results indicate that the proposed family of estimators achieves substantial improvements in both precision and efficiency, offering a versatile and effective alternative to conventional approaches. Their consistently high performance across multiple populations and simulation settings suggests strong potential for application in real-world survey data, especially in contexts where auxiliary information is available and reliable.

4. Discussion

The performance evaluation of the proposed estimator requires not only theoretical justification but also empirical evidence that reflects its robustness in practical applications. To this end, we carried out an extensive simulation study, complemented by an empirical investigation across three distinct populations, to validate the theoretical properties established in the earlier sections. The discussion presented here emphasizes both the statistical implications and the applied relevance of the findings.

From the theoretical perspective, the derivations in Section 3 demonstrated that the proposed family of estimators consistently achieves a lower minimum mean squared error (MSE) compared to conventional alternatives such as $\widehat{G}\left(y^{\ast }\right)$, ${\widehat{G}}_R\left(y^{\ast }\right)$, ${\widehat{G}}_{BT,R}\left(y^{\ast }\right)$, ${\widehat{G}}_{Reg}\left(y^{\ast }\right)$, ${\widehat{G}}_{RD}\left(y^{\ast }\right)$, and ${\widehat{G}}_{GK}\left(y^{\ast }\right)$. This advantage was shown to hold under general conditions, thereby establishing a strong foundation for the efficiency gains observed in practice.

On the empirical side, the results provide compelling numerical evidence. As depicted in Figure 3, the proposed estimators ${\widehat{\mathcal{F}}}_{1,SM}$ through ${\widehat{\mathcal{F}}}_{8,SM}$ consistently yield substantially lower MSE values across all three populations, thereby confirming the robustness of the theoretical results. The magnitude of improvement is not marginal; rather, it is systematic and pronounced. In particular, the efficiency gains are clearly illustrated in Figure 3, where the percentage relative efficiency (PRE) values of the proposed estimators exceed those of the existing estimators, ranging from 136% to 328% across populations. Such high PRE values underscore the substantial improvements in precision and efficiency achieved by incorporating auxiliary information into the PPS sampling framework.

From an applied standpoint, these findings are particularly significant. The improved estimation of the population cumulative distribution function (CDF) has direct implications for fields where accurate distributional inference is critical, such as economics, social sciences, official statistics, and biomedical studies. For instance, survey practitioners working with unequal probability designs often face challenges in balancing design efficiency and estimator bias; the proposed family of estimators provides a viable solution that reduces estimation error while maintaining design consistency. Moreover, the graphical comparisons not only enhance the interpretability of the results but also underscore the stability of the proposed estimators across heterogeneous population structures, making them more attractive for practical implementation.

Beyond these theoretical and applied contributions, the study also underscores the role of computational advances in modern survey sampling and inference. The use of simulation-based validation enables the exploration of estimator performance across a wide range of population structures and sampling designs, providing insights that would be difficult to obtain through purely analytical derivations. Furthermore, the integration of auxiliary information into both the design and estimation stages exemplifies how computational statistics can bridge theory and application: leveraging additional covariates enhances estimator efficiency. At the same time, simulation frameworks ensure reproducibility and scalability in practice. This synergy between computational methods, auxiliary information, and theoretical efficiency directly aligns with the goals of contemporary computational statistics, as emphasized in this special issue.

Therefore, the discussion consolidates both theoretical and empirical perspectives: the proposed estimators achieve provable efficiency gains under PPS sampling, supported by extensive numerical validation. The joint evidence from analytical derivations, numerical tables, and graphical results confirms that the proposed family of estimators offers a substantial improvement over the existing approaches, thereby advancing the toolkit available for distribution function estimation in modern computational statistics and its applications.

Looking ahead, the methodological framework introduced here could be further extended to meet the challenges posed by contemporary data environments. In particular, integrating the proposed estimators with big data survey designs, Bayesian computational frameworks, or machine learning-based auxiliary information extraction presents exciting avenues for future research. Such extensions would not only enhance scalability and adaptability in high-dimensional or complex population settings but also strengthen the role of computational statistics in bridging traditional theory with modern data-driven applications. Likewise, can also be extended to other scenarios with different datasets [38,39,40,41,42].

5. Conclusions

This study emphasizes the fundamental importance of probability proportional to size (PPS) sampling for improving the estimation of distribution functions by strategically incorporating auxiliary information. By extending the theoretical framework to cumulative distribution functions (CDFs) for both study and auxiliary variables, we developed a novel, computationally efficient family of estimators specifically tailored to estimate the population CDF of the study variable. Theoretical analyses reveal that the proposed estimators achieve notable reductions in mean squared error (MSE). At the same time, empirical evidence across multiple populations shows percentage relative efficiency (PRE) gains ranging from 136% to 328% relative to the existing PPS-based estimators. Beyond methodological refinement, this work directly advances modern survey methodology by integrating dual auxiliary information into both design and estimation stages, thereby improving estimator precision without increasing sample size requirements. Although the current empirical evaluations were based on moderately sized datasets (e.g., fisheries, wine chemistry, and demographics), future research will extend this framework to large-scale survey environments to assess computational scalability and performance under high-dimensional data structures. Thus, the proposed PPS-based estimation framework bridges theoretical innovation with computational practicality, providing a robust and efficient tool for contemporary survey statisticians and data scientists.