Exactly Solvable Model of a System with a Non-Conserved Number of Particles

Abstract

An exactly solvable, one-component model originating from a unitary scenario of spontaneous particle production in curved spacetimes is proposed. The properties of such a system with a time-independent and a time-dependent Hamiltonian are discussed.

1. Introduction

It is a well-known fact that quantization of a scalar-free field in a curved spacetime may lead to particle production, e.g., the creation of particles inside a Schwarzschild black hole [1] and particle creation in an Expanding Universe(s) [2,3]. Such a system reveals spontaneous particle production whose rate has been the subject of numerous discussions in QFT in a range of curved spacetimes (see e.g., [1,2,4,5,6,7,8,9,10,11,12,13]). In order to describe its dynamics, one may invoke the Bogolyubov transformation between the time-dependent annihilation/creation operators and their initial counterparts. Most of these treatments have been based on different adiabatic approximations (see e.g., [2,4,5,7,8,9,10]). The quantized field function is expanded into a complete set of solutions of the appropriate Klein–Gordon equation; these solutions are expressed by WKB-like functions and an adiabatic approximation is finally formulated. The subtlety of the adiabatic approximation is its non-unitary character (see [6,10]).

A different kind of approach based on the principle of the unitarity of temporal evolution, referred to as a unitary scenario, was recently proposed [6]. The Hamiltonian of the scalar field (see e.g., [2,4,5,6]) is derived: it is expressed in terms of annihilation and creation operators and it comprises harmonic oscillator system terms and symmetry-dependent terms representing the creation and annihilation of pairs of particles. The dynamical properties of the system are studied by applying Heisenberg’s equations for the annihilation/creation operators, and their approximate solutions are then sought.

Yet another treatment, based on the diagonalization of the original Hamiltonian, i.e., its transformation into a form of non-interacting harmonic oscillatory systems should be mentioned as a possible way to lead to exact solvability (see [8]). However, this kind of transformation can be performed only within some particular ranges of the Hamiltonian’s parameters (see below); moreover, the transformation coefficients turn out to be time-dependent, thus precluding the hope of exact solvability.

These activities justify exploration of the exact solvability of the dynamics of a system with a non-conserved particle number. On the one hand, an exactly solvable model, though interesting in itself like every exact solution, should turn out to be both peculiar and specific. On the other hand it should also throw light on the properties of the overall process of spontaneous particle production (including curved space-times). It would also provide a clue to help tackle some technical problems associated with the solution of the Heisenberg equations of motion (see below). This is the motivation for our considerations.

The aim of this paper is to search for a model system, a simplified version of the general case of the scalar field quantized in curved space-time, allowing an exact solution of the Heisenberg equation for annihilation/creation operators. An exactly solvable model allowing spontaneous particle, or excitation production, even highly transformed from the original one, would be a useful tool in establishing the status of the ansatz given in the form of the Bogolyubov transformations. Its illustrative character, as will be shown below, provides significant added value. We will show that there exists a particular class of models whose dynamics is exactly solved. The exact solutions will be given and their properties will be discussed.

The paper is organized as follows. In Section 2 the problem is formulated: a simplified, time-dependent Hamiltonian is proposed. In Section 3 the properties of a time-independent Hamiltonian allowing an exact description of the dynamics of annihilation/creation operators are discussed. A time-dependent model is considered in Section 4 and the conditions for its solvability are derived. The discussion is presented in Section 5 and results of the paper are summarized in Section 6. In Appendix A we apply a squeezed operator for the “diagonalization” of the Hamiltonian with a non-conserved number of particles. In Appendix B an interesting property resulting from the commutation of a time-dependent Hamiltonian and a corresponding unitary evolution operator is discussed. In Appendix C we present a non-trivial relationship between seemingly different systems of equations for Bogolyubov coefficients.

2. Formulation of the Problem

The Hamiltonian of the scalar field quantized in a wide class of curved space-time may be written in the following form [6,7,8]:

$$\widehat{H}={\displaystyle \frac{1}{2}}\sum _{\mathbf{k}}\left[{\omega }_{\mathbf{k}}\left(t\right)\left\{{\widehat{A}}_{\mathbf{k}},{\widehat{A}}_{\mathbf{k}}^{+}\right\}+{\gamma }_{\mathbf{k}}\left(t\right){\widehat{A}}_{\mathbf{k}}{\widehat{A}}_{-\mathbf{k}}+{\gamma }_{\mathbf{k}}^{*}\left(t\right){\widehat{A}}_{\mathbf{k}}^{+}{\widehat{A}}_{-\mathbf{k}}^{+}\right]$$

(1)

where the time-dependent parameters ${\omega }_{\mathbf{k}}\left(t\right)$ and ${\gamma }_{\mathbf{k}}\left(t\right)$ are determined by the solutions of the appropriate Klein–Gordon (KG) (or Euler–Lagrange) equation (see e.g., [6]). In general, these parameters also contain quantities related to the geometry of spacetime through the KG equation. The specific form of the parameters depends on the classical gravitational field (spacetime) under considerations with which the quantum scalar field described by operators ${\widehat{A}}_{\mathbf{k}}$, ${\widehat{A}}_{\mathbf{k}}^{+}$ is coupled. However, we will not consider here the specific form of the classical gravitational field. Thus annihilation and creation operators ${\widehat{A}}_{\mathbf{k}},{\widehat{A}}_{\mathbf{k}}^{+}$ satisfy standard commutation relations

$$\left[{\widehat{A}}_{\mathbf{k}},{\widehat{A}}_{\mathbf{k}}^{+}\right]=1,$$

(2)

$$\left[{\widehat{A}}_{\mathbf{k}},{\widehat{A}}_{{\mathbf{k}}^{\prime }}\right]=\left[{\widehat{A}}_{\mathbf{k}}^{+},{\widehat{A}}_{{\mathbf{k}}^{\prime }}^{+}\right]=0.$$

(3)

The Heisenberg equation of motion for annihilation operators

$$i\hslash {\displaystyle \frac{d{\widehat{A}}_{\mathbf{k}}}{dt}}=\left[{\widehat{A}}_{\mathbf{k}},\widehat{H}\right]$$

(4)

may be discussed by using the following ansatz

$${\widehat{A}}_{\mathbf{k}}\left(t\right)={\alpha }_{\mathbf{k}}\left(t\right){\widehat{A}}_{\mathbf{k}}+{\beta }_{\mathbf{k}}\left(t\right){\widehat{A}}_{-\mathbf{k}}^{+}$$

(5)

that turns out to be a Bogolyubov transformation. The dynamics of the system may be formulated in terms of the differential equations for the coefficients ${\alpha }_{\mathbf{k}}\left(t\right)$, ${\beta }_{\mathbf{k}}\left(t\right)$ and the approximate solution provides $|{\beta }_{\mathbf{k}}\left(t\right){|}^2$, which represents the average number of “particles”, spontaneously produced in an initial vacuum state, $\left|0\right.〉$. The Hamiltonian (Equation (1)), (see [6]) might be diagonalized for ${\omega }_{\mathbf{k}}^2\left(t\right)-{\left|{\gamma }_{\mathbf{k}}\left(t\right)\right|}^2>0$.

The approach based on ansatz (Equation (5)) presents some concerns. The first of these refers to the dual role of substitution (Equation (5)). In the Heisenberg equation (Equation (4)), the explicit time derivative of ${\widehat{A}}_{\mathbf{k}}\left(t\right)$ is taken on the LHS and on the RHS ${\widehat{A}}_{\mathbf{k}}\left(t\right)$ is used in the commutation relations: ambiguity arises when one uncovers two apparently distinct forms of differential equations for ${\alpha }_{\mathbf{k}}\left(t\right)$ and ${\beta }_{\mathbf{k}}\left(t\right)$ (see below). These pose a question for the applicability and the status of the Bogolyubov transformation presented here.

One can therefore search for a Hamiltonian having on the one hand the form of the original Hamiltonian (Equation (1)) and on the other hand being sufficiently simplified so that it permits an exact solution. This would provide a model that is interesting due to its exact solvability. While the role of the diagonalization of the Hamiltonian is rather obvious—it defines a system of non-interacting (harmonic) oscillators—the meaning of the case when one cannot diagonalize the Hamiltonian is much less obvious, and in such a situation an exactly solvable model would provide an illustrative explanation. Moreover, an exact solution would allow us to resolve the above-mentioned concerns. We will therefore consider a single-mode system described by the following Hamiltonian

$$\stackrel{\sim }{H}\left(t\right)={\displaystyle \frac{1}{2}}\left[\omega \left(t\right)\left\{\widehat{A},{\widehat{A}}^{+}\right\}+\gamma \left(t\right){\left(\widehat{A}\right)}^2+{\gamma }^{*}\left(t\right){\left({\widehat{A}}^{+}\right)}^2\right].$$

(6)

Such a model preserves one of the key features of the original system (Equation (1)): Hamiltonian (Equation (6)) comprises terms with coefficients $\gamma$ and ${\gamma }^{*}$ representing the annihilation and creation of pairs of particles. On the other hand $k,-k$ symmetry, which reflects momentum conservation in the model (Equation (1)), is no longer present in model (Equation (6)). This implies that a significant property of system (Equation (1)), namely the creation/annihilation of particles in $k,-k$ branches, cannot be observed in system (Equation (6)). The physical meaning of this is that particles are still created or annihilated in pairs (Equation (6)) but not in $k,-k$ pairs (Equation (1)). Further implications of this lost symmetry are noted below (see Section 5). The dynamic properties of system (Equation (6)) are studied by using the Heisenberg equation of motion (we will use a system of units such that $\hslash =1$, although at the end of Section 5, ℏ will be restored)

$$i{\displaystyle \frac{d\widehat{A}}{dt}}={\widehat{U}}^{+}\left(t\right)\left[\widehat{A},\stackrel{\sim }{H}\right]\widehat{U}\left(t\right)=\omega \left(t\right)\widehat{A}\left(t\right)+{\gamma }^{*}\left(t\right){\widehat{A}}^{+}\left(t\right).$$

(7)

where $\widehat{A}\left(t\right)$ in the Heisenberg picture

$$\widehat{A}\left(t\right)={\widehat{U}}^{+}\left(t\right)\widehat{A}\widehat{U}\left(t\right),$$

(8)

is expressed via a unitary evolution operator $\widehat{U}\left(t\right)$

$$i{\displaystyle \frac{d\widehat{U}\left(t\right)}{dt}}=\stackrel{\sim }{H}\left(t\right)\widehat{U}\left(t\right).$$

(9)

In order to solve (Equation (7)) one can apply an ansatz (Equation (5)), that, in this case, takes the following form:

$$\widehat{A}\left(t\right)=\alpha \left(t\right)\widehat{A}+\beta \left(t\right){\widehat{A}}^{+}.$$

(10)

The ansatz (Equation (5)) is accurate for Hamilton operators that are combinations of bilinear operators $\widehat{A}$, as shown by Equation (A2). An example of such a Hamilton operator is Equation (6).

Imposing canonical commutation relations for operators $\widehat{A}\left(t\right),$ and ${\widehat{A}}^{+}\left(t\right)$, one obtains

$${\left|\alpha \right|}^2-{\left|\beta \right|}^2=1,$$

(11)

i.e., the relation (Equation (10)) is a Bogolyubov transformation. Inserting $\widehat{A}\left(t\right)$ in the form Equation (10) into Equation (7) one finds

$$i{\displaystyle \frac{d\alpha }{dt}}\widehat{A}+i{\displaystyle \frac{d\beta }{dt}}{\widehat{A}}^{+}=\left[\omega \left(t\right)\alpha \left(t\right)+{\gamma }^{*}\left(t\right){\beta }^{*}\left(t\right)\right]\widehat{A}+\left[\omega \left(t\right)\beta \left(t\right)+{\gamma }^{*}\left(t\right){\alpha }^{*}\left(t\right)\right]{\widehat{A}}^{+}.$$

(12)

This means that the Bogolyubov coefficients satisfy the following differential equations

$$i{\displaystyle \frac{d\alpha }{dt}}=\omega \left(t\right)\alpha \left(t\right)+{\gamma }^{*}\left(t\right){\beta }^{*}\left(t\right),$$

(13)

$$i{\displaystyle \frac{d\beta }{dt}}=\omega \left(t\right)\beta \left(t\right)+{\gamma }^{*}\left(t\right){\alpha }^{*}\left(t\right).$$

(14)

One may notice that if the Hamiltonian $\stackrel{\sim }{H}\left(t\right)$ commutes with $\widehat{U}\left(t\right),$

$$\left[\stackrel{\sim }{H}\left(t\right),\widehat{U}\left(t\right)\right]=0,$$

(15)

which occurs if $\stackrel{\sim }{H}\left(t\right)$ commutes at different instants in time,

$$\left[\stackrel{\sim }{H}\left(t_1\right),\stackrel{\sim }{H}\left(t_2\right)\right]=0,$$

(16)

then Equation (7) can be rewritten as

$$\begin{array}{c}i{\displaystyle \frac{d\widehat{A}}{dt}}={\widehat{U}}^{+}\left[\widehat{A},\stackrel{\sim }{H}\left(t\right)\right]\widehat{U}=\left[\widehat{A}\left(t\right),\stackrel{\sim }{H}\left(t\right)\right]=\\ =\left[\omega \left(t\right)\alpha \left(t\right)-\gamma \left(t\right)\beta \left(t\right)\right]\widehat{A}-\left[\omega \left(t\right)\beta \left(t\right)-{\gamma }^{*}\left(t\right)\alpha \left(t\right)\right]{\widehat{A}}^{+}.\end{array}$$

(17)

Inserting Equation (10) into the LHS of the Equation (17) one obtains the differential equations

$$i{\displaystyle \frac{d\alpha }{dt}}=\omega \left(t\right)\alpha \left(t\right)-\gamma \left(t\right)\beta \left(t\right),$$

(18)

$$i{\displaystyle \frac{d\beta }{dt}}=-\omega \left(t\right)\beta \left(t\right)+{\gamma }^{*}\left(t\right)\alpha \left(t\right),$$

(19)

which are alternatives to those given above Equations (13) and (14). In Appendix C, the equivalence of systems of Equations (12), (13), (18) and (19) at the solution level is formally proven.

Our task is to establish the relation(s) between the model parameters $\omega \left(t\right)$ and $\gamma \left(t\right)$ of system (Equation (6)) which permits the exact description of the annihilation/creation operator dynamics. An exact solution would provide ${\left|\beta \right|}^2$, i.e., give an insight into the rate of particle production in system (Equation (1)). On the other hand it would also help us to resolve any ambiguity in the equation of motion which arises from the two forms (Equations (12)–(14)) vs. (Equations (18) and (19)).

We will start from the time-independent case which will provide a useful background for the discussion of the exactly solvable, time-dependent model (Equation (6)).

3. Exact Solution for a Time-Independent System

Let us consider the time-independent version of the Hamiltonian (Equation (6)), $\omega \left(t\right)=\omega ,$ $\gamma \left(t\right)=\gamma ,$

$$H={\displaystyle \frac{1}{2}}\left[\omega \left\{\widehat{A},{\widehat{A}}^{+}\right\}+\gamma {\left(\widehat{A}\right)}^2+{\gamma }^{*}{\left({\widehat{A}}^{+}\right)}^2\right].$$

(20)

The time evolution is then described by the unitary operator

$$U\left(t\right)=e^{-iHt}.$$

In this case (Equations (12)–(14), (18) and (19)) lead to a simple, second order differential equation

$${\displaystyle \frac{d^2\phi }{d{t}^2}}+{\Omega }^2\phi \left(t\right)=0,$$

(21)

where

$${\Omega }^2={\omega }^2-{\left|\gamma \right|}^2,$$

(22)

and $\phi \left(t\right)=\left\{\alpha \left(t\right),\beta \left(t\right)\right\}.$ Indeed, applying the operator $i{\displaystyle \frac{d}{dt}}$ to (Equations (13) and (14)) one gets

$$-{\displaystyle \frac{d^2\alpha }{d{t}^2}}=\omega i{\displaystyle \frac{d}{dt}}\alpha \left(t\right)+{\gamma }^{*}i{\displaystyle \frac{d}{dt}}{\beta }^{*}\left(t\right)={\Omega }^2\alpha \left(t\right),$$

(23)

$$-{\displaystyle \frac{d^2\beta }{d{t}^2}}=\omega i{\displaystyle \frac{d}{dt}}\beta \left(t\right)+{\gamma }^{*}i{\displaystyle \frac{d}{dt}}{\alpha }^{*}\left(t\right)={\Omega }^2\beta \left(t\right).$$

(24)

The initial conditions are imposed to be as follows

$$\alpha \left(t=0\right)=1,\beta \left(t=0\right)=0.$$

(25)

One can consider two cases parametrized by the sign of ${\Omega }^2$.

3.1. ${\Omega }^2>0$

In this case, the coefficients $\alpha \left(t\right),\beta \left(t\right)$ satisfying Equation (21) with initial conditions (Equation (25)) have the form

$$\alpha \left(t\right)=cos\Omega t-i{\displaystyle \frac{\omega }{\Omega }}sin\Omega t,$$

(26)

$$\beta \left(t\right)=-i{\displaystyle \frac{{\gamma }^{*}}{\Omega }}sin\Omega t,$$

(27)

and the “particle production” term

$${\left|\beta \left(t\right)\right|}^2={\displaystyle \frac{{\left|\gamma \right|}^2}{{\Omega }^2}}{sin}^2\Omega t$$

(28)

fluctuates between 0 and ${\displaystyle \frac{{\left|\gamma \right|}^2}{{\Omega }^2}}$ with a frequency $\Omega$ (see Figure 1).

3.2. ${\Omega }^2<0$

Making the substitution

$$\Omega \to i\Delta =i\sqrt{{\left|\gamma \right|}^2-{\omega }^2}$$

(29)

one finds that $\alpha \left(t\right),$ and $\beta \left(t\right)$ are of the form

$$\alpha \left(t\right)=cosh\Delta t-i{\displaystyle \frac{\omega }{\Delta }}sinh\Delta t,$$

(30)

$$\beta \left(t\right)=-i{\displaystyle \frac{{\gamma }^{*}}{\Delta }}sinh\Delta t,$$

(31)

and the “particle production”

$${\left|\beta \left(t\right)\right|}^2={\displaystyle \frac{{\left|\gamma \right|}^2}{{\Delta }^2}}{sinh}^2\Delta t.$$

(32)

turns out to grow exponentially for times greater than the characteristic time $t_1\sim {\Delta }^{-1}$ (see Figure 2).

The outcome characteristic of derivations (Equations (26), (27), (30) and (31)) should be underlined. Coefficients $\alpha \left(t\right)$ and $\beta \left(t\right)$ are complex and imaginary, respectively, functions of time satisfying normalization condition (Equation (11)) and initial conditions (Equation (25)). Similar behaviour, with the former function being complex and the latter one imaginary is observed in the case of the dynamics of the scalar-free field quantized in de Sitter spacetime (to be discussed elsewhere)—the question of whether this is a more general property than this specific case remains open.

4. Exact Solution for a Time-Dependent System

Let us consider now the time-dependent case (Equation (6)). In order to solve the Heisenberg equation of motion (Equation (7)), i.e., to find $\alpha \left(t\right)$ and $\beta \left(t\right)$, we will start from the case.

4.1. ${\omega }^2\left(t\right)-{\left|\gamma \right|}^2\left(t\right)>0$

Following this, the Hamiltonian may be diagonalized, i.e., transformed into the harmonic oscillator form

$$\stackrel{\sim }{H}\left(t\right)={\displaystyle \frac{1}{2}}\Omega \left(t\right)\left\{\widehat{B},{\widehat{B}}^{+}\right\},$$

(33)

where

$$\Omega \left(t\right)=\sqrt{{\omega }^2\left(t\right)-{\left|\gamma \right|}^2\left(t\right)}.$$

(34)

Operators $\widehat{B},{\widehat{B}}^{+}$ satisfy the canonical commutation relations (Equations (2)–(4)) and are expressed via operators $\widehat{A},{\widehat{A}}^{+}$ as follows

$$\widehat{A}=\lambda \widehat{B}+\sigma {\widehat{B}}^{+},$$

(35)

$${\left|\lambda \right|}^2-{\left|\sigma \right|}^2=1.$$

(36)

Coefficients $\lambda$ and $\sigma$ are found to be given as

$${\displaystyle \frac{\sigma }{{\lambda }^{*}}}={\displaystyle \frac{1}{{\gamma }^{*}}}\left(-\omega +\sqrt{{\omega }^2-{\left|\gamma \right|}^2}\right).$$

(37)

The dynamics of the annihilation operators $\widehat{B}$ is well-known

$$\widehat{B}\left(t\right)=b_0{e}^{-iG\left(t\right)}\widehat{B},$$

(38)

where $b_0$ is fixed by the initial conditions and $G\left(t\right)$ is

$$G\left(t\right)={\int }^t\Omega \left(t^{\prime }\right)d{t}^{\prime }.$$

(39)

Hence, if $\lambda$ and $\sigma$ are time-independent, the dynamics of $\widehat{A}\left(t\right)$ (see Equation (10)) are given as follows. The Bogolyubov coefficients $\alpha \left(t\right)$ and $\beta \left(t\right)$ take the following form:

$$\alpha \left(t\right)=cos\left[G\left(t\right)\right]+iEsin\left[G\left(t\right)\right],$$

(40)

$$\beta \left(t\right)=iHsin\left[G\left(t\right)\right],$$

(41)

where the constants E and H (see Section 5) are

$$E=-{\displaystyle \frac{\omega \left(t\right)}{\Omega \left(t\right)}},$$

(42)

$$H=-{\displaystyle \frac{{\gamma }^{*}\left(t\right)}{\Omega \left(t\right)}},$$

(43)

i.e.,

$${\displaystyle \frac{\omega \left(t\right)}{\gamma \left(t\right)}}=C=const.$$

Therefore, the “particle production” rate fluctuates in this case

$${\left|\beta \left(t\right)\right|}^2={\displaystyle \frac{{\left|\gamma \right|}^2}{{\omega }^2-{\left|\gamma \right|}^2}}{sin}^2\left[G\left(t\right)\right]={\displaystyle \frac{1}{{\left|C\right|}^2-1}}{sin}^2\left[G\left(t\right)\right]$$

(44)

in a manner similar to the time-independent case (see Equation (28)).

4.2. ${\omega }^2\left(t\right)-{\left|\gamma \right|}^2\left(t\right)<0$

In this case the Hamiltonian (Equation (6)) cannot be diagonalized (see Appendix A). The coefficients $\alpha \left(t\right)$ and $\beta \left(t\right)$ are found by assuming their form to be

$$\alpha \left(t\right)=cosh\left[g\left(t\right)\right]+iesinh\left[g\left(t\right)\right],$$

(45)

$$\beta \left(t\right)=2ihsinh\left[g\left(t\right)\right],$$

(46)

where $g\left(t\right)$ is defined as

$$g\left(t\right)={\int }^t\Delta \left(t^{\prime }\right)d{t}^{\prime },$$

(47)

and

$$\Delta \left(t\right)=\sqrt{{\left|\gamma \right|}^2\left(t\right)-{\omega }^2\left(t\right)}.$$

(48)

Inserting the solutions (Equations (45) and (46)) into the RHS of Equations (12)–(14) one finds the coefficients e and h

$$e=-{\displaystyle \frac{\omega \left(t\right)}{\Delta \left(t\right)}},$$

(49)

$$h=-{\displaystyle \frac{{\gamma }^{*}\left(t\right)}{\Delta \left(t\right)}}.$$

(50)

Then one verifies that $\alpha \left(t\right)$ and $\beta \left(t\right)$ given in the form (Equations (45) and (46)) are the solutions of Equations (12)–(14) if the coefficients $e,h$ are constant (see Section 5). This means that if the ratio

$${\displaystyle \frac{\omega \left(t\right)}{\gamma \left(t\right)}}={\psi }_0$$

(51)

is constant then the system is exactly solvable (where ${\psi }_0$ is a complex number). In such a case “particle production”

$${\left|\beta \left(t\right)\right|}^2={\displaystyle \frac{{\left|\gamma \right|}^2}{{\left|\gamma \right|}^2-{\omega }^2}}{sinh}^2\left[g\left(t\right)\right]={\displaystyle \frac{1}{1-{\left|{\psi }_0\right|}^2}}{sinh}^2\left[g\left(t\right)\right],$$

(52)

turns out to grow exponentially with time, $g\left(t\right)>>1$ (c.f. Equation (32)).

Some implications of the considerations in this section are as follows. In the case of the scalar-free field quantized in different bacgrounds the sign of the expression ${\omega }_k^2\left(t\right)-{\left|{\gamma }_k\left(t\right)\right|}^2$ is positive, both for the interior of Schwarzschild Black Hole [6] and for de Sitter spacetime while it may be negative, in particular regions of k-space, as in the case of Conformal Flat Spacetime (CFS). Hence, in the case of CFS, one can refer to a ‘gravitationally driven instability’. Here, for ${\omega }^2\left(t\right)-{\left|\gamma \left(t\right)\right|}^2<0$, one can refer to the instability itself, as suggested by a reviewer of the manuscript of this paper and to whom the authors are thankful. Such an instability is manifested by an exponentially growing number of spontaneously produced particles.

5. Discussion

Considering the time-dependent Hamiltonian (Equation (6)), originating from the scalar field quantized in curved space-time, one may search for a version of this whose dynamics allows exact solvability. The first consideration is of a time-independent Hamiltonian (Equation (20)) that in the range ${\omega }^2-{\left|\gamma \right|}^2>0$ permits diagonalization, i.e., transformation into a harmonic oscillator form, leading to the exact dynamics of the annihilation/creation operators. In such a case, the Bogolyubov coefficients $\alpha \left(t\right)$ and $\beta \left(t\right)$ can be found. The physical meaning of this result is as follows. If the initial state is a vacuum one $\left|0\right.〉$

$$\widehat{A}\left|0\right.〉=0,$$

(53)

its time evolution is given as

$$\left|0\left(t\right)\right.〉=\widehat{U}\left(t\right)\left|0\right.〉.$$

(54)

One finds that during the evolution, the “particles” are spontaneously created. Indeed, the average value of the particle number operator ${\widehat{A}}^{+}\widehat{A}$ at the instant t is formally given as

$$\left.〈0\left(t\right)\right|{\widehat{A}}^{+}\widehat{A}\left|0\left(t\right)\right.〉=\left.〈0\right|{\widehat{A}}^{+}\left(t\right)\widehat{A}\left(t\right)\left|0\right.〉,$$

(55)

and inserting $\widehat{A}\left(t\right)$ expressed via $\widehat{A}$ and ${\widehat{A}}^{+}$ (see Equation (10)) one finds

$$\left.〈0\right|{\widehat{A}}^{+}\left(t\right)\widehat{A}\left(t\right)\left|0\right.〉=\left.〈0\right|{\left[\alpha \left(t\right)\widehat{A}+\beta \left(t\right){\widehat{A}}^{+}\right]}^{+}\left[\alpha \left(t\right)\widehat{A}+\beta \left(t\right){\widehat{A}}^{+}\right]\left|0\right.〉={\left|\beta \left(t\right)\right|}^2$$

(56)

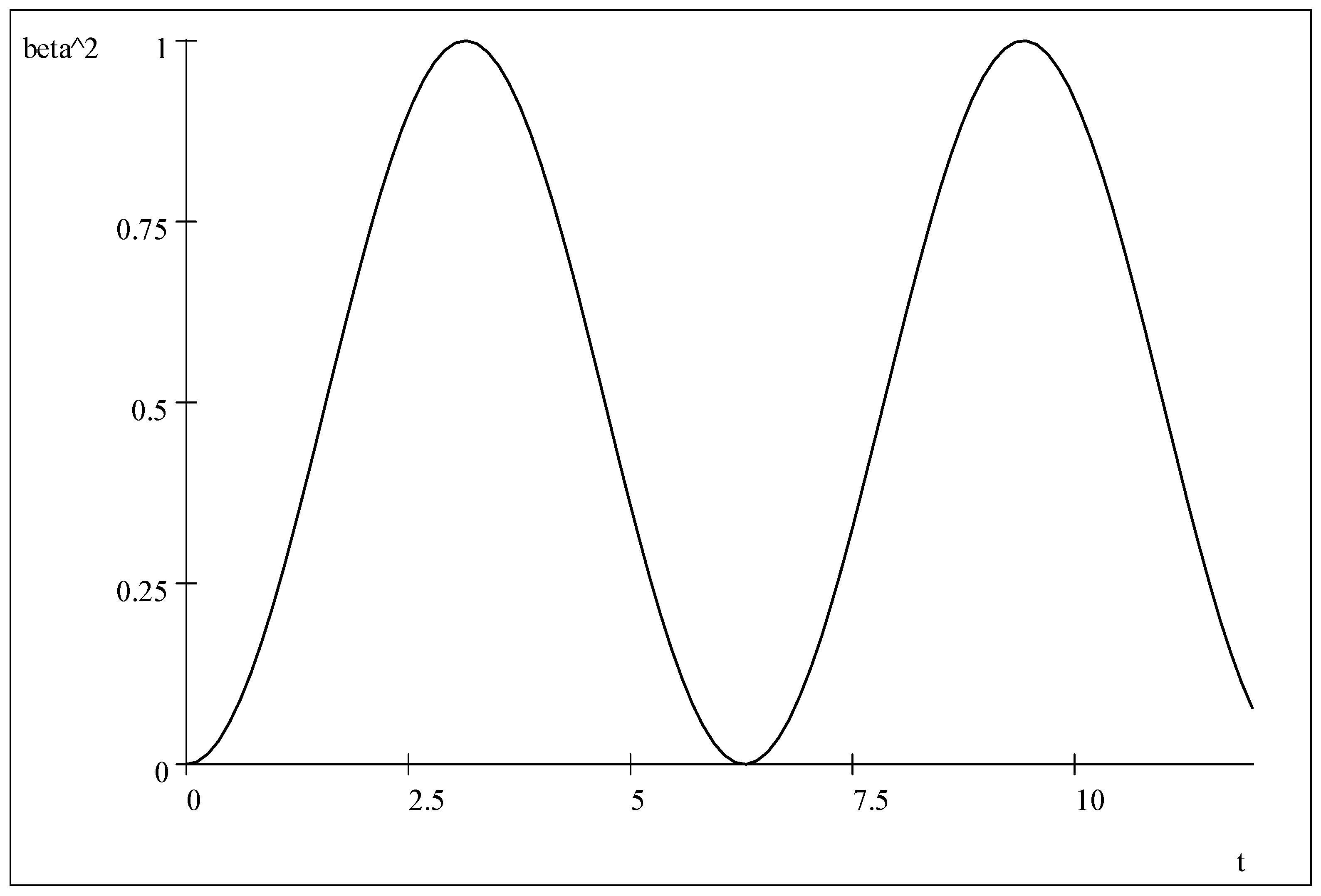
which ${\left|\beta \left(t\right)\right|}^2$ represents the temporal evolution of the average number of “particles” (or “excitations”), spontaneously produced in an initial vacuum state, $\left|0\right.〉.$ Let us underline here that for ${\left|{\beta }_k\left(t\right)\right|}^2$ represented in (Equation (1)), their average number of particles created in the branch k and also created in the branch $-k$ were created in such pairs. In an exactly solvable single-mode model (Equation (6)), ${\left|\beta \left(t\right)\right|}^2$ is simply the average number of particles created in a vacuum. The coefficient ${\left|\beta \left(t\right)\right|}^2$ turns out to fluctuate in a simple manner with a characteristic frequency $\Omega =\sqrt{{\omega }^2-{\left|\gamma \right|}^2}.$ Two interesting features are revealed in the range ${\omega }^2-{\left|\gamma \right|}^2<0$. Firstly, the Hamiltonian (Equation (20)) can not be diagonalized. Secondly, even in such a case, one can find an exact description of the dynamics of the system (Equation (20)). One can conclude then that the temporal evolution of the initial vacuum state reveals in that case an exponentially growing number of spontaneously produced “particles” (“excitations”), where the characteristic time turns out to be ${\Delta }^{-1}={\left(\sqrt{{\left|\gamma \right|}^2-{\omega }^2}\right)}^{-1}.$

Experience with the exactly solved dynamics of the time-independent system enables us to formulate the time-dependent Hamiltonian (Equation (33)) allowing the operator’s dynamics to be exactly solved. Namely, the exact solution is found in a special class of systems, where the ratio

$${\displaystyle \frac{\omega \left(t\right)}{\gamma \left(t\right)}}={\psi }_0$$

(57)

is constant. This property turns out to have a deeper sense. It has been shown in an extended discussion (Appendix B and Appendix C) that the constant value of the ratio ${\displaystyle \frac{\omega \left(t\right)}{\gamma \left(t\right)}}$ results from the commutation of the Hamiltonian $\stackrel{\sim }{H}\left(t\right)$ at the different time instants. But, according to a remark from an anonymous reviewer, formally verified in Appendix B, a fundamental point is an $SU\left(1,1\right)$ algebra lies behind Equations (16) and (57). Namely, $\stackrel{\sim }{H}\left(t\right)$ is composed of the generators $SU\left(1,1\right)$ hence the relation Equation (16) implies Equation (57) and in consequence the equivalence of Equations (15) and (16). In such a case, i.e., Equation (57) the time-dependence of the Hamiltonian takes a particular form

$$\stackrel{\sim }{H}\left(t\right)=\omega \left(t\right){\displaystyle \frac{1}{2}}\left[\left\{\widehat{A},{\widehat{A}}^{+}\right\}+{\psi }_0^{-1}{\left(\widehat{A}\right)}^2+{\left({\psi }_0^{*}\right)}^{-1}{\left({\widehat{A}}^{+}\right)}^2\right]$$

(58)

and one can consider two ranges of parameters, $1-{\left|{\psi }_0^{-1}\right|}^2>0$ and $1-{\left|{\psi }_0^{-1}\right|}^2<0,$ allowing and not allowing, respectively, its diagonalization. In the former case one can diagonalize the Hamiltonian and the average number of the excitations ${\left|\beta \left(t\right)\right|}^2$ in the initial vacuum state; $\left|0\right.〉$ fluctuates with a frequency, $G\left(t\right)=\sqrt{1-{\left|{\psi }_0^{-1}\right|}^2}{\int }^t\omega \left(t^{\prime }\right)d{t}^{\prime }.$ In the latter case, one cannot diagonalize the Hamiltonian and the number of excitations during the temporal evolution of the initial vacuum state, which grows exponentially fast. Exponential growth of the number of excitations indicates an instability of the system.

Some questions related to the general problem of spontaneous particle production (Equation (1)) arise in the context of the above discussion. How is the property of the temporal fluctuation of the number of “particles” produced during the evolution from the initial vacuum state observed in the exactly solvable model (Equation (58)) for ${\omega }^2\left(t\right)-{\left|\gamma \right|}^2\left(t\right)>0$ manifested (if at all) in the general case Equation (1) (and/or Equation (6))? What is the meaning of the lack of the diagonalizability of model (Equation (58)) in the case ${\omega }^2\left(t\right)-{\left|\gamma \right|}^2\left(t\right)<0$ and the exponential growth of the “particles” produced then, and what is its relation to the general properties of the scalar field quantized in curved spacetime?

Without answering those questions specifically here let us instead make a general remark about the properties of the time-independent model (Equation (20)).

This model can be expressed in a coordinate representation by using the following well-known transformation (we will later restore the usual meaning of Planck’s constant ℏ),

$$\widehat{A}={\left({\displaystyle \frac{m{\omega }_0}{2\hslash }}\right)}^{1/2}\left(\widehat{x}+{\displaystyle \frac{i}{m{\omega }_0}}\widehat{p}\right),$$

(59)

where $m,$ and ${\omega }_0$ are parameters to be specified later. Hamiltonian (Equation (20)) takes the form

$$\widehat{H}={\displaystyle \frac{1}{2}}\left[{\lambda }_1{\widehat{p}}^2+{\lambda }_2{\widehat{x}}^2+{\lambda }_3\left\{\widehat{x},\widehat{p}\right\}\right],$$

(60)

where ${\lambda }_1={\displaystyle \frac{1}{m}}\left({\displaystyle \frac{\hslash \omega -{\gamma }_1}{\hslash {\omega }_0}}\right),{\lambda }_2=\left({\displaystyle \frac{\hslash \omega +{\gamma }_1}{\hslash {\omega }_0}}\right)m{\omega }_0^2,$ ${\lambda }_3={\displaystyle \frac{{\gamma }_2}{2\hslash }}$ and $\gamma ={\gamma }_1+i{\gamma }_2$. Making the following substitution:

$$\widehat{P}=\widehat{p}+{\displaystyle \frac{{\lambda }_3}{{\lambda }_1}}\widehat{x}$$

(61)

one transforms Hamiltonian (Equation (60)) into the harmonic oscillator-like form

$$\widehat{H}={\displaystyle \frac{1}{2}}\left[{\lambda }_1{\widehat{P}}^2+{\lambda }_4{\widehat{x}}^2\right],$$

(62)

where

$${\lambda }_4=m{\omega }_0^2\left[{\displaystyle \frac{{\left(\hslash \omega \right)}^2-{\left|\gamma \right|}^2}{{\left(\hslash {\omega }_0\right)}^2}}{\displaystyle \frac{1}{\frac{\hslash \omega -{\gamma }_1}{\hslash {\omega }_0}}}\right].$$

(63)

One can choose parameter ${\omega }_0$ as follows

$${\left(\hslash {\omega }_0\right)}^2=\left|{\left(\hslash \omega \right)}^2-{\left|\gamma \right|}^2\right|.$$

(64)

This derivation provides us with a Hamiltonian of dual character expressed in coordinate representation—see Equations (60) and (62),

$$\widehat{H}={\displaystyle \frac{1}{2M}}{\widehat{P}}^2\pm {\displaystyle \frac{1}{2}}M{\omega }_0^2{\widehat{x}}^2$$

(65)

where $M={\displaystyle \frac{m}{\frac{\hslash \omega -{\gamma }_1}{\hslash {\omega }_0}}},$ and the sign “$\pm$” corresponds to the sign of the difference $\left|{\left(\hslash \omega \right)}^2-{\left|\gamma \right|}^2\right|=\pm \left[{\left(\hslash \omega \right)}^2-{\left|\gamma \right|}^2\right].$ The duality of the Hamiltonian (Equation (65)) is represented as

(a) $“+”$—a particle of mass M placed within a parabolic well, i.e., the standard harmonic oscillator;

(b) $“-”$—a particle of mass M placed in an inverted potential, i.e., an unstable case.

In the former case one can transform the Hamiltonian (Equation (65)) into the diagonal form

$$H={\displaystyle \frac{1}{2}}\hslash {\omega }_0\left\{\widehat{B},{\widehat{B}}^{+}\right\}.$$

(66)

In the latter case, the Hamiltonian, when transformed into the annihilation/creation representation, takes the off-diagonal form

$$H=-{\displaystyle \frac{1}{2}}\hslash {\omega }_0\left[{\left(\widehat{B}\right)}^2+{\left({\widehat{B}}^{+}\right)}^2\right].$$

(67)

Therefore, the status of the discussion in Section 3 and Section 4 is as follows.

In the range ${\Omega }^2={\left(\hslash \omega \right)}^2-{\left|\gamma \right|}^2>0,$ with parameter ${\left|\beta \left(t\right)\right|}^2$, the average number of “particles” produced in the initial vacuum state fluctuates with a frequency $\Omega$ (Equation (28)). In this case the Hamiltonian (Equation (20)) may be diagonalized (Equation (66)) and in the coordinate representation it is represented by a particle within a parabolic well—a harmonic oscillator (HO)—and the system becomes stable.

In the range ${\Omega }^2={\left(\hslash \omega \right)}^2-{\left|\gamma \right|}^2<0,$ the parameter ${\left|\beta \left(t\right)\right|}^2$ grows exponentially which indicates the instability of the system. In such a case the Hamiltonian (Equation (20)) cannot be diagonalized, and it takes the off-diagonal form (Equation (67)). For the coordinate representation Hamiltonian, (Equation (65)) describes a particle moving in a reversed parabolic well—a so-called reversed harmonic oscillator (RHO)—and the system is unstable.

The detailed derivation of this and a discussion of the last paragraph and Equations (59)–(67) will be given elsewhere. Let us make two comments here though: (a) the problem of the RHO has recently been the subject of intensive studies (see e.g., [14,15]), (b) the possible utilisation of the interplay between the annihilation/creation operator representation (Equation (6)) and the coordinate representation Equation (60), and/or their variations in the range of questions associated with a quantum formulation of the damped harmonic oscillator, e.g., [16,17,18], still seems to be an open and interesting topic.

6. Final Remarks

In this paper we have proposed a single-mode, exactly solvable model characterized by the Hamiltonian (Equation (6)). It arose from a drastic simplification of the Hamiltonian of the scalar field quantized in a curved spacetime. Applying a Bogolyubov ansatz, we have derived and solved differential equations for the coefficients $\alpha \left(t\right)$ and $\beta \left(t\right).$ This provided us with a rigorous description of the dynamics of a time-independent system and a specific class of time-dependent systems (Equation (6))—the justification of the self-consistency of the approach based on ansatz (Equation (10)) is one of the main outcomes of our considerations. There are two regimes for the model parameters in case Equation (6) (but also in case Equation (1)): when one can and when one cannot diagonalize the Hamiltonian (Equation (6)). We have shown that the former regime corresponds to a stable situation, where the number of “particles” produced fluctuates and the system may be represented by a harmonic oscillator. In the latter regime, the system is unstable; it may be represented by a so-called reversed harmonic oscillator and the number of “particles” exponentially grows. An interesting link between those stability properties and a hidden symmetry of system (Equation (6)) was discovered. Namely, Hamiltonian (Equation (6)) is composed of the generators of the $SU\left(1,1\right)$ group (see Appendix B and also [19]). It commutes at different time instants (Equation (16)) if the ratio ${\displaystyle \frac{\omega \left(t\right)}{\gamma \left(t\right)}}$ is constant and this implies the equivalence or compatibility of the relations Equations (12)–(14), (18) and (19). There are three regions parameterized by the complex parameter which correspond to the two regimes of the stability $\left({\Omega }^2>0\right)$, instability $\left({\Omega }^2<0\right)$ of Hamiltonian (Equation (6)), and a third “in-between” option $\left({\Omega }^2=0\right).$ These regimes correspond to three regions in the complex plane in which the SU(1,1) group acts (see Section 5, [19]): the unit circle, Equation (A34), its interior, (see Equation (A30)), and its exterior (see Equation (A31)). Hence, the complex plane is foliated into three orbits of SU(1,1). This means that SU$\left(1,1\right)$ acts transitively inside the circle, outside the circle, and on the circle itself. This shows that the structure of the SU(1,1) group is deeply rooted in the model under consideration.

Which of the properties described above of the exactly solvable system (Equation (6)) would be reflected in the systems characterized by Hamiltonian (Equation (1))? There is one obvious property in common for systems (Equations (1) and (6)). If an analogy of the condition ${\Omega }^2<0$ occurs, i.e., ${\Omega }_k^2={\left(\hslash {\omega }_k\right)}^2-{\left|{\gamma }_k\right|}^2<0$ then in system (Equation (1)), there is an instability that should be referred to as being “gravitationally driven” (which we will discuss in future works). More or less regular oscillations as opposed to the exponential growth of parameter ${\left|{\beta }_k\left(t\right)\right|}^2$ would be expected in an appropriate domain, ${\Omega }_k^2>0$, for system (Equation (1)). The difference in the interpretation of the parameters ${\left|\beta \left(t\right)\right|}^2$ and ${\left|{\beta }_k\left(t\right)\right|}^2$ appears to be obvious: the former represents the number of “particles” (“excitations”), and the latter one represents the number of the particles spontaneously produced during the evolution of a vacuum state in the branches k and $-k,$ in curved spacetime.