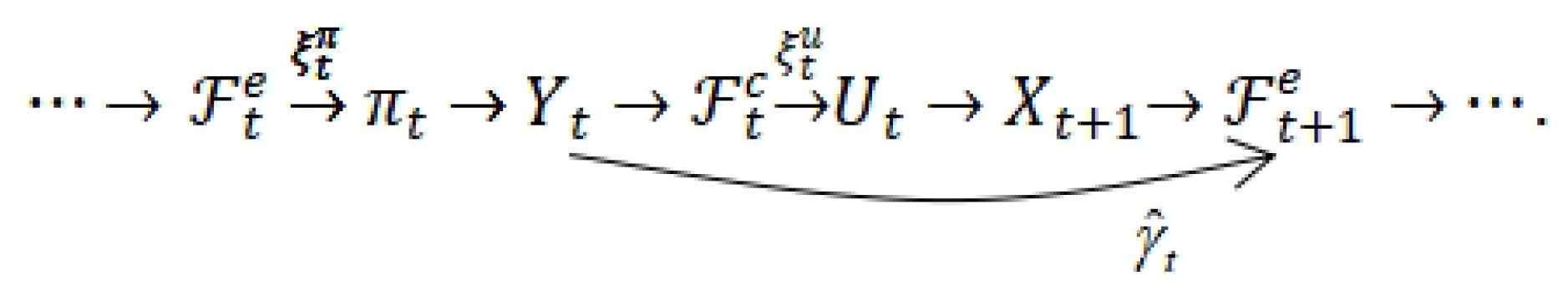Energy Management and Control for Linear–Quadratic–Gaussian Systems with Imperfect Acknowledgments and Energy Constraints

Abstract

This paper explores the optimal control issue for a linear–quadratic–Gaussian (LQG) system under the conditions of imperfect feedback and constraints related to energy harvesting. The system is equipped with various energy options, which allow it to gather energy for information transmission while also receiving imperfect feedback from an auxiliary filter that estimates packet loss. The primary goal of this study is to jointly design the energy selector and the controller to achieve an optimal balance between transmission costs and control performance. Initially, we separate the controller’s synthesis task from the energy selection task. The subproblem of optimal controller synthesis is characterized by a Riccati equation that takes continuous packet loss into account. Simultaneously, the energy selection task, influenced by imperfect feedback and constraints on energy costs, is reformulated as a Markov decision process (MDP) that operates with perfect acknowledgments through iterative updates of state information. Ultimately, the optimal energy selection policy that guarantees filtering performance is derived by solving a Bellman equation. The effectiveness of the proposed approach is confirmed through simulation results.

1. Introduction

As a result of swift advancements in networking, communication technology, and computing, the management of these systems intertwines the cyber and physical realms closely. To ensure the stability of these systems, it is essential to have dependable signals that are transmitted among the components over a common communication network. As demonstrated in references [1,2], implementing improvements to performance and reliability will be subject to challenges when undertaken in the presence of resource constraints. Due to resource constraints, measurement errors are inevitable when predicting actual systems and making decisions. In such cases, these errors are often handled in probabilistic terms to achieve better results [3,4].

Linear–quadratic–Gaussian (LQG) control, a classical and widely used optimal control method in modern control theory, primarily addresses the optimal control problem of linear stochastic systems. It achieves optimal feedback control laws by solving the Riccati equation, integrating state feedback with Kalman filtering. In practical applications, LQG control has been successfully implemented in various fields such as aerospace, robotic control, and power systems. However, as modern industries transition towards intelligence and networking, the dependence of control systems on networks has increased significantly. In this context, the impact of communication constraints on system performance cannot be overlooked [5,6,7]. Taking smart grids as an example, limited communication bandwidth restricts the amount of real-time data transmission between power nodes. When there are sudden changes in grid loads, various nodes may fail to timely exchange power adjustment information, leading to exacerbated voltage fluctuations and potentially triggering local grid failures. Aghaee, Fateme et al. focused on the impact of communication delays and data packet loss on distributed secondary control for microgrids [8]. The study presented in [9] investigates the safety of surgical robots with autonomous control in the context of surgical procedures, focusing on the modeling and control of nonlinear tissue compression and heating utilizing LQG methods. The authors in [10] showcase the balance between the expenses associated with control and the data transmission rates in infinite-horizon LQG systems. Furthermore, the work in [11] examines the ideal tracking capabilities of single-input single-output networked control systems when faced with restricted communication channels. In a similar vein, this paper delves into the LQG control issue under the conditions of communication limitations.

Prior research efforts [12,13,14] have examined the energy transmission issue in systems incorporating energy harvesters, which play a crucial role in transforming various environmental energy types into electricity. In [15], the authors demonstrated that the distributed resource allocation game algorithm significantly enhances energy efficiency and reduces network interference, thereby ensuring successful data transmission. Additionally, In [16], the authors investigated the challenges related to energy transmission for a sensor that harvests energy for remote state estimation, utilizing a continuous-time methodology alongside perturbation analysis. Building on this foundation, they demonstrated the existence of an optimal policy for the allocation of deterministic and stationary power transmission [17]. It is evident that the integration of energy harvesters substantially improves system performance. Consequently, it is posited that the energy selector possesses the capability to efficiently harvest energy.

Generally speaking, control strategies and energy selection strategies need to be co-designed for a long time. For example, researchers demonstrated that the ideal controller does not display the separation principle [2]. On the other hand, they offered the essential criteria for the controller to manifest a separation principle [5]. Based on the principle of separation proposed in [5], a novel framework is introduced in [18] that integrates a controller with a quantization selector, enabling the dynamic determination of the optimal quantization level from a specified set of quantization levels. Nevertheless, the optimal structure of the controller and the energy selector has not been sufficiently investigated. This paper adopts a similar approach and investigates the separation structure between the controller and the energy selector. In contrast to [18], this paper considers a situation where the communication channel is unreliable, which may lead to packet loss. In [19], the authors addressed the issue of energy management for a controller that transmits information to a sensor over communication channels characterized by unknown packet loss. Unlike the approach taken in [19], this paper examines a scenario where the plant transmits information through an unknown packet-dropping link to the filter. In a manner akin to the channel model outlined in reference [17], the energy used for transmission impacts the frequency of packet loss. Apart from scenarios involving flawless receipt acknowledgments [17,20], this study also takes into account a feedback channel that operates as a flawed packet-dropping link between the filter and the plant.

This study examines a challenge related to inefficient control and energy scheduling that stems from a faulty feedback channel. During each time interval, the energy selector assesses the power allocated for data transmission, relying on imperfect acknowledgments and the currently available energy supply. Simultaneously, the controller produces outputs to sustain an ideal equilibrium between control effectiveness and expenses. The optimal control issue, assuming that the state is estimated optimally, is defined by a Riccati equation that incorporates packet loss. The problem of energy selection is addressed by reinterpreting it as a Markov decision process (MDP) with accurate acknowledgments. In conclusion, this study outlines three main contributions:

(1) The LQG optimal control problem under the optimal estimated state with given energy levels is investigated by considering imperfect acknowledgments and energy constraints.

(2) In the case of the packet loss information and transmission cost, a novel optimal controller structure under the optimal estimated state is derived by using backward induction.

(3) The optimal energy selection strategies to ensure filtering performance and the suboptimal controller gain are co-designed, which can be computed offline and independently.

Notations: The symbols $X^{\top }$ and tr(X) denote the transpose and the trace of a real-valued matrix denoted by X, respectively. The inverse of the matrix X is expressed as $X^{-1}$. The sets of non-negative integers and positive integers are represented by ${\mathbb{N}}_0$ and ${\mathbb{N}}_{+}$, respectively. The n-dimensional Euclidean space is referred to as ${\mathbb{R}}^n$. Additionally, $\mathbb{P}\left[X\right]$ signifies the probability of X, while $E\left[X\right|Y]$ indicates the conditional expectation of X given Y.

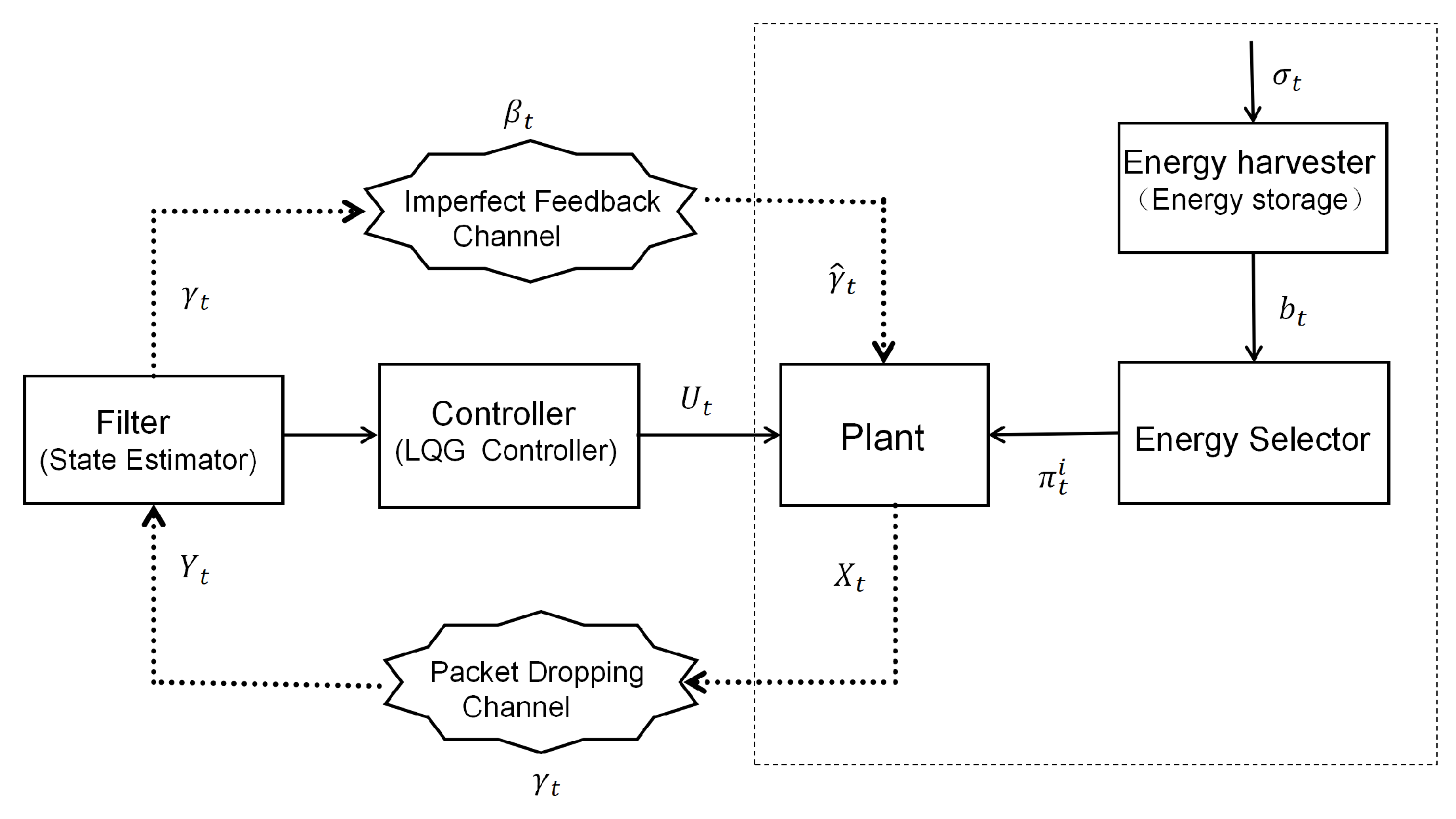
As shown in Figure 1, the plant, on one hand, acquires energy from the environment via its integrated energy-harvesting subsystem (comprising an energy collector, an energy storage battery, and an energy selector) to generate ${\sigma }_t$. This energy is stored in the battery as $b_t$, and then, the energy selector chooses the optimal transmission energy $p_t$ from M energy levels to power the transmission of the state value. On the other hand, the plant transmits its own state $X_t$ to the filter through a wireless channel with packet loss. The filter performs state estimation based on the received state value $Y_t$, obtains the estimated value, and sends it to the controller. The controller, relying on its own information set, calculates the optimal control signal $U_t$ in accordance with the separation principle and feeds it back to the plant to stabilize its state. Meanwhile, the filter sends an imperfect acknowledgment signal ${\widehat{\gamma }}_t$ to the plant. The plant uses this feedback signal to adjust the subsequent energy-selection strategy, ultimately forming a complete closed loop of “state → energy optimization → estimation → control → feedback regulation” and enabling the stable operation of the system under energy constraints and imperfect feedback. In the following sections, we will detail the different submodules represented in the plant diagram.

2. Plant

2.1. LQG System

Consider the following time-invariant LQG system:

$$X_{t+1}=A{X}_t+B{U}_t+W_t$$

(1)

For every $t\in {\mathbb{N}}_0$, let $X_t\in {\mathbb{R}}^n$ represent the state of the system, while $U_t\in {\mathbb{R}}^m$ denotes the control input. The matrices A and B are constants with dimensions that are compatible. The sequence ${\left\{W_t\right\}}_{t\in {\mathbb{N}}_0}$ corresponds to a series of independent and identically distributed (i.i.d.) noise values, each following a zero-mean Gaussian distribution denoted by $W_t\sim \mathcal{N}(0,\mathcal{W})$. The initial state $X_0$ is characterized by a Gaussian distribution with parameters specified as $\mathcal{N}({\mu }_0,\mathsf{\Sigma })$.

In a wireless communication scenario plagued by packet loss, the plant conveys the measurement data to the filter. It is assumed that the wireless channel operates as an additive white Gaussian noise (AWGN) channel, where the relationship between the bit error rate (BER) and the transmission energy $p_t$ is detailed in [17]:

$$\begin{array}{cc}\hfill \mathrm{BER}& =2\mathsf{\Phi }\left(\sqrt{{\displaystyle \frac{\alpha p_t}{S_{0}K}}}\right)\hfill \end{array}$$

(2)

where

$$\begin{array}{c}\hfill \mathsf{\Phi }\left(x\right)\triangleq {\displaystyle \frac{1}{\sqrt{2\pi }}}{\int }_x^{\infty }exp(-t^2/2)dt\end{array}$$

(3)

and $\alpha$ represents a constant parameter, with $S_0$ denoting the spectral density of the noise power, while K signifies the bandwidth of the wireless channel.

This study examines a situation in which energy availability is limited and the required volume of transmitted information is typically constrained. For simplicity, we consider that each data packet consists of a single bit (similar to what is employed for parity checks). If a packet is lost during transmission, the receiving end will not verify the parity correctly, meaning that the packet dropout corresponds to $\mathrm{BER}$. Various data-check methods outlined in [16] can identify packet errors.

We can represent the transmission processes using a binary random variable ${\gamma }_t$, where ${\gamma }_t=1$ indicates that the transmitted signal is received without errors by the filter, while ${\gamma }_t=0$ signifies a dropout scenario. The probability of dropout for the transmitted signals is denoted by

$$\begin{array}{c}\hfill \mathbb{P}[{\gamma }_t=0]=2\mathsf{\Phi }\left(\sqrt{\alpha {\displaystyle \frac{p_t}{S_{0}K}}}\right).\end{array}$$

(4)

It can be deduced from Equation (4) that different transmission energy values may give rise to different dropout probabilities, which subsequently impact the estimation performance at the filter. Depending on the above indicator function ${\gamma }_t$, the state available to the filter is represented as

$$Y_t=(1-{\gamma }_t)X_t+{\gamma }_t(A{X}_{t-1}+B{U}_{t-1}).$$

(5)

2.2. Energy Harvesting and Storage

The energy selector is equipped with an energy harvester that could gather energy from the environment. Denote the amount of harvested energy from the beginning to the end at step t as ${\sigma }_t$. The process of energy harvesting, denoted as ${\sigma }_t$, is considered to be a first-order homogeneous Markov process operating in discrete time and demonstrating stationarity. Let C represent the maximum energy storage capacity of the battery, with the condition that $C\ge p_t$. Following the work of [4], we assume that the evolution of the battery’s available energy is expressed as

$$\begin{array}{c}\hfill b_{t+1}=min\{b_t-p_t+{\sigma }_{t+1},C\},t\in {\mathbb{N}}_0.\end{array}$$

(6)

2.3. Energy Selection

Divide the transmission energy into M levels, and select the transmission energy $p_t$ among M energy levels. The energy for transmission at the i-th level, symbolized as ${\mathcal{Q}}^i$ ($i\in \{1,2,\dots ,M\}$), is associated with a cost denoted by $\lambda \left({\mathcal{Q}}^i\right)={\lambda }_i\in {\mathbb{N}}_{+}$. Let us define the new decision variable ${\pi }_t^i$ for the selection of transmission energy as follows: ${\pi }_t^i=1$ if the i-th transmission energy level is employed at time t, and ${\pi }_t^i=0$ in all other cases. Consequently, the vector ${\pi }_t\triangleq {[{\pi }_t^1,{\pi }_t^2,\dots ,{\pi }_t^M]}^{\top }\in {\{0,1\}}^M$ represents the choices made regarding the switching of transmission energy at the specified time t. Because the transmission energy selector selects only one transmission energy at each time step, hence, we can have ${\mathsf{\Sigma }}_{i=1}^M{\pi }_t^i=1$ for all $t\in {\mathbb{N}}_0$.    

3. Filter and Imperfect Feedback

The filter receives the state value $Y_t$ transmitted by the plant, performs state estimations based on historical measurements and control information, and transmits the estimated results to the controller; at the same time, it sends an imperfect feedback signal to the plant.

3.1. Imperfect Feedback

A signal acknowledging transmission is dispatched from the filter to the plant at every time step. This study addresses a feedback channel that may contain errors. The packet loss sequence $\{{\gamma }_t,t\in {\mathbb{N}}_0\}$ remains unknown to the plant. Instead, an imperfect acknowledgment sequence $\{{\widehat{\gamma }}_t,t\in {\mathbb{N}}_0\}$ is received by the plant from the filter. According to [4], the modeling of the erroneous feedback channel is presented as follows:

$$\begin{array}{c}\hfill {\widehat{\gamma }}_t=\left\{\begin{array}{cc}0\mathrm{or}1\hfill & \mathrm{if}{\beta }_t=1\hfill \\ 2\hfill & \mathrm{if}{\beta }_t=0\hfill \end{array}\right..\end{array}$$

(7)

When ${\beta }_t=0$, all feedback signals are completely lost with a specified dropout probability $\eta$ where $\eta \in [0,1]$. Conversely, when ${\beta }_t=1$, the likelihood of a transmission error arises with a probability of $ϵ$ such that $ϵ\in [0,1]$. This error in transmission results in ${\widehat{\gamma }}_t=0$ if ${\gamma }_t=1$ and ${\widehat{\gamma }}_t=1$ if ${\gamma }_t=0$. The conditional probability matrix for the feedback channel is formulated as follows:

$$\begin{array}{c}\hfill \mathbb{A}=\left(a_{mn}\right)=\left[\begin{array}{ccc}(1-ϵ)(1-\eta )& ϵ(1-\eta )& \eta \\ ϵ(1-\eta )& (1-ϵ)(1-\eta )& \eta \end{array}\right]\end{array}$$

(8)

where $a_{mn}:=\mathbb{P}(\widehat{\gamma }=n-1|\gamma =m-1)$ for $m\in \{1,2\}$ and $n\in \{1,2,3\}$. The system receives perfect packet reception acknowledgments when both $ϵ$ and $\eta$ are set to 0.

3.2. State Estimation

Let us define the sets as follows: ${\mathcal{X}}_t\triangleq \{X_0,X_1,\dots ,X_t\}$ represents the set of state history, ${\mathcal{Y}}_t\triangleq \{Y_0,Y_1,\dots ,Y_t\}$ represents the history of state values that the filter can receive, ${\mathcal{U}}_t\triangleq \{U_0,U_1,\dots ,U_t\}$ denotes the control history, ${\widehat{\gamma }}_t\triangleq \{{\widehat{\gamma }}_0,{\widehat{\gamma }}_1,\dots ,{\widehat{\gamma }}_t\}$ corresponds to the history of feedback signals, and finally, ${\mathsf{\Pi }}_t\triangleq \{{\pi }_0,{\pi }_1,\dots ,{\pi }_t\}$ signifies the history of transmission selection.

The data accessible to the controller at time t is represented as

$${\mathcal{F}}_t^c=\sigma (Y_0,{\pi }_0,Y_1,U_0,{\pi }_1,\dots ,Y_t,U_{t-1},{\pi }_t)$$

(9)

with the initial state being ${\mathcal{F}}_0^c=\{Y_0,{\pi }_0\}$, where $\sigma (·)$ a $\sigma$ algebra. Based on Equation (9)’s definition, one can interpret an admission control strategy as a function that maps ${\mathcal{F}}_t^c$ to ${\mathbb{R}}^m$. We label these strategies as ${\xi }_t^u$. In contrast to the feedback-based control methods described in [2], our approach involves transmitting $W_{t-1}$ rather than $X_t$ at time t. It is important to note that $W_{t-1}$ can be easily calculated using the values of $X_t$, $X_{t-1}$, and $U_{t-1}$.

Now, we introduce notation ${\widehat{X}}_t=E\left[X_t\right|{\mathcal{F}}_{t-1}^c]$, which we will call the prediction of $X_t$. Additionally, we define ${\tilde{X}}_t=E\left[X_t\right|{\mathcal{F}}_t^c]$ as the filtered version of $X_t$. Consequently, we express $\widehat{{\omega }_t}\left({\pi }_{t+1}\right)=E\left[W_t\right|{\mathcal{F}}_{t+1}^c]$.

Using (1) and because $U_t$ is ${\mathcal{F}}_t^c$-measurable, we have

$${\widehat{X}}_{t+1}=A{\tilde{X}}_t+B{U}_t$$

(10)

$$\begin{array}{c}\hfill {\tilde{X}}_t=E\left[X_t\right|{\mathcal{F}}_t^c]={\widehat{X}}_t+{\widehat{\omega }}_{t-1}\left({\pi }_t\right).\end{array}$$

(11)

Let us introduce the error ${\Delta }_t=X_t-{\tilde{X}}_t$. From this, it can be derived that

$$\begin{array}{c}\hfill {\Delta }_{t+1}=A{\Delta }_t+W_t-{\widehat{\omega }}_t=···=A^{t+1}{\Delta }_0+\sum _{k=0}^t{A}^{t-k}(W_k-{\widehat{\omega }}_k)\end{array}$$

(12)

where ${\Delta }_0=W_{-1}-{\widehat{\omega }}_{-1}\left({\pi }_0\right)$. The estimation error of the state ${\Delta }_t$ is influenced by the sequence $\{{\pi }_0,\dots ,{\pi }_t\}$ via the variables $\{{\widehat{\omega }}_{-1},\dots ,{\widehat{\omega }}_{t-1}\}$. However, it is independent of the control strategy ${\xi }^{\mathcal{U}}$.

4. Suboptimal Control and Energy Selection Strategy

The controller receives the state estimation transmitted by the filter and, based on its own information set ${\mathcal{F}}_t^c$, outputs the optimal control signal $U_t$ to ensure the stability of the equipment state and minimize the total cost. The energy transmission selector at time t has access to the information given by

$${\mathcal{F}}_t^e=\sigma \left(X_0,U_0,{\widehat{\gamma }}_0,{\pi }_0,\dots ,X_t,U_{t-1},{\widehat{\gamma }}_t,{\pi }_{t-1}\right)={\mathcal{F}}_{t-1}^e\vee \sigma \left(X_t,U_{t-1},{\widehat{\gamma }}_t,{\pi }_{t-1}\right)$$

(13)

with ${\mathcal{F}}_0^e=\left\{X_0\right\}$. The strategies for selecting the transmitter can likewise be considered as a mapping: ${\mathcal{F}}_t^e$ to ${\{0,1\}}^M$. These strategies are denoted as ${\xi }_t^{\pi }$. Thus, the decision-making process during a single time step is illustrated in Figure 2.

The cooperative minimization of the cost function undertaken by the controller and the energy transmission selector involves a finite horizon quadratic criterion, and it is expressed as follows:

$$\begin{array}{cc}\hfill J_T({\xi }^{\mathcal{U}},{\xi }^{\mathsf{\Pi }})& =E[\sum _{t=0}^{T-1}(X_t^{\top }{Q}_1{X}_t+U_t^{\top }R{U}_t+{\pi }_t^{\top }\wedge )\hfill \\ \hfill & +X_T^{\top }{Q}_2{X}_T|U_t={\xi }_t^u\left({\mathcal{F}}_t^c\right),{\pi }_t={\xi }_t^{\pi }\left({\mathcal{F}}_t^e\right)]\hfill \end{array}$$

(14)

where $\wedge ={[{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_M]}^{\top }$, $R\succ 0$, $Q_1$, $Q_2⪰0$, ${\xi }^{\mathsf{\Pi }}$ represents the entire sequence $\{{\xi }_0^{\pi },{\xi }_1^{\pi },\dots ,{\xi }_{T-1}^{\pi }\}$; likewise, ${\xi }^{\mathcal{U}}$ is defined similarly.

Remark 1. 

The overall cost function to minimize is a weighted combination of control efficiency and transmission cost, directly reflecting their balance. Then, penalize the state deviation from the equilibrium ($X_t^{\top }{Q}_1{X}_t$) and control input consumption ($U_t^{\top }R{U}_t$)—smaller values mean better control stability. High-cost energy selection is then penalized—smaller values mean lower energy expenditure (driven by Λ). To avoid the complexity of joint optimization, we use the separation principle to decompose the problem into two decoupled but mutually constrained subproblems—ensuring that neither control efficiency nor energy selection (costΛ)) is sacrificed excessively.

It is essential to identify the optimal mappings ${\xi }^{{\mathcal{U}}^{*}}$ and ${\xi }^{{\mathsf{\Pi }}^{*}}$ that minimize the cost function (14) across all permissible strategies:

$$({\xi }^{{\mathcal{U}}^{*}},{\xi }^{{\mathsf{\Pi }}^{*}})=\underset{{\xi }^{\mathcal{U}},{\xi }^{\mathsf{\Pi }}}{argmin}{J}_T({\xi }^{\mathcal{U}},{\xi }^{\mathsf{\Pi }}).$$

(15)

4.1. Optimal Control Under the Optimal Estimated State with the Separate Principle

When packet loss occurs during the process of transmission, the controller cannot receive ${\widehat{\omega }}_t$, and we have the following function:

$$\begin{array}{c}\hfill {\tilde{X}}_t=\left\{\begin{array}{ccc}\hfill g\left({\tilde{X}}_{t-1}\right),& & \gamma \left(t\right)=0\hfill \\ \hfill {\tilde{X}}_t,& & \gamma \left(t\right)=1\hfill \end{array}\right.\end{array}$$

(16)

where $g\left(X\right)\triangleq AX+BU$. It is clear that the values of ${\tilde{X}}_t$ belong to a countably infinite collection: $\{{\tilde{X}}_t,g\left({\tilde{X}}_{t-1}\right),g^2\left({\tilde{X}}_{t-2}\right),\dots \}$.

We may introduce a random variable ${\tau }_t$ to represent the length of the most recent successful transfer before time t:

$${\tau }_t=t-max\{t^{*}:\gamma \left(t^{*}\right)=1,0⩽t^{*}⩽t\}$$

(17)

The analysis presented suggests a distinction in structure between the controller and the selection of transmitters. In the subsequent sections, we will formally demonstrate the emergence of a separation principle related to this issue. Associated with the cost function (14), let us define the value function as

$$\begin{array}{cc}\hfill V_k({\mathcal{F}}_k^c,{\mathcal{F}}_k^e)& =\underset{{\xi }_t^u,{\xi }_t^{\pi }}{min}E[\sum _{t=k}^{T-1}(X_t^{\top }{Q}_1{X}_t+U_t^{\top }R{U}_t+{\pi }_t^{\top }\wedge )\hfill \\ \hfill & +X_T^{\top }{Q}_2{X}_T|U_t={\xi }_t^u,{\pi }_t={\xi }_t^{\pi },t=k,\dots ,T-1].\hfill \end{array}$$

(18)

Expression (18) is rewritten as follows by using the dynamic programming principle:

$$\begin{array}{cc}\hfill V_k({\mathcal{F}}_k^c,{\mathcal{F}}_k^e)& =\underset{{\xi }_k^u,{\xi }_k^{\pi }}{min}E[(X_k^{\top }{Q}_1{X}_k+U_k^{\top }R{U}_k+{\pi }_k^{\top }\wedge )\hfill \\ & +V_{k+1}({\mathcal{F}}_{k+1}^c,{\mathcal{F}}_{k+1}^e)|U_k={\xi }_k^u,{\pi }_k={\xi }_k^{\pi }].\hfill \end{array}$$

(19)

If ${\xi }_k^{u^{*}}$ and ${\xi }_k^{{\pi }^{*}}$ serve to minimize the right side of (19), then we have $U_k^{*}={\xi }_k^{u^{*}}\left({\mathcal{F}}_k^c\right)$ and ${\pi }_k^{*}={\xi }_k^{{\pi }^{*}}\left({\mathcal{F}}_k^e\right)$. Additionally, from (18), we can derive the following:

$$\underset{{\xi }^{\mathcal{U}},{\xi }^{\mathsf{\Pi }}}{min}{J}_T({\xi }^{\mathcal{U}},{\xi }^{\mathsf{\Pi }})=E\left[V_0({\mathcal{F}}_0^c,{\mathcal{F}}_0^e)\right]$$

(20)

Here, the expectation in Equation (20) pertains to the random variables ${\mathcal{F}}_0^c$ and ${\mathcal{F}}_0^e$. For conciseness in the upcoming analysis, we will denote $V_k({\mathcal{F}}_k^c,{\mathcal{F}}_k^e)$ as follows:

$$\begin{array}{c}\hfill V_k({\mathcal{F}}_k^c,{\mathcal{F}}_k^e)=\underset{{\xi }_k^u,{\xi }_k^{\pi }}{min}E[(X_k^{\top }{Q}_1{X}_k+U_k^{\top }R{U}_k+{\pi }_k^{\top }\wedge )+V_{k+1}({\mathcal{F}}_{k+1}^c,{\mathcal{F}}_{k+1}^e)|{\mathcal{F}}_k]\end{array}$$

(21)

where ${\mathcal{F}}_k=\{{\mathcal{F}}_k^c,{\mathcal{F}}_k^e\}$ is the combined information set. Note that the information set ${\mathcal{F}}_k^e$ (and, consequently, ${\mathcal{F}}_k$) encompasses the realization $x_k$ of the state $X_k$. The subsequent theorem describes the optimal policy ${\xi }_k^{u^{*}}$ for every $k=0,1,\dots ,T-1$.

Theorem 1. 

Given the information set ${\mathcal{F}}_k^c$ at time k provided to the controller, the optimal control policy ${\xi }_k^{u^{*}}:{\mathcal{F}}_k^c\to {\mathbb{R}}^m$, which operates under the optimal estimated state to minimize the right-hand side of Equation (19), can be expressed in the following manner:

$$U_k^{*}={\xi }_k^{u^{*}}\left({\mathcal{F}}_k^c\right)=-G_k{g}^{{\tau }_k}\left(E\left[X_{k-{\tau }_k}\right|{\mathcal{F}}_k^c]\right).$$

(22)

This holds for every $k=0,1,\dots ,T-1$.

$$\begin{array}{cc}{G}_k\hfill & ={(R+B^{\top }{P}_{k+1}B)}^{-1}{B}^{\top }{P}_{k+1}A,\hfill \end{array}$$

(23a)

$$\begin{array}{cc}{P}_k\hfill & =Q_1+A^{\top }{P}_{k+1}A-G_k^{\top }(R+B^{\top }{P}_{k+1}B)G_k,\hfill \end{array}$$

(23b)

$$\begin{array}{cc}{P}_T\hfill & =Q_2.\hfill \end{array}$$

(23c)

Proof. 

To ensure conciseness, we will refer to $g^{{\tau }_k}$ rather than $g^{{\tau }_k}\left(x_{k-{\tau }_k}\right)$, and $g_{\Delta }^{{\tau }_k}$ will denote $g^{{\tau }_k}\left({\Delta }_{k-{\tau }_k}\right)$. The proof of this theorem relies on the dynamic programming principle. The central concept is to establish that the value function linked to the optimal control problem, assuming the best estimate of the state, is represented as follows:

$$V_k({\mathcal{F}}_k^c,{\mathcal{F}}_k^e)={g^{{\tau }_k}}^{\top }{P}_k{g}^{{\tau }_k}+C_k+o_k$$

(24)

where $x_k$ signifies the outcome of the state $X_k$, and $P_k$ is defined similarly to that in (23b); this is applicable for all $k=0,1,\dots ,T-1$.

$$C_k=\underset{{\left\{{\xi }_t^{\pi }\right\}}_{t=k}^{T-1}}{min}E\left[\sum _{t=k}^{T-1}{g_{\Delta }^{{\tau }_t}}^{\top }{H}_t{g}_{\Delta }^{{\tau }_t}+{\pi }_t^{\top }\wedge |{\mathcal{F}}_k^e\right].$$

(25)

The matrix $H_k\in {\mathbb{R}}^{n\times m}$ and the scalar $o_k$ are defined by the following equations:

$$\begin{array}{cc}\hfill H_k& =G_k^{\top }(R+B^{\top }{P}_{k+1}B)G_k,\hfill \end{array}$$

(26a)

$$\begin{array}{cc}\hfill o_k& =o_{k+1}+tr\left(P_{k+1}\mathcal{W}\right),\hfill \end{array}$$

(26b)

$$\begin{array}{cc}\hfill o_T& =0.\hfill \end{array}$$

(26c)

Neither $H_k$ nor $o_k$ relies on previous or forthcoming control or energy selection decisions. Thus, these values can be calculated offline. Additionally, from (12), it can be deduced that ${\Delta }_t$ is independent of the earlier control history ${\mathcal{U}}_t$, being solely determined by ${\mathsf{\Pi }}_t$. Consequently, $C_k$ is not influenced by the control action $U_k$. Equation (25) can be reformulated as follows.

$$C_k=\underset{{\xi }_k^{\pi }}{min}E\left[{g_{\Delta }^{{\tau }_k}}^{\top }{H}_k{g}_{\Delta }^{{\tau }_k}+{\pi }_k^{\top }\wedge +C_{k+1}|{\mathcal{F}}_k^e\right].$$

(27)

Based on the definition of $V_k(·)$ presented in (18), we can express $V_T({\mathcal{F}}_T^c,{\mathcal{F}}_T^e)$ as follows:

$$V_T({\mathcal{F}}_T^c,{\mathcal{F}}_T^e)={g^{{\tau }_T}}^{\top }{Q}_2{g}^{{\tau }_T}={g^{{\tau }_T}}^{\top }{P}_T{g}^{{\tau }_T}.$$

(28)

Following this, we need to confirm that $V_{T-1}({\mathcal{F}}_{T-1}^c,{\mathcal{F}}_{T-1}^e)$ conforms to the structure outlined in (24):

$$\begin{array}{c}\hfill V_{T-1}({\mathcal{F}}_{T-1}^c,{\mathcal{F}}_{T-1}^e)=\underset{{\xi }_{T-1}^u,{\xi }_{T-1}^{\pi }}{min}E\left[{g^{{\tau }_{T-1}}}^{\top }{Q}_1{g}^{{\tau }_{T-1}}+U_{T-1}^{\top }R{U}_{T-1}+{\pi }_{T-1}^{\top }\wedge +{g^{{\tau }_T}}^{\top }{P}_T{g}^{{\tau }_T}\right].\end{array}$$

(29)

Substituting Equation (1) and performing a series of simplifications result in the following expression:

$$\begin{array}{cc}\hfill V_{T-1}({\mathcal{F}}_{T-1}^c,{\mathcal{F}}_{T-1}^e)& =\underset{{\xi }_{T-1}^u,{\xi }_{T-1}^{\pi }}{min}E\left[\right||U_{T-1}+G_{T-1}{g}^{{\tau }_{T-1}}{\left|\right|}_{(R+B^{\top }{P}_{T}B)}^2\hfill \\ & +{g^{{\tau }_{T-1}}}^{\top }{P}_{T-1}{g}^{{\tau }_{T-1}}+{\pi }_{T-1}^{\top }\wedge +tr\left(P_T\mathcal{W}\right)|{\mathcal{F}}_k].\hfill \end{array}$$

(30)

In Formula (30), the term $\left|\right|U_{T-1}+G_{T-1}{g}^{{\tau }_{T-1}}{\left|\right|}_{(R+B^{\top }{P}_{T}B)}^2$ is the sole component that is influenced by $U_{T-1}$. Therefore, $U_{T-1}$ serves as the minimum mean squared estimate for $G_{T-1}{g}^{{\tau }_{T-1}}$.Then,

$$\begin{array}{cc}\hfill U_{T-1}^{*}& ={\xi }_{T-1}^{u^{*}}\left({\mathcal{F}}_{T-1}^c\right)=-G_{T-1}{g}^{{\tau }_{T-1}}\left(E\left[X_{T-1-{\tau }_{T-1}}\right|{\mathcal{F}}_{T-1}^c]\right).\hfill \end{array}$$

(31)

After replacing the optimal $U_{T-1}^{*}$ in (29), we derive

$$\begin{array}{cc}\hfill V_{T-1}({\mathcal{F}}_{T-1}^c,{\mathcal{F}}_{T-1}^e)=& \underset{{\xi }_{T-1}^{\pi }}{min}E\left[{g_{\Delta }^{{\tau }_{T-1}}}^{\top }{H}_{T-1}{g}_{\Delta }^{{\tau }_{T-1}}+{\pi }_{T-1}^{\top }\wedge |{\mathcal{F}}_{T-1}^e\right]\hfill \\ & +{g^{{\tau }_{T-1}}}^{\top }{P}_{T-1}{g}^{{\tau }_{T-1}}+tr\left(P_T\mathcal{W}\right)\hfill \end{array}$$

(32)

Consequently, applying the definitions of $C_{T-1}$ and $o_{T-1}$ leads us to the conclusion that

$$\begin{array}{c}\hfill V_{T-1}({\mathcal{F}}_{T-1}^c,{\mathcal{F}}_{T-1}^e)=C_{T-1}+{g^{{\tau }_{T-1}}}^{\top }{P}_{T-1}{g}^{{\tau }_{T-1}}+o_{T-1}.\end{array}$$

(33)

Therefore, the expression $V_{T-1}({\mathcal{F}}_{T-1}^c,{\mathcal{F}}_{T-1}^e)$ is certainly in the format described by Equation (24). To confirm that Equation (24) is also valid for time k, we apply backward induction, presuming that it is true for some time $k+1$. Toward that end, we obtain

$$\begin{array}{cc}\hfill V_k({\mathcal{F}}_k^c,{\mathcal{F}}_k^e)& =\underset{{\xi }_k^u,{\xi }_k^{\pi }}{min}E[({g^{{\tau }_k}}^{\top }{Q}_1{g}^{{\tau }_k}+U_k^{\top }R{U}_k+{\pi }_k^{\top }\wedge )\hfill \\ & +{g^{{\tau }_{k+1}}}^{\top }{P}_{k+1}{g}^{{\tau }_{k+1}}+C_{k+1}+o_{k+1}\left|{\mathcal{F}}_k\right].\hfill \end{array}$$

(34)

Using Equations (1), (23a) and (23b), one can obtain

$$\begin{array}{cc}\hfill V_k({\mathcal{F}}_k^c,{\mathcal{F}}_k^e)& =\underset{{\xi }_k^u,{\xi }_k^{\pi }}{min}E\left[\right||U_k+G_k{g}^{{\tau }_k}{\left|\right|}_{(R+B^{\top }{P}_{k+1}B)}^2+{g^{{\tau }_k}}^{\top }{P}_k{g}^{{\tau }_k}\hfill \\ & +{\pi }_k^{\top }\wedge )+tr\left(P_{k+1}\mathcal{W}\right)+C_{k+1}+o_{k+1}|{\mathcal{F}}_k].\hfill \end{array}$$

(35)

The optimal control, denoted as $U_k^{*}$, which is derived under the best estimated state to minimize (35), is expressed as follows:

$$U_k^{*}={\xi }_k^{u^{*}}\left({\mathcal{F}}_k^c\right)=-G_k{g}^{{\tau }_k}\left(E\left[X_{k-{\tau }_k}\right|{\mathcal{F}}_k^c]\right).$$

(36)

After substituting the optimal control under the optimal estimated state from (36) in (35), we can obtain

$$\begin{array}{cc}\hfill V_k({\mathcal{F}}_k^c,{\mathcal{F}}_k^e)& =\underset{{\xi }_k^{\pi }}{min}E\left[\right({g_{\Delta }^{{\tau }_k}}^{\top }\left(G_k^{\top }(R+B^{\top }{P}_{k+1}B)G_k\right)g_{\Delta }^{{\tau }_k}\hfill \\ & +{\pi }_k^{\top }\wedge +C_{k+1}\left)\right|{\mathcal{F}}_k^e]+{g^{{\tau }_k}}^{\top }{P}_k{g}^{{\tau }_k}+tr\left(P_{k+1}\mathcal{W}\right)+o_{k+1}\hfill \\ & =\underset{{\xi }_k^{\pi }}{min}{E}_{{\mathcal{F}}_k^e}[{g_{\Delta }^{{\tau }_k}}^{\top }{H}_k{g}_{\Delta }^{{\tau }_k}+{\pi }_k^{\top }\wedge +C_{k+1}]+{g^{{\tau }_k}}^{\top }{P}_k{g}^{{\tau }_k}+o_k\hfill \\ & ={g^{{\tau }_k}}^{\top }{P}_k{g}^{{\tau }_k}+C_k+o_k.\hfill \end{array}$$

(37)

Consequently, the value function can be expressed in the form of (24), and the optimal control based on the best estimated state at times $k=0,1,\dots ,T-1$ is provided in (36).    □

Remark 2. 

The optimal feedback controller for the separated control problem is given by Theorem 1 in [5]; it indicates that there exists a separation principle if the policy satisfies the structure of Equation (4) in [5]. In this paper, Equation (23a) is exactly the same as the structure of Equation (4) in [5], which shows that the optimal control strategy proposed by us satisfies the separation principle.

Remark 3.

The problem of designing a controller based on the filter requires the consideration of both filtering performance and control performance simultaneously. One typical method is to prioritize filtering performance before ensuring control performance. For example, the separation structure between the controller and the quantizer is studied in [18] to ensure the filtering performance and control performance individually. Through a similar analytical approach, we find that the state estimation error ${\Delta }_t$ at the filter depends only on the energy selection policy ${\xi }_t^{\mathsf{\Pi }}$ through the variable $\{{\widehat{\omega }}_{-1},\dots ,{\widehat{\omega }}_{t-1}\}$ and not on the control ${\xi }_t^U$. Likewise, we obtain a separation principle between the energy selector and the controller.

Note that, in contrast to [18], this paper takes into account delay: ${\tau }_t=t-max\{t^{*}:\gamma \left(t^{*}\right)=1,0⩽t^{*}⩽t\}$. In the presence of delay, the information available at the controller will be affected since some of the measurements’ arrival will be delayed, and hence, state estimations will be affected. Theorem 1 incorporates the consideration of delay and provides the optimal controller structure for this scenario: $U_k^{*}=-G_k{g}^{{\tau }_k}\left(E\left[X_{k-{\tau }_k}\right|{\mathcal{F}}_k^c]\right)$.

4.2. Optimal Energy Selection to Ensure Filtering Performance and MDP

Affected by the energy constraint, packet dropouts may occur during the information transmission of the plant. Consequently, the system determines the most efficient transmission energy to reduce the error covariance at the filter, as well as the energy selection cost. The optimization challenge can be reformulated as follows:

$$\underset{{\xi }_t^{\pi }}{min}E\left[\sum _{t=0}^{T-1}\left(tr\left(P_t\right)+{\pi }_t^{\top }\wedge \right)\right]$$

(38)

This subsection aims to identify the ideal energy selection strategy that guarantees filtering efficacy while minimizing the above cost function. Due to the presence of an imperfect feedback communication channel, the system cannot verify the receipt of packets by the filter. Thus, at time t, the system acquires “imperfect state information” regarding $\left\{P_t\right\}$ through the acknowledgment sequence $\left\{{\widehat{\gamma }}_t\right\}$. This optimization problem can be interpreted as a Markov decision process (MDP) with flawed state information. Furthermore, the issue characterized as an MDP with imperfect acknowledgments may be transformed into an MDP with accurate acknowledgments by utilizing the information-state framework.

Let all observations obtained from the filter up to time t be represented as

$$\begin{array}{c}\hfill z^t:=\{P_0,{\widehat{\gamma }}_0,\dots ,{\widehat{\gamma }}_t,p_0,\dots ,p_{t-1}\}\end{array}$$

(39)

for $t\ge 0$, with $z^{-1}:=\left\{P_0\right\}$. Next, we define the information state as

$$\begin{array}{c}\hfill f_{t+1}\left(P_{t+1}\right|z^t,p_t)=\mathbb{P}\left(P_{t+1}\right|z^t,p_t),\end{array}$$

(40)

representing the conditional probability of the estimation error covariance $P_{t+1}$ given $z^t$ and $p_t$. The ensuing theorem illustrates how $f_{t+1}(·|z^t,p_t)$ can be determined from $f_t(·|z^{t-1},p_{t-1})$ in conjunction with ${\widehat{\gamma }}_t$ and $p_t$. From reference [4], we have the following lemma.

Lemma 1

([4]). The dynamics of the information-state function $f_{(·)}$ is described as follows:

$$\begin{array}{cc}& f_{t+1}\left(P_{t+1}\right|z^t,p_t)\hfill \\ \hfill =& \sum _{{\gamma }_t\in \{0,1\}}[{\int }_{P_t}\left(\mathbb{P}\left(P_{t+1}\right|P_t,{\gamma }_t)\times f_t\left(P_t\right|z^{t-1},p_{t-1})\right)d{P}_t\hfill \\ & \times {\displaystyle \frac{\mathbb{P}\left({\widehat{\gamma }}_t\right|{\gamma }_t)\times \mathbb{P}\left({\gamma }_t\right|p_t)}{{\sum }_{{\gamma }_t\in \{0,1\}}\mathbb{P}\left({\widehat{\gamma }}_t\right|{\gamma }_t)\times \mathbb{P}\left({\gamma }_t\right|p_t)}}],\hfill \end{array}$$

(41)

with the initial condition given by $f_0\left(P_0\right|z^{-1})=\delta \left(P_0\right)$, where δ denotes the Dirac delta function.

In light of the function ${\gamma }_t$, the estimation error covariances at the filter satisfy the following iteration expression:

$$\begin{array}{c}\hfill P_{t+1}={\gamma }_t\mathcal{W}+(1-{\gamma }_t)(A{P}_t{A}^{\top }+\mathcal{W})\end{array}$$

(42)

The condition of having perfect state information is characterized by the information-state $f_{(·)}$. Define a binary random variable $\gamma$, akin to ${\gamma }_t$. For a given P, we express the following

$$\begin{array}{c}\hfill \mathcal{L}(P,\gamma ):=\gamma \mathcal{W}+(1-\gamma )(AP{A}^{\top }+\mathcal{W})\end{array}$$

(43)

as the operator of the random Riccati equation. Let ${\mathcal{S}}_{+}^n$ denote the collection of all non-negative definite matrices. We denote the space of all probability density functions defined on ${\mathcal{S}}_{+}^n$ as $\mathsf{\Psi }$, characterized by the condition ${\int }_{{\mathcal{S}}_{+}^n}\phi \left(P\right)dP=1$ for any $\phi \in \mathsf{\Psi }$. Building on the recursion of the information-state, we define

$$\begin{array}{c}\hfill \tilde{\phi }:=\sum _{\gamma \in \{0,1\}}\left[{\int }_P\mathbb{P}\left(\mathcal{L}(P,\gamma )|P,\gamma \right)\phi \left(P\right)dP\times {\displaystyle \frac{\mathbb{P}\left(\widehat{\gamma }\right|\gamma )\times \mathbb{P}\left(\gamma \right|p)}{{\sum }_{\gamma \in \{0,1\}}\mathbb{P}\left(\widehat{\gamma }\right|\gamma )\times \mathbb{P}\left(\gamma \right|p)}}\right]\end{array}$$

(44)

for a given $\phi \in \mathsf{\Psi }$, as well as for $\widehat{\gamma }$ and p. It is important to highlight that when both $ϵ$ and $\eta$ are set to zero, the optimization issue transforms into a stochastic control problem with perfect state information.

We formulate a Markov decision process (MDP) to address the stochastic control issue. At time t, the MDP is characterized by the state $s_t=({\phi }_t,{\sigma }_t,b_t)$, which resides within the state space $\mathbb{S}$. Let $\mathbb{A}=\{0,p_t\left(1\right),\dots ,p_t\left(M\right)\}$ represent the set of actions corresponding to transmission energy, while $\mathbb{A}\left(s\right)$ denotes the collection of permissible actions for the state $s\in \mathbb{S}$. The reward for a single stage is given by

$$\begin{array}{cc}\hfill r(s,\gamma )& =E\left[\left(tr\left(\mathcal{L}\right(P,\gamma \left)\right)|\phi ,p\right)+{\pi }^{\top }\wedge \right]\hfill \\ & =\mathbb{P}(\gamma =1)\times tr\left(\mathcal{W}\right){\int }_P\phi \left(P\right)dP+\mathbb{P}(\gamma =0)\hfill \\ & \times {\int }_{P}tr(AP{A}^{\top }+\mathcal{W})\phi \left(P\right)dP+{\pi }^{\top }\wedge .\hfill \end{array}$$

(45)

The best approach for selecting energy to guarantee effective filtering performance is calculated offline using the Bellman dynamic programming equations presented below.

Theorem 2. 

Given the initial condition ${\mathcal{I}}_0=\{{\sigma }_0,b_0,P_0\}$, the finite-time horizon minimization problem, which accounts for imperfect acknowledgments, fulfills the following Bellman optimal iterative equation:

$$\begin{array}{c}\hfill V_k(\phi ,\sigma ,b)=\underset{p\in \mathbb{A}}{min}\left\{r(s,\gamma )+E\left[V_{k+1}(\tilde{\phi },\tilde{\sigma },\tilde{b})|\phi ,\sigma ,p\right]\right\}\end{array}$$

(46)

and the termination condition is

$$\begin{array}{c}\hfill V_T(\phi ,\sigma ,b):=\underset{p\in \mathbb{A}}{min}E\left[tr\left(\mathcal{L}\right(P,\gamma \left)\right)|\phi ,p\right]=E\left[tr\left(\mathcal{L}\right(P,\gamma \left)\right)|\phi ,b\right]\end{array}$$

(47)

where all available energy is used for transmission in the final time T.

Accordingly, the optimal selection policy ${\xi }^{{\pi }^{*}}$ is obtained by

$$\begin{array}{c}\hfill {\xi }^{{\pi }^{*}}=arg\underset{p\in \mathbb{A}}{min}\left\{r(s,\gamma )+E\left[V_{k+1}(\tilde{\phi },\tilde{\sigma },\tilde{b})|\phi ,\sigma ,p\right]\right\}\end{array}$$

(48)

Proof. 

For this proof, please consult Theorem $7.1$ in reference [21].    □

To facilitate the calculations, we express

$$\begin{array}{c}\hfill E\left[V_{k+1}(\tilde{\phi },\tilde{\sigma },\tilde{b})|\phi ,\sigma ,p\right]={\sum }_{i=1}^N{V}_{k+1}(\tilde{\phi },i,\tilde{b}\left(i\right))\times {\left(\mathbb{P}\left(\sigma \right)\mathbb{H}\right)}_i,\end{array}$$

(49)

where the energy harvesting sequence $\left\{{\sigma }_k\right\}$ is characterized by finite-state Markov chains. The matrix $\mathbb{H}$ represents the state transition probabilities of the energy harvesting processes, and $\mathbb{P}\left(\sigma \right):=\left[\mathbb{P}\right(\sigma =1),\dots ,\mathbb{P}(\sigma =N\left)\right]$.

Remark 4. 

The energy selection problem with the imperfect state information problem is reduced to ones with perfect state information using the notion of information-state [21]. The information state is the entire probability density function $\tilde{\phi }$ and not just its value at any particular $P_t$. We note that discretized versions of the Bellman equations (46), which, in particular, includes the discretization of the space of probability density functions Ψ, is used for the numerical computation to find the suboptimal solution to the energy selection problem. As the degree of discretization increases, the suboptimal solution will converge to the optimal solution [22]. For Bellman optimal (46), we can solve it by applying the value iteration algorithm [23].

4.3. Algorithm

Algorithm 1 is the algorithm flow of this article.

Algorithm 1 Joint Optimization of Control and Energy Selection for LQG Systems.

Require: Set Time horizon T, system matrices $A,B$, noise covariance $\mathcal{W}$, state penalty Q, control cost R, energy cost vector $\mathsf{\Lambda }$, energy levels $\mathcal{A}$, battery capacity C, energy harvesting transition matrix T, harvesting set ${\sigma }_t$,$\alpha$, noise spectral density S, bandwidth K, feedback error probabilities $ϵ,\eta$ Initialize the distributions: System initial state $X_0\sim \mathcal{N}(0,I)$, initial battery level $b_0$; Estimation error covariance initial value $P_0$ (Dirac delta distribution $f_0\left(P_0\right|z^{-1})=\delta \left(P_0\right)$), information state ${\phi }_0=f_0$; Energy selection decision variable ${\pi }_0\in \{0,1\}$, Offline Calculation: Controller and Energy Policy (Backward Induction):   1: for $k=T-1$ down to 0 do   2:       Solve Riccati equation for optimal control gain   3:       if $k=T-1$ then   4:             Initialize terminal matrix $P_T=Q_2$ (Equation (23c))   5:       end if   6:       Calculate $P_k$ (Equation (23b))   7:       Compute control gain $G_k$ (Equation (23a))   8:       Store $\{G_0,G_1,\dots ,G_{T-1}\}$   9:       MDP value iteration for optimal energy policy 10:       while MDP value function $V_k$ not converged do 11:           Prediction of information state: Update √ via Lemma 1 12:           Update of value function: Calculate one-stage reward $r(s_t,\gamma )$ (Equation (45)) 13:           Update $V_k$ (Equation (46)) 14:       end while 15:       Determine optimal energy policy: ${\xi }_k^{{\pi }^{*}}$ (Equation (48)) 16:       Store $\{{\xi }_0^{{\pi }^{*}},\dots ,{\xi }_{T-1}^{{\pi }^{*}}\}$ 17: end for Online Simulation: System Operation (Forward Propagation)): for $t=0$ to $T-1$ do   2:     Select transmission energy $p_t={\xi }_t^{*}({\phi }_t,{\sigma }_t,b_t)$ (feasibility constraint: $p_t\le b_t$)     Compute packet loss probability $\mathbb{P}[{\gamma }_t=0]=2\mathsf{\Phi }\left(\sqrt{{\displaystyle \frac{\alpha p_t}{S_{0}K}}}\right)$   4:     Generate binary loss indicator ${\gamma }_t\sim \mathrm{Bern}(1-\mathbb{P}[{\gamma }_t=0])$     Generate measurement $Y_t$ (Equation (5))   6:     Calculate continuous loss duration ${\tau }_t$ (Equation (17))     Filtered state ${\tilde{X}}_t=g^{{\tau }_t}\left({\tilde{X}}_{t-{\tau }_t}\right)$   8:     Compute optimal control $U_t^{*}=-G_t{g}^{{\tau }_t}\left(\mathbb{E}\left[X_{t-{\tau }_t}\right|{\mathcal{F}}_t^c]\right)$ (Equation (22))     Update state $X_{t+1}$ (Equation (1)), where $W_t\sim \mathcal{N}(0,\mathcal{W})$ 10:     Update battery $b_{t+1}$ (Equation (6))     Generate next harvesting energy ${\sigma }_{t+1}\sim \mathrm{Markov}\left(T\right)$ 12:     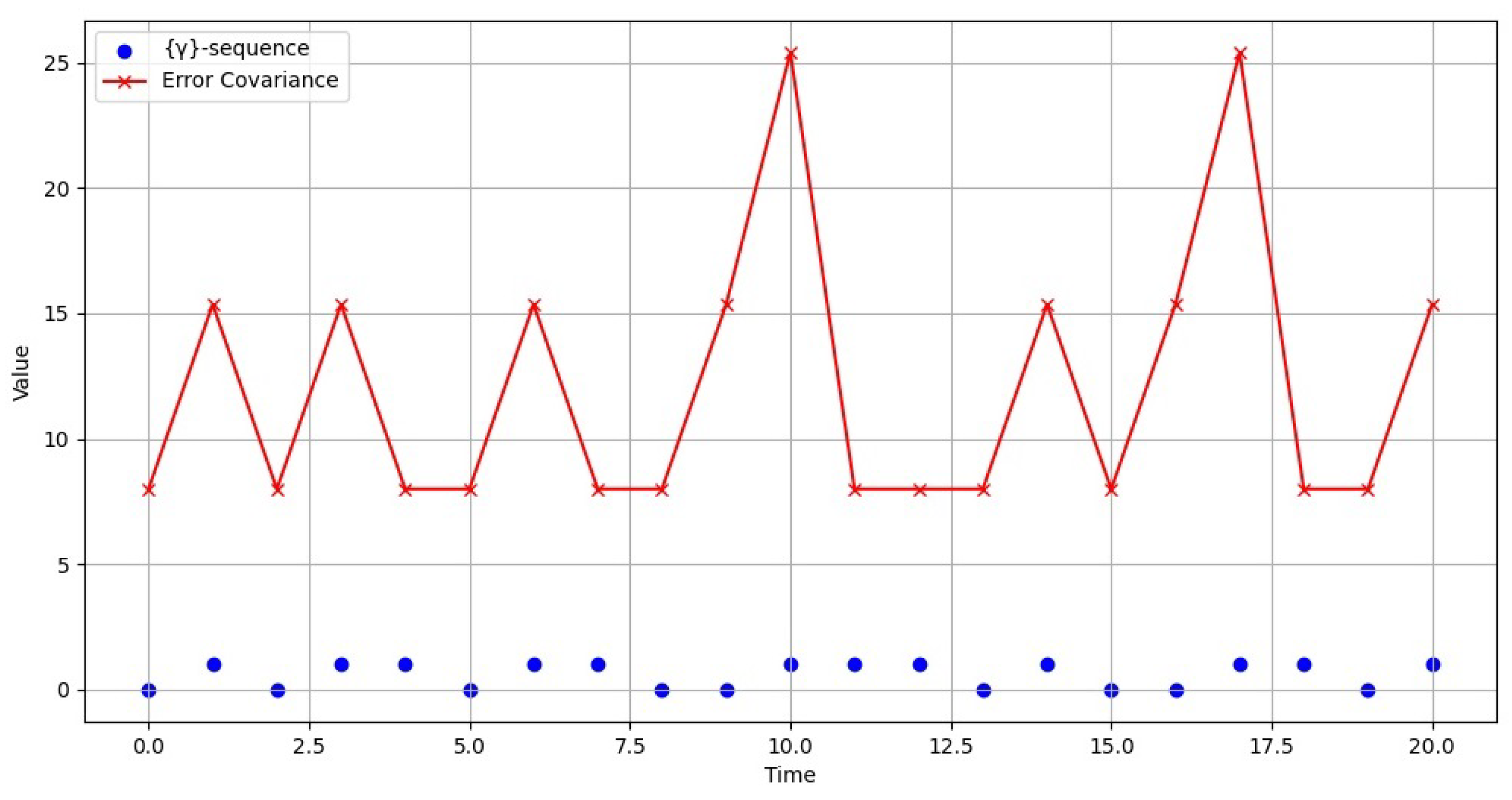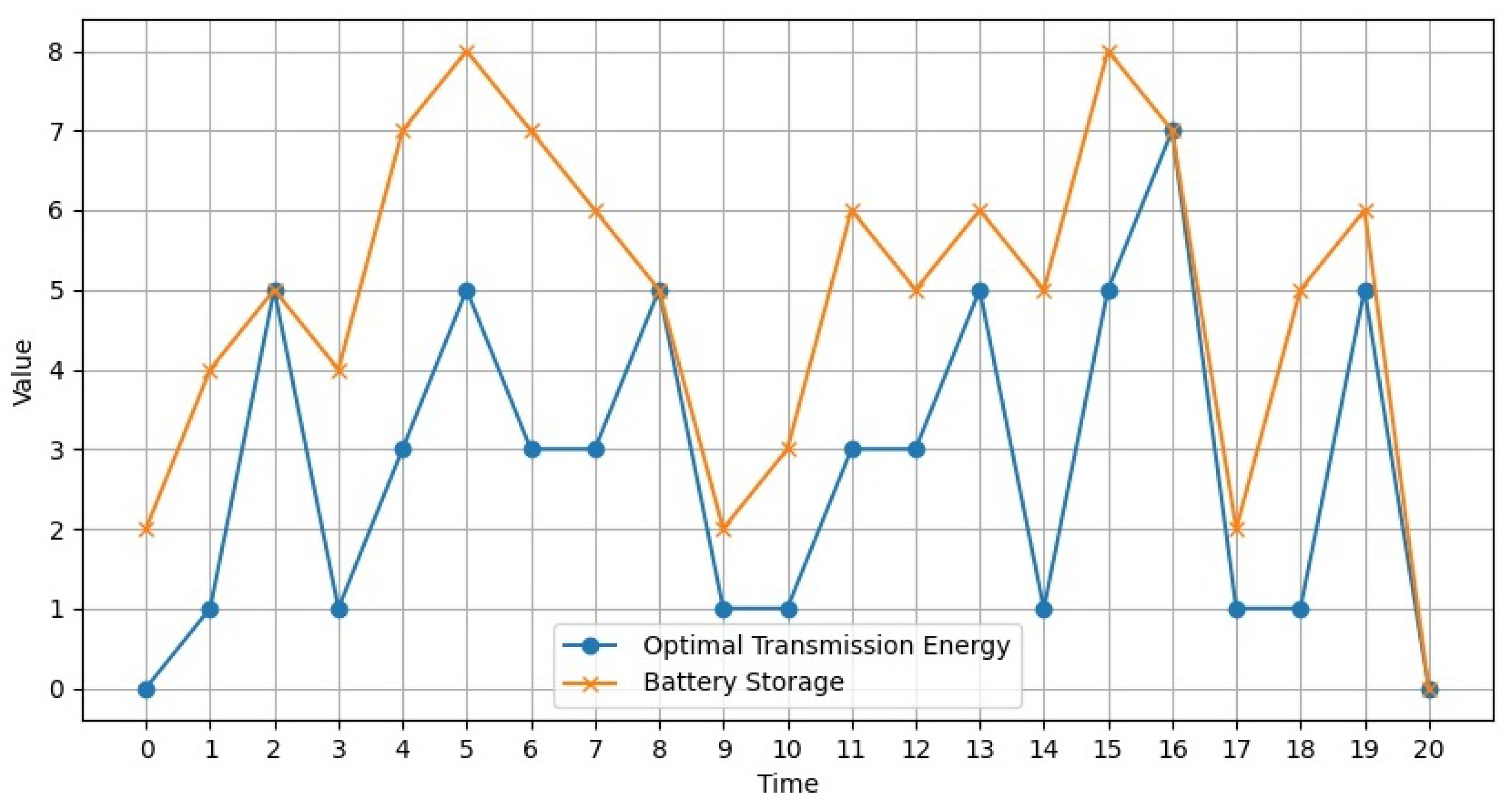Record performance indicators:       estimation error covariance $P_t=\mathbb{E}\left[{\Delta }_t{\Delta }_t^{\top }\right]$, transmission cost ${\pi }_t^{\top }\mathsf{\Lambda }$, control cost $U_t^{*\top }R{U}_t^{*}$ end for

5. Simulation Results

Example 1. 

Let us consider the two-dimensional (unstable) system

$$X_{t+1}=\left[\begin{array}{cc}1.03& 0.5\\ 0& 1.2\end{array}\right]X_t+\left[\begin{array}{cc}0.1& 0\\ 0& 0.18\end{array}\right]U_t+W_t,$$

(50)

where the starting condition is defined as $X_0\sim \mathcal{N}(0,I)$, while $W_t$ follows a distribution of $W_t\sim \mathcal{N}(0,2I)$. The parameters for the control cost are specified as $Q_1=Q_2=R={\displaystyle \frac{1}{2}}I$, with the time horizon established at $T=40$.

The harvested energies are modeled as two-level discrete Markov chains with the transition matrix $T=[0.4,0.6;0.3,0.7]$ and the energy-harvesting set $\left\{{\sigma }_t\right\}=\{2,4\}$. The parameters of the channel are $\beta =0.5$, $S_0=0.8$, and $K=2$. The simulation was performed with seven energy selectors corresponding to the action set $\{0,1,3,5,7,9\}$ and a one-to-one mapping $\left\{p_t\right\}=\{0,1,3,5,7,9\}\mapsto \left\{{\pi }_t\right\}=\{{\pi }_t^1,{\pi }_t^2,{\pi }_t^3,{\pi }_t^4,{\pi }_t^5,{\pi }_t^6\}$ (where ↦ denotes the mapping from $p_t$ to the decision variable ${\pi }_t$). The costs associated with the energy selectors are $\wedge ={[0,0.1,0.2,0.3,0.4,0.5]}^T$.

To simplify the discussion, we initially consider a scenario where the plant operates with ideal acknowledgments (i.e., $\eta =0$ and $ϵ=0$). In Figure 3, a single simulation run of the packet loss process $\left\{{\gamma }_t\right\}$ is depicted, with the red line illustrating the filter’s error covariance, while the blue dots represent the values of γ (where $\gamma =0$ signifies packet loss, and $\gamma =1$ denotes successful data transmission). Meanwhile, Figure 4 presents battery storage $\left\{b_t\right\}$ along with the corresponding optimal energy distribution $\left\{p_t\right\}$ for $C=10$, and the control effect comparison is illustrated in Figure 5.

We set $\tau =\{0,1,2\}$ (continuous packet dropping time). Without the proposed strategy, the system state is unstable; implementing this strategy leads to overall stabilization. An increase in τ will result in a corresponding increase in the time required for the system to regain stability. The control gain is calculated by Theorem 1 (removed redundant period) and given in

Table 1. Control gain for Example 1.

Time	0	⋯	38	39
$-G$	$\left[\begin{array}{cc}-0.593& -0.743\\ -0.703& -3.470\end{array}\right]$	⋯	$\left[\begin{array}{cc}-0.206& -0.155\\ -0.085& -0.566\end{array}\right]$	$\left[\begin{array}{cc}-0.101& -0.049\\ 0& -0.209\end{array}\right]$

.

Example 2. 

We consider an unstable batch reactor (a large-scale system) with parameters from [24] as follows:

$$A=\left[\begin{array}{cccc}1.1782& 0.0015& 0.5116& -0.4033\\ -0.0515& 0.6619& -0.0110& 0.0613\\ 0.0762& 0.3351& 0.5607& 0.3824\\ -0.0006& 0.3353& 0.0893& 0.8494\end{array}\right],B=\left[\begin{array}{cc}0.0045& -0.0876\\ 9.4672& 0.0012\\ 0.2132& -0.2353\\ 0.2131& -0.0161\end{array}\right],$$

where the starting condition is represented as $X_0\sim \mathcal{N}(0,I)$ and $W_t\sim \mathcal{N}(0,2I_{4\times 4})$. The parameters for control costs are defined as $Q_1=Q_2={\displaystyle \frac{1}{2}}{I}_{4\times 4}$ and $R={\displaystyle \frac{1}{2}}{I}_{2\times 2}$, while the time horizon is established at $T=40$. All other parameters remain consistent with those detailed in Example 1.

If we assume that packet loss may occur within this system, we derive an energy selection policy (specifically, $\eta =0$ and $ϵ=0$) and assess the control performance of the proposed approach. As illustrated in Figure 6, we note that the estimated error covariance rises with an increase in the continuous packet dropping duration τ. The optimal energy allocation under this policy when C = 10 is presented in Figure 7, where the blue curve denotes optimal transmission energy and the orange curve represents battery storage, providing quantitative insights into energy management. In Figure 8, the state after control diminishes to 0 (in contrast to the state prior to control), which validates the effectiveness of the designed controller. The control gain for the system is computed using Theorem 1 and is presented in

Table 2. Control gain for Example 2.

Time	$-\mathit{G}$
0	$\left[\begin{array}{cccc}0.0137& -0.0999& -0.0122& -0.08168\\ 2.1389& 0.1310& 1.4990& -0.9285\end{array}\right]$
1	$\left[\begin{array}{cccc}0.0137& -0.0999& -0.0122& -0.08168\\ 2.1389& 0.1310& 1.4990& -0.9285\end{array}\right]$
⋮	⋮
39	$\left[\begin{array}{cccc}0.0051& -0.0706& -0.0003& -0.0092\\ 0.1141& 0.0757& 0.1675& 0.0638\end{array}\right]$

.

6. Conclusions

In this study, we examine a traditional LQG problem that involves flawed acknowledgments and constraints related to energy harvesting. The transmitter is required to determine the optimal energy level based on incomplete feedback data, aiming to minimize the overall costs associated with transmission and control efficacy. By addressing the classical Riccati equation linked to the LQG problem, we have computed the optimal control gains. The challenge of energy selection under imperfect feedback is reformulated into a Markov decision process (MDP) concerning ideal acknowledgments through the iterative processing of state information. Ultimately, we derive the optimal energy selection approach needed to maintain filtering performance by solving the finite horizon Bellman optimal dynamic equation. In our upcoming research, we intend to investigate and evaluate this matter within a more realistic context.