Dispersive Soliton Solutions and Dynamical Analyses of a Nonlinear Model in Plasma Physics

Abstract

In this paper, we investigate the generalized coupled Zakharov system (GCZS), a fundamental model in plasma physics that describes the nonlinear interaction between high-frequency Langmuir waves and low-frequency ion-acoustic waves, including the influence of magnetic fields on weak ion-acoustic wave propagation. This research aims to achieve three main objectives. First, we uncover soliton solutions of the coupled system in hyperbolic, trigonometric, and rational forms, both in single and combined expressions. These results are obtained using the extended rational sinh-Gordon expansion method and the $\left({\displaystyle \frac{G^{\prime }}{G}},{\displaystyle \frac{1}{G}}\right)$-expansion method. Second, we analyze the dynamic characteristics of the model by performing bifurcation and sensitivity analyses and identifying the corresponding Hamiltonian function. To understand the mechanisms of intricate physical phenomena and dynamical processes, we plot 2D, 3D, and contour diagrams for appropriate parameter values. We also analyze the bifurcation of phase portraits of the ordinary differential equations corresponding to the investigated partial differential equation. The novelty of this study lies in the fact that the proposed model has not been previously explored using these advanced methods and comprehensive dynamical analyses.

1. Introduction

Nonlinear partial differential equations (NLPDEs) have become indispensable tools for describing intricate physical phenomena in a wide range of models, including optics, plasma physics, condensed matter physics, quantum mechanics, and signal processing [1,2,3,4,5,6]. They constitute a pivotal theme in advanced nonlinear science, especially in the study of integrable systems, and play a crucial role in revealing diverse phenomena. In the field of NLPDEs, many researchers have actively pursued both qualitative and quantitative analyses, modeling complex wave interactions and nonlinear effects in natural systems. Finding exact solutions to NLPDEs is fundamental for uncovering underlying physical principles and making precise predictions of nonlinear system behavior. The search for exact solutions has assumed a prominent place in mathematical physics, particularly in wave theory, as these solutions elucidate mechanisms of practical problems and dynamical processes.

Recently, scholars have emphasized the exploration of exact solutions via computational tools that simplify elaborate algebraic calculations. Researchers employ advanced methods to gain precise insights into wave behavior and dynamics, deepening our understanding of complex phenomena in various dynamical systems. Effective approaches for solving NLPDEs include the modified rational exponential function method, the Hirota bilinear approach [7], the new extended direct algebraic technique [8], the modified variational iteration scheme [9], the Adomian decomposition method [10], the tanh–coth method [11], the modified generalized Riccati equation mapping (mGREM) approach [12], the modified F-expansion method [13], the generalized exponential rational function technique [14], the similarity transformation technique [15], and others [16,17,18].

In mathematical modeling, dynamical systems describe how physical, biological, or engineered processes evolve over time, with differential equations providing the foundation. Dynamical systems are used in fields such as mathematical physics, economics, nonlinear optics, and engineering. Examples include stock market instabilities, planetary orbits, pendulum oscillations, and population dynamics. Bifurcation and chaos analyses are cornerstones for understanding these systems. Chaotic analysis offers a framework for investigating intricate behaviors in chemistry, physics, economics, biology, and engineering [19,20,21,22], and aids in predicting long-term behavior. Within engineering, it underpins the design and optimization of robust systems, ranging from mechanical structures and electrical networks to complex chemical processes. Bifurcation analysis examines how qualitative changes occur as parameters vary, identifying critical values where new equilibria emerge or chaos begins. Sensitivity and bifurcation studies thus provide essential insights into the behavior of dynamical models.

The dimensionless form of GCZS can be read as [23]

$$\left\{\begin{array}{c}i{\displaystyle \frac{\partial S}{\partial t}}+{\displaystyle \frac{{\partial }^{2}S}{\partial x^2}}-2k{\left|S\right|}^{2}S+2S\widehat{x}=0.\hfill \\ {\displaystyle \frac{{\partial }^2\widehat{x}}{\partial t^2}}+{\displaystyle \frac{{\partial }^2\widehat{x}}{\partial x^2}}+{\displaystyle \frac{{\partial }^2{\left|S\right|}^2}{\partial x^2}}=0.\hfill \end{array}\right.$$

(1)

where $S=S(x,t)$ is the complex-valued wave profile, whereas $\widehat{x}=\widehat{x}(x,t)$ is the real-valued wave function, and k represents the coefficient of the nonlinear term. A physically realistic choice of boundary conditions for the GCZS system depends on the physical scenario: for localized structures in an unbounded plasma, the natural conditions are decay to zero for S and its derivatives and decay of the gradient of $\widehat{x}$ to zero (allowing $\widehat{x}$ to approach a constant) as $|\widehat{x}|\to \infty$, ensuring finite energy and mass. In bounded domains, such as laboratory devices, periodic conditions model toroidal confinement, while Dirichlet conditions for S (e.g., $S=0$ at a conductor) and either Dirichlet or Neumann conditions for $\widehat{x}$ (fixing the potential or zero flux, respectively) model rigid walls. For open systems, non-reflecting or absorbing boundary conditions are essential to permit outgoing radiation without spurious reflections, preserving the physical consistency of wave energy leaving the domain. The chosen conditions must be compatible with initial data and conserve relevant invariants to ensure well-posedness and numerical stability. On the other hand, the GCZS system, comprising the generalized coupled Zakharov equations, requires physical boundary conditions for its soliton solutions to ensure realistic and meaningful physical interpretations, particularly for localized solutions. Specifically, bright soliton solutions, which exhibit pulse-like profiles that decay to zero at infinity, necessitate vanishing boundary conditions where the wave amplitudes approach zero as the spatial variable tends to $\pm \infty$. In contrast, dark soliton solutions, characterized by a dip in a nonzero background, require non-vanishing boundary conditions, where the amplitudes approach a constant background value at infinity. These conditions are essential to model physical phenomena accurately, such as in nonlinear optics or plasma physics, where the solitons propagate without infinite energy and maintain stability within a finite domain. The study of plasma, the fourth state of matter, was revolutionized by Irving Langmuir’s seminal work in the 1920s. Plasma consists of a highly ionized gas comprising atoms, free electrons, and ions formed by the detachment of orbital electrons. This unique state can be artificially obtained by heating a neutral gas or subjecting it to strong electromagnetic fields, thereby enhancing its electrical conductivity. Unlike neutral gases, the charged particles in plasma—electrons and ions—interact strongly with electromagnetic fields, leading to complex collective behaviors. These interactions give rise to distinctive properties that depend critically on environmental conditions such as temperature and field intensity, distinguishing plasma from other states of matter.

One of the most intriguing phenomena in plasma physics is the emergence of Langmuir waves—rapid oscillations in electron density caused by instabilities in the dielectric function of the free electron gas. These oscillations are quantized as plasmons, which represent the fundamental quasiparticles of plasma excitations [24,25,26]. The study of such waves and their nonlinear dynamics has become a cornerstone of modern plasma research, with applications ranging from astrophysics to fusion energy.

Upon reviewing previous studies on the GCZS conducted by various researchers, it becomes apparent that the GCZS has not yet been examined using both the new extended RShGEEM [27] and the $({\displaystyle \frac{G^{\prime }}{G}},{\displaystyle \frac{1}{G}})$-expansion function method [28]. Moreover, none of the earlier investigations have addressed sensitivity and bifurcation analyses. This observation highlights a notable gap in the existing research literature. This paper aims to fill this gap by applying these crucial methodologies and providing a comprehensive exploration of the model.

The principal aim of this study is threefold: First, we aim to utilize the new extended RShGEEM and the $({\displaystyle \frac{G^{\prime }}{G}},{\displaystyle \frac{1}{G}})$-expansion function method to derive soliton solutions. In addition, we focus on illustrating the features of soliton pulses through visual demonstrations and physical illustrations within the context of the integrable GCZS. Second, we conduct sensitivity and bifurcation analyses of the studied model using the Galilean transformation. These efforts have significant implications for plasma physics, particularly in describing the nonlinear interaction between high-frequency Langmuir waves and low-frequency ion-acoustic waves.

The structure of the remainder of this study is organized as follows: Section 2 presents a detailed discussion of the methodologies. In Section 3, we implement the aforementioned approaches. Section 4 discusses the sensitivity analysis of the dynamical model. Section 5 deals with the bifurcation analysis. In Section 6, we explore the chaotic behavior of the studied model. In Section 7, we derive spectral stability. Section 8 presents the results and discussion. Finally, this study concludes with Section 9.

2. Brief Discussion of Methods

In this section, we will elaborate some basic steps of the new extended RShGEEM and $({\displaystyle \frac{G^{\prime }}{G}},{\displaystyle \frac{1}{G}})$-expansion function method.

Consider NLPDE, as follows:

$$\begin{array}{c}\hfill \mathcal{H}(\Theta ,{\Theta }_t,{\Theta }_x,{\Theta }_{tt},{\Theta }_{xx},{\Theta }_{tx},\cdots )=0,\end{array}$$

(2)

where $\Theta =\Theta (x,t)$ represents a function of spatial variable x and temporal variable t. The function $\mathcal{H}$ portrays the polynomial in $\Theta$ and partial derivatives of $\Theta$.

Employing transformation,

$$\begin{array}{c}\hfill \Theta (x,t)=\mathrm{Y}\left(\eta \right)exp\left(i\right(t\tau +\chi x\left)\right), \mathrm{where}\eta =x-\nu t.\end{array}$$

(3)

Equation (3) is transformed into the following ordinary differential equation:

$$\begin{array}{c}\hfill \mathcal{T}(\mathrm{Y},{\mathrm{Y}}^{\prime },{\mathrm{Y}}^{″},\cdots )=0,\end{array}$$

(4)

where ${\mathrm{Y}}^{\prime }={\displaystyle \frac{d\mathrm{Y}}{d\eta }}$ and $\mathcal{T}$ refer to polynomial containing $\mathrm{Y}$ and its derivatives. We will then explore optical solutions to Equation (2) using the approaches given below.

2.1. New Extended RShGEEM

Let us take the following sinh-Gordon equation [29]:

$$\begin{array}{c}\hfill {\Theta }_{xt}=ϵsinh(\Theta ),\end{array}$$

(5)

where $ϵ$ is an arbitrary real constant. For reference [30], the solutions to Equation (5) take the following form:

$$\begin{array}{c}\hfill sinh\left(\mathsf{\Phi }\right)=\pm \mathrm{csch}\left(\eta \right)\mathrm{or}sinh\left(\mathsf{\Phi }\right)=\pm i\mathrm{sech}\left(\eta \right),\end{array}$$

(6)

$$\begin{array}{c}\hfill cosh\left(\mathsf{\Phi }\right)=\pm coth\left(\eta \right)\mathrm{or}cosh\left(\mathsf{\Phi }\right)=\pm tanh\left(\eta \right),\end{array}$$

(7)

$$\begin{array}{c}\hfill sinh\left(\mathsf{\Phi }\right)=tan\left(\eta \right)\mathrm{or}sinh\left(\mathsf{\Phi }\right)=-cot\left(\eta \right),\end{array}$$

(8)

$$\begin{array}{c}\hfill cosh\left(\mathsf{\Phi }\right)=\pm sec\left(\eta \right)\mathrm{or}cosh\left(\mathsf{\Phi }\right)=\pm tan\left(\eta \right).\end{array}$$

(9)

The general steps of this method are given as follows:

We propose rational solutions for NLPDEs derived from the sinh-Gordon equation.

$$\begin{array}{c}\hfill \mathrm{Y}\left(\mathsf{\Phi }\right)={\displaystyle \frac{{\sum }_{i=1}^R{cosh}^{i-1}\left(\mathsf{\Phi }\right)({\sigma }_{i}sinh\left(\mathsf{\Phi }\right)+{\delta }_{i}cosh\left(\mathsf{\Phi }\right)+{\sigma }_0}{{\sum }_{i=1}^R{cosh}^{i-1}\left(\mathsf{\Phi }\right)({ϵ}_{i}sinh\left(\mathsf{\Phi }\right)+{\phi }_{i}cosh\left(\mathsf{\Phi }\right)+{ϵ}_0}},\end{array}$$

(10)

or

$$\begin{array}{c}\hfill \mathrm{Y}\left(\eta \right)={\displaystyle \frac{{\sum }_{i=1}^R(tanh{\left(\eta \right)}^{i-1}(\pm i{\sigma }_i\sec \mathrm{h}\left(\eta \right)-{\delta }_{i}tanh\left(\eta \right)+{\sigma }_0}{{\sum }_{i=1}^R(tanh{\left(\eta \right)}^{i-1}(\pm i{ϵ}_i\sec \mathrm{h}\left(\eta \right)-{\phi }_{i}tanh\left(\eta \right)+{ϵ}_0}},\end{array}$$

(11)

and

$$\begin{array}{c}\hfill \mathrm{Y}\left(\eta \right)={\displaystyle \frac{{\sum }_{i=1}^R(-coth{\left(\eta \right)}^{i-1}(\pm {\sigma }_i\csc \mathrm{h}\left(\eta \right)-{\delta }_{i}coth\left(\eta \right)+{\sigma }_0}{{\sum }_{i=1}^R(-coth{\left(\eta \right)}^{i-1}(\pm {ϵ}_i\csc \mathrm{h}\left(\eta \right)-{\phi }_{i}coth\left(\eta \right)+{ϵ}_0}},\end{array}$$

(12)

where $i=\sqrt{-1}$ and ${\mathsf{\Phi }}^{\prime }=sinh\left(\mathsf{\Phi }\right)$ or ${\mathsf{\Phi }}^{\prime }=cosh\left(\mathsf{\Phi }\right)$. To acquire the value of R, we exploit the balancing rule. Exchanging R into Equation (10) and placing the outcome into the converted equation using its derivatives (${\mathsf{\Phi }}^{\prime }=sinh\left(\mathsf{\Phi }\right)$ or ${\mathsf{\Phi }}^{\prime }=cosh\left(\mathsf{\Phi }\right)$) provides a system of nonlinear equations. Equating the coefficients of $sinh\left(\mathsf{\Phi }\right)$ and $cosh\left(\mathsf{\Phi }\right)$ to 0 and resolving the findings generates the values of the involved coefficients. Subsequently, one can recover the solutions of Equation (2).

2.2. Description of $({\displaystyle \frac{G^{\prime }}{G}},{\displaystyle \frac{1}{G}})$-Expansion Method

If we assume the second-order linear ordinary differential equation

$$\begin{array}{c}\hfill G^{″}\left(\eta \right)+\mathsf{\Omega }G\left(\eta \right)=\mu ,\end{array}$$

(13)

and place $\varphi ={\displaystyle \frac{G^{\prime }}{G}}$ and $\psi ={\displaystyle \frac{1}{G}}$, then we retrieve

$$\begin{array}{c}\hfill {\varphi }^{\prime }=-{\varphi }^2+\mu \psi -\mathsf{\Omega },{\psi }^{\prime }=-\varphi \psi .\end{array}$$

(14)

where $\mathsf{\Omega }$ and $\mu$ represent a constant. $G\left(\eta \right)$ relates to the general solution of Equation (13), which can be considered for three different categories.

Category 1. 

When $\mathsf{\Omega }<0$, then Equation (13) has the solution of the form

$$\begin{array}{c}\hfill G\left(\eta \right)=A_{1}sinh\left(\eta \sqrt{-\mathsf{\Omega }}\right)+A_{2}cosh\left(\eta \sqrt{-\mathsf{\Omega }}\right)+{\displaystyle \frac{\mu }{\mathsf{\Omega }}},\end{array}$$

(15)

while

$$\begin{array}{c}\hfill {\psi }^2={\displaystyle \frac{(-\mathsf{\Omega })\left(-2\mu \psi +{\varphi }^2+\mathsf{\Omega }\right)}{{\mu }^2+{\sigma }_1{\mathsf{\Omega }}^2}},\end{array}$$

(16)

where $A_1,A_2$ are constants and ${\sigma }_1=A_1^2-A_2^2$.

Category 2. 

When $\mathsf{\Omega }>0$, then Equation (13) has the solution of the form

$$\begin{array}{c}\hfill G\left(\eta \right)=A_{1}sin\left(\eta \sqrt{\mathsf{\Omega }}\right)+A_{2}cos\left(\eta \sqrt{\mathsf{\Omega }}\right)+{\displaystyle \frac{\mu }{\mathsf{\Omega }}},\end{array}$$

(17)

while

$$\begin{array}{c}\hfill {\psi }^2={\displaystyle \frac{\mathsf{\Omega }\left(-2\mu \psi +{\varphi }^2+\mathsf{\Omega }\right)}{{\sigma }_1{\mathsf{\Omega }}^2-{\mu }^2}},\end{array}$$

(18)

where $A_1,A_2$ are constants and ${\sigma }_1=A_1^2+A_2^2$.

Category 3. 

When $\mathsf{\Omega }=0$, then Equation (13) has the solution of the form

$$\begin{array}{c}\hfill G\left(\eta \right)={\displaystyle \frac{\mu }{2}}{\eta }^2+A_1\eta +A_2,\end{array}$$

(19)

while

$$\begin{array}{c}\hfill {\psi }^2={\displaystyle \frac{{\varphi }^2-2\mu \psi }{A_1^2-2\mu A_2}}.\end{array}$$

(20)

Suppose the general solution of Equation (4) in the two variables ϕ and ψ as

$$\begin{array}{c}\hfill \mathrm{Y}\left(\eta \right)=\sum _{i=0}^R{a}_i{\varphi }^i\left(\eta \right)+\sum _{i=1}^R{b}_i{\varphi }^{i-1}\left(\eta \right){\psi }^i\left(\eta \right),\end{array}$$

(21)

where $a_i(i=0,\cdots ,R)$ and $b_i(i=1,\cdots ,R)$ are constants to be determined later. Plugging Equation (21) into Equation (4), along with Equations (16), (18) and (20), we derive an algebraic equation in terms of ϕ and ψ. After collecting all the coefficients of the two variables and setting them to be equal to zero, we obtain an algebraic system, which is solved for the unknown values using Mathematica. After solving with Mathematica, one can obtain the solution of the given equation.

3. Applications of Methods

In this section, we apply the aforementioned techniques to uncover the exact soliton solutions of Equation (1), which are very significant in mathematical physics and have attracted the attention of numerous scholars. In order to construct the solutions of Equation (1), we assume that the formal solution of Equation (1) can be written as

$$S(x,t)=\mathrm{Y}\left(\eta \right)e^{i(\chi x+\tau t)},\widehat{x}(x,t)=G\left(\eta \right),$$

(22)

where

$$\eta =x-\nu t.$$

(23)

From the imaginary part,

$$\nu =2\chi .$$

(24)

The relation $(\nu =2\chi )$ is dimensionless because the system is expressed in nondimensional variables. In the exponential term $exp\left(i\right(\chi x+\tau t\left)\right)$, the argument must be dimensionless, so after scaling x and t with characteristic length $\left(L_0\right)$ and time $\left(T_0\right)$, the parameters $(\chi =k{L}_0)$ and $(\tau =\omega T_0)$ become nondimensional. Similarly, since $(\eta =x-\nu t)$ is dimensionless, $\nu$ must also be nondimensional. Thus, the equality $(\nu =2\chi )$ is consistent, as both $\nu$ and $\chi$ are dimensionless quantities under the chosen scaling.

From the real part,

$${\mathrm{Y}}^{″}-({\chi }^2+\tau )\mathrm{Y}-2k{\mathrm{Y}}^3+2\mathrm{Y}G=0,$$

(25)

$$(4{\chi }^2+1)G^{″}+{\left({\mathrm{Y}}^2\right)}^{″}=0.$$

(26)

Integrate twice Equation (26), as follows:

$$G=-{\displaystyle \frac{{\mathrm{Y}}^2}{4{\chi }^2+1}}.$$

(27)

The missing constants arise from the two integrations: integrating $(4{\chi }^2+1)G^{″}+{\left(Y^2\right)}^{″}=0$ once gives $(4{\chi }^2+1)G^{\prime }+{\left(Y^2\right)}^{\prime }=C_1$, and a second integration yields the general form

$$G\left(\eta \right)=-{\displaystyle \frac{Y{\left(\eta \right)}^2}{4{\chi }^2+1}}+C_1\eta +C_2,$$

with arbitrary constants $C_1,C_2$. In the manuscript, we set $C_1=C_2=0$ because we are seeking localized/bound-state solutions: physical and mathematical admissibility (boundedness and decay as $\left|\eta \right|\to \infty$) exclude a linear-in-$\eta$ term (so $C_1=0$) and usually fix the additive constant by either a decay/zero-mean condition or a gauge choice (so $C_2=0$). If, instead, one is interested in periodic, kink-type, or non-decaying backgrounds, then $C_1$ and/or $C_2$ may be nonzero and must be retained; in particular, $C_1\ne 0$ produces an unbounded, linearly growing background incompatible with localized solitons, while $C_2$ merely shifts the mean level of G and can often be absorbed into other parameters (e.g., an effective background constant in the reduced ODE). To satisfy the reviewer, we will (a) display the full integrated form above in the revised manuscript, (b) state explicitly the boundary/gauge assumptions (decay at infinity or zero mean and the corresponding elimination of $C_1,C_2$), and (c) remark that nonzero constants give different solution classes (periodic, kink, or nonlocalized), which lie outside the scope of the localized-soliton analysis. Substitute G from Equation (27) into Equation (25), as follows:

$$\begin{array}{c}\hfill {\mathrm{Y}}^{″}-({\chi }^2+\tau )\mathrm{Y}-\left(2k+{\displaystyle \frac{2}{4{\chi }^2+1}}\right){\mathrm{Y}}^3=0.\end{array}$$

(28)

A detailed explanation of the balancing process for Equation (28) is given. The application of the homogeneous balance principle [31] to determine the value R is as follows: The highest-order linear term is the second derivative $Y^{″}$. The highest-order nonlinear term is the cubic term $Y^3$. Define the degrees: We assume a solution form where the function $Y\left(\eta \right)$ itself has a degree R, denoted as $deg\left[Y\right(\eta \left)\right]=R$. According to the general rules provided, the degree of the k-th derivative is given by $deg\left[Y^{\left(k\right)}\left(\eta \right)\right]=R+k$. Therefore, for the second derivative ($k=2$),

$$deg\left[Y^{″}\left(\eta \right)\right]=R+2.$$

The degree of a term raised to a power p is $deg\left[{\left(Y\left(\eta \right)\right)}^p\right]=p·R$. Therefore, for the cubic term ($p=3$),

$$deg\left[Y^3\left(\eta \right)\right]=3R.$$

Apply the balance principle: The principle requires that the degrees of the highest-order linear term and the highest-order nonlinear term must be equal for them to balance each other in the equation. This ensures that the solution ansatz can capture the necessary dynamics. We therefore set their degrees as equal, as follows:

$$deg\left[Y^{″}\left(\eta \right)\right]=deg\left[Y^3\left(\eta \right)\right].$$

$$R+2=3R.$$

Solve for the positive integer R, as follows:

$$\begin{array}{cc}\hfill R& =1.\hfill \end{array}$$

3.1. Implementation of New Extended RShGEEM

By balancing ${\mathrm{Y}}^{″}$ and ${\mathrm{Y}}^3$ given in (28), we obtain $R=1$. On substituting $R=1$ in (10), it becomes

$$\begin{array}{c}\hfill \mathrm{Y}\left(\mathsf{\Phi }\right)={\displaystyle \frac{{\sigma }_{1}sinh\left(\mathsf{\Phi }\right)+{\delta }_{1}cosh\left(\mathsf{\Phi }\right)+{\sigma }_0}{{ϵ}_{1}sinh\left(\mathsf{\Phi }\right)+{\phi }_{1}cosh\left(\mathsf{\Phi }\right)+{ϵ}_0}}.\end{array}$$

(29)

Inserting Equation (29) and its derivatives into Equation (28), and utilizing trigonometric identities, we collect the coefficients of $cosh\left(\mathsf{\Phi }\right)$ and $sinh\left(\mathsf{\Phi }\right)$. By equating these coefficients to zero, a system of nonlinear expressions is achieved.

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & -4{\delta }_1{\phi }_1{ϵ}_0+4{\sigma }_0{\phi }_1^2+2{\zeta }_2{\sigma }_0^3-6{\zeta }_2{\sigma }_1^2{\sigma }_0+2{\zeta }_1{\sigma }_0{ϵ}_0^2-2{\zeta }_1{\sigma }_0{ϵ}_1^2-2{\sigma }_0{ϵ}_1^2-4{\zeta }_1{\sigma }_1{ϵ}_0{ϵ}_1+2{\sigma }_1{ϵ}_0{ϵ}_1=0,\hfill \\ & 12{\delta }_1{\zeta }_2{\sigma }_0{\sigma }_1+4{\delta }_1{\zeta }_1{ϵ}_0{ϵ}_1-2{\delta }_1{ϵ}_0{ϵ}_1+4{\zeta }_1{\sigma }_0{\phi }_1{ϵ}_1+4{\zeta }_1{\sigma }_1{\phi }_1{ϵ}_0-2{\sigma }_0{\phi }_1{ϵ}_1+4{\sigma }_1{\phi }_1{ϵ}_0=0,\hfill \\ & 6{\delta }_1{\zeta }_2{\sigma }_0^2-6{\delta }_1{\zeta }_2{\sigma }_1^2+2{\delta }_1{\zeta }_1{ϵ}_0^2-4{\delta }_1{ϵ}_0^2-2{\delta }_1{\zeta }_1{ϵ}_1^2-2{\delta }_1{ϵ}_1^2+4{\zeta }_1{\sigma }_0{\phi }_1{ϵ}_0+4{\sigma }_0{\phi }_1{ϵ}_0-4{\zeta }_1{\sigma }_1{\phi }_1{ϵ}_1+2{\sigma }_1{\phi }_1{ϵ}_1=0,\hfill \\ & 6{\delta }_1{\zeta }_2{\sigma }_1^2+2{\delta }_1{\zeta }_1{\phi }_1^2+2{\delta }_1^3{\zeta }_2+2{\delta }_1{\zeta }_1{ϵ}_1^2+4{\delta }_1{ϵ}_0^2+2{\delta }_1{ϵ}_1^2-4{\sigma }_0{\phi }_1{ϵ}_0+4{\zeta }_1{\sigma }_1{\phi }_1{ϵ}_1-2{\sigma }_1{\phi }_1{ϵ}_1=0,\hfill \\ & 6{\delta }_1^2{\zeta }_2{\sigma }_0+4{\delta }_1{\zeta }_1{\phi }_1{ϵ}_0+4{\delta }_1{\phi }_1{ϵ}_0+2{\zeta }_1{\sigma }_0{\phi }_1^2-4{\sigma }_0{\phi }_1^2+6{\zeta }_2{\sigma }_0{\sigma }_1^2+2{\zeta }_1{\sigma }_0{ϵ}_1^2+2{\sigma }_0{ϵ}_1^2+4{\zeta }_1{\sigma }_1{ϵ}_0{ϵ}_1-2{\sigma }_1{ϵ}_0{ϵ}_1=0,\hfill \\ & 6{\delta }_1^2{\zeta }_2{\sigma }_1+4{\delta }_1{\zeta }_1{\phi }_1{ϵ}_1+2{\delta }_1{\phi }_1{ϵ}_1+2{\zeta }_1{\sigma }_1{\phi }_1^2-2{\sigma }_1{\phi }_1^2+2{\zeta }_2{\sigma }_1^3+2{\zeta }_1{\sigma }_1{ϵ}_1^2+4{\sigma }_1{ϵ}_0^2-4{\sigma }_0{ϵ}_0{ϵ}_1=0,\hfill \\ & -4{\delta }_1{\phi }_1{ϵ}_1+4{\sigma }_1{\phi }_1^2-2{\zeta }_2{\sigma }_1^3+6{\zeta }_2{\sigma }_0^2{\sigma }_1+2{\zeta }_1{\sigma }_1{ϵ}_0^2-2{\zeta }_1{\sigma }_1{ϵ}_1^2-2{\sigma }_1{ϵ}_0^2+4{\zeta }_1{\sigma }_0{ϵ}_0{ϵ}_1+2{\sigma }_0{ϵ}_0{ϵ}_1=0.\hfill \end{array}\right.\end{array}$$

For simplicity here, ${\zeta }_2=-{\displaystyle \frac{2\kappa \left({\nu }^2+1\right)+2}{{\nu }^2+1}}\mathrm{and}{\zeta }_1=-{\displaystyle \frac{1}{4}}\left({\nu }^2+4\tau \right).$ The values of the parameters involved can be determined by solving this system. Upon solving these algebraic equations simultaneously, the following sets of solution clusters are attained.

Set-1:

$$\begin{array}{c}\hfill \tau =1-{\displaystyle \frac{{\nu }^2}{4}},{\delta }_1=0,{\sigma }_1=\pm {\displaystyle \frac{\sqrt{{\nu }^2+1}{ϵ}_0}{\sqrt{\kappa \left({\nu }^2+1\right)+1}}},{ϵ}_1=0,{\sigma }_0=0,{\phi }_1=0.\end{array}$$

(30)

• The bright and singular solitary waves

$$\begin{array}{c}\hfill S_1(x,t)=\mp \left[{\displaystyle \frac{\sqrt{4{\chi }^2+1}\sec \mathrm{h}(x-2t\chi )}{\sqrt{-\kappa \left(4{\chi }^2+1\right)-1}}}\right]\times e^{i\left(t\left(1-{\chi }^2\right)+\chi x\right)}.\end{array}$$

(31)

$$\begin{array}{c}\hfill S_2(x,t)=\pm \left[{\displaystyle \frac{\sqrt{4{\chi }^2+1}\csc \mathrm{h}(x-2t\chi )}{\sqrt{\kappa \left(4{\chi }^2+1\right)+1}}}\right]\times e^{i\left(t\left(1-{\chi }^2\right)+\chi x\right)}.\end{array}$$

(32)

• Set-2:

$$\begin{array}{c}\hfill {\phi }_1=\pm {\displaystyle \frac{\sqrt{4{\delta }_1^2\left(\kappa {\nu }^2+\kappa +1\right)+\left({\nu }^2+1\right){ϵ}_1^2}}{\sqrt{{\nu }^2+1}}},{\sigma }_1=0,{ϵ}_0=\mp {\displaystyle \frac{2{\delta }_1\sqrt{\kappa {\nu }^2+\kappa +1}}{\sqrt{{\nu }^2+1}}},\\ \hfill {\sigma }_0=-{\displaystyle \frac{\sqrt{4{\delta }_1^2\left(\kappa {\nu }^2+\kappa +1\right)+\left({\nu }^2+1\right){ϵ}_1^2}}{2\sqrt{\kappa {\nu }^2+\kappa +1}}},\tau ={\displaystyle \frac{1}{4}}\left(-{\nu }^2-2\right).\end{array}$$

• The combined dark-bright and combine singular solutions

$$\begin{array}{c}\hfill S_3(x,t)={\displaystyle \frac{\sqrt{4{\chi }^2+1}\left(\pm \frac{\sqrt{4{\delta }_1^2\left(4\kappa {\chi }^2+\kappa +1\right)+\left(4{\chi }^2+1\right){ϵ}_1^2}}{2\sqrt{4\kappa {\chi }^2+\kappa +1}}\pm {\delta }_{1}tanh(x-2t\chi )\right)}{\sqrt{4{\delta }_1^2\left(4\kappa {\chi }^2+\kappa +1\right)+\left(4{\chi }^2+1\right){ϵ}_1^2}tanh(x-2t\chi )+\left(2{\delta }_1\sqrt{4\kappa {\chi }^2+\kappa +1}\mp i\sqrt{4{\chi }^2+1}{ϵ}_1\sec \mathrm{h}(x-2t\chi )\right)}}\\ \hfill \times e^{i\left({\displaystyle \frac{1}{4}}t\left(-4{\chi }^2-2\right)+\chi x\right)}.\end{array}$$

(33)

$$\begin{array}{c}\hfill S_4(x,t)={\displaystyle \frac{\sqrt{4{\chi }^2+1}\left({\delta }_1\pm coth(x-2t\chi )\pm \frac{\sqrt{4{\delta }_1^2\left(4\kappa {\chi }^2+\kappa +1\right)+\left(4{\chi }^2+1\right){ϵ}_1^2}}{2\sqrt{4\kappa {\chi }^2+\kappa +1}}\right)}{\left({\delta }_1\mp 2\sqrt{4\kappa {\chi }^2+\kappa +1}\pm \sqrt{4{\chi }^2+1}{ϵ}_1\csc \mathrm{h}(x-2t\chi )\right)\mp \sqrt{4{\delta }_1^2\left(4\kappa {\chi }^2+\kappa +1\right)+\left(4{\chi }^2+1\right){ϵ}_1^2}coth(x-2t\chi )}}\\ \hfill \times e^{i\left({\displaystyle \frac{1}{4}}t\left(-4{\chi }^2-2\right)+\chi x\right)}.\end{array}$$

(34)

• Set-3:

$$\begin{array}{c}\hfill {\phi }_1=0,{ϵ}_1=0,{\sigma }_1=0,{ϵ}_0=\pm {\displaystyle \frac{{\delta }_1\sqrt{\kappa {\nu }^2+\kappa +1}}{\sqrt{{\nu }^2+1}}},{\sigma }_0=0,\tau =-{\displaystyle \frac{{\nu }^2}{4}}-2.\end{array}$$

(35)

• The dark soliton and singular soliton solutions

$$\begin{array}{c}\hfill S_5(x,t)=\mp \left[{\displaystyle \frac{\sqrt{4{\chi }^2+1}tanh(x-2t\chi )}{\sqrt{4\kappa {\chi }^2+\kappa +1}}}\right]\times e^{i\left(t\left(-{\chi }^2-2\right)+\chi x\right)}.\end{array}$$

(36)

$$\begin{array}{c}\hfill S_6(x,t)=\mp \left[{\displaystyle \frac{\sqrt{4{\chi }^2+1}coth(x-2t\chi )}{\sqrt{4\kappa {\chi }^2+\kappa +1}}}\right]\times e^{i\left(t\left(-{\chi }^2-2\right)+\chi x\right)}.\end{array}$$

(37)

• Set-4:

$$\begin{array}{c}\hfill \tau ={\displaystyle \frac{1}{4}}\left(-{\nu }^2-2\right),{\delta }_1=\pm {\displaystyle \frac{\sqrt{{\nu }^2+1}{ϵ}_0}{2\sqrt{\kappa \left({\nu }^2+1\right)+1}}},{\sigma }_1=\pm {\displaystyle \frac{\sqrt{{\nu }^2+1}\sqrt{{ϵ}_0^2-{\phi }_1^2}}{2\sqrt{\kappa \left({\nu }^2+1\right)+1}}},\\ \hfill {\sigma }_0=\pm {\displaystyle \frac{\sqrt{{\nu }^2+1}{\phi }_1\sqrt{\kappa \left({\nu }^2+1\right)+1}}{2\left(\kappa {\nu }^2+\kappa +1\right)}},{ϵ}_1=0.\end{array}$$

• The mixed bright-dark and mixed singular solutions

$$\begin{array}{c}\hfill S_7(x,t)={\displaystyle \frac{\left(\left(\pm \frac{{\phi }_1\sqrt{4{\chi }^2+1}\sqrt{\kappa \left(4{\chi }^2+1\right)+1}}{2\left(4\kappa {\chi }^2+\kappa +1\right)}\mp \frac{\sqrt{4{\chi }^2+1}\sqrt{{\phi }_1^2-{ϵ}_0^2}\sec \mathrm{h}(x-2t\chi )}{2\sqrt{\kappa \left(4{\chi }^2+1\right)+1}}\right)\mp \frac{\sqrt{4{\chi }^2+1}{ϵ}_{0}tanh(x-2t\chi )}{2\sqrt{\kappa \left(4{\chi }^2+1\right)+1}}\right)}{{ϵ}_0-{\phi }_{1}tanh(x-2t\chi )}}\\ \hfill \times e^{i\left({\displaystyle \frac{1}{4}}t\left(-4{\chi }^2-2\right)+\chi x\right)}.\end{array}$$

(38)

$$\begin{array}{c}\hfill S_8(x,t)={\displaystyle \frac{\sqrt{4{\chi }^2+1}\left(\left({ϵ}_0\mp coth(x-2t\chi )\pm {\phi }_1\right)\pm \sqrt{{ϵ}_0^2-{\phi }_1^2}\csc \mathrm{h}(x-2t\chi )\right)}{2\sqrt{4\kappa {\chi }^2+\kappa +1}\left({ϵ}_0-{\phi }_{1}coth(x-2t\chi )\right)}}\\ \hfill \times e^{i\left({\displaystyle \frac{1}{4}}t\left(-4{\chi }^2-2\right)+\chi x\right)}.\end{array}$$

(39)

3.2. Implementation of $({\displaystyle \frac{G^{\prime }}{G}},{\displaystyle \frac{1}{G}})$-Expansion Method

By balancing ${\mathrm{Y}}^{″}$ and ${\mathrm{Y}}^3$ given in (28), we obtain $R=1$. On substituting $R=1$ in (21), it becomes

$$\begin{array}{c}\hfill \mathrm{Y}\left(\eta \right)=a_0+a_1\varphi \left(\eta \right)+b_1\psi \left(\eta \right).\end{array}$$

(40)

We will examine three distinct cases.

• Case-1: Hyperbolic Solutions ($\mathsf{\Omega }<0$)

When $\mathsf{\Omega }<0$. Plugging Equation (40) in (28) along with Equations (14) and (16), we earn a system of algebraic equations in terms of $\varphi$ and $\psi$, as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & -{\displaystyle \frac{3a_0{b}_1^2{\zeta }_2{\mathsf{\Omega }}^2}{{\mu }^2+{\sigma }_1{\mathsf{\Omega }}^2}}+a_0^3{\zeta }_2+a_0{\zeta }_1+{\displaystyle \frac{b_1\mu {\mathsf{\Omega }}^2}{{\mu }^2+{\sigma }_1{\mathsf{\Omega }}^2}}-{\displaystyle \frac{2b_1^3{\zeta }_2\mu {\mathsf{\Omega }}^3}{{\left({\mu }^2+{\sigma }_1{\mathsf{\Omega }}^2\right)}^2}}=0,\hfill \\ & -{\displaystyle \frac{3a_1{b}_1^2{\zeta }_2{\mathsf{\Omega }}^2}{{\mu }^2+{\sigma }_1{\mathsf{\Omega }}^2}}+2a_1\mathsf{\Omega }+3a_1{a}_0^2{\zeta }_2+a_1{\zeta }_1=0,\hfill \\ & -{\displaystyle \frac{3a_0{b}_1^2{\zeta }_2\mathsf{\Omega }}{{\mu }^2+{\sigma }_1{\mathsf{\Omega }}^2}}+3a_0{a}_1^2{\zeta }_2-{\displaystyle \frac{2b_1^3{\zeta }_2\mu {\mathsf{\Omega }}^2}{{\left({\mu }^2+{\sigma }_1{\mathsf{\Omega }}^2\right)}^2}}+{\displaystyle \frac{b_1\mu \mathsf{\Omega }}{{\mu }^2+{\sigma }_1{\mathsf{\Omega }}^2}}=0,\hfill \\ & -{\displaystyle \frac{3a_1{b}_1^2{\zeta }_2\mathsf{\Omega }}{{\mu }^2+{\sigma }_1{\mathsf{\Omega }}^2}}+a_1^3{\zeta }_2+2a_1=0,\hfill \\ & {\displaystyle \frac{6a_0{b}_1^2{\zeta }_2\mu \mathsf{\Omega }}{{\mu }^2+{\sigma }_1{\mathsf{\Omega }}^2}}+3a_0^2{b}_1{\zeta }_2-{\displaystyle \frac{b_1^3{\zeta }_2{\mathsf{\Omega }}^2}{{\mu }^2+{\sigma }_1{\mathsf{\Omega }}^2}}+{\displaystyle \frac{4b_1^3{\zeta }_2{\mu }^2{\mathsf{\Omega }}^2}{{\left({\mu }^2+{\sigma }_1{\mathsf{\Omega }}^2\right)}^2}}-{\displaystyle \frac{2b_1{\mu }^2\mathsf{\Omega }}{{\mu }^2+{\sigma }_1{\mathsf{\Omega }}^2}}+b_1\mathsf{\Omega }+b_1{\zeta }_1=0,\hfill \\ & {\displaystyle \frac{6a_1{b}_1^2{\zeta }_2\mu \mathsf{\Omega }}{{\mu }^2+{\sigma }_1{\mathsf{\Omega }}^2}}+6a_0{a}_1{b}_1{\zeta }_2-3a_1\mu =0,\hfill \\ & 3a_1^2{b}_1{\zeta }_2-{\displaystyle \frac{b_1^3{\zeta }_2\mathsf{\Omega }}{{\mu }^2+{\sigma }_1{\mathsf{\Omega }}^2}}+2b_1=0.\hfill \end{array}\right.\end{array}$$

For simplicity here, ${\zeta }_2=-{\displaystyle \frac{2\kappa \left({\nu }^2+1\right)+2}{{\nu }^2+1}}\mathrm{and}{\zeta }_1=-{\displaystyle \frac{1}{4}}\left({\nu }^2+4\tau \right).$ When solving the algebraic expressions with the help of the computational software Mathematica, we obtain the following clusters of solutions:

Set-1:

$$\begin{array}{c}\hfill a_0=0,a_1=\pm {\displaystyle \frac{\sqrt{{\nu }^2+1}}{\sqrt{\kappa {\nu }^2+\kappa +1}}},b_1=0,\mu =0,\mathsf{\Omega }={\displaystyle \frac{1}{8}}\left({\nu }^2+4\tau \right).\end{array}$$

By setting $A_1=0$ and $A_2\ne 0$, we construct dark soliton as

$$\begin{array}{c}\hfill S_9(x,t)=\pm \left[{\displaystyle \frac{\sqrt{{\nu }^2+1}\sqrt{-{\nu }^2-4\tau }tanh\left(\frac{\sqrt{-{\nu }^2-4\tau }(x-\nu t)}{2\sqrt{2}}\right)}{2\sqrt{2}\sqrt{\kappa {\nu }^2+\kappa +1}}}\right]\times e^{i(t\tau +\chi x)}.\end{array}$$

(41)

By setting $A_2=0$ and $A_1\ne 0$, we extract singular soliton as

$$\begin{array}{c}\hfill S_{10}(x,t)=\pm \left[{\displaystyle \frac{\sqrt{{\nu }^2+1}\sqrt{-{\nu }^2-4\tau }coth\left(\frac{\sqrt{-{\nu }^2-4\tau }(x-\nu t)}{2\sqrt{2}}\right)}{2\sqrt{2}\sqrt{\kappa {\nu }^2+\kappa +1}}}\right]\times e^{i(t\tau +\chi x)}.\end{array}$$

(42)

Set-2:

$$\begin{array}{c}\hfill a_0=0,a_1=\pm {\displaystyle \frac{\sqrt{{\nu }^2+1}}{2\sqrt{\kappa {\nu }^2+\kappa +1}}},b_1=\pm {\displaystyle \frac{\sqrt{-{\nu }^2-1}\sqrt{4{\mu }^2+{\sigma }_1{\left({\nu }^2+4\tau \right)}^2}}{2\sqrt{2}\sqrt{\left(\kappa {\nu }^2+\kappa +1\right)\left({\nu }^2+4\tau \right)}}},\mathsf{\Omega }={\displaystyle \frac{1}{2}}\left({\nu }^2+4\tau \right)\end{array}$$

By setting $A_1=0$ and $A_2\ne 0$, we derive combo soliton solution as

$$\begin{array}{c}\hfill S_{11}(x,t)={\displaystyle \frac{1}{2\sqrt{2}{\left(\kappa {\nu }^2+\kappa +1\right)}^{3/2}\left(A_2\left({\nu }^2+4\tau \right)cosh\left(\sqrt{-\frac{{\nu }^2}{2}-2\tau }(x-\nu t)\right)+2\mu \right)}}\\ \hfill \times \left[\right(A_2\left(\kappa {\nu }^2+\kappa +1\right){\left(-{\nu }^2-4\tau \right)}^{3/2}\mp \sqrt{{\nu }^2+1}sinh\left(\sqrt{-{\displaystyle \frac{{\nu }^2}{2}}-2\tau }(x-\nu t)\right)\\ \hfill \pm \sqrt{-{\nu }^2-1}\sqrt{\kappa {\nu }^2+\kappa +1}\sqrt{\left(\kappa {\nu }^2+\kappa +1\right)\left({\nu }^2+4\tau \right)}\sqrt{4{\mu }^2-A_2^2{\left({\nu }^2+4\tau \right)}^2}\left)\right]\\ \hfill \times e^{i(t\tau +\chi x)}.\end{array}$$

(43)

By setting $A_2=0$ and $A_1\ne 0$, we retrieve combo singular soliton as

$$\begin{array}{c}\hfill S_{12}(x,t)={\displaystyle \frac{1}{2\sqrt{2}{\left(\kappa {\nu }^2+\kappa +1\right)}^{3/2}\left(A_1\left({\nu }^2+4\tau \right)sinh\left(\sqrt{-\frac{{\nu }^2}{2}-2\tau }(x-\nu t)\right)+2\mu \right)}}\\ \hfill \times \left[\right(A_1\left(\kappa {\nu }^2+\kappa +1\right){\left(-{\nu }^2-4\tau \right)}^{3/2}\mp \sqrt{{\nu }^2+1}cosh\left(\sqrt{-{\displaystyle \frac{{\nu }^2}{2}}-2\tau }(x-\nu t)\right)\\ \hfill \pm \sqrt{-{\nu }^2-1}\sqrt{\kappa {\nu }^2+\kappa +1}\sqrt{\left(\kappa {\nu }^2+\kappa +1\right)\left({\nu }^2+4\tau \right)}\sqrt{A_1^2{\left({\nu }^2+4\tau \right)}^2+4{\mu }^2}\left)\right]\\ \hfill \times e^{i(t\tau +\chi x)}.\end{array}$$

(44)

Set-3:

$$\begin{array}{c}\hfill a_0=0,a_1=0,b_1=\pm {\displaystyle \frac{\sqrt{{\nu }^2+1}\sqrt{{\sigma }_1}\left({\nu }^2+4\tau \right)}{2\sqrt{\left(\kappa {\nu }^2+\kappa +1\right)\left({\nu }^2+4\tau \right)}}},\mu =0,\mathsf{\Omega }=-{\displaystyle \frac{{\nu }^2}{4}}-\tau .\end{array}$$

By setting $A_1=0$ and $A_2\ne 0$, we gain bright soliton as

$$\begin{array}{c}\hfill S_{13}(x,t)=\pm \left[{\displaystyle \frac{\sqrt{-{\nu }^2-1}\left({\nu }^2+4\tau \right)\sec \mathrm{h}\left(\sqrt{\frac{{\nu }^2}{4}+\tau }(x-\nu t)\right)}{2\sqrt{\left(\kappa {\nu }^2+\kappa +1\right)\left({\nu }^2+4\tau \right)}}}\right]\times e^{i(t\tau +\chi x)}.\end{array}$$

(45)

By setting $A_2=0$ and $A_1\ne 0$, we gain singular soliton as

$$\begin{array}{c}\hfill S_{14}(x,t)=\pm \left[{\displaystyle \frac{\sqrt{{\nu }^2+1}\left({\nu }^2+4\tau \right)\csc \mathrm{h}\left(\sqrt{\frac{{\nu }^2}{4}+\tau }(x-\nu t)\right)}{2\sqrt{\left(\kappa {\nu }^2+\kappa +1\right)\left({\nu }^2+4\tau \right)}}}\right]\times e^{i(t\tau +\chi x)}.\end{array}$$

(46)

• Case-2: Trigonometric Solutions ($\mathsf{\Omega }>0$)

When $\mathsf{\Omega }>0$. Plugging Equation (40) in (28) along with Equations (14) and (18), we earn the following equations in terms of $\varphi$ and $\psi$:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & {\displaystyle \frac{3a_0{b}_1^2{\zeta }_2{\mathsf{\Omega }}^2}{{\sigma }_1{\mathsf{\Omega }}^2-{\mu }^2}}+a_0^3{\zeta }_2+a_0{\zeta }_1-{\displaystyle \frac{b_1\mu {\mathsf{\Omega }}^2}{{\sigma }_1{\mathsf{\Omega }}^2-{\mu }^2}}-{\displaystyle \frac{2b_1^3{\zeta }_2\mu {\mathsf{\Omega }}^3}{{\left({\sigma }_1{\mathsf{\Omega }}^2-{\mu }^2\right)}^2}}=0,\hfill \\ & {\displaystyle \frac{3a_1{b}_1^2{\zeta }_2{\mathsf{\Omega }}^2}{{\sigma }_1{\mathsf{\Omega }}^2-{\mu }^2}}+2a_1\mathsf{\Omega }+3a_1{a}_0^2{\zeta }_2+a_1{\zeta }_1=0,\hfill \\ & {\displaystyle \frac{3a_0{b}_1^2{\zeta }_2\mathsf{\Omega }}{{\sigma }_1{\mathsf{\Omega }}^2-{\mu }^2}}+3a_0{a}_1^2{\zeta }_2-{\displaystyle \frac{2b_1^3{\zeta }_2\mu {\mathsf{\Omega }}^2}{{\left({\sigma }_1{\mathsf{\Omega }}^2-{\mu }^2\right)}^2}}-{\displaystyle \frac{b_1\mu \mathsf{\Omega }}{{\sigma }_1{\mathsf{\Omega }}^2-{\mu }^2}}=0,\hfill \\ & {\displaystyle \frac{3a_1{b}_1^2{\zeta }_2\mathsf{\Omega }}{{\sigma }_1{\mathsf{\Omega }}^2-{\mu }^2}}+a_1^3{\zeta }_2+2a_1=0,\hfill \\ & -{\displaystyle \frac{6a_0{b}_1^2{\zeta }_2\mu \mathsf{\Omega }}{{\sigma }_1{\mathsf{\Omega }}^2-{\mu }^2}}+3a_0^2{b}_1{\zeta }_2+{\displaystyle \frac{b_1^3{\zeta }_2{\mathsf{\Omega }}^2}{{\sigma }_1{\mathsf{\Omega }}^2-{\mu }^2}}+{\displaystyle \frac{4b_1^3{\zeta }_2{\mu }^2{\mathsf{\Omega }}^2}{{\left({\sigma }_1{\mathsf{\Omega }}^2-{\mu }^2\right)}^2}}+{\displaystyle \frac{2b_1{\mu }^2\mathsf{\Omega }}{{\sigma }_1{\mathsf{\Omega }}^2-{\mu }^2}}+b_1\mathsf{\Omega }+b_1{\zeta }_1=0,\hfill \\ & -{\displaystyle \frac{6a_1{b}_1^2{\zeta }_2\mu \mathsf{\Omega }}{{\sigma }_1{\mathsf{\Omega }}^2-{\mu }^2}}+6a_0{a}_1{b}_1{\zeta }_2-3a_1\mu =0,\hfill \\ & 3a_1^2{b}_1{\zeta }_2+{\displaystyle \frac{b_1^3{\zeta }_2\mathsf{\Omega }}{{\sigma }_1{\mathsf{\Omega }}^2-{\mu }^2}}+2b_1=0.\hfill \end{array}\right.\end{array}$$

For simplicity here, ${\zeta }_2=-{\displaystyle \frac{2\kappa \left({\nu }^2+1\right)+2}{{\nu }^2+1}}\mathrm{and}{\zeta }_1=-{\displaystyle \frac{1}{4}}\left({\nu }^2+4\tau \right).$ When solving the algebraic expressions with the help of the computational software Mathematica, we obtain the following clusters of solutions.

Set-1:

$$\begin{array}{c}\hfill a_0=0,a_1=\pm {\displaystyle \frac{\sqrt{{\nu }^2+1}}{\sqrt{\kappa {\nu }^2+\kappa +1}}},b_1=0,\mu =0,\mathsf{\Omega }={\displaystyle \frac{1}{8}}\left({\nu }^2+4\tau \right).\end{array}$$

By setting $A_1=0$ and $A_2\ne 0$, we retrieve periodic solution

$$\begin{array}{c}\hfill S_{15}(x,t)=\mp \left[{\displaystyle \frac{\sqrt{{\nu }^2+1}\sqrt{{\nu }^2+4\tau }tan\left(\frac{\sqrt{{\nu }^2+4\tau }(x-\nu t)}{2\sqrt{2}}\right)}{2\sqrt{2}\sqrt{\kappa {\nu }^2+\kappa +1}}}\right]\times e^{i(t\tau +\chi x)}.\end{array}$$

(47)

By setting $A_2=0$ and $A_1\ne 0$, we explore trigonometric solution

$$\begin{array}{c}\hfill S_{16}(x,t)=\pm \left[{\displaystyle \frac{\sqrt{{\nu }^2+1}\sqrt{{\nu }^2+4\tau }cot\left(\frac{\sqrt{{\nu }^2+4\tau }(x-\nu t)}{2\sqrt{2}}\right)}{2\sqrt{2}\sqrt{\kappa {\nu }^2+\kappa +1}}}\right]\times e^{i(t\tau +\chi x)}.\end{array}$$

(48)

Set-2:

$$\begin{array}{c}\hfill a_0=0,a_1=\pm {\displaystyle \frac{\sqrt{{\nu }^2+1}}{2\sqrt{\kappa {\nu }^2+\kappa +1}}},b_1=\pm {\displaystyle \frac{\sqrt{{\nu }^2+1}\sqrt{{\sigma }_1{\left({\nu }^2+4\tau \right)}^2-4{\mu }^2}}{2\sqrt{2}\sqrt{\left(\kappa {\nu }^2+\kappa +1\right)\left({\nu }^2+4\tau \right)}}},\mathsf{\Omega }={\displaystyle \frac{1}{2}}\left({\nu }^2+4\tau \right).\end{array}$$

By setting $A_1=0$ and $A_2\ne 0$, we attain combined periodic solutions

$$\begin{array}{c}\hfill S_{17}(x,t)=\pm [{\displaystyle \frac{\sqrt{{\nu }^2+1}\sqrt{A_2^2{\left({\nu }^2+4\tau \right)}^2-4{\mu }^2}}{2\sqrt{2}\sqrt{\left(\kappa {\nu }^2+\kappa +1\right)\left({\nu }^2+4\tau \right)}\left(A_{2}cos\left(\frac{\sqrt{{\nu }^2+4\tau }(x-\nu t)}{\sqrt{2}}\right)+\frac{2\mu }{{\nu }^2+4\tau }\right)}}\\ \hfill -{\displaystyle \frac{A_2\sqrt{{\nu }^2+1}\sqrt{{\nu }^2+4\tau }sin\left(\frac{\sqrt{{\nu }^2+4\tau }(x-\nu t)}{\sqrt{2}}\right)}{2\sqrt{2}\sqrt{\kappa {\nu }^2+\kappa +1}\left(A_{2}cos\left(\frac{\sqrt{{\nu }^2+4\tau }(x-\nu t)}{\sqrt{2}}\right)+\frac{2\mu }{{\nu }^2+4\tau }\right)}}]\\ \hfill \times e^{i(t\tau +\chi x)}.\end{array}$$

(49)

By setting $A_2=0$ and $A_1\ne 0$, we compile combined periodic solutions

$$\begin{array}{c}\hfill S_{18}(x,t)=\pm [{\displaystyle \frac{\sqrt{{\nu }^2+1}\sqrt{A_2^2{\left({\nu }^2+4\tau \right)}^2-4{\mu }^2}}{2\sqrt{2}\sqrt{\left(\kappa {\nu }^2+\kappa +1\right)\left({\nu }^2+4\tau \right)}\left(A_{2}cos\left(\frac{\sqrt{{\nu }^2+4\tau }(x-\nu t)}{\sqrt{2}}\right)+\frac{2\mu }{{\nu }^2+4\tau }\right)}}-\\ \hfill {\displaystyle \frac{A_2\sqrt{{\nu }^2+1}\sqrt{{\nu }^2+4\tau }sin\left(\frac{\sqrt{{\nu }^2+4\tau }(x-\nu t)}{\sqrt{2}}\right)}{2\sqrt{2}\sqrt{\kappa {\nu }^2+\kappa +1}\left(A_{2}cos\left(\frac{\sqrt{{\nu }^2+4\tau }(x-\nu t)}{\sqrt{2}}\right)+\frac{2\mu }{{\nu }^2+4\tau }\right)}}]\\ \hfill \times e^{i(t\tau +\chi x)}.\end{array}$$

(50)

Set-3:

$$\begin{array}{c}\hfill a_0=0,a_1=0,b_1=\pm {\displaystyle \frac{\sqrt{-{\nu }^2-1}\sqrt{{\sigma }_1}\left({\nu }^2+4\tau \right)}{2\sqrt{\left(\kappa {\nu }^2+\kappa +1\right)\left({\nu }^2+4\tau \right)}}},\mu =0,\mathsf{\Omega }=-{\displaystyle \frac{{\nu }^2}{4}}-\tau .\end{array}$$

By setting $A_1=0$ and $A_2\ne 0$, we obtain trigonometric solutions

$$\begin{array}{c}\hfill S_{19}(x,t)=\pm \left[{\displaystyle \frac{\sqrt{-{\nu }^2-1}\left({\nu }^2+4\tau \right)sec\left(\sqrt{-\frac{{\nu }^2}{4}-\tau }(x-\nu t)\right)}{2\sqrt{\left(\kappa {\nu }^2+\kappa +1\right)\left({\nu }^2+4\tau \right)}}}\right]\times e^{i(t\tau +\chi x)}.\end{array}$$

(51)

By setting $A_2=0$, and $A_1\ne 0$, we obtain trigonometric solutions

$$\begin{array}{c}\hfill S_{20}(x,t)=\pm \left[{\displaystyle \frac{\sqrt{-{\nu }^2-1}\left({\nu }^2+4\tau \right)csc\left(\sqrt{-\frac{{\nu }^2}{4}-\tau }(x-\nu t)\right)}{2\sqrt{\left(\kappa {\nu }^2+\kappa +1\right)\left({\nu }^2+4\tau \right)}}}\right]\times e^{i(t\tau +\chi x)}.\end{array}$$

(52)

• Case-3: Rational Solutions ($\mathsf{\Omega }$ = 0)

When $\mathsf{\Omega }=0$. Plugging Equation (40) in (28) along with Equations (14) and (20), we earn the following algebraic equations in terms of $\varphi$ and $\psi$:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & a_0^3{\zeta }_2+a_0{\zeta }_1=0,\hfill \\ & 3a_1{a}_0^2{\zeta }_2+a_1{\zeta }_1=0,\hfill \\ & {\displaystyle \frac{3a_0{b}_1^2{\zeta }_2}{A_1^2-2A_2\mu }}+3a_0{a}_1^2{\zeta }_2-{\displaystyle \frac{2b_1^3{\zeta }_2\mu }{{\left(A_1^2-2A_2\mu \right)}^2}}-{\displaystyle \frac{b_1\mu }{A_1^2-2A_2\mu }}=0,\hfill \\ & {\displaystyle \frac{3a_1{b}_1^2{\zeta }_2}{A_1^2-2A_2\mu }}+a_1^3{\zeta }_2+2a_1=0,\hfill \\ & -{\displaystyle \frac{6a_0{b}_1^2{\zeta }_2\mu }{A_1^2-2A_2\mu }}+3a_0^2{b}_1{\zeta }_2+{\displaystyle \frac{4b_1^3{\zeta }_2{\mu }^2}{{\left(A_1^2-2A_2\mu \right)}^2}}+{\displaystyle \frac{2b_1{\mu }^2}{A_1^2-2A_2\mu }}+b_1{\zeta }_1=0,\hfill \\ & -{\displaystyle \frac{6a_1{b}_1^2{\zeta }_2\mu }{A_1^2-2A_2\mu }}+6a_0{a}_1{b}_1{\zeta }_2-3a_1\mu =0,\hfill \\ & 3a_1^2{b}_1{\zeta }_2+{\displaystyle \frac{b_1^3{\zeta }_2}{A_1^2-2A_2\mu }}+2b_1=0.\hfill \end{array}\right.\end{array}$$

For simplicity here, ${\zeta }_2=-{\displaystyle \frac{2\kappa \left({\nu }^2+1\right)+2}{{\nu }^2+1}}\mathrm{and}{\zeta }_1=-{\displaystyle \frac{1}{4}}\left({\nu }^2+4\tau \right).$ When solving the algebraic expressions with the help of the computational software Mathematica, we obtain the following clusters of solutions.

Set-1:

$$\begin{array}{c}\hfill a_0=0,a_1=\pm {\displaystyle \frac{\sqrt{{\nu }^2+1}}{\sqrt{\kappa {\nu }^2+\kappa +1}}},b_1=0,\mu =0,\tau =-{\displaystyle \frac{{\nu }^2}{4}}.\end{array}$$

We deduce the rational solution as follows:

$$\begin{array}{c}\hfill S_{21}(x,t)=\pm \left[{\displaystyle \frac{A_1\sqrt{{\nu }^2+1}}{\sqrt{\kappa {\nu }^2+\kappa +1}\left(A_1(x-\nu t)+A_2\right)}}\right]\times e^{i\left(\chi x-{\displaystyle \frac{{\nu }^{2}t}{4}}\right)}.\end{array}$$

(53)

Set-2:

$$\begin{array}{c}\hfill a_0=0,a_1=\pm {\displaystyle \frac{\sqrt{{\nu }^2+1}}{2\sqrt{\kappa {\nu }^2+\kappa +1}}},b_1=\pm {\displaystyle \frac{\sqrt{{\nu }^2+1}\sqrt{A_1^2-2A_2\mu }}{2\sqrt{\kappa \left({\nu }^2+1\right)+1}}},\tau =-{\displaystyle \frac{{\nu }^2}{4}}.\end{array}$$

For this set, we establish the following solution:

$$\begin{array}{c}\hfill S_{22}(x,t)=\pm \left[{\displaystyle \frac{\sqrt{{\nu }^2+1}\left(A_1+\mu (x-\nu t)\right)}{2\sqrt{\kappa {\nu }^2+\kappa +1}\left(A_1(x-\nu t)+A_2+\frac{1}{2}\mu {(x-\nu t)}^2\right)}}+{\displaystyle \frac{\sqrt{{\nu }^2+1}\sqrt{A_1^2-2A_2\mu }}{2\sqrt{\kappa \left({\nu }^2+1\right)+1}\left(A_1(x-\nu t)+A_2+\frac{1}{2}\mu {(x-\nu t)}^2\right)}}\right]\\ \hfill \times e^{i\left(\chi x-{\displaystyle \frac{{\nu }^{2}t}{4}}\right)}.\end{array}$$

(54)

Remark 1. 

For the above twenty-two solutions, we can derive expressions for $\widehat{x}(x,t)$ using the relation $\widehat{x}(x,t)=-{\displaystyle \frac{{\left|S\right|}^2}{4{\chi }^2+1}}$.

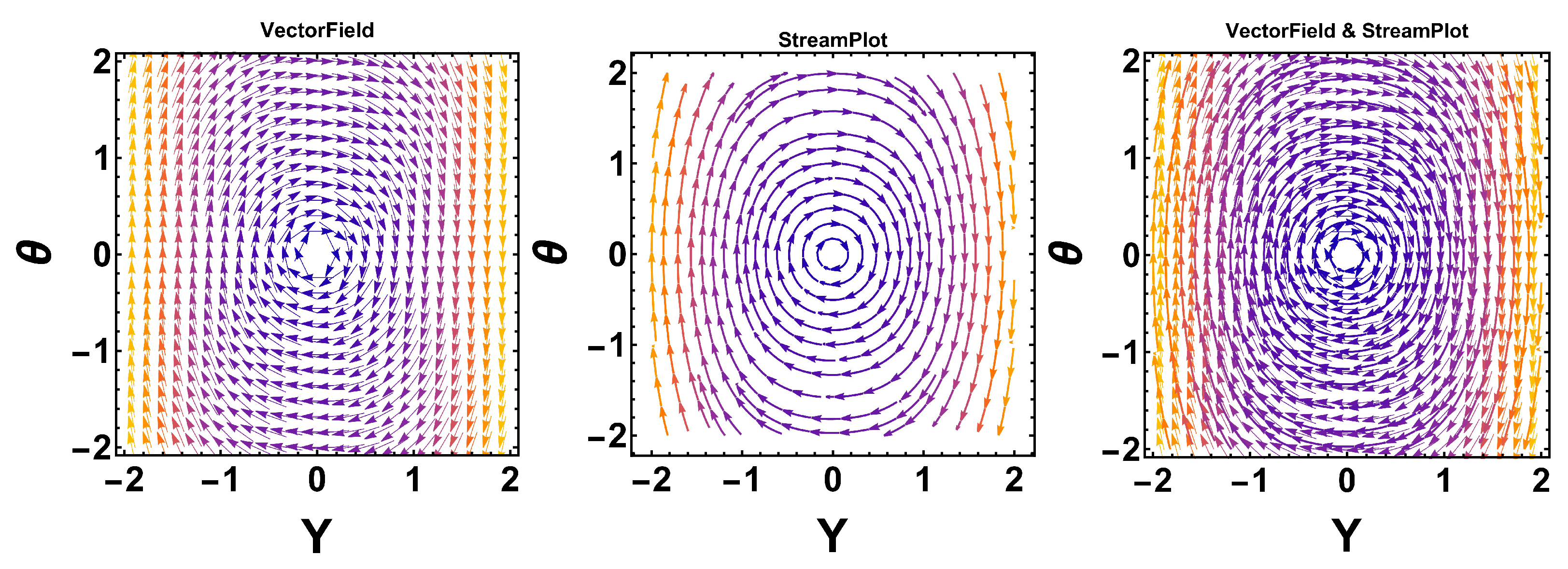
4. Sensitivity Analysis

This section investigates the sensitivity of the governing model. Sensitivity analysis [3] of dynamical systems yields vital information regarding the system’s dynamics. It enables the validation and refinement of models, assists in evaluating and mitigating risks, guides the development of optimization and control approaches, and plays a key role in quantifying uncertainties. Our approach focuses on assessing the influence of small perturbations in initial conditions on the system’s dynamics.

We analyze Equation (28) and transform it into the following dynamical system:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d\mathrm{Y}}{d\varsigma }}& =& \Theta \left(\varsigma \right),\hfill \\ \hfill {\displaystyle \frac{d\Theta }{d\varsigma }}& =& f_1\mathrm{Y}{\left(\varsigma \right)}^3+f_2\mathrm{Y}\left(\varsigma \right),\hfill \end{array}$$

(55)

where $f_1=\left(2k+{\displaystyle \frac{2}{4{\chi }^2+1}}\right)$ and $f_2=({\chi }^2+\tau )$.

Two solution curves are formulated and illustrated in Figure 1, Figure 2, Figure 3 and Figure 4 using different parameter values: $\tau =1$, $\kappa =-2$, $\chi =1$.

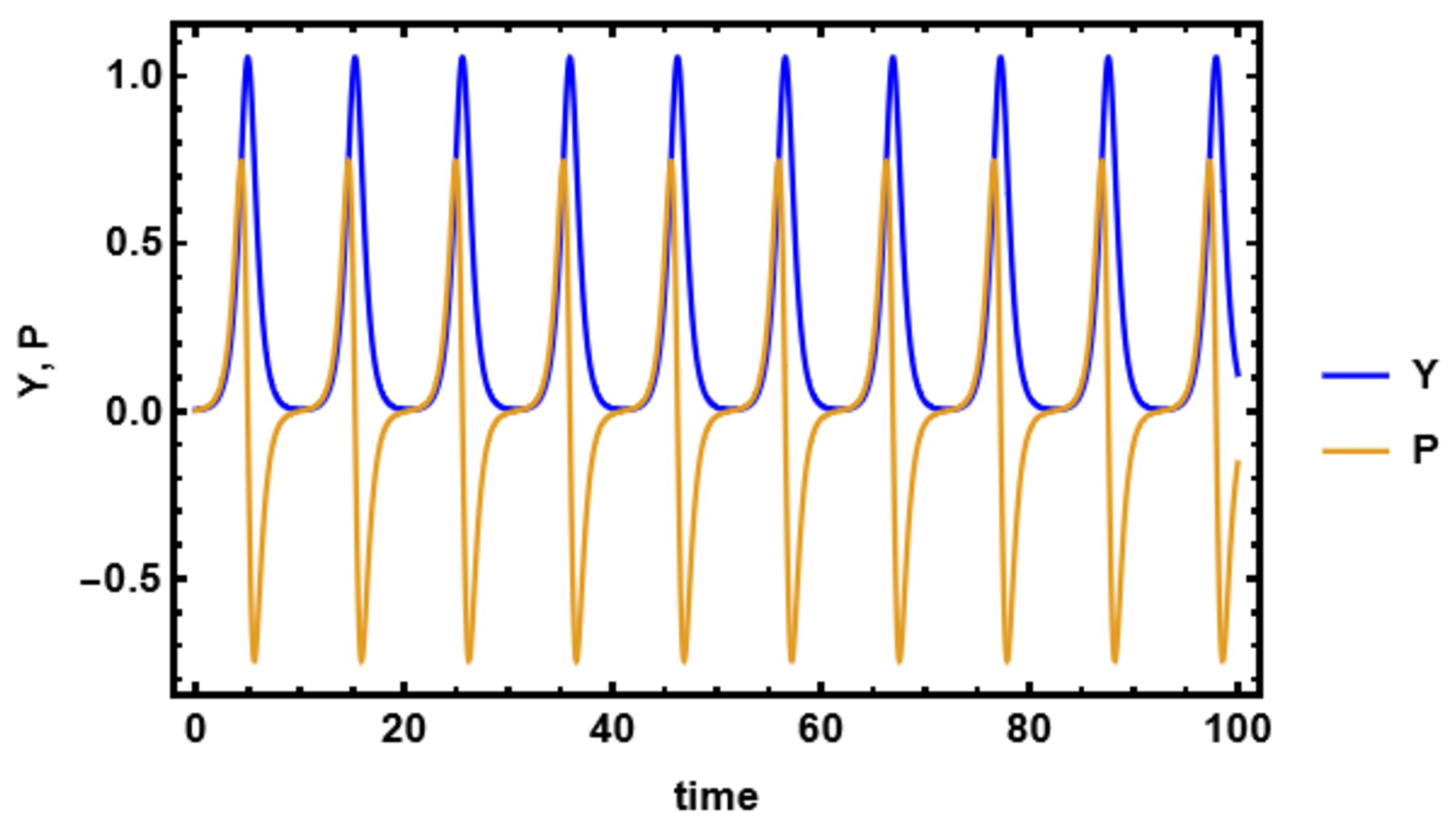
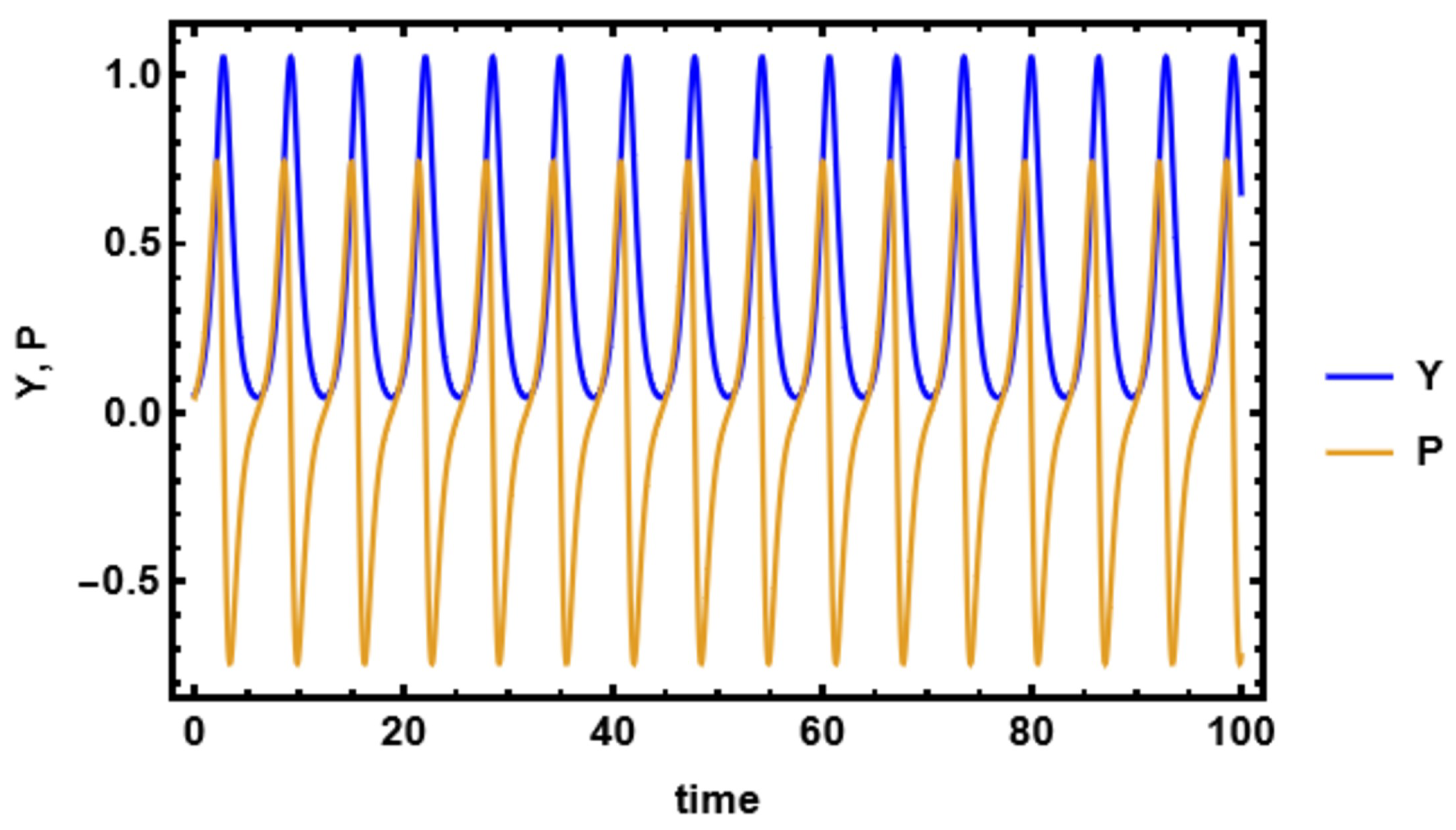
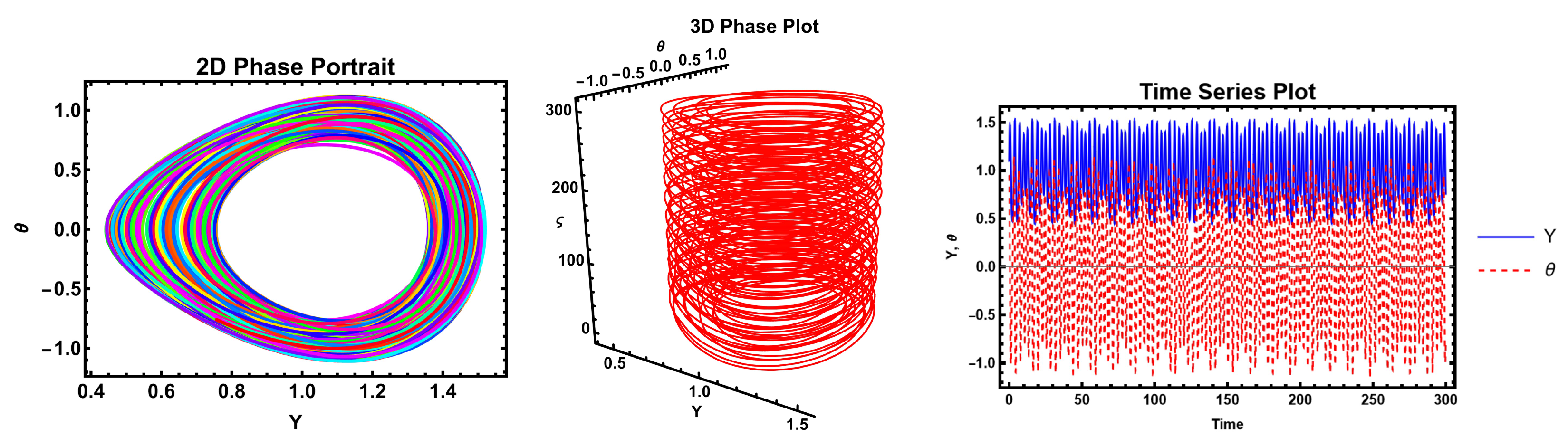
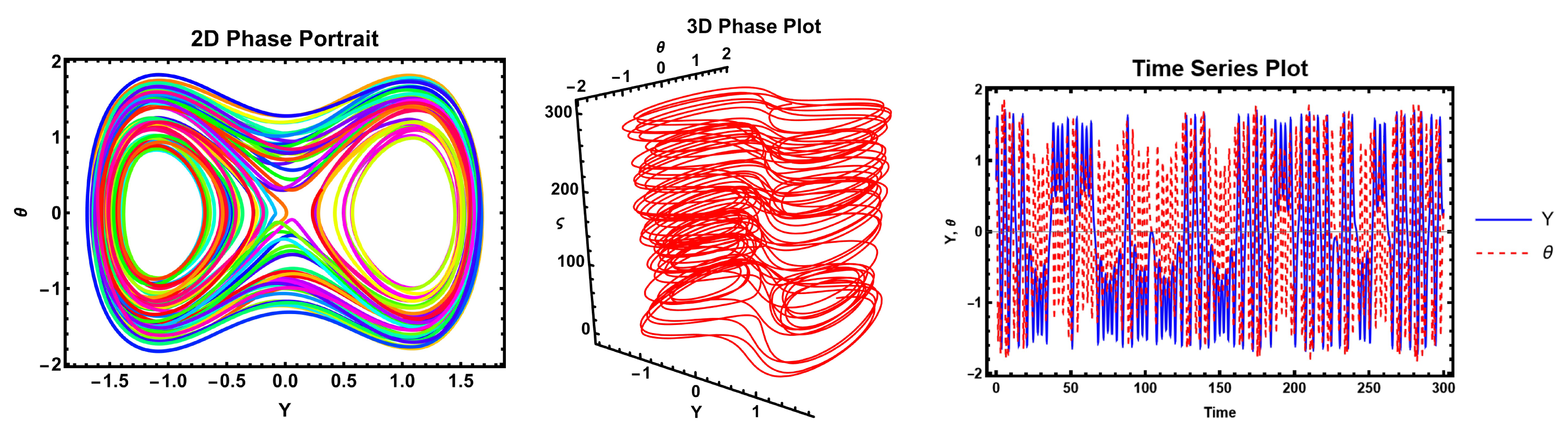
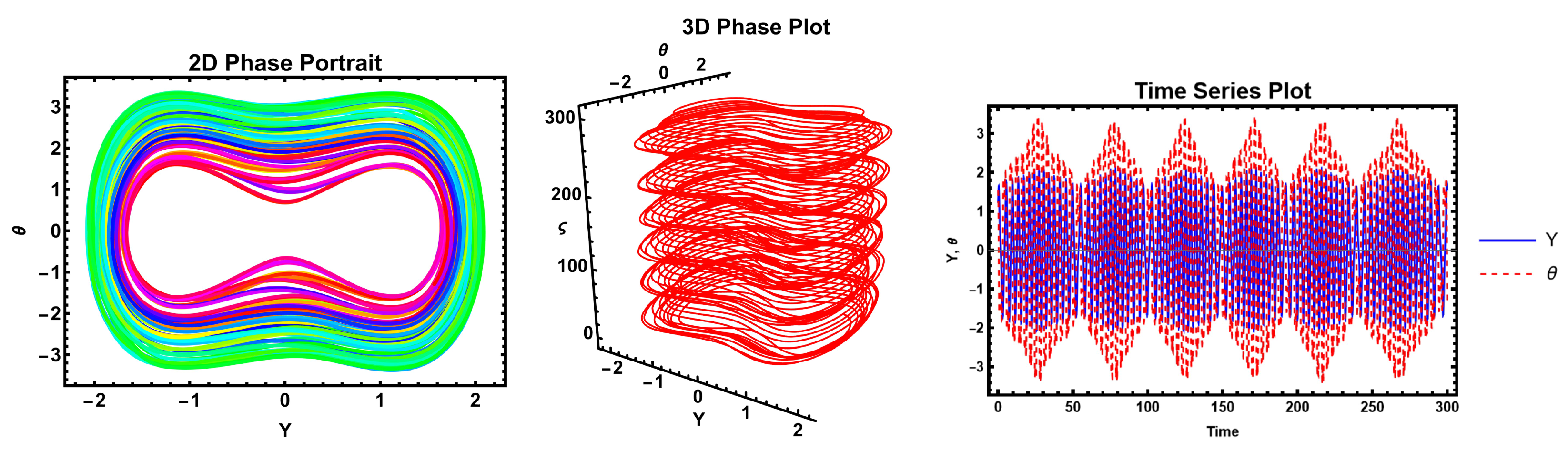
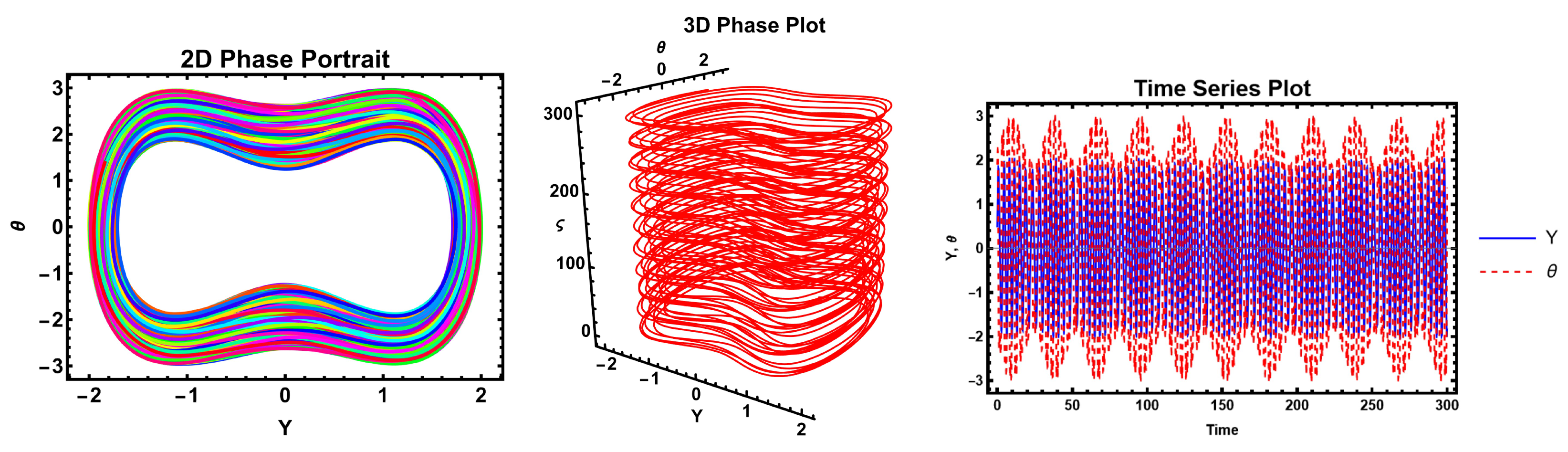
The figures demonstrate that a minor adjustment in the initial conditions leads to a substantial difference in the resulting solution, indicating that the model exhibits high sensitivity. Sensitivity analysis is an essential technique for understanding complex systems and making informed decisions across various fields of nonlinear science.

These figures illustrate the sensitivity analysis of the system by showing the time evolution of the two state variables, Y (blue curve) and $\theta$ (yellow curve). The plot demonstrates that both variables exhibit periodic oscillatory behavior with sharp peaks and troughs, highlighting the system’s nonlinear response to parameter variations. The close correspondence between the oscillations of Y and $\theta$ indicates their strong dynamical coupling, while the differences in amplitude and phase reveal how small perturbations can influence each variable differently. Such behavior is crucial in sensitivity analysis, as it reflects how variations in parameters propagate through the system and affect its stability and long-term dynamics. These figures, therefore, provide clear evidence of the sensitivity of the system to initial conditions and parameters, which is a key aspect in understanding bifurcation and potential transition to more complex behaviors.

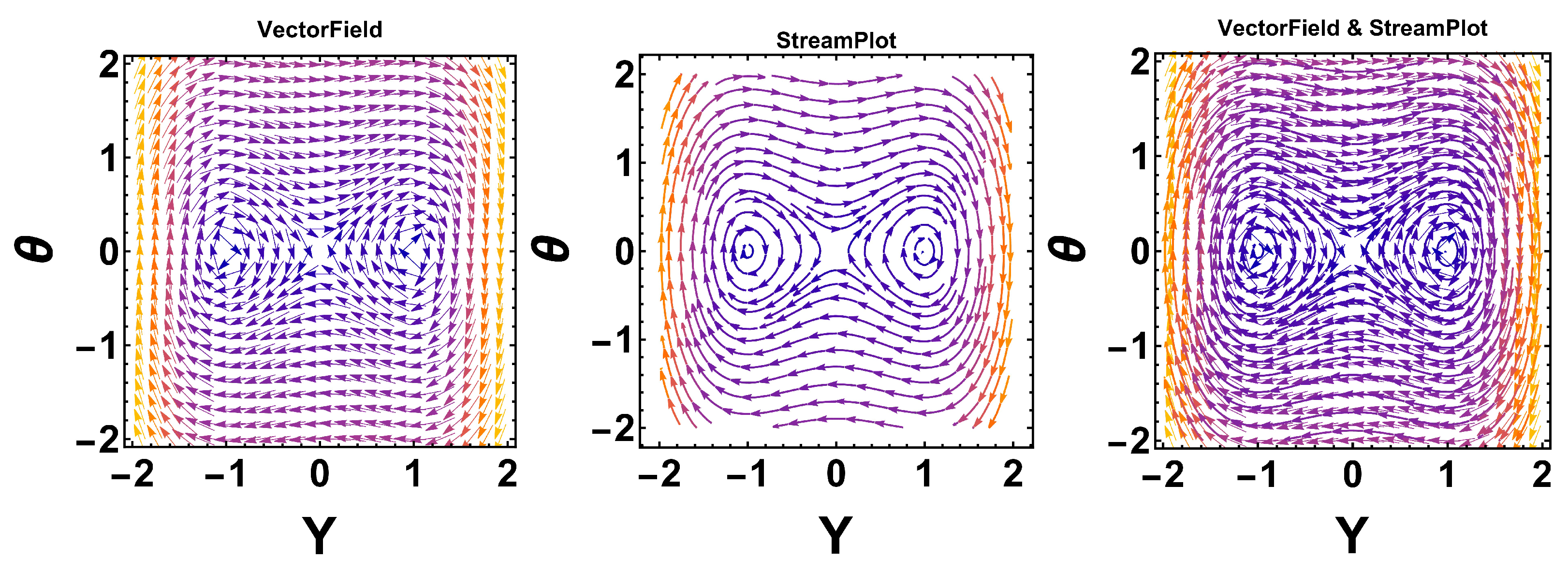
5. Bifurcation Analysis

Bifurcation analysis investigates how the qualitative behavior of a dynamical system changes as a critical parameter is varied. A bifurcation occurs when such variations lead to significant alterations in the system’s dynamics. As the parameter changes, equilibria, periodic orbits, or other features of the system may appear, disappear, or undergo changes in stability [32,33].

In this part, we apply bifurcation theory to analyze Equation (1). By applying a Galilean transformation through the Runge–Kutta fourth-order (RK4) method, the governing equation can be recast as a planar dynamical system, allowing a more thorough investigation of its behavior. The RK4 method is a reliable and accurate scheme for bifurcation analysis; its performance is indeed sensitive to the choice of time step. An inappropriate time step may either lead to numerical instability or suppress important dynamical features, especially near critical bifurcation points. In our study, we carefully selected a sufficiently small time step to ensure numerical stability and accuracy, and we verified that further refinement of the step size does not qualitatively alter the observed bifurcation structures.

The Hamiltonian function for Equation (55) is

$$\begin{array}{c}\hfill \mathcal{H}(\mathrm{Y},\Theta )={\displaystyle \frac{{\Theta }^2}{2}}-f_1{\displaystyle \frac{{\mathrm{Y}}^4}{4}}-f_1{\displaystyle \frac{{\mathrm{Y}}^2}{2}}.\end{array}$$

(56)

To solve system (55), we first find its equilibrium points. The system states the following three equilibrium solutions: $P_1=(0,0)$, $P_2=\left(-\sqrt{-{\displaystyle \frac{f_2}{f_1}}},0\right)$, $P_3=\left(\sqrt{-{\displaystyle \frac{f_2}{f_1}}},0\right)$.

For system (55), the Jacobian matrix determinant is

$$\begin{array}{c}\hfill D(\mathrm{Y},\Theta )=\left|\begin{array}{cc}0& 1\\ 3f_1{\mathrm{Y}}^2+f_2& 0\end{array}\right|=-3f_1{\mathrm{Y}}^2-f_2.\end{array}$$

(57)

We know the following:

• If $D(\mathrm{Y},\Theta )<0$, then $(\mathrm{Y},\Theta )$ is a saddle.
• If $D(\mathrm{Y},\Theta )>0$, then $(\mathrm{Y},\Theta )$ is a center.
• If $D(\mathrm{Y},\Theta )=0$, then $(\mathrm{Y},\Theta )$ is cuspidal.

The results that may be achieved by varying the relevant parameter are listed below.

• Case-1: When $f_1>0$ and $f_2>0$.

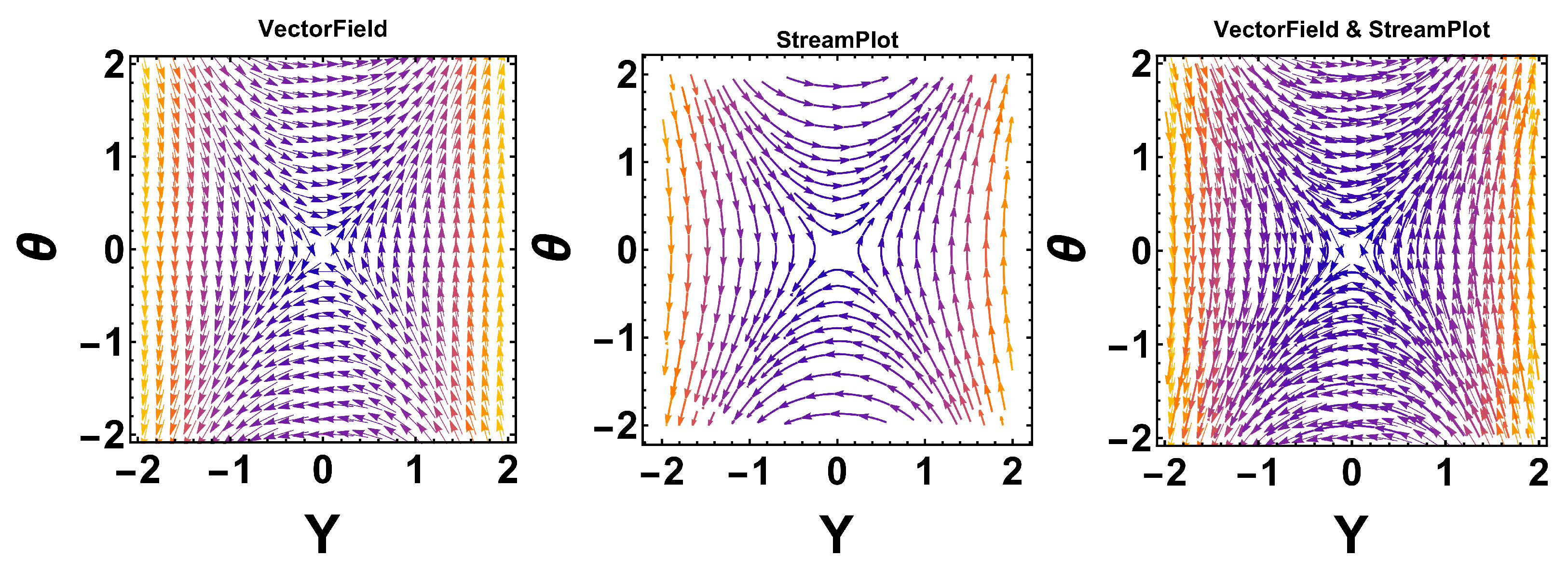
By picking certain values for the parameters, $\kappa =1$, $\chi =1$, and $\tau =2$, we observe that $(0,0)$ is the only real equilibrium point (EqP), as illustrated in Figure 5. Clearly, $(0,0)$ corresponds to a saddle point.

• Case-2: When $f_1<0$ and $f_2>0$.

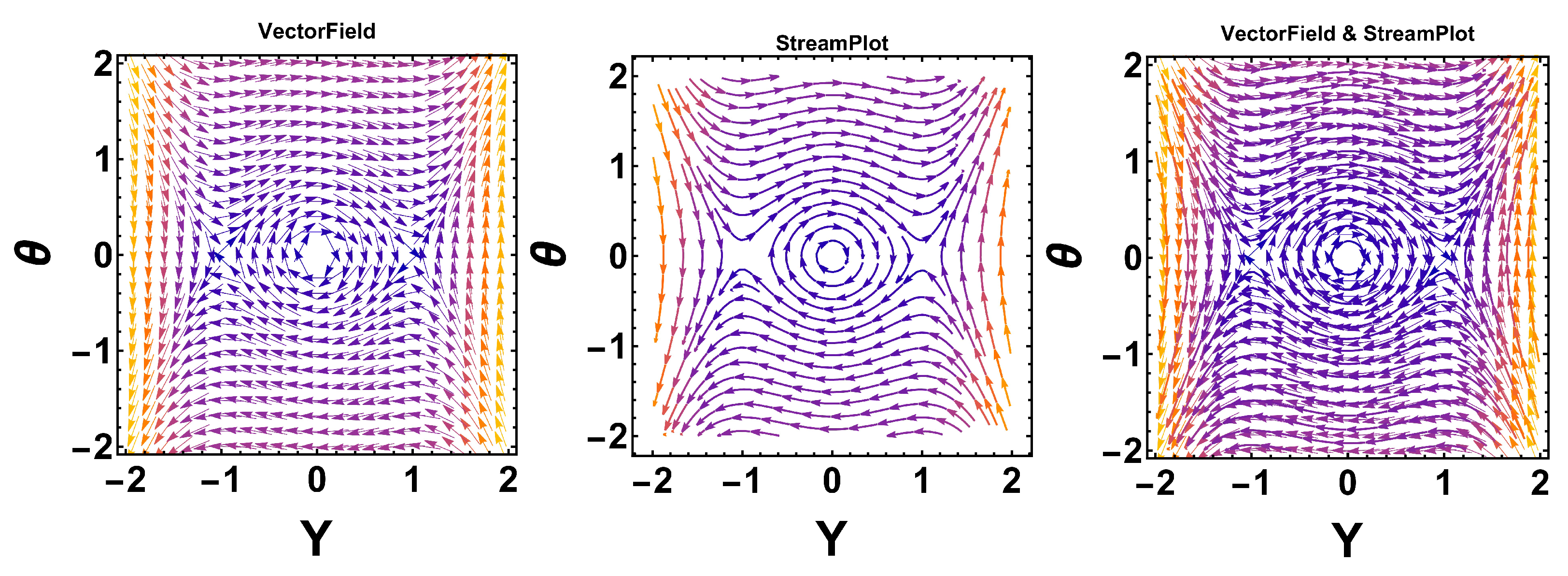
By setting the parameters $\kappa =-1$, $\chi =1$, and $\tau =2$, we find that $(0,0)$, $(1.3693,0)$, and $(-1.3693,0)$ are three equilibrium points. Among them, $(0,0)$ behaves as a saddle point, as shown in Figure 6, while $(1.3693,0)$ and $(-1.3693,0)$ act as center points.

• Case-3: When $f_1<0$ and $f_2<0$.

By taking the parameters $\kappa =-1$, $\chi =1$, and $\tau =-2$, we find that $P_2$ and $P_3$ are imaginary points, whereas $P_1$ is evidently a center point in this case, as elucidated in Figure 7.

• Case-4: When $f_1>0$ and $f_2<0$.

By choosing the parameters $\kappa =1$, $\chi =1$, and $\tau =-2$, we find that $(0,0)$, $(0.6454,0)$, and $(-0.6454,0)$ are three equilibrium points. Among them, $(0,0)$ behaves as a center point, whereas $(0.6454,0)$ and $(-0.6454,0)$ behave as saddle points, as illustrated in Figure 8.

6. Chaotic Behavior

To examine the chaotic dynamics of Equation (55), we consider the dynamics of the following Duffing-type oscillator system [34]:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d\mathrm{Y}}{d\varsigma }}& =& \Theta \left(\varsigma \right),\hfill \\ \hfill {\displaystyle \frac{d\Theta }{d\varsigma }}& =& f_1\mathrm{Y}{\left(\varsigma \right)}^3+f_2\mathrm{Y}\left(\varsigma \right)+\beta cos\left(\lambda \varsigma \right),\hfill \end{array}$$

(58)

where $f_1=\left(2k+{\displaystyle \frac{2}{4{\chi }^2+1}}\right)$ and $f_2=({\chi }^2+\tau )$. The perturbative effects in the system are governed by two critical parameters: $\beta$, which quantifies the perturbation amplitude, and $\lambda$, which corresponds to its oscillatory frequency.

To study the potential for chaotic behavior in the system described by Equation (58), we introduce these parameters into the system, as illustrated in Figure 9, Figure 10, Figure 11 and Figure 12. The chaotic behavior curves are formulated and presented in these figures using the parameter values $\kappa =-1.3$, $\tau =1.2$, and $\chi =1.3$. For all figures depicting chaotic behavior, the parameter values used are $\beta =0.20$ and $\lambda =1.6$.

The figures demonstrate that even a minor adjustment in the initial conditions (ICs) leads to a substantial difference in the resulting solutions, indicating that the model exhibits strong chaotic behavior.

7. Spectral Stability

Here, we observe the spectral (linear) stability analysis [31] for the considered system (1), together with the principal analytical reductions used when studying solitary waves, the linearization, the resulting eigenvalue problem, the structure of the continuous spectrum, and the role of symmetry (zero) modes. The “GSS/VK” route refers to the methodologies developed by Grillakis, Shatah, and Strauss (GSS) and independently by Vakhitov and Kolokolov (VK) that one uses to deduce spectral/orbital stability from the spectral problem [35,36].

We seek a standing/steady wave of the form

$$S(x,t)=e^{i\omega t}Q\left(x\right),\widehat{x}(x,t)=K\left(x\right),$$

with $Q:\mathbb{R}\to \mathbb{R}$ and $K:\mathbb{R}\to \mathbb{R}$. Substitute into system (1) and factor out $e^{i\omega t}$. System (1) reduces to the system

$$\begin{array}{c}\hfill Q_{xx}-\omega Q-2\kappa Q^3+2KQ=0,\end{array}$$

(59)

$$\begin{array}{c}\hfill -K_{xx}+{\left(Q^2\right)}_{xx}=0.\end{array}$$

(60)

Integrating Equation (60) twice gives the general relation

$$K\left(x\right)=Q{\left(x\right)}^2+Ax+B,$$

with constants $A,B$. For physically relevant localized solutions, we require boundedness of K as $\left|x\right|\to \infty$, so $A=0$. (If $A\ne 0$, one obtains a linearly growing background for $\widehat{x}$, and that changes both existence and spectral conclusions.) With $A=0$, one has $K=Q^2+B$. Substituting into the Equation (59) yields the scalar ODE

$$Q_{xx}-\mu Q+\gamma Q^3=0,\mu =\omega -2B,\gamma =2-2\kappa .$$

This ODE admits the standard first integral (multiply by $Q_x$ and integrate)

$${\left(Q_x\right)}^2-\mu Q^2+{\displaystyle \frac{\gamma }{2}}{Q}^4=C,$$

and for a localized, decaying solitary wave, one typically takes the integration constant $C=0$. If $C\ne 0$, one obtains periodic or nonlocalized families; the choice $C=0$ is compatible with decaying boundary conditions $Q\to 0,Q_x\to 0$ at $\left|x\right|\to \infty$.

Linearize system (1) about the standing wave $S_0=e^{i\omega t}Q\left(x\right),{\widehat{x}}_0=K\left(x\right)$. Write a small perturbation, as follows:

$$S(x,t)=e^{i\omega t}\left(Q\left(x\right)+\epsilon \left[a\right(x,t)+ib(x,t\left)\right]\right),\widehat{x}(x,t)=K\left(x\right)+\epsilon w(x,t),$$

with real $a,b,w$. Substitute in system (1), keep only $O\left(\epsilon \right)$ terms, and separate real/imaginary parts. After straightforward algebra, one obtains the linearized system as

$$\begin{array}{cc}\hfill a_t& =L_{-}b,\hfill \\ \hfill b_t& =-L_{+}a+2Qw,\hfill \\ \hfill w_{tt}& =w_{xx}-2{\left(Qa\right)}_{xx},\hfill \end{array}$$

where the two Schrödinger-type self-adjoint operators $L_{\pm }$ are

$$L_{-}=-{\partial }_x^2+\omega -2K+2\kappa Q^2,L_{+}=-{\partial }_x^2+\omega -2K+6\kappa Q^2.$$

Now, put $a(x,t)=e^{\lambda t}A\left(x\right),b(x,t)=e^{\lambda t}B\left(x\right),w(x,t)=e^{\lambda t}W\left(x\right)$. The linearized system becomes the spectral system as

$$\begin{array}{cc}\hfill \lambda A& =L_{-}B,\hfill \end{array}$$

(61)

$$\begin{array}{cc}\hfill \lambda B& =-L_{+}A+2QW,\hfill \end{array}$$

(62)

$$\begin{array}{cc}\hfill {\lambda }^{2}W& =W_{xx}-2{\left(QA\right)}_{xx}.\hfill \end{array}$$

(63)

Eliminate B by applying $L_{-}$ to Equation (62) and using Equation (61), applying $L_{-}$ to $\lambda B=-L_{+}A+2QW$, and substituting $L_{-}B=\lambda A$ gives

$${\lambda }^{2}A+L_{-}{L}_{+}A-2L_{-}\left(QW\right)=0,$$

while Equation (63) reads

$${\lambda }^{2}W-W_{xx}+2{\left(QA\right)}_{xx}=0.$$

Thus, the linear spectral problem reduces to the coupled system for $(A,W)$, as follows:

$$\begin{array}{cc}\hfill \left({\lambda }^2+L_{-}{L}_{+}\right)A& =2L_{-}\left(QW\right),\hfill \end{array}$$

(64)

$$\begin{array}{cc}\hfill \left({\lambda }^2-{\partial }_x^2\right)W& =2{\left(QA\right)}_{xx}.\hfill \end{array}$$

(65)

For $\lambda \ne 0$, one may solve Equation (65) for W as follows:

$$W={\left({\partial }_x^2-{\lambda }^2\right)}^{-1}2{\left(QA\right)}_{xx},$$

and substitute back into Equation (64) to obtain a single (nonlocal) eigenvalue equation for A,

$$\begin{array}{c}\hfill \left[{\lambda }^2+L_{-}{L}_{+}-4L_{-}\left(Q{({\partial }_x^2-{\lambda }^2)}^{-1}{\partial }_x^2(Q·)\right)\right]A=0.\end{array}$$

(66)

This is the exact spectral condition; eigenvalues $\lambda$ are those complex numbers for which the above operator has a nontrivial kernel in $L^2\left(\mathbb{R}\right)$. To find the continuous spectrum, analyze the linear operator at spatial infinity where $Q\left(x\right)\to 0$ and $K\left(x\right)\to B$. Set $Q\equiv 0$ and $K\equiv B$. Then $L_{\pm }$ reduces to the constant-coefficient operator

$$L_{\infty }=-{\partial }_x^2+\mu ,\mu =\omega -2B.$$

The asymptotic dispersion relations come from putting $A,W\propto e^{i\widehat{x}x}$; Equation (66) becomes ${\lambda }^2+{({\widehat{x}}^2+\mu )}^2=0$; hence,

$$\lambda =\pm i({\widehat{x}}^2+\mu ),\widehat{x}\in \mathbb{R},$$

while the wave component gives ${\lambda }^2=-{\widehat{x}}^2$, i.e., $\lambda =\pm i|\widehat{x}|$. Therefore, the essential spectrum is contained in the imaginary axis, two branches $\lambda =\pm i({\widehat{x}}^2+\mu )$ and $\lambda =\pm i|\widehat{x}|$. Instabilities (spectral eigenvalues with $\Re \lambda >0$) can only arise as discrete eigenvalues bifurcating off the imaginary axis; they are not part of the continuous spectrum.

8. Results and Discussion

In this paper, we employed the new extended RShGEEM and the $({\displaystyle \frac{G^{\prime }}{G}},{\displaystyle \frac{1}{G}})$-expansion method to derive new hyperbolic, trigonometric, and rational solutions for the studied model. We identified several solutions, including dark, bright, singular, combo soliton, periodic, and plane wave solutions. The characteristics and dynamics of these solutions are elucidated through two-dimensional, three-dimensional, and contour plots, created by varying the model’s parameters. The methodologies adopted in this work are particularly effective, as evidenced by their capacity to generate extensive families of solutions, suggesting broad applicability to other NLPDEs. The results computed in this study have significant physical implications, particularly in the context of soliton theory and applications in other fields of applied sciences such as physics, electrical engineering, control theory, and wave phenomena. The graphical representations were carefully constructed, with meticulous attention to selecting appropriate parameter values.

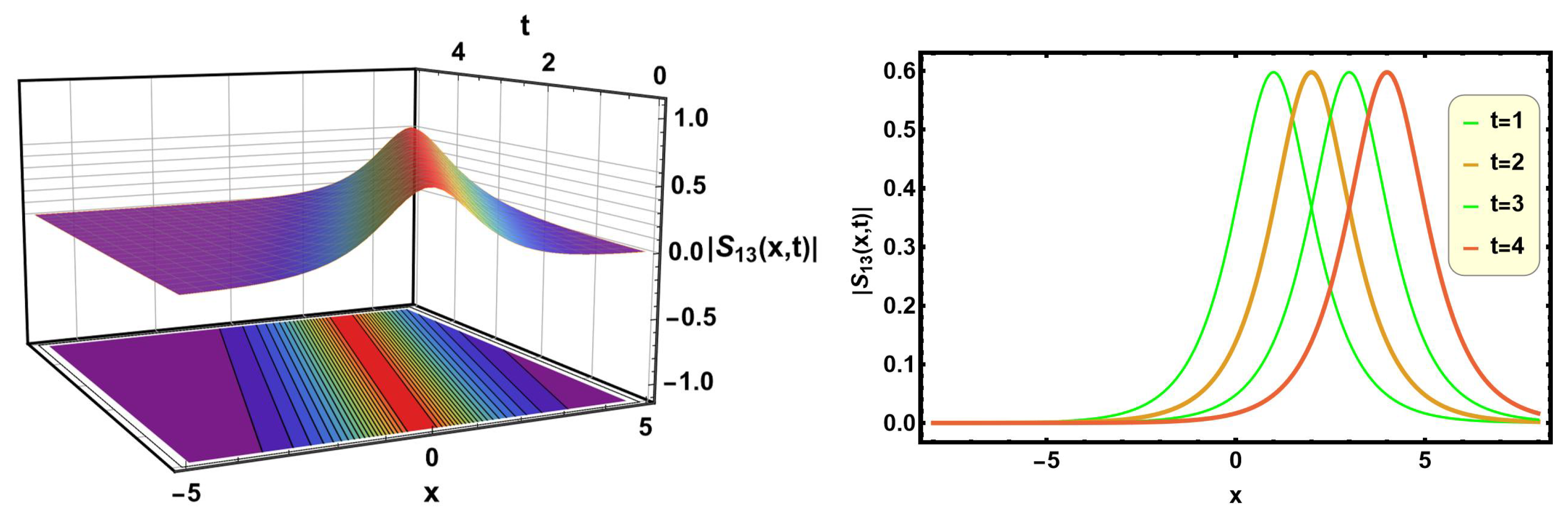
Figure 13 and Figure 14 describe the bright soliton solutions of Equations (31) and (45) with suitable parametric values $\chi =0.38$, $\kappa =0.55$, and $\kappa =0.2$, $\nu =1$, $\tau =0.9$, $\chi =0.9$, respectively. Bright solitons are characterized by a peak or maximum in amplitude, unlike dark solitons, which have a localized dip or minimum. Bright solitons are crucial in fiber-optic communications, where they can transmit information over long distances without distortion, enabling high-speed data transfer and reducing the need for signal regeneration.

Figure 15 and Figure 16 portray the combined soliton solutions of Equations (38) and (43) with appropriate parametric values ${\epsilon }_0=0.04$, $\kappa =0.01$, $\chi =0.01$, ${\phi }_1=0.05$, and $\nu =0.1$, $\chi =1.7$, $A_2=4.5$, $\tau =0.1$, $\kappa =1.8$, $\mu =1.4$, respectively. A dark-bright soliton is a composite soliton solution that showcases dual behavior with both lower and higher intensities. These kinds of solitons are important for developing advanced techniques in optical signal processing and transmission, where maintaining signal integrity across different channels is essential.

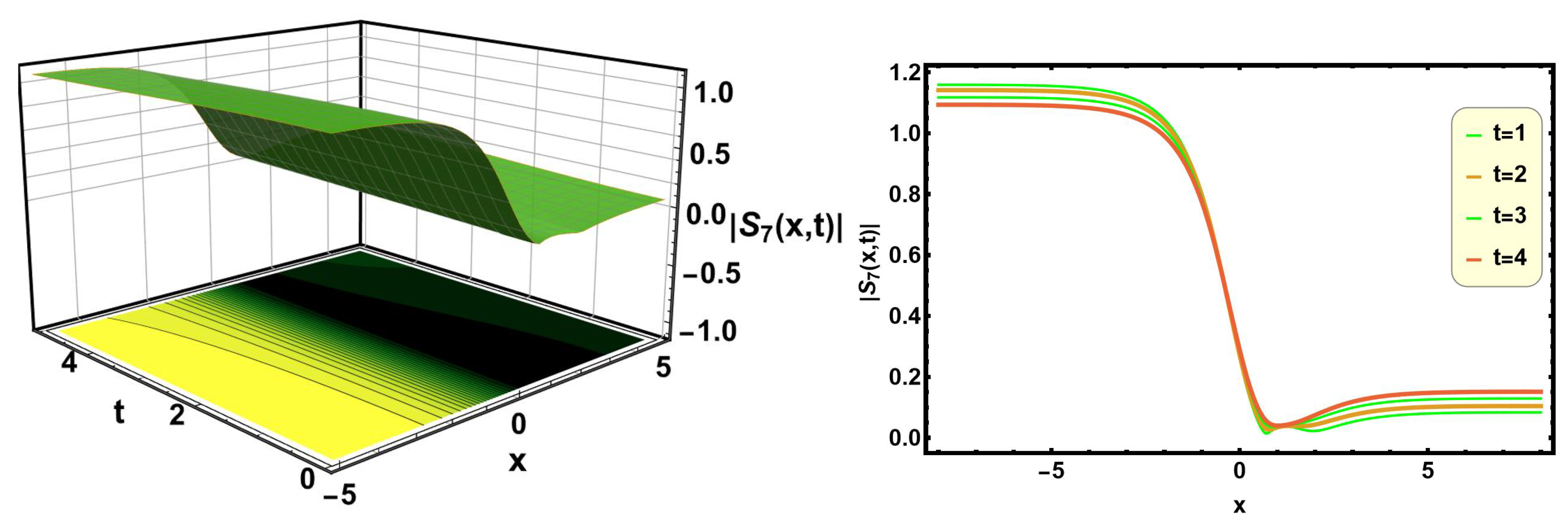
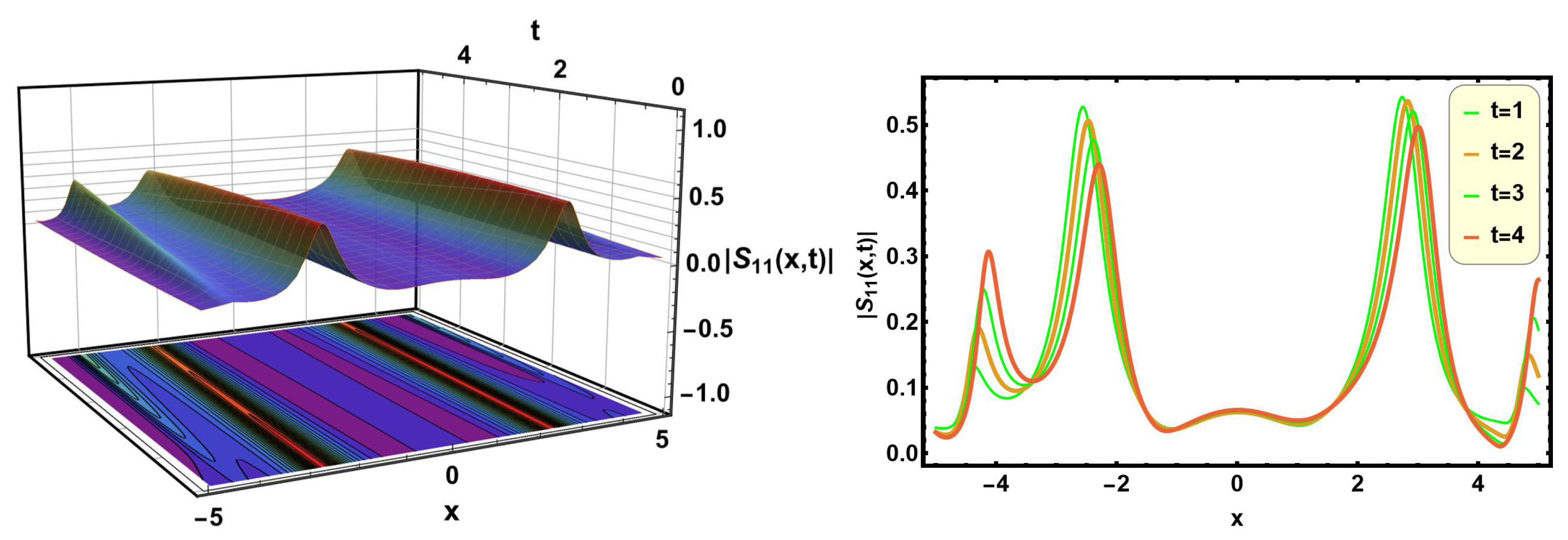
Figure 17 and Figure 18 exemplify the dark soliton solutions of Equations (36) and (41) with proper parametric values $\kappa =0.15$, $\chi =0.20$, and $\tau =-1.5$, $\kappa =0.15$, $\nu =0.25$, $\chi =0.8$, respectively. A dark soliton is characterized by a localized drop in the amplitude of a continuous wave. Dark solitons typically occur in nonlinear dispersive media, where they appear as dips in the background of a continuous wave, maintaining their shape and velocity during propagation. These solitons are crucial in nonlinear fiber optics, where they assist in understanding the propagation of light pulses in optical fibers. They can enhance the design of fiber-optic communication systems by reducing signal degradation over long distances.

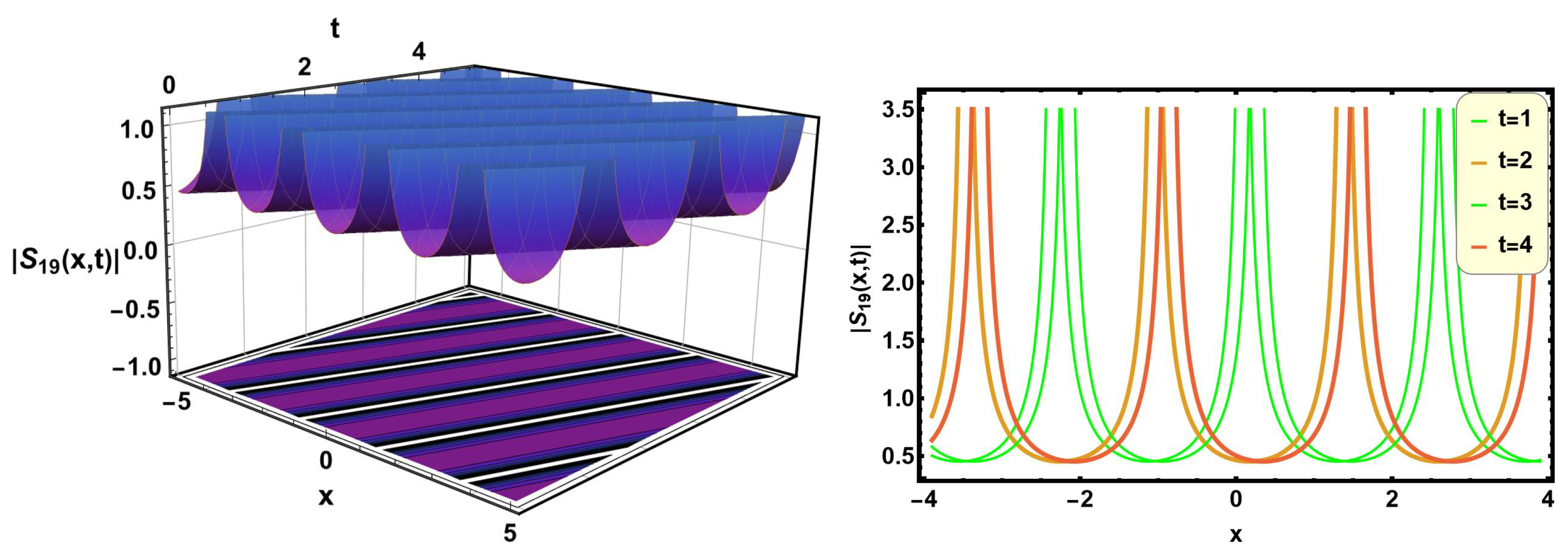
Figure 19 characterizes the periodic solutions of Equation (51) with suitable parametric values $\tau =-2.7$, $\kappa =-1.55$, $\nu =1.3$, $\chi =1.38$. A periodic solution is a type of wave that repeats its pattern consistently over time or space.

Furthermore, singular solutions (e.g., those with poles leading to infinite amplitude at certain points) are typically non-physical artifacts arising from the specific mathematical ansatz (like the $sec{h}^p$ or $tan{h}^p$ methods) when parameters satisfy certain relations that cause the exponent p to be non-integer or when integration constants are neglected; however, these singularities can be regularized into finite-amplitude, physically admissible pulses through appropriate parameter choices that satisfy existence conditions, such as enforcing a positive nonlinearity coefficient to ensure a real and bounded width, selecting a wave velocity c sufficiently greater than the linear wave speed to maintain a positive argument for the root defining the pulse width, and strictly adhering to boundary conditions that eliminate divergent terms, thereby yielding a smooth, sech-type soliton profile with finite energy.

The derived results are exceptional and novel, significantly advancing upon previous outcomes in the literature. We briefly compare our obtained solutions with those presented in earlier research. Our findings lead to the following conclusions, presented in

Table 1. Novelty of current study.

Ref.	Soliton Solutions	Sensitivity	Bifurcation	Chaotic Behavior
In [23]	Yes	No	No	No
Our study	Yes	Yes	Yes	Yes

, which highlight the novelty of the present work.

9. Conclusions

In this research, we have meticulously analyzed the GCZS to obtain soliton solutions by employing two proposed approaches. We successfully extracted diverse solitonic structures for the investigated model, including singular, dark, bright, combo, hyperbolic, mixed trigonometric forms, and singular periodic waves. Furthermore, by incorporating sensitivity and bifurcation analyses into our study, we gained deeper insights into the behavior of the GCZS equation and further validated the effectiveness of the applied methodologies.

The physical configurations are illustrated through 2D, 3D, and contour graphs, examining the effects of dispersion and nonlinearity for several parametric values. The results presented in this manuscript not only offer potential solutions to mitigate the growing issue in plasma physics but also demonstrate the efficiency of the analytical tools in investigating complex dynamical systems encountered in advanced research and engineering fields.

Moreover, this study lays the groundwork for future investigations on soliton solutions of the GCZS by integrating a conformable fractional derivative (CFD), because selecting this derivative is suitable for modeling nonlocal transport and memory effects in complex plasma or fluid systems, as the CFD’s kernel-free definition and adherence to these classical calculus rules facilitate a straightforward traveling wave reduction, which transforms the fractional partial differential equation into a tractable ordinary differential equation, thereby enabling the analytical construction of solitary wave and soliton solutions that capture the system’s underlying anomalous diffusion and wave propagation dynamics. This research contributes significantly to understanding wave dynamics in shallow water and plasma physics, and the results obtained will play a significant role in future investigations of nonlinear equations. Furthermore, as part of future recommendations, it is important to acknowledge that while bifurcation diagrams derived from the reduced ODE provide valuable local insight into solution structures, the global bifurcation behavior of the full PDE system may differ, particularly regarding stability changes and the multiplicity of bound states. A natural extension of the present work would therefore involve the numerical continuation of full-PDE branches using tools such as AUTO or related bifurcation software, in order to validate the reduction assumptions and to capture phenomena beyond the ODE framework. Moreover, in advancing the physical applicability of the generalized coupled Zakharov system, it is crucial to address heterogeneity and noise in a principled manner. Rather than relying on ad hoc stochastic perturbations, a promising strategy is to derive stochastic terms systematically from microscopic random-walk models of particle or energy transport in inhomogeneous plasma patches. Taking the continuum limit of such models may naturally yield spatially varying coefficients or stochastic forcing terms and, in certain regimes, fractional operators arising from continuous time random walks. This approach grounds the stochastic generalizations in identifiable physical mechanisms, ensures interpretability of the parameters, and provides a systematic pathway toward fractional Zakharov models. Future studies could therefore explore fractional generalizations of the GCZS by employing fractional traveling-wave transforms and established numerical schemes, such as Grunwald–Letnikov discretization or spectral fractional operators. Incorporating these directions would significantly broaden the scope of the model and enhance its relevance both mathematically and in plasma physics applications.