Approximating Solutions of General Class of Variational Inclusions Involving ${\mathcal{B}}^l$-Co-Monotone Mappings in Banach Spaces

Abstract

The goal of the current study is to introduce a new class of proximal-point mappings that are associated with a new class of ${\mathcal{B}}^l$-co-monotone mappings that are being defined. The ${\mathcal{B}}^l$-co-monotone mapping is the sum of co-coercive and symmetric monotone mappings and an extension of the $C_n$-monotone mapping. The investigation is further discussed, along with its application, which involves a variational inclusion problem (VIP) in Banach spaces. Moreover, the study proposes an iterative algorithm and systematically investigates the convergence characteristics of its generated sequences. For the purpose of illustrating our findings, a simplified numerical example is created to show the convergence graph by using the MATLAB 2015a.

1. Introduction and Preliminaries

Let X be a real Banach space with the norm $\parallel .\parallel$ and $X^{\ast }$ the topological dual of X. Let $\langle .,.\rangle$ denote the duality pairing between X and $X^{\ast }$ and $2^X$ the power set of X. Set $X^l=\underset{l}{\underbrace{X\times X\times ...X}}$. For each $i\in \{1,2,...,l\},l\ge 3$, consider the following variational inclusion: find $d\in X$ such that

$$0\in \mathcal{K}\left(d\right)+\mathcal{M}(f_1\left(d\right),f_2\left(d\right),...,f_l\left(d\right)),$$

(1)

where $\mathcal{K}:X\to X^{\ast }$, $f_i:X\to X$ are single-valued mappings and $\mathcal{M}:X^l\rightrightarrows X^{\ast }$ is a multi-valued mapping.

Variational inclusions, which are the generalization of variational inequalities, have received considerable attention in recent years in the literature. The reason we emphasize this is that variational inclusions have a wide range of applications in different fields (for instance, in management sciences, engineering sciences, optimization, economics, transportation equilibrium, etc.); see [1]. This increasing interest has motivated the investigation of many existence results and the introduction of efficient iterative algorithms for such applications. Of the many approaches used by researchers, some of the most successful have been those based on proximal-point mapping (resolvent operator) techniques for studying variational inclusions. For more on these developments and methods, see [2,3,4].

In recent past, Xia and Huang [5] proposed and investigated a general H-monotone operator and with the aim of investigating a class of varitional inclusions that involve such a kind of operator in Banach spaces. Ding and Feng [6], along with Feng and Ding [7], further explored the general H-monotone operator, including its applications to variational inclusions. Leveraging the proximal mapping, the authors proposed new classes of variational inclusions characterized by general H-monotone and A-monotone operators. Concurrently, some iterative algorithms were developed for the solution of these classes in Banach spaces. In contrast, Sun et al. [8] proposed and studied a new class of M-monotone operators in Hilbert spaces. Utilizing the resolvent operator for M-monotone operator, a proximal point algorithm is designed to address variational inequalities in Hilbert spaces. In this continuation, Zou and Huang [9,10] recently made a significant contribution by defining and analyzing a novel class of $H(.,.)$-accretive operators in Banach spaces. Their research revealed key properties of the resolvent operators associated with these operators and its applications for addressing the variational inclusions in Banach spaces. Cocoercive mappings, a generalization of monotone mappings, were defined by Tseng [11], Magnanti and Perakis [12], and Zhu and Marcotte [13]. Ahmad et al. [2,3,14] pioneered the study of $H(.,.)$-cocoercive mappings, $H(.,.)$-co-accretive mappings, and $H(.,.)$-co-monotone mappings and elucidated their characteristics and fundamental properties.

Luo and Huang [15] presented B-monotone operators in Banach spaces, which was a significant achievement. Their contribution not only defined these operators but also provided their proximal mapping, therefore guiding arguments on the solution to a new class of variational inclusions in Banach spaces. In this continuation, S. Z. Nazemi [16] made a recent and noteworthy contribution by investigating a new class of $C_n$-monotone mappings and their associated proximal point mapping. Nazemi’s study played a very crucial role in finding an approximate solution to a novel class of variational inclusions.

Motivated by significant progress in the field, this current study offers a new angle for continuing research. Building upon these strides, we embark on a comprehensive examination of a novel class of ${\mathcal{B}}^l$-co-monotone mappings, a generalization of $C_n$-monotone mappings. This class is defined as the amalgamation of cocoercive and symmetric monotone mappings, inspired by the concept of $H(.,.)$-co-accretive mappings pioneered by Ahmad et al. [3].

Based on previous studies, this work presents the fresh idea of ${\mathcal{B}}^l$-co-monotone mappings in Banach spaces. This new notion extends the definitions of B-monotone mappings from [15] and $C_n$-monotone mappings from [16]. We also develop a new proximal mapping specifically designed for these ${\mathcal{B}}^l$-co-monotone mappings via B-monotone and $C_n$-monotone mappings. We establish a broad framework for an implicit algorithm that involves a sequence of multi-valued ${\mathcal{B}}^l$-co-monotone mappings. Moving forward, we delve into convergence analysis within a Banach space, addressing a broad class of nonlinear implicit variational inclusion problems. Our proof of the algorithm’s iterative sequence convergence is extended by modifying the condition from a uniformly smooth Banach space (defined by ${\rho }_X\left(t\right)\le C{t}^2$) to a q-uniformly smooth Banach space. Crucially, the performed convergence analysis of the iterative sequences generated by the proposed algorithm significantly extends the results established in [15,16]. Overall, the findings presented herein broaden and generalize several important results previously reported in the literature. Its novel, integrative approach propels it into numerous exciting applications in economics, optimization, control theory, and more, fostering dynamic academic discourse and laying the foundation for pioneering future research and real-world solutions. To substantiate our theoretical advancements, we have included a numerical experiment, visually represented using MATLAB 2015a.

Let $C\left(X\right)$ and $CB\left(X\right)$ denote the families of all nonempty compact subsets of X, and the families of all nonempty closed, and bounded subsets of $\left(X\right)$, respectively. Let $\mathcal{D}(.,.)$ be the Hausdorff metric on $CB\left(X\right)$ defined by

$$\mathcal{D}(U,V)=\max \left\{\underset{d\in U}{\sup }(d,V),\underset{e\in V}{\sup }(U,e)\right\},\forall U,V\in CB\left(X\right).$$

(2)

Definition 1

 ([17]). For $q>1$, a generalized duality mapping ${\mathcal{J}}_q:X\rightrightarrows X^{\ast }$ is defined by

$$\begin{array}{ccc}& & {\mathcal{J}}_q\left(d\right)=\{g\in X^{\ast }:\langle d,g\rangle ={\parallel d\parallel }^q{,\parallel d\parallel }^{q-1}=\parallel g\parallel \},\forall d\in X.\hfill \end{array}$$

In particular, ${\mathcal{J}}_2$ is the usual normalized duality mapping on X. It is well known that

$$\begin{array}{c}\hfill {\mathcal{J}}_q\left(d\right)={\parallel d\parallel }^{q-2}{\mathcal{J}}_2\left(d\right),(d\ne 0)\in X.\end{array}$$

Note that if $X=H$ is a real Hilbert space, then ${\mathcal{J}}_2$ becomes the identity mapping on H.

Definition 2

 ([17]). A Banach space X is said to be smooth if, for each $d\in X$ with $\parallel d\parallel =1$, there exists a unique $g\in X^{\ast }$ such that $\parallel g\parallel =g\left(d\right)=1$. The modulus of smoothness of X is the function ${\rho }_X:[0,\infty )\to [0,\infty )$, which is defined by

$$\begin{array}{c}\hfill {\rho }_X\left(t\right)=\sup \left\{{\displaystyle \frac{\parallel d+e\parallel +\parallel d-e\parallel }{2}}-1:,d,e\in X,\parallel d\parallel =1,\parallel e\parallel \le t\right\}.\end{array}$$

A Banach space X is called uniformly smooth if

$$\underset{t\to 0}{\lim }{\displaystyle \frac{{\rho }_X\left(t\right)}{t}}=0.$$

X is called q-uniformly smooth if there exists $c_q>0$ such that

$${\rho }_X\left(t\right)\le c_q{t}^q,q>1.$$

It is well known that

$$l_q(or L_q)=\left\{\begin{array}{cc}\mathrm{q}\text{-}\mathrm{uniformly}\mathrm{smooth},\mathrm{if}\hfill & 1<q\le 2\hfill \\ 2\text{-}\mathrm{uniformly}\mathrm{smooth},\mathrm{if}\hfill & q\ge 2.\hfill \end{array}\right.$$

Xu [17] established the following lemma concerning characteristic inequalities in q-uniformly smooth Banach spaces, which applies when X is uniformly smooth.

Lemma 1.

 ([17]). Let $q>1$ be a real number and X be a real smooth Banach space. Then X is q-uniformly smooth iff there exists a non-negative constant $c_q>0$ such that for each $d,e\in X,$

$${\parallel d+e\parallel }^q\le {\parallel d\parallel }^q+q\langle e,{\mathcal{J}}_q\left(e\right)\rangle +c_q{\parallel e\parallel }^q.$$

Lemma 2.

 ([18]). Let two non-negative real sequences $\left\{c_k\right\}$ and $\left\{d_k\right\}$, satisfying $c_{k+1}\le (1-{\widehat{\alpha }}_k)c_k+d_k,k\ge 0,$ with ${\widehat{\alpha }}_k\in [0,1]$, ${\sum }_{k=0}^{\infty }{\widehat{\alpha }}^k=\infty$ and $d_k=o\left({\widehat{\alpha }}_k\right)$. Then $c_k⟶0$ as $k⟶\infty .$

Definition 3.

A multi-valued mapping $T:X\rightrightarrows CB\left(X\right)$ is said to be $\mathcal{D}$-Lipschitz-continuous if there exists a constant $\lambda >0$ such that

$$\begin{array}{c}\hfill \mathcal{D}(Td,Te)\le \lambda \parallel d-e\parallel ,\forall d,e\in X,\end{array}$$

where $\mathcal{D}(.,.)$ represents the Hausdorff metric on $CB\left(X\right)$.

We briefly state the following well-known terminology before providing crucial definitions for the demonstration of this research.

Definition 4.

Let $g:X\to X$ be single-valued mappings; then,

(i) 

g is called r-strongly monotone if there exists some constant $r>0$ such that

$$\begin{array}{c}\hfill 〈g\left(d\right)-g\left(e\right),d-e〉\ge r{\parallel d-e\parallel }^2,\forall d,e\in X;\end{array}$$

(ii) 

g is called s-relaxed monotone if there exists some constant $s>0$ such that

$$\begin{array}{c}\hfill 〈g\left(d\right)-g\left(e\right),d-e〉\ge -s{\parallel d-e\parallel }^2,\forall d,e\in X;\end{array}$$

(iii) 

g is called t-Lipschitz-continuous if there exists some constant $t>0$ such that

$$\begin{array}{c}\hfill \parallel g\left(d\right)-g\left(e\right)\parallel \le t\parallel d-e\parallel ,\forall d,e\in X;\end{array}$$

(iv) 

g is called α-expansive if there exists some constant $\alpha >0$ such that

$$\begin{array}{c}\hfill \parallel g\left(d\right)-g\left(e\right)\parallel \ge \alpha \parallel d-e\parallel ,\forall d,e\in X.\end{array}$$

Definition 5.

A single-valued mapping $p:X\to X$ is $(\beta ,\gamma )$-cocoercive iff there exist $j_q(d-e)\in {\mathcal{J}}_q(d-e)$ and some constants $\beta ,\gamma >0$ such that

$$\begin{array}{c}\hfill 〈j_q(d-e),p\left(d\right)-p\left(e\right)〉\ge {-\beta \parallel p\left(d\right)-p\left(e\right)\parallel }^q+\gamma {\parallel d-e\parallel }^q,\forall d,e\in X,\end{array}$$

where ${\mathcal{J}}_q$ is the normalized duality mapping.

Definition 6.

Let ${\mathcal{B}}^l:X\times X\to X^{\ast }$, $g_1,g_2:X\to X$ be single-valued mappings. Then ${\mathcal{B}}^l$ is called

(i) 

${\gamma }_1$-cocoercive with respect to $g_1$ if there exists some constant ${\gamma }_1>0$ such that

$$\begin{array}{c}\hfill 〈{\mathcal{B}}^l(g_1\left(d\right),u)-{\mathcal{B}}^l(g_1\left(e\right),u),d-e〉\ge {\gamma }_1{\parallel g_1\left(d\right)-g_2\left(e\right)\parallel }^2,\forall d,e,u\in X;\end{array}$$

(ii) 

${\gamma }_2$-relaxed cocoercive with respect to $g_2$ if there exists some constant ${\gamma }_2>0$ such that

$$\begin{array}{c}\hfill 〈{\mathcal{B}}^l(u,g_2\left(d\right))-{\mathcal{B}}^l(u,g_2\left(e\right)),d-e〉\ge -{\gamma }_2{\parallel g_1\left(d\right)-g_2\left(e\right)\parallel }^2,\forall d,e,u\in X;\end{array}$$

(iii) 

${\gamma }_1{\gamma }_2$-symmetric cocoercive with respect to $g_1,g_2$ if ${\mathcal{B}}^l$ is ${\gamma }_1$-cocoercive with respect to $g_1$ and ${\gamma }_2$-relaxed cocoercive with respect to $g_2$.

(iv) 

$l_1$-Lipschitz-continuous in the first component if there exists some constant $l_1>0$ such that

$$\begin{array}{c}\hfill \parallel {\mathcal{B}}^l(d,u)-{\mathcal{B}}^l(e,u)\parallel \le l_1\parallel d-e\parallel ,\forall d,e,u\in X;\end{array}$$

(v)

$l_2$-Lipschitz-continuous in the second component if there exists some constant $l_2>0$ such that

$$\begin{array}{c}\hfill \parallel {\mathcal{B}}^l(u,d)-{\mathcal{B}}^l(u,e)\parallel \le l_2\parallel d-e\parallel ,\forall d,e,u\in X.\end{array}$$

Definition 7.

Let $i\in \{1,2,...,l\}$, where $l\ge 3$ and $\mathcal{M}:X^l\rightrightarrows X^{\ast }$ bisa multi-valued mapping and $f_1,f_2,...,f_l:X⊸X$ are the single-valued mappings. Then $\mathcal{M}$ is called

(i) 

${\mu }_i$-strongly monotone with respect to $f_i$ if there exists some constant ${\mu }_i>0$ such that

$$\begin{array}{ccc}& & 〈v_i-v_i^{\prime },d-e〉\ge {\mu }_i{\parallel d-e\parallel }^2,\forall d,e,u_1,...,u_{i-1},u_{i+1},...,u_l\in X,\hfill \\ & & v_i\in \mathcal{M}(u_1,...,u_{i-1},f_i\left(d\right),u_{i+1},...,u_l),v_i^{\prime }\in \mathcal{M}(u_1,...,u_{i-1},f_i\left(e\right),u_{i+1},...,u_l);\hfill \end{array}$$

(ii) 

${\overline{\mu }}_i$-relaxed monotone with respect to $f_i$ if there exists some constant ${\overline{\mu }}_i>0$ such that

$$\begin{array}{ccc}& & 〈v_i-v_i^{\prime },d-e〉\ge -{\overline{\mu }}_i{\parallel d-e\parallel }^2,\forall d,e,u_1,...,u_{i-1},u_{i+1},...,u_l\in X,\hfill \\ & & v_i\in \mathcal{M}(u_1,...,u_{i-1},f_i\left(d\right),u_{i+1},...,u_l),v_i^{\prime }\in \mathcal{M}(u_1,...,u_{i-1},f_i\left(e\right),u_{i+1},...,u_l);\hfill \end{array}$$

(iii) 

${\mu }_1{\overline{\mu }}_2{\mu }_3{\overline{\mu }}_4...{\mu }_{l-1}{\overline{\mu }}_l$-symmetric monotone with respect to $f_1,f_2,...,f_l$ iff for $i\in \{1,3,...,l-1\}$, $\mathcal{M}$ is ${\mu }_i$-strongly monotone with respect to $f_i$ and for $i\in \{2,4,...,l\}$, and $\mathcal{M}$ is ${\overline{\mu }}_i$-relaxed monotone with respect to $f_i$, where l is even, satisfying

$$\sum _{i=odd}{\mu }_i\ge \sum _{j=even}{\overline{\mu }}_i,\mathrm{and}\sum _{i=odd}{\mu }_i=\sum _{i=even}{\overline{\mu }}_i\mathrm{iff}d=e;$$

(iv) 

${\mu }_1{\overline{\mu }}_2{\mu }_3{\overline{\mu }}_4...{\overline{\mu }}_{l-1}{\mu }_l$-symmetric monotone with respect to $f_1,f_2,...,f_l$ iff for $i\in \{1,3,...,l\}$, $\mathcal{M}$ is ${\mu }_i$-strongly monotone with respect to $f_i$ and for $i\in \{2,4,...,l-1\}$, and $\mathcal{M}$ is ${\overline{\mu }}_i$-relaxed monotone with respect to $f_i$, where l is odd, satisfying

$$\sum _{i=odd}{\mu }_i\ge \sum _{i=even}{\overline{\mu }}_i,\mathrm{and}\sum _{i=odd}{\mu }_i=\sum _{i=even}{\overline{\mu }}_i\mathrm{iff}d=e.$$

Definition 8.

Let $i\in \{1,2,...,l\},$ with $l\ge 3$. Let multi-valued mappings $T_i:X\rightrightarrows X^{\ast }$ and single-valued mapping $F:X^l\to X^{\ast }$; then, F is said to be ${\gamma }_i$-Lipschitz-continuous in the $i^{th}$ component if there exists some constant ${\gamma }_{T_i}>0$ such that

$$\begin{array}{ccc}& & \parallel F(v_1,..,v_{i-1},d,v_{i+1}...v_l)-F(v_1,..,v_{i-1},e,v_{i+1}...v_l)\parallel \le {\gamma }_{T_i}\parallel d-e\parallel ,\hfill \\ & & \forall w_1,w_2,v_1,..,v_{i-1},v_{i+1}...v_l\in X,d\in T_i\left(w_1\right),e\in T_i\left(w_2\right).\hfill \end{array}$$

2. ${\mathcal{B}}^l$-Co-Monotone Mappings

Let $i\in \{1,2,...,l\}$, where $l\ge 3$. Assume that $\mathcal{M}:X^l\rightrightarrows X^{\ast }$ is a multi-valued mapping and ${\mathcal{B}}^l:X\times X\to X^{\ast }$, $g_1,g_2,f_1,f_2,...f_l:X\to X$ are single-valued mappings. The new class of generalized ${\mathcal{B}}^l$-co-monotone mapping is now introduced and studied.

Definition 9.

Let X be a Banach space with its dual space $X^{\ast }$. Let $l\ge 3$ and $g_1,g_2,f_1,f_2,...,f_l:X\to X$ be single-valued mappings. Let ${\mathcal{B}}^l$ be ${\gamma }_1{\gamma }_2$-symmetric cocoercive with respect to $g_1,g_2$; then, $\mathcal{M}$ is said to be a generalized ${\mathcal{B}}^l$-co-monotone with respect to mappings $(g_1,g_2,f_1,f_2,...,f_l)$

(i) 

iff $\mathcal{M}$ is ${\mu }_1{\overline{\mu }}_2{\mu }_3{\overline{\mu }}_4...{\mu }_{l-1}{\overline{\mu }}_l$-symmetric monotone with respect to $f_1,f_2,...,f_l$ and

$\left({\mathcal{B}}^l(g_1,g_2)+\lambda \mathcal{M}(f_1,f_2,...,f_l)\right)$$\left(X\right)=X^{\ast }$ for each $\lambda >0$ if l is even;

(ii) 

iff $\mathcal{M}$ is ${\mu }_1{\overline{\mu }}_2{\mu }_3{\overline{\mu }}_4...{\overline{\mu }}_l{\mu }_{l-1}$-symmetric monotone with respect to $f_1,f_2,...,f_l$ and

$\left({\mathcal{B}}^l(g_1,g_2)+\lambda \mathcal{M}(f_1,f_2,...,f_l)\right)$$\left(X\right)=X^{\ast }$ for each $\lambda >0$ if l is odd.

Remark 1.

(i) 

If $\mathcal{M}(.,.,...)=\mathcal{M}(.,.)$, then ${\mathcal{B}}^l$-co-monotone reduces to $H(.,.)$-co-monotone mapping, proposed and studied by Ahmad et al. [2],

(ii) 

If ${\mathcal{B}}^l(.,.)$ is accretive with $g_1,g_2$ and $\mathcal{M}(.,.,...)=\mathcal{M}(.)$, then ${\mathcal{B}}^l$-co-monotone reduces to $H(.,.)$-accretive mapping, proposed and studied by Zou and Huang et al. [9,10].

(iii) 

If $g_1=g_2\equiv 0$ and $\mathcal{M}(.,.,...)=\mathcal{M}(.,.)$, generalized ${\mathcal{B}}^l$-co-monotone reduces to B-monotone mapping, proposed and studied by Luo and Huang [15];

(iv) 

If $g_1=g_2\equiv 0$, generalized ${\mathcal{B}}^l$-co-monotone reduces to $C_n$-monotone mapping, proposed and studied by Nazemi [16];

(v) 

If ${\mathcal{B}}^l(.,.)$ is accretive with $g_1,g_2$ and $\mathcal{M}(.,.,...)=\mathcal{M}(.,.)$, then ${\mathcal{B}}^l$-co-monotone reduces to generalized $\alpha \beta$-$H(.,.)$-accretive mapping, proposed and studied by Kazmi et al. [19],

Whenever $\mathcal{M}$ is ${\mathcal{B}}^l$-co-monotone, it provides the following information:

(i)

${\mathcal{B}}^l$ is ${\gamma }_1{\gamma }_2$ symmetric cocoercive with respect to $g_1.g_2$ and ${\gamma }_1>{\gamma }_2$, respectively;

(ii)

$\mathcal{M}$ is symmetric monotone with respect to $f_1,f_2,...,f_l$ with constants ${\mu }_1,{\overline{\mu }}_2,...,{\mu }_{l-1},{\overline{\mu }}_l$, respectively, if l is even;

(iii)

$\mathcal{M}$ is symmetric monotone with respect to $f_1,f_2,...,f_l$ with constants ${\mu }_1,{\overline{\mu }}_2,...,{\overline{\mu }}_{l-1},{\mu }_l$, respectively, if l is odd.

To simplify our discussion, we can assume that l is an even number in the next text.

Lemma 3.

Let X be a Banach space with its dual space $X^{\ast }$. Let $l\ge 3$ and $f_1,f_2,...,f_l:X\to X$ be single-valued mappings, and let $\mathcal{M}:X^l\rightrightarrows X^{\ast }$ be a ${\mu }_1{\overline{\mu }}_2{\mu }_3{\overline{\mu }}_4...{\mu }_{l-1}{\overline{\mu }}_l$-symmetric monotone with respect to mappings $(f_1,f_2,...,f_l)$. Then for any $d,e\in X$,

$$〈v^{\ast }-w^{\ast },d-e〉\ge K_l{\parallel d-e\parallel }^2,$$

(3)

where $K_l={\mu }_1-{\overline{\mu }}_1+{\mu }_2-{\overline{\mu }}_2+...-{\mu }_{l-1}+{\overline{\mu }}_l.$

Proof. 

Let $u_1^{\ast }\in \mathcal{M}(f_{1}d,f_{2}e,...,f_{l}e)$, $u_2^{\ast }\in \mathcal{M}(f_{1}d,f_{2}d,...,f_{l}e)$, and $u_{l-1^{\ast }}\in \mathcal{M}(f_{1}d,f_{2}d,...,f_{l-1}d,f_{l}e)$. From Definition 7, we have

$$\begin{array}{c}〈v^{\ast }-w^{\ast },d-e〉\ge 〈v^{\ast }-u_1^{\ast },d-e〉+〈u_1^{\ast }-u_2^{\ast },d-e〉+...+〈u_{l-1}^{\ast }-w^{\ast },d-e〉\hfill \\ \ge {\mu }_1{\parallel d-e\parallel }^2-{\overline{\mu }}_1{\parallel d-e\parallel }^2+...+{\overline{\mu }}_l{\parallel d-e\parallel }^2\hfill \\ \ge K_1{\parallel d-e\parallel }^2,\hfill \end{array}$$

(4)

where $K_l={\mu }_1-{\overline{\mu }}_1+{\mu }_2-{\overline{\mu }}_2+...-{\mu }_{l-1}+{\overline{\mu }}_l$. Hence, we obtain the required result. □

Theorem 1.

Let X be a Banach space with its dual space $X^{\ast }$. Let $l\ge 3$ and $g_1,g_2,f_1,f_2,...,f_l:X\to X$ be single-valued mappings. Let $g_1$ be a ${\alpha }_1$-expansive and $g_2$ be a ${\alpha }_2$-Lipschitz-continuous, and let $\mathcal{M}:X^l\rightrightarrows X^{\ast }$ be a ${\mathcal{B}}^l$-co-monotone mapping with respect to mappings $(g_1,g_2,f_1,f_2,...,f_l)$ and ${\gamma }_1>{\gamma }_2,{\alpha }_1>{\alpha }_2,\sum {\mu }_i>\sum {\overline{\mu }}_j$; then, $({\mathcal{B}}^l(g_1,g_2)+\lambda \mathcal{M}$$(f_1,f_2,...,f_l){)}^{-1}$ is single-valued.

Proof. 

Suppose, on the contrary, that there exists $d,e\in W,$$d^{\ast }\in X^{\ast }$ such that $d,e\in {\left({\mathcal{B}}^l(g_1,g_2)+\lambda \mathcal{M}(f_1,f_2,...,f_l)\right)}^{-1}\left(d^{\ast }\right)$. It follows that

$$\begin{array}{ccc}& & d={\left({\mathcal{B}}^l(g_1,g_2)+\lambda \mathcal{M}(f_1,f_2,...,f_l)\right)}^{-1}\left(d^{\ast }\right),\hfill \\ & & e={\left({\mathcal{B}}^l(g_1,g_2)+\lambda \mathcal{M}(f_1,f_2,...,f_l)\right)}^{-1}\left(d^{\ast }\right).\hfill \end{array}$$

This implies that

$$\begin{array}{ccc}& & -{\mathcal{B}}^l(g_{1}d,g_{2}d)+d^{\ast }\in \lambda \mathcal{M}(f_1,f_2,...,f_l)\left(d\right),\hfill \\ & & -{\mathcal{B}}^l(g_{1}e,g_{2}e)+d^{\ast }\in \lambda \mathcal{M}(f_1,f_2,...,f_l)\left(e\right).\hfill \end{array}$$

By using the Lemma 3 and ${\mathcal{B}}^l$ is ${\gamma }_1{\gamma }_2$-symmetric cocoercive with respect to $g_1,g_2$, respectively, we have

$$\begin{array}{ccc}& & K_l{\parallel d-e\parallel }^2\le 〈{\displaystyle \frac{1}{\lambda }}\left(-{\mathcal{B}}^l(g_{1}d,g_{2}d)+d^{\ast }\right)-{\displaystyle \frac{1}{\lambda }}\left(-{\mathcal{B}}^l(g_{1}e,g_{2}e)+d^{\ast })\right),d-e〉\hfill \end{array}$$

After simplifying, we get

$$\begin{array}{ccc}& & ({\gamma }_1{{\alpha }_1}^2-{\gamma }_2{{\alpha }_2}^2+\lambda K_l{)\parallel d-e\parallel }^2\le 0.\hfill \end{array}$$

Since $K_l>0$, ${\alpha }_1>{\alpha }_2$, ${\gamma }_1>{\gamma }_2$, it implies that $d=e$. Hence ${({\mathcal{B}}^l(g_1,g_2)+\lambda \mathcal{M}(f_1,f_2,...,f_l))}^{-1}$ is single-valued. Similarly, the result can be established if l is odd. □

Using Theorem 1, we can establish the proximal-point mapping ${\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}$.

Definition 10.

Let X be a Banach space with its dual space $X^{\ast }$. Let $l\ge 3$ and $g_1,g_2,f_1,f_2,...,f_l:X\to X$ be single-valued mappings. Let $\mathcal{M}:X^l\rightrightarrows X^{\ast }$ be a ${\mathcal{B}}^l$-co-monotone mapping with respect to mappings $(g_1,g_2,f_1,f_2,...,f_l)$; then, proximal-point mapping ${\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}:X^{\ast }\to X$ is defined as

$$\begin{array}{ccc}\hfill & & {\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d^{\ast }\right)={\left({\mathcal{B}}^l(g_1,g_2)+\lambda \mathcal{M}(f_1,f_2,...,f_l)\right)}^{-1}\left(d^{\ast }\right),\forall d^{\ast }\in X^{\ast }.\hfill \end{array}$$

(5)

Theorem 2.

Let X be a Banach space with its dual space $X^{\ast }$. Let $l\ge 3$ and $g_1,g_2,f_1,f_2,...,f_l:X\to X$ be single-valued mappings. Let $g_1$ be a ${\alpha }_1$-expansive and $g_2$ be a ${\alpha }_2$-Lipschitz-continuous, and Let $\mathcal{M}:X^l\rightrightarrows X^{\ast }$ be a ${\mathcal{B}}^l$-co-monotone mapping with respect to mappings $(g_1,g_2,f_1,f_2,...,f_l)$ and ${\gamma }_1>{\gamma }_2,{\alpha }_1>{\alpha }_2,\sum {\mu }_i>\sum {\overline{\mu }}_j$; then, proximal-point mapping ${\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}:X^{\ast }\to X$ is ${\displaystyle \frac{1}{\left[{\gamma }_1{{\alpha }_1}^2-{\gamma }_2{{\alpha }_2}^2+\lambda K_l\right]}}$-Lipschitz-continuous, where $K_l=\sum {\mu }_i-\sum {\overline{\mu }}_j$.

Proof. 

Let any given $d^{\ast },e^{\ast }\in X^{\ast }$, and from Definition 10, it follows that

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d^{\ast }\right)={\left({\mathcal{B}}^l(g_1,g_2)+\lambda \mathcal{M}(f_1,f_2,...,f_l)\right)}^{-1}\left(d^{\ast }\right),\hfill \\ {\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(e^{\ast }\right)={\left({\mathcal{B}}^l(g_1,g_2)+\lambda \mathcal{M}(f_1,f_2,...,f_l)\right)}^{-1}\left(e^{\ast }\right).\hfill \end{array}\right.\end{array}$$

This implies that

$$\begin{array}{ccc}& & {\lambda }^{-1}\left(d^{\ast }-{\mathcal{B}}^l\left(g_1\left({\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d^{\ast }\right)\right),g_2\left({\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d^{\ast }\right)\right)\right)\right)\hfill \\ & & \in \mathcal{M}\left(f_1\left({\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d^{\ast }\right)\right),f_2\left({\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d^{\ast }\right)\right),...,f_l\left({\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d^{\ast }\right)\right)\right),\hfill \\ & & {\lambda }^{-1}\left(e^{\ast }-{\mathcal{B}}^l\left(g_1\left({\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(e^{\ast }\right)\right),g_2\left({\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(e^{\ast }\right)\right)\right)\right)\hfill \\ & & \in \mathcal{M}\left(f_1\left({\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(e^{\ast }\right)\right),f_2\left({\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(e^{\ast }\right)\right),...,f_l\left({\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(e^{\ast }\right)\right)\right).\hfill \end{array}$$

By using Lemma 3, and when ${\mathcal{B}}^l$ is ${\gamma }_1{\gamma }_2$-symmetric cocoercive with respect to $g_1,g_2$, respectively, we have

$$\begin{array}{ccc}\hfill & & {\displaystyle \frac{1}{\lambda }}\langle \left(d^{\ast }-{\mathcal{B}}^l\left(g_1\left({\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d^{\ast }\right)\right),g_2\left({\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d^{\ast }\right)\right)\right)\right)-\left(e^{\ast }-{\mathcal{B}}^l\left(g_1\left({\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(e^{\ast }\right)\right),g_2\left({\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(e^{\ast }\right)\right)\right)\right),\hfill \\ & & {\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d^{\ast }\right)-{\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(e^{\ast }\right)\rangle \ge K_l\parallel {\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d^{\ast }\right)-{\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(e^{\ast }\right){\parallel }^2.\hfill \end{array}$$

(6)

Since ${\mathcal{B}}^l$ is symmetric cocoercive mapping with respect to mappings $g_1,g_2$ and $\mathcal{M}$ is symmetric monotone, then we have

$$\begin{array}{ccc}\hfill & & \parallel d^{\ast }-e^{\ast }\parallel \parallel {\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d^{\ast }\right)-{\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(e^{\ast }\right)\parallel \ge {\lambda }^{-1}〈d^{\ast }-e^{\ast },{\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d^{\ast }\right)-{\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(e^{\ast }\right)〉\hfill \\ & & \ge \langle {\mathcal{B}}^l\left(g_1\left({\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d^{\ast }\right)\right),g_2\left({\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d^{\ast }\right)\right)\right)-{\mathcal{B}}^l\left(g_1\left({\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(e^{\ast }\right)\right),g_2\left({\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(e^{\ast }\right)\right)\right),\hfill \\ & & {\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d^{\ast }\right)-{\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(e^{\ast }\right)\rangle +\lambda K_l\parallel {\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d^{\ast }\right)-{\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(e^{\ast }\right){\parallel }^2\hfill \\ & & \ge \left(\lambda K_l+{\gamma }_1{{\alpha }_1}^2-{\gamma }_2{{\alpha }_2}^2\right)\parallel {\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d^{\ast }\right)-{\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(e^{\ast }\right){\parallel }^2.\hfill \end{array}$$

(7)

From (6) and (7), we obtain the following result:

$$\begin{array}{ccc}& & \parallel {\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d^{\ast }\right)-{\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(e^{\ast }\right)\parallel \le {\displaystyle \frac{1}{\left({\gamma }_1{{\alpha }_1}^2-{\gamma }_2{{\alpha }_2}^2+\lambda K_l\right)}}\parallel d^{\ast }-e^{\ast }\parallel ,\forall d^{\ast },e^{\ast }\in X^{\ast },\hfill \end{array}$$

where $K_l=\sum {\mu }_i-\sum {\overline{\mu }}_j$. □

3. Main Result

In this section, we will demonstrate how the new ${\mathcal{B}}^l$-co-monotone operator might be useful for resolving variational inclusions problem [VIP] of type (1) in Banach spaces with the proper assumptions.

Let $l\ge 3$, $g_1,g_2,f_1,f_2,...,f_l:X\to X$, $p:X\to X$, $\mathcal{K}:X\to X^{\ast }$, ${\mathcal{B}}^l:X\times X\to X^{\ast }$, and $F:X^l\to X^{\ast }$ be single-valued mappings and $T_i:X\rightrightarrows CB\left(X^{\ast }\right)$, $(i=1,2,...,l)$ be multi-valued mappings. Let multi-valued mapping $\mathcal{M}:X^l\rightrightarrows X^{\ast }$ be a ${\mathcal{B}}^l$-co-monotone mapping with respect to mappings $(g_1,g_2,f_1,f_2,...,f_l)$. Now, the VIP is to find for any given $c\in X^{\ast }$$d\in X,v_1\in T_1\left(d\right),v_2\in T_2\left(d\right),...,v_l\in T_l\left(d\right)$ such that

$$c\in \mathcal{K}((d-p\left(d\right))-F(v_1,v_2,...,v_l)+\mathcal{M}(f_1\left(d\right),f_2\left(d\right),...,f_l\left(d\right)).$$

(8)

We note that problem (8) contains many different types of variational inclusion. The following are some examples of special cases:

(i)

If $F(v_1,v_2,...,v_l)=F(v_1,v_2,v_3)$ and $\mathcal{M}(f_1\left(d\right),f_2\left(d\right),...,f_l\left(d\right))=\mathcal{M}(f_1\left(d\right),f_2\left(d\right))$, then problem (8) coincides with (9) studied in [15]: for given $c\in X^{\ast }$, $d\in X, v_1\in T_1\left(d\right),v_2\in T_2\left(d\right),v_3\in T_3\left(d\right)$ such that

$$c\in \mathcal{K}\left(d\right)-F(v_1,v_2,v_3)+\mathcal{M}(f_1\left(d\right),f_2\left(d\right)).$$

(9)

(ii)

If $F(v_1,v_2,...,v_l)=F(v_1,v_2,v_3)$ and $\mathcal{M}(f_1\left(d\right),f_2\left(d\right),...,f_l\left(d\right))=\mathcal{M}(f_1\left(d\right),d)$, then problem (8) coincides with (10) studied in [5]: for given $c\in X^{\ast }$, $d\in X,v_1\in T_1\left(d\right),v_2\in T_2\left(d\right),v_3\in T_3\left(d\right)$ such that

$$c\in \mathcal{K}\left(d\right)-F(v_1,v_2,v_3)+\mathcal{M}(f_1\left(d\right),d)).$$

(10)

(iii)

If $c=0,F=0,$$f_2,f_3=...=f_l=0$ and $\mathcal{M}(f_1\left(d\right),f_2\left(d\right),...,f_l\left(d\right))=\mathcal{M}\left(f_1\left(d\right)\right)$, then problem (8) coincides with (11) studied in [6]: for given $d\in X$ such that

$$0\in \mathcal{K}\left(d\right)+\mathcal{M}\left(f_1\left(d\right)\right).$$

(11)

(iv)

If $c=0,F=0,$ and $\mathcal{M}(f_1\left(d\right),f_2\left(d\right),...,f_l\left(d\right))=\mathcal{M}\left(d\right)$, then problem (8) coincides with (12) studied in [20,21,22]: for given $d\in X$ such that

$$0\in \mathcal{K}\left(d\right)+\mathcal{M}\left(d\right).$$

(12)

Lemma 4.

Let us consider VIP (8). If $(d,v_1,v_2,...,v_l)$, where $d\in X$, $v_1\in T_1\left(d\right),v_2\in T_2\left(d\right),...,v_l\in T_l\left(d\right)$ is a solution of VIP (8) if and only if $(d,v_1,v_2,...,v_l)$ satisfies the following relation:

$$\begin{array}{c}\hfill d={\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}[{\mathcal{B}}^l(g_1,g_2)\left(d\right)-\lambda \mathcal{K}((d-p\left(d\right))+\lambda c+\lambda F(v_1,v_2,...,v_l)].\end{array}$$

(13)

Proof. 

Let $(d,v_1,v_2,...,v_l)$ be a solution of VIP (8); then, $(d,v_1,v_2,...,v_l)$ satisfy the following condition:

$$\begin{array}{ccc}& & c\in \mathcal{K}((d-p\left(d\right))-F(v_1,v_2,...,v_l)+\mathcal{M}(f_1\left(d\right),f_2\left(d\right),...,f_l\left(d\right)).\hfill \\ & & \iff \lambda c+\lambda F(v_1,v_2,...,v_l)-\lambda \mathcal{K}((d-p\left(d\right))\in \lambda \mathcal{M}(f_1\left(d\right),f_2\left(d\right),...,f_l\left(d\right)).\hfill \\ & & \iff {\mathcal{B}}^l(g_{1}d,g_{2}d)-\lambda \mathcal{K}((d-p\left(d\right))+\lambda c+\lambda F(v_1,v_2,...,v_l)\hfill \\ & & \in {\mathcal{B}}^l(g_{1}d,g_{2}d)+\lambda \mathcal{M}(f_1\left(d\right),f_2\left(d\right),...,f_l\left(d\right)).\hfill \end{array}$$

Let

$$\begin{array}{ccc}\hfill & & d^{\ast }={\mathcal{B}}^l(g_{1}d,g_{2}d)-\lambda \mathcal{K}((d-p\left(d\right))+\lambda c+\lambda F(v_1,v_2,...,v_l).\hfill \end{array}$$

(14)

By using the resolvant operator ${\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}$, we obtain

$$\begin{array}{c}\hfill d={\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d^{\ast }\right)={\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}[{\mathcal{B}}^l(g_1,g_2)\left(d\right)-\lambda \mathcal{K}((d-p\left(d\right))+\lambda c+\lambda F(v_1,v_2,...,v_l)].\end{array}$$

(15)

□

Building upon Lemma 4, we propose a general iterative scheme to find an approximate solution of VIP (8) along with its variant formulations. A key distinguishing feature of this procedure, unlike existing methods in the literature, is the incorporation of a sequence of multi-valued A-maximal monotone mappings within the framework of Hilbert spaces. In the current context, however, the newly introduced Algorithm 1 extends this concept further by generalizing it to a broader class of proximal-point (or resolvent) mappings, thereby paving the way for more recent algorithmic innovations.

Algorithm 1.

For any given $d_0\in X$, select $v_0^1\in T_1\left(d_0\right),v_0^2\in T_2\left(d_0\right),...,v_0^l\in T_l\left(d_0\right)$ and obtain $\left\{d_k\right\}$, $\left\{v_k^1\right\}$, $\left\{v_k^2\right\}$,..., $\left\{v_k^l\right\}$ via the following iterative algorithm:

$$\begin{array}{ccc}& & d_{k+1}=(1-{\widehat{\alpha }}_k)d_k+{\widehat{\alpha }}_k{\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}[{\mathcal{B}}^l(g_1,g_2)\left(d_k\right)-\lambda \mathcal{K}(d_k-p\left(d_k\right))\hfill \\ & & +\lambda c+\lambda F(v_k^1,v_k^2,...,v_k^l)],\hfill \\ & & v_k^l\in T_1\left(d_k\right):\parallel v_{k+1}^l-v_k^1\parallel \le \mathcal{D}\left(T_1\left(d_{k+1}\right),T_1\left(d_k\right)\right),\hfill \\ & & v_k^2\in T_2\left(d_k\right):\parallel v_{k+1}^2-v_k^2\parallel \le \mathcal{D}\left(T_2\left(d_{k+1}\right),T_2\left(d_k\right)\right),\hfill \\ & & :\hfill \\ & & :\hfill \\ & & v_k^l\in T_l\left(d_k\right):\parallel v_{k+1}^l-v_k^l\parallel \le \mathcal{D}\left(T_1\left(d_{k+1}\right),T_1\left(d_k\right)\right),\hfill \end{array}$$

where $0\le {\widehat{\alpha }}_k\le 1,$$\lambda >0,$ and $k=0,1,2,....$.

Now we present a theorem in which we investigate the existence of a unique solution to the variational inclusion problem (8) as follows:

Theorem 3.

Let X be a q-uniformly smooth Banach space with its dual space $X^{\ast }$. Let $l\ge 3$ and $g_1,g_2,f_1,f_2,...,f_l:X\to X$, $p:X\to X$ be single-valued mappings such that p is $(\beta ,\gamma )$-relaxed cocoercive and ${\lambda }_p$-Lipschitz-continuous, $g_1$ be a ${\alpha }_1$-Lipschitz-continuous and $g_2$ be ${\alpha }_2$-expansive, and $\mathcal{M}:X^l\rightrightarrows X^{\ast }$ be ${\mathcal{B}}^l$-co-monotone mapping. Let $\mathcal{K}:X\to X^{\ast }$ be a ${\lambda }_{\mathcal{K}}$-Lipschitz-continuous mapping and $T_1,T_2,...,T_l:X\rightrightarrows CB\left(X\right)$ be $\mathcal{D}$-Lipschitz-continuous with constant ${\lambda }_1,{\lambda }_2,...,{\lambda }_l$, respectively. Suppose that $F:X^l\to X^{\ast }$ is ${\gamma }_{T_i}$ - Lipschitz-continuous with $T_i,(i=1,2,...,l)$ and the following condition is satisfied:

$$\begin{array}{ccc}\hfill & & 0<{\displaystyle \frac{\left[\left(l_1{\alpha }_1+l_2{\alpha }_2\right)+\lambda {\lambda }_{\mathcal{K}}{\left(1+q\beta {\lambda }_p^q-q\gamma +c_q{\lambda }_p^q\right)}^{\frac{1}{q}}+\lambda \left({\gamma }_{T_1}{\lambda }_1+{\gamma }_{T_2}{\lambda }_2+...+{\gamma }_{T_l}{\lambda }_l\right)\right]}{\left({\gamma }_1{{\alpha }_1}^2-{\gamma }_2{{\alpha }_2}^2+\lambda K_l\right)}}<1,\hfill \end{array}$$

(16)

where $K_l=\sum {\mu }_i-\sum {\overline{\mu }}_j$. Then, the general nonlinear operator Equation (8) based on ${\mathcal{B}}^l$-co-monotone mapping framework has a unique solution $(d,v^1,v^2,..,v^l)$ in X.

Proof. 

Let us consider the mapping $\mathcal{Q}:X\to X$, given by

$$\begin{array}{ccc}\hfill & & \mathcal{Q}\left(d\right)={\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left[{\mathcal{B}}^l(g_1,g_2)\left(d\right)-\lambda \mathcal{K}\left(d\right)+\lambda c+\lambda F(v_1,v_2,...,v_l)\right].\hfill \end{array}$$

(17)

Using (17) and Theorem 2, we have

$$\begin{array}{ccc}\hfill & & \parallel \mathcal{Q}\left(d\right)-\mathcal{Q}\left(e\right)\parallel =\parallel {\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left[{\mathcal{B}}^l(g_1,g_2)\left(d\right)-\lambda \mathcal{K}((d-p\left(d\right))+\lambda c+\lambda F(v_1,v_2,...,v_l)\right]\hfill \\ & & -{\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left[{\mathcal{B}}^l(g_1,g_2)\left(e\right)-\lambda \mathcal{K}((e-p\left(e\right))+\lambda c+\lambda F(w_1,w_2,...,w_l)\right]\parallel \hfill \\ & & \le {\displaystyle \frac{1}{\left({\gamma }_1{{\alpha }_1}^2-{\gamma }_2{{\alpha }_2}^2+\lambda K_l\right)}}\parallel {\mathcal{B}}^l(g_1,g_2)\left(d\right)-\lambda \mathcal{K}((d-p\left(d\right))+\lambda c+\lambda F(v_1,v_2,...,v_l)\hfill \\ & & -\left({\mathcal{B}}^l(g_1,g_2)\left(e\right)-\lambda \mathcal{K}((e-p\left(e\right))+\lambda c+\lambda F(w_1,w_2,...,w_l)\right)\parallel \hfill \\ & & \le {\displaystyle \frac{1}{\left({\gamma }_1{{\alpha }_1}^2-{\gamma }_2{{\alpha }_2}^2+\lambda K_l\right)}}[\parallel {\mathcal{B}}^l(g_1,g_2)\left(d\right)-{\mathcal{B}}^l(g_1,g_2)\left(d\right)\parallel \hfill \\ & & +\lambda \parallel \mathcal{K}((d-p\left(d\right))-\mathcal{K}((e-p\left(e\right))\parallel +\lambda \parallel F(v_1,v_2,...,v_l)-F(w_1,w_2,...,w_l)\parallel ].\hfill \end{array}$$

(18)

As $\mathcal{B}$ satisfies $(l_1,l_2)$-Lipschitz continuity in both arguments, and given that $g_1$ is ${\alpha }_1$-expansive while $g_2$ is ${\alpha }_2$-Lipschitz-continuous, then we have

$$\begin{array}{ccc}\hfill & & \parallel {\mathcal{B}}^l(g_1,g_2)\left(d\right)-{\mathcal{B}}^l(g_1,g_2)\left(e\right)\parallel \le \parallel {\mathcal{B}}^l(g_{1}d,g_{2}d)-{\mathcal{B}}^l(g_{1}e,g_{2}d)\parallel \hfill \\ & & +\parallel {\mathcal{B}}^l(g_{1}e,g_{2}d)-{\mathcal{B}}^l(g_{1}e,g_{2}e)\parallel \hfill \\ & & \le l_1\parallel g_1\left(d\right)-g_1\left(e\right)\parallel +l_2\parallel g_2\left(d\right)-g_2\left(e\right)\parallel \hfill \\ & & \le l_1{\alpha }_1\parallel d-e\parallel +l_2{\alpha }_2\parallel d-e\parallel \hfill \\ & & \le \left(l_1{\alpha }_1+l_2{\alpha }_2\right)\parallel d-e\parallel .\hfill \end{array}$$

(19)

Since $\mathcal{K}$ is a $l_{\mathcal{K}}$-Lipschitz-continuous, we have

$$\begin{array}{ccc}\hfill & & \parallel \mathcal{K}(d-p\left(d\right))-\mathcal{K}(e-p\left(e\right))\parallel \le {\lambda }_{\mathcal{K}}\parallel \mathcal{K}(d-p\left(d\right))-\mathcal{K}(e-p\left(e\right))\parallel \hfill \\ & & \le {\lambda }_{\mathcal{K}}\parallel d-e-\left(p\left(d\right)-p\left(e\right)\right)\parallel .\hfill \end{array}$$

(20)

Since p is a $(\beta ,\gamma )$-relaxed cocoercive mapping and ${\lambda }_p$-Lipschitz-continuous, and using the Lemma 1, we have

$$\begin{array}{ccc}\hfill & & \parallel d-e-(p\left(d\right)-p\left(e\right)){\parallel }^q\le \parallel d-e{\parallel }^q-q〈p\left(d\right)-p\left(e\right),{\mathcal{J}}_q(d-e)〉+c_q\parallel p\left(d\right)-p\left(e\right){\parallel }^q\hfill \\ & & \le \parallel d-e{\parallel }^q+q\beta \parallel p\left(d\right)-p\left(e\right){\parallel }^q-q\gamma \parallel d-e{\parallel }^q+c_q\parallel p\left(d\right)-p\left(e\right){\parallel }^q\hfill \\ & & \le \parallel d-e{\parallel }^q+q\beta {\lambda }_p^q\parallel d-e{\parallel }^q-q\gamma \parallel d-e{\parallel }^q+c_q{\lambda }_p^q\parallel d-e{\parallel }^q\hfill \\ & & \le \left(1+q\beta {\lambda }_p^q-q\gamma +c_q{\lambda }_p^q\right)\parallel d-e{\parallel }^q.\hfill \end{array}$$

(21)

Since F is ${\gamma }_{T_i}$-Lipschitz-continuous with respect to mapping $T_i$ and $T_i$ is ${\lambda }_i$-$\mathcal{D}$-Lipschitz-continuous, $i\in \{1,2,...,l\}$, we have

$$\begin{array}{ccc}\hfill & & \parallel F(v^1,v^2,...,v^l)-F(w^1,w^2,...,w^l)\parallel \hfill \\ & & \le \parallel F\left(v^1,v^2,...,v^l\right)-F\left(w^1,v^2,...,v^l\right)\parallel +\parallel F\left(w^1,v^2,...,v^l\right)-F\left(w^1,w^2,...,v^l\right)\parallel \hfill \\ & & +\parallel F\left(w^1,w^2,...,v^l\right)-F\left(w^1,w^2,...,w^l\right)\parallel \hfill \\ & & \le {\gamma }_{T_1}\parallel v^1-w^1\parallel +{\gamma }_{T_2}\parallel v^2-w^2\parallel +...+{\gamma }_{T_l}\parallel v^l-w^l\parallel \hfill \\ & & \le {\gamma }_{T_1}\mathcal{D}\left(T_1\left(d\right),T_1\left(e\right)\right)+{\gamma }_{T_2}\mathcal{D}\left(T_2\left(d\right),T_2\left(e\right)\right)+...+{\gamma }_{T_l}\mathcal{D}\left(T_l\left(d\right),T_l\left(e\right)\right)\hfill \\ & & \le \left({\gamma }_{T_1}{\lambda }_1+{\gamma }_{T_2}{\lambda }_2+...+{\gamma }_{T_l}{\lambda }_l\right)\parallel d-e\parallel .\hfill \end{array}$$

(22)

Using Equations (19)–(22) in Equation (18), we have

$$\begin{array}{ccc}& & \parallel \mathcal{Q}\left(d\right)-\mathcal{Q}\left(e\right)\parallel \le {\displaystyle \frac{1}{\left({\gamma }_1{{\alpha }_1}^2-{\gamma }_2{{\alpha }_2}^2+\lambda K_l\right)}}[\left(l_1{\alpha }_1+l_2{\alpha }_2\right)+\lambda {\lambda }_{\mathcal{K}}{\left(1+q\beta {\lambda }_p^q-q\gamma l+c_q{\lambda }_p^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ & & +\lambda ({\gamma }_{T_1}{\lambda }_1+{\gamma }_{T_2}{\lambda }_2+...+{\gamma }_{T_l}{\lambda }_l\left)\right]\parallel d-e\parallel .\hfill \end{array}$$

Let

$$\begin{array}{ccc}\hfill & & \parallel \mathcal{Q}\left(d\right)-\mathcal{Q}\left(e\right)\parallel \le \theta \parallel d-e\parallel ,\hfill \end{array}$$

(23)

where

$$\begin{array}{c}\hfill \theta ={\displaystyle \frac{\left[\left(l_1{\alpha }_1+l_2{\alpha }_2\right)+\lambda {\lambda }_{\mathcal{K}}{\left(1+q\beta {\lambda }_p^q-q\gamma +c_q{\lambda }_p^q\right)}^{\frac{1}{q}}+\lambda \left({\gamma }_{T_1}{\lambda }_1+{\gamma }_{T_2}{\lambda }_2+...+{\gamma }_{T_l}{\lambda }_l\right)\right]}{\left({\gamma }_1{{\alpha }_1}^2-{\gamma }_2{{\alpha }_2}^2+\lambda K_l\right)}}.\end{array}$$

(24)

From condition (16), we have

$$\begin{array}{c}\hfill {\displaystyle \frac{\left[\left(l_1{\alpha }_1+l_2{\alpha }_2\right)+\lambda {\lambda }_{\mathcal{K}}{\left(1+q\beta {\lambda }_p^q-q\gamma +c_q{\lambda }_p^q\right)}^{\frac{1}{q}}+\lambda \left({\gamma }_{T_1}{\lambda }_1+{\gamma }_{T_2}{\lambda }_2+...+{\gamma }_{T_l}{\lambda }_l\right)\right]}{\left({\gamma }_1{{\alpha }_1}^2-{\gamma }_2{{\alpha }_2}^2+\lambda K_l\right)}}<1.\end{array}$$

(25)

Thus, we have $0\le \theta <1$. It follows from (23) that mapping Q, given below, is a contraction mapping in $\mathcal{W}$, and, consequently, it has a unique fixed point d in $\mathcal{W}$,

$$\mathcal{Q}\left(d\right)={\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left[{\mathcal{B}}^l(g_1,g_2)\left(d\right)-\lambda \mathcal{K}(d-p\left(d\right))+\lambda c+\lambda F(v_1,v_2,...,v_l)\right],\forall d\in X.$$

Hence $(d,v^1,v^2,..,v^l)$ is a unique solution of VIP (8). □

Under the assumption that l is an even number $(l\ge 3)$, we next present a theorem in which a generalized algorithm is utilized to approximate a solution of VIP (8). With appropriate conditions, we demonstrate that the generated sequence exhibits linear convergence. The following assumptions further support the convergence of the sequence constructed by Algorithm 1.

Theorem 4.

Let X be a q-uniformly smooth Banach space with its dual space $X^{\ast }$. Let $l\ge 3$ and $g_1,g_2,f_1,f_2,...,f_l:X\to X$, $p:X\to X$ be single-valued mappings such that p is $(\beta ,\gamma )$-relaxed cocoercive and ${\lambda }_p$-Lipschitz-continuous, $g_1$ is ${\alpha }_1$-Lipschitz-continuous, and $g_2$ is ${\alpha }_2$-expansive, and let $\mathcal{M}:X^l\rightrightarrows X^{\ast }$ be a ${\mathcal{B}}^l$-co-monotone mapping. Let $\mathcal{K}:X\to X^{\ast }$ be a ${\lambda }_{\mathcal{K}}$-Lipschitz-continuous mapping and $T_1,T_2,...,T_l:X\rightrightarrows CB\left(X\right)$ be $\mathcal{D}$-Lipschitz-continuous with constant ${\lambda }_1,{\lambda }_2,...,{\lambda }_l$, respectively. Suppose that $F:X^l\to X^{\ast }$ is ${\gamma }_{T_i}$- Lipschitz-continuous with $T_i,(i=1,2,...,l)$ and the following condition is satisfied:

$$\begin{array}{ccc}\hfill & & 0<{\displaystyle \frac{\left[\left(l_1{\alpha }_1+l_2{\alpha }_2\right)+\lambda {\lambda }_{\mathcal{K}}{\left(1+q\beta {\lambda }_p^q-q\gamma +c_q{\lambda }_p^q\right)}^{\frac{1}{q}}+\lambda \left({\gamma }_{T_1}{\lambda }_1+{\gamma }_{T_2}{\lambda }_2+...+{\gamma }_{T_l}{\lambda }_l\right)\right]}{\left({\gamma }_1{{\alpha }_1}^2-{\gamma }_2{{\alpha }_2}^2+\lambda K_l\right)}}<1,\hfill \end{array}$$

(26)

${\widehat{\alpha }}_k\in [0,1]$ and ${\sum }_{k=0}^{\infty }{\widehat{\alpha }}_k=\infty$, where $K_l=\sum {\mu }_i-\sum {\overline{\mu }}_j$. Then the iterative sequences

$(\left\{d_k\right\},\left\{v_k^1\right\},\left\{v_k^2\right\},....,\left\{v_k^l\right\})$ developed by Algorithm 1 converge strongly to $(d,v^1,v^2,..,v^l)$ a solution of SVLIP (8).

Proof. 

We proceed to prove that the sequence $\left\{d_k\right\}$ converges to d as $k\to \infty$. This result is a direct consequence of Theorem 2 in conjunction with the structure of Algorithm 1 that

$$\begin{array}{ccc}& & \parallel d_{k+1}-d_k\parallel \hfill \\ & & =\parallel (1-{\widehat{\alpha }}_k)d_k+{\widehat{\alpha }}_k{\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left[{\mathcal{B}}^l(g_1,g_2)\left(d_k\right)-\lambda \mathcal{K}\left(d_k-p\left(d_k\right)\right)+\lambda c+\lambda F\left(v_k^1,v_k^2,...,v_k^l\right)\right]\hfill \\ & & -(1-{\widehat{\alpha }}_k)d_{k-1}+{\widehat{\alpha }}_k{\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left[{\mathcal{B}}^l(g_1,g_2)\left(d_{k-1}\right)-\lambda \mathcal{K}\left(d_{k-1}-p(d_{k-1}\right)\right)\hfill \\ & & +\lambda c+\lambda F\left(v_{k-1}^1,v_{k-1}^2,...,v_{k-1}^l\right)]\parallel \hfill \\ & & \le \parallel (1-{\widehat{\alpha }}_k)\left(d_k-d_{k-1}\right)+{\displaystyle \frac{{\alpha }_k}{\left({\gamma }_1{{\alpha }_1}^2-{\gamma }_2{{\alpha }_2}^2+\lambda K_l\right)}}\times \hfill \\ & & [\left({\mathcal{B}}^l(g_1,g_2)\left(d_k\right)-\lambda \mathcal{K}\left(d_k-p\left(d_k\right)\right)+\lambda c+\lambda F\left(v_k^1,v_k^2,...,v_k^l\right)\right)\hfill \\ & & -\left({\mathcal{B}}^l(g_1,g_2)\left(d_{k-1})-\lambda \mathcal{K}\left(d_{k-1}-p(d_{k-1}\right)\right)+\lambda c+\lambda F\left(v_{k-1}^1,v_{k-1}^2,...,v_{k-1}^l\right)\right)]\parallel \hfill \\ & & \le (1-{\widehat{\alpha }}_k)\parallel (d_k-d_{k-1})\parallel +{\displaystyle \frac{{\alpha }_k}{\left({\gamma }_1{{\alpha }_1}^2-{\gamma }_2{{\alpha }_2}^2+\lambda K_l\right)}}\times \hfill \end{array}$$

$$\begin{array}{ccc}\hfill & & \parallel \left({\mathcal{B}}^l(g_1,g_2)\left(d_k\right)-{\mathcal{B}}^l(g_1,g_2)\left(d_{k-1}\right)\right)+\lambda \left(\mathcal{K}(d_k-p\left(d_k\right))-\mathcal{K}(d_{k-1}-p\left(d_{k-1}\right))\right)\hfill \\ & & +\lambda \left(F\left(v_k^1,v_k^2,...,v_k^l\right)-F\left(v_{k-1}^1,v_{k-1}^2,...,v_{k-1}^l\right)\right)\parallel \hfill \\ & & \le (1-{\widehat{\alpha }}_k)\parallel d_k-d_{k-1}\parallel +{\displaystyle \frac{{\alpha }_k}{\left({\gamma }_1{{\alpha }_1}^2-{\gamma }_2{{\alpha }_2}^2+\lambda K_l\right)}}\times \hfill \\ & & [\parallel {\mathcal{B}}^l(g_1,g_2)\left(d_k\right)-{\mathcal{B}}^l(g_1,g_2)\left(d_{k-1}\right)\parallel +\lambda \parallel \mathcal{K}\left(d_k-p\left(d_k\right)\right)-\mathcal{K}\left(d_{k-1}-p\left(d_{k-1}\right)\right)\parallel \hfill \\ & & +\lambda \parallel F\left(v_k^1,v_k^2,...,v_k^l\right)-F\left(v_{k-1}^1,v_{k-1}^2,...,v_{k-1}^l\right)\parallel ].\hfill \end{array}$$

(27)

As ${\mathcal{B}}^l$ satisfies $(l_1,l_2)$-Lipschitz continuity in both arguments, and given that $g_1$ is ${\alpha }_1$-expansive while $g_2$ is ${\alpha }_2$-Lipschitz-continuous, in light of Equation (19) with these arguments, we have

$$\begin{array}{ccc}\hfill & & \parallel {\mathcal{B}}^l(g_1,g_2)\left(d_k\right)-{\mathcal{B}}^l(g_1,g_2)\left(d_{k-1}\right)\parallel \le \left(l_1{\alpha }_1+l_2{\alpha }_2\right)\parallel d_k-d_{k-1}\parallel \hfill \end{array}$$

(28)

Since $\mathcal{K}$ is a ${\lambda }_{\mathcal{K}}$-Lipschitz-continuous, we have

$$\begin{array}{ccc}\hfill & & \parallel \mathcal{K}\left(d_k-p\left(d_k\right)\right)-\mathcal{K}\left(d_{k-1}-p\left(d_{k-1}\right)\right)\parallel \le {\lambda }_{\mathcal{K}}\parallel d_k-d_{k-1}-\left(p\left(d_k\right)-p\left(d_{k-1}\right)\right)\parallel .\hfill \end{array}$$

(29)

Since p is a $(\beta ,\gamma )$-relaxed cocoercive and ${\lambda }_p$-Lipschitz-continuous mapping, by applying Lemma 1 and considering Equation (20) under these assumptions, we obtain the following result:

$$\begin{array}{ccc}\hfill & & \parallel d_k-d_{k-1}-(p\left(d_k\right)-p\left(d_{k-1}\right)){\parallel }^q\le \left(1+q\beta {\lambda }_p^q-q\gamma +c_q{\lambda }_p^q\right)\parallel d_k-d_{k-1}{\parallel }^q.\hfill \end{array}$$

(30)

Using (30) in (29), we obtain

$$\parallel \mathcal{K}\left(d_k-p\left(d_k\right)\right)-\mathcal{K}\left(d_{k-1}-p\left(d_{k-1}\right)\right)\parallel \le {\lambda }_{\mathcal{K}}{\left(1+q\beta {\lambda }_p^q-q\gamma +c_q{\lambda }_p^q\right)}^{{\displaystyle \frac{1}{q}}}\parallel d_k-d_{k-1}\parallel .$$

(31)

Given that F is ${\gamma }_{T_i}$-Lipschitz-continuous with respect to $T_i$, and $T_i$ is ${\lambda }_i$-$\mathcal{D}$-Lipschitz-continuous for each $i\in \{1,2,...l\}$, in view of Equation (21), we obtain the following:

$$\begin{array}{ccc}\hfill & & \parallel F\left(v_k^1,v_k^2,...,v_k^l)-F(v_{k-1}^1,v_{k-1}^2,...,v_{k-1}^l\right)\parallel \le \left({\gamma }_{T_1}{\lambda }_1+{\gamma }_{T_2}{\lambda }_2+...+{\gamma }_{T_l}{\lambda }_l\right)\parallel d_k-d_{k-1}\parallel .\hfill \end{array}$$

(32)

Using (28), (31), and (32) in (27), we obtain

$$\begin{array}{ccc}& & \parallel d_{k+1}-d_k\parallel \le (1-{\widehat{\alpha }}_k)\parallel d_k-d_{k-1}\parallel \hfill \\ & & +{\displaystyle \frac{(l_1{\alpha }_1+l_2{\alpha }_2)+\lambda {\lambda }_{\mathcal{K}}{\left(1+q\beta {\lambda }_p^q-q\gamma +c_q{\lambda }_p^q\right)}^{\frac{1}{q}}+\lambda +\lambda \left({\gamma }_{T_1}{\lambda }_1+{\gamma }_{T_2}{\lambda }_2+...+{\gamma }_{T_l}{\lambda }_l\right)}{\left({\gamma }_1{{\alpha }_1}^2-{\gamma }_2{{\alpha }_2}^2+\lambda K_l\right)}}\hfill \\ & & \times {\widehat{\alpha }}_k\parallel d_k-d_{k-1}\parallel \hfill \\ & & =\left[1-{\widehat{\alpha }}_k\left(1-{\displaystyle \frac{(l_1{\alpha }_1+l_2{\alpha }_2)+\lambda {\lambda }_{\mathcal{K}}{\left(1+q\beta {\lambda }_p^q-q\gamma +c_q{\lambda }_p^q\right)}^{\frac{1}{q}}+\lambda +\lambda \left({\gamma }_{T_1}{\lambda }_1+...+{\gamma }_{T_l}{\lambda }_l\right)}{\left({\gamma }_1{{\alpha }_1}^2-{\gamma }_2{{\alpha }_2}^2+\lambda K_l\right)}}\right)\right]\hfill \end{array}$$

$$\begin{array}{ccc}\hfill & & \times \parallel d_k-d_{k-1}\parallel \hfill \\ & & =\left[1-{\widehat{\alpha }}_k(1-{\theta }_k)\right]\parallel d_k-d_{k-1}\parallel ,\hfill \end{array}$$

(33)

where

$$\begin{array}{c}\hfill {\theta }_k={\displaystyle \frac{(l_1{\alpha }_1+l_2{\alpha }_2)+\lambda {\lambda }_{\mathcal{K}}{\left(1+q\beta {\lambda }_p^q-q\gamma +c_q{\lambda }_p^q\right)}^{\frac{1}{q}}+\lambda +\lambda \left({\gamma }_{T_1}{\lambda }_1+{\gamma }_{T_2}{\lambda }_2+...+{\gamma }_{T_l}{\lambda }_l\right)}{\left({\gamma }_1{{\alpha }_1}^2-{\gamma }_2{{\alpha }_2}^2+\lambda K_l\right)}}.\end{array}$$

From (26), $0<{\theta }_k<1$. This implies that $(1-{\theta }_k)\in (0,1]$ and ${\sum }_{k=0}^{\infty }{\delta }_k(1-{\theta }_k)=\infty$. Using the Lemma 2, we obtain

$$\begin{array}{ccc}& & \underset{k\to \infty }{\lim }\parallel d_{k+1}-d_k\parallel ⟶0.\hfill \end{array}$$

Thus, $\left\{d_k\right\}$ becomes a Cauchy sequence in X. Therefore, there exists $d\in X$ as $d_k⟶d$ as $k⟶0$. From Algorithm 1, we have

$$\begin{array}{ccc}& & \parallel v_{k+1}^1-v_k^1\parallel \le \mathcal{D}\left(T_1\left(d_{k+1}\right),T_1\left(d_k\right)\right)\le {\gamma }_{T_1}\parallel d_{k+1}-d_k\parallel ,\hfill \\ & & \parallel v_{k+1}^2-v_k^2\parallel \le \mathcal{D}\left(T_2\left(d_{k+1}\right),T_2\left(d_k\right)\right)\le {\gamma }_{T_2}\parallel d_{k+1}-d_k\parallel ,\hfill \\ & & :\hfill \\ & & :\hfill \\ & & \parallel v_{k+1}^l-v_k^l\parallel \le \mathcal{D}\left(T_l\left(d_{k+1}\right),T_l\left(d_k\right)\right)\le {\gamma }_{T_l}\parallel d_{k+1}-d_k\parallel .\hfill \end{array}$$

This shows that $\left\{v_k^1\right\},\left\{v_k^2\right\},....,\left\{v_k^l\right\}$ are Cauchy sequences; then, there exists $v^1,v^2,...v^l$ such that $v_k^1\to v^1,v_k^2\to v^2,...,v_k^l\to v^l,$ as $k\to \infty$.

Via the continuity of ${\mathcal{B}}^l,g_1,g_2,f_1,f_2,...f_l,T_1,T_2,...,T_l$, and ${\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}$, we know that $(d,v^1,v^2,...,v^l)$ is satisfying the following relation:

$$\begin{array}{c}\hfill d={\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left[{\mathcal{B}}^l(g_1,g_2)\left(d\right)-\lambda \mathcal{K}\left((d-p(d)\right)+\lambda c+\lambda F\left(v_1,v_2,...,v_l\right)\right].\end{array}$$

Now, we show that $v^1\in T_1\left(d\right)$. Since $v_k^1\in T_1\left(d_k\right)$, we have

$$\begin{array}{ccc}& & d\left(v^1,T_1\left(d\right)\right)\le \parallel v^1-v_k^1\parallel +d\left(v_k^1,T_1\left(d\right)\right)\hfill \\ & & \le \parallel v^2-v_k^2\parallel +\mathcal{D}\left(T_1\left(d_k\right),T_1\left(d\right)\right)\hfill \\ & & \le \parallel v^l-v_k^l\parallel +{\gamma }_{T_1}\parallel d_k-d\parallel ⟶0ask\to \infty .\hfill \end{array}$$

Since $T_1\left(d\right)$ is closed, thus $v^1\in T_1\left(d\right)$. Similarly, we can prove $v^2\in T_2\left(d\right), v^3\in T_3\left(d\right),...,v^l\in T_l\left(d\right)$. By Lemma 4, VIP (8) has a solution $\left(d^1,v^1,v^2,...,v^l\right)$. □

4. Numerical Experiment

We provide the following numerical example to show the convergence graph of Theorem 4 with the computation table using MATLAB 2015a.

Example 1.

Let X be 2-uniformly smooth Banach space and $X=\mathbb{R}$. If l is even and $g_1,g_2:\mathbb{R}\to \mathbb{R}$ are given by

$$\begin{array}{ccc}& & g_1\left(d\right)={\displaystyle \frac{7d}{5}},g_2\left(d\right)={\displaystyle \frac{4d}{5}},\forall d\in \mathbb{R}.\hfill \end{array}$$

Assume that $B^l:\mathbb{R}\times \mathbb{R}\to \mathbb{R}$ is defined by

$$\begin{array}{ccc}& & B^l(g_1\left(d\right),g_2\left(d\right))=g_1\left(d\right)-g_2\left(d\right).\hfill \end{array}$$

Let for any $u\in \mathbb{R}$,

$$\begin{array}{c}\begin{array}{cc}\hfill 〈B^l\left(g_1\left(d\right),u\right)-B^l\left(g_1\right.& \left(e\right),u),d-e\rangle =〈g_1\left(d\right)-u-g_1\left(e\right)+u,d-e〉\hfill \\ \hfill & =〈g_1\left(d\right)-g_1\left(e\right),d-e〉\hfill \\ \hfill & =〈{\displaystyle \frac{7d}{5}}-{\displaystyle \frac{7e}{5}},d-e〉\hfill \\ \hfill & ={\displaystyle \frac{7}{5}}{(d-e)}^2={\displaystyle \frac{7}{5}}{\parallel d-e\parallel }^2;\hfill \\ \hfill {∥g_i\left(d\right)-g_1\left(e\right)∥}^2& =〈g_1\left(d\right)-g_1\left(e\right),g_1\left(d\right)-g_1\left(e\right)〉\hfill \\ \hfill & =〈{\displaystyle \frac{7d}{5}}-{\displaystyle \frac{7e}{5}},{\displaystyle \frac{7d}{5}}-{\displaystyle \frac{7e}{5}}〉\hfill \\ \hfill & ={\displaystyle \frac{49}{25}}{(d-e)}^2={\displaystyle \frac{49}{25}}{\parallel d-e\parallel }^2.\hfill \end{array}\hfill \\ Thus,〈B^l\left(g_1\left(d\right),u\right)-B^l\left(g_1\left(e\right),u\right),d-e〉={\displaystyle \frac{5}{7}}{\parallel d-e\parallel }^2\ge {\displaystyle \frac{9}{14}}{\parallel d-e\parallel }^2.\hfill \end{array}$$

Therefore, $B^l$ is ${\displaystyle \frac{9}{14}}$-strongly cocoercive with respect to $g_1$.

$$\begin{array}{ccc}& & 〈B^l(u,g_2\left(d\right))-B^l(u,g_2\left(e\right)),d-e〉=〈u-g_2\left(d\right)-u+g_2\left(e\right),d-e〉\hfill \\ & & =-〈g_2\left(d\right)-g_2\left(e\right),d-e〉\hfill \\ & & =-〈{\displaystyle \frac{4d}{5}}-{\displaystyle \frac{4e}{5}},d-e〉\hfill \\ & & =-{\displaystyle \frac{4}{5}}{(d-e)}^2=-{\displaystyle \frac{4}{5}}{\parallel d-e\parallel }^2;\hfill \\ & & \parallel g_2\left(d\right)-g_2\left(e\right){\parallel }^2=〈g_2\left(d\right)-g_2\left(e\right),g_2\left(d\right)-g_2\left(e\right)〉\hfill \\ & & =〈{\displaystyle \frac{4d}{5}}-{\displaystyle \frac{4e}{5}},{\displaystyle \frac{4d}{5}}-{\displaystyle \frac{4e}{5}}〉\hfill \\ & & ={\displaystyle \frac{16}{25}}{\parallel d-e\parallel }^2.\hfill \\ & & \mathrm{Thus},〈B^l(u,g_2\left(d\right))-B^l(u,g_2\left(e\right)),d-e〉=-{\displaystyle \frac{5}{4}}\parallel g_2\left(d\right)-g_2\left(e\right){\parallel }^2\ge -{\displaystyle \frac{11}{8}}\parallel g_2\left(d\right)-g_2\left(e\right){\parallel }^2.\hfill \end{array}$$

Therefore, $B^l$ is ${\displaystyle \frac{11}{8}}$-relaxed cocoercive with respect to $g_2$.

$$\begin{array}{ccc}& & \parallel g_1\left(d\right)-g_1\left(e\right)\parallel =\parallel {\displaystyle \frac{7d}{5}}-{\displaystyle \frac{7e}{5}}\parallel ={\displaystyle \frac{7}{5}}\parallel d-e\parallel \ge {\displaystyle \frac{13}{10}}\parallel d-e\parallel ;\hfill \\ & & \parallel g_2\left(d\right)-g_2\left(e\right)\parallel =\parallel {\displaystyle \frac{4d}{5}}-{\displaystyle \frac{4e}{5}}\parallel ={\displaystyle \frac{4}{5}}\parallel d-e\parallel \le {\displaystyle \frac{8}{9}}\parallel d-e\parallel .\hfill \end{array}$$

This implies that $g_1$ is ${\displaystyle \frac{13}{10}}$-expansive and $g_2$ is ${\displaystyle \frac{8}{9}}$-Lipschitz-continuous.

Let l be even, and for each $i\in \{1,2,...,p\}$, $f_i:\mathbb{R}\to \mathbb{R}$ is given by

$$\begin{array}{ccc}& & f_1\left(d\right)={\displaystyle \frac{2d}{5}},f_3\left(d\right)={\displaystyle \frac{2d}{5}},....,f_{l-1}\left(d\right)={\displaystyle \frac{2d}{5}},\hfill \\ & & f_2\left(d\right)={\displaystyle \frac{d}{15}},f_4\left(d\right)={\displaystyle \frac{d}{15}},...,f_l\left(d\right)={\displaystyle \frac{d}{15}}.\hfill \end{array}$$

Let the multi-valued mapping $\mathcal{M}:{\mathbb{R}}^l\rightrightarrows \mathbb{R}$ be defined by

$$\begin{array}{ccc}& & \mathcal{M}(f_1\left(d\right),f_2\left(d\right),...,f_{l-1}\left(d\right),f_l\left(d\right))=f_1\left(d\right)-f_2\left(d\right)+...+f_{l-1}\left(d\right)-f_l\left(d\right).\hfill \end{array}$$

For any $u_2,u_3,...,u_l\in \mathbb{R}$,

$$\begin{array}{ccc}& & 〈\mathcal{M}(f_1\left(d\right),u_2,...,u_l)-\mathcal{M}(f_1\left(e\right),u_2,...,u_l),d-e〉\hfill \\ & & =〈f_1\left(d\right)-f_1\left(e\right),d-e〉\hfill \\ & & =〈{\displaystyle \frac{2d}{5}}-{\displaystyle \frac{2e}{5}},d-e〉\hfill \\ & & ={\displaystyle \frac{2}{5}}{(y-z)}^2\hfill \\ & & \ge {\displaystyle \frac{3}{10}}{(d-e)}^2={\displaystyle \frac{3}{10}}{\parallel d-e\parallel }^2.\hfill \end{array}$$

Thus, $\mathcal{M}$ is ${\displaystyle \frac{3}{10}}$-strongly monotone with respect to $f_1$. Similarly, we can show that $\mathcal{M}$ is ${\displaystyle \frac{3}{10}}$-strongly monotone with respect to $f_i$ for each $i\in \{1,3,...,l-1\}$.

Let for any $u_i,u_3,...,u_l\in \mathbb{R}$,

$$\begin{array}{ccc}& & 〈\mathcal{M}(u_1,f_2\left(d\right),...,u_l)-\mathcal{M}(u_1,f_2\left(e\right),...,u_l),d-e〉\hfill \\ & & =-〈f_2\left(d\right)-f_2\left(e\right),d-e〉\hfill \\ & & =-〈{\displaystyle \frac{d}{15}}-{\displaystyle \frac{e}{15}},d-e〉\hfill \\ & & =-{\displaystyle \frac{1}{15}}{(d-e)}^2\hfill \\ & & \ge -{\displaystyle \frac{3}{30}}{(d-e)}^2=-{\displaystyle \frac{1}{10}}{\parallel d-e\parallel }^2.\hfill \end{array}$$

Thus, $\mathcal{M}$ is ${\displaystyle \frac{16}{15}}$-relaxed monotone with respect to $f_2$. Similarly, we can show that $\mathcal{M}$ is ${\displaystyle \frac{1}{10}}$-relaxed monotone with respect to $f_i$ for each $i\in \{2,4,...,l\}$.

One can easily verify the following for $\lambda =1$:

$$\begin{array}{ccc}& & [B^l(g_1,g_2)+\lambda \mathcal{M}(f_1,f_2,...,f_l)]\left(\mathbb{R}\right)=\mathbb{R}.\hfill \end{array}$$

The proximal-point mappings for $l=8,\lambda =1$, is given by

$$\begin{array}{ccc}& & {\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d\right)={[{\mathcal{B}}^l(g_1,g_2)+\mathcal{M}(f_1,f_2,...,f_l)]}^{-1}\left(d\right)={\displaystyle \frac{15d}{17}}.\hfill \end{array}$$

In addition

$$\begin{array}{ccc}& & \parallel {\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(d\right)-{\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left(e\right)\parallel =\parallel {\displaystyle \frac{15d}{17}}-{\displaystyle \frac{15e}{17}}\parallel ={\displaystyle \frac{15}{17}}\parallel d-e\parallel \le {\displaystyle \frac{31}{34}}\parallel d-e\parallel .\hfill \end{array}$$

Hence, the proximal-point mapping is for ${\displaystyle \frac{31}{34}}$-Lipschitz-continuous.

Let $p,\mathcal{K}:\mathbb{R}\to \mathbb{R}$ be given by $p\left(d\right)={\displaystyle \frac{d}{4}},\mathcal{K}\left(d\right)={\displaystyle \frac{6d}{5}}$

$$\begin{array}{ccc}& & \parallel p\left(d\right)-p\left(e\right)\parallel =\parallel {\displaystyle \frac{d}{4}}-{\displaystyle \frac{e}{4}}\parallel ={\displaystyle \frac{1}{4}}\parallel d-e\parallel \le {\displaystyle \frac{2}{7}}\parallel d-e\parallel ;\hfill \\ & & \parallel \mathcal{K}\left(d\right)-\mathcal{K}\left(e\right)\parallel =\parallel {\displaystyle \frac{6d}{5}}-{\displaystyle \frac{6e}{5}}\parallel ={\displaystyle \frac{6}{5}}\parallel d-e\parallel \le {\displaystyle \frac{12}{9}}\parallel d-e\parallel .\hfill \end{array}$$

Thus, mappings $p,\mathcal{K}$ are ${\displaystyle \frac{2}{7}},{\displaystyle \frac{12}{9}}$-Lipschitz-continuous, respectively.

Assume that single-valued mapping $F:{\mathbb{R}}^l\to \mathbb{R}$ is defined by

$$\begin{array}{ccc}& & F(v_1,v_2,...,v_{l-1},v_l)={\displaystyle \frac{1}{2}}{v}_1+{\displaystyle \frac{1}{3}}{v}_2+...+{\displaystyle \frac{1}{l}}{v}_{l-1}+{\displaystyle \frac{1}{l+1}}{v}_l.\hfill \end{array}$$

$$\begin{array}{ccc}& & \parallel F(v_1,v_2,...,v_{l-1},v_l)-F(w_1,w_2,...,w_{l-1},w_l)\parallel \hfill \\ & & =\parallel \left({\displaystyle \frac{1}{2}}{v}_1+{\displaystyle \frac{1}{3}}{v}_2+...+{\displaystyle \frac{1}{l}}{v}_{l-1}+{\displaystyle \frac{1}{l+1}}{v}_l\right)-\left({\displaystyle \frac{1}{2}}{w}_1+{\displaystyle \frac{1}{3}}{w}_2+...+{\displaystyle \frac{1}{l}}{w}_{l-1}+{\displaystyle \frac{1}{l+1}}{w}_l\right)\parallel \hfill \\ & & \le {\displaystyle \frac{1}{2}}\parallel v_1-w_1\parallel +{\displaystyle \frac{1}{3}}\parallel v_2-w_2\parallel +...+{\displaystyle \frac{1}{l-1}}\parallel v_{l-1}-w_{l-1}\parallel +{\displaystyle \frac{1}{l}}\parallel v_l-w_l\parallel \hfill \\ & & \le {\displaystyle \frac{2}{3}}\parallel d-e\parallel +{\displaystyle \frac{2}{5}}\parallel d-e\parallel +...+{\displaystyle \frac{2}{2l-3}}\parallel d-e\parallel +{\displaystyle \frac{2}{2l+1}}\parallel d-e\parallel .\hfill \end{array}$$

Thus, F is ${\displaystyle \frac{2}{3}},{\displaystyle \frac{2}{5}},...{\displaystyle \frac{2}{2l-3}},{\displaystyle \frac{2}{2l+1}}$-Lipschitz-continuous with respect to $T_i$ for each $i\in \{1,2,...,l\}$.

For each $i\in \{1,2,...,l\}$, let $T_i:\mathbb{R}\to \mathbb{R}$ such that $T_i\left(d\right)={\displaystyle \frac{d}{5}}$ is an identity mapping. Therefore $T_i$ is Lipschitz-continuous with constant ${\lambda }_i={\displaystyle \frac{2}{9}}$.

In view of the constants computed above, all the conditions of Theorem 4 are fulfilled.

For ${\alpha }_k={\displaystyle \frac{1}{n+1}}$ and $c=0$, the iterative sequence generated by Algorithm 1 has the following model:

$$\begin{array}{ccc}& & d_{k+1}=(1-{\widehat{\alpha }}_k)d_k+{\widehat{\alpha }}_k{\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left[{\mathcal{B}}^l(g_1,g_2)\left(d_k\right)-\lambda \mathcal{K}(d_k-p\left(d_k\right))+\lambda c+\lambda F(v_k^1,v_k^2,...,v_k^l)\right],\hfill \\ & & =(1-{\widehat{\alpha }}_k)d_k+{\widehat{\alpha }}_k{\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left[{\displaystyle \frac{3d_k}{5}}-{\displaystyle \frac{9d_k}{10}}+\left({\displaystyle \frac{1}{2}}{v}_k^1+{\displaystyle \frac{1}{3}}{v}_k^2+...+{\displaystyle \frac{1}{8}}{v}_k^7+{\displaystyle \frac{1}{9}}{v}_k^8\right)\right],\hfill \\ & & =(1-{\widehat{\alpha }}_k)d_k+{\widehat{\alpha }}_k{\mathcal{R}}_{\mathcal{M}}^{\lambda ,{\mathcal{B}}^l}\left[-{\displaystyle \frac{3d_k}{5}}+{\displaystyle \frac{2d_k}{9}}\log {\displaystyle \frac{19}{3}}\right],\hfill \\ & & =(1-{\widehat{\alpha }}_k)d_k+{\widehat{\alpha }}_k\left[-{\displaystyle \frac{9d_k}{17}}+{\displaystyle \frac{10d_k}{51}}\log {\displaystyle \frac{19}{3}}\right].\hfill \end{array}$$

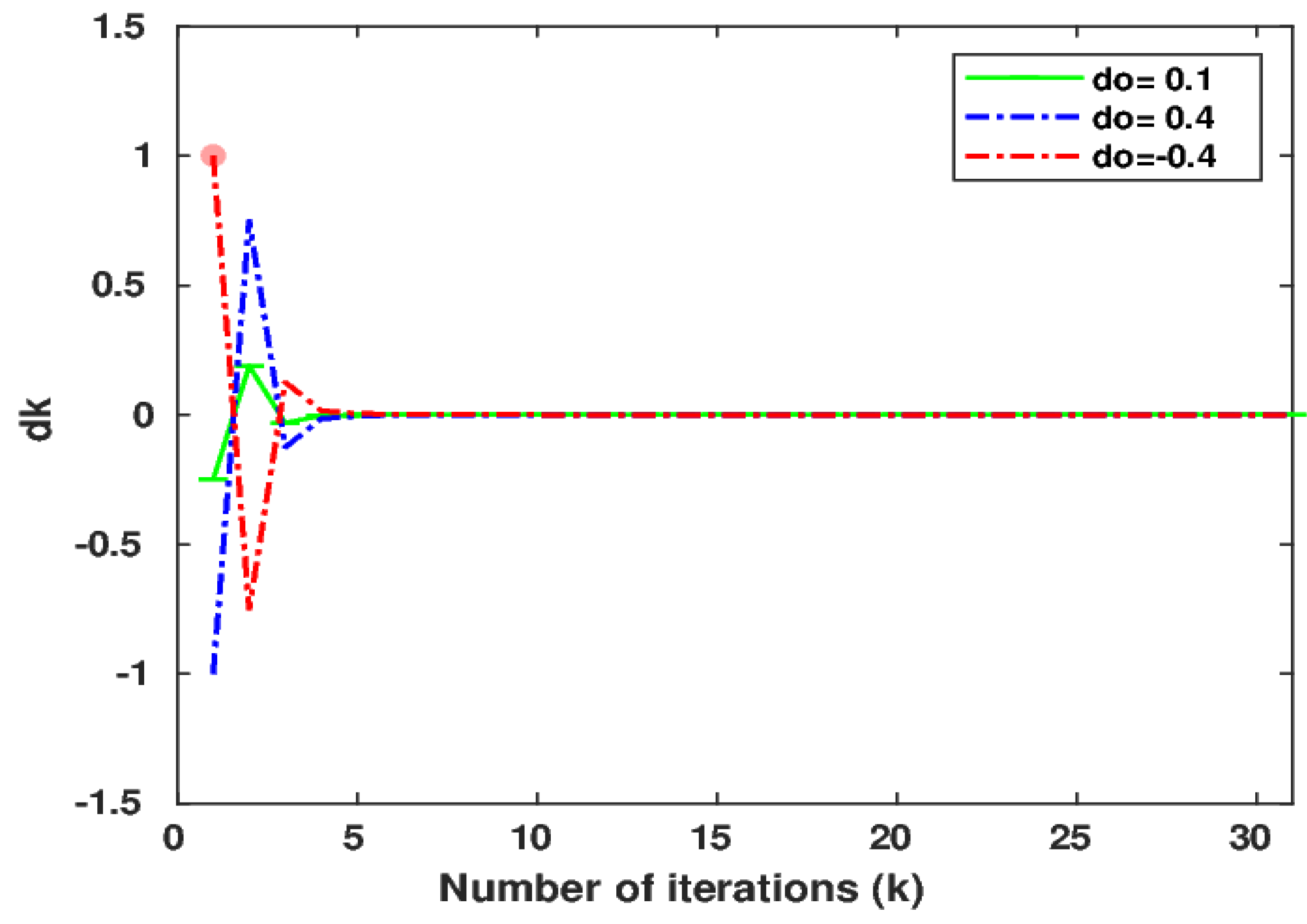
Figure 1 (

Table 1. Computations of outputs $d_k$ for different values of $d_0$.

Number of Iterations	${\mathit{d}}_0=0.1$ ${\mathit{d}}_{\mathit{k}}$	${\mathit{d}}_0=0.4$ ${\mathit{d}}_{\mathit{k}}$	${\mathit{d}}_0=-0.4$ ${\mathit{d}}_{\mathit{k}}$
1.	−0.2502	−1.0010	1.0010
2.	0.1880	0.7520	−0.7520
3.	−0.0315	−0.1259	0.1259
4.	−0.0039	−0.0157	0.0157
5.	−0.0012	−0.0047	0.0047
6.	−0.0005	−0.0020	0.0020
7.	−0.0002	−0.0010	0.0010
8.	−0.0001	−0.0005	0.0005
9.	−0.0001	−0.0003	0.0003
10.	−0.0001	−0.0002	0.0002
11.	−0.0000	−0.0001	0.0001
12.	−0.0000	−0.0001	0.0001
13.	−0.0000	−0.0001	0.0001
14.	0.0000	−0.0001	0.0001
15–30.	0.0000	0.0000	0.0000

) shows the convergence of the sequence $\left\{d_k\right\}$ for the different initial values $d_0=0.1$, $0.4$ and $-0.4$, respectively.

5. Conclusions

This article is a discussion on ${\mathcal{B}}^l$-co-monotone mappings, which consist of $\mathcal{B}$-monotone, $C_n$-monotone, $\left(H\right(.,.)$-monotone mappings, and $H(.,.)$-co-monotone mappings, etc. as special cases. We analyzed and investigated VIP (8) with ${\mathcal{B}}^l$-co-monotone mapping due to the widespread applicability of variational inclusions in fields such as economics, finance, applied sciences, and management sciences. Using the proximal-point mapping approach, the uniqueness and existence of solution of VIP (8) in q-uniformly smooth Banach spaces is shown. We concentrate our study on the convergence analysis of VIP (8) using the Algorithm 1. In order to illustrate our findings, a simplified numerical example is drafted. This article can be continued in the future to include the Yosida inclusion problems in the setting of semi-inner product spaces.