Extending the Applicability of Newton-Jarratt-like Methods with Accelerators of Order 2m + 1 for Solving Nonlinear Systems
Abstract
1. Introduction
| Algorithm 1-step Newton-Jarratt Method (2) |
|
- Motivation for our paper
- (P1)
- The existence of at least the fifth derivative is assumed in [20] to show the local convergence and provided that , where m is a natural number. Let us consider , and define the function byHere are real numbers with and . It follows by the definition of the function f that is a solution of the equation . But the fifth derivative of the function f is not bounded, since it is not continuous at . Therefore the results in [20] cannot assure the convergence of the method to . However, the method converges to if we take . Thus, the sufficient convergence conditions in [20] can be weakened. It is also worth noting that only F and appear on the method.
- (P2)
- There is no knowledge in advance about the natural number K such that , where is the error tolerance. Thus, the number of such iterations K is unknown.
- (P3)
- Information about the isolation of is not available.
- (P4)
- The most important and challenging semi-local convergence is not given.
- (P5)
- The convergence is established only for .
- Novelty of our Paper
- (P1)′
- The local convergence is based on the operators F and , which only appear on the method. Moreover, generalized continuity assumptions [21] are used to control the derivative and sharpen the error distances .
- (P2)′
- The number of iterations K is known in advance, since a priori estimates on become available.
- (P3)′
- Domains are determined containing only one solution.
- (P4)′
- (P5)′
2. Local Convergence
- Suppose:
- (C1)
- There exists a continuous and nondecreasing function such that the function has a smallest zero in the interval . We shall denote such zero by and set .
- (C2)
- There exists a continuous and nondecreasing function such that for the functions:, ,the functions , are defined byare such that the functions , , have smallest zeros in the interval . We shall denote such zeros by . SetThis parameter shall be shown to be the radius of convergence for the method (2) in Theorem 1. It follows from the definition of r that for each :andThe real functions and w relate to the operators on the method (2).
- (C3)
- There exists a solution of the equation and an invertible operator such that for eachDefine the region .
- (C4)
- for each .
- (C5)
- .
- (1)
- The limit point r can be replaced by in the condition ().
- (2)
- Under all the conditions ()–() one can set and in the Proposition 1.
3. Semi-Local Convergence
- (a)
- The midpoint is taken as an approximation to the solution .
- (b)
- The interval is replaced by if , or, if . The convergence of this method can then always be guaranteed.
- Suppose:
- (H1)
- There exists a continuous and nondecreasing function such that the function has a smallest zero in the interval . Let us denote such zero by s and set .
- (H2)
- There exists a continuous and nondecreasing function . Define the scalar sequences for ; ; , some byandThese sequences are shown to be majorizing for the sequences generated by method (2). But let us first present a convergence result for them.
- (H3)
- There exists such that for each ,
- (H4)
- There exists and an invertible operator such that for eachDefine the region . By this condition and () it follows that for : . So the linear operator is invertible. Therefore, we can take .
- (H5)
- .
- (H6)
- .
- The semi-local analysis for the method (2) follows next.
- (1)
- The limit point can be replaced by s in the condition ().
- (2)
- Under all the conditions ()–() we can take and in the Proposition 2.
- (3)
- The sufficient semi-local convergence conditions ()–() are very general. Clearly, if the functions and v are specialized more, concrete results can be obtained, which include the rate and order of convergence. But in this paper, we wanted to minimize the limitations of our approach.
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Argyros, I.K.; Shakhno, S. Extended Local Convergence for the Combined Newton-Kurchatov Method Under the Generalized Lipschitz Conditions. Mathematics 2019, 7, 207. [Google Scholar] [CrossRef]
- Costabile, F.; Gualtieri, M.; Capizzano, S. An iterative method for the computation of the solutions of nonlinear equations. Calcolo 1999, 36, 17–34. [Google Scholar] [CrossRef]
- Nisha, S.; Parida, P.K. An improved bisection Newton-like method for enclosing simple zeros of nonlinear equations. SeMA J. 2015, 72, 83–92. [Google Scholar] [CrossRef]
- Ortega, J.M.; Rheinboldt, W.C. Iterative Solution of Nonlinear Equations in Several Variables; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Traub, J.F. Iterative Methods for the Solution of Equations; Prentice-Hall: Hoboken, NJ, USA, 1964. [Google Scholar]
- Ostrowski, A.M. Solution of Equations and Systems of Equations; Academic Press: New York, NY, USA, 1960. [Google Scholar]
- Darvishi, M.T.; Barati, A. Super cubic iterative methods to solve systems of nonlinear equations. Appl. Math. Comput. 2007, 188, 1678–1685. [Google Scholar] [CrossRef]
- Homeier, H.H.H. A modified Newton method with cubic convergence: The multivariate case. J. Comput. Appl. Math. 2004, 169, 161–169. [Google Scholar] [CrossRef]
- Noor, M.A.; Saleem, M. Some iterative methods for solving a system of nonlinear equations. Comput. Math. Appl. 2009, 57, 101–106. [Google Scholar] [CrossRef]
- Xiao, X.; Yin, H. A new class of methods with higher order of convergence for solving systems of nonlinear equations. Appl. Math. Comput. 2016, 264, 300–309. [Google Scholar] [CrossRef]
- Behl, R.; Cordero, A.; Motsa, S.S.; Torregrosa, J.R. Stable high-order iterative methods for solving nonlinear models. Appl. Math. Comput. 2017, 303, 70–80. [Google Scholar] [CrossRef]
- Cordero, A.; Feng, L.; Magreñán, Á.A.; Torregrosa, J.R. A new fourth-order family for solving nonlinear problems and its dynamics. J. Math. Chem. 2015, 53, 893–910. [Google Scholar] [CrossRef]
- Cordero, A.; Hueso, J.L.; Martínez, E.; Torregrosa, J.R. Increasing the convergence order of an iterative method for nonlinear systems. Appl. Math. Lett. 2012, 25, 2369–2374. [Google Scholar] [CrossRef]
- Esmaeili, H.; Ahmadi, M. An efficient three-step method to solve system of non linear equations. Appl. Math. Comput. 2015, 266, 1093–1101. [Google Scholar]
- Sharma, J.R.; Sharma, R.; Bahl, A. An improved Newton-Traub composition for solving systems of nonlinear equations. Appl. Math. Comput. 2016, 290, 98–110. [Google Scholar]
- Sharma, J.R.; Arora, H. An efficient derivative-free family of seventh order methods for systems of nonlinear equations. SeMA J. 2016, 73, 39–75. [Google Scholar] [CrossRef]
- Weerakoon, S.; Fernando, T.G.I. A Variant of Newton’s Method with Accelerated Third-Order Convergence. Appl. Math. Lett. 2000, 13, 87–93. [Google Scholar] [CrossRef]
- Xiao, X.Y.; Yin, H.W. Increasing the order of convergence for iterative methods to solve nonlinear systems. Calcolo 2016, 53, 285–300. [Google Scholar]
- Xiao, X.; Yin, H. Accelerating the convergence speed of iterative methods for solving nonlinear systems. Appl. Math. Comput. 2018, 333, 8–19. [Google Scholar] [CrossRef]
- Sharma, J.R.; Kumar, S. A class of accurate Newton–Jarratt-like methods with applications to nonlinear models. Comput. Appl. Math. 2022, 41, 46. [Google Scholar] [CrossRef]
- Argyros, I.K. The Theory and Application of Iteration Methods, 2nd ed.; Taylor and Francis: Boca Raton, FL, USA, 2022. [Google Scholar]
- Argyros, I.K.; Shakhno, S. Extended Two-Step-Kurchatov Method for Solving Banach Space Valued Nondifferentiable Equations. Int. J. Appl. Comput. Math. 2020, 6, 2. [Google Scholar] [CrossRef]
- Argyros, I.K.; Shakhno, S.; Yarmola, H. Two-Step Solver for Nonlinear Equations. Symmetry 2019, 11, 128. [Google Scholar] [CrossRef]
- Alzahrani, A.K.H.; Behl, R.; Alshomrani, A.S. Some higher-order iteration functions for solving nonlinear models. Appl. Math. Comput. 2018, 334, 80–93. [Google Scholar] [CrossRef]
- Cordero, A.; Lotfi, T.; Bakhtiari, P.; Mahdiani, K.; Torregrosa, J.R. Some new efficient multipoint iterative methods for solving nonlinear systems of equations. Int. J. Comput. Math. 2015, 92, 1921–1934. [Google Scholar]
- Jang, T.S. An integral equation formalism for solving the nonlinear Klein–Gordon equation. Appl. Math. Comput. 2014, 243, 322–338. [Google Scholar] [CrossRef]
- Madhu, K.; Elango, A.; Landry, R.J.; Al-arydah, M. New Multi-Step Iterative Methods for Solving Systems of Nonlinear Equations and Their Application on GNSS Pseudorange Equations. Sensors 2020, 20, 5976. [Google Scholar] [CrossRef]
- Moré, J.J.; Garbow, B.S.; Hillstrom, K.H. Testing Unconstrained Optimization Software. ACM Trans. Math. Softw. 1981, 7, 17–41. [Google Scholar] [CrossRef]
- Moré, J.J.; Cosnard, M.Y. Numerical solution of nonlinear equations. ACM Trans. Math. Softw. 1979, 5, 64–85. [Google Scholar] [CrossRef]
- Motsa, S.S.; Shateyi, S. New Analytic Solution to the Lane–Emden Equation of Index 2. Math. Probl. Eng. 2012, 614796. [Google Scholar] [CrossRef]
- Regmi, S. Optimized Iterative Methods with Applications in Diverse Disciplines; Nova Science Publisher: New York, NY, USA, 2021. [Google Scholar]
- Sharma, J.R.; Arora, H. Improved Newton-like methods for solving systems of nonlinear equations. SeMA J. 2016, 74, 147–163. [Google Scholar] [CrossRef]
- Sharma, J.R.; Arora, H. Efficient derivative-free numerical methods for solving systems of nonlinear equations. Comput. Appl. Math. 2016, 35, 269–284. [Google Scholar] [CrossRef]
- Sharma, J.R.; Gupta, P. An efficient fifth order method for solving systems of nonlinear equations. Comput. Math. Appl. 2014, 67, 591–601. [Google Scholar] [CrossRef]
- Ullah, M.Z.; Serra-Capizzano, S.; Ahmad, F.; Al-Aidarous, E.S. Higher order multi-step iterative method for computing the numerical solution of systems of nonlinear equations: Application to nonlinear PDEs and ODEs. Appl. Math. Comput. 2015, 269, 972–987. [Google Scholar] [CrossRef]
- Usman, M.; Iqbal, J.; Khan, A.; Ullah, I.; Khan, H.; Alzabut, J.; Alkhawar, H.M. A new iterative multi-step method for solving nonlinear equation. MethodsX 2025, 15, 103394. [Google Scholar] [CrossRef] [PubMed]
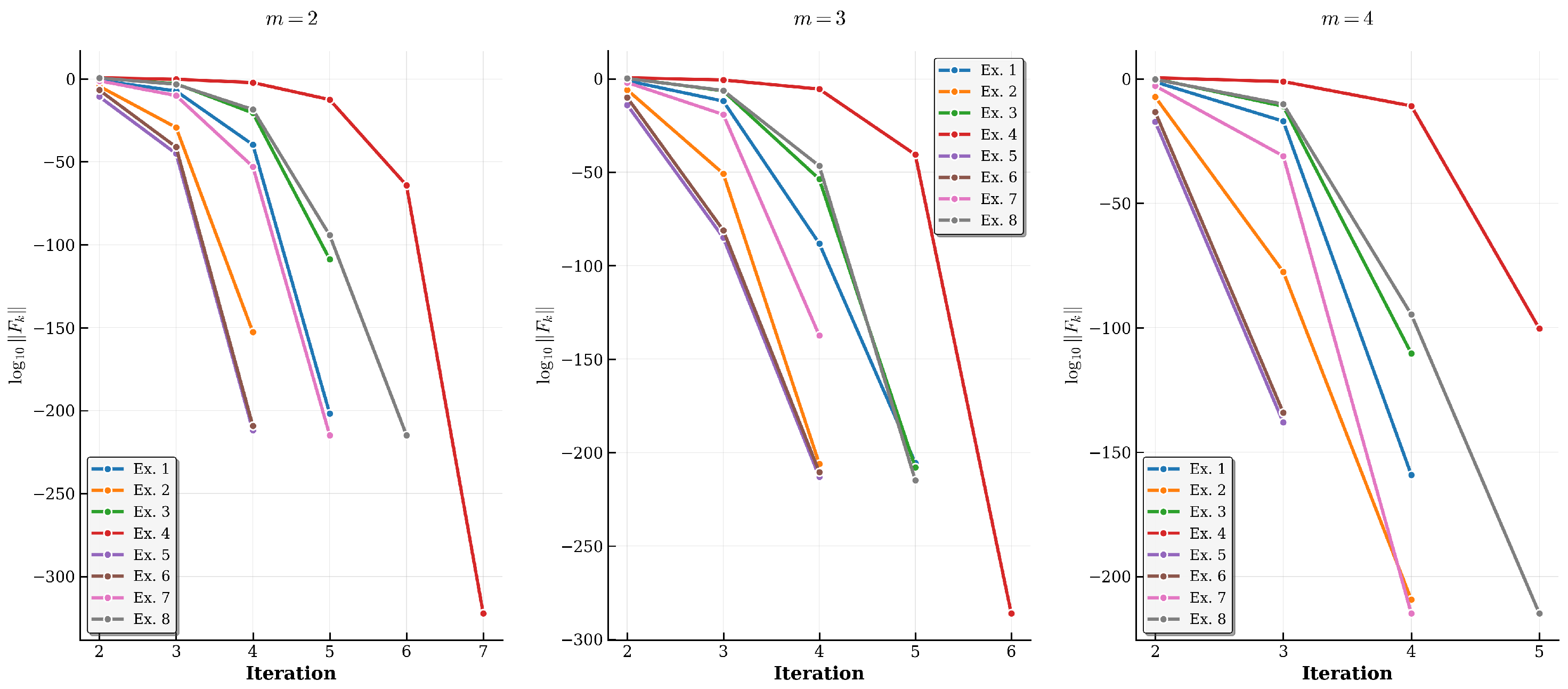
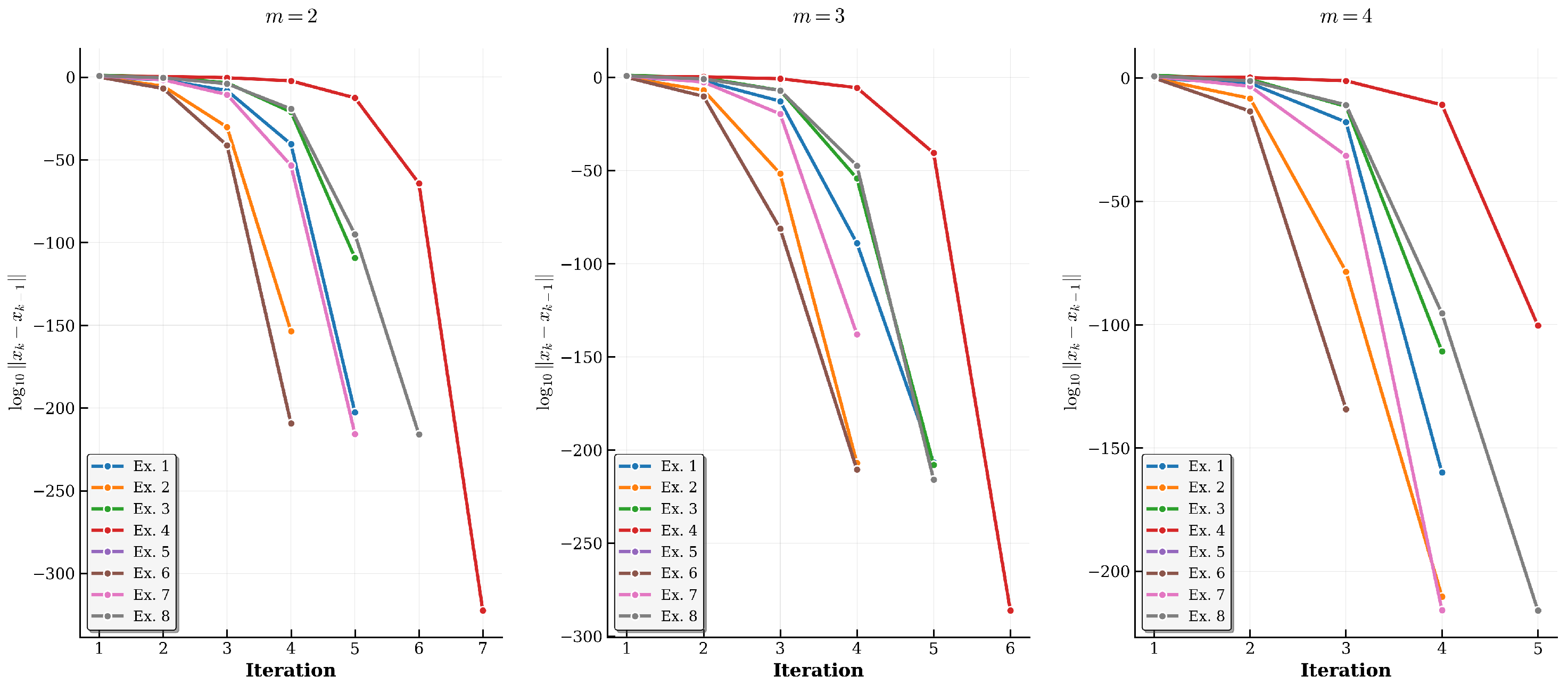
| Value of m | |||
|---|---|---|---|
| Metric | 2 | 3 | 4 |
| Example 1 | |||
| k | 5 | 5 | 4 |
| COC | 5.010 | 6.995 | 9.003 |
| e-time (s) | 0.014 | 0.014 | 0.013 |
| 1.61 × 10−206 | 1.61 × 10−206 | 1.61 × 10−206 | |
| 3.11 × 10−203 | 2.45 × 10−207 | 1.16 × 10−160 | |
| Example 2 | |||
| k | 4 | 4 | 4 |
| COC | 4.975 | 6.635 | 8.680 |
| e-time (s) | 0.018 | 0.020 | 0.021 |
| 3.28 × 10−207 | 6.24 × 10−211 | 8.55 × 10−215 | |
| 2.52 × 10−154 | 1.22 × 10−207 | 6.12 × 10−211 | |
| Example 3 | |||
| k | 5 | 5 | 4 |
| COC | 5.000 | 6.973 | 8.988 |
| e-time (s) | 17.74 | 28.07 | 24.30 |
| 0 | 5.77 × 10−209 | 0 | |
| 6.16 × 10−110 | 1.37 × 10−208 | 1.62 × 10−111 | |
| Example 4 | |||
| k | 7 | 6 | 5 |
| COC | 5.396 | 7.240 | 9.150 |
| e-time (s) | 0.021 | 0.017 | 0.015 |
| 0 | 0 | 0 | |
| 4.59 × 10−323 | 7.56 × 10−287 | 4.23 × 10−101 | |
| Example 5 | |||
| k | 4 | 4 | 3 |
| COC | 4.982 | 6.981 | 8.980 |
| e-time (s) | 16.16 | 15.65 | 15.66 |
| 1.58 × 10−215 | 5.51 × 10−214 | 1.23 × 10−213 | |
| 4.84 × 10−210 | 2.52 × 10−211 | 5.62 × 10−135 | |
| Example 6 | |||
| k | 4 | 4 | 3 |
| COC | 4.982 | 6.981 | 8.980 |
| e-time (s) | 162.7 | 160.2 | 118.9 |
| 2.75 × 10−211 | 7.19 × 10−212 | 4.08 × 10−211 | |
| 5.08 × 10−210 | 3.76 × 10−211 | 5.62 × 10−135 | |
| Example 7 | |||
| k | 5 | 4 | 4 |
| COC | 4.788 | 6.912 | 7.004 |
| e-time (s) | 17.52 | 16.72 | 15.41 |
| 1.12 × 10−215 | 1.10 × 10−215 | 8.89 × 10−216 | |
| 2.31 × 10−216 | 1.40 × 10−138 | 1.82 × 10−216 | |
| Example 8 | |||
| k | 6 | 5 | 5 |
| COC | 4.989 | 6.463 | 8.664 |
| e-time (s) | 27.17 | 22.84 | 29.26 |
| 1.21 × 10−215 | 1.22 × 10−215 | 1.10 × 10−215 | |
| 1.40 × 10−216 | 1.43 × 10−216 | 1.26 × 10−216 | |
| r |
| Iterative Methods | NJM (2) | NRM (41) |
|---|---|---|
| Number of iterations | 1 | 1 |
| Size of problem | 500 | 500 |
| Number of steps | 16 | 23 |
| Theoretical convergence-order | 31 | 24 |
| Function evaluations per iteration | 16 | 23 |
| Solutions of system of linear equations per iteration | 16 | 23 |
| when right side is vector | ||
| Solutions of system of linear equations per iteration | 1 | 0 |
| when right side is matrix | ||
| Number of Jacobian evaluations per iteration | 2 | 1 |
| Number of Jacobian LU-factorization per iteration | 1 | 1 |
| Number of matrix vector multiplications per iteration | 15 | 0 |
| Steps | ||
| 1 | 6.8402 × 10−1 | 6.2052 × 10−1 |
| 2 | 5.5152 × 10−1 | 5.5165 × 10−1 |
| 3 | 8.1764 × 10−1 | 6.4046 × 10−1 |
| 4 | 1.5322 | 8.5943 × 10−1 |
| 5 | 1.2030 | 1.1858 |
| 6 | 2.3728 | 1.2422 |
| 7 | 7.9603 × 10−1 | 1.3089 |
| 8 | 8.2595 × 10−1 | 2.0382 |
| 9 | 8.5373 × 10−1 | 1.3065 |
| 10 | 7.8730 × 10−1 | 1.8401 |
| 11 | 4.7382 × 10−1 | 9.4516 × 10−1 |
| 12 | 1.6708 × 10−1 | 8.9284 × 10−1 |
| 13 | 3.7363 × 10−2 | 9.1266 × 10−1 |
| 14 | 6.1138 × 10−3 | 9.3032 × 10−1 |
| 15 | 7.9369 × 10−4 | 9.1482 × 10−1 |
| 16 | 8.5210 × 10−5 | 6.9886 × 10−1 |
| 17 | 3.7548 × 10−1 | |
| 18 | 1.4397 × 10−1 | |
| 19 | 4.3176 × 10−2 | |
| 20 | 1.0867 × 10−2 | |
| 21 | 2.3786 × 10−3 | |
| 22 | 4.6137 × 10−4 | |
| 23 | 8.0241 × 10−5 | |
| CPU time (s) | 0.029 | 0.043 |
| Iterative Methods | NJM (2) | NRM (41) |
|---|---|---|
| Number of iterations | 1 | 1 |
| Size of problem | 4420 | 4420 |
| Number of steps | 3 | 4 |
| Theoretical convergence-order | 5 | 5 |
| Function evaluations per iteration | 3 | 4 |
| Solutions of system of linear equations per iteration | 3 | 3 |
| when right side is vector | ||
| Solutions of system of linear equations per iteration | 1 | 0 |
| when right side is matrix | ||
| Number of Jacobian evaluations per iteration | 2 | 1 |
| Number of Jacobian LU-factorization per iteration | 1 | 1 |
| Number of matrix vector multiplications per iteration | 2 | 0 |
| Steps | ||
| 1 | 3.3122 × 10−1 | 1.1253 × 10−1 |
| 2 | 6.8391 × 10−3 | 6.8391 × 10−3 |
| 3 | 3.5588 × 10−5 | 1.5342 × 10−4 |
| 4 | 1.8717 × 10−6 | |
| CPU time (s) | 5.8 | 1.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Argyros, I.K.; Shakhno, S.; Shakhov, M. Extending the Applicability of Newton-Jarratt-like Methods with Accelerators of Order 2m + 1 for Solving Nonlinear Systems. Axioms 2025, 14, 734. https://doi.org/10.3390/axioms14100734
Argyros IK, Shakhno S, Shakhov M. Extending the Applicability of Newton-Jarratt-like Methods with Accelerators of Order 2m + 1 for Solving Nonlinear Systems. Axioms. 2025; 14(10):734. https://doi.org/10.3390/axioms14100734
Chicago/Turabian StyleArgyros, Ioannis K., Stepan Shakhno, and Mykhailo Shakhov. 2025. "Extending the Applicability of Newton-Jarratt-like Methods with Accelerators of Order 2m + 1 for Solving Nonlinear Systems" Axioms 14, no. 10: 734. https://doi.org/10.3390/axioms14100734
APA StyleArgyros, I. K., Shakhno, S., & Shakhov, M. (2025). Extending the Applicability of Newton-Jarratt-like Methods with Accelerators of Order 2m + 1 for Solving Nonlinear Systems. Axioms, 14(10), 734. https://doi.org/10.3390/axioms14100734







