The Density Function of the Stochastic SIQR Model with a Two-Parameters Mean-Reverting Process
Abstract
1. Introduction
2. Existence and Uniqueness of the Global Positive Solution of System (2)
3. Existence of a Stationary Distribution of System (2)
4. Density Function and Extinction of System (2)
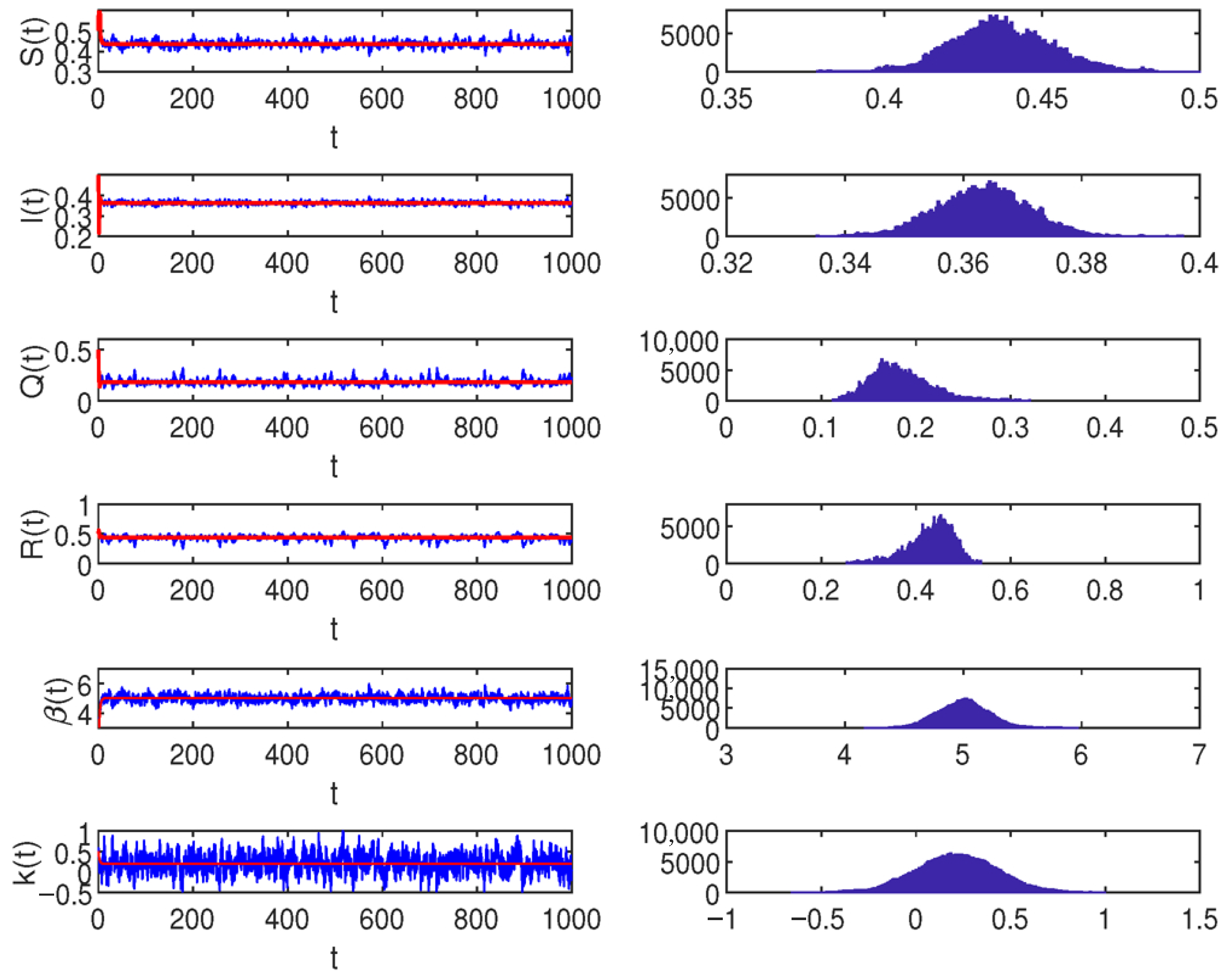
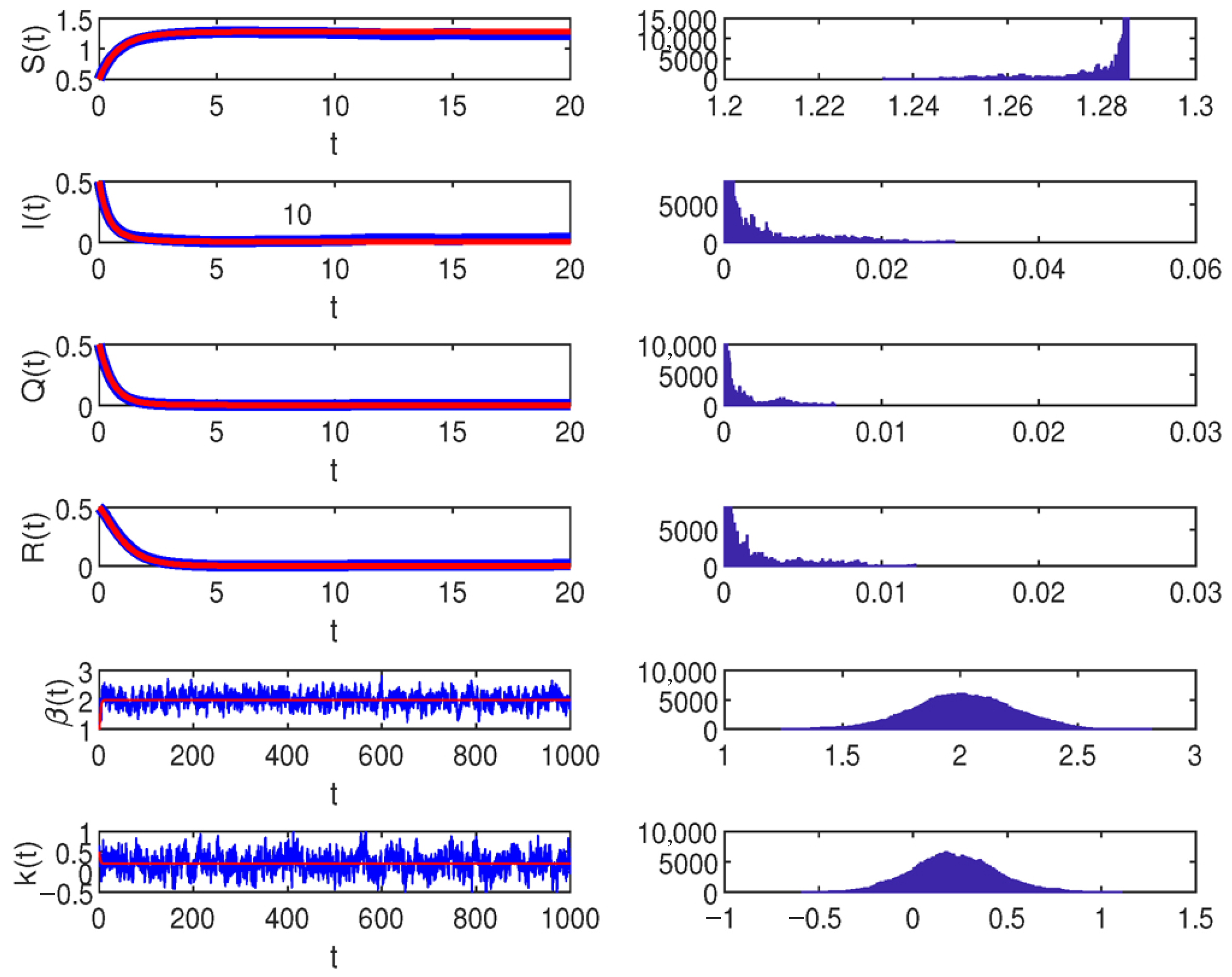
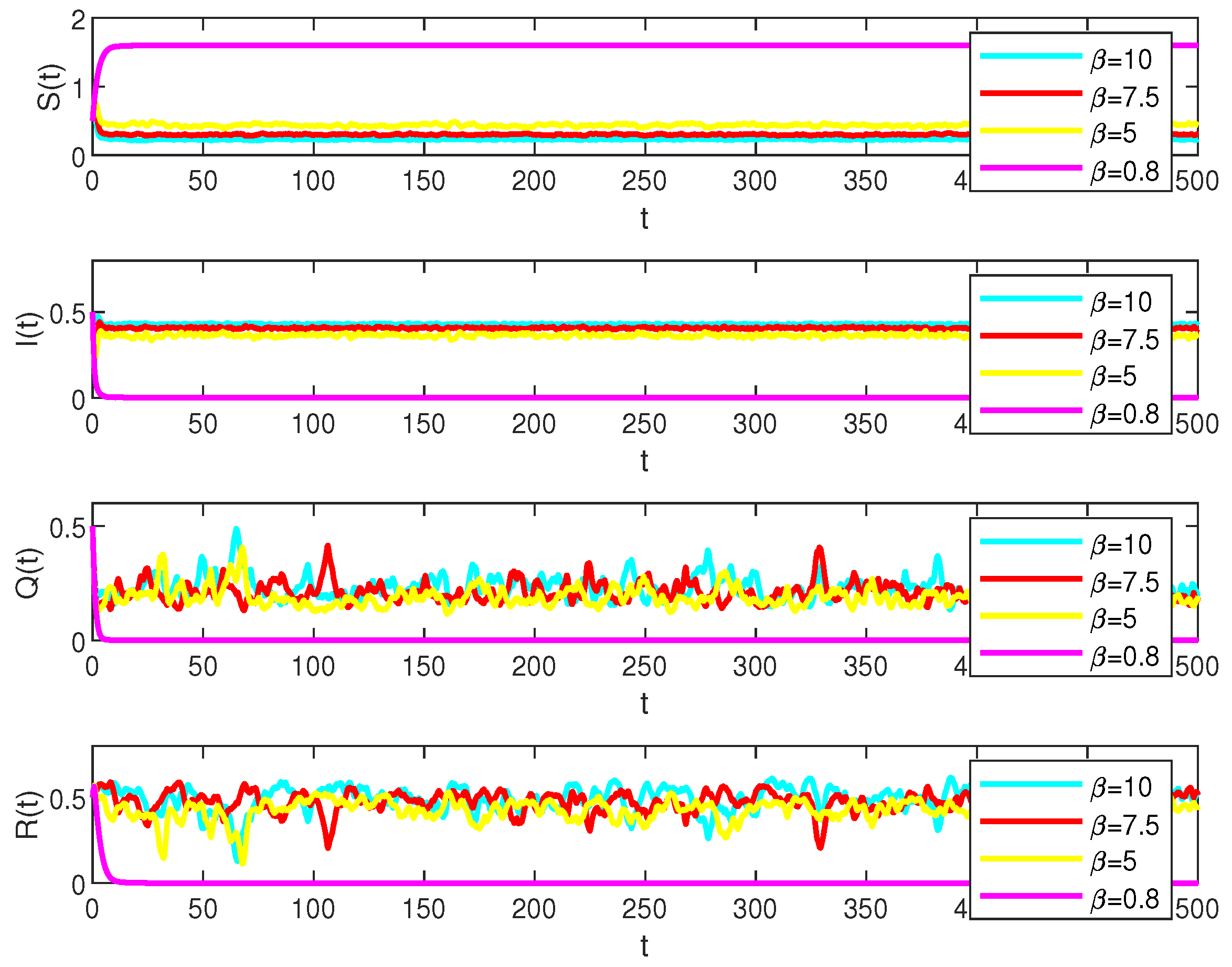
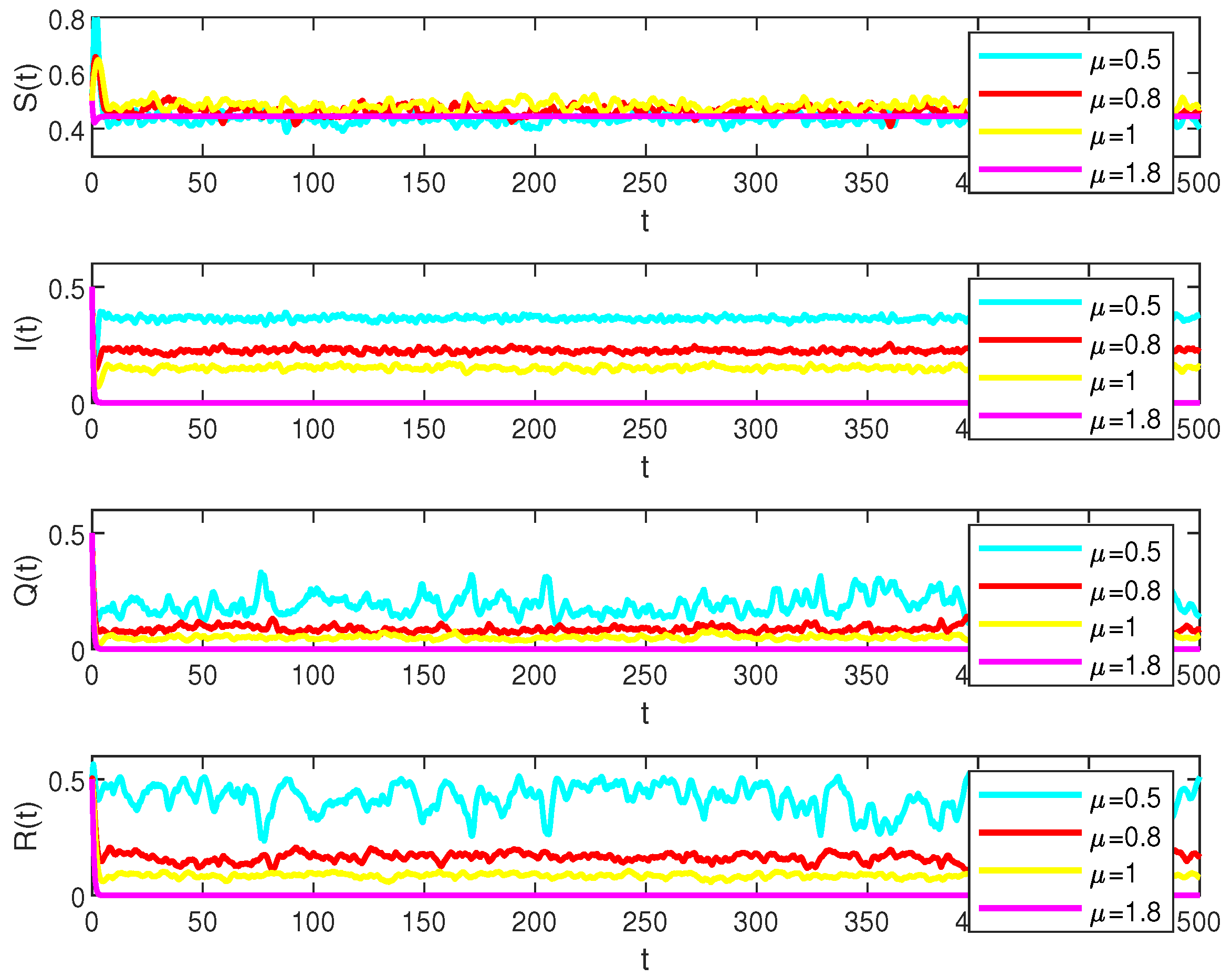
5. Numerical Simulations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans: Dynamics and Control; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Diekmann, O.; Kretzschmar, M. Patterns in the effects of infectious diseases on population growth. J. Math. Biol. 1991, 29, 539–570. [Google Scholar] [CrossRef] [PubMed]
- Gardiner, C.W. Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences; Springer: Berlin/Heidelberg, Germany, 1893. [Google Scholar]
- Li, W.; Liu, S. Dynamic analysis of a stochastic epidemic model incorporating the double epidemic hypothesis and Crowley-Martin incidence term. Electron. Res. Arch. 2023, 31, 6134–6159. [Google Scholar] [CrossRef]
- Hethcote, H.W.; Zhien, M.; Liao, S. Effect of Quarantine in Six Endemic Models for Infectious Diseases. Math. Biosci. Eng. 2002, 180, 141–160. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Liu, M.; Chen, L. Optimal quarantine strategies in stochastic SIR models with white noise. IEEE Trans. Biomed. Eng. 2020, 67, 3542–3551. [Google Scholar]
- Nirwani, N.; Badshah, V.H.; Khandelwal, R. Dynamical Study of an SIQR Model with Saturated Incidence Rate. Nonlinear Anal. Differ. Equ. 2016, 4, 43–50. [Google Scholar] [CrossRef]
- Higham, D.J. An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
- Divine, W. Estimating white noise intensity regions for comparable properties of a class of SEIRs stochastic and deterministic epidemic models. J. Appl. Anal. Comput 2021, 11, 1095–1137. [Google Scholar]
- Wang, X.; Wang, K.; Teng, Z. Dynamical properties and density function in a stochastic epidemic model with incomplete and temporal immunization. Adv. Contin. Discret. Model. 2025, 2025, 110. [Google Scholar] [CrossRef]
- Mao, X.; Marion, G.; Renshaw, E. Environmental brownian noise suppresses explosions in population dynamics. Stoch. Process. Appl. 2002, 97, 95–110. [Google Scholar] [CrossRef]
- Khasminskii, R. Stochastic Stability of Differential Equations; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Mao, X. Stochastic Differential Equations and Applications; Horwood Publishing: Chichester, UK, 1997. [Google Scholar]
- Roozen, H. An Asymptotic Solution to a Two-Dimensional Exit Problem Arising in Population Dynamics. SIAM J. Appl. Math. 1989, 49, 1793–1810. [Google Scholar] [CrossRef]
- Zhou, B.; Jiang, D.; Dai, Y.; Hayat, T. Stationary distribution and density function expression for a stochastic SIQRS epidemic model with temporary immunity. Nonlinear Dyn. 2021, 105, 931–955. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Wang, S.; Chen, R.; Zhang, C.; Zhang, Y.; Gao, J.; Du, S. Reliability estimation method based on nonlinear Tweedie exponential dispersion process and evidential reasoning rule. Comput. Ind. Eng. 2025, 206, 111205. [Google Scholar] [CrossRef]

| Parameter | Definition |
|---|---|
| susceptible individuals | |
| infected individuals | |
| quarantined individuals | |
| recovered individuals | |
| the recruitment rate of susceptible | |
| the average number of adequate contacts | |
| the per capita natural mortality rate | |
| the removal rate constant from the compartment I | |
| k | the removal rate constant from the compartment Q |
| the rate at which individuals recover from compartment I and move to compartment R | |
| the extra disease-related death rate constant in compartments I | |
| the extra disease-related death rate constant in compartments Q |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Ni, Z.; Jiang, D.; Sun, J. The Density Function of the Stochastic SIQR Model with a Two-Parameters Mean-Reverting Process. Axioms 2025, 14, 732. https://doi.org/10.3390/axioms14100732
Zhang H, Ni Z, Jiang D, Sun J. The Density Function of the Stochastic SIQR Model with a Two-Parameters Mean-Reverting Process. Axioms. 2025; 14(10):732. https://doi.org/10.3390/axioms14100732
Chicago/Turabian StyleZhang, Huina, Zhiming Ni, Daqing Jiang, and Jianguo Sun. 2025. "The Density Function of the Stochastic SIQR Model with a Two-Parameters Mean-Reverting Process" Axioms 14, no. 10: 732. https://doi.org/10.3390/axioms14100732
APA StyleZhang, H., Ni, Z., Jiang, D., & Sun, J. (2025). The Density Function of the Stochastic SIQR Model with a Two-Parameters Mean-Reverting Process. Axioms, 14(10), 732. https://doi.org/10.3390/axioms14100732







