Abstract
The contraction method is a procedure that allows to establish non-trivial relations between Lie algebras and has had successful applications in both mathematics and theoretical physics. This work deals with generalizations of the contraction procedure, with a main focus on the so-called S-expansion method, as it includes most of the other generalized contractions. Basically, the S-expansion combines a Lie algebra with a finite abelian semigroup S in order to define new S-expanded algebras. After giving a description of the main ingredients used in this paper, we present a Java library that automates the S-expansion procedure. With this computational tool, we are able to represent Lie algebras and semigroups, so we can perform S-expansions of Lie algebras using arbitrary semigroups. We explain how the library methods have been constructed and how they work; then, we give a set of example programs aimed to solve different problems. They are presented so that any user can easily modify them to perform their own calculations, without necessarily being an expert in Java. Finally, some comments about further developments and possible new applications are made.
MSC:
22E70; 17B99; 05E15; 83E50
1. Introduction
The theory of Lie groups and algebras plays an important role in physics, as it allows us to describe the continuous symmetries of a given physical system. Due to the well-known relation between symmetries and conservation laws, via the Noether theorem, the Lie theory represents an essential ingredient in the construction of quantum field theories, particularly in the Standard Model of particles, as well as in general relativity and its generalizations. Since the second half of the last century, the study of non-trivial relations between Lie algebras and groups has also appeared as a problem of great interest in both mathematics and modern theoretical physics. (By “non-trivial relations”, we mean that starting from a given algebra, there are mechanisms allowing us to generate new algebras that are not isomorphic to the original one, i.e., they cannot be obtained by a simple change in basis.) Examples of these procedures are known as contractions [1,2,3,4] and deformations [5,6,7,8] of Lie algebras, both sharing the property of preserving the dimension of the algebras involved in the process.
The idea that led to the concept of contractions was first introduced in [1] and consists of the observation that if two physical theories are related by means of a limit process, then the corresponding symmetry groups under which those theories are invariant should be related through a limit process too. For example, Newtonian mechanics can be obtained from special relativity by taking (where c is the speed of light) and thus, the non-relativistic limit that brings the Poincaré algebra to the Galilean algebra is a good example of what is called a contraction process. On the other hand, a deformation can be regarded as the inverse of a contraction, which means that in the previous example, the Poincaré algebra is a deformation of the Galilean algebra. However, in the present article, we will not work with deformations, but rather with generalizations of the contraction method.
The contractions were formally introduced in [2,3] in a way that nowadays is known as Inönü-Wigner (IW) contraction. The contraction of an algebra is made with respect to a subalgebra of . The procedure basically consists of rescaling the generators of by a parameter and then performing a singular limit for that parameter. As a result, the generators of become abelian and the subalgebra acts on them. Further details and explicit examples, including the mentioned relation between Galileo and Poincaré algebras, can be found in [9,10]. Remarkably, if the original algebra has a more general subspace structure, it is possible to perform more general contractions which are known as Weimar–Woods (WW) contractions [11,12,13].
Recently, an interesting generalization has been introduced in parallel in the context of string theory [14] and supergravity [15,16,17]. This procedure, known as the expansion method, is not only able to reproduce the WW contractions when the dimension is preserved in the process, but also may lead to expanded algebras whose dimension is higher than the original one (a result that cannot be obtained by any contraction process). Another distinguishing feature is that the algebra is described in its dual formalism, i.e., in terms of the Maurer–Cartan (MC) forms on the manifold of its associated Lie group (a good introduction to the dual formulation of Lie algebras can be found in Chapter 5.6 of [18]). Instead of rescaling the generators by a real parameter , as is usually carried out in the contraction methods, the rescaling is performed on some of the group coordinates. As a consequence, the MC forms can be expanded as power series in that, under certain conditions, can be truncated in such a way that assures the closure of a new, bigger algebra.
In this work, we deal with an even more general procedure called S-expansion [19] that not only reproduces the results of the expansion method described above (which, in turn, means that it also reproduces all WW contractions) but also allows us to establish relations between Lie algebras that cannot be obtained by the previous expansion procedure. Instead of performing a rescaling of some of the algebra generators or the group coordinates, it combines the structure constants of the algebra with the inner multiplication law of an abelian semigroup S in order to define the Lie bracket of a new S-expanded algebra. Under certain conditions, it is possible to extract smaller algebras which are called resonant subalgebras and reduced algebras. Under these conditions, S-expansion is able to reproduce the results of the previous expansion method [14,15,16,17] for a particular family of semigroups denoted by .
An important advantage of the S-expansion method is related to the construction of invariant tensors (and their duals known as Casimir operators) whose full classification is known only for semi-simple Lie algebras. The classification of all invariant tensors and Casimirs for non-semi-simple algebras is still an open problem in Lie theory. The standard procedure to construct an invariant tensor of range r is to use the symmetrized trace (or supertrace for superalgebras) for the product of r generators in some matrix representation. A good feature of S-expansion is that if we know the invariant tensors of a certain semi-simple Lie algebra, then the mechanism gives the invariant tensors for the expanded algebras even if they are not semi-simple (the same result was extended in [20] for the Casimir operators). Those invariant tensors of the S-expanded algebra are, in general, different from the symmetrized trace, so it would be interesting to analyze if S-expansion could help to solve the classification of invariant tensors for non-semi-simple Lie algebras. Indeed, it has already been supposed in the early 1960s that solvable Lie algebras could be obtained as contractions of semi-simple algebras of the same dimension [21,22]. The incorrectness of that conjecture was shown in [23] and, recently, that problem has been revisited in terms of S-expansions [24]. However, knowing whether S-expansions are able to fit the classification of non-semi-simple Lie algebras and their invariant tensors remains an open problem. Independent of the answer, what we do know is that the S-expansion gives invariant tensors that are, in general, different from the symmetrized trace, and this fact has already been useful for the construction of Chern–Simons (CS) gauge theories of (super)gravity [25,26] and their interrelations.
The dual formulation [27] in terms of MC forms has also been very useful, as it allows us to perform the S-expansion procedure directly on the Lagrangian of a given gravity theory. This has been used in [28,29,30,31,32] to show that general relativity (GR) in even and odd dimensions may emerge as a special limit of a Born–Infeld [33] and CS Lagrangian, respectively. Black hole and cosmological solutions have been studied for gravity theories based on expanded algebras [34,35,36,37], as well as some aspects about their non-relativistic limits [38]. In addition, the S-expansion has also been extended to other mathematical structures, like the case of higher order Lie algebras and infinite dimensional loop algebras [39,40,41].
At the beginning, the applications considered only the specific family of semigroups that allows for reproducing the previous expansion method [14,15,16,17]. These semigroups were denoted by and led to the so called algebras [19]. The use of other abelian semigroups to perform S-expansions of Lie algebras was first considered in [42]. It was shown that some Bianchi algebras [43,44] can be obtained as S-expansions from the two-dimensional isometries acting transitively in a two-dimensional space. The semigroups that allow us to obtain those relations do not all belong to the family and, thus, it is clear that these results can only be obtained in the context of the S-expansion, i.e., they cannot be reached by using the previous expansion procedure [15,16,17]. This procedure was then used in [20] to show that the semi-simple version of the so-called Maxwell algebra (introduced in [45,46,47]) can be obtained as an expansion of the AdS algebra. Later, this result was generalized in [48,49] to new families of semigroups generating algebras denoted by and , which have been useful to construct new (super)gravity models [50,51,52,53,54,55,56,57]. Other recent applications can also be found in [58,59].
On the other hand, a general study of the properties of S-expansion with arbitrary semigroups, in the context of the classification of Lie algebras, was performed in [60]. It was shown that under the S-expansions, some properties of the original algebra are always preserved, while others are not, in general. The explicit examples that allowed us to check the results in [42,60] were obtained with a set of computing programs that, in this work, we have improved and further developed to give them in the form of a Java library [61], allowing us to perform S-expansions with arbitrary finite abelian semigroups. We will present this library as a handbook with examples and all the necessary information to use its methods.
This work is organized as follows: In Section 2, we introduce the basic ingredients we will use. First, we give a brief description of discrete semigroups and the S-expansion method. Then, we give a brief review of the existing literature on the classification of non-isomorphic semigroups and finite semigroup computer programs. We conclude that section with a general description of the library and notation used. In Section 3 and Section 4, we describe the library, which consists of a set of classes containing different methods allowing us to perform S-expansions with any given finite abelian semigroup. The reader who is not an expert in Java language and/or is probably more interested in applying the computational tools presented in this paper might skip Section 3 and Section 4 and go directly to Section 5. There, we describe some of the 45 programs provided in [61] (see the list in Appendix A) as examples to use the library. With those instructions, the user can easily create new programs to perform their own calculations just by changing the inputs and even without knowing about the Java language. Finally, Section 6 contains some comments about possible new applications.
2. Preliminars
2.1. Discrete Semigroups
We consider a set of n elements . We say that S is a semigroup if it is equipped with an associative product
Notice the following:
- The identity element e satisfying does not necessarily exist.
- The elements do not need to have an inverse.
- If there exists an element such that , we will call it a zero element.
- n is the order of the semigroup
- If , the discrete semigroup is said to be commutative or abelian.
We can give the product by means of a multiplication table, an matrix:
with entries in . Thus, a visual way to describe a semigroup is given by the table in Figure 1. For instance, it allows us to check easily if a semigroup is commutative, because in that case, its multiplication table is symmetric.

Figure 1.
A table of certain multiplication laws for the semigroup elements.
An informal way (but useful for our purposes) of expressing the multiplication group law is by means of the quantities , called selectors, which are defined in the following way:
Then, the semigroup law can be expressed as follows:
As shown explicitly in [19], from the associativity and closure of the semigroup, it follows that the selectors provide a matrix representation for S, and this fact will be used in the next section to define the S-expansion method.
Equation (3) takes into account the matrix representation of K-selectors. A semigroup must be closed with respect to the associative binary operation of multiplication. The representation (3) of the multiplication law in terms of the K-selectors is not necessary because this suggests a second binary operation of addition and includes the binary scalars (0,1) into the multiplication law of the semigroup. However, K-selectors were the main ingredient in the construction of S-expansion in [19]. On the right-hand side of (3), there is only one term, and the second binary operation for the semigroup does not need to be introduced.
2.1.1. Isomorphisms of Semigroups
Consider the semigroups given by the table in Figure 2.
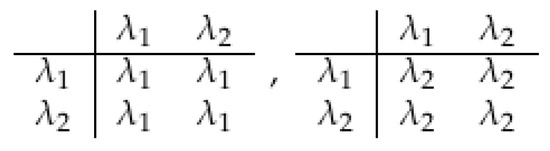
Figure 2.
The first example of two isomorphic semigroups.
These two semigroups have exactly the same structure if we rename by and vice versa. This is an example of an isomorphism of semigroups.
The group of isomorphisms between semigroups of order n is isomorphic to the group of permutations of n elements . For simplicity, we choose to represent a permutation by
which means change by , change by , ⋯, and finally change by . Then, isomorphisms between semigroups can be defined in terms of their multiplication tables. Let and be the multiplication tables of two semigroups of order n. According to the definitions given in [62], A and B describe two isomorphic semigroups if there exists a permutation such that
If, instead, we have
we say that A and B are related by an anti-isomorphism.
2.2. S-Expansion of Lie Algebras
Here, we briefly describe the general abelian semigroup expansion procedure (S-expansion for short). We refer the interested reader to [19] for further details.
First, we need to consider a Lie algebra with generators and Lie bracket
where are the structure constants. Next, we need a finite abelian semigroup , whose multiplication law is given in terms of the selectors defined in Equations (2) and (3). According to Theorem 3.1 from [19], the direct product
is also a Lie algebra, which is called expanded algebra. In the proof, it can be seen that the commutativity property of the semigroup is crucial for the Jacobi identity to be satisfied in . The elements of this expanded algebra are denoted by
where ⊗ is the Kronecker product of the matrix representations of the generators and the semigroup elements . The Lie bracket in is defined as
and therefore, the structure constants of the expanded algebra are fully determined by the selectors and the structure constants of the original Lie algebra , i.e.,
There are different cases in which it is possible to systematically extract smaller algebras from . One of them occurs when the Lie algebra has a decomposition in a direct sum of vectorial subspaces , where I is a set of indices encoding the information of the internal subspace structure of the algebra through the mapping , where stands for the set of all subsets of I, and the relation
If the semigroup S has a decomposition in subsets , , where denotes the set of all the products of all elements from with all elements from , satisfying the condition
which is said to be resonant with respect to the subspace structure (12) of the algebra; then, the subset
is a Lie algebra by itself, which is called resonant subalgebra of (see Theorem 4.2 from [19]).
Before explaining the next procedures to extract a smaller algebra from , we need to briefly explain what is called a reduction of an algebra. Suppose that we have a Lie algebra with a subspace decomposition . If the condition is satisfied, then it is possible to show that the structure constants on satisfies the Jacobi identity by themselves (the proof can be found in Chapter 4.1.2 of [63]). The structure constants whose indices take values only on then define a Lie algebra, which is called a reduced algebra . Notice that this definition does not require that is a subalgebra.
Now, the second case, in which it is possible to obtain a smaller algebra, occurs when there is a zero element in the semigroup . In that case, the commutation relations of are given by,
Thus, the expanded algebra admits a decomposition , with
which clearly satisfies the reduction condition . According to definition III.2 of [19], the structure constants satisfy the Jacobi identity on and then the commutators
define a Lie algebra by themselves, which is called the -reduced algebra. Thus, the reduction process is then equivalent to remove the whole sector from the expanded algebra. As we can see from Equation (15), the reduced algebra defined in this way is not a subalgebra of .
The existence of a resonant decomposition (a resonance for short) and a zero element for the semigroup are mutually independent issues and, consequently, the same is true for the extraction of a resonant subalgebra and a reduced algebra. That is, there are semigroups with resonances but with no zero element, and vice versa. Thus, the third way to obtain smaller algebras happens when a given semigroup has both properties simultaneously. In that case, it is possible to perform a reduction of the resonant subalgebra, and the resulting algebra, denoted by , is called a -reduced resonant subalgebra.
A fourth way to extract smaller algebras from is called resonant reduction. It can be applied when the semigroup has a resonant decomposition , satisfying Equation (16) for which, in addition, each subset admits a partition such that
This partition induce a descomposition on the resonant subalgebra where,
Using conditions (17) and (18), it can be shown that . This implies that is a reduction of the resonant subalgebra , which is called the resonant reduction.
Interestingly, the -reduction of a resonant subalgebra can be regarded as a particular case of the resonant reduction. Indeed, consider a semigroup S with a element and a resonant decomposition such that for each . If is the corresponding resonant subalgebra, then the following partition
satisfies the conditions (17) y (18) and, therefore, in this particular case, the resonant reduction of coincides with the -reduction of . Further details and explicit examples can be found in [19].
A last independent method to extract smaller algebras from can be carried out with the so-called H-condition, introduced in [64], that applies when the semigroup is a cyclic group of even order. However, as that procedure applies only to that family of semigroups, the techniques developed in this work are not necessarily needed for that case.
2.3. S-Expansions and the Classification of Lie Algebras
The properties of the S-expansion in the general context of the classification of Lie algebras have been studied in [60]. It was shown that abelian, solvable, and nilpotent algebras under expansions with any semigroup remain, respectively, abelian, solvable, and nilpotent (see Figure 3). However, for semi-simple and compact algebras, the situation is different. It was shown that the quantity
called a semigroup metric, can be used to predict if properties like semi-simplicity and compactness are preserved or broken under the S-expansion. To see this, let us first remember the following:
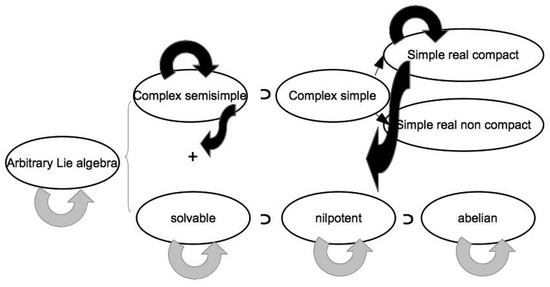
Figure 3.
Action of the expansion methods on the scheme of the theory of the classification of Lie algebras.
- A Lie algebra is semi-simple if and only if the Killing–Cartan (KC) metric,is non degenerate, i.e., if .
- The KC metric is diagonalizable, so if we denote its spectra of eigenvalues by , then a semi-simple Lie algebra is compact if and only if .
Now, the Killing–Cartan (KC) metric of an S-expanded Lie algebra is given by
This means that is the Kronecker product of and ,
with the last two matrices being diagonalizable. Denoting, the spectra of eigenvalues of and by and , respectively, from the general theory of Kronecker products, we know the following:
- The eigenvalues of are ;
- , where n is the order of the semigroup.
Therefore, is semi-simple (), and is semi-simple if and only if . In addition, if is compact (), then is compact only if . In other words, the real form of strongly depends on the signs of .
A similar analysis and the definition of the KC metric for the resonant subalgebra and reduced algebra that will be used in our library (see Section 4) can be found in Section 3.2 of [60]. In terms of the eigenvalues of the matrices , , and , it was shown that under the action of the S-expansion procedure, some properties of the Lie algebras (like commutativity, solvability, and nilpotency) are always preserved, while others (like semi-simplicity and compactness) are not in general. This was analyzed for the expanded algebra , the resonant subalgebra , and the reduced algebras and . The same analysis was carried out for the expansion of a general Lie algebra on its Levi–Malcev decomposition , where represents the semidirect sum of the semi-simple subalgebra and the maximal solvable ideal (also known as radical). The results are summarized in Table 1.

Table 1.
Properties preserved by the action of the S-expansion procedure.
Figure 3 illustrates the general scheme of the classification theory of Lie algebras, and the arrows represent the action of the expansion method on this classification. Grey arrows are used when the expansion method maps algebras of one set onto the same set, i.e., they preserve some specific property. On the other hand, black arrows indicate that the expansion methods can map algebras of one specific set onto the same set and also can lead us outside the set, to an algebra that will have a Levi–Malcev decomposition.
The Cartan decomposition of the expanded algebra was also obtained when the expansion preserves compactness. To check all these theoretical results, an example was given by studying all the possible expansions of the semi-simple algebra with semigroups of order up to 6. This check was made with some computer programs that have been the starting point of constructing the Java library that we will present in the next Sections. Before showing how the library is constructed and how it works, we give a brief review of the classification of semigroups.
2.4. Review of Finite Semigroups Programs
Discrete semigroups have been a subject of intensive research in mathematics, and its classifications have been made by many different authors (see, e.g., [62,65,66,67,68,69,70,71,72,73,74] and references therein). In particular, the number of finite non-isomorphic semigroups of order n is given in Table 2.

Table 2.
The number of discrete semigroups for each rank.
As shown in the table, the problem of enumerating all non-isomorphic finite semigroups of a certain order is a non-trivial problem. In fact, the number Q of semigroups increases very quickly with the order of the semigroup. Since the original algorithms proposed by Plemmons [62,67,68] to computationally generate non-isomorphic semigroups, a lot of work has been aided by computers. Remarkably, order 9 has only been reached with the aid of supercomputers, and the number (but not the explicit list of semigroup tables) for order 10 has been obtained very recently [75].
Particularly, in [76], very useful algorithms were constructed to make calculations with finite semigroups. First, the program gen.f generates in lexicographical ordering the lists of all the non-isomorphic semigroups of order . This means that if we find a semigroup table , which is not contained in one of those lists, then
- does not have lexicographical ordering;
- is isomorphic to one and only one table of the lists generated by gen.f.
In each list, a semigroup of order n is univocally identified by the number and the semigroup elements are denoted by with .
The second program of [76] is com.f, which takes one of these lists generated by gen.f and selects only the abelian semigroups. For example, for the elements are labeled by , and the program com.f gives the semigroups from the table in Figure 4.
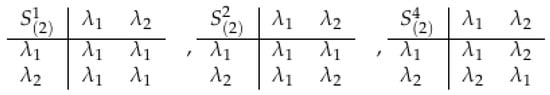
Figure 4.
The semigroups of rank .
Note that the semigroup is not given in the list in Figure 4 because it is not abelian. In the library that will be described in the next section, it will be easier to use the full lists of semigroups generated by gen.f. When needed, we will select the abelian ones using a method similar to com.f.
2.5. Description of the Library and Notation
As a preliminary step, we have used the program gen.f of [76] to generate the files sem.2, sem.3, sem.4, sem.5, and sem.6, which contain all the non-isomorphic semigroups up to order 6. In principle, with the program gen.f, it is possible to generate the full lists of non-isomorphic semigroups up to order 8. In our case we were able to compute the lists up to order 6. However, various methods of our library are able to perform calculations with semigroups of order higher than 6, like checking associativity, finding zero elements, isomorphisms, and resonances (see, e.g., Section 5.1 and Section 5.4). As we will see, those files are the input data for many of our programs.
To use the Java library that we present in this work, it is necessary to download the linear algebra package jama.jar from [77] and the list of files from [61] given in Table 3. In particular, we use the methods belonging to the class Matrix of the library jama.jar.

Table 3.
The list of files that we have to download from [61].
A ReadMe.pdf file is also provided with detailed installation instructions, should they be needed.
Our library is composed of the following classes (to see the source code unzip the file sexpansion.jar):
- 1.
- Semigroup.java;
- 2.
- SetS.java;
- 3.
- Selector.java;
- 4.
- SelectorReduced.java;
- 5.
- SelectorResonant.java;
- 6.
- SelectorResonantReduced.java;
- 7.
- StructureConstantSet.java;
- 8.
- StructureConstantSetExpanded.java;
- 9.
- StructureConstantSetExpandedReduced.java;
- 10.
- StructureConstantSetExpandedResonant.java;
- 11.
- StructureConstantSetExpandedResonantReduced.java.
Each class contains different methods. A brief description can be found in the code at the beginning of each class and method. As the full documentation of the library is available in [78], in this article, we will describe only the most important methods of these classes (see Section 3 and Section 4).
In addition, there are 45 programs included as examples in the file examples.zip whose aim is to show how the methods of our library work. They are named with the prefixes I, II, and III, which stand for the following classification:
- I
- General computations with semigroups;
- II
- Examples of S-expansions of Lie algebras;
- III
- Programs related to the calculations made in [60].
The list of these example programs is given in Appendix A, and most of them will be described in Section 5.
2.5.1. The Type of Resonances Implemented on This First Version
The methods that will be described in Section 3 and Section 4, are able to work with algebras having a decomposition with the subspace structure given by
Correspondingly, the type of resonant decomposition that will be considered has the form and satisfies
Then, the resonant subalgebras that will be obtained have the form
We will also deal with the case in which the semigroup may have a element. Therefore, the library will allow us to extract the following three types of smaller algebras from :
- —Reduced algebras, when the semigroup has a element;
- —Reduction of the resonant subalgebra when the semigroup has simultaneously a element and the resonant decomposition given by Equation (26).
In a first stage, the situation described by Equations (25)–(27) (particular cases of Equations (12)–(14)) will be enough for the applications we want to consider in this work. However, as our library has an open GNU licence, we expect that it can be extended in order to perform S-expansions of algebras having more general subspace structures. This type of licence basically means that anyone can download, use, and modify the library. We do appreciate the corresponding citation to our original version.
2.5.2. Conventions and Notation
For programming language reasons, the semigroup elements must be labeled by their sub-index number
with . With this convention, the closure is given by
so that the multiplication Table 1 can be written as
Thus, properties like associative and commutativity, respectively, read,
which, in terms of the multiplication table, can be expressed as
An isomorphism, like the one described in Equation (4), will be then denoted by
and means change 1 by , change 2 by , … and finally change n by .
In the codes, Latin characters are used to label both semigroup elements and generators of the Lie algebra, and their meanings are specified.
3. Methods for Semigroup Calculations
3.1. Loading All the Non-Isomorphic Semigroups
Using the conventions and notations adopted in Section 2.5, we define the Semigroup class in Fragment 1 of the code to represent a discrete semigroup and all the operations which can be performed with them.
| Fragment 1. Definition of class for discrete semigroups. |
| public class Semigroup { int [][] data; int order; int ID; |
Obviously, the code is bigger, but for space reasons, we restrict ourselves only to describing the main parts of the methods and classes. We remind the reader that the library, containing the full code of all the programs described here, is available in [61]. Thus, we use three variables to save the information of a semigroup : an integer ID, which corresponds to the identifier a of the semigroup, a second integer order, which tells us the order n of the semigroup, and a matrix of integers data, where we save the multiplication table of the semigroup .
As explained in Section 2.5, in many of the calculations that will be carried out, it is necessary to load the semigroups generated by the program gen.f of [76]. This is carried out by the method loadFile, which loads all the semigroups of a given order (up to order 6), returning us an array of Semigroup objects. To load all the available semigroups from order 2 to 6, we use the method loadFromFile, which uses the method loadFile. In Section 5, we will show how the method loadFromFile is used in different problems.
3.2. Associativity, Commutativity, and -Element
To check if a given multiplication table of a set of elements is a semigroup, we must check if it is associative. This means to check the relations for all . We perform this task with the method isAssociative in Fragment 2 of the code. Basically, this method returns true if a given multiplication table is associative.
| Fragment 2. A simple check of associativity for discrete semigroups. |
| public boolean isAssociative() { int i , j , k ; for ( i = 0 ; i < order ; ++ i) { for ( j = 0 ; j < order ; ++j) { for ( k = 0 ; k < order ; ++ k) { if ( ! (data[i][data[j][k]-1] == data[data[i][j]-1][k])) { return false ; }}}} return true; } |
On the other hand, as described in Section 2.2, to perform an S-expansion, the semigroup used must be commutative. The method isCommutative is given in Fragment 3 of the code. It returns true if a given semigroup is commutative, i.e., .
| Fragment 3. Checking commutativity for discrete semigroups. |
| public boolean isCommutative(){ int i, j; for ( i = 0 ; i < order ; ++i) { for( j = 0 ; j < order ; ++j ) { if ( ! (data[i][j] == data[j][i])) { return false; }}} return true; } |
In Section 2.2, we have explained that when a commutative semigroup has a zero element satisfying , it is possible to perform a -reduction of the expanded algebra. To be able to automatize that procedure we need a method which can look for the zero element for any semigroup. Such a method is written in Fragment 4 of the code. The method findZero gives the zero element when the semigroup does have it; otherwise, it returns as a result.
| Fragment 4. Looking for the zero element inside a given discrete semigroup. |
| public int findZero() { int i, j ; boolean isZero = false ; for ( i = 0 ; i < order ; ++ i ) { if ( isZero == true ) { return i ; } j = 0 ; isZero = true; while ( isZero && (j < order )) { if ( data[j][i] != i+1) { isZero = false ; } ++j; }} if ( isZero == true ) { return order ; } return −1 ; } |
On the other hand, it is also useful to have an auxiliary method in some cases to check for the equality of two given semigroups. The method isEqualTo in Fragment 5 returns true if they are equal.
| Fragment 5. Checking for the equality of two given discrete semigroups. |
| public boolean isEqualTo ( Semigroup B ) { int i,j; if ( this.order != B.order ) { return false; } for ( i = 0 ; i < this.order ; ++i ) { for ( j = 0 ; j < B.order ; ++j) { if ( this.data[i][j] != B.data[i][j]){ return false; }}} return true; } |
In Section 5, we will show how the methods loadFromFile, isAssociative, isCommutative, findZero, and isEqualTo are used in different problems.
3.3. Creating Sets and the Permutation Group
As explained in Section 2.1, the group of isomorphisms of the semigroups or order n is the group of permutations of n elements, . Thus, we define in Fragment 6 of the code the SetS class to represent a permutation.
| Fragment 6. Definition of class to represent a permutation. |
| public class SetS { int [] list ; int nElements ; |
A SetS object contains an integer nElements representing the number of elements to which we want to apply the permutation and a list, where we save the permutation with the notation given in Equation (33) in Section 2.5. These objects will also serve us to save any set of non-repeated integers, like the one we will use for the resonant decomposition of a discrete semigroup.
Again, for space reasons, we are not able to reproduce the complete definition of the SetS class here, and only its main methods will be described in what follows (remind that the full library is available on [61]).
To create a SetS object just from an array of integers, we can use Fragment 7 of the code.
| Fragment 7. Creating the object SetS. |
| public SetS( int [] elements ) { list = elements ; nElements = elements.length; } |
while to create a SetS of n elements containing the identity permutation in we should use Fragment 8 of the code.
| Fragment 8. Creating the object SetS. |
| public SetS( int n ){ nElements = n; list = new int[n]; int i ; for ( i = 0 ; i < n ; ++i) { list[i] = i +1 ; }} |
Now, to check if two given semigroups are isomorphic, we have to try all the existing isomorphisms for a given order. This means using all the elements in . This is performed by the method allPermutations in Fragment 9, which returns an array of SetS objects containing all the elements in .
| Fragment 9. Creating an array of SetS objects. |
| SetS [] allPermutations( ) { SetS result = new SetS(0) ; return this.permutationsAux( this, result); } |
This method uses the auxiliary method permutationsAux, which actually performs most of the work. This is a recursive method that takes an original SetS object and reorders its elements in all the possible ways. This is, given the identity permutation
it returns all the possible ways to permute it, i.e., all the elements of the permutation group . As we can see in what follows in Fragment 10 of the code, permutationsAux uses the methods addElement and eraseElement, whose definition is obvious and we do not reproduce here.
| Fragment 10. The methods addElement and eraseElement in use. |
| SetS [] permutationsAux( SetS original, SetS result ) { int i, j; SetS original2, result2 ; SetS [] list = null; SetS [] totalList = null; SetS [] previousList = null; int N = 0 ; if ( original.nElements == 0 ) { list = new SetS[1]; list[0] = result ; return list ; } for ( i = 0 ; i < original.nElements ; i++ ){ result2 = result.addElement( original.elementAt(i) ) ; original2 = original.eraseElement(i) ; list = permutationsAux( original2, result2) ; N = N + list.length ; previousList = totalList ; totalList = new SetS[N]; for ( j = 0 ; j < N − list.length ; ++j) { totalList[j] = previousList[j]; } for ( j = 0 ; j < list.length ; ++j) { totalList[ j + N − list.length ] = list[j]; }} return totalList; } |
As explained in Section 2.1, two given semigroups are isomorphic or anti-isomorphic if there exists a permutation that relates them through Equations (5) and (6). Here, we will describe two basic operations related to isomorphisms. First, the method that applies a given isomorphism to a semigroup is permuteWith written in Fragment 11 of the following code:
| Fragment 11. Applying a given isormorphism to a semigroup. |
| public Semigroup permuteWith( SetS s ) { int i,j; int [][] matrix = new int[this.order][ this.order]; SetS inverse = s.inversePermutation() ; for ( i = 0 ; i < this.order ; ++i) { for ( j = 0 ; j < this.order ; ++j) { matrix[i][j] = this.data[ inverse.elementAt(i) − 1] [ inverse.elementAt(j) -1] ; }} for ( i = 0 ; i < this.order ; ++i) { for ( j = 0 ; j < this.order ; ++j) { if ( matrix[i][j] != -1 ) { matrix[i][j] = s.elementAt( matrix[i][j] − 1 ); }}} return new Semigroup(matrix); } |
In other cases, what we need is to find all the isomorphic forms of a given semigroup, i.e., apply all the possible permutations to a given semigroup. In that case, we use the method permute in Fragment 12, which returns an array of Semigroup objects containing all the permutations of a given one:
| Fragment 12. Getting all the possible permutations of a given semigroup. |
| public Semigroup [] permute() { SetS identity = new SetS( this.order); SetS [] permutations = identity.allPermutations() ; int k; Semigroup [] result = new Semigroup [permutations.length]; for ( k = 0 ; k < permutations.length ; ++k) { result[k ] = this.permuteWith(permutations[k]); } return result; } |
Then, a simple method to check anti-isomorphisms is given in Fragment 13 of the code.
| Fragment 13. Checking anti-isomorphisms. |
| public Semigroup [] antiPermute () { return (this.transpose()).permute( ); } |
In Section 5, we will show different examples using these methods.
3.4. Resonant Decompositions
In Section 2.2, we explained that a resonant subalgebra can be extracted from the expanded algebra when the original algebra has a certain subspace structure and the semigroup satisfies a so-called resonant decomposition (see Equations (12) and (13)). As mentioned in Section 2.5, for our purposes, it will be enough to consider the case given by Equations (25) and (26), i.e., we will study resonant conditions of the type
A previous step to check if two given subsets and satisfy the resonance condition is to check that their union reproduces the full semigroup, i.e., . This is carried out in Fragment 14 by the method fillTheSpace of the SetS class.
| Fragment 14. Checking the resonance condition. |
| public static boolean fillTheSpace(SetS s1,SetS s2,int order){ int i ; for ( i = 0 ; i < order ; ++i) { if ( ! s1.find( i+1) && ! s2.find(i +1) ){ return false; }} return true; } |
The parameter order tells the method the order of the semigroup for which s1 and s2 must be a resonant decomposition.
In Fragment 15, the method isResonant returns true if the two SetS objects s0 and s1 represent a resonant decomposition for the current Semigroup object.
| Fragment 15. Checking the resonance condition. |
| public boolean isResonant( SetS s0, SetS s1) { int i,j, n0 = s0.nElements, n1 = s1.nElements ; if ( SetS.fillTheSpace(s0, s1, order) ) { for ( i = 0 ; i < n0 ; ++i ) { for ( j = 0 ; j < n0 ; ++j ) { if ( ! s0.find(this.data[s0.elementAt(i) -1] [s0.elementAt(j)-1] ) ) { return false ; }}} for ( i = 0 ; i < n0 ; ++i ){ for ( j = 0 ; j < n1 ; ++j) { if ( ! s1.find( this.data[s0.elementAt(i)-1] [s1.elementAt(j)-1])) { return false; }}} for ( i = 0 ; i < n1 ; ++i) { for ( j = 0 ; j < n1 ; ++j) { if (! s0.find( this.data[s1.elementAt(i)-1] [s1.elementAt(j)-1])) { return false; }}}} else { return false; } return true; } |
Once we are able to check if a given decomposition of a semigroup is resonant, we want to be able to look for resonant decompositions. In Fragment 16, the method findResonances looks for all the possible resonances of a semigroup, with and having, respectively, n1 and n2 elements.
| Fragment 16. Looking for all the possible resonances of a given semigroup. |
| public SetS [][] findResonances( int n1, int n2 ) { SetS total = new SetS(this.order) ; SetS [] list1 = total.subSets(n1) ; SetS [] list2 = total.subSets(n2) ; SetS [][] result = null; SetS [][] auxiliar = null ; int foundResonances = 0 ; int i, j, k = 0; for ( i = 0 ; i < list1.length ; ++ i) { for ( j = 0 ; j < list2.length ; ++j) { if ( this.isResonant( list1[i], list2[j]) && SetS.fillTheSpace( list1[i], list2[j], this.order)) { foundResonances = foundResonances + 1 ; auxiliar = result ; result = new SetS[foundResonances ] [2] ; for ( k = 0 ; k < foundResonances -1 ; ++k) { result[k][0] = auxiliar[k][0]; result[k][1] = auxiliar[k][1]; } result[ foundResonances − 1 ] [0] = list1[i]; result[ foundResonances − 1] [1] = list2[j]; }}} return result; } |
In case it finds any resonant decomposition, this method returns a two-dimensional array whose element is the and is for the ith decomposition found. In Fragment 17, this method uses the auxiliary method subSets, which returns all the subsets with n element of a given SetS object.
| Fragment 17. The method auxSubset is used by the method subSets. |
| public SetS [] subSets( int n) { SetS result = new SetS(); return SetS.cleanDuplicates(auxSubset( this, result, n)); } |
This method is just a more convenient way to use the recursive method auxSubset in Fragment 18:
| Fragment 18. The method auxSubset is used by the method subSets. |
| public SetS[] auxSubset( SetS original, SetS result, int n) { int i; SetS [] list = null; SetS [] totalList = null; if ( n == 0) { totalList = new SetS[1]; totalList[0] = result; return totalList ; } SetS aux1; SetS aux2; for ( i = 0 ; i < original.nElements ; ++i) { aux1= original.eraseElement(i); aux2= result.addElement( original.elementAt(i)); list = auxSubset(aux1, aux2, n-1); totalList = SetS.add(list, totalList); if ( totalList != null) { }} return totalList ; } |
In Fragment 19, the auxiliary method cleanDuplicates just cleans possible duplicates in an array of SetS objects.
| Fragment 19. Removing possible duplicates. |
| public static SetS[] cleanDuplicates( SetS [] lst) { int i, j ; int n = lst.length ; int elements = n; SetS [] newList ; for ( i = 0 ; i < n ; ++i) { lst[i] = SetS.sort(lst[i]); } for ( i = 0 ; i < n ; ++i) { for ( j = i +1 ; j < n ; ++j){ if (lst[i] != null && lst[j] != null && lst[i].equalTo(lst[j])){ lst[j] = null ; elements = elements − 1 ; }}} newList = new SetS[elements] ; j = 0 ; for ( i = 0 ; i < n ; ++i) { if ( lst[i] != null) { newList[j] = lst[i]; ++j; }} return newList ; } |
To find all the possible resonant decompositions of a given semigroup, we define the method findAllResonances in Fragment 20 of the code.
| Fragment 20. Finding all the possible resonant decompositions. |
| public SetS [][] findAllResonances() { int i, j, k; SetS [][] result = null; SetS [][] auxiliar ; SetS [][] intermediateResult; int N = 0; for ( i = 1 ; i < this.order ; ++i) { for ( j = 1 ; j < this.order ; ++j) { intermediateResult = this.findResonances( i, j) ; if ( intermediateResult != null) { auxiliar = result ; N = N + intermediateResult.length ; result = new SetS[ N][2]; for ( k = 0 ; k < N − intermediateResult.length ; ++k) { result[k][0] = auxiliar[k][0]; result[k][1] = auxiliar[k][1]; } for (k = 0 ; k < intermediateResult.length ; ++k) { result[ N − intermediateResult.length + k][0 ] = intermediateResult[k][0]; result[ N − intermediateResult.length + k][ 1 ] = intermediateResult[k][1]; }}}} return result; } |
In the following sections, we will see the usefulness of these methods.
4. Methods for S-Expansions
In this section, we will explain the construction of the classes, which will allow us to
- Represent a semigroup of order n and compute the metric defined in Equation (21));
- Represent Lie algebras in terms of their structure constants (adjoint representation) and compute the Killing–Cartan (KC) metric defined in Equation (22);
- Show the selector in a fancy way, by using n boxes of dimension , so the component is found in box a, row b, column c (and carry out something similar for the structure constants of the original and expanded algebras);
- Obtain the S-expanded algebra, resonant subalgebra, -reduced algebra and the -reduction of a resonant subalgebra;
- Compute the KC metric of the original Lie algebra, the S-expanded algebra, the resonant subalgebra, the -reduced algebra and the -reduction of a resonant subalgebra (see Equation (24) and Section 3.2 of [60]).
4.1. A Reminder
For space reasons, we will only explain the main parts of those classes here. The full source code of the library is available in [61] and its documentation can be found in [78].
4.2. Representing Semigroups and Lie Algebras
In Section 2.1, it was shown that an informal but useful way to represent the multiplication law of a semigroup is by means of the selectors , whose definition was given in Equation (2). Thus, in Fragment 21, we define the Selector class to represent these quantities.
| Fragment 21. Definition of class for K-selectors. |
| public class Selector { int order ; int [][][] data ; |
It has two variables: an integer to save the order of the semigroup and an array to save all the selectors in the semigroup as follows:
The methods Selector, SetS, and get allow the creation of a selector object for a semigroup of order n to set and return the value of the component of the selector. The method show gives the selector by means of n boxes of dimension , so the component is found in box a, row b, column c. According to Equation (3), this means that box a is indeed the adjoint representation of the element .
For example, consider the semigroup given by the table in Figure 5.

Figure 5.
An example of an associative commutative discrete semigroup of rank 4.
The following piece of code (part of program 26 in Appendix A) given in Fragment 22 illustrates how the Selector class works together with the method getSelector of the Semigroup class to build and print a selector object for this semigroup.
| Fragment 22. Creating and printing K-selectors for the semigroup from Figure 5. |
| int [][] mS = {{1,2,3,4},{2,3,4,4},{3,4,4,4}, {4,4,4,4}}; Semigroup S = new Semigroup(mS) ; Selector Adj = S.getSelector() ; Adj.show(); |
The output in Figure 6 reads

Figure 6.
List of K-selectors for the semigroup from the table in Figure 5.
This class also contains the methods selectorMetric and expandedMetric, which computes the metrics and defined in Equations (21)–(23). Explicit examples with them will be given in Section 5.5.
In a similar way, we construct the classes SelectorReduced, SelectorResonant, and SelectorResonantReduced, which extend the Selector class for the cases where the semigroup has a zero element, a resonance, and both simultaneously.
On the other hand, to represent a Lie algebra by means of its structure constants, we define the StructureConstantSet class in Fragment 23.
| Fragment 23. Definition of StructureConstantSet class. |
| public class StructureConstantSet { double [][][] constants ; int N ; |
The integer N in Fragment 23 is the number of generators of the Lie algebra, and with the convention
we choose
This class contains methods that allow the introduction of the values of the structure constants and show them in a similar way to what was carried out for the selectors. In particular, the following method given in Fragment 24 sets the values of and .
| Fragment 24. Setting the values of the structure constants. |
| public void setStructureConstant(int i, int j, int k, double fijk){ constants[i][j][k] = fijk ; constants[j][i][k] = − fijk; } |
As the first position of an array [ ] is usually [0], the method setStructureConstant must be used to introduce the non-vanishing structure constants as follows:
where . However, the outputs will usually be given in such a way that .
NameOfTheAlgebra.setStructureConstant(i, j, k, value of C_{ij}^{k})
As an example, the following piece of code in Fragment 25 (also part of program 26 in Appendix A) illustrates how to introduce the structure constants of the algebra,
in order to obtain its adjoint representation.
| Fragment 25. Obtaining the adjoint representation for algebra. |
| sl2.setStructureConstant(0, 1, 2, -2); sl2.setStructureConstant(0, 2, 1, 2); sl2.setStructureConstant(1, 2, 0, 2); sl2.show(); |
The output in Figure 7 reads,

Figure 7.
Matrices of the adjoint representation of the elements of the algebra .
Several simple operations can be performed by the methods of the StructureConstantSet class. For example, the method in Fragment 26 computes the Killing–Cartïn metric of a given Lie algebra.
| Fragment 26. Computing the Killing–Cartïn metric of a given Lie algebra. |
| public Matrix cartanKillingMetric(){ int i, j, k, l; double sum = 0 ; double [][] metric = new double[N][N] ; for (i = 0 ; i < N ; ++i) { for (j = 0 ; j < N ; ++j) { sum = 0 ; for (k = 0 ; k < N ; ++k) { for (l = 0 ; l < N ; ++l) { sum = sum + this.structureConstant(i,k,l) * this.structureConstant(j,l,k); }} metric[i][j] = sum ; }} return new Matrix(metric); } |
Explicit examples using this and other methods included in the classes Selector and StructureConstantSet will be given in Section 5.5.
4.3. The S-Expanded Algebra
In double index notation, the Lie bracket of the S-expanded algebra is written here as
To use this double index notation internally in our library, we create the class StructureConstantSetExpanded in Fragment 27.
| Fragment 27. Creating the class StructureConstantSetExpanded. |
| public class StructureConstantSetExpanded { int n,m ; double [][][][][][] data ; |
Thus, an object of this class has information about the dimension n of the original Lie algebra and the order m of the semigroup used to perform the S-expansion and uses the six-dimensional array data to save the structure constants, in such a way that
To obtain the S-expanded algebra, we must follow the next steps:
- 1.
- Create a StructureConstantSet object to store the original Lie algebra;
- 2.)
- Create a Semigroup object S to store the semigroup which we want to use for the S-expansion;
- 3.
- Use the method getExpandedStructureConstant to perform the S-expansion of the Lie algebra with the semigroup object;
- 4.
- Use the method showCommut to obtain the non-vanishing commutators of the expanded algebra ;
- 5.
- Use the method showSC to obtain the non-vanishing structure constants of ;
- 6.
- Use the method cartanKillingMetric to compute the KC metric of .
A piece of code performing the steps above for the algebra and the semigroup given by Figure 5 and by Equation (34) would be in Fragment 28.
| Fragment 28. Computing the Killing–Cartïn metric of an extended algebra of . |
| StructureConstantSet sl2 = new StructureConstantSet(3) ; sl2.setStructureConstant(0, 1, 2,-2) ; sl2.setStructureConstant(0, 2, 1, 2) ; sl2.setStructureConstant(1, 2, 0, 2) ; int [][] SemigroupTable = {{1,2,3,4},{2,3,4,4},{3,4,4,4}, {4,4,4,4}}; Semigroup S = new Semigroup(SemigroupTable) ; StructureConstantSetExpanded Gexp = S.getExpandedStructureConstant(sl2); Gexp.showCommut(); Gexp.showSC(); Matrix metricaGexp = Gexp.cartanKillingMetric(); metricaGexp.print(0,0); |
Further examples with sample outputs will be given in Section 5.5.
4.4. The Resonant Subalgebra
To obtain a resonant subalgebra of an S-expanded algebra, we define the StructureConstantSetExpandedResonant class, which is a child of the StructureConstantSetExpanded class in Fragment 29.
| Fragment 29. Definition of the StructureConstantSetExpandedResonant class. |
| public class StructureConstantSetExpandedResonant extends StructureConstantSetExpanded { SetS S0, S1, V0, V1; |
Here, S0 and S1 represent the resonant decomposition of the semigroup, whilst V0 and V1 give the graded decomposition of the Lie algebra. To obtain the resonant subalgebra of an S-expanded algebra, we must
- 1.
- Obtain the correspondent S-expanded algebra, following the steps in the previous section;
- 2.
- Introduce the resonant decomposition and with the method SetS;
- 3.
- Introduce the graded decomposition and also with the method SetS;
- 4.
- Use all these objects to create a StructureConstantSetExpandedResonant object;
- 5.
- Use methods showCommutRes, showSCRes, and cartanKillingMetricPretty to obtain the non-vanishing commutators, structure constants, and KC metric of the resonant subalgebra.
For example, the algebra considered in Equation (34) has a subspace decomposition given by , where
Considering the semigroup given in Figure 5 again, we see that it admits a decomposition with
which is resonant, i.e., it satisfies Equation (26). Thus, the piece of code in Fragment 30 performs the S-expansion of , and it calculates the resonant subalgebra.
| Fragment 30. Calculating the resonant subalgebra. |
| StructureConstantSet sl2 = new StructureConstantSet(3) ; sl2.setStructureConstant(0, 1, 2,-2) ; sl2.setStructureConstant(0, 2, 1, 2) ; sl2.setStructureConstant(1, 2, 0, 2) ; int [][] SemigroupTable = {{1,2,3,4},{2,3,4,4},{3,4,4,4}, {4,4,4,4}}; Semigroup S = new Semigroup(SemigroupTable) ; int[] mS0 = {1,3,4} ; SetS S0 = new SetS(mS0) ; int[] mS1 = {2,4} ; SetS S1 = new SetS(mS1) ; int[] mV0 = {1}; SetS V0 = new SetS(mV0); int[] mV1 = {2,3}; SetS V1 = new SetS(mV1); StructureConstantSetExpanded Gexp = S.getExpandedStructureConstant(sl2); StructureConstantSetExpandedResonant ResGexp = new StructureConstantSetExpandedResonant(Gexp.data,S0,S1,V0,V1) ; ResGexp.showCommutRes(); ResGexp.showSCRes(); Matrix metricaResGexp = ResGexp.cartanKillingMetricPretty(); metricaResGexp.print(0,0); |
Other examples with samples of their outputs will be described in detail in Section 5.5.
4.5. S-Expanded Algebra Followed by a 0S-Reduction
To perform the reduction by the zero element of an S-expanded Lie algebra, we define the StructureConstantSetExpandedReduced class in Fragment 31, which is a child of the StructureConstantSetExpanded class.
| Fragment 31. Definition of the class for performing -reduction. |
| public class StructureConstantSetExpandedReduced extends StructureConstantSetExpanded { int zero ; |
With respect to the StructureConstantSetExpanded class, it only adds an integer variable to save the zero element.
To perform the reduction by zero of an S-expanded algebra, we have to
- 1.
- Obtain the S-expanded algebra in a StructureConstantSetExpanded;
- 2.
- Use it to create a StructureConstantSetExpandedReduced;
- 3.
- Use other methods in the class to obtain the non-vanishing commutators, structure constants, and KC metric of the reduced algebra.
For example, the semigroup given in Figure 5 has as the zero element. Thus, the piece of code in Fragment 32 calculates the -reduction of the S-expansion of the algebra .
| Fragment 32. -reduction of the S-expansion of the algebra . |
| StructureConstantSet sl2 = new StructureConstantSet(3) ; sl2.setStructureConstant(0, 1, 2,-2) ; sl2.setStructureConstant(0, 2, 1, 2) ; sl2.setStructureConstant(1, 2, 0, 2) ; int [][] SemigroupTable = {{1,2,3,4},{2,3,4,4},{3,4,4,4}, {4,4,4,4}}; Semigroup S = new Semigroup(SemigroupTable); StructureConstantSetExpandedReduced RedGexp = new StructureConstantSetExpandedReduced (S.getExpandedStructureConstant(sl2).data,4); RedGexp.showCommutRed(); RedGexp.showSCRed(); Matrix metricaRedGexp = RedGexp.cartanKillingMetricPretty(); metricaRedGexp.print(0,0); |
4.6. Resonant Subalgebra Followed by a 0S-Reduction
In Fragment 33, we define the class StructureConstantSetExpandedResonantReduced, which is a child of the class StructureConstantSetExpandedResonant.
| Fragment 33. Defining class for the resonant subalgebra followed by a -reduction. |
| public class StructureConstantSetExpandedResonantReduced extends StructureConstantSetExpandedResonant { int zero; |
We just add an integer to save the zero element. Its use is analogous to that of the StructureConstantSetExpandedResonant described in Section 4.4. Explicit examples using this class and its methods are given in Section 5.5.
5. Applications
Here, we will describe most of the programs listed in Appendix A in order to explicitly show the kind of calculations that can be carried out with the methods described in Section 3 and Section 4. Mainly, we will explain the ones that allow us to carry out the following:
- Check associativity and commutativity, find the zero element and resonances for any given multiplication table;
- Apply permutations and find isomorphisms between any set of semigroups;
- Perform S-expansions with any given semigroup and, if the semigroup fulfills the necessary conditions, to find the resonant subalgebra , the reduced algebra and the reduction of the resonant subalgebra ;
- Identify S-expansions, preserving semi-simplicity.
With these examples, the user can easily create new programs to perform their own calculations. Along this section, we will refer to the example programs by their Appendix A number. When the output is short, the results are directly printed onto the screen. Longer outputs are printed in .txt-files in the folder “./Output_examples/”, with the naming convention Output_ + name of the program. For a good visualization, those files must opened with Notepad++. In addition, most of the outputs can be found in the file Output_examples.zip available in [61]. Finally, we remind the reader that a brief description of the general structure of these programs can be found in Section 2.5.
5.1. Examples of Associativity and Commutativity
The first two programs (program 1 and program 2) listed in Appendix A allow us to check the associativity and commutativity of the multiplication in the tables given in Figure 8, Figure 9 and Figure 10.
| Fragment 34. The main parts of program 1 from Appendix A are described here. |
| package examples; import sexpansion.Semigroup; public class I_associative_checking { public static void main(String[] args) { // Manually enter the semigroups as matrices int[][] ms_ex1 = {{1,2,3},{2,1,2},{3,2,1}}; // and do the same for the other tables. // Next, we use these tables to define Semigroup objects: Semigroup s_ex1 = new Semigroup(ms_ex1) ; // and define s_ex2,..., s_ex6 in the same way. // Now, the method isAssociative can be used as follows: if (s_ex1.isAssociative()) { System.out.println(‘‘The semigroup S_ex1 is associative’’);} else { System.out.println(‘‘The semigroup S_ex1 is not associative’’);} // and proceed similarly with the other tables. }} |

Figure 8.
Examples of associative commutative discrete semigroup of rank 3.

Figure 9.
Examples of associative commutative discrete semigroup of rank 4 and rank 5.
Figure 10.
An example of associative commutative discrete semigroup of rank 10.
The output in Figure 11 reads
| Fragment 35. Program 2 is defined in a similar way. |
| package examples; import sexpansion.Semigroup; public class I_commutative_checking { public static void main(String[] args) { |

Figure 11.
Output of program 1 from Appendix A.
After introducing the tables, in the same way as was carried out for program 1, in Fragment 36, we use the method isCommutative.
| Fragment 36. The method isCommutative is used in program 2 from Appendix A. |
| if (s_ex1.isCommutative()) { System.out.println(‘‘S_ex1 is commutative’’);} else { System.out.println(‘‘S_ex1 is not commutative’’);} // and repeat the same for the other tables. }} |
Thus, we have in Figure 12 the following result:

Figure 12.
Output of the method isCommutative.
In particular, the semigroup is an example of a non-commutative semigroup of order 10 that has been used in [75].
Another example is given by program 3, which selects the abelian semigroups from the lists of all non-isomorphic semigroups sem.n (with ). The outputs are printed in the folder “./Output_examples/” in text files named with the convention explained at the beginning of this section.
5.2. Examples with Zero Element and Resonances

Figure 13.
Examples of multiplication tables for abelian semigroups with zero element .

Figure 14.
Examples of multiplication tables for abelian semigroups with zero element .

Figure 15.
Examples of multiplication tables for abelian semigroups with zero element .
With a simple program, like the ones described in the previous Section 5.1, it can be checked that the tables given in Figure 13, Figure 14 and Figure 15 actually represent abelian semigroups. Indeed, they have been used in different works related to S-expansions. First, the semigroups , , , , and were used in [42] to obtain some Bianchi as an S-expansion from the two-dimensional solvable algebra . Then, semigroup and were constructed in [20] to show that the semi-simple version of the Maxwell algebra [45] can be obtained as an S-expansion of the AdS algebra, . Later, in [48], the semigroup was renamed as and extended to a family of semigroups , which lead to a generalization of the Maxwell algebras.
Now, we will explicitly show how the methods of our library can be used to find the zero element and all resonant decompositions (of the type (26)) for these semigroups. First, program 19 introduces those semigroups as tables and then as semigroup objects, in the same way as explained in Section 5.1 for program 1.
| Fragment 37. Manual input of the multiplication table in program 19. |
| package examples; import sexpansion.Semigroup; public class II_findzero_ex { public static void main(String[] args) { // Manually enter the semigroups table |
The only important issue is that the element in the multiplication tables , , , , and cannot be represented by the number 0, because the library recognizes only positive interger numbers to represent semigroup elements. For example, the matrix associated with must be introduced as
where we have identified with 1, with 2, and with 3. A similar change must be applied to introduce the other semigroups having the element .
int[][] ms_ex1 = {{1,2,3},{2,3,2},{3,2,3}};
Then, program 19 uses the method findZero in Fragment 38 of the class Semigroup to define an integer for each semigroup to save its zero element. It also defines the integer nozero that is used when a given semigroup has no zero element.
| Fragment 38. Method findZero is used in program 19 from Appendix A. |
| int zero_S_E2 = S_E2.findZero(); // and do the same for the others. int nozero = −1; |
| Fragment 39. Obtaining the results of program 19 from Appendix A. |
| if (zero_S_E2 == nozero){ System.out.println(‘‘The semigroup S_E2 has no zero element’’);} else { System.out.println(‘‘The zero element of S_E2 is ’’ +zero_S_E2);} // and repeat for the others. }} |
Thus, the output in Figure 16 reads

Figure 16.
Output of the results of program 19 from Appendix A searching for zero element.
On the other hand, program 15 finds the resonances of the semigroups given in the tables in Figure 13 and Figure 14. Program 16 carries out the same procedure as program 15, but prints the result in the folder “./Output_examples/”. After introducing the semigroup tables, it defines the following variables: two auxiliary SetS objects S0 and S1, the integers j, and nResonances to count the different resonances that a given semigroup may have.
| Fragment 40. Manual input for the multiplication table in program 15. |
| package examples; import sexpansion.Semigroup; import sexpansion.SetS; public class II_findresonances_ex_console { public static void main(String[] args) { // Manually enter the semigroups table SetS S0; SetS S1; int j, nResonances = 0; |
Then, it defines a two-dimensional array for each semigroup, whose elements are SetS objects in Fragment 41. To find the resonant decompositions of each semigroup, the method findAllResonances is used in Fragment 42.
| Fragment 41. Defining a 2-dimensional array of SetS objects. |
| SetS[][] rS_E2; ... // Similarly define rS_N1, ..., rS_M4 for each semigroup. |
| Fragment 42. Finding all the resonant decompositions for a given semigroup. |
| rS_E2 = S_E2.findAllResonances(); ... // And similarly define rS_K3, ..., rS_M4 for the other semigroups. |
This means that for each element in the array, let us call it , [j][0] and [j][1] will play, respectively, the role of and in the jth resonant decomposition for the semigroup . This can be explicitly seen in Fragment 43, which is used to print the result.
| Fragment 43. Printing the result for the resonant decomposition of a given semigroup. |
| if (rS_E2 != null) { System.out.println(‘‘The semigroup S_E2 has ’’+rS_E2.length+ ‘‘ resonances:’’); for (j = 0 ; j < rS_E2.length ; ++j) { nResonances = nResonances + 1; S0 = rS_E2[j][0] ; S1 = rS_E2[j][1] ; System.out.println(‘‘Resonance #’’ +nResonances); System.out.print(‘‘S0: ’’); S0.show(); System.out.print(‘‘S1: ’’) ; S1.show(); } nResonances = 0; } ... // And repeat a similar code for rS_K3, ..., rS_M4. }} |
A sample output looks as follows (Figure 17).

Figure 17.
Output of the method findAllResonances.
Remarkably, a semigroup having more than one resonant decomposition might lead, through the S-expansion procedure, to different non-isomorphic expanded Lie algebras. This is the case of the semigroup , which, according to the summary given in Table 5 and Equations (34) and (36) of [42], allows us to obtain the Type III and V Bianchi algebras with the following resonant conditions:
and
According to the previous output sample, they correspond to the resonances #1 and #2.
5.3. All the Semigroups with Resonances and/or Zero Element
In some applications, it is useful to have a list containing all the resonant decompositions of semigroups of a given order, e.g., if we want to study all the possible resonant subalgebras of the S-expansions of a given Lie algebra. Program 13 performs this task for order 4 in Fragment 44.
| Fragment 44. The method findAllResonances is used in program 13 of Appendix A. |
| package examples; import sexpansion.Semigroup; import sexpansion.SetS; public class II_findAllResonances_console_ord4 { public static void main(String[] args) { Semigroup [] list = Semigroup.loadFromFile(‘‘src/data/’’); SetS [][] Resonances; SetS S0, S1; int i, j, nResonances=0, nSemigroupWithResonance=0, TotalResonances=0; for (i=0; i < list.length ; i++) { if (list[i].order == 4 && list[i].isCommutative()) { Resonances = list[i].findAllResonances(); if (Resonances != null) { nSemigroupWithResonance = nSemigroupWithResonance +1; TotalResonances = TotalResonances + Resonances.length; System.out.println(‘‘The semigroup #’’+list[i].ID+‘‘ has ’’ +Resonances.length+‘‘ resonances’’); list[i].show(); for (j = 0; j < Resonances.length ; j++) { nResonances = nResonances + 1; S0 = Resonances[j][0]; S1 = Resonances[j][1]; System.out.println(‘‘Resonance #’’ +nResonances); System.out.print(‘‘S0: ’’); S0.show(); System.out.print(‘‘S1 :’’); S1.show(); } nResonances = 0; }}} System.out.println(‘‘There are ’’+nSemigroupWithResonance+ ‘‘ semigroups with at least one resonance and there are’’ +‘‘ in total ’’+TotalResonances+‘‘ different resonances.’’); }} |
For space reasons, we cannot give the full output here, but a sample is given in Figure 18.

Figure 18.
Output of program 13 from Appendix A.
Thus, apart from explicitly giving the resonances of all the non-isomorphic semigroups of a given order, program 13 also gives the total number of semigroups having at least one resonance and the total number of different resonances. By changing the value of the variable list[i].order, one can easily obtain the results for other orders. For orders 5 and 6, the output is so big that, depending on the Java environment that is being used, it could not be fully printed onto the screen. For this reason, program 14 makes the same calculation for the orders and prints the output in the folder “./Output_examples/”. In particular, these outputs can also be found as pdf documents in the file Output examples.zip which is available together with the library in [61]. Using a font size of 10, those documents contain 13 pages for , 130 for , and 1668 for .
On the other hand, a list with all the semigroups of a given order having a zero element is also useful if we want to study all the possible S-expansions followed by a -reduction for a given Lie algebra. Program 18 makes this for order 4.
| Fragment 45. Creating a list of semigroups with a element by program 18. |
| package examples; import sexpansion.Semigroup; public class II_findzero_console_ord4 { public static void main(String[] args) { Semigroup[] list = Semigroup.loadFromFile(‘‘src/data/’’); Semigroup s ; int elementoCero ; int i,j; j = 0; for (i = 0 ; i < list.length ; ++i){ s = list[i]; elementoCero = list[i].findZero(); if (s.order == 4 && elementoCero != -1 && list[i].isCommutative()) { ++j; System.out.println(‘‘#’’ +list[i].ID); list[i].show(); System.out.print(‘‘The zero element is’’); System.out.println(elementoCero); }} System.out.println(‘‘Number of semigroups with zero element:’’ +j); }} |
Again, changing the value in the variable s.order one can easily obtain the results for other orders. In particular, program 20 performs the same calculation for and prints the results in the folder “./Output_examples/”.
Finally, program 17 mix both types of codes described above in order to give the list of all semigroups having simultaneously both zero element and at least one resonance (the outputs are also printed to a file). It is also worth to point out that the type of programs described here were used in Sections 4.1 and 4.2 of [60] to study the general properties of the expansions with semigroups up to order 6. These results will be summarized in the table of Section 5.6, where also the number of semigroups preserving semi-simplicity will be given.
5.4. Examples of Isomorphisms
As shown in [19,29,48], the following families of semigroups
allows us to generate the algebras and which, as explained in the introduction, have been recently used in many applications in gravity theories. For each order n, the semigroups and represent non-isomorphic semigroups. For example, the semigroups corresponding to order 7 are given by the tables in Figure 19.
| Fragment 46. Program 4 determines if there are isomorphisms between and . |
| package examples; import sexpansion.Semigroup; public class I_isomorphisms_ex1 { public static void main(String[] args) { |

Figure 19.
Multiplication tables for the semigroups and .
After introducing the semigroups as carried out before (reminding us to rename the semigroup elements in such a way that they are represented by positive integer numbers), we use the isotest method in Fragment 47.
| Fragment 47. The isotest method. |
| if (SE_5.isotest(SM_6)[0]) { System.out.println(‘‘SE_5 is isomorphic to SM_6‘‘); } else { System.out.println(‘‘SE_5 is not isomorphic to SM_6’’); }}} The output reads, SE_5 is not isomorphic to SM_6 |
Similar programs were used in [42] to check that the semigroups , , , , and are not isomorphic between them and, thus, that they represent different solutions to relate two- and three-dimensional algebras. Indeed, with the same kind of code, one could easily check that all the semigroups of order 4 given by the tables in Figure 13 and Figure 14 are not isomorphic between them.
On the other hand, there are cases where we need to identify the specific semigroup of the lexicographical classification to which a given semigroup is isomorphic. We remind the reader that those semigroups were labeled in Section 2.4 by , where identify a specific semigroup of order n and Q is the total number of semigroups in that order. For example, let us consider the semigroup from the table in Figure 14. Using the method isEqualTo of the Semigroup class, one may check that its multiplication table does not coincide with any table of the list sem.4 (and, in general, this will happen for any semigroup table which does not have a lexicographical order). However, that list is exhaustive, i.e., it contains all the non-isomorphic semigroups of order 4 and, thus, must be isomorphic to one and only one semigroup in the list sem.4.
Before showing how we can find the semigroup , which is isomorphic to , it is worth first seeing how the methods of our library generate all the permutations (and the corresponding inverses) of a given set with n elements. Program 8 performs that task for using the methods allPermutations and inversePermutation. First, it defines a SetS object n_elements with n elements and stores all its permutations in the SetS object called allpermut in Fragment 48.
| Fragment 48. Generating all the possible permutations for a given semigroup. |
| package examples; import sexpansion.SetS; public class I_Permutations_and_inverses_console_n4 { public static void main(String[] args) { int n = 4, i; SetS [] allpermut ; SetS n_elements ; n_elements = new SetS(n); allpermut = n_elements.allPermutations() ; Then, with the following piece of code, we obtain the result. for (i = 0 ; i < allpermut.length; ++i) { System.out.println(‘‘Permutation #’’ +i); allpermut[i].show(); System.out.println(‘‘The inverse permutation is:’’); allpermut[i].inversePermutation().show(); }}} |
In the same way, program 9 generates the list of all permutations with their corresponding inverses for a set of n elements, with . The results are directly printed in the folder “./Output_examples/”, and in each case, the permutations are labeled here by , with .
Now, it is easy to see in Fragment 49 how program 5 finds the semigroup of the lexicographic classification, which is isomorphic to . First, it reads the semigroup nd the full list of semigroups of order 4 and defines some useful variables with the method allPermutations explained before.
| Fragment 49. Method allPermutations is used by program 5 for the semigroup |
| package examples; import sexpansion.Semigroup; import sexpansion.SetS; public class I_isomorphisms_ex2 { public static void main(String[] args) { int [][] mSN3 = {{4,1,4,4},{1,2,3,4},{4,3,4,4},{4,4,4,4}}; Semigroup SN3 = new Semigroup(mSN3); Semigroup[] lista = Semigroup.loadFromFile(‘‘src/data/’’); int i,k ; Semigroup [] permutations ; SetS [] p = (new SetS(4)).allPermutations(); After introducing as usual, the following piece of code performs the task. for (i = 0 ; i < lista.length ; ++i){ if (lista[i].order == 4) { if (lista[i].isotest(SN3)[0]) { System.out.println(‘‘The semigroup #’’ + lista[i].ID); lista[i].show(); System.out.println(‘‘is isomorphic to SN3.’’); permutations = lista[i].permute(); for (k = 0 ; k < permutations.length; ++k) { if (permutations[k].isEqualTo(SN3)) { System.out.print(‘‘A permutation that brings #’’ + lista[i].ID + ‘‘ to SN3 is P#’’); System.out.println(k); p[k].show(); System.out.println(‘‘The inverse permutation is:’’); p[k].inversePermutation().show(); }}}}}}} |
The output in Figure 20 reads,

Figure 20.
Output of the method allPermutations used in program 5.
Interestingly, more than one permutation may represent the isomorphism. To show how the permutation must be applied according to the definition given by Equation (33), let us explicitly see the relation with (Table 4):

Table 4.
Certain example of permutations inside a semigroup of order 4.
In addition, program 10 uses the methods permuteWith and equalTo to check the result in both senses, i.e, it checks the following:
- can be obtained by applying the permutations and to the semigroup ;
- can be obtained by applying the permutations the permutations and to the semigroup .
With those isomorphisms, one can directly check that the five resonances found for and , respectively, in Section 5.2 and Section 5.3, are in one-to-one correspondence.
With simple modifications on the inputs of the program described above, the reader may check if there exist isomorphisms for any given set of semigroups. Indeed, this type of code was used to find the isomorphisms given in Section 6 of [42].
5.5. Examples with S-Expanded Algebras
As explained in Section 4.2, given a semigroup, we can use the method getSelector to obtain the adjoint representation of any semigroup. An explicit example to carry this out is provided by program 26. Now, we are going to describe the main characteristics of the programs 28–35 in order to illustrate how to perform S-expansions.
Let us first consider the Lie algebra with the following commutation relations:
Consider also the semigroup given by the table in Figure 21, which has the resonant decompositions and and where is the zero element.

Figure 21.
One more example of the semigroup multiplication law.
Program 28 gives the non-vanishing commutators and structure constants of as follows:
- The expanded algebra ;
- The resonant subalgebra ;
- The reduced algebra ;
- The reduction of the resonant subalgebra .
| Fragment 50. To run program 28, we need the following classes. |
| package examples; import Jama.Matrix; import sexpansion.Semigroup; import sexpansion.SetS; import sexpansion.StructureConstantSet; import sexpansion.StructureConstantSetExpanded; import sexpansion.StructureConstantSetExpandedReduced; import sexpansion.StructureConstantSetExpandedResonant; import sexpansion.StructureConstantSetExpandedResonantReduced; public class II_SExp_sl2_S770 { public static void main(String[] args) { |
Then, in Fragment 51, we define an object called metric with the class Matrix of the jama library and use the method setStructureConstant of the class StructureConstantSet to introduce the non-vanishing structure constants of the original algebra. According to the convention explained at the end of Section 4.2, this is carried out in such a way that where n is the dimension of . Similarly, in the functions , where m is the order of the semigroup. However, the outputs will be given in such a way that and .
| Fragment 51. Defining KC metric as an object with the class Matrix. |
| Matrix metric ; StructureConstantSet sl2 = new StructureConstantSet(3) ; sl2.setStructureConstant(0, 1, 2,-2) ; sl2.setStructureConstant(0, 2, 1, 2) ; sl2.setStructureConstant(1, 2, 0, 2) ; metric = sl2.cartanKillingMetric() ; metric.print(2,2); // Show its KC metric System.out.println(metric.det()); // Prints its determinant |
In addition, the KC metric and its determinant are calculated. Next, in Fragment 52, the program loads the semigroup and its resonant decomposition using the classes Semigroup and SetS.
| Fragment 52. Loading the semigroup and its resonant decomposition. |
| int [][] mS770 = {{1,1,1,1,1},{1,2,1,1,5},{1,1,3,4,1}, {1,1,4,3,1},{1,5,1,1,2}}; Semigroup S770 = new Semigroup(mS770) ; int[] mS0 = {1,2,3} ; SetS S0 = new SetS(mS0) ; int[] mS1 = {1,4,5} ; SetS S1 = new SetS(mS1) ; int[] mV0 = {1}; SetS V0 = new SetS(mV0); int[] mV1 = {2,3}; SetS V1 = new SetS(mV1); |
Now, in Fragment 53, we use the methods showCommut, showSC, and cartanKillingMetric to compute the commutators, structure constants, and KC metric of expanded algebra (here, some prints which explain the output are omitted for space reasons).
| Fragment 53. Methods for the algebra expanded by the semigroup |
| // 1) the expanded algebra StructureConstantSetExpanded Gexp = S770.getExpandedStructureConstant (sl2); Gexp.showCommut(); Gexp.showSC(); Matrix metricaGexp = Gexp.cartanKillingMetric(); metricaGexp.print(0,0); System.out.println(metricaGexp.det()); |
This way, we have reproduced the six steps explained in Section 4.3 for the specific expansion of with the semigroup .
Similarly, in Fragment 54, program 28 follows the steps given in Section 4.4 and Section 4.5 to obtain the resonant subalgebra and reduced algebra.
| Fragment 54. Methods used to obtain the resonant subalgebra and reduced algebra. |
| // 2) the resonant subalgebra StructureConstantSetExpandedResonant ResGexp = new StructureConstantSetExpandedResonant(Gexp.data,S0,S1,V0,V1); ResGexp.showCommutRes(); ResGexp.showSCRes(); Matrix metricaResGexp = ResGexp.cartanKillingMetricPretty(); metricaResGexp.print(0,0); System.out.println(metricaResGexp.det()); // 3) the reduced algebra showCommutRel StructureConstantSetExpandedReduced RedGexp = new StructureConstantSetExpandedReduced (S770.getExpandedStructureConstant(sl2).data,1); RedGexp.showCommutRed(); RedGexp.showSCRed(); Matrix metricaRedGexp = RedGexp.cartanKillingMetricPretty(); metricaRedGexp.print(0,0); System.out.println(metricaRedGexp.det()); |
Finally, the reduction of the resonant subalgebra is realized in Fragment 55.
| Fragment 55. Methods to reduce the resonant subalgebra. |
| // 4) the reduction of the resonant subalgebra StructureConstantSetExpandedResonantReduced RedResGexp = new StructureConstantSetExpandedResonantReduced(ResGexp,1) ; RedResGexp.showCommutResRed(); RedResGexp.showSCResRed(); Matrix metricaRedResGexp = RedResGexp.cartanKillingMetricPretty(); metricaRedResGexp.print(0,0); System.out.println(metricaRedResGexp.det()); }} |
A sample output for the expanded algebra may be found in Figure 22, Figure 23, Figure 24 and Figure 25.

Figure 22.
Output for the Killing–Cartan metric.

Figure 23.
Output of the method showCommut.

Figure 24.
Output of the method showSC.
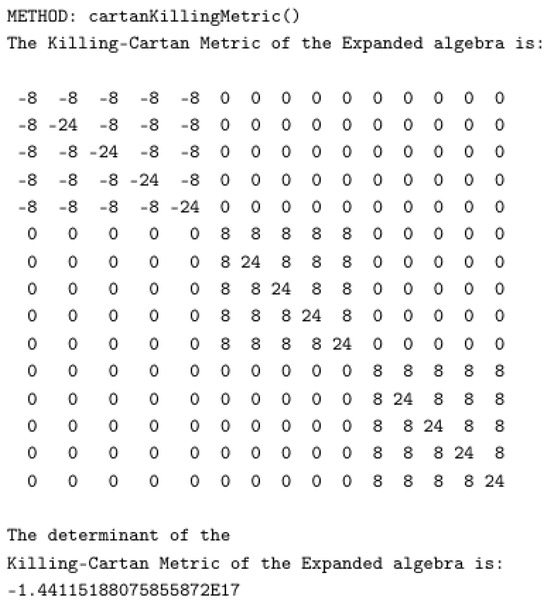
Figure 25.
Output of the method cartanKillingMetric.
Now, the parts of the output corresponding to the reduction of the resonant sublgebra are given in Figure 26, Figure 27 and Figure 28.

Figure 26.
Output of the method showCommutResRed.

Figure 27.
Output of the method showSCResRed.

Figure 28.
Output of the method cartanKillingMetricPretty.
The programs 29–31 perform the same kind of calculation for the semigroups , , and . According to Section 5 of [60], these are the semigroups of lowest order that lead (after extracting reduced and resonant subalgebras) to non-trivial expansions of in such a way that semi-simplicity is preserved. In addition, the programs 32–35 use the method showPretty to generate the adjoint representations for expansions of with the same semigroups. A sample output for the reduction of the resonant subalgebra obtained with the semigroup is given in Figure 29.

Figure 29.
Output of the programs 29–31 for the semigroups of lowest order that lead to non-trivial expansions of , preserving semi-simplicity.
The full output of the programs described in this section can be found in the file Output_examples.zip available in [61].
5.6. Identifying S-Expansions That Preserve Semi-Simplicity
In [60], it was shown that commutativity, solvability, and nilpotency are properties preserved under the S-expansions of any semigroup, whilst properties like semi-simplicity and compactness are preserved only for semigroups satisfying certain conditions (see the summary given in Section 2.2). In what follows, we will show how our library can be used to identify all the semigroups preserving semi-simplicity up to order 6.
Let us consider the algebra, whose commutation relations are given in Equation (39). Program 42 in Fragment 56 calculates the S-expanded algebras for all the non-isomorphic semigroups of the lists sem.n for . As shown in what follows, for each expansion, it checks if the determinant of the expanded Killing–Cartan metric is different than zero (again, for space reasons, some prints explaining the output are omitted).
| Fragment 56. Calculating the S-expanded algebras for all the semigroups. |
| package examples; import Jama.Matrix; import sexpansion.Semigroup; import sexpansion.StructureConstantSet; import sexpansion.StructureConstantSetExpanded; public class III_sl2_SExp_ord2_to_6_console { // To change the order modify the value of the interger ’order’ // (only for values between 2 and 6) private static int order=3 ; public static void main(String[] args) { Matrix metric ; Semigroup [] listSemigroups = Semigroup.loadFromFile(‘‘src/data/’’) ; StructureConstantSet sl2 = new StructureConstantSet(3) ; sl2.setStructureConstant(0, 1, 2, -2) ; sl2.setStructureConstant(0, 2, 1, 2) ; sl2.setStructureConstant(1, 2, 0, 2) ; metric = sl2.cartanKillingMetric() ; metric.print(2, 2) ; System.out.println(metric.det()); Semigroup semigroup ; StructureConstantSetExpanded expandedAlgebra ; int nCommutativos = 0 ; int nSemi-simples = 0 ; int i ; for (i = 0 ; i < listSemigroups.length ; ++i) { semigroup = listSemigroups[i] ; if (semigroup.order == order && semigroup.isCommutative()) { nCommutativos = nCommutativos + 1 ; expandedAlgebra = semigroup.getExpandedStructureConstant( sl2); metric = expandedAlgebra.cartanKillingMetric() ; if (metric.det() != 0) { nSemi-simples = nSemi-simples + 1 ; System.out.println(‘‘A semi-simple algebra has been found’’ +‘‘expanding with the semigroup #’’+semigroup.ID); semigroup.show(); System.out.println(‘‘The metric of the expanded algebra is:’’); metric.print(2, 2); System.out.print(‘‘whose determinant is: ’’); System.out.println(metric.det()); }}} System.out.print(‘‘There are ’’+nCommutativos+ ‘‘ commutative semigroups of order ’’+order+‘‘ and ’’+nSemi-simples+ ‘‘ expansions that give a semi-simple algebra.’’); }} |
A sample of output reads in Figure 30.
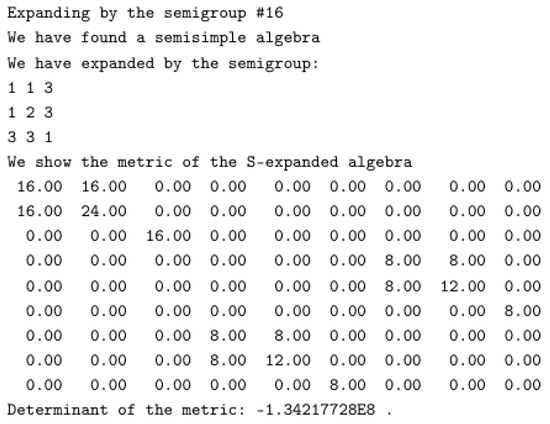
Figure 30.
Output of program 42 for Killing–Cartan metric of the S-expanded algebras .
Similarly, the programs 43–45 were used in [60] to perform S-expansions with all the non-isomorphic semigroups which have a zero element and/or at least one resonance. In each case, these programs dentify the expanded algebras , , and , which are semi-simple. In particular, Figure 31 illustrates the different kinds of expansions that can be carried out using the results of these programs for order 3.

Figure 31.
Expansions of with abelian semigroups of order 3.
For space reasons, only the label ‘a’ of the semigroup was written in Figure 31. The vertical axis illustrates the different types of expansions that can be performed, and the boxes over the horizontal axis contain the semigroups that can be used for each case. The semigroups that preserve semi-simplicity are labeled with a gray number and, as we can see, it might happen that a semigroup preserves semi-simplicity in one level but not in another. This is the case of the semigroup , appearing in the sample output above, which preserves semi-simplicity for the expanded algebra but not for the resonant subalgebra.
The results of the programs 42–45 (which can also be found in the file Output_examples.zip available in [61]) are summarized in Table 5.

Table 5.
Number of semigroups which allow to us generate from different types of S-expanded algebras such as , , and .
Table 5 gives, for each order, the number of semigroups which allows us to generate S-expanded algebras , reduced algebras , resonant subalgebras , and reductions of the resonant subalgebras . The number of expansions preserving semi-simplicity, denoted by #pss, is given for each case. As shown in Section 5.2 and Section 5.3, a given semigroup might have more than one resonance and, thus, for the cases with resonances, we also give the total number of resonances #r.
The fraction of semigroups preserving semi-simplicity is very small and remarkably, as shown explicitly in Section 4.2 of [60], expansions performed with those semigroups always contain the original algebra as a subalgebra. For example, the semigroups of order with a zero element and a resonant decomposition that preserve semi-simplicity are as follows:
For some of them, it is possible to perform more than one reduction consecutively and, thus, it can be shown that the semigroups , , , and leads after the whole process to the trivial result . Expansions with , , and essentially lead to , as can be shown by performing a suitable change in basis. Finally, the expansion the semigroup leads to .
One of the motivations used in [60] to study S-expansions preserving semi-simplicity was the possibility of establishing some relations between the classical simple Lie algebras , , , , and the special ones. The detailed analysis revealed that the expansions preserving semi-simplicity generate only direct sums of simple algebras, always containing the original one as a subalgebra This is consistent with the result obtained recently in [79], where it was stated that the expansion of simple algebras leads in general to non-simple algebras.. This leads to the conjecture that there is no S-expansion procedure relating them (at least with the resonant conditions considered here). However, a general proof for this statement still remains as an open problem.
Finally, the programs 36–41 are examples to study the compactness property of S-expanded alegbras (with semigroups of order ) in terms of the eigenvalues of the semigroup metric and the expanded Killing–Cartan metric given, respectively, in Equations (21) and (24). Following the procedure described in the previous section, these programs can be extended in order to study the compactness of resonant subalgebras and reduced algebras.
6. Final Remarks and Conclusions
Motivated by the growing number of applications that the S-expansion method has had recently, mainly in the construction of higher-dimensional gravity theories and the understanding of their interrelations, we have developed a computational tool to automate this procedure. It is given as a Java library which is composed of 11 classes (listed in Section 2.5 and described in Section 3 and Section 4), whose methods allow the following:
- To perform basic operations with semigroups (check associativity and commutativity, find the zero element, resonances, and isomorphisms);
- To represent arbitrary Lie algebras and semigroups in order to perform S-expansions with arbitrary semigroups.
Many examples have been provided in Section 5 to solve a considerable number of problems. They are presented such that any user, not necessarily an expert in Java, can easily modify them to perform their own calculations.
An important input we have used in many of our algorithms is the list of all the non-isomorphic semigroups generated by the Fortran program gen.f given in [76]. Consequently, this is an input based on the results of many works related to the classification of semigroups (some of them, the most important for our purposes, were cited in Section 2.4). As mentioned in [76], the program gen.f should be able to generate, in principle, the full lists up to order 8. However, in our case, we obtained them only up to order 6, because for some reason, the program stops when it reaches the 835,927th of the 836,021 semigroups of order 7. That is why, when we need to have the list of all non-isomorphic semigroups of a given order, we restrict our calculations to order 6. However, with our library, we can still perform calculations with semigroups of order higher than 6 (see, e.g., the examples in Section 5.1 and Section 5.4). The only issue is that we do not have the full list of non-isomorphic tables for those higher orders.
As our library has an open licence GNU (as mentioned, before anyone can download, use and modify the library—the corresponding citation to this original version is appreciated), we expect not only that these lists can be updated soon for semigroups up to order 8 but also that some of its methods can be improved and extended. For example, a superalgebra has usually a subspace structure given by
so, according to [19], in order to perform S-expansions of superalgebras, one needs to consider resonant decompositions satisfying
Therefore, an extension of the method described in Section 3.4 for this kind of resonances would allow to perform S-expansions of superalgebras with all the machinery developed in this work. It would also be useful to extend the library to perform resonant reductions which, as briefly mentioned at the end of Section 2.2, are more general than the -reduction process.
Interestingly, in [80], an analytic method was proposed to answer whether two given Lie algebras can be S-related. They consider resonances in which an element, different than zero, is not allowed to be repeated in the subsets of the considered decomposition of the semigroup. As our methods are able to find all possible resonant decompositions (allowing non-zero elements to be repeated), a method selecting the decompositions with non-repeated elements may be implemented in such a way that our library can also be useful for this kind of problem, at least for the case . We will provide those methods in [81] as a first extension of this library, together with an independent and complementary procedure that we developed in parallel, in order to answer whether two given Lie algebras can be S-related.
On the other hand, as mentioned in the introduction, in the early 1960s, it was conjectured that all solvable Lie algebras could be obtained as a contraction of a semi-simple Lie algebra of the same dimension (see, e.g., [21,22]). Although in 2006 some contra-examples were found that disproved this supposition [23], that problem has been revisited very recently in the context of S-expansion [24]. Whether this method fixes the classification of solvable Lie algebras still remains an open problem; therefore, we think that the computational tools developed in this work might be useful to work this out.
It is also worth mentioning that the fact that S-expansion reproduces all the WW contractions does not imply that S-expansion covers all possible contractions. As noticed in [24], there exist contractions that cannot be realized by a WW contraction (see, e.g., [82,83]), and that is why it is still unclear whether all contractions can be obtained from S-expansions. On the other hand, we do know that there exist S-expansions that are not equivalent to any contraction (an explicit example is given in [24]) and, in general, this is the case of S-expansions with semigroups that do not belong to the family and/or the case of expansions that lead to algebras of dimension bigger than the original one. Thus, the computational tool provided in this article might also be useful to answer whether S-expansions exhaust all possible contractions or not.
From the theoretical physics point of view, the S-expansion method has been used to show that Chern–Simons (CS) or Born–Infeld (BI) type gravities constructed with the family lead, in a certain limit, to higher-dimensional general relativity. Thus, among the possible new applications, the techniques developed in this paper might help to analyze if it is possible to uncover and classify all the relations of this type (some results on this particular problem will be submitted soon [84]). An extension of the method to calculate resonant decompositions able to expand superalgebras might also be very useful in the context of supergravity (see, e.g., [85,86]). In particular, it might be analyzed whether it is possible to obtain standard five-dimensional supergravity (see [87]) from a Chern–Simons supergravity based on a suitable expanded superalgebra.
Another application is related to the so-called Pure Lovelock (PL) theory [88,89,90], which is a higher-dimensional theory that has recently been called into the attention by the fact that their black hole solutions are asymptotically indistinguishable from the ones in general relativity. In [91,92], an attempt to obtain PL gravity from CS- and BI-type gravities has been carried out using the expanded algebras. The relation is obtained at the level of the action but presents some problems at the level of the field equations, which can be fixed only by performing suitable identifications of the fields. Thus, the methods of this library could be used to look for a suitable S-expanded algebra giving the right dynamical limit and without performing identification of the fields (see [93]).
In ref. [42], Lie algebras of isometry on two-dimensional manifolds were S-expanded via the procedure of S-expansion to algebras of isometry on certain three-dimensional manifolds. It was mentioned in [42] that in a similar way (via S-expansion), the algebras of isometries on two-dimensional manifolds may be expanded to the algebras of isometries on manifolds of a dimension higher than three. Even if we do not engage in S-expansion at all, an algebra of differential operators, that represent the generators of isometry for a given metric of a given manifold, may coincide with the algebra of isometry for another metric of another manifold of a different dimension. The reduced differential operators of the same isometry algebra would act on the metric of another manifold. Killing vectors of both manifolds are determined by the equations for these manifolds in the embedding space. The realizations of the Killing vectors in the differential operators that generate isometries are different for different manifolds in different dimensions, even if their algebras of isometries coincide. The geodesics on both the manifolds may be found from their metric or from the Killing vectors of the isometry algebras, for example, in the same way as was carried out in [43]. These geodesics may be related by a certain type of projective maps. If a given algebra of isometries is S-expanded to another algebra of isometries on a different manifold of a higher dimension, their geodesics may be related by another type of projective maps.
On the practical side, each dynamic Hamiltonian system may be written as a geodesic on a certain manifold [94]. By knowing the connection coefficients (Christoffel symbols) of the manifold from the geodesic equation, we determine a metric of the original manifold and the corresponding algebra of isometry, which may then be S-expanded. By fixing the metric of this new manifold by the S-expanded isometry algebra constructed in this procedure of S-expansion, we may write the geodesic equation on this S-expanded manifold, and then we may write the dynamic Hamiltonian system which corresponds to the geodesic of the S-expanded manifold. The original Hamiltonian system from which we started and the new system will be related by S-expansion. These two dynamic systems will be related by certain projective maps because the corresponding geodesics are related by these maps. A part of conservative quantities, such as energy of the original system, for example, may be found from geometric concepts of the S-expanded system.
Apart from the mentioned applications in gravity theories and Lie group theory, it would be interesting to analyze if this tool could also have applications in other physical theories related to symmetries, as well as in other branches, like semigroup theory and constraint logic programming. Lie algebras and semigroups have been recently applied in robotics and artificial intelligence, so it would also be interesting to explore possible applications of these methods in this area.
Author Contributions
Conceptualization, C.I., I.K., N.M. and F.N. All authors have read and agreed to the published version of the manuscript.
Funding
C.I. was supported by a Mecesup PhD grant and the Término de tesis grant from CONICYT (Chile). I.K. was supported by Fondecyt (Chile) grant 1050512 and by DIUBB (Chile) Grant Nos. 102609 and GI 153209/C. N.M. was supported by the FONDECYT (Chile) grant 3130445 and by a Becas-Chile postdoctoral grant during the first stage of this work. In the last stage of this work N.M. was also supported by the Agencia Nacional de Investigación y Desarrollo (ANID), Chile, vía Fondecyt Regular Grant No. 1231133. F. N. wants to thank CSIC for a JAE-Predoc grant cofunded by the European Social Fund.
Data Availability Statement
Data is contained within the article.
Acknowledgments
We are grateful to all four referees of this manuscript for their careful revision and many generous suggestions, which improved it.
Conflicts of Interest
Carlos Inostroza is employed by Amazon LLC. Felip Nadal is employed by Edicom Capital, S. L. Igor Kondrashuk and Nelson Merino declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A. List of Program Examples
Appendix A.1
In this Appendix, we give the list of 45 example programs included in the file examples.zip available in [61]. Most of them have been described in Section 5 and, according to the classification explained in Section 2.5, they are called generically as “prefix_name”.
- I_associative_checking.java;
- I_commutative_checking.java;
- I_commutative_ord2_to_6.java;
- I_isomorphisms_ex1.java;
- I_isomorphisms_ex2.java;
- I_isomorphisms_ex3.java;
- I_isomorphisms_SE_N.java;
- I_Permutations_and_inverses_console_n4.java;
- I_Permutations_and_inverses_Order_2_to_7.java;
- I_PermuteWith_ex.java;
- II_AdjointRep_Casimirs_ex.java;
- II_Example_diagonalization.java;
- II_findAllResonances_console_ord4.java;
- II_findAllResonances_ord2_to_6.java;
- II_findresonances_ex_console.java;
- II_findresonances_ex.java;
- II_findzero_and_AllResonances_ord2_to_6.java;
- II_findzero_console_ord4.java;
- II_findzero_ex.java;
- II_findzero_ord2_to_6.java;
- II_isresonant_ex.java;
- II_isresonant_permute_ex1.java;
- II_isresonant_permute_ex2.java;
- II_isresonant_permute_ex3.java;
- II_isresonant_permute_ex4.java;
- II_S_and_G_AdjointRep_ex.java;
- II_SExp_CheckingByHand.java;
- II_SExp_sl2_S770.java;
- II_SExp_sl2_S968.java;
- II_SExp_sl2_S990.java;
- II_SExp_sl2_S991.java;
- II_SExpStructConst_sl2_S770.java;
- II_SExpStructConst_sl2_S968.java;
- II_SExpStructConst_sl2_S990.java;
- II_SExpStructConst_sl2_S991.java;
- III_EigenVectors_SExp_sl2_ord2.java;
- III_EigenVectors_SExp_sl2_ord3.java;
- III_EigenVectors_SExp_sl2_ord4.java;
- III_Signature_Sem_ord2.java;
- III_Signature_Sem_ord3.java;
- III_Signature_Sem_ord4.java;
- III_sl2_SExp_ord2_to_6_console.java;
- III_sl2_SExp_Red_ord2_to_6_console.java;
- III_sl2_SExp_Res_ord2_to_6_console.java;
- III_sl2_SExp_Res_Red_ord2_to_6_console.java.
References
- Segal, I.E. A class of operator algebras which are determined by groups. Duke Math. J. 1951, 18, 221. [Google Scholar] [CrossRef]
- Inönü, E.; Wigner, E.P. On the contraction of groups and their representations. Proc. Nat. Acad. Sci. USA 1953, 39, 510–524. [Google Scholar] [CrossRef] [PubMed]
- Inönü, E. Contractions of Lie groups and their representations. In Group Theoretical Concepts in Elementary Particle Physics; Gürseyed, F., Ed.; Gordon and Breach: Abingdon, UK, 1964; pp. 391–402. [Google Scholar]
- Saletan, E.J. Contractions of Lie groups. J. Math. Phys. 1961, 2, 1–21. [Google Scholar] [CrossRef]
- Gerstenhaber, M. On the deformations of rings and algebras. Ann. Math. 1964, 79, 59–103. [Google Scholar] [CrossRef]
- Nijenhuis, A.; Richardson, R.W., Jr. Cohomology and deformations in graded Lie algebras. Bull. A Math. Soc. 1966, 72, 1–29. [Google Scholar] [CrossRef]
- Nijenhuis, A.; Richardson, R.W., Jr. Deformations of Lie algebra structures. J. Math. Mech. 1967, 171, 89–105. [Google Scholar] [CrossRef]
- Richardson, R.W. On the rigidity of semi-direct products of Lie algebras. Pac. J. Math. 1967, 22, 339–344. [Google Scholar] [CrossRef]
- Barut, A.O.; Ratzka, R. Theory of Group Representations and Applications; World Scientific: Singapore, 1986. [Google Scholar]
- Gilmore, R. Lie Groups, Lie Algebras, and Some of their Applications; Wiley-Interscience: New York, NY, USA, 1974. [Google Scholar]
- Weimar-Woods, E. Contractions of Lie algebras: Generalized Inonu-Wigner contractions versus graded contractions. J. Math. Phys. 1995, 36, 4519–4548. [Google Scholar] [CrossRef]
- Weimar-Woods, E. Contraction of Lie algebra representations. J. Math. Phys. 1991, 32, 2028–2665. [Google Scholar] [CrossRef]
- Weimar-Woods, E. Contractions, generalized Inönü and Wigner contractions and deformations of finite-dimensional Lie algebras. Rev. Math. Phys. 2000, 12, 1505–1529. [Google Scholar] [CrossRef]
- Hatsuda, M.; Sakaguchi, M. Wess-Zumino term for the AdS superstring and generalized Inonu-Wigner contraction. Prog. Theor. Phys. 2003, 109, 853. [Google Scholar] [CrossRef]
- de Azcarraga, J.A.; Izquierdo, J.M.; Picon, M.; Varela, O. Generating Lie and gauge free differential (super)algebras by expanding Maurer-Cartan forms and Chern-Simons supergravity. Nucl. Phys. B 2003, 662, 185–219. [Google Scholar] [CrossRef]
- de Azcarraga, J.A.; Izquierdo, J.M.; Picon, M.; Varela, O. Extensions, expansions, Lie algebra cohomology and enlarged superspaces. Class. Quant. Grav. 2004, 21, 1375–1384. [Google Scholar] [CrossRef]
- de Azcarraga, J.A.; Izquierdo, J.M.; Picon, M.; Varela, O. Expansions of algebras and superalgebras and some applications. Int. J. Theor. Phys. 2007, 46, 2738–2752. [Google Scholar] [CrossRef]
- Nakahara, M. Geometry, Topology and Physics; Institute of Physics Publishing: Bristol, UK, 1990. [Google Scholar]
- Izaurieta, F.; Rodriguez, E.; Salgado, P. Expanding Lie (super)algebras through Abelian semigroups. J. Math. Phys. 2006, 47, 123512. [Google Scholar] [CrossRef]
- Díaz, J.; Fierro, O.; Izaurieta, F.; Merino, N.; Rodríguez, E.; Salgado, P.; Valdivia, O. A generalized action for (2 + 1)-dimensional Chern-Simons gravity. J. Phys. A 2012, 45, 255207. [Google Scholar] [CrossRef][Green Version]
- Zaitsev, G.A. Group-Invariant Study of the Sets of Limiting Geometrie and Special Lie Subalgebras. In Talk thesises of All-USSR Geometric Conference; Kiev, USSR, 1961. pp. 1–48. (In Russian).[Green Version]
- Celeghini, E.; Tarlini, M. Contraction of group representations II. Nuovo Cimento B 1981, 65, 172–180. [Google Scholar] [CrossRef]
- Nesterenko, M.; Popovych, R. Contractions of low-dimensional Lie algebras. J. Math. Phys. 2006, 47, 123515. [Google Scholar] [CrossRef]
- Nesterenko, M. S-Expansions of Three-Dimensional Lie Algebras. In Proceedings of the 6th International Workshop on Group Analysis of Differential Equations and Integrable Systems, Protaras, Cyprus, 17–21 June 2012; Vaneeva, O.O., Ed.; University of Cyprus: Nicosia, Cyprus, 2013; pp. 147–154. [Google Scholar]
- Zanelli, J. Lecture Notes on Chern-Simons (Super-)Gravities, 2nd ed. 2008. Available online: https://arxiv.org/abs/hep-th/0502193 (accessed on 23 August 2025).
- Izaurieta, F.; Rodriguez, E.; Salgado, P. Eleven-dimensional gauge theory for the M algebra as an Abelian semigroup expansion of osp(32|1). Eur. Phys. J. C 2008, 54, 675. [Google Scholar] [CrossRef]
- Izaurieta, F.; Rodriguez, E.; Salgado, P. Dual Formulation of the Lie Algebra S-expansion Procedure. J. Math. Phys. 2009, 50, 073511. [Google Scholar] [CrossRef]
- Edelstein, J.D.; Hassaine, M.; Troncoso, R.; Zanelli, J. Lie-algebra expansions, Chern-Simons theories and the Einstein-Hilbert Lagrangian. Phys. Lett. B 2006, 640, 278. [Google Scholar] [CrossRef]
- Izaurieta, F.; Rodriguez, E.; Minning, P.; Salgado, P.; Perez, A. Standard General Relativity from Chern-Simons Gravity. Phys. Lett. B 2009, 678, 213. [Google Scholar] [CrossRef]
- Concha, P.K.; Peñafiel, D.M.; Rodríguez, E.K.; Salgado, P. Even-dimensional General Relativity from Born-Infeld gravity. Phys. Lett. B 2013, 725, 419. [Google Scholar] [CrossRef]
- Concha, P.K.; Peñafiel, D.M.; Rodríguez, E.K.; Salgado, P. Chern-Simons and Born-Infeld gravity theories and Maxwell algebras type. Eur. Phys. J. C 2014, 74, 2741. [Google Scholar] [CrossRef]
- Concha, P.K.; Peñafiel, D.M.; Rodríguez, E.K.; Salgado, P. Generalized Poincaré algebras and Lovelock-Cartan gravity theory. Phys. Lett. B 2015, 742, 310. [Google Scholar] [CrossRef]
- Deser, S.; Gibbons, G.W. Born-Infeld-Einstein Actions? Class. Quant. Grav. 1998, 15, L35. [Google Scholar] [CrossRef]
- Quinzacara, C.A.C.; Salgado, P. Black hole for the Einstein-Chern-Simons gravity. Phys. Rev. D 2012, 85, 124026. [Google Scholar] [CrossRef]
- Quinzacara, C.A.C.; Salgado, P. Stellar equilibrium in Einstein-Chern-Simons gravity. Eur. Phys. J. C 2013, 73, 2479. [Google Scholar] [CrossRef][Green Version]
- Crisóstomo, J.; Gómez, F.; Salgado, P.; Quinzacara, C.; Cataldo, M.; del Campo, S. Accelerated FRW Solutions in Chern-Simons Gravity. Eur. Phys. J. C 2014, 74, 3087. [Google Scholar][Green Version]
- Crisóstomo, J.; Gómez, F.; Quinzacara, C.; Salgado, P. Static solutions in Einstein-Chern-Simons gravity. J. Cosmol. Astropart. Phys. 2016, 1606, 49. [Google Scholar] [CrossRef][Green Version]
- González, N.; Rubio, G.; Salgado, P.; Salgado, S. Generalized Galilean algebras and Newtonian gravity. Phys. Lett. B 2016, 755, 433. [Google Scholar] [CrossRef]
- Caroca, R.; Merino, N.; Salgado, P. S-Expansion of Higher-Order Lie Algebras. J. Math. Phys. 2009, 50, 013503. [Google Scholar] [CrossRef]
- Caroca, R.; Merino, N.; Perez, A.; Salgado, P. Generating Higher-Order Lie Algebras by Expanding Maurer Cartan Forms. J. Math. Phys. 2009, 50, 123527. [Google Scholar] [CrossRef]
- Caroca, R.; Merino, N.; Salgado, P.; Valdivia, O. Generating infinite-dimensional algebras from loop algebras by expanding Maurer-Cartan forms. J. Math. Phys. 2011, 52, 043519. [Google Scholar] [CrossRef]
- Caroca, R.; Kondrashuk, I.; Merino, N.; Nadal, F. Bianchi spaces and their three-dimensional isometries as S-expansions of two-dimensional isometries. J. Phys. A 2013, 46, 225201. [Google Scholar] [CrossRef]
- Bianchi, L. Sugli Spazi a tre Dimensioni che Ammettono un Gruppo Continuo di Movimenti; Memorie di Matematica e di Fisica della Societa Italiana delle Scienze, Serie Terza Tomo XI; Accademia Nazionale delle Scienze: Roma, Italy, 1898; pp. 267–352. [Google Scholar]
- Bianchi, L. On the Three-Dimensional Spaces Which Admit a Continuous Group of Motions. Gen. Relativ. Gravit. 2001, 33, 2171–2253. [Google Scholar] [CrossRef]
- Soroka, D.V.; Soroka, V.A. Semi-simple extension of the (super)Poincare algebra. Adv. High Energy Phys. 2009, 2009, 234147. [Google Scholar] [CrossRef]
- Durka, R.; Kowalski-Glikman, J.; Szczachor, M. Gauged AdS-Maxwell algebra and gravity. Mod. Phys. Lett. A 2011, 26, 2689. [Google Scholar] [CrossRef]
- Durka, R.; Kowalski-Glikman, J.; Szczachor, M. AdS-Maxwell superalgebra and supergravity. Mod. Phys. Lett. A 2012, 27, 1250023. [Google Scholar] [CrossRef]
- Salgado, P.; Salgado, S. (D-1,1)⊗(D-1,2) algebras and gravity. Phys. Lett. B 2014, 728, 5. [Google Scholar] [CrossRef]
- Concha, P.K.; Durka, R.; Merino, N.; Rodríguez, E.K. New family of Maxwell like algebras. Phys. Lett. B 2016, 759, 507. [Google Scholar] [CrossRef]
- Salgado, P.; Szabo, R.J.; Valdivia, O. Topological gravity and transgression holography. Phys. Rev. D 2014, 89, 084077. [Google Scholar] [CrossRef]
- Fierro, O.; Izaurieta, F.; Salgado, P.; Valdivia, O. Minimal AdS-Lorentz supergravity in three-dimensions. Phys. Lett. B 2019, 788, 198–205. [Google Scholar] [CrossRef]
- Concha, P.K.; Rodríguez, E.K. Maxwell Superalgebras and Abelian Semigroup Expansion. Nucl. Phys. B 2014, 886, 1128. [Google Scholar] [CrossRef]
- Concha, P.K.; Rodríguez, E.K. N = 1 Supergravity and Maxwell superalgebras. J. High Energy Phys. 2014, 1409, 090. [Google Scholar] [CrossRef]
- Concha, P.K.; Rodríguez, E.K.; Salgado, P. Generalized supersymmetric cosmological term in N=1 Supergravity. J. High Energy Phys. 2015, 1508, 009. [Google Scholar] [CrossRef]
- Concha, P.K.; Fierro, O.; Rodríguez, E.K.; Salgado, P. Chern-Simons supergravity in D=3 and Maxwell superalgebra. Phys. Lett. B 2015, 750, 117. [Google Scholar] [CrossRef]
- Ipinza, M.C.; Concha, P.K.; Ravera, L.; Rodríguez, E.K. On the Supersymmetric Extension of Gauss-Bonnet like Gravity. J. High Energy Phys. 2016, 1609, 007. [Google Scholar] [CrossRef][Green Version]
- Concha, P.K.; Fierro, O.; Rodríguez, E.K. Inönü-Wigner Contraction and D=2+1 Supergravity. Eur. Phys. J. C 2017, 77, 48. [Google Scholar] [CrossRef]
- Durka, R. Resonant algebras and gravity. J. Phys. A: Math. Theor. 2017, 50, 145202. [Google Scholar] [CrossRef]
- Peñafiel, D.M.; Ravera, L. Infinite S-Expansion with Ideal Subtraction and Some Applications. J. Math. Phys. 2017, 58, 081701. [Google Scholar] [CrossRef]
- Andrianopoli, L.; Merino, N.; Nadal, F.; Trigiante, M. General properties of the expansion methods of Lie algebras. J. Phys. A 2013, 46, 365204. [Google Scholar] [CrossRef]
- Available online: https://github.com/SemigroupExp/Sexpansion/releases/tag/v1.0.0 (accessed on 23 August 2025).
- Plemmons, R. A survey of computer applications to semigroups and related structures. ACM Sigsam 1969, 12, 28–39. [Google Scholar] [CrossRef]
- Izaurieta, F. Semigroup Expansion and M-Supergravity in Eleven Dimensions. arXiv 2006, arXiv:hep-th/0611238. [Google Scholar] [CrossRef]
- González, N.; Salgado, P.; Rubio, G.; Salgado, S. Einstein-Hilbert action with cosmological term from Chern-Simons gravity. J. Geom. Phys. 2014, 86, 339. [Google Scholar] [CrossRef]
- Forsythe, G.E. SWAC computes 126 distinct semigroups of order 4. Proc. Amer. Math. Soc. 1955, 6, 443–447. [Google Scholar] [CrossRef][Green Version]
- Motzkin, T.S.; Selfridge, J.L. Semigroups of order five. Bull. Amer. Math. Soc. 1956, 62, 13–23. [Google Scholar][Green Version]
- Plemmons, R. Construction and analysis of non-equivalent finite semigroups. In Computational Problems in Abstract Algebra; Pergamon: Oxford, UK, 1967; pp. 223–228. [Google Scholar][Green Version]
- Plemmons, R. There are 15973 semigroups of order 6. Math Algorithms 1967, 2, 2–17. [Google Scholar][Green Version]
- Jürgensen, H.; Wick, P. Die Halbgruppen der Ordnungen ≤ 7. Semigroup Forum 1977, 14, 69–79. [Google Scholar] [CrossRef]
- Satoh, S.; Yama, K.; Tokizawa, M. Semigroups of order 8. Semigroup Forum 1994, 49, 7–29. [Google Scholar] [CrossRef]
- Distler, A.; Kelsey, T. The monoids of orders eight, nine & ten. Ann. Math. Artif. Intell. 2009, 56, 3–21. [Google Scholar] [CrossRef]
- Distler, A.; Kelsey, T. The monoids of order eight and nine. In Lecture Notes in Computer Science Proceedings of the Artificial Intelligence and Symbolic Computation, 8th International Conference, AISC 2008, Birmingham, UK, 31 July–2 August 2008; Autexier, S., Campbell, J., Rubio, J., Sorge, V., Suzuki, M., Wiedijk, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5144, pp. 61–76. [Google Scholar]
- Distler, A.; Mitchell, J.D. Smallsemi—A library of Small Semigroups. Available online: https://gap-packages.github.io/smallsemi/ (accessed on 23 August 2025).
- Distler, A.; Kelsey, T.; Mitchell, J.D. Available online: https://circa.st-andrews.ac.uk/research-software/ (accessed on 23 August 2025).
- Distler, A.; Jefferson, C.; Kelsey, T.; Kotthoff, L. The Semigroups of Order 10. In Principles and Practice of Constraint Programming 18th International Conference, CP 2012, Quïbec City, QC, Canada, 8–12 October 2012; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7514, pp. 883–899. [Google Scholar]
- Hildebrant, J. Handbook of Finite Semigroup Programs (LSU Mathematics Electronic Preprint Series). 2001; preprint 2001-24. [Google Scholar]
- Available online: http://math.nist.gov/javanumerics/jama/ (accessed on 23 August 2025).
- Available online: https://github.com/SemigroupExp/Sexpansion/wiki (accessed on 23 August 2025).
- Artebani, M.; Caroca, R.; Ipinza, M.C.; Peñafiel, D.M.; Salgado, P. Geometrical aspects of the Lie algebra S-expansion procedure. J. Math. Phys. 2016, 57, 023516. [Google Scholar] [CrossRef]
- Ipinza, M.C.; Lingua, F.; Peñafiel, D.M.; Ravera, L. An Analytic Method for S-Expansion involving Resonance and Reduction. Fortsch. Phys. 2016, 64, 854. [Google Scholar] [CrossRef]
- Inostroza, C.; Kondrashuk, I.; Merino, N.; Nadal, F. Algorithm to find S-related Lie algebras. unpublished.
- Burde, D. Degenerations of 7-dimensional nilpotent Lie algebras. Comm. Algebra 2005, 33, 1259. [Google Scholar] [CrossRef]
- Popovych, D.R.; Popovych, R.O. Lowest dimensional example on non-universality of generalized Inönü-Wigner contractions. J. Algebra 2010, 324, 2742–2756. [Google Scholar] [CrossRef][Green Version]
- Concha, P.K.; Inostroza, C.; Merino, N.; Rodríguez, E.K. Chern-Simons gravities related with General Relativity. unpublished.[Green Version]
- Arnowitt, R.L.; Nath, P.; Zumino, B. Superfield Densities and Action Principle in Curved Superspace. Phys. Lett. 1975, 56B, 81. [Google Scholar] [CrossRef]
- Akulov, V.P.; Volkov, D.V.; Soroka, V.A. Gauge Fields on Superspaces with Different Holonomy Groups. JETP Lett. 1975, 22, 187. [Google Scholar]
- Castellani, L.; D’Auria, R.; Fre, P. Supergravity and Superstrings: A Geometric Perspective; World Scientific: Singapore, 1991. [Google Scholar]
- Cai, R.G.; Ohta, N. Black Holes in Pure Lovelock Gravities. Phys. Rev. D 2006, 74, 064001. [Google Scholar] [CrossRef]
- Dadhich, N.; Pons, J.M.; Prabhu, K. On the static Lovelock black holes. Gen. Rel. Grav. 2013, 45, 1131. [Google Scholar] [CrossRef]
- Dadhich, N.; Durka, R.; Merino, N.; Miskovic, O. Dynamical structure of Pure Lovelock gravity. Phys. Rev. D 2016, 93, 064009. [Google Scholar] [CrossRef]
- Concha, P.K.; Durka, R.; Inostroza, C.; Merino, N.; Rodriguez, E.K. Pure Lovelock gravity and Chern-Simons theory. Phys. Rev. D 2016, 94, 024055. [Google Scholar] [CrossRef]
- Concha, K.P.; Merino, N.; Rodríguez, E.K. Lovelock gravities from Born–Infeld gravity theory. Phys. Lett. B 2017, 765, 395–401. [Google Scholar] [CrossRef][Green Version]
- Durka, R.; Inostroza, C.; Merino, N. Pure Lovelock gravity from Chern-Simons theory. unpublished.[Green Version]
- Dubrovin, B.A.; Fomenko, A.T.; Novikov, S.P. Modern Geometry—Methods and Applications. Part I: The Geometry of Surfaces, Transformation Groups, and Fields; Transl. from the Russian by Robert G. Burns. Graduate Texts in Mathematics, 93; Springer: New York, NY, USA, 2012; 464 p. [Google Scholar][Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).