Extending the Applicability of Newton-Jarratt-like Methods with Accelerators of Order 2m + 1 for Solving Nonlinear Systems

Abstract

The local convergence analysis of the $m+1$-step Newton-Jarratt composite scheme with order $2m+1$ has been shown previously. But the convergence order $2m+1$ is obtained using Taylor series and assumptions on the existence of at least the fifth derivative of the mapping involved, which is not present in the method. These assumptions limit the applicability of the method. A priori error estimates or the radius of convergence or uniqueness of the solution results have not been given either. These drawbacks are addressed in this paper. In particular, the convergence is based only on the operators on the method, which are the operator and its first derivative. Moreover, the radius of convergence is established, a priori estimates and the isolation of the solution is discussed using generalized continuity assumptions on the derivative. Furthermore, the more challenging semi-local convergence analysis, not previously studied, is presented using majorizing sequences. The convergence for both analyses depends on the generalized continuity of the Jacobian of the mapping involved, which is used to control it and sharpen the error distances. Numerical examples validate the sufficient convergence conditions presented in the theory.

1. Introduction

The problem of solving nonlinear equations and systems of nonlinear equations is a fundamental and challenging task in numerical analysis with significant applications in many branches of science and engineering. Since closed-form or analytical solutions are rarely available, research has focused heavily on developing and analyzing iterative methods to approximate a solution $x^{*}$ to an equation of the form

$$F\left(x\right)=0,$$

(1)

where F is a Fréchet-differentiable operator defined on a convex subset D of a Banach space $B_0$ with values in a Banach space B. The solution is typically found as the limit of a sequence $\left\{x_k\right\}$ generated by an iterative method. The results obtained here hold for any norm denoted by $||·||$. There are a variety of iterative methods for solving such equations and nonlinear systems [1,2,3,4,5]. The most well-known is Newton’s method, which is renowned for its quadratic convergence under standard assumptions [6]. To achieve a higher order of convergence, numerous modified Newton- or Newton-like methods have been proposed in the literature [7,8,9,10]. Among the most efficient and widely studied families are multipoint methods, which can attain a high order of convergence while keeping the number of function evaluations low. In this context, the Newton-Jarratt family and its variants are particularly prominent, offering fourth-order convergence or higher [11,12]. The development of even more efficient high-order multipoint methods continues to be an active area of research [10,13,14,15,16,17,18,19].

Recently, Sharma and Kumar [20] introduced an efficient and elegant class of Newton-Jarratt-like methods. Their approach involves a multi-step scheme designed to increase the order of convergence systematically. As described in their work, the key innovation is that in each step, the order of convergence is increased by two at the cost of only a single additional function evaluation. Furthermore, the computationally expensive inverse of the Fréchet derivative, $F^{\prime }{\left(x_n\right)}^{-1}$, is calculated only once per iteration and then reused in all subsequent sub-steps. This design, which they term a method with a ’frozen inverse operator’, makes the algorithm highly efficient, especially for large systems of equations.

We provide a complete theoretical framework, covering both local and the more challenging semi-local convergence. The local analysis establishes a radius of convergence. It gives uniqueness of the results, improving the study in [20] by using larger convergence domains and tighter error bounds under our weaker hypotheses. Critically, and in a significant extension to this work, we also present the first semi-local convergence analysis for this class of methods using majorizing sequences. Owing to this analysis, we can guarantee convergence with a given initial point without assuming the existence of a solution beforehand. It is a crucial aspect for practical applications, where the existence of a solution is often not known. The theoretical results are then validated through numerical examples.

We extend the applicability of the multi-step method, introduced in [20], which is defined for a natural number $m\ge 2$, $x_0^{\left(0\right)}=x_0\in D$, $j=2,\dots ,m$ and each $n=0,1,2,\dots$.

$$\begin{array}{cc}\hfill & y_n^{\left(0\right)}=x_n-{\displaystyle \frac{2}{3}}{F}^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right),\hfill \\ \hfill & A_n=F^{\prime }{\left(x_n\right)}^{-1}{F}^{\prime }\left(y_n^{\left(0\right)}\right),\hfill \\ \hfill & y_n^{\left(1\right)}=y_n^{\left(0\right)}-{\displaystyle \frac{1}{12}}(13I-9A_n)F^{\prime }{\left(x_k\right)}^{-1}F\left(x_k\right),\hfill \\ \hfill & E_n=E(x_n,y_n^{\left(0\right)})={\displaystyle \frac{1}{2}}(5I-3A_n),\hfill \\ \hfill & y_n^{\left(j\right)}=y_n^{(j-1)}-E_n{F}^{\prime }{\left(x_n\right)}^{-1}F\left(y_n^{(j-1)}\right),\hfill \\ \hfill & \dots \hfill \\ \hfill & x_{n+1}=y_n^{\left(m\right)}=y_n^{(m-1)}-E_n{F}^{\prime }{\left(x_n\right)}^{-1}F\left(y_n^{(m-1)}\right).\hfill \end{array}$$

(2)

The structure of the method begins with a Newton-Jarratt-like predictor step to find $y_n^{\left(0\right)}$ and then is followed by a series of additional steps. It is important to note that the operators $A_n$ and $E_n$, and the inverse operator $F^{\prime }{\left(x_n\right)}^{-1}$, are computed only once per iteration. The steps at $j\ge 2$ use the fixed operator $E_n{F}^{\prime }{\left(x_n\right)}^{-1}$ to iteratively improve the solution, enhancing the order of convergence without requiring additional costly derivative evaluations or inversions. The pseudo-code for the particular method is provided in Algorithm 1.

Algorithm 1$(m+1)$-step Newton-Jarratt Method (2)

1: Input: 2:    Function F and its Jacobian J 3:    Initial guess $x_0$ 4:    Number of steps of the algorithm m 5:    Maximum iterations n 6:    Tolerance $ϵ$ 7: Output: 8:    Approximate root $x^{*}$ 9:    Convergence status (boolean) 10: $x_k\leftarrow x_0$ 11: for  $k=1,\dots ,n$  do 12:     Compute $f_k=F\left(x_k\right)$ 13:     Compute Jacobian $J_k=J\left(x_k\right)$ 14:     Perform LU factorization: $J_k=L_k{U}_k$, store $L_k$ and $U_k$ 15:     Solve system of linear equation $J_k{c}_k=f_k$ for $c_k$ using the LU factors 16:     $w_{k,0}\leftarrow x_k-{\displaystyle \frac{2}{3}}{c}_k$ 17:     Compute Jacobian $J_{w_{k,0}}=J\left(w_{k,0}\right)$ 18:     Solve system of linear equations $J_k{A}_k=J_{w_{k,0}}$ for $A_k$ using the LU factors 19:     $w_{k,1}\leftarrow w_{k,0}-{\displaystyle \frac{1}{12}}(13I-9A_k)c_k$ 20:     $E_k\leftarrow {\displaystyle \frac{1}{2}}(5I-3A_k)$ 21:     for $j=2,\dots ,m$ do 22:         Compute $f_{w_{k,j-1}}=F\left(w_{k,j-1}\right)$ 23:         Solve system of linear equations $J_{k}d=f_{w_{k,j-1}}$ for d using the LU factors 24:         $w_{k,j}\leftarrow w_{k,j-1}-E_{k}d$ 25:     end for 26:     $x_{k+1}\leftarrow w_{k,m}$ 27:     if $\left|\right|x_k-x_{k+1}\left|\right|+\left|\right|F\left(x_{k+1}\right)\left|\right|<ϵ$ then 28:         return $x_{k+1}$, True 29:     end if 30:     $x_k\leftarrow x_{k+1}$ 31: end for 32: return $x_n$, False

But there is a number of problems with the Taylor series approach which restrict the applicability of the method (2).

• Motivation for our paper

  (P₁)

  The existence of at least the fifth derivative is assumed in [20] to show the local convergence and provided that $B_0=B={\mathbb{R}}^m$, where m is a natural number. Let us consider $m=1$, $D=[-2,2]$ and define the function $f:D\to \mathbb{R}$ by

  $$f\left(x\right)=\left\{\begin{array}{cc}{s}_1{x}^{5}lnx+s_2{x}^6+s_3{x}^7,\hfill & x\ne 0,\hfill \\ 0,\hfill & x=0.\hfill \end{array}\right.$$

  Here $s_1,s_2,s_3$ are real numbers with $s_1\ne 0$ and $s_2+s_3=1$. It follows by the definition of the function f that $x^{*}=1\in D$ is a solution of the equation $f\left(x\right)=0$. But the fifth derivative of the function f is not bounded, since it is not continuous at $x=0\in D$. Therefore the results in [20] cannot assure the convergence of the method to $x^{*}$. However, the method converges to $x^{*}$ if we take $x_0=0.95$. Thus, the sufficient convergence conditions in [20] can be weakened. It is also worth noting that only F and $F^{\prime }$ appear on the method.

  (P₂)

  There is no knowledge in advance about the natural number K such that $||x_n-x^{*}||<\epsilon$, where $\epsilon >0$ is the error tolerance. Thus, the number of such iterations K is unknown.

  (P₃)

  Information about the isolation of $x^{*}$ is not available.

  (P₄)

  The most important and challenging semi-local convergence is not given.

  (P₅)

  The convergence is established only for $B_0=B={\mathbb{R}}^m$.

The problems (${\mathrm{P}}_1$)–(${\mathrm{P}}_5$) appear in studies utilizing the Taylor series approach. In this paper, we positively handle these problems in order to extend the applicability of the method.

• Novelty of our Paper

  (P₁)′

  The local convergence is based on the operators F and $F^{\prime }$, which only appear on the method. Moreover, generalized continuity assumptions [21] are used to control the derivative and sharpen the error distances $||x_n-x^{*}||$.

  (P₂)′

  The number of iterations K is known in advance, since a priori estimates on $||x_n-x^{*}||$ become available.

  (P₃)′

  Domains are determined containing only one solution.

  (P₄)′

  The semi-local convergence is developed using majorizing sequences [4,21,22,23].

  (P₅)′

  The local and semi-local convergence is given in the more general setting of a Banach space. Notice that although our technique is applied on method (2) it can also be used on other methods with problems (${\mathrm{P}}_1$)–(${\mathrm{P}}_5$) along the same lines [11,12,15,22,24,25,26,27,28,29,30,31,32,33,34,35,36].

The rest of this paper is organized as follows. Section 2 is devoted to the local convergence analysis of method (2), where we establish a radius of convergence and provide uniqueness results under our weaker hypotheses. The more demanding semi-local convergence analysis is presented in Section 3, based on the use of majorizing sequences. In Section 4, there are numerical results for validation of the theoretical conditions and demonstration of the performance of the method on several problems. Finally, we provide concluding remarks in Section 5.

2. Local Convergence

The analysis uses some scalar functions. Set $T=[t_0,+\infty )$.

• Suppose:

  (C₁)

  There exists a continuous and nondecreasing function $w_0:T\to T$ such that the function $1-w_0\left(t\right)$ has a smallest zero in the interval $T-\left\{0\right\}$. We shall denote such zero by $R_0$ and set $T_0=[0,R_0)$.

  (C₂)

  There exists a continuous and nondecreasing function $w:T_0\to T$ such that for the functions:

  ${\overline{w}}^{\left(s\right)}\left(t\right):T_0\to T$, $s=0,1,\dots ,m-1$,

  $${\overline{w}}^{\left(s\right)}\left(t\right)=\left\{\begin{array}{c}w\left((1+g_s\left(t\right))t\right)\hfill \\ or\hfill \\ w_0\left(t\right)+w_0\left(g_s\left(t\right)t\right),\hfill \end{array}\right.$$

  the functions $g_0,g_1,g_j:T_0\to T$, $j=2,\dots ,m$ are defined by

  $$g_0\left(t\right)={\displaystyle \frac{{\int }_0^{1}w\left((1-\theta )t\right)d\theta +\frac{1}{3}(1+{\int }_0^{1}w\left(\theta t\right)d\theta )}{1-w_0\left(t\right)}},$$

  $$g_1\left(t\right)={\displaystyle \frac{{\int }_0^1{w}_0\left((1-\theta )t\right)d\theta }{1-w_0\left(t\right)}}+{\displaystyle \frac{{\overline{w}}^{\left(0\right)}\left(t\right)(1+{\int }_0^1{w}_0\left(\theta t\right)d\theta )}{{(1-w_0\left(t\right))}^2}},$$

  $$g_j\left(t\right)=[{\displaystyle \frac{{\int }_0^{1}w\left((1-\theta )g_{j-1}\left(t\right)t\right)d\theta }{1-w_0\left(g_{j-1}\left(t\right)t\right)}}+{\displaystyle \frac{{\overline{w}}^{(j-1)}\left(t\right)(1+{\int }_0^1{w}_0\left(\theta g_{j-1}\left(t\right)t\right)d\theta )}{(1-w_0\left(t\right))(1-w_0\left(g_{j-1}\left(t\right)t\right))}}$$

  $$+{\displaystyle \frac{3}{2}}{\displaystyle \frac{w^{\left(0\right)}\left(t\right)(1+{\int }_0^1{w}_0\left(\theta g_{j-1}\left(t\right)t\right)d\theta )}{{(1-w_0\left(t\right))}^2}}]g_{j-1}\left(t\right)$$

  are such that the functions $1-g_{\delta }\left(t\right)$, $\delta =0,1,2,\dots ,m$, have smallest zeros in the interval $T_0-\left\{0\right\}$. We shall denote such zeros by $r_{\delta }$. Set

  $$r=min\left\{r_{\delta }\right\}\mathrm{and}{T}_1=[0,r).$$

  (3)

  This parameter shall be shown to be the radius of convergence for the method (2) in Theorem 1. It follows from the definition of r that for each $t\in T_1$:

  $$0\le w_0\left(t\right)<1,$$

  (4)

  $$0\le w_0\left(g_{j-1}\left(t\right)t\right)<1,$$

  (5)

  and

  $$0\le g_s\left(t\right)<1.$$

  (6)

  The real functions $w_0$ and w relate to the operators on the method (2).

  (C₃)

  There exists a solution $x^{*}\in D$ of the equation $F\left(x\right)=0$ and an invertible operator $M\in L(B_0,B)$ such that for each $u\in D$

  $$||M^{-1}(F^{\prime }\left(u\right)-M)||\le w_0(||u-x^{*}||).$$

  Define the region $D_0=S(x^{*},R_0)\cap D$.

  (C₄)

  $||M^{-1}(F^{\prime }\left(u_1\right)-F^{\prime }\left(u\right))||\le w(||u_1-u||)$ for each $u,u_1\in D_0$.

  (C₅)

  $S[x^{*},r]\subset D$.

Remark 1. 

Some choices of M can be $M=I$, the identity operator on $B_0$ or $M=F^{\prime }\left(\tilde{x}\right)$ for some auxiliary point $\tilde{x}\in D$ other than $x^{*}$, or $M=F^{\prime }\left(x^{*}\right)$. In the last case, it follows by ($C_3$) that $x^{*}$ is a simple solution of the equation $F\left(x\right)=0$. The main local convergence result for the method (2) follows in the next result.

Theorem 1. 

Suppose that conditions ($P_1$)–($P_5$) hold. Then, the sequence $\left\{x_n\right\}$ generated by the method (2) converges to $x^{*}$, provided that $x_0\in S_0:=S(x^{*},r)-\left\{x^{*}\right\}$. Moreover, the following items hold:

$$||x_{n+1}-x^{*}||\le c^{n+1}||x_0-x^{*}||,$$

(7)

where

$$c=d^m\in [0,1),$$

(8)

and for $e_0=||x_0-x^{*}||$

$$d=min\{g_1\left(e_0\right),g_2\left(e_0\right),\dots ,g_m\left(e_0\right)\}\in [0,1).$$

(9)

Proof. 

Notice that by the definition of the radius r, (4), (7)–(9), it follows that r, c, d exist and belong to the interval $[0,1)$. We shall show by induction that for each $n=0,1,2,\dots$

$$||y_n^{\left(0\right)}-x^{*}||\le g_0(||x_n^{\left(0\right)}-x^{*}||)||x_n^{\left(0\right)}-x^{*}||\le ||x_n^{\left(0\right)}-x^{*}||<r,$$

(10)

$$||y_n^{\left(1\right)}-x^{*}||\le g_1(||x_n^{\left(0\right)}-x^{*}||)||x_n^{\left(0\right)}-x^{*}||\le ||x_n^{\left(0\right)}-x^{*}||,$$

(11)

and for $j=2,...,m$

$$||y_n^{\left(j\right)}-x^{*}||\le g_j(||y_n^{(j-1)}-x^{*}||)||y_n^{(j-1)}-x^{*}||.$$

(12)

Let $u\in S_0$. By the condition (${\mathrm{C}}_3$), (3) and (4) we have the estimate

$$||M^{-1}(F^{\prime }\left(u\right)-M)||\le w_0(||u-x^{*}||)\le w_0\left(r\right)<1.$$

(13)

It follows by (13) and the Banach lemma on invertible operators that $F^{\prime }\left(u\right)$ is invertible and

$$||{\left[F^{\prime }\left(u\right)\right]}^{-1}M||\le {\displaystyle \frac{1}{1-w_0(||u-x^{*}||)}}.$$

(14)

In particular, for $u=x_0$, the operator $F^{\prime }\left(x_0\right)$ is invertible. So, the iterates $y_0^{\left(0\right)},y_0^{\left(1\right)},...,y_0^{\left(m\right)}$ are well defined by the method (2). Then, by the first substep, we can write in turn

$$\begin{array}{cc}\hfill & y_0^{\left(0\right)}-x^{*}=x_0-x^{*}-F^{\prime }{\left(x_0\right)}^{-1}F\left(x_0\right)+{\displaystyle \frac{1}{3}}{F}^{\prime }{\left(x_0\right)}^{-1}F\left(x_0\right)\hfill \\ \hfill & =\left[F^{\prime }{\left(x_0\right)}^{-1}M\right]\left[{\int }_0^1{M}^{-1}(F^{\prime }(x^{*}+\theta (x_0-x^{*}))-F^{\prime }\left(x_0\right))d\theta \right](x_0-x^{*})\hfill \\ \hfill & +{\displaystyle \frac{1}{3}}\left[F^{\prime }{\left(x_0\right)}^{-1}M\right]\left[M^{-1}F\left(x_0\right)\right].\hfill \end{array}$$

(15)

We need estimates

$$||{\int }_0^1{M}^{-1}\left(F^{\prime }\left(x^{*}+\theta (x_0-x^{*})\right)-F^{\prime }\left(x_0\right)\right)d\theta ||\le {\int }_0^{1}w\left((1-\theta )||x_0-x^{*}||\right)d\theta$$

(16)

by ($C_4$),

$$F\left(x_0\right)=F\left(x_0\right)-F\left(x^{*}\right)={\int }_0^1{F}^{\prime }(x^{*}+\theta (x_0-x^{*}))d\theta (x_0-x^{*}),$$

so

$$\begin{array}{cc}\hfill & ||M^{-1}F\left(x_0\right)||=||{\int }_0^1{M}^{-1}(F^{\prime }(x^{*}+\theta (x_0-x^{*}))-M+M)d\theta (x_0-x^{*})||\hfill \\ \hfill & \le \left(1+{\int }_0^1{w}_0(\theta ||x_0-x^{*}||)d\theta \right)||x_0-x^{*}||.\hfill \end{array}$$

(17)

Then, by (3), (6) (for $\delta =1$), (14) (for $u=x_0$), (16) and (17), identity (15) can give

$$\begin{array}{cc}\hfill & ||y_0^{\left(0\right)}-x^{*}||\hfill \\ \hfill & \le {\displaystyle \frac{\left[{\int }_0^{1}w((1-\theta )||x_0-x^{*}||d\theta +\frac{1}{3}\left(1+{\int }_0^1{w}_0(\theta ||x_0-x^{*}||)d\theta \right)\right]||x_0-x^{*}||}{1-w_0(||x_0-x^{*}||)}}\hfill \\ \hfill & \le g_0(||x_0-x^{*}||)||x_0-x^{*}||\le ||x_0-x^{*}||<r.\hfill \end{array}$$

(18)

Thus, the iterate $y_0^{\left(0\right)}\in S(x^{*},r)$ and item (10) hold if $n=0$. Then, by the second substep of the method (2), we get in turn that

$$\begin{array}{cc}\hfill & y_0^{\left(1\right)}-x^{*}=x_0-x^{*}-F^{\prime }{\left(x_0\right)}^{-1}F\left(x_0\right)+\left({\displaystyle \frac{1}{3}}I-{\displaystyle \frac{1}{12}}(13I-9A_0)\right)F^{\prime }{\left(x_0\right)}^{-1}F\left(x_0\right)\hfill \\ \hfill & =x_0-x^{*}-F^{\prime }{\left(x_0\right)}^{-1}F\left(x_0\right)+{\displaystyle \frac{3}{4}}\left(F^{\prime }{\left(x_0\right)}^{-1}{F}^{\prime }\left(y_0^{\left(0\right)}\right)-I\right)F^{\prime }{\left(x_0\right)}^{-1}F\left(x_0\right).\hfill \end{array}$$

(19)

Notice that

$$\begin{array}{cc}\hfill & F^{\prime }{\left(x_0\right)}^{-1}{F}^{\prime }\left(y_0^{\left(0\right)}\right)-I=F^{\prime }{\left(x_0\right)}^{-1}\left(F^{\prime }\left(y_0^{\left(0\right)}\right)-F^{\prime }\left(x_0\right)\right), \mathrm{so}\hfill \\ \hfill & ||M^{-1}(F^{\prime }\left(y_0\right)-F^{\prime }\left(x_0\right))||\hfill \\ \hfill & \le w\left(||y_0^{\left(0\right)}-x_0||\right)\le w\left(||x_0-x^{*}||+||y_0-x^{*}||\right)\hfill \\ \hfill & \le w\left(\right(1+g_0(||x_0-x^{*}||\left)\right)||x_0-x^{*}||)\le w_0^{\left(0\right)}\hfill \end{array}$$

(20)

or

$$\begin{array}{cc}\hfill & ||M^{-1}(F^{\prime }\left(y_0^{\left(0\right)}\right)-F^{\prime }\left(x_0\right))||\le ||M^{-1}(F^{\prime }\left(x_0\right)-M)||\hfill \\ \hfill & +||M^{-1}(F^{\prime }\left(y_0^{\left(0\right)}\right)-M)||\le w_0(||x_0-x^{*}||)+w_0(||y_0^{\left(0\right)}-x^{*}||)\le w_0^{\left(0\right)}.\hfill \end{array}$$

(21)

Hence, the identity (19) can give

$$\begin{array}{cc}\hfill & ||y_0^{\left(1\right)}-x^{*}||\le \left[{\displaystyle \frac{{\int }_0^1{w}_0\left((1-\theta )||x_0-x^{*}||\right)d\theta }{1-w_0(||x_0-x^{*}||)}}\right.\hfill \\ \hfill & +\left.{\displaystyle \frac{w_0^{\left(0\right)}\left(1+{\int }_0^1{w}_0\left(\theta ||x_0-x^{*}||\right)d\theta \right)}{(1-w_0(||x_0-x^{*}{||\left)\right)}^2}}\right]||x_0-x^{*}||\hfill \\ \hfill & \le g_1(||x_0-x^{*}||)||x_0-x^{*}||\le ||x_0-x^{*}||.\hfill \end{array}$$

(22)

So, the iterate $y_0^{\left(1\right)}\in S(x^{*},r)$ and the item (11) holds if $n=0$. Then, we can write for $j=2,\dots ,m$ by method (2) if $n=0$

$$\begin{array}{cc}\hfill & y_0^{\left(j\right)}-x^{*}=y_0^{(j-1)}-x^{*}-F^{\prime }{\left(y_0^{(j-1)}\right)}^{-1}F\left(y_0^{(j-1)}\right)\hfill \\ \hfill & +(F^{\prime }{\left(y_0^{(j-1)}\right)}^{-1}-F^{\prime }{\left(x_0\right)}^{-1})F\left(y_0^{(j-1)}\right)\hfill \\ \hfill & +(I-E_0)F^{\prime }{\left(x_0\right)}^{-1}F\left(y_0^{(j-1)}\right)\hfill \\ \hfill & =y_0^{(j-1)}-x^{*}-F^{\prime }{\left(y_0^{(j-1)}\right)}^{-1}F\left(y_0^{(j-1)}\right)\hfill \\ \hfill & +F^{\prime }{\left(y_0^{(j-1)}\right)}^{-1}(F^{\prime }\left(x_0\right)-F^{\prime }\left(y_0^{(j-1)}\right))F^{\prime }{\left(x_0\right)}^{-1}F\left(y_0^{(j-1)}\right)\hfill \\ \hfill & +{\displaystyle \frac{3}{4}}(A_0-I)F^{\prime }{\left(x_0\right)}^{-1}F\left(y_0^{\left(1\right)}\right).\hfill \end{array}$$

(23)

In view of (3), (6) (for $\delta =1$) and (20)–(22), identity (23) can give

$$\begin{array}{cc}\hfill & ||y_0^{\left(j\right)}-x^{*}||\le \left[{\displaystyle \frac{{\int }_0^{1}w((1-\theta )||y_0^{(j-1)}-x^{*}||)d\theta }{1-w_0(||y_0^{(j-1)}-x^{*}||)}}\right.\hfill \\ \hfill & +{\displaystyle \frac{w_0^{(j-1)}\left(1+{\int }_0^1{w}_0(\theta ||y_0^{(j-1)}-x^{*}||)d\theta \right)}{(1-w_0(||x_0-x^{*}||\left)\right)(1-w_0(||y_0^{(j-1)}-x^{*}||\left)\right)}}\hfill \\ \hfill & \left.+{\displaystyle \frac{3}{2}}{\displaystyle \frac{w_0^{\left(0\right)}\left(1+{\int }_0^1{w}_0(\theta ||y_0^{(j-1)}-x^{*}||)d\theta \right)}{(1-w_0(||x_0-x^{*}{||\left)\right)}^2}}\right]||y_0^{(j-1)}-x^{*}||\hfill \\ \hfill & \le g_j(||y_0^{(j-1)}-x^{*}||)||y_0^{(j-1)}-x^{*}||\le ||y_0^{(j-1)}-x^{*}||.\hfill \end{array}$$

(24)

Thus, the iterate $y_0^{\left(j\right)}\in S(x^{*},r)$, the items (12) hold for $n=0$ and $j=2,\dots ,m$. Simply, exchange $x_0,y_0,\dots ,y_0^{\left(j\right)}$ by $x_1,y_1,\dots ,y_1^{\left(j\right)}$ respectively in the preceding calculations to complete the induction for items (10)–(12). Notice also that all the iterates of the method (2) belong to $S(x^{*},r)$. Moreover, the existence of d is guaranteed by (3)–(6) and items (10)–(12). Finally, by letting $n\to +\infty$ in (7), we deduce that ${lim}_{n\to \infty }{x}_n=x^{*}$. □

The following result provides a region inside which the only solution of the equation $F\left(x\right)=0$ is $x^{*}$.

Proposition 1. 

Suppose the condition ($C_3$) holds in the ball $S(x^{*},R)$ for some $R>0$ and there exists $R_1\ge R$ such that

$${\int }_0^1{w}_0\left(\theta R_1\right)d\theta <1.$$

(25)

Define the region $D_1=S[x^{*},R_1]\cap D$. Then, the only solution of the equation $F\left(x\right)=0$ in the region $D_1$ is $x^{*}$.

Proof. 

Suppose that there exists a solution $z\in D_1$ of the equation $F\left(x\right)=0$ such that $z\ne x^{*}$. Define the linear operator $H_0={\int }_0^1{F}^{\prime }(x^{*}+\theta (z-x^{*}))d\theta$. Then, it follows by the condition (${\mathrm{C}}_3$) and (25) that

$$||M^{-1}(H_0-M)||\le {\int }_0^1{w}_0(\theta ||z-x^{*}||)d\theta \le {\int }_0^1{w}_0\left(\theta R_1\right)d\theta <1.$$

(26)

Therefore, the operator $H_0$ is invertible. Finally, from the identity

$$z-x^{*}=H_0^{-1}\left(F\left(z\right)-F\left(x^{*}\right)\right)=H_0^{-1}\left(0\right)=0,$$

we deduce that $z=x^{*}$. □

Remark 2. 

(1) 

The limit point r can be replaced by $R_0$ in the condition ($C_5$).

(2) 

Under all the conditions ($C_1$)–($C_5$) one can set $R=r$ and $z=x^{*}$ in the Proposition 1.

3. Semi-Local Convergence

The choice of the initial point $x_0$ is challenging in the general setting of a Banach space. In the special case when $B_0=B=\mathbb{R}$ one can certainly employ the bisection method [2,3]:

(a)

The midpoint $m={\displaystyle \frac{s+t}{2}}$ is taken as an approximation to the solution $x^{*}$.

(b)

The interval $[s,t]$ is replaced by $[s,m]$ if $f\left(s\right)f\left(t\right)<0$, or, $[m,t]$ if $f\left(m\right)f\left(t\right)<0$. The convergence of this method can then always be guaranteed.

One can refer to [2,3] and the references therein for more information on the bisection method and its assistance in the determination of initial points.

We shall first recall the definition of a majorizing sequence [4,21,22,23].

Definition 1. 

Let $\left\{z_n\right\}$ be a sequence in a complete normed linear space. Suppose that there exists a nonnegative scalar sequence $\left\{p_n\right\}$ such that for each $n=0,1,2,\dots$

$$||z_{n+1}-z_n||\le p_{n+1}-p_n.$$

It is worth noting that if the inequality above holds, then $p_{n+1}-p_n\ge 0$. Hence, the scalar sequence $\left\{p_n\right\}$ is nonnegative. Then, the sequence $\left\{p_n\right\}$ is majorizing for $\left\{z_n\right\}$. Moreover, if the sequence $\left\{p_n\right\}$ converges to $p^{*}$, then so does $\left\{z_n\right\}$ and

$$||z_n-z^{*}||\le p^{*}-p_n,$$

where $z^{*}={lim}_{n\to \infty }{z}_n$.

As in the local case, the analysis relies on some scalar functions. Moreover, the formulas and calculations are the same, but $x^{*}$, $w_0$, and w are replaced by $x_0$, $v_0$, and v, respectively.

• Suppose:

  (H₁)

  There exists a continuous and nondecreasing function $v_0:T\to T$ such that the function $1-v_0\left(t\right)$ has a smallest zero in the interval $T-\left\{0\right\}$. Let us denote such zero by s and set $T_2=[0,s)$.

  (H₂)

  There exists a continuous and nondecreasing function $v:T_2\to T$. Define the scalar sequences $\left\{{\alpha }_n^{\left(j\right)}\right\},\left\{b_n^{\left(j\right)}\right\}$ for $j=2,\dots ,m$; $n=0,1,2,\dots$; ${\alpha }_n^{\left(0\right)}=0$, some $b_0^{\left(0\right)}\ge 0$ by

  $$\begin{array}{c}\hfill {\overline{v}}_n=\left\{\begin{array}{c}v(b_n^{\left(0\right)}-{\alpha }_n^{\left(0\right)})\hfill \\ \mathrm{or}\hfill \\ v_0\left({\alpha }_n^{\left(0\right)}\right)+v_0\left(b_n^{\left(0\right)}\right),\hfill \end{array}\right.\end{array}$$

  (27)

  $$b_n^{\left(1\right)}=b_n^{\left(0\right)}+{\displaystyle \frac{1}{2}}\left[1+{\displaystyle \frac{9}{4}}·{\displaystyle \frac{{\overline{v}}_n}{1-v_0\left({\alpha }_0^{\left(0\right)}\right)}}\right](b_n^{\left(0\right)}-{\alpha }_n^{\left(0\right)}),$$

  $$\begin{array}{cc}\hfill & {\lambda }_n^{\left(j\right)}={\int }_0^{1}v\left((1-\theta )(b_n^{(j-1)}-{\alpha }_n^{\left(0\right)})\right)d\theta (b_n^{(j-1)}-{\alpha }_n^{\left(0\right)})\hfill \\ \hfill & +(1+v_0\left({\alpha }_n^{\left(0\right)}\right))(b_n^{(j-1)}-b_n^{\left(0\right)})\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\left(1+v_0\left({\alpha }_n^{\left(0\right)}\right)\right)[b_n^{\left(0\right)}-{\alpha }_n^{\left(0\right)}],\hfill \end{array}$$

  $$b_n^{\left(j\right)}=b_n^{(j-1)}+{\displaystyle \frac{1}{2\left(1-v_0\left({\alpha }_n^{\left(0\right)}\right)\right)}}\left(1+{\displaystyle \frac{3{\overline{v}}_n}{1-v_0\left({\alpha }_n^{\left(0\right)}\right)}}\right){\lambda }_n^{(j-1)},$$

  $$\begin{array}{cc}\hfill & {\xi }_{n+1}={\int }_0^{1}v\left((1-\theta )({\alpha }_{n+1}^{\left(0\right)}-{\alpha }_n^{\left(0\right)})\right)d\theta ({\alpha }_{n+1}^{\left(0\right)}-{\alpha }_n^{\left(0\right)})\hfill \\ \hfill & +(1+v_0\left({\alpha }_n^{\left(0\right)}\right))({\alpha }_{n+1}^{\left(0\right)}-b_n^{\left(0\right)})+{\displaystyle \frac{1}{2}}(1+v_0\left({\alpha }_n^{\left(0\right)}\right))(b_n^{\left(0\right)}-{\alpha }_n^{\left(0\right)}),\hfill \end{array}$$

  $$b_{n+1}^{\left(0\right)}={\alpha }_{n+1}^{\left(0\right)}+{\displaystyle \frac{2}{3}}{\displaystyle \frac{{\xi }_{n+1}}{1-v_0\left({\alpha }_{n+1}^{\left(0\right)}\right)}},$$

  and

  $${\alpha }_{n+1}=b_n^{\left(m\right)}.$$

  These sequences are shown to be majorizing for the sequences generated by method (2). But let us first present a convergence result for them.

  (H₃)

  There exists $s_0\in [0,s)$ such that for each $n=0,1,2,\dots$, $i=0,1,2,\dots ,m$

  $$v\left({\alpha }_n^{\left(0\right)}\right)<1,{\alpha }_n^{\left(0\right)}\le s_0\mathrm{and}{b}_n^{\left(i\right)}\le s_0.$$

  This condition and (27) imply that these sequences are nondecreasing and bounded above by $s_0$, and as such they converge to their unique least upper bound ${\alpha }^{*}\in [0,s_0)$, $0\le {\alpha }_n^{\left(0\right)}\le b_n^{\left(0\right)}\le s_0\mathrm{and}{\beta }_n^{(j-1)}\le b_n^{\left(j\right)}\le s_0.$ The functions $v_0$ and v relate to the operators on the method (2).

  (H₄)

  There exists $x_0\in D$ and an invertible operator $M\in L(B_0,B)$ such that for each $u\in D$

  $$||M^{-1}(F^{\prime }\left(u\right)-M)||\le v_0(||u-x_0||).$$

  Define the region $D_2=S(x_0,s_0)\cap D$. By this condition and (${\mathrm{H}}_1$) it follows that for $u=x_0$: $||M^{-1}(F^{\prime }\left(x_0\right)-M)||\le v_0\left(0\right)<1$. So the linear operator $F^{\prime }\left(x_0\right)$ is invertible. Therefore, we can take $b_0^{\left(0\right)}\ge {\displaystyle \frac{2}{3}}||{\left[F^{\prime }\left(x_0\right)\right]}^{-1}F\left(x_0\right)||$.

  (H₅)

  $||M^{-1}\left(F^{\prime }\left(u_1\right)-F^{\prime }\left(u\right)\right)||\le v\left(||u_1-u||\right)$.

  (H₆)

  $S[x_0,{\alpha }^{*}]\subset D$.

Remark 3. 

Possible selections for $M=I$ or $M=F^{\prime }\left(\overline{x}\right)$, $\overline{x}\in D$ with $\overline{x}\ne x_0$.

• The semi-local analysis for the method (2) follows next.

Theorem 2. 

Suppose the conditions ($H_1$)–($H_6$) hold. Then, the sequence $\left\{x_n\right\}$ generated by method (2) exists and converges to some $x^{*}\in S[x_0,{\alpha }^{*}]$ such that

$$||x^{*}-x_n||\le {\alpha }^{*}-{\alpha }_n.$$

(28)

Proof. 

We shall establish by induction. Items for $i=2,\dots ,m$ and each $n=0,1,2,\dots$

$$||y_n^{\left(0\right)}-x_n||\le b_n^{\left(0\right)}-{\alpha }_n^{\left(0\right)},$$

(29)

$$||y_n^{\left(1\right)}-y_n^{\left(0\right)}||\le b_n^{\left(1\right)}-b_n^{\left(0\right)},$$

(30)

$$||y_n^{\left(i\right)}-y_n^{(i-1)}||\le b_n^{\left(i\right)}-b_n^{(i-1)}.$$

(31)

Notice that for $i=m$, (31) gives by the method (2) and (27) that

$$||x_{n+1}-x_n||\le {\alpha }_{n+1}-{\alpha }_n.$$

(32)

Item (29) holds if $n=0$ by the definition of $b_0^{\left(0\right)}$ in (${\mathrm{H}}_4$) and (27), since

$$||y_0^{\left(0\right)}-x_0||={\displaystyle \frac{2}{3}}||{\left[F^{\prime }\left(x_0\right)\right]}^{-1}F\left(x_0\right)||\le b_0^{\left(0\right)}-{\alpha }_0^{\left(0\right)}=b_0^{\left(0\right)}<{\alpha }^{*}.$$

Moreover, the iterate $y_0^{\left(0\right)}\in S(x_0,{\alpha }^{*})$. Let $u\in S(x_0,{\alpha }^{*})$. Then, we have by (${\mathrm{H}}_2$) and (${\mathrm{H}}_4$)

$$||M^{-1}(F^{\prime }\left(u\right)-M)||\le v_0(||u-x_0||)\le v_0\left({\alpha }^{*}\right)<1,$$

so $F^{\prime }\left(u\right)\in L(B,B_0)$

$$||{\left[F^{\prime }\left(u\right)\right]}^{-1}M||\le {\displaystyle \frac{1}{1-v_0(||u-x_0||)}}$$

(33)

and iterates for $u=x_0=x_0^{\left(0\right)},x_0^{\left(1\right)},\dots ,x_0^{\left(m\right)}=x_1$ exist by the method (2) for $n=0$.

Then, we can write by the second substep and induction

$$y_n^{\left(1\right)}-y_n^{\left(0\right)}=-{\displaystyle \frac{1}{3}}{F}^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right)+{\displaystyle \frac{3}{4}}(A_n-I)F^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right),$$

which can give

$$\begin{array}{cc}\hfill & ||y_n^{\left(1\right)}-y_n^{\left(0\right)}||\le {\displaystyle \frac{1}{2}}||y_n^{\left(0\right)}-x_n||+{\displaystyle \frac{9}{8}}·{\displaystyle \frac{{\overline{v}}_n}{1-v_0\left({\alpha }_n^{\left(0\right)}\right)}}||y_n^{\left(0\right)}-x_n||\hfill \\ \hfill & \le {\displaystyle \frac{1}{2}}(b_n^{\left(0\right)}-{\alpha }_n^{\left(0\right)})+{\displaystyle \frac{9}{8}}{\overline{v}}_n(b_n^{\left(0\right)}-{\alpha }_n^{\left(0\right)})=b_n^{\left(1\right)}-b_n^{\left(0\right)},\hfill \end{array}$$

where we also used the estimates

$$||F^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right)||\le {\displaystyle \frac{3}{2}}||y_n^{\left(0\right)}-x_n||\le {\displaystyle \frac{3}{2}}(b_n^{\left(0\right)}-{\alpha }_n^{\left(0\right)}),$$

$$\begin{array}{cc}\hfill & ||A_n-I||=||F^{\prime }{\left(x_n\right)}^{-1}(F^{\prime }\left(y_n^{\left(0\right)}\right)-F^{\prime }\left(x_n\right))||\hfill \\ \hfill & \le ||F^{\prime }{\left(x_n\right)}^{-1}M||||M^{-1}(F^{\prime }\left(y_n^{\left(0\right)}\right)-F^{\prime }\left(x_n\right))||\hfill \\ \hfill & \le {\displaystyle \frac{{\overline{v}}_n}{1-v_0\left(||x_n-x_0||\right)}}\le {\displaystyle \frac{{\overline{v}}_n}{1-v_0\left({\alpha }_n^{\left(0\right)}\right)}}.\hfill \end{array}$$

We also have

$$\begin{array}{cc}\hfill & ||y_n^{\left(1\right)}-x_0||\le ||y_n^{\left(1\right)}-y_n^{\left(0\right)}||+||y_n^{\left(0\right)}-x_0||\hfill \\ \hfill & \le b_n^{\left(1\right)}-b_n^{\left(0\right)}+b_n^{\left(0\right)}-{\alpha }_0=b_n^{\left(1\right)}<{\alpha }^{*}.\hfill \end{array}$$

So, the iterate $y_n^{\left(1\right)}\in S(x^{*},{\alpha }^{*})$.

By the first substep of the method (2), we have the identity

$$\begin{array}{cc}\hfill & F\left(y_n^{(i-1)}\right)=F\left(y_n^{(i-1)}\right)-F\left(x_n\right)-{\displaystyle \frac{3}{2}}{F}^{\prime }\left(x_n\right)(y_n^{\left(0\right)}-x_n)\hfill \\ \hfill & =F\left(y_n^{(i-1)}\right)-F\left(x_n\right)-F^{\prime }\left(x_n\right)(y_n^{(i-1)}-x_n)\hfill \\ \hfill & +F^{\prime }\left(x_n\right)(y_n^{(i-1)}-y_n^{\left(0\right)})-{\displaystyle \frac{1}{2}}{F}^{\prime }\left(x_n\right)(y_n^{\left(0\right)}-x_n)\hfill \end{array}$$

leading to

$$\begin{array}{cc}\hfill & ||M^{-1}F\left(y_n^{(i-1)}\right)||\le {\int }_0^{1}v(1-\theta )(b_n^{(i-1)}-{\alpha }_n^{\left(0\right)})d\theta (b_n^{(i-1)}-{\alpha }_n^{\left(0\right)})\hfill \\ \hfill & +(1+v_0\left({\alpha }_n^{\left(0\right)}\right))(b_n^{(i-1)}-{\alpha }_n^{\left(0\right)})+{\displaystyle \frac{1}{2}}(1+v_0\left({\alpha }_n^{\left(0\right)}\right))(b_n^{\left(0\right)}-{\alpha }_n^{\left(0\right)})=b_n^{(i-1)},\hfill \end{array}$$

(34)

so by the third, fourth …, i-th substep of the method (2)

$$\begin{array}{cc}\hfill & ||y_n^{\left(i\right)}-y_n^{(i-1)}||\le ||E_n||||F^{\prime }{\left(x_n\right)}^{-1}M||||M^{-1}F\left(y_n^{(i-1)}\right)||\hfill \\ \hfill & \le {\displaystyle \frac{1}{2}}||F^{\prime }{\left(x_n\right)}^{-1}M||||M^{-1}F\left(y_n^{(i-1)}\right)||\hfill \\ \hfill & +{\displaystyle \frac{3}{2}}||A_n-I||||F^{\prime }{\left(x_n\right)}^{-1}M||||M^{-1}F\left(y_n^{(i-1)}\right)||\hfill \\ \hfill & \le {\displaystyle \frac{1}{2(1-v_0\left({\alpha }_n^{\left(0\right)}\right))}}\left(1+{\displaystyle \frac{3{\overline{v}}_0}{1-v_0\left({\alpha }_n^{\left(0\right)}\right)}}\right){\alpha }_n^{(i-1)}\hfill \\ \hfill & =b_n^{\left(i\right)}-b_n^{(i-1)}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & ||y_n^{\left(i\right)}-x_0||\le ||y_n^{\left(i\right)}-y_n^{(i-1)}||+||y_n^{(i-1)}-x_0||\hfill \\ \hfill & \le b_n^{\left(i\right)}-b_n^{(i-1)}+b_n^{(i-1)}-{\alpha }_0=b_n^{\left(i\right)}<{\alpha }^{*}.\hfill \end{array}$$

Thus, the items (31) hold and the iterate $y_n^{\left(i\right)}\in S(x_0,{\alpha }^{*})$.

Given the first substep for n exchanged by $n+1$, we have then

$$\begin{array}{cc}\hfill & F\left(x_{n+1}\right)=F\left(x_{n+1}\right)-F\left(x_n\right)-{\displaystyle \frac{3}{2}}{F}^{\prime }\left(x_n\right)(y_n^{\left(0\right)}-x_n)\hfill \\ \hfill & =F\left(x_{n+1}\right)-F\left(x_n\right)-F^{\prime }\left(x_n\right)(x_{n+1}-x_n)\hfill \\ \hfill & +F^{\prime }\left(x_n\right)(x_{n+1}-y_n^{\left(0\right)})-{\displaystyle \frac{1}{2}}{F}^{\prime }\left(x_n\right)(y_n^{\left(0\right)}-x_n),\hfill \end{array}$$

so,

$$\begin{array}{cc}\hfill & ||M^{-1}F\left(x_{n+1}\right)||\le {\int }_0^{1}v\left((1-\theta )({\alpha }_{n+1}^{\left(0\right)}-{\alpha }_n^{\left(0\right)})\right)d\theta ({\alpha }_{n+1}^{\left(0\right)}-{\alpha }_n^{\left(0\right)})\hfill \\ \hfill & +\left(1+v_0\left({\alpha }_n^{\left(0\right)}\right)\right)({\alpha }_{n+1}^{\left(0\right)}-b_n^{\left(0\right)})+{\displaystyle \frac{1}{2}}(1+v_0\left({\alpha }_n^{\left(0\right)}\right))(b_n^{\left(0\right)}-{\alpha }_n^{\left(0\right)})={\xi }_{n+1}.\hfill \end{array}$$

(35)

Then, it also follows by (27), (33) (for $u=x_{n+1}$) and the first substep of the method (2)

$$\begin{array}{cc}\hfill & ||y_{n+1}^{\left(0\right)}-x_{n+1}||\le {\displaystyle \frac{2}{3}}||F^{\prime }{\left(x_{n+1}\right)}^{-1}M||||M^{-1}F\left(x_{n+1}\right)||\hfill \\ \hfill & \le {\displaystyle \frac{2}{3}}{\displaystyle \frac{{\xi }_{n+1}}{1-v_0\left({\alpha }_{n+1}^{\left(0\right)}\right)}}=b_{n+1}^{\left(0\right)}-{\alpha }_{n+1}^{\left(0\right)}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & ||y_{n+1}^{\left(0\right)}-x_0||\le ||y_{n+1}^{\left(0\right)}-x_{n+1}||+||x_{n+1}-x_0||\hfill \\ \hfill & \le b_{n+1}^{\left(0\right)}-{\alpha }_{n+1}^{\left(0\right)}+{\alpha }_{n+1}^{\left(0\right)}-{\alpha }_0=b_{n+1}^{\left(0\right)}<{\alpha }^{*}.\hfill \end{array}$$

The induction for items (29)–(32) is completed and all iterates $\left\{x_n\right\}$ belong to $S(x_0,{\alpha }^{*})$. By the triangle inequality (32) gives

$$||x_{n+q}-x_n||\le {\alpha }_{n+q}-{\alpha }_n,q=0,1,2,\dots$$

(36)

Therefore, the sequence $\left\{x_n\right\}$ is complete in the Banach space $B_0$ and, as such, it converges to some $x^{*}\in S[x_0,{\alpha }^{*}]$ (since $S[x_0,{\alpha }^{*}]$ is a closed set). Moreover, by letting $n\to \infty$ in (35) and using the continuity of the operator F, we obtain $F\left(x^{*}\right)=0$. Finally, by letting $q\to \infty$ in (36) we show item (28). □

As in the local case, a domain is determined with only one solution of the equation $F\left(x\right)=0$.

Proposition 2. 

Suppose there exists a solution $z\in S(x_0,\mu )$ of the equation $F\left(x\right)=0$ for some $\mu >0$, the condition $\left(H_4\right)$ holds in the ball $S(x_0,\mu )$ and there exists ${\mu }_1\ge \mu$ such that

$${\int }_0^1{v}_0\left((1-\theta )\mu +\theta {\mu }_1\right)d\theta <1.$$

(37)

Define the domain $D_4=S[x_0,{\mu }_1]\cap D_0$. Then, z is the only solution of the equation $F\left(x\right)=0$ in the domain $D_4$.

Proof. 

Suppose there exists a solution $z_1\in D_4$ of the equation $F\left(x\right)=0$ such that $z\ne z_1$. Define the linear operator

$$L={\int }_0^1{F}^{\prime }(z+\theta (z_1-z))d\theta .$$

Then, it follows by (${\mathrm{H}}_4$) and (37) that

$$\begin{array}{cc}\hfill & ||M^{-1}(L-M)||\le {\int }_0^1{v}_0\left((1-\theta )\right(||z-x_0||+\theta ||z_1-x_0||)d\theta \hfill \\ \hfill & \le {\int }_0^1{v}_0((1-\theta )\mu +\theta {\mu }_1)d\theta <1.\hfill \end{array}$$

So L is invertible, and from

$$z_1-z=L^{-1}(F\left(z_1\right)-F\left(z\right))=L^{-1}\left(0\right)=0$$

we conclude that $z_1=z$. □

Remark 4. 

(1) 

The limit point ${\alpha }^{*}$ can be replaced by s in the condition ($H_6$).

(2) 

Under all the conditions ($H_1$)–($H_6$) we can take $z=x^{*}$ and $\mu ={\alpha }^{*}$ in the Proposition 2.

(3) 

The sufficient semi-local convergence conditions ($H_1$)–($H_6$) are very general. Clearly, if the functions $v_0$ and v are specialized more, concrete results can be obtained, which include the rate and order of convergence. But in this paper, we wanted to minimize the limitations of our approach.

4. Numerical Results

In this section, we present numerical results to validate the theoretical analysis discussed in the preceding sections. We apply our proposed $(m+1)$-step method, given by (2), to several nonlinear systems of equations to demonstrate its efficiency and confirm its high order of convergence. The numerical experiments were performed using the C++ programming language on a machine equipped with an Intel(R) Core(TM) i7-10510U CPU @ 1.80 GHz processor. For more precise calculations, we used the Boost Multiprecision Library. It allowed us to utilize high-precision floating-point arithmetic, which was configured to 200 digits, to get more accurate results that are close to theoretical ones.

To validate our results, we tested the implemented approach on some test examples. As in paper [20], for all test cases, the iteration process is terminated when the following condition is met:

$$\left|\right|x_{k+1}-x_k\left|\right|+\left|\right|F\left(x_k\right)\left|\right|<{10}^{-100}.$$

For each example, we track the error at each iteration. To numerically verify the theoretical convergence rate, we use the Computational Order of Convergence (COC), which is approximated using the following formula based on four consecutive iterations [17]:

$$\mathrm{COC}={\displaystyle \frac{log\left(||x_{k+2}-x_{k+1}||/||x_{k+1}-x_k||\right)}{log\left(||x_{k+1}-x_k||/||x_k-x_{k-1}||\right)}},$$

(38)

where $x_{k-1},x_k,x_{k+1},$ and $x_{k+2}$ are iterates close to the final solution.

We have tested the method (2) on several examples that were used in [20] and also added some general functions that are used for testing algorithms for solving systems of nonlinear equations that are suggested in the article [28]. We used the exact initial approximations that were utilized in the previously mentioned articles. The numerical results will be presented for problems including the following:

Example 1.

A system of 2 equations given by:$\left\{\begin{array}{c}{e}^{-x_1^2}+8x_{1}sin{x}_2=0,\hfill \\ x_1+x_2-1=0\hfill \end{array}\right.$ with initial approximation $x_0={({\displaystyle \frac{4}{10}},-{\displaystyle \frac{4}{10}})}^T$ (see [32]).

Example 2. 

A system of 3 equations [16] given by:$\left\{\begin{array}{c}10x_1+sin(x_1+x_2)-1=0,\hfill \\ 8x_2-{cos}^2(x_3-x_2)-1=0,\hfill \\ 12x_3+sin\left(x_3\right)-1=0\hfill \end{array}\right.$ with initial approximation $x_0={(0,1,0)}^T$.

Example 3. 

A system of n equations [33] given by:

$$\left\{\begin{array}{c}{x}_i^2{x}_{i+1}=0,i=1,\dots ,n-1,\hfill \\ x_i^2{x}_1-1=0,i=n\hfill \end{array}\right.$$

with initial approximation $x_0={({\displaystyle \frac{18}{10}},\dots ,{\displaystyle \frac{18}{10}})}^T$, where the solution is: $x_i^{*}=1$ for $i=1,\dots ,n$. We select $n=300$.

Example 4. 

A system of three equations:

$$\left\{\begin{array}{c}{e}^{x_1}-1=0,\hfill \\ {\displaystyle \frac{e-1}{2}}{x}_2^2+x_2=0,\hfill \\ x_3=0,\hfill \end{array}\right.$$

$x_0={(3.5,0.5,2.5)}^T$, $x^{*}={(0,0,0)}^T$.

Example 5. 

Discrete boundary value function [29]

$$f_i\left(x\right)=2x_i-x_{i-1}-x_{i+1}+h^2{(x_i+t_i+1)}^{3/2},$$

where $h={\displaystyle \frac{1}{n+1}}$, $t_i=ih$, $i=0,\dots ,n$, and $x_0=x_{n+1}=0$ $x_0=\left({\xi }_j\right)$, where ${\xi }_j=t_j(t_j-1)$. We take $n=300$.

Example 6. 

Discrete integral equation function [29]

$$\begin{array}{c}{f}_i\left(x\right)=x_i+{\displaystyle \frac{h}{2}}\left[(1-t_i)\sum _{j=1}^i{t}_j{(x_j+t_j+1)}^3\right.\\ \left.+t_i\sum _{j=i+1}^n(1-t_j){(x_j+t_j+1)}^3\right],\end{array}$$

where $h={\displaystyle \frac{1}{n+1}}$, $t_i=ih$,$i=0,\dots ,n$, and $x_0=x_{n+1}=0$. $x_0=\left({\xi }_j\right)$, where ${\xi }_j=t_j(t_j-1)$. We take $n=300$.

Example 7. 

Broyden tridiagonal function [28]

$$\begin{array}{c}{f}_i\left(x\right)=(3-2x_i)x_i-x_{i-1}-2x_{i+1}+1,\end{array}$$

where $x_0=x_{n+1}=0$, $x_0={(-1,\dots ,-1)}^T$. We take $n=300$.

Example 8. 

Broyden banded function [28].

$$\begin{array}{c}{f}_i\left(x\right)=x_i(2+5x_i^2)+1-\sum _{j\in J_i}{x}_j(1+x_j),\end{array}$$

where $J_i=\{j:j\ne i,max(1,i-m_l)\le j\le min(n,i+m_u)\}$, $m_l=5$, and $m_u=1$ $x_0={(-1,\dots ,-1)}^T$. We take $n=300$.

The results for each problem are summarized in Table 1, showing the total number of iterations that are required for meeting the stopping criterion (k), the elapsed time (e-time), norm of the difference between approximate solution $x_k$ and $x_{k-1}$ ($||x_k-x_{k-1}||$), norm of $F_k$ ($||F_k||$), and the calculated $COC$. It enables a comprehensive comparison of the method’s performance for various values of m. From these tables, we can conclude that the computational order of convergence is quite close to the theoretical one for almost all examples (the theoretical order of convergence for m = 2, 3, 4 will be 5, 7, and 9, respectively). $||F_k||$ and $||x_k-x_{k-1}||$ converge even further to smaller number than established accuracy. Increasing the value of m does not always lead to better performance time, as it may not always result in a decrease in the number of iterations. For instance, in Example 8, there is no need to increase m from 3 to 4, since the iteration number is not reduced; however, it is a good idea to increase it from 2 to 3. For example, in Example 6, it is more crucial to increase m from 3 to 4, as it leads to a significant reduction in performance time.

Table 1. Performance of $(m+1)$-step Newton-Jarrat (2) (Examples 1–8).

	Value of m
Metric	2	3	4
Example 1
k	5	5	4
COC	5.010	6.995	9.003
e-time (s)	0.014	0.014	0.013
$\left|\right|F_k\left|\right|$	1.61 × 10−206	1.61 × 10−206	1.61 × 10−206
$\left|\right|x_k-x_{k-1}\left|\right|$	3.11 × 10−203	2.45 × 10−207	1.16 × 10−160
Example 2
k	4	4	4
COC	4.975	6.635	8.680
e-time (s)	0.018	0.020	0.021
$\left|\right|F_k\left|\right|$	3.28 × 10−207	6.24 × 10−211	8.55 × 10−215
$\left|\right|x_k-x_{k-1}\left|\right|$	2.52 × 10−154	1.22 × 10−207	6.12 × 10−211
Example 3
k	5	5	4
COC	5.000	6.973	8.988
e-time (s)	17.74	28.07	24.30
$\left|\right|F_k\left|\right|$	0	5.77 × 10−209	0
$\left|\right|x_k-x_{k-1}\left|\right|$	6.16 × 10−110	1.37 × 10−208	1.62 × 10−111
Example 4
k	7	6	5
COC	5.396	7.240	9.150
e-time (s)	0.021	0.017	0.015
$\left|\right|F_k\left|\right|$	0	0	0
$\left|\right|x_k-x_{k-1}\left|\right|$	4.59 × 10−323	7.56 × 10−287	4.23 × 10−101
Example 5
k	4	4	3
COC	4.982	6.981	8.980
e-time (s)	16.16	15.65	15.66
$\left|\right|F_k\left|\right|$	1.58 × 10−215	5.51 × 10−214	1.23 × 10−213
$\left|\right|x_k-x_{k-1}\left|\right|$	4.84 × 10−210	2.52 × 10−211	5.62 × 10−135
Example 6
k	4	4	3
COC	4.982	6.981	8.980
e-time (s)	162.7	160.2	118.9
$\left|\right|F_k\left|\right|$	2.75 × 10−211	7.19 × 10−212	4.08 × 10−211
$\left|\right|x_k-x_{k-1}\left|\right|$	5.08 × 10−210	3.76 × 10−211	5.62 × 10−135
Example 7
k	5	4	4
COC	4.788	6.912	7.004
e-time (s)	17.52	16.72	15.41
$\left|\right|F_k\left|\right|$	1.12 × 10−215	1.10 × 10−215	8.89 × 10−216
$\left|\right|x_k-x_{k-1}\left|\right|$	2.31 × 10−216	1.40 × 10−138	1.82 × 10−216
Example 8
k	6	5	5
COC	4.989	6.463	8.664
e-time (s)	27.17	22.84	29.26
$\left|\right|F_k\left|\right|$	1.21 × 10−215	1.22 × 10−215	1.10 × 10−215
$\left|\right|x_k-x_{k-1}\left|\right|$	1.40 × 10−216	1.43 × 10−216	1.26 × 10−216

We also prepared plots that show the values of the previously mentioned norms at each iteration on a logarithmic scale (see Figure 1 and Figure 2). The convergence of the method (2) for different values of m is graphically shown, and the comparison for all examples (colors represent different examples). The lines in Figure 1 show how quickly the function approaches zero, in other words, how quickly the algorithm converges to an approximate solution with accuracy ${10}^{-100}$. As you can see, an increasing number of m from 2 to 4 leads to either faster convergence or smaller error. For instance, Example 4 requires one fewer iteration with each increase in the value of m by one. Example 7 does not reduce the number of iterations when we increase m from 3 to 4, but we can clearly see that the norm of the function is closer to zero. Also, from all these plots, we can conclude that the most significant step the algorithm makes is at the last iteration. A similar situation is also shown in Figure 2. Notice that the convergence plots for Example 5 and Example 6 are identical for all tested values of m (m = 2, 3, 4).

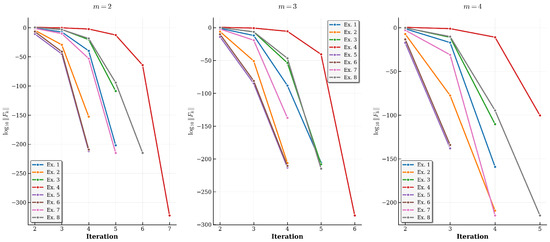
Figure 1. Convergence Analysis of $\left|\right|F_k\left|\right|$ for different values of m.

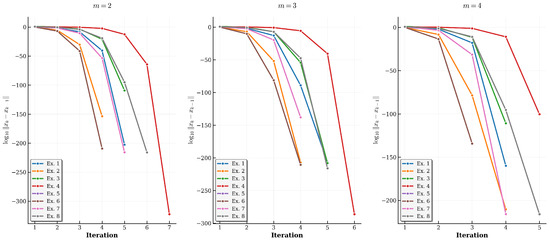
Figure 2. Convergence Analysis of $\left|\right|x_k-x_{k-1}\left|\right|$ for different values of m.

We have also provided an example of a nonlinear equation involving a mapping $F:{\mathbb{R}}^3\to {\mathbb{R}}^3$ where the majorant functions $w_0$ and w are determined without the usage of high-order differentiability (see Example 9). Moreover, this example has error bounds on the distances $||x_n-x^{*}||$ that involve Lipschitz constants, as you requested. Notice that such a priori bounds are not available in [20] or other studies using Taylor series.

Example 9. 

Let us consider the mapping $F:{\mathbb{R}}^3\to {\mathbb{R}}^3$ for $D=S[0,1]$, $s={(s_1,s_2,s_3)}^T$ defined by

$$F\left(s\right)=\left(e^{s_1}-1,{\displaystyle \frac{1}{2}}(e-1)s_2^2+s_2,s_3\right).$$

Then, notice that $s^{*}=0$ solves the equation $F\left(s\right)=0$. Moreover, the Fréchet derivative of the mapping F is given by

$$F^{\prime }\left(s\right)=\left[\begin{array}{ccc}{e}^{s_1}& 0& 0\\ 0& (e-1)s_2+1& 0\\ 0& 0& 1\end{array}\right].$$

It follows that $F^{\prime }\left(s^{*}\right)=I$. We shall take $M=F^{\prime }\left(s^{*}\right)$. Furthermore the conditions ($C_1$), ($C_3$) and ($C_4$) are validated if we choose $w_0\left(s\right)=(e-1)s$, $R_0={\displaystyle \frac{1}{e-1}}$ and $w\left(s\right)=e^{{\displaystyle \frac{1}{e-1}}}s$. For this case, we can calculate the radius of convergence. In the case $m=2$, we must calculate $g_0\left(t\right)$, $g_1\left(t\right)$ and $g_2\left(t\right)$ using formulas from ($C_2$). After getting these functions, we find such $r_0,r_1,r_2$ for which $g_j\left(r_j\right)-1=0$, where $j=0,1,2$. Then we can find the radius of convergence $r=min\left(r_j\right)$. Notice that we can take two options of taking ${\overline{w}}^{\left(s\right)}\left(t\right)$:

$${\overline{w}}^{\left(s\right)}\left(t\right)=\left\{\begin{array}{c}w\left((1+g_s\left(t\right))t\right)\hfill \\ or\hfill \\ w_0\left(t\right)+w_0\left(g_s\left(t\right)t\right).\hfill \end{array}\right.$$

We calculated $r_j$ and r for both options and collected results in Table 2. So, when we take ${\overline{w}}^{\left(s\right)}\left(t\right)=w\left((1+g_s\left(t\right))t\right)$ radius of convergence is greater in comparison with the selection ${\overline{w}}^{\left(s\right)}\left(t\right)=w_0\left(t\right)+w_0\left(g_s\left(t\right)t\right)$.

Table 2. Radii of Convergence for Newton-Jarrat Method (2).

	${\overline{\mathit{w}}}^{\left(\mathit{s}\right)}\left(\mathit{t}\right)=\mathit{w}\left((1+{\mathit{g}}_{\mathit{s}}\left(\mathit{t}\right))\mathit{t}\right)$	${\overline{\mathit{w}}}^{\left(\mathit{s}\right)}\left(\mathit{t}\right)={\mathit{w}}_0\left(\mathit{t}\right)+{\mathit{w}}_0\left({\mathit{g}}_{\mathit{s}}\left(\mathit{t}\right)\mathit{t}\right)$
$r_0$	$0.228990$	$0.228990$
$r_1$	$0.142601$	$0.043682$
$r_2$	$0.123565$	$0.069096$
r	$0.123565$	$0.043682$

We also wanted to test our method on some ordinary and partial differential equations. For this purpose, we take the Lene–Emden equation [30], which states as

$$x^{″}\left(t\right)+{\displaystyle \frac{2}{t}}{x}^{\prime }\left(t\right)+x{\left(t\right)}^5=0,x^{\prime }\left(0\right)=0,x\left(0\right)=1,$$

(39)

and Klein–Gordon equation [26]:

$$u_{tt}(z,t)-c^2{u}_{zz}(z,t)+f\left(u\right)=p(z,t),-\infty <x<\infty ,t>0.$$

(40)

We compare results with the $(s-1)$-step version of Newton–Raphson (NRM) presented in [35]:

$$\left\{\begin{array}{c}{y}_1=x_k-F^{\prime }{\left(x_k\right)}^{-1}F\left(x_k\right),\hfill \\ y_2=y_1-F^{\prime }{\left(x_k\right)}^{-1}F\left(y_1\right),\hfill \\ y_3=y_2-F^{\prime }{\left(x_k\right)}^{-1}F\left(y_2\right),\hfill \\ ⋮\hfill \\ x_{k+1}=y_{s-1}=y_{s-2}-F^{\prime }{\left(x_k\right)}^{-1}F\left(y_{s-2}\right).\hfill \end{array}\right.$$

(41)

We also employ the Chebyshev pseudo-spectral collocation method for temporal and spatial discretizations, as was done in the previously mentioned article:

$$F\left(x\right)=\left(D_t^2+\mathrm{diag}\left({\displaystyle \frac{2}{t}}\right)D_t\right)x+x^5=0$$

for (39), and

$$F\left(u\right)=((I_z\otimes D_t^2)-c^2(D_z^2\otimes I_z))u+f\left(u\right)=0$$

for (40).

We tested this solution in a slightly different environment; we did not use a high-precision library. We made this choice to ensure that our results were more representative in a realistic computing environment that relies on standard hardware floating-point types. We also set the dimension of our system to 500 for (39) and 4420 for (40) to test our method on high-dimensional problems. We set the same initial approximation and domain as was done in [35]. For (39), the method (2) converges to the solution with accuracy $O\left({10}^{-5}\right)$ after 16 steps, while Newton-Raphson needs 23 ones. For (40), it took only three steps for the Newton-Jarrat-like method to converge with such accuracy, while for Newton-Raphson it took four steps. The results of the described experiments are presented in Table 3 and Table 4, and they are in the same format as they are presented in [35] for comparison purposes. As you might notice, the method (2) is quite expensive in comparison with NRM, since it requires additional evaluation of Jacobian, matrix vector multiplications, and solving a system of linear equations per iteration when the right side is a matrix. In the case of partial derivative (40), it plays a crucial role, since both algorithms converge in a small number of steps that also leads to the same theoretical order of convergence, and because of these costly operations, it takes more time for the method (14) to converge with the previously mentioned accuracy. However, in the case of (39), the order of convergence of the method (2) is greater than that of NRM, and it plays a more crucial role in terms of performance time. So, in this case, the method (2) takes less time to converge.

Table 3. Comparison of performances for the $(m+1)$-step Newton-Jarrat method (NJM) (2) and Multi-step Newton-Raphson (NRM) (41) for the Lene–Emden Equation (39); initial guess 1; domain [0, 9] [35].

Iterative Methods	NJM (2)	NRM (41)
Number of iterations	1	1
Size of problem	500	500
Number of steps	16	23
Theoretical convergence-order	31	24
Function evaluations per iteration	16	23
Solutions of system of linear equations per iteration	16	23
when right side is vector
Solutions of system of linear equations per iteration	1	0
when right side is matrix
Number of Jacobian evaluations per iteration	2	1
Number of Jacobian LU-factorization per iteration	1	1
Number of matrix vector multiplications per iteration	15	0
Steps	$\left|\right|{\mathbf{x}}_m-{\mathbf{x}}^{*}{\left|\right|}_{\infty }$	$\left|\right|{\mathbf{x}}_m-{\mathbf{x}}^{*}{\left|\right|}_{\infty }$
1	6.8402 × 10−1	6.2052 × 10−1
2	5.5152 × 10−1	5.5165 × 10−1
3	8.1764 × 10−1	6.4046 × 10−1
4	1.5322	8.5943 × 10−1
5	1.2030	1.1858
6	2.3728	1.2422
7	7.9603 × 10−1	1.3089
8	8.2595 × 10−1	2.0382
9	8.5373 × 10−1	1.3065
10	7.8730 × 10−1	1.8401
11	4.7382 × 10−1	9.4516 × 10−1
12	1.6708 × 10−1	8.9284 × 10−1
13	3.7363 × 10−2	9.1266 × 10−1
14	6.1138 × 10−3	9.3032 × 10−1
15	7.9369 × 10−4	9.1482 × 10−1
16	8.5210 × 10−5	6.9886 × 10−1
17		3.7548 × 10−1
18		1.4397 × 10−1
19		4.3176 × 10−2
20		1.0867 × 10−2
21		2.3786 × 10−3
22		4.6137 × 10−4
23		8.0241 × 10−5
CPU time (s)	0.029	0.043

Table 4. Comparison of performances for the $(m+1)$-step Newton-Jarrat method (NJM) (2) and Multi-step Newton-Raphson (NRM) (41) for the Klein–Gordon Equation (40); initial guess $u(z_j,t_j)=0$, $u(z,t)=\delta \sec \mathrm{h}\left(\kappa \right(z-vt\left)\right)$, $\kappa =\sqrt{{\displaystyle \frac{k}{c^2-v^2}}}$, $\delta =\sqrt{{\displaystyle \frac{2k}{\gamma }}}$, $c=1$, $\gamma =1$, $v=0.5$, $k=0.5$, $n_z=170$, $n_t=26$, $z\in [-22,22]$, $t\in [0,0.5]$ [35].

Iterative Methods	NJM (2)	NRM (41)
Number of iterations	1	1
Size of problem	4420	4420
Number of steps	3	4
Theoretical convergence-order	5	5
Function evaluations per iteration	3	4
Solutions of system of linear equations per iteration	3	3
when right side is vector
Solutions of system of linear equations per iteration	1	0
when right side is matrix
Number of Jacobian evaluations per iteration	2	1
Number of Jacobian LU-factorization per iteration	1	1
Number of matrix vector multiplications per iteration	2	0
Steps	$\left|\right|{\mathbf{x}}_m-{\mathbf{x}}^{*}{\left|\right|}_{\infty }$	$\left|\right|{\mathbf{x}}_m-{\mathbf{x}}^{*}{\left|\right|}_{\infty }$
1	3.3122 × 10−1	1.1253 × 10−1
2	6.8391 × 10−3	6.8391 × 10−3
3	3.5588 × 10−5	1.5342 × 10−4
4		1.8717 × 10−6
CPU time (s)	5.8	1.6

5. Conclusions

In this work, we have presented a significant extension of the convergence analysis for the class of multi-step Newton-Jarratt-like methods of order $2m+1$, initially proposed in the paper [20]. While the computational efficiency of their scheme is noteworthy, its practical application was limited by a theoretical framework that relied on strong conditions, namely the existence and boundedness of derivatives up to the fifth order. Other limitations of the Taylor series approach and how to handle them can be found in items (${\mathrm{P}}_1$)–(${\mathrm{P}}_5$) and (${\mathrm{P}}_1$)’–(${\mathrm{P}}_5$)’ of the Introduction.

The primary contribution of this paper is the removal of these restrictive assumptions. We have developed a new convergence analysis using only conditions on the first Fréchet derivative. This approach, based on generalized Lipschitz-type continuity, not only confirms the local convergence of the method but does so under a much weaker and more practical set of hypotheses. This significantly broadens the range of nonlinear problems to which this efficient method can be applied with confidence.

Furthermore, we have established the first semi-local convergence analysis for this family of methods. By employing the concept of majorizing sequences, we provide criteria that guarantee convergence from an initial guess without prior knowledge of the existence of a solution. This is a crucial step forward, as it provides a practical tool for verifying the method’s applicability to real-world problems where the solution’s location is unknown.

The theoretical results were rigorously validated through numerical experiments. We expanded the range of challenging examples for testing the method (2) by using the large-scale problems from [28], and thereby proved the effectiveness of such method. The computational order of convergence (COC) was found to be in close agreement with the theoretical order of $2m+1$. We also tested the method on ordinary and partial differential equations and compared the results with the existing famous method.

In summary, by providing a more robust theoretical foundation with both local and semi-local convergence under weaker assumptions, our work substantially extends the applicability and utility of this powerful class of Newton-Jarratt-like methods for solving systems of nonlinear equations. The ideas in this paper shall be used to extend the applicability of other methods in our future research [11,12,15,22,24,25,26,27,28,29,30,31,32,33,34,35,36].