A Mathematical Model of the Generalized Finite Strain Consolidation Process and Its Deep Galerkin Solution

Abstract

Developing classical three-dimensional consolidation theories considers the small-strain assumption. This small-strain assumption is inappropriate when studying the consolidation process of soft or very soft clay layers. Instead, this study derives a novel generalized mathematical model describing a three-dimensional finite-strain consolidation process and applies the deep Galerkin method to deduce its novel numerical solution. Developing this mathematical model uses the Reynolds transport theorem to describe mass and momentum balances for clay grain and pore water phases. The governing equation is the sum of the resulting mass and momentum balance equations. Next, the deep Galerkin method is applied to train a deep neural network to minimize the loss function defined by the governing equation and available initial and boundary conditions. The unknowns are the average velocity, effective stress, and pore water pressure. Predicting consolidation settlements is implemented by updating the problem domain using the resulting average velocity. Beneficial from the deep Galerkin method, two real-world examples demonstrate that the current mathematical model provides accurate predictions of consolidation settlements caused by the self-weight of two very soft clay layers. The deep Galerkin method helps resolve ill-posed problems by fitting a family of fields constrained by sampling/regularization rather than physics if the physics is under-determined.

1. Introduction

Consolidation represents the time-dependent process by which clay decreases its volume due to the expulsion of pore water under an external loading or its self-weight. A consolidation theory or a mathematical model describing the consolidation process is essential in many actual problems, such as estimating the consolidation settlements due to a construction loading (e.g., [1]), evaluating the results of a sand drain scheme (e.g., [2]), and scheduling a land reclamation project (e.g., [3]). Unexpected consolidation settlements may damage a building and delay a land reclamation project.

Nevertheless, developing classical mathematical models describing consolidation processes considers the small-strain assumption (e.g., [4]) in which consolidation settlements do not substantially change the thickness of a clay layer. It is invalid for a soft or very soft clay layer since it may be significantly thinner due to its consolidation settlements. These consolidation settlements may be caused only by their self-weight. A real example may be the Kansai airport, which may gradually sink into the sea due to excessive settlements of undersea clay layers. However, we only had one-dimensional [5] or quasi multi-dimensional mathematical models [6] to describe the consolidation process of a soft or very soft clay layer. Developing these mathematical models assumes that a soft or very soft clay layer deforms only in the vertical direction. This assumption is inconsistent with the actual condition.

Therefore, the author’s thesis [7] developed a generalized mathematical model describing a generalized finite-strain consolidation process. The Reynolds transport theorem [8] is employed to represent mass and momentum balances. The previous thesis [7] further combined the resulting mass and momentum equations into one single governing equation. Nevertheless, the resulting governing equation is long and complex. Applying it to model a real problem is difficult since we have few numerical methods to solve it. To solve this drawback, this study applies the deep Galerkin method (DGM) [9] to minimize the loss function defined by the sum of resulting momentum equations, initial, and boundary conditions. The unknowns are the average velocity field, effective stress, and pore water pressure. Calculating consolidation settlements is implemented by updating the problem domain according to the resulting average velocity field.

This DGM (e.g., [9]) is a meshless deep algorithm for solving high-dimensional partial differential equations. Choosing it considers the difficulties of collecting necessary data to define the boundary conditions (for example, a deep boundary) of a soft or very soft clay layer. By using the DGM, we train a deep neural network to provide a solution to a partial differential equation at random points in a problem domain. Defining complete boundary conditions is unnecessary.

The principal contributions of this study are as follows:

• Compensate for the absence of a useful mathematical model for describing a generalized finite-strain consolidation process. It advances the simulation of the finite-strain consolidation process of soft or very soft clay layers. Compared with traditional small-strain consolidation theories (e.g., [4]), the proposed mathematical model has more applications, such as estimating settlements of dredge fill deposits.
• Extend the application of the DGM to ill-posed problems. Specifying complete boundary conditions is unnecessary.

The remainder of this article is divided into four sections. Section 2 presents a review of published articles relevant to this study. Section 3 presents the development of a generalized finite strain consolidation theory and its DGM solution. Section 4 presents the numerical results generated using the current mathematical model. This section compares the numerical results with the observed settlements of the phosphatic waste clay and Osaka Bay mud. Based on this comparison, Section 5 presents a discussion. Section 6 presents the conclusion and concluding remarks of this research.

2. Related Works

This study intends to develop a mathematical model to describe a generalized finite-strain consolidation process and apply the DGM to solve the unknowns. Therefore, relevant references are those articles presenting a two- or three-dimensional finite strain consolidation theory and applications of the DGM to solve various partial differential equations.

2.1. Finite Strain Consolidation Theory

When we intend to develop a generalized finite strain consolidation theory, the origin is usually the one-dimensional finite strain consolidation theory proposed by Gibson et al. [3,5]. Different from Biot [4], they used the void ratio as the main unknown of their mathematical model. Considering that consolidation settlements may substantially thin a soft clay layer, they defined a convective coordinate system to describe the changes in a clay layer’s thickness. Besides, Gibson et al. [3,5] accounted for the effects of a thick clay layer’s self-weight on its consolidation process.

After the one-dimensional finite strain consolidation theory [3,5], few articles presented a truly generalized finite strain consolidation theory. However, quasi-two- or three-dimensional theories are available. For example, Jeeravipoolvarn et al. [6] developed a quasi-three-dimensional finite strain consolidation theory, which assumed that pore water flows in any direction and pore pressure dissipation causes only vertical deformations. Huerta and Rodriguez (1992) [10] calculated finite-strain consolidation settlements of soft sediment fillings at high water levels. They considered one-dimensional deformations and two-dimensional fluxes. Liu et al. [11] assumed vertical strains. They evaluated the vertical drains combined with vacuum pressure using a quasi-axisymmetric finite strain consolidation theory.

The author’s Ph.D. thesis [7] presented a truly three-dimensional finite strain consolidation theory. This generalized finite strain consolidation theory extended the one-dimensional works provided by Gibson et al. [3,5]. Creating this extension used the Reynolds transport theory to model the mass and momentum balances for the clay grain and pore water phases. Limiting the deformation and pore water dissipation in the vertical direction is not required. Besides, the effect of the self-weight of a thick clay layer on its consolidation process is studied. However, the resulting mathematical model may be complex.

2.2. Deep Galerkin Method

Since this study chooses the DGM (e.g., [9]) to solve the proposed mathematical model, it is necessary to review the representative partial differential equations, which were solved using the DGM.

Kumar et al. [12] used the DGM to solve the one-dimensional Burger-Huxley and Huxley equations. They are second-order partial differential equations with initial and boundary conditions. In the application of DGM, estimating the time derivatives using a finite difference scheme was not required. Approximating a time derivative by a finite difference scheme is frequently seen in the application of the finite element method in solving a time-dependent partial differential equation.

Sirignano and Spiliopoulos [9] applied the DGM to a free boundary equation. It is a one-dimensional and second-order partial differential equation. Its theoretical background is stock price dynamics. One of the boundaries is a time-dependent function. It enters into the derivation of the loss function defined to implement the DGM.

Masaharu [13] employed the DGM to solve a compressible Navier–Stokes equation. The Navier–Stokes equation contains convective accelerations. They are highly nonlinear differential terms. We may notice that Masaharu (2021) [13] studied supersonic flows around a blunt body without specifying full boundary conditions. This example is quite different from the application of a finite element method.

We may notice that only the third published study [13] applied the DGM to ill-posed problems. It encourages the current study to apply the DGM to solve finite strain consolidation problems.

3. Generalized Finite Strain Consolidation Theory

Presenting the following subsections frequently employs the following symbols: t is the time, $\Omega$ is the problem domain, V is its volume, S is its boundary, v is the velocity, $\mathbf{a}$ denotes the Lagrangian coordinate, $\mathbf{x}$ represents the convective coordinate, the subscript _s denotes the clay grain phase, the subscript _w denotes the pore water phase, the subscript ₀ represents the Lagrangian coordinate $\mathbf{a}$, $\Theta$ denotes the total amount of an extensive property (such as mass and momentum) within ${\Omega }_0$, $\theta$ is its density, ${\displaystyle \frac{d}{dt}}$ is the total derivative with respect to t, $\mathbf{v}$ is the velocity field, n is the porosity, e is the void ratio, $\mathbf{n}$ denotes a unit normal vector, $\rho$ is the density, $\mathsf{\sigma }$ denotes the total stress tensor, ${\mathsf{\sigma }}^{\mathbf{\prime }}$ denotes the effective stress tensor, p is the pore water pressure, g is the gravitational acceleration, $\Gamma$ represents the boundary (for specifying boundary conditions), $\beta$ is the learning rate, $Loss$ denotes the loss function, ‖‖ represents the size, and $\varphi$ is the neural network’s parameter.

Based on the above symbols, the aim of Section 3.1 is to develop a mathematical model describing a finite strain consolidation process. The aim of Section 3.2 is to present the DGM solution of this mathematical model, whereas the aim of Section 3.3 is to discuss the aim of the resulting DGM solution.

3.1. Mathematical Model

Suppose a homogeneous and saturated soil layer. Besides, clay grains and pore water are incompressible. The convective coordinate $\mathbf{x}$ is defined to identify a point in a problem domain $\Omega$.

The Reynolds transport theorem states that the conservation of the extensive property $\Theta$ can be represented by [8]

$${\displaystyle \frac{d\Theta }{dt}}={\displaystyle \frac{d}{dt}}\left({\int }_{\Omega }\theta dV\right)+{\int }_S\theta \left({\mathbf{v}}_S·{\mathbf{n}}_S\right)dS=0$$

(1)

where the dot · is the dot operator and ${\mathbf{n}}_S$ is a unit vector normal to S.

3.1.1. Mass Balance for the Clay Grain Phase

Substituting $\theta =(1-n){\rho }_s$ into Equation (1) results in

$${\displaystyle \frac{d}{dt}}\left[{\int }_{\Omega }(1-n){\rho }_{s}dV\right]+{\int }_S(1-n){\rho }_s\left({\mathbf{v}}_s·{\mathbf{n}}_S\right)dS=0$$

(2)

where f is a function. Applying the definition of total derivative ${\displaystyle \frac{df}{dt}}={\displaystyle \frac{\partial f}{\partial t}}+\nabla f·\mathbf{v}$ and coordinate transform to simplify Equation (2) yields

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d}{dt}}\left[{\int }_{\Omega }(1-n){\rho }_{s}dV\right]+{\int }_S(1-n){\rho }_s\left({\mathbf{v}}_s·{\mathbf{n}}_S\right)dS={\displaystyle \frac{d}{dt}}\left[{\int }_{{\Omega }_0}(1-n_0){\rho }_{s0}Jd{V}_0\right]\hfill \\ & +{\int }_S(1-n){\rho }_s\left({\mathbf{v}}_s·{\mathbf{n}}_S\right)dS={\int }_{{\Omega }_0}{\displaystyle \frac{d\left[(1-n_0){\rho }_{s0}J\right]}{dt}}d{V}_0+{\int }_S(1-n){\rho }_s\left({\mathbf{v}}_s·{\mathbf{n}}_S\right)dS\hfill \\ & ={\int }_{{\Omega }_0}\left\{{\displaystyle \frac{\partial \left[(1-n_0){\rho }_{s0}J\right]}{\partial t}}+{\mathbf{v}}_{s0}·\nabla \left[(1-n_0){\rho }_{s0}J\right]\right\}d{V}_0+{\int }_S(1-n){\rho }_s\left({\mathbf{v}}_s·{\mathbf{n}}_S\right)dS=0\hfill \end{array}$$

(3)

in which ∇ is the gradient vector, $J=\left|{\displaystyle \frac{\partial (x_1,x_2,x_3)}{\partial (a_1,a_2,a_3)}}\right|$ is the Jacobian, $x_i(i=1,2,3)$ are the components of convective coordinate $\mathbf{x}$, and $a_i$ are the components of Lagrangian coordinate $\mathbf{a}$.

Applying the Gauss theorem [14] $\left({\int }_S\pi ·dS=\int {\int }_{\Omega }\pi dV\right.$, and $\pi$ denotes a continuously differentiable vector field) and coordinate transform to simplify the final term of Equation (3) yields

$${\int }_S(1-n){\rho }_s\left({\mathbf{v}}_s·{\mathbf{n}}_S\right)dS={\int }_{{\Omega }_0}(1-n){\rho }_s\nabla ·{\mathbf{v}}_{s}dV={\int }_{{\Omega }_0}(1-n_0){\rho }_{s0}\nabla ·{\mathbf{v}}_{s0}Jd{V}_0$$

(4)

Combining the final term of Equation (4) with the eighth term $\left({\int }_{{\Omega }_0}{\mathbf{v}}_{s0}·\nabla \left[(1-n_0){\rho }_{s0}J\right]d{V}_0\right)$ in Equation (3) yields ${\int }_{{\Omega }_0}\nabla ·\left[(1-n_0){\rho }_{s0}J{\mathbf{v}}_{s0}\right]d{V}_0$. Substituting the resulting expression into Equation (3) yields

$${\int }_{{\Omega }_0}\left\{{\displaystyle \frac{\partial \left[(1-n_0){\rho }_{s0}J\right]}{\partial t}}+\nabla ·\left[(1-n_0){\rho }_{s0}{\mathbf{v}}_{s0}J\right]\right\}d{V}_0=0$$

(5)

Since Equation (5) holds for any problem domain ${\Omega }_0$, we can reduce it by considering the localization:

$${\displaystyle \frac{\partial \left[(1-n_0){\rho }_{s0}J\right]}{\partial t}}+\nabla ·\left[(1-n_0){\rho }_{s0}{\mathbf{v}}_{s0}J\right]=0$$

(6)

Equation (6) is the mass balance equation for the clay grain phase. Furthermore, simplifying Equation (5) by considering that only the pore water dissipation from the $dV$ causes the consolidation settlements yields

$${\int }_{{\Omega }_0}\nabla ·\left[(1-n_0){\rho }_{s0}J{\mathbf{v}}_{s0}\right]d{V}_0=0\mathrm{and}{\int }_{{\Omega }_0}{\displaystyle \frac{\partial \left[(1-n_0){\rho }_{s0}J\right]}{\partial t}}d{V}_0=0$$

(7)

Further simplifying the final expression of Equation (7) leads to

$$(1-n_0){\rho }_{s0}J=C=[1-n_0(t=0)]{\rho }_{s0}(t=0)$$

(8)

where C is independent of time t. Since this study assumed that clay grains are incompressible, we can obtain ${\rho }_{s0}={\rho }_{s0}(t=0)$ and simplify Equation (8) to

$$J={\displaystyle \frac{1-n_0(t=0)}{1-n_0}}$$

(9)

3.1.2. Mass Balance for the Pore Water Phase

Substituting $\theta =n{\rho }_w$ into Equation (1) yields

$${\displaystyle \frac{d}{dt}}\left({\int }_{\Omega }n{\rho }_{w}dV\right)+{\int }_{S}n{\rho }_w\left({\mathbf{v}}_w·{\mathbf{n}}_S\right)dS=0$$

(10)

Referring to Section 3.1.1 to simplify Equation (10) results in

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d}{dt}}\left({\int }_{\Omega }n{\rho }_{w}dV\right)+{\int }_{S}n{\rho }_w\left({\mathbf{v}}_w·{\mathbf{n}}_S\right)dS={\int }_{{\Omega }_0}\left[{\displaystyle \frac{\partial \left(n_0{\rho }_{w0}J\right)}{\partial t}}+{\mathbf{v}}_{w0}·\nabla \left(n_0{\rho }_{w0}J\right)\right]d{V}_0\hfill \\ & +{\int }_{{\Omega }_0}{n}_0{\rho }_{w0}\left(\nabla ·{\mathbf{v}}_{w0}\right)Jd{V}_0={\int }_{{\Omega }_0}\left[{\displaystyle \frac{\partial \left(n_0{\rho }_{w0}J\right)}{\partial t}}+\nabla ·\left(n_0{\rho }_{w0}{\mathbf{v}}_{w0}J\right)\right]d{V}_0=0\hfill \end{array}$$

(11)

Since Equation (11) holds for any problem domain ${\Omega }_0$, considering the localization to simplify Equation (11) yields

$${\displaystyle \frac{\partial \left(n_0{\rho }_{w0}J\right)}{\partial t}}+\nabla ·\left(n_0{\rho }_{w0}{\mathbf{v}}_{w0}J\right)=0$$

(12)

Equation (12) is the mass balance equation for the pore water phase.

3.1.3. Momentum Balance for the Clay Grain Phase

Substituting $\theta =(1-n){\rho }_s{\mathbf{v}}_s$ into Equation (1) yields

$${\displaystyle \frac{d}{dt}}\left[{\int }_{\Omega }(1-n){\rho }_s{\mathbf{v}}_{s}dV\right]+{\int }_S(1-n){\rho }_s{\mathbf{v}}_s\left({\mathbf{v}}_s·{\mathbf{n}}_S\right)dS=0$$

(13)

Similar to the derivation of Equation (3), one can simplify Equation (13) to

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d}{dt}}\left[{\int }_{\Omega }(1-n){\rho }_s{\mathbf{v}}_{s}dV\right]+{\int }_S(1-n){\rho }_s{\mathbf{v}}_s\left({\mathbf{v}}_s·{\mathbf{n}}_S\right)dS={\displaystyle \frac{d}{dt}}\left[{\int }_{{\Omega }_0}(1-n_0){\rho }_{s0}{\mathbf{v}}_{s0}Jd{V}_0\right]\hfill \\ & +{\int }_S(1-n){\rho }_s{\mathbf{v}}_s\left({\mathbf{v}}_s·{\mathbf{n}}_S\right)dS={\int }_{{\Omega }_0}{\displaystyle \frac{d\left[(1-n_0){\rho }_{s0}{\mathbf{v}}_{s0}J\right]}{dt}}d{V}_0+{\int }_S(1-n){\rho }_s{\mathbf{v}}_s\left({\mathbf{v}}_s·{\mathbf{n}}_S\right)dS\hfill \\ & ={\int }_{{\Omega }_0}{\rho }_{s0}(1-n_0)J{\displaystyle \frac{d{\mathbf{v}}_{s0}}{dt}}d{V}_0+{\int }_{{\Omega }_0}{\mathbf{v}}_{s0}{\displaystyle \frac{d\left[{\rho }_{s0}(1-n_0)J\right]}{dt}}d{V}_0+{\int }_S(1-n){\rho }_s{\mathbf{v}}_s\left({\mathbf{v}}_s·{\mathbf{n}}_S\right)dS\hfill \end{array}$$

(14)

By simplifying Equation (14) using the Gauss theorem and transforming the final term of the same equation using the coordinate transformation, we can reduce the equation to

$$\begin{array}{cc}\hfill & {\int }_{{\Omega }_0}{\rho }_{s0}(1-n_0)J{\displaystyle \frac{d{\mathbf{v}}_{s0}}{dt}}d{V}_0+{\int }_{{\Omega }_0}{\mathbf{v}}_{s0}{\displaystyle \frac{d\left[{\rho }_{s0}(1-n_0)J\right]}{dt}}d{V}_0+{\int }_S(1-n){\rho }_s{\mathbf{v}}_s\left({\mathbf{v}}_s·{\mathbf{n}}_S\right)dS\hfill \\ & ={\int }_{{\Omega }_0}{\rho }_{s0}(1-n_0)J{\displaystyle \frac{d{\mathbf{v}}_{s0}}{dt}}d{V}_0+{\int }_{{\Omega }_0}{\mathbf{v}}_{s0}{\displaystyle \frac{d\left[{\rho }_{s0}(1-n_0)J\right]}{dt}}d{V}_0+{\int }_{{\Omega }_0}(1-n_0){\rho }_{s0}{\mathbf{v}}_{s0}J\left(\nabla ·{\mathbf{v}}_{s0}\right)d{V}_0\hfill \end{array}$$

(15)

Combining the final two terms of Equation (15) yields

$$\begin{array}{cc}\hfill & {\int }_{{\Omega }_0}{\mathbf{v}}_{s0}{\displaystyle \frac{d\left[{\rho }_{s0}(1-n_0)J\right]}{dt}}d{V}_0+{\int }_{{\Omega }_0}(1-n_0){\rho }_{s0}{\mathbf{v}}_{s0}J\left(\nabla ·{\mathbf{v}}_{s0}\right)d{V}_0\hfill \\ & ={\int }_{{\Omega }_0}{\mathbf{v}}_{s0}\left\{{\displaystyle \frac{\partial \left[{\rho }_{s0}(1-n_0)J\right]}{\partial t}}+\nabla \left[{\rho }_{s0}(1-n_0)J\right]·{\mathbf{v}}_{s0}+(1-n_0){\rho }_{s0}J\left(\nabla ·{\mathbf{v}}_{s0}\right)\right\}d{V}_0\hfill \\ & ={\int }_{{\Omega }_0}{\mathbf{v}}_{s0}\left\{{\displaystyle \frac{\partial \left[{\rho }_{s0}(1-n_0)J\right]}{\partial t}}+\nabla ·\left[{\rho }_{s0}(1-n_0)J{\mathbf{v}}_{s0}\right]\right\}d{V}_0\hfill \end{array}$$

(16)

Based on Equation (6), Equation (16) is equal to 0. We then simplify Equation (13) to

$${\int }_{{\Omega }_0}{\rho }_{s0}(1-n_0)J{\displaystyle \frac{d{\mathbf{v}}_{s0}}{dt}}d{V}_0=0$$

(17)

where the term ${\displaystyle \frac{d\mathbf{v}}{dt}}$ is the acceleration field and ${\rho }_{s0}(1-n_0)$ denotes the mass of clay grains (in $Jd{V}_0$). Therefore, this equation is equal to the forces exerted on clay grains. Thus, we can define

$${\int }_{{\Omega }_0}{\rho }_{s0}(1-n_0)J{\displaystyle \frac{d{\mathbf{v}}_{s0}}{dt}}d{V}_0={\int }_{{\Omega }_0}{\mathbf{f}}_s(1-n_0)d{V}_0+{\int }_{{\Omega }_0}{\mathbf{h}}^{s}d{V}_0+{\int }_{S_0}\left({\mathit{\sigma }}_0^{\prime }·{\mathbf{n}}_{S_0}\right)d{S}_0$$

(18)

in which ${\mathbf{h}}^s$ is the seepage force vector per unit volume arising from the frictional drag of pore water, and ${\mathbf{f}}_s$ is the body force vector. This study considers that the ${\mathbf{f}}_s$ comes from the weights of clay grains. It and ${\mathit{\sigma }}_0^{\prime }$ can be further equated by

$${\mathit{\sigma }}_0^{\prime }=\left[\begin{array}{ccc}{{\sigma }^{\prime }}_{11,0}& {{\sigma }^{\prime }}_{12,0}& {{\sigma }^{\prime }}_{13,0}\\ {{\sigma }^{\prime }}_{21,0}& {{\sigma }^{\prime }}_{22,0}& {{\sigma }^{\prime }}_{23,0}\\ {{\sigma }^{\prime }}_{31,0}& {{\sigma }^{\prime }}_{32,0}& {{\sigma }^{\prime }}_{33,0}\end{array}\right]\mathsf{and}{\mathbf{f}}_s=\pm {\rho }_{s0}\mathbf{g}$$

(19)

where $\mathbf{g}={(0,0,g)}^T$. The sign ± depends upon the direction of $a_3$. If the direction of $a_3$ is opposite to the direction of the gravitational force, the sign + is adopted. Meanwhile, applying the Gauss theorem to simplify the final term of Equation (18) yields ${\int }_{S_0}\left({\mathit{\sigma }}_0^{\prime }·{\mathbf{n}}_{S_0}\right)d{S}_0={\int }_{{\Omega }_0}\left(\nabla ·{\mathit{\sigma }}_0^{\prime }\right)d{V}_0$. Substituting the resulting expression into Equation (18) and considering that the resulting integral equation holds for any problem domain ${\Omega }_0$, we can further simplify the resulting integral equation by considering localization. The result is

$${\rho }_{s0}(1-n_0)J{\displaystyle \frac{d{\mathbf{v}}_{s0}}{dt}}=\pm {\rho }_{s0}(1-n_0)\mathbf{g}+{\mathbf{h}}^s+\nabla ·{\mathit{\sigma }}_0^{\prime }$$

(20)

Equation (20) is the momentum balance equation for the clay grain phase.

3.1.4. Momentum Balance for the Pore Water Phase

Substituting $\theta =n{\rho }_w{\mathbf{v}}_s$ into Equation (1) yields

$${\displaystyle \frac{d}{dt}}\left({\int }_{\Omega }n{\rho }_w{\mathbf{v}}_{w}dV\right)+{\int }_{S}n{\rho }_w{\mathbf{v}}_w\left({\mathbf{v}}_w·{\mathbf{n}}_S\right)dS=0$$

(21)

Referring to the derivation of Equation (14) to simplify the first term of Equation (21) and applying the Gauss theorem and coordinate transform to the final term of the same equation, the resulting equation is

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d}{dt}}\left({\int }_{\Omega }n{\rho }_w{\mathbf{v}}_{w}dV\right)+{\int }_{S}n{\rho }_w{\mathbf{v}}_w\left({\mathbf{v}}_w·{\mathbf{n}}_S\right)dS={\displaystyle \frac{d}{dt}}\left({\int }_{{\Omega }_0}{n}_0{\rho }_{w0}{\mathbf{v}}_{w0}Jd{V}_0\right)\hfill \\ & +{\int }_{S}n{\rho }_w{\mathbf{v}}_w\left({\mathbf{v}}_w·{\mathbf{n}}_S\right)dS={\int }_{{\Omega }_0}{\rho }_{w0}{n}_{0}J{\displaystyle \frac{d{\mathbf{v}}_{w0}}{dt}}d{V}_0+{\int }_{{\Omega }_0}{\mathbf{v}}_{w0}{\displaystyle \frac{d\left({\rho }_{w0}{n}_{0}J\right)}{dt}}d{V}_0\hfill \\ & +{\int }_{S_0}{n}_0{\rho }_{w0}{\mathbf{v}}_{w0}J\left(\nabla ·{\mathbf{v}}_{w0}\right)d{V}_0\hfill \end{array}$$

(22)

The final two terms of Equation (22) are combined and reduced to

$$\begin{array}{cc}\hfill & {\int }_{{\Omega }_0}{\mathbf{v}}_{w0}{\displaystyle \frac{d\left({\rho }_{w0}{n}_{0}J\right)}{dt}}d{V}_0+{\int }_{{\Omega }_0}{n}_0{\rho }_{w0}{\mathbf{v}}_{w0}J\left(\nabla ·{\mathbf{v}}_{w0}\right)d{V}_0\hfill \\ & ={\int }_{{\Omega }_0}{\mathbf{v}}_{w0}\left[{\displaystyle \frac{\partial \left({\rho }_{w0}{n}_{0}J\right)}{\partial t}}+\nabla ·\left({\rho }_{w0}{n}_{0}J{\mathbf{v}}_{w0}\right)\right]d{V}_0\hfill \end{array}$$

(23)

Based on Equation (12), Equation (23) is equal to 0. Thus, we can reduce Equation (21) to

$${\int }_{{\Omega }_0}{\rho }_{w0}{n}_{0}J{\displaystyle \frac{d{\mathbf{v}}_{w0}}{dt}}d{V}_0=0$$

(24)

Similar to Equation (17), Equation (24) is equal to the forces exerted on the pore water phase. Thus [8],

$${\int }_{{\Omega }_0}{\rho }_{w0}{n}_{0}J{\displaystyle \frac{d{\mathbf{v}}_{w0}}{dt}}d{V}_0={\int }_{{\Omega }_0}{\mathbf{f}}_w{n}_{0}d{V}_0+{\int }_{{\Omega }_0}{\mathbf{h}}^{w}d{V}_0+{\int }_{S_0}\left({\mathbf{p}}_0·{\mathbf{n}}_{S_0}\right)d{S}_0$$

(25)

where $\mathbf{p}$ denotes the pore water pressure tensor, ${\mathbf{h}}^w$ is the reactive force vector per unit volume exerted by clay grains on the pore water phase as the pore water seeps through the clay, and ${\mathbf{f}}_w$ is the body force vector. The ${\mathbf{p}}_0$ and ${\mathbf{f}}_w$ are further defined by

$${\mathbf{p}}_0=\left[\begin{array}{ccc}{p}_0& 0& 0\\ 0& p_0& 0\\ 0& 0& p_0\end{array}\right]\mathsf{and}{\mathbf{f}}_w=\pm {\rho }_{w0}\mathbf{g}$$

(26)

in which setting the sign ± still depends upon the direction of $a_3$. On the other hand, applying the Gauss theorem to the final term of Equation (25) yields ${\int }_{S_0}\left({\mathbf{p}}_0·{\mathbf{n}}_{S_0}\right)d{S}_0={\int }_{{\Omega }_0}\left(\nabla ·{\mathbf{p}}_0\right)d{V}_0$. Substituting the resulting expression into Equation (25) and considering that the resulting expression holds for any problem domain ${\Omega }_0$, we can further simplify the resulting integral equation by considering localization. The result is

$${\rho }_{w0}{n}_{0}J{\displaystyle \frac{d{\mathbf{v}}_{w0}}{dt}}=\pm n_0{\rho }_{w0}\mathbf{g}+{\mathbf{h}}^w+\nabla ·{\mathbf{p}}_0$$

(27)

Equation (27) is the momentum balance equation for the pore water phase.

3.2. DGM Formulation

Summing Equations (20) and (27) results in

$${\rho }_{total}J{\displaystyle \frac{d{\mathbf{v}}_{avg}}{dt}}=\pm {\rho }_{total}\mathbf{g}+{\mathbf{h}}^w+{\mathbf{h}}^s+\nabla ·{\mathbf{p}}_0+\nabla ·{\mathit{\sigma }}_0^{\prime }$$

(28)

where ${\mathbf{v}}_{avg}={\displaystyle \frac{{\rho }_{s0}(1-n_0){\mathbf{v}}_{s0}+{\rho }_{w0}{n}_0{\mathbf{v}}_{w0}}{{\rho }_{total}}}$ denotes the average velocity field, ${\displaystyle \frac{d{\mathbf{v}}_{avg}}{dt}}$ represents the average acceleration field, and ${\rho }_{total}={\rho }_{s0}(1-n_0)+{\rho }_{w0}{n}_0$ is the total mass density. Different from the author’s thesis [7], this study does not try to combine Equations (9), (12), (20) and (27) into a governing equation. Thus, deriving a DGM solution of the current mathematical model is simpler.

Furthermore, focusing on the macro behaviors of clay grains and pore water, this study assumes ${\mathbf{h}}^w+{\mathbf{h}}^s=0$ [7] or neglects the interaction between pore water and clay grains. Simplifying Equation (28) with this consideration yields

$${\rho }_{total}J{\displaystyle \frac{d{\mathbf{v}}_{avg}}{dt}}=\pm {\rho }_{total}\mathbf{g}+\nabla ·{\mathbf{p}}_0+\nabla ·{\mathit{\sigma }}_0^{\prime }$$

(29)

A DGM solution of Equation (29) is next derived: Suppose the time t is between 0 and T. The initial and boundary conditions are

$${\displaystyle \frac{d{\mathbf{v}}_{avg}\left(t=0\right)}{dt}}=0,\hspace{1em}\mathbf{p}(t=0)={\mathbf{p}}_{ini},\hspace{1em}\mathrm{and}\hspace{1em}{\mathit{\sigma }}^{\prime }(t=0)={\mathit{\sigma }}_{ini}^{\prime }$$

(30)

$${\mathit{\sigma }}^{\prime }={\mathit{\sigma }}_d\hspace{1em}\mathrm{on}\hspace{1em}{\Gamma }_f$$

(31)

$$p=0\hspace{1em}\mathrm{on}\hspace{1em}{\Gamma }_D$$

(32)

$${\mathbf{v}}_{avg}=0\hspace{1em}\mathrm{on}\hspace{1em}{\Gamma }_F$$

(33)

$${\displaystyle \frac{\partial p_0}{\partial n_{Uj}}}=0\hspace{1em}\mathrm{on}\hspace{1em}{\Gamma }_U$$

(34)

where ${\Gamma }_f$, ${\Gamma }_D$, ${\Gamma }_F$, and ${\Gamma }_U$ are free, drained, fixed, and undrained boundaries, respectively, ${\mathbf{p}}_{ini}$ is the initial pore water pressure tensor, ${\mathit{\sigma }}_{ini}^{\prime }$ represents the initial effective stress tensor, ${\mathit{\sigma }}_d$ denotes an imposed loading, and $n_{Uj}(j=1,2,3)$ is the component of a unit vector ${\mathbf{n}}_U$ normal to the undrained boundary ${\Gamma }_U$. Note that Equations (31)–(34) do not mean that ${\Gamma }_f$, ${\Gamma }_D$, ${\Gamma }_F$, and ${\Gamma }_U$ exist separately in a particular problem domain ${\Omega }_0$. Also, the computation of ${\mathit{\sigma }}_{ini}^{\prime }$ and ${\mathbf{p}}_{ini}$ depends upon a particular problem domain ${\Omega }_0$.

Based on Equations (29)–(34), this study applied the DGM algorithm to approximate the ${\mathbf{v}}_{avg}$ using $\mathit{\alpha }(\mathbf{a},t,\varphi )$, ${\mathbf{p}}_0$ using $\mathbf{P}(\mathbf{a},t,\varphi )$, and ${\mathit{\sigma }}_0^{\prime }$ using $\mathbf{S}(\mathbf{a},t,\varphi )$ in which $\varphi$ is the neural network’s parameter. The DGM algorithm defines the loss function by (e.g., [9])

$$\begin{array}{c}Loss={∥{\rho }_{total}J{\displaystyle \frac{d\mathit{\alpha }}{dt}}-\nabla ·\mathbf{P}-\nabla ·\mathbf{S}∥}_{(0,T)\times {\Omega }_0,{\nu }_1}^2+{∥\mathit{\alpha }(t=0)∥}_{{\Omega }_0,{\nu }_2}^2\\ +{∥\mathbf{P}(t=0)-{\mathbf{p}}_{ini}∥}_{{\Omega }_0,{\nu }_2}^2+{∥{\mathit{\sigma }}^{\prime }(t=0)-{\mathit{\sigma }}_{ini}^{\prime }∥}_{{\Omega }_0,{\nu }_2}^2\\ +{∥\mathbf{P}∥}_{(0,T)\times {\Gamma }_D,{\nu }_3}^2+{∥\mathbf{S}-{\mathit{\sigma }}_d∥}_{(0,T)\times {\Gamma }_f,{\nu }_4}^2+{∥{\displaystyle \frac{\partial P_{ij}}{\partial n_{Uj}}}∥}_{(0,T)\times {\Gamma }_U,{\nu }_5}^2\end{array}$$

(35)

where ${\nu }_1={\displaystyle \frac{1}{\left|\Omega \right|}}$, ${\nu }_2={\displaystyle \frac{1}{T}}$, ${\nu }_3={\displaystyle \frac{1}{\left|{\Gamma }_D\right|}}$, ${\nu }_4={\displaystyle \frac{1}{\left|{\Gamma }_f\right|}}$, ${\nu }_5={\displaystyle \frac{1}{\left|{\Gamma }_U\right|}}$, denotes the size, $P_{ij}(i,j=1,2,3)$ is the component of the $\mathbf{P}$ tensor, the symbol represents the $L^2$ norm function in which $Loss$ measures how well the functions $\mathit{\alpha }$, $\mathbf{P}$, and $\mathbf{S}$ satisfy Equations (29)–(34). If we can obtain $Loss=0$, the $\mathit{\alpha }$, $\mathbf{P}$, and $\mathbf{S}$ are the solutions of Equation (29).

The goal of defining Equation (35) is to find the $\varphi$ parameter with which the corresponding $\mathit{\alpha }(\mathbf{a},t,\varphi )$, $\mathbf{P}(\mathbf{a},t,\varphi )$, and $\mathbf{S}(\mathbf{a},t,\varphi )$ minimize the $Loss$ function. Then, they are solutions of the ${\mathbf{v}}_{avg}$, $\mathbf{p}$, and ${\mathit{\sigma }}^{\prime }$. The best $\varphi$ value is estimated using an existing optimization method (for example, the Adam optimizer). Discretizing the problem domain $\Omega$ into some elements is unnecessary.

Algorithm 1 [13] illustrates the proposed steps of implementing the DGM algorithm and three post-processing steps (6–8 th steps) in which k denotes an iteration number, E denotes an error, $\beta$ represents the learning rate, and $\mathbf{C}$ is the compliance matrix, R denotes the void ratio-effective stress relationship, and $\mathit{ϵ}$ is the strain tensor. The sixth step provides the void ratio e. Optionally, calculating the strain tensor $\mathit{ϵ}$ may be implemented. The seventh step outputs the numerical results for updating the Jacobian J and ${\rho }_{total}$. Since the initial displacement and velocity fields are zero, the eighth step is employed to update the coordinates $x_j(j=1,2,3)$. Updating the coordinates $x_j$ also provides the consolidation settlements. Note that this study does not calculate consolidation settlements from the strain tensor $\mathit{ϵ}$ since collecting undisturbed samples of soft or very soft clay to construct its stress-strain and void ratio–stress relationships is difficult.

The learning rate ${\beta }_k$ in Algorithm 1 decreases with the iteration number k. The calculation ${\nabla }_{\varphi }E$ is an unbiased estimation of ${\nabla }_{\varphi }\left(Loss\right)$:

$$\mathbb{E}\left[{\nabla }_{\varphi }E(·|{\varphi }_k)\right]={\nabla }_{\varphi }\left[Loss\left(·:{\varphi }_k\right)\right]$$

(36)

where $\mathbb{E}$ denotes the mathematical expectation. Under technical conditions, the $\varphi$ parameter will converge to a critical point of the $Loss$ function as $k\to \infty$:

$$\underset{k\to \infty }{lim}∥{\nabla }_{\varphi }Loss\left(·:{\varphi }_k\right)∥=0$$

(37)

Algorithm 1 DGM algorithm

Input: A problem domain $\Omega$, a time interval (0, T), initial and boundary conditions, the neural network’s parameter $\varphi$, a learning rate $\beta$, a maximum iteration number, and a compliance matrix $\mathbf{C}$ or a void ratio-effective stress relationship R.

Output: Solutions of the ${\mathbf{v}}_{avg}$, $\mathbf{p}$ and ${\mathit{\sigma }}^{\prime }$. 1: Generate random points from $\Omega \times [0,T]$ and existing boundaries 2: while a maximum iteration number is not exceeded do 3:     Calculate the ${\mathit{\sigma }}_{ini}^{\prime }$ and ${\mathbf{p}}_{ini}$ according to the initial problem domain $\Omega$. 4:     Calculate: $\begin{array}{c}E\leftarrow {\left[{\rho }_{total}J{\displaystyle \frac{d\mathit{\alpha }(\mathbf{a},t,{\varphi }_k)}{dt}}-\nabla ·\mathbf{P}(\mathbf{a},t,{\varphi }_k)-\nabla ·\mathbf{S}(\mathbf{a},t,{\varphi }_k)\right]}_{\Omega }^2+{\left[\mathit{\alpha }(t=0,{\varphi }_k)\right]}_{\Omega }^2\\ +{\left[\mathbf{P}(t=0,{\varphi }_k)-{\mathbf{p}}_{ini}\right]}_{\Omega }^2+{\left[{\mathit{\sigma }}^{\prime }(t=0,{\varphi }_k)-{\mathit{\sigma }}_{ini}^{\prime }\right]}_{\Omega }^2+{\left[\mathbf{P}(\mathbf{a},t,{\varphi }_k)\right]}_{{\Gamma }_D}^2\\ +{\left[\mathbf{S}(\mathbf{a},t,{\varphi }_k)-{\mathit{\sigma }}_d\right]}_{{\Gamma }_f}^2+{\left[{\displaystyle \frac{\partial P_{ij}}{\partial n_{Uj}}}\right]}_{{\Gamma }_U}^2\end{array}$ 5:     Update ${\varphi }_{k+1}\leftarrow {\varphi }_k-{\beta }_k{\nabla }_{\varphi }E$. 6:     Calculate $e\leftarrow R\left({\mathit{\sigma }}^{\prime }\right)$. If available, compute $\mathit{ϵ}\leftarrow \mathbf{C}{\mathit{\sigma }}^{\prime }$. 7:     Update J and ${\rho }_{total}$. 8:     Update $\mathbf{x}=\mathbf{x}+\int {\mathbf{v}}_{avg}dt$. 9:     $k\leftarrow (k+1)$. 10: end while

Figure 1 (e.g., [12,13]) shows an example of the neural network’s architecture for implementing the DGM. It approximates the ${\mathbf{v}}_{avg}$ by $\mathit{\alpha }(\mathbf{a},t,\varphi )$, $\mathbf{p}$ by $\mathbf{P}(\mathbf{a},t,\varphi )$, and $\mathit{\sigma }$ by $\mathbf{S}(\mathbf{a},t,\varphi )$ in which $\varphi$ is the neural network’s parameter. In mathematical expressions, the deep neural network contains three types of layers:

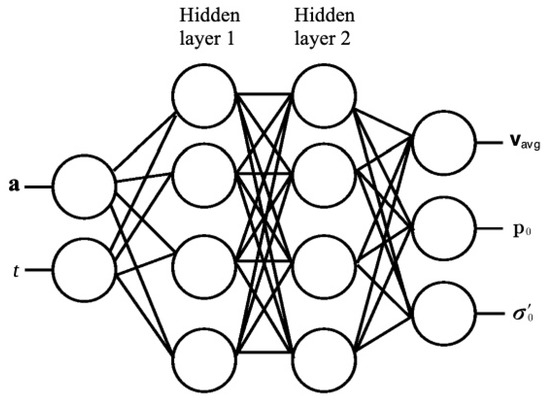
Figure 1. An example of the neural network’s architecture for implementing the DGM (e.g., [9]).

• Input layer: The neural network calculates

  $${\mathbf{Z}}^{\left(0\right)}=\psi \left({\mathbf{W}}_0\mathbf{X}+{\mathbf{b}}_0\right)$$

  (38)

  in which $\mathbf{X}={\left(\mathbf{a},t\right)}^T$, $\mathbf{Z}$ is the intermediate hidden feature vector, $\psi$ represents the activation function, ${\mathbf{W}}_0$ denotes the input weight matrix, and ${\mathbf{b}}_0$ represents the input bias vector.
• Hidden layer: Suppose L hidden layers are generated. For each hidden layer, the neural network computes

  $$\begin{array}{c}{\mathbf{F}}^{\left(k\right)}=\psi \left[{\mathbf{W}}_f^{\left(k\right)}{\mathbf{Z}}^{(k-1)}+{\mathbf{b}}_f^{\left(k\right)}\right]\\ {\mathbf{r}}^{\left(k\right)}=\psi \left[{\mathbf{W}}_r^{\left(k\right)}{\mathbf{Z}}^{(k-1)}+{{\mathbf{b}}_r}^{\left(k\right)}\right]\\ {\tilde{\mathbf{Z}}}^{\left(k\right)}=tanh\left\{{\mathbf{W}}_h^{\left(k\right)}\left[{\mathbf{r}}^{\left(k\right)}\odot {\mathbf{Z}}^{(k-1)}\right]+{\mathbf{b}}_h^{\left(k\right)}\right\}\\ {\mathbf{Z}}^{\left(k\right)}=\left[1-{\mathbf{F}}^{\left(k\right)}\right]\odot {\mathbf{Z}}^{(k-1)}+{\mathbf{F}}^{\left(k\right)}\odot {\tilde{\mathbf{Z}}}^{\left(k\right)}\end{array}$$

  (39)

  where $k=1,2\dots ,L$ denotes the L-th hidden layer, $\mathbf{F}$ is the gate vector, the subscripts _f, _r, and _h denote the update gate, reset gate, and candidate hidden gate, respectively, $\mathbf{r}$ represents the reset gate. $\tilde{\mathbf{Z}}$ represents the candidate hidden state, ⊙ is the Hadamard product, and tanh is the hyperbolic tangent function. This tanh function serves as a nonlinear activation function.
• Output layer:

  $$\mathbf{U}={\mathbf{W}}_{out}{\mathbf{Z}}^{\left(L\right)}+{\mathbf{b}}_{out}$$

  (40)

  where $\mathbf{U}={\left({\mathbf{v}}_{avg},\mathbf{p},{\mathit{\sigma }}^{\prime }\right)}^T$ represents the output of the neural network, ${\mathbf{W}}_{out}$ is the weight matrix of the output layer, and ${\mathbf{b}}_{out}$ is the bias vector of the output layer.

3.3. Implementation of the DGM

This study uses PyTorch 2.8.0 in coding a Python program for implementing Algorithm 1. It has an automatic differentiation function that can easily output the derivatives with respect to independent variables. Moreover, back propagation is adopted to train a deep neural network. Besides, optimizing the training process adopts the Adam optimizer based on the stochastic gradient descent method. Furthermore, an Apple Mac Pro with 8 MB of RAM, an M2 CPU, and 16 GPUs was employed to generate numerical results.

4. Application

Considering the acquisition of experimental data, this study introduces the recorded consolidation settlements of the phosphatic waste clay [15] and Osaka Bay [16] mud to test the proposed mathematical model.

4.1. Phosphatic Waste Clay

The phosphate waste clay is the byproduct of the beneficiation process of the phosphate ore. This phosphate ore occurs in a gravely, clayey sand and contains ${\displaystyle \frac{1}{3}}$ phosphate, ${\displaystyle \frac{1}{3}}$ granular materials (sand), and ${\displaystyle \frac{1}{3}}$ clays. Merely the phosphate is collected as the primary source of phosphorus in inorganic fertilizers. After extracting the phosphate, the phosphate waste clay is pumped into large retention ponds and allowed to consolidate without any imposed loading. For designing the storage capacity of the retention ponds, we must predict well the consolidation settlements of the phosphate waste clay caused by its self-weight.

The phosphate waste clay has a liquid limit between 100 and 200, a plastic index between 70 and 150, and a specific yield $G_s$ equal to 2.71 [15]. Some previous studies have constructed empirical relationships between the void ratio and effective stress. Equation (41) provides an example [17]:

$$e=\left(e_b-e_{\infty }\right)exp\left[-\lambda {\sigma }_{33}^{\prime }\left({\mathrm{kg}/\mathrm{cm}}^2\right)\right]+e_{\infty }$$

(41)

where $e_b$ and $e_{\infty }$ are the anticipated void ratios before and after the consolidation process, and $\lambda$ is an empirical parameter. This word, ‘anticipated’, denotes the difficulty of measuring the void ratio within the whole phosphate waste clay layer.

Testing the performance of the current mathematical model is through the results of a field test [17]. In this field test, a retention pond settled due to the self-weight of poured phosphate waste clay. Cargill [3] derived a one-dimensional mathematical model to predict the consolidation settlements. Instead, this study applied the two-dimensional version of the proposed mathematical model to predict the consolidation settlements and compare the measured results. The initial problem domain is $0\le a_j\le H$ ($j=1,3$) in which H is the depth of the retention pond, the direction of $a_3$ is identical to the direction of the gravitational force, and the $a_1$ is from right to left. Equation (35) is employed to fit the ${\mathbf{v}}_{avg}$, $\mathbf{p}$, and ${\mathit{\sigma }}^{\prime }$ in this problem domain. If the physics is under-determined, Equation (35) fits the ${\mathbf{v}}_{avg}$, $\mathbf{p}$, and ${\mathit{\sigma }}^{\prime }$, constrained by sampling/regularization rather than physics. A small figure inside the subsequent Figure 2 also illustrates the initial problem domain. The two-dimensional version of Equation (29) is the governing equation in the subsection:

$$\begin{array}{c}{\rho }_{total}J{\displaystyle \frac{d{v}_{avg,1}}{dt}}={\displaystyle \frac{\partial p_0}{\partial a_1}}+{\displaystyle \frac{\partial {\sigma }_{11,0}^{\prime }}{\partial a_1}}+{\displaystyle \frac{\partial {\sigma }_{13,0}^{\prime }}{\partial a_3}}\\ {\rho }_{total}J{\displaystyle \frac{d{v}_{avg,3}}{dt}}=-{\rho }_{total}g+{\displaystyle \frac{\partial p_0}{\partial a_3}}+{\displaystyle \frac{\partial {\sigma }_{13,0}^{\prime }}{\partial a_1}}+{\displaystyle \frac{\partial {\sigma }_{33,0}^{\prime }}{\partial a_3}}\end{array}$$

(42)

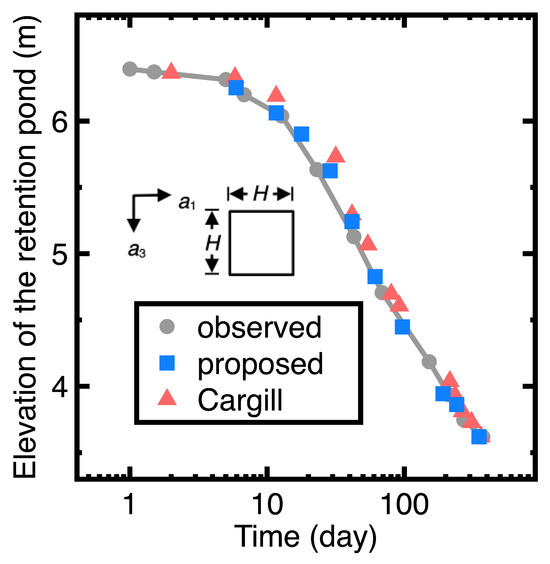
Figure 2. Comparison of the predicted and observed elevations of the retention pond [17].

The initial and boundary conditions are

$$\begin{array}{c}{\mathbf{v}}_{avg}\left(t=0\right)=0,p(t=0)={\gamma }_w{a}_3,\\ {\sigma }_{11}^{\prime }(t=0)={\sigma }_{13}^{\prime }(t=0)=0,\\ {\sigma }_{33}^{\prime }(t=0)={\displaystyle \frac{{\gamma }_w(G_s-1)a_3}{1+e(t=0)}},\\ {\mathit{\sigma }}^{\prime }(a_3=0)=p(a_3=0)=0\end{array}$$

(43)

where ${\gamma }_w$ is the unit weight of pore water. Equation (43) means that $a_3=0$ is a free boundary and also a drained one. Moreover, the previous study [17] provided the following data:

$$T=633 \mathrm{days},\hspace{1em}\lambda =3.53\hspace{1em}H=6.33\mathrm{m},\hspace{1em}{e}_b=6.936,\hspace{1em}\mathrm{and}\hspace{1em}{e}_{\infty }=3.64$$

(44)

in which the high ratio $e_b$ value implies that the phosphate waste clay layer is very soft. Meanwhile, training a deep neural network uses the Adam optimizer, learning rate $\beta$ equal to ${10}^{-3}$, and ${10}^5$ epochs. This deep neural network has three hidden layers, and each hidden layer has 128 neurons. Discretizing the problem domain ${\Omega }_0$ and ${\Gamma }_f$ uses $2^{22}$ random interior nodes and $2^9$ random boundary nodes.

After subtracting predicted consolidation settlements from the elevation of the retention pond, Figure 2 compares the remaining elevation. Figure 3a–d selectively show the predicted ${\sigma }_{11,0}^{\prime }$, ${\sigma }_{33,0}^{\prime }$, ${\sigma }_{13,0}^{\prime }$, and $p_0$ at the time t = 30 days. The unit of predicted ${\sigma }_{11,0}^{\prime }$, ${\sigma }_{33,0}^{\prime }$, ${\sigma }_{13,0}^{\prime }$, and $p_0$ is kPa. Creating the data for plotting Figure 2 and Figure 3a–d takes the GPU time = 1546.87 s.

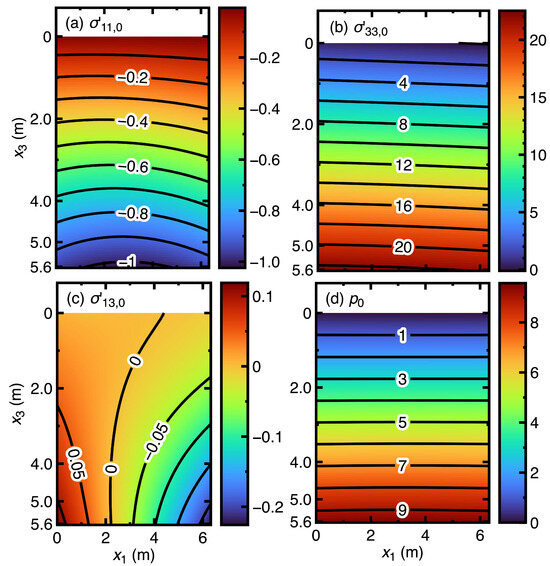
Figure 3. Predicted ${\sigma }_{11,0}^{\prime }$, ${\sigma }_{33,0}^{\prime }$, ${\sigma }_{13,0}^{\prime }$, and $p_0$ of a phosphate waste layer consolidated by its self-weight at the time t = 30 days (${\sigma }_{11,0}^{\prime }$, ${\sigma }_{33,0}^{\prime }$, ${\sigma }_{13,0}^{\prime }$ in kPa).

Figure 2 shows the necessity of developing a general mathematical model for studying a finite strain consolidation process. Considering the horizontal pore water dissipation, the current mathematical model provides more accurate predicted elevations of the retention pond, especially during 10–100 days. The corresponding maximum error $\left(={\displaystyle \frac{\left|\mathrm{predicted}\mathrm{value}-\mathrm{true}\mathrm{value}\right|}{\mathrm{true}\mathrm{value}}}\right)$ is about 2.3%, whereas the previous one-dimensional model [17] outputs the maximum error about 4.2%. Figure 3a,b show that the ${\sigma }_{11,0}^{\prime }$ and ${\sigma }_{33,0}^{\prime }$ vary symmetrically to two skewed vertical axes. Besides, Figure 3c demonstrates that a nonuniform ${\sigma }_{13,0}^{\prime }$ exerts on the retention pond. It is impossible to use a one-dimensional mathematical model to output variations of the ${\sigma }_{11,0}^{\prime }$, ${\sigma }_{33,0}^{\prime }$, and ${\sigma }_{13,0}^{\prime }$ shown in Figure 3a–c. Meanwhile, Figure 3d demonstrates that the pore water pressure $p_0$ varies uniformly across the depth of the retention pond.

Figure 4 demonstrates the convergence of the $Loss$ value with respect to the number of epochs. This figure indicates that the $Loss$ value decreases to a low value after running Algorithm 1 sufficiently.

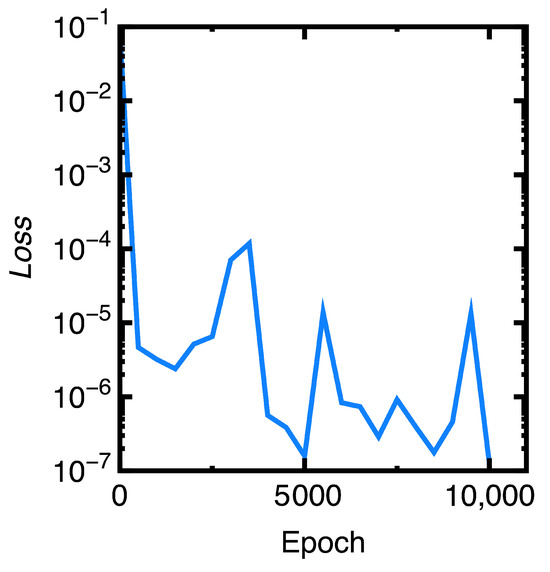
Figure 4. Convergence of the $Loss$ value in predicting consolidation settlements of a phosphate waste clay layer.

If we desire the $Loss$ values below ${10}^{-4}$, Figure 4 indicates that we can adopt merely 4000 to 5000 epochs to generate such predictions. However, it may be interesting to study how to investigate the variation of $Loss$ values with respect to the learning rate $\beta$ and the number of interior or boundary nodes.

4.2. Osaka Bay Mud

Since Japan has limited land and a dense population, it has no choice but to build some offshore public facilities. Therefore, some published studies (e.g., [16]) investigated the consolidation behaviors of offshore clay layers near big cities such as Tokyo and Osaka. This study uses the results of a model test [16] whose goal is to monitor the consolidation process induced by the self-weight of an Osaka Bay mud layer to test the current mathematical model.

The previous study [16] reported that Osaka Bay mud has a liquid limit equal to 102.8, a plastic index equal to 45.8, and a specific yield $G_s$ equal to 2.59. Another published study [18] provided an empirical relationship between the void ratio and vertical effective stress ${\sigma }_{33}^{\prime }$:

$$e=1.35-0.45log\left({\displaystyle \frac{{{\sigma }^{\prime }}_{33}}{25\mathrm{kPa}}}\right)$$

(45)

Similar to Section 4.1, Equation (42) is still the governing equation for predicting consolidation settlements of the Osaka Bay mud layer, with the initial problem domain set equal to $0\le a_j\le H$ ($j=1,3$), where H is the thickness of the Osaka Bay mud layer. The direction of $a_3$ is identical to the direction of the gravitational force, whereas the direction of $a_1$ is from left to right. Equation (35) is employed to fit the ${\mathbf{v}}_{avg}$, $\mathbf{p}$, and ${\mathit{\sigma }}^{\prime }$ in this problem domain. If the physics is under-determined, Equation (35) fits the ${\mathbf{v}}_{avg}$, $\mathbf{p}$, and ${\mathit{\sigma }}^{\prime }$ constrained by sampling/regularization rather than physics. The small figure inside the subsequent Figure 5 further illustrates this problem domain ${\Omega }_0$. The initial and boundary conditions are

$$\begin{array}{c}{\mathbf{v}}_{avg}\left(t=0\right)=0,p(t=0)={\gamma }_w{a}_3{\sigma }_{33}^{\prime }(t=0)={\displaystyle \frac{{\gamma }_w(G_s-1)a_3}{1+e(t=0)}}\\ {\sigma }_{11}^{\prime }(t=0)={\sigma }_{13}^{\prime }(t=0)=0\\ {\mathit{\sigma }}^{\prime }(a_3=0)=0,p(a_3=0)=0\\ {\displaystyle \frac{\partial p\left(a_1=0\right)}{\partial a_1}}={\displaystyle \frac{\partial p\left(a_1=H\right)}{\partial a_1}}=v_{avg,1}\left(a_1=0\right)=v_{avg,1}\left(a_1=H\right)=0\\ {\displaystyle \frac{\partial p\left(a_3=H\right)}{\partial a_3}}=v_{avg,3}\left(a_3=H\right)=0\end{array}$$

(46)

where $a_1=0$ is a fixed boundary and also an undrained one, $a_3=H$ is a fixed boundary and also an undrained one. Other necessary data are [16]:

$$T=112.5\mathrm{days},\hspace{1em}H=80\mathrm{cm},\hspace{1em}e(t=0)=7.849$$

(47)

in which the initial void ratio $e(t=0)$ indicates that the Osaka mud layer is softer than the phosphate waste clay layer in Section 4.1. Meanwhile, training a deep neural network uses the Adam optimizer, a learning rate $\beta$ equal to ${10}^{-3}$, and ${10}^5$ epochs. This deep neural network has three hidden layers, and each hidden layer has 128 neurons. Discretizing the problem domain ${\Omega }_0$ and ${\Gamma }_f$ uses $2^{22}$ random interior nodes and $2^9$ random boundary nodes. Figure 5 compares the predicted and measured vertical settlements. Figure 6a–d selectively show variations of the predicted ${\sigma }_{11,0}^{\prime }$, ${\sigma }_{33,0}^{\prime }$, ${\sigma }_{13,0}^{\prime }$, and $p_0$ at the time t = $1.55\times {10}^4$ min. The unit of the ${\sigma }_{11,0}^{\prime }$, ${\sigma }_{33,0}^{\prime }$, ${\sigma }_{13,0}^{\prime }$, and $p_0$ is kPa. Creating the data for plotting Figure 2 and Figure 3a–d takes the GPU time = 1299.66 s.

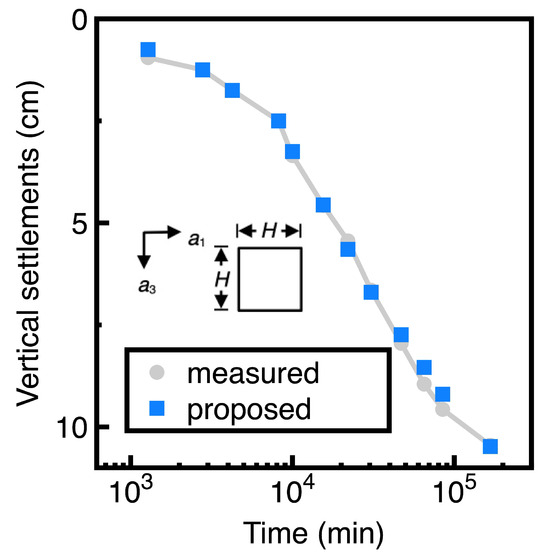
Figure 5. Comparison of predicted and measured vertical settlements of an Osaka Bay mud layer at the time $t=1.55\times {10}^4$ min [16].

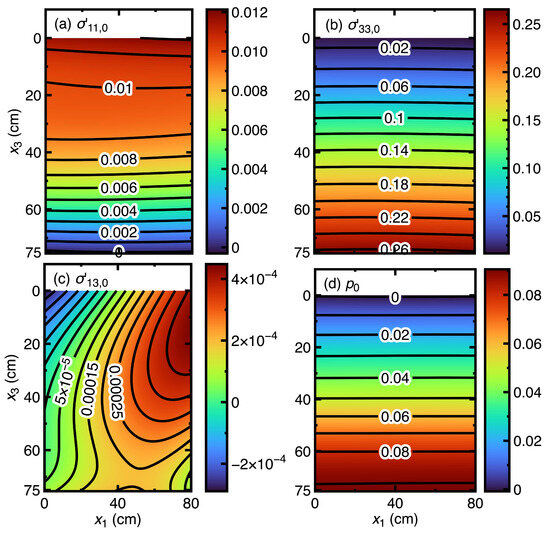
Figure 6. Predicted ${\sigma }_{11,0}^{\prime }$, ${\sigma }_{33,0}^{\prime }$, ${\sigma }_{13,0}^{\prime }$, and $p_0$ of an Osaka Bay mud layer consolidated by its self-weights at the time $t=1.55\times {10}^4$ min (${\sigma }_{11,0}^{\prime }$, ${\sigma }_{33,0}^{\prime }$, ${\sigma }_{13,0}^{\prime }$ in kPa).

Figure 5 indicates that the current mathematical model provides accurate predictions of vertical settlements. Further inspection of the data used to plot this figure finds that the maximum error is below 5%. Although the Osaka Bay mud layer in this section is thinner than the phosphate waste clay layer in Section 4.1, Figure 6a still shows that nonuniform ${\sigma }_{11,0}^{\prime }$ imposes the Osaka Bay mud layer. Larger stresses ${\sigma }_{11,0}^{\prime }$ are imposed on the middle part of the Osaka Bay mud layer. Similarly, Figure 6c demonstrates that the shear stress ${\sigma }_{13,0}^{\prime }$ varies nonuniformly. In contrast, Figure 6b,d shows that variations of the ${\sigma }_{33,0}^{\prime }$ and $p_0$ are uniform.

Figure 7 visualizes the convergence of the $Loss$ value with respect to the number of epochs. Similar to Section 4.1, if the desired $Loss$ value is below ${10}^{-4}$, this figure shows that we can adopt merely 2000 epochs to obtain such $Loss$ values. Convergence of the $Loss$ value is even faster in this section than in Section 4.1, although more complex boundary conditions are in this section.

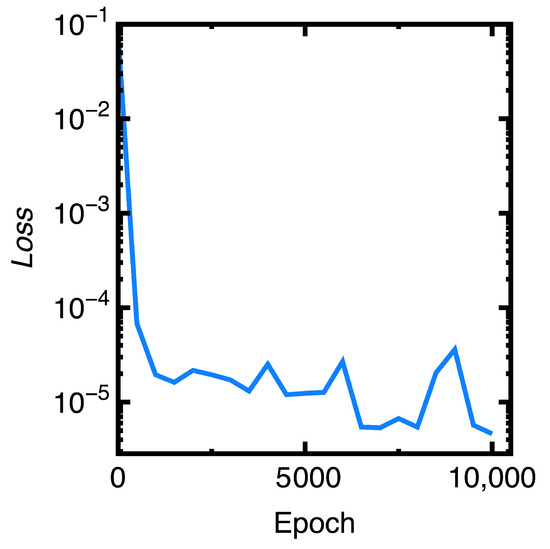
Figure 7. Convergence of the $Loss$ value in predicting consolidation settlements of an Osaka Bay mud layer.

4.3. Ablation Study

In Section 3.2, Equation (32) defines the $Loss$ value. Several parameters can affect its convergence. Compared with the error analysis in the application of other numerical methods (for example, the finite element method) to solve a partial differential equation, this study chooses to inspect the $Loss$ value with respect to different learning rates $\beta$ and numbers of interior and boundary nodes. Obviously, increasing the number of hidden layers or neurons can provide lower $Loss$ values. Discussing the influence of the number of hidden layers or neurons on the $Loss$ value cannot deliver new results.

Figure 8a,b compare the $Loss$ values with respect to the learning rates $\beta ={10}^{-2}$ and ${10}^{-4}$. Except for the learning rate $\beta$, creating Figure 8a uses the required data or settings for plotting Figure 2, Figure 3a–d and Figure 4, whereas generating Figure 8b employs the required data or settings for drawing Figure 5, Figure 6a–d and Figure 7.

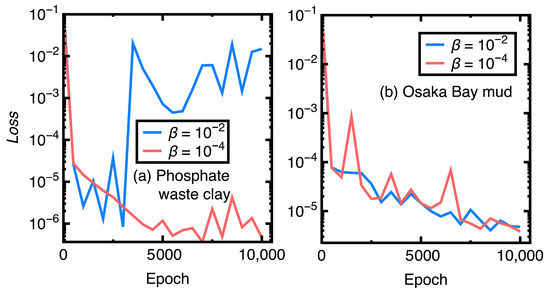
Figure 8. Comparison of the $Loss$ values with respect to different learning rates $\beta$: (a) the phosphate waste clay, (b) Osaka Bay mud.

Observing Figure 8a,b, one may find that training the deep neural network using a faster learning rate $\beta ={10}^{-2}$ is not appropriate. The corresponding $Loss$ value does not converge to an acceptable value (below ${10}^{-4}$) in Figure 8a. In contrast, the $Loss$ value is below ${10}^{-4}$ when training the deep neural network for over 4000 to 5000 epochs with a learning rate $\beta ={10}^{-4}$.

Figure 9a,b compare the $Loss$ values versus different numbers of interior and boundary nodes. Except for the number of interior or boundary nodes, editing Figure 9a uses the data and settings required to prepare Section 4.1 while creating Figure 9b is based on the necessary data and settings employed to generate Figure 5, Figure 6a–d and Figure 7. For keeping a particular nodal spacing, the total number of interior and boundary nodes is simultaneously increased in creating Figure 9a,b.

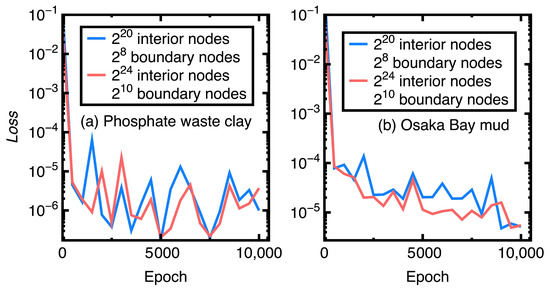
Figure 9. Comparison of the $Loss$ values with respect to different numbers of interior and boundary nodes: (a) phosphate waste clay and (b) Osaka Bay mud.

Increasing the total number of interior and boundary nodes means a finer discretization of the problem domain. Since this study creates random interior and boundary nodes, Figure 9a,b indicate that generating a finer discretization of the problem domain does not apparently improve the $Loss$ value. These two figures may show a distinguishing characteristic that does not exist in other existing numerical methods (for example, the finite element method). A finer discretization of the problem domain can apparently improve the accuracy of numerical results.

5. Discussion

Section 4.1 and Section 4.2 reveal four difficulties of developing a mathematical model for an engineering problem; however, this study resolves these difficulties to a certain extent:

• The first difficulty is the challenge of balancing the number of assumptions and the simplicity of the corresponding governing equations. This study eliminates the assumption that a clay layer consolidates only in the vertical direction in modeling a finite strain consolidation process; however, the current governing equation (Equation (29)) is not complex.
• The second difficulty is the challenge of choosing a suitable numerical method for solving a real-world problem. For this study, two real-world problems are ill-posed; nevertheless, boundary conditions are prerequisites for implementing existing numerical methods (for example, the finite element method). Section 4.1 provides an example. Probably due to the lack of field measurements, some boundary conditions were unavailable in the previous study [17]. However, the DGM can resolve this difficulty since its goal is to minimize the $Loss$ value at random nodes.
• The third difficulty arises from the fact that a finite strain consolidation problem is usually ill-posed. For example, limited boundary conditions are available, or the number of unknowns exceeds the number of equations. The DGM helps resolve an ill-posed problem. It fits a family of fields constrained by sampling/regularization rather than physics if the physics is under-determined. In Section 4.1 and Section 4.2, two governing equations are available, but six unknowns (pore water pressure, two average velocity components, and three effective stress components) exist. If this study does not adopt the DGM, modifying the problem to be well-posed must be implemented using available material properties (for example, a void ratio–stress relationship). The author’s Ph.D. thesis provided an example in which the void ratio is the unknown of a single and complex governing equation.
• The fourth difficulty is the non-homogeneity of clay’s properties. This difficulty represents the limitation of this study. Natural clay’s properties are non-homogeneous. Although we can create a particular probability model to regress the distribution of a clay’s property, there must be enough clay samples to provide accurate regression points. However, gathering clay samples of a natural soft clay layer is not easy. Probably due to this reason, it is unavoidable that the accuracy of predicted consolidation settlements is limited.

Meanwhile, Section 4.3 demonstrates that the DGM may be a promising numerical method for studying engineering problems. Even in a finite-strain engineering problem, we only need to adjust the learning rate $\beta$ in implementing a particular deep neural network.

6. Conclusions and Concluding Remarks

This study develops a mathematical model for describing a generalized finite strain consolidation process and its DGM solution. Developing this mathematical model adopts the Reynolds transport theorem to describe mass and momentum balances for clay grain and pore water phases. The governing equation is the sum of the resulting mass and momentum balance equations. Applying the DGM to train a deep neural network to minimize a loss function defined using the resulting governing equation, available initial, and boundary conditions, is next implemented. Two real-world problems show that the current mathematical model outperforms previous one-dimensional models in predicting the consolidation settlements caused by the self-weights of two natural soft clay layers. Besides, an additional ablation study finds that the learning rate has an apparent effect on the value of the loss function.

Based on Section 4.1, Section 4.2 and Section 4.3, the conclusions of this study are

• Deriving the current mathematical model advances the modeling of a finite-strain engineering problem. The current governing equation is simple but adapts to the changes in the problem domain. Based on this, we can make more accurate predictions about settlements.
• The DGM helps resolve an ill-posed problem in which the number of unknowns exceeds the number of equations, or limited boundary conditions are available. If the physics is under-determined, it fits a family of fields constrained by sampling/regularization rather than physics.
• To obtain the desired accuracy of numerical results provided by the DGM, adopting a lower learning rate in training a deep neural network is preferred.

Furthermore, the limitation of this study is the non-homogeneity of clay properties. Since implementing the DGM uses random interior and boundary nodes, constructing particular probability models to regress the distributions of clay properties and combining the resulting probability model with a DGM solution may be the main interest of future research.