A Parametric Method for Proving Some Analytic Inequalities
Abstract
1. Introduction
2. On a Sign of Mixed Trigonometric Polynomial Functions
2.1. A Positivity of MTP Functions
2.2. Isolation Methods
2.2.1. A Method for Isolating Zeros of an MTP Function
- 1.
- f has a constant sign on and on under the condition that ;
- 2.
- has a constant sign on ;
2.2.2. A Method for Isolating Extrema of an MTP Function
- 1.
- has a constant sign on and on under the condition that ;
- 2.
- has a constant sign on ;
3. On the Parametric Method
- (a)
- and for each , , ;
- (b)
- the functions are continuous with respect to for each ;
- 1.
- the family of functions is increasingly (decreasingly) stratified on the interval ;
- 2.
- there exists a continuous monotonically increasing function that satisfies (4);
- 3.
- there exist limits and in such that .
- (i)
- If , then
- (ii)
- If , then the equality has a unique solution and it holds thatand
- (iii)
- If , then
- 1.
- the family of functions is increasingly (decreasingly) stratified on the interval ;
- 2.
- there exists a continuous monotonically decreasing function that satisfies (4);
- 3.
- there exist limits and in such that .
- (i)
- If , then
- (ii)
- If , then the equality has a unique solution and it holds thatand
- (iii)
- If , then
- 1.
- the family of functions is increasingly (decreasingly) stratified on the interval ;
- 2.
- there exists a continuous function that satisfies (4) and that is monotonically decreasing on and monotonically increasing on for some ;
- 3.
- there exist limits and in such that for:it holds that .
- (i)
- If , then
- (ii)
- If , then the equality has exactly two solutions such that , and it holds thatand
- (iii)
- If , then the equality has a unique solution .If , thenandIf , thenand
- (iv)
- If , then
4. Applications
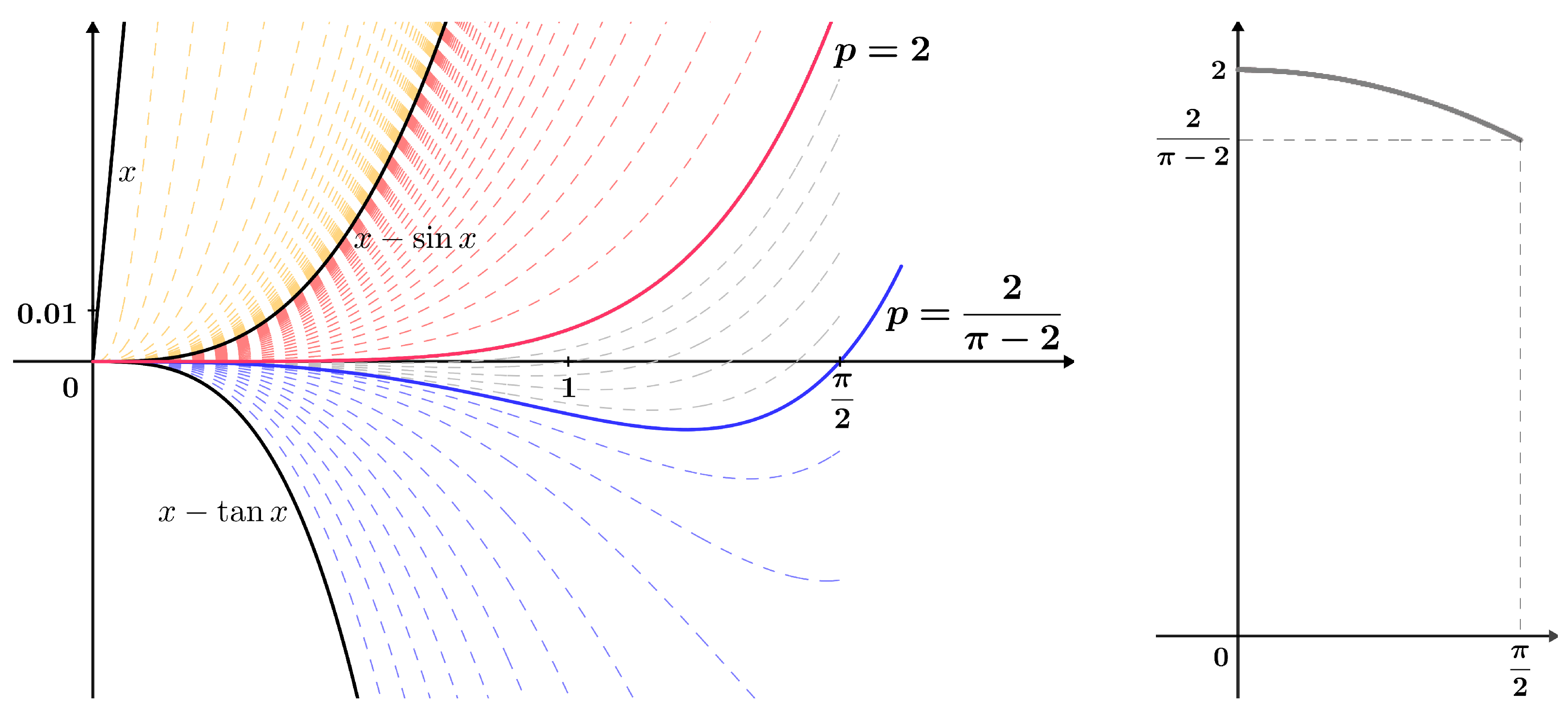
4.1. Application 1 (Cusa–Huygens Inequality)
- (i)
- If , then
- (ii)
- If , then the equality
- (iii)
- If , then
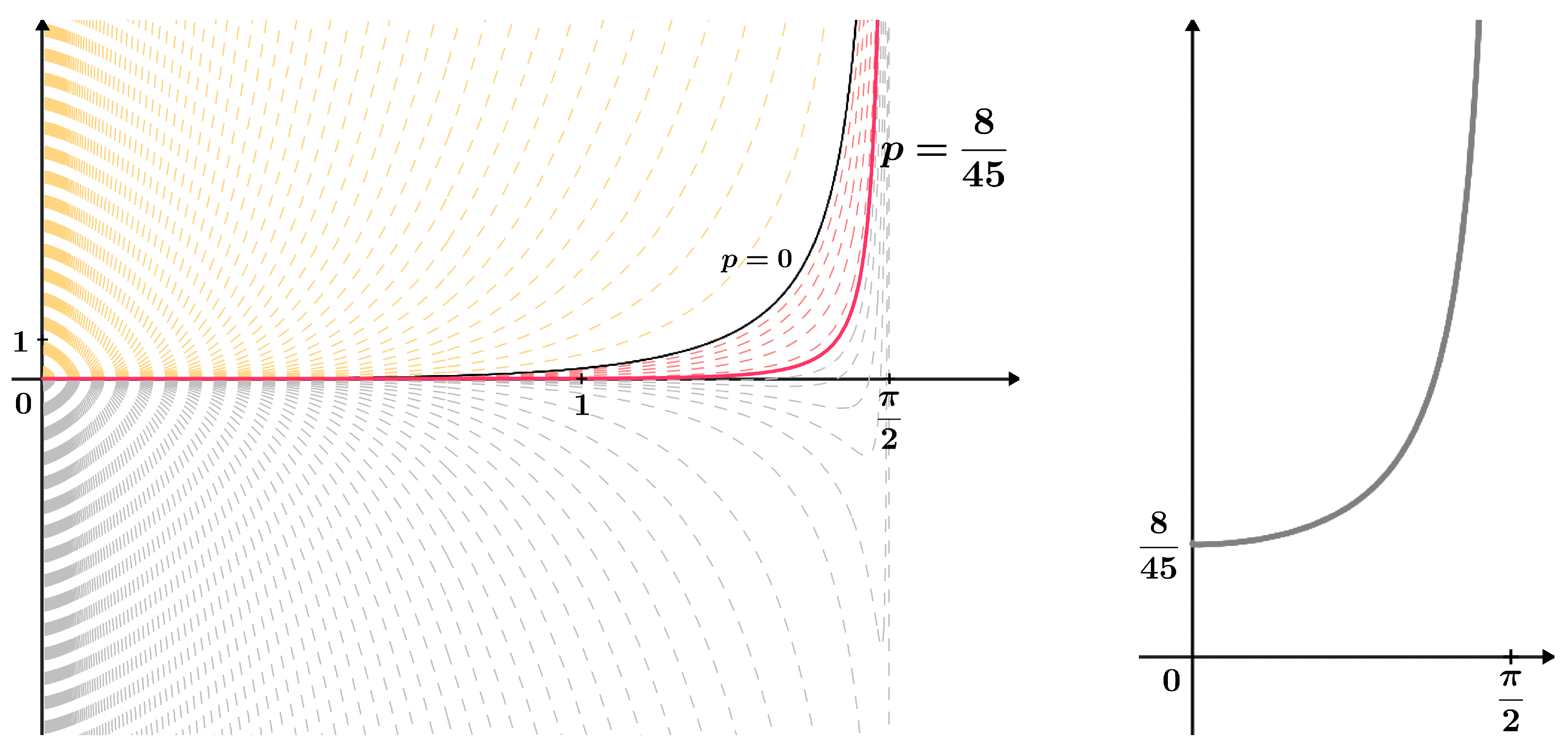
4.2. Application 2 (Wilker-Type Inequality)
- (i)
- If , then
- (ii)
- If , then the equality
4.3. Applications 3 and 4 (Mitrinović–Adamović-Type Inequalities)
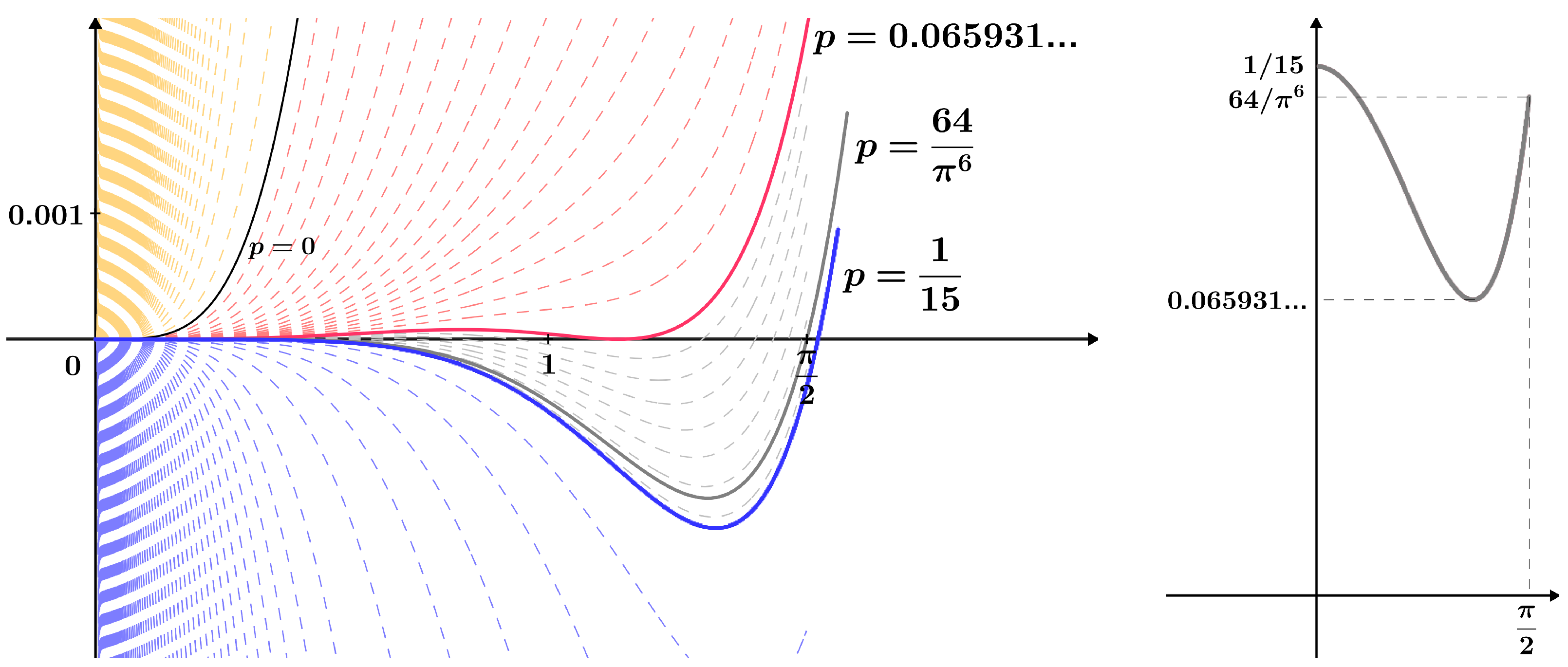
4.3.1. Application 3
- (i)
- If , then
- (ii)
- If , then the equality
- (iii)
- If , then the equality
- (iv)
- If , then
- 1. We prove that for and that for by applying the method for proving MTP inequalities.
- 1.1.
- By approximating the functions , , and with the Maclaurin polynomials of degrees 18, 16, 15 and 13, respectively, we obtain the downward polynomial approximation
- 1.2.
- By approximating the functions , , and with the Maclaurin polynomials of degrees 16, 14, 17 and 15, respectively, we obtain the downward polynomial approximation
- 2. We prove that for .
- It holds that
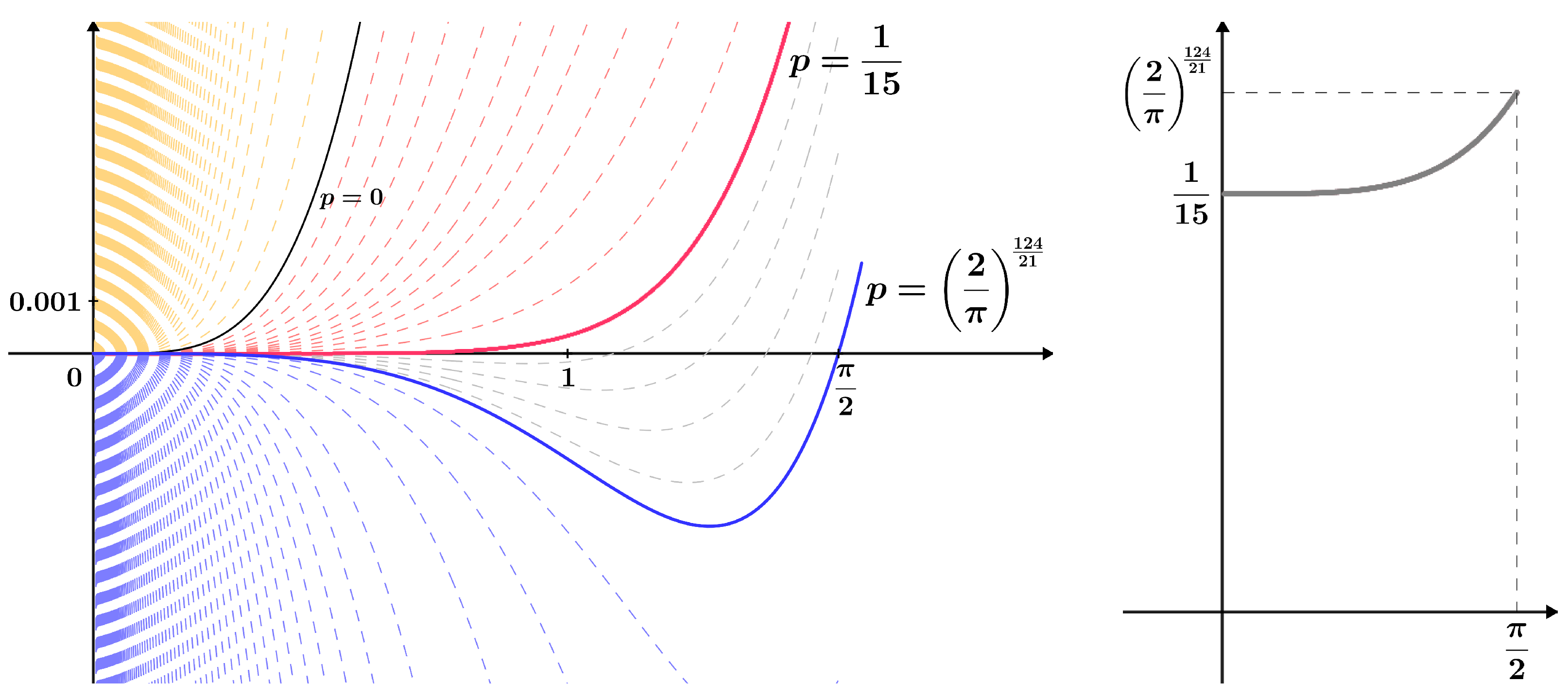
4.3.2. Application 4
- (i)
- If , then
- (ii)
- If , then the equality
- (iii)
- If , then
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviation
| MTP | Mixed Trigonometric Polynomial |
References
- Malešević, B.; Mihailović, B. A minimax approximant in the theory of analytic inequalities. Appl. Anal. Discret. Math. 2021, 15, 486–509. [Google Scholar] [CrossRef]
- Malešević, B.; Mihailović, B.; Nenezić Jović, M.; Mićović, M.; Milinković, L. Some generalisations and minimax approximants of D’Aurizio trigonometric inequalities. HAL 2024, hal-03550277v2. [Google Scholar]
- Malešević, B.; Jovanović, D. Frame’s Types of Inequalities and Stratification. Cubo 2024, 26, 1–19. [Google Scholar] [CrossRef]
- Malešević, B.; Mićović, M. Exponential Polynomials and Stratification in the Theory of Analytic Inequalities. J. Sci. Arts 2023, 23, 659–670. [Google Scholar] [CrossRef]
- Mićović, M.; Malešević, B. Jordan-Type Inequalities and Stratification. Axioms 2024, 13, 262. [Google Scholar] [CrossRef]
- Banjac, B.; Malešević, B.; Mićović, M.; Mihailović, B.; Savatović, M. The best possible constants approach for Wilker-Cusa-Huygens inequalities via stratification. Appl. Anal. Discret. Math. 2024, 18, 244–288. [Google Scholar] [CrossRef]
- Rahmatollahi, G.; Abreu, G. Closed-Form Hop-Count Distributions in Random Networks with Arbitrary Routing. IEEE Trans. Commun. 2012, 60, 429–444. [Google Scholar] [CrossRef]
- De Abreu, G.T.F. Jensen-Cotes Upper and Lower Bounds on the Gaussian Q-Function and Related Functions. IEEE Trans. Commun. 2009, 57, 3328–3338. [Google Scholar] [CrossRef]
- De Abreu, G.T.F. Arbitrarily Tight Upper and Lower Bounds on the Gaussian Q-Function and Related Functions. In Proceedings of the 2009 IEEE International Conference on Communications, Dresden, Germany, 14–18 June 2009. [Google Scholar]
- Ali, F.; Zahid, M.; Hou, Y.; Manafian, J.; Rana, M.A.; Hajar, A. A Theoretical Study of Reverse Roll Coating for a Non-Isothermal Third-Grade Fluid under Lubrication Approximation Theory. Math. Probl. Eng. 2022, 2022, 1–18. [Google Scholar] [CrossRef]
- Malešević, B.; Makragić, M. A Method for Proving Some Inequalities on Mixed Trigonometric Polynomial Functions. J. Math. Inequal. 2016, 10, 849–876. [Google Scholar] [CrossRef]
- Malešević, B.; Banjac, B. One method for proving polynomial inequalities with real coefficients. In Proceedings of the 28th TELFOR Conference, Belgrade, Serbia, 24–25 November 2020. [Google Scholar]
- Malešević, B.; Banjac, B. Automated Proving Mixed Trigonometric Polynomial Inequalities. In Proceedings of the 27th TELFOR Conference, Belgrade, Serbia, 26–27 November 2019. [Google Scholar]
- Yu, B.; Dong, B. A Hybrid Polynomial System Solving Method for Mixed Trigonometric Polynomial Systems. SIAM J. Numer. Anal. 2008, 46, 1503–1518. [Google Scholar] [CrossRef]
- Chen, S.; Liu, Z. Automated proving of trigonometric function inequalities using Taylor expansion. J. Syst. Sci. Math. Sci. 2016, 36, 1339–1348. (In Chinese) [Google Scholar]
- Chen, S.; Liu, Z. Automated proof of mixed trigonometric-polynomial inequalities. J. Symbolic Comput. 2020, 101, 318–329. [Google Scholar] [CrossRef]
- Chen, S.; Ge, X. Square-free factorization of mixed trigonometric-polynomials. J. Class. Anal. 2023, 22, 45–53. [Google Scholar] [CrossRef]
- Guessab, A.; Schmeisser, G. Sharp integral inequalities of the Hermite-Hadamard type. J. Approx. Theory 2002, 115, 260–288. [Google Scholar] [CrossRef]
- Dell’Accio, F.; Di Tommaso, F.; Guessab, A.; Nudo, F. A unified enrichment approach of the standard three-node triangular element. Appl. Numer. Math. 2023, 187, 1–23. [Google Scholar] [CrossRef]
- Alzer, H.; Guessab, A. An integral inequality for cosine polynomials. Appl. Math. Comput. 2014, 249, 532–534. [Google Scholar] [CrossRef]
- Chen, X.-D.; Shi, J.; Wang, Y.; Xiang, P. A New Method for Sharpening the Bounds of Several Special Functions. Results Math. 2017, 72, 695–702. [Google Scholar] [CrossRef]
- Chen, X.-D.; Wang, L.-Q.; Wang, Y.-G. A constructive method for approximating trigonometric functions and their integrals. Appl. Math. J. Chin. Univ. 2020, 35, 293–307. [Google Scholar] [CrossRef]
- Sturm, J.C.F. Mémoire sur la résolution des équations numériques. Bull. Des Sci. Ferussac 1829, 11, 419–425. [Google Scholar]
- Cutland, N. Computability: An Introduction to Recursive Function Theory; Cambridge University Press: Cambridge, UK, 1980. [Google Scholar]
- Chen, R.; Li, H.; Xia, B.; Zhao, T.; Zheng, T. Isolating all the real roots of a mixed trigonometric-polynomial. J. Symb. Comput. 2024, 121, 102250. [Google Scholar] [CrossRef]
- Rudin, W. Principles of Mathematical Analysis, 3rd ed.; McGraw-Hill: Singapore, 1976. [Google Scholar]
- Mortici, C. The natural approach of Wilker-Cusa-Huygens inequalities. Math. Inequal. Appl. 2011, 14, 535–541. [Google Scholar] [CrossRef]
- Qi, F.; Niu, D.-W.; Guo, B.-N. Refinements, Generalizations, and Applications of Jordan’s Inequality and Related Problems. J. Inequal. Appl. 2009, 2009, 271923. [Google Scholar] [CrossRef]
- Qi, F.; Guo, B.-N. On generalizations of Jordan’s inequality. Coal High. Educ. Suppl. 1993, 32–33. (In Chinese) [Google Scholar]
- Qi, F. Extensions and sharpenings of Jordan’s and Kober’s inequality. J. Math. Technol. 1996, 12, 98–102. (In Chinese) [Google Scholar]
- Deng, K. The noted Jordan’s inequality and its extensions. J. Xiangtan Min. Inst. 1995, 10, 60–63. (In Chinese) [Google Scholar]
- Jiang, W.D.; Yun, H. Sharpening of Jordan’s inequality and its applications. J. Inequalities Pure Appl. Math. 2006, 7, 1–4. [Google Scholar]
- Li, J.-L.; Li, Y.-L. On the Strengthened Jordan’s Inequality. J. Inequal. Appl. 2008, 2007, 074328. [Google Scholar] [CrossRef][Green Version]
- Huy, D.Q.; Hieu, P.T.; Van, D.T.T. New sharp bounds for sinc and hyperbolic sinc functions via cos and cosh functions. Afr. Mat. 2024, 35, 1–13. [Google Scholar] [CrossRef]
- Jiang, W.-D. New sharp inequalities of Mitrinović-Adamović type. Appl. Anal. Discret. Math. 2023, 17, 76–91. [Google Scholar] [CrossRef]
- Hung, L.-C.; Li, P.-Y. On generalization of D’Aurizio-Sándor inequalities involving a parameter. J. Math. Inequal. 2018, 12, 853–860. [Google Scholar] [CrossRef]
- Sándor, J. Extensions of D’Aurizio’s trigonometric inequality. Notes Number Theory Discret. Math. 2017, 23, 81–83. [Google Scholar]
- Li, W.-H.; Guo, B.-N. Several inequalities for bounding sums of two (hyperbolic) sine cardinal functions. Filomat 2024, 38, 3937–3943. [Google Scholar]
- Zhu, L. New inequalities of Wilker’s type for circular functions. AIMS Math. 2020, 5, 4874–4888. [Google Scholar] [CrossRef]
- Shinde, R.; Chesneau, C.; Darkunde, N.; Ghodechor, S.; Lagad, A. Revisit of an Improved Wilker Type Inequality. Pan-Am. J. Math. 2023, 2, 13. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, R. New inequalities of Mitrinović-Adamović type. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Math. RACSAM 2022, 116, 1–15. [Google Scholar] [CrossRef]
- Malešević, B.; Nenezić, M.; Zhu, L.; Banjac, B.; Petrović, M. Some new estimates of precision of Cusa-Huygens and Huygens approximations. Appl. Anal. Discret. Math. 2021, 15, 243–259. [Google Scholar] [CrossRef]
- Bagul, Y.J.; Banjac, B.; Chesneau, C.; Kostić, M.; Malešević, B. New Refinements of Cusa-Huygens Inequality. Results Math. 2021, 76, 107. [Google Scholar] [CrossRef]
- Bagul, Y.J.; Chesneau, C.; Kostić, M. On the Cusa-Huygens inequality. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Math. RACSAM 2021, 115, 29. [Google Scholar] [CrossRef]
- Chouikha, A.R.; Chesneau, C.; Bagul, Y.J. Some refinements of well-known inequalities involving trigonometric functions. J. Ramanujan Math. Soc. 2021, 36, 193–202. [Google Scholar]
- Bagul, Y.J.; Chesneau, C. Refined forms of Oppenheim and Cusa-Huygens type inequalities. Acta Comment. Univ. Tartu. Math. 2020, 24, 183–194. [Google Scholar] [CrossRef]
- Bagul, Y.J.; Chesneau, C.; Kostić, M. The Cusa-Huygens inequality revisited. Novi Sad J. Math. 2020, 50, 149–159. [Google Scholar]
- Dhaigude, R.M.; Chesneau, C.; Bagul, Y.J. About Trigonometric-polynomial Bounds of Sinc Function. Math. Sci. Appl. E-Notes 2020, 8, 100–104. [Google Scholar] [CrossRef]
- Zhu, L. New Inequalities of Cusa-Huygens Type. Mathematics 2021, 9, 2101. [Google Scholar] [CrossRef]
- Sándor, J.; Oláh-Gál, R. On Cusa-Huygens type trigonometric and hyperbolic inequalities. Acta Univ. Sapientiae Math. 2012, 4, 145–153. [Google Scholar]
- Wu, Y.; Bercu, G. New refinements of Becker-Stark and Cusa-Huygens inequalities via trigonometric polynomials method. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Math. RACSAM 2021, 115, 87. [Google Scholar] [CrossRef]
- Chen, C.-P.; Mortici, C. The relationship between Huygens’ and Wilker’s inequalities and further remarks. Appl. Anal. Discret. Math. 2023, 17, 92–100. [Google Scholar] [CrossRef]
- Malešević, B.; Lutovac, T.; Rašajski, M.; Mortici, C. Extensions of the natural approach to refinements and generalizations of some trigonometric inequalities. Adv. Differ. Equ. 2018, 2018, 90. [Google Scholar] [CrossRef]
- Chouikha, A.R. Global approaches of trigonometric and hyperbolic inequalities. HAL 2024, hal-04637327. [Google Scholar]
- Yang, Z.-H.; Chu, Y.-M.; Song, Y.-Q.; Li, Y.-M. A Sharp Double Inequality for Trigonometric Functions and Its Applications. Abstr. Appl. Anal. 2014, 2014, 1–9. [Google Scholar] [CrossRef]
- Chen, C.-P.; Malešević, B. Sharp inequalities related to the Adamović-Mitrinović, Cusa, Wilker and Huygens results. Filomat 2023, 37, 6319–6334. [Google Scholar] [CrossRef]
- Chouikha, A.R. On natural approaches related to classical trigonometric inequalities. Open J. Math. Sci. 2023, 7, 299–320. [Google Scholar] [CrossRef]
- Chouikha, A.R. New sharp inequalities related to classical trigonometric inequalities. J. Inequal. Spec. Funct. 2020, 11, 27–35. [Google Scholar]
- Zhu, L. An unity of Mitrinovic–Adamovic and Cusa–Huygens inequalities and the analogue for hyperbolic functions. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Math. RACSAM 2019, 113, 3399–3412. [Google Scholar] [CrossRef]
- Yang, Z.-H.; Chu, Y.-M. A Note on Jordan, Adamović-Mitrinović, and Cusa Inequalities. Abstr. Appl. Anal. 2014, 2014, 1–12. [Google Scholar] [CrossRef]
- Yang, Z.-H. Refinements of a two-sided inequality for trigonometric functions. J. Math. Inequal. 2013, 7, 601–615. [Google Scholar] [CrossRef]
- Malešević, B. Application of lambda method on Shafer-Fink’s inequality. Publ. Elektrotehničkog Fak.-Ser. Mat. 1997, 8, 90–92. [Google Scholar]
- Wilker, J.B. Problem E3306. Am. Math. Mon. 1989, 96, 55. [Google Scholar]
- Chen, S.; Ge, X. A solution to an open problem for Wilker-type inequalities. J. Math. Inequal. 2021, 15, 59–65. [Google Scholar] [CrossRef]
- Bercu, G. Refinements of Huygens-Wilker-Lazarović inequalities via the hyperbolic cosine polynomials. Appl. Anal. Discrete Math. 2022, 16, 91–110. [Google Scholar] [CrossRef]
- Nenezić, M.; Malešević, B.; Mortici, C. New approximations of some expressions involving trigonometric functions. Appl. Math. Comput. 2016, 283, 299–315. [Google Scholar] [CrossRef]
- Chouikha, A.R. Sharp inequalities related to Wilker results. Open J. Math. Sci. 2023, 7, 19–34. [Google Scholar] [CrossRef]
- Chouikha, A.R. On the 1-parameter trigonometric and hyperbolic inequalities chains. HAL 2024, hal-04435124. [Google Scholar]
- Zhang, B.; Chen, C.-P. Sharp Wilker and Huygens type inequalities for trigonometric and inverse trigonometric functions. J. Math. Inequal. 2020, 14, 673–684. [Google Scholar] [CrossRef]
- Chen, C.-P.; Paris, R.B. On the Wilker and Huygens-type inequalities. J. Math. Inequal. 2020, 14, 685–705. [Google Scholar] [CrossRef]
- Jiang, W.-D.; Luo, Q.-M.; Qi, F. Refinements and Sharpening of some Huygens and Wilker Type Inequalities. Turk. J. Anal. Number Theory 2014, 2, 134–139. [Google Scholar] [CrossRef][Green Version]
- Bercu, G. Refinements of Wilker-Huygens-Type Inequalities via Trigonometric Series. Symmetry 2021, 13, 1323. [Google Scholar] [CrossRef]
- Zhu, L.; Sun, Z. Refinements of Huygens- and Wilker- type inequalities. AIMS Math. 2020, 5, 2967–2978. [Google Scholar] [CrossRef]
- Guo, B.-N.; Qiao, B.-M.; Qi, F.; Li, W. On new proofs of Wilker’s inequalities involving trigonometric functions. Math. Inequal. Appl. 2003, 6, 19–22. [Google Scholar] [CrossRef]
- Zhu, L. Some New Wilker-Type Inequalities for Circular and Hyperbolic Functions. Abstr. Appl. Anal. 2009, 2009, 1–9. [Google Scholar] [CrossRef]
- Sun, Z.; Zhu, L. On New Wilker-Type Inequalities. ISRN Math. Anal. 2011, 2011, 1–7. [Google Scholar] [CrossRef][Green Version]
- Zhu, L. Wilker inequalities of exponential type for circular functions. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Math. RACSAM 2021, 115, 35. [Google Scholar] [CrossRef]
- Mortici, C. A subtly analysis of Wilker inequality. Appl. Math. Comput. 2014, 231, 516–520. [Google Scholar] [CrossRef]
- Wu, S.-H.; Srivastava, H.M. A weighted and exponential generalization of Wilker’s inequality and its applications. Integral Transforms Spec. Funct. 2007, 18, 529–535. [Google Scholar] [CrossRef]
- Wu, S.-H.; Srivastava, H.M. A further refinement of Wilker’s inequality. Integral Transforms Spec. Funct. 2008, 19, 757–765. [Google Scholar] [CrossRef]
- Rašajski, M.; Lutovac, T.; Malešević, B. Sharpening and generalizations of Shafer-Fink and Wilker type inequalities: A new approach. J. Nonlinear Sci. Appl. 2018, 11, 885–893. [Google Scholar] [CrossRef][Green Version]
- Chouikha, A.R.; Chesneau, C. Contributions to trigonometric 1-parameter inequalities. HAL 2024, hal-04500965. [Google Scholar]
- Wu, S.-H.; Yue, H.-P.; Deng, Y.-P.; Chu, Y.-M. Several improvements of Mitrinović-Adamović and Lazarević’s inequalities with applications to the sharpening of Wilker-type inequalities. J. Nonlinear Sci. Appl. 2016, 9, 1755–1765. [Google Scholar] [CrossRef]
- Wu, S.-H.; Li, S.-G.; Bencze, M. Sharpened versions of Mitrinović-Adamović, Lazarević and Wilker’s inequalities for trigonometric and hyperbolic functions. J. Nonlinear Sci. Appl. 2016, 9, 2688–2696. [Google Scholar] [CrossRef]
- Mitrinović, D.S.; Adamović, D.D. Sur une inégalité élémentaire où interviennent des fonctions trigonométriques. Publ. Elektrotehničkog Fak. Ser. Mat. Fiz. 1965, 149, 23–34. [Google Scholar]
- Zhu, L.; Nenezić, M. New approximation inequalities for circular functions. J. Inequal. Appl. 2018, 2018, 313. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L. New Mitrinović-Adamović type inequalities. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Math. RACSAM 2020, 114, 119. [Google Scholar] [CrossRef]
- Qian, G.; Chen, X.-D. Improved bounds of Mitrinović-Adamović-type inequalities by using two-parameter functions. J. Inequal. Appl. 2023, 2023, 25. [Google Scholar] [CrossRef]
- Sándor, J. Refinements of the Mitrinović-Adamović inequality, with application. Notes Number Theory Discret. Math. 2017, 23, 4–6. [Google Scholar]
- Wu, S.; Baricz, Á. Generalizations of Mitrinović, Adamović and Lazarević’s inequalities and their applications. Publ. Math. Debr. 2009, 75, 447–458. [Google Scholar] [CrossRef]
- Zhu, L. Sharp inequalities of Mitrinovic-Adamovic type. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Math. RACSAM 2019, 113, 957–968. [Google Scholar] [CrossRef]
- Banjac, B. System for Automatic Proving of Some Classes of Analytic Inequalities. Ph.D. Thesis, School of Electrical Engineering, University of Belgrade, Belgrade, Serbia, 2019. (In Serbian). [Google Scholar]
- Nenezić Jović, M. Stratified Families of Functions in the Theory of Analytical Inequalities with Applications. Ph.D. Thesis, School of Electrical Engineering, University of Belgrade, Belgrade, Serbia, 2023. (In Serbian). [Google Scholar]
- Mitrinović, D. Analytic Inequalities; Springer: Berlin, Germany, 1970. [Google Scholar]
- Anderson, G.D.; Vuorinen, M.; Zhang, X. Topics in Special Functions III. In Analytic Number Theory, Approximation Theory and Special Functions; Milovanović, G., Rassias, M., Eds.; Springer: New York, NY, USA, 2014; pp. 297–345. [Google Scholar]
- Cloud, M.J.; Drachman, B.C.; Lebedev, L.P. Inequalities with Applications to Engineering; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Pachpatte, B.G. Analytic Inequalities: Recent Advances; Atlantis Press: Paris, France, 2012. [Google Scholar]
- Anastassiou, G.A. Intelligent Comparisons: Analytic Inequalities; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Kazarinoff, N.D. Analytic Inequalities; Holt, Rinehart and Winston: New York, NY, USA, 1961. [Google Scholar]
- Qin, Y. Analytic Inequalities and Their Applications in PDEs; Birkhäuser: Cham, Switzerland, 2017. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malešević, B.; Mićović, M.; Mihailović, B. A Parametric Method for Proving Some Analytic Inequalities. Axioms 2024, 13, 520. https://doi.org/10.3390/axioms13080520
Malešević B, Mićović M, Mihailović B. A Parametric Method for Proving Some Analytic Inequalities. Axioms. 2024; 13(8):520. https://doi.org/10.3390/axioms13080520
Chicago/Turabian StyleMalešević, Branko, Miloš Mićović, and Bojana Mihailović. 2024. "A Parametric Method for Proving Some Analytic Inequalities" Axioms 13, no. 8: 520. https://doi.org/10.3390/axioms13080520
APA StyleMalešević, B., Mićović, M., & Mihailović, B. (2024). A Parametric Method for Proving Some Analytic Inequalities. Axioms, 13(8), 520. https://doi.org/10.3390/axioms13080520





