Abstract
We define biequivalent planar graphs, which are a generalisation of the uniform polyhedron graphs, as planar graphs made out of two families of equivalent nodes. Such graphs are required to identify polyhedral cages with geometries suitable for artificial protein cages. We use an algebraic method, which is followed by an algorithmic method, to determine all such graphs with up to 300 nodes each with valencies ranging between three and six. We also present a graphic representation of every graph found.
Keywords:
planar graphs; Cayley graphs; uniform polyhedron; regular solids; polyhedral cages; protein cage MSC:
00A69
1. Introduction
Recently, we showed that to construct a polyhedral cage (p-cages for short) one must use planar graphs to characterise how the different faces of a p-cage are linked together [1]. P-cages are assemblies of regular or nearly regular polygons but with holes. The nodes of the graph correspond to the faces of the p-cage, while the edges determine which of the faces are sharing an edge. P-cages correspond to the mathematical description of the geometry of artificial protein cages, which are being developed for targeted drug delivery [2]. To form spontaneously, such protein cages must be symmetric so that each face is equivalent, modulo a rotation, to all the other faces. The simplest p-cages candidates for artificial protein cages are hence p-cages made out of a single type of polygon, where all the faces are equivalent, thus having modulo rotation [3]. To be good candidates, p-cages must have small holes, and each face should have at least four neighbours each. Unfortunately, the number of such p-cages is relatively small. As an alternative, it is natural to consider protein cages made out of two types of polygons. In [4], we have constructed such p-cages but with the restriction that each face of a given type must be connected to face of the other type. Unfortunately, very few of these p-cages have small holes.
The next step is then to construct p-cages made out of two types of polygons but allowing each face to be adjacent to any type of face. To achieve this task, as explained in [1], one must characterise all the planar graphs made out of two families of nodes such that the nodes of a given family are equivalent to each other modulo to achieve automorphism of the graph. Planar graphs for which all the nodes are equivalent to each other correspond to the planar graphs of all the convex uniform polyhedra [5] (They are examples of Cayley graphs). The aim of this paper is to determine a list of all the planar graphs made out of two equivalent types of nodes with valencies ranging from three to six. This restriction comes from the fact that the faces of a p-cage must have at least three neighbours and cannot have more than six without being heavily irregular.
Artificial protein cages have been experimentally generated by a number of research groups. One of the first ones was the TRAP-cage made out of 24 hendecagonal faces, which are also called TRAP-rings [2,6]. More recently, a smaller protein cage was shown to be made out of 12 of the same TRAP-protein hendecagonal rings [7].
A number of other artificial protein cages have been made experimentally [8,9,10,11]. These cages are similar to virus capsids but require metal atoms to bind together [12]. The motivation to create these protein nanocages is to develop new method of drug delivery [13,14,15,16,17] by enclosing the drug inside such cages. By adding to the protein cages receptors that can bind to a target cell, such as cancer cells for example [13], the protein cages can be swallowed by the cell, where the drug is then released [18]. For expensive drugs, this method would greatly reduce the cost of medical treatment, and as only the targeted cells receives the drug, thus greatly reducing the side effects. Our ultimate aim it to identify geometries that can be used by nanobioengineers to create new protein cages.
The study of the structure of protein cages is quite new, and most investigations have so far been mostly experimental [19,20]. The formal mathematical description of polyhedral cages, as well as the connection between their structure and planar graphs, were identified in our previous work [1].
Graphs do occur in a number of areas of science such as the study of complex protein networks [21], quantum field theory [22], neurology [23], or mathematics [24]. The symmetry of graphs has been studied extensively [25], but here, we restrict ourselves to planar graphs. As we have stated above, planar graphs where all the nodes are equivalent, modulo of an automorphism of the graphs, and correspond to the planar graphs of convex uniform polyhedra. In this paper, we are constructing planar graphs made out of two families of equivalent nodes.
2. Characteristics of Potential Graphs
We define a biequivalent planar graph as a planar graph made out of nodes split in two families such that any node of a given family can be mapped to any other node of the same family via an automorphism of the graph. For the reasons mentioned in the introduction, in what follows, we restrict ourselves to graphs with a node valency ranging from three to six. Notice that loops are excluded from planar graphs.
Each planar graph is made of a number of nodes connected together by edges that then define faces. Each face is then characterised by the number of nodes from each family, as well as their cyclic order around the face. To be equivalent, the nodes of a given family must all be adjacent to the same type of faces and in the same order. To find biequivalent graphs, we start by using the Euler formula that states that for any planar graph consisting of F faces, E edges, and V nodes/vertices, the following condition is always satisfied: . This will allow us to find restrictions on the number of nodes, as well as the number and types of faces belonging to the graphs. We must emphasise that in the Euler formula, the outside of the graph is considered as a face. This is easy to understand when one visualises the graphs as a planar projection of a 3D polyhedron.
Considering planar graphs made out of nodes of type 1, with each having valency and nodes of type 2 of valency , we denote as the number of faces with nodes of type 1 and nodes of type 2. Then, we have that the total number of edges E and faces F are given by
Moreover,
Then, as a result,
Substituting these expressions for F, E, and V into the Euler formula, we have
Now, by multiplying (5) by , we obtain
If each node of type j belongs to faces with nodes of type 1 and nodes of type 2, we have
and similarly for any :
Indeed, for every face with nodes of type 1 and nodes of type 2, is the number of nodes of type 1, and is multiplied by the number of faces of that type adjacent to nodes of type 1 and similarly for nodes of type 2. This only works because all the nodes of a given type are equivalent.
Then, by definition, we also have
To construct all biequivalent planar graphs, we must find the integers , , and satisfying (6). We must then compute and using (3) and reject the cases where and are not integers. We must next compute and using (7) and (8), thus keeping only the cases for which they are integers that satisfy (9).
To do so, we have written a computer program (available from zenodo), which when given values for and , scans all the possible combinations of polygons made out of type 1 and type 2 nodes, thus considering polygonal faces such that , with a maximum of 300 faces.
We have restricted ourselves to decagonal faces, because they are the largest polygons occurring in Archimedean solids and also because they already lead to p-cages with very large holes. We restricted ourselves to 300 faces to capture all the graphs, which are derivatives of the planar graphs corresponding to the Archimedean solids. We did so for and . When , the program completes in a few minutes, but for it ran for 3 months on a powerful workstation. We did run the program for larger polygons and more faces (up to 1000) for some of the smaller values of and but did not obtain any more graphs other than the one derived from the prisms and antiprisms, of which there is an infinite number.
The program generates a list of potential graph characteristics (PGCs) of the type
| [4 5; | 5 4 0, 10 2 1; | 2 0, 2 1; | 5 1; | 10 2] |
| valencies | faces 0 & 1 | node 1 | node 2 | # nodes |
The first two numbers correspond to the valencies of the graphs 4 and 5 for nodes of type 1 and 2, respectively. The value 5 4 0, 10 2 1 indicates that the graph is made out of five squares of valency, four nodes, and 10 triangles made out of two valency 4 and one valency 5 nodes. The value 2 0, 2 1 indicates that the type 1 nodes are adjacent to two faces of type 0 (the squares) and two faces of type 1 (the triangles). The value 5 1 indicates that the nodes of type 2 are adjacent to five faces of type 1. The value 10 2 specifies that there are 10 nodes of type 1 and 2 nodes of type 2. The total number of faces is hence 15 in this case.
Between the nine pairs of valencies considered and after filtering out double entries when and in cases where there are no edges linking the two types of nodes, the program generated over 30,000 PGCs, but only just over 1% of these correspond to an actual planar graph. As an example of an impossible graph, the PGC [3 3; 1 0 4, 2 2 1, 2 4 0; 1 1, 2 2; 1 1, 2 0; 4 2] specifies that the type 2 nodes must be adjacent to two squares 0 4, but as there is only one square, this is not possible.
As the next step, we must consider all the PGCs and try to convert them into actual graphs, thus discarding those for which this is not possible.
3. Construction of the Graphs
3.1. The Faces of the Graph
Each graph is made out of the faces and nodes as specified in the PGC described in the previous section. A face with nodes of type 1 and nodes of type 2 can assume different configurations referring to the order in which the nodes are distributed. For example, up to cyclic rotations, an hexagon can have the following configurations: , , or . In the first case, all the nodes 1 are equivalent, and there are two types of nodes of type 2 (Some nodes 2 have the cyclic sequence on the right, while others have ). For the last two cases, there are two types of node 1 and four types of node 2. In what follows, we refer to these as the C-signature of the face, and we call the number of different C-signatures for the face . We then label these configurations as , where indexes the different configurations. In the example above, , , , and .
The cycle of the configuration, , is the smallest number of single cyclic rotations needed to recover the configuration. In the example above, we have and .
Each node on a face will have an index number, as well as a reduced index number corresponding to the lowest index amongst all the equivalent nodes of the same type. The reduced index of index i is simply (Notice that the index corresponds to an offset and hence starts at 0). For example, the reduced indices of are , while the reduced indices of and are the actual indices: .
We call the node multiplicity of a face configuration as the number of nonequivalent nodes of type t that it contains, and we label it as . The multiplicity of a type t node for a given configuration is simply given by .
In the example above, , and ; as well, , and .
Having described the faces of the graph, we must now consider the nodes.
3.2. The Nodes of the Graph
The planar graphs we are considering are of two types and can be of different valencies. Each node of a given type will be surrounded by a sequence of faces of the different types, and to be equivalent, that sequence must be the same for every node, thus being modulo for a cyclic rotation.
As described above, each node of type t will be surrounded by faces made out of nodes of type 1 and nodes of type 2, and for the type t nodes to be equivalent, it is not just the type of face that must be in the same sequence, but the C-signatures of these faces must be in the same sequence as well. Moreover, every nodes of type t must have the same reduced indices for each of the matching face signatures in the sequence. By convention, we label them in the anticlockwise order.
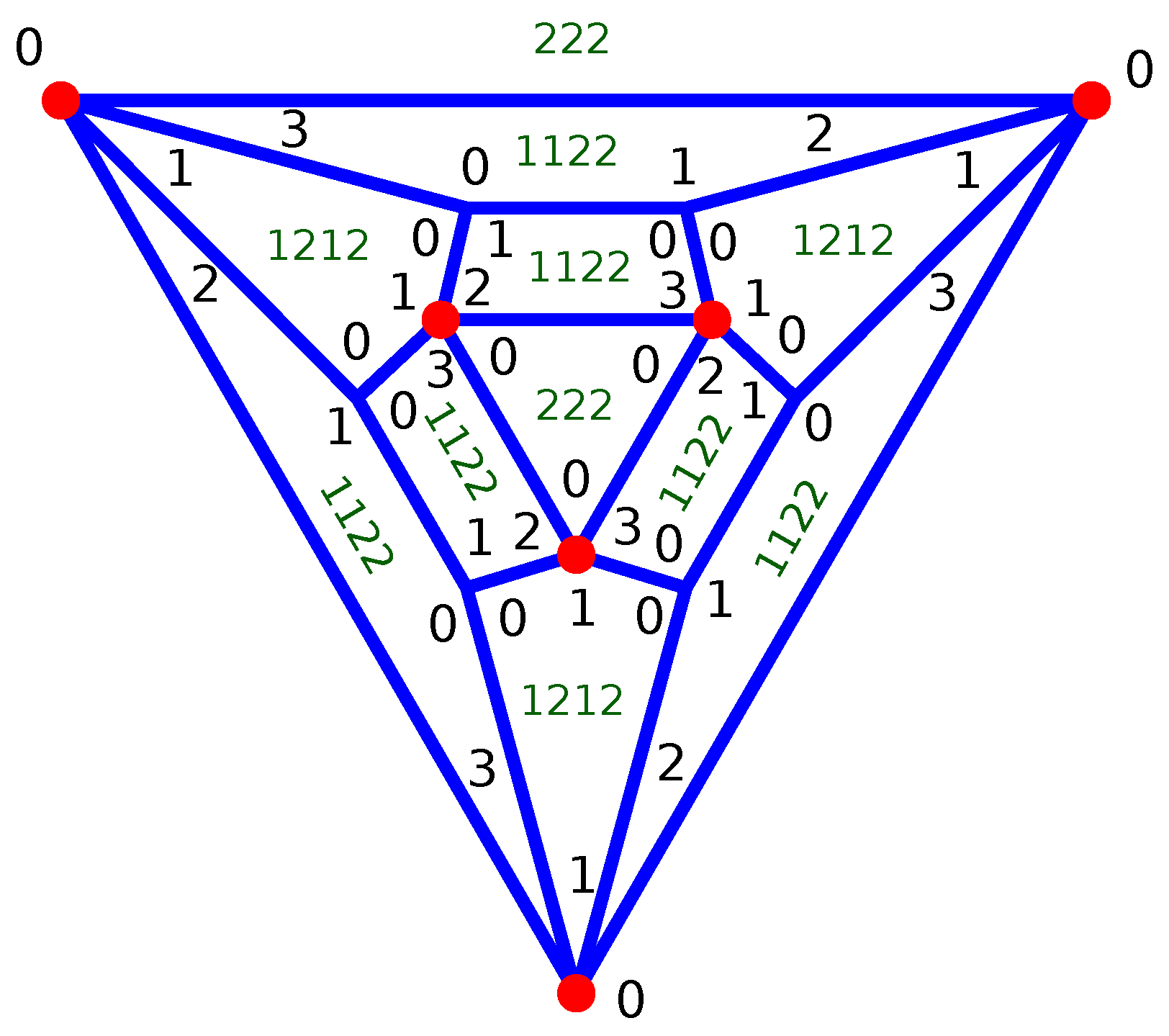
Figure 1 illustrates this as an example where the nodes of type 1 have valency 3, and the nodes of type 2, marked with a read dot, have valency 4. The graph is made out of two triangles, , and nine squares, . So, we have and , and we define , , and . Notice that one of the 222 face sits outside the graph, but if we picture the graph as a polyhedron, it corresponds to the bottom of the polyhedron. In what follows, we call that face the outside face.
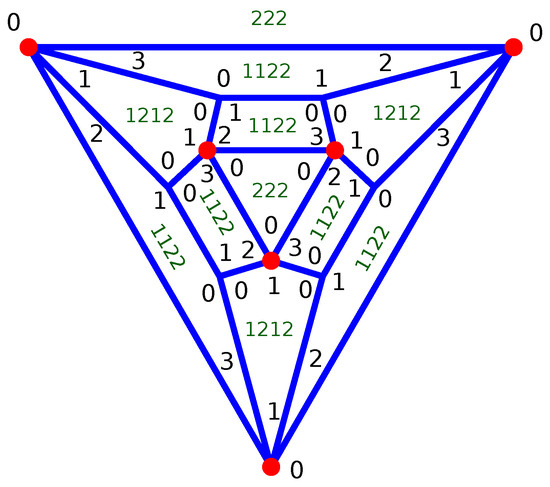
Figure 1.
Graph made out of six valency 3 nodes (type 1), six valency 4 nodes (type 2) and the following faces: 2 , 3 , and 6 . , and . The reduced indices of each node are the black digits in the corner of each face.
The nodes of type 1 have the face sequence with the corresponding reduce indices . This also means that , and . The multiplicity of the face configurations are then , , and .
The nodes of type 2 have the face sequence with the corresponding reduced indices . This also means that , and . The multiplicity of the face configurations are then , , and .
Notice that the sum of the multiplicities of a type t node for the different configurations must be less than or equal to :
In the example above, we have
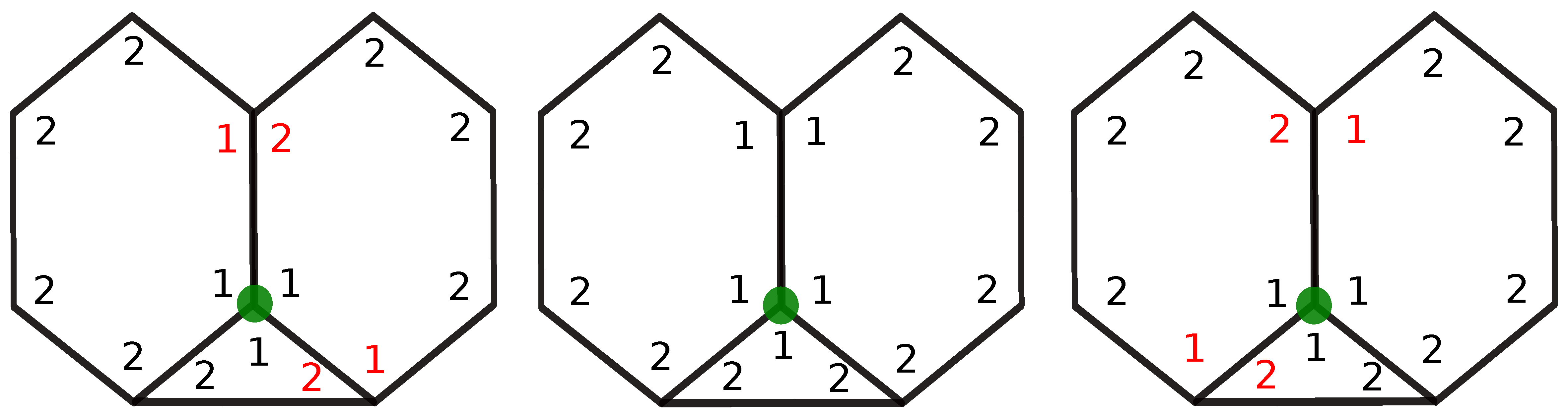
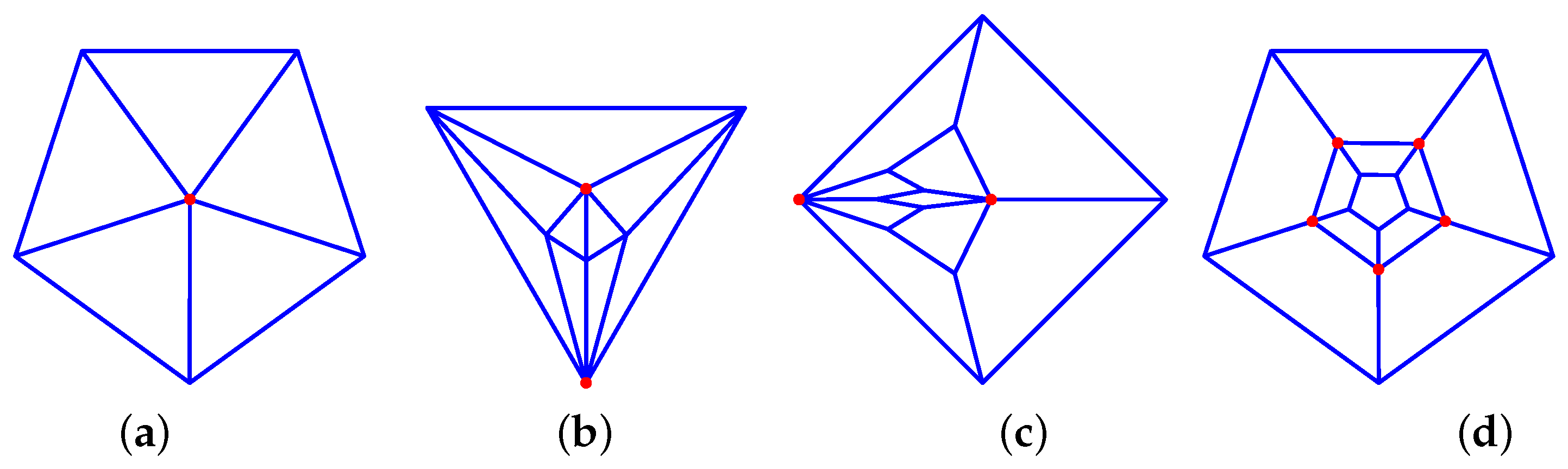
To determine the possible arrangements of faces around a node, we must consider all the permutations of the different face signatures for each of their possible configurations. For example, if a trivalent node of type 1 is surrounded by one face and two faces, the possible arrangements are as follows: (We order the faces in the anticlockwise order around the node, and the nodes are also ordered in the anticlockwise order around a face. The first node on the face signature is the node considered).
- (1,2,2), (1,1,2,2,2,2), (1,1,2,2,2,2)
- (1,2,2), (1,2,2,2,2,1), (1,1,2,2,2,2)
- (1,2,2), (1,2,2,2,2,1), (1,2,2,2,2,1)
- (1,2,2), (1,1,2,2,2,2), (1,2,2,2,2,1)
The first three configurations are illustrated in the same order in Figure 2, where we see that only the second configuration leads to compatible nodes. Indeed, not all configurations are compatible, and the neighbouring faces must have matching node types: on the first arrangement, the second face must have a second node of type 2 to match the face, and the two hexagons have a node mismatch above the green dot. One sees graphically that the only compatible configuration is the middle one: .
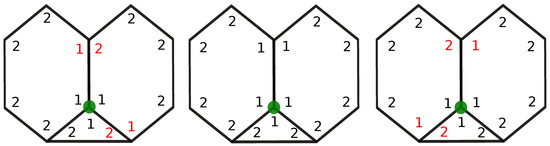
Figure 2.
Fitting of a triangle and two hexagon around a trivalent node. The green dot corresponds to the node being fitted. Red labels indicate incompatible node types.
If we denote as the index of the configuration , the condition is that if A and B are two successive configurations in that order around a node with respective index a and b for the node, we must have
where and are the number of edges of, respectively, face A and B.
To construct a graph from a given PGC, we start by selecting a C-signature for each of the faces making the graph. For both types of node, we order the different faces around the node, as well as select a reduced index of the node for each face. We then pick a face as the outside face, as well as a node on that face. We then try to add the different faces around that node in the preselected order. Once a node is completed, we move to the adjacent node and keep working our way through all the nodes but stop when the addition of a face leads to a node type clash. We must then move one step backward and skip the addition of the previous face. One must also stop and move one step back when all the faces or all the nodes have been used. This is a recursive algorithm which, in some cases, can take a very long time. When the graph is completed, one can stop and move on to the next potential node and face configuration.
To find all the possible graphs for a given PGC, we must consider all the possible combinations of the face C-signatures, as well as all the possible orders of these faces around each type of node. This leads to a very large number of possibilities, but most of them can be easily ruled out using simple matching node incompatibility, as described above.
To understand how to construct a graph, we start by describing how to deconstruct one. If we start from a full graph and remove a given face, keeping the nodes and the edges belonging to the other faces, the graph acquires a hole (the graph still looks the same, as we have not removed any edges yet, but the removed face should be viewed as a hole in the graph). We then remove a second face by removing the edges common to the holes and that face. In the process, the hole becomes larger. We keep removing faces adjacent to the hole until we are left with the outside face with just a hole in it.
To build a graph, we proceed the other way round, thus starting from the outside face and adding faces inside the hole. We must consider every type of face that the graph is made of, as well as every rotation of the nodes. There is a very large number of ways to do this: many face additions can be ruled out by the constrains described above. When adding any face at a given location fails to satisfy all the constraints, we must remove the previous face and try again with another face instead. This is a recursive algorithm. We output a graph when it is completed.
We have written a computer program, available from Zenodo, (the link is given at the end of the paper), which builds a planar graph using the algorithm described above, thus using as input a PGC generated by the program described in the previous section.
It is usually best to take the largest face as the outside face, but sometimes, taking a different face generates or rejects a graph much faster. For some parameters, the program takes several weeks to complete, but in most cases, the graphs are rejected within a few minutes.
Some of the graphs have a chiral symmetry and hence correspond to two different graphs. Most of the time, the characteristics of a potential graph correspond to a single graph, modulo to the chiral symmetry, but in some instances, they actually correspond to two or even three totally different graphs.
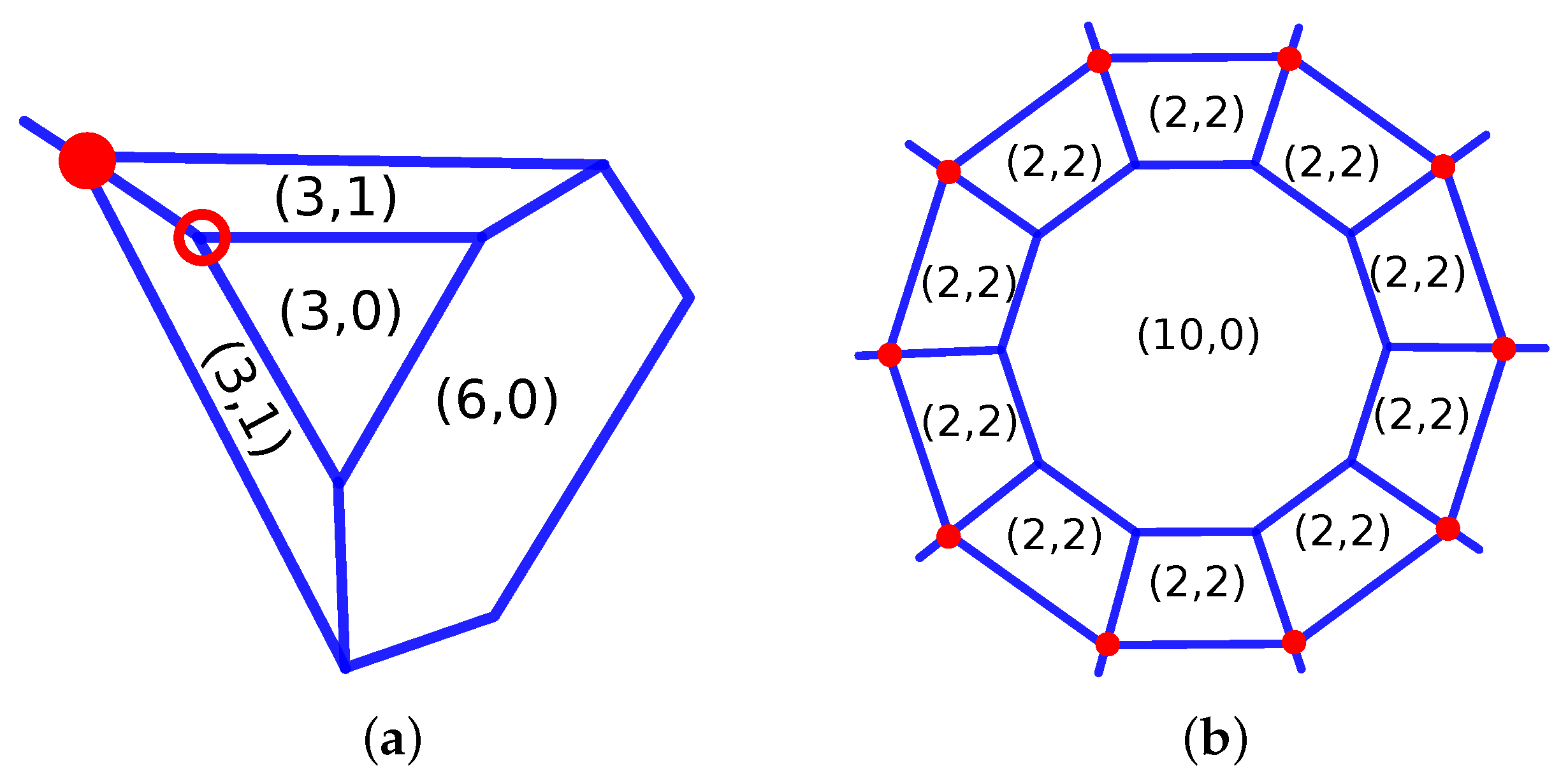
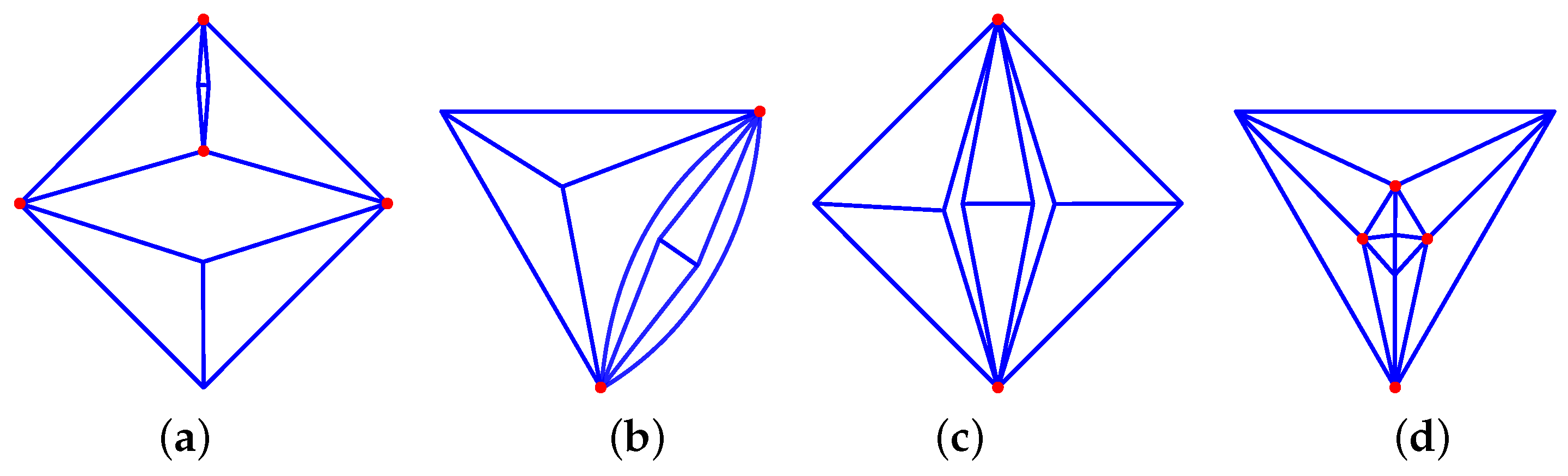
Some graphs can be excluded easily though. For example, the graph corresponding to the PGC [3 4; 1 6 0, 2 0 3, 2 3 0, 2 3 1; 1 0, 1 2, 1 3; 1 3, 3 1; 6 2] has to contain one hexagon made out of valency 3 nodes, as well as a triangle made out of valency 3 nodes (see Figure 3a). The triangle 3 0 must share an edge with the hexagon 6 0 so that two of the valency 3 nodes are adjacent to a 3 0 and a 6 0 face. The remaining two edges of the triangle must then be shared with an edge from the 3 1, but as a result, the third node of the triangle is adjacent to two 3 1, which is not one as requested.
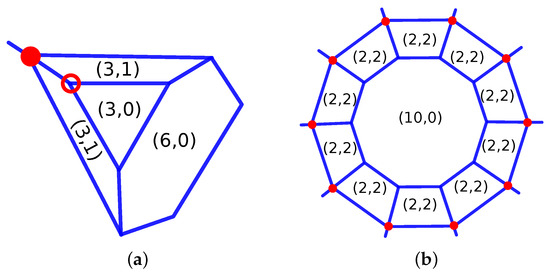
Figure 3.
Examples of impossible PGCs: (a) 34_F9_1-6-0_2-0-3_2-3-0_2-3-1_V6_2; (b) 34_F122_10-0-8_12-10-0_120-2-2_V120_80.
As another example, the PGC [3 4; 10 0 8, 12 10 0, 120 2 2; 1 2, 2 3; 1 1, 3 3; 120 80] specifies that each face 10 0 must be surrounded by 10 2 2 forming a compound decagon (see Figure 3b). We must then find a way to form the planar graph of a uniform polyhedra made out of twelve decagons and ten octagons, but this is known to not exist, as there is no corresponding regular polyhedron.
We have run our computer program to construct all the biequivalent graphs with valencies ranging from three to six and made at most 300 faces ranging from triangle to decagons. In the next section, we describe each of these graphs.
4. Results
Most of the biequivalent graphs can be seen as modifications of the planar graph of a uniform polyhedron, where extra nodes and edges are added in symmetrically. So, we will present these graphs as different categories of such modifications, but we will start with the graphs derived from simple polygons. As shown in Appendix A, there are no planar graphs made exclusively out of valency 6 nodes. As a result, we can only consider the following pairs of valency values : (3,3), (3,4), (3,5), (3,6), (4,4), (4,5), (4,6), (5,5) and (5,6). The data files describing the PGC, the graph connectivities, and the vector graphic representations of the graphs are available from Zenodo.
The drawing of a graph depends on the choice of the outside face, and most of the time, we have chosen the largest polygon for it. The connectivity between the different nodes, on the other hand, remains the same, regardless of the chosen outside face, and a description of each graph as a set of pair of nodes linked together can be found as plain text files available from Zenodo.
Most graphs can be seen as a member of a family of similarly obtained graphs, such as, for example, the addition of a pyramid on the bases of prisms. As we have identified over 400 different graphs, we only include one example of each family in the main text, but the supplementary file contains a graphic representation of every graph that we have found. On the figures, the nodes of type 2 are indicated with a red dot.
The names of the graphs are derived from their PGC and are of the type , where and , with , are the valencies of the nodes, n is the total number of faces of the graph, is the number of faces of type , and is the number of nodes of type k. For example, |45_F15_5-4-0_10-2-1_V10_2| is a graph made out of ten valency 4 nodes and two valency 5 nodes, with a total of fifteen faces: five squares and ten triangles . When more than one graph correspond to a given PGC, we add the suffix _a, _b, or _c at the end of the name to differentiate them. We also add a ∗ after the p-cage name when the graph is chiral.
To describe the families of graphs, we sometimes use some parameters, say P, and include an arithmetic expression inside curly brackets. For example, {2P+1} should be thought of as the value of .
We now proceed by describing each graph and how they can be described as modifications of known structures. As an abuse of language, we use the names of regular solids to refer to their planar graphs.
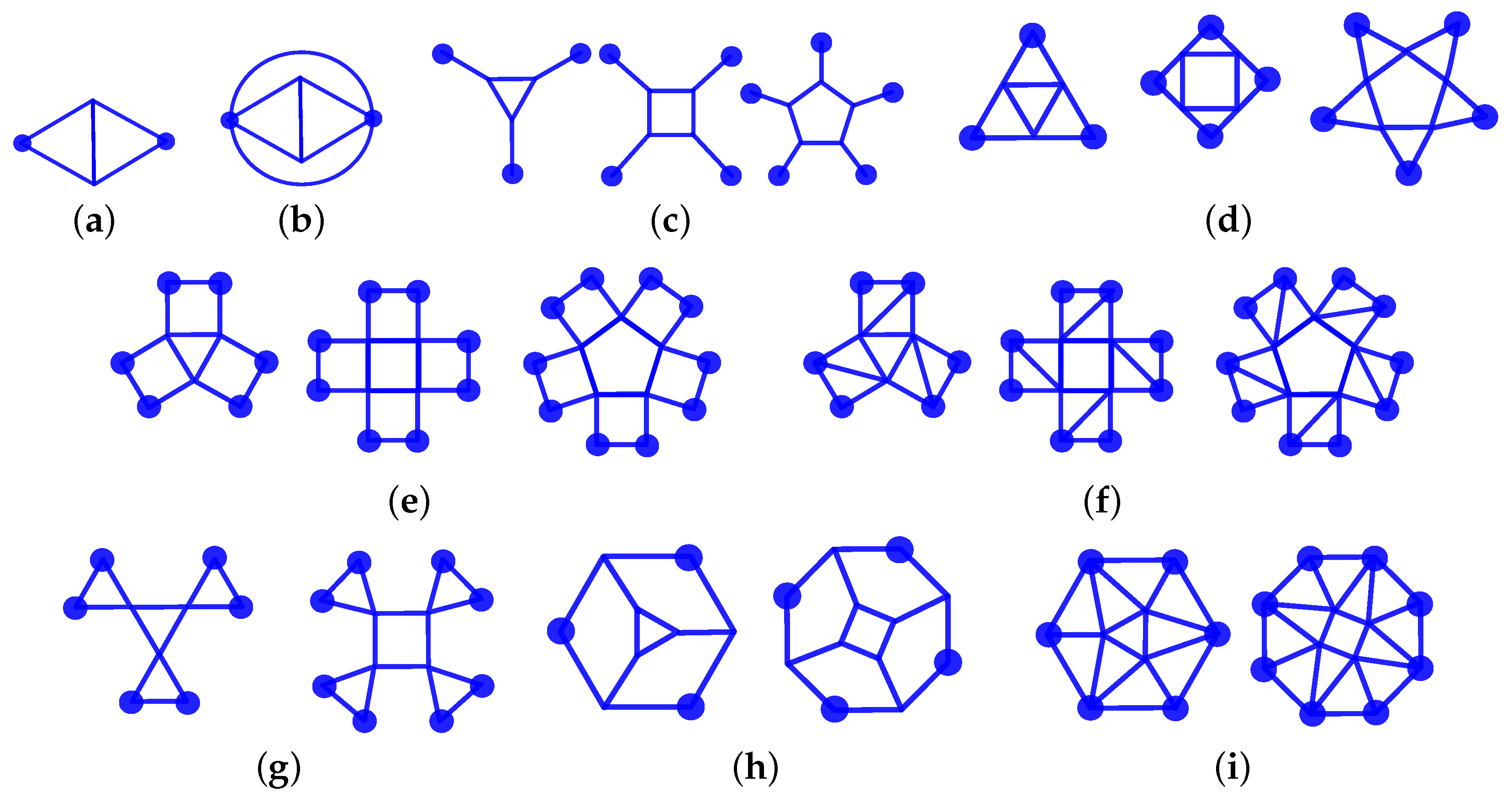
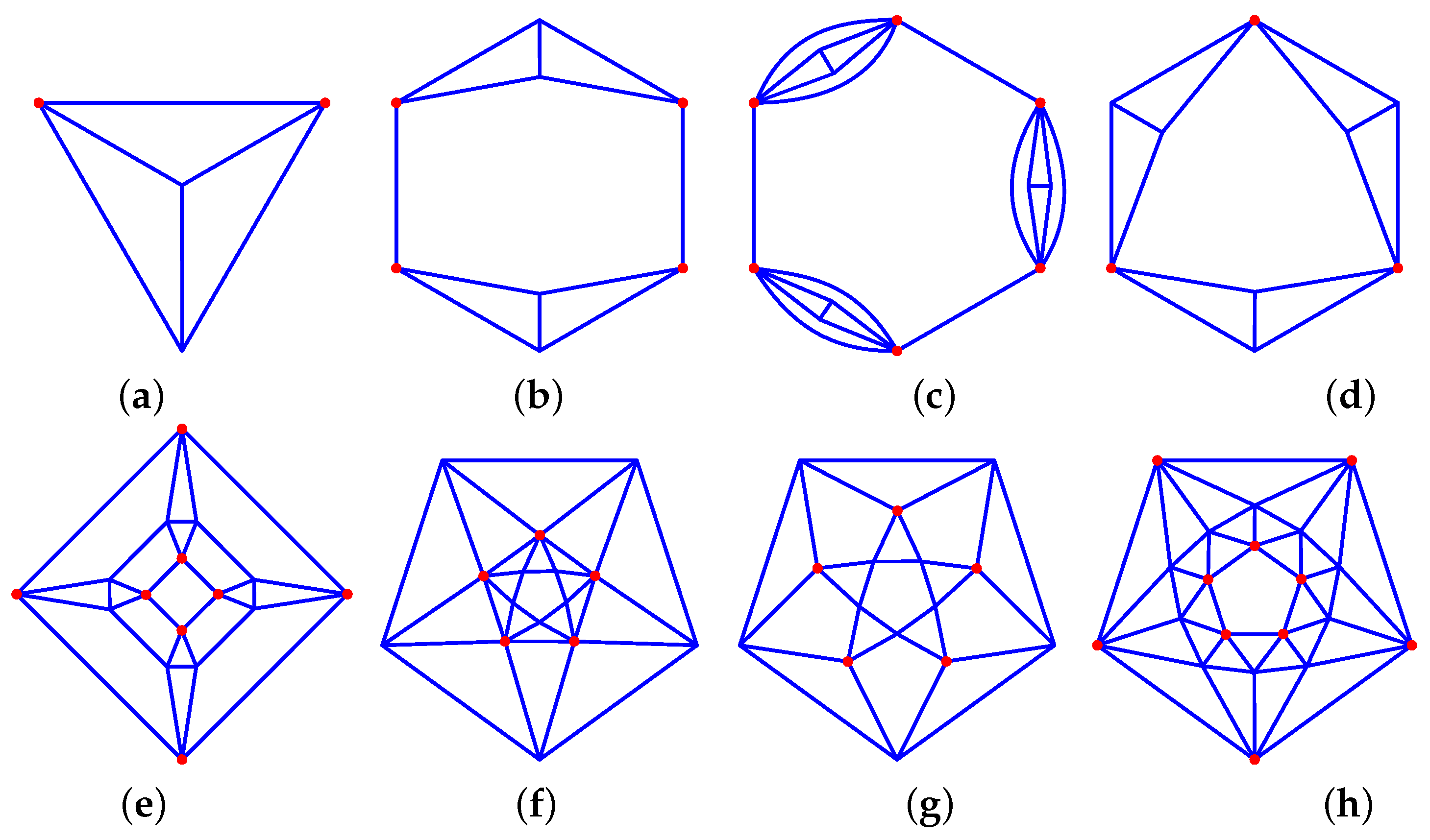
In what follows, we will be using some graph components to describe the biequivalent graphs. They are presented in Figure 4, where the blue dots represent the nodes that will be linked to the rest of the graph. We will also use the following abbreviations: P-gone for a polygon with P edges, P-star for a polygonal star with P branches, P-fan for polygonal fan with P blades, split P-fan for a split polygonal fan with P blades, inverted P-fan for inverted polygonal fans with P blades, and P-mosaic for mosaic with a P-gon at its centre. We also refer to pyramids, prisms, and antiprisms with a P-gonal base as, respectively, P-pyramids, P-prisms, and P-antiprisms.
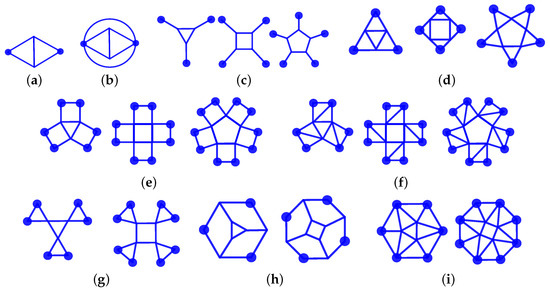
Figure 4.
(a) 2D diamond, (b) 2D bubble diamond, (c) linked P-gon. (d) polygonal stars, (e) polygonal fans, (f) polygonal split fans, (g) polygonal inverted fans, (h) linked P-gon face, (i) mosaic polygon.
4.1. Special Graphs
Some graphs do not fall in any special category and should be considered as special:
- Two alternating diamonds: 34_F8_4-1-3_4-2-1_V4_4, (see Figure 5a).
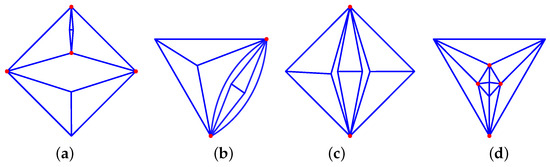 Figure 5. Special graphs: (a) 34_F8_4-1-3_4-2-1_V4_4, (b) 36_F8_4-1-2_4-2-1_V4_2, (c) 36_F9_3-2-2_6-2-1_V6_2, (d) 45_F12_4-2-1_8-1-2_V4_4.
Figure 5. Special graphs: (a) 34_F8_4-1-3_4-2-1_V4_4, (b) 36_F8_4-1-2_4-2-1_V4_2, (c) 36_F9_3-2-2_6-2-1_V6_2, (d) 45_F12_4-2-1_8-1-2_V4_4. - One 2D diamond and one 2D bubble diamond: 36_F8_4-1-2_4-2-1_V4_2, (see Figure 5b)
- Three 2D diamonds: 36_F9_3-2-2_6-2-1_V6_2, (see Figure 5c)
- Multitriangles: 45_F12_4-2-1_8-1-2_V4_4 (see Figure 5d).
4.2. Polygonal Dressing Graphs
- Replacing every second edge of a 2P-gone by a 2D diamond yields the following: 33_F2P+2_2-P-2P_2P-2-1_VP_P, , (see Figure 6a,b)
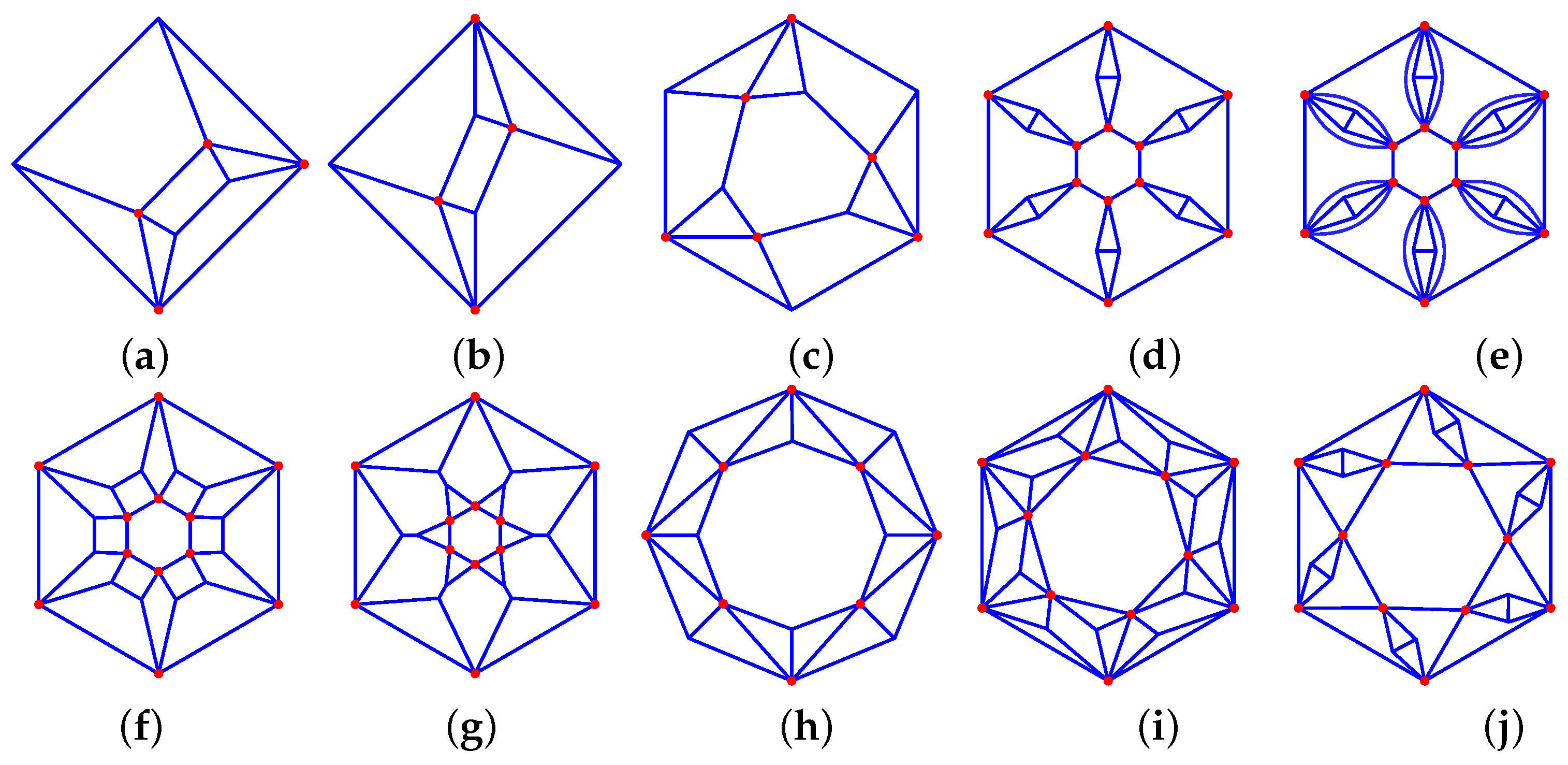
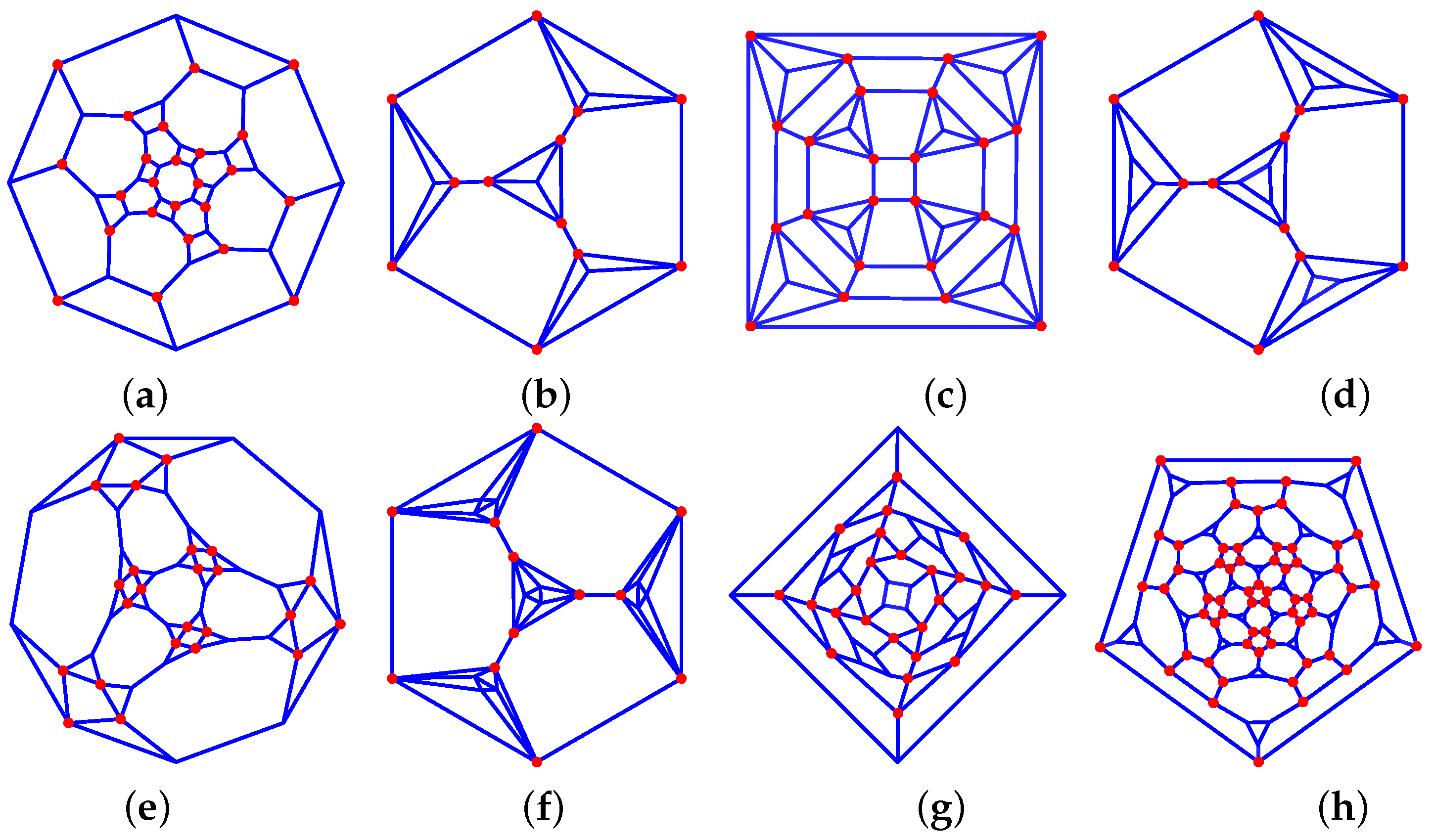
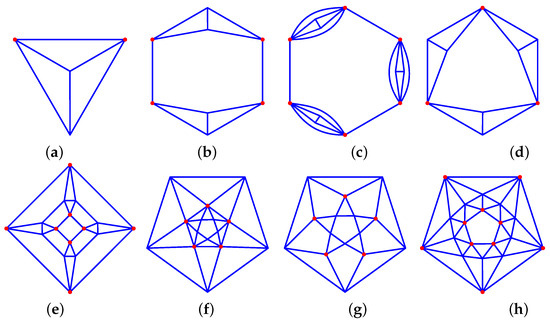 Figure 6. Dressed polygons: (a) 33_F4_2-1-2_2-2-1_V2_2, (b) 33_F6_2-2-4_4-2-1_V4_4, (c) 35_F14_2-0-6_6-1-2_6-2-1_V6_6, (d) 34_F8_2-3-3_6-2-1_V6_3, (e) 44_F18_2-0-4_8-2-1_8-2-2_V8_8, (f) 46_F18_2-4-0_8-1-2_8-2-1_V8_4. (g) 44_F17_2-5-0_5-2-2_10-2-1_V10_9, (h) 55_F32_2-0-5_10-1-2_20-2-1_V10_10.
Figure 6. Dressed polygons: (a) 33_F4_2-1-2_2-2-1_V2_2, (b) 33_F6_2-2-4_4-2-1_V4_4, (c) 35_F14_2-0-6_6-1-2_6-2-1_V6_6, (d) 34_F8_2-3-3_6-2-1_V6_3, (e) 44_F18_2-0-4_8-2-1_8-2-2_V8_8, (f) 46_F18_2-4-0_8-1-2_8-2-1_V8_4. (g) 44_F17_2-5-0_5-2-2_10-2-1_V10_9, (h) 55_F32_2-0-5_10-1-2_20-2-1_V10_10. - Replacing every second edge of a 2P-gon by a 2D bubble diamond yields the following: 35_F{4P+2}_2-0-{2P}_{2P}-1-2_{2P}-2-1_V{2P}_{2P}, (see Figure 6c).
- P joined up 2D diamonds yield the following: 34_F{2P+2}_2-{P}-{P}_{2P}-2-1_V4_2, , (see Figure 6d)
- Inverted P-fans on both sides of a P-gon: 44_F{4P+2}_2-0-P_{2P}-2-1_{2P}-2-2_V{2P}_{2P}, . (see Figure 6e).
- Two back-to-back P-stars on a polygon: 46_F{4P+2}_2-0-P_{2P}-1-2_{2P}-2-1_V{2P}_{P}, . (see Figure 6f).
- Two back-to-back P-stars: 44_F{3P+2}_2-P-0_P-2-2_2P}-2-1_V{2P}_{P}, . (see Figure 6g).
- Two P-mosaics back to back: 55_F{6P+2}_2-0-P_{2P}-1-2_{4P}-2-1_V{2P}_{2P}, . When , this is an icosahedron. (see Figure 6h).
4.3. Pyramid Derived Graphs
- P-pyramids with graphs of the following type: 3P_F{P+1}_1-P-0_0-P-2-1_VP_1, . (see Figure 7a).
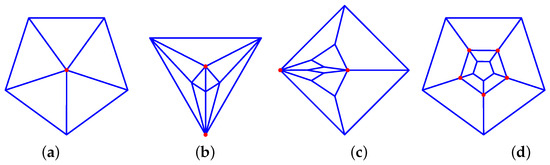 Figure 7. Dressed polygons: (a) 35_F6_1-5-0_5-2-1_V5_1, (b) 45_F10_10-1-2_V5_2, (c) 35_F10_10-3-1_V10_2, (d) 34_F12_2-5-0_10-2-2_V10_5.
Figure 7. Dressed polygons: (a) 35_F6_1-5-0_5-2-1_V5_1, (b) 45_F10_10-1-2_V5_2, (c) 35_F10_10-3-1_V10_2, (d) 34_F12_2-5-0_10-2-2_V10_5. - Two P-pyramids joined at the base: 4P_F{2P}_{2P}-1-2_V2_P, . is the octahedron. (see Figure 7b).
- P squares joined at a vertex, with two of them joined together: 3P_F{2P}_2P-1-3_V{2P}_2. (see Figure 7c).
- Two truncated P-pyramids joined at the base: 34_F{2P+2}_2-P-0_{2P}-2-2_V{2P}_P, , (see Figure 7d).
4.4. Prism Derived Graphs
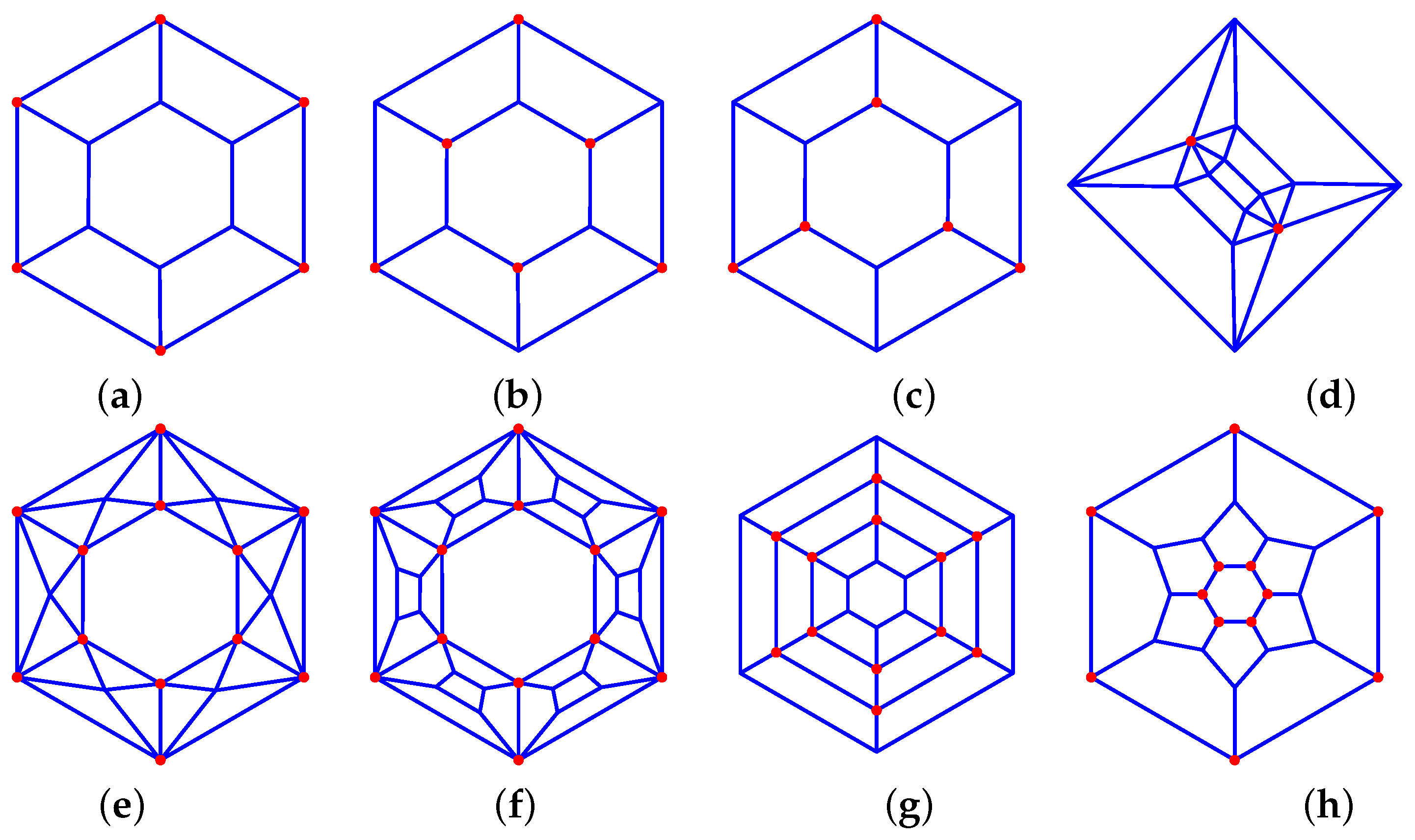
- The nodes of the prisms can be split in two symmetric subsets in two different ways: top base and bottom base nodes, F{P+2}_1-0-P_1-P-0_P-2-2_VP_P (see Figure 8a), or, for even P values, alternating nodes on top and bottom base F{2P}_{2P}-2-{P/2}-{P/2}_P-2-2_V6_6_a * (see Figure 8b), as well as F{2P}_{2P}-2-{P/2}-{P/2}_P-2-2_V6_6_b (see Figure 8c).
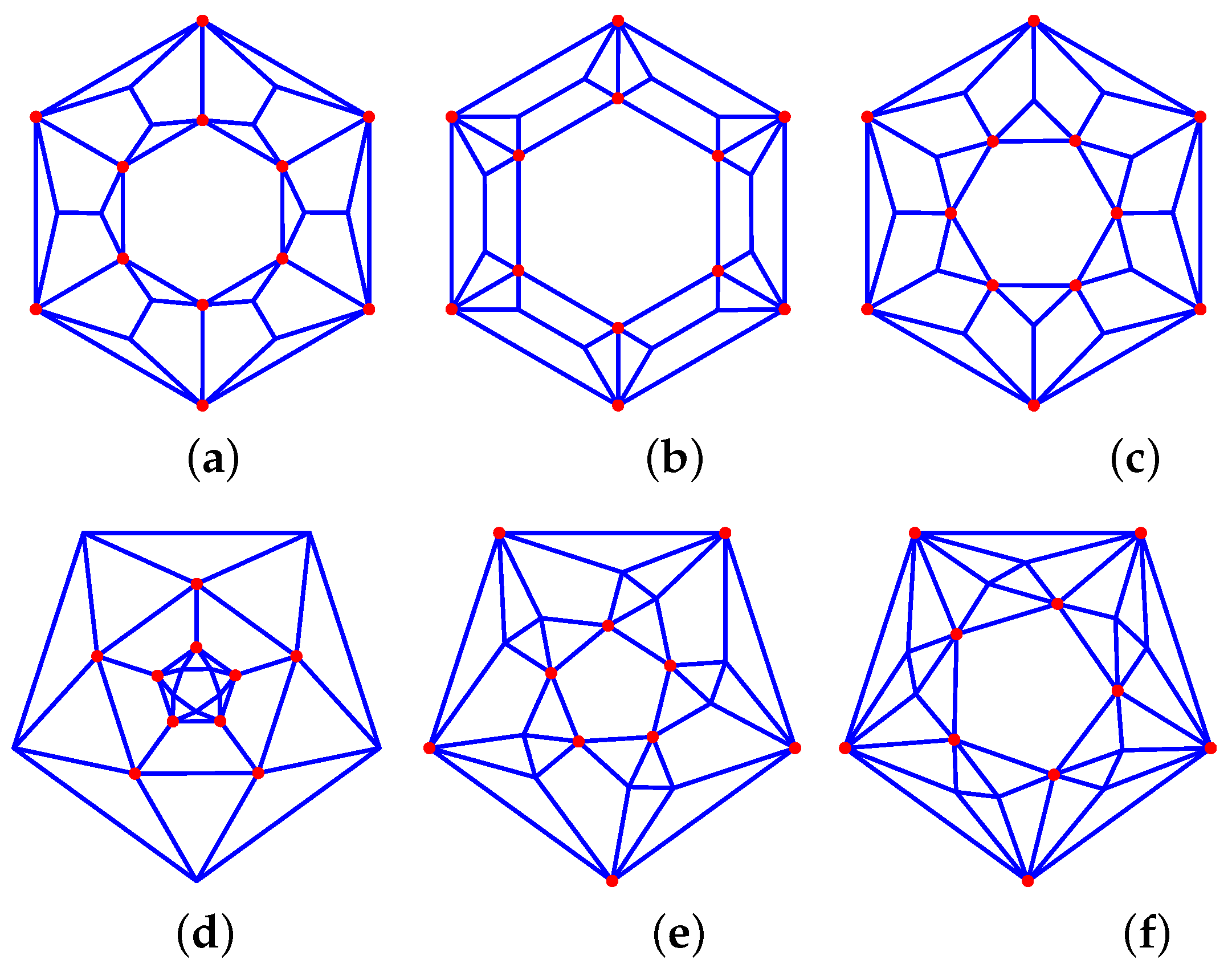
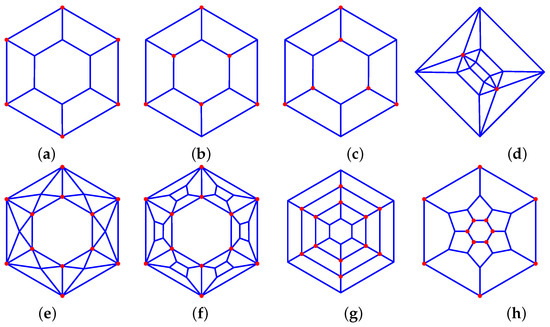 Figure 8. Prism-derived graphs: (a) 33_F8_1-0-6_1-6-0_6-2-2_V6_6, (b) 33_F8_2-3-3_6-2-2_V6_6_a *, (c) 33_F8_2-3-3_6-2-2_V6_6_b, (d) 46_F18_6-4-0_12-2-1_V12_2, (e) 45_F26_2-0-6_24-1-2_V6_12, (f) 35_F32_2-0-6_6-4-0_24-2-2_V24_12, (g) 34_F20_2-6-0_6-0-4_12-2-2_V12_12, (h) 33_F14_2-0-6_12-3-2_V12_12.
Figure 8. Prism-derived graphs: (a) 33_F8_1-0-6_1-6-0_6-2-2_V6_6, (b) 33_F8_2-3-3_6-2-2_V6_6_a *, (c) 33_F8_2-3-3_6-2-2_V6_6_b, (d) 46_F18_6-4-0_12-2-1_V12_2, (e) 45_F26_2-0-6_24-1-2_V6_12, (f) 35_F32_2-0-6_6-4-0_24-2-2_V24_12, (g) 34_F20_2-6-0_6-0-4_12-2-2_V12_12, (h) 33_F14_2-0-6_12-3-2_V12_12. - P-prisms with a P-pyramid on each base: 3P_F{3P}_P-0-4_{2P}-1-2_V2_{2P} (see Figure 8d).
- P-risms with 4-pyramids on the square faces: 44_F{4P+2}_2-0-P_{4P}-1-2_V{P}_{2P} , (see Figure 8e).
- P-prism with a truncated 4-pyramid on each side face: 35_F{5P+2}_2-0-P_P-4-0_{4P}_2-2_V{2P}_{2P} *, (see Figure 8f).
- P-prisms with a truncated P-pyramid on each base: 34_F{3P+2}_2-P-0_P-0-4_{2P}-2-2_V{2P}_{2P}, (see Figure 8g).
- P-prisms where the base is replaced by a linked P-gon: 33_F14_2-0-P_{2P}-3-2_V{2P}_{2P}, (see Figure 8h).
- A P-prism where every other side is split in two triangles: 34_F{3P+2}_2-P-P_P-2-2_{2P}-1-2_V{2P}_{2P} *, (see Figure 9a–c).
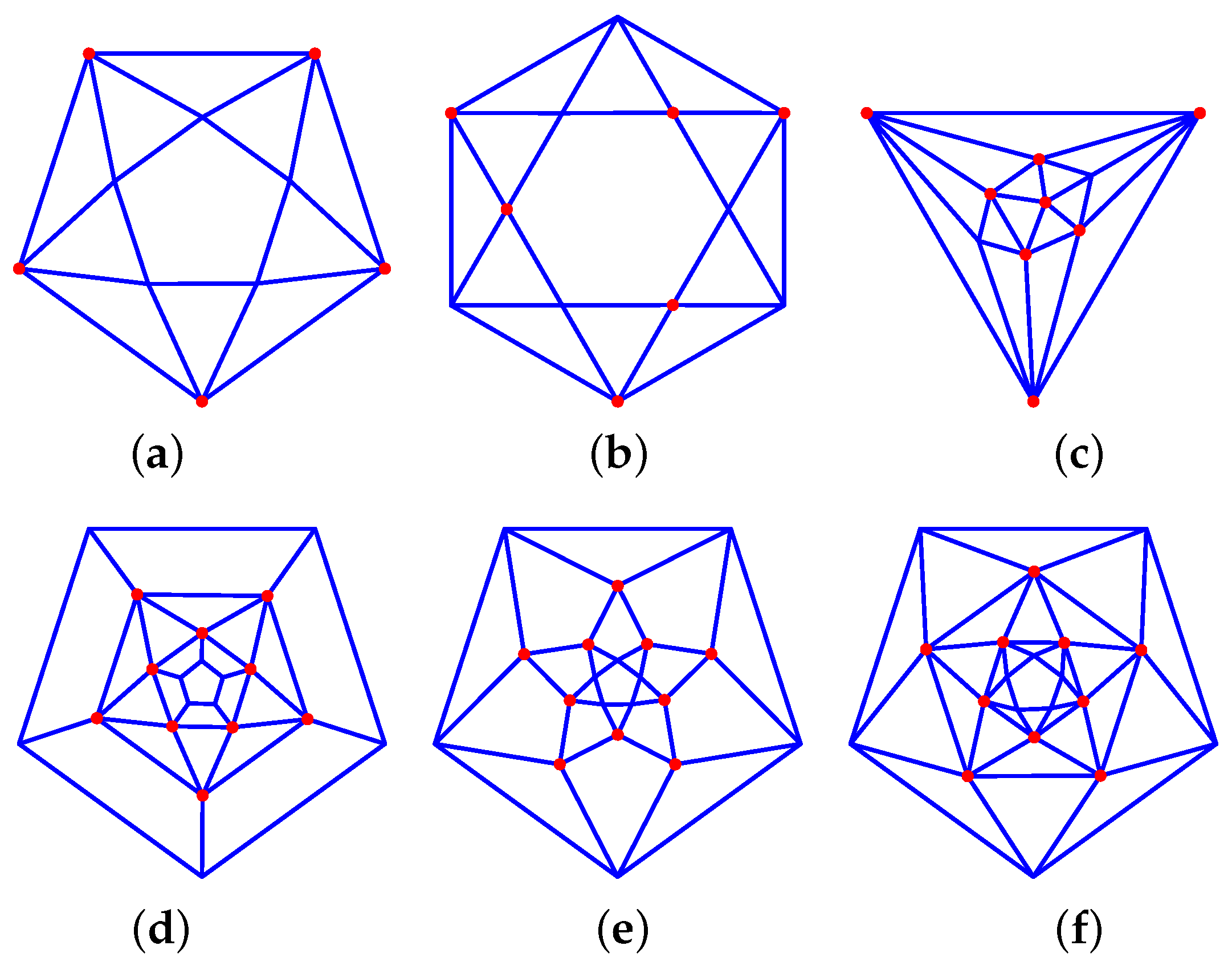
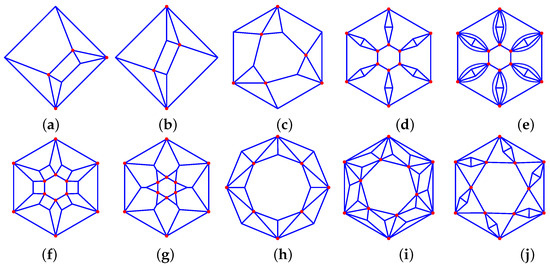 Figure 9. Prism-derived graphs: (a) 34_F8_4-1-2_4-2-2_V4_4_a (parallel cut), (b) 34_F8_4-1-2_4-2-2_V4_4_b *, (c) 34_F11_2-3-3_3-2-2_6-1-2_V6_6 *, (d) 34_F20_2-0-6_6-2-4_12-2-1_V12_12, (e) 36_F32_2-0-6_6-0-4_12-1-2_12-2-1_V12_12, (f) 34_F20_2-0-6_18-2-2_V12_12, (g) 34_F20_2-0-6_6-4-2_12-1-2_V12_12 (h) 35_F18_2-4-4_16-1-2_V8_8, (i) 36_F32_2-0-6_6-2-2_24-1-2_V12_12 *, (j) 35_F26_2-0-6_12-1-3_12-2-1_V12_12 *.
Figure 9. Prism-derived graphs: (a) 34_F8_4-1-2_4-2-2_V4_4_a (parallel cut), (b) 34_F8_4-1-2_4-2-2_V4_4_b *, (c) 34_F11_2-3-3_3-2-2_6-1-2_V6_6 *, (d) 34_F20_2-0-6_6-2-4_12-2-1_V12_12, (e) 36_F32_2-0-6_6-0-4_12-1-2_12-2-1_V12_12, (f) 34_F20_2-0-6_18-2-2_V12_12, (g) 34_F20_2-0-6_6-4-2_12-1-2_V12_12 (h) 35_F18_2-4-4_16-1-2_V8_8, (i) 36_F32_2-0-6_6-2-2_24-1-2_V12_12 *, (j) 35_F26_2-0-6_12-1-3_12-2-1_V12_12 *. - P-prisms where every side edge becomes a 2D diamond: 34_F{3P+2}_2-0-P_P-2-4_{2P}-2-1_V{2P}_{2P}, , (see Figure 9d)
- P-prisms where the links between the two bases become a 2D bubble diamond: 36_F{5P+2}_2-0-P_P-0-4_{2P}-1-2_{2P}-2-1_V{2P}_{2P}, , (see Figure 9e)
- P-prisms where the edges joining the bases are split into a square, and the two new nodes are merged with the adjacent one, hence tiling the sides of the prism with squares: 34_F{3P+2}_2-0-P_{3P}-2-2_V{2P}_{2P}, , (see Figure 9f).
- P-prims with P-star bases, where : 34_F{3P+2}_2-0-P_P-4-2_{2P}-1-2_V{2P}_{2P} (see Figure 9g).
- A 2P-prism where the squares are split asymmetrically into two triangles: 35_F{4P+2}_2-P-P_{4P}-1-2_V{2P}_{2P}, (see Figure 9h).
- P-prisms where the squares are split into four triangles and one square: 36_F{5P+2}_2-0-P_P-2-2_{4P}-1-2_V{2P}_{2P} *, , (see Figure 9i).
- P-prisms where every other vertex between the two bases becomes a 2D diamond: 35_F{4P+2}_2-0-P_{2P}-1-3_{2P}_2-1_V{2P}_{2P} *, , (see Figure 9j).
- P-prisms where the faces are split into two squares and two triangles: 35_F{4P+2}_2-0-P_{2P}-1-2_{2P}_2-2_V{2P}_{2P}, . This can be done in three different ways (see Figure 10a–c).
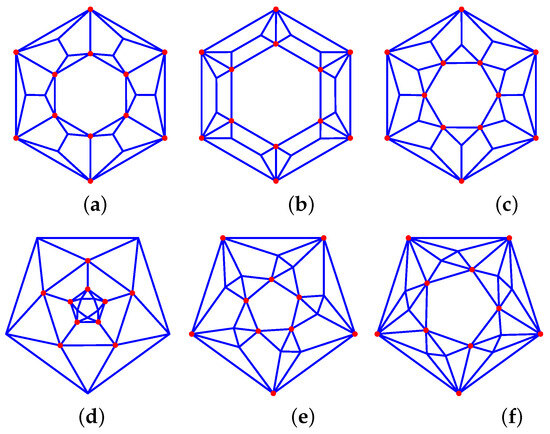 Figure 10. Prism-derived graphs: (a) 35_F26_2-0-6_12-1-2_12-2-2_V12_12_a, (b) 35_F26_2-0-6_12-1-2_12-2-2_V12_12_b, (c) 35_F26_2-0-6_12-1-2_12-2-2_V12_12_c, (d) 45_F27_2-5-0_5-0-4_10-1-2_10-2-1_V10_10, (e) F27_2-0-5_5-2-2_10-1-2_10-2-1_V10_10 *, (f) 46_F32_2-0-5_10-2-1_20-1-2_V10_10 *.
Figure 10. Prism-derived graphs: (a) 35_F26_2-0-6_12-1-2_12-2-2_V12_12_a, (b) 35_F26_2-0-6_12-1-2_12-2-2_V12_12_b, (c) 35_F26_2-0-6_12-1-2_12-2-2_V12_12_c, (d) 45_F27_2-5-0_5-0-4_10-1-2_10-2-1_V10_10, (e) F27_2-0-5_5-2-2_10-1-2_10-2-1_V10_10 *, (f) 46_F32_2-0-5_10-2-1_20-1-2_V10_10 *. - P-prism with a P-star on each base: 45_F{5P+2}_2-P-0_P-0-4_{2P}-1-2_{2P}-2-1_V{2P}_{2P}, , (see Figure 10d).
- P-prisms where the squares are split into three triangles and a square: 45_F{5P+2}_2-0-P_P-2-2_{2P}-1-2_{2P}-2-1_V{2P}_{2P} *, , (see Figure 10e).
- P-prisms where the squares are split into six triangles: 46_F{6P+2}_2-0-P_{2P}-2-1_{4P}-1-2_V{2P}_{2P} *, , (see Figure 10f).
4.5. Antiprism-Derived Graphs
- P-antiprisms where the two types of nodes are on each of the bases: 44_F{2P+2}_1-0-P_1-P-0_P-1-2_P-2-1_VP_P, (see Figure 11a).
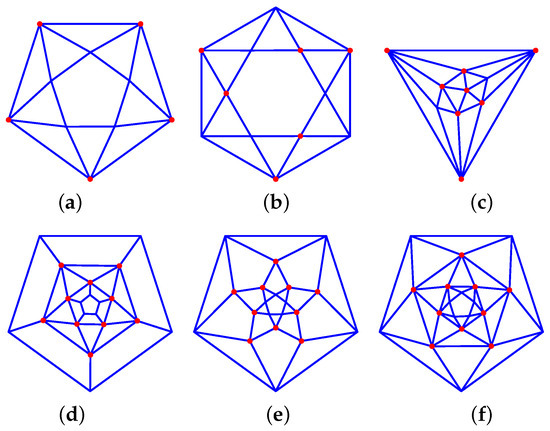 Figure 11. Antiprism-derived graphs: (a) 44_F12_1-0-5_1-5-0_5-1-2_5-2-1_V5_5, (b) 44_F14_2-3-3_6-1-2_6-2-1_V6_6 *, (c) 45_F16_8-0-3_8-1-2_V2_8, (d) 35_F22_2-5-0_10-0-3_10-2-2_V10_10, (e) 44_F22_2-5-0_10-1-3_10-2-1_V10_10, (f) 46_F32_2-5-0_10-0-3_10-1-2_10-2-1_V10_10.
Figure 11. Antiprism-derived graphs: (a) 44_F12_1-0-5_1-5-0_5-1-2_5-2-1_V5_5, (b) 44_F14_2-3-3_6-1-2_6-2-1_V6_6 *, (c) 45_F16_8-0-3_8-1-2_V2_8, (d) 35_F22_2-5-0_10-0-3_10-2-2_V10_10, (e) 44_F22_2-5-0_10-1-3_10-2-1_V10_10, (f) 46_F32_2-5-0_10-0-3_10-1-2_10-2-1_V10_10. - P-antiprisms where the two types of nodes alternate between the bases: 44_F{2P+2}_2-{P/2}-{P/2}_P-1-2_P-2-1_VP_P *, even, (see Figure 11b).
- P-antiprisms with a P-pyramid on each base: P5_F{4P}_{2P}-0-3_{2P}-1-2_V{2P}_{2P}, , (see Figure 11c).
- P-antiprisms with two truncated P-gonal base pyramids: 35_F{4P+2}_2-P-0_{2P}-0-3_{2P}_2-2_V{2P}_{2P}, , (see Figure 11d).
- P-antiprism with a P-star base: 44_F{4P+2}_2-P-0_{2P}-1-3_{2P}-2-1_V{2P}_{2P}, , (see Figure 11e).
- P-antiprisms with P-fans added to the two bases: 46_F{6P+2}_2-P-0_{2P}-0-3_{2P}-1-2_{2P}-2-1_V{2P}_{2P} *, , (see Figure 11f).
4.6. Platonic Solids-Derived Graphs
The nodes of the Platonic solids can be split into two symmetric families, but these graphs will also be characterised as part of other categories further done.
- Tetrahedron: 33_F4_2-1-2_2-2-1_V2_2.
- Cube: 33_F6_6-3-1_V6_2.
- Octahedron: 44_F8_8-2-1_V4_2.
- Dodecahedron: 33_F12_2-5-0_10-2-3_V10_10.
- Icosahedron: selecting two nodes on the poles of the solid 55_F20_10-2-1_10-3-0_V10_2.
- Icosahedron: selecting six nodes on the equator: 55_F20_2-3-0_6-2-1_12-1-2_V6_6.
- Platonic solids where the vertices become polygons, and the edges become two squares so that the faces of the solids end up with twice as many edges:
- –
- Tetrahedron: 34_F20_4-0-3_4-3-3_12-2-2_V12_12.
- –
- Cube: 34_F38_6-4-4_8-0-3_24-2-2_V24_24.
- –
- Octahedron: 34_F38_6-0-4_8-3-3_24-2-2_V24_24 (see Figure 12a).
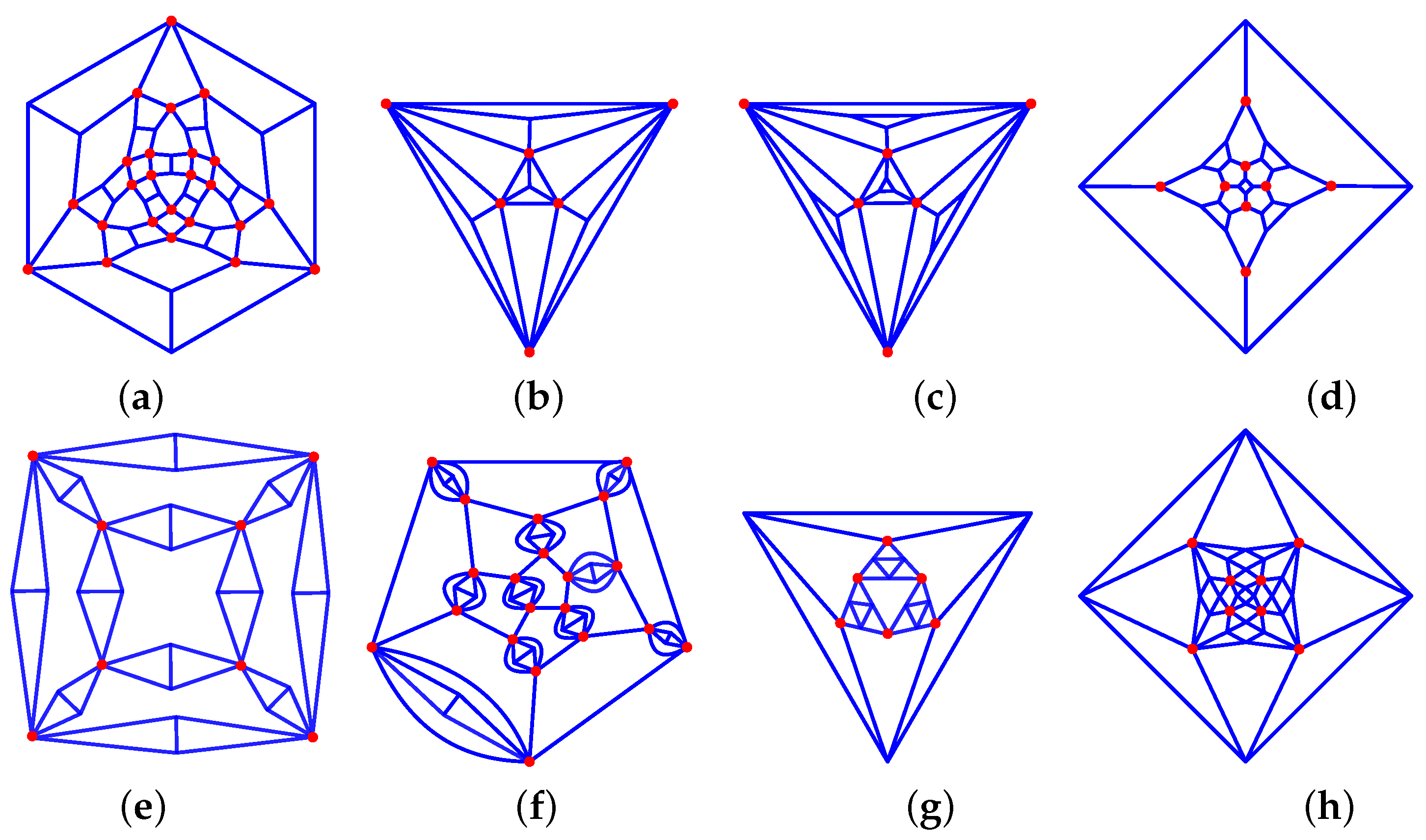
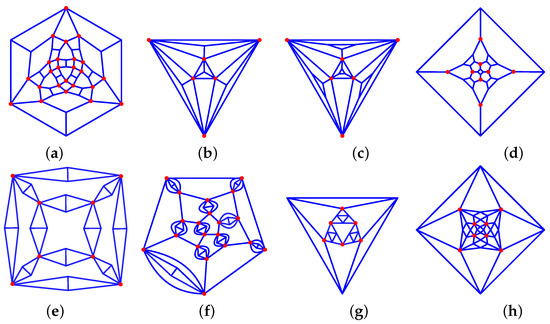 Figure 12. Platonic solids-derived graphs: (a) 34_F38_6-0-4_8-3-3_24-2-2_V24_24, (b) 36_F16_4-0-3_12-1-2_V4_6, (c) 36_F20_4-0-3_4-3-0_12-2-2_V12_6, (d) 33_F18_6-4-0_12-4-2_V24_8, (e) 36_F30_6-4-4_24-2-1_V24_8, (f) 36_F52_12-0-5_20-1-2_20-2-1_V20_20. (g) 44_F20_4-3-0_4-3-3_12-2-1_V12_6, (h) 46_F42_6-4-0_12-2-2_24-2-1_V24_8.
Figure 12. Platonic solids-derived graphs: (a) 34_F38_6-0-4_8-3-3_24-2-2_V24_24, (b) 36_F16_4-0-3_12-1-2_V4_6, (c) 36_F20_4-0-3_4-3-0_12-2-2_V12_6, (d) 33_F18_6-4-0_12-4-2_V24_8, (e) 36_F30_6-4-4_24-2-1_V24_8, (f) 36_F52_12-0-5_20-1-2_20-2-1_V20_20. (g) 44_F20_4-3-0_4-3-3_12-2-1_V12_6, (h) 46_F42_6-4-0_12-2-2_24-2-1_V24_8. - –
- Dodecahedron: 34_F92_12-5-5_20-0-3_60-2-2_V60_60.
- –
- Icosahedron: 34_F92_12-0-5_20-3-3_60-2-2_V60_60.
- Platonic solids where a pyramid is placed on four faces:
- –
- Octhedron: 36_F16_4-0-3_12-1-2_V4_6 (see Figure 12b).
- –
- Icosahedron: 36_F28_12-1-2_16-0-3_V4_12.
- Platonic solids where some faces become truncated pyramids:
- –
- Tetrahedron: 36_F16_4-3-0_12-2-2_V12_4.
- –
- Octahedron: 36_F20_4-0-3_4-3-0_12-2-2_V12_6 (see Figure 12c).
- –
- Icosahedron: 36_F32_4-3-0_12-2-2_16-0-3_V12_12.
- Platonic solids where some P-gonal faces become P-stars. Doing this, the tetrahedron becomes an octahedron, the cube becomes an the octahedron, and both become a cuboctahedron, while the dodecahedron and icosahedron both become an icosidodecahedron.
- Platonic solid where a face becomes a linked P-gon:
- –
- Tetrahedron: 33_F10_4-3-0_6-4-2_V12_4.
- –
- Cube: 33_F18_6-4-0_12-4-2_V24_8 (see Figure 12d).
- –
- Octahedron: 34_F20_8-3-0_12-4-2_V24_6.
- –
- Dodecahedron: 33_F42_12-5-0_30-4-2_V60_20.
- –
- Icosahedron: 35_F50_20-3-0_30-4-2_V60_12.
- Platonic solids where every edge becomes a 2D diamond. The octahedron and icosahedron lead to graphs with valency exceeding 6:
- –
- Tetrahedron: 36_F16_4-3-3_12-2-1_V12_4,
- –
- Cube: 36_F30_6-4-4_24-2-1_V24_8 (see Figure 12e),
- –
- Dodecahedron: 36_F72_12-5-5_60-2-1_V60_20.
- Platonic solids where some edges become a 2D bubble diamond:
- –
- Tetrahedron: 36_F12_4-0-3_4-1-2_4-2-1_V4_4.
- –
- Dodecahedron: 36_F52_12-0-5_20-1-2_20-2-1_V20_20 (see Figure 12f).
- Octahedrom where every other face is a P-star: 44_F20_4-3-0_4-3-3_12-2-1_V12_6 (see Figure 12g).
- Platonic solids with inverted P-fans replacing the faces. The octahedron and the icosahedron have, respectively, valency 4 and 5 nodes, and this leads to graphs with a valency exceeding six:
- –
- Tetrahedron: 46_F22_4-3-0_6-2-2_12-2-1_V12_4.
- –
- Cube: 46_F42_6-4-0_12-2-2_24-2-1_V24_8.
- –
- Dodecahedron: 46_F102_12-5-0_30-2-2_60-2-1_V60_20.
4.7. Archimedean Solids-Derived Graphs
- Truncated Platonic solids (the nodes of the other Archimedean solids cannot be split into two equivalent families):
- –
- Truncated octahedron: 33_F14_6-2-2_8-3-3_V12_12.
- –
- Truncated cube: 33_F14_4-0-3_4-3-0_6-4-4_V12_12.
- –
- Truncated cuboctahedron: 33_F26_6-4-4_8-3-3_12-2-2_V24_24 (see Figure 13a).
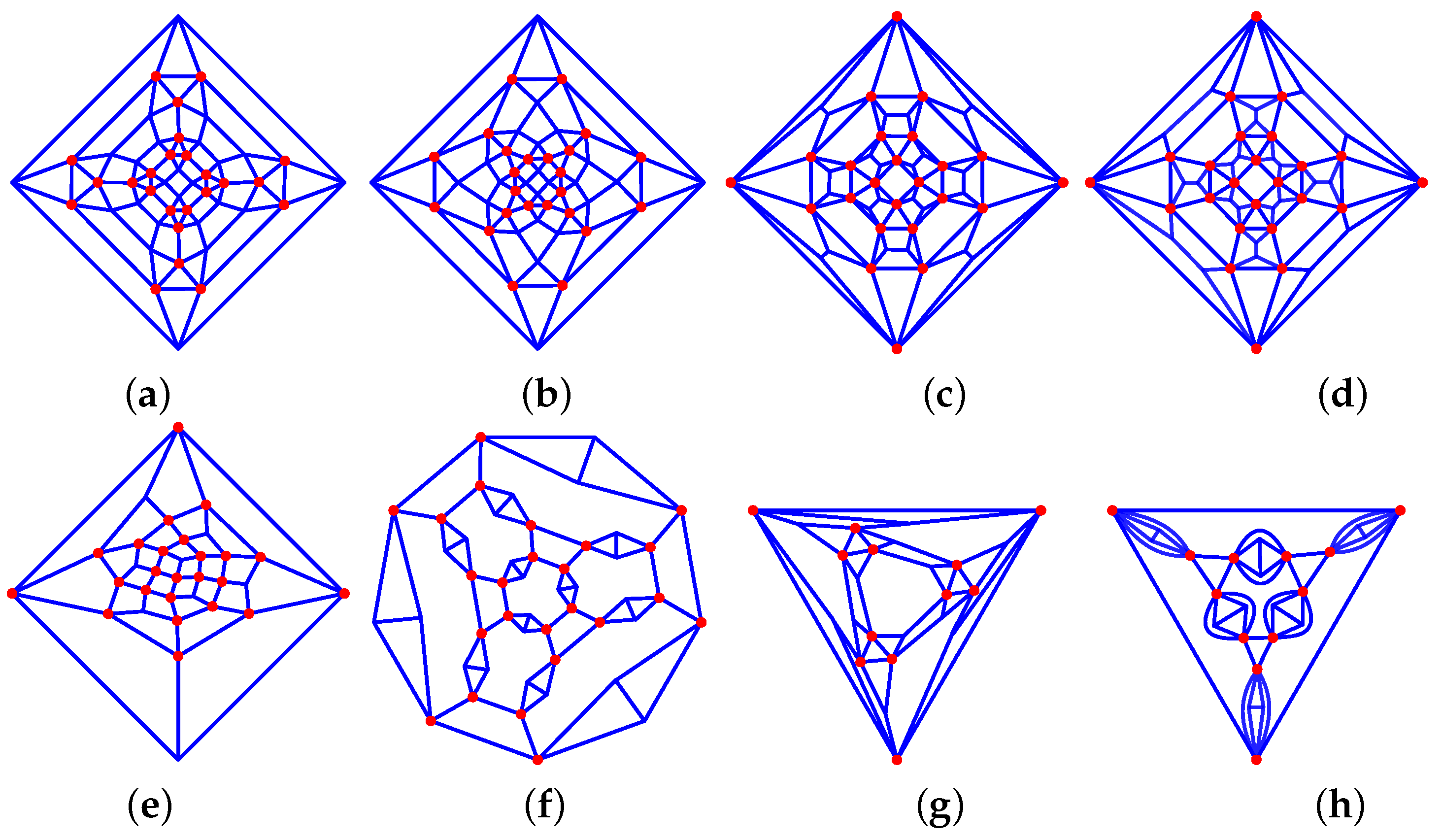
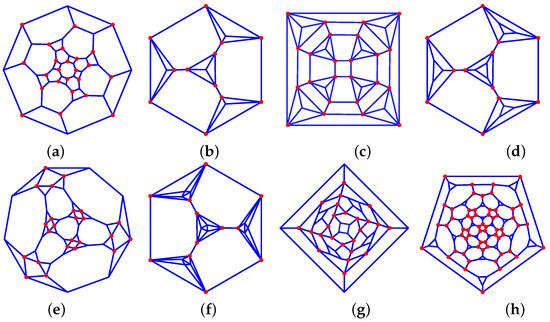 Figure 13. Archimedean solids-derived graphs: (a) 33_F26_6-4-4_8-3-3_12-2-2_V24_24, (b) 34_F16_4-0-6_12-1-2_V4_12, (c) 35_F42_18-0-4_24-1-2_V8_24, (d) 34_F20_4-0-6_4-3-0_12-2-2_V12_12, (e) 34_F38_6-0-4_8-6-3_24-1-2_V24_24, (f) 45_F32_4-0-6_4-3-0_12-1-2_12-2-1_V12_12 (g) 34_F38_6-4-0_8-0-3_24-2-3_V24_24 *, (h) 35_F26_6-0-4_8-3-0_12-4-4_V24_24.
Figure 13. Archimedean solids-derived graphs: (a) 33_F26_6-4-4_8-3-3_12-2-2_V24_24, (b) 34_F16_4-0-6_12-1-2_V4_12, (c) 35_F42_18-0-4_24-1-2_V8_24, (d) 34_F20_4-0-6_4-3-0_12-2-2_V12_12, (e) 34_F38_6-0-4_8-6-3_24-1-2_V24_24, (f) 45_F32_4-0-6_4-3-0_12-1-2_12-2-1_V12_12 (g) 34_F38_6-4-0_8-0-3_24-2-3_V24_24 *, (h) 35_F26_6-0-4_8-3-0_12-4-4_V24_24. - –
- Truncated icosidodecahedron: 33_F62_12-5-5_20-3-3_30-2-2_V60_60.
- Solids where a pyramid is placed on some of the faces of the truncated Platonic solids. Only the face that does not touch similar faces can be tiled like this, as otherwise, the equivalence is broken:
- –
- Truncated tetrahedron (triangles): 34_F16_4-0-6_12-1-2_V4_12 (see Figure 13b).
- –
- Truncated tetrahedron (hexagons): 56_F28_4-3-0_24-2-1_V12_4.
- –
- Truncated cube (triangles): 34_F30_6-0-8_24-1-2_V8_24.
- –
- Truncated octahedron (squares): 44_F32_8-6-0_24-2-1_V24_6.
- –
- Truncated octahedron (hexagons): 56_F54_6-4-0_48-2-1_V24_8.
- –
- Truncated dodecahedron (triangles): 34_F72_12-0-10_60-1-2_V20_60.
- –
- Truncated icosahedron (pentagons): 45_F80_20-6-0_60-2-1_V60_12.
- –
- Truncated icosahedron (hexagons): 56_F132_12-5-0_120-2-1_V60_20.
- Solids where a pyramid is placed on some faces of the Archimedean solids:
- –
- Cuboctahedron (every other triangle): 35_F22_4-0-3_6-0-4_12-1-2_V4_12.
- –
- Cuboctahedron (triangles): 36_F30_6-0-4_24-1-2_V8_12.
- –
- Cuboctahedron (squares): 46_F32_8-0-3_24-1-2_V6_12.
- –
- Rhombicuboctahedron (triangles): 35_F42_18-0-4_24-1-2_V8_24 (see Figure 13c).
- –
- Rhombicuboctahedron (6 squares): 45_F44_8-0-3_12-0-4_24-1-2_V6_24.
- –
- Rhombicuboctahedron (8 squares): 46_F62_6-0-4_8-0-3_48-1-2_V12_24.
- –
- Icosidodecahedron (triangles): 36_F72_12-0-5_60-1-2_V20_30.
- –
- Icosidodecahedron (pentagons): 56_F80_20-0-3_60-1-2_V12_30.
- –
- Snub dodecahedron (pentagons): 56_F140_60-1-2_80-0-3_V12_60 *.
- –
- Snub dodecahedron (20 triangles): 36_F132_12-0-5_60-0-3_60-1-2_V20_60 *.
- –
- Rhombicosididecahedron (triangles): 35_F102_12-0-5_30-0-4_60-1-2_V20_60.
- –
- Rhombicosididecahedron (squares): 46_F152_12-0-5_20-0-3_120-1-2_V30_60.
- –
- Rhombicosididecahedron (pentagons): 55_F110_20-3-0_30-4-0_60-2-1_V60_12.
- Truncated pyramid on truncated Platonic solids:
- –
- Truncated tetrahedron (triangles): 34_F20_4-0-6_4-3-0_12-2-2_V12_12 (see Figure 13d).
- –
- Truncated tetrahedron (hexagons): 35_F32_4-0-3_4-6-0_24-2-2_V24_12.
- –
- Truncated cube (triangles): 34_F38_6-0-8_8-3-0_24-2-2_V24_24.
- –
- Truncated cube (octagons): 35_F62_6-8-0_8-0-3_48-2-2_V48_24.
- –
- Truncated dodecahedron (decagons): 35_F152_12-10-0_20-0-3_120-2-2_V120_60.
- –
- Truncated icosahedron (pentagon): 34_F92_12-5-0_20-0-6_60-2-2_V60_60.
- –
- Truncated icosahedron (hexagon): 35_F152_12-0-5_20-6-0_120-2-2_V120_60.
- –
- Truncated octahedron (squares): 34_F38_6-4-0_8-0-6_24-2-2_V24_24.
- –
- Truncated octahedron (hexagons): 35_F62_6-0-4_8-6-0_48-2-2_V48_24.
- –
- Truncated dodecahedron (triangles): 34_F82_12-0-10_20-3-0_60-2-2_V60_60.
- Truncated pyramid on other Archimedean solids:
- –
- Snub cube (squares): 36_F62_6-4-0_24-2-2_32-0-3_V24_24 *.
- –
- Snub cube (8 triangles): 36_F62_6-0-4_8-3-0_24-0-3_24-2-2_V24_24 *.
- –
- Rhombicuboctahedron (triangles): 35_F50_8-3-0_18-0-4_24-2-2_V24_24.
- –
- Snub dodecahedron (pentagons): 36_F152_12-5-0_60-2-2_80-0-3_V60_60 *.
- –
- Snub dodecahedron (triangles): 36_F152_12-0-5_20-3-0_60-0-3_60-2-2_V60_60 *.
- –
- Cuboctahedron (squares): 36_F38_6-4-0_8-0-3_24-2-2_V24_12.
- –
- Cuboctahedron(triangles): 36_F38_6-0-4_8-3-0_24-2-2_V24_12.
- –
- Cuboctahedron (every other triangles): 35_F26_4-0-3_4-3-0_6-0-4_12-2-2_V12_12.
- –
- Rhombicuboctahedron (6 squares): 35_F50_6-4-0_8-0-3_12-0-4_24-2-2_V24_24.
- –
- Rhombicuboctahedron (8 squares): 36_F74_6-0-4_8-0-3_12-4-0_48-2-2_V48_24.
- –
- Icosidodecahedron (pentagons): 36_F92_12-5-0_20-0-3_60-2-2_V60_30.
- –
- Icosidodecahedron (triangles): 36_F92_12-0-5_20-3-0_60-2-2_V60_30.
- –
- Rhombicosidodecahedron (triangles): 35_F122_12-0-5_20-3-0_30-0-4_60-2-2_V60_60.
- –
- Rhombicosidodecahedron (pentagons): 35_F122_12-5-0_20-0-3_30-0-4_60-2-2_V60_60.
- Archimedean solids where some P-gonal faces become P-stars. This is only possible when there is a P-fold rotation symmetry around the center of the P-gonal face:
- –
- Truncated tetrahedron (triangles): 34_F20_4-0-3_4-6-3_12-1-2_V12_12.
- –
- Truncated octahedron (squares): 34_F38_6-0-4_8-6-3_24-1-2_V24_24.
- –
- Truncated icosahedron (pentagons): 34_F92_12-0-5_20-6-3_60-1-2_V60_60.
- –
- Cuboctahedron (triangles): 44_F38_6-4-4_8-3-0_24-2-1_V24_12.
- –
- Cuboctahedron (every other triangle): 44_F26_4-0-3_4-3-0_6-2-4_12-2-1_V12_12.
- –
- Cuboctahedron (squares): 44_F38_6-4-0_8-3-3_24-2-1_V24_12.
- –
- Rhombicuboctahedron (triangles): 44_F50_6-0-4_8-3-0_12-2-4_24-2-1_V24_24.
- –
- Rhombicuboctahedron (squares): 44_F50_6-0-4_8-3-0_12-4-2_24-1-2_V24_24.
- –
- Icosidodecahedron(triangles): 44_F92_12-5-5_20-3-0_60-2-1_V60_30.
- –
- Icosidodecahedron (pentagons): 44_F92_12-0-5_20-3-3_60-2-1_V60_30.
- –
- Snub cube (squares): 45_F62_6-4-0_8-0-3_24-1-3_24-2-1_V24_24 *.
- –
- Snub cube (eight triangles): 45_F62_6-0-4_8-3-0_24-1-3_24-2-1_V24_24 *.
- –
- Snub dodecahedron (pentagons): 45_F152_12-5-0_20-0-3_60-1-3_60-2-1_V60_60 *.
- –
- Snub dodecahedron (20 triangles): 45_F152_12-0-5_20-3-0_60-1-3_60-2-1_V60_60 *.
- –
- Rhombicosidodecahedron (triangles): 44_F122_12-0-5_20-3-0_30-2-4_60-2-1_V60_60.
- –
- Rhombicosidodecahedron (pentagons): 44_F122_12-0-5_20-3-0_30-4-2_60-1-2_V60_60.
- Archimedean solids with some P-faces filled with a P-stars.
- A P-star-filled cuboactahedron and icosidodecahedron have valency 8 nodes. The following solids have nodes with valencies that are too large: truncated cubes (octagons), truncated octagons (hexagons), snub cubes, snub dodecahedrons, truncated dodecahedrons (decagons), and truncated icosahedron (hexagons).
- –
- Truncated tetrahedron (triangles): 45_F32_4-0-6_4-3-0_12-1-2_12-2-1_V12_12 (see Figure 13f).
- –
- Truncated tetrahedron (hexagons): 45_F32_4-0-3_4-3-0_12-1-3_12-2-1_V12_12 *.
- –
- Truncated cube (triangles): 45_F62_6-0-8_8-3-0_24-1-2_24-2-1_V24_24.
- –
- Truncated octahedron (squares): 45_F62_6-4-0_8-0-6_24-1-2_24-2-1_V24_24.
- –
- Truncated dodecahedron (triangles): 45_F152_12-0-10_20-3-0_60-1-2_60-2-1_V60_60.
- –
- Truncated icosahedron (pentagons): 45_F152_12-5-0_20-0-6_60-1-2_60-2-1_V60_60.
- –
- Cuboctahedron (four triangles): 34_F20_4-0-3_4-6-3_12-1-2_V12_12.
- –
- Rhomicuboctahedron (six squares): 46_F74_6-4-0_8-0-3_12-0-4_24-1-2_24-2-1_V24_24.
- –
- Rhomicuboctahedron (triangles): 46_F74_8-3-0_18-0-4_24-1-2_24-2-1_V24_24.
- –
- Rhomicosidodecahedron (pentagon): 46_F182_12-5-0_20-0-3_30-0-4_60-1-2_60-2-1.
- –
- Rhomicosidodecahedron (triangles): 46_F182_12-0-5_20-3-0_30-0-4_60-1-2_60-2-1.
- Linked P-gon-filled truncated Platonic solids:
- –
- Truncated tetrahedron: 34_F20_4-0-3_4-3-0_12-2-3_V12_12 *.
- –
- Truncated cube: 34_F38_6-4-0_8-0-3_24-2-3_V24_24 * (see Figure 13g).
- –
- Truncated octahedron: 34_F38_6-0-4_8-3-0_24-2-3_V24_24 *.
- –
- Truncated dodecahedron: 34_F92_12-5-0_20-0-3_60-2-3_V60_60 *.
- –
- Truncated icosahedron: 34_F92_12-0-5_20-3-0_60-2-3_V60_60 *.
- Archimedean solids where a face becomes a linked P-gon. When applying this to the cuboctahedron, one obtains the truncated cube and the truncated octahedron. When applying this to the icosidodecahedron, one obtains the truncated dodecahedron and the truncated icosahedron. This cannot be applied to the truncated Platonic solids, as this gives the same solid (truncation face) of an nonequivalent graph (adjacent faces):
- –
- The snub cube (eight triangles) gives 34_F38_6-0-4_8-3-0_24-2-3_V24_24 (a linked P-gon-filled truncated octahedron).
- –
- The snub cube (squares) gives 34_F38_6-4-0_8-0-3_24-2-3_V24_24 (a linked P-gon-filled truncated cube).
- –
- The snub dodecahedron (20 triangles) gives 34_F92_12-0-5_20-3-0_60-2-3_V60_60 (a linked P-gon-filled truncated icosahedron).
- –
- The snub dodecahedron (pentagons) gives 34_F92_12-5-0_20-0-3_60-2-3_V60_60 (a linked P-gon-filled truncated dodecahedron).
- –
- Rhombicuboctahedron: 35_F26_6-0-4_8-3-0_12-4-4_V24_24 (see Figure 13h),.
- –
- Rhombicosidodecahedron: 33_F62_12-0-5_20-3-0_30-4-4_V60_60.
- Truncated Platonic solids where some the 2P faces are filled with P-fans (). This can be done in two different ways:
- –
- Truncated tetrahedron: 45_F32_4-0-3_4-3-0_12-1-2_12-2-2_V12_12_a.
- –
- Truncated tetrahedron: 45_F32_4-0-3_4-3-0_12-1-2_12-2-2_V12_12_b.
- –
- Truncated cube 1: 45_F62_6-4-0_8-0-3_24-1-2_24-2-2_V24_24_a (see Figure 14a).
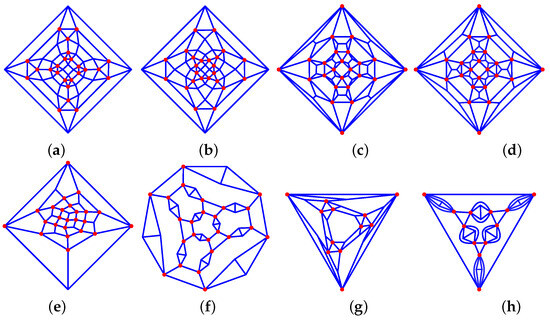 Figure 14. Archimedean solids-derived graphs: (a) 45_F62_6-4-0_8-0-3_24-1-2_24-2-2_V24_24_a, (b) 45_F62_6-4-0_8-0-3_24-1-2_24-2-2_V24_24_b, (c) 36_F62_6-0-4_8-0-3_24-1-2_24-2-2_V24_24_a, (d) 36_F62_6-0-4_8-0-3_24-1-2_24-2-2_V24_24_b, (e) 34_F30_6-0-4_24-1-3_V8_24 *, (f) 34_F38_6-0-4_8-3-6_24-2-1_V24_24, (g) 35_F26_4-0-3_4-3-3_6-2-2_12-1-2_V12_12 *, (h) 36_F32_4-0-3_4-0-6_12-1-2_12-2-1_V12_12.
Figure 14. Archimedean solids-derived graphs: (a) 45_F62_6-4-0_8-0-3_24-1-2_24-2-2_V24_24_a, (b) 45_F62_6-4-0_8-0-3_24-1-2_24-2-2_V24_24_b, (c) 36_F62_6-0-4_8-0-3_24-1-2_24-2-2_V24_24_a, (d) 36_F62_6-0-4_8-0-3_24-1-2_24-2-2_V24_24_b, (e) 34_F30_6-0-4_24-1-3_V8_24 *, (f) 34_F38_6-0-4_8-3-6_24-2-1_V24_24, (g) 35_F26_4-0-3_4-3-3_6-2-2_12-1-2_V12_12 *, (h) 36_F32_4-0-3_4-0-6_12-1-2_12-2-1_V12_12. - –
- Truncated cube 2: 45_F62_6-4-0_8-0-3_24-1-2_24-2-2_V24_24_b (see Figure 14b).
- –
- Truncated cctahedron 1: 45_F62_6-0-4_8-3-0_24-1-2_24-2-2_V24_24_a.
- –
- Truncated octahedron 2: 45_F62_6-0-4_8-3-0_24-1-2_24-2-2_V24_24_b.
- –
- Truncated dodecahedron 1: 45_F152_12-5-0_20-0-3_60-1-2_60-2-2_V60_60_a.
- –
- Truncated dodecahedron 2: 45_F152_12-5-0_20-0-3_60-1-2_60-2-2_V60_60_b.
- –
- Truncated icosahedron 1: 45_F152_12-0-5_20-3-0_60-1-2_60-2-2_V60_60_a.
- –
- Truncated icosahedron 2: 45_F152_12-0-5_20-3-0_60-1-2_60-2-2_V60_60_b.
- Archimedean solids where squares are split into two squares and two triangles. This can be done in two different ways:
- –
- Rhombicubotcahedron: 36_F62_6-0-4_8-0-3_24-1-2_24-2-2_V24_24_a (see Figure 14c).
- –
- Rhombicubotcahedron: 36_F62_6-0-4_8-0-3_24-1-2_24-2-2_V24_24_b (see Figure 14d).
- –
- Rhombicosidodecahedron: 36_F152_12-0-5_20-0-3_60-1-2_60-2-2_V60_60_a.
- –
- Rhombicosidodecahedron: 36_F152_12-0-5_20-0-3_60-1-2_60-2-2_V60_60_b.
- Truncated Platonic solids with 2P-gon faces split into P squares:
- –
- Truncated tetrahedron: 34_F16_4-0-3_12-1-3_V4_12 *.
- –
- Truncated cube: 44_F32_8-3-0_24-3-1_V24_6 *.
- –
- Truncated octahedron: 34_F30_6-0-4_24-1-3_V8_24 * (see Figure 14e).
- –
- Truncated icosahedron: 34_F72_12-0-5_60-1-3_V20_60 *.
- –
- Truncated dodecahedron: 45_F80_20-3-0_60-3-1_V60_12 *.
- As truncated Platonic solids have a 2-fold symmetry around the centre of the edges shared by two identical faces, one can replace the edge with a 2D diamond. For the truncated cube and truncated dodecahedron, this leads to faces with more than 10 edges:
- –
- Truncated tetrahedron: 34_F20_4-0-3_4-3-6_12-2-1_V12_12.
- –
- Truncated octahedron: 34_F38_6-0-4_8-3-6_24-2-1_V24_24 (see Figure 14f).
- –
- Truncated icosahedron: 34_F92_12-0-5_20-3-6_60-2-1_V48_60.
- Archimedean solids with squares linking triangles are split into two triangles and a square. This requires a 2-fold rotation symmetry of the solid around the split square:
- –
- Split cuboctahedron: 35_F26_4-0-3_4-3-3_6-2-2_12-1-2_V12_12 * (see Figure 14g).
- –
- Rhombicuboctahedron: 35_F50_6-4-4_8-0-3_12-2-2_24-1-2_V24_24 *.
- –
- Rhombicuboctahedron: 35_F50_6-0-4_8-3-3_12-2-2_24-1-2_V24_24 *.
- –
- Rhombicosidodecahedron: 35_F122_12-0-5_20-3-3_30-2-2_60-1-2_V60_60 *.
- –
- Rhombicosidodecahedron: 35_F122_12-5-5_20-0-3_30-2-2_60-1-2_V60_60 *.
- Archimedean solids where some edges become a 2D bubble diamonds:
- –
- Truncated tetrahedron: 36_F32_4-0-3_4-0-6_12-1-2_12-2-1_V12_12 (see Figure 14h).
- –
- Truncated cube: 36_F62_6-0-8_8-0-3_24-1-2_24-2-1_V24_24.
- –
- Truncated octahedron: 36_F62_6-0-4_8-0-6_24-1-2_24-2-1_V24_24.
- –
- Truncated dodecahedron: 36_F152_12-0-10_20-0-3_60-1-2_60-2-1_V60_60.
- –
- Truncated icosahedron: 36_F152_12-0-5_20-0-6_60-1-2_60-2-1.
- Archimedean solids where some squares are split intro four triangles:
- –
- Cuboctahedron: 36_F32_4-0-3_4-3-3_24-1-2_V12_12 * (see Figure 15a).
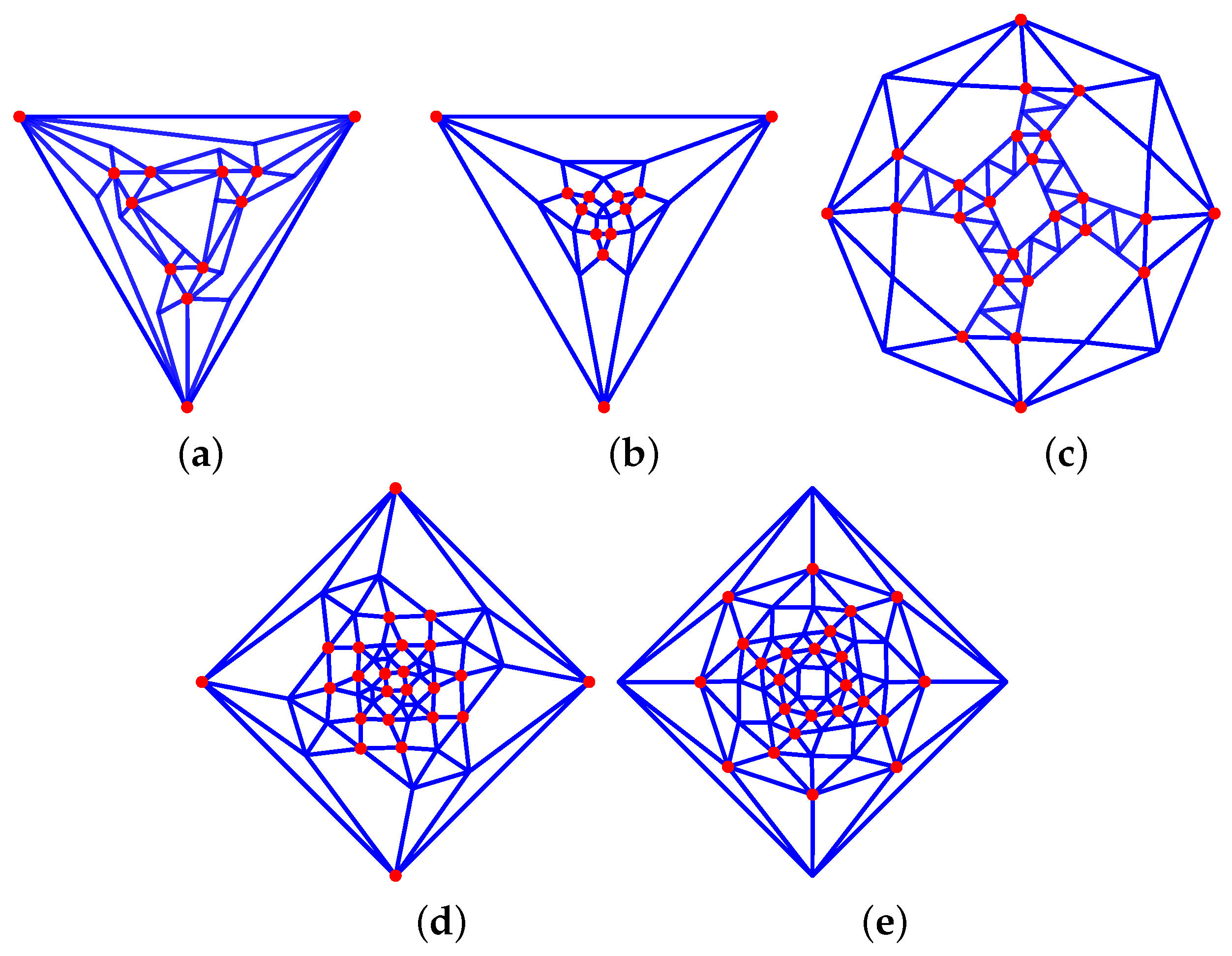
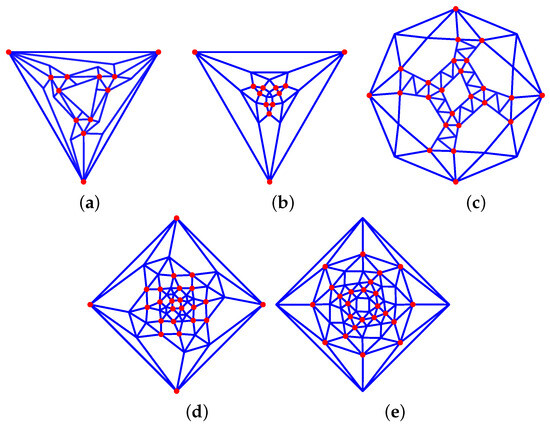 Figure 15. Archimedean solids-derived graphs: (a) 36_F32_4-0-3_4-3-3_24-1-2_V12_12 *, (b) 44_F26_4-0-3_4-3-0_18-2-2_V12_12, (c) 45_F62_6-4-4_8-0-3_24-1-2_24-2-1_V24_24 *, (d) 55_F74_6-0-4_8-3-0_12-2-2_24-1-2_24-2-1_V24_24 *, (e) 56_F86_6-4-0_8-0-3_24-2-1_48-1-2_V24_24 *.
Figure 15. Archimedean solids-derived graphs: (a) 36_F32_4-0-3_4-3-3_24-1-2_V12_12 *, (b) 44_F26_4-0-3_4-3-0_18-2-2_V12_12, (c) 45_F62_6-4-4_8-0-3_24-1-2_24-2-1_V24_24 *, (d) 55_F74_6-0-4_8-3-0_12-2-2_24-1-2_24-2-1_V24_24 *, (e) 56_F86_6-4-0_8-0-3_24-2-1_48-1-2_V24_24 *. - –
- Rhombicuboctahedron: 36_F32_4-0-3_4-3-3_24-1-2_V12_12 *.
- –
- Rhombicuboctahedron: 36_F62_6-4-4_8-0-3_48-1-2_V24_24 *.
- –
- Rhombicosidodecahedron: 36_F152_12-0-5_20-3-3_120-1-2_V60_60 *.
- –
- Rhombicosidodecahedron: 36_F152_12-5-5_20-0-3_120-1-2_V60_60 *.
- Truncated Platonic solids where the faces are replaced by P-fans. This can only be done with valency 3 graphs without exceeding the maximum valency, which we consider as follows:
- –
- Truncated tetrahedron: 44_F26_4-0-3_4-3-0_18-2-2_V12_12.
- –
- Truncated cube and truncated octahedron:44_F26_4-0-3_4-3-0_6-2-4_12-2-1_V12_12 (see Figure 14b).
- –
- Truncated dodecahedron and truncated icosahedron:44_F122_12-0-5_20-3-0_90-2-2_V60_60.
- Archimedean solids where the squares are split into four triangles to form braided links:
- –
- Cuboctahedron: 45_F32_4-0-3_4-3-3_12-1-2_12-2-1_V12_12 *.
- –
- Rhombicuboctahedron that is parallel braided: 45_F62_6-0-4_8-3-3_24-1-2_24-2-1_V24_24 *.
- –
- Rhombicuboctahedron that is perpendicular braided: 45_F62_6-4-4_8-0-3_24-1-2_24-2-1_V24_24 * (see Figure 14c).
- –
- Rhombicosidodecahedron that is parallel braided: 45_F152_12-5-0_20-0-3_60-1-3_60-2-1_V60_6 *.
- –
- Rhombicosidodecahedron that is perpendicular braided: 45_F152_12-5-5_20-0-3_60-1-2_60-2-1_V60_60 *.
- Truncated Platonic solids with 2P-gonal faces replaced by split P-fans. For the truncated cube and truncated icosahedron, this leads to nodes with valencies exceeding six:
- –
- Truncated tetrahedron: 55_F38_4-0-3_4-3-0_6-2-2_12-1-2_12-2-1_V12_12 *.
- –
- Truncated octahedron: 55_F74_6-0-4_8-3-0_12-2-2_24-1-2_24-2-1_V24_24 * (see Figure 14d).
- –
- Truncated dodecahedron: 55_F182_12-0-5_20-3-0_30-2-2_60-1-2_60-2-1_V60_60 *.
- Truncated Platonic solids where the faces are P-mosaics:
- –
- Truncated tetrahedron: 56_F44_4-0-3_4-3-0_12-2-1_24-1-2_V12_12 *.
- –
- Truncated cube: 56_F86_6-4-0_8-0-3_24-2-1_48-1-2_V24_24 *.
- –
- Truncated octahedron: 56_F86_6-0-4_8-3-0_24-2-1_48-1-2_V24_24 *.
- –
- Truncated icosahedron: 56_F212_12-0-5_20-3-0_60-2-1_120-1-2_V60_60 *.
- –
- Truncated dodecahedron: 56_F212_12-5-0_20-0-3_60-2-1_120-1-2_V60_60 *.
4.8. Other Solids-Derived Graphs
- For solids with valency 4 nodes and a 2-fold rotational symmetry around each node, one can replace the node with a 2D diamond:
- –
- Octahedron: 34_F20_8-3-3_12-1-2_V12_12 * (see Figure 16a).
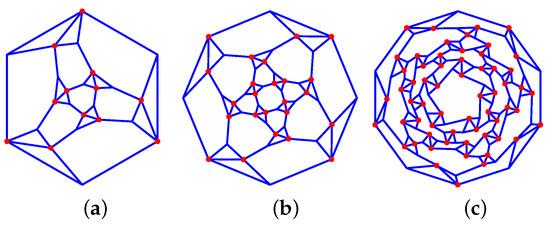 Figure 16. Other solids-derived graphs: (a) 34_F20_8-3-3_12-1-2_V12_12 *, (b) 34_F38_6-4-4_8-3-3_24-1-2_V24_24 *, (c) 34_F92_12-5-5_20-3-3_60-1-2_V60_60 *.
Figure 16. Other solids-derived graphs: (a) 34_F20_8-3-3_12-1-2_V12_12 *, (b) 34_F38_6-4-4_8-3-3_24-1-2_V24_24 *, (c) 34_F92_12-5-5_20-3-3_60-1-2_V60_60 *. - –
- Cuboctahedron: 34_F38_6-4-4_8-3-3_24-1-2_V24_24 * (see Figure 16b).
- –
- Icosidodecahedron: 34_F92_12-5-5_20-3-3_60-1-2_V60_60 * (see Figure 16c).
4.9. Dual of Archimedean Solids Graphs
The planar graphs of the dual of Archimedean solids with two inequivalent type of faces have nodes that can be split into two families. These are the following:
- Triakis tetrahedron: 36_F12_12-1-2_V4_4 (see Figure 17a).
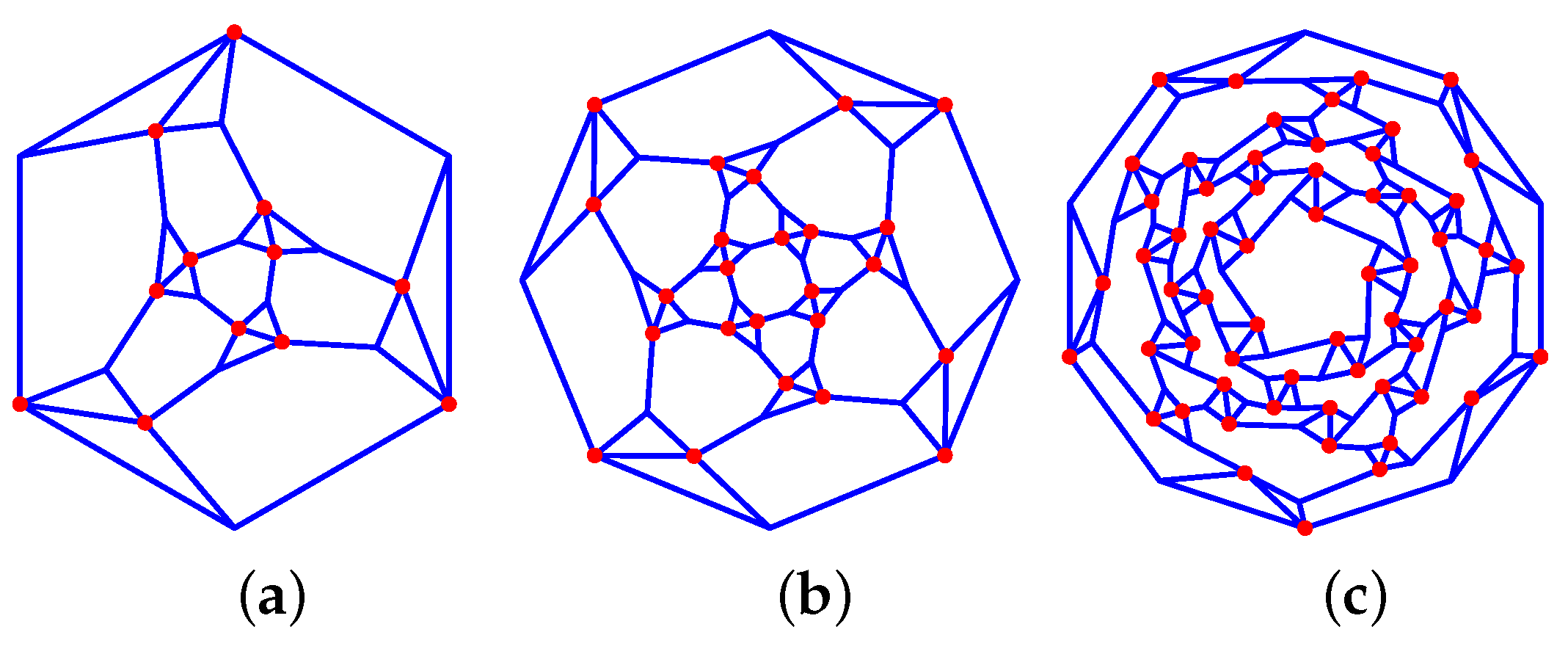
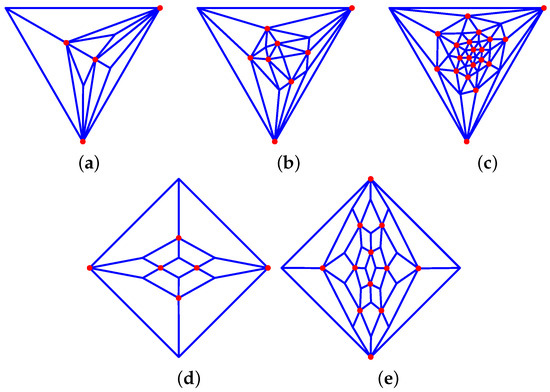 Figure 17. Archimedean solids-derived graphs: (a) Triakis tetrahedron: 36_F12_12-1-2_V4_4. (b) Triakis hexahedron: 46_F24_24-1-2_V6_8. (c) Pentakis dodecahedron: 56_F60_60-1-2_V12_20. (d) Rhomic dodecahedron: 34_F12_12-2-2_V8_6. (e) Rhomic tricontahedron: 35_F30_30-2-2_V20_12.
Figure 17. Archimedean solids-derived graphs: (a) Triakis tetrahedron: 36_F12_12-1-2_V4_4. (b) Triakis hexahedron: 46_F24_24-1-2_V6_8. (c) Pentakis dodecahedron: 56_F60_60-1-2_V12_20. (d) Rhomic dodecahedron: 34_F12_12-2-2_V8_6. (e) Rhomic tricontahedron: 35_F30_30-2-2_V20_12. - Triakis hexahedron: 46_F24_24-1-2_V6_8 (see Figure 17b).
- Pentakis dodecahedron: 56_F60_60-1-2_V12_20 (see Figure 17c).
- Rhomic dodecahedron: 34_F12_12-2-2_V8_6 (see Figure 17d).
- Rhomic tricontahedron: 35_F30_30-2-2_V20_12 (see Figure 17e).
The planar graphs of the dual of the truncated cube and the truncated dodecahedron have valencies exceeding six and are hence not presented here.
5. Conclusions
In this paper, we have defined biequivalent graphs as graphs made out of two families of nodes equivalent in modulo to an automorphism of the graph. We have found 430 graphs made out of up to 300 faces ranging from triangles to decagons and with valencies ranging between three and six.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/axioms13070437/s1. graphs_full_list.pdf: a graphic representation of all the graphs that we have identified.
Funding
This research was funded by the Leverhulme Trust Research Project Grants RPG-2020-306.
Data Availability Statement
The software to determine all the biequivalent planar graphs is available from Zenodo: https://doi.org/10.5281/zenodo.11059064. The PGC node links and vector graphics for all the graphs are available from Zenodo: https://doi.org/10.5281/zenodo.11059440.
Acknowledgments
I would like to thank Árpad Lukács for our useful discussions. Some of the graphics where created or edited using Inkscape: https://inkscape.org/ (accessed on 20 June 2024).
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| p-cage | Polyhedral cages |
| PGC | Potential graph characteristics |
| TRAP | trp RNA-binding attenuation protein |
Appendix A
A maximal planar graph is a graph for which adding one edge would render the graph nonplanar. Every maximal planar graph is made out of triangles. This means that using F, E, and V for, respectively, the number of faces, edges, and nodes, we have
As the sum of the valencies of each node of the graph is , the average valency of the graph is
which is then strictly smaller than six. This means that maximal planar graphs must have at least one node of a valency less than six, and as nonmaximal graphs, they can be obtained by removing edges from some maximal graphs; this implies that it is impossible to have planar graphs where all the nodes have a valency of six.
References
- Piette, B.M.A.G.; Kowalczyk, A.; Heddle, J.G. Characterization of near-miss connectivity-invariant homogeneous convex polyhedral cages. Proc. R. Soc. A 2022, 478, 20210679. [Google Scholar] [CrossRef] [PubMed]
- Malay, A.D.; Heddle, J.G.; Tomita, S.; Iwasaki, K.; Miyazaki, N.; Sumitomo, K.; Yanagi, H.; Yamashita, I.; Uraoka, Y. Gold nanoparticle-induced formation of artificial protein capsids. Nano Lett. 2012, 12, 2056–2059. [Google Scholar] [CrossRef] [PubMed]
- Piette, B.M.A.G.; Lukács, A. Near-Miss Symmetric Polyhedral Cages. Symmetry 2023, 15, 717. [Google Scholar] [CrossRef]
- Piette, B.M.A.G.; Lukács, A. Near-Miss Bi-Homogenous Symmetric Polyhedral Cages. Symmetry 2023, 15, 1804. [Google Scholar] [CrossRef]
- Coxeter, H.S.M. Regular Polytopes; Dover Publications: Mineola, NY, USA, 1973. [Google Scholar]
- Malay, A.D.; Miyazaki, N.; Biela, A.; Chakraborti, S.; Majsterkiewicz, K.; Stupka, I.; Kaplan, C.S.; Kowalczyk, A.; Piette, B.M.; Hochberg, G.K.; et al. An ultra-stable gold-coordinated protein cage displaying reversible assembly. Nature 2019, 569, 438–442. [Google Scholar] [CrossRef] [PubMed]
- Stupka, I.; Biela, A.P.; Piette, B.; Kowalczyk, A.; Majsterkiewicz, K.; Borzęcka-Solarz, K.; Naskalska, A.; Heddle, J.G. An artificial protein cage made from a 12-membered ring. J. Mater. Chem. B 2024, 12, 436–447. [Google Scholar] [CrossRef] [PubMed]
- Chakraborti, S.; Lin, T.Y.; Glatt, S.; Heddle, J.G. Enzyme encapsulation by protein cages. RSC Adv. 2020, 10, 13293–13301. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Gao, R.; Tan, H.; Li, S.; Ma, S.; Tang, Y.; Zhang, K.; Zhang, Z.; Fan, Q.; Yang, J.; Zhang, X.E.; et al. A prototype protein nanocage minimized from carboxysomes with gated oxygen permeability. Proc. Natl. Acad. Sci. USA 2022, 119, e2104964119. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Avakyan, N.; Kakkis, A.; Hoffnagle, A.M.; Han, K.; Li, Y.; Zhang, Z.; Choi, T.S.; Na, Y.; Yu, C.J.; et al. Protein Assembly by Design. Chem. Rev. 2021, 121, 13701–13796. [Google Scholar] [CrossRef]
- Percastegui, E.G.; Ronson, T.K.; Nitschke, J.R. Design and Applications of Water-Soluble Coordination Cages. Chem. Rev. 2020, 120, 13480–13544. [Google Scholar] [CrossRef]
- Cristie-David, A.S.; Marsh, E.N.G. Metal-dependent assembly of a protein nano-cage. Protein Sci. 2019, 28, 1620–1629. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Furukawa, H.; Sakamoto, K.; Inaba, H.; Matsuura, K. Anticancer Activity of Reconstituted Ribonuclease S-Decorated Artificial Viral Capsid. ChemBioChem 2022, 23, e202200220. [Google Scholar] [CrossRef] [PubMed]
- Olshefsky, A.; Richardson, C.; Pun, S.H.; King, N.P. Engineering Self-Assembling Protein Nanoparticles for Therapeutic Delivery. Bioconjug Chem. 2022, 33, 2018–2034. [Google Scholar] [CrossRef] [PubMed]
- Luo, X.; Liu, J. Ultrasmall Luminescent Metal Nanoparticles: Surface Engineering Strategies for Biological Targeting and Imaging. Adv. Sci. 2022, 9, e2103971. [Google Scholar] [CrossRef] [PubMed]
- Naskalska, A.; Borzęcka-Solarz, K.; Różycki, J.; Stupka, I.; Bochenek, M.; Pyza, E.; Heddle, J.G. Artificial Protein Cage Delivers Active Protein Cargos to the Cell Interior. Biomacromolecules 2021, 22, 4146–4154. [Google Scholar] [CrossRef] [PubMed]
- Edwardson, T.G.W.; Tetter, S.; Hilvert, D. Two-tier supramolecular encapsulation of small molecules in a protein cage. Nat. Commun. 2020, 11, 5410. [Google Scholar] [CrossRef] [PubMed]
- Stupka, I.; Azuma, Y.; Biela, A.P.; Imamura, M.; Scheuring, S.; Pyza, E.; Woźnicka, O.; Maskell, D.P.; Heddle, J.G. Chemically induced protein cage assembly with programmable opening and cargo release. Sci. Adv. 2022, 8, eabj9424. [Google Scholar] [CrossRef] [PubMed]
- Miller, J.E.; Castells-Graells, R.; Arbing, M.A.; Munoz, A.; Jiang, Y.X.; Espinoza, C.T.; Nguyen, B.; Moroz, P.; Yeates, T.O. Design of Beta-2 Microglobulin Adsorbent Protein Nanoparticles Biomolecules. Biomolecules 2023, 13, 1122. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, E.; Böhringer, D.; Van De Waterbeemd, M.; Leibundgut, M.; Zschoche, R.; Heck, A.J.; Ban, N.; Hilvert, D. Structure and assembly of scalable porous protein cages. Nat. Commun. 2017, 8, 14663. [Google Scholar] [CrossRef]
- Mashaghi, A.R.; Ramezanpour, A.; Karimipour, V. Investigation of a protein complex network. Eur. Phys. J. B 2004, 41, 113–121. [Google Scholar] [CrossRef][Green Version]
- Bjorken, J.D.; Drell, S.D. Relativistic Quantum Fields; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Vecchio, F. Brain network connectivity assessed using graph theory in frontotemporal dementia. Neurology 2013, 81, 134–143. [Google Scholar] [CrossRef]
- Biggs, N.; Lloyd, E.; Wilson, R. Graph Theory; Oxford University Press: Oxford, UK, 1986. [Google Scholar]
- Biggs, N. Algebraic Graph Theory, 2nd ed.; Cambridge University Press: Cambridge, UK, 1993; pp. 118–140. ISBN 0-521-45897-8. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).