Bicubic Splines for Fast-Contracting Control Nets
Abstract
1. Introduction
- is a 8-piece bi-3 (bi-cubic) construction.
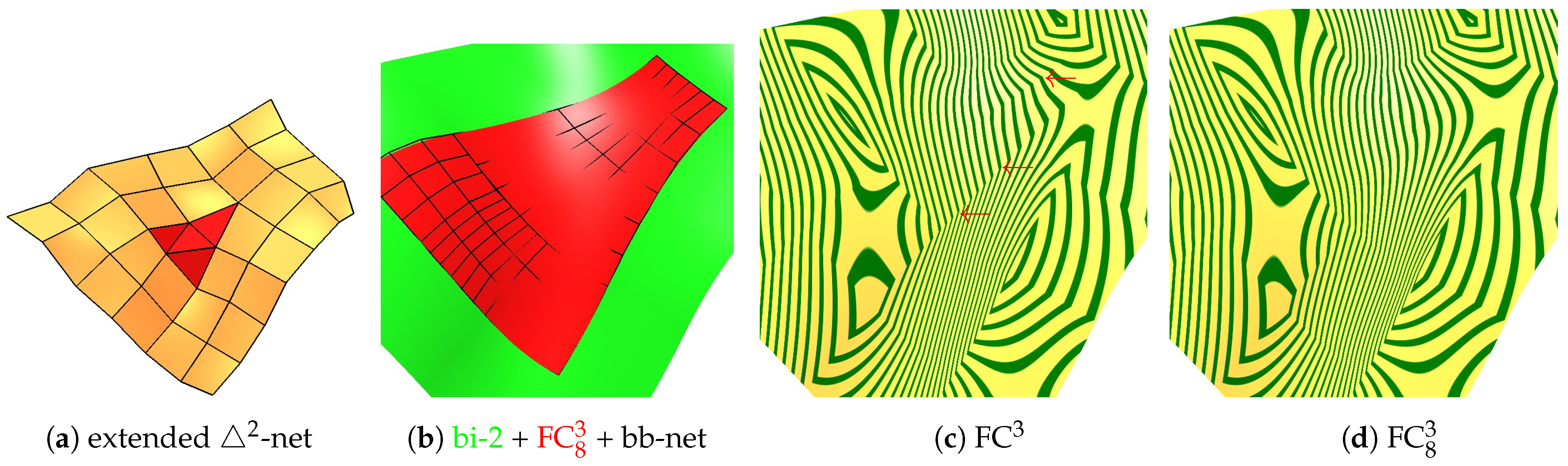
- yields improved shape compared to FC3, measured empirically with a more uniformly highlighted line distribution, and has fewer polynomial pieces, the minimal number required for a good shape.
- The formulas for generating bi-3 patches are linear in the input control net, and hence can be collected into a matrix.
- The implementation of can so be reduced to gathering the control net in a vector of points and multiplying the vector by a matrix.
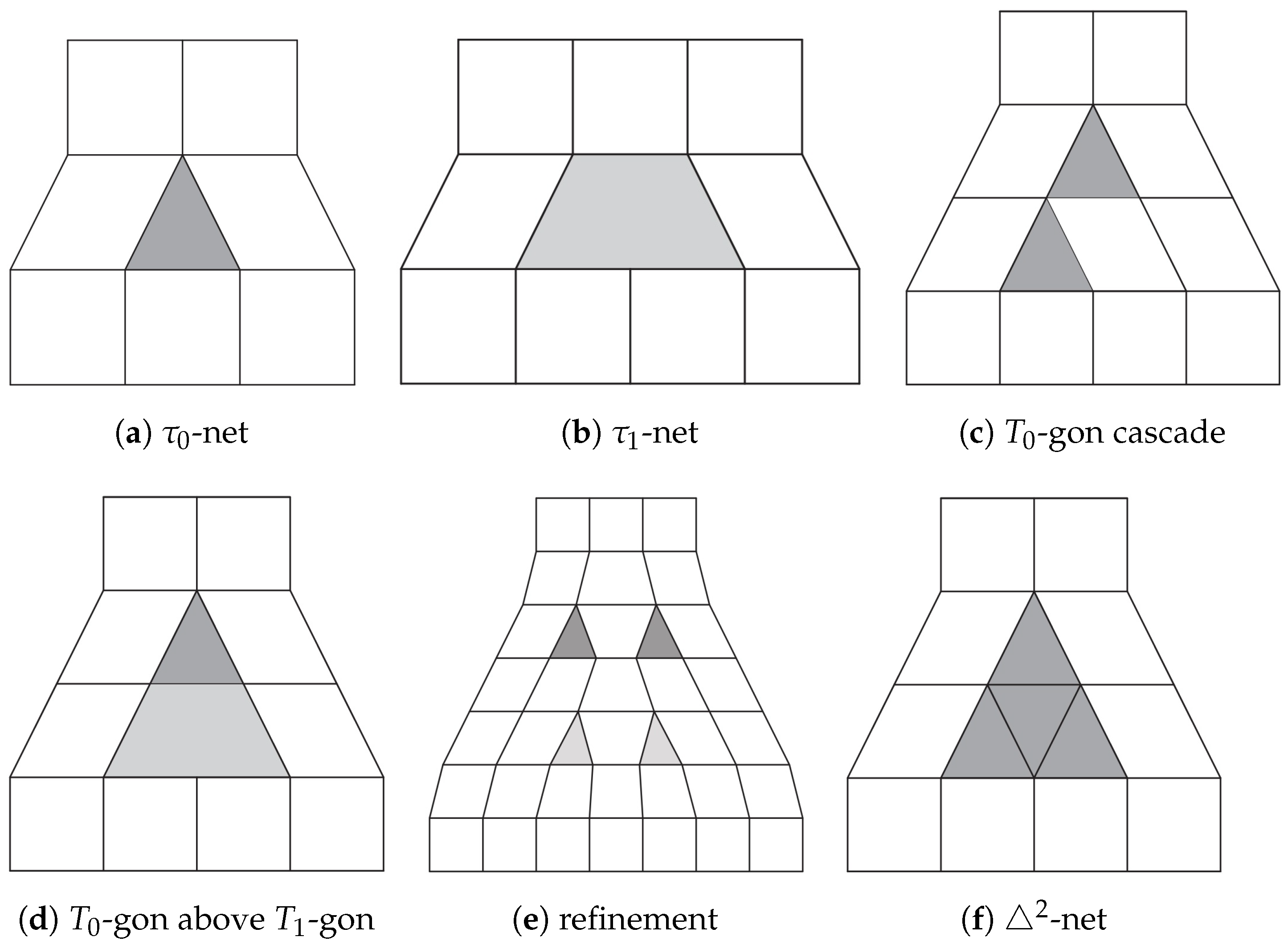
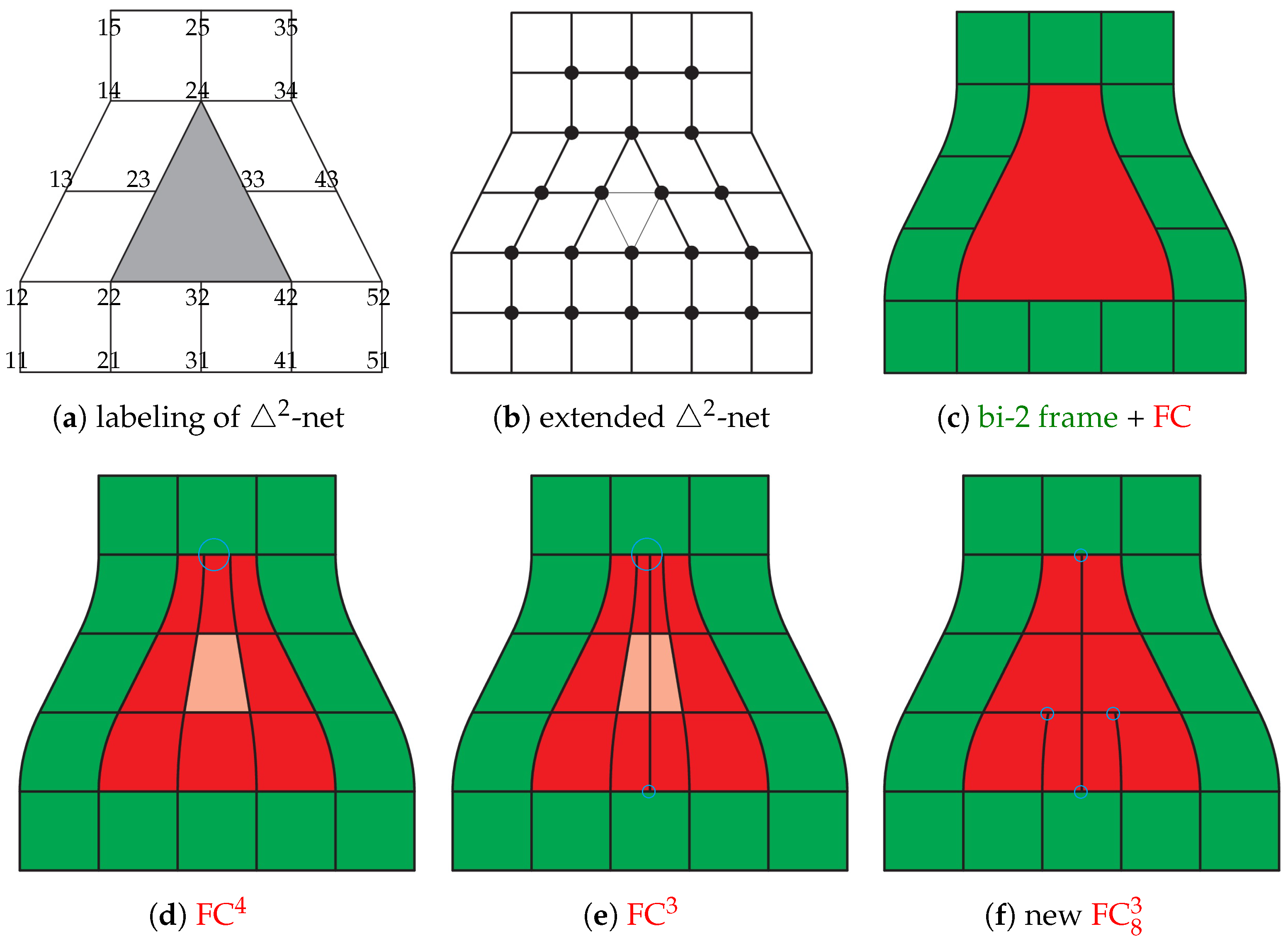
Related Work
2. Control Nets, Macro-Patches, FC3 and FC4
2.1. Control Nets
2.2. Polynomial Pieces
2.3. Summary of FC4 and FC3
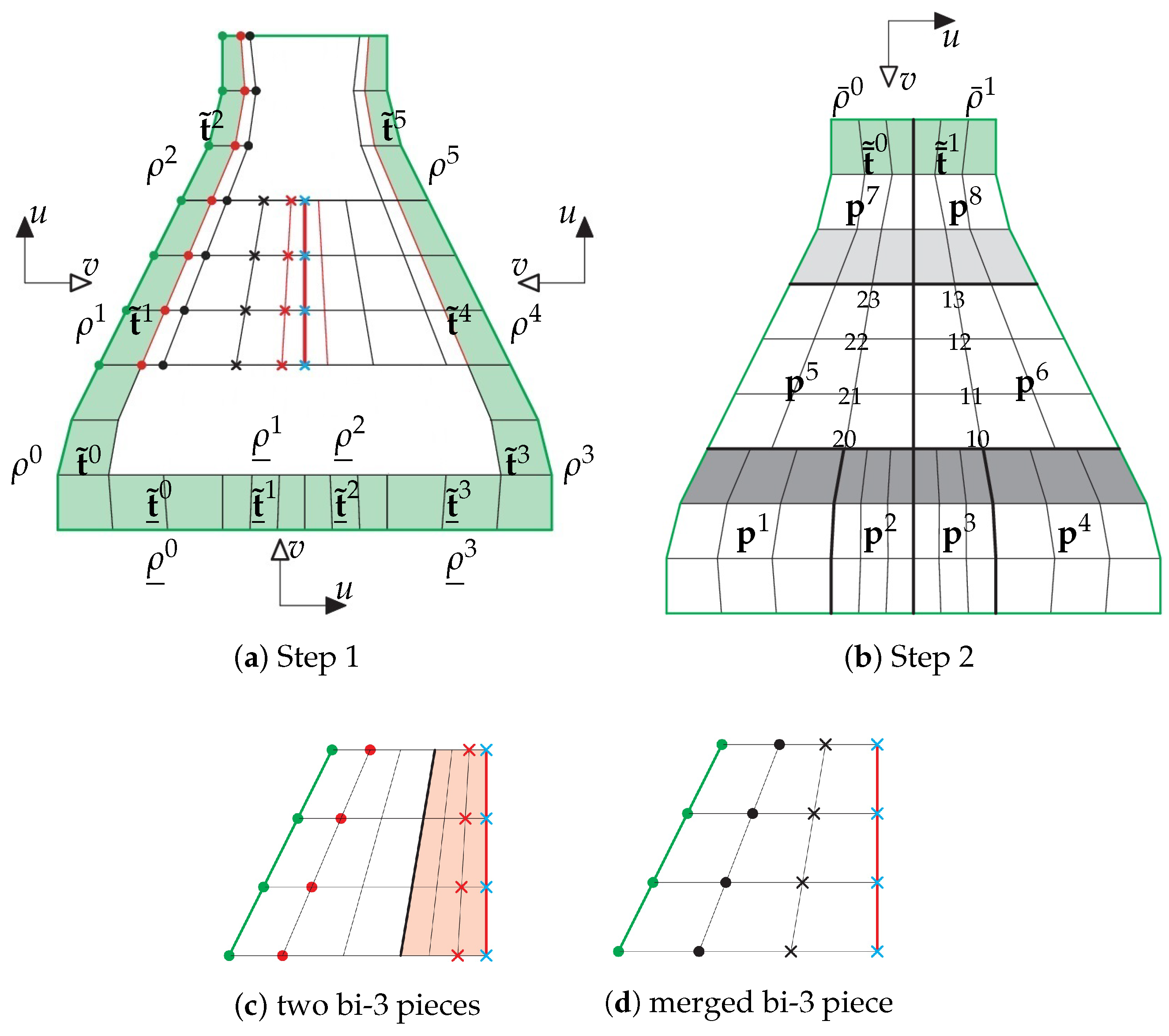
3. The Construction
4. Assessments and Comparisons
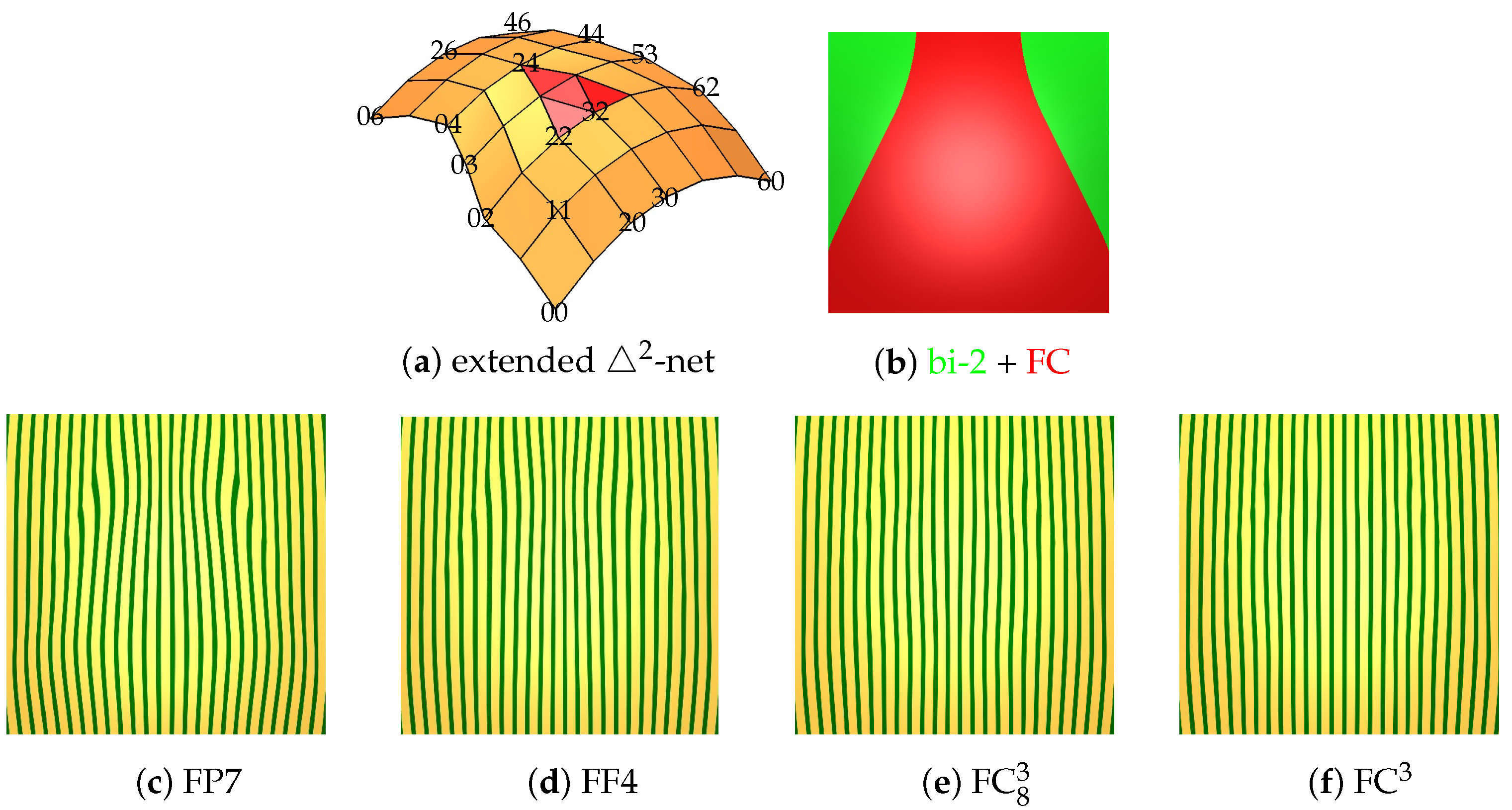
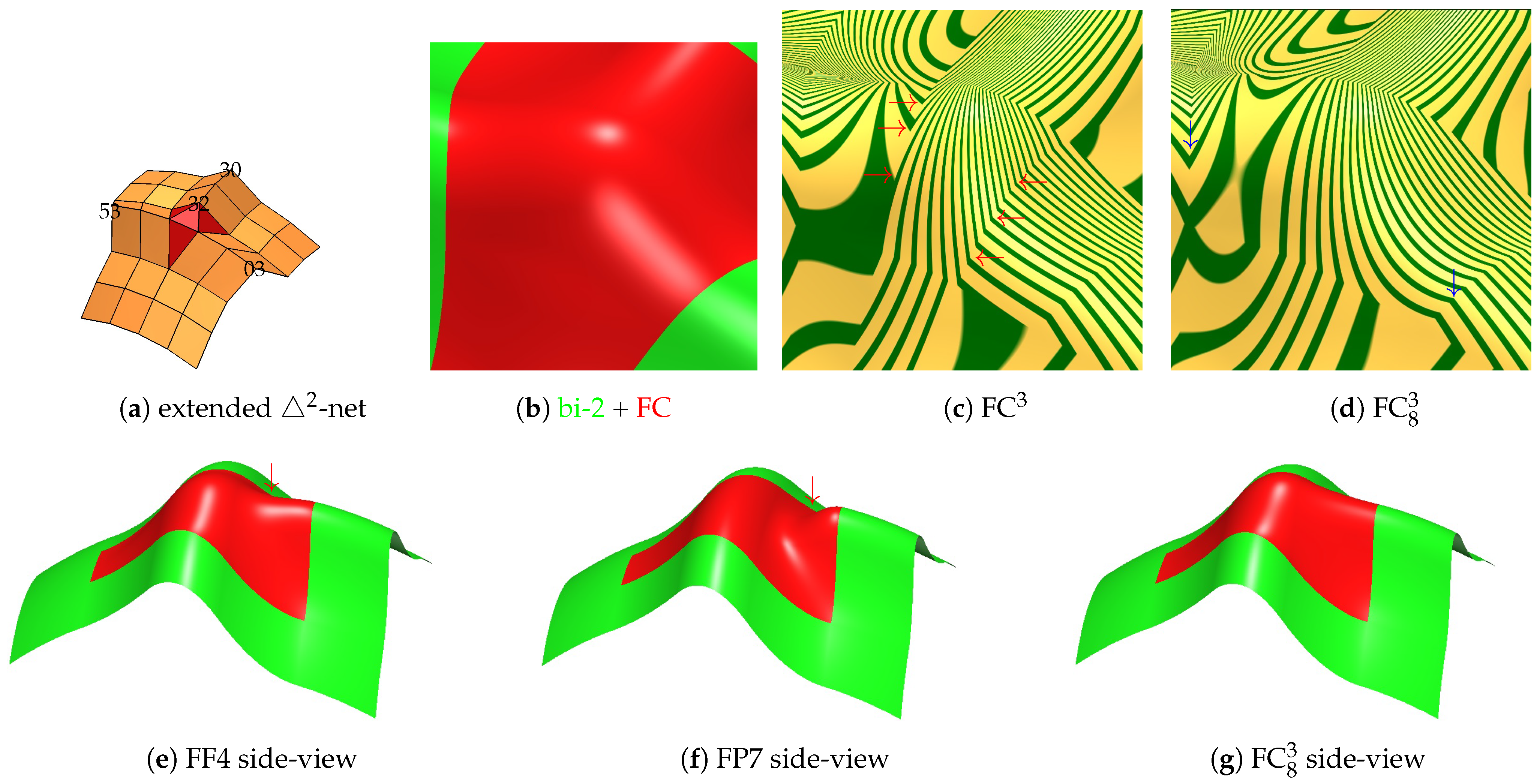
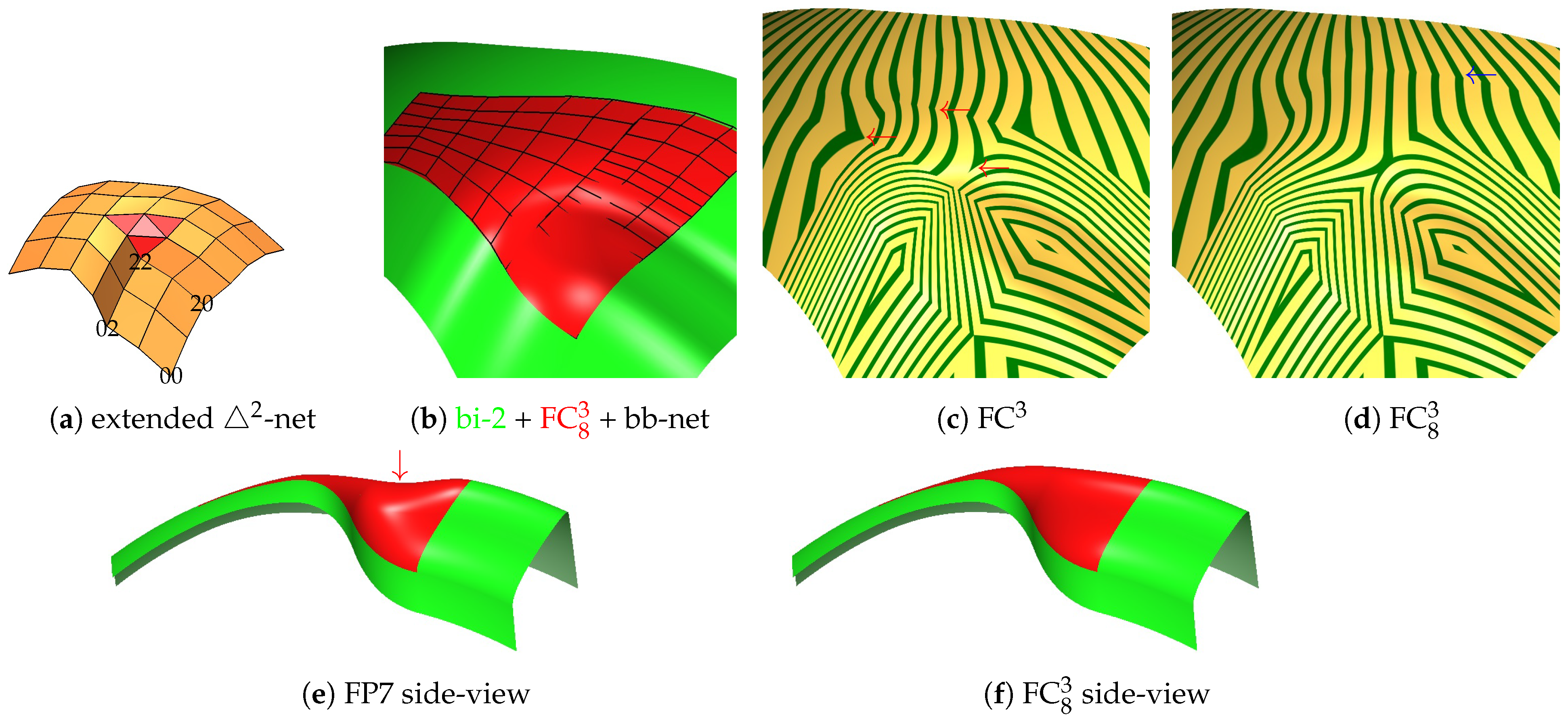
4.1. Small Local Challenge Nets
4.2. Large Hand-Crafted Models
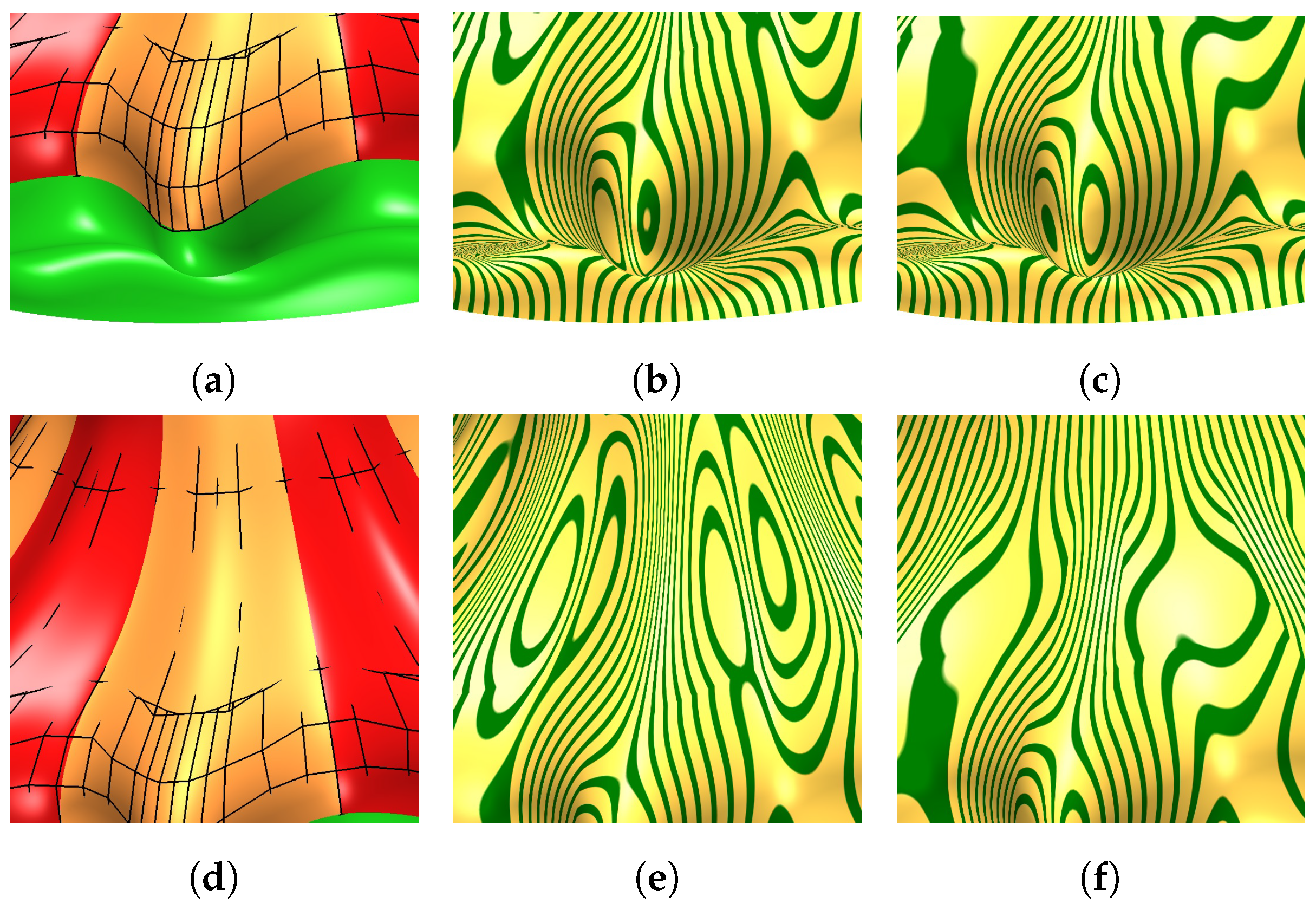
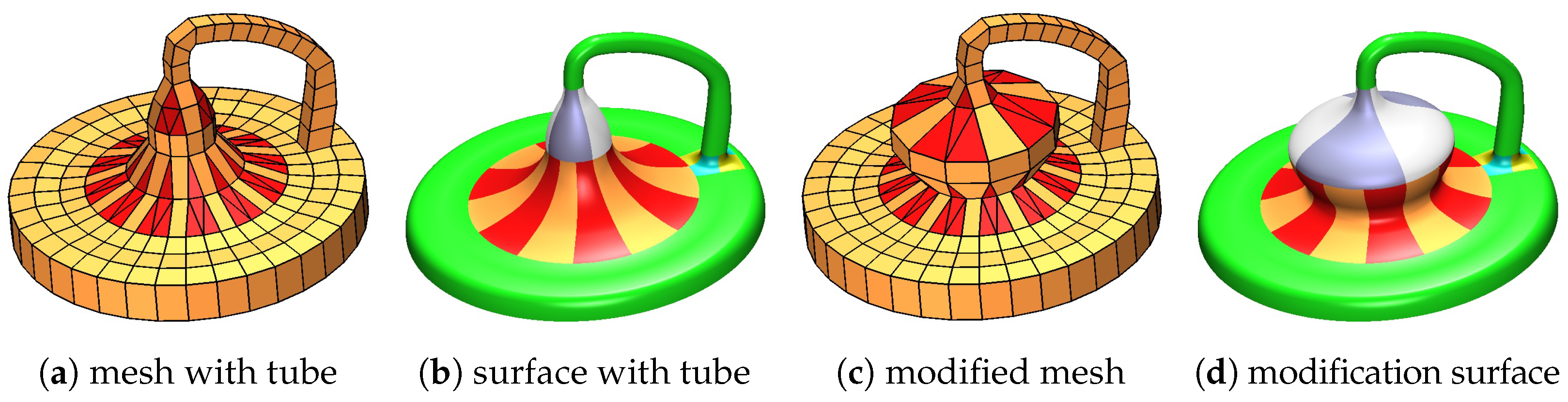


5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schertler, N.; Tarini, M.; Jakob, W.; Kazhdan, M.; Gumhold, S.; Panozzo, D. Field-Aligned Online Surface Reconstruction. ACM Trans. Graph. 2017, 36, 77:1–77:13. [Google Scholar] [CrossRef]
- Jakob, W.; Tarini, M.; Panozzo, D.; Sorkine-Hornung, O. Instant Field-Aligned Meshes. ACM Trans. Graph. 2015, 34, 189:1–189:15. [Google Scholar] [CrossRef]
- Doo, D.; Sabin, M. Behaviour of recursive division surfaces near extraordinary points. Comput.-Aided Des. 1978, 10, 356–360. [Google Scholar] [CrossRef]
- Karčiauskas, K.; Peters, J. Point-augmented biquadratic C1 subdivision surfaces. Graph. Models 2015, 77, 18–26. [Google Scholar] [CrossRef]
- Karčiauskas, K.; Peters, J. Localized remeshing for polyhedral splines. Comput. Graph. 2022, 106, 58–65. [Google Scholar] [CrossRef]
- Gunpinar, E.; Karčiauskas, K.; Peters, J. Splines for fast-contracting polyhedral control nets. Comput.-Aided Des. 2024, 173, 103727. [Google Scholar] [CrossRef]
- Catmull, E.; Clark, J. Recursively generated B-spline surfaces on arbitrary topological meshes. Comput.-Aided Des. 1978, 10, 350–355. [Google Scholar] [CrossRef]
- Karčiauskas, K.; Peters, J. Low degree splines for locally quad-dominant meshes. Comput. Aided Geom. Des. 2020, 83, 101934. [Google Scholar] [CrossRef]
- Karčiauskas, K.; Peters, J. Refinable smooth surfaces for locally quad-dominant meshes with T-gons. Comput. Graph. 2019, 82, 193–202. [Google Scholar] [CrossRef]
- Salvi, P.; Várady, T. Multi-sided surfaces with fullness control. In Proceedings of the Eighth Hungarian Conference on Computer Graphics and Geometry, Budapest, Hungary, 30–31 March 2016; pp. 61–69. [Google Scholar]
- Hettinga, G.J.; Kosinka, J. A multisided C2 B-spline patch over extraordinary vertices in quadrilateral meshes. Comput.-Aided Des. 2020, 127, 102855. [Google Scholar] [CrossRef]
- Vaitkus, M.; Várady, T.; Salvi, P.; Sipos, Á. Multi-sided B-spline surfaces over curved, multi-connected domains. Comput. Aided Geom. Des. 2021, 89, 102019. [Google Scholar] [CrossRef]
- Karčiauskas, K.; Peters, J. Point-augmented bi-cubic subdivision surfaces. In Proceedings of the Pacific Graphics 2022; Umetani, N., Vouga, E., Wojtan, C., Eds.; The Eurographics Association and John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2022; Volume 41, pp. 13–23, Computer Graphics Forum. [Google Scholar]
- Karčiauskas, K.; Peters, J. Evolving Guide Subdivision. Comput. Graph. Forum 2023, 42, 321–332. [Google Scholar] [CrossRef]
- Karčiauskas, K.; Peters, J. Quadratic-Attraction Subdivision. Comput. Graph. Forum 2023, 42, e14900. [Google Scholar] [CrossRef]
- Myles, A.; Peters, J. C2 Splines Covering Polar Configurations. Comput. Aided Des. 2011, 43, 1322–1329. [Google Scholar] [CrossRef]
- Toshniwal, D.; Speleers, H.; Hiemstra, R.R.; Hughes, T.J. Multi-degree smooth polar splines: A framework for geometric modeling and isogeometric analysis. Comput. Methods Appl. Mech. Eng. 2017, 316, 1005–1061. [Google Scholar] [CrossRef]
- Karčiauskas, K.; Peters, J. Smooth polar caps for locally quad-dominant meshes. Comput. Aided Geom. Des. 2020, 81, 101908. [Google Scholar] [CrossRef]
- Peters, J. Parametrizing singularly to enclose vertices by a smooth parametric surface. In Proceedings of the Graphics Interface’91, Calgary, Alberta, 3–7 June 1991; MacKay, S., Kidd, E.M., Eds.; Canadian Information Processing Society: Toronto, ON, Canada, 1991; pp. 1–7. [Google Scholar]
- Reif, U. A refineable space of smooth spline surfaces of arbitrary topological genus. J. Approx. Theory 1997, 90, 174–199. [Google Scholar] [CrossRef]
- Nguyen, T.; Karčiauskas, K.; Peters, J. C1 finite elements on non-tensor-product 2d and 3d manifolds. Appl. Math. Comput. 2016, 272, 148–158. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, Y.J.; Toshniwal, D.; Speleers, H.; Li, X.; Manni, C.; Evans, J.A.; Hughes, T.J. Blended B-spline construction on unstructured quadrilateral and hexahedral meshes with optimal convergence rates in isogeometric analysis. Comput. Methods Appl. Mech. Eng. 2018, 341, 609–639. [Google Scholar] [CrossRef]
- Gregory, J.A. Smooth interpolation without twist constraints. In Computer Aided Geometric Design; Barnhill, R.E., Riesenfeld, R.F., Eds.; Academic Press: Cambridge, MA, USA, 1974; pp. 71–88. [Google Scholar]
- Loop, C.T.; Schaefer, S.; Ni, T.; Castaño, I. Approximating subdivision surfaces with Gregory patches for hardware tessellation. ACM Trans. Graph 2009, 28, 151:1–151:9. [Google Scholar] [CrossRef]
- Loop, C.T.; Schaefer, S. G2 Tensor Product Splines over Extraordinary Vertices. Comput. Graph. Forum 2008, 27, 1373–1382. [Google Scholar] [CrossRef]
- Karčiauskas, K.; Peters, J. Minimal bi-6 G2 completion of bicubic spline surfaces. Comput. Aided Geom. Des. 2016, 41, 10–22. [Google Scholar] [CrossRef]
- Karčiauskas, K.; Peters, J. Improved shape for multi-surface blends. Graph. Models 2015, 82, 87–98. [Google Scholar] [CrossRef]
- Kapl, M.; Sangalli, G.; Takacs, T. Dimension and basis construction for analysis-suitable G1 two-patch parameterizations. Comput. Aided Geom. Des. 2017, 52–53, 75–89. [Google Scholar] [CrossRef]
- Blidia, A.; Mourrain, B.; Xu, G. Geometrically smooth spline bases for data fitting and simulation. Comput. Aided Geom. Des. 2020, 78, 101814. [Google Scholar] [CrossRef]
- Marsala, M.; Mantzaflaris, A.; Mourrain, B. G1-Smooth biquintic approximation of Catmull-Clark subdivision surfaces. Comput. Aided Geom. Des. 2022, 99, 102158. [Google Scholar] [CrossRef]
- Karčiauskas, K.; Peters, J. Bi-cubic scaffold surfaces. Comput.-Aided Des. 2022, 150, 103310. [Google Scholar] [CrossRef]
- Bonneau, G.P.; Hahmann, S. Flexible G1 interpolation of quad meshes. Graph. Model. 2014, 76, 669–681. [Google Scholar] [CrossRef]
- Karčiauskas, K.; Nguyen, T.; Peters, J. Generalizing bicubic splines for modeling and IGA with irregular layout. Comput.-Aided Des. 2016, 70, 23–35. [Google Scholar] [CrossRef]
- Beier, K.P.; Chen, Y. Highlight-line algorithm for realtime surface-quality assessment. Comput.-Aided Des. 1994, 26, 268–277. [Google Scholar] [CrossRef]
- Peters, J.; Lo, K.; Karčiauskas, K. Algorithm 1032: Bi-cubic splines for polyhedral control nets. ACM Trans. Math. Softw. 2023, 49, 7:1–7:12. [Google Scholar] [CrossRef]
- Karčiauskas, K.; Peters, J. Smooth multi-sided blending of biquadratic splines. Comput. Graph. 2015, 46, 172–185. [Google Scholar] [CrossRef]
- Sederberg, T.W.; Zheng, J.; Bakenov, A.; Nasri, A. T-splines and T-NURCCs. ACM Trans. Graph. 2003, 22, 477–484. [Google Scholar] [CrossRef]
- Karčiauskas, K.; Panozzo, D.; Peters, J. T-junctions in spline surfaces. ACM Trans. Graph. 2017, 36, 170:1–170:9. [Google Scholar] [CrossRef]
- Campen, M.; Zorin, D. Similarity maps and field-guided T-splines: A perfect couple. ACM Trans. Graph. 2017, 36, 91:1–91:16. [Google Scholar] [CrossRef]
- Tong, Y.; Alliez, P.; Cohen-Steiner, D.; Desbrun, M. Designing quadrangulations with discrete harmonic forms. In Proceedings of the Eurographics Symposium on Geometry Processing, Sardinia, Italy, 26–28 June 2006. [Google Scholar]
- Peng, C.H.; Barton, M.; Jiang, C.; Wonka, P. Exploring quadrangulations. ACM Trans. Graph. (TOG) 2014, 33, 12:1–12:13. [Google Scholar] [CrossRef]
- Bommes, D.; Campen, M.; Ebke, H.C.; Alliez, P.; Kobbelt, L. Integer-grid maps for reliable quad meshing. ACM Trans. Graph. (TOG) 2013, 32, 98:1–98:12. [Google Scholar] [CrossRef]
- Farin, G. Curves and Surfaces for Computer Aided Geometric Design: A Practical Guide; Academic Press: Cambridge, MA, USA, 1988. [Google Scholar]
- De Rose, T.D. Necessary and sufficient conditions for tangent plane continuity of Bézier surfaces. Comput. Aided Geom. Des. 1990, 7, 165–179. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karčiauskas, K.; Lo, K.S.-H.; Gunpinar, E.; Peters, J. Bicubic Splines for Fast-Contracting Control Nets. Axioms 2024, 13, 390. https://doi.org/10.3390/axioms13060390
Karčiauskas K, Lo KS-H, Gunpinar E, Peters J. Bicubic Splines for Fast-Contracting Control Nets. Axioms. 2024; 13(6):390. https://doi.org/10.3390/axioms13060390
Chicago/Turabian StyleKarčiauskas, Kȩstutis, Kyle Shih-Huang Lo, Erkan Gunpinar, and Jörg Peters. 2024. "Bicubic Splines for Fast-Contracting Control Nets" Axioms 13, no. 6: 390. https://doi.org/10.3390/axioms13060390
APA StyleKarčiauskas, K., Lo, K. S.-H., Gunpinar, E., & Peters, J. (2024). Bicubic Splines for Fast-Contracting Control Nets. Axioms, 13(6), 390. https://doi.org/10.3390/axioms13060390








