Spectral Curves for Third-Order ODOs

Abstract

Spectral curves are algebraic curves associated to commutative subalgebras of rings of ordinary differential operators (ODOs). Their origin is linked to the Korteweg–de Vries equation and to seminal works on commuting ODOs by I. Schur and Burchnall and Chaundy. They allow the solvability of the spectral problem $Ly=\lambda y$, for an algebraic parameter $\lambda$ and an algebro-geometric ODO L, whose centralizer is known to be the affine ring of an abstract spectral curve $\Gamma$. In this work, we use differential resultants to effectively compute the defining ideal of the spectral curve $\Gamma$, defined by the centralizer of a third-order differential operator L, with coefficients in an arbitrary differential field of zero characteristic. For this purpose, defining ideals of planar spectral curves associated to commuting pairs are described as radicals of differential elimination ideals. In general, $\Gamma$ is a non-planar space curve and we provide the first explicit example. As a consequence, the computation of a first-order right factor of $L-\lambda$ becomes explicit over a new coefficient field containing $\Gamma$. Our results establish a new framework appropriate to develop a Picard–Vessiot theory for spectral problems.

1. Introduction

Picard–Vessiot theory is a Galois theory for linear ordinary differential equations. It studies the space of solutions of the operator in relation to an algebraic group, its differential Galois group. This theory has important connections with a long-standing conjecture, the Jacobian conjecture [1], which is related with the theory of commuting differential operators through the Dixmier conjecture [2] and Beret’s conjecture [3].

At the beginning of the 20th century, the solutions of differential equations as a function of a parameter caught the attention of some mathematicians. This interest seems clearly reflected in the work of J. Drach [4]. Recently, differential Galois theories began to be used to study spectral problems $Ly=\lambda y$, for ordinary differential operators L of second order [5,6,7,8]. Following Drach’s ideology [4], the spectral parameter $\lambda$ was considered an algebraic variable in [8], where a Picard–Vessiot theory for algebro-geometric operators with parameters began to develop. We can say that it is a Picard–Vessiot theory for commuting differential operators and, consequently, $\lambda$ is governed by a spectral curve. Parametric Galoisian theories, for free algebraic parameters, have existed since the pioneer parametric Picard–Vessiot theory of Cassidy and Singer [9], and have been studied for second-order operators in [10], and for third-order operators in [11], but their connection with spectral problems has not been established thus far.

It has been well-known since the beginning of the 20th century [12,13], that the existence of an operator M that commutes with L forces the consideration of the spectral problem $Ly=\lambda y$ as a coupled spectral problem:

$$Ly=\lambda y,My=\mu y,$$

(1)

where $\lambda$ and $\mu$ are tied by the constant coefficient polynomial equation $f(\lambda ,\mu )=0$ that defines an algebraic curve $\Gamma$. In the case of a Schrödinger operator L, the existence of a non-trivial M commuting with L is closely related to the Korteweg–de Vries hierarchy of integrable non-linear differential equations. The solutions of (1) depend on the geometry of the spectral curve $\Gamma$, as it is exhaustively studied in the works of J. J. Morales-Ruiz and the authors of [7,8], where spectral Picard–Vessiot theory appears for the first time.

In this work, we study the spectral problem $Ly=\lambda y$ for a third-order operator L, under the assumption that L has a nontrivial centralizer and that it contains M as in (1). The development of a spectral Picard–Vessiot theory for this type of operator is an open problem. Since a third-order L is related to a more complicated integrable hierarchy, the Boussinesq hierarchy, there is even a lack of explicit examples due to computational problems [14,15].

A famous theorem by I. Schur [16] implies that the centralizer of an ordinary differential operator L, with analytic coefficients, has as quotient field a function field in one variable. Therefore, such a centralizer can be seen as the affine ring of an algebraic curve $\Gamma$ [17]. In this work, we will call this curve the spectral curve of the operator L, and assume that L has coefficients in an arbitrary differential field $\Sigma$ of zero characteristic.

A fundamental goal driving this work is the development of a Picard–Vessiot theory for spectral problems $(L-\lambda )\left(y\right)=0$, in the case of an algebro-geometric differential operator L and an algebraic parameter $\lambda$ over $\Sigma$. In order to construct a splitting field for $(L-\lambda )\left(y\right)=0$, it is crucial to note that $\lambda$ is not a free parameter, but rather it is governed by the spectral curve $\Gamma$ of L. For this purpose, to achieve the factorization of $L-\lambda$, a new coefficient field $\Sigma (\Gamma )$, containing $\Sigma$ and $\Gamma$, must be considered.

We believe that the novel results that emerge from the study of the order three case will be important for the development of a spectral Picard–Vessiot theory for arbitrary order. Specifically, our main contribution is the identification of the spectral curve of L, as the curve defined by its centralizer, and the computation of its defining ideal in the case of third-order operators. The field of functions $\Sigma (\Gamma )$ on the spectral curve of L is now controlled and allows effective computation of the first-order intrinsic right factor of $L-\lambda$. It is intrinsic because, via the specialization of the parameter $\lambda$ to each constant value ${\lambda }_0$, it gives the rank one sheaf over $\Gamma$, made famous by the works of Krichever [18] and Mumford [19], where the correspondence between commutative subrings of ODOs and affine spectral curves is established; see [20] for a recent review. In Section 2, an extended version of this contributions is included.

2. Contributions

We consider ordinary differential operators with coefficients in an arbitrary differential field $\Sigma$, whose field of constants $\mathbf{C}$ is algebraically closed and of zero characteristic. We use differential algebra, differential Galois theory and algebraic geometry to give a constructive proof of the following theorem.

Theorem 1.

The centralizer of a third-order ordinary differential operator L, with non-constant coefficients in Σ, is either isomorphic to a polynomial ring in one variable or to the coordinate ring $\mathbf{C}[\Gamma ]$ of an irreducible (space) algebraic curve Γ.

A differential operator L whose centralizer is not a polynomial ring in one variable is often called algebro-geometric [21,22]. Our results establish a new framework to study spectral problems for algebro-geometric ODOs.

The authors defined spectral Picard–Vessiot fields for algebro-geometric second-order operators in [8] and provided algebraic tools to effectively compute a basis of solutions for the spectral problem in this case. The extension to a higher order of the techniques developed for second-order operators poses several important issues. The main problem treated in this paper is the definition and computation of spectral curves for algebro-geometric ODOs.

Computing algebro-geometric ODOs amounts to computing Gelfand–Dikii hierarchies and solutions of them [23], which are non-trivial problems. It is well-known that solutions of the KdV hierarchy provide algebro-geometric Schrödinger ODOs [7,8,24]. Solutions of the Boussinesq hierarchy [25] provide algebro-geometric operators of third order, and investigating those, we discovered that planar algebraic curves do not explain all nontrivial centralizers of third-order ODOs. We found an example of an algebro-geometric third-order ODO whose centralizer is the commutative $\mathbf{C}$-algebra generated by three ODOs [26]. Explaining the nature of this example was the seed for the results presented here. A general study of algebro-geometric differential operators of prime order is postponed until meaningful examples are found, for order five and higher.

Planar spectral curves have been commonly defined for pairs of commuting differential operators P and Q, since the seminal work of Burchnall and Chaundy [12]; see also [18,19] and the recent review [20]. Most results have been obtained in the case of commuting pairs $P,Q$ with coprime orders, called the rank 1 case; see, for instance, [20]. Without this restriction, hence for any rank $r=\gcd \left(\right(\mathrm{ord}\left(P\right),\mathrm{ord}\left(Q\right))$, we define an isomorphism between the coordinate ring of the planar spectral curve, an irreducible plane algebraic curve ${\Gamma }_{P,Q}$, and the commutative ring of differential operators $\mathbf{C}[P,Q]$. Namely, we prove that the ideal of the curve ${\Gamma }_{P,Q}$ equals the ideal of all constant coefficient polynomials $g(\lambda ,\mu )$ that are satisfied by the differential operators, commonly denoted $g(P,Q)=0$, and known as Burchnall and Chaundy polynomials. We introduce in this paper the notion of Burchnall and Chaundy ideal of a pair $P,Q$ and denote it by $\mathtt{BC}(P,Q)$. Since P and Q are differential operators in a Euclidean domain, the ideal $\mathtt{BC}(P,Q)$ is naturally proved to be a prime ideal. These results are included in Theorem 3. From now on, we will call ${\Gamma }_{P,Q}$ the spectral curve of the pair $P,Q$ to distinguish it from the spectral curve associated with the centralizer of an ordinary differential operator.

It was known by E. Previato [27] and G. Wilson [14], in the case of differential operators with analytic coefficients, that a Burchnall and Chaundy polynomial for a commuting pair $P,Q$ can be obtained by computing the differential resultant $\partial \mathrm{Res}(P-\lambda ,Q-\mu )$ of $P-\lambda$ and $Q-\mu$. In particular, they proved that such a resultant is a constant coefficient polynomial. We generalize this result in Theorem 5 to differential operators with coefficients in $\Sigma$. We go further, proving that the ideal of all Burchnall and Chaundy polynomials for the pair $P,Q$ is generated by an irreducible polynomial $f(\lambda ,\mu )$, the radical of $\partial \mathrm{Res}(P-\lambda ,Q-\mu )$. For this purpose, we use the differential elimination ideal determined by $P-\lambda$ and $Q-\mu$,

$$\mathcal{E}(P-\lambda ,Q-\mu )=(P-\lambda ,Q-\mu )\cap \Sigma [\lambda ,\mu ],$$

the ideal of all differential operators generated by $P-\lambda$ and $Q-\mu$ in $\Sigma [\lambda ,\mu ]$, for which the derivation has been eliminated. Our main result about arbitrary commuting pairs of ODOs establishes the intrinsic nature of the differential resultant of $P-\lambda$ and $Q-\mu$. We prove the following result in Theorem 8.

Theorem 2.

Given commuting ordinary differential operators P and Q with coefficients in Σ, let $f(\lambda ,\mu )$ be the radical of $\partial \mathrm{Res}(P-\lambda ,Q-\mu )$. The following statements hold:

• The principal ideal $\left(f\right)$ generated by f in $\mathbf{C}[\lambda ,\mu ]$ equals the prime ideal $\mathtt{BC}(P,Q)$.
• The differential ideal $\left[f\right]$ generated by f in $\Sigma [\lambda ,\mu ]$ equals the radical of the elimination ideal $\mathcal{E}(P-\lambda ,Q-\mu )$.

For an algebraically closed field of constants, the classical theory of Picard and Vessiot [28] allows us to formally manage solutions, and it will be important to give formal proofs of our results. Specializing the parameter $\lambda$ to ${\lambda }_0\in \mathbf{C}$, the Picard–Vessiot extension of $\Sigma$ for $(P-{\lambda }_0)\left(y\right)=0$ is the splitting field for $(P-{\lambda }_0)\left(y\right)=0$. If algebraic variables $\lambda$ and $\mu$ over $\Sigma$ are considered, the differential operators $P-\lambda$ and $Q-\mu$ belong to the differential field $\mathcal{F}=\Sigma (\lambda ,\mu )$ and to use classical Picard–Vessiot theory, the algebraic closure of $\mathcal{F}$ can be considered to prove Theorem 5.

Centralizers are maximal commutative rings. In some cases, the centralizer $\mathcal{Z}\left(L\right)$ of a differential operator L is the affine ring of a planar curve, as in the case of algebro-geometric Schrödinger operators where $\mathcal{Z}\left(L\right)=\mathbf{C}[L,A]$. Let us fix now an algebro-geometric differential operator L of third order with coefficients in $\Sigma$. One of the motivations to give a constructive proof of Theorem 1 is to show that in general, $\mathcal{Z}\left(L\right)$ is not the coordinate ring of the planar curve. As a consequence of the results of K. Goodearl in [29], it has the structure of a free $\mathbf{C}\left[L\right]$-module

$$\mathcal{Z}\left(L\right)=\mathbf{C}[L,A_1,A_2]=\mathbf{C}\left[L\right]\oplus \mathbf{C}\left[L\right]A_1\oplus \mathbf{C}\left[L\right]A_2,$$

where $A_i$ is of minimal order congruent with $i\left(\mathrm{mod}3\right)$. Observe that $\mathcal{Z}\left(L\right)$ contains the rank one algebras $\mathbf{C}[L,A_i]$, but also $\mathbf{C}[A_1,A_2]$, whose rank may be grater than one, being the rank of a set, the greatest common divisor of the orders of its elements; see [17]. We introduce the notion of Burchnall–Chaundy ideal $\mathtt{BC}\left(L\right)$ of L to explain the ring multiplicative structure of $\mathcal{Z}\left(L\right)$. This is the ideal of all polynomials $g(\lambda ,{\mu }_1,{\mu }_2)$ in $\mathbf{C}[\lambda ,{\mu }_1,{\mu }_2]$ such that $g(L,A_1,A_2)=0$. We prove that $\mathtt{BC}\left(L\right)$ is a prime ideal that naturally contains the Burchnall–Chaundy ideals of pairs of differential operators in the centralizer of L. Three BC ideals are of crucial importance in this work:

$$\mathtt{BC}(L,A_1)=\left(f_1\right),\mathtt{BC}(L,A_2)=\left(f_2\right),\mathtt{BC}(A_1,A_2)=\left(f_3\right),$$

all of them contained in $\mathtt{BC}\left(L\right)$, but even more so we prove in Theorem 10 that

$$\mathtt{BC}\left(L\right)=(f_1,f_2,f_3),$$

which is one of the main contributions of this article, since it allows the computation of the spectral curve. The constructive proof of Theorem 1 is achieved in Corollary 3, where $\mathcal{Z}\left(L\right)$ is shown to be isomorphic to the coordinate ring

$$\mathbf{C}[\Gamma ]=\frac{\mathbf{C}[\lambda ,{\mu }_1,{\mu }_2]}{\mathtt{BC}\left(L\right)}=\frac{\mathbf{C}[\lambda ,{\mu }_1,{\mu }_2]}{(f_1,f_2,f_3)}$$

of an irreducible space algebraic curve $\Gamma$ in ${\mathbf{C}}^3$, which we define as the spectral curve of L.

An important consequence of the constructive proof of Theorem 1 is to discover the appropriate coefficient field where a third-order algebro-geometric operator $L-\lambda$ would have an intrinsic right factor. Recall that $\lambda$ is not a free parameter; it is governed by the space spectral curve $\Gamma$ of L. Extending the ideal $\mathtt{BC}\left(L\right)$ to the ring of polynomials in three variables with coefficients in $\Sigma$, we can think of an extended curve whose ring of regular functions is

$$\Sigma [\Gamma ]=\frac{\Sigma [\lambda ,{\mu }_1,{\mu }_2]}{\left[\mathtt{BC}\right(L\left)\right]}.$$

Over its quotient field $\Sigma (\Gamma )$, a factorization of $L-\lambda$ is guaranteed,

$$L-\lambda =N·(\partial +\varphi ),$$

where $\partial +\varphi$ can be computed by means of the greatest common right divisors $\mathrm{gcrd}(L-\lambda ,A_1-{\mu }_1)$ or $\mathrm{gcrd}(L-\lambda ,A_2-{\mu }_2)$, which are proved to coincide over $\Sigma (\Gamma )$. The precise statement is contained in Theorem 12. We can think of $\partial +\varphi$ as a global factor, since for almost every point $P_0\in \Gamma$, our methods produce a factorization of $L-{\lambda }_0=N_{P_0}·(\partial +\varphi \left(P_0\right)$. The specialization of $(\lambda ,{\mu }_1,{\mu }_2)$ to each point $P_0$ of $\Gamma$ provides the rank one sheaf given by the solutions of $\partial +\varphi \left(P_0\right)$. Therefore, starting with the centralizer of L, both the spectral curve $\Gamma$ and the previous rank one sheaf of the Mumford correspondence in [19] are now effectively computed.

It remains as a future project to define and prove the existence of the spectral Picard–Vessiot field of $L-\lambda$, for an algebro-geometric differential operator L. It would be a differential field extension of $\Sigma (\Gamma )$, the minimal extension containing all the solutions, and it requires a full factorization of $L-\lambda$ over $\Sigma (\Gamma )$. This requires further investigations where the parametric Picard–Vessiot theory, introduced by Cassidy and Singer in [9] and studied in [10,11], may be relevant.

The paper is organized as follows. In Section 3, we establish the appropriate framework to study algebro-geometric differential operators, in the case of a third-order operator L. The novel notions of Burchnall–Chaundy (BC) ideal, of a pair $P,Q$ of ODOs and the BC ideal $\mathtt{BC}\left(L\right)$ of a fixed differential operator L are introduced in Section 4. These BC ideals are proved to be prime ideals describing the algebra $\mathbf{C}[P,Q]$ and the centralizer $\mathcal{Z}\left(L\right)$, as coordinate rings of algebraic curves, respectively, in Theorems 3 and 4. These allow the definitions of the spectral curves of a pair $P,Q$ and of a third-order operator L.

Section 5 and Section 6 are dedicated to computing generators of these BC ideals. Section 5 contains the proof of Theorem 2, the first part in Theorem 6 and the second in Theorem 8. The effective description of $\mathtt{BC}\left(L\right)$ is achieved by means of any basis of the centralizer $\mathcal{Z}\left(L\right)$ and the computation of differential resultants. The choice of a basis of $\mathcal{Z}\left(L\right)$ is discussed in Section 6.1. We use Gröbner bases in Section 6.2 to control the projection of the space spectral curve onto the plane $\lambda =0$ and obtain a set of generators of $\mathtt{BC}\left(L\right)$ in Theorem 10.

In Section 7, we show that the algebro-geometric hypothesis implies the existence of a right factor $\partial +\varphi$ of $L-\lambda$, over a new differential field of coefficients $\Sigma (\Gamma )$, defined in Section 7.1. The computation of $\varphi$ is delicate and it is achieved by means of differential subresultants in Section 7.2. Finally, Section 8 contains the first computed example of a non-planar spectral curve. It is used to illustrate how to globally factor the linear operator $L-\lambda$. All computations in this work are performed with Maple [30].

To make this work as self-contained as possible, two appendices are included. Appendix A contains the results needed to understand centralizers of differential operators, giving special importance to Goodearl’s construction of a basis of $\mathcal{Z}\left(L\right)$. In Appendix B, we review definitions and proofs of results on differential resultants and subresultants in relation to the factorization of ODOs.

Notation. 

For concepts in differential algebra, we refer to [28,31,32]. A differential ring is a ring R with a derivation ∂ on R. A differential ideal I is an ideal of R invariant under the derivation. We denote by

$$Const\left(R\right)=\{r\in R|\partial \left(r\right)=0\},$$

which is called the ring of constants of R. Assuming that R is a differential domain, its field of fractions $Fr\left(R\right)$ is a differential field with extended derivation

$$\partial (f/g)=(\partial \left(f\right)g-f\partial \left(g\right))/g^2.$$

A differential field $(\Sigma ,\partial )$ is a differential ring which is a field. Given $a\in \Sigma$, we denote $\partial \left(a\right)$ by $a^{\prime }$. Note that $Const(\Sigma )$ is a field whenever $\Sigma$ is. We assume that $\mathbf{C}:=Const(\Sigma )$ is algebraically closed and has characteristic 0.

Let us consider algebraic variables $\lambda$ and $\mu$ with respect to ∂. Thus, $\partial \left(\lambda \right)=0$ and $\partial \left(\mu \right)=0$, and we can extend the derivation ∂ of $\Sigma$ to the polynomial ring $\Sigma [\lambda ,\mu ]$ having ring of constants $\mathbf{C}[\lambda ,\mu ]$. Similarly, we consider algebraic variables ${\mu }_1$ and ${\mu }_2$ with respect to ∂ and extend the derivation to the polynomial ring $\Sigma [\lambda ,{\mu }_1,{\mu }_2]$ having ring of constants $\mathbf{C}[\lambda ,{\mu }_1,{\mu }_2]$.

We denote by $\mathbb{N}$ the set of non-negative integers including 0. Notation regarding ODOs in $\Sigma [\partial ]$ and their centralizers is included in Appendix A.

3. Algebro-Geometric ODOs

Let us consider an ordinary differential operator L in $\Sigma [\partial ]$, with non-constant coefficients, that is $L\in \Sigma [\partial ]\setminus \mathbf{C}[\partial ]$. We will assume throughout this work that L has a non-trivial centralizer, as in Definition A1; this means that the centralizer of L in $\Sigma [\partial ]$

$$\mathcal{Z}\left(L\right)=\{A\in \Sigma [\partial ]\mid LA=AL\},$$

does not equal the polynomial ring $\mathbf{C}\left[L\right]$. Therefore, we have a chain of strict inclusions

$$\mathbf{C}\left[L\right]\subset \mathcal{Z}\left(L\right)\subset \Sigma [\partial ].$$

In Appendix A, we review results of K. Goodearl in [29] regarding the structure of centralizers.

Definition 1.

We call a differential operator $L\in \Sigma [\partial ]\setminus \mathbf{C}[\partial ]$ algebro-geometric if its centralizer $\mathcal{Z}\left(L\right)$ is non-trivial.

By the generalization of Schur’s theorem in [16], (A6) in the Appendix A, we know that $\mathcal{Z}\left(L\right)$ is commutative, it is a differential domain, and $\mathrm{Spec}\left(\mathcal{Z}\right(L\left)\right)$ is an (abstract) algebraic curve. Spectral curves are defined for any commutative subring B of $\Sigma [\partial ]$ as $\mathrm{Spec}\left(B\right)$; see [19,20]. As observed in [17], Section 2.1, the centralizer $\mathcal{Z}\left(L\right)$ is a maximal commutative subring of $\Sigma [\partial ]$. We emphasize in this work the importance of spectral curves for maximal commutative subrings of $\Sigma [\partial ]$, namely spectral curves for centralizers.

Definition 2.

Given an algebro-geometric differential operator $L\in \Sigma [\partial ]\setminus \mathbf{C}[\partial ]$, we define the spectral curve of L as ${\Gamma }_L:=\mathit{Spec}\left(\mathcal{Z}\left(L\right)\right)$.

Let us consider now a third-order ordinary differential operator L in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$. We will assume throughout this work that L has a non-trivial centralizer. In this work, we identify a defining ideal for the abstract curve ${\Gamma }_L$. This is Corollary 3, obtained as a consequence of Theorem 10.

By Theorem A1, the centralizer $\mathcal{Z}\left(L\right)$ is a free $\mathbf{C}\left[L\right]$-module of rank 3. Let $\mathcal{B}\left(L\right)=\{1,A_1,A_2\}$ be a basis of $\mathcal{Z}\left(L\right)$ as a $\mathbf{C}\left[L\right]$-module. The construction of a basis is reviewed in Appendix A. Each $A_i$ is a monic operator in $\mathcal{Z}\left(L\right)\setminus \mathbf{C}\left[L\right]$ of minimal order $o_i:=\mathrm{ord}\left(A_i\right)\equiv i\left(\mathrm{mod}3\right)$. Therefore,

$$\mathcal{Z}\left(L\right)=\mathbf{C}\left[L\right]\oplus \mathbf{C}\left[L\right]A_1\oplus \mathbf{C}\left[L\right]A_2=\{p_0\left(L\right)+p_1\left(L\right)A_1+p_2\left(L\right)A_2\mid p_i\in \mathbf{C}\left[\lambda \right]\}.$$

(2)

From the composition of the basis, we obtain the following result.

Corollary 1.

Let L be a third-order operator in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$. The following statements are equivalent:

• L has a nontrivial centralizer $\mathcal{Z}\left(L\right)\ne \mathbf{C}\left[L\right]$.
• There exists an operator A in $\Sigma [\partial ]$ of order m, relatively prime with 3, such that $[L,A]=0$.

The second statement of Corollary 1 is the traditional definition of algebro-geometric operator; see, for instance, [21,22]. This statement highlights that $\mathcal{Z}\left(L\right)$ contains a pair of operators $L,A$ of rank one, the rank of the pair being the greatest common divisor of their orders. A discussion on the rank of a set of differential operators appears in [17] .

Since centralizers are maximal commutative subrings of $\Sigma [\partial ]$, given a differential operator M that commutes with L, we have the sequence of inclusions

$$\mathbf{C}\left[L\right]\subseteq \mathbf{C}[L,M]\subseteq \mathcal{Z}\left(L\right),$$

and all of them could be strict. In the case of a third-order operator, the following ring diagram of inclusions illustrates the ring structure of $\mathcal{Z}\left(L\right)$.

(3)

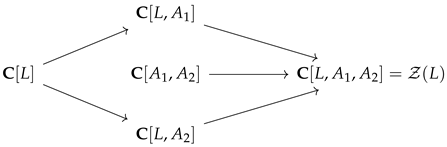
Remark 1.

Making use of the ring structure of $\mathcal{Z}\left(L\right)$, it may happen that $A_1$ equals a polynomial in $A_2$ or vice versa, $A_1=q\left(A_2\right)$, with q a univariate polynomial. In this situation, $\mathcal{Z}\left(L\right)=\mathbf{C}[L,A_2]$. For instance, this is the case whenever $\mathrm{ord}\left(A_2\right)=2$, then $A_1=A_2^2$ has order 4 and $\mathcal{Z}\left(L\right)=\mathcal{Z}\left(A_2\right)$ is the centralizer of a second-order operator.

4. Burchnall–Chaundy Ideals and Spectral Curves

A polynomial $f(\lambda ,\mu )$ with constant coefficients satisfied by a commuting pair of differential operators P and Q is called a Burchnall–Chaundy (BC) polynomial of the pair P, Q, since the first result of this sort appeared in the 1923 paper [12] by Burchnall and Chaundy. We define in this section the ideal of all BC-polynomials associated to an arbitrary pair of commuting differential operators. For a fixed differential operator L of order 3, we also define an ideal of BC-polynomials.

4.1. Burchnall–Chaundy Ideal of a Pair

Given commuting differential operators P and Q in $\Sigma [\partial ]$, to avoid meaningless situations, we will assume that $P,Q\notin \mathbf{C}[\partial ]$ and both have positive order. We define the ring homomorphism

$$e_{P,Q}:\mathbf{C}[\lambda ,\mu ]\to \Sigma [\partial ]by{e}_{P,Q}\left(\lambda \right)=P,e_{P,Q}\left(\mu \right)=Q.$$

(4)

It is a ring homomorphism since P and Q commute, and they commute with the elements of $\mathbf{C}$, the field of constants of $\Sigma$. The image of $e_{P,Q}$ is the $\mathbf{C}$-algebra

$$\mathbf{C}[P,Q]=\left\{\sum _{i,j}{\sigma }_{i,j}{P}^i{Q}^j\mid {\sigma }_{i,j}\in \mathbf{C}\right\}.$$

Observe that $\mathrm{Ker}\left(e_{P,Q}\right)$ is an ideal of $\mathbf{C}[\lambda ,\mu ]$. In this setting, given $g\in \mathbf{C}[\lambda ,\mu ]$, we will denote

$$g(P,Q):=e_{P,Q}\left(g\right).$$

(5)

Thus, a polynomial g belongs to the kernel of $e_{P,Q}$ if and only if $g(P,Q)=0$, that is,

$$\mathrm{Ker}\left(e_{P,Q}\right)=\{g\in \mathbf{C}[\lambda ,\mu ]\mid g(P,Q)=0\}.$$

Definition 3.

Given commuting differential operators P and Q in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$, both of positive order, we define the BC-ideal of a pair P and Q as

$$\mathtt{BC}(P,Q):=\mathrm{Ker}\left(e_{P,Q}\right)=\{g\in \mathbf{C}[\lambda ,\mu ]\mid g(P,Q)=0\}.$$

We will call BC-polynomials the elements of the BC-ideal.

An important consequence of working with differential operators in a Euclidean domain $\Sigma [\partial ]$ is the following lemma.

Lemma 1.

Given commuting differential operators P and Q in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$, both of positive order, the ideal $\mathtt{BC}(P,Q)$ is a prime ideal in $\mathbf{C}[\lambda ,\mu ]$.

Proof. 

To start, $\mathtt{BC}(P,Q)$ is a nonzero ideal by [29], Theorem 1.13. For details, let us consider the centralizer $\mathcal{Z}\left(P\right)$ of P. Since $\mathcal{Z}\left(P\right)$ is a finitely generated $\mathbf{C}\left[P\right]$-module, there exists $p_0,\dots ,p_t\in \mathbf{C}\left[\lambda \right]$ such that

$$g(\lambda ,\mu )=p_0\left(\lambda \right)+p_1\left(\lambda \right)\mu +\dots +p_{t-1}\left(\lambda \right){\mu }^{t-1}+{\mu }^t\in \mathtt{BC}(P,Q).$$

Given $h_1$ and $h_2$ in $\mathbf{C}[\lambda ,\mu ]$, let us assume that $h_1·h_2\in \mathtt{BC}(P,Q)$. Observe that $h_1(P,Q)=e_{P,Q}\left(h_1\right)$ and $h_2(P,Q)=e_{P,Q}\left(h_2\right)$ are differential operators in the Euclidean domain $\Sigma [\partial ]$. Since $e_{P,Q}$ is a ring homomorphism

$$0=e_{P,Q}(h_1·h_2)=e_{P,Q}\left(h_1\right)·e_{P,Q}\left(h_2\right)$$

implies $e_{P,Q}\left(h_1\right)=0$ or $e_{P,Q}\left(h_2\right)=0$. Thus, $h_1\in \mathtt{BC}(P,Q)$ or $h_2\in \mathtt{BC}(P,Q)$, proving that $\mathtt{BC}(P,Q)$ is prime. □

Definition 4.

Given commuting differential operators P and Q in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$, both of positive order, we define the spectral curve of the pair $P,Q$ as the irreducible algebraic variety of the prime ideal $\mathtt{BC}(P,Q)$, that is,

$${\Gamma }_{P,Q}:=V\left(\mathtt{BC}(P,Q)\right)=\left\{({\lambda }_0,{\mu }_0)\in {\mathbf{C}}^2\mid g({\lambda }_0,{\mu }_0)=0,\mathit{for}\mathit{all}g\in \mathtt{BC}(P,Q)\right\}.$$

(6)

Remark 2.

We proved in Lemma 1 that $\mathtt{BC}(P,Q)$ is a prime ideal. Then the algebraic variety ${\Gamma }_{P,Q}$ is an irreducible algebraic variety in ${\mathbf{C}}^2$. This variety cannot be a single point $({\lambda }_0,{\mu }_0)$, because this would mean that $\mathtt{BC}(P,Q)=(\lambda -{\lambda }_0,\mu -{\mu }_0)$, implying $P-{\lambda }_0=0$ and $Q-{\mu }_0=0$, which contradicts $P,Q\notin \mathbf{C}$. Therefore, ${\Gamma }_{P,Q}$ is an irreducible algebraic curve in ${\mathbf{C}}^2$.

The following result summarizes the situation.

Theorem 3.

Given differential operators P and Q in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$, both of positive order, if P and Q commute, then the following statements hold:

• $\mathbf{C}[P,Q]$ is a commutative domain isomorphic to $\mathbf{C}[\lambda ,\mu ]/\mathtt{BC}(P,Q)$, the coordinate ring of the spectral curve ${\Gamma }_{P,Q}$.
• There exists an irreducible polynomial $f\in \mathbf{C}[\lambda ,\mu ]$ such that $\mathtt{BC}(P,Q)=\left(f\right)$.

Proof. 

As a consequence of the construction of $e_{P,Q}$ and Lemma 1, we obtain 1. In addition, recall that $\mathbf{C}$ is an algebraically closed field. By Remark 2, ${\Gamma }_{P,Q}$ is an irreducible algebraic curve in ${\mathbf{C}}^2$, meaning that its defining ideal $\mathtt{BC}(P,Q)=\left(f\right)$ is generated by an irreducible polynomial $f\in \mathbf{C}[\lambda ,\mu ]$. □

In Section 5, we treat the computation of the defining polynomial f of the spectral curve ${\Gamma }_{P,Q}$.

4.2. Burchnall–Chaundy Ideal of a Third-Order Operator

Let us consider a third-order operator L in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$ with nontrivial centralizer $\mathcal{Z}\left(L\right)$. We will define next the Burchnall–Chaundy ideal of the operator L.

Given a basis $\mathcal{B}\left(L\right)=\{1,A_1,A_2\}$ of $\mathcal{Z}\left(L\right)$, we can define the ring homomorphism

$$e_L:\mathbf{C}[\lambda ,{\mu }_1,{\mu }_2]\to \Sigma [\partial ]by{e}_{P,Q}\left(\lambda \right)=L,e_{P,Q}\left({\mu }_1\right)=A_1,e_{P,Q}\left({\mu }_2\right)=A_2.$$

(7)

We will denote monomials in $\mathbf{C}[\lambda ,{\mu }_1,{\mu }_2]$ by $M_{\alpha }={\lambda }^{{\alpha }_0}{\mu }_1^{{\alpha }_1}{\mu }_2^{{\alpha }_2}$, $\alpha =({\alpha }_0,{\alpha }_1,{\alpha }_2)\in {\mathbb{N}}^3$, whose image is $e_L\left(M_{\alpha }\right)=L^{{\alpha }_0}{A}_1^{{\alpha }_1}{A}_2^{{\alpha }_2}$. Thus, the image of $e_L$ is the centralizer of L,

$$\mathcal{Z}\left(L\right)=\mathbf{C}[L,A_1,A_2]=\left\{\sum _{\alpha \in {\mathbb{N}}^3}{\sigma }_{\alpha }{e}_L\left(M_{\alpha }\right)\mid {\sigma }_{\alpha }\in \mathbf{C}\right\}.$$

Given $g\in \mathbf{C}[\lambda ,{\mu }_1,{\mu }_2]$, we will denote

$$g(L,A_1,A_2):=e_L\left(g\right).$$

(8)

Definition 5.

Given a third-order operator L in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$, with nontrivial centralizer and given a basis $\mathcal{B}\left(L\right)=\{1,A_1,A_2\}$ of $\mathcal{Z}\left(L\right)$, we define a BC-ideal of an operator L as

$$\mathtt{BC}\left(L\right):=\mathrm{Ker}\left(e_L\right)=\{g\in \mathbf{C}[\lambda ,{\mu }_1,{\mu }_2]\mid g(L,A_1,A_2)=0\}.$$

(9)

We will call the elements of the BC ideal BC-polynomials.

Lemma 2.

Given a third-order operator L in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$, with nontrivial centralizer $\mathcal{Z}\left(L\right)$, the ideal $\mathtt{BC}\left(L\right)$ is a prime ideal in $\mathbf{C}[\lambda ,{\mu }_1,{\mu }_2]$.

Proof. 

Given a basis $\mathcal{B}\left(L\right)=\{1,A_1,A_2\}$, since L and $A_i$ commute, by Lemma 1, $\mathtt{BC}(L,A_i)$ is a nonzero ideal. Observe that $\mathtt{BC}(L,A_i)\subseteq \mathtt{BC}\left(L\right)$, which implies that $\mathtt{BC}\left(L\right)$ is also a nonzero ideal.

As in Lemma 1, we can prove that $\mathtt{BC}\left(L\right)$ is a prime ideal using the fact that $e_L$ is a ring homomorphism and that $\Sigma [\partial ]$ is a Euclidean domain. □

We obtain the following result as a consequence of the construction of ${\epsilon }_{P,Q}$ and Lemma 2.

Theorem 4.

Given a third-order operator L in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$, with nontrivial centralizer $\mathcal{Z}\left(L\right)$, and given any basis $\{1,A_1,A_2\}$ of $\mathcal{Z}\left(L\right)$, then the next isomorphism holds:

$$\mathcal{Z}\left(L\right)=\mathbf{C}[L,A_1,A_2]\simeq \frac{\mathbf{C}[\lambda ,{\mu }_1,{\mu }_2]}{\mathtt{BC}\left(L\right)}.$$

Thus, $\mathcal{Z}\left(L\right)$ is the affine ring of an algebraic curve whose defining ideal is $\mathtt{BC}\left(L\right)$.

Definition 6.

Given a third-order operator L in $\Sigma [\partial ]$, with nontrivial centralizer $\mathcal{Z}\left(L\right)$, we define the spectral curve of Las the irreducible algebraic variety of the prime ideal $\mathtt{BC}\left(L\right)$, that is,

$${\Gamma }_L:=\{P_0\in {\mathbf{C}}^3\mid g\left(P_0\right)=0,\forall g\in \mathtt{BC}\left(L\right)\}.$$

We will compute in Section 6.2 a finite set of defining polynomials for ${\Gamma }_L$. In general, the spectral curve of a third-order operator will be a space curve, and only in some special cases will it be a planar curve.

Remark 3.

In some cases, described in Remark 1, if $\mathcal{Z}\left(L\right)=\mathbf{C}[L,A]$ then $\mathtt{BC}\left(L\right)=\mathtt{BC}(L,A)$. Therefore, the spectral curve of L would be the spectral curve of the pair $L,A,$ a plane curve.

5. Elimination Ideals for Commuting Pairs of ODOs

Given a pair of commuting differential operators $P,Q$ in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$, both of positive order, we know that the BC-ideal $\mathtt{BC}(P,Q)$ is a prime ideal by Lemma 1. This section is dedicated to the proof of Theorem 2, which is obtained as a consequence of Theorem 8 in this section. Moreover, we start proving in Theorem 5 a generalization of a known result of E. Previato [27] and G. Wilson [14] to the case of a pair of commuting operators with coefficients in $\Sigma$.

5.1. Generalized Previato–Wilson Theorem

Let us assume that P and Q have positive orders n and m, and leading coefficients $a_n$ and $b_m$, respectively. Observe that the operators $P-\lambda$ and $Q-\mu$ have coefficients in the differential domain $(\Sigma [\lambda ,\mu ],\partial )$; see the notation in Section 1. Let us consider the differential resultant of $P-\lambda$ and $Q-\mu$, as defined in Appendix B:

$$h(\lambda ,\mu ):=\partial \mathrm{Res}(P-\lambda ,Q-\mu ).$$

By (A8), it provides a nonzero polynomial in $\Sigma [\lambda ,\mu ]$,

$$h(\lambda ,\mu )=a_n^m{\mu }^n-b_m^n{\lambda }^m+\cdots =a_n^m{\mu }^n+\sum _{j=0}^{n-1}{a}_j\left(\lambda \right){\mu }^j\ne 0,$$

where $a_j\left(\lambda \right)$ belong to $\Sigma \left[\lambda \right]$ and have degree less than or equal to m.

The next theorem was proved by E. Previato in [27], for differential operators whose coefficients are analytic functions; see also [14]. For completion, we review the proof given in [7], on this occasion for differential operators with coefficients in an arbitrary differential field $\Sigma$ with algebraically closed field of constant $\mathbf{C}$ of zero characteristic.

Theorem 5.

Let us consider differential operators P and Q in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$, both of positive order. If P and Q commute, then $\partial \mathrm{Res}(P-\lambda ,Q-\mu )$ is a polynomial in $\mathbf{C}[\lambda ,\mu ]$.

Proof. 

Recall that $P-\lambda$ and $Q-\mu$ are differential operators with coefficients in $\Sigma [\lambda ,\mu ]$, whose field of fractions is $\mathcal{F}=\Sigma (\lambda ,\mu )$. We can extend the derivation of $\mathcal{F}$ to its algebraic closure $\overline{\mathcal{F}}$, whose field of constants $\mathcal{C}$ is known to be algebraically closed; see [33], Corollary 3.3.1. Since the ring of constants of $\Sigma [\lambda ,\mu ]$ is $\mathbf{C}[\lambda ,\mu ]$, then it holds that $\Sigma [\lambda ,\mu ]\cap \mathcal{C}=\mathbf{C}[\lambda ,\mu ]$.

Let us consider a fundamental system of solutions ${\psi }_1,\dots ,{\psi }_n$ of $(P-\lambda )\left(y\right)=0$ in a Picard–Vessiot extension $(\mathcal{E},\overline{\partial })$ of $\overline{\mathcal{F}}$ for $(P-\lambda )\left(y\right)=0$, whose field of constants is $\mathcal{C}$ and whose derivation $\overline{\partial }$ is defined by $P-\lambda$. The natural extension of $Q-\mu$ to $(\mathcal{E},\overline{\partial })$ allows us to consider the action of $Q-\mu$ on the $\mathcal{C}$-linear space of the solutions of $(P-\lambda )\left(y\right)=0$.

Since $P-\lambda$ and $Q-\mu$ commute, then $(Q-\mu )\left({\psi }_i\right)$ are solutions of $P-\lambda$. Therefore, there exists an $n\times n$ matrix M with coefficients in $\mathcal{C}$ such that

$$W\left((Q-\mu )\left({\psi }_i\right)\right)=MW\left({\psi }_i\right).$$

Taking determinants and using Poisson’s formula in Theorem A4, we obtain

$$\partial \mathrm{Res}(P-\lambda ,Q-\mu )=\frac{detW\left((Q-\mu )\left({\psi }_i\right)\right)}{detW\left({\psi }_i\right)}=detM\in \mathcal{C}.$$

Thus, $\partial \mathrm{Res}(P-\lambda ,Q-\mu )\in \Sigma [\lambda ,\mu ]\cap \mathcal{C}=\mathbf{C}[\lambda ,\mu ]$. □

Let us consider $({\lambda }_0,{\mu }_0)\in {\mathbf{C}}^2$. For a commuting pair P, Q, the next corollary characterizes the existence of common solutions of the eigenvalue problem

$$Py={\lambda }_{0}y,Qy={\mu }_{0}y.$$

(10)

It follows from Theorem A5 and the fact that $h({\lambda }_0,{\mu }_0)=\partial \mathrm{Res}(P-{\lambda }_0,Q-{\mu }_0).$

Corollary 2.

Given commuting differential operators P and Q in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$, both of positive order, the spectral problem (10) has a non-trivial (common) solution in a Picard–Vessiot extension of Σ for $P-{\lambda }_0$ (or $Q-{\mu }_0$) if and only if $h({\lambda }_0,{\mu }_0)=0$.

5.2. Computing the Burchnall–Chaundy Ideal of a Pair

It is ensured by Theorem 5 that the differential resultant $h(\lambda ,\mu )=\partial \mathrm{Res}(P-\lambda ,Q-\mu )$ is a polynomial in $\mathbf{C}[\lambda ,\mu ]$. Resultants are also called eliminants, and this is the feature of resultants we will emphasize next. Let us consider the left ideal generated by $P-\lambda$ and $Q-\mu$ in $\Sigma [\lambda ,\mu ][\partial ]$:

$$(P-\lambda ,Q-\mu )=\left\{C\right(P-\lambda )+D(Q-\mu )\mid C,D\in \Sigma [\lambda ,\mu \left]\right[\partial \left]\right\}$$

(11)

and the elimination ideal

$$\mathcal{E}(P-\lambda ,Q-\mu ):=(P-\lambda ,Q-\mu )\cap \Sigma [\lambda ,\mu ],$$

(12)

which is a two-sided ideal of $\Sigma [\lambda ,\mu ]$, and

$${\mathcal{E}}_{\mathbf{C}}(P-\lambda ,Q-\mu ):=(P-\lambda ,Q-\mu )\cap \mathbf{C}[\lambda ,\mu ],$$

(13)

which is a two-sided ideal of $\mathbf{C}[\lambda ,\mu ]$. Observe that by Lemma A3, with differential domain of coefficients $\Sigma [\lambda ,\mu ]$, and by Theorem 5, it follows that

$$h(\lambda ,\mu )=\partial \mathrm{Res}(P-\lambda ,Q-\mu )\in {\mathcal{E}}_{\mathbf{C}}(P-\lambda ,Q-\mu ).$$

Thus, both elimination ideals are nonzero.

It was proved by Wilson in [14] that $h(P,Q)=0$, that is, $h(\lambda ,\mu )\in \mathtt{BC}(P,Q)$, in the case of differential operators P and Q whose coefficients are complex-valued smooth functions of x defined in some (real or complex) neighborhood of $x=0$. We use here the argument of [14], Proposition 5.3 in a more general framework, where differential operators have coefficients in an arbitrary differential field $\Sigma$, with field of constants algebraically closed of zero characteristic. For this purpose, we develop the following construction.

Considering $\Sigma [\lambda ,\mu ]$ as a $\Sigma$-vector space with basis $\left\{{\lambda }^i{\mu }^j\right\}$, we can define the $\Sigma$-linear map

$${\epsilon }_{P,Q}:\Sigma [\lambda ,\mu ]\to \Sigma [\partial ], \mathrm{defined} \mathrm{by} {\epsilon }_{P,Q}\left(\sum _{i,j}{\sigma }_{i,j}{\lambda }^i{\mu }^j\right)=\sum _{i,j}{\sigma }_{i,j}{e}_{P,Q}\left({\lambda }^i{\mu }^j\right).$$

(14)

In this setting, given $g\in \Sigma [\lambda ,\mu ]$, we will also denote $g(P,Q):={\epsilon }_{P,Q}\left(g\right)$. Thus,

$$\mathrm{Ker}\left({\epsilon }_{P,Q}\right)=\{g\in \Sigma [\lambda ,\mu ]\mid g(P,Q)=0\}.$$

Observe that the restriction of ${\epsilon }_{P,Q}$ to the subring of constants $\mathbf{C}[\lambda ,\mu ]$ of $\Sigma [\lambda ,\mu ]$ is the ring homomorphism $e_{P,Q}$ defined in (4), and also that

$$\mathtt{BC}(P,Q)=\mathrm{Ker}\left(e_{P,Q}\right)=\mathrm{Ker}\left({\epsilon }_{P,Q}\right)\cap \mathbf{C}[\lambda ,\mu ].$$

(15)

We will proceed next to calculate a generator for both kernels. We will begin by demonstrating that the differential resultant $\partial \mathrm{Res}(P-\lambda ,Q-\mu )$ belongs to the ideal $\mathtt{BC}(P,Q)$, that is, h is a Burchnall–Chaundy polynomial. This is Theorem 6, and to prove it, we will need some auxiliary results.

Lemma 3.

Given commuting differential operators P and Q in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$, both of positive order, with the previous notation, it holds that

$$\mathcal{E}(P-\lambda ,Q-\mu )\subseteq \mathrm{Ker}\left({\epsilon }_{P,Q}\right).$$

Proof. 

Given a polynomial g in $\mathcal{E}(P-\lambda ,Q-\mu )$, then

$$g(\lambda ,\mu )=C(P-\lambda )+D(Q-\mu ),C,D\in \Sigma [\lambda ,\mu ][\partial ].$$

Observe that the differential operator $g(P,Q)={\epsilon }_{P,Q}\left(g\right)$ has finite order, $q=\mathrm{ord}\left(g\right(P,Q\left)\right)$.

Let ${\lambda }_0$ be a constant in $\mathbf{C}$. Since $\mathbf{C}$ is algebraically closed, there exists ${\mu }_0$ in the nonempty set $\{\mu \in \mathbf{C}\mid h({\lambda }_0,\mu )=0\}$. By Corollary 2, there exists a common eigenfunction ${\psi }_{{\lambda }_0}$ for the coupled spectral problem (10). Consequently, the following is an infinite set of linearly independent eigenfunctions

$$\Psi =\{{\psi }_{{\lambda }_0}\mid {\lambda }_0\in \mathbf{C}\},$$

since eigenfunctions associated to different eigenvalues are linearly independent. Now, for every ${\psi }_{{\lambda }_0}\in \Psi$, it holds that

$$g(P,Q)\left({\psi }_{{\lambda }_0}\right)=g({\lambda }_0,{\mu }_0)·{\psi }_{{\lambda }_0}=C^0(P-{\lambda }_0)\left({\psi }_{{\lambda }_0}\right)+D^0(Q-{\mu }_0)\left({\psi }_{{\lambda }_0}\right)=0,$$

where $C^0$ and $D^0$ are the result of evaluating the coefficients of C and D in $({\lambda }_0,{\mu }_0)$. Moreover, $\Psi$ is included in the $\mathbf{C}$-linear space of solutions of the equation $g(P,Q)\left(y\right)=0$, whose dimension is q. Then $g(P,Q)$ is the zero operator. □

As a consequence of Lemma 3, Formula (15) and Theorem 5, the following result is proved.

Theorem 6.

Given commuting differential operators P and Q in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$, both of positive order, then

$$h(\lambda ,\mu )=\partial \mathrm{Res}(P-\lambda ,Q-\mu )\in \mathtt{BC}(P,Q).$$

Moreover, $h=f^{\overline{r}}$ for some non-zero natural number $\overline{r}$ and f is the irreducible polynomial such that $\mathtt{BC}(P,Q)=\left(f\right)$.

The radical of the ideal $\left(h\right)$ generated by h in $\mathbf{C}[\lambda ,\mu ]$ equals $\left(f\right)$; see, for instance, [34], page 178, Proposition 9, where f is the radical of h, that is,

$$f=\sqrt{h}=h/\gcd (h,h^{\prime })$$

(16)

is the square-free part of h. If $n=\mathrm{ord}\left(P\right)$ and $m=\mathrm{ord}\left(Q\right)$, observe that, by Section 5.1, the degrees in $\mu$ and $\lambda$ of h are, respectively,

$$n={deg}_{\mu }\left(h\right)=\overline{r}{deg}_{\mu }\left(f\right),m={deg}_{\lambda }\left(h\right)=\overline{r}{deg}_{\lambda }\left(f\right),$$

(17)

then $\overline{r}$ divides $\mathbf{r}:=\gcd (n,m)$, and $\overline{n}={deg}_{\mu }\left(f\right)\le n$, $\overline{m}={deg}_{\lambda }\left(f\right)\le m$.

Let us consider the pure lexicografic monomial ordering in $\Sigma [\lambda ,\mu ]$ with $\mu >\lambda$. Given $g\in \Sigma [\lambda ,\mu ]$, by the Division Theorem (see [34], Theorem 3, page 64), we can write $g=qf+g_N$, where $q,g_N\in \Sigma [\lambda ,\mu ]$,

$$g_N(\lambda ,\mu )={\alpha }_{\overline{n}-1}\left(\lambda \right){\mu }^{\overline{n}-1}+\cdots +{\alpha }_1\left(\lambda \right)\mu +{\alpha }_0\left(\lambda \right),\mathrm{with} {\alpha }_j\in \Sigma \left[\lambda \right],$$

(18)

since the leading monomial $LT\left(f\right)={\mu }^{\overline{n}}$ of f does not divide $g_N$. We call $g_N$ the normal form of g with respect to f, and for short we write that $g_N$ is the normal form of g w.r.t. f.

Let us consider a polynomial $g\in \mathbf{C}[\lambda ,\mu ]$, and the differential ideal $\left[g\right]$ generated by g in the differential ring $\Sigma [\lambda ,\mu ]$, whose field of constants is $\mathbf{C}[\lambda ,\mu ]$. Observe that $\left[g\right]=\{\ell g\mid \ell \in \Sigma [\lambda ,\mu \left]\right\}$ and ${(\ell g)}^{\prime }={\ell }^{\prime }g$, since $g\in \mathbf{C}[\lambda ,\mu ]$. Furthermore, $\left[g\right]$ is the ideal of $\Sigma [\lambda ,\mu ]$ generated by g, but we use the notation $\left[g\right]$ to distinguish it from the ideal $\left(g\right)$ generated in $\mathbf{C}[\lambda ,\mu ]$ by g.

Lemma 4.

Given commuting differential operators P and Q in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$, both of positive order, with the previous notation, it holds that $\mathrm{Ker}\left({\epsilon }_{P,Q}\right)=\left[f\right]$.

Proof. 

By Theorem 6, we know that $\mathtt{BC}(P,Q)=\left(f\right)$. We observe that $\left[\mathtt{BC}(P,Q)\right]=\left[f\right]\subseteq \mathrm{Ker}\left({\epsilon }_{P,Q}\right)$. Let us prove the other inclusion.

Given $g\in \mathrm{Ker}\left({\epsilon }_{P,Q}\right)$, let us consider its normal form $g_N$ w.r.t. f as in (18). If we denote $d_j=deg\left({\alpha }_j\right)$, then $\mathrm{ord}\left({\alpha }_j\left(P\right)Q^j\right)=n{d}_j+jm$, $j=0,1,\dots ,\overline{n}-1$. Let us define

$$\mathcal{O}=\{n{d}_j+jm\mid {\alpha }_j\left(P\right)Q^j\ne 0,j\in \{0,1,\dots ,\overline{n}-1\}\}.$$

Observe that ${\epsilon }_{P,Q}\left(g\right)={\epsilon }_{P,Q}\left(qf\right)+{\epsilon }_{P,Q}\left(g_N\right)$ and ${\epsilon }_{P,Q}\left(qf\right)={\epsilon }_{P,Q}\left(q\right){\epsilon }_{P,Q}\left(f\right)$, only because f is constant. Since $g(P,Q)={\epsilon }_{P,Q}\left(g\right)=0$ and $f(P,Q)={\epsilon }_{P,Q}\left(f\right)=e_{P,Q}\left(f\right)=0$ then $H=g_N(P,Q)=0$ is a zero operator. If we assume that at least one of the terms of H is nonzero, that is, $\mathcal{O}\ne Ø$, then by (A3)

$$n{d}_{j_1}+j_{1}m=n{d}_{j_2}+j_{2}m$$

for distinct $j_1,j_2\in \{0,1,\dots ,\overline{n}-1\}$. Reorganizing and dividing by $\mathbf{r}=\gcd (n,m)$, it holds that

$$\widehat{n}|d_{j_1}-d_{j_2}|=\widehat{m}|j_1-j_2|,$$

(19)

where $n=\widehat{n}\mathbf{r}$ and $m=\widehat{m}\mathbf{r}$, $\gcd (\widehat{n},\widehat{m})=1$. By (17), we have $\widehat{n}\le \overline{n}\le n$. If $|j_1-j_2|<\widehat{n}$, then by (19), $|d_{j_1}-d_{j_2}|<\widehat{m}$ and $\widehat{m}\mid \widehat{n}$, contradicting that $\widehat{n}$ and $\widehat{m}$ are coprime. If $\widehat{n}\le |j_1-j_2|$, then $|j_1-j_2|=\widehat{n}t+\widehat{j}$, with $0\le \widehat{j}<\widehat{n}$. Hence, $\widehat{n}\left(\right|d_{j_1}-d_{j_2}|-\widehat{m}t)=\widehat{m}\widehat{j}$, implying $\widehat{n}\mid \widehat{m}$, which is a contradiction. Therefore, we conclude that $\mathcal{O}=Ø$, in other words, that $g_N$ is the zero polynomial. This proves that $g=qf$, that is, $g\in \left[f\right]$. □

Theorem 7.

Let us consider commuting differential operators P and Q in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$, both of positive order, and $f=\sqrt{h}$, with $h=\partial \mathrm{Res}(P-\lambda ,Q-\mu )$. Then $\left[f\right]$ is a prime differential ideal in $\Sigma [\lambda ,\mu ]$.

Proof. 

As defined in (6), let ${\Gamma }_{P,Q}$ be the spectral curve of the pair $P,Q$. For each point $({\lambda }_0,{\mu }_0)\in {\Gamma }_{P,Q}$, by Corollary 2, there exists a common solution ${\psi }_0$ in a Picard–Vessiot extension of $\Sigma$ for $P-{\lambda }_0$.

Let us consider $g_1,g_2\in \Sigma [\lambda ,\mu ]$ and assume that $g_1·g_2\in \left[f\right]$. Observe that

$$0=g_1({\lambda }_0,{\mu }_0)·g_2({\lambda }_0,{\mu }_0)\in \Sigma .$$

Thus, we can write the following partition of ${\Gamma }_{P,Q}$:

$${\Gamma }_{P,Q}={\Gamma }_1\cup {\Gamma }_2 \mathrm{where} {\Gamma }_i=\{({\lambda }_0,{\mu }_0)\in {\Gamma }_{P,Q}\mid g_i({\lambda }_0,{\mu }_0)=0\}.$$

Having an algebraically closed field of constants $\mathbf{C}$ implies that at least one of the two components, say ${\Gamma }_1$, has an infinite number of points.

We then have an infinite set of linearly independent eigenfunctions $\Psi =\{{\psi }_0\mid ({\lambda }_0,{\mu }_0)\in {\Gamma }_1\}$. For every ${\psi }_0\in \Psi$, we have

$$0=g_1({\lambda }_0,{\mu }_0)·{\psi }_0=g_1(P,Q)\left({\psi }_0\right)$$

This contradicts the fact that $g_1(P,Q)$ is a finite-order differential operator. This proves that $g_1\in \mathrm{Ker}\left({\epsilon }_{P,Q}\right)$. By Lemma 4, $g_1\in \left[f\right]$. □

We proceed next to emphasize the relationship between the elimination ideals defined in (12) and (13) and the ideal of Burchnall–Chaundy polynomials of a commuting pair of ODOs.

Theorem 8.

Let us consider commuting differential operators P and Q in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$, both of positive order, and $f=\sqrt{h}$, with $h=\partial \mathrm{Res}(P-\lambda ,Q-\mu )$. It holds that

• The radical of the elimination ideal ${\mathcal{E}}_{\mathbf{C}}(P-\lambda ,Q-\mu )$ equals $\mathtt{BC}(P,Q)=\left(f\right)$.
• The radical of the elimination ideal $\mathcal{E}(P-\lambda ,Q-\mu )$ equals $\left[f\right]$.

Proof. 

By Lemma 3 and Lemma 4, we obtain

$$\begin{array}{cc}\hfill \mathcal{E}(P-\lambda ,Q-\mu )\subseteq & \mathrm{Ker}\left({\epsilon }_{P,Q}\right)=\left[f\right],\hfill \\ \hfill {\mathcal{E}}_{\mathbf{C}}(P-\lambda ,Q-\mu )=\mathcal{E}(P-\lambda ,Q-\mu )\cap \mathbf{C}[\lambda ,\mu ]\subseteq & \mathrm{Ker}\left({\epsilon }_{P,Q}\right)\cap \mathbf{C}[\lambda ,\mu ]=\mathtt{BC}(P,Q)=\left(f\right),\hfill \end{array}$$

using also Equality (15) and Theorem 6. Now, taking radicals and applying Theorem 7, the following inclusions hold:

$$\begin{array}{cc}\hfill \sqrt{\mathcal{E}(P-\lambda ,Q-\mu )}\subseteq & \mathrm{Ker}\left({\epsilon }_{P,Q}\right)=\left[f\right]\hfill \\ \hfill \sqrt{{\mathcal{E}}_{\mathbf{C}}(P-\lambda ,Q-\mu )}=& \mathtt{BC}(P,Q)=\left(f\right),\hfill \end{array}$$

where the last equality is satisfied since $\mathbf{C}$ is an algebraically closed field; see [35].

Moreover, the differential resultant $h=f^{\overline{r}}$ is a polynomial in $\mathcal{E}(P-\lambda ,Q-\mu )$, by Theorem 6. Consequently, f belongs to the radical $\sqrt{\mathcal{E}(P-\lambda ,Q-\mu )}$. Thus, we have $\sqrt{\mathcal{E}(P-\lambda ,Q-\mu )}=\left[f\right]$. □

Summarizing, the spectral curve ${\Gamma }_{P,Q}$ of a commuting pair $P,Q\in \Sigma [\partial ]\setminus \mathbf{C}[\partial ]$ is defined by the irreducible polynomial $f=\sqrt{h}$, with $h=\partial \mathrm{Res}(P-\lambda ,Q-\mu )$. The commutative $\mathbf{C}$-algebra $\mathbf{C}[P,Q]$ is isomorphic to the coordinate ring $\mathbf{C}\left[{\Gamma }_{P,Q}\right]$ of this curve:

$$\mathbf{C}[P,Q]\simeq \mathbf{C}\left[{\Gamma }_{P,Q}\right]:=\frac{\mathbf{C}[\lambda ,\mu ]}{\mathtt{BC}(P,Q)}=\frac{\mathbf{C}[\lambda ,\mu ]}{\left(f\right)}.$$

In addition, the prime differential ideal $\left[f\right]$ determines a differential domain

$$\Sigma \left[{\Gamma }_{P,Q}\right]:=\frac{\Sigma [\lambda ,\mu ]}{\left[f\right]},$$

whose fraction field, denoted by $\Sigma \left({\Gamma }_{P,Q}\right)$, will play a key role in the study of the coupled spectral problem:

$$Py=\lambda y,Qy=\mu y.$$

Remark 4.

In some cases, the centralizer $\mathcal{Z}\left(L\right)$ of a differential operator L is the affine ring of a planar curve, as in the case of algebro-geometric Schrödinger operators where $\mathcal{Z}\left(L\right)=\mathbf{C}[L,A]$. The spectral Picard–Vessiot extension of $\Sigma \left({\Gamma }_{L,A}\right)$ for $(L-\lambda )\left(y\right)=0$, introduced in [8], is a Liouvillian extension of $\Sigma \left({\Gamma }_{L,A}\right)$ determined by the solution of the first-order greatest common right divisor of $L-\lambda$ and $A-\mu$, as differential operators with coefficients in $\Sigma \left({\Gamma }_{L,A}\right)$.

6. Centralizers as Coordinate Rings

Let $L\in \Sigma [\partial ]\setminus \mathbf{C}[\partial ]$ be a third-order operator, whose centralizer is non-trivial. We proved in Lemma 2 that $\mathtt{BC}\left(L\right)$ is a prime ideal, and in Theorem 4 that

$$\mathcal{Z}\left(L\right)\simeq \frac{\mathbf{C}[\lambda ,{\mu }_1,{\mu }_2]}{\mathtt{BC}\left(L\right)}.$$

Our next goal is to obtain a computational description of $\mathtt{BC}\left(L\right)$. We will use differential resultants for this purpose.

6.1. Normalized Basis

By Theorem 6, each operator A in the centralizer $\mathcal{Z}\left(L\right)$, together with L, satisfies the algebraic equation defined by an irreducible polynomial $f_A(\lambda ,\mu )\in \mathbf{C}[\lambda ,\mu ]$ defined by the differential resultant $\partial \mathrm{Res}(L-\lambda ,A-\mu )$, that is,

$$f_A(L,A)=0, \mathrm{with} f_A(\lambda ,\mu )={\mu }^3+a_2\left(\lambda \right){\mu }^2+a_1\left(\lambda \right)\mu +a_0\left(\lambda \right).$$

The Tschirnhaus transformation of $f_A(\lambda ,\mu )$ gives a new polynomial

$$f_{\tilde{A}}(\lambda ,\mu )=f_A(\lambda ,\mu -\frac{1}{3}{a}_2\left(\lambda \right))={\mu }^3+{\tilde{a}}_1\left(\lambda \right)\mu +{\tilde{a}}_0\left(\lambda \right).$$

(20)

satisfied by L and the operator

$$\tilde{A}:=A-\frac{1}{3}{a}_2\left(L\right).$$

(21)

Observe that, by Theorems 3 and 8,

$$\frac{\mathbf{C}[\lambda ,\mu ]}{\left(f_A\right)}\simeq \mathbf{C}[L,A]=\mathbf{C}[L,\tilde{A}]\simeq \frac{\mathbf{C}[\lambda ,\mu ]}{\left(f_{\tilde{A}}\right)}.$$

In addition, $f_{\tilde{A}}\in \mathtt{BC}(L,\tilde{A})$ and by (20) $f_{\tilde{A}}$, is an irreducible polynomial because $f_A$ is irreducible over $\mathbf{C}[\lambda ,\mu ]$. Thus, Theorem 8 implies

$$f_{\tilde{A}}(\lambda ,\mu )=\partial \mathrm{Res}(L-\lambda ,\tilde{A}-\mu ).$$

Recall that any basis of $\mathcal{Z}\left(L\right)$ is a minimal-order basis; see Proposition A2 in Appendix A.

Definition 7.

Let $L\in \Sigma [\partial ]\setminus \mathbf{C}[\partial ]$ be a third-order operator, whose centralizer is non-trivial. We will call $A\in \mathcal{Z}\left(L\right)\ne \mathbf{C}\left[L\right]$ a normalized operator of $\mathcal{Z}\left(L\right)$if $\partial \mathit{Res}(L-\lambda ,A-\mu )$ has no term of degree 2 in μ. A basis $\mathcal{B}\left(L\right)=\{1,A_1,A_2\}$ of $\mathcal{Z}\left(L\right)$ as a $\mathbf{C}\left[L\right]$-module is called a normalized basis of $\mathcal{Z}\left(L\right)$if $A_1$ and $A_2$ are normalized operators of $\mathcal{Z}\left(L\right)$.

The next result shows that any other basis of $\mathcal{Z}\left(L\right)$ as a $\mathbf{C}\left[L\right]$-module is determined by a normalized basis.

Theorem 9.

Let $L\in \Sigma [\partial ]\setminus \mathbf{C}[\partial ]$ be a third-order operator, whose centralizer is non-trivial. Let us consider a normalized basis $\mathcal{B}\left(L\right)=\{1,A_1,A_2\}$ of $\mathcal{Z}\left(L\right)$. Then for any other basis $\{1,B_1,B_2\}$ of $\mathcal{Z}\left(L\right)$, it holds that

$$B_i={\alpha }_i{A}_i+q_i\left(L\right),i=1,2,$$

(22)

with ${\alpha }_i\in \mathbf{C}$, $q_i\left(\lambda \right)\in \mathbf{C}\left[\lambda \right]$, ${deg}_{\lambda }\left(q_i\left(\lambda \right)\right)\le \frac{\mathrm{ord}{A}_i-i}{3}$. Moreover, if $\{1,B_1,B_2\}$ is also a normalized basis, then

$$B_i={\alpha }_i{A}_i,i=1,2.$$

Proof. 

We know that $\mathcal{Z}\left(L\right)=\mathbf{C}[L,A_1,A_2]=\mathbf{C}[L,B_1,B_2]$. W.l.o.g., let us assume that $o_1=\mathrm{ord}\left(A_1\right)<o_2=\mathrm{ord}\left(A_2\right)$. Since $\{1,B_1,B_2\}$ is a minimal-order basis, let us assume that $B_i$ has minimal-order congruence with i ($\mathrm{mod}3$). Then $\mathrm{ord}\left(B_i\right)=o_i$ and $o_1<o_2$, together with (2), implies

$$B_1={\alpha }_1{A}_1+q_1\left(L\right) \mathrm{and} B_2={\alpha }_2{A}_2+p\left(L\right)A_1+q_2\left(L\right),$$

with ${\alpha }_i\in \mathbf{C}$, $p\left(\lambda \right),q_i\left(\lambda \right)\in \mathbf{C}\left[\lambda \right]$ and ${deg}_{\lambda }\left(q_i\left(\lambda \right)\right)\le \frac{\mathrm{ord}{A}_i-i}{3}$.

Let us prove that $p\left(\lambda \right)$ is identically zero. We know that $\mathtt{BC}(L,B_2)=\left(f\right)$, where $f=\partial \mathrm{Res}(L-\lambda ,B_2-\mu )\in \mathbf{C}[\lambda ,\mu ]$ is a polynomial of degree 3 in $\mu$. Thus,

$$B_2^3={\beta }_2\left(L\right)B_2^2+{\beta }_1\left(L\right)B_2+{\beta }_0\left(L\right),{\beta }_j\in \mathbf{C}\left[\lambda \right].$$

(23)

Since $\mathcal{B}\left(L\right)$ is a normalized basis, it holds that

$$A_i^3={\gamma }_{i,1}\left(L\right)A_i+{\gamma }_{i,0}\left(L\right),{\gamma }_{i,k}\in \mathbf{C}\left[\lambda \right].$$

(24)

Computing $B_2^3={({\alpha }_2{A}_2+p\left(L\right)A_1+q_2\left(L\right))}^3$, for instance, with Maple and using (24) to replace $A_i^3$, we obtain only the monomials $A_1^2{A}_2$ and $A_1{A}_2^2$ of degree three in $A_1$ and $A_2$ in (25). Comparing with the r.h.s. of (23), we obtain that the coefficients of the monomials of degree three must vanish:

$${({\alpha }_2{A}_2+p\left(L\right)A_1+q_2\left(L\right))}^3=3{\alpha }_{2}p{\left(L\right)}^2{A}_1^2{A}_2+3{\alpha }_2^{2}p\left(L\right)A_1{A}_2^2+\cdots .$$

(25)

Thus, $p\left(\lambda \right)$ must be identically zero and we obtain

$$B_2^3={({\alpha }_2{A}_2+q_2\left(L\right))}^3=3{\alpha }_2^2{q}_2\left(L\right)A_2^2+({\alpha }_2^3{\gamma }_{2,1}\left(L\right)+3{\alpha }_2{q}_2{\left(L\right)}^2)A_2+{\alpha }_2^3{\gamma }_{2,0}\left(L\right)+q_2{\left(L\right)}^3.$$

If $\{1,B_1,B_2\}$ is also a normalized basis, the r.h.s. of (23) cannot have a term $A_2^2$, then $q_2\left(\lambda \right)$ must be the zero polynomial and $B_2={\alpha }_2{A}_2$. We analogously prove that $B_1={\alpha }_1{A}_1$. □

The previous result explains that a normalized basis is unique up to multiplication by constants. We include this result for completion but we do not need to choose the normalized basis in the remaining parts of this work.

6.2. Generators of the Burchnall–Chaundy Ideal of a Third-Order ODO

Let us consider a basis $\mathcal{B}\left(L\right)=\{1,A_1,A_2\}$ of $\mathcal{Z}\left(L\right)$. Let us denote

$$f_i(\lambda ,{\mu }_i):=\partial \mathrm{Res}(L-\lambda ,A_i-{\mu }_i)={\mu }_i^3-{\lambda }^{o_i}+\cdots \in \mathbf{C}[\lambda ,{\mu }_i],$$

if $\mathcal{B}\left(L\right)$ is the normalized basis, then

$$f_i(\lambda ,{\mu }_i):={\mu }_i^3-{\gamma }_{i,1}\left(\lambda \right){\mu }_i-{\gamma }_{i,0}\left(\lambda \right).$$

Recall that $f_i$ are irreducible and $\mathtt{BC}(L,A_i)=\left(f_i\right)$, $i=1,2$; see Section 5.2. In addition, let us denote by $f_3$ the irreducible polynomial in $\mathbf{C}[{\mu }_1,{\mu }_2]$ obtained as the radical of

$$\partial \mathrm{Res}(A_1-{\mu }_1,A_2-{\mu }_2)={\mu }_2^{o_1}-{\mu }_1^{o_2}+\cdots .$$

We have $\mathtt{BC}(A_1,A_2)=\left(f_3\right)$.

The situation so far is described by the following chain of ideals in $\mathbf{C}[\lambda ,{\mu }_1,{\mu }_2]$ and we will determine first if the last two inclusions are identities:

$$\left(0\right)\subset \left(f_i\right)\subset (f_1,f_2)\subseteq (f_1,f_2,f_3)\subseteq \mathtt{BC}\left(L\right),i=1,2.$$

(26)

Let us consider the following algebraic varieties defined by the previous ideals:

$$\Gamma :=V\left(\mathtt{BC}\left(L\right)\right),\gamma :=V(f_1,f_2,f_3),\beta :=V(f_1,f_2).$$

By the inclusions in (26), we obtain $\Gamma \subseteq \gamma \subseteq \beta$. Observe that $\beta =V\left(f_1\right)\cap V\left(f_2\right)$ is the intersection of the irreducible surfaces defined by $f_1(\lambda ,{\mu }_1)=0$ and $f_2(\lambda ,{\mu }_2)=0$; therefore, $\beta$ is a space algebraic curve.

The Zariski closure of the projection $\overline{{\Pi }_{\lambda }\left(\beta \right)}$ of $\beta$ onto the plane $\lambda =0$ is a plane algebraic curve defined by the square free part $r({\mu }_1,{\mu }_2)$ of the algebraic resultant ${\mathrm{Res}}_{\lambda }(f_1,f_2)$ w.r.t. $\lambda$; see [34], Chapter 3, §2 and [36], Section 2. This projected curve $\overline{{\Pi }_{\lambda }\left(\beta \right)}=V\left(r\right)$ could be irreducible or not. Observe that $r(A_1,A_2)=0$, and therefore, $r\in \mathtt{BC}(A_1,A_2)=\left(f_3\right)$. Thus, there are two possible situations:

• Irreducible. If $r({\mu }_1,{\mu }_2)$ is irreducible, then $(f_1,f_2)=(f_1,f_2,f_3)$ and $V\left(r\right)$ is an irreducible curve.
• Non-irreducible. If $r({\mu }_1,{\mu }_2)$ is not irreducible, then $f_3$ properly divides r and $(f_1,f_2)\ne (f_1,f_2,f_3)$. Including $f_3$ in the ideal allows us to select one irreducible component of $V\left(r\right)$. The example in Section 8 illustrates this situation.

We will prove next that $(f_1,f_2,f_3)$ is the defining ideal of an irreducible space curve, in both situations. By Remark 2, the irreducible component of ${\Pi }_{\lambda }\left(\beta \right)$ determined by $f_3$ is a proper curve; it cannot be a point.

Remark 5.

Let us assume that the projection over the plane $\lambda =0$ of the algebraic curve β, and therefore, γ is birational. Note that this holds for almost all projections (see [35] [Fulton], p. 155), and hence, we can make this assumption w.l.o.g. More precisely, a valid projection direction can be achieved by an affine change of coordinates (see [36], Section 2, which establishes an isomorphism between coordinate rings; see, for instance, [37], Theorem 2.24).

A Gröbner basis $\mathcal{F}=\{F_0,F_1,\dots ,F_s\}\subset \mathbf{C}[\lambda ,{\mu }_1,{\mu }_2]$ of $(f_1,f_2,f_3)$ w.r.t. the pure lexicographic monomial ordering with $\lambda >{\mu }_1>{\mu }_2$ verifies:

• The polynomial $F_0\in \mathbf{C}[{\mu }_1,{\mu }_2]$ is an implicit representation of the Zariski closure of the projection $\overline{{\Pi }_{\lambda }\left(\gamma \right)}$ of γ onto the plane $\lambda =0$. Furthermore, $F_0=f_3$ because $f_3$ is irreducible over $\mathbf{C}$. Thus, this projection is an irreducible algebraic curve $\overline{{\Pi }_{\lambda }\left(\gamma \right)}=V\left(f_3\right)$.
• On the other hand, since this projection is assumed birational on γ, then $\mathcal{F}$ contains a linear polynomial in λ, say $F_1=g_2({\mu }_1,{\mu }_2)\lambda -g_1({\mu }_1,{\mu }_2)$.

Let us consider the pure lexicographic monomial ordering with $\lambda >{\mu }_1>{\mu }_2$ in $\Sigma [\lambda ,{\mu }_1,{\mu }_2]$. Given $g\in \Sigma [\lambda ,{\mu }_1,{\mu }_2]$, by the Division Theorem [34], Theorem 3, page 64, we can write

$$g=\sum _j{q}_j{F}_j+g^{\mathcal{F}}$$

(27)

where $q_j,g^{\mathcal{F}}\in \Sigma [\lambda ,{\mu }_1,{\mu }_2]$. We call $g^{\mathcal{F}}$ the normal form of g w.r.t $\mathcal{F}$.

Lemma 5.

Let us consider a Gröbner basis $\mathcal{F}$ of $(f_1,f_2,f_3)$ w.r.t. the pure lexicographic order with $\lambda >{\mu }_1>{\mu }_2$. The normal form $g^{\mathcal{F}}$ of $g\in \Sigma [\lambda ,{\mu }_1,{\mu }_2]$ w.r.t $\mathcal{F}$ is a polynomial in $\Sigma [{\mu }_1,{\mu }_2]$ whose degree in ${\mu }_1$ is less than ${deg}_{{\mu }_1}\left(f_3\right)$.

Proof. 

By the Division Theorem, no monomial of $g^{\mathcal{F}}$ is divisible by the leading terms $LT\left(F_1\right)=\lambda$ and $LT\left(F_0\right)=LT\left(f_3\right)$; thus, the result follows. □

We are ready to prove that $\mathtt{BC}\left(L\right)\subseteq (f_1,f_2,f_3)$.

Theorem 10.

Let L be a third-order operator in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$, whose centralizer is non-trivial. Given a basis $\{1,A_1,A_2\}$ of the centralizer, let $f_i$, $i=1,2,3$ be the irreducible polynomials over $\mathbf{C}$ such that $\mathtt{BC}(L,A_i)=\left(f_i\right)$ and $\mathtt{BC}(A_1,A_2)=\left(f_3\right)$. Then $\mathtt{BC}\left(L\right)=(f_1,f_2,f_3)$

Proof. 

Given $g\in \mathtt{BC}\left(L\right)$, let $g^{\mathcal{F}}$ be its normal form w.r.t $\mathcal{F}$. Then $g^{\mathcal{F}}\in \mathtt{BC}\left(L\right)$. Furthermore, by Lemma 5, then $g^{\mathcal{F}}\in \mathtt{BC}(A_1,A_2)\subset \mathbf{C}[{\mu }_1,{\mu }_2]$ and ${deg}_{{\mu }_1}\left(g^{\mathcal{F}}\right)<{deg}_{{\mu }_1}\left(f_3\right)$. We conclude that $g^{\mathcal{F}}$ is identically zero, that is, $g\in \left(\mathcal{F}\right)=(f_1,f_2,f_3)$. □

Corollary 3.

Let $L\in \Sigma [\partial ]\setminus \mathbf{C}[\partial ]$ be a third-order operator, whose centralizer is non-trivial. Then

$$\Gamma =V\left(\mathtt{BC}\right(L\left)\right)$$

is an irreducible algebraic curve whose defining ideal is $\mathtt{BC}\left(L\right)=(f_1,f_2,f_3)$, with $f_i$ defined above. Furthermore,

$$\mathcal{Z}\left(L\right)\simeq \frac{\mathbf{C}[\lambda ,{\mu }_1,{\mu }_2]}{(f_1,f_2,f_3)}.$$

7. Parametric Factorization of Algebro-Geometric ODOs

Let L be a third-order operator in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$, whose centralizer is non-trivial. We consider next the factorization of $L-\lambda$, for $\lambda$ an algebraic parameter over $\Sigma$. We know that $\lambda$ is not a free parameter, but that it is governed by the spectral curve $\Gamma$ of L. Thus,

$$L-\lambda \in \Sigma \left[\lambda \right][\partial ]\subset \Sigma [\lambda ,{\mu }_1,{\mu }_2][\partial ].$$

Recall that $\Sigma [\lambda ,{\mu }_1,{\mu }_2]$ is a differential ring with the extended derivation ∂; see the notation in Section 1.

Let us consider a basis $\{1,A_1,A_2\}$ of $\mathcal{Z}\left(L\right)$ and the irreducible polynomials $f_i$, $i=1,2,3$ in $\mathbf{C}[\lambda ,{\mu }_1,{\mu }_2]$ such that $\mathtt{BC}(L,A_1)=\left(f_i\right)$ and $\mathtt{BC}(A_1,A_2)=\left(f_3\right)$. By Theorem 10,

$$\left[\mathtt{BC}\left(L\right)\right]=[f_1,f_2,f_3].$$

(28)

As differential operators in $\Sigma (\lambda ,{\mu }_1,{\mu }_2)[\partial ]$, the pairs $L-\lambda$ and $A_i-{\mu }_i$ are right coprime, since their differential resultants are nonzero, by Theorem A2. To consider the factorization of $L-\lambda$, we need an appropriate differential field of coefficients.

7.1. Coefficient Field for Factorization

Associated to L we have defined in (9) the prime ideal $\mathtt{BC}\left(L\right)$; see Lemma 2. We will prove in this section that the differential ideal $\left[\mathtt{BC}\right(L\left)\right]$ is a prime ideal in $\Sigma [\lambda ,{\mu }_1,{\mu }_2]$. Thus, we can define the differential domain

$$\Sigma [\Gamma ]=\frac{\Sigma [\lambda ,{\mu }_1,{\mu }_2]}{\left[\mathtt{BC}\right(L\left)\right]}$$

(29)

and its fraction field $\Sigma (\Gamma )$, which therefore is a differential field.

Considering $\Sigma [\lambda ,{\mu }_1,{\mu }_2]$ as a $\Sigma$-vector space with basis

$$\{M_{\alpha }={\lambda }^{{\alpha }_0}{\mu }_1^{{\alpha }_1}{\mu }_2^{{\alpha }_2}\mid \alpha =({\alpha }_0,{\alpha }_1,{\alpha }_2)\in {\mathbb{N}}^3\},$$

we can define the $\Sigma$-linear map

$${\epsilon }_L:\Sigma [\lambda ,{\mu }_1,{\mu }_2]\to \Sigma [\partial ], \mathrm{defined} \mathrm{by} {\epsilon }_L\left(\sum _{\alpha }{\sigma }_{\alpha }{M}_{\alpha }\right)=\sum _{\alpha }{\sigma }_{\alpha }{e}_L\left(M_{\alpha }\right),$$

(30)

where $e_L$ is the ring homomorphism defined in (7). Observe that given $g={\sum }_{\alpha }{\sigma }_{\alpha }{M}_{\alpha }\in \Sigma [\lambda ,{\mu }_1,{\mu }_2]$ and $F\in \mathbf{C}[\lambda ,{\mu }_1,{\mu }_2]$, then

$${\epsilon }_L\left(gF\right)=\sum _{\alpha }{\sigma }_{\alpha }{e}_L\left(M_{\alpha }F\right)={\epsilon }_L\left(g\right)e_L\left(F\right).$$

(31)

Lemma 6.

Let us consider a Gröbner basis $\mathcal{F}$ of $(f_1,f_2,f_3)$ w.r.t. the pure lexicographic order with $\lambda >{\mu }_1>{\mu }_2$. Given $g\in \mathrm{Ker}\left({\epsilon }_L\right)$, the normal form $g^{\mathcal{F}}$ of g w.r.t $\mathcal{F}$ verifies

$$g^{\mathcal{F}}\in \left[\mathtt{BC}(A_1,A_2)\right]=\left[f_3\right].$$

Proof. 

With notation as in (27), by (31), we have

$$0={\epsilon }_L\left(g\right)=\sum _j{\epsilon }_L\left(q_j\right)e_L\left(F_j\right)+{\epsilon }_L\left(g^{\mathcal{F}}\right)={\epsilon }_L\left(g^{\mathcal{F}}\right).$$

Thus, $g^{\mathcal{F}}\in \mathrm{Ker}\left({\epsilon }_L\right)$ and by Lemma 5, we know that $g^{\mathcal{F}}\in \Sigma [{\mu }_1,{\mu }_2]$. Therefore, by Lemma 4,

$$g^{\mathcal{F}}\in \mathrm{Ker}\left({\epsilon }_{A_1,A_2}\right)=\left[\mathtt{BC}(A_1,A_2)\right]=\left[f_3\right].$$

□

Lemma 7.

With the previous notation, it holds that $\mathit{Ker}\left({\epsilon }_L\right)=\left[\mathtt{BC}\left(L\right)\right]$.

Proof. 

We will show next that the inclusion of $\left[\mathtt{BC}\left(L\right)\right]=[f_1,f_2,f_3]$ in $\mathrm{Ker}\left({\epsilon }_L\right)$ is natural. Since $f_i$ has constant coefficients, the next differential ideal coincides with the ideal generated by $f_1,f_2,f_3$ in $\Sigma [\lambda ,{\mu }_1,{\mu }_2]$:

$$[f_1,f_2,f_3]=\{g_1{f}_1+g_2{f}_2+g_3{f}_3\mid g_i\in \Sigma [\lambda ,{\mu }_1,{\mu }_2]\}.$$

In addition, by (31), ${\epsilon }_L\left(g_i{f}_i\right)={\epsilon }_L\left(g_i\right)e_L\left(f_i\right)=0$, which proves that $[\mathtt{BC}\left(L\right)\subseteq \mathrm{Ker}\left({\epsilon }_L\right)]$.

Conversely, given $g\in \mathrm{Ker}\left({\epsilon }_L\right)$, by Lemma 6, $g^{\mathcal{F}}\in \left[f_3\right]$. In addition, by Lemma 5, ${deg}_{{\mu }_1}\left(g^{\mathcal{F}}\right)<{deg}_{{\mu }_1}\left(f_3\right)$. Therefore $g^{\mathcal{F}}$ is identically zero, proving that $g\in \left[\mathcal{F}\right]=\left[\mathtt{BC}\right(L\left)\right]$. □

Theorem 11.

Let L be a third-order operator in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$, whose centralizer is non-trivial. Then the differential ideal $\left[\mathtt{BC}\right(L\left)\right]$ is a prime ideal in $\Sigma [\lambda ,{\mu }_1,{\mu }_2]$.

Proof. 

Given $g\in \left[\mathtt{BC}\right(L\left)\right]$, let us assume that $g=g_1·g_2$, with $g_1,g_2\in \Sigma [\lambda ,{\mu }_1,{\mu }_2]$. By Lemma 6, $g^{\mathcal{F}}\in Ker\left({\epsilon }_L\right)$. By Lemma 5, $g_i^{\mathcal{F}}\in \Sigma [{\mu }_1,{\mu }_2]$ and using (27), we can write

$$g_i={\Delta }_i+g_i^{\mathcal{F}},\mathrm{with} {\Delta }_i\in \left[\mathtt{BC}\left(L\right)\right].$$

Thus,

$$g_1·g_2={\Delta }_1{\Delta }_2+{\Delta }_1{g}_2^{\mathcal{F}}+{\Delta }_2{g}_1^{\mathcal{F}}+g_1^{\mathcal{F}}{g}_2^{\mathcal{F}}.$$

Therefore, $0={\epsilon }_L\left(g\right)={\epsilon }_L(g_1·g_2)={\epsilon }_L\left(g_1^{\mathcal{F}}{g}_2^{\mathcal{F}}\right)$. This implies that $g_1^{\mathcal{F}}{g}_2^{\mathcal{F}}\in \left[f_3\right]$, which is a prime ideal in $\Sigma [{\mu }_1,{\mu }_2]$, by Theorem 7. We can conclude that $g_i^{\mathcal{F}}\in \left[f_3\right]$, which shows that $g_i\in \left[\mathtt{BC}\left(L\right)\right]$, for $i=1$ or $i=2$, proving that $\left[\mathtt{BC}\right(L\left)\right]$ is a prime ideal. □

We are now ready to work over the field $\Sigma (\Gamma )$, the fraction field of the domain $\Sigma [\Gamma ]$ defined in (29). Regarding the differential structure of $\Sigma (\Gamma )$, we consider the standard differential structure of the quotient ring $\Sigma [\Gamma ]$ given by a derivation $\tilde{\partial }$ defined by:

$$\tilde{\partial }(q+\left[\mathtt{BC}\left(L\right)\right]):=\partial \left(q\right)+\left[\mathtt{BC}\left(L\right)\right],q\in \Sigma [\lambda ,{\mu }_1,{\mu }_2].$$

(32)

Observe that $\tilde{\partial }$ is a derivation in $\Sigma [\Gamma ]$ because $\left[\mathtt{BC}\right(L\left)\right]$ is a differential ideal. By abuse of notation, we will denote by ∂ the derivation $\tilde{\partial }$ and its extension to the fraction field $\Sigma (\Gamma )$.

7.2. The Intrinsic Right Factor

We will study next the factorization of $L-\lambda$ as a differential operator with coefficients in the differential field $(\Sigma (\Gamma ),\partial )$, as defined in Section 7.1.

As differential operators in $\Sigma (\Gamma )[\partial ]$, $L-\lambda$ and $A_i-{\mu }_i$, $i=1,2$ have a non-trivial common factor, namely their monic greatest common right divisor ${\mathcal{L}}_i:=\mathrm{gcrd}(L-\lambda ,A_i-{\mu }_i)$. For instance, this follows from the Resultant Theorem A5, since $f_i=\partial \mathrm{Res}(L-\lambda ,A_i-{\mu }_i)$ is zero in $\Sigma (\Gamma )$. Similarly, for some positive integer r, it holds that $f_3^r=\partial \mathrm{Res}(A_1-{\mu }_1,A_2-{\mu }_2)$, which is zero in $\Sigma (\Gamma )$, implying that ${\mathcal{L}}_3:=\mathrm{gcrd}(A_1-{\mu }_1,A_2-{\mu }_2)$ is a differential operator of order greater than or equal to one.

We will prove next that ${\mathcal{L}}_1$ and ${\mathcal{L}}_2$ are indeed differential operators of order 1 in $\Sigma (\Gamma )[\partial ]$. Moreover, the goal of this section is to show that ${\mathcal{L}}_1$ and ${\mathcal{L}}_2$ are equal as differential operators in $\Sigma (\Gamma )[\partial ]$, providing a right factor of $L-\lambda$ that is intrinsic to the nature of L. This factor is linked to the hypothesis of having a nontrivial centralizer.

We chose differential subresultants to compute greatest common right divisors, because they have fairly explicit expressions for their computation that also allow us to obtain some important theoretical conclusions. As defined in Appendix B.1, let us consider the first differential subresultants:

$$\begin{array}{cc}\hfill & \mathrm{s}\partial {\mathrm{Res}}_1(L-\lambda ,A_i-{\mu }_i)={\varphi }_{i,0}+{\varphi }_{i,1}\partial ,i=1,2,\hfill \\ \hfill & \mathrm{s}\partial {\mathrm{Res}}_1(A_1-{\mu }_1,A_2-{\mu }_2)={\varphi }_{3,0}+{\varphi }_{3,1}\partial \hfill \end{array}$$

where, for $j=0,1$

$$\begin{array}{cc}\hfill & {\varphi }_{i,j}(\lambda ,{\mu }_i):=det\left(S_1^j(L-\lambda ,A_i-{\mu }_i)\right),i=1,2\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill & {\varphi }_{3,j}({\mu }_1,{\mu }_2):=det\left(S_1^j(A_1-{\mu }_1,A_2-{\mu }_2)\right).\hfill \end{array}$$

(34)

Observe that the coefficients ${\varphi }_{i,j}$ are nonzero polynomials in $\Sigma [\lambda ,{\mu }_1,{\mu }_2]$, but we need to check if they are nonzero in $\Sigma (\Gamma )$. Recall that from Section 3, $o_i=\mathrm{ord}\left(A_i\right)\equiv i\left(\mathrm{mod}3\right)$.

Lemma 8.

With the notation established above, the class ${\varphi }_{i,j}+\left[\mathtt{BC}\left(L\right)\right]$, $i=1,2$, $j=0,1$ in $\Sigma (\Gamma )$ is non-zero. In addition, if $\gcd (o_1,o_2)=1$, then the class of ${\varphi }_{3,j}+\left[\mathtt{BC}\left(L\right)\right]$ is non-zero.

Proof. 

By the construction of the matrices $S_1^j$ as in (A11), the degree in ${\mu }_i$ of ${\varphi }_{i,j}$ is less than 3, for $i=1,2$. Thus, ${\varphi }_{i,j}$, $i=1,2$ does not belong to $\left[\mathtt{BC}\right(L\left)\right]$ because otherwise it is included in

$$\left[\mathtt{BC}\left(L\right)\right]\cap \Sigma [\lambda ,{\mu }_i]=\left[\mathtt{BC}(L,A_i)\right]=\left[f_i\right],$$

which is not possible. Similarly, if $\gcd (o_1,o_2)=1$, then the degree in ${\mu }_1$ of ${\varphi }_{3,j}$ is less than $o_2$ and ${\varphi }_{3,j}$ does not belong to $\left[\mathtt{BC}\right(L\left)\right]$ because otherwise, it is included in

$$\left[\mathtt{BC}\left(L\right)\right]\cap \Sigma [{\mu }_1,{\mu }_2]=\left[\mathtt{BC}(A_1,A_2)\right]=\left[f_3\right].$$

Observe that in the case $\gcd (o_1,o_2)=1$ then $f_3=\partial \mathrm{Res}(A_1-{\mu }_1,A_2-{\mu }_2)$ has degree $o_2$ in ${\mu }_1$. □

By Lemma 8, $\mathrm{s}\partial {\mathrm{Res}}_1(L-\lambda ,A_i-{\mu }_i)$ are nonzero differential operators in $\Sigma (\Gamma )[\partial ]$ of order one. The First Subresultant Theorem A3 implies that ${\mathcal{L}}_i=\mathrm{gcrd}(L-\lambda ,A_i-{\mu }_i)$ equals the first subresultant. We can make them monic and write

$${\mathcal{L}}_i=\mathrm{gcrd}(L-\lambda ,A_i-{\mu }_i)=\partial +{\varphi }_i+\left[\mathtt{BC}\left(L\right)\right],\mathrm{with} {\varphi }_i:=\frac{{\varphi }_{i,0}}{{\varphi }_{i,1}}.$$

(35)

The next lemma will be important to prove that the right factors ${\mathcal{L}}_i$ coincide over the field of the spectral curve $\Sigma (\Gamma )$. For this purpose, let us define the elimination ideal

$$\mathcal{E}\left(L\right):=(L-\lambda ,A_1-{\mu }_1,A_2-{\mu }_2)\cap \Sigma [\lambda ,{\mu }_1,{\mu }_2].$$

(36)

Proposition 1.

With the previous notation, it holds that $\mathcal{E}\left(L\right)\subset \left[\mathtt{BC}\right(L\left)\right]$.

Proof. 

Given a polynomial g in $\mathcal{E}\left(L\right)$, then

$$g(\lambda ,{\mu }_1,{\mu }_2)=C(L-\lambda )+D_1(A_1-{\mu }_1)+D_2(A_2-{\mu }_2),C,D_1,D_2\in \Sigma [\lambda ,{\mu }_1,{\mu }_2][\partial ].$$

(37)

With the notation in Remark 5 and by Corollary 3, every point of $\Gamma$ is determined by a point $({\eta }_1,{\eta }_2)$ of the projection of the curve $\Gamma$ onto the plane $\lambda =0$, in the following way:

$$\left(\frac{g_1({\eta }_1,{\eta }_2)}{g_2({\eta }_1,{\eta }_2)},{\eta }_1,{\eta }_2\right) \mathrm{with} f_3({\eta }_1,{\eta }_2)=0,$$

(38)

except for a finite number of points such that $g_2({\eta }_1,{\eta }_2)=0$.

As in Remark 5, let us consider a Gröbner basis $\mathcal{F}=\{F_0,F_1,\dots ,F_s\}\subset \mathbf{C}[\lambda ,{\mu }_1,{\mu }_2]$ of $(f_1,f_2,f_3)$ w.r.t. the pure lexicographic monomial ordering with $\lambda >{\mu }_1>{\mu }_2$. Recall that $F_1=g_2({\mu }_1,{\mu }_2)\lambda -g_1({\mu }_1,{\mu }_2)$, with $g_i\in \mathbf{C}[{\mu }_1,{\mu }_2]$. By (38), since $\mathtt{BC}\left(L\right)=(f_1,f_2,f_3)=\left(\mathcal{F}\right)$, we have

$$F_1(L,A_1,A_2)=g_2(A_1,A_2)L-g_1(A_1,A_2)=0.$$

(39)

Given ${\eta }_1\in \mathbf{C}$, there exists $\eta =({\eta }_1,{\eta }_2)\in {\Pi }_{\lambda }(\Gamma )$, the Zariski closure of the projection of $\Gamma$ onto the plane $\lambda =0$. Let ${\mathcal{E}}_1$ be the Picard–Vessiot extension of $\Sigma$ for $A_1-{\eta }_1$. By Corollary 2, since $f_3({\eta }_1,{\eta }_2)=0$, there exists ${\psi }_1\in {\mathcal{E}}_1$, a common eigenfunction of the spectral problem

$$A_{1}y={\eta }_{1}y,A_{2}y={\eta }_{2}y.$$

(40)

Thus, $\Psi :=\{{\psi }_1\mid {\eta }_1\in \mathbf{C}\}$ is an infinite set of linearly independent eigenfunctions for (40). Observe that, by (39),

$$0=(L{g}_2(A_1,A_2)-g_1(A_1,A_2))\left({\psi }_1\right)=L(g_2\left(\eta \right)·{\psi }_1)-g_1\left(\eta \right)·{\psi }_1$$

Thus,

$$L\left({\psi }_1\right)=\frac{g_1\left(\eta \right)}{g_2\left(\eta \right)}·{\psi }_1.$$

(41)

To finish the argument, for every ${\psi }_1\in \Psi$, by (40) and (41),

$$\begin{array}{c}g(L,A_1,A_2)\left({\psi }_1\right)=\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill & g\left(\frac{g_1\left(\eta \right)}{g_2\left(\eta \right)},{\eta }_1,{\eta }_2\right)·{\psi }_1=\left(\tilde{C}\left(L-\frac{g_1\left(\eta \right)}{g_2\left(\eta \right)}\right)+{\tilde{D}}_1(A_1-{\eta }_1)+{\tilde{D}}_2(A_2-{\eta }_2)\right)\left({\psi }_1\right)=0,\hfill \end{array}$$

(43)

using (37) and obtaining $\tilde{C}$, ${\tilde{D}}_1$ and ${\tilde{D}}_2$ in $\Sigma [\partial ]$. Since $\Psi$ is an infinite set, we can conclude that $g(L,A_1,A_2)=0$, which proves the result. □

Let us denote by ${\overline{\varphi }}_i$ the class ${\varphi }_i+\left[\mathtt{BC}\left(L\right)\right]$ in $\Sigma (\Gamma )$. Looking at these functions as representatives of objects in $\Sigma (\Gamma )$, we can establish the following result.

Lemma 9.

With the previous notation. Let us consider ${\varphi }_i$ as in (35), then

$$\varphi :={\overline{\varphi }}_1={\overline{\varphi }}_2\in \Sigma (\Gamma ).$$

(44)

If $\mathit{gcd}(o_1,o_2)=1$, then $\varphi ={\overline{\varphi }}_3$.

Proof. 

By the definition of subresultants in Appendix B.1, we know that

$${\mathcal{L}}_i=\partial +{\varphi }_i\in (L-\lambda ,A_i-{\mu }_i).$$

The next one is a differential polynomial in $\Sigma [\lambda ,{\mu }_1,{\mu }_2]$:

$$g={\varphi }_{1,1}{\varphi }_{2,1}({\mathcal{L}}_1-{\mathcal{L}}_2)={\varphi }_{1,0}{\varphi }_{2,1}-{\varphi }_{2,0}{\varphi }_{1,1}.$$

Observe that it belongs to the elimination ideal $\mathcal{E}\left(L\right)$ as defined in (36). In addition, by Lemma 1,

$$g\in \mathcal{E}\left(L\right)\subseteq \left[\mathtt{BC}\right(L\left)\right].$$

Therefore, $\overline{g}\equiv 0$ in $\Sigma (\Gamma )$. This proves (44). □

We are ready to state an important application of the results of this paper.

Theorem 12.

Let L be a third-order operator in $\Sigma [\partial ]\setminus \mathbf{C}[\partial ]$, whose centralizer is non-trivial. Let Γ be the spectral curve of L. Then $L-\lambda$ has an order one factor $\partial +\varphi$ in $\Sigma (\Gamma )[\partial ]$. We call $\partial +\varphi$ the intrinsic right factor of L. Moreover, given any basis $\{1,A_1,A_2\}$ of $\mathcal{Z}\left(L\right)$ as a $\mathbf{C}\left[L\right]$-module, this factor is the greatest common right divisor in $\Sigma (\Gamma )[\partial ]$:

$$\partial +\varphi =\mathrm{gcrd}(L-\lambda ,A_1-{\mu }_1,A_2-{\mu }_2).$$

(45)

Proof. 

By the First Subresultant Theorem A3,

$$\partial +\overline{{\varphi }_i}=\mathrm{gcrd}(L-\lambda ,A_i-{\mu }_i),i=1,2$$

and by Lemma 9,

$$\partial +\varphi =\partial +\overline{{\varphi }_1}=\partial +\overline{{\varphi }_2}$$

Thus, (45) follows. □

As a consequence of (45) and (35) $\partial +\varphi$, the intrinsic right factor of $L-\lambda$ as a differential operator in $\Sigma [\Gamma ][\partial ]$ can be computed as $\mathrm{gcrd}(L-\lambda ,A_i-{\mu }_i)$, for any $A_i\in \mathcal{Z}\left(L\right)$ of minimal order $i\left(\mathrm{mod}3\right)$ for $i=1$ or $i=2$.

Remark 6.

Let us assume that $L={\partial }^3+u_1\partial +u_0$ is in normal form. By direct computation, we obtain the factorization

$$L-\lambda =\left({\partial }^2-\varphi \partial +u_1-2{\varphi }^{\prime }+{\varphi }^2\right)·(\partial +\varphi ),$$

(46)

in $\Sigma (\Gamma )[\partial ]$, under the condition

$${\varphi }^3+u_1\varphi -3\varphi {\varphi }^{\prime }-u_0+{\varphi }^{″}+\lambda =0.$$

(47)

Factorization at each point $P_0$ of $\Gamma$. 

The intrinsic right factor is a global factor in the following sense. For every $P_0=({\lambda }_0,{\eta }_1,{\eta }_2)\in \Gamma \setminus Z$, where Z is a finite number of points in ${\mathbf{C}}^3$, we obtain a right factor in $\Sigma [\partial ]$ of

$$L-{\lambda }_0=N_i·(\partial +{\varphi }_i\left(P_0\right)),i=1,2$$

where $\partial +{\varphi }_i\left(P_0\right)$ is the greatest common right divisor of $L-{\lambda }_0$ and $A_i-{\eta }_i$ in $\Sigma [\partial ]$ and ${\varphi }_i\left(P_0\right)$ is the result of replacing $(\lambda ,{\mu }_1,{\mu }_2)$ in ${\varphi }_i$ by $({\lambda }_0,{\eta }_1,{\eta }_2)$. The set of points Z to be removed can be described as

$$Z=\{({\lambda }_0,{\eta }_1,{\eta }_2)\in {\mathbf{C}}^3\mid ({\lambda }_0,{\eta }_i)\in Z_i,i=1,2\}$$

where $Z_i=\{({\lambda }_0,{\eta }_i)\in {\mathbf{C}}^2\mid {\varphi }_{i,1}({\lambda }_0,{\eta }_i)=0\}$, i = 1, 2, are finite sets of points, which is a consequence of (33) together with Remark 5. Furthermore, $\partial +{\varphi }_1\left(P_0\right)=\partial +{\varphi }_2\left(P_0\right)$ is the greatest common right divisor of $L-{\lambda }_0$, $A_1-{\eta }_1$ and $A_2-{\eta }_2$ for every $P_0=({\lambda }_0,{\eta }_1,{\eta }_2)\in \Gamma \setminus Z$.

Remark 7.

The factorization of an ordinary differential operator with coefficient in a differential field $(\Sigma =\mathbf{C}(x),\partial =d/dx)$ can be achieved by means of the so-called eigenring of L, defined by M. Singer in [38] as

$$\mathcal{E}\left(L\right)=\{\overline{R}\in \Sigma [\partial ]/\Sigma [\partial ]·L\mid LR is divisible by L\},$$

where $\overline{R}$ denotes the equivalence class of $R\in \Sigma [\partial ]$ in the module $\Sigma [\partial ]/\Sigma [\partial ]·L$. The centralizer $\mathcal{Z}\left(L\right)$ can be seen as a subring of the eigenring, but note that the representative of order smaller than 3 in the eigenring of an element of the centralizer may not belong itself to the centralizer. In the example of Section 8, since $\mathit{ord}\left(A_1\right)=4$, then $A_1$ has a representative in $\mathcal{E}\left(L\right)$ that does not belong to the centralizer.

One could study the factorization of $L-{\lambda }_0$, for any ${\lambda }_0\in \mathbf{C}$ by means of the algorithms based on the eigenring, as in [39]. What these algorithms would not do is to identify the spectral curve. Furthermore, these algorithms would not allow a formal treatment of λ as an algebraic parameter over the coefficient field Σ. These algorithms would partially identify the spectral curve. They would treat the parameter λ in the algebraic closure of $\Sigma \left(\lambda \right)$ and therefore consider a branch of the spectral curve. See the example in Section 8.

8. Example of Non-Planar Spectral Curve

There are many examples of rank 1 operators whose centralizers are the ring of a plane algebraic curve; see references in. In this section, we present the first explicit example of a centralizer isomorphic to the ring of a non-planar spectral curve. We explained the computational method used to obtain this example in [15,26], based on Wilson’s almost commuting bases [14]. We use this example to illustrate the new results of this paper.

Let us consider the differential operator in $\mathbb{C}\left(x\right)[\partial ]$, where $\partial =\frac{d}{dx}$:

$$L={\partial }^3-\frac{6}{x^2}\partial +\frac{12}{x^3}+1.$$

(48)

The centralizer of L equals $\mathcal{Z}\left(L\right)=\mathbb{C}[L,A_1,A_2]$ with

$$\begin{array}{cc}\hfill A_1=& {\partial }^4-\frac{8}{x^2}{\partial }^2+\frac{24}{x^3}\partial -\frac{24}{x^4},\hfill \\ \hfill A_2=& {\partial }^5-\frac{10}{x^2}{\partial }^3+\frac{40}{x^3}{\partial }^2-\frac{80}{x^4}\partial +\frac{80}{x^5}.\hfill \end{array}$$

The Burchall–Chaundy ideal of L equals

$$\mathtt{BC}\left(L\right)=(f_1,f_2,f_3),$$

generated by the irreducible polynomials

$$\begin{array}{cc}\hfill & f_1(\lambda ,{\mu }_1)=\partial \mathrm{Res}(L-\lambda ,A_1-{\mu }_1)=-{\mu }_1^3+{(\lambda -1)}^4,\hfill \\ \hfill & f_2(\lambda ,{\mu }_2)=\partial \mathrm{Res}(L-\lambda ,A_2-{\mu }_2)=-{\mu }_2^3+{(\lambda -1)}^5,\hfill \\ \hfill & f_3({\mu }_1,{\mu }_2)=\partial \mathrm{Res}(A_1-{\mu }_1,A_2-{\mu }_2)={\mu }_2^4-{\mu }_1^5.\hfill \end{array}$$

Since ${\mathrm{Res}}_{\lambda }(f_1,f_2)=p{f}_3$ with $p={\mu }_1^{10}+{\mu }_1^5{\mu }_2^4+{\mu }_2^8$, then $(f_1,f_2)$ is strictly contained in $(f_1,f_2,f_3)$. A Gröbner basis of $\mathtt{BC}\left(L\right)$ in $\mathbb{C}[\lambda ,{\mu }_1,{\mu }_2]$ w.r.t. the pure lexicographic order $\lambda >{\mu }_1>{\mu }_2$ is

$$\mathcal{F}=\{f_3({\mu }_1,{\mu }_2),F_1=g_2({\mu }_1,{\mu }_2)\lambda +g_1({\mu }_1,{\mu }_2),\dots ,F_5\}$$

with $g_1=-{\mu }_2^4-{\mu }_1^2{\mu }_2^3$ and $g_2={\mu }_2^4$.

The curve defined by $\mathtt{BC}\left(L\right)$ is a non-planar curve $\Gamma$ parameterized by

$$\aleph \left(\tau \right)=(-{\tau }^3+1,{\tau }^4,-{\tau }^5),\tau \in \mathbb{C}.$$

(49)

This is the first explicit example of a non-planar spectral curve.

The first differential subresultants of $L-\lambda$, $A_1-{\mu }_1$ and $A_2-{\mu }_2$ pairwise are equal to

$${\varphi }_{i,0}+{\varphi }_{i,1}\partial ,i=1,2,3,j=0,1;$$

see (33), with

$$\begin{array}{cc}{\varphi }_{1,0}=(1-\lambda ){\mu }_1-\frac{4{\mu }_1}{x^3}+\frac{8(\lambda -1)}{x^4},\hfill & {\varphi }_{1,1}={(\lambda -1)}^2-\frac{2{\mu }_1}{x^2}+4\frac{(\lambda -1)}{x^3},\hfill \\ {\varphi }_{2,0}={(1-\lambda )}^3-\frac{4{(1-\lambda )}^2}{x^2}+\frac{8{\mu }_2}{x^4},\hfill & {\varphi }_{2,1}={(\lambda -1)}^3-\frac{4{(1-\lambda )}^2}{x^2}+\frac{8{\mu }_2}{x^3},\hfill \\ {\varphi }_{3,0}=-{\mu }_2\left({\mu }_1^2+\frac{4{\mu }_2}{x^3}-\frac{8{\mu }_1}{x^4}\right),\hfill & {\varphi }_{3,1}={\mu }_1^3-\frac{2{\mu }_2^2}{x^2}+\frac{4{\mu }_2{\mu }_1}{x^3}.\hfill \end{array}$$

We have $o_1=4$ and $o_2=5$; thus, $\gcd (o_1,o_2)=1$ and

$$\varphi ={\overline{\varphi }}_i=\frac{{\varphi }_{0,i}}{{\varphi }_{1,i}}+\left[\mathtt{BC}\left(L\right)\right],i=1,2,3.$$

Let us call $\varphi \left(\tau \right)$ the result of replacing $(\lambda ,{\mu }_1,{\mu }_2)$ by the parameterization $\aleph \left(\tau \right)$ of $\Gamma$ in $\varphi$, which equals

$$\varphi \left(\tau \right):={\varphi }_i(\aleph \left(\tau \right))=\frac{-{\tau }^3{x}^3+2{\tau }^2{x}^2-4\tau x+4}{({\tau }^2{x}^2-2\tau x+2)x}.$$

(50)

Thus, $L+{\tau }^3-1=\left({\partial }^2+\varphi \left(\tau \right)\partial +\varphi {\left(\tau \right)}^2+2\varphi {\left(\tau \right)}^{\prime }-\frac{6}{x^2}\right)·(\partial +\varphi \left(\tau \right))$ as in (46). At every point $P_0=\aleph \left({\tau }_0\right)$ of the spectral curve $\Gamma$ of L, we recover a right factor $\partial +\varphi \left({\tau }_0\right)$, for ${\tau }_0\ne 0$.

Observe that whenever the spectral curve $\Gamma$ is a rational curve with rational parameterization $\aleph \left(\tau \right)=({\aleph }_1\left(\tau \right),{\aleph }_2\left(\tau \right),{\aleph }_3\left(\tau \right))$, as in the previous example, one can consider the factorization of $L-{\aleph }_1\left(\tau \right)$ as a differential operator in $\Sigma \left(\tau \right)[\partial ]$, since the algebraic variable $\tau$ with $\partial \left(\tau \right)=0$, would be a free parameter over $\Sigma$. To achieve a full factorization, it is a future project to use the parameterized Picard–Vessiot theory introduced by Cassidy and Singer in [9], and studied in [11]. It would be interesting to explore how this theory explains the factorization over the field of the spectral curve, using the results on second-order operators in [10] combined with the intrinsic factorization of Section 7.2.

9. Discussion

In this work, the computation of the space algebraic curve $\Gamma$ that describes the centralizer of third-order ODO L was achieved. We proved that $\Gamma$ is the spectral curve of a commutative algebra with three generators and, in general, it is a non-planar curve. We provided an effective description of the defining ideal of $\Gamma$ that will allow a parametric factorization of $L-\lambda$, for an algebraic parameter $\lambda$. The computation of the intrinsic right factor, of the Mumford correspondence [19], of $L-\lambda$ was only described before in the case of planar spectral curves [25], in connection with the Baker–Akheizer function.

It is an ongoing project to develop the spectral Picard–Vessiot theory of the third-order operator $L-\lambda$. We intend to follow our previously successful strategy, in the case of second-order Schrödinger operators [8]. In analogy with the Galois theory of univariate polynomials, a full factorization of $L-\lambda$ will be studied, in combination with ideas coming from the parametric Picard–Vessiot theory [9,10,11], that must be adapted to a non-free algebraic parameter $\lambda$. Through this journey, spectral curves, planar or not, will govern the factorization of $L-\lambda$ and the hidden free parameters will emerge.

Appendix B.1. First Differential Subresultant

The differential resultant of two differential operators is a condition on their coefficients that guaranties the existence of a right common factor. We introduce next the first differential subresultant as a tool to compute such a factor in case it is a first-order factor. Differential subresultants were introduced in [43]; see also [44].

Let us consider the $\mathbb{K}$-linear map

$${\mathrm{s}}_1:{\mathcal{M}}_{n-1}\oplus {\mathcal{M}}_{m-1}\to {\mathcal{M}}_{n+m-1}definedby(C,D)\mapsto CP+DQ.$$

(A9)

In the basis $\{{\partial }^{\ell },\dots ,\partial ,1\}$, for each ${\mathcal{M}}_{\ell }$, the matrix of ${\mathrm{s}}_1$ is a matrix ${\mathrm{s}}_1(P,Q)$ with $n+m-2$ rows and $n+m-1$ columns, with entries in $\mathbb{D}$, whose rows are the coefficient of the extended system

$${\Xi }_1=\{{\partial }^{m-2}P,\dots ,\partial P,P,{\partial }^{n-2}Q,\dots ,\partial Q,Q\}.$$

(A10)

Observe that Im(s₁) is the $\mathbb{K}$-vector space spanned by ${\Xi }_1$ and that $\mathrm{I}\mathrm{m}\left({\mathrm{s}}_1\right)\subset (P,Q)$. Let us consider the squared matrix ${\hat{\mathrm{S}}}_1(P,Q)$ obtained by adding ${\mathrm{S}}_1(P,Q)$ the first row (0,⋯, 0, 1, −∂). The first differential subresultant of P and Q is the determinant

$$\mathrm{s}\partial {\mathrm{Res}}_1(P,Q):=det{\widehat{\mathrm{s}}}_1(P,Q)=det\left(S_1^0\right)+det\left(S_1^1\right)\partial ,$$

(A11)

where ${\mathrm{s}}_1^0$ and ${\mathrm{s}}_1^1$ are the submatrices of s₁ (P,Q) obtained by removing the columns indexed by ∂ and 1, respectively.

Lemma A4.

Given $P,Q$ in $\mathbb{D}[\partial ]$, then $\partial \mathrm{Res}(P,Q)$ belongs to the image of $s_1$, that is,

$$\mathrm{s}\partial {\mathit{Res}}_1(P,Q)=C_{1}P+D_{1}Q\in \mathit{Im}\left({\mathrm{s}}_1\right),$$

with $\mathit{ord}\left(C_1\right)=m-2$ and $\mathit{ord}\left(D_1\right)=n-2$.

Proof. 

Multiply ${\widehat{\mathrm{s}}}_1(P,Q)$ on the right by the squared matrix E of size $n+m-1$ whose i-th row contains 1 in the i-th position and ${\partial }^{n+m-1-i}$ in the last position. Observe that $detE=1$ and that ${\widehat{\mathrm{s}}}_1(P,Q)E$ has entries in $\mathbb{D}[\partial ]$; in particular, its last column contains 0 followed by the elements of ${\Xi }_1$. Thus,

$$det\left({\mathrm{s}}_1(P,Q)\right)=det\left({\widehat{\mathrm{s}}}_1(P,Q)E\right)=C_{1}P+D_{1}Q$$

after developing ${\mathrm{s}}_1(P,Q)E$ by its last two columns. □

Theorem A3

(First Subresultant Theorem). Let us consider $P,Q\in \mathbb{D}[\partial ]$. If $\partial \mathrm{Res}(P,Q)=0$ and $\mathrm{s}\partial {\mathrm{Res}}_1(P,Q)\ne 0$, then:

• $\mathrm{s}\partial {\mathit{Res}}_1(P,Q)$ is a differential operator of order 1;
• $\mathit{gcrd}(P,Q)$ equals $\mathrm{s}\partial {\mathit{Res}}_1(P,Q)$ up to multiplication by an element of $\mathbb{K}$.

Proof. 

If $\mathrm{s}\partial {\mathrm{Res}}_1(P,Q)$ has order zero, then it equals $det\left(S_1^0\right)$. Therefore, $\mathrm{Im}\left({\mathrm{s}}_0\right)\cap \mathbb{D}\ne 0$, contradicting, by Theorem A2, that $\partial \mathrm{Res}(P,Q)=0$.

By Lemma A4, we have $\mathrm{s}\partial {\mathrm{Res}}_1(P,Q)\in \mathrm{Im}\left({\mathrm{s}}_1\right)\subset (P,Q)$, then $\mathrm{s}\partial {\mathrm{Res}}_1(P,Q)$ is a multiple of $\mathrm{gcrd}(P,Q)$, which proves 2. □

Appendix B.2. Characterizing Common Solutions

Given a differential operator $L\in \mathbb{K}[\partial ]$, a Picard–Vessiot extension $\mathcal{E}$ of $\mathbb{K}$ for L is a differential field extension $\mathcal{E}=\mathbb{K}⟨{\psi }_1,\dots ,{\psi }_n⟩$, where $\{{\psi }_1,\dots ,{\psi }_n\}$ is a fundamental set of solutions, with no new constants in $\mathcal{E}$. It is the equivalent of a splitting field for $L\left(y\right)=0$. Under the assumption that the field of constants $\mathbf{C}$ is algebraically closed, the classical Picard–Vessiot theory guaranties the existence and uniqueness (up to differential automorphisms) of the Picard–Vessiot field for the equation $L\left(y\right)=0$. See [28], Proposition 1.22.

Given differential operators P and Q in $\mathbb{K}[\partial ]$, let us consider the Picard–Vessiot extensions $({\mathcal{E}}_P,{\partial }_P)$ and $({\mathcal{E}}_Q,{\partial }_Q)$ of $\Sigma$ for the equations $P\left(y\right)=0$ and $Q\left(y\right)=0$, respectively, whose field of constants is $\mathbf{C}$. As a consequence, $\mathbb{K}[\partial ]$ can be included in ${\mathcal{E}}_P\left[{\partial }_P\right]$ and Q can be naturally extended to act on ${\mathcal{E}}_P$. Analogously, P can be naturally extended to act on ${\mathcal{E}}_Q$.

We give next a proof of Poisson’s formula in [43], Theorem 5 using the strategy of E. Previato in [27]. Given a fundamental system of solutions ${\psi }_1,\dots ,{\psi }_n$ of $P\left(y\right)=0$ in $({\mathcal{E}}_P,{\partial }_P)$, we denote its Wronskian matrix by

$$W\left({\psi }_i\right)=\left(\begin{array}{ccc}{\psi }_1& \cdots & {\psi }_n\\ {\partial }_P\left({\psi }_1\right)& \cdots & {\partial }_P\left({\psi }_n\right)\\ ⋮& \ddots & ⋮\\ {\partial }_P^{n-1}\left({\psi }_1\right)& \cdots & {\partial }_P^{n-1}\left({\psi }_n\right)\end{array}\right).$$

Note that the natural extension of Q to $({\mathcal{E}}_P,{\partial }_P)$ allows us to consider its action on solutions of $P\left(y\right)=0$ and to write $Q\left({\psi }_i\right)$. Analogously, the action of P on solutions of $Q\left(y\right)=0$ is naturally defined.

Theorem A4

(Poisson’s Formula). Let us consider differential operators P and Q in $\mathbb{K}[\partial ]$ of orders n and m, and leading coefficients $a_n$ and $b_m$, respectively. Given fundamental systems of solutions ${\psi }_1,\dots ,{\psi }_n$ of $P\left(y\right)=0$ in ${\mathcal{E}}_P$ and ${\varphi }_1,\dots ,{\varphi }_m$ of $Q\left(y\right)=0$ in ${\mathcal{E}}_Q$ then

$$\partial \mathit{Res}(P,Q)=a_n^m\frac{detW\left(Q\left({\psi }_i\right)\right)}{detW\left({\psi }_i\right)}={(-1)}^{mn}{b}_m^n\frac{detW\left(P\left({\varphi }_i\right)\right)}{detW\left({\varphi }_i\right)}.$$

(A12)

Proof. 

Let us consider the following decomposition of the Sylvester matrix:

$$S_0(P,Q)=\left(\begin{array}{cc}{M}_1& M_2\\ M_3& M_4\end{array}\right)$$

where $M_1$ is an upper triangular $m\times m$ matrix with $a_n$ in the main diagonal. By the following matrix manipulation, where $I_n$ is the identity matrix of size n and 0 is the zero matrix of the appropriate size,

$$\left(\begin{array}{cc}{M}_1& M_2\\ M_3& M_4\end{array}\right)\left(\begin{array}{cc}{M}_1^{-1}& -M_1^{-1}{M}_2\\ 0& I_n\end{array}\right)=\left(\begin{array}{cc}{I}_m& 0\\ M_3{M}_1^{-1}& M_4-M_3{M}_1^{-1}{M}_2\end{array}\right)$$

we obtain that

$$\partial \mathrm{Res}(P,Q)=a_n^{m}det(M_4-M_3{M}_1^{-1}{M}_2).$$

(A13)

From the action of the system ${\Xi }_0$ on the fundamental system of solutions $\left\{{\psi }_i\right\}$, we obtain

$$W\left(Q\left({\psi }_i\right)\right)=(M_4-M_3{M}_1^{-1}{M}_2)W\left({\psi }_i\right).$$

(A14)

Taking determinants in (A14), the first part of formula (A12) follows. □

We are ready to review Theorem A5.

Theorem A5

(Resultant Theorem). Let us consider differential operators P and Q in $\mathbb{K}[\partial ]$. Let $\mathcal{E}$ be a Picard–Vessiot extension of Σ for $P\left(y\right)=0$ (or $Q\left(y\right)=0$). Then the system

$$P\left(y\right)=0,Q\left(y\right)=0$$

(A15)

has a nontrivial solution in $\mathcal{E}$ if and only if $\partial \mathrm{Res}(P,Q)=0$.

Proof. 

Let us consider a fundamental system of solutions ${\psi }_1,\dots ,{\psi }_n$ of $P\left(y\right)=0$ in $({\mathcal{E}}_P,{\partial }_P)$, whose field of constants is $\mathbf{C}$. Thus, $V={\oplus }_i\mathbf{C}{\psi }_i\subset {\mathcal{E}}_P$ is the solution set of $P\left(y\right)=0$. A nontrivial solution of the system (A15) in ${\mathcal{E}}_P$ is therefore a nonzero $\psi \in V$ such that $Q\left(\psi \right)=0$.

By Poisson’s formula, $\partial \mathrm{Res}(P,Q)=0$ if and only if $det\left(W\left(Q\left({\psi }_i\right)\right)\right)=0$. Equivalently, the columns of $W\left(Q\left({\psi }_i\right)\right)$ must be linearly dependent over $\mathbf{C}$, namely for some $c_i\in \mathbf{C}$, not all zero,

$$\sum _i{c}_i{\partial }_P^j\left(Q\left({\psi }_i\right)\right)=0,j=0,1,\dots ,n-1.$$

In other words, $det\left(W\left(Q\left({\psi }_i\right)\right)\right)=0$ is equivalent to the existence of a nonzero $\psi ={\sum }_i{c}_i{\psi }_i$ in V such that $Q\left(\psi \right)=0$. □

Remark A1.

Observe that as a result of Theorems A2 and A5, the differential operators P and Q have a common factor F in $\mathbb{K}[\partial ]$ if and only if they have a non-trivial solution in ${\mathcal{E}}_P\cap {\mathcal{E}}_Q$.