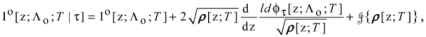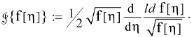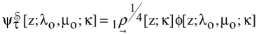Double-Step Shape Invariance of Radial Jacobi-Reference Potential and Breakdown of Conventional Rules of Supersymmetric Quantum Mechanics

Abstract

The paper reveals some remarkable form-invariance features of the ‘Jacobi-reference’ canonical Sturm–Liouville equation (CSLE) in the particular case of the density function with the simple pole at the origin. It is proven that the CSLE under consideration preserves its form under the two second-order Darboux–Crum transformations (DCTs) with the seed functions represented by specially chosen pairs of ‘basic’ quasi-rational solutions (q-RSs), i.e., such that their analytical continuations do not have zeros in the complex plane. It is proven that both transformations generally either increase or decrease by 2 the exponent difference (ExpDiff) for the mentioned pole while keeping two other parameters unchanged. The change is more complicated in the latter case if the ExpDiff for the pole of the original CSLE at the origin is smaller than 2. It was observed that the DCTs in question do not preserve bound energy levels according to the conventional supersymmetry (SUSY) rules. To understand this anomaly, we split the DCT in question into the two sequential Darboux deformations of the Liouville potentials associated with the CSLEs of our interest. We found that the first Darboux transformation turns the initial CSLE into the Heun equation written in the canonical form while the second transformation brings us back to the canonical form of the hypergeometric equation. It is shown that the first of these transformations necessarily places the mentioned ExpDiff into the limit-circle (LC) range and then the second transformation keeps the pole within the LC region, violating the conventional prescriptions of SUSY quantum mechanics.

1. Introduction

Half a century ago, the author [1] constructed the two families of ‘implicit’ potentials exactly solvable in terms of hypergeometric or confluent hypergeometric functions. Below we refer to them as Jacobi-reference (JRef) and Laguerre-reference (LRef) potentials accordingly, keeping in mind that they are quantized via classical Jacobi and classical Laguerre polynomials, respectively, with degree-dependent indices.

The cited paper was later used by Cooper et al. [2] to demonstrate that the Darboux transformation (DT) using the nodeless eigenfunction as the transformation function (TF) converts the JRef potential into a completely different rational function referred to by us [3,4,5] simply as ‘CGK potential’. This illustration implied that the exactly solvable potential discovered in [1] is not shape-invariant, contrary to Gendenshtein’s [6] renowned assertion that any exactly solvable potential must be shape-invariant. A thorough examination of the rational formulas derived in [2] revealed [3] that the ground-energy eigenfunction has the ‘basic’ form

$${}_1\mathsf{\varphi }_{\mathbf{t},0}[\mathrm{z}]:=\hspace{0.17em}{\mathrm{z}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\mathsf{\lambda }}_{0;\mathbf{t},0}+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{(1-\mathrm{z})}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\mathsf{\lambda }}_{1;\mathbf{t},0}+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\hspace{0.17em}(0<\mathrm{z}<1),$$

(1)

which assures that its analytical continuation into the complex plane remains finite at any regular point of the JRef canonical Sturm–Liouville equation (CSLE) where the subscript 0 indicates that the corresponding ‘quasi-rational’ [7] solution (q-RS) is composed of the Jacobi polynomial of degree 0. In following our early study [8] on DTs of centrifugal-barrier potentials (published long before the birth of the supersymmetric (SUSY) quantum mechanics [9,10,11]), we found it convenient to identify the four possible types of basic solutions (1) by the letters t = a, b, c, and d; namely, the labels a and b are used to identify principal Frobenius solutions (PFSs) near the lower and upper ends of the quantization interval [0, 1], whereas the q-RS of type d diverges near both singular endpoints (types I, II, and III in Quesne’s terms [12]). Alternatively, we will specify the type of the given q-RSs by the double indices

$$+-\equiv \mathbf{a},\hspace{0.17em}-+\equiv \mathbf{b},\hspace{0.17em}++\equiv \mathbf{c},\hspace{0.17em}--\equiv \mathbf{d}$$

specifying signs of the exponent parameters ${\mathsf{\lambda }}_{0;\mathbf{t},0}$ and ${\mathsf{\lambda }}_{1;\mathbf{t},0}$. For our purposes, a certain advantage of the four-letter labeling comes from the fact that two q-RSs formed by Jacobi polynomials with an identical positive degree m may be of the same type if the Sturm–Liouville problem in question has less than m−1 eigenvalues. In this case, we mark the q-RSs in the second sequence (not starting from one of the basic solutions) by prime. For example, it will be shown in Section 2 that, in addition to the eigenfunctions, the radial potential of our current interest has the distinguished pairs of q-RSs vanishing at the origin which are labeled by us as $|\mathbf{a},\mathrm{m})$ and $|{\mathbf{a}}^{\prime },\mathrm{m})$, with the sequence $|\mathbf{a},\mathrm{m})$ starting from the basic solution $|\mathbf{a},0)$.

It was originally proven in [3] and then more scrupulously analyzed in [13] that the ground-energy eigenfunction $|\mathbf{c},0)$ of the JRef CSLE is accompanied by three other basic solutions $|\mathbf{a},0),$ $|\mathbf{b},0),$ and $|\mathbf{d},0)$ if the polynomial numerator of the density function

$${}_1\mathit{\rho }[\mathrm{z};T_2]=\frac{{\mathrm{T}}_2[\mathrm{z};{\overline{\mathrm{z}}}_{\mathrm{T}}]}{4{\mathrm{z}}^2{(1-\mathrm{z})}^2}>0$$

(2)

the so-called [3,4,5] ‘tangent polynomial’ (TP),

$${\mathrm{T}}_2[\mathrm{z};{\overline{\mathrm{z}}}_{\mathrm{T}}]:={\mathrm{a}}_2(\mathrm{z}-{\mathrm{z}}_{\mathrm{T};1})(\mathrm{z}-{\mathrm{z}}_{\mathrm{T};2})$$

(3)

with ${\overline{\mathrm{z}}}_{\mathrm{T}}:={\mathrm{z}}_{\mathrm{T};1},{\mathrm{z}}_{\mathrm{T};2}$, has a positive discriminant. Excluding the simple-pole density function [14]

$${}_1\mathit{\rho }_{\diamond }[\mathrm{z}]=\frac{1}{4\mathrm{z}(1-\mathrm{z})}>0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(0<\mathrm{z}<1)$$

(4)

associated with the Darboux/Pöschl–Teller potential [15,16], we (for the reasons explained in [13]) define the TP leading coefficient via the condition

$${\mathrm{T}}_2[1;{\overline{\mathrm{z}}}_{\mathrm{T}}]=1.$$

(5)

Concurrently with [2], Rudyak and Zakhariev published their pioneering study [17] on the so-called [18] ‘generalized’ DTs of the generic CSLE, which (for the reasons explained in Section 5) are referred to below as the Liouville–Darboux transformations (LDTs). Our analysis [3] of Rudyak and Zakhariev’s reciprocal formula for the TF of the companion intertwining operator

$${}_1{}^{\ast }\mathsf{\varphi }_{\mathbf{t},0}[\mathrm{z}]:=\hspace{0.17em}{}_1\mathit{\rho }^{-1}[\mathrm{z};T_2]/{}_1\mathsf{\varphi }_{\mathbf{t},0}[\mathrm{z}]$$

(6)

then revealed that the resultant rational CSLE (RCSLE) may have new poles only at TP zeros. Since the TP degree cannot exceed 2, the rational DT (RDT) of the JRef CSLE using each of the basic solutions (1) as its TF generally leads to the Fuchsian RCSLEs with five regular singular points (including infinity). Their common remarkable feature (compared with the general case examined in [19,20]) is that the eigenfunctions of the RCSLEs constructed in such a way are expressible in terms of finite sequences of polynomials referred to by us as ‘Jacobi-seed’ (JS) Heine polynomials, though it is worth mentioning that the coefficient functions of the first derivative in the corresponding Fuchsian equations generally depend on the polynomial degree (in contrast with the standard definition of Heine polynomials [21,22,23]).

If the TP has a zero at one and only one regular point of the JRef CSLE outside the quantization interval [0, 1], then the constructed quartet of solvable RCSLEs turns into the quartet of Heun equations written in the normal form [24] such that the associated potentials of Heun class [25] are quantized by polynomials. Since at least one of the ‘exponent parameters’ [24] depends on the polynomial degree, the given polynomial solutions of the Heun equation are not the Heun polynomials in the conventional sense [26,27].

There are three types of TPs which fall into this category:

(i)

Second-degree TP with one zero at the origin (radial JRef potential [28,29,30,31,32,33,34]);

(ii)

Linear TP (LTP) [3,9];

(iii)

Double-root TP (DRtTP) with zero discriminant [35,36].

In Ishkhanyan’s classification scheme [37], the corresponding Liouville potentials represent the Lemieux–Bose potentials [38] of types (1, 1/2, −1/2), (1, 1, −1/2), and (1, 1, −1) with ${\mathrm{z}}_1$ = 1, ${\mathrm{z}}_2$ = 0 under some additional constraints allowing one to express the eigenfunctions in terms of polynomial solutions of the Heun equation.

Since the TP discriminants for the instances (i) and (ii) are positive, there are four basic solutions in both cases. However, as already proven for the radial Heun-reference (HRef) potentials in [34] and explicitly demonstrated below for the LTP with a negative zero, this quartet of exactly solvable HRef potentials can be split into sibling pairs such that the potentials in each pair are interrelated by two sequential LDTs. As a consequence, we have only two sibling Lemieux–Bose potentials for both instances (i) and (ii).

On the other hand, each of the two exponents specifying the basic solutions (1) is determined by roots of the cubic polynomials for the DRtTP [36], contrary to the general case [13] with each exponent determined by one of the four real roots of the corresponding quartic equations. (It has been proven in [13] that there is a unique way to relate each root of one quartic equation to the corresponding root of the second equation.) As a result, there are only three basic solutions for the instance (iii), and therefore, the quartet of the sibling SUSY partners solvable by polynomial solutions of the Heun equation collapses into a triplet.

The main purpose of this paper is to demonstrate that the double shape invariance of the Liouville potentials associated with the instances (i) and (ii) is the intrinsic feature of the given CSLE rather than the potential itself. It is a natural extension of our approach [39] to translationally shape-invariant (TSI) potentials of groups A and B [40], where we introduced the concept of the translationally form-invariant (TFI) rational CSLEs (RCSLEs). In the particular case of the JRef CSLE, the TPs in question have the following form:

$${\mathrm{T}}_2[\mathrm{z};{\mathrm{a}}_{\mathrm{K}};\mathsf{\kappa },\mathrm{K}-\mathsf{\kappa }]:={\mathrm{z}}^{\mathsf{\kappa }}{(\mathrm{z}-1)}^{\mathrm{K}-\mathsf{\kappa }}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(2\mathsf{\kappa }\ge \mathrm{K}=0,1,2).$$

(7)

It was demonstrated that the two TSI potentials, namely, Morse and hyperbolic Pöschl–Teller (h-PT) potentials, can be alternatively included either in Group A or Group B depending on the choice of the TFI CSLE for their rational representation. Specifically, the h-PT potential can be included either in Group B or Group A by choosing $\mathsf{\kappa }=\mathrm{K}=1$ [1] or alternatively ($\mathsf{\kappa }=1,\hspace{0.17em}\hspace{0.17em}\mathrm{K}=2)$ performing the Liouville transformation [41,42,43,44] of the CSLE with single-pole density (4) on the infinite interval [1, ∞), as originally suggested in [45,46] and then broadly adopted in the physical literature in following the renowned review [47] by Cooper et al. and their textbook [48].

In Section 2, we extend our results for the radial JRef potential [33] to the instance (ii) by extending the corresponding JRef CSLE to the positive semi-axis. Depending on the location of the TP zero

$${\mathrm{z}}_{\mathrm{T}}(\mathsf{\kappa })=1-1/\mathsf{\kappa }$$

(8)

outside of the interval [0, 1],

$${\mathrm{z}}_{\mathrm{T}}(\mathsf{\kappa })>1 \mathrm{i}\mathrm{f} \mathsf{\kappa }<0 \mathrm{or} {\mathrm{z}}_{\mathrm{T}}(\mathsf{\kappa })<0 \mathrm{i}\mathrm{f} 0<\mathsf{\kappa }<1$$

and the density function

$${\hspace{0.17em}}_1\underrightarrow{\rho }(\mathrm{z};\mathsf{\kappa })=\hspace{0.17em}\hspace{0.17em}\frac{\mathsf{\kappa }\mathrm{z}+1-\mathsf{\kappa }}{4|\mathrm{z}|{(1-\mathrm{z})}^2}>0$$

(9)

remains positive either on the interval (−∞, 1) or on the positive semi-axis (0, ∞).

It has been demonstrated in [33] that there are four infinite sequences of q-RSs unambiguously specified by the roots of two quadratic equations with positive discriminants. The range of the definition for these q-RSs is now extended to the infinite intervals (−∞, 0) and (1, ∞).

In Section 3, we again group the four basic solutions into the two pairs chosen in such a way that the two solutions from the given pair are specified by the roots of the same quadratic equation. We then use the paired basic solutions as seed functions for the second-order Darboux–Crum [49] transformation (DCT) making use of Schnizer and Leeb’s general formula [18,50] for the Darboux–Crum transforms (DCs) of the generic CSLE. It was proven that the only effect of both second-order DCTs on the JRef CSLE is either the increase or decrease in the exponent difference (ExpDiff) for the pole at the origin by 2.

It is worth mentioning in this connection that the reference to Krein’s paper [51] in [17,50] was obviously an overkill. The distinction between the Crum Wronskian (CW) [49] and the Krein determinant (KD) [51] arises only for the CW of more than two seed functions, and Leeb never discussed the solutions of the ‘double-step’ SLEs which indeed require the computation of the CW of three seed functions.

To our knowledge, the rigorous extension of the notion of the KDs to the theory of the DCs of CSLEs was first formulated in our works [52,53]. It was shown that the CW of seed solutions of a CSLE and the corresponding KD differ by either a half-integer or integer power of the density function. As expected, this factor disappears for the Schrödinger equation since the density function is identically equal to 1. The distinctive feature of the KDs is that they, in contrast with the CWs, are formed only by the seed functions and their first derivatives. In Section 3, we explicitly replace the CW of three seed functions with the corresponding KD to avoid the computation of the second derivative of the hypergeometric series under consideration.

After the CWs of three seed functions have been replaced with the KDs, the DCs of the principal Frobenius solution (PFS) can be represented as the first-order differential expressions for the hypergeometric series in question. In Section 3, we explicitly confirm these differential expressions using the renowned contiguous formulas for hypergeometric functions. While our analysis of these differential equations in [33] was focused mostly on the DCT increasing the ExpDiff for the pole at the origin, here we treat both DCTs in a parallel way as far as the ExpDiff in question is larger than 2. On the other hand, if its value is smaller than 2, then the DCT generally decreasing the ExpDiff by 2 converts the given PFS into a non-principal FS of the transformed CSLE. This anomaly constitutes one of the most interesting results of this paper.

In Section 4, we formulate the Dirichlet problem with the boundary conditions imposed at the ends of the finite interval [0, 1] and show that the DCT decreasing the ExpDiff by 2 does not preserve the existent energy spectrum if the value of the ExpDiff is smaller than 2, in violation of the conventional rules of SUSY quantum mechanics [47,48].

In Section 5, we decompose the second-order DCTs under consideration into two sequential LDTs and then examine the action of the first LDT on the JRef CSLE. It is proven that (as stated above) these LDTs result in the four Heun equations written in their canonical form. It turns out that each CSLE constructed in such a way also preserves its form under two sequential LDTs and, as a result, the quartet of HRef CSLEs can be split into the two pairs such that the CSLEs in each pair differ only by the values of the ExpDiff for the pole at the origin.

In Section 6, we finally reveal the source of the mentioned anomaly for smaller-than-2 values of the mentioned ExpDiff. It is shown that the LDTs of our interest either decrease or increase this ExpDiff by 1. If the value of the ExpDiff lies between 1 and 2 (i.e., if the pole of the initial JRef CSLE at the origin is the limit point (LP) singularity), then the LDT decreasing the ExpDiff by 1 brings the ExpDiff of our interest into the limit circle (LC) region of the HRef CSLE, while keeping it within the LC region if the original value of this ExpDiff is smaller than 1. As a result, the pole of the resultant HRef CSLE at the origin is necessarily within the LC region. The second LDT then keeps this pole within the LC region. On the other hand, it has been proven by the author in a separate article [53] that the LDTs keeping the ExpDiff within the LC range violate the conventional rules of SUSY quantum mechanics (see [14,54] for more examples). As a direct consequence of this anomaly, the second-order DCT in question brings us to the JRef CSLE with a completely different energy spectrum if the initial value of the ExpDiff under consideration is smaller than 2.

2. Radical Formulas for Energies of q-RSs in Special Case of Density Function with Simple Pole at Origin

Regardless of the choice of the density function, the reference polynomial fraction (RefPF) of the JRef CSLE [13]

$$\left\{\hspace{0.17em}\frac{{\mathrm{d}}^2\hspace{0.17em}\hspace{0.17em}}{\mathrm{d}{\mathrm{z}}^2}+{}_1\mathrm{I}^{\mathrm{o}}[\mathrm{z}\hspace{0.17em};\hspace{0.17em}{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}}]+{\mathsf{\epsilon }}_{\hspace{0.17em}1}\underrightarrow{\rho }(\mathrm{z};\mathsf{\kappa })\hspace{0.17em}\right\}\hspace{0.17em}{}_1\mathsf{\Phi }[\mathrm{z}\hspace{0.17em};\hspace{0.17em}{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }]=\hspace{0.17em}0$$

(10)

has the following common form:

$${}_1\mathrm{I}^{\mathrm{o}}[\mathrm{z}\hspace{0.17em};\hspace{0.17em}{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}}]=\hspace{0.17em}\hspace{0.17em}\frac{1-{\mathsf{\lambda }}_{\mathrm{o}}^2}{{4\mathrm{z}}^2(1-\mathrm{z})}+\frac{1}{4{(1-\mathrm{z})}^2}+\frac{{\mathsf{\mu }}_{\mathrm{o}}^2}{4\mathrm{z}(1-\mathrm{z})}$$

(11)

Here, the energy measurement point is chosen via the requirement that the characteristic exponents (ChExps) for the pole of CSLE (10) at z = 1 are both real iff ε < 0. In this paper, we restrict our discussion solely to the JRef CSLE with the density function (9).

It is crucial that the TP of our interest vanishes at z = 0 and, as a result, the ExpDiff for the pole of the CSLE at the origin becomes energy-independent. Setting

$$\mathsf{\vartheta }\hspace{0.17em}[\mathrm{z};\mathsf{\lambda },\Xi ]:=\hspace{0.17em}|\mathrm{z}{|}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.(\mathsf{\lambda }+1)}|1-\mathrm{z}{|}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.(\Xi +1)}$$

(12)

and restricting our analysis solely to negative energies, we can represent the corresponding Frobenius solutions (FSs) near the poles at 0 and 1 for an arbitrary negative energy ε as

$$\begin{array}{l}{}_1\mathsf{\Phi }_0^{\pm }[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }]=\mathsf{\vartheta }\hspace{0.17em}[\mathrm{z};\pm {\mathsf{\lambda }}_{\mathrm{o}},-\sqrt{-\mathsf{\epsilon }}]\times \\ \mathrm{F}\hspace{0.17em}[\mathsf{\alpha }(\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };-\sqrt{-\mathsf{\epsilon }})\hspace{0.17em},\mathsf{\beta }(\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };-\sqrt{-\mathsf{\epsilon }});1\pm {\mathsf{\lambda }}_{\mathrm{o}};\mathrm{z}]\\ (-1<\mathrm{z}<0 \mathrm{or} 0<\mathrm{z}<1)\end{array}$$

(13)

and

$$\begin{array}{l}{}_1\mathsf{\Phi }_1^{\pm }[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }]=\mathsf{\vartheta }\hspace{0.17em}[\mathrm{z};-{\mathsf{\lambda }}_{\mathrm{o}},\pm \sqrt{-\mathsf{\epsilon }}]\times \\ \mathrm{F}\hspace{0.17em}[\mathsf{\alpha }(-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\pm \sqrt{-\mathsf{\epsilon }})\hspace{0.17em},\mathsf{\beta }(-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\pm \sqrt{-\mathsf{\epsilon }});1\pm \sqrt{-\mathsf{\epsilon }};1-\mathrm{z}]\\ (0<\mathrm{z}<1 \mathrm{or} 1<\mathrm{z}<2)\end{array}$$

(14)

respectively. By definition, $\mathsf{\alpha }(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\Xi )$ and $\mathsf{\beta }(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\Xi )$ are two roots of the indicial equation

$${\mathrm{X}}^2-(\mathsf{\lambda }+\Xi +1\hspace{0.17em})\mathrm{X}+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.{\left(\mathsf{\lambda }\hspace{0.17em}+\Xi +1\right)}^2\hspace{0.17em}-{\mathsf{\mu }}^2({\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }{\Xi }^2)=0$$

(15)

with

$$|\Xi |:=\sqrt{|\mathsf{\epsilon }|}$$

(16)

and

$$\mathsf{\mu }({\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }{\Xi }^2):=\sqrt{{\mathsf{\mu }}_{\mathrm{o}}^2+\mathsf{\kappa }{\Xi }^2}$$

(17)

standing for the ExpDiff for the pole of the CSLE at infinity; i.e., by definition,

$$\mathsf{\alpha }(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\Xi )+\mathsf{\beta }(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\Xi )=\mathsf{\lambda }+\Xi +1.$$

(18)

Also [1]

$$\mathsf{\beta }(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\Xi )-\mathsf{\alpha }(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\Xi )=\mathsf{\mu }({\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }{\Xi }^2)>0$$

(19)

Combining (18) and (19) gives

$$\mathsf{\alpha }(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\Xi )=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.[\mathsf{\lambda }+\Xi +1-\mathsf{\mu }({\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }{\Xi }^2)],\hspace{0.17em}$$

(20)

$$\mathsf{\beta }(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\Xi )=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.[\mathsf{\lambda }+\Xi +1+\mathsf{\mu }({\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }{\Xi }^2)]\hspace{0.17em}$$

(21)

and therefore,

$$\mathsf{\alpha }(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\Xi )\hspace{0.17em}\mathsf{\beta }(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\Xi )=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.[{(\mathsf{\lambda }\hspace{0.17em}+\Xi +1)}^2\hspace{0.17em}-{\mathsf{\mu }}^2({\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }{\Xi }^2)]$$

(22)

in agreement with (15).

If

$$\mathsf{\alpha }(\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };{\Xi }_{\pm ,\upsilon ,\mathrm{m}})=-\mathrm{m}$$

(23)

then both FSs (13) and (14) at the energies

$$\hspace{0.17em}{\mathsf{\epsilon }}_{\pm ,\upsilon ,\mathrm{m}}=-{\Xi }_{\pm ,\upsilon ,\mathrm{m}}^2$$

(24)

become quasi-rational:

$$\begin{array}{l}{}_1\mathsf{\Phi }_0^{\pm }[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };{\mathsf{\epsilon }}_{+,\upsilon ,\mathrm{m}}]={}_1\mathsf{\varphi }_{\upsilon ,\mathrm{m}}^{\pm }[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]:=\mathsf{\vartheta }\hspace{0.17em}[\mathrm{z};\pm {\mathsf{\lambda }}_{\mathrm{o}},{\Xi }_{+,\upsilon ,\mathrm{m}}]\times \\ \mathrm{F}\hspace{0.17em}[-\mathrm{m}\hspace{0.17em},\pm {\mathsf{\lambda }}_{\mathrm{o}}+{\Xi }_{\pm ,\upsilon ,\mathrm{m}}+\mathrm{m}+1;1\pm {\mathsf{\lambda }}_{\mathrm{o}};\mathrm{z}],\end{array}$$

(25)

where m stands for an arbitrary nonnegative integer and the index $\upsilon$ = ± will be specified below.

Making use of (18.5.7) in [24],

$$\mathrm{F}[-\mathrm{m},\hspace{0.17em}\mathsf{\lambda }+\Xi +\mathrm{m}+1,\mathsf{\lambda }+1;\mathrm{z}]=\hspace{0.17em}\frac{\hspace{0.17em}{(-1)}^{\mathrm{m}}\mathrm{m}!}{{\langle \mathsf{\lambda }+1\rangle }_{\mathrm{m}}}{\mathrm{P}}_{\mathrm{m}}^{(\Xi ,\mathsf{\lambda })}(2\mathrm{z}-1),$$

(26)

we can then represent the q-RSs in question as

$${}_1\mathsf{\varphi }_{\upsilon ,\mathrm{m}}^{\pm }[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]=\hspace{0.17em}\frac{\hspace{0.17em}{(-1)}^{\mathrm{m}}\mathrm{m}!}{{\langle 1\pm {\mathsf{\lambda }}_{\mathrm{o}}\rangle }_{\mathrm{m}}}\mathsf{\vartheta }\hspace{0.17em}[\mathrm{z};\pm {\mathsf{\lambda }}_{\mathrm{o}},{\Xi }_{\pm ,\upsilon ,\mathrm{m}}]\hspace{0.17em}{\mathrm{P}}_{\mathrm{m}}^{({\Xi }_{\pm ,\upsilon ,\mathrm{m}}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}\pm {\mathsf{\lambda }}_{\mathrm{o}})}(2\mathrm{z}-1)$$

(27)

Combining (18)–(20) and (23), we come to the following pair of the quadratic equations:

$${[{\Xi }_{\pm ,\upsilon ,\mathrm{m}}\pm {\mathsf{\lambda }}_{\mathrm{o}}+2\mathrm{m}+1]}^2={\mathsf{\mu }}_{\mathrm{o}}^2+\mathsf{\kappa }\hspace{0.17em}{\Xi }_{\pm ,\upsilon ,\mathrm{m}}^2$$

(28)

Setting ${\Xi }_{\pm ,\upsilon ,\mathrm{m}}\equiv {\mathsf{\lambda }}_{\upsilon ,\mathrm{m}}(\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })$ and re-writing the quadratic Equation (28) in the standard form

$$\begin{array}{c}(1-\mathsf{\kappa })\hspace{0.17em}{\mathsf{\lambda }}_{\upsilon ,\mathrm{m}}^2(\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })+2(\pm {\mathsf{\lambda }}_{\mathrm{o}}+2\mathrm{m}+1){\mathsf{\lambda }}_{\upsilon ,\mathrm{m}}(\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })\hspace{0.17em}+\\ {(\pm {\mathsf{\lambda }}_{\mathrm{o}}+2\mathrm{m}+1)}^2-{\mathsf{\mu }}_{\mathrm{o}}^2=0\end{array}$$

(29)

we find that their roots are given by the radical formulas

$${\mathsf{\lambda }}_{\upsilon ,\mathrm{m}}(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })=\left[\upsilon \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\sqrt{{\mathsf{\Delta }}_{\mathrm{m}}(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })}-\mathsf{\lambda }-2\mathrm{m}-1\right]\hspace{0.17em}/(1-\mathsf{\kappa })\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(\upsilon =\pm )$$

(30)

with the positive discriminant

$${\mathsf{\Delta }}_{\mathrm{m}}(\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })=4\hspace{0.17em}[\mathsf{\kappa }\hspace{0.17em}{(2\mathrm{m}+1\pm {\mathsf{\lambda }}_{\mathrm{o}})}^2+(1-\mathsf{\kappa }\hspace{0.17em}){\mathsf{\mu }}_{\mathrm{o}}^2]$$

(31)

for $0\le \mathsf{\kappa }\le 1$.

We therefore proved the following:

Theorem 1.

CSLE (10) with the density function (9) has four infinite sequences of q-RSs (29) unambiguously specified by roots (30) of two quadratic Equation (29), if the corresponding TP has a negative root (0 < κ <1).

On the contrary, all four sequences of the q-RSs (27) are finite if the non-zero TP root is larger than 1 (κ < 0); namely, the number of the q-RSs in each pair of the sequences $(\mathsf{\lambda }=\pm {\mathsf{\lambda }}_{\mathrm{o}})$ is equal to

$${\mathrm{m}}_{\max }^{\pm }=\lceil \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\sqrt{1-1\hspace{0.17em}/\mathsf{\kappa }}\hspace{0.17em}{\mathsf{\mu }}_{\mathrm{o}}-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.(1\pm {\mathsf{\lambda }}_{\mathrm{o}})\rceil$$

(32)

Since both quadratic Equation (29) have positive leading coefficients, we conclude that each equation has two real roots of the opposite sign iff

$$0\le 2\mathrm{m}<{\mathsf{\mu }}_{\mathrm{o}}-\hspace{0.17em}{\mathsf{\lambda }}_{\mathrm{o}}-1.$$

(33)

Below, we refer to the q-RSs (27) simply as |±,υ,m) with the label υ specifying the sign of the Jacobi index (30) as far as the polynomial degrees restricted by the constraint (33). This is the range of the polynomial degrees where the type of the q-RS can be unambiguously specified by the label t = a, b, c, or d mentioned in the Introduction. (In particular, this is true for the quartet of the basic solutions |t,0) assuming that the potential has the discrete energy spectrum.) For larger m values, the q-RSs |++,m) diverge at z = 1, and therefore, we mark them as |a′,m). Similarly, if each quadratic equation has a positive free term then the q-RSs |−+,m) diverge at both 0 and 1, and therefore, we refer to them as |d′,m).

3. Double-Step Form Invariance of JRef CSLE (10)

Let us now consider the double-step DCT using a pair of basic seed functions

$$\begin{array}{l}{}_1\mathsf{\varphi }_{\upsilon ,0}[\mathrm{z};\pm {\mathsf{\lambda }}_{\mathrm{o}},{\Xi }_{\pm ,\upsilon ,0}]:={}_1\mathsf{\varphi }_{\upsilon ,0}^{\pm }[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]\\ =\hspace{0.17em}|\mathrm{z}{|}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\pm \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\mathsf{\lambda }}_{\mathrm{o}}}|1-\mathrm{z}{|}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\mathsf{\lambda }}_{\upsilon ,0}(\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })}.\end{array}$$

(34)

The RefPF for the transformed CSLE

$$\begin{array}{l}\left\{\hspace{0.17em}\frac{{\mathrm{d}}^2\hspace{0.17em}\hspace{0.17em}}{\mathrm{d}{\mathrm{z}}^2}+{\mathrm{I}}^{\mathrm{o}}[\mathrm{z};\hspace{0.17em}{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }|\pm ,+,0;\pm ,-,0]+\mathsf{\epsilon }\hspace{0.17em}{}_1\rho [\mathrm{z};T_{\mathrm{K}}]\hspace{0.17em}\right\}\hspace{0.17em}\times \\ {}_1\mathsf{\Phi }[\mathrm{z};\hspace{0.17em}{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};T_{\mathrm{K}};\mathsf{\epsilon }|\pm ,+,0;\pm ,-,0]=\hspace{0.17em}0\end{array}$$

(35)

can be represented in the standard way [18]

$$\begin{array}{l}{\mathrm{I}}^{\mathrm{o}}[\mathrm{z};\hspace{0.17em}{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }|\pm ,+,0;\pm ,-,0]={\mathrm{I}}^{\mathrm{o}}[\mathrm{z};\hspace{0.17em}\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}}]+\\ 2\sqrt{{\hspace{0.17em}}_1\underrightarrow{\rho }[\mathrm{z};\hspace{0.17em}\mathsf{\kappa }]}\frac{\mathrm{d}\hspace{0.17em}}{\mathrm{d}\mathrm{z}}\frac{ld\hspace{0.17em}{}_1\mathrm{W}[\mathrm{z};\hspace{0.17em}\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]}{\sqrt{{\hspace{0.17em}}_1\underrightarrow{\rho }[\mathrm{z};\hspace{0.17em}\mathsf{\kappa }]}}\end{array}$$

(36)

where

$${}_1\mathrm{W}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]\equiv \mathrm{W}\{{}_1\mathsf{\varphi }_{+,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }],\hspace{0.17em}{}_1\mathsf{\varphi }_{-,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]\}$$

(37)

Substituting (34) into (37) shows that the Wronskian of the selected pair of the basic solutions is given by the simple formula

$$\begin{array}{l}{}_1\mathrm{W}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]=\frac{{\mathsf{\lambda }}_{-,0}(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })-{\mathsf{\lambda }}_{+,0}(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })}{2(\mathrm{z}-1)}]\hspace{0.17em}\times \\ {}_1\mathsf{\varphi }_{+,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]\hspace{0.17em}{}_1\mathsf{\varphi }_{-,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }],\end{array}$$

(38)

which represents the core of our derivation. Combining it with the general formula for the derivative of the Wronskian of two solutions of the generic CSLE

$$\begin{array}{l}{}_1\stackrel{•}{\mathrm{W}}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]=\left|\begin{array}{cc}{}_1\mathsf{\varphi }_{+,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]& {}_1\mathsf{\varphi }_{-,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]\\ {}_1\stackrel{••}{\mathsf{\varphi }}_{+,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]& {}_1\stackrel{••}{\mathsf{\varphi }}_{-,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]\end{array}\right|\\ =\left[{\mathsf{\epsilon }}_{+,0}(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })-{\mathsf{\epsilon }}_{-,0}(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })\right]{\hspace{0.17em}}_1\underrightarrow{\rho }\hspace{0.17em}[\mathrm{z};\hspace{0.17em}\mathsf{\kappa }]\times \end{array}$$

(39)

$$\hspace{0.17em}{}_1\mathsf{\varphi }_{+,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\hspace{0.17em}\mathsf{\kappa }]\hspace{0.17em}{}_1\mathsf{\varphi }_{-,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\hspace{0.17em}\mathsf{\kappa }]$$

(40)

one can represent the logarithmic derivative of Wronskian (38) as

$$ld\hspace{0.17em}{}_1\mathrm{W}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]=\hspace{0.17em}[{\mathsf{\lambda }}_{+,0}(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })+{\mathsf{\lambda }}_{-,0}(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })]\frac{\mathsf{\kappa }\hspace{0.17em}[\mathrm{z}-{\mathrm{z}}_{\mathrm{T}}(\mathsf{\kappa })]}{2\mathrm{z}(\mathrm{z}-1)}$$

(41)

where we also made use of (24) to express the energy difference in terms of the ExpDiffs for the pole at z = 1:

$${\mathsf{\epsilon }}_{\upsilon ,0}\hspace{0.17em}(\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }):={\mathsf{\epsilon }}_{\pm ,\upsilon ,0}\hspace{0.17em}({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })\equiv -{\mathsf{\lambda }}_{\upsilon ,0}^2(\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })$$

(42)

By definition, ${\mathsf{\lambda }}_{\pm ,0}(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })$ are two roots of quadratic Equation (29) with $\pm {\mathsf{\lambda }}_{\mathrm{o}}$ replaced by λ, and therefore,

$${\mathsf{\lambda }}_{+,0}(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })+{\mathsf{\lambda }}_{-,0}(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })=\frac{2(\mathsf{\lambda }+1)}{\mathsf{\kappa }-1}$$

(43)

We can consequently re-write (41) as

$$ld{}_1\mathrm{W}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]=\hspace{0.17em}\frac{\mathsf{\lambda }+1}{{\mathrm{z}}_{\mathrm{T}}(\mathsf{\kappa })}\times \frac{\hspace{0.17em}\mathrm{z}-{\mathrm{z}}_{\mathrm{T}}(\mathsf{\kappa })}{\hspace{0.17em}\hspace{0.17em}\mathrm{z}(\mathrm{z}-1)}$$

(44)

Consequently,

$$\stackrel{•}{ld}\hspace{0.17em}{}_1\mathrm{W}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]=\hspace{0.17em}\frac{\mathsf{\lambda }+1}{{\mathrm{z}}_{\mathrm{T}}(\mathsf{\kappa })}\times \left\{\frac{\hspace{0.17em}1}{\hspace{0.17em}\hspace{0.17em}\mathrm{z}(\mathrm{z}-1)}-\frac{\hspace{0.17em}\mathrm{z}-{\mathrm{z}}_{\mathrm{T}}(\mathrm{k})}{\hspace{0.17em}\hspace{0.17em}{\mathrm{z}}^2(\mathrm{z}-1)}-\frac{\hspace{0.17em}\mathrm{z}-{\mathrm{z}}_{\mathrm{T}}(\mathrm{k})}{\hspace{0.17em}\hspace{0.17em}\mathrm{z}{(\mathrm{z}-1)}^2}\right\}$$

(45)

Representing the second summand in (36) in the rational form

$$\begin{array}{l}2\sqrt{{\hspace{0.17em}}_1\underrightarrow{\rho }[\mathrm{z};\hspace{0.17em}\mathsf{\kappa }]}\frac{\mathrm{d}\hspace{0.17em}}{\mathrm{d}\mathrm{z}}\frac{ld\hspace{0.17em}{}_1\mathrm{W}[\mathrm{z};\hspace{0.17em}\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]}{\sqrt{{\hspace{0.17em}}_1\underrightarrow{\rho }[\mathrm{z};\hspace{0.17em}\mathsf{\kappa }]}}=2\stackrel{•}{ld}\hspace{0.17em}{}_1\mathrm{W}[\mathrm{z};\hspace{0.17em}\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]\\ -ld\hspace{0.17em}{\hspace{0.17em}}_1\underrightarrow{\rho }[\mathrm{z};\hspace{0.17em}\mathsf{\kappa }]\hspace{0.17em}ld\hspace{0.17em}{}_1\mathrm{W}[\mathrm{z};\hspace{0.17em}\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }],\end{array}$$

(46)

taking into account that

$$ld{\hspace{0.17em}}_1\underrightarrow{\rho }(\mathrm{z};\mathsf{\kappa })=\hspace{0.17em}\frac{1}{\mathrm{z}-{\mathrm{z}}_{\mathrm{T}}(\mathsf{\kappa })}-\frac{1}{\mathrm{z}}-\frac{2}{\mathrm{z}-1}$$

(47)

and substituting (44), (45), and (47) into the right-hand side of (46) then gives

$$\begin{array}{l}{\mathrm{I}}^{\mathrm{o}}[\mathrm{z};\hspace{0.17em}{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }|\pm ,+,0;\pm ,-,0]={}_1\mathrm{I}^{\mathrm{o}}[\mathrm{z}\hspace{0.17em};\hspace{0.17em}{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}}]+\frac{\hspace{0.17em}1\pm {\mathsf{\lambda }}_{\mathrm{o}}}{\hspace{0.17em}\hspace{0.17em}{\mathrm{z}}^2(\mathrm{z}-1)}\\ ={\mathrm{I}}^{\mathrm{o}}[\mathrm{z};\hspace{0.17em}|{\mathsf{\lambda }}_{\mathrm{o}}\pm 2|,{\mathsf{\mu }}_{\mathrm{o}}].\end{array}$$

(48)

Note that representing the summand (46) in its rational form makes the derivation applicable for the whole real axis, in contrast with [33], where our analysis was artificially restricted to the finite interval 0 < z < 1. This modification of the arguments also helped the author to eliminate an erroneous shift [33] in the energy measurement point for the transformed potential in the original version of (48).

Note that the DCT decreasing the ExpDiff for the pole at the origin in general changes it for 2 − ${\mathsf{\lambda }}_{\mathrm{o}}$ if 0 < ${\mathsf{\lambda }}_{\mathrm{o}}$ < 2. This results in the anomaly which makes the latter region very special. We shall come back to the discussion of this anomaly in the next section.

We thus proved the following:

Theorem 2.

Putting aside the mentioned anomaly, the DCTs using the pairs of the basic seed functions $\pm ,+,0$ and $\pm ,-,0$ preserve the form of the given JRef CSLE while changing by 2 the ExpDiff for its pole at the origin.

The derived Formula (48) constitutes the cornerstone of this paper. It allows us to assert that the DCTs in question generate the first-order differential expressions in the space of hypergeometric series provided that the CWs [49] are replaced by the corresponding KDs [51] as outlined in the Introduction. In the next section, we directly confirm these expressions taking advantage of the renowned contiguous relations.

4. Dirichlet Problem for the Finite Quantization Interval [0, 1]

Our next step is to investigate the spectral problem for the SLE defined on the finite interval (0, 1). The analysis of the supplementary spectral problems on the infinite intervals (−∞, 0) and (1, ∞) was postponed for a separate publication. As outlined in Section 7 below, the Liouville transformation on the finite interval results in the Schrödinger equation with the radial potential [28,29,30,31,54] while its counterparts on the infinite intervals lead to the Schrödinger equation with the LTP potential on the line [3,13].

To formulate the Sturm–Liouville problem of our interest we introduce the so-called [53] ‘prime’ SLE

$$\left\{\hspace{0.17em}\frac{\mathrm{d}\hspace{0.17em}\hspace{0.17em}}{\mathrm{d}\mathrm{z}}\cancel{\rho }[\mathrm{z}]\frac{\mathrm{d}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{\mathrm{d}\mathrm{z}}-\cancel{\mathrm{q}}\hspace{0.17em}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}}]+\mathsf{\epsilon }\hspace{0.17em}{}_1\underrightarrow{\cancel{\mathrm{w}}}[\mathrm{z};\mathsf{\kappa }]\right\}\hspace{0.17em}\cancel{\mathsf{\Psi }}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }]=\hspace{0.17em}0$$

(49)

By definition, it is obtained from the JRef CSLE (10) by the gauge transformation

$$\hspace{0.17em}\cancel{\mathsf{\Psi }}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }]={\cancel{\rho }}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}[\mathrm{z}]\hspace{0.17em}\mathsf{\Phi }[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }]$$

(50)

chosen in such a way that the ChExps of the Frobenius solutions of SLE (49) near each singular endpoint have exactly the same absolute value but opposite signs. Note that the weight function for SLE (49) has the form

$${}_1\underrightarrow{\cancel{\mathrm{w}}}[\mathrm{z};\mathsf{\kappa }]:={\hspace{0.17em}}_1\underrightarrow{\mathit{\rho }}[\mathrm{z};\mathsf{\kappa }]\hspace{0.17em}\cancel{\rho }[\mathrm{z}]\hspace{0.17em}\hspace{0.17em}$$

(51)

regardless of the particular choice of the leading coefficient function $\cancel{\rho }[\mathrm{z}].$ In our case, we choose [5,53]

$$\cancel{\rho }[\mathrm{z}]=\mathrm{z}(1-\mathrm{z})\hspace{0.17em}.$$

(52)

It has been demonstrated in [5] that the free term

$$\cancel{\mathrm{q}}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}}]=-\hspace{0.17em}\cancel{\rho }[\mathrm{z}]\hspace{0.17em}{\mathrm{I}}^{\mathrm{o}}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}}]+\frac{1}{4\mathrm{z}}+\frac{1}{4(1-\mathrm{z})}$$

(53)

has the simple poles in the finite plane, and therefore, the corresponding indicial equations do not have linear terms. The latter requirement ensures [5] that the sum of the ChExps for both singular ends of the interval (0, 1) is equal to 0, as asserted.

We thus affirm that the PFSs in question are unambiguously selected by the Dirichlet boundary conditions (DBCs):

$$\underset{\mathrm{z}\to \ell }{lim}{\cancel{\mathsf{\Psi }}}_{\ell }[\mathrm{z};{\mathsf{\Lambda }}_{\mathrm{o}};{\mathrm{T}}_{\mathrm{K}};\mathsf{\epsilon }]=0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(\ell =0,1).$$

(54)

One of the advantages of formulating the spectral problem in such a form is that we can automatically adopt the rigorous theorems proven in [55] for the generic SLE solved under the DBCs.

Prime SLE (49) has two infinite sequences of quasi-rational PFSs near the origin:

$$\begin{array}{l}{}_1\cancel{\mathsf{\psi }}_{\mathbf{a},\mathrm{m}}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]:={}_1\cancel{\mathsf{\psi }}_{-,\mathrm{m}}^{+}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]\\ =\hspace{0.17em}\frac{\hspace{0.17em}{(-1)}^{\mathrm{m}}\mathrm{m}!}{{\langle 1+{\mathsf{\lambda }}_{\mathrm{o}}\rangle }_{\mathrm{m}}}{\mathrm{z}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\mathsf{\lambda }}_{\mathrm{o}}}{(1-\mathrm{z})}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\Xi }_{+,-,\mathrm{m}}}\hspace{0.17em}{\mathrm{P}}_{\mathrm{m}}^{({\Xi }_{+,-,\mathrm{m}}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}{\mathsf{\lambda }}_{\mathrm{o}})}(2\mathrm{z}-1)\end{array}$$

(55)

and

$${}_1\cancel{\mathsf{\psi }}_{+,\mathrm{m}}^{+}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]=\hspace{0.17em}\frac{\hspace{0.17em}{(-1)}^{\mathrm{m}}\mathrm{m}!}{{\langle 1+{\mathsf{\lambda }}_{\mathrm{o}}\rangle }_{\mathrm{m}}}{\mathrm{z}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\mathsf{\lambda }}_{\mathrm{o}}}|1-\mathrm{z}{|}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\Xi }_{+,+,\mathrm{m}}}\hspace{0.17em}{\mathrm{P}}_{\mathrm{m}}^{({\Xi }_{+,+,\mathrm{m}}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}{\mathsf{\lambda }}_{\mathrm{o}})}(2\mathrm{z}-1)$$

(56)

An examination of the linear term of the quadratic Equation (29) specifying the PFSs near the origin reveals that the positive root exists iff the given quadratic polynomial has a negative free term, i.e., the infinite sequence (56) is composed of the eigenfunctions

$${}_1\cancel{\mathsf{\psi }}_{\mathbf{c},\mathrm{n}}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]={}_1\cancel{\mathsf{\psi }}_{+,\mathrm{n}}^{+}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }] \mathrm{for} \mathrm{n}<{\mathrm{n}}_{\max }$$

(57)

and

$${}_1\cancel{\mathsf{\psi }}_{{\mathbf{a}}^{\prime },\mathrm{m}}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]={}_1\cancel{\mathsf{\psi }}_{+,\mathrm{m}}^{+}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }] \mathrm{for} \mathrm{m}>{\mathrm{n}}_{\max },$$

(58)

with

$${\mathrm{n}}_{\max }=\lfloor ({\mathsf{\mu }}_{\mathrm{o}}-{\mathsf{\lambda }}_{\mathrm{o}}-1)/2\rfloor .$$

(59)

Let us now apply the second-order DCTs discussed in Section 3 to the PFS in the pair (13). Making use of Schulze-Halberg’s [56] general formula for solutions of the generic CSLE undergoing an arbitrary DCT, we can represent the DCs of the PFS marked by a superscript ‘+’ in {13) as follows:

$$\begin{array}{l}{\hspace{0.17em}}_1{\mathsf{\Phi }}_0^{+}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }|\pm ,+,0;\pm ,-,0]:=\\ \frac{\mathrm{W}\{{}_1\mathsf{\varphi }_{+,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }],\hspace{0.17em}{}_1\mathsf{\varphi }_{-,0}[\mathrm{z};\hspace{0.17em}\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }],{}_1\mathsf{\Phi }_0^{+}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }]\}}{{\hspace{0.17em}}_1\underrightarrow{\mathit{\rho }}\hspace{0.17em}[\mathrm{z};\mathsf{\kappa }]\hspace{0.17em}{}_1\mathrm{W}[\mathrm{z};\hspace{0.17em}\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]},\end{array}$$

(60)

Converting the CW to the KD gives

$$\begin{array}{l}\mathrm{W}\{{}_1\mathsf{\varphi }_{+,0}[\mathrm{z};\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }],\hspace{0.17em}{}_1\mathsf{\varphi }_{-,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }],{}_1\mathsf{\Phi }_0^{+}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }]\}=\\ -{\hspace{0.17em}}_1\underrightarrow{\mathit{\rho }}\hspace{0.17em}[\mathrm{z};\mathsf{\kappa }]{\hspace{0.17em}}_1\mathrm{K}[\mathrm{z};\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }],\end{array}$$

(61)

where

$$\begin{array}{l}{\hspace{0.17em}}_1\mathcal{K}[\mathrm{z};\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }]:=\\ \left|\begin{array}{ccc}{}_1\mathsf{\varphi }_{+,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]& {}_1\mathsf{\varphi }_{-,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]& {}_1\mathsf{\Phi }[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }]\\ {}_1\stackrel{•}{\mathsf{\varphi }}_{+,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]& {}_1\stackrel{•}{\mathsf{\varphi }}_{-,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]& {}_1\stackrel{•}{\mathsf{\Phi }}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }]\\ {\mathsf{\epsilon }}_{+,0}(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }){}_1\mathsf{\varphi }_{+,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]& {\mathsf{\epsilon }}_{-,0}(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }){}_1\mathsf{\varphi }_{-,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]& \mathsf{\epsilon }\hspace{0.17em}{}_1\mathsf{\Phi }[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }]\end{array}\right|\\ ={}_1\mathsf{\varphi }_{+,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]\hspace{0.17em}{}_1\mathsf{\varphi }_{-,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]\times \\ \left|\begin{array}{ccc}1& 1& {}_1\mathsf{\Phi }[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }]\\ ld{}_1\mathsf{\varphi }_{+,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]& ld{}_1\mathsf{\varphi }_{-,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]& {}_1\stackrel{•}{\mathsf{\Phi }}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }]\\ -{\mathsf{\lambda }}_{+,0}^2(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })& -{\mathsf{\lambda }}_{-,0}^2(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })& \mathsf{\epsilon }\hspace{0.17em}{}_1\mathsf{\Phi }[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }]\end{array}\right|.\end{array}$$

(62)

Note that the density function disappeared from the denominator of the fraction

$${}_1\mathsf{\Phi }[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }|\pm ,+,0;\pm ,-,0]=\frac{\hspace{0.17em}{\hspace{0.17em}}_1\mathcal{K}[\mathrm{z};\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }]}{\hspace{0.17em}{}_1\mathrm{W}[\mathrm{z};\hspace{0.17em}\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]}$$

(63)

This is one of the additional advantages of the KD representation compared with the Crum formula. It directly follows from (38) and (62) that fraction (63) does not have a pole at the TP zero ${\mathrm{z}}_{\mathrm{T}}(\mathsf{\kappa })$ as expected from the fact that RefPF (36) is regular at this point.

Making use of (38) and introducing the first-order differential operator

$$\begin{array}{l}{\hspace{0.17em}}_1\mathbf{D}\left\{\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }\right\}:=\frac{2}{{\mathsf{\lambda }}_{-,0}(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })-{\mathsf{\lambda }}_{+,0}(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })}\mathrm{z}(\mathrm{z}-1)\\ \left|\begin{array}{ccc}1& 1& 1\\ ld{}_1\mathsf{\varphi }_{+,0}[\mathrm{z};\hspace{0.17em}\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]& ld{}_1\mathsf{\varphi }_{-,0}[\mathrm{z};\hspace{0.17em}\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]& \frac{\mathrm{d}\hspace{0.17em}\hspace{0.17em}}{\mathrm{d}\mathrm{z}}\\ -{\mathsf{\lambda }}_{+,0}^2(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })& {\mathsf{\lambda }}_{-,0}^2(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })& \mathsf{\epsilon }\end{array}\right|\end{array}$$

(64)

we can represent the solution (63) of RCSLE (35) as follows:

$${}_1\mathsf{\Phi }_0[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }|\pm ,+,0;\pm ,-,0]={\mathrm{z}}^{-1}{\hspace{0.17em}}_1\mathbf{D}\left\{{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }\right\}{}_1\mathsf{\Phi }_0[\mathrm{z};\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }].$$

(65)

Let us formally represent the solution (60) as

$$\begin{array}{l}{}_1\mathsf{\Phi }_0[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }|\pm ,+,0;\pm ,-,0]={\mathrm{z}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.({\mathsf{\lambda }}_{\mathrm{o}}-1)}{(1-\mathrm{z})}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\hspace{0.17em}(-\sqrt{-\mathsf{\epsilon }}+1)}\times \\ {}_1\mathrm{F}_0[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }|\pm ,+,0;\pm ,-,0] (0<\mathrm{z}<1),\end{array}$$

(66)

where

$$\begin{array}{l}{}_1\mathrm{F}_0[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }|\pm ,+,0;\pm ,-,0]:={\hspace{0.17em}}_1{\mathbf{D}}_0^{\pm }\left\{{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };-\sqrt{-\mathsf{\epsilon }}\right\}\times \hspace{0.17em}\\ \mathrm{F}\hspace{0.17em}[\mathsf{\alpha }({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };-\sqrt{-\mathsf{\epsilon }})\hspace{0.17em},\mathsf{\beta }({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };-\sqrt{-\mathsf{\epsilon }});{\mathsf{\lambda }}_{\mathrm{o}}+1;\mathrm{z}]\hspace{0.17em}(0<\mathrm{z}<1),\end{array}$$

(67)

with the corresponding first-order differential operators defined as follows:

$$\begin{array}{l}{}_1\mathbf{D}_0^{+}\left\{{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\Xi \right\}:=\\ \mathrm{z}\left|\underset{-{\mathsf{\lambda }}_{+,0}^2({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}2({\mathsf{\lambda }}_{\mathrm{o}}+1)/(1-\mathsf{\kappa })\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-{\Xi }^2\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{\overset{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathsf{\lambda }}_{+,0}({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Xi +2(\mathrm{z}-1)\frac{\mathrm{d}\hspace{0.17em}\hspace{0.17em}}{\mathrm{d}\mathrm{z}}\hspace{0.17em}\hspace{0.17em}}}\right|\end{array}$$

(68)

and

$$\begin{array}{l}{}_1\mathbf{D}_0^{-}\left\{{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\Xi \right\}=\\ =\hspace{0.17em}\left|\underset{-{\mathsf{\lambda }}_{+,0}^2(-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}2(1-{\mathsf{\lambda }}_{\mathrm{o}})/(1-\mathsf{\kappa })\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-{\Xi }^2\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{\overset{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathsf{\lambda }}_{+,0}(-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })\mathrm{z}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{z}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Xi \hspace{0.17em}\mathrm{z}+2(\mathrm{z}-1)\left({\mathsf{\lambda }}_{\mathrm{o}}+\mathrm{z}\frac{\mathrm{d}\hspace{0.17em}}{\mathrm{d}\mathrm{z}}\right)\hspace{0.17em}}}\right|\end{array}$$

(69)

bearing in mind that

$${\mathsf{\lambda }}_{+,0}(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })+{\mathsf{\lambda }}_{-,0}(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })=2(\mathsf{\lambda }+1)/(\mathsf{\kappa }-1).$$

(70)

We will refer to functions (67) and to the first-order differential operator (68) or (69) as the ‘Darboux–Crum–Krein transforms’ (DCKs) of the hypergeometric functions and as the ‘DCK’ generators, respectively.

Theorem 3.

DCK generators (68) or (69) respectively increase or decrease by 1 the first two parameters of the hypergeometric function on the right-hand side of (66) while respectively increasing or decreasing by 2 the third parameter.

Proof of Theorem 3.

Let us first present the explicit expressions for the coefficient functions of the DCK generators (68) and (69). Namely, again taking into account that we deal with the two roots (30) of quadratic Equation (29), coupled with (17), one finds

$$(1-\mathsf{\kappa }){\hspace{0.17em}}_1{\mathbf{D}}_0^{+}\left\{\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\Xi \right\}\hspace{0.17em}=\hspace{0.17em}\mathrm{z}{\mathsf{\Lambda }}_2(\Xi ;\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })+4(\mathsf{\lambda }+1)\mathrm{z}(1-\mathrm{z})\frac{\mathrm{d}\hspace{0.17em}\hspace{0.17em}}{\mathrm{d}\mathrm{z}}$$

(71)

and

$$(1-\mathsf{\kappa }){\hspace{0.17em}}_1{\mathbf{D}}_0^{-}\left\{{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\Xi \right\}\hspace{0.17em}={\mathsf{\Lambda }}_2(\Xi ;-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })+4(1-{\mathsf{\lambda }}_{\mathrm{o}})(1-\mathrm{z})\left({\mathsf{\lambda }}_{\mathrm{o}}+\mathrm{z}\frac{\mathrm{d}\hspace{0.17em}}{\mathrm{d}\mathrm{z}}\right),$$

(72)

where the quadratic polynomial in $\Xi$ is defined as follows:

$${\mathsf{\Lambda }}_2(\Xi ;\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }):=(1-\mathsf{\kappa })[\Xi \hspace{0.17em}-{\mathsf{\lambda }}_{+,0}(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })]\times [\Xi \hspace{0.17em}-{\mathsf{\lambda }}_{-,0}(\mathsf{\lambda },{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })]$$

(73)

$$\equiv {\mathsf{\mu }}^2({\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }{\Xi }^2)-{(\Xi +\mathsf{\lambda }+1)}^2.$$

(74)

Making use of (18) and (22) with $\mathsf{\lambda }={\mathsf{\lambda }}_{\mathrm{o}}$ gives

$${\mathsf{\Lambda }}_2(\Xi ;{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })=-4\mathsf{\alpha }({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\Xi )\hspace{0.17em}\mathsf{\beta }({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\Xi )$$

(75)

On the other hand, setting $\mathsf{\lambda }=-{\mathsf{\lambda }}_{\mathrm{o}}$ in (43) and $\mathsf{\lambda }={\mathsf{\lambda }}_{\mathrm{o}}$ in (18) shows that the resultant value of quadratic polynomial (74) is related to (75) via the simple shift

$${\mathsf{\Lambda }}_2(\Xi ;-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })={\mathsf{\Lambda }}_2(\Xi ;{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })+4{\mathsf{\lambda }}_{\mathrm{o}}(\Xi +1).$$

(76)

Substituting (75) into the latter relation gives

$${\mathsf{\Lambda }}_2(\Xi ;-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })=-4\left[\mathsf{\alpha }({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\Xi )-{\mathsf{\lambda }}_{\mathrm{o}}\hspace{0.17em}\right]\times \left[\mathsf{\beta }({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\Xi )-{\mathsf{\lambda }}_{\mathrm{o}}\right].$$

(77)

Our next step is to explicitly confirm that the DCK of the hypergeometric function generated by operator (68) has the double zero at the origin as expected from the fact that the DCT in question increases by 2 the ExpDiff for this pole of the CSLE while keeping the parameter ${\mathsf{\mu }}_{\mathrm{o}}$ unchanged. First bearing in mind that

$$({\mathsf{\lambda }}_{\mathrm{o}}+1)(\mathsf{\alpha }+\mathsf{\beta }-{\mathsf{\lambda }}_{\mathrm{o}}-1)=\mathsf{\alpha }\mathsf{\beta }-({\mathsf{\lambda }}_{\mathrm{o}}+1-\mathsf{\alpha })({\mathsf{\lambda }}_{\mathrm{o}}+1-\mathsf{\beta })$$

(78)

we represent contiguous relation (13) in §33 in [57] as

$$\begin{array}{l}({\mathsf{\lambda }}_{\mathrm{o}}+1)(1-\mathrm{z})\frac{\mathrm{d}\hspace{0.17em}}{\mathrm{d}\mathrm{z}}\mathrm{F}\hspace{0.17em}(\mathsf{\alpha }\hspace{0.17em},\mathsf{\beta };{\mathsf{\lambda }}_{\mathrm{o}}+1;\mathrm{z})=\mathsf{\alpha }\hspace{0.17em}\mathsf{\beta }\hspace{0.17em}\mathrm{F}\hspace{0.17em}(\mathsf{\alpha }\hspace{0.17em},\mathsf{\beta };{\mathsf{\lambda }}_{\mathrm{o}}+1;\mathrm{z})-\\ (\mathsf{\alpha }\hspace{0.17em}-{\mathsf{\lambda }}_{\mathrm{o}}-1)(\mathsf{\beta }-{\mathsf{\lambda }}_{\mathrm{o}}-1)\left[\mathrm{F}(\mathsf{\alpha },\mathsf{\beta };{\mathsf{\lambda }}_{\mathrm{o}}+1;\mathrm{z})-\mathrm{F}\hspace{0.17em}(\mathsf{\alpha }\hspace{0.17em},\mathsf{\beta };{\mathsf{\lambda }}_{\mathrm{o}}+2;\mathrm{z})\right] (|\mathrm{z}|<1).\end{array}$$

(79)

Also note that making use of contiguous relation (9) in the cited monograph

$$\left({\mathsf{\lambda }}_{\mathrm{o}}+\mathrm{z}\frac{\mathrm{d}\hspace{0.17em}}{\mathrm{d}\mathrm{z}}\right)\hspace{0.17em}\hspace{0.17em}\mathrm{F}\left(\mathsf{\alpha },\mathsf{\beta };{\mathsf{\lambda }}_{\mathrm{o}}+1;\mathrm{z}\right)={\mathsf{\lambda }}_{\mathrm{o}}\mathrm{F}\left(\mathsf{\alpha },\mathsf{\beta };{\mathsf{\lambda }}_{\mathrm{o}};\mathrm{z}\right) (|\mathrm{z}|<1)$$

(80)

coupled with the conventional formula for the derivative of the hypergeometric function

$$\frac{\mathrm{d}\hspace{0.17em}}{\mathrm{d}\mathrm{z}}\mathrm{F}\hspace{0.17em}(\mathsf{\alpha }\hspace{0.17em},\mathsf{\beta };{\mathsf{\lambda }}_{\mathrm{o}}+2;\mathrm{z})=\frac{\mathsf{\alpha }\mathsf{\beta }}{{\mathsf{\lambda }}_{\mathrm{o}}+2}\mathrm{F}\hspace{0.17em}(\mathsf{\alpha }+1\hspace{0.17em},\mathsf{\beta }+1;{\mathsf{\lambda }}_{\mathrm{o}}+3;\mathrm{z}) (|\mathrm{z}|<1)$$

(81)

one can re-write the difference between the hypergeometric functions in the second term in the right-hand of (79) as

$$\begin{array}{c}\mathrm{F}(\mathsf{\alpha },\mathsf{\beta };{\mathsf{\lambda }}_{\mathrm{o}}+1;\mathrm{z})-\mathrm{F}(\mathsf{\alpha },\mathsf{\beta };{\mathsf{\lambda }}_{\mathrm{o}}+2;\mathrm{z})=\frac{\mathsf{\alpha }\mathsf{\beta }}{({\mathsf{\lambda }}_{\mathrm{o}}+1)({\mathsf{\lambda }}_{\mathrm{o}}+2)}\mathrm{z}\hspace{0.17em}\mathrm{F}(\mathsf{\alpha }+1\hspace{0.17em},\mathsf{\beta }+1;{\mathsf{\lambda }}_{\mathrm{o}}+3;\mathrm{z})\\ (|\mathrm{z}|<1).\end{array}$$

(82)

Consequently, function (67) for the DCT in question takes the form

$$\begin{array}{l}{}_1\mathrm{F}_0[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }|+,+,0;+,-,0]=[{({\mathsf{\lambda }}_{\mathrm{o}}\hspace{0.17em}-\sqrt{|\mathsf{\epsilon }|}\hspace{0.17em}+1)}^2\hspace{0.17em}-{\mathsf{\mu }}^2({\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }|\mathsf{\epsilon }|)]\times \\ \frac{[\mathsf{\alpha }({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };-\sqrt{|\mathsf{\epsilon }|})-{\mathsf{\lambda }}_{\mathrm{o}}-1]\times [\mathsf{\beta }({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };-\sqrt{|\mathsf{\epsilon }|})-{\mathsf{\lambda }}_{\mathrm{o}}-1]}{(\mathsf{\kappa }-1)({\mathsf{\lambda }}_{\mathrm{o}}+1)({\mathsf{\lambda }}_{\mathrm{o}}+2)}\times \\ {\mathrm{z}}^2\mathrm{F}\left(\mathsf{\alpha }({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };-\sqrt{|\mathsf{\epsilon }|})+1\hspace{0.17em},\mathsf{\beta }({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };-\sqrt{|\mathsf{\epsilon }|})+1;{\mathsf{\lambda }}_{\mathrm{o}}+3;\mathrm{z}\right) (0<\mathrm{z}<1)\end{array}$$

(83)

which completes the proof of Theorem 3 for DCK generator (68).

Coming back to DCK generator (69), let us show that

$$\begin{array}{l}({\mathsf{\lambda }}_{\mathrm{o}}-1)(1-\mathrm{z})\left({\mathsf{\lambda }}_{\mathrm{o}}+\mathrm{z}\frac{\mathrm{d}\hspace{0.17em}}{\mathrm{d}\mathrm{z}}\right)\hspace{0.17em}\mathrm{F}(\mathsf{\alpha }\hspace{0.17em},\mathsf{\beta };{\mathsf{\lambda }}_{\mathrm{o}}+1;\mathrm{z})={\mathsf{\lambda }}_{\mathrm{o}}({\mathsf{\lambda }}_{\mathrm{o}}-1)\mathrm{F}(\mathsf{\alpha }\hspace{0.17em}-1,\mathsf{\beta }-1;{\mathsf{\lambda }}_{\mathrm{o}}-1;\mathrm{z})-\\ ({\mathsf{\lambda }}_{\mathrm{o}}-\mathsf{\alpha })({\mathsf{\lambda }}_{\mathrm{o}}-\mathsf{\beta })\mathrm{z}\hspace{0.17em}\mathrm{F}(\mathsf{\alpha }\hspace{0.17em},\mathsf{\beta };{\mathsf{\lambda }}_{\mathrm{o}}+1;\mathrm{z}) (|\mathrm{z}|<1).\end{array}$$

(84)

and therefore, function (67) for the DCT in question takes the form

$$\begin{array}{l}{}_1\mathrm{F}_0[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }|-,+,0;-,-,0]=\frac{4{\mathsf{\lambda }}_{\mathrm{o}}({\mathsf{\lambda }}_{\mathrm{o}}-1)\hspace{0.17em}}{\mathsf{\kappa }-1}\times \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{F}\left(\mathsf{\alpha }(-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };-\sqrt{|\mathsf{\epsilon }|})-1\hspace{0.17em},\mathsf{\beta }(-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };-\sqrt{|\mathsf{\epsilon }|})-1;{\mathsf{\lambda }}_{\mathrm{o}}-1;\mathrm{z}\right) (0<\mathrm{z}<1)\end{array}$$

(85)

as anticipated. Indeed, making use of contiguous relation (9) in §33 in [57], one finds

$$\left({\mathsf{\lambda }}_{\mathrm{o}}+\mathrm{z}\frac{\mathrm{d}\hspace{0.17em}}{\mathrm{d}\mathrm{z}}\right)\hspace{0.17em}\hspace{0.17em}\mathrm{F}(\mathsf{\alpha },\mathsf{\beta };{\mathsf{\lambda }}_{\mathrm{o}}+1;\mathrm{z})={\mathsf{\lambda }}_{\mathrm{o}}\mathrm{F}(\mathsf{\alpha }\hspace{0.17em},\mathsf{\beta };{\mathsf{\lambda }}_{\mathrm{o}};\mathrm{z}) (|\mathrm{z}|<1);$$

(86)

while decreasing ${\mathsf{\lambda }}_{\mathrm{o}}$ by 1 in (81) and substituting the resultant expression into contiguous relation (13) in the same paragraph of [57] brings us to another contiguous relation

$$\begin{array}{l}\mathsf{\alpha }\mathsf{\beta }(1-\mathrm{z})\mathrm{F}\hspace{0.17em}(\mathsf{\alpha }+1\hspace{0.17em},\mathsf{\beta }+1;{\mathsf{\lambda }}_{\mathrm{o}}+2;\mathrm{z})=\mathsf{\alpha }\hspace{0.17em}\mathsf{\beta }\hspace{0.17em}\mathrm{F}\hspace{0.17em}(\mathsf{\alpha }\hspace{0.17em},\mathsf{\beta };{\mathsf{\lambda }}_{\mathrm{o}}+1;\mathrm{z})-\\ (\mathsf{\alpha }\hspace{0.17em}-{\mathsf{\lambda }}_{\mathrm{o}}-1)(\mathsf{\beta }-{\mathsf{\lambda }}_{\mathrm{o}}-1)\left[\mathrm{F}(\mathsf{\alpha },\mathsf{\beta };{\mathsf{\lambda }}_{\mathrm{o}}+1;\mathrm{z})-\mathrm{F}\hspace{0.17em}(\mathsf{\alpha }\hspace{0.17em},\mathsf{\beta };{\mathsf{\lambda }}_{\mathrm{o}}+2;\mathrm{z})\right] (|\mathrm{z}|<1).\end{array}$$

(87)

not listed in [57]. Taking into account that

$$({\mathsf{\lambda }}_{\mathrm{o}}+1)(\mathsf{\alpha }+\mathsf{\beta }-{\mathsf{\lambda }}_{\mathrm{o}}-1)=\mathsf{\alpha }\mathsf{\beta }-({\mathsf{\lambda }}_{\mathrm{o}}+1-\mathsf{\alpha })({\mathsf{\lambda }}_{\mathrm{o}}+1-\mathsf{\beta })$$

(88)

we can then re-write (87) as

$$\begin{array}{l}(1-\mathrm{z})\mathrm{F}\hspace{0.17em}(\mathsf{\alpha }+1\hspace{0.17em},\mathsf{\beta }+1;{\mathsf{\lambda }}_{\mathrm{o}}+2;\mathrm{z})=\mathrm{F}(\mathsf{\alpha },\mathsf{\beta };{\mathsf{\lambda }}_{\mathrm{o}}+1;\mathrm{z})-\\ \frac{({\mathsf{\lambda }}_{\mathrm{o}}+1-\mathsf{\alpha })({\mathsf{\lambda }}_{\mathrm{o}}+1-\mathsf{\beta })}{\mathsf{\alpha }\hspace{0.17em}\mathsf{\beta }}[\mathrm{F}(\mathsf{\alpha },\mathsf{\beta };{\mathsf{\lambda }}_{\mathrm{o}}+1;\mathrm{z})-\mathrm{F}(\mathsf{\alpha },\mathsf{\beta };{\mathsf{\lambda }}_{\mathrm{o}}+2;\mathrm{z})] (|\mathrm{z}|<1).\end{array}$$

(89)

Substituting (82) in the right-hand side of (89) and replacing $\mathsf{\alpha }+1\hspace{0.17em},\mathsf{\beta }+1$, and ${\mathsf{\lambda }}_{\mathrm{o}}+2$ with $\mathsf{\alpha },\mathsf{\beta }$, and ${\mathsf{\lambda }}_{\mathrm{o}}$, respectively, we finally come to the sought-for contiguous relation

$$\begin{array}{c}{\mathsf{\lambda }}_{\mathrm{o}}({\mathsf{\lambda }}_{\mathrm{o}}-1)(1-\mathrm{z})\mathrm{F}(\mathsf{\alpha },\mathsf{\beta };{\mathsf{\lambda }}_{\mathrm{o}};\mathrm{z})={\mathsf{\lambda }}_{\mathrm{o}}({\mathsf{\lambda }}_{\mathrm{o}}-1)\mathrm{F}(\mathsf{\alpha }-1,\mathsf{\beta }-1;{\mathsf{\lambda }}_{\mathrm{o}}-1;\mathrm{z})-\\ ({\mathsf{\lambda }}_{\mathrm{o}}-\mathsf{\alpha })({\mathsf{\lambda }}_{\mathrm{o}}-\mathsf{\beta })\mathrm{z}\hspace{0.17em}\mathrm{F}(\mathsf{\alpha },\mathsf{\beta };{\mathsf{\lambda }}_{\mathrm{o}}+1;\mathrm{z}) (|\mathrm{z}|<1),\end{array}$$

(90)

which, coupled with (88), brings us back to (85). This completes the proof of Theorem 3 for the second DCK generator (69). □

Combining (66), (67), (83), and (85) we come to the conclusion that the functions

$$\begin{array}{c}{}_1\cancel{\mathsf{\Psi }}_0[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }|+,+,0;+,-,0]:={\cancel{\rho }}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}[\mathrm{z}]{\hspace{0.17em}}_1{\mathsf{\Phi }}_0[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }|+,+,0;+,-,0]\\ =[{({\mathsf{\lambda }}_{\mathrm{o}}\hspace{0.17em}-\sqrt{|\mathsf{\epsilon }|}\hspace{0.17em}+1)}^2\hspace{0.17em}-{\mathsf{\mu }}^2({\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }|\mathsf{\epsilon }|)]\hspace{0.17em}{\mathrm{z}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.({\mathsf{\lambda }}_{\mathrm{o}}+2)}{(1-\mathrm{z})}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\sqrt{-\mathsf{\epsilon }}}\times \\ \frac{[\mathsf{\alpha }({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };-\sqrt{|\mathsf{\epsilon }|})-{\mathsf{\lambda }}_{\mathrm{o}}-1]\times [\mathsf{\beta }({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };-\sqrt{|\mathsf{\epsilon }|})-{\mathsf{\lambda }}_{\mathrm{o}}-1]}{(\mathsf{\kappa }-1)({\mathsf{\lambda }}_{\mathrm{o}}+1)({\mathsf{\lambda }}_{\mathrm{o}}+2)}\times \\ \hspace{0.17em}\mathrm{F}\left(\mathsf{\alpha }({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };-\sqrt{|\mathsf{\epsilon }|})+1\hspace{0.17em},\mathsf{\beta }({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };-\sqrt{|\mathsf{\epsilon }|})+1;{\mathsf{\lambda }}_{\mathrm{o}}+3;\mathrm{z}\right)\end{array}$$

(91)

and

$$\begin{array}{l}{}_1\cancel{\mathsf{\Psi }}_0[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }|-,+,0;-,-,0]:={\cancel{\rho }}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}[\mathrm{z}]{\hspace{0.17em}}_1{\mathsf{\Phi }}_0[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }|-,+,0;-,-,0]\\ =\frac{4{\mathsf{\lambda }}_{\mathrm{o}}({\mathsf{\lambda }}_{\mathrm{o}}-1)\hspace{0.17em}}{\mathsf{\kappa }-1}{\mathrm{z}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.({\mathsf{\lambda }}_{\mathrm{o}}-2)}{(1-\mathrm{z})}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\sqrt{-\mathsf{\epsilon }}}\times \\ \mathrm{F}\left(\mathsf{\alpha }(-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };-\sqrt{|\mathsf{\epsilon }|})-1\hspace{0.17em},\mathsf{\beta }(-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };-\sqrt{|\mathsf{\epsilon }|})-1;{\mathsf{\lambda }}_{\mathrm{o}}-1;\mathrm{z}\right),\end{array}$$

(92)

with ${\mathsf{\lambda }}_{\mathrm{o}}>2$ in the latter case, are the solutions of the prime SLEs

$$\begin{array}{l}\left\{\hspace{0.17em}\frac{\mathrm{d}\hspace{0.17em}\hspace{0.17em}}{\mathrm{d}\mathrm{z}}\cancel{\rho }[\mathrm{z}]\frac{\mathrm{d}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{\mathrm{d}\mathrm{z}}-\cancel{\mathrm{q}}\hspace{0.17em}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }|\pm ,+,0;\pm ,-,0]+\mathsf{\epsilon }\hspace{0.17em}{}_1\underrightarrow{\cancel{\mathrm{w}}}[\mathrm{z};\mathsf{\kappa }]\right\}\times \\ {}_1\cancel{\mathsf{\Psi }}_0[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }|\pm ,+,0;\pm ,-,0]=\hspace{0.17em}0\end{array}$$

(93)

satisfying the DBCs

$${\underset{\mathrm{z}\to 0}{lim}}_1{\cancel{\mathsf{\Psi }}}_0[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }|\pm ,+,0;\pm ,-,0]=\hspace{0.17em}0,$$

(94)

where by definition

$$\begin{array}{l}\cancel{\mathrm{q}}\hspace{0.17em}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }|\pm ,+,0;\pm ,-,0]:=-\hspace{0.17em}\cancel{\rho }[\mathrm{z}]\hspace{0.17em}{\mathrm{I}}^{\mathrm{o}}\hspace{0.17em}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }|\pm ,+,0;\pm ,-,0]+\\ \frac{1}{4\mathrm{z}}+\frac{1}{4(1-\mathrm{z})}\end{array}$$

(95)

Again, note that the solution (92) infinitely grows near the origin if $0<{\mathsf{\lambda }}_{\mathrm{o}}<2$. We shall come back to this puzzling issue in Section 6.

Note that all the results were obtained by us with no reference to the Liouville transformations leading to quantum-mechanical applications. To be able to apply the developed formalism to quantum-mechanical problems, one simply needs to convert the JRef CSLE to the radial Schrödinger equation by the Liouville transformation on the finite interval [0, 1] as thoroughly elaborated in [33].

5. Decomposition of Second-Order DCT into Two Sequential LDTs

To understand the source behind the anomalous behavior of the solution (92) in the region $0<{\mathsf{\lambda }}_{\mathrm{o}}<2$, let us decompose the given second-order DCTs into two sequential LDTs.

Let ${\mathsf{\varphi }}_{\tau }[\mathrm{z};{\mathsf{\Lambda }}_{\mathrm{o}};T]$ be a nodeless solution of the generic CSLE

$$\left\{\hspace{0.17em}\frac{{\mathrm{d}}^2\hspace{0.17em}\hspace{0.17em}}{\mathrm{d}{\mathrm{z}}^2}+{\mathrm{I}}^{\mathrm{o}}[\mathrm{z};{\mathsf{\Lambda }}_{\mathrm{o}};T]+\mathsf{\epsilon }\mathit{\rho }[\mathrm{z};T]\hspace{0.17em}\right\}\hspace{0.17em}\hspace{0.17em}{\mathsf{\Phi }}_{\tau }[\mathrm{z};{\mathsf{\Lambda }}_{\mathrm{o}};T;\mathsf{\epsilon }]=\hspace{0.17em}0$$

(96)

at an energy ${\mathsf{\epsilon }}_{\tau }({\mathsf{\Lambda }}_{\mathrm{o}};T)$. We define the LD of CSLE with the TF, ${\mathsf{\varphi }}_{\tau }[\mathrm{z};{\mathsf{\Lambda }}_{\mathrm{o}};T]$, as the CSLE with the solution

$${}^{\ast }\mathsf{\varphi }_{\tau }[\mathrm{z};{\mathsf{\Lambda }}_{\mathrm{o}};T]={\mathit{\rho }}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\hspace{0.17em}[\mathrm{z};T]/{\mathsf{\varphi }}_{\tau }[\mathrm{z};{\mathsf{\Lambda }}_{\mathrm{o}};T]$$

(97)

at the same energy. As originally pointed out by Rudjak and Zakhariev [17], the zero-energy free term of the resultant CSLE has the form

(98)

where the so-called [53] ‘universal correction’ is defined via the following generic formula [18]:

(99)

In [4], we identified this transformation as the following three-step operation:

(i)

The Liouville transformation of the generic CSLE to the Schrödinger equation by the change in variable $\mathrm{z}(\mathrm{x};T)$ determined up to a constant shift by the following first-order ordinary differential equation (ODE):

$$\frac{\mathrm{d}\mathrm{x}}{\mathrm{d}\mathrm{z}}={}_1\mathit{\rho }^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}[\mathrm{z};T];$$

(100)

(ii)

The Darboux deformation of the Liouville potential with the TF

$${\mathsf{\chi }}_{\tau }[\mathrm{z}(\mathrm{x};T);{\mathsf{\Lambda }}_{\mathrm{o}};T)=\frac{1}{\sqrt{{\mathrm{z}}^{\prime }(\mathrm{x};T)}}{\mathsf{\varphi }}_{\tau }[\mathrm{z}(\mathrm{x};T);{\mathsf{\Lambda }}_{\mathrm{o}};T];$$

(101)

(iii)

The reverse Liouville transformation of the Schrödinger equation with the deformed potential to the new CSLE with the original density function $\mathit{\rho }\hspace{0.17em}[\mathrm{z};\mathrm{T}]$.

It should be stressed that our definition of the LDT is given with no relation to the corresponding Darboux deformation of the associated Liouville potential. However, the mentioned interrelationship between the LDTs of the generic CSLE and conventional DTs of the Schrödinger equation makes it easier to apply our scrupulous mathematical analysis of some remarkable features of the LDTs to the one-dimensional SUSY quantum mechanics. We shall come back to the discussion of this dualism between the two approaches in Section 7.

Let us now consider the four LDTs using the basic solutions (34) as their TFs. These LDTs formally result in the quartet of the new exactly solvable CSLEs which have the quasi-rational functions

$${}_1{}^{\ast }\mathsf{\varphi }_{\upsilon ,0}[\mathrm{z};\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]=\frac{2}{\sqrt{|\mathsf{\kappa }\mathrm{z}+1-\mathsf{\kappa }|}}\hspace{0.17em}\hspace{0.17em}|\mathrm{z}{|}^{\mp \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\mathsf{\lambda }}_{\mathrm{o}}}|1-\mathrm{z}{|}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\mathsf{\lambda }}_{\upsilon ,0}(\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })}$$

(102)

as their solutions. An examination of these functions reveals [34] that these SLEs must have the form of Fuchsian equations with five poles (including the pole at infinity). It is crucial that the positions of the two poles outside of the interval [0, 1] are independent of the parameters specifying the JRef PF. We thus come to the following Heun equations written in the canonical form

$$\begin{array}{l}\left\{\hspace{0.17em}\frac{{\mathrm{d}}^2\hspace{0.17em}\hspace{0.17em}}{\mathrm{d}{\mathrm{z}}^2}+{}_1\mathrm{I}^{\mathrm{o}}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}}\pm 1,{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }|\pm ,\upsilon ,0]+{\mathsf{\epsilon }}_{\hspace{0.17em}1}\underrightarrow{\rho }(\mathrm{z};\mathsf{\kappa })\hspace{0.17em}\right\}\times \\ {}_1\mathsf{\Phi }[\mathrm{z};\hspace{0.17em}{\mathsf{\lambda }}_{\mathrm{o}}\pm 1,{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa };\mathsf{\epsilon }|\pm ,\upsilon ,0]=\hspace{0.17em}0,\end{array}$$

(103)

with

$$\begin{array}{l}{}_1\mathrm{I}^{\mathrm{o}}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}}\pm 1,{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }|\pm ,\upsilon ,0]={}_1\mathrm{I}^{\mathrm{o}}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}}\pm 1,{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]-\frac{3}{4{[\mathrm{z}-{\mathrm{z}}_{\mathrm{T}}(\mathsf{\kappa })]}^2}+\frac{3}{4\mathrm{z}(\mathrm{z}-1)}\\ +\frac{1\pm {\mathsf{\lambda }}_{\mathrm{o}}+(1-\mathsf{\kappa })[{\mathsf{\lambda }}_{\upsilon ,0}(\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })-2]+1}{2\mathsf{\kappa }\mathrm{z}(\mathrm{z}-1)[\mathrm{z}-{\mathrm{z}}_{\mathrm{T}}(\mathsf{\kappa })]}.\end{array}$$

(104)

Theorem 4.

The quartet of the PFs (104) can be split into two pairs such that the RefPFs in each pair represent the same HRef CSLE form-invariant under two sequential LDTs.

Proof of Theorem 4.

Let us first re-write (104) as

$$\begin{array}{l}{}_1\mathrm{I}^{\mathrm{o}}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}}\pm 1,{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }|\pm ,\upsilon ,0]={}_1\mathrm{I}^{\mathrm{o}}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}}\pm 1,{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]-\frac{3}{4{[\mathrm{z}-{\underrightarrow{\mathrm{z}}}_{\mathrm{T}}(\mathsf{\kappa })]}^2}+\frac{3}{4\mathrm{z}(\mathrm{z}-1)}\\ +\frac{\upsilon \sqrt{{\mathsf{\Delta }}_0(\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })/2}+2\mathsf{\kappa }-1}{2\mathsf{\kappa }\mathrm{z}(\mathrm{z}-1)[\mathrm{z}-{\mathrm{z}}_{\mathrm{T}}(\mathsf{\kappa })]},\end{array}$$

(105)

where

$${\mathsf{\Delta }}_0(\pm {\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })=4\hspace{0.17em}[\mathsf{\kappa }\hspace{0.17em}{({\mathsf{\lambda }}_{\mathrm{o}}\pm 1)}^2+(1-\mathsf{\kappa }\hspace{0.17em}){\mathsf{\mu }}_{\mathrm{o}}^2]$$

(106)

is the discriminant of the quadratic Equation (29) for m = 0. Setting $*{\mathsf{\lambda }}_{\mathrm{o}}:={\mathsf{\lambda }}_{\mathrm{o}}+1$ gives

$$\begin{array}{l}{}_1\mathrm{I}^{\mathrm{o}}[\mathrm{z};*{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }|+,\upsilon ,0]=\\ {}_1\mathrm{I}^{\mathrm{o}}[\mathrm{z};*{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]-\frac{3}{4{[\mathrm{z}-{\underrightarrow{\mathrm{z}}}_{\mathrm{T}}(\mathsf{\kappa })]}^2}+\frac{3}{4\mathrm{z}(\mathrm{z}-1)}+\frac{\upsilon \sqrt{\mathsf{\kappa }\hspace{0.17em}*{\mathsf{\lambda }}_{\mathrm{o}}^2+(1-\mathsf{\kappa }\hspace{0.17em}){\mathsf{\mu }}_{\mathrm{o}}^2}+2\mathsf{\kappa }-1}{2\mathsf{\kappa }\mathrm{z}(\mathrm{z}-1)[\mathrm{z}-{\mathrm{z}}_{\mathrm{T}}(\mathsf{\kappa })]}\end{array}$$

(107)

and

$${}_1\mathrm{I}^{\mathrm{o}}[\mathrm{z};*{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }|-,\upsilon ,0]={}_1\mathrm{I}^{\mathrm{o}}[\mathrm{z};*{\mathsf{\lambda }}_{\mathrm{o}}-2,{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }|+,\upsilon ,0].$$

(108)

The derived expression confirms one of the most important results of this paper: the two sequential LDTs with the TFs ${}_1{}^{\ast }\mathsf{\varphi }_{\upsilon ,0}[\mathrm{z};*{\mathsf{\lambda }}_{\mathrm{o}}-1,{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]$ and ${}_1\mathsf{\varphi }_{\upsilon ,0}[\mathrm{z};1-*{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]$ accordingly decrease by 2 the ExpDiff $*{\mathsf{\lambda }}_{\mathrm{o}}$ > 2 for the pole of the HRef CSLE at the origin while keeping two other parameters ${\mathsf{\mu }}_{\mathrm{o}}$ and $\mathsf{\kappa }$ unchanged. □

It should be stressed that Theorem 4 fails if the ExpDiff for the pole of the HRef CSLE at the origin lies between 0 and 2. We shall come back to the discussion of this issue in Section 6.

6. Breakup of SUSY Rules for Radial Potential with Centrifugal Barrier in LC Range

As pointed out at the end of Section 4, the solution (92) is not the PFS of the corresponding RCSLE (35) near the origin if ${\mathsf{\lambda }}_{\mathrm{o}}<2$. This is the direct consequence of the fact that one of the two sequential LDTs necessarily converts the given LC region of the given RCSLE into the LC region of the transformed RCSLE if both TFs are represented by non-principal solutions near the origin.

Let us start from the instance 1 < ${\mathsf{\lambda }}_{\mathrm{o}}$< 2. Under this restriction, the LDT of JRef CSLE (10) with the TF ${}_1\mathsf{\varphi }_{\upsilon ,0}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]$ places the given spectral problem into the LC region of the HRef CSLE (35) with the ExpDiff of our interest, $*{\mathsf{\lambda }}_{\mathrm{o}}={\mathsf{\lambda }}_{\mathrm{o}}-1$, lying between 0 and 1 while the second LDT with the TF ${}_1{}^{\ast }\mathsf{\varphi }_{\upsilon ,0}[\mathrm{z};2-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]$ keeps this ExpDiff within the LC region, changing its original value ${\mathsf{\lambda }}_{\mathrm{o}}$ for $2-{\mathsf{\lambda }}_{\mathrm{o}}$, with the absolute value smaller than 1. As proven in [53], the LDTs of such a kind result in the violation of the conventional rules of SUSY quantum mechanics. On the contrary, the DTs using the PFSs as their TFs always convert the LC region outside of the LC region of the transformed CSLE.

If ${\mathsf{\lambda }}_{\mathrm{o}}$ lies in the LC range of the JRef CSLE (10), i.e., if 0 < ${\mathsf{\lambda }}_{\mathrm{o}}$ < 1, then the LDT with the TF ${}_1\mathsf{\varphi }_{\upsilon ,0}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]$ keeps the ExpDiff within the LC region of the HRef CSLE, $*{\mathsf{\lambda }}_{\mathrm{o}}=1-{\mathsf{\lambda }}_{\mathrm{o}}$, while the second LDT with the TF ${}_1{}^{\ast }\mathsf{\varphi }_{\upsilon ,0}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]$ converts the latter region into the LC region of the JRef CSLE (10), bringing the ExpDiff back to its original value ${\mathsf{\lambda }}_{\mathrm{o}}$ < 1. Each LDT results in the violation of the conventional rules of SUSY quantum mechanics.

In particular, the solutions (92) at the energies $\mathsf{\epsilon }={\mathsf{\epsilon }}_{\mathrm{c}\mathrm{n}}({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })$,

$$\begin{array}{l}{}_1\cancel{\mathsf{\psi }}_{\mathbf{b},\mathrm{n}}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}}-2,{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]\propto \\ \frac{\mathrm{W}\{{}_1\mathsf{\varphi }_{+,0}[\mathrm{z};\hspace{0.17em}-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }],\hspace{0.17em}{}_1\mathsf{\varphi }_{-,0}[\mathrm{z};\hspace{0.17em}-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }],{}_1\cancel{\mathsf{\psi }}_{\mathrm{c},\mathrm{n}}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]\}}{{\hspace{0.17em}}_1\underrightarrow{\mathit{\rho }}\hspace{0.17em}[\mathrm{z};\mathsf{\kappa }]\hspace{0.17em}{}_1\mathrm{W}[\mathrm{z};\hspace{0.17em}-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]}\\ =\frac{4{\mathsf{\lambda }}_{\mathrm{o}}({\mathsf{\lambda }}_{\mathrm{o}}-1)\hspace{0.17em}}{\mathsf{\kappa }-1}{\mathrm{z}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.({\mathsf{\lambda }}_{\mathrm{o}}-2)}{(1-\mathrm{z})}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\sqrt{-{\mathsf{\epsilon }}_{\mathrm{c}\mathrm{n}}({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })}}\times \\ \mathrm{F}\left(-\mathrm{n}-1\hspace{0.17em},\mathrm{n}-{\mathsf{\lambda }}_{\mathrm{o}}-\sqrt{-{\mathsf{\epsilon }}_{\mathrm{c}\mathrm{n}}({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })};{\mathsf{\lambda }}_{\mathrm{o}}-1;\mathrm{z}\right),\\ \mathrm{for} 0<{\mathsf{\lambda }}_{\mathrm{o}}<2\end{array}$$

(109)

do not satisfy the DBCs at the origin and therefore do not represent the eigenfunctions of the prime SLE (49). The latter are given by the supplementary relation

$$\begin{array}{l}{}_1\cancel{\mathsf{\psi }}_{\mathrm{c},\mathrm{n}}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]\propto \\ \frac{\mathrm{W}\{{}_1\mathsf{\varphi }_{+,0}[\mathrm{z};\hspace{0.17em}-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }],\hspace{0.17em}{}_1\mathsf{\varphi }_{-,0}[\mathrm{z};\hspace{0.17em}-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }],{}_1\cancel{\mathsf{\psi }}_{\mathbf{b},\mathrm{n}}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]\}}{{\hspace{0.17em}}_1\underrightarrow{\mathit{\rho }}\hspace{0.17em}[\mathrm{z};\mathsf{\kappa }]\hspace{0.17em}{}_1\mathrm{W}[\mathrm{z};\hspace{0.17em}-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]}\\ \mathrm{for} 0<{\mathsf{\lambda }}_{\mathrm{o}}<2\end{array}$$

(110)

and the energy spectrum of the resultant Sturm–Liouville problem is given by a completely different formula,

$$\begin{array}{l}\hspace{0.17em}{\mathsf{\epsilon }}_{+,+,\mathrm{n}}(2-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })=-{\mathsf{\lambda }}_{+,+,\mathrm{n}}^2(2-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })\\ \mathrm{for} 0<{\mathsf{\lambda }}_{\mathrm{o}}<2 \mathrm{and} 0\le \mathrm{n}\le \lfloor ({\mathsf{\mu }}_{\mathrm{o}}+{\mathsf{\lambda }}_{\mathrm{o}}-3)/2\rfloor ,\end{array}$$

(111)

compared with the energy spectrum of the initial potential,

$${\mathsf{\epsilon }}_{+,+,\mathrm{n}}({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })=-{\mathsf{\lambda }}_{+,+,\mathrm{n}}^2({\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa })\hspace{0.17em}\hspace{0.17em}0\le \mathrm{n}\le \lfloor ({\mathsf{\mu }}_{\mathrm{o}}-{\mathsf{\lambda }}_{\mathrm{o}}-1)/2\rfloor .$$

(112)

Similar arguments explain the anomalous behavior of the HRef CSLE for 1 < $*{\mathsf{\lambda }}_{\mathrm{o}}$ < 2. In this case, the LDT with the TF ${}_1{}^{\ast }\mathsf{\varphi }_{\upsilon ,0}[\mathrm{z};*{\mathsf{\lambda }}_{\mathrm{o}}-1,{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]$ places the given spectral problem into the LC region of the JRef CSLE (10), $0<{\mathsf{\lambda }}_{\mathrm{o}}<1$, and the next LDT with the TF ${}_1\mathsf{\varphi }_{\upsilon ,0}[\mathrm{z};-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]$ keeps the CSLE within the LC region.

If $1<{\mathsf{\lambda }}_{\mathrm{o}}<2$, then the ExpDiff $*{\mathsf{\lambda }}_{\mathrm{o}}={\mathsf{\lambda }}_{\mathrm{o}}-1$ of the HRef CSLE obtained from the JRef CSLE by the LDT with the TF ${}_1\mathsf{\varphi }_{\upsilon ,0}[\mathrm{z};-{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]$ lies within its LC range: $0<*{\mathsf{\lambda }}_{\mathrm{o}}<1$. However, it remains unclear whether there exists any LDT which would place the given spectral problem into the LC region of the JRef CSLE.

7. Discussion

Before proceeding to the examination of the presented results, let us remind the reader how our advancements [53] in the singular Sturm–Liouville theory are related to the renowned recipes of SUSY quantum mechanics. First, the gauge transformation

(113)

brings us to the (self-adjoint) SLE

(114)

termed in [53] as the ‘algebraic’ Schrödinger equation. Note that both the leading coefficient function and weight for this SLE are represented by the square roots of positive rational functions, whereas the rational function

$$\mathrm{V}\hspace{0.17em}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]=-{\hspace{0.17em}}_1{\underrightarrow{\rho }}^{-1}[\mathrm{z};\mathsf{\kappa }]\hspace{0.17em}{\mathrm{I}}^{\mathrm{o}}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}}]\hspace{0.17em}-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\mathrm{Schw}\{{\hspace{0.17em}}_1{\underrightarrow{\rho }}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}[\mathrm{z};\mathsf{\kappa }]\}$$

(115)

coincides with the quantum-mechanical potential expressed in terms of the variable z, with the change in variable r[z] defined by the ODE

$$\frac{\mathrm{d}\mathrm{r}}{\mathrm{d}\mathrm{z}}=\frac{\sqrt{\mathsf{\kappa }+(1-\mathsf{\kappa })/\mathrm{z}}}{2(1-\mathrm{z})}$$

(116)

on the interval [0, 1) with the boundary condition r[0] = 0. The so-called [53] ‘Schwarzian’

$$Schw\{\mathrm{f}[\mathrm{z}]\}=\mathrm{f}[\mathrm{z}]\stackrel{••}{\mathrm{f}}[\mathrm{z}]-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{(\stackrel{•}{\mathrm{f}}[\mathrm{z}])}^2$$

(117)

turns into the conventional Schwarzian derivative [41] if we set

$$\mathrm{f}[\mathrm{z}]={\hspace{0.17em}}_1{\underrightarrow{\rho }}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}[\mathrm{z};\mathsf{\kappa }].$$

(118)

It has been shown in [33] that the Schwarzian (118) for the density function (9) has the following rational form:

$$\begin{array}{l}Schw\left\{{\hspace{0.17em}}_1{\underrightarrow{\rho }}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}(\mathrm{z};\mathsf{\kappa })\right\}=-\frac{3{(1-\mathrm{z})}^2}{2\mathrm{z}(\mathsf{\kappa }\mathrm{z}+1-\mathsf{\kappa })}-\frac{2}{\hspace{0.17em}\hspace{0.17em}\mathsf{\kappa }\mathrm{z}+1-\mathsf{\kappa }}+\frac{2\mathsf{\kappa }\hspace{0.17em}(1-\mathrm{z})}{{(\mathsf{\kappa }\mathrm{z}+1-\mathsf{\kappa })}^2}\\ -\frac{\mathsf{\kappa }\hspace{0.17em}\hspace{0.17em}{(1-\mathrm{z})}^2}{2{(\mathsf{\kappa }\mathrm{z}+1-\mathsf{\kappa })}^2}-\frac{5\mathsf{\kappa }(1-\mathsf{\kappa })\hspace{0.17em}\hspace{0.17em}{(1-\mathrm{z})}^2}{2{(\mathsf{\kappa }\mathrm{z}+1-\mathsf{\kappa })}^3}\end{array}$$

(119)

As outlined in Section 5, the LDT of the generic CSLE with a TF ${\mathsf{\varphi }}_{\tau }[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }]$ is defined by us in such a way that the DT with the TF

(120)

converts the potential (116) into the Liouville potential of the transformed CSLE:

$$\mathrm{V}\hspace{0.17em}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}};\mathsf{\kappa }|\tau ]=-{\hspace{0.17em}}_1{\underrightarrow{\rho }}^{-1}[\mathrm{z};\mathsf{\kappa }]\hspace{0.17em}{\mathrm{I}}^{\mathrm{o}}[\mathrm{z};{\mathsf{\lambda }}_{\mathrm{o}},{\mathsf{\mu }}_{\mathrm{o}}|\tau ]\hspace{0.17em}-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\mathrm{S}\mathrm{c}\mathrm{h}\mathrm{w}\{{\hspace{0.17em}}_1{\underrightarrow{\rho }}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}[\mathrm{z};\mathsf{\kappa }]\}.$$

(121)

This trivial interrelationship between the two techniques allows one to easily implement the new mathematical scheme in quantum-mechanical applications when necessary.

In this paper, we focused solely on the Liouville transformation on the finite interval (0, 1) which results in the radial Schrödinger equation. Alternatively, this transformation can be performed on the infinite interval (−∞, 0) or (1, ∞) which results in the Schrödinger equation on the line. The corresponding change in variable x[z] is obtained by integrating the ODE

$$\frac{\mathrm{d}\mathrm{x}}{\mathrm{d}\mathrm{z}}=\frac{\sqrt{|\mathsf{\kappa }+(1-\mathsf{\kappa })/\mathrm{z}|}}{2|\mathrm{z}-1|}$$

(122)

either from −∞ to 0 or from 1 to ∞. It directly follows from the arguments presented in Section 3 that the resultant Liouville potentials on the line must be double-step shape-invariant.

Note that the reciprocal transformation

$$\underset{˜}{\mathrm{z}}(\mathrm{x})={\mathrm{z}}^{-1}(\mathrm{x})$$

(123)

satisfies the ODE

$$\frac{\mathrm{d}\mathrm{x}}{\mathrm{d}\underset{˜}{\mathrm{z}}}=-\frac{1}{{\mathrm{z}}^2}\frac{\mathrm{d}\mathrm{x}}{\mathrm{d}\mathrm{z}}=\frac{\sqrt{\mathsf{\kappa }+(1-\mathsf{\kappa })\underset{˜}{\mathrm{z}}}}{2\underset{˜}{\mathrm{z}}(1-\underset{˜}{\mathrm{z}})} (0<\underset{˜}{\mathrm{z}}<1)$$

(124)

associated with the LTP density function

$${\hspace{0.17em}}_1\underset{˜}{\rho }(\underset{˜}{\mathrm{z}};\mathsf{\kappa })=\frac{\mathsf{\kappa }+(1-\mathsf{\kappa })\underset{˜}{\mathrm{z}}}{4{\underset{˜}{\mathrm{z}}}^2{(1-\underset{˜}{\mathrm{z}})}^2}>0 (0<\underset{˜}{\mathrm{z}}<1)$$

(125)

if $\hspace{0.17em}0<\mathsf{\kappa }<1$. It can be easily verified that one comes to a similar LTP density function

$${\hspace{0.17em}}_1\underset{˜}{\rho }(\underset{˜}{\mathrm{z}};\mathsf{\kappa })=\frac{1-\mathsf{\kappa }-\underset{˜}{\mathrm{z}}}{4{\underset{˜}{\mathrm{z}}}^2{(1-\underset{˜}{\mathrm{z}})}^2}>0 (0<\underset{˜}{\mathrm{z}}<1)$$

(126)

by using the variable

$$\underset{˜}{\mathrm{z}}(\mathrm{x})=\frac{\mathrm{z}(\mathrm{x})}{\mathrm{z}(\mathrm{x})-1}$$

(127)

if $\mathsf{\kappa }<0$. We infer that the LTP potential on the line [13] must be also double-step shape-invariant regardless of the position of the zero of the first-degree polynomial in the numerator of the density function (126) or (127).

The very important element of our approach is the concept of the ‘prime’ SLE chosen in such a way that the two ChExps for the poles at the endpoints differ only by sign. As a result, the energy spectrum of the given Sturm–Liouville problem can be obtained by solving the prime SLE under the DBCs. This in turn allows one to take advantage of the rigorous theorems proven in [55] for eigenfunctions of the generic SLE solved under the DBCs.

It has been explicitly demonstrated that the JRef CSLE in the particular case of the density function with the simple pole at the origin has two pairs of quasi-rational solutions such that their analytical continuations do not have zeros at any regular point of the complex plane. It is essential that the absolute values of ChExps for the pole at the origin coincide for all four ‘basic’ solutions which can be thereby grouped into the pairs via the requirement that the paired solutions share the same characteristic exponent for the mentioned singular endpoint. Each pair of the basic solutions was then used as seed functions for the second-order DCT on the positive semi-axis. It is proven that both transformations simply shift by 2 the ExpDiff for the pole of the CSLE at the origin while keeping two other parameters unchanged.

In Section 5, we decomposed the second-order DCT into two sequential DTs. The two separate Liouville transformations on the finite interval (0, 1) and on the infinite interval (1, inf) then result in the supplementary pair of double-step shape-invariant potentials defined on the positive semi-axis and on the real axis, respectively, and solvable by polynomial solutions of the Heun equation.

In theory, the quantization can be also performed on the infinite interval (−∞, ${\mathrm{z}}_{\mathrm{T}}$) and on the finite interval [${\mathrm{z}}_{\mathrm{T}}$, 0). In this sense, the classification of the Lemieux–Bose potentials suggested in [37] is inconclusive. It is not sufficient to simply specify the order of the TP zeros—one must also indicate which poles are selected as the endpoints for the quantization interval.

In this paper, we focused mostly on the HRef CSLEs associated with the ‘radial’ CGK potential and its ‘surviving’ SUSY sibling exactly solvable by polynomial solutions of the Heun equation. (Remember that CGK potential [2] generally has the three SUSY siblings [3,4,5], but the two pairs of these sibling potentials merge into the pair of the double-step shape-invariant potentials in the limiting case of the TP vanishing at the origin.) One can extend the arguments presented in Section 5 to prove the double-step shape invariance of the CGK potential in the LTP limit and its (‘surviving’) shape-invariant SUSY sibling also exactly solvable by polynomial solutions of the Heun equation (regardless of the position of the TP zero outside the interval [0, 1]).

Our analysis [53] of the solutions of two prime SLEs related by an LDT allowed the author to conclude that conventional rules of SUSY quantum mechanics fail in the LC regions of the corresponding Liouville potentials iff the DLT in question converts one region into the other (see [8,54] for some examples). In particular, this happens if the ExpDiff for the poles of the JRef CSLE (10) or the two HRef CSLEs (35) at the common singular endpoint z = 0 is smaller than 2 and, as a result, at least one of the sequential LDTs turns the centrifugal barrier of the radial rational potential into the infinitely deep well. If the second DT turns the well back into the centrifugal barrier, then the barrier height is necessarily within the LC range.

8. Conclusions

As stressed at the end of Section 3, the major results of this study are based on Theorem 2 asserting that the two second-order DCTs under consideration preserve the form of the CSLE, only changing the ExpDiff for its pole at the origin (putting aside the anomalous case mentioned in the theorem). It is essential that the derivation of the core Formula (48) was performed using only logarithmic derivatives of the rational density function (9), not the derivative of its square root as in [33]. As a result, the theorem is automatically applied to all three quantization intervals (−∞, 0), (0, 1), and (1, $\infty$). The Liouville transformations performed on these intervals then lead to the three different quantum-mechanical potentials shape-invariant under the DCTs in question.

As the direct corollary of Theorem 2, we conclude that the mentioned second-order DCTs generate the first-order differential expressions in the space of hypergeometric functions after the CWs [49] are replaced by the KDs [51]. Using the conventional contiguous relations for hypergeometric series, we explicitly confirmed the predicted differential equations for the PFSs near the origin.

The mentioned anomalous case presents a remarkable example of the breakup of the conventional rules of SUSY quantum mechanics for DCTs between the LP and LC regions. The source of this anomaly was explained by decomposing the corresponding second-order DCT into the two sequential LDTs and demonstrating that the first LDT places the ExpDiff into the LC range while the second LDT keeps its value within the same range. As it has been proven in [53], the LDT keeping the given spectral problem within the LC region necessarily violates the conventional SUSY rules.

This paper also has much more general implications than the brief outline of its results presented above. It presents a very specific illustration of the recently advanced SUSY theory of the so-called [4] ‘Gauss-reference’ (GRef) potentials representing the Liouville potentials for either two Fuchsian RCSLEs with three second-order poles (including infinity) or the confluent RCSLE with a single pole in the finite plane (commonly placed at the origin). We refer to these three Liouville potentials [1,43] as ‘Jacobi-reference’ (JRef), ‘Routh-reference’ (RRef) and ‘Laguerre-reference’ (LRef) CSLE, where the terms ‘JRef’ and ‘LRef’ have a slightly different meaning compared with their simplistic definition in the Introduction. Namely, we refer to the RCSLE as ‘JRef’, ‘RRef’ or ‘LRef’ if it has q-RSs composed of (‘generalized’ [58]) Jacobi, Routh [59,60,61,62], or (‘generalized’ [63]) Laguerre polynomials. The difference between the two definitions comes from the fact that the RRef CSLE is quantized in terms of finite orthogonal sequences of Romanovski/pseudo-Jacobi [64,65,66] polynomials (‘Romanovski–Routh’ [60,61,62] polynomials in our terms), while the eigenfunctions of the JRef and LRef CSLEs are composed of infinite sequences of classical Jacobi and classical Laguerre polynomials (with the polynomial indices generally dependent on the polynomial degrees in all the three cases).

From our perspective, the concept of the LDTs advanced in [4,53,61,62] provides the rigorous mathematical grounds for SUSY quantum mechanics of the rational potentials under consideration. In [39], we showed that the GRef Liouville potentials are shape-invariant in Gendenshtein’s sense [6] iff the corresponding RCSLEs preserve their form under the LDTs using the basic solutions as the TFs. In this paper, we extend the concept of form-invariant RCSLEs to the JRef CSLE (10) with the density function (9). As mentioned in the previous section, the Liouville transformation can be independently performed on the three distinguished quantization intervals (0, 1), (−∞, 0), and (1, $\infty )$, which brings us to the three Liouville potentials: the radial potential discussed here and two branches of the LTP potential on the line which turned out to be shape-invariant under the action of the second-order DCTs using the pairs of the basic solutions as the seed functions. The only effect of these DCTs on the CSLE under consideration is that they shift by 2 the translational shape-invariance parameter represented by the ExpDiff for the pole of the CSLE at the origin.

As discussed in [4,53], a similar technique can be advanced for the rational SUSY partners of the LRef potentials [1,67]. By analogy with the three families of the HRef potentials mentioned in the Introduction, there are three families of their confluent counter-parts (c-HRef potentials) obtained by the ‘basic’ LDTs of the three LRef potentials:

(i)

Radial LRef potential [28,29,54,68];

(ii)

Confluent LTP potential with the parabolic barrier at infinity [67];

(iii)

DRtTP LRef potential on the line [69] transformable to its rational form by the Lambert W-function [70].

Again, we selected the latter potentials via the requirement that the corresponding TP has a single zero outside the interval [0, 1]. Each family of the c-HRef potentials constructed in such a way represents conditionally exactly solvable reductions of the confluent Lemieux–Bose potentials [38,71,72] with the eigenfunctions expressible in terms of the polynomial solutions of the confluent Heun equation.

By analogy with the two double-step form-invariant JRef potentials discussed here, we expect that both the radial LRef potential and parabolic-barrier potential well are double-step shape-invariant under two sequential LDTs with the ‘basic’ TFs (i.e., with no zeros at the regular points after being analytically continued into the complex plane).

One of our top priorities will be to re-examine the latest study by Lévai [73] on the solvable-by-polynomials potentials of the confluent Heun class [25], keeping in mind the progress achieved in our recent studies [4,53,54,67,74] not mentioned in the paper.

We hope that the presented sketch of possible extensions of our analysis of the exactly solvable Fuchsian SLEs to their confluent counterparts helps the reader to realize the full might and comprehensiveness of our approach to the SUSY theory of rational potentials.