Numerical Simulation of Flows Using the Fourier Pseudospectral Method and the Immersed Boundary Method

Abstract

The present work proposes the application of a computational methodology based on the coupling of the Fourier Pseudospectral Method (FPSM) and the Immersed Boundary Method (IBM) for conducting flow simulations over slender airfoils. This methodology, termed IMERSPEC, leverages the benefits of both high accuracy and low computational cost inherent in pseudospectral methods, thanks to the utilization of the Fast Fourier Transform algorithm. IBM is employed to impose non-periodic boundary conditions in the Navier–Stokes equations, addressing the requirement of periodicity at boundaries for FPSM convergence and to accurately represent the immersed slender airfoil in the flow. The aerodynamic behavior of the analyzed profiles was assessed by calculating lift and drag coefficients, which were then compared with existing literature results. Consistently favorable outcomes were observed, particularly in flows at lower Reynolds numbers, demonstrating the effectiveness of the IMERSPEC methodology for simulating complex flows computationally. Additionally, weight functions, fundamental to IBM, are employed flexibly for aerodynamic force calculations. Specifically, within the same simulation, a Cubic function is utilized for drag calculation while a Hat function is employed for lift calculation, yielding results more closely aligned with the literature’s findings. This approach offers an alternative to previously proposed methods for IBM implementation.

1. Introduction

The continuity and Navier–Stokes equations form a system of second-order nonlinear partial differential equations (PDEs) used to describe fluid motion. These equations, grounded in the principles of mass balance and linear momentum, mathematically capture the dynamic behavior of viscous fluids. Despite their formulation in the 19th century, the Navier–Stokes equations remain a formidable mathematical challenge. Analytical solutions often rely on simplifications that limit their applicability to idealized scenarios and specific flow problems. As a result, numerical methodologies are essential for obtaining more realistic results. By solving the comprehensive differential mathematical model developed at the continuum level within a discrete domain, these methodologies provide a means to tackle the complexity of real-world fluid dynamics. Transforming the PDEs into systems of algebraic equations allows for the generation of coherent approximate solutions, facilitating the analysis and comprehension of a broad range of complex flow phenomena encountered in practical applications.

The development and application of numerical and computational methods for solving the Navier–Stokes equations are of great interest to researchers in Computational Fluid Dynamics (CFD). CFD finds widespread use across various fields and applications, including aerodynamics, weather forecasting, heat and mass transfer analysis, chemical engineering processes, metallurgical processes, refrigeration and air conditioning system design, and turbomachinery design [1]. Additionally, CFD is employed in verifying aerodynamic forces on buildings [2], analyzing fluid–structure interactions [3], studying the aerodynamics of land, aquatic, and aerial vehicles [4,5], and determining hydrodynamic forces on submerged structures [6], among other applications.

The primary focus of this study is the flow over airfoils, a critical aspect of aircraft aerodynamic performance and the design of turbomachinery, including hydraulic turbines, wind turbines, and fans. Understanding the flow around a blade typically starts with investigating two-dimensional flow over the airfoil, which represents the cross-sectional shape of the blade.

Existing studies in the literature provide valuable insights into the complexity of such flows and serve as essential resources for validating computational models. Menon and Mittal (2019) [7] investigated the aerodynamic performance of three airfoils—NACA 0012, NACA 0015, and NACA 4415—at Reynolds numbers (Re) of 500, 1000, and 2000, with angles of attack ($\alpha$) ranging from 0° to 50° Despite the low Re and the laminar flow characteristics, the authors observed significant complexities, including the generation of Karman vortex shedding and the shedding of Leading-Edge Vortex (LEV).

Aerodynamic forces acting on wings operating at very low Reynolds numbers, below ${10}^4$, are of interest for small remotely piloted vehicles at high altitudes and the development of small-scale wind turbines [8], which have spurred advancements in Micro Aerial Vehicles (MAVs). In a doctoral thesis, Ref. [9] examined different aerodynamic profiles at ultralow Reynolds numbers for subsequent application in micro-rotor design. Ref. [10] conducted numerical analyses of incompressible flows over airfoils at Reynolds numbers ranging from 400 to 6000. They employed a pseudotime integration method and adopted artificial compressibility to solve the Navier–Stokes equations, comparing their findings with data from [9] to validate the proposed methodology.

In their work, Ref. [11] discuss the flow dynamics over helicopters, emphasizing the significant impact of wingtip vortices generated by the rotor on aerodynamic load. These vortices travel numerous revolutions before reaching the body, underscoring the necessity of accurately resolving them over a considerable distance to determine aerodynamic forces. In vortex-dominated flows, high-order convergence methods are indispensable. First- and second-order methodologies tend to dissipate the unstable flow structures crucial for the aerodynamic performance of flying vehicles. While high-accuracy solutions yield precise results, they often entail a significant computational cost.

Classical high-order methodologies, such as high-order finite differences, finite volumes, and compact schemes, are known to be computationally expensive [12,13], primarily due to the necessity of solving large and numerous linear systems.

Among high-order methodologies, the Fourier Pseudospectral Method (FPM) presents all the intrinsic advantages of this class of methods, while concurrently having lower computational cost compared to others. The low computational cost is associated with the use of the Fast Fourier Transform (FFT) [14], an algorithm that efficiently calculates the derivatives required for solving the PDEs, reducing the computational cost from $O\left(N^2\right)$ operations of traditional high-order methodologies to $O\left(Nlo{g}_{2}N\right)$ [15], where N is the number of mesh nodes. Additionally, by utilizing the Navier–Stokes equations to model incompressible flows in spectral space, it is possible to employ a pressure gradient term projection method [16], which eliminates the need to solve the Poisson equation, necessary for coupling pressure and velocity, thereby saving significant processing time. The method allows for the decoupling of the pressure field from the Navier–Stokes equations and its subsequent retrieval for post-processing.

The primary limitation of the FPM, however, lies in the boundary conditions [17], as to maintain convergence order coupled with low computational cost, only periodic boundary conditions are permitted. This restriction limits the use of the technique to very specific flows, such as simulations of homogeneous and isotropic turbulence and temporally developing jets [18]. Nevertheless, the pseudospectral methodology’s applicability has been expanded to other CFD problems by coupling it with the Immersed Boundary Method (IBM) [15,19].

The Immersed Boundary Method (IBM) was developed to handle complex, movable, and deformable geometries by introducing a source term for force in the governing equations. This method involves creating two distinct Cartesian grids: the Lagrangian mesh, representing the boundary of the body immersed in the flow, and the Eulerian mesh, where the equations governing fluid flow are solved [20]. The integration of the FPM and IBM resulted in the hybrid methodology known as IMERSPEC [3,15]. With IMERSPEC, the Navier–Stokes equations are solved using the Fourier pseudospectral method, while physical boundary conditions are imposed through the source term of the immersed boundary. This approach enables the solution of non-periodic problems with high accuracy and computational efficiency.

The present study employs the IMERSPEC methodology to simulate flows around airfoils, particularly focusing on low Reynolds numbers ($Re\le {10}^4$). It investigates flow phenomena over different thin airfoil geometries, including both symmetric (NACA 0008) and asymmetric (NACA 4404) profiles. The numerical study involves two-dimensional, transient, and incompressible flows around these aerodynamic profiles, aiming to validate the applicability of the IMERSPEC methodology. The analysis assesses the influence of curvature and thickness of NACA airfoils on the flow and determines aerodynamic coefficients. Convergence between the obtained results and those available in the literature is verified, with a specific focus on analyzing the influence of simulation parameters within the IMERSPEC methodology to adjust the model for improved accuracy.

In addition, an alternative approach for calculating aerodynamic forces is introduced. This approach utilizes weight functions, fundamental in the Immersed Boundary Method (IBM) algorithm, in a novel manner for the calculation of aerodynamic forces. Specifically, in the same simulation, both the Cubic function for drag calculation and the Hat function for lift calculation are employed. This adjustment leads to results that closely align with those presented in the literature, showcasing a different alternative from existing methods for IBM usage.

2. Numerical Methods

In this study, we utilize the IMERSPEC methodology, implemented in the Fortran 90 programming language, which results from the fusion of the Fourier Pseudospectral Method and the Immersed Boundary Method [15]. To achieve this integration, the Navier–Stokes equations are solved with the imposition of a source term derived from the IBM. This source term creates a force field essential for simulating immersed bodies within the fluid.

2.1. Immersed Boundary Method

The Immersed Boundary Method operates simultaneously within two distinct and independent computational domains: the Eulerian domain ($\Omega$), which is Cartesian and stationary, where the equations are solved, and the Lagrangian domain ($\Gamma$), which characterizes the geometry of the solid interface representing the boundary between the fluid and the immersed body. Figure 1 illustrates the depiction of the NACA 0008 airfoil, considering the two grids utilized by the IBM.

The fluid equations are solved throughout the entire Eulerian domain ($\Omega$), including the region delimited by the Lagrangian interface ($\Gamma$). To account for the presence of the immersed body within the fluid, a source term of force is incorporated into the Navier–Stokes equations. This addition simulates the influence of the body at specific points within the domain, enabling the fluid to interact with the immersed geometry and trace a path consistent with physical expectations.

The mathematical model for incompressible flow of Newtonian fluids with constant physical properties is established by the Navier–Stokes equations (Equation (1)), which express the principle of momentum conservation (Newton’s second law), and by the continuity equation (Equation (2)), which ensures mass balance in the domain.

$$\frac{\partial u_i}{\partial t}+\frac{\partial {(u}_i{u}_j)}{\partial x_j}=-\frac{\partial p}{\partial x_i}+\nu \frac{{\partial }^2{u}_i}{\partial x_j\partial x_j}+f_i$$

(1)

$$\frac{\partial u_j}{\partial x_j}=0$$

(2)

where $\frac{\partial p}{\partial x_i}=\frac{1}{\rho }\frac{\partial p^{*}}{\partial x_i}$, with $p^{*}$ representing the static pressure in [N.${\mathrm{m}}^{-2}$]. Here, $u_i$ denotes the velocity component in [m.${\mathrm{s}}^{-1}$] along direction $i=1,2$, while $\rho$ and $\nu$ stand for the mass density in [kg.${\mathrm{m}}^{-3}$] and the kinematic viscosity of the fluid in [${\mathrm{m}}^2$.${\mathrm{s}}^{-1}$], respectively. The variable $f_i=\frac{f_{i*}}{\rho }$, where $f_{i*}$ represents the source term in [${\mathrm{N.m}}^{-3}$]. In this context, this term originates from the Immersed Boundary Method and serves to represent the immersed body within the fluid.

The Lagrangian domain represents the immersed interface in the flow. Being independent of the Eulerian domain, the Lagrangian mesh enables the simulation of flows over complex geometries using a Cartesian domain, eliminating the need for remeshing, even in the case of moving geometries, as only the Lagrangian interface will move [3]. The fundamental characteristic of always working with a fixed Cartesian domain, even for flows over complex, deformable, or moving geometries, is the main reason why researchers opt for the IBM.

Eulerian–Lagrangian Coupling

The communication between the two domains, Lagrangian and Eulerian, is performed considering the Navier–Stokes equations, valid in the domain $\Omega$, as shown in Figure 2. The force source term is computed by a discontinuous function, which can take nonzero values in cases where there is coincidence between Eulerian and Lagrangian nodes, or zero otherwise, as shown in Equation (3), where $f_i\left(\overrightarrow{x,}t\right)$ is the Lagrangian force defined in the domain $\Gamma$.

$$f_i\left(\overrightarrow{x},t\right)=\left\{\begin{array}{ccc}{F}_i\left(\overrightarrow{X},t\right)& \hspace{1em}if& \overrightarrow{x}=\overrightarrow{X}\\ 0& if& \overrightarrow{x}\ne \overrightarrow{X}\end{array}\right.$$

(3)

Ensuring coincidence between points in the domains is particularly challenging for complex geometries. Hence, the Lagrangian force field is computed in a region near the solid interface by interpolating and distributing it over its neighborhood, utilizing a force distribution function, $D_h\left(\overrightarrow{x}-\overrightarrow{X}\right)$, proposed by [20]. This function is described in Equations (4)–(6). Consequently, the Eulerian force field virtually models the presence of a body.

$$f_i\left(\overrightarrow{x}\right)=\sum _{\Gamma }{D}_h\left(\overrightarrow{x}-\overrightarrow{X}\right)F_i\left(\overrightarrow{x}\right)\Delta s^2$$

(4)

$$D_h\left(\overrightarrow{x}-\overrightarrow{X}\right)=\frac{1}{h^2}{W}_g\left(r_x\right)W_g\left(r_y\right)$$

(5)

$$W_g\left(r\right)=\left\{\begin{array}{ccc}\frac{3-2\left|r\right|+\sqrt{1+4\left|r\right|-4{\left|r\right|}^2}}{8}& \hspace{1em}if& 0<\left|r\right|\le 1\\ \frac{5-2\left|r\right|+\sqrt{-7+12\left|r\right|-4{\left|r\right|}^2}}{8}& if& 1<\left|r\right|\le 2\\ 0& if& 2<\left|r\right|\end{array}\right.$$

(6)

where $f_i(\overrightarrow{x},t)$ represents the Eulerian force field, and $F_i(\overrightarrow{x},t)$ denotes the Lagrangian force field. Here, $r_x=\frac{x-X}{h}$ and $r_y=\frac{y-Y}{h}$. The function $W_g$ resembles a Gaussian shape and maintains the property of unit integral over the interval $\left[-\infty ,\infty \right]$.

Other authors have proposed alternative mathematical formulations for the force distribution function, diverging from the Gaussian function introduced by [20]. These formulations differ primarily in their choice of weight function, denoted as $W\left(r\right)$. The Cubic function, $W_c$ (Equation (7)), was proposed by [21], while the Hat function, $W_h$ (Equation (8)), akin to bilinear interpolation, was introduced by [22].

$$W_c\left(r\right)=\left\{\begin{array}{ccc}1-\frac{1}{2}\left|r\right|-{\left|r\right|}^2+\frac{1}{2}{\left|r\right|}^3& \hspace{1em}if& 0<\left|r\right|\le 1\\ 1+\frac{11}{6}\left|r\right|+{\left|r\right|}^2-\frac{1}{6}{\left|r\right|}^3& if& 1<\left|r\right|\le 2\\ 0& if& 2<\left|r\right|\end{array}\right.$$

(7)

$$W_h\left(r\right)=\left\{\begin{array}{ccc}1-\left|r\right|& \hspace{1em}if& 0<\left|r\right|\le 1\\ 0& if& 1<\left|r\right|\end{array}\right.$$

(8)

Not all weight functions available in the literature satisfy the necessary mathematical properties of distribution functions. However, even those that do not satisfy them can produce superior results compared to some that meet all properties [15]. The weight function, $W\left(r\right)$, is fundamental for the accuracy and numerical convergence order of the methodology.

Given the no-slip condition, it is expected that the velocity of fluid particles is equal to the velocity of the boundary. However, due to the spatial discretization of the IBM methodology and the application of distribution and interpolation functions, errors may arise that compromise the accuracy of this condition. The studies of [23] propose an improvement of the calculation through an iterative method applied to the corrected Eulerian velocity field, the Multi-Direct Forcing (MDF) model adopted in the present work.

The immersed boundary method based on MDF requires a mathematical model for calculating the Lagrangian force. Starting from Equation (1), the Eulerian force field $f_i$ is isolated, as shown in Equation (9), and developed under the assumption of continuity. Given that the Lagrangian domain ($\Gamma$) is contained within the Eulerian domain ($\Omega$), the Lagrangian force $F_i(\overrightarrow{X},t)$ can be defined through Equation (10). Here, lowercase primitive variables denote points in the domain $\Omega$, while uppercase primitive variables represent points in the domain $\Gamma$.

$$f_i\left(\overrightarrow{x},t\right)=\frac{\partial u_i}{\partial t}+\frac{\partial {(u}_i{u}_j)}{\partial x_j}+\frac{\partial p}{\partial x_i}-\nu \frac{{\partial }^2{u}_i}{\partial x_j\partial x_j}$$

(9)

$$F_i\left(\overrightarrow{X},t\right)=\frac{\partial U_i}{\partial t}+\frac{\partial {(U}_i{U}_j)}{\partial X_j}+\frac{\partial P}{\partial X_i}-\nu \frac{{\partial }^2{U}_i}{\partial X_j\partial x{X}_j}$$

(10)

Initially, the application of the MDF method consists of adding and subtracting a temporary parameter ${U_i}^{*}$ in the discretized temporal derivative of Equation (10), as shown in Equation (11). In Equation (11), the temporal derivative was discretized using the explicit Euler scheme. However, this choice was merely explanatory and didactic for better understanding of the modeling. The temporal discretization in the present work was performed using the fourth-order Runge–Kutta method with six steps (RK46), as presented in the work of [24].

$$F_i(\overrightarrow{X},t)=\frac{U_i^{(t+\Delta t)}-U_i^{*}+U_i^{*}-U_i^t}{\Delta t}+{\mathrm{RHS}}_i^t$$

(11)

where $U_i^{(t+\Delta t)}$ is the velocity of a Lagrangian point at the subsequent time step, $U_i^t$ is the velocity of a Lagrangian point at the current time step, $\Delta t$ is the time step, and RHS is the sum of the remaining terms of Equation (10).

Based on the addition and subtraction of $U_i^{*}$, Equation (11) can be subdivided into:

$$\frac{U_i^{*}-U_i^t}{\Delta t}+{\mathrm{RHS}}_i^t=0$$

(12)

$$F_i(\overrightarrow{X},t)=\frac{U_i^{(t+\Delta t)}-U_i^t}{\Delta t}$$

(13)

Equation (12) can be defined in both the domain $\Gamma$ and the domain $\Omega$, as shown in Equation (14).

$$\frac{u_i^{*}-u_i^t}{\Delta t}+{\mathrm{rhs}}_i^t=0$$

(14)

where $u_i^{*}$ is the temporary parameter in the Eulerian domain, understood as the estimate of the Eulerian velocity field at the subsequent time step, without taking into account the imposition of boundary conditions inserted by the source term of $f_i$.

The calculation of $F_i(\overrightarrow{X},t)$ requires the determination of the temporary parameter $U_i^{*}$. For this, the interpolation process is employed. By Equation (15), the information from the Eulerian domain $u_i^{*}$ is transferred to the Lagrangian domain. In this process, similar to distribution, the information from the Eulerian field is transmitted to the nearest neighboring Lagrangian points, with a weighting according to the distance between these points. This implies that Lagrangian points close to Eulerian points have a greater contribution from the Eulerian information, while those farther away have a smaller contribution.

$$U_i^{*}=\sum _{\Omega }{u}_i^{*}{D}_h(\overrightarrow{x}-\overrightarrow{X})h^2$$

(15)

With the temporary parameter $U_i^{*}$, we can determine $F_i(\overrightarrow{X_i},t)$ using Equation (13). Here, the term $U_i^{t+\Delta t}$ represents the desired velocity at the immersed interface, denoted as ${U_i}^{IM}$. Thus,

$$F_i(\overrightarrow{X},t)=\frac{U_i^{\mathrm{IM}}-U_i^t}{\Delta t}$$

(16)

For flows over stationary airfoils, $U_i^{IM}=0$. After defining the Lagrangian source term, $F(\overrightarrow{X},t)$, this information is transmitted to the Eulerian domain according to Equation (3). Subsequently, it is used to determine $u^{t+\Delta t}$ through Equation (17), which is applied in $\Omega$ under the continuum assumption.

$$u_i^{(t+\Delta t)}=u_i^{*}+\Delta t{f}_i$$

(17)

The MDF improves the accuracy of velocity and Eulerian force field calculation, approximating, at each iteration, the fluid velocity over the immersed boundary to the velocity the boundary would theoretically have. A condition for the MDF iteration process is adopted, based on considering the maximum difference of Eulerian forces between consecutive iterations, as presented in Equation (18).

$$max|f_i^{it+1}-f_i^{it}|\le \epsilon$$

(18)

where $\epsilon$ is a tolerance value for the maximum difference, which tends to zero and determines the termination of the iterations. With this condition, the computational effort is reduced, since more iterations are performed only in the transient phase of the flow.

In this study, the calculation of the Lagrangian force in the x direction utilizes the Cubic function, whereas the Hat function is employed for the y direction. The results obtained through this hybrid approach exhibit greater physical consistency compared to using the same function for both directions in simulations of airflow over airfoils.

2.2. Fourier Pseudospectral Method

The Fourier transform aims to convert a function defined in the time or spatial domain into the frequency domain, also known as the spectral domain. Transforming the Navier–Stokes and continuity equations (Equations (1) and (2)) from physical space to spectral space is particularly interesting, because such expressions, when analyzed in the spectral domain, do not depend on the pressure field [17]. This characteristic simplifies the analysis compared to other numerical methods that necessitate pressure–velocity coupling [15].

Transforming the Navier–Stokes Equations into the Fourier Pseudospectral Space

Transforming the continuity equation, Equation (2), into the spectral domain and applying the properties of the Fourier transform yields Equation (19).

$${\mathrm{ik}}_i{\widehat{u}}_i=0$$

(19)

When the dot product between two vectors is zero, they must be orthogonal. Therefore, observing Equation (19), it is concluded that the wave number vector ($k_i$) is orthogonal to the transformed velocity (${\widehat{u}}_i$). Thus, a plane perpendicular to the wave number vector, $\pi$-plane, is defined, which will contain the transformed velocity vector $\widehat{u_i}(\overrightarrow{k},t)$ [25].

Transforming Equation (1) into Fourier space, with the necessary manipulations required by the properties of Fourier transforms, yields Equation (20):

$$\frac{\partial u_i}{\partial t}+\frac{\partial \left(u_i{u}_j\right)}{\partial x_j}=-i{k}_i\widehat{p}-v{k}^2{u}_i+{\widehat{f}}_i$$

(20)

where $k^2$ is the squared norm of the wave number vector, that is, $k^2=k_j{k}_j$.

Since pressure is a scalar function, the pressure gradient is collinear with the wave number vector, and therefore perpendicular to the $\pi$-plane. The vector representing the pressure gradient disappears when projected. This procedure decouples the pressure field from the incompressible Navier–Stokes equations.

The nonlinear term in Equation (20) results in a convolution integral, as shown in Equation (21).

$$\left(u_i{u}_j\right)\left(\overrightarrow{k}\right)=\int u_i\left(\overrightarrow{r}\right)u_j(\overrightarrow{k}-\overrightarrow{r})d\overrightarrow{r}$$

(21)

The presence of this integral would strictly require the use of some numerical integration methodology, a computationally intensive procedure. If performed, the computational gain obtained by the projection operation would likely be lost. The convolution integral here is replaced by the pseudospectral method, which is more computationally feasible [15].

With the terms defined in the previous equations, we apply the projection method, starting from Equation (21). The sum of the viscous term with the transient term belongs to the $\pi$-plane; therefore, the addition of the pressure gradient to the nonlinear term and the source term should also belong to this plane. Since the sum of two collinear vectors is zero, the sum of all four terms should also be zero, as evidenced in Equation (22).

$${\left[\frac{\partial u_i}{{\partial }_t}+{\mathrm{vk}}^2{u}_i\right]}_{\in \pi }+{\left[\frac{\partial u_i{u}_j}{\partial x_j}+{\mathrm{ik}}_i\widehat{p}+{\widehat{f}}_i\right]}_{\in \pi }=0$$

(22)

The position of the transformed nonlinear term in relation to the $\pi$-plane is indeterminate. Therefore, we employ a projection tensor $\overline{\overline{p}}$, which can project any vector onto the $\pi$-plane [25]. Since the term ${\mathrm{ik}}_l\widehat{p}$ is orthogonal to the plane $\pi$, it is essential that its sum with the nonlinear term also lies within this plane, leading to:

$${\left[\frac{\partial u_i{u}_j}{\partial x_j}+{\mathrm{ik}}_i\widehat{p}\right]}_{\in \pi }={\overline{\overline{p}}}_{lm}\left[\frac{\partial u_m{u}_j}{\partial x_j}+{\widehat{f}}_i\right]$$

(23)

From Equation (23), it is evident that the sum of the transformed vectors of the pressure gradient, the nonlinear term, and the transformed source term is the projection of the transformed nonlinear and source terms onto the $\pi$-plane. Finally, the Navier–Stokes equations in the Fourier space for incompressible flows become Equation (24):

$$\frac{\partial u_i\left(\overrightarrow{k}\right)}{{\partial }_t}+v{k}^2{u}_i\left(\overrightarrow{k}\right)=-i{k}_j{\overline{\overline{p}}}_{lm}\int u_m\left(\overrightarrow{r}\right)u_j(\overrightarrow{k}-\overrightarrow{r})d\overrightarrow{r}+{\widehat{f}}_i$$

(24)

Despite the absence of the pressure field in the Navier–Stokes equations, it can be retrieved for post-processing, as demonstrated in [15].

3. Results

The relative motion between a flowing fluid and an immersed object generates a specific resultant force. This is characterized by exerting pressures in the normal direction of the body, as well as tangential shear stresses due to the viscous effect of the boundary layer. As shown in Figure 3, the resultant force ($F_R$) can be decomposed into four components: the normal ($F_N$), the axial ($F_A$), the drag ($F_D$), and the lift ($F_L$) forces. The normal and the axial forces represent the components of $F_R$ in the normal and axial directions, respectively, while the drag and the lift forces are relative to the undisturbed velocity (V).

Figure 4 illustrates an airfoil with an infinitely long surface area, where $dS=ds\times 1$. In the figure, $S_e$ and $S_i$ represent the distances from the leading edge to the arbitrary points $O_e$ and $O_i$, respectively, measured along the surface of the upper and lower sides of the profile. $\overline{P_e}\left(s_e\right),\overline{{\tau }_e}\left(s_e\right),\overline{P_i}\left(s_i\right)$, and $\overline{{\tau }_i}\left(s_i\right)$ define the static pressures and shear stresses on the upper and lower surfaces. The static pressures are normal to the airfoil surface and inclined at an angle $\theta$ with respect to the y-axis, while the shear stresses are tangential to the surface and inclined at an angle $\theta$ with respect to the x-axis.

The drag coefficient, $C_d$, and the lift coefficient, $C_l$, as defined by [26], represent the ratio of the drag force (for $C_d$) or the lift force (for $C_l$) to the force that would be generated by bringing the fluid approaching directly from the wing’s surface area to a state of rest. Mathematically, this can be expressed as follows:

$$C_d=\frac{F_D}{\frac{1}{2}\rho A{V}^2}$$

(25)

$$C_l=\frac{F_L}{\frac{1}{2}\rho A{V}^2}$$

(26)

The lift force ($F_L$) and drag force ($F_D$) are derived from the iterative process of the MDF. In these equations, $\rho$ represents the fluid density, and A denotes the airfoil’s area as viewed from above. For the two-dimensional case, a unit depth is considered, corresponding to $A=C\times 1$, where C is the chord of the aerodynamic profile. V denotes the relative flow velocity.

The dimensionless coefficients $C_l$ and $C_d$ are employed to assess the aerodynamic efficiency of a profile and to evaluate its key geometric attributes. An airfoil is deemed efficient when it achieves higher lift coefficients $C_l$, accompanied by lower drag coefficients $C_d$.

In the present study, the aim was to validate the computational program IMERSPEC for conducting numerical simulations of two-dimensional flows over airfoils. The objective was to achieve results consistent with those available in the literature, based on solutions that represent the relevant aspects of the physical phenomenon. The simulations involve incompressible flow of a homogeneous, Newtonian fluid with constant physical properties. The airfoil is the only immersed body considered, without the influence of barriers or other interfacial phenomena.

The aerodynamic coefficients, namely drag and lift coefficients (Equations (25) and (26)), are the main parameters considered in the quantitative comparison between the obtained results and those available in the literature. When calculated for each time step, the values of these coefficients exhibit fluctuations resulting from vortex-shedding processes in the boundary layer. However, the mean values are adopted for comparison. Tests were conducted with both symmetric and asymmetric airfoils at different angles of attack to assess the numerical model’s capability in simulating flows around profiles with non-zero curvature.

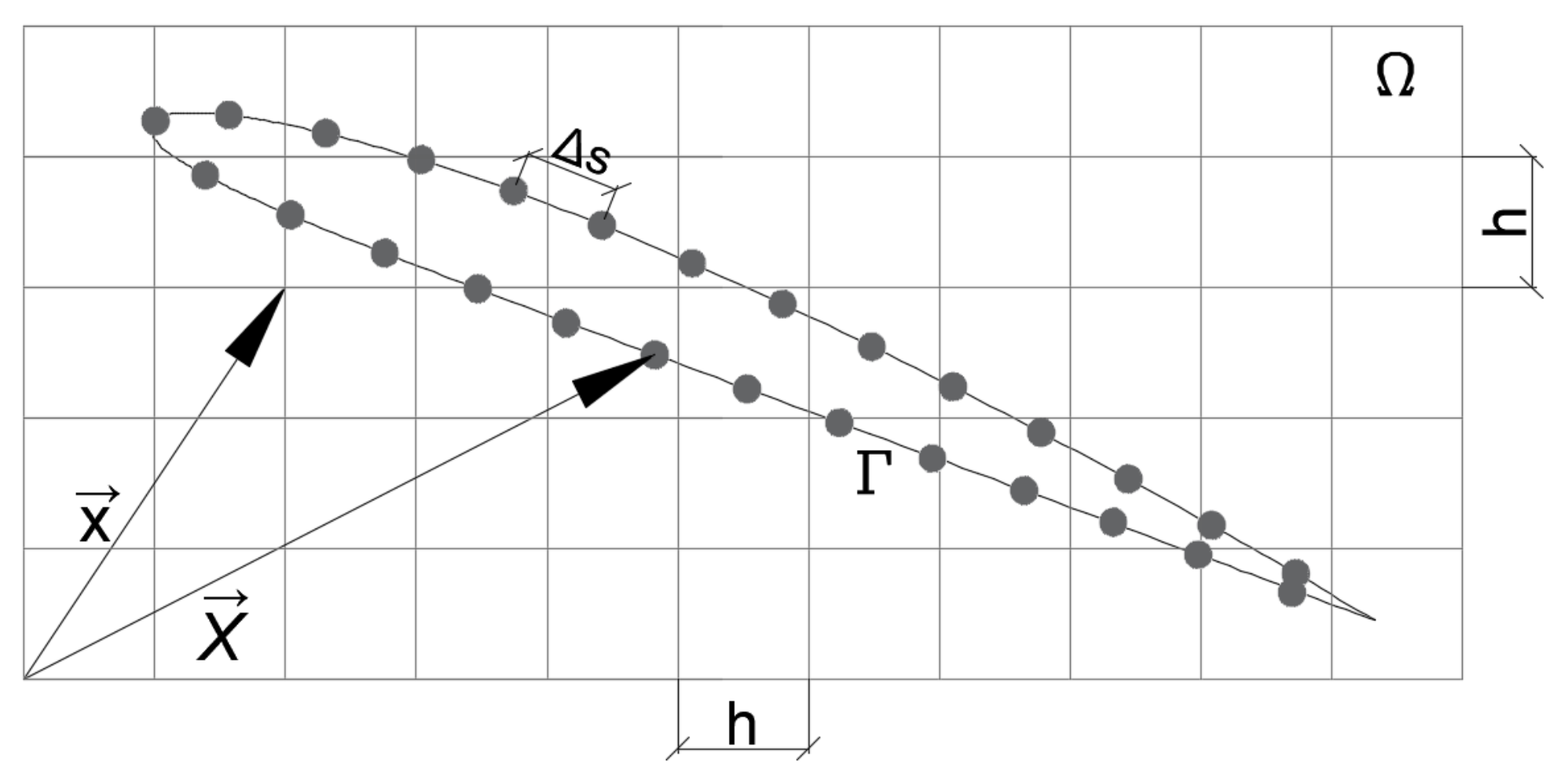
For the simulations, the Eulerian domain was discretized to ensure the best performance of the FFT subroutine [27], considering a regular grid and equally spaced grid points, with $2^M$ collocation nodes, where M is an integer.

The dimensions of the computational domain are illustrated in Figure 5. The Eulerian domain is determined by $L_x\times L_y$, where $L_x=\frac{N_x}{N_y}{L}_y$, ensuring the condition of equal spacing between the Eulerian nodes, and is divided into three different regions: the buffer zone ($L_{bz}$), the forcing zone, and the physical domain ($L_c$). The combination of these regions generates a periodic domain, which is required by the FPSM, resulting in identical boundary conditions at the domain’s exit and entrance. Due to periodicity, physical instabilities exiting the Eulerian domain (fluid recirculations, for example) are reintroduced at its entrance, justifying the presence of the buffer region and the forcing zone [3,15].

In all simulations, the airfoils were centrally positioned within a domain of sufficiently large dimensions to accurately represent the external flow over the profiles. This positioning minimizes the influence of the upper walls on the immersed geometry, ensuring a more realistic simulation of the flow behavior around the airfoils.

This study will commence by investigating the influence of different interpolation and distribution functions on simulations of two-dimensional flows over the NACA 4404 profile, renowned for its exceptional slimness. The effectiveness of these functions in producing accurate aerodynamic coefficients will then be evaluated. Following this, we will analyze the emergence of fluid dynamic effects by plotting curves of the drag coefficient and lift coefficient against the angle of attack for the airfoil.

3.1. Different Types of Interpolation and Distribution Functions

The geometry of the studied airfoil, NACA 4404, is depicted in Figure 6. This profile features a thickness of 4% and a maximum curvature of 4%, located at 40% of the chord length, measured from the leading edge.

The examination of slender airfoil profiles is highly significant for methodological testing. This significance arises chiefly due to convergence issues at the trailing edge and numerical errors leading to exceedingly high vorticity fields at the profile exit over time, particularly when periodic boundary conditions are utilized. Although thin airfoils provide benefits at low Reynolds numbers, such as a favorable lift-to-drag ratio, they frequently encounter notable lift fluctuations, mainly attributed to the unstable flow separation at the trailing edge.

For the proposed cases, Eulerian grids with $1024\times 256$ collocation points were employed, which are relatively refined and have ensured convergent results in previous works [28]. The angle of attack varied between 0° and 7°. An Eulerian domain of $32\mathrm{m}\times 8\mathrm{m}$ was considered, with a distance of 24 m between the trailing edge and the outlet, and a forcing zone of 0.625 m. The free-stream velocity was $U_0=1.0\mathrm{m}/\mathrm{s}$. The fluid had a density of $\rho =1.0{\mathrm{kg}/\mathrm{m}}^3$. The kinematic viscosity of the fluid was given by $\nu =U_{0}c/Re$, where c is the airfoil chord. In the Multi-Direct Forcing iterative process, the tolerance was set to $\epsilon ={10}^{-3}$, as shown in Equation (18).

The NACA 4404 airfoil was discretized into 400 Lagrangian collocation points, with a more refined distribution at the leading and trailing edges. Increasing the number of Lagrangian nodes enhances the representation of the immersed body boundary within the Eulerian domain, as more discrete points highlight the Lagrangian force field. Consequently, the flow around the bodies becomes more accurately captured, especially in critical flow regions, justifying the higher concentration of points at the leading and trailing edges, as depicted in Figure 7. In this work, as shown in Figure 7, an average of three Lagrangian points per Eulerian mesh cell is adopted, following the recommendation in the literature [15] to use a minimum of two.

The profiles used had a chord length of 2.0 m. Increasing the chord length of the profile results in more Eulerian points within the airfoil region. Since the Navier–Stokes and continuity equations (Equations (1), (2) and (24)) are solved for the entire Eulerian domain, including the nodes inside the Lagrangian domain, a higher number of discrete points within the airfoil ensures better delineation of the body’s boundary. This prevents the inflow and outflow of fluid, which could distort the physical phenomenon and deviate from reality. In essence, a refined Eulerian mesh should yield similar results, as it also increases the number of Eulerian nodes within the profile.

The initial analysis aimed to determine which interpolation method, among Gaussian, Cubic, and Hat functions, would yield results closer to those found by [29]. These authors presented a numerical analysis via CFD of the velocity field around slender airfoil profiles, using software to numerically solve the Navier–Stokes equations, considering incompressible laminar flow. The algorithm they used is based on the two-dimensional finite element method, with semi-implicit fractional step schemes.

The interpolation process determines the convergence order of the methodology, so it is important to use a high-order convergence weight function for its evaluation [15].

Table 1. Average aerodynamic coefficients of the NACA 4404 airfoil for different functions.

$\mathit{\alpha }{[}^0]$	Distribution Function	${\mathit{C}}_{\mathit{l}}$	${\mathit{C}}_{\mathit{d}}$	Difference ${\mathit{C}}_{\mathit{l}}$	Difference ${\mathit{C}}_{\mathit{d}}$
	Cubic	0.088	0.107	44.51%	1.49%
	Gaussian	0.166	0.218	5.02%	101.82%
0	Hat	0.157	0.207	0.53%	91.16%
	[29]	0.158	0.108	-	-
	Cubic	0.157	0.108	34.06%	1.50%
	Gaussian	0.252	0.216	6.01%	96.72%
1	Hat	0.245	0.202	2.70%	84.12%
	[29]	0.238	0.110	-	-
	Cubic	0.224	0.112	28.68%	0.16%
	Gaussian	0.336	0.198	6.87%	76.66%
2	Hat	0.325	0.206	3.39%	84.16%
	[29]	0.314	0.112	-	-
	Cubic	0.284	0.115	26.73%	0.13%
	Gaussian	0.417	0.212	7.81%	84.93%
3	Hat	0.409	0.214	5.65%	86.88%
	[29]	0.387	0.114	-	-
	Cubic	0.477	0.118	4.67%	0.72%
	Gaussian	0.644	0.233	41.46%	98.42%
5	Hat	0.482	0.155	5.80%	32.44%
	[29]	0.455	0.117	-	-
	Cubic	0.414	0.125	20.10%	2.27%
	Gaussian	0.496	0.249	4.21%	103.40%
6	Hat	0.499	0.183	3.72%	49.18%
	[29]	0.518	0.122	-	-
	Cubic	0.464	0.134	25.39%	1.11%
	Gaussian	0.574	0.243	7.86%	82.38%
7	Hat	0.599	0.252	3.76%	89.21%
	[29]	0.623	0.133	-	-

shows the average values of the lift coefficient, $C_l$, and drag coefficient, $C_d$, obtained in the present simulations for the asymmetric profile, considering different distribution/interpolation functions and a Reynolds number flow $Re=800$. For all angles of attack considered, it was observed that simulations using the Cubic function obtained results closer to the reference for the drag coefficient, $C_d$, with relative differences not exceeding 2.27%. However, this function did not achieve satisfactory performance for the lift coefficient, $C_l$, which was better calculated in simulations using the Hat function.

The angles of attack studied were small, but sufficient to potentially generate adverse pressure gradients over the airfoil, leading to flow separation or turbulence due to boundary layer detachment and low-pressure regions. Graphically, the results can be observed in Figure 8, Figure 9 and Figure 10. The uniform application of identical functions in both the x and y directions compromised the accuracy of the methodology. An illustration of this is the stall region observed between $\alpha =5$ and 7 in Figure 9, showing how the isolated use of the Cubic function yielded inconsistent outcomes. The analyses indicate that using a hybrid distribution, employing the Cubic function for $C_d$ and the Hat function for $C_l$, may be appropriate.

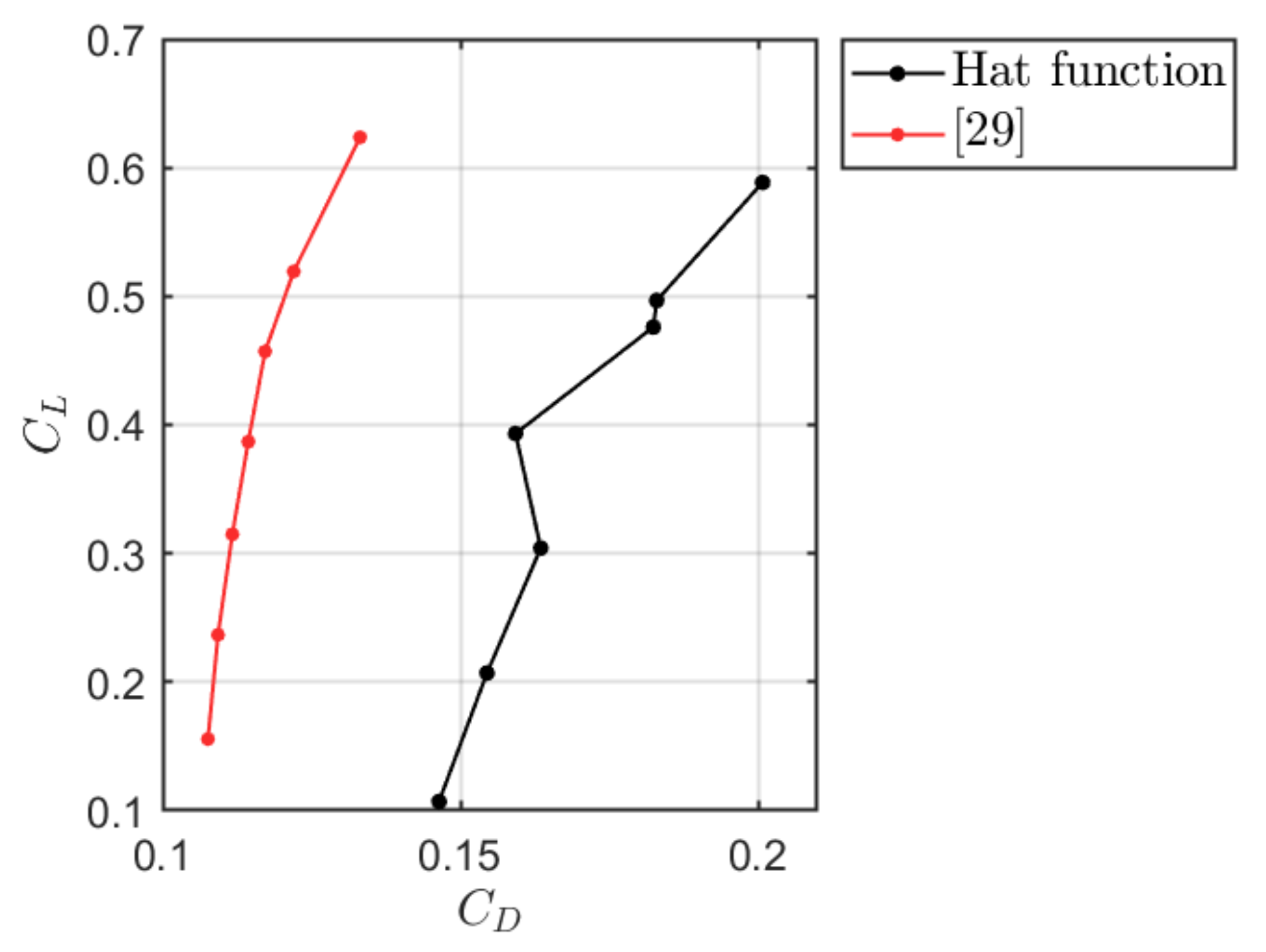
In the simulation results presented in Figure 11 and Figure 12, the values of $C_d$ were obtained using the Cubic function, while the values of $C_l$ were obtained using the Hat function. Figure 11 depicts the polar curve of the flow over the NACA 4404 airfoil at $Re=800$, obtained using the Hat function for both coefficients. Figure 12 shows the same curve, now obtained using different distribution functions, highlighting the improvements achieved.

In

Table 2. Average aerodynamic coefficients of the NACA 0008 airfoil for different functions.

Distribution Functions	${\mathit{C}}_{\mathit{l}}$	${\mathit{C}}_{\mathit{d}}$	${\mathit{C}}_{\mathit{l}}$/${\mathit{C}}_{\mathit{d}}$	Difference ${\mathit{C}}_{\mathit{l}}$	Difference ${\mathit{C}}_{\mathit{d}}$
Gaussian	0.1474	0.1628	0.91	28.014%	127.416%
Cubic	0.2414	0.0727	3.32	17.914%	1.537%
Hat	0.2404	0.0979	2.46	17.455%	36.800%
Hybrid (Cubic and Hat)	0.2050	0.0820	2.50	0.135%	14.595%
[29]	0.2047	0.0716	2.86	–	–

, the enhancements, resulting from the adoption of the hybrid methodology in calculating the lift coefficient, drag coefficient, and aerodynamic efficiency for the symmetric NACA 0008 profile (shown in Figure 13) are highlighted. These improvements bring the values closer to those proposed by [29], who simulated flows over the same profile under conditions of $Re=2000$ and an angle of attack of 3°. For this simulation, the same domain and numerical simulation parameters as before were utilized; however, a less refined Eulerian mesh of $512\times 128$ collocation points was employed. Despite the coarser mesh, the obtained results were already quite satisfactory.

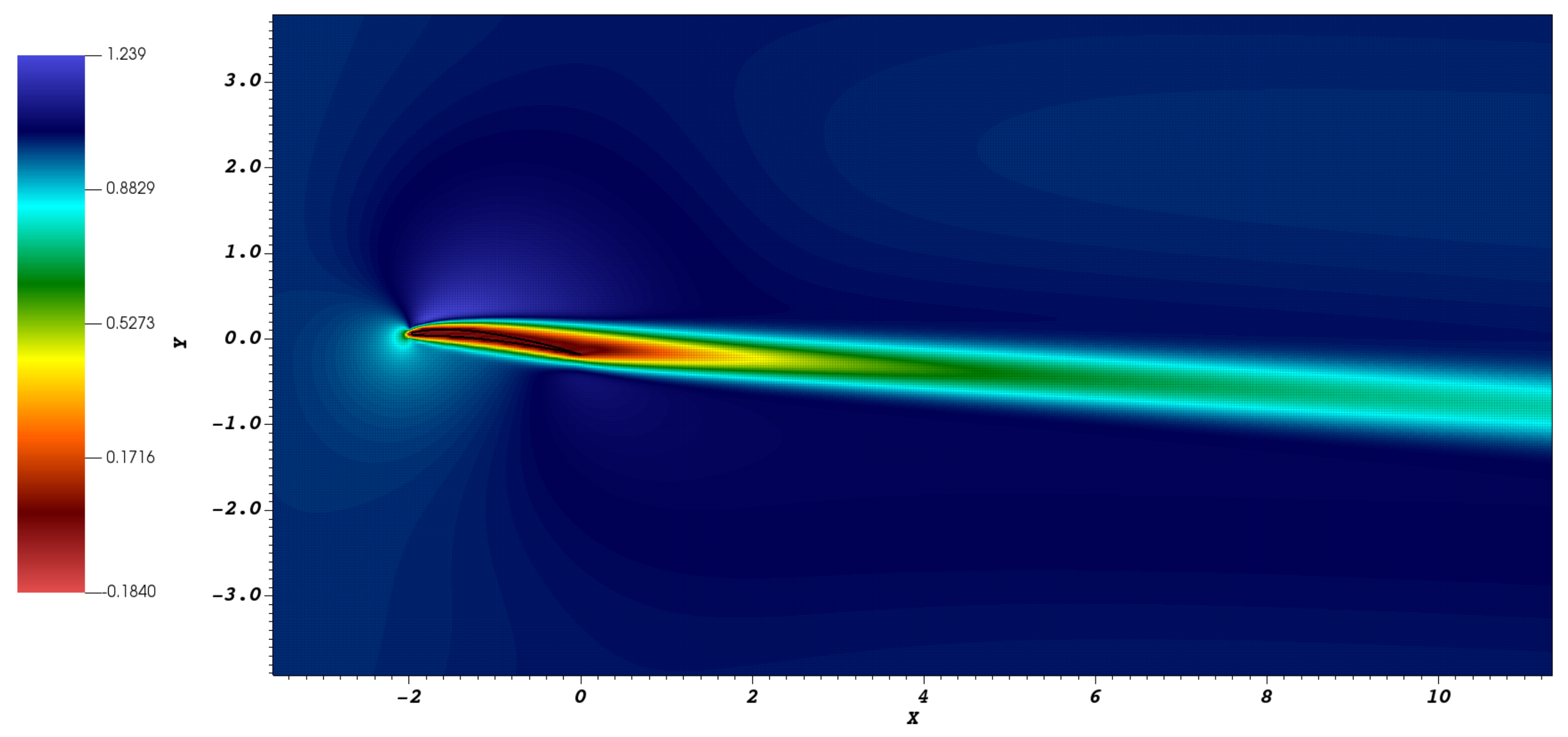
Figure 14 displays the velocity fields around the NACA 0008 airfoil at the time instant of 100 s, derived from the simulation using the Gaussian function and the simulation using the Hybrid function.

From the velocity fields, it is evident how crucial it is to select the appropriate function for accurately representing fluid dynamic phenomena around the airfoil. The flow obtained using the Gaussian function showed the development of recirculation zones near the trailing edge, due to boundary layer separation occurring close to the leading edge. This led to an expansion of the low-pressure region over the airfoil and an adverse pressure gradient between the front and rear of the profile. In contrast, in the flow obtained using the hybrid function, streamlines exhibited laminar flow without vortex shedding, and boundary layer separation occurred near the trailing edge. This minimized the effects of negative pressure at the rear of the profile and in the wake region. The flow behavior observed with the hybrid function is consistent with those reported in the study by [29].

3.2. Analysis of Airfoil Geometry on Aerodynamic Coefficients

Given the influence of the distribution/interpolation functions, as observed in the previous section, numerical simulations of incompressible flows over asymmetric airfoils were conducted. The objective is to analyze the influence of geometric parameters of the profiles on their aerodynamic coefficients, as well as to verify the adequacy of the hybrid distribution methodology in the simulations. The dimensional parameters of the domain, as well as the numerical simulation parameters, previously presented, remain the same for the numerical simulations in this section. These are analyses of two-dimensional flows, without the use of turbulence models, with a grid of 1024 × 256 Eulerian placement points and 400 Lagrangian discretization points for the airfoil.

In Figure 15, Figure 16, Figure 17 and Figure 18, the velocity fields $u(x,y,t)$ in [m/s] of NACA 4404 profile are shown, respectively, for angles of attack of 0°, 2°, 7°, and 12°, in a flow with $Re=800$.

The increase in angle of attack induces noticeable alterations in the flow dynamics, particularly on the upper surface of the profile, where boundary layer separation occurs. Even at a 0° angle of attack, differences in velocity distribution between the lower and upper surfaces are apparent, accentuating with increasing angles due to the pressure differential across the surfaces. At a 2° angle of attack, negative velocities close to the trailing edge indicate extensive boundary layer separation, affecting larger areas of the upper surface as the angle increases further.

At a 12° angle of attack, the formation of vortices due to boundary layer separation becomes pronounced. The curvature of asymmetric profiles significantly influences the pressure distribution dynamics between the lower surface and the upper surface. As the flow traverses over the upper region, it encounters a more pronounced adverse pressure gradient, especially upon reaching the point of maximum curvature.

In Figure 19, the lift curve, $C_l$, vs. $\alpha$, and the calculated aerodynamic efficiency, $C_l/C_d$ vs. $\alpha$, for the NACA 4404 profile are shown, compared to the results from [29].

For low Reynolds number flows, the methodology studied here yielded consistent results, in close agreement with expectations and existing literature. These conditions were relatively benign compared to turbulent flow scenarios characterized by extensive vortex generation across different frequency ranges, which are commonly encountered and analyzed for airfoils. Further accurate calculations are necessary to capture these physical phenomena more faithfully, necessitating additional testing of mesh refinement capabilities to ensure convergent results. Nevertheless, the simulations demonstrate significant potential for the methodology.

4. Conclusions

The present study conducted simulations of incompressible flows over two different slender airfoils at low Reynolds numbers. To achieve this, the IMERSPEC methodology was employed, utilizing the pseudo-spectral Fourier method for spatial discretization of the Navier–Stokes equations and continuity, in conjunction with the Immersed Boundary Method for enforcing boundary conditions.

Validation of the methodology was demonstrated through simulations of flows at different Reynolds numbers and various angles of attack, revealing the influence of curvature and thickness of different airfoils on the flow. Additionally, quantitative results of drag and lift coefficients were presented, confirming convergence between the obtained results and those available in the literature.

Specifically, the main contribution of this work lies in showcasing the influence of the distribution function on the obtained drag and lift coefficients. It was found that the drag coefficient is more accurate when obtained using the Cubic function, while the lift coefficient is more accurately obtained using the Hat function. Therefore, it is suggested to consider employing different distribution functions based on the specific coefficient being calculated in the same computational simulation of airfoil flows.

It is crucial to acknowledge, however, that enhancing accuracy encompasses various factors beyond function selection. These factors include increasing mesh density, adjusting iteration counts or tolerance levels in the Multi-Direct Forcing method, and applying mathematical filters to manage numerical oscillations inherent in spectral methods, among others.

This work facilitates future progress in conducting numerical simulations using turbulence models in conjunction with the IMERSPEC methodology, specifically tailored for numerical studies in airfoils. This allows for the investigation of induced drag effects and complex fluid dynamic phenomena that arise at high Reynolds numbers, while maintaining low computational costs through efficient programming.