Two Different Analytical Approaches for Solving the Pantograph Delay Equation with Variable Coefficient of Exponential Order
Abstract
1. Introduction
2. The MSE: Exact Solution
3. The LTADM: Closed-Form Solution
4. Convergence
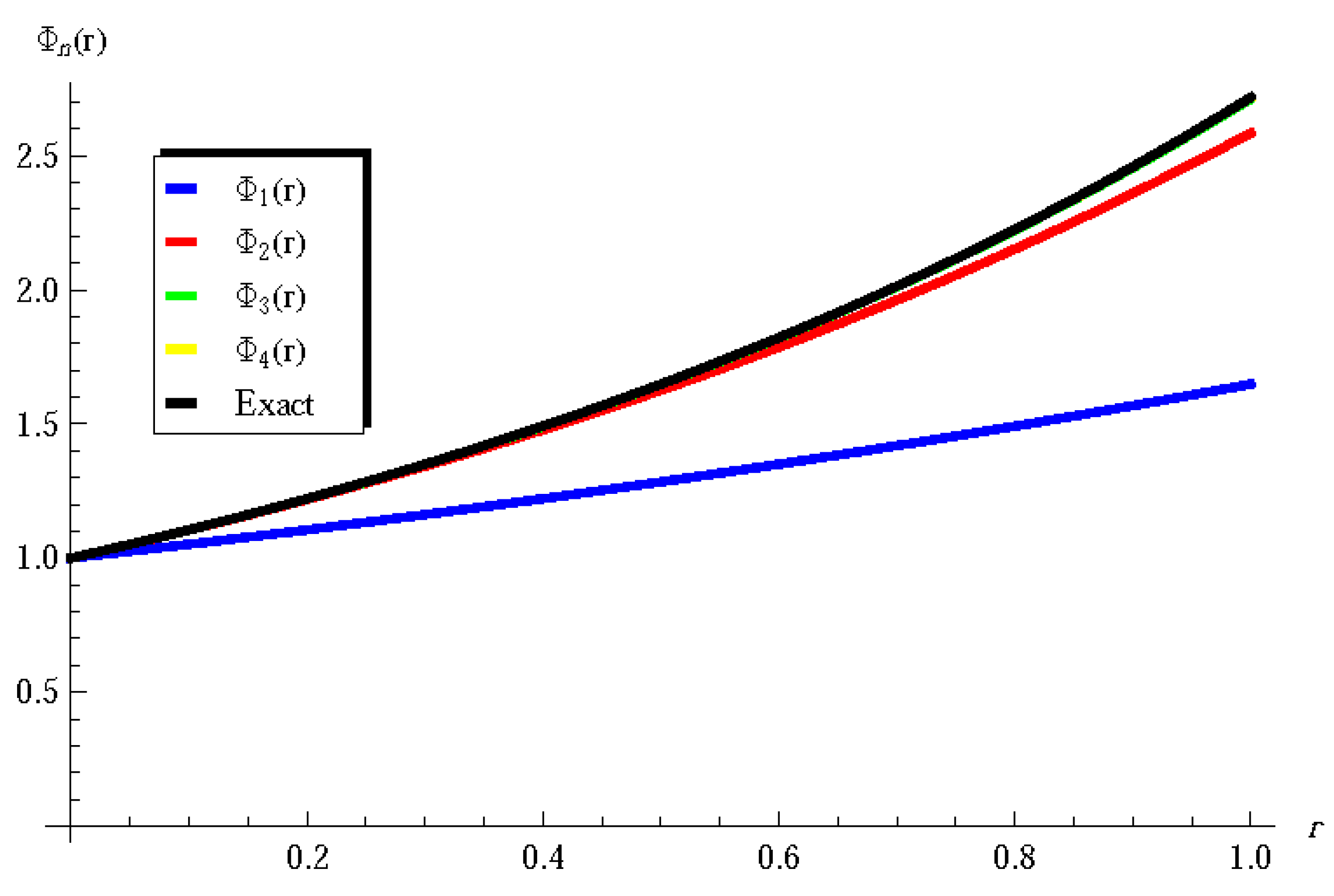
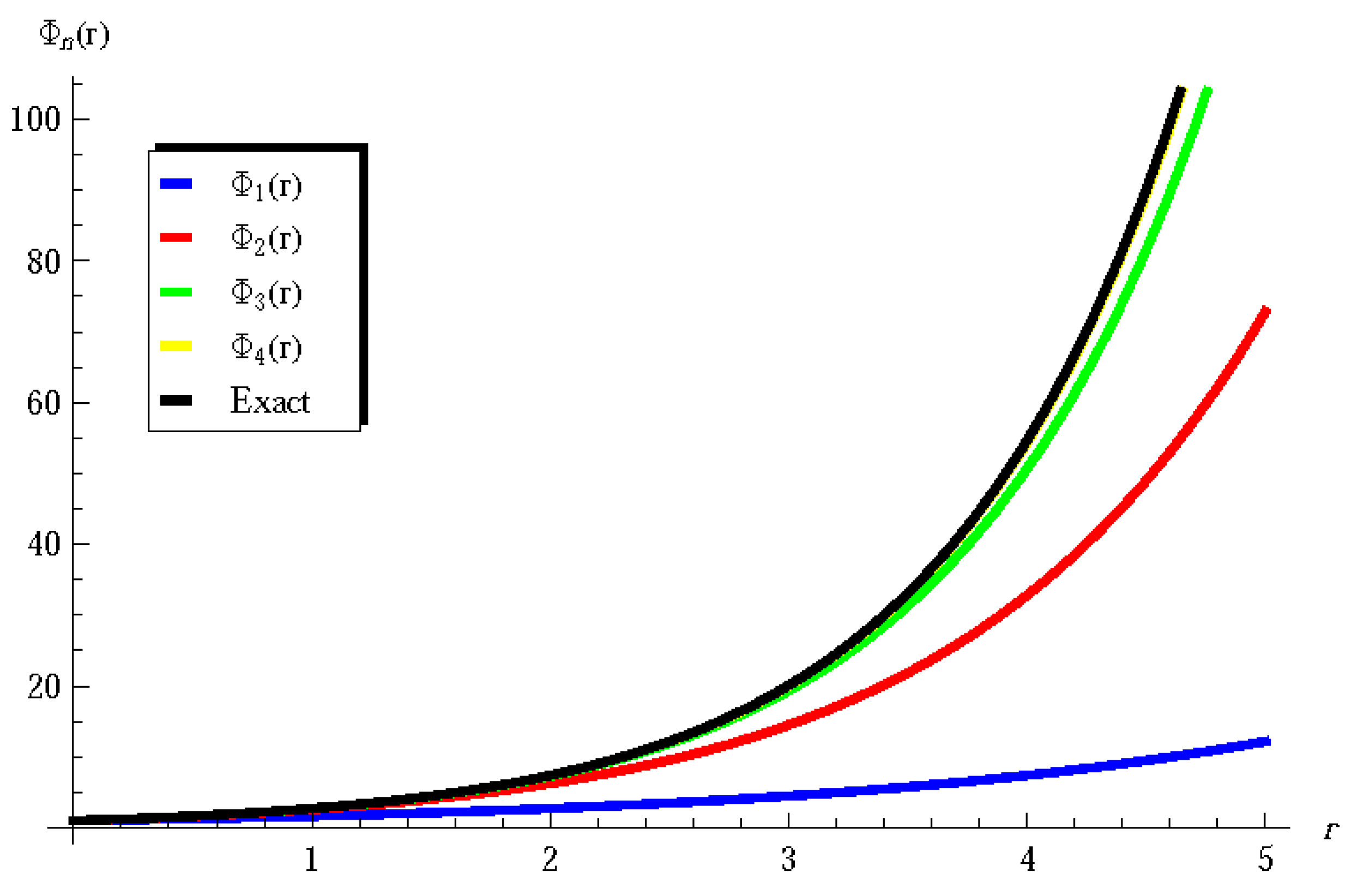
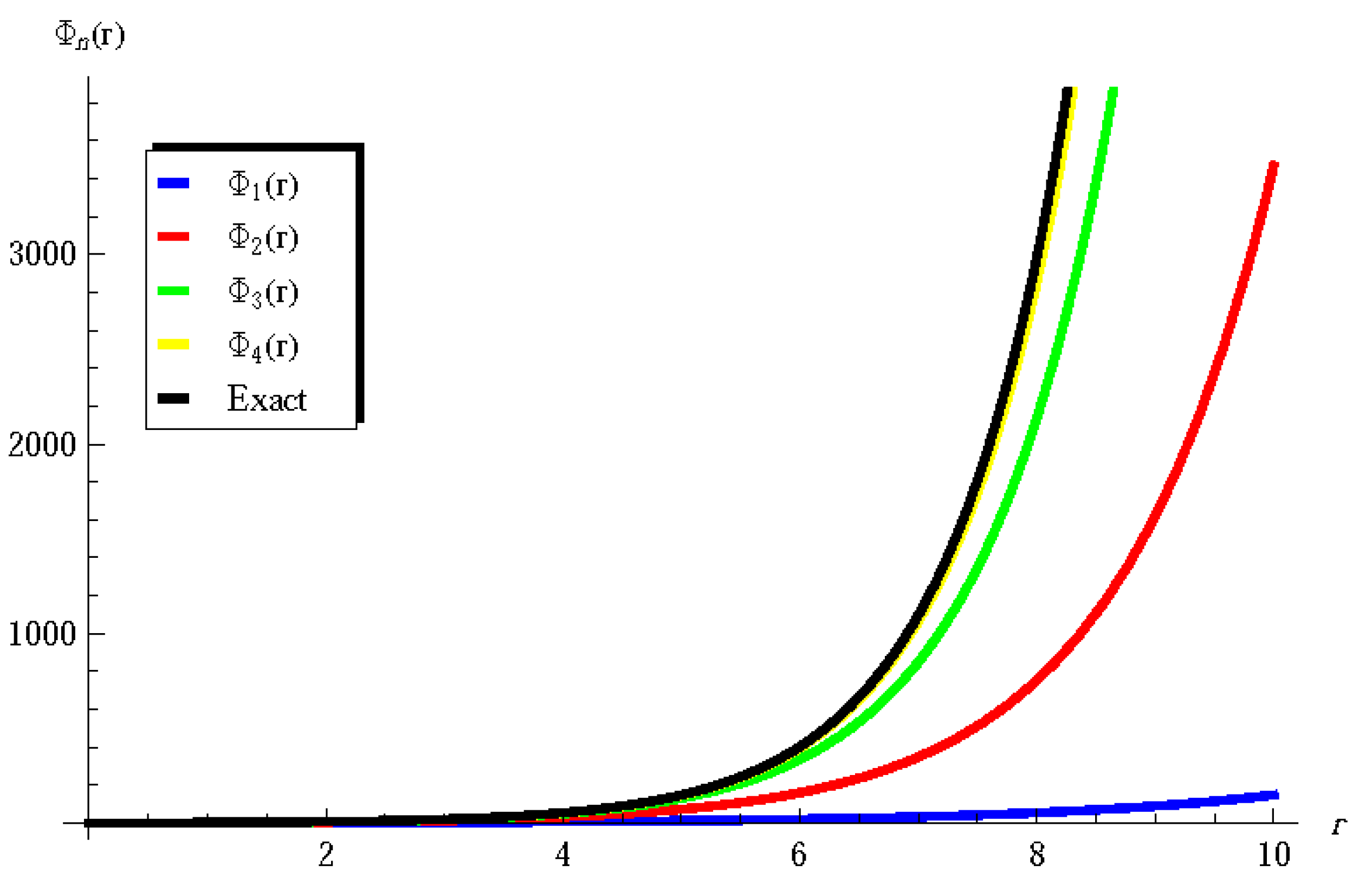
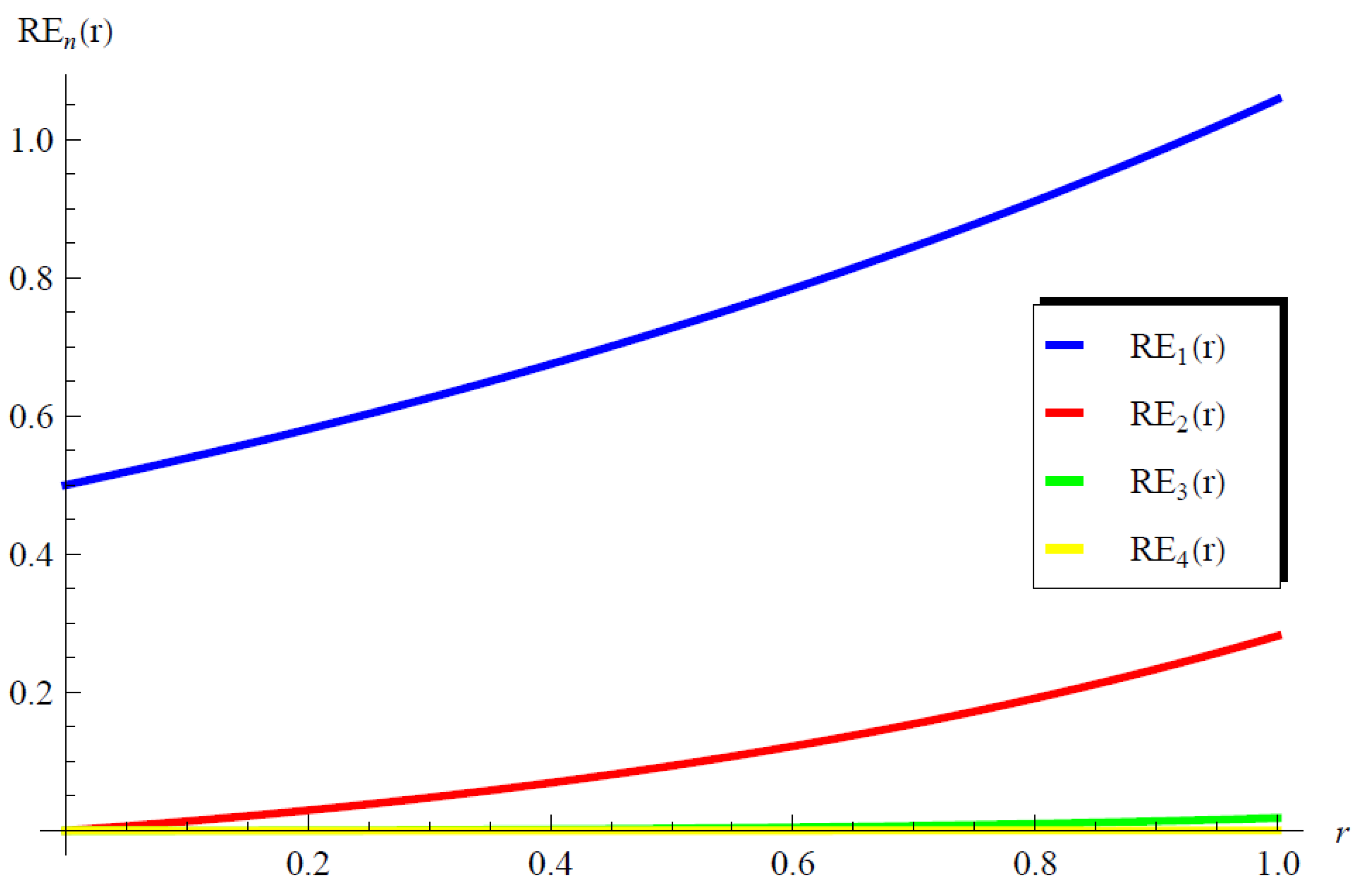
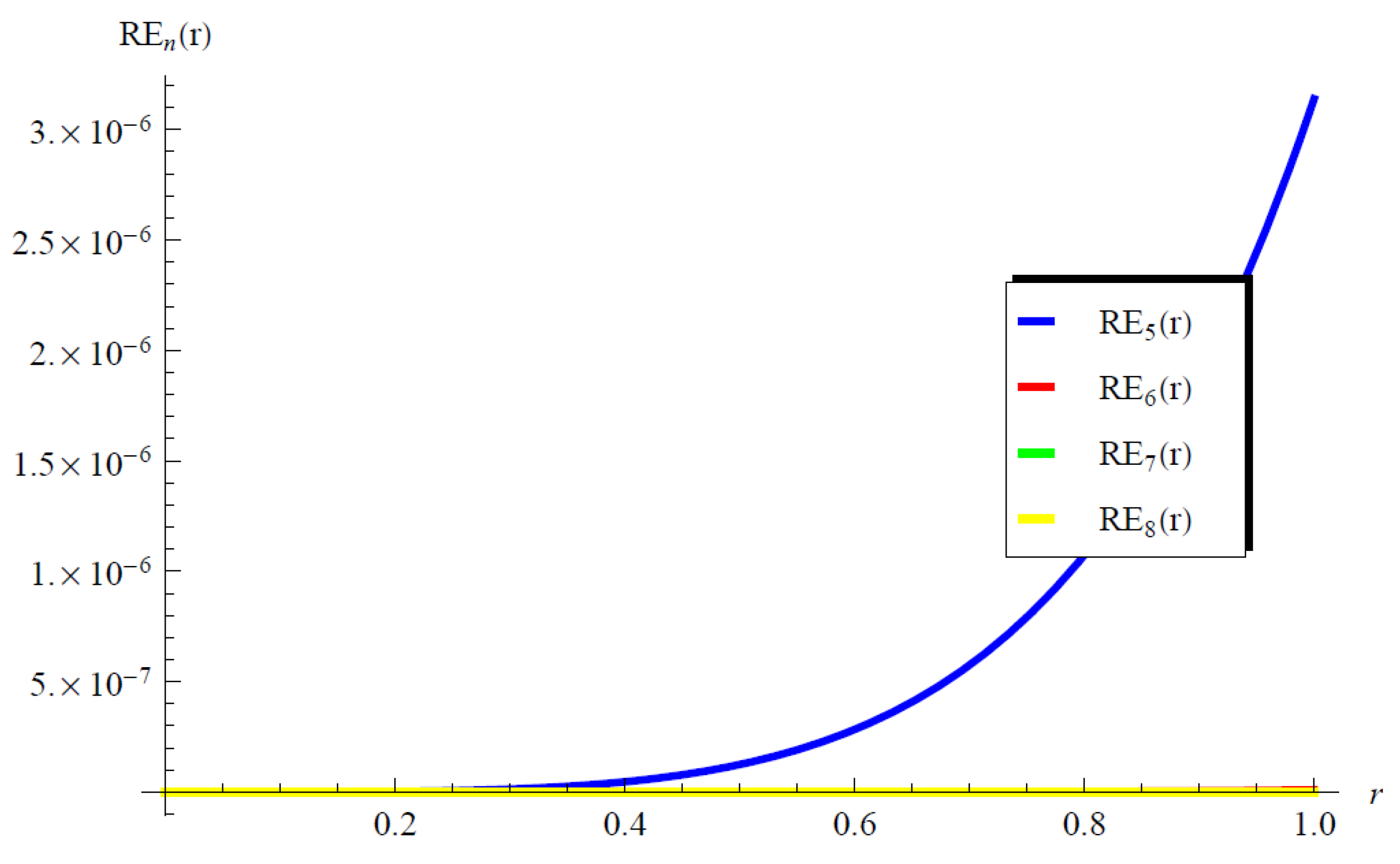
5. Results and Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sedaghat, S.; Ordokhani, Y.; Dehghan, M. Numerical solution of the delay differential equations of pantograph type via Chebyshev polynomials. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4815–4830. [Google Scholar] [CrossRef]
- Tohidi, E.; Bhrawy, A.H.; Erfani, K. A collocation method based on Bernoulli operational matrix for numerical solution of generalized pantograph equation. Appl. Math. Model. 2013, 37, 4283–4294. [Google Scholar] [CrossRef]
- Javadi, S.; Babolian, E.; Taheri, Z. Solving generalized pantograph equations by shifted orthonormal Bernstein polynomials. J. Comput. Appl. Math. 2016, 303, 1–14. [Google Scholar] [CrossRef]
- Shen, J.; Tang, T.; Wang, L. Spectral Methods: Algorithms, Analysis and Applications; Springer: Berlin/Heidelberg, Germany, 2011; Volume 41. [Google Scholar]
- Ezz-Eldien, S.S. On solving systems of multi-pantograph equations via spectral tau method. Appl. Math. Comput. 2018, 321, 63–73. [Google Scholar] [CrossRef]
- Yang, C.; Hou, J.; Lv, X. Jacobi spectral collocation method for solving fractional pantograph delay differential equations. Eng. Comput. 2022, 38, 1985–1994. [Google Scholar] [CrossRef]
- Al-Enazy, A.H.S.; Ebaid, A.; Algehyne, E.A.; Al-Jeaid, H.K. Advanced Study on the Delay Differential Equation y′(t) = ay(t) + by(ct). Mathematics 2022, 10, 4302. [Google Scholar] [CrossRef]
- Albidah, A.B.; Kanaan, N.E.; Ebaid, A.; Al-Jeaid, H.K. Exact and Numerical Analysis of the Pantograph Delay Differential Equation via the Homotopy Perturbation Method. Mathematics 2023, 11, 944. [Google Scholar] [CrossRef]
- Isik, O.R.; Turkoglu, T. A rational approximate solution for generalized pantograph-delay differential equations. Math. Methods Appl. Sci. 2016, 39, 2011–2024. [Google Scholar] [CrossRef]
- Jafari, H.; Mahmoudi, M.; Noori Skandari, M.H. A new numerical method to solve pantograph delay differential equations with convergence analysis. Adv. Differ. Equ. 2021, 2021, 129. [Google Scholar] [CrossRef]
- El-Zahar, E.R.; Ebaid, A. Analytical and Numerical Simulations of a Delay Model: The Pantograph Delay Equation. Axioms 2022, 11, 741. [Google Scholar] [CrossRef]
- Bakodah, H.O.; Ebaid, A. Exact solution of Ambartsumian delay differential equation and comparison with Daftardar-Gejji and Jafari approximate method. Mathematics 2018, 6, 331. [Google Scholar] [CrossRef]
- Dogan, N. Solution of the system of ordinary differential equations by combined Laplace transform-Adomian decomposition method. Math. Comput. Appl. 2012, 17, 203–211. [Google Scholar] [CrossRef]
- Ra, P. Application of Laplace transforms to solve ODE using MATLAB. J. Inform. Math. Sci. 2015, 7, 93–97. [Google Scholar]
- Handibag, S.S.; Karande, B.D. Laplace substitution method for n th-order linear and non-linear PDEs involving mixed partial derivatives. Int. Res. J. Eng. Technol. 2015, 2, 378–388. [Google Scholar]
- Alshikh, A.A.; Mahgob, M.M. A comparative study between Laplace transform and two new integrals “Elzaki” transform and “Aboodh” transform. Pure Appl. Math. J. 2016, 5, 145–150. [Google Scholar] [CrossRef]
- Atangana, A.; Alkaltani, B.S. A novel double integral transform and its applications. J. Nonlinear Sci. Appl. 2016, 9, 424–434. [Google Scholar] [CrossRef]
- Zhou, H.; Yang, L.; Agarwal, P. Solvability for fractional p-Laplacian differential equations with multipoint boundary conditions at resonance on infinite interval. J. Appl. Math. Comput. 2017, 53, 51–76. [Google Scholar] [CrossRef]
- Liang, X.; Gao, F.; Gao, Y.N.; Yang, X.J. Applications of a novel integral transform to partial differential equations. J. Nonlinear Sci. Appl. 2017, 10, 528–534. [Google Scholar] [CrossRef]
- Khaled, S.M. The exact effects of radiation and joule heating on Magnetohydrodynamic Marangoni convection over a flat surface. Therm. Sci. 2018, 22, 63–72. [Google Scholar] [CrossRef]
- Pavani, P.V.; Priya, U.L.; Reddy, B.A. Solving differential equations by using Laplace transforms. Int. J. Res. Anal. Rev. 2018, 5, 1796–1799. [Google Scholar]
- Agarwal, P.; Ntouyas, S.K.; Jain, S.; Chand, M.; Singh, G. Fractional kinetic equations involving generalized k-Bessel function via Sumudu transform. Alex. Eng. J. 2018, 57, 1937–1942. [Google Scholar] [CrossRef]
- Restrepo, J.E.; Piedrahita, A.; Agarwal, P. Multidimensional Fourier transform and fractional derivative. Proc. Jangjeon Math. Soc. 2019, 22, 269–277. [Google Scholar]
- Faraj, B.M.; Ahmed, F.W. On the MATLAB technique by using Laplace transform for solving second order ODE with initial conditions exactly. Matrix Sci. Math. 2019, 3, 8–10. [Google Scholar] [CrossRef]
- Mousa, A.; Elzaki, M. Solution of volterra integro-differential equations by triple Laplace transform. Irish Interdiscip. J. Sci. Res. 2019, 3, 67–72. [Google Scholar]
- Dhunde, R.R.; Waghmare, G.L. Double Laplace iterative method for solving nonlinear partial differential equations. New Trends Math. Sci. 2019, 7, 138–149. [Google Scholar] [CrossRef]
- Ziane, D.; Cherif, M.H.; Cattani, C.; Belghaba, K. Yang-Laplace decomposition method for nonlinear system of local fractional partial differential equations. Appl. Math. Nonlinear Sci. 2019, 4, 489–502. [Google Scholar] [CrossRef]
- Mastoi, S.; Othman, W.A.; Nallasamy, K. Randomly generated grids and Laplace Transform for partial differential equations. Int. J. Disaster Recovery Bus. Contin. 2020, 11, 1694–1702. [Google Scholar]
- Ebaid, A.; Alharbi, W.; Aljoufi, M.D.; El–Zahar, E.R. The exact solution of the falling body problem in three–dimensions: Comparative study. Mathematics 2020, 8, 1726. [Google Scholar] [CrossRef]
- Spiegel, M.R. Spiegel, Laplace Transforms; McGraw-Hill. Inc.: New York, NY, USA, 1965. [Google Scholar]
- Alrebdi, R.; Al-Jeaid, H.K. Accurate Solution for the Pantograph Delay Differential Equation via Laplace Transform. Mathematics 2023, 11, 2031. [Google Scholar] [CrossRef]
- Srinivasa, K.; Mundewadi, R.A. Wavelets approach for the solution of nonlinear variable delay differential equations. Int. J. Math. Comput. Eng. 2023, 1, 139–148. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alrebdi, R.; Al-Jeaid, H.K. Two Different Analytical Approaches for Solving the Pantograph Delay Equation with Variable Coefficient of Exponential Order. Axioms 2024, 13, 229. https://doi.org/10.3390/axioms13040229
Alrebdi R, Al-Jeaid HK. Two Different Analytical Approaches for Solving the Pantograph Delay Equation with Variable Coefficient of Exponential Order. Axioms. 2024; 13(4):229. https://doi.org/10.3390/axioms13040229
Chicago/Turabian StyleAlrebdi, Reem, and Hind K. Al-Jeaid. 2024. "Two Different Analytical Approaches for Solving the Pantograph Delay Equation with Variable Coefficient of Exponential Order" Axioms 13, no. 4: 229. https://doi.org/10.3390/axioms13040229
APA StyleAlrebdi, R., & Al-Jeaid, H. K. (2024). Two Different Analytical Approaches for Solving the Pantograph Delay Equation with Variable Coefficient of Exponential Order. Axioms, 13(4), 229. https://doi.org/10.3390/axioms13040229





