Abstract
This study investigates a green multimodal routing problem with soft time window. The objective of routing is to minimize the total costs of accomplishing the multimodal transportation of a batch of goods. To improve the feasibility of optimization, this study formulates the routing problem in an uncertain environment where the capacities and carbon emission factors of the travel process and the transfer process in the multimodal network are considered fuzzy. Taking triangular fuzzy numbers to describe the uncertainty, this study proposes a fuzzy nonlinear programming model to deal with the specific routing problem. To make the problem solvable, this study adopts the fuzzy chance-constrained programming approach based on the possibility measure to remove the fuzziness of the proposed model. Furthermore, we use linear inequality constraints to reformulate the nonlinear equality constraints represented by the continuous piecewise linear functions and realize the linearization of the nonlinear programming model to improve the computational efficiency of problem solving. After model processing, we can utilize mathematical programming software to run exact solution algorithms to solve the specific routing problem. A numerical experiment is given to show the feasibility of the proposed model. The sensitivity analysis of the numerical experiment further clarifies how improving the confidence level of the chance constraints to enhance the possibility that the multimodal route planned in advance satisfies the real-time capacity constraint in the actual transportation, i.e., the reliability of the routing, increases both the total costs and carbon emissions of the route. The numerical experiment also finds that charging carbon emissions is not absolutely effective in emission reduction. In this condition, bi-objective analysis indicates the conflicting relationship between lowering transportation activity costs and reducing carbon emissions in routing optimization. The sensitivity of the Pareto solutions concerning the confidence level reveals that reliability, economy, and environmental sustainability are in conflict with each other. Based on the findings of this study, the customer and the multimodal transport operator can organize efficient multimodal transportation, balancing the above objectives using the proposed model.
Keywords:
green multimodal transportation; routing; soft time window; twofold uncertainty; triangular fuzzy numbers; fuzzy chance-constrained programming; linear programming model MSC:
90-08
1. Introduction
Currently, transportation accounts for 9.17% of carbon emissions in China, and road transportation accounts for 72.3% of total transportation emissions [1]. The transportation industry has been the key to promoting China’s ‘Dual Carbon’ strategy. The Chinese government and industry are focused on optimizing the transportation structure dominated by roads by encouraging the transfer of long-distance freight flows from roads to railways and waterways that are acknowledged as sustainable transportation modes. The aim of optimizing the transportation structure is to establish a multimodal transportation system that can integrate the various advantages of different transportation modes [2]. With the motivation of this national policy, multimodal transportation in China has developed rapidly since 2015. The volume of multimodal transportation has increased from 5.35 million TEU in 2015 to 263.9 million TEU in 2021, with an average annual growth of more than 30%. Compared to road transportation, multimodal transportation significantly reduces transportation costs by 118.5% [3].
Multimodal transportation is suitable for long-distance and bulk transportation, especially for container transportation in this setting. Although it shows a great advantage in reducing cost and improving timeliness compared to unimodal transportation, it still consumes high transportation costs and time, and meanwhile, produces large amounts of carbon emissions, which affects the economy, timeliness, and environmental sustainability of transportation [4]. To improve the quality of the multimodal transportation service, the optimization of routes that are based on the best utilization of transportation resources to meet the demand of customers has become a highlight in the field of transportation planning, which needs mathematical methods to support decision making [5]. In addition to taking cost minimization as the optimization objective, recent multimodal routing studies in the literature have formulated a soft time window to improve the timeliness and flexibility of the transportation service. Fazayeli et al. [6] and Zhang et al. [7] explore the multimodal (location) routing problem with a soft time window under fuzzy demand and propose continuous piecewise linear functions to determine the storage costs and penalty costs caused by the early and delayed delivery of the goods. All studies verify the feasibility of the soft time window, which provides the basis for this article.
To further exploit the potential of multimodal transportation to achieve environmental benefits, multimodal routing studies consider reducing carbon emissions in their optimization. The most widely used method in the existing literature is to charge carbon emissions and formulate carbon emissions as a part of the costs of multimodal transportation, whose minimization is the objective of the routing. Based on this method, Guo et al. [8] discuss the green multimodal routing problem under transportation time uncertainty and build a robust stochastic optimization model. Hrusovsky et al. [9] developed a hybrid simulation and optimization approach for a green multimodal routing problem considering the same uncertainty as Guo et al. [8]. Wang et al. [10] addressed a green multimodal scheduling problem considering seaborn arrival uncertainty. In the existing literature represented by the above studies, the carbon emission factors of transportation activities are the key elements to calculate the emissions of the multimodal route(s) and are modeled as deterministic parameters. However, the carbon emission factors of transportation activities are influenced by various man-machine–environment factors, including but only limited to manual driving and operation, the working environment of the equipment and facility, the fuel type, traffic status, and weather conditions. As a result, it is difficult to accurately determine the emission factors. Moreover, multimodal routing is an advanced work that should be conducted before actual transportation. The constantly changing factors mentioned above make it impossible to predict the carbon emission factors of transportation activities in advanced routing. Consequently, the carbon emission factors are uncertain. Currently, only Sun et al. [2,4] considered carbon emission factor uncertainty in multimodal routing. However, this consideration is only associated with the travel process of road transportation rather than with the entire multimodal network.
In addition to the uncertainty of carbon emission factors, the capacity of a multimodal network is also uncertain in the routing phase. The total capacity of the network cannot be fully saved for a certain transportation order/task. It becomes occupied by other transportation orders/tasks that are difficult to know and predicate. The available capacity increases or decreases when other transportation orders/tasks start or end. Additionally, some influencing factors (e.g., bad weather, accidents, and breakdowns) also worsen the stability of the capacity. Therefore, it is difficult to exactly determine the capacity available for multimodal routing. The capacity for multimodal routing is, therefore, uncertain. However, recent relevant studies focus on multimodal routing under capacity certainty. A few studies can be found that cope with capacity uncertainty. Uddin & Huynh [11] fit the probability distribution of capacity uncertainty and use stochastic programming to model the road-rail multimodal routing problem with arc transportation capacity and node transfer capacity uncertainty. Lu et al. [12] presented an international road-rail multimodal location-routing problem constrained by triangular fuzzy capacity. Sun et al. [2,4,13] explored a road-rail multimodal routing problem considering trapezoidal fuzzy capacity. Both Lu et al. [12] and Sun et al. [2,4,13] developed chance-constrained programming models for their specific problems.
Above all, existing studies widely investigate the multimodal routing problem and obtain solid progress. However, in green multimodal routing, the current studies neglect the uncertainty of carbon emission factors in transportation activities. The performance and feasibility of charging carbon emissions on emission reduction are not adequately analyzed in these works. There are studies showing that this emission reduction method depends on extremely high unit emission costs to lower emissions [14], making its performance evaluation and feasibility analysis meaningful. Regarding capacity uncertainty, the stochastic programming used by Uddin & Huynh [11] requires large numbers of historical data to fit the probability distribution of uncertainty. However, enough reliable historical data are unattainable in most cases [15]. As an effective alternative, fuzzy numbers based on the fuzzy set theory can be adopted to model the uncertainty [16], in which limited historical information and decision makers’ expertise can be combined to determine the presentation of uncertainty easily. The fuzzy programming model can thereby be established to formulate the optimization problem under uncertainty [17]. Although adopting fuzzy programming is a more feasible method, Lu et al. [12] and Sun et al. [2,4,13] considered that only railway transportation yields capacity uncertainty in its travel process and consequently makes the formulation of the capacity uncertainty of the multimodal network incomplete. To the best of our knowledge, there are few articles that comprehensively model the capacity uncertainty and carbon emission factor uncertainty of the entire multimodal network when studying the green multimodal routing problem with soft time window.
To fix these research weaknesses, this study explores a green multimodal routing problem with soft time window under twofold uncertainty. The following works were conducted in our study:
- (1)
- Using triangular fuzzy numbers, the most commonly used form of fuzzy numbers [18], to describe the capacity uncertainty and carbon emission factor uncertainty of the travel process and transfer process in the multimodal network;
- (2)
- Building a fuzzy nonlinear optimization model, the aim of which was to minimize the total travel costs, transfer costs, storage costs, penalty costs, and carbon emission costs;
- (3)
- Adopting the fuzzy chance-constrained programming approach that is the most successful method applied in fuzzy optimization [19] to make the problem solvable and further use linearization transformation to improve the computational efficiency of problem solving by overcoming the difficulty of finding a global optimum solution to the nonlinear programming model;
- (4)
- Presenting a systematic numerical experiment in which we discuss the influence of improving the confidence level of the chance constraints on the total costs and carbon emissions of the routing, evaluate the performance and feasibility of the emission-charging method, and analyze the relationship among the economy, environmental sustainability, and reliability of the routing.
2. Problem Description
In this study, we consider the railway–road–waterway multimodal transportation for a batch of goods carried by standardized TEU containers. The goods have a fixed departure time at the origin and yield a deterministic time window at the destination. When the goods arrive at the destination later than the upper bound of the time window, penalty costs should be paid, as the delay could cause economic loss to the receiver. When the goods arrive at the destination earlier than the lower bound of the time window, they should be stored before the further processing of the receiver. In this case, the storage costs should be paid. Penalty costs and storage costs are integrated into the total costs. By reducing the total costs, the penalty costs and storage costs can be reduced, and the timeliness of multimodal transportation can be strengthened.
In multimodal routing, we assume that the goods volume, transportation origin and destination, fixed departure time, and time window are all known and deterministic. The multimodal network is also deterministic, in which the network structure and the parameters that govern time and costs are known and deterministic. Finally, we assume that the goods are unsplittable during the entire transportation process.
This study formulates the uncertainty of both capacities and carbon emission factors of the multimodal network when modeling multimodal routing. We use to denote an uncertain parameter. When is a random parameter in stochastic programming, and determine the support of the random parameter, and can be presented by the expectation. However, considering the limitations of stochastic programming, this study uses fuzzy programming to deal with the routing problem under twofold uncertainty, in which represents a triangular fuzzy parameter. In this case, and are the minimum and maximum possible values of , respectively, and is its most likely value. and reflect two extreme conditions and appear in practice at a low possibility, while represents the condition of in most cases. For triangular fuzzy capacity, and show the conditions in which the multimodal network suffers capacity shortage and has sufficient capacity, respectively. On the contrary, for a triangular fuzzy carbon emission factor, and separately represent the best and worst conditions. For any triangular fuzzy parameters, gives their conditions in most cases. As a result, the triangular fuzzy number can include all the possible conditions of an uncertain parameter.
3. Optimization Model
3.1. Notation
- (1)
- Sets, indices, and parameters
: a multimodal network in which , and represent the sets of nodes, arcs and transportation modes, respectively.
, , : indices of nodes and , , .
: arc from node to node , and .
, : indices of transportation modes, and , .
: predecessor node set to node , and .
: successor node set to node , and .
: transportation mode set to connecting node , and .
: transportation mode set on arc , and .
: travel distance of transportation mode on arc (unit: km).
: travel speed of transportation mode on arc (unit: km/h).
: unit of time to transfer goods from transportation mode to transportation mode at node (unit: h/TEU).
: triangular fuzzy capacity of transportation mode on arc (unit: TEU).
: triangular fuzzy capacity to transfer goods from transportation mode to transportation mode at node (unit: TEU).
: triangular fuzzy carbon emission factor of transportation mode on arc (unit: kg/TEU·km).
: triangular fuzzy carbon emission factors to transfer the goods from transportation mode to transportation mode at node (unit: kg/TEU).
: unit travel costs of transportation mode on arc (unit: CNY/TEU).
: unit costs of transferring the goods from transportation mode to transportation mode at node (unit: CNY/TEU).
: unit carbon emissions costs (unit: CNY/kg).
: unit storage costs at the destination (unit: CNY/TEU·h).
: unit penalty costs at the destination (unit: CNY/TEU·h).
: index of the origin and .
: index of the destination and .
: departure time of the goods at the origin.
: volume of the goods (unit: TEU).
: time window at the destination.
- (2)
- Variables
: 0–1 variable. If the goods are moved by transportation mode on arc ,, otherwise, .
: 0–1 variable. If the goods are transferred from transportation mode to transportation mode at node , ; otherwise, .
: non-negative variable representing the period from the arrival time of the goods at the destination to the lower bound of the time window for early delivery (unit: h).
: non-negative variable representing the period from the upper bound of the time window to the arrival time of the goods at the destination for delayed delivery (unit: h).
3.2. Fuzzy Nonlinear Programming Model
s.t.
In the optimization model, Equation (1) is the objective function that minimizes the total costs of accomplishing multimodal transportation. The objective function consists of five formulas that successively represent the travel costs, transfer costs, storage costs, penalty costs, and carbon emission costs. Equation (2) is the constraint to the equilibrium of the flow of goods. It ensures that the selected transportation modes on the route are smoothly connected at the nodes to link the origin and destination. Equations (3) and (4) ensure that the goods are unsplittable in the travel process and transfer process of multimodal transportation. Equations (5) and (6) ensure that the travel process and transfer process are connected smoothly at the transfer nodes on the planned route; that is, when the goods arrive at a transfer node by a transportation mode, they will be transferred from this mode to another one at the node, and vice versa. Equations (7) and (8) use the continuous piecewise linear function to calculate the storage and penalty periods caused by the early and delayed delivery of the goods at the destination. Equations (9) and (10) are the capacity constraints to ensure that the volume of goods does not exceed the travel capacity of the selected transportation mode and the transfer capacity between the two selected transportation modes at the selected node on the planned route. Equations (11)–(14) are the constraints of the variable domain.
4. Model Processing
The model proposed in Section 3.2 cannot be solved straightforwardly since it contains imprecise information on both the objective function and the constraints. Thus, we should process the model to realize its defuzzification to ensure the multimodal routing problem under uncertainty is solvable. In this study, we used the chance-constrained programming approach to obtain the crisp reformulation that is equivalent to the initial fuzzy optimization model. The chance-constrained programming approach first uses the fuzzy expected value operator to generate the crisp objective function of the model and then transforms the fuzzy constraints into chance constraints [20].
Consequently, the objective of the crisp model is to minimize the fuzzy expected value of the initial fuzzy objective. Both the fuzzy expected value operator and the fuzzy objective function (1) are linear. Therefore, only the fuzzy carbon emissions in Equation (1) should be converted into their fuzzy expected value, as shown in Equation (15).
By replacing fuzzy carbon emissions, as shown in Equation (15), we can obtain a crisp objective function, as indicated by Equation (16):
The chance-constrained programming approach then transforms the fuzzy constraints, i.e., Equations (9) and (10), into their respective chance constraints. Based on the possibility measure [21], the chance constraint reformulations of Equations (8) and (10) are shown as Equations (17) and (18), respectively.
The chance constraints shown as Equations (17) and (18) mean that the possibility that the volume of goods does not exceed the two types of fuzzy capacities of the planned route should not be lower than a given confidence level denoted by . is determined by the customer according to his/her preference. The higher is, the higher the possibility that the planned route satisfies real-time capacity constraints in the actual transportation, which means that the planned route is more reliable in practice.
We took a non-negative triangular fuzzy number , and a non-negative deterministic number . According to Peykani et al. [22], the possibility that is bigger than or equal to can be calculated by Equation (19).
When there is a confidence level , can be rewritten as Equation (20). Equation (20) realizes the defuzzification of the chance constraint.
According to Equation (20), Equations (17) and (18) are equivalent to Equations (21) and (22) that are crisp, respectively.
Based on the model processing given above, we can obtain a fuzzy chance-constrained model for the specific multimodal routing problem. The objective of this model is Equation (16), and the constraint set includes Equations (2)–(8), (11)–(14), (21) and (22). This model removes the fuzziness of the initial model and is, thereby, solvable.
However, the fuzzy chance-constrained model is nonlinear since it contains nonlinear Equations (13) and (14) that use the continuous piecewise linear function. Currently, there is no efficient method to find the global optimum solution to the nonlinear programming models [23]. Therefore, we need to find the linear equivalence of the nonlinear programming model to enable the global optimum solution to be found in acceptable computational time. To improve the computational efficiency, we linearize Equations (13) and (14) to generate their equivalent linear forms as follows. Under the minimization control of variables and from Equation (16) and their domain constraints, i.e., Equations (13) and (14), nonlinear Equations (7) and (8) can be linearized by Equations (23) and (24), respectively [13].
After the linearization, we obtained a mixed integer linear optimization model for the problem. Although this model belongs to the multi-parameter optimization models, its linearity characteristic enables it to be efficiently solved using the exact solution algorithms implemented by mathematical programming software. The successful use of this standard method can be found in the work of Xie et al. [24] and Zandkarimkhani et al. [25]. Therefore, this study uses the mathematical programming software Lingo to run the Branch-and-Bound algorithm to solve the specific multimodal routing problem formulated by the proposed linear programming model. Based on this method, we can obtain the global optimum solution to the problem.
5. Numerical Experiment
With reference to Sun & Lang [26], this study designed a numerical experiment in the Chinese scenario, in which the multimodal network is illustrated in Figure 1.
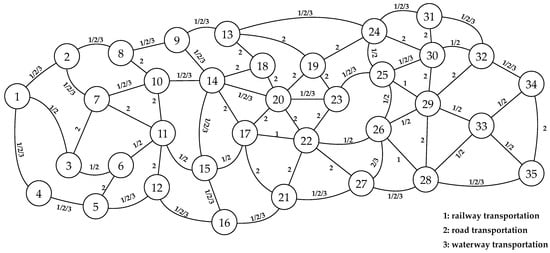
Figure 1.
Multimodal network in the numerical experiment [26].
This numerical experiment assumes that a batch of goods should be moved from Node 1 to Node 35. The goods are carried by 20 ft containers, and the volume is 40 TEU. The goods depart from the origin at 7:00 on the first day, and their time window at the destination is 13:00 to 19:00 on the second day. Unit storage costs are CNY 10/TEU·h, and unit penalty costs are CNY 30/TEU·h at the destination.
In the multimodal network, the average travel speeds of railway, road, and waterway transportation are 60 km/h, 80 km/h, and 30 km/h, respectively [27]. The travel distances of these transportation modes on different arcs referred to by Sun & Lang [26]. Furthermore, according to the definition of the triangular fuzzy number, we used the capacities in Reference [26] as the maximum possible capacities and set 70% and 60% as the most likely capacities and minimum possible capacities, respectively, to generate the prominent points of the triangular fuzzy capacities of the multimodal network. In the numerical experiment, the unit costs and time to transfer goods between different transportation modes at the nodes are shown in Table 1 [26].

Table 1.
Unit costs and time to transfer goods between different transportation modes.
In the numerical experiment, the unit travel costs of different transportation modes are determined by Equation (25) [28]:
This study uses the data presented by Li & Lv [29] as benchmarks to determine the triangular fuzzy carbon emission factors of transportation activities, which can be seen in Table 2 and Table 3. Furthermore, the unit carbon emission costs are set at CNY 10/kg, according to Yuan et al. [30].

Table 2.
Triangular fuzzy carbon emission factors of different transportation modes.

Table 3.
Triangular fuzzy carbon emission factors to transfer goods between different transportation modes.
Under a confidence level of 0.8, we used mathematical programming software Lingo version 12 in a ThinkPad Laptop with Intel Core i5-5200U 2.20 GHz CPU and 8 GB RAM to run the Branch-and-Bound algorithm to solve the problem efficiently and obtain the planned route for the goods shown in Table 4.

Table 4.
Planned route with confidence level of 0.8.
In this study, the confidence level reflects the customer’s preference for the reliability of transportation. To analyze the influence of the confidence level on the optimization results, we took 0.1 as the step and calculated the total costs of the planned routes under different confidence levels from 0.1 to 1.0. The results of this sensitivity are indicated in Figure 2.
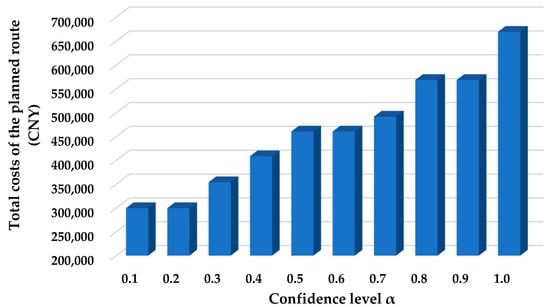
Figure 2.
Sensitivity of the total costs of the planned route concerning confidence level.
As seen in Figure 2, improving the confidence level of the chance constraints increases the total costs of the planned route stepwise. The improvement of the confidence level represents the enhancement of the reliability of the routing. Consequently, we can conclude that the economy and reliability of routing are in conflict with each other. Improving one objective worsens the other one. Based on the sensitivity indicated in Figure 2, the customer can make tradeoffs between the total costs and the reliability of the routing based on his/her preference. The multimodal transport operator can then plan the best multimodal route using the model given in our study.
Meanwhile, this study calculates the carbon emissions of the planned route under different confidence levels and obtains the sensitivity illustrated in Figure 3.
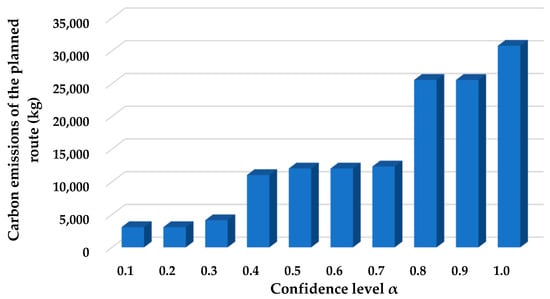
Figure 3.
Sensitivity of the carbon emissions of the planned route concerning the confidence level.
As indicated in Figure 3, the carbon emissions of the planned route increase with the improvement of the confidence level in a stepwise manner. Therefore, the reliability and environmental sustainability of the route are also in conflict with each other. The increase in carbon emissions is an important reason that leads to the increase in the total costs of the planned route.
Under a confidence level of 0.5, this study analyzes the sensitivity of the carbon emissions of the planned route concerning the unit emission costs. When unit emission costs increase from CNY 10/kg to CNY 100/kg with a step of CNY 10/kg, the variations in the total costs, carbon emission costs, and transportation activity costs (the sum of travel costs, transfer costs, storage costs, and penalty costs) of the planned route are those shown in Figure 4.
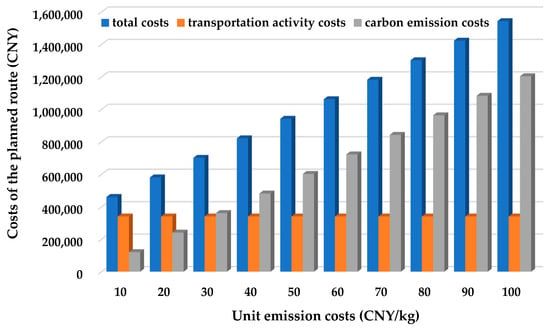
Figure 4.
Sensitivity of the costs of the planned route concerning the unit carbon emission costs under a confidence level of 0.5.
Figure 4 clarifies that the transportation activity costs remain the same since the planned route is unchanged. The increase in the total costs only results from the increase in the unit carbon emission costs. Therefore, charging carbon emissions does not contribute to emission reduction. Under this condition, the emission reduction method is unfeasible, which verifies that charging carbon emissions does not always work in all cases.
In this case, we discuss the bi-objective optimization for the green multimodal routing problem that takes the minimization of transportation activity costs and carbon emissions as two separate objectives. In bi-objective optimization, the economic objective and environmental objective are Equations (26) and (27), respectively, and the constraint set includes Equations (2)–(6), (11)–(14), and (21)–(24).
In this study, we adopted the weighted compromise method [31] to solve the bi-objective optimization model by converting the two objectives into a single one, as shown in Equation (28). In Equation (28), and are the optimum values of the economic and environmental objective functions, while and are the objective function values when another one reaches its optimum. By modifying the weight assigned to the economic objective within its domain, as indicated by Equation (29), we can obtain the Pareto solutions to the problem.
When confidence levels are 0.3, 0.5, and 0.7, the Pareto solutions generated by the weighted compromise method are shown in Figure 5.
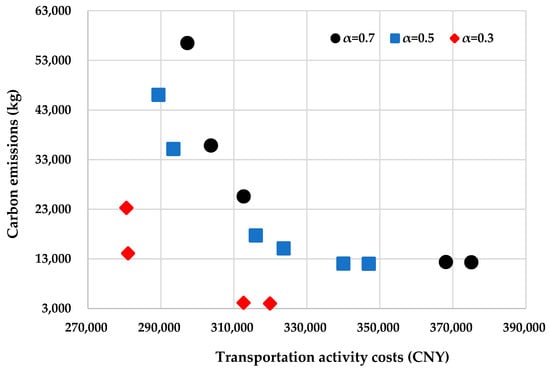
Figure 5.
Pareto solutions to the multi-objective multimodal routing optimization under different confidence levels.
As we can see from Figure 5, bi-objective optimization is more effective than the emission-charging method in reducing carbon emissions when the confidence level is 0.5. Figure 5 clarifies that lowering the transportation activity costs and reducing carbon emissions are the two conflicting objectives of the multimodal routing problem and cannot reach their respective optimum simultaneously. Furthermore, improving the confidence level makes Pareto solutions move to the upper right, which means that improving the reliability worsens both the economy and environmental sustainability of the routing. Based on the sensitivity of Figure 5, we found conflicting relationships among the economy, environmental sustainability, and reliability of the multimodal routing. Therefore, the customer and the multimodal transport operator can make tradeoffs among these three objectives. A multimodal routing scheme that achieves the best comprehensive performance on the objectives can be planned by comparing the various solutions using multiple attribute decision-making methods (e.g., the Analytic Hierarchy Process method).
6. Conclusions
In this study, we explore a green multimodal routing problem with soft time window under capacity and carbon emission factor uncertainty. Triangular fuzzy numbers are used to model the twofold uncertainty of the entire multimodal network, and a fuzzy nonlinear optimization model is accordingly established to deal with the problem. We used a chance-constrained programming approach and linearization transformation to process the model to make the problem easily solvable. The findings from the numerical experiment are summarized as follows:
- (1)
- Improving the confidence level increases the total costs of the planned route, which means that the customer needs to prepare more budget for transportation if more reliable transportation is demanded.
- (2)
- Charging carbon emissions is not always effective in the emission reduction in multimodal routing. As an alternative, bi-objective optimization can provide Pareto solutions to help the customer and multimodal transport operator make tradeoffs between lowering the transportation activity costs and reducing carbon emissions.
- (3)
- When planning a green multimodal route, the multimodal transport operator should first test the feasibility of the emission charging method to avoid extra costs brought to the customer without any helpful effects.
- (4)
- In the bi-objective optimization framework, improving the confidence level increases both the transportation activity costs and carbon emissions of the planned route, which means that the economy, environmental sustainability, and reliability of the multimodal routing in this case are in conflict with each other.
- (5)
- The proposed model can effectively deal with twofold uncertainty and help the customer and the multimodal transport operator to plan the best multimodal route based on their attitudes toward the three objectives.
Based on the conclusions above, in practical decision making, the multimodal transport operator can first help the customer determine a suitable confidence level with reference to the sensitivity analysis. The customer can select the confidence level that satisfies his/her attitude on the reliability of transportation. Then, the multimodal transport operator should check the feasibility of the emission charging method compared to the bi-objective optimization under the given confidence level. If this method is feasible, the multimodal transport operator can, hence, plan the multimodal route based on the prescribed unit emission costs. Otherwise, the multimodal transport operator needs to provide the customers with Pareto solutions for bi-objective optimization. The customer finally makes the decision by making tradeoffs between improving the economy and enhancing the environmental sustainability of transportation. In this case, the customer’s decision might be influenced by the low carbon policy, the willingness of the sustainable development of the company, and the budget for transportation that the customer can afford. However, the proposed optimization model can always find the best solution for the customer and the multimodal transport operator once they determine their attitudes toward the economy, environmental sustainability, and reliability.
Author Contributions
Conceptualization, X.L., Y.S. and D.W.; Formal analysis, X.L., Y.S., J.Q. and D.W.; Funding acquisition, Y.S.; Investigation, X.L., Y.S., J.Q. and D.W.; Methodology, X.L., Y.S., J.Q. and D.W.; Software, Y.S., J.Q. and D.W.; Supervision, Y.S.; Validation, X.L., Y.S. and D.W.; Writing—original draft, X.L., Y.S. and J.Q.; Writing—review and editing, Y.S. and D.W. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the Shandong Provincial Natural Science Foundation of China under Grant No. ZR2023MG020 and the University-Industry Collaborative Education Program of the Ministry of Education of China under Grant Nos. 230711255407320 and 220601369102256.
Data Availability Statement
All data used in this study are included in this paper and can be obtained from the cited reference [26].
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Guo, X.; He, J.; Lan, M.; Yu, H.; Yan, W. Modeling carbon emission estimation for hinterland-based container intermodal network. J. Clean. Prod. 2022, 378, 134593. [Google Scholar] [CrossRef]
- Sun, Y.; Sun, G.; Huang, B.; Ge, J. Modeling a carbon-efficient road–rail intermodal routing problem with soft time windows in a time-dependent and fuzzy environment by chance-constrained programming. Systems 2023, 11, 403. [Google Scholar] [CrossRef]
- A New Mode of Green Transportation System Should Be Constructed by Taking the Multimodal Transportation in the Major Trunk Lines as a Breakthrough. Available online: https://www.zgjtb.com/2022-10/25/content_329922.html (accessed on 10 March 2024).
- Sun, Y.; Yu, N.; Huang, B. Green road-rail intermodal routing problem with improved pickup and delivery services integrating truck departure time planning under uncertainty: An interactive fuzzy programming approach. Complex Intell. Syst. 2022, 8, 1459–1486. [Google Scholar] [CrossRef]
- Caris, A.; Macharis, C.; Janssens, G.K. Decision support in intermodal transport: A new research agenda. Comput. Ind. 2013, 64, 105–112. [Google Scholar] [CrossRef]
- Fazayeli, S.; Eydi, A.; Kamalabadi, I.N. Location-routing problem in multimodal transportation network with time windows and fuzzy demands: Presenting a two-part genetic algorithm. Comput. Ind. Eng. 2018, 119, 233–246. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, F.Y.; Yuan, X.M.; Zhang, H.Y. Low-carbon multimodal transportation path optimization under dual uncertainty of demand and time. Sustainability 2021, 13, 8180. [Google Scholar] [CrossRef]
- Guo, W.; Atasoy, B.; Beelaerts van Blokland, W.; Negenborn, R.R. A global intermodal shipment matching problem under travel time uncertainty. Lect. Notes Comput. Sci. 2020, 12433, 553–568. [Google Scholar]
- Hrusovsky, M.; Demir, E.; Jammernegg, W.; Van Woensel, T. Hybrid simulation and optimization approach for green intermodal transportation problem with travel time uncertainty. Flex. Serv. Manuf. J. 2018, 30, 486–516. [Google Scholar] [CrossRef]
- Wang, W.; Xu, X.; Jiang, Y.; Xu, Y.; Cao, Z.; Liu, S. Integrated scheduling of intermodal transportation with seaborne arrival uncertainty and carbon emission. Transp. Res. Part D Transp. Environ. 2020, 88, 102571. [Google Scholar] [CrossRef]
- Uddin, M.; Huynh, N. Reliable routing of road-rail intermodal freight under uncertainty. Netw. Spat. Econ. 2019, 19, 929–952. [Google Scholar] [CrossRef]
- Lu, Y.; Lang, M.; Sun, Y.; Li, S. A fuzzy intercontinental road-rail multimodal routing model with time and train capacity uncertainty and fuzzy programming approaches. IEEE Access 2020, 8, 27532–27548. [Google Scholar] [CrossRef]
- Sun, Y. Fuzzy approaches and simulation-based reliability modeling to solve a road-rail intermodal routing problem with soft delivery time windows when demand and capacity are uncertain. Int. J. Fuzzy Syst. 2020, 22, 2119–2148. [Google Scholar] [CrossRef]
- Cheng, X.Q.; Jin, C.; Wang, C.; Mamatok, Y. Impacts of different low-carbon policies on route decisions in intermodal freight transportation: The case of the west river region in China. In International Forum on Shipping, Ports and Airports (IFSPA) 2019Hong Kong Polytechnic University; National Academics: Washington, DC, USA, 2019. [Google Scholar]
- Zheng, Y.; Liu, B. Fuzzy vehicle routing model with credibility measure and its hybrid intelligent algorithm. Appl. Math. Comput. 2006, 176, 673–683. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Fuzzy set theory. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 317–332. [Google Scholar] [CrossRef]
- Sahinidis, N.V. Optimization under uncertainty: State-of-the-art and opportunities. Comput. Chem. Eng. 2004, 28, 971–983. [Google Scholar] [CrossRef]
- Chen, S.M. Evaluating weapon systems using fuzzy arithmetic operations. Fuzzy Sets Syst. 1996, 77, 265–276. [Google Scholar] [CrossRef]
- Arriola, E.R.; Ubando, A.T.; Chen, W.H. A bibliometric review on the application of fuzzy optimization to sustainable energy technologies. Int. J. Energy Res. 2022, 46, 6–27. [Google Scholar] [CrossRef]
- Xu, J.; Zhou, X. Approximation based fuzzy multi-objective models with expected objectives and chance constraints: Application to earth-rock work allocation. Inf. Sci. 2013, 238, 75–95. [Google Scholar] [CrossRef]
- Mula, J.; Peidro, D.; Poler, R. The effectiveness of a fuzzy mathematical programming approach for supply chain production planning with fuzzy demand. Int. J. Prod. Econ. 2010, 128, 136–143. [Google Scholar] [CrossRef]
- Peykani, P.; Hosseinzadeh Lotfi, F.; Sadjadi, S.J.; Ebrahimnejad, A.; Mohammadi, E. Fuzzy chance-constrained data envelopment analysis: A structured literature review, current trends, and future directions. Fuzzy Optim. Decis. Mak. 2022, 21, 197–261. [Google Scholar] [CrossRef]
- Asghari, M.; Fathollahi-Fard, A.M.; Mirzapour Al-E-Hashem, S.M.J.; Dulebenets, M.A. Transformation and linearization techniques in optimization: A state-of-the-art survey. Mathematics 2022, 10, 283. [Google Scholar] [CrossRef]
- Xie, Y.; Lu, W.; Wang, W.; Quadrifoglio, L. A multimodal location and routing model for hazardous materials transportation. J. Hazard. Mater. 2012, 227, 135–141. [Google Scholar] [CrossRef] [PubMed]
- Zandkarimkhani, S.; Mina, H.; Biuki, M.; Govindan, K. A chance constrained fuzzy goal programming approach for perishable pharmaceutical supply chain network design. Ann. Oper. Res. 2020, 295, 425–452. [Google Scholar] [CrossRef]
- Sun, Y.; Lang, M. Bi-objective optimization for multi-modal transportation routing planning problem based on Pareto optimality. J. Ind. Eng. Manag. 2015, 8, 1195–1217. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H.Y.; Yuan, X.M.; Hao, Y.C. Path optimization of low-carbon multimodal transportation under dual uncertainty. J. Beijing Jiaotong Univ. (Soc. Sci. Ed.) 2022, 21, 113–121. [Google Scholar]
- Jiang, Q.W.; Lin, Y.; Feng, F.L. Research on multimodal transport path optimization problem considering carbon tax value changes under fuzzy time. J. Ind. Technol. Econ. 2020, 39, 81–88. [Google Scholar]
- Li, Y.L.; Lv, Y.B. Study on economy of multi-modal transport considering carbon emission and time cost. China Transp. Rev. 2023, 45, 143–147. [Google Scholar]
- Yuan, X.M.; Jiang, Y.D.; Zhang, X. Research on robust optimization of interval-based fuzzy multimodal transport paths under low-carbon policies. Ind. Eng. Manag. 2021, 26, 134–141. [Google Scholar]
- Hu, H.; Li, X.; Zhang, Y.; Shang, C.; Zhang, S. Multi-objective location-routing model for hazardous material logistics with traffic restriction constraint in inter-city roads. Comput. Ind. Eng. 2019, 128, 861–876. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).