On Proximity Spaces Constructed on Rough Sets

Abstract

Based on equivalence relation R on X, equivalence class $\left[x\right]$ of a point and equivalence class $\left[A\right]$ of a subset represent the neighborhoods of x and A, respectively. These neighborhoods play the main role in defining separation axioms, metric spaces, proximity relations and uniformity structures on an approximation space $(X,R)$ depending on the lower approximation and the upper approximation of rough sets. The properties and the possible implications of these definitions are studied. The generated approximation topology ${\tau }_R$ on X is equivalent to the generated topologies associated with metric d, proximity $\delta$ and uniformity $\mathcal{U}$ on X. Separated metric spaces, separated proximity spaces and separated uniform spaces are defined and it is proven that both are associating exactly discrete topology ${\tau }_R$ on X.

1. Introduction

Originally, Pawlak in [1] initiated the notions of lower approximation set $L\left(A\right)$ and upper approximation set $U\left(A\right)$ of subset A of universal set X depending on the equivalence classes formed by equivalence relation R on X. The pair $(X,R)$ is then called an approximation space. From the set difference, $U\left(A\right)\setminus L\left(A\right)$, a boundary region area is formed and is called the boundary region set $B\left(A\right)$. Any subset in $(X,R)$ is then a rough set (whenever $B\left(A\right)\ne \varnothing$) or an exact set (whenever $B\left(A\right)=\varnothing$). The importance of this boundary region set is in its role in many real applications; refs. [2,3] are samples of research work of such applications. Decision Theory and Data Mining are the most intercept branches with the concept of rough sets. Yao in [4,5] extended the research work on rough sets and explained the algebraic properties of rough sets. Some researchers paid their attention to the approximation spaces $(X,R)$ constructed by an arbitrary (not equivalence) relation R on X. As an example, ref. [6] objected to the effects on the notion of rough sets by reflexive relations or transitive relation or both. Generating approximation topology ${\tau }_R$ associated with $(X,R)$ is explained well in [7,8], whenever $(X,R)$ is constructed by arbitrary relation R on X. Then, we obtain left approximation neighborhoods $R<x>$ and right approximation neighborhoods $<x>R$ at each point $x\in X$. That is, the notion of rough sets has a generalized form (as found in [4,9]) in which the definition of Pawlak is a special case. Kozae, in [10], introduced a generalization of rough sets using the intersection of left and right approximation neighborhoods $R<x>$ and $<x>R$, respectively, at point $x\in X$. The resulting rough sets (in [10]) have fewer boundary region sets than those defined in [1,4,9], and so it is a good generalized definition. Following that generalized definition in [10], Ibedou et al. [11,12] introduced two types of generalizations of rough sets in the fuzzy case. Also, in this paper, we follow the same strategy. For all basics in general topology, please refer to [13,14,15].

The aim of this paper is to construct a proximity relation and a uniformity structure on an approximation space $(X,R)$, and also define a metric function and separation axioms based on the rough sets in $(X,R)$. In Section 2, we present (in the sense of Pawlak) some basics of rough sets and introduce the definitions of separation axioms $T_i,i=0,1,2,3,4$ in $(X,R)$. In Section 3, we focus on defining metric d on approximation space $(X,R)$ and study its usual properties. In Section 4, we define proximity relation $\delta$ on $(X,R)$ and study its properties. In Section 5, we define a uniform structure $\mathcal{U}$, similar to that defined in [16], on $(X,R)$. We study the relations in between notion separation axioms $T_i,i=0,1,2,3,4$ in $(X,R)$, metric spaces $(X,d)$, proximity spaces $(X,\delta )$ and uniform spaces $(X,\mathcal{U})$ based on the rough sets defined by an equivalence relation R on X. Finally, in Section 6, we explain the deviations in these notions whenever R is not an equivalence relation on X.

2. Preliminaries

Throughout the paper, we let X be a universal set of objects, let $P\left(X\right)$ be the power set of X and let $2^X$ denote the set of all characteristic functions on X. Then, in the set theory, it is well known that there is a one-to-one correspondence between $P\left(X\right)$ and $2^X$. Thus, we use subset A and characteristic function A without distinction.

Relation R on X is mapping $R:X\times X\to \{0,1\}$ defined by the following: for any $x,y\in X,$

$$R(x,y)=1\mathrm{i}\mathrm{f}x\mathrm{a}\mathrm{n}\mathrm{d}y\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}\mathrm{a}\mathrm{n}\mathrm{d}R(x,y)=0\mathrm{i}\mathrm{f}x\mathrm{a}\mathrm{n}\mathrm{d}y\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{o}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}.$$

R is called an equivalence relation on X if it satisfies the following conditions:

(1)

R is reflexive, that is, for all $x\in X,$ we have $R(x,x)=1$,

(2)

R is symmetric, that is, $R(x,y)=R(y,x)$ for any $x,y\in X$,

(3)

R is transitive, that is, $R(x,z)\le R(x,y)\wedge R(y,z)$ for any $x,y,z\in X$,

where $R(x,y)\wedge R(y,z)=min\left\{R\right(x,y),R(y,z\left)\right\}.$

The pair $(X,R)$ is called an approximation space (see [1]).

The equivalence relation R is partitioning X into equivalence classes $\left[x\right]$ for each $x\in X$, where an equivalence class $\left[x\right]$ is mapping $\left[x\right]:X\to \{0,1\}$ defined, for each $y\in X$, as follows:

$$\left[x\right]\left(y\right)=1\mathrm{iff}R(y,x)=1\mathrm{a}\mathrm{n}\mathrm{d}\left[x\right]\left(y\right)=0\mathrm{iff}R(y,x)=0.$$

Then, for any $x,y\in X$, we have

$$x\in \left[y\right]\mathrm{iff}y\in \left[x\right]\mathrm{iff}\left[x\right]=\left[y\right]\mathrm{iff}\left[x\right]\cap \left[y\right]\ne \varphi ,$$

and moreover, $\left[x\right]$ and $\left[y\right]$ are disjointed:

$$\left[x\right]\cap \left[y\right]=\varnothing \mathrm{iff}R(x,y)=0\mathrm{iff}\left[x\right]\left(z\right)\ne \left[y\right]\left(z\right)\mathrm{for}\mathrm{all}z\in X.$$

Now, for each $A\in 2^X$, the equivalence class $\left[A\right]$ of A is defined by

$$\left[A\right]=\underset{x\in A}{\bigvee }\left[x\right].$$

Then, $\left[A\right]=\{z\in X:\mathrm{there}\mathrm{exists}x\in A\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}R(x,z)=1\}$ that is,

$$\left[A\right]\left(z\right)=1\mathrm{iff}R(x,z)=1\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{m}\mathrm{e}x\in A.$$

For each $x\in X$ and each $A\in 2^X$, we have $\left\{x\right\}\subseteq \left[x\right]$ and $A\subseteq \left[A\right]$, respectively, and these equivalence classes, $\left[x\right]$ and $\left[A\right]$, are called the neighborhoods of x and A, respectively.

In general, let us define an equivalence class $\left[B\right]$ as follows:

$$\left[B\right]\left(x\right)=\underset{y\in X}{\bigvee }\left(B\left(y\right)\wedge R(y,x)\right)\equiv \underset{y\in X}{\bigvee }(B\cap \left[x\right])\left(y\right).$$

(1)

Remark 1.

For $A,B\subseteq X$ where A which is not a singleton or B is not a singleton, we have $\left[A\right]\cap \left[B\right]=\varnothing ,whichimpliesA\cap B=\varnothing$ but not the converse. For example, we let $X=\{a,b,c,d,e,f\}$, $R=\left\{\right(a,a),(b,b),(c,c),(d,d),(e,e),(f,f),(b,d),(d,b),(e,f),(f,e\left)\right\}$, $K=\{a,c,d\}$, $H=\{b,e\}$. Then, $\left[K\right]=\{a,b,c,d\}$, $\left[H\right]=\{b,d,e,f\}$. That is, $K\cap H=\varnothing$ while $\left[K\right]\cap \left[H\right]=\{b,d\}\ne \varnothing$. Thus, for non-singleton sets, $A,B$ may be found $\left[A\right]\cap \left[B\right]\ne \varnothing$ but $\left[A\right],\left[B\right]$ are not identical as the case with two singletons. $A\subseteq \left[B\right]$ and $B\subseteq \left[A\right]$ implies $\left[A\right]=\left[B\right]$, and in general ${\left[A\right]}^c\subseteq A^c\subseteq \left[A^c\right]$, $\left[\right[A\left]\right]=\left[A\right]$. Moreover, $A\subseteq B$ implies $\left[A\right]\subseteq \left[B\right]$. We recall that

$$\begin{array}{ccc}\hfill \left[A\right]\cap \left[B\right]=\varnothing & implies& \left(\right[A]\cap \{x\}=\varnothing \mathrm{for}\mathrm{all}x\in B)\hfill \\ & equivuivalent to& \left(\right[B]\cap \{y\}=\varnothing \mathrm{for}\mathrm{all}y\in A)\hfill \\ & implies& \left(\right[x]\cap [y]=\varnothing \mathrm{for}\mathrm{all}x\in B,y\in A).\hfill \end{array}$$

Lemma 1.

For any $A,B\in 2^X$, the following properties are fulfilled:

 (1) 

$\left[A\right]\subseteq B$ implies $A\subseteq B$,

 (2) 

$[A\cup B]=\left[A\right]\cup \left[B\right]$,

 (3) 

$\left[A\right]\subseteq B$ implies $\left[B^c\right]\subseteq A^c$, while $A\subseteq B$ implies ${\left[B\right]}^c\subseteq A^c$,

 (4) 

If $\left[A\right]\subseteq B$, then there is $K\in 2^X$ such that $\left[A\right]\subseteq K$ and $\left[K\right]\subseteq B$.

Proof. 

(1)

This is easily proven using Remark 1.

(2)

$\left[A\right]\cup \left[B\right]\subseteq [A\cup B]$ is clear. Now, we let $x\in [A\cup B]$. Then, there is $y\in A\cup B$ such that $R(x,y)=1$; that is, there is $y\in A$ or $y\in B$ such that $R(x,y)=1$. Thus, $x\in \left[A\right]$ or $x\in \left[B\right]$. So, $x\in \left[A\right]\cup \left[B\right]$; that is, $[A\cup B]\subseteq \left[A\right]\cup \left[B\right]$. Hence, $[A\cup B]=\left[A\right]\cup \left[B\right]$.

(3)

$\left[A\right]\subseteq B$ implies $B^c\subseteq {\left[A\right]}^c$; that is, ${\left[B\right]}^c\subseteq \left[B^c\right]\subseteq {\left[A\right]}^c\subseteq A^c$, while $A\subseteq B$ implies that ${\left[B\right]}^c\subseteq {\left[A\right]}^c\subseteq A^c$.

(4)

The proof is straightforward.

□

Based on the meaning of neighborhoods $\left[x\right],\left[A\right]$, the lower and the upper approximations of any subset of X were defined. For subset A of X, we define approximation subsets $A_{\ast },A^{\ast }:X\to \{0,1\}$ using

$$A_{\ast }=\{x\in X:\left[x\right]\cap A^c=\varnothing \},A^{\ast }=\{x\in X:\left[x\right]\cap A\ne \varnothing \};\mathrm{that}\mathrm{is},\mathrm{for}\mathrm{each}\mathrm{x}\in \mathrm{X},$$

$$\begin{array}{c}\hfill A_{\ast }\left(x\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\left[x\right]\cap A^c=\varnothing \hfill \\ 0\hfill & \mathrm{if}\left[x\right]\cap A^c\ne \varnothing ,\hfill \end{array}\right.\end{array}$$

(2)

$$\begin{array}{c}\hfill A^{\ast }\left(x\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}\left[x\right]\cap A=\varnothing \hfill \\ 1\hfill & \mathrm{if}\left[x\right]\cap A\ne \varnothing .\hfill \end{array}\right.\end{array}$$

(3)

Lemma 2.

If $(X,R)$ is an approximation space with R an arbitrary relation on X, then, for any $A,B\in 2^X,$

 (1) 

$X_{\ast }=X,{\varnothing }^{\ast }=\varnothing ,$

 (2) 

$A⊈A_{\ast }⊈A,A⊈A^{\ast }⊈A,$

 (3) 

${\left(A_{\ast }\right)}_{\ast }\subseteq A_{\ast },$${\left(A^{\ast }\right)}^{\ast }\supseteq A^{\ast },$

 (4) 

${(A\cap B)}^{\ast }\subseteq A^{\ast }\cap B^{\ast },{(A\cup B)}_{\ast }\supseteq A_{\ast }\cup B_{\ast },$

 (5) 

${(A\cup B)}^{\ast }\supseteq A^{\ast }\cup B^{\ast },{(A\cap B)}_{\ast }\subseteq A_{\ast }\cap B_{\ast },$

 (6) 

$A\subseteq B$ implies that $A_{\ast }\subseteq B_{\ast },$ $A^{\ast }\subseteq B^{\ast }.$

Proof. 

The proof is direct. □

Whenever R is reflexive, for any $A,B\in 2^X,$ we have $A_{\ast }\subseteq A,A\subseteq A^{\ast }$, $X^{\ast }=X,{\varnothing }_{\ast }=\varnothing ,{(A\cup B)}^{\ast }=A^{\ast }\cup B^{\ast },{(A\cap B)}_{\ast }=A_{\ast }\cap B_{\ast }.$

If R is also transitive, $A_{\ast \ast }=A_{\ast },A^{\ast \ast }=A^{\ast }$. For any subset A of X, the lower approximation $A_R$ and the upper approximation $A^R$ are defined by

$$A_R=A\cap A_{\ast },A^R=A\cup A^{\ast }.$$

The boundary region set $A^B$ is defined by the set difference, $A^R\setminus A_R=A^B$, and moreover, the accuracy value $\alpha \left(A\right)$ of rough set A is given by the ratio

$$\alpha \left(A\right)=\frac{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{e}\mathrm{l}\mathrm{e}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s} \mathrm{o}\mathrm{f} A_R}{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{e}\mathrm{l}\mathrm{e}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s} \mathrm{o}\mathrm{f} A^R}.$$

Whenever $A^R⊈A_R$, $A^B$ is not empty and set A has a roughness region. Thus, A is called a rough set. As a special case, if $A^R=X,A_R=\varnothing$. Then, $A^B=X$, and A is called a totally rough set. However, if $A^R\subseteq A_R$, then $A^B=\varnothing$, and set A is called an exact set.

From Lemma 2 and the definitions of $A_R$ and $A^R$, we have the following consequences.

Lemma 3.

Let $(X,R)$ be an approximation space with R as an arbitrary relation. Then, for any $A,B\in 2^X$, the following properties are fulfilled:

 (1) 

$X_R=X^R=X,$${\varnothing }_R={\varnothing }^R=\varnothing ,$

 (2) 

$A_R\subseteq A\subseteq A^R,$

 (3) 

${\left(A_R\right)}_R\subseteq A_R,$${\left(A^R\right)}^R\supseteq A^R,$

 (4) 

${(A\cap B)}^R\subseteq A^R\cap B^R,$${(A\cup B)}_R\supseteq A_R\cup B_R,$

 (5) 

${(A\cup B)}^R\supseteq A^R\cup B^R,$${ (A\cap B)}_R\subseteq A_R\cap B_R,$

 (6) 

$A\subseteq B$ implies that $A_R\subseteq B_R,$$A^R\subseteq B^R.$

Proof. 

The proof is straightforward from Lemma 2. □

Note that if R is a reflexive relation, the equality holds in (5), Lemma 3, and moreover, if R is a transitive relation, the equality holds in (3), Lemma 3. Thus, we can deduce that approximation topology ${\tau }_R$ on approximation space $(X,R)$ is associated, for each $A\subseteq X$, with the interior $A^{\circ }$ and the closure $\overline{A}$ defined by $A^{\circ }=A_R$ and $\overline{A}=A^R$.

Now, we recall two operators on X and both operators generate topologies on X, respectively (both are dual).

Mapping $c:2^X\to 2^X$ is called a closure operator on X (see [14]) if it satisfies the following conditions: for any $A,B\in 2^X,$

(C.1) $c(\varnothing )=\varnothing ,$

(C.2) $A\subseteq c\left(A\right),$

(C.3) $c\left(c\right(A\left)\right)=c\left(A\right),$

(C.4) $c(A\cup B)=c\left(A\right)\cup c\left(B\right).$

Mapping $i:2^X\to 2^X$ is called an interior operator on X (see [14]) if it satisfies the following conditions: for any $A,B\in 2^X,$

(I.1) $i\left(X\right)=X,$

(I.2) $i\left(A\right)\subseteq A,$

(I.3) $i\left(i\right(A\left)\right)=i\left(A\right),$

(I.4) $i(A\cap B)=i\left(A\right)\cap i\left(B\right).$

Lemma 4

([14]). Let c be a closure operator on X. Then, topology ${\tau }_c$ is generated on X such that $c\left(A\right)=\overline{A}$ for each $A\in 2^X$, where $\overline{A}$ is the closure of A with respect to topology ${\tau }_c$. In fact, ${\tau }_c=\{F\in 2^X:c\left(F^c\right)=F^c\}.$

Lemma 5

([14]). Let i be an interior operator on X. Then, topology ${\tau }_i$ is generated on X such that $i\left(A\right)=A^{\circ }$ for each $A\in 2^X$, where $A^{\circ }$ is the interior of A with respect to topology ${\tau }_i$. In fact, ${\tau }_i=\{U\in 2^X:i\left(U\right)=U\}.$

We let $(X,R)$ be an approximation space. We define mappings $i,c:2^X\to 2^X$, respectively, for each $A\in 2^X,$ as follows:

$$i\left(A\right)=\bigcup _{\left[x\right]\cap A^c=\varphi }\left\{x\right\}\equiv A_R,$$

(4)

$$c\left(A\right)=\bigcup _{\left[x\right]\cap A\ne \varphi }\left\{x\right\}\equiv A^R.$$

(5)

Then, from Lemma 3, we can easily check that i is an interior operator and c is a closure operator on X. Thus, by Lemmas 5 and 4, there are topologies ${\tau }_i$ and ${\tau }_c$ on X such that $i\left(A\right)=A^{\circ }$ and $c\left(A\right)=\overline{A}$ for each $A\in 2^X$. Furthermore, we have $c\left(A^c\right)=i{\left(A\right)}^c$ and $i\left(A^c\right)=c{\left(A\right)}^c$. So, ${\tau }_i={\tau }_c$, and we denote both of the topologies by ${\tau }_R$. Hence, we consider approximation space $(X,R)$ as the topological space equipped with the interior operator defined by (4) or the closure operator defined by (5). Moreover, the generated topology on X is given by

$${\tau }_R=\{A\subseteq X:A=A^{\circ }\}\equiv \{A\subseteq X:A^c=\overline{A^c}\}.$$

Since $A^{\circ }=A\mathrm{iff}\left[A\right]=A$, $\left[A^c\right]=A^c$. Also, since $\overline{A}=A\mathrm{iff}\left[A^c\right]=A^c$, $\left[A\right]=A$. In general, each $A\in 2^X$ with $\left[A\right]=A$ is an open and closed set in $(X,R)$. That is, $A_R=A^R=A$, and then A is an exact set. That means no roughness of A.

Example 1.

Let $X=\{a,b,c\}$ and $R=\left\{\right(a,a),(b,b),(c,c),(a,b),(b,a\left)\right\}$. Then,

$$\left[a\right]=\left[b\right]=\left[\right\{a,b\left\}\right]=\{a,b\},\left[c\right]=\left\{c\right\}and\left[\right\{a,c\left\}\right]=\left[\right\{b,c\left\}\right]=\left[X\right]=X.$$

(1) If $A=\{a,c\}$ or $A=\{b,c\}$. Then, obtain

$$A_R=\bigcup _{\left[x\right]\cap \left\{b\right\}=\varnothing }\left\{x\right\}=\bigcup _{\left[x\right]\cap \left\{a\right\}=\varnothing }\left\{x\right\}=\left\{c\right\},$$

$$A^R=\bigcup _{\left[x\right]\cap \{a,c\}\ne \varnothing }\left\{x\right\}=\bigcup _{\left[x\right]\cap \{b,c\}\ne \varnothing }\left\{x\right\}=X.$$

(2) If $A=\left\{a\right\}$ or $A=\left\{b\right\}$. Then, obtain

$$A_R=\bigcup _{\left[x\right]\cap \{b,c\}=\varnothing }\left\{x\right\}=\bigcup _{\left[x\right]\cap \{a,c\}=\varnothing }\left\{x\right\}=\varnothing ,$$

$$A^R=\bigcup _{\left[x\right]\cap \left\{a\right\}\ne \varnothing }\left\{x\right\}=\bigcup _{\left[x\right]\cap \left\{b\right\}\ne \varnothing }\left\{x\right\}=\{a,b\}.$$

(3) Since $\left[\right\{a,b\left\}\right]=\{a,b\}$, $\left[c\right]=\left\{c\right\}$ and $\left[X\right]=X$, the lower approximation and the upper approximation of any of these subsets are equal, $A_R=A=A^R$, and then only subsets $\{a,b\},\left\{c\right\},X$ are exact sets and the other four non-empty subsets are rough sets.

Example 2.

Let $X=\{a,b,c,d\}$ and $R=\left\{\right(a,a),(b,b),(c,c),(d,d),(a,b),(b,a),(c,d),(d,c\left)\right\}$. Then, have

$$\begin{array}{cc}\hfill \left[a\right]=\left[b\right]=& \left[\right\{a,b\left\}\right]=\{a,b\},\left[c\right]=\left[d\right]=\left[\right\{c,d\left\}\right]=\{c,d\},\hfill \\ \hfill \left[\right\{a,c\left\}\right]=& \left[\right\{b,c\left\}\right]=\left[\right\{a,d\left\}\right]=\left[\right\{b,d\left\}\right]=\left[\right\{a,b,c\left\}\right]\hfill \\ \hfill =& \left[\right\{a,b,d\left\}\right]=\left[\right\{a,c,d\left\}\right]=\left[\right\{b,c,d\left\}\right]=\left[X\right]=X.\hfill \end{array}$$

(1) If $A\in \left\{\right\{a,c\},\{b,c\},\{a,d\},\{b,d\left\}\right\}$, $A_R=\varnothing$ and $A^R=X$. Thus, these subsets are totally rough sets.

(2) If $A\in \left\{\right\{a,b,c\},\{a,b,d\left\}\right\}$, $A_R=\{a,b\}$ and $A^R=X$.

(3) If $A\in \left\{\right\{a,c,d\},\{b,c,d\left\}\right\}$, $A_R=\{c,d\}$ and $A^R=X$.

(4) If $A\in \left\{\right\{a\},\{b\left\}\right\}$, $A_R=\varnothing$ and $A^R=\{a,b\}$.

(5) If $A\in \left\{\right\{c\},\{d\left\}\right\}$, $A_R=\varnothing$ and $A^R=\{c,d\}$. These subsets appearing in he previous items (2)–(5) are rough sets.

(6) If $A\in \left\{\right\{a,b\},\{c,d\},X\}$, determine that the lower approximation and the upper approximation of any of these subsets are equal, that is, $A_R=A=A^R$. Thus, these subsets are exact sets without roughness.

Example 3.

Let $X=\{a,b,c,d\}$ and $R=\left\{\right(a,a),(b,b),(c,c),(d,d),(b,c),(c,b),(b,d),(d,b),(c,d),(d,c\left)\right\}$. Then, have

$$\begin{array}{c}\left[a\right]=\left\{a\right\},\hfill \\ \left[b\right]=\left[c\right]=\left[d\right]=\left[\right\{b,c\left\}\right]=\left[\right\{b,d\left\}\right]=\left[\right\{c,d\left\}\right]=\left[\right\{b,c,d\left\}\right]=\{b,c,d\},\hfill \\ \left[\right\{a,b\left\}\right]=\left[\right\{a,c\left\}\right]=\left[\right\{a,d\left\}\right]=\left[\right\{a,b,c\left\}\right]=\left[\right\{a,b,d\left\}\right]=\left[\right\{a,c,d\left\}\right]=\left[X\right]=X.\hfill \end{array}$$

(1) If $A\in \left\{\right\{a,b\},\{a,c\},\{a,d\},\{a,b,c\},\{a,b,d\},\{a,c,d\left\}\right\}$, $A_R=\left\{a\right\}$ and $A^R=X.$ These subsets are rough sets. Moreover, the boundary set is $A^B=\{b,c,d\}$, and the accuracy is $\frac{1}{4}$.

(2) If $A\in \left\{\right\{b\},\{c\},\{d\},\{b,c\},\{b,d\},\{c,d\left\}\right\}$, $A_R=\varnothing$ and $A^R=\{b,c,d\}$. These subsets are rough sets. Moreover, the boundary set is $A^B=\{b,c,d\}$, and the accuracy is $\frac{0}{3}=0$.

(3) If $A\in \left\{\right\{a\},\{b,c,d\},X\}$, $A_R=A=A^R$. These non-empty subsets are exact sets. Moreover, the boundary set is $A^B=\varnothing$, and the accuracy is 1.

Example 4.

Let $(X,R)$ be a finite approximation space such that $\left[x\right]=\left\{x\right\}$ for all $x\in X$ (only equal elements are related). Then, $\left[A\right]=A$ for each $A\in 2^X$. Thus, any subset A of X is open and closed, that is, $A_R=A=A^R$ for all $A\in 2^X$, and hence the boundary set is ∅. So, each $A\in 2^X$ is an exact subset of X without roughness.

Definition 1.

An approximation space $(X,R)$ is said to be

(i) a $T_0$-space if for all $x\ne y\in X$, then $t\notin \left[y\right]$ for all $t\in \left[x\right]$ or $s\notin \left[x\right]$ for all $s\in \left[y\right]$,

(ii) a $T_1$-space if for all $x\ne y\in X$, then $t\notin \left[y\right]$ for all $t\in \left[x\right]ands\notin \left[x\right]$ for all $s\in \left[y\right]$, that is, $\left[x\right]\cap \left[y\right]=\varnothing$,

(iii) a $T_2$-space if for all $x\ne y\in X$, then $\left[x\right]\cap \left[y\right]=\varnothing$,

(iv) regular if for all $x\notin F=\overline{F}$, then $t\notin \left[F\right]$ for all $t\in \left[x\right]ands\notin \left[x\right]$ for all $s\in \left[F\right]$, that is, $\left[x\right]\cap \left[F\right]=\varnothing$,

(v) a $T_3$ space if it is regular and $T_1$,

(vi) normal if for all $F=\overline{F},G=\overline{G}$ with $F\cap G=\varnothing$, $t\notin \left[G\right]$ for all $t\in \left[F\right]ands\notin \left[F\right]$ for all $s\in \left[G\right]$, that is, $\left[F\right]\cap \left[G\right]=\varnothing$,

(vii) a $T_4$ space if it is normal and $T_1$.

Remark 2.

 (1) 

Suppose $(X,R)$ is a $T_0$-space and let $x\ne y\in X$. Then, either $\left[x\right]\cap \left[y\right]=\varnothing$ or $\left[x\right]=\left[y\right]$. Thus, every approximation space $(X,R)$ cannot be a $T_0$-space except $\left[x\right]=\left\{x\right\}$ for all $x\in X$.

 (2) 

$(X,R)$ is a $T_1$-space if and only if $\left[x\right]=\left\{x\right\}$ for all $x\in X$ if and only if $\overline{\left\{x\right\}}=\left\{x\right\}$ for all $x\in X$ from Equation (5).

 (3) 

It is obvious that $T_0$, $T_1$ and $T_2$ separation axioms are equivalent definitions in an approximation space $(X,R)$.

Proposition 1.

From Definition 1, $T_4\Rightarrow T_3\Rightarrow T_2\iff T_1\iff T_0$.

3. Metric Distance in Approximation Spaces

Let $d:X\times X\to \{0,1\}$ be a mapping satisfying the following conditions:

(D1)

$x=y$ implies that $d(x,y)=0$,

(D2)

$d(x,y)=d(y,x)$ for all $x,y\in X$,

(D3)

$d(x,z)\le d(x,y)+d(y,z)$ for all $x,y,z\in X$,

(D4)

$d(x,y)=0$ implies that $x=y$.

d is called a metric on X if mapping d satisfies only conditions (D1)–(D3). Then, d is called a pseudo-metric on X if d satisfies only conditions (D1), (D3). Then, d is called a quasi-pseudo-metric on X, and if d satisfies only conditions (D1), (D3), (D4), d is called a quasi-metric on X.

Let $(X,R)$ be an approximation space with an equivalence relation R on X and $d:X\times X\to \{0,1\}$ a mapping defined as a relation on X in the following way:

$$\begin{array}{c}\hfill d(x,y)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\left[x\right]\cap \left\{y\right\}=\varnothing \hfill \\ 0\hfill & \mathrm{if}\left[x\right]\cap \left\{y\right\}\ne \varnothing .\hfill \end{array}\right.\end{array}$$

(6)

From (6), it is obvious that $x=y$ implies $d(x,y)=0$. Since $\left[x\right]\cap \left\{y\right\}=\varnothing \equiv \left[y\right]\cap \left\{x\right\}=\varnothing$, $d(x,y)=d(y,x)$. Also, it is clear that $d(x,z)\le d(x,y)+d(y,z)$. On the other hand, if $\left[x\right]=\left[y\right]=\{x,y\}$, then, clearly, $d(x,y)=0$ but $x\ne y.$ Thus, d defines a pseudo-metric on X. In this case, the pair $(X,d)$ is called a pseudo-metric space induced by $(X,R)$ and we write the topology on X induced by d or associated to d as ${\tau }_d$. The pair $(X,{\tau }_d)$ is the associated topological space.

It is clear that there is a distance between x and y in X if and only if $\left[x\right]\cap \left\{y\right\}=\varnothing$.

For each $x\in X$ and each $A\in 2^X$, the distance between x and A, denoted by $d(x,A)$, is defined as follows:

$$d(x,A)=\underset{y\in A}{\bigwedge }d(x,y)$$

which is equivalent to

$$\begin{array}{c}\hfill d(x,A)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\left[x\right]\cap A=\varnothing \hfill \\ 0\hfill & \mathrm{if}\left[x\right]\cap A\ne \varnothing .\hfill \end{array}\right.\end{array}$$

(7)

For any $A,B\in 2^X$, the distance between A and B, denoted by $d(A,B)$, is defined as follows:

$$d(A,B)=\underset{x\in A}{\bigwedge }\underset{y\in B}{\bigwedge }d(x,y)$$

which is equivalent to

$$\begin{array}{c}\hfill d(A,B)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\left[A\right]\cap B=\varnothing \hfill \\ 0\hfill & \mathrm{if}\left[A\right]\cap B\ne \varnothing .\hfill \end{array}\right.\end{array}$$

(8)

Then, from (7), we can rewrite Equations (2) and (3), respectively, as follows:

$$\begin{array}{c}\hfill A_{\ast }\left(x\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}d(x,A^c)=1\hfill \\ 0\hfill & \mathrm{if}d(x,A^c)=0,\hfill \end{array}\right.\end{array}$$

(9)

$$\begin{array}{c}\hfill A^{\ast }\left(x\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}d(x,A)=1\hfill \\ 1\hfill & \mathrm{if}d(x,A)=0.\hfill \end{array}\right.\end{array}$$

(10)

Thus, from Equations (4) and (5), obtain

$${\mathrm{int}}_{{\tau }_d}\left(A\right)=A^{\circ }=A_R=A_{\ast }=\bigcup _{d(x,A^c)=1}\left\{x\right\},$$

(11)

$${\mathrm{cl}}_{{\tau }_d}\left(A\right)=\overline{A}=A^R=A^{\ast }=\bigcup _{d(x,A)=0}\left\{x\right\},$$

(12)

where ${\mathrm{int}}_{{\tau }_d}\left(A\right)$ and ${\mathrm{cl}}_{{\tau }_d}\left(A\right)$ denote the interior and the closure of A with respect to topology ${\tau }_d$, respectively. So, it can easily be seen that ${\tau }_d={\tau }_R.$

Pseudo-metric d on the approximation space $(X,R)$ is a metric on X, if $x\ne y\in X$ implies $d(x,y)=1$, that is, $\left[x\right]=\left\{x\right\}$ for all $x\in X$. The associated topological space $(X,{\tau }_d)$ proves that it is a normal topological space. Based on the definition of a metric d, and that R is given by $R(x,x)=1$ for all $x\in X$, otherwise $R(x,y)=0$, $(X,{\tau }_d)$ is a $T_1$ space. Thus, $(X,{\tau }_d)$ is a $T_4$ space, which means satisfying all the $T_i$ separation axioms; $i=0,1,2,3$. Recall that $(X,{\tau }_d)$ in this case is exactly a discrete topological space, i.e., all subsets are open and closed. Moreover, Equations (7) and (8) could be rewritten as

$$\begin{array}{c}\hfill d(x,A)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}x\notin A\hfill \\ 0\hfill & \mathrm{if}x\in A,\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill d(A,B)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}A\cap B=\varnothing \hfill \\ 0\hfill & \mathrm{if}A\cap B\ne \varnothing .\hfill \end{array}\right.\end{array}$$

Proposition 2.

Let $(X,d)$ be a pseudo-metric space and let ${\tau }_d$ be the topology associated to d. Then, $(X,{\tau }_d)$ is a normal space. Moreover, if d is a metric, then $(X,{\tau }_d)$ is a $T_4$ space.

Proof. 

We suppose d is a metric on X. From Equation (6), we determine that $x\ne y$ if $d(x,y)=1$ if $\left[x\right]\cap \left\{y\right\}=\left[y\right]\cap \left\{x\right\}=\varnothing$, and then $y\notin \left[x\right]$ and $x\notin \left[y\right]$. Hence, $(X,{\tau }_d)$ is a $T_1$ space.

We let $F={\mathrm{cl}}_{{\tau }_d}F\in 2^X$, $G={\mathrm{cl}}_{{\tau }_d}G\in 2^X$ with $F\cap G=\varnothing$. Then, we have

$$F\subseteq G^c={\mathrm{int}}_{{\tau }_d}\left(G^c\right)\mathrm{a}\mathrm{n}\mathrm{d}G\subseteq F^c={\mathrm{int}}_{{\tau }_d}\left(F^c\right).$$

Thus, $\left[F\right]\subseteq \left[G^c\right]=G^c$ and $\left[G\right]\subseteq \left[F^c\right]=F^c$. We assume that $\left[F\right]\cap \left[G\right]\ne \varnothing ,$ say, $t\in \left[F\right]\cap \left[G\right]$. Then, there exist $x\in F$ and $y\in G$ such that $R(x,t)=1$ and $R(t,y)=1$. Thus, $R(x,y)=1$. So, $x\in \left[G\right]\subseteq F^c$ and $y\in \left[F\right]\subseteq G^c$ and both are contradictions. Hence, $\left[F\right]\cap \left[G\right]=\varnothing$. Therefore, $(X,{\tau }_d)$ is normal. □

4. Proximity Relation in Approximation Spaces

Binary relation $\delta$ on $2^X$ is called a nearness relation or a proximity on X, provided that the negation of $\delta$, denoted by $\overline{\delta }$ (called a farness relation), for any $A,B,K\in 2^X$, fulfills the following conditions (see [15]):

(P1) $A\overline{\delta }B$ implies $B\overline{\delta }A$,

(P2) $(A\cup B)\overline{\delta }K$ if and only if $A\overline{\delta }K$ and $B\overline{\delta }K$,

(P3) $A=\varnothing$ or $B=\varnothing$ implies $A\overline{\delta }B$,

(P4) $A\overline{\delta }B$ implies $A\cap B=\varnothing$,

(P5) if $A\overline{\delta }B$. Then, there is $L\in 2^X$ such that $A\overline{\delta }L$ and $L^c\overline{\delta }B$.

The pair $(X,\delta )$ is called a proximity space. Note that $\delta$ is the negation of $\overline{\delta }$, that is, $A\delta B\equiv A/\overline{\delta }B$.

(P1) and (P2) imply the following condition:

(P2^′) $K\overline{\delta }(A\cup B)$ if and only if $K\overline{\delta }A$ and $K\overline{\delta }B$.

In the following proposition, we show that there is a proximity on an approximation space $(X,R)$.

Proposition 3.

Let $(X,R)$ be an approximation space and let δ be a binary relation on $2^X$ defined, for any $A,B\in 2^X$, as follows:

$$A\overline{\delta }B\mathrm{if} \mathrm{and} \mathrm{only} \mathrm{if}\left[A\right]\cap B=\varnothing .$$

Then, δ is a proximity on X. In this case, δ is called a proximity on X induced by R and the pair $(X,\delta )$ is called a proximity space of $(X,R).$

Proof. 

(P1) Suppose $A\overline{\delta }B$ for any $A,B\in 2^X$. Then, by the definition of $\delta$, $\left[A\right]\cap B=\varnothing .$ Thus, $\left[A\right]\subseteq B^c$. So, by Lemma 1 (3), $\left[B\right]\subseteq A^c$. Hence, $B\overline{\delta }A$.

(P2) Suppose $(A\cup B)\overline{\delta }K$ for any $A,B,K\in 2^X.$ Then, clearly, $[A\cup B]\cap K=\varnothing .$ Thus, by Lemma 1 (2), $\left(\right[A]\cup [B\left]\right)\cap K=\varnothing ,$ that is, $\left(\right[A]\cap K)\cup \left(\right[B]\cap K)=\varnothing .$ So, $\left[A\right]\cap K=\varnothing$ and $\left[B\right]\cap K=\varnothing$. Hence, $A\overline{\delta }K$ and $B\overline{\delta }K$.

Conversely, suppose $A\overline{\delta }K$ and $B\overline{\delta }K$. Assume that $(A\cup B)\delta K$, that is, $[A\cup B]\cap K\ne \varnothing$. Then, there is $x\in K$ and $R(x,y)=1$ for some $y\in A\cup B$. Thus, $R(x,y)=1$ for some $y\in A$ or $y\in B$. So, $x\in \left[A\right]$ or $x\in \left[B\right]$, that is, $\left[A\right]\cap K\ne \varnothing$ or $\left[B\right]\cap K\ne \varnothing$. Both are contradicting $A\overline{\delta }K$ and $B\overline{\delta }K$. Hence, $(A\cup B)\overline{\delta }K$.

(P3), (P4) The proofs are straightforward.

(P5) Suppose $A\overline{\delta }B$ for any $A,B\in 2^X.$ Then, clearly, $\left[A\right]\cap B=\varnothing$, that is, $\left[A\right]\subseteq B^c$. Thus, there is $H\subseteq B^c$ such that $\left[A\right]\subseteq H\subseteq \left[H\right]\subseteq B^c$. Thus, $A\overline{\delta }{H}^c$ and $H\overline{\delta }B$, which is equivalent to there is $L\in 2^X$ such that $A\overline{\delta }L$ and $L^c\overline{\delta }B$. □

Let $\delta$ be a proximity on an approximation space $(X,R)$. Consider two mappings, $in{t}_{\delta },c{l}_{\delta }:2^X\to 2^X$ defined, for each $A\in 2^X,$ respectively, as follows:

$${\mathrm{int}}_{\delta }A=\bigcup _{\left\{x\right\}\overline{\delta }{A}^c}\left\{x\right\}\equiv \bigcup _{\left[x\right]\cap A^c=\varnothing }\left\{x\right\}\equiv \bigcup _{d(x,A^c)=1}\left\{x\right\}\equiv A_R\equiv A^{\circ }$$

(13)

and

$${\mathrm{cl}}_{\delta }A=\bigcup _{\left\{x\right\}/\overline{\delta }A}\left\{x\right\}\equiv \bigcup _{\left[x\right]\cap A\ne \varnothing }\left\{x\right\}\equiv \bigcup _{d(x,A)=0}\left\{x\right\}\equiv A^R\equiv \overline{A}.$$

(14)

Then, it can easily be checked that $in{t}_{\delta }$ is an interior operator and $c{l}_{\delta }$ a closure operator on X. Thus, by Lemmas 4 and 5, there is topology ${\tau }_{\delta }$ (called the topology associated to) on X. In fact,

$${\tau }_{\delta }=\{K\subseteq X:K={\mathrm{int}}_{\delta }K\}\equiv \{K\subseteq X:K^c={\mathrm{cl}}_{\delta }\left(K^c\right)\}.$$

The pair $(X,{\tau }_{\delta })$ is the associated topological space to $(X,\delta )$. It is obvious that ${\tau }_{\delta }={\tau }_R$.

Proximity $\delta$ on approximation space $(X,R)$ is said to be separated if $x\ne y\in X$ implies $\left\{x\right\}\overline{\delta }\left\{y\right\}$. It is obvious that $\delta$ is a separated proximity if and only if $\left[x\right]=\left\{x\right\}$ for all $x\in X$, that is, $(X,{\tau }_{\delta })$ is a $T_1$-space if and only if the pseudo-metric d is a metric.

In the following Proposition, it is proven that topological space $(X,{\tau }_{\delta })$ associated to proximity space $(X,\delta )$ is a $T_4$ space.

Proposition 4.

Let $(X,\delta )$ be the proximity space for an approximation space $(X,R)$ and let ${\tau }_{\delta }$ be the topology associated to δ. Then, $(X,{\tau }_{\delta })$ is a normal space. Moreover, if δ is separated, $(X,{\tau }_{\delta })$ is a $T_4$ space.

Proof. 

Clear as given in Proposition 2 and from Equations (13) and (14). □

Proposition 5.

Let $(X,{\tau }_R)$ be a topological approximation space. Then, the constructed proximity δ on X fulfills, for any $A,B\in 2^X,$ the following property:

$$A\overline{\delta }B\mathrm{if} \mathrm{and} \mathrm{only} \mathrm{if}\overline{A}\overline{\delta }\overline{B}.$$

Proof. 

From conditions (P1), (P2), $\overline{A}\overline{\delta }\overline{B}\mathrm{if}A\overline{\delta }\overline{B}\mathrm{if}A\overline{\delta }B$. Also, $\overline{A}\overline{\delta }\overline{B}\mathrm{if}\overline{A}\overline{\delta }B\mathrm{if}A\overline{\delta }B$. □

Let $(X,d)$ be the pseudo-metric space induced by an approximation space $(X,R)$. Then, we can define proximity $\delta$ on X in the following way: for any $A,B\in 2^X,$

$$A\overline{\delta }B\mathrm{iff}d(A,B)=1orA\delta B\mathrm{iff}d(A,B)=0.$$

(15)

It is easy to see that $\delta$ satisfies Conditions (P1)–(P5) depending on the properties of the pseudo-metric d. Moreover, if d is a metric on X, $\delta$ is a separated proximity on X. Thus, the resulting interior operators and closure operators in both of $(X,d)$ and $(X,\delta )$ (as shown in Equations (11)–(14)) generate equivalent topologies ${\tau }_d$ and ${\tau }_{\delta }$. So, both of them are equivalent to discrete topology ${\tau }_R$ generated on X. Hence, all subsets of X have identical lower approximations and upper approximations.

In this case,

$$d(A,B)=1\mathrm{iff}A\overline{\delta }B\mathrm{iff}A\cap B=\varnothing ,d(A,B)=0\mathrm{iff}A\delta B\mathrm{iff}A\cap B\ne \varnothing .$$

5. Uniform Structure in Approximation Spaces

In this section, we study the relation between the uniform spaces and the $T_i$ separation axioms given in Section 2, the defined pseudo-metric in Section 3 and the defined proximity in Section 4.

For a non-empty set X, the top relation and the bottom relation on X, denoted by $\mathbf{T}$ and $\mathbf{B}$, are relations on X, respectively, defined, for any $x,y\in X$, as follows:

$$\mathbf{T}(x,y)=1\mathrm{a}\mathrm{n}\mathrm{d}\mathbf{B}(x,y)=0.$$

$2^{X\times X}$ denotes the bounded set of all relations on X.

For each $R\in 2^{X\times X},$ the inverse relation of R, denoted by $R^{-1}$, is a relation on X defined, for any $x,y\in X$, as follows:

$$R^{-1}(x,y)=R(y,x).$$

Binary operations ∧ and ∨ on $2^{X\times X}$ between arbitrary relations are defined, for any $R_1,R_2\in 2^{X\times X}$ and any $x,y\in X,$ by

$$(R_1\wedge R_2)(x,y)=R_1(x,y)\wedge R_2(x,y)\mathrm{a}\mathrm{n}\mathrm{d}(R_1\vee R_2)(x,y)=R_1(x,y)\vee R_2(x,y).$$

For any $R_1,R_2\in 2^{X\times X},$ the composition of $R_1$ and $R_2$, denoted by $R_1\circ R_2$, is a relation on X defined as follows: for any $x,z\in X$,

$$(R_1\circ R_2)(x,z)=\underset{y\in X}{\bigvee }{R}_1(x,y)\wedge R_2(y,z).$$

(16)

The order relation ≤ on $2^{X\times X}$ is defined, for any $R_1,R_2\in 2^{X\times X}$ and $x,y\in X,$ by

$$R_1\le R_2\mathrm{iff}{R}_1(x,y)\le R_2(x,y).$$

Definition 2.

Filter $\mathcal{M}$ on $X\times X$ is mapping $\mathcal{M}:2^{X\times X}\to \{0,1\}$ satisfying the following conditions:

(i) $\mathcal{M}\left(\mathbf{T}\right)=1$, ($\mathcal{M}\left(\mathbf{B}\right)=0$ to be a proper filter),

(ii) $R_1\le R_2$ implies $\mathcal{M}\left(R_1\right)\le \mathcal{M}\left(R_2\right)$ for all $R_1,R_2\in 2^{X\times X}$,

(iii) $\mathcal{M}(R_1\wedge R_2)\ge \mathcal{M}\left(R_1\right)\wedge \mathcal{M}\left(R_2\right)$ for all $R_1,R_2\in 2^{X\times X}$.

The inverse ${\mathcal{M}}^{-1}$ of $\mathcal{M}$ is defined by ${\mathcal{M}}^{-1}\left(R\right)=\mathcal{M}\left(R^{-1}\right)$ for all $R\in 2^{X\times X}$.

The principal filter $[x,y]$ on $X\times X$ of a pair $(x,y)$ in $X\times X$ is defined, for each $R\in 2^{X\times X},$ by

$$[x,y]\left(R\right)=R(x,y).$$

It is clear that $[x,x]\left(R\right)=R(x,x)$ for all $R\in 2^{X\times X}$. Then, $R_{\mathrm{ref}}\left(X\right)\subseteq [x,x],$ where $R_{\mathrm{ref}}\left(X\right)$ denotes the set of all reflexive relations on X.

For any two filters $\mathcal{M}$ and $\mathcal{K}$, we say that $\mathcal{M}$ is finer than $\mathcal{K}$, denoted by $\mathcal{M}\prec \mathcal{K}$, if for each $R\in 2^{X\times X},$

$$\mathcal{M}\prec \mathcal{K}\mathrm{iff}\mathcal{M}\left(R\right)\le \mathcal{K}\left(R\right).$$

Definition 3.

Let $\mathcal{M}$ and $\mathcal{K}$ be two filters on $X\times X$ such that $[x,y]\prec \mathcal{M}$ and $[y,z]\prec \mathcal{K}$ for any $x,y,z\in X.$ Then, the composition of $\mathcal{M}$ and $\mathcal{K}$, denoted by $\mathcal{M}\circ \mathcal{K}$, is a filter on $X\times X$ defined, for each $R\in 2^{X\times X},$ by

$$(\mathcal{M}\circ \mathcal{K})\left(R\right)=\underset{(R_1\circ R_2)\le R}{\bigvee }\mathcal{M}\left(R_1\right)\wedge \mathcal{K}\left(R_2\right).$$

(17)

The notion of uniformity was introduced by Weil in [15]. Here, we construct a uniform structure in an approximation space $(X,R)$.

Definition 4.

Uniformity $\mathcal{U}$ on X is a filter on $X\times X$ satisfying the following conditions:

(U1) $[x,x]\prec \mathcal{U}$ for all $x\in X$,

(U2) $\mathcal{U}={\mathcal{U}}^{-1}$,

(U3) $(\mathcal{U}\circ \mathcal{U})\prec \mathcal{U}$.

The pair $(X,\mathcal{U})$ is called a uniform space.

From the above definition, we can easily see that $R_{\mathrm{eq}}\left(X\right)\subseteq \mathcal{U}$, where $R_{\mathrm{eq}}\left(X\right)$ denotes the set of all equivalence relations on X.

Definition 5.

Let $\mathcal{U}$ be a filter on $X\times X$ such that $[x,x]\prec \mathcal{U}$ for all $x\in X$ and let $\mathcal{M}:2^X\to 2$ be a filter on X. Then, the image of $\mathcal{M}$ with respect to $\mathcal{U}$, denoted by $\mathcal{U}\left[\mathcal{M}\right]$, is the mapping $\mathcal{U}\left[\mathcal{M}\right]:2^X\to 2$ defined in [16], for each $R\in 2^{X\times X}$ and each $B\in 2^X,$ by

$$\left(\mathcal{U}\left[\mathcal{M}\right]\right)\left(A\right)=\underset{R\left[B\right]\cap A^c=\varnothing }{\bigvee }\left(\mathcal{U}\left(R\right)\wedge \mathcal{M}\left(B\right)\right),$$

(18)

where $R\in 2^{X\times X}$, $B\in 2^X$ and set $R\left[B\right]\in 2^X$ is defined so that

$$\left(R\left[B\right]\right)\left(x\right)=\underset{y\in X}{\bigvee }\left(B\left(y\right)\wedge R(y,x)\right)\equiv \left[B\right]\left(x\right).$$

(19)

From Equation (1), determine that $R\left[B\right]\equiv \left[B\right]$ for all $B\in 2^X$.

It is obvious that $\mathcal{U}\left[\mathcal{M}\right]$ is a filter on X.

The principal filter $\left[\dot{x}\right]$ on X at a point $x\in X$ is defined by $\left[\dot{x}\right]\left(A\right)=A\left(x\right)$ for all $A\in 2^X$. It is clear that $\left[\dot{x}\right]\left(\left\{x\right\}\right)=1$ for all $x\in X$.

Let $\mathcal{U}$ be a uniformity on a set X and let ${\mathrm{int}}_{\mathcal{U}},{\mathrm{cl}}_{\mathcal{U}}:2^X\to 2^X$ be the mappings defined, respectively, as follows: for each $R\in 2^{X\times X}$, any $A,B\in 2^X$ and each $x\in X$:

$$\left({\mathrm{int}}_{\mathcal{U}}A\right)\left(x\right)=\left(\mathcal{U}\left[\dot{x}\right]\right)\left(A\right)\equiv \underset{\left[B\right]\cap A^c=\varnothing }{\bigvee }\left(\mathcal{U}\left(R\right)\wedge B\left(x\right)\right),$$

(20)

$$\left({\mathrm{cl}}_{\mathcal{U}}A\right)\left(x\right)=\underset{\left[B\right]\cap A\ne \varnothing }{\bigvee }\left(\mathcal{U}\left(R\right)\wedge B\left(x\right)\right).$$

(21)

Then, it can easily be proven that ${\mathrm{int}}_{\mathcal{U}}$ and ${\mathrm{cl}}_{\mathcal{U}}$ are the interior and the closure operators on X, respectively. Thus, there is topology ${\tau }_{\mathcal{U}}$ on X induced by ${\mathrm{int}}_{\mathcal{U}}$ or ${\mathrm{cl}}_{\mathcal{U}}$.

Since any equivalence relation R on X is an element of a uniformity $\mathcal{U}$ on X, in an approximation space $(X,R)$, from Equations (4) and (5), obtain

$${\mathrm{int}}_{\mathcal{U}}A\equiv {\mathrm{int}}_{\delta }A\equiv {\mathrm{int}}_{{\tau }_d}A\equiv A^{\circ }\equiv A_R$$

(22)

and

$${\mathrm{cl}}_{\mathcal{U}}A\equiv {\mathrm{cl}}_{\delta }A\equiv {\mathrm{cl}}_{{\tau }_d}A\equiv \overline{A}\equiv A^R.$$

(23)

Uniformity $\mathcal{U}$ on X is said to be separated, if for all $x\ne y\in X$ there is $R\in R_E\left(X\right)$ such that $\mathcal{U}\left(R\right)=1$ and $R(x,y)=0$, that is, $\left[x\right]\cap \left[y\right]=\varnothing$. In this case, pair $(X,\mathcal{U})$ is called a separated uniform space.

As in Section 2, $T_2\equiv T_1\equiv T_0$ as separation axioms. So, separated uniform spaces satisfy all these axioms.

Generated topology ${\tau }_R$ on approximation space $(X,R)$ is explained during the lower and the upper sets of a rough set. It is equivalent to induced topology ${\tau }_{\delta }$ generated by constructed proximity $\delta$ on X, and also is equivalent to the generated topology ${\tau }_d$ by pseudo-metric d constructed on X. Moreover, all these topologies are equivalent to generated topology ${\tau }_{\mathcal{U}}$ the constructed uniformity $\mathcal{U}$ on X. According to the definitions of a metric, a separated proximity and a separated uniformity, obtain a similar result to Proposition 2 and Proposition 4 related to the defined separation axioms in Section 2.

Proposition 6.

Let X be a set, $\mathcal{U}$ a uniform structure on X and ${\tau }_{\mathcal{U}}$ the topology induced by $\mathcal{U}$. Then, $(X,{\tau }_{\mathcal{U}})$ is a normal space, and moreover

$$(X,\mathcal{U})\mathit{separated} \mathit{if} \mathit{and} \mathit{only} \mathit{if} (X,{\tau }_{\mathcal{U}})\mathit{is} \mathit{a} T_4-\mathit{space}.$$

Proof. 

The proof is coming from Equations (22) and (23) and from the proofs of Proposition 2 and Proposition 4. □

6. Arbitrary Relation in Approximation Spaces

In this section, we recall the strategy of Kozae in [10]. We let R be an arbitrary relation on X. Then, the right and left neighborhoods (the after and fore sets) of element $x\in X$ are sets in $2^X$ given, respectively, by

$$xR=\{y\in X:R(x,y)=1\},Rx=\{y\in X:R(y,x)=1\}.$$

We let $<x>R\in 2^X$ be defined as

$$<x>R=\left\{\begin{array}{cc}{\displaystyle \bigcap _{x\in pR}}pR\hfill & \mathrm{if}\mathrm{there}\mathrm{exists}p:x\in pR,\hfill \\ \varnothing \hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(24)

and $R<x>\in 2^X$ be defined as

$$R<x>=\left\{\begin{array}{cc}{\displaystyle \bigcap _{x\in Rp}}Rp\hfill & \mathrm{if}\mathrm{there}\mathrm{exists}p:x\in Rp,\hfill \\ \varnothing \hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(25)

$<x>R,R<x>$ are called minimal right neighborhoods and minimal left neighborhoods of $x\in X$;

$$R<x>R=<x>R\cap R<x>$$

(26)

is called the minimal neighborhood of $x\in X$.

For any subset A of X, the lower approximation $A_R$ and the upper approximation $A^R$ are defined by $A_R=A\cap A_{\ast },A^R=A\cup A^{\ast },$ where

$$A_{\ast }=\{x\in X:R<x>R\cap A^c=\varnothing \},A^{\ast }=\{x\in X:R<x>R\cap A\ne \varnothing \}$$

(27)

The resulting lower and upper approximation sets $A_R,A^R$ of set A are typically those defined by Kozae in [10]. The interior operator and the closure operator defined, respectively, in Equations (4) and (5) did not satisfy the common properties of interior and closure operators to generate a topology on $(X,R)$. In the case R is a reflexive relation, $A^{\circ }=A_R=A_{\ast },\overline{A}=A^R=A^{\ast }$, but this is still not sufficient to generate a topology on $(X,R)$. At least, in Equations (4) and (5), R needs to be reflexive and transitive to produce topology ${\tau }_R$ on $(X,R)$. In the case R is an equivalence relation, the well-known definition of Pawlak [1] is obtained, and Equations (4) and (5) define topology ${\tau }_R$ on X.

In the case R is an arbitrary relation on $(X,R)$, the separation axiom $T_0$ could be satisfied and the separation axiom $T_1$ is not satisfied. That is, the given equivalence $T_0\mathrm{iff}{T}_1\mathrm{iff}{T}_2$ in Section 2 is not correct.

Remark 3.

Whenever R is arbitrary relation on X, we have to replace $\left[x\right]$ with $R<x>R$ in all the notations introduced in Section 2, Section 3, Section 4 and Section 5. If R is not reflexive, it may be $R(x,x)=0$, that is, $R<x>R\cap \left\{x\right\}=\varnothing$. Hence, condition (D1) is not satisfied and we can not build pseudo-metric d on $(X,R)$ according to Equation (6). According to Equation (13), we may have $\left\{x\right\}\overline{\delta }\left\{x\right\}$ which is a contradiction to condition (P4), and then we cannot build proximity δ on $(X,R)$. Also, condition (U1) is not satisfied, and so construction of uniformity $\mathcal{U}$ on $(X,R)$ is not possible. If R is not symmetric, Conditions (D2), (P1) and (U2) are not satisfied, and thus it fails to build a metric (pseudo-metric), a proximity or a uniformity in $(X,R)$, but it could be a quasi-metric (quasi-pseudo-metric), a quasi-proximity or a quasi-uniformity in $(X,R)$. Also, if R is not transitive, Conditions (D3), (P5) and (U3) are not satisfied, and thus it fails to build any of metric (pseudo-metric), proximity or uniformity in $(X,R)$.

Examples 1–4 are given for equivalence relations. Now, we offer an example of arbitrary relation R on X.

Example 5.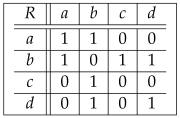

Let R be a relation on set $X=\{a,b,c,d\}$ as shown below.

$aR=\{1,1,0,0\}$, $bR=\{1,0,1,1\}$, $cR=\{0,1,0,0\}$, $dR=\{0,1,0,1\}$ and $Ra=\{1,1,0,0\}$, $Rb=\{1,0,1,1\}$, $Rc=\{0,1,0,0\}$, $Rd=\{0,1,0,1\}$. Then, $<a>R=\{1,0,0,0\}$, $<b>R=\{0,1,0,0\}$, $<c>R=\{1,0,1,1\}$, $<d>R=\{0,0,0,1\}$ and $R<a>=\{1,0,0,0\}$, $R<b>=\{0,1,0,0\}$, $R<c>=\{1,0,1,1\}$, $R<d>=\{0,0,0,1\}$ and then, $R<a>R=\{1,0,0,0\}$, $R<b>R=\{0,1,0,0\}$, $R<c>R=\{1,0,1,1\}$, $R<d>R=\{0,0,0,1\}$.

(1) For subset $A=\{1,1,0,0\}$, we compute $A_{\ast },A^{\ast }$ as follows: $A_{\ast }=A_R=\{1,1,0,0\}=A$, $A^{\ast }=A^R=\{1,1,1,0\}$, and thus $A^B=\{0,0,1,0\}$, and the accuracy value is $\frac{2}{3}$.

(2) For subset $K=\{0,0,1,0\}$, we compute $K_{\ast },K^{\ast }$ as follows: $K_{\ast }=\{0,0,0,0\}\equiv \varnothing ,K^{\ast }=K=\{0,0,1,0\}$, and then $K_R=\{0,0,0,0\},K^R=K=\{0,0,1,0\}$, and thus $K^B=\{0,0,1,0\}$, and the accuracy value is $\frac{0}{1}=0$.

(3) For subset $H=\{1,1,0,1\}$ we have $H_{\ast }=\{1,1,0,1\}=H_R=H$, $H^{\ast }=H^R=\{1,1,1,1\}\equiv X$, and thus $H^B=\{0,0,1,0\}$, and the accuracy value is $\frac{3}{4}$.

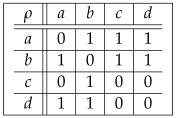
From Remark 3, we determine that $R<c>R=\{1,0,1,1\}\ne \{0,0,1,0\}$, and thus this example cannot satisfy any axiom of the separation axioms as given in Definition 1.

Also, from $R<a>R,R<b>R,R<c>R,R<d>R$ computed in this example, we can deduce function ρ (neither a metric nor a pseudo-metric) as follows:

7. Conclusions

This aim of paper was to construct a proximity relation and a uniformity structure on approximation space $(X,R)$ and also define metric function and separation axioms based on the rough sets in $(X,R)$. We presented some basics of rough sets and introduced the definitions of separation axioms $T_i,i=0,1,2,3,4$ in $(X,R)$. We focused on defining metric d on approximation space $(X,R)$ and studied its usual properties. We defined proximity relation $\delta$ on $(X,R)$ and studied its properties. Following the definition of uniformity structure $\mathcal{U}$ introduced by Gahler on $(X,R)$, we studied the relations in between notion separation axioms $T_i,i=0,1,2,3,4$ in $(X,R)$, metric spaces $(X,d)$, proximity spaces $(X,\delta )$ and uniform spaces $(X,\mathcal{U})$ based on the rough sets defined by an equivalence relation R on X. At last, we explained the deviations in these notions whenever R is not an equivalence relation on X. In a future work, we will discuss these results and their applications in the fuzzy approximation spaces, the soft approximation spaces and the soft fuzzy approximation spaces.