Iterative Stability Analysis for Generalized α-Nonexpensive Mappings with Fixed Points

Abstract

This article introduces a novel iterative process, denoted as $F^{★}$, designed for the class of generalized $\alpha$-Nonexpensive mappings. The study establishes strong and weak convergence theorems within the context of Banach spaces, supported by carefully chosen assumptions. The convergence results contribute to the theoretical foundation of iterative processes in functional analysis. The presented framework is applied to address nonlinear integral equations, showcasing the versatility and applicability of the proposed $F^{*}$ for the class of generalized iteration process. Additionally, the article includes numerical examples that not only validate the theoretical findings but also provide insights into the practical utility of the developed methodology.

1. Introduction

When the presence of a solution for a given operator is affirmed, ordinary analytical approaches often fall short of obtaining such solutions. To surmount this challenge, resorting to approximation methods becomes imperative. One of the key findings in fixed point (FP) theory is the Banach contraction theorem, which Polish mathematician Stefan Banach presented in 1922 [1]. The Banach contraction theorem relies on the convergence of a fundamental iterative process known as the sequence of successive approximations or the Picard iteration process. This theorem addresses an FP problem for a contraction mapping defined on a complete metric space [2]. It has evolved into a crucial tool for demonstrating the existence and approximation of solutions to nonlinear functional equations, including those arising in differential, integral, and partial differential equations. While certain scenarios ensure the existence of a solution to the FP problem, determining the exact solution may be infeasible. In these situations, there is a great desire to approximate the solution to the given problem, which prompts the creation of numerous iterative procedures. In the domain of nonexpansive mappings, denoted as NonExp mappings, the assurance of Picard iteration process convergence to a FP is not guaranteed for specific classes of NonExp mappings [2]. Consequently, alternative iterative approaches are employed, incorporating different procedural steps and parameter sets. Several iterative processes, such as those introduced by Mann [3], Ishikawa [4], Noor [5], S iteration by Agarwal et al. [6], Abbas [7], and Picard-S [8], have undergone extensive investigation.

In 2018, Ullah and Arshad [9] introduced the M iterative scheme for Suzuki mappings, showcasing its faster convergence compared to the aforementioned processes. In 2008, Suzuki [10] proved analogous FP theorems in Banach space, denoted as (BS), showing that the class of maps meeting condition (C) is weaker than the idea of NonExp mappings. Browder in 1965 [11] focused on uniformly convex BS, while Kirk [12], in a reflexive BS, established FPs for NonExp mappings. More recently, Ullah et al. [13] applied the M iteration scheme to find FPs of generalized $\alpha$-Nonexpensive mappings, denoted as GNZ-$\alpha$-NonExp mappings, in BS.

In 2020, Ali and Ali [14] introduced a novel iteration process, the F iterative process, for generalized contractions. They demonstrated the stability and superior convergence rate of this F iterative scheme compared to other iteration processes in the context of generalized contractions.

In 2021, Junaid et al. [2] established a connection between the F iteration process and the class of GNZ-$\alpha$-NonExp mappings. Under suitable assumptions, they derived both strong and weak convergence outcomes within the framework of BS. The following iteration process (1) for uniformly convex Banach space, denoted as UCBS, as given in [2], is described as follows:

$$\begin{array}{cc}\hfill w_1& \in \mathcal{S},\hfill \\ \hfill u_t& =\Omega ((1-{\alpha }_t)w_t+{\alpha }_t\Omega w_t),\hfill \\ \hfill v_t& =\Omega u_t,\hfill \\ \hfill w_{t+1}& =\Omega v_t,t\ge 1,\hfill \end{array}$$

(1)

where $\Omega$ is GNZ-$\alpha$-NonExp mapping and ${\alpha }_t\in (0,1)$.

In this paper, we modify the iterative process given in [2] for GNZ-$\alpha$-NonExp mappings. For this purpose a new function $x_t=\Omega x_t$ is defined in the above iterative process (1). By using this new function, we observe early convergence with high accuracy. This finding is supported by providing two different examples. The obtained numerical results are presented in

Table 1. Convergence comparison of $F^{*}$ scheme (2) for GNZ-$\alpha$-NonExp mapping given in Example 1 with other schemes with respect to the number of iterations.

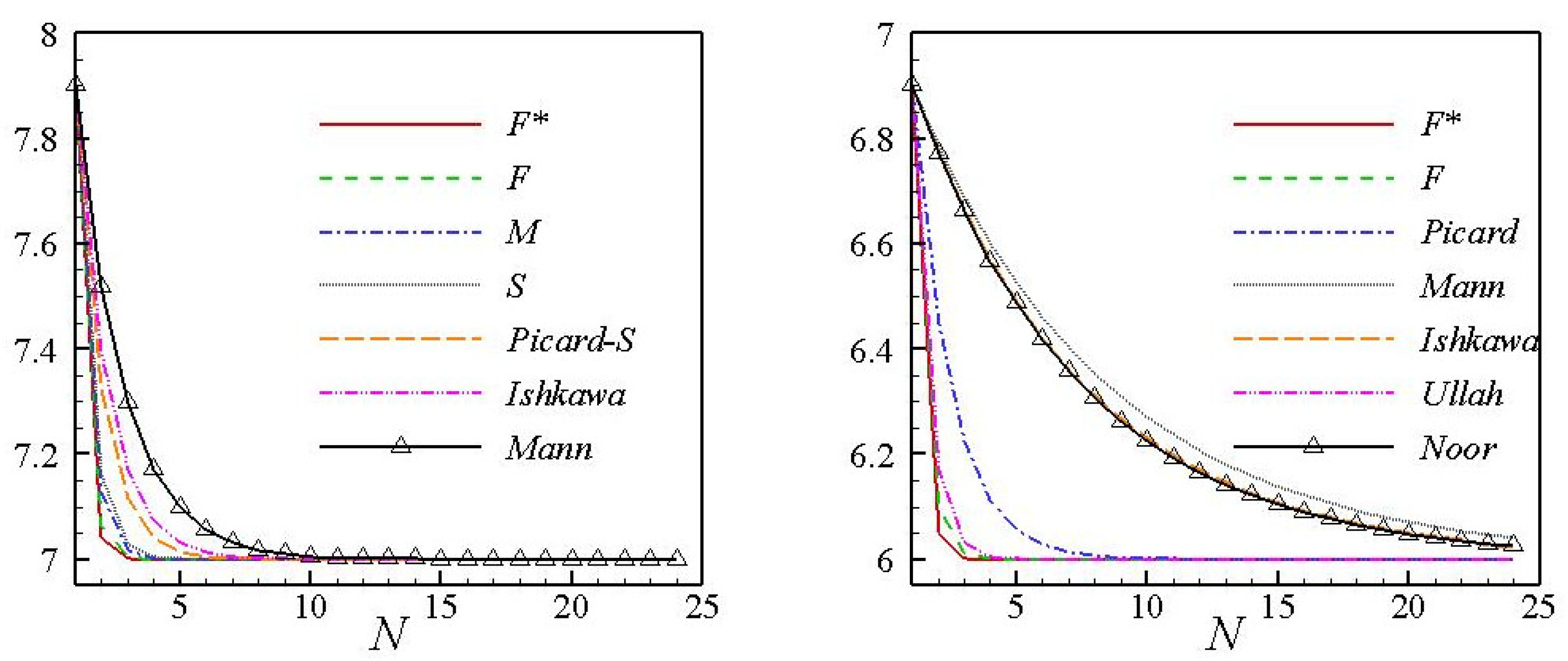
N	${\mathit{F}}^{*}$	F [2]	M [9]	S [6]	Picard-S [8]	Ishikawa [4]	Mann [3]
1	7.9	7.9	7.9	7.9	7.9	7.9	7.9
2	7.042188	7.06468750	7.12937500	7.3256875	7.1628437	7.3931875	7.51750000
3	7.001978	7.00464941	7.01859766	7.11785816	7.02946454	7.17177379	7.29756250
4	7.000093	7.00033418	7.00267341	7.04264992	7.00533124	7.07504367	7.17109844
5	7.000004	7.00002402	7.00038430	7.01543394	7.00096462	7.03278471	7.09838160
6	7	7.00000173	7.00005524	7.00558516	7.00017454	7.01432282	7.05656942
7	7	7.00000012	7.00000794	7.00202113	7.00003158	7.00625728	7.0325 2742
8	7	7.00000001	7.00000114	7.0007314	7.00000571	7.00273365	7.01870 326
9	7	7	7.00000016	7.00026467	7.00000103	7.00119426	7.0107543 8
10	7	7	7.00000002	7.00009578	7.00000019	7.00052174	7.00618377
11	7	7	7	7.00000003	7.00003466	7.00022794	7.00355567
12	7	7	7	7.00001254	7.00000001	7.00009959	7.00204451
13	7	7	7	7.00000454	7	7.00004350	7.00117559
14	7	7	7	7.00000164	7	7.00001901	7.00067597
15	7	7	7	7.00000059	7	7.00000830	7.00038868
16	7	7	7	7.00000022	7	7.00000363	7.00022349
17	7	7	7	7.00000008	7	7.00000158	7.00012851
18	7	7	7	7.00000003	7	7.00000069	7.00007389
19	7	7	7	7.00000001	7	7.00000030	7.00004249
20	7	7	7	7	7	7.00000013	7.00002443
21	7	7	7	7	7	7.00000006	7.00001405
22	7	7	7	7	7	7.00000003	7.00000808
23	7	7	7	7	7	7.00000001	7.00000464
24	7	7	7	7	7	7	7.00000260

and

Table 2. Convergence comparison of $F^{*}$ scheme (2) for GNZ-$\alpha$-NonExp mapping given in Example 2 with other schemes with respect to the number of iterations.

N	${\mathit{F}}^{\mathbf{★}}$	F [2]	Picard [1]	Mann [3]	Ishikawa [4]	M [9]	Noor [5]
1	6.9	6.9	6.9	6.9	6.9	6.9	6.9
2	6.04921875	6.0984387	6.45	6.7875	6.773438	6.172266	6.77168
3	6.002692	6.010767	6.225	6.689063	6.664673	6.032973	6.661655
4	6.000147	6.001178	6.1125	6.60293	6.571203	6.006311	6.567318
5	6.000008	6.000129	6.05625	6.527563	6.490878	6.001208	6.48643
6	6	6.000014	6.028125	6.461618	6.421848	6.000231	6.417076
7	6	6.000002	6.014063	6.403916	6.362526	6.000044	6.35761
8	6	6	6.007031	6.353426	6.311546	6.0000088	6.306623
9	6	6	6.003516	6.309248	6.267734	6.000002	6.262905
10	6	6	6.001758	6.270592	6.230084	6	6.225421
11	6	6	6.000879	6.236768	6.197729	6	6.193281
12	6	6	6.000439	6.207172	6.169923	6	6.165723
13	6	6	6.00022	6.181276	6.146028	6	6.142094
14	6	6	6.00011	6.158616	6.125493	6	6.121835
15	6	6	6.000055	6.138789	6.107845	6	6.104464
16	6	6	6.000027	6.12144	6.092679	6	6.08957
17	6	6	6.000014	6.10626	6.079646	6	6.076799
18	6	6	6.000007	6.092978	6.068446	6	6.065849
19	6	6	6.000003	6.081356	6.058821	6	6.05646
20	6	6	6.000002	6.0711867	6.050549	6	6.04841
21	6	6	6.000001	6.062288	6.043441	6	6.041508
22	6	6	6	6.0545027	6.037332	6	6.03559
23	6	6	6	6.047689	6.027571	6	6.030516
24	6	6	6	6.041728	6.023693	6	6.026165

. These results are compared with the previous iterative processes. Another interesting property of the above process is that if the number of functions similar to $x_t$ is increased, then rapid convergence along with high accuracy can be obtained. However, for simplicity, we consider only one function ${\mathit{x}}_{\mathit{t}}$ in our study.

In this manuscript, we have six sections. Section 1, includes the introduction of our research, and Section 2 is related to the preliminaries and results, which are helpful to construct the main result of the paper. Section 3 is the main part of the paper where we define our main scheme and the strong and weak convergence results of the scheme, whereas Section 4 and Section 5 are about the useability of our results. Here, we apply our findings for the solution of non-linear integral equation. In the last section, we conclude our findings.

2. Preliminaries

This section deals with the preliminaries and results, which help construct the main results of this article.

Definition 1 

([2]). Suppose that $\mathcal{T}$ is a BS and $\mathcal{S}\subseteq \mathcal{T}$ is a nonempty subset. Let $\Omega :\mathcal{S}\to \mathcal{S}$ be a mapping. Then Ω is said to be

1. 

NonExp if $||\Omega d^{\prime }-\Omega d^{″}\Vert \le \Vert d^{\prime }-d^{″}\Vert$, for all $d^{\prime },d^{″}\in \mathcal{S}$;

2. 

endowed with condition (C) if for all $d^{\prime },d^{″}\in \mathcal{S}$ with $\frac{1}{2}\Vert d^{\prime }-\Omega d^{\prime }\Vert \le \Vert d^{\prime }-d^{″}\Vert \Rightarrow$

$\Vert \Omega {\mathit{d}}^{\prime }-\Omega {\mathit{d}}^{″}\Vert \le \Vert d^{\prime }-d^{″}\Vert$.

Definition 2 

([2]). Suppose that $\mathcal{T}$ is a BS and $\mathcal{S}\subseteq \mathcal{T}$ is a nonempty subset. Let $\Omega :\mathcal{S}⟶\mathcal{S}$ be a mapping. Then Ω is said to be GNZ-α-NonExp if for all $d^{\prime },d^{″}$$\in \mathcal{S}$ with

$$\frac{1}{2}\Vert d^{\prime }-\Omega d^{\prime }\Vert \le \Vert d^{\prime }-d^{″}\Vert ,$$

⇒

$$\Vert \Omega d^{\prime }-\Omega d^{″}\Vert \le \alpha \Vert d^{\prime }-\Omega {\mathit{d}}^{″}\Vert +\alpha \Vert d^{″}-\Omega d^{\prime }\Vert +(1-2\alpha )\Vert d^{\prime }-d^{″}\Vert$$

for some $\alpha \in [0,1)$.

Definition 3 

([15]). A BS $\mathcal{T}$ is said to satisfy the Opial condition (OpCd), if for every sequence $w_t\subseteq \mathcal{T}$ that weakly converges to $j\in \mathcal{T}$, the following condition holds:

$$\underset{t\to \infty }{lim\; sup}\Vert w_t-j\Vert <\underset{t\to \infty }{lim\; sup}\Vert w_t-j^{\prime }\Vert ,\forall j^{\prime }\in \mathcal{S}-\left\{j\right\}.$$

Definition 4 

([2]). Suppose that $\mathcal{T}$ is a BS and $\mathcal{S}\subseteq \mathcal{T}$ is nonempty and $\left\{w_t\right\}\subseteq \mathcal{T}$ is a bounded sequence. For a fix $j\in \mathcal{T}$ the following assumptions hold:

1. 

at the point j of asymptotic radius of bounded sequence $\left\{w_t\right\}$ by

$$R(j,\left\{w_t\right\})=\underset{t\to \infty }{lim\; sup}||j-w_t||;$$

2. 

the connection of $\mathcal{S}$ with asymptotic radius of bounded sequence $\left\{w_t\right\}$ by

$$R(\mathcal{S},\left\{w_t\right\})=inf\{r(j,\left\{w_t\right\}):j\in \mathcal{S}\};$$

3. 

the connection of asymptotic center of bounded sequence $\left\{w_t\right\}$ with $\mathcal{S}$ by

$$A(\mathcal{S},\left\{w_t\right\})=\{j\in \mathcal{S}:r(j,\left\{w_t\right\})\}=r(\mathcal{S},\left\{w_t\right\})\}.$$

In the case of UCBS, $A(\mathcal{S},\left\{w_t\right\})$ has a cardinality equal to one [6,16].

Pant and Shukla [17] described the following facts about GNZ-$\alpha$-NonExp mappings.

Proposition 1 

([17]). For a BS $\mathcal{T}$ with a closed, nonempty subset $\mathcal{S}\subseteq \mathcal{T}$, and a mapping $\Omega :\mathcal{S}\to \mathcal{S}$ with $\alpha \in [0,1)$, the following statements hold:

1. 

If Ω satisfies condition (C), it is considered a GNZ-α-NonExp mapping.

2. 

If Ω is a GNZ-α-NonExp mapping with a nonempty FP, then for any $d^{\prime }\in \mathcal{S}$ and $d^{★}$ as the FP of Ω, $||\Omega d^{\prime }-d^{★}||\le ||{\mathit{d}}^{\prime }-d^{★}||$.

3. 

When Ω is a GNZ-α-NonExp mapping, the set $F_{\Omega }^{★}$ is closed. Additionally, if the fundamental space $\mathcal{T}$ is strictly convex and $\mathcal{S}$ is convex, then $F_{\Omega }^{★}$ is convex.

4. 

For all $d^{\prime },d^{″}\in \mathcal{S}$, if Ω is a GNZ-α-NonExp mapping, the inequality holds:

$$||{\mathit{d}}^{\prime }-\Omega {\mathit{d}}^{″}\Vert \le \left(\frac{3+\alpha }{1-\alpha }\right)\Vert {\mathit{d}}^{\prime }-\Omega {\mathit{d}}^{\prime }\Vert +\Vert {\mathit{d}}^{\prime }-{\mathit{d}}^{″}\Vert .$$

5. 

If the fundamental space $\mathcal{T}$ satisfies the OpCd, then Ω is a GNZ-α-NonExp mapping. Moreover, if $\left\{w_t\right\}$ weakly converges to $\mathit{l}$ and ${lim}_{t\to \infty }\Vert \Omega w_t-w_t\Vert =0$, then $\mathit{l}\in F_{\Omega }^{★}$.

We have an interesting property of a UCBS [18].

Lemma 1 

([18]). Suppose that $\mathcal{T}$ is any UCBS for which the $r,{\alpha }_t,s$ are defined as $0<r\le {\alpha }_t\le s<1$ and $\left\{w_t\right\},\left\{x_t\right\}\subseteq \mathcal{J}$ such that

$$\underset{t\to \infty }{lim\; sup}\Vert w_t\Vert \le q,$$

$$\underset{t\to \infty }{lim\; sup}\Vert x_t\Vert \le q,$$

$$\underset{t\to \infty }{lim\; sup}\Vert {\alpha }_t{w}_t+(1-{\alpha }_t)x_t\Vert =q$$

for some $q\ge 0$. Then ${lim}_{t\to \infty }||w_t-x_t||=0$.

3. Generalized Iterative Scheme for $\mathbf{\alpha }$-NonExp Mappings

Suppose that $\mathcal{S}$ is a UCBS and $\Omega :\mathcal{S}\to \mathcal{S}$ is a GNZ-$\alpha$-NonExp mapping. Then a modified iteration process for the present study is described as

$$\begin{array}{cc}\hfill w_1& \in \mathcal{S},\hfill \\ \hfill u_t& =\Omega ((1-{\alpha }_t)w_t+{\alpha }_t\Omega w_t),\hfill \\ \hfill x_t& =\Omega u_t,\hfill \\ \hfill {\gamma }_t& =\Omega x_t,\hfill \\ \hfill w_{t+1}& =\Omega {\gamma }_t,t\ge 1,\hfill \end{array}$$

(2)

where $\Omega$ is GNZ-$\alpha$-NonExp mapping and ${\alpha }_t\in (0,1)$.

In the mentioned procedure, a novel function $x_t=\Omega x_t$ is introduced. It is noted that attaining early convergence with enhanced accuracy is possible by augmenting the number of functions akin to $x_t$ utilized in the aforementioned approach. However, for the sake of simplicity in the current scenario, we focus on a single function $x_t$. We term this innovative iterative method as $F^{★}$, representing a generalized version of the scheme proposed by Junaid [2].

In this section, the results related to the strong and weak convergence for the new iterative scheme $F^{★}$ are described.

Lemma 2.

Suppose that $\mathcal{T}$ is any UCBS and $\mathcal{S}\subseteq \mathcal{T}$ is closed, nonempty and convex. Let $\Omega :\mathcal{S}⟶\mathcal{S}$ be a GNZ-α-NonExp mapping satisfying $F_{\Omega }^{★}\ne \varnothing$ and $\left\{w_t\right\}$ be a sequence of $F^{★}$ iterates (2). Then ${lim}_{t\to \infty }||w_t-d^{★}||$ always exists for every $d^{★}\in F_{\Omega }^{★}$.

Proof. 

Suppose $d^{★}\in F_{\Omega }^{★}$. Using Proposition 1(2), we have

$$\begin{array}{ccc}\hfill ||u_t-d^{★}||& =& ||\Omega ((1-{\alpha }_t)w_t+{\alpha }_t\Omega w_t)-d^{★}||\hfill \\ & \le & ||(1-{\alpha }_t)w_t+{\alpha }_t\Omega w_t-d^{★}||\hfill \\ & \le & ((1-{\alpha }_t)||w_t-d^{★}||+{\alpha }_t||\Omega w_t-d^{★}||\hfill \\ & \le & (1-{\alpha }_t)||w_t-d^{★}||+{\alpha }_t||w_t-d^{★}||\hfill \\ & \le & ||w_t-d^{★}||,\hfill \end{array}$$

$$\Vert {\mathit{w}}_{\mathit{t}+\mathit{1}}-{\mathit{d}}^{★}\Vert =\Vert \Omega {\mathit{v}}_{\mathit{t}}-{\mathit{d}}^{★}\Vert \le \Vert {\mathit{v}}_{\mathit{t}}-{\mathit{d}}^{★}\Vert =\Vert \Omega {\mathit{u}}_{\mathit{t}}-{\mathit{d}}^{★}\Vert \le \Vert {\mathit{u}}_{\mathit{t}}-{\mathit{d}}^{★}\Vert \le \Vert {\mathit{w}}_{\mathit{t}}-{\mathit{d}}^{★}\Vert .$$

(3)

Consequently,

$$\Vert w_{t+1}-d^{★}\Vert \le \Vert w_t-d^{★}\Vert ,$$

which means that $\{||w_t-d^{★}||\}$ is bounded as well as non-increasing. It follows that ${lim}_{t\to \infty }\Vert w_t-d^{★}\Vert$, exists for each $d^{★}\in F_{\Omega }^{★}$. □

We now provide the necessary and sufficient requirements for the existence of FP for any GNZ-$\alpha$-NonExp mapping in UCBS.

Theorem 1.

Consider any UCBS, where $\mathcal{T}$ is the space, and $\mathcal{S}\subseteq \mathcal{T}$ is a closed, nonempty, and convex subset. Assume that $\Omega :\mathcal{S}⟶\mathcal{S}$ is a GNZ-α-NonExp mapping, and $\left\{w_t\right\}$ represents a sequence of $F^{★}$ iterates (2). Then $F_{\Omega }^{★}\ne \varnothing$ if and only if $\left\{w_t\right\}$ is bounded and ${lim}_{t\to \infty }||\Omega w_t-w_t||=0$.

Proof. 

Assuming $F^{★}\Omega \ne \varnothing$ and $d^{★}\in F^{★}\Omega$, for any $d^{★}\in F^{★}\Omega$, utilizing Lemma 1, we observe that $limt\to \infty \Vert w_t-d^{★}\Vert$ exists and $w_t$ is bounded. Let us denote this limit as $\epsilon$, i.e.,

$$\underset{t\to \infty }{lim}\Vert w_t-d^{★}\Vert =\epsilon .$$

(4)

From Lemma 1, we have

$$\Vert u_t-d^{★}\Vert \le \Vert w_t-d^{★}\Vert .$$

By applying the lim and using (4), we have

$$\underset{t\to \infty }{lim\; sup}\Vert u_t-d^{★}\Vert \le \underset{t\to \infty }{lim\; sup}\Vert w_t-d^{★}\Vert =\epsilon .$$

(5)

Since $d^{★}$ is in the set $F_{\Omega }^{★}$, and by using Proposition 1(2), we get the following:

$$\begin{array}{c}\hfill ||\Omega w_t-d^{★}||\le ||w_t-d^{★}||,\\ \hfill \underset{t\to \infty }{lim\; sup}||\Omega w_t-d^{★}||\le \underset{t\to \infty }{lim\; sup}||w_t-d^{★}||=\epsilon .\end{array}$$

From Lemma 1, we have

$$\begin{array}{ccc}\hfill ||w_{t+1}-d^{★}||& \le & ||u_t-d^{★}||,\hfill \\ \hfill \epsilon & =& \underset{t\to \infty }{lim\; inf}||w_{t+1}-d^{★}||\le \underset{t\to \infty }{lim\; inf}||u_t-d^{★}||.\hfill \end{array}$$

(6)

From (5) and (6), we have

$$\epsilon =\underset{t\to \infty }{lim}\Vert u_t-d^{★}\Vert .$$

By (3) and (1), we have

$$\begin{array}{ccc}\hfill \epsilon & =& \underset{t\to \infty }{lim}||u_t-d^{★}||\hfill \\ & =& \underset{t\to \infty }{lim}||\Omega ((1-{\alpha }_t)w_t+{\alpha }_t\Omega w_t)-d^{★}||\hfill \\ & \le & \underset{t\to \infty }{lim}||((1-{\alpha }_t)({\mathit{w}}_{\mathit{t}}-d^{★})+{\alpha }_t(\Omega {\mathit{w}}_{\mathit{t}}-d^{★})||\hfill \\ & \le & \underset{t\to \infty }{lim}||((1-{\alpha }_t)(w_t-d^{★})||+\underset{t\to \infty }{lim}||{\alpha }_t(\Omega w_t-d^{★})||\hfill \\ & \le & \underset{t\to \infty }{lim}((1-{\alpha }_t)||(w_t-d^{★})||+\underset{t\to \infty }{lim}{\alpha }_t||w_t-d^{★}||\hfill \\ & =& l\underset{t\to \infty }{lim}||(w_t-d^{★})||\hfill \\ & \le & \epsilon .\hfill \end{array}$$

Thus,

$$\epsilon =\underset{t\to \infty }{lim}\Vert ((1-{\alpha }_t)(w_t-d^{★})+{\alpha }_t(\Omega w_t-d^{★})\Vert .$$

By Lemma 1, we get

$$\underset{t\to \infty }{lim}\Vert \Omega {\mathit{w}}_{\mathit{t}}-{\mathit{w}}_{\mathit{t}}\Vert =0.$$

Conversely, we will demonstrate the non-emptiness of the set ${\mathit{F}}_{\Omega }^{★}$ under the conditions that $\left\{w_t\right\}$ is bounded and approaches zero as ${lim}_{t\to \infty }\Vert \Omega {\mathit{w}}_{\mathit{t}}-{\mathit{w}}_{\mathit{t}}\Vert =0$. If we apply the Proposition 1(4), we have

$$\begin{array}{ccc}\hfill r(\Omega d^{★},\left\{w_t\right\})& =& \underset{t\to \infty }{lim\; sup}||w_t-\Omega d^{★}||\hfill \\ & \le & \left(\frac{3+\alpha }{1-\alpha }\right)\underset{t\to \infty }{lim\; sup}||\Omega w_t-w_t||+\underset{t\to \infty }{lim\; sup}||w_t-d^{★}||\hfill \\ & =& \underset{t\to \infty }{lim\; sup}||w_t-d^{★}||\hfill \\ & =& r(d^{★},\left\{w_t\right\}).\hfill \end{array}$$

We observe that $\Omega d^{★}\in A(\mathcal{S},\left\{w_t\right\})$. In the case of UCBS, the set $A(\mathcal{S},\left\{w_t\right\})$ has cardinality equal to one. This concludes that $\Omega {\mathit{d}}^{★}={\mathit{d}}^{★}$. Thus, the set ${\mathit{F}}_{\Omega }^{★}$ is nonempty. □

The weak and strong convergences of $F^{★}$ iteration (2) are established as follows.

Theorem 2.

Consider any UCBS $\mathcal{T}$ satisfying the OpCd, where $\mathcal{S}\subseteq \mathcal{T}$ is a closed, nonempty, and convex subset. If $\Omega :\mathcal{S}\to \mathcal{S}$ is a GNZ-α-NonExp mapping with $F_{\Omega }^{★}\ne \varnothing$, and $\left\{w_t\right\}$ represents a sequence of $F^{★}$ iterates (2), then $\left\{w_t\right\}$ weakly converges to a FP of Ω.

Proof. 

By Theorem 1, $\left\{w_t\right\}$ is bounded in $\mathcal{S}$. Since $\mathcal{T}$ is a UCBS, $\mathcal{T}$ will be reflexive; hence, the bounded sequence $\left\{w_t\right\}$ admits a weakly convergent sub sequence $\left\{w_{t_r}\right\}$ with weak limit, namely, $w_1\in \mathcal{S}$. If we apply Theorem 1 on this subsequence, we obtain ${lim}_{t\to \infty }\Vert w_{t_r}-\mathrm{\Omega }{w}_{t_r}\Vert =0$. Thus, by Proposition 1(5), one has $w_1\in F_{\Omega }^{★}$. If we prove that $w_1$ is a weak limit for $\left\{w_t\right\}$, then the proof will be finished. We prove this by contradiction. Suppose $w_1$ is not a weak limit for $\left\{w_t\right\}$; that is, another subsequence $\left\{w_{t_s}\right\}$ of $\left\{w_t\right\}$ exists that admits a weak limit $w_2\in \mathcal{S}$. The same calculations give $w_2\in F_{\Omega }$. Now we know that $\mathcal{J}$ admits the OpCd. Thus, one has

$$\begin{array}{ccc}\hfill \underset{t\to \infty }{lim}||w_t-w_1||& =& \underset{s\to \infty }{lim}||w_{t_s}-w_1||\hfill \\ & <& \underset{s\to \infty }{lim}||w_{t_s}-w_2||\hfill \\ & =& \underset{t\to \infty }{lim}||w_t-w_2||\hfill \\ & =& \underset{s\to \infty }{lim}||w_{t_s}-w_2||\hfill \\ & <& \underset{s\to \infty }{lim}||w_{t_s}-w_1||\hfill \\ & =& \underset{t\to \infty }{lim}||w_t-w_1||.\hfill \end{array}$$

The above estimate suggests a contradiction and, hence, we must accept that $w_1=w_2$. Accordingly, $\left\{w_t\right\}$ converges weakly to $w_1\in F_{\Omega }^{★}$. □

Theorem 3.

Assuming that $\mathcal{T}$ is a UCBS satisfying the OpCd, and $\mathcal{S}\subseteq \mathcal{T}$ is a convex, nonempty, and compact subset. If $\Omega :\mathcal{S}\to \mathcal{S}$ is a GNZ-α-NonExp mapping with ${\mathit{F}}_{\Omega }^{★}\ne \varnothing$, and $\left\{w_t\right\}$ denotes a sequence of ${\mathit{F}}^{★}$ iterates (2), then $\left\{w_t\right\}$ exhibits strong convergence to a FP of Ω.

Proof. 

Due to the convexity of $\mathcal{S}$, we have $\left\{w_t\right\}\subseteq \mathcal{S}$. Accordingly, we have a subsequence $\left\{w_{t_s}\right\}$ of $\left\{w_t\right\}$ with ${lim}_{s\to \infty }\Vert w_{t_s}-{\mathit{d}}^{★★}\Vert =0$ for some ${\mathit{d}}^{★★}\in \mathcal{S}$. On the other hand, using Theorem 1, ${lim}_{s\to \infty }\Vert \mathrm{\Omega }{w}_{t_s}-w_{t_s}\Vert =0$. Thus, by Proposition 1(4), one has

$$\Vert w_{t_s}-\mathrm{\Omega }{\mathit{d}}^{★★}\Vert \le \left(\frac{3+\alpha }{1-\alpha }\right)\Vert w_{t_s}-\mathrm{\Omega }{w}_{t_s}\Vert +\Vert w_{t_s}-{\mathit{d}}^{★★}\Vert .$$

Hence, if we let $s\to \infty$, then $\mathrm{\Omega }{\mathit{d}}^{★★}={\mathit{d}}^{★★}$. Hence, ${\mathit{d}}^{★★}$ is a FP of $\mathrm{\Omega }$, and by Lemma 2, ${lim}_{t\to \infty }\Vert w_t-{\mathit{d}}^{★★}\Vert$ exists. Accordingly, ${\mathit{d}}^{★★}$ is also a strong limit of $\left\{w_t\right\}$. □

Theorem 4.

Assuming $\mathcal{T}$ is a UCBS equipped with the OpCd, and $\mathcal{S}\subseteq \mathcal{T}$ is a closed, nonempty, and convex subset. If $\Omega :\mathcal{S}\to \mathcal{S}$ is a GNZ-α-NonExp mapping with ${\mathit{F}}_{\Omega }^{★}\ne \varnothing$, and $\left\{w_t\right\}$ represents a sequence of ${\mathit{F}}^{★}$ iterates (2) such that ${lim\; inf}_{t\to \infty }\mathit{d}({\mathit{w}}_{\mathit{t}},{\mathit{F}}_{\Omega }^{★})=0$, then $\left\{w_t\right\}$ strongly converges to an FP of Ω.

Proof. 

According to Lemma 2, the limit ${lim}_{t\to \infty }\Vert {\mathit{w}}_{\mathit{t}}-{\mathit{c}}^{★}\Vert$ exists for every FP of $\Omega$. Consequently, ${lim}_{t\to \infty }\mathit{d}({\mathit{w}}_{\mathit{t}},{\mathit{F}}_{\Omega }^{★})$ also exists, and

$$\underset{t\to \infty }{lim}\mathit{d}({\mathit{w}}_{\mathit{t}},{\mathit{F}}_{\Omega }^{★})=0.$$

The above limit provides us two subsequences $\left\{w_{t_s}\right\}$ and $\left\{d_s\right\}$ of $\left\{w_t\right\}$ and ${\mathit{F}}_{\Omega }^{★}$, respectively, in the following way

$$\Vert {\mathit{w}}_{{\mathit{t}}_{\mathit{s}}}-{\mathit{d}}_{\mathit{s}}\Vert \le \frac{1}{2^s},\forall \mathit{s}\ge 1.$$

By Lemma 2, we see that $\left\{w_t\right\}$ is non increasing and so

$$\Vert {\mathit{w}}_{{\mathit{t}}_{\mathit{s}+\mathit{1}}}-{\mathit{d}}_{\mathit{s}}\Vert \le \Vert {\mathit{w}}_{{\mathit{t}}_{\mathit{s}}}-{\mathit{d}}_{\mathit{s}}\Vert \le \frac{1}{2^s}.$$

It follows that if $\mathit{s}\to \infty$, then

$$\Vert {\mathit{d}}_{\mathit{s}+\mathit{1}}-{\mathit{d}}_{\mathit{s}}\Vert \le \Vert {\mathit{d}}_{\mathit{s}+\mathit{1}}-{\mathit{w}}_{{\mathit{t}}_{\mathit{s}+\mathit{1}}}\Vert +\Vert {\mathit{w}}_{{\mathit{t}}_{\mathit{s}+\mathit{1}}}-{\mathit{d}}_{\mathit{s}}\Vert \le \frac{1}{2^{s+1}}+\frac{1}{2^s}\le \frac{1}{2^{s1}}\to 0.$$

Consequently, we obtain that ${lim}_{s\to \infty }\Vert {\mathit{d}}_{\mathit{s}+\mathit{1}}-{\mathit{d}}_{\mathit{s}}\Vert =0$, which shows that $\left\{d_s\right\}$ is a Cauchy sequence in ${\mathit{F}}_{\Omega }^{★}$ and so it converges to an element ${\mathit{d}}^{★★}$. By Proposition 1(3), ${\mathit{F}}_{\Omega }^{★}$ is closed and so ${\mathit{d}}^{★★}\in {\mathit{F}}_{\Omega }^{★}$. By Lemma 2, ${lim}_{t\to \infty }\Vert {\mathit{w}}_{\mathit{t}}-{\mathit{d}}^{★★}\Vert$ exists and, hence, ${\mathit{d}}^{★★}$ is the strong limit of $\left\{w_t\right\}$. □

Theorem 5.

Assume that $\mathcal{T}$ is a UCBS with the OpCd, and $\mathcal{S}\subseteq \mathcal{J}$ is a closed, nonempty, and convex subset. Let $\Omega :\mathcal{S}⟶\mathcal{S}$ be a mapping satisfying condition (C), with ${\mathit{F}}_{\Omega }^{★}\ne \varnothing$ and $\left\{w_t\right\}$ representing a sequence of ${\mathit{F}}^{★}$ iterates (2). Then, $\left\{w_t\right\}$ exhibits strong convergence to a FP of Ω.

Proof. 

From (1), we have

$$lim\underset{t\to \infty }{inf}\Vert \Omega {\mathit{w}}_{\mathit{t}}-{\mathit{w}}_{\mathit{t}}\Vert =0.$$

(7)

By using the definition of condition (I) [2], we have

$$\Vert {\mathit{w}}_{\mathit{t}}-\Omega {\mathit{w}}_{\mathit{t}}\Vert \ge \mathit{f}\left(\mathit{d}({\mathit{w}}_{\mathit{t}},{\mathit{F}}_{\Omega }^{★})\right).$$

(8)

Applying (7) and (8), we have

$$lim\underset{t\to \infty }{inf}\mathit{f}\left(\mathit{d}({\mathit{w}}_{\mathit{t}},{\mathit{F}}_{\Omega }^{★})\right)=0.$$

It follows that

$$lim\underset{t\to \infty }{inf}\mathit{d}({\mathit{w}}_{\mathit{t}},{\mathit{F}}_{\Omega }^{★})=0.$$

By Theorem 4, $\left\{w_t\right\}$ is strongly convergent to an FP of $\Omega$. □

To support the main results, we provide two examples by Proposition 1(1) of GNZ-$\alpha$-NonExp mapping, which is provided with C. By using these examples, we implement our new proposed method to obtain numerical results. These results are compared with other iteration schemes that are used for GNZ-$\alpha$-NonExp mappings.

Example 1.

Consider the closed and bounded subset $\mathcal{S}=[7,13]$ of the real number space $\mathbb{R}$. Define $\Omega :\mathcal{S}⟶\mathcal{S}$ as

$$\Omega d=\left\{\begin{array}{cc}\frac{d+7}{2},\hfill & \hfill \mathrm{for}d<13,\\ 7,\hfill & \hfill \mathrm{for}d=13.\end{array}\right.$$

Our aim is to establish that Ω is a GNZ-α-NonExp mapping with $\alpha =\frac{1}{2}$, while it does not fall under the category of Suzuki mappings. This example, therefore, extends beyond the class of Suzuki mappings.

Case I: If $d^{\prime },d^{″}=13$, then we have

$$\frac{1}{2}\mid d^{\prime }-\Omega {\mathit{d}}^{″}\mid +\frac{1}{2}\mid {\mathit{d}}^{″}-\Omega {\mathit{d}}^{\prime }\mid +(1-2\left(\frac{1}{2}\right))\mid {\mathit{d}}^{\prime }-{\mathit{d}}^{″}\mid \ge 0=\mid \Omega {\mathit{d}}^{\prime }-\Omega {\mathit{d}}^{″}\mid .$$

Case II: If $d^{\prime },d^{″}\le 13$, then we have

$$\begin{array}{ccc}\hfill & & \frac{1}{2}|d^{\prime }-\Omega d^{″}|+\frac{1}{2}|d^{″}-\Omega d^{\prime }|+(1-2\left(\frac{1}{2}\right))|d^{\prime }-d^{″}|\hfill \\ & & =\frac{1}{2}|d^{″}-\left(\frac{d^{\prime }+7}{2}\right)|+\frac{1}{2}|d^{\prime }-\left(\frac{d^{″}+7}{2}\right)|\hfill \\ & & \ge \frac{1}{4}|(d^{″}-\left(\frac{d^{\prime }+7}{2}\right))-(d^{\prime }-\left(\frac{d^{″}+7}{2}\right))|\hfill \\ & & =\frac{1}{2}|\frac{3d^{″}-3d^{\prime }}{2}|\hfill \\ & & =\frac{3}{4}|d^{\prime }-d^{″}|\hfill \\ & & \ge \frac{1}{2}|d^{\prime }-d^{″}|\hfill \\ & & =|\Omega d^{\prime }-\Omega d^{″}|.\hfill \end{array}$$

Case III: If $d^{\prime }=13$ and $d^{″}<13$, then we have

$$\begin{array}{ccc}\hfill \frac{1}{2}|d^{\prime }-\Omega d^{\prime }|+\frac{1}{2}|d^{″}-\Omega d^{\prime }|+(1-2\left(\frac{1}{2}\right))|d^{\prime }-d^{″}|& =& \frac{1}{2}|d^{\prime }-7|+\frac{1}{2}|d^{″}-\left(\frac{d^{\prime }+7}{2}\right)|\hfill \\ & \ge & \frac{1}{2}|7d^{\prime }|\hfill \\ & =& |\frac{d^{\prime }-7}{2}|\hfill \\ & =& |\Omega d^{\prime }-\Omega d^{″}|.\hfill \end{array}$$

So

$$|\Omega {\mathit{d}}^{\prime }-\Omega {\mathit{d}}^{″}|\le \frac{1}{2}\mid {\mathit{d}}^{\prime }-\Omega {\mathit{d}}^{″}\mid +\frac{1}{2}\mid {\mathit{d}}^{″}-\Omega {\mathit{d}}^{\prime }\mid +(1-2\left(\frac{1}{2}\right))\mid {\mathit{d}}^{\prime }-{\mathit{d}}^{″}\mid$$

for all ${\mathit{d}}^{\prime },{\mathit{d}}^{″}\in \Omega$.

Example 2.

Consider the closed and bounded subset $\mathcal{S}=[6,15]$ within the Banach space $\mathbb{R}$. Let $\Omega :\mathcal{S}\to \mathcal{S}$ be defined as

$$\Omega d^{\prime }=\left\{\begin{array}{cc}\frac{d^{\prime }+6}{2},\hfill & \hfill \mathrm{for}{d}^{\prime }<15,\\ 6,\hfill & \hfill \mathrm{for}{d}^{\prime }=15.\end{array}\right.$$

In this example, we prove again that Ω is a GNZ-α-NonExp mapping with $\alpha =\frac{1}{4}$, but not a Suzuki mapping. This example thus exceeds the class of Suzuki mappings.

Case I: If ${\mathit{d}}^{\prime }=15={\mathit{d}}^{″}$, then we have

$$\frac{1}{4}|d^{\prime }-\Omega d^{″}|+\frac{1}{4}|d^{″}-\Omega d^{\prime }|+(1-2\left(\frac{1}{4}\right))|d^{\prime }-d^{″}|\ge 0=|\Omega d^{\prime }-\Omega d^{″}|.$$

Case II: If ${\mathit{d}}^{\prime },{\mathit{d}}^{″}\le 15$, then we have

$$\begin{array}{ccc}\hfill & & \frac{1}{4}|d^{\prime }-\Omega d^{″}|+\frac{1}{4}|d^{″}-\Omega d^{\prime }|+(1-2\left(\frac{1}{4}\right))|d^{\prime }-d^{″}|\hfill \\ & & =\frac{1}{4}|d^{″}-\left(\frac{d^{\prime }+6}{2}\right)|+\frac{1}{4}|d^{\prime }-\left(\frac{d^{″}+6}{2}\right)|\hfill \\ & & \ge \frac{1}{4}|\frac{3d^{″}-3d^{\prime }}{2}|\hfill \\ & & =\frac{3}{8}|d^{\prime }-d^{″}|\hfill \\ & & \ge \frac{1}{4}|d^{\prime }-d^{″}|\hfill \\ & & =|\Omega d^{\prime }-\Omega d^{″}|.\hfill \end{array}$$

Case III: If ${\mathit{d}}^{\prime }=15$ and ${\mathit{d}}^{″}<15$, then we have

$$\begin{array}{ccc}\hfill \frac{1}{4}|d^{\prime }-\Omega d^{″}||+\frac{1}{4}|d^{″}-\Omega d^{\prime }|+(1-2\left(\frac{1}{4}\right))|d^{\prime }-d^{″}|& =& \frac{1}{4}|d^{\prime }-6||+\frac{1}{4}|d^{″}-\left(\frac{d^{\prime }+6}{2}\right)|\hfill \\ & \ge & \frac{1}{4}|d^{\prime }-6|\hfill \\ & =& |\frac{d^{\prime }-6}{4}|\hfill \\ & =& |\Omega d^{\prime }-\Omega d^{″}|.\hfill \end{array}$$

So,

$$|\Omega d^{\prime }-\Omega d^{″}|\le \frac{1}{4}|d^{\prime }-\Omega d^{″}|+\frac{1}{4}|d^{″}-\Omega d^{\prime }|+(1-2\left(\frac{1}{4}\right))|d^{\prime }-d^{″}|$$

for all $d^{\prime },d^{″}\in \Omega$.

We will now assess the efficiency of the proposed iteration scheme $F^{*}$ in comparison to other prominent schemes, namely F [2], M [9], Noor [5], S [6], Picard-S [8], Picard [1], Ishikawa [4], and Mann [3], within the broader context of GNZ-$\alpha$-NonExp mappings. Each of these schemes exhibits distinct convergence rates for GNZ-$\alpha$-NonExp mappings. Upon comparing these leading schemes, it becomes evident that F [2], M [9], and S [6] demonstrate a higher rate of convergence when compared to Noor [5], Picard-S [8], Picard [1], Ishikawa [4], and Mann [3]. Essentially, the former set of schemes proves to be more efficient for contractions and NonExp mappings. The effectiveness of $F^{*}$ is clearly observed in Table 1 and Table 2, which provide results for GNZ-$\alpha$-NonExp mappings as presented in Examples 1 and 2. Additionally, Figure 1 offers insights into the performance of these leading schemes. It is evident that the $F^{*}$ iterative scheme surpasses the other schemes in the general context of GNZ-$\alpha$-NonExp mappings.

4. Application to Nonlinear Integral Equation

In this section, we explore the application of our findings to a nonlinear integral equation of the form

$$d^{\prime }\left(t\right)=w\left(t\right)+{\int }_c^{d}Y(t,s)z(t,d^{\prime }\left(s\right))ds,$$

where $Y:[c,d]\times [c,d]\to {\mathbb{R}}^{+}$, $z:[c,d]\times \mathbb{R}\to \mathbb{R}$, and $w:[c,d]\to \mathbb{R}$ are continuous functions. Let $\mathcal{S}=C\left(\right[c,d],\mathbb{R})$ denote the space of all continuous functions defined on $[c,d]$, and the order relations ≤ in $\mathcal{S}$ are defined as follows: For $d^{\prime },d^{″}\in \mathcal{S}$, $d^{\prime }\le d^{″}\iff d^{\prime }\left(s\right)\le d^{″}\left(s\right)$ for all $s\in [c,d]$. Define $||.||:\mathcal{S}\times \mathcal{S}\to [0,\infty )$ by

$$||d^{\prime }-d^{″}||=\underset{s\in [c,d]}{inf}|d^{\prime }\left(s\right)-d^{″}\left(s\right)|.$$

Theorem 6.

Consider the space $\mathcal{S}=C\left(\right[c,d],\mathbb{R})$ representing all continuous real-valued functions defined on $[c,d]$. Let $\Omega :\mathcal{S}\to \mathcal{S}$ be the mapping defined as

$$\Omega d^{\prime }\left(t\right)=w\left(t\right)+{\int }_c^{d}Y(t,s)z(t,d^{\prime }\left(s\right))ds,$$

where $Y:[c,d]\times [c,d]\to {\mathbb{R}}^{+}$, $z:[c,d]\times \mathbb{R}\to \mathbb{R}$, and $w:[c,d]\to \mathbb{R}$ are continuous functions. Additionally, suppose the following conditions are met:

1. 

There exists a continuous mapping $\eta :\mathcal{S}\times \mathcal{S}\to [0,\infty )$ such that

$$|z(s,d^{\prime }\left(s\right))-z(s,d^{″}\left(s\right))|\le \eta (d^{\prime },d^{″})|d^{\prime }\left(s\right)-d^{\prime \prime }\left(s\right)|,$$

for all $s\in [c,d]$ and $d^{\prime },d^{″}\in \mathcal{S}$.

2. 

There exists $\sigma \in [0,1)$ such that

$${\int }_c^{d}Y(t,s)\eta (d^{\prime },d^{″})ds\le \sigma .$$

Then the integral Equation (4) possesses a solution.

Proof. 

Suppose $d^{\prime }\le d^{″}$. If

$$|d^{″}\left(s\right)-d^{\prime }\left(s\right)|\ge inf\parallel \Omega d^{\prime }\left(s\right)-d^{\prime }\left(s\right)|$$

for all $s\in [c,d]$, then

$$\frac{1}{2}\Vert \Omega d^{\prime }-d^{\prime }\Vert \le \Vert d^{″}-d^{\prime }\Vert .$$

Thus, we

$$\begin{array}{cc}\hfill |\Omega d^{″}\left(s\right)-\Omega d^{\prime }\left(s\right)|& =||w\left(t\right)+{\int }_c^{d}Y(t,s)z(t,d^{″}\left(s\right))ds-w\left(t\right)+{\int }_c^{d}Y(t,s)z(t,d^{\prime }\left(s\right))ds\parallel \hfill \\ & \le {\int }_c^d|Y(t,s)[z(t,d^{″}\left(s\right))-z(t,d^{\prime }\left(s\right))]|ds\hfill \\ & \le {\int }_c^{d}Y(t,s)\eta (d^{\prime },d^{″})|d^{″}\left(s\right)-,d^{\prime }\left(s\right)]ds\hfill \\ & \le \underset{s\in [c,d]}{inf}|d^{″}\left(s\right)-d^{\prime }\left(s\right)|{\int }_c^{d}Y(t,s)\sigma (d^{\prime },d^{″})ds\hfill \\ & \le \sigma \Vert d^{″}-d^{\prime }\Vert \hfill \\ & \le \Vert d^{″}-d^{\prime }\Vert .\hfill \end{array}$$

Thus, we have

$$\frac{1}{2}\Vert d^{\prime }-\Omega d^{\prime }\Vert \le \Vert d^{\prime }-d^{″}\Vert$$

and

$$\Vert \Omega d^{\prime }-\Omega d^{″}\Vert \le \alpha \Vert d^{\prime }-\Omega {\mathit{d}}^{″}\Vert +\alpha \Vert d^{″}-\Omega d^{\prime }\Vert +(1-2\alpha )\Vert d^{\prime }-d^{″}\Vert$$

for all $d^{\prime },d^{″}\in \mathcal{S}$ and $\alpha \in [0,1)$.

Clearly, $\Omega$ satisfies the condition (C) and by Definition 2, $\Omega$ is a GNZ-$\alpha$-NonExp mapping. All the conditions given in Theorem 5 are satisfied. Thus, $\Omega$ has an FP that is the solution of the nonlinear integral Equation (4). □

5. Experimental Results

We have a nonlinear integral equation of the form

$$d^{\prime }\left(t\right)=f\left(t\right)+{\int }_c^{d}K(t,s)w(s,d\left(s\right))ds.$$

The equation represents a relationship between the derivative of an unknown function $d\left(t\right)$ and the integral of a function $w(s,d(s\left)\right)$ over a given interval $[c,d]$, weighted by the kernel function $K(t,s)$. The function $f\left(t\right)$ represents a driving force.

To solve this equation, we will employ the FP Iteration method. We start with an initial approximation $d_0\left(t\right)$ and update it iteratively by using the following formula:

$$d_{n+1}\left(t\right)=d_0\left(t\right)+{\int }_c^{d}K(t,s)w(s,d_n\left(s\right))ds,$$

(9)

where n represents the iteration number.

In the example, we will consider specific functions for $f\left(t\right)$, $w(s,d)$, and $K(t,s)$, and the interval $[c,d]$. We will solve (9) by using the FP Iteration method with an initial approximation $d_0\left(t\right)$. We will evaluate the solution at various points within the interval $[c,d]$.

Table 3. Approximation, exact, and error values for different iterations.

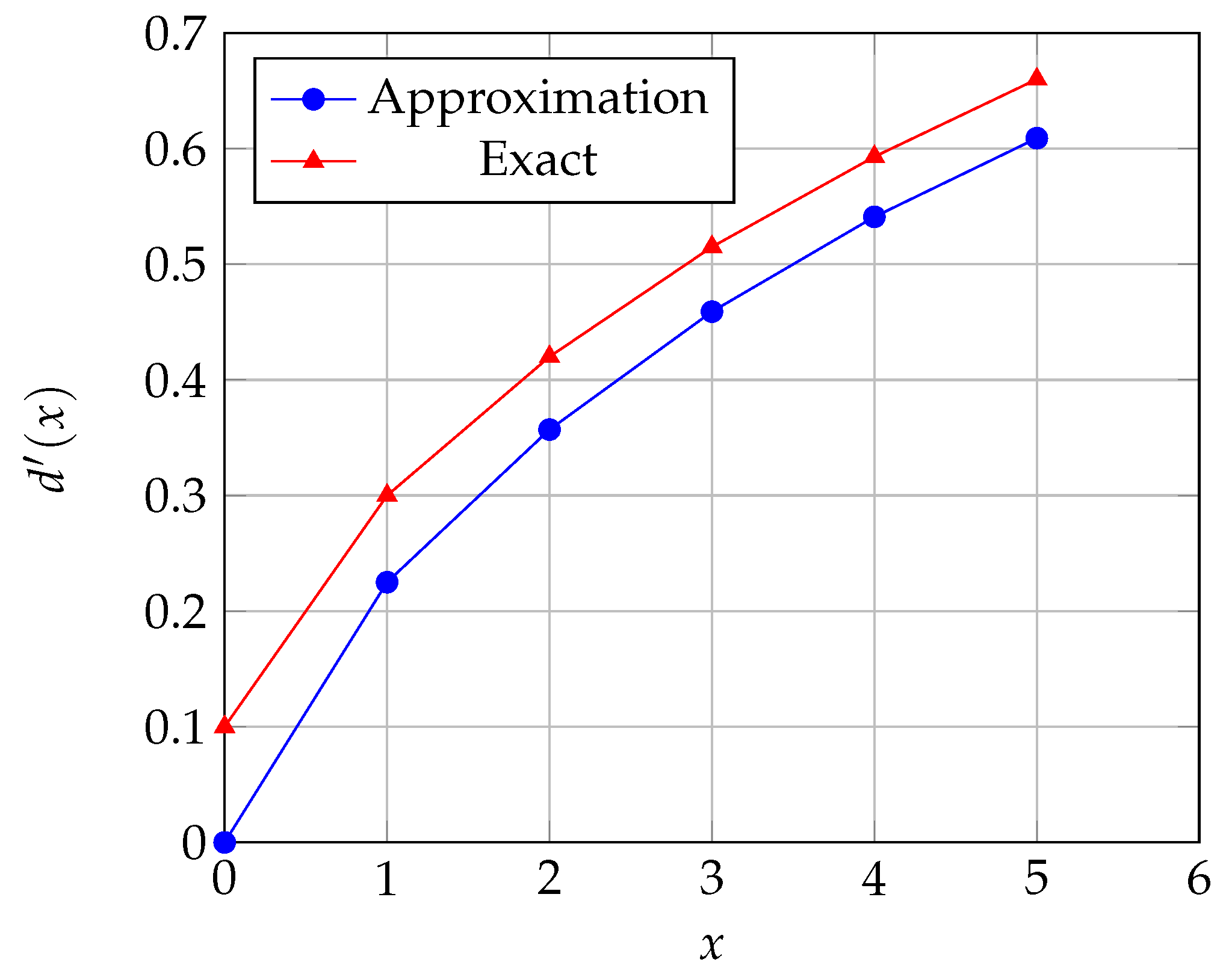
Iteration	Approximation	Exact	Error
0	0.000	0.100	-
1	0.225	0.300	0.075
2	0.357	0.420	0.063
3	0.459	0.515	0.056
4	0.541	0.593	0.052
5	0.609	0.660	0.051

provided in the example shows the approximation, exact value, and error at each iteration. Each row corresponds to a specific iteration, with the approximation denoted as $d_n\left(t\right)$, the exact value denoted as $d\left(t\right)$, and the calculated error being the absolute difference between the approximation and the exact value $|d_n\left(t\right)-d\left(t\right)|$.

Furthermore, a graphical representation will be given to visualize the convergence behavior of the iterative scheme. The graph will show the exact solution and the iteratively computed approximations $d_n\left(t\right)$ for each iteration.

Overall, the example will demonstrate the process of solving a nonlinear integral equation by using the FP Iteration method and provide insights into the convergence behavior through the table and graph.

Example 3.

Consider the following nonlinear integral equation:

$$d^{\prime }\left(t\right)=f\left(t\right)+{\int }_c^{d}K(t,s)w(s,d\left(s\right))ds,$$

(10)

where $f\left(t\right)$ and $w(s,d)$ are continuous functions, and $K(t,s)$ is a kernel function. To solve (10), we can use an iterative scheme called the FP Iteration method. We start with an initial approximation $d_0\left(t\right)$ and iteratively update it by using the following formula:

$$d_{n+1}\left(t\right)=d_0\left(t\right)+{\int }_c^{d}K(t,s)w(s,d_n\left(s\right))ds,$$

where n represents the iteration number.

Now, we assume the following specific functions for our example:

$$f\left(t\right)=t^2,w(s,d)=d^2+2s,K(t,s)=\frac{1}{1+t+s}$$

and the interval $[c,d]$ as $[0,1]$.

We will solve (10) by using the FP Iteration method with an initial approximation $d_0\left(t\right)=t$. We will evaluate the solution at various points in the interval $[0,1]$. Table 3 shows the approximation, exact value, and error at each iteration while

Table 4. Solution function $d\left(t\right)$ and the iteratively computed approximations $d_n\left(t\right)$ for different iterations.

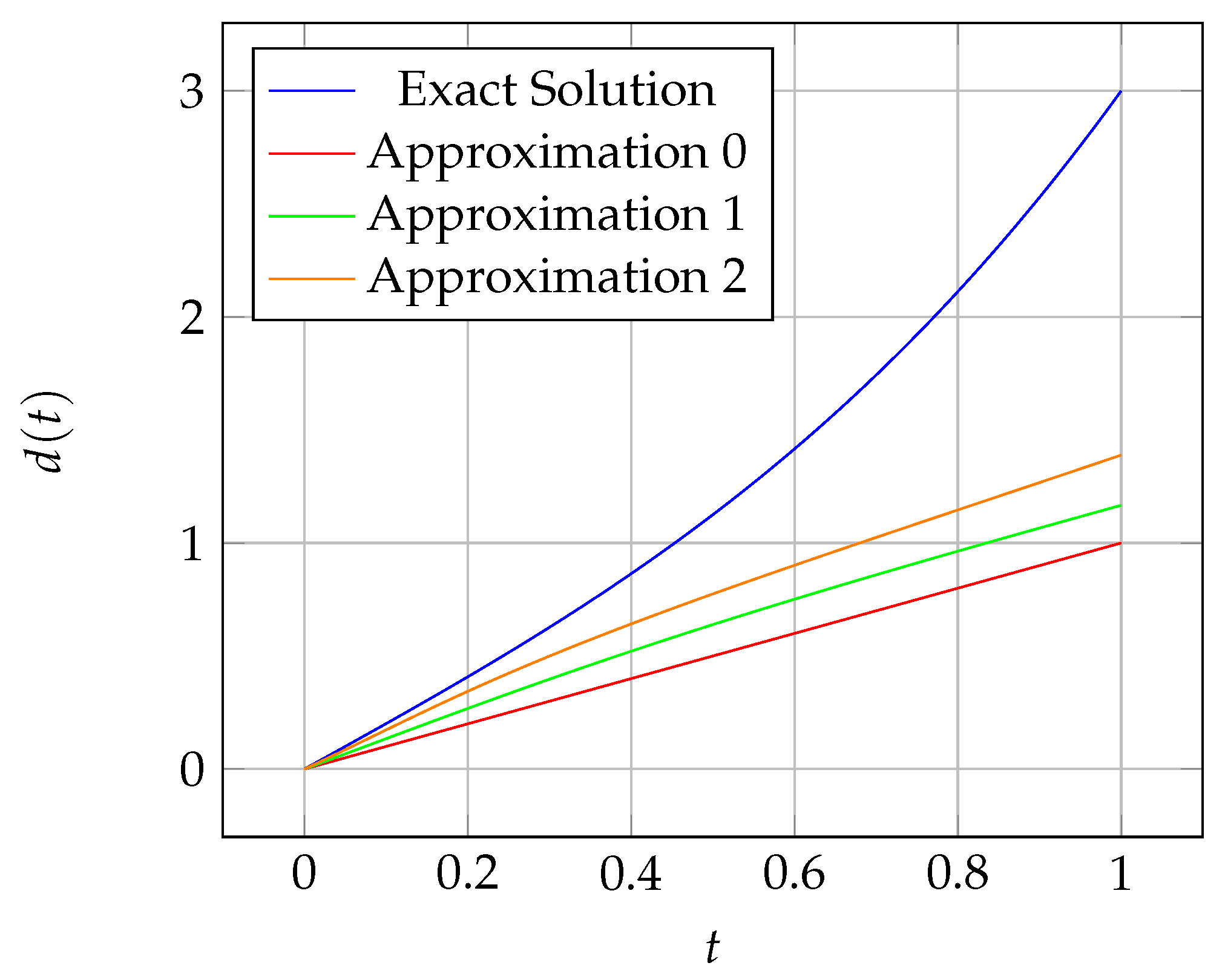
Iteration	Approximation	Exact	Error
0	$d_0\left(t\right)$	$d\left(t\right)$	$|d_0\left(t\right)-d\left(t\right)|$
1	$d_1\left(t\right)$	$d\left(t\right)$	$|d_1\left(t\right)-d\left(t\right)|$
2	$d_2\left(t\right)$	$d\left(t\right)$	$|d_2\left(t\right)-d\left(t\right)|$
…	…	…	…

shows the solution function $d\left(t\right)$ and the iteratively computed approximations $d_n\left(t\right)$ for each iteration.

Finally, we can plot the graph of the solution function $d\left(t\right)$ and the iteratively computed approximations $d_n\left(t\right)$ for each iteration. Figure 2 and Figure 3 provide a visual representation of the convergence behavior for each iteration.

6. Conclusions

This paper presents several novel contributions:

(i)

We introduce a new iterative scheme, denoted as $F^{*}$, specifically designed for GNZ-$\alpha$-NonExp mappings. Our findings indicate that the inclusion of an additional function facilitates rapid convergence for $\alpha$-NonExp mappings. We establish both weak and strong convergence for the modified iterative scheme.

(ii)

The key outcomes of this paper are substantiated through numerical experiments, enhancing the results established by Ali and Ali [14] and Ahmad et al. [2].

(iii)

We provide diverse examples to illustrate and support our findings, showcasing the efficiency of the proposed algorithm across various iterative algorithms in the existing literature. This is achieved through different parameter choices and initial guesses.

(iv)

Consequently, our results extend the core findings of Ahmad et al. [2], serving as generalizations and refinements of the outcomes presented by Ali and Ali [14] and Ahmad et al. [2]. We extend our results from contraction to NonExp mappings and GNZ-$\alpha$-NonExp mappings, emphasizing enhanced convergence speed.

(v)

To demonstrate the practical applicability of our results, we apply our findings to ascertain solutions for nonlinear integral equations.