Asymptotic Behavior of Some Differential Inequalities with Mixed Delays and Their Applications
Abstract
1. Introduction
- (1)
- Halanay inequality and generalized Halanay inequality are the special forms of delay inequality (1). Therefore, the theoretical results of this article can be used to study more general delay dynamical systems. Specifically, the results of this paper can be used to conveniently study neutral-type differential dynamical systems.
- (2)
- Specifically, the results of this paper can be used to conveniently study neutral-type differential dynamical systems. Example 1 contains a first-order neutral-type differential equation, which can be used to model models of biological populations and lossless transmission systems. Examples 2 and 3 contain first-order nonlinear equations with mixed delays. Many neural networks, physical models, chemical models, and infectious disease models can be described by Examples 2 and 3.
- (3)
2. Main Results
- (i)
- and
- (ii)
- as .
- (i)
- (ii)
- as .
- (i)
- (ii)
- as .
- (i)
- (ii)
- as .
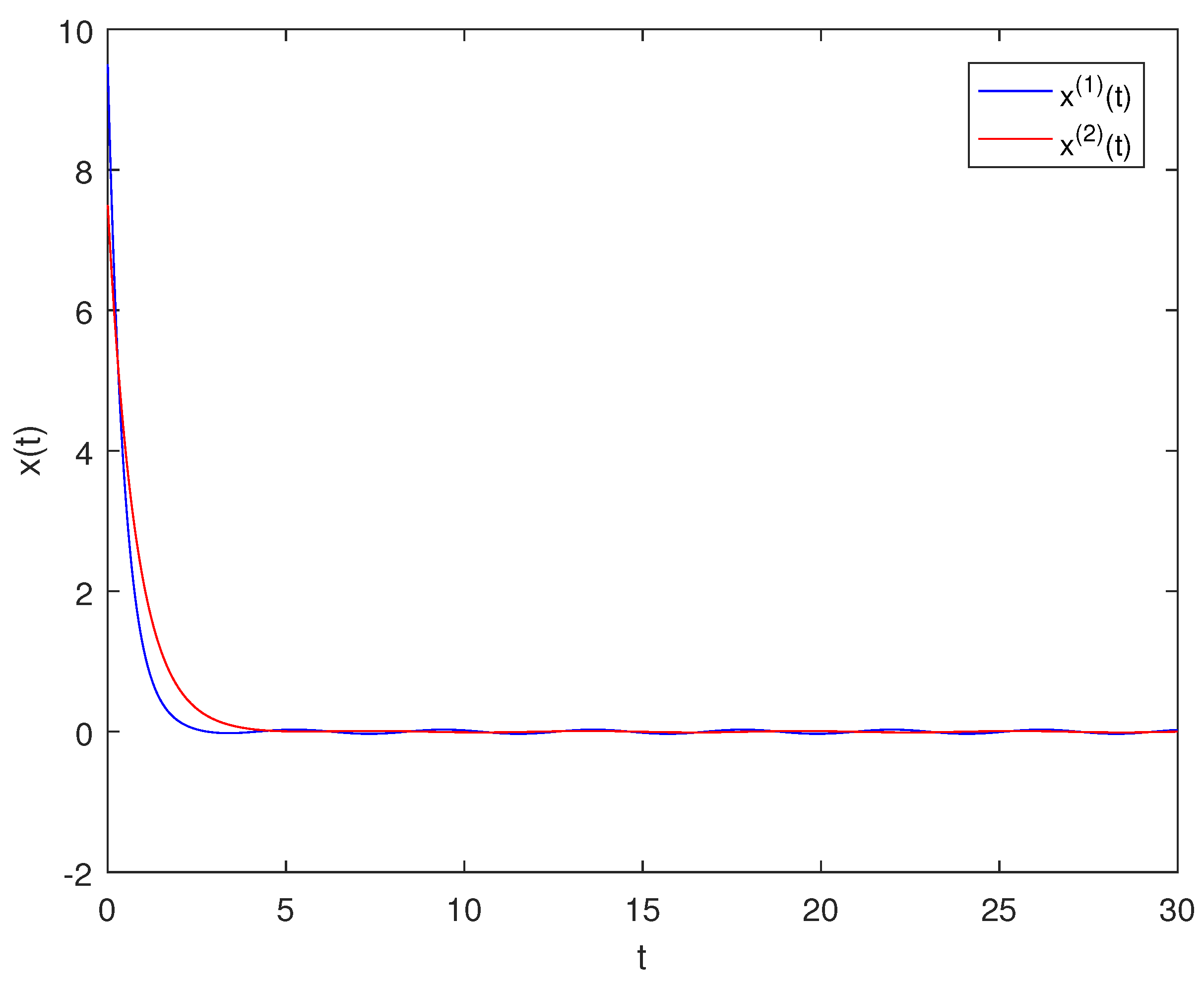
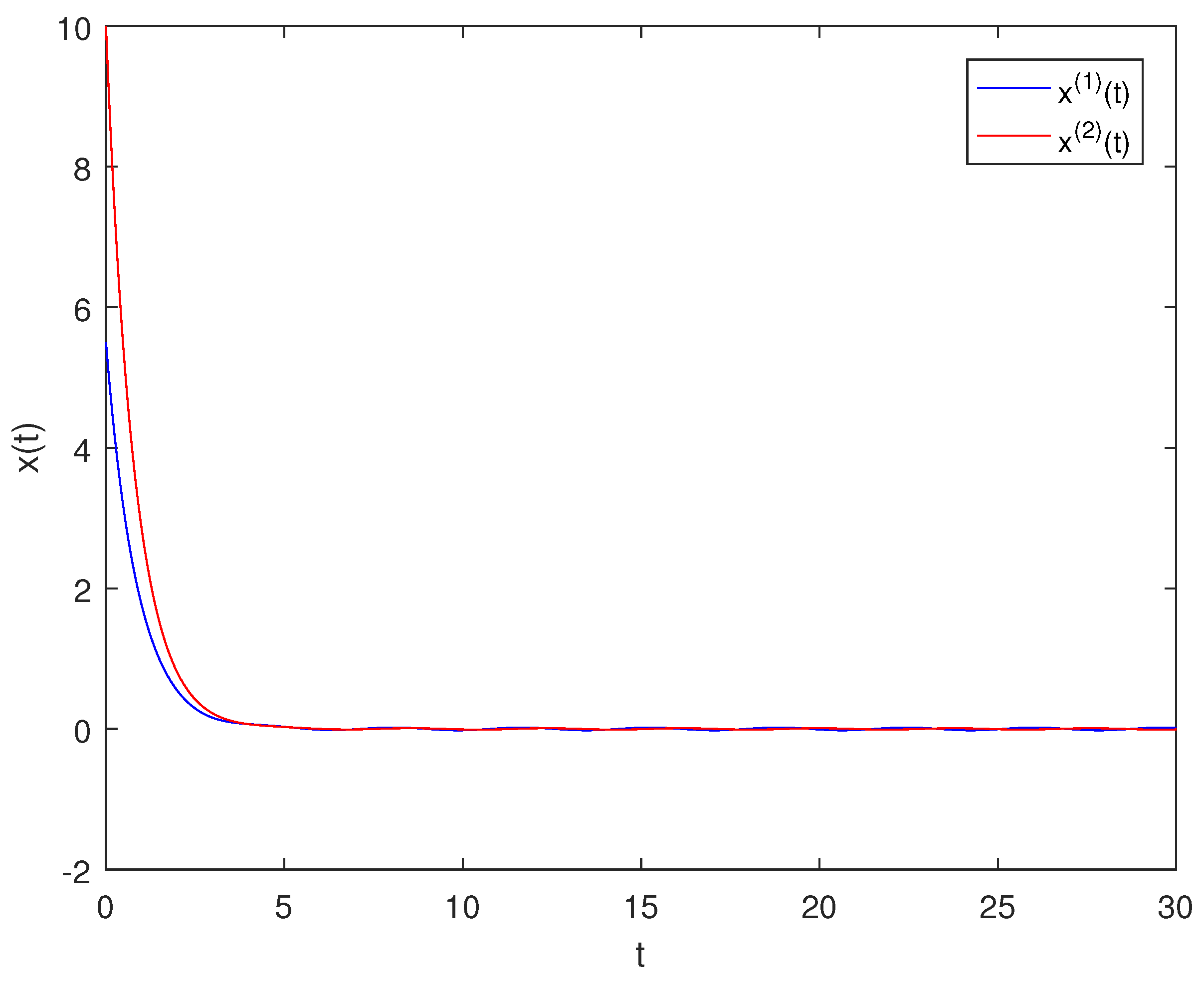
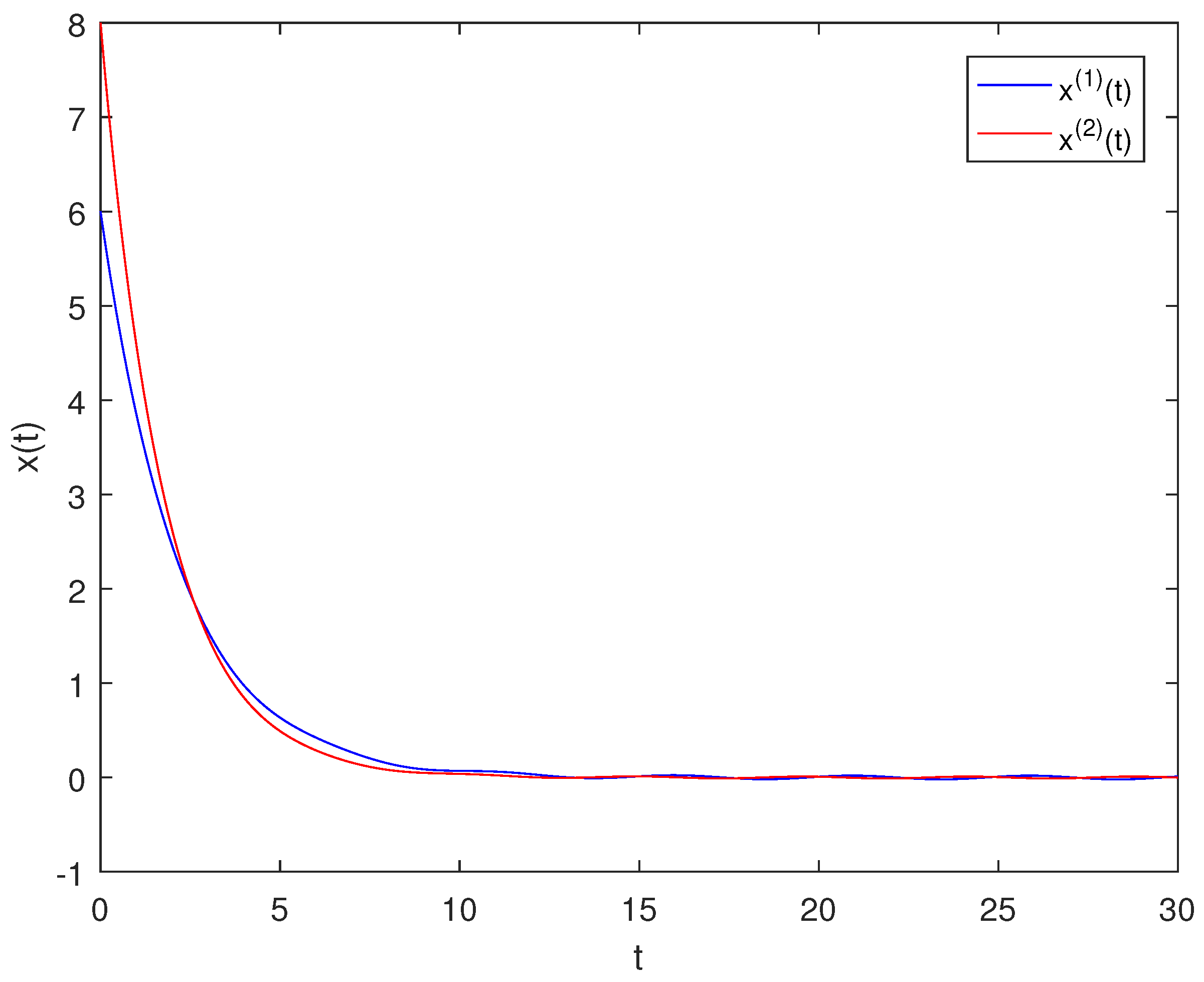
3. Examples
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hale, J.; Lunel, S. Introduction to Functional Differential Equations; Springer-Verlag: Berlin, Germany, 1993. [Google Scholar]
- Yu, Y. Global exponential convergence for a class of neutral functional differential equations with proportional delays. Math. Methods Appl. Sci. 2016, 39, 4520–4525. [Google Scholar] [CrossRef]
- Shi, K.; Zhu, H.; Zhong, S.; Zeng, Y.; Zhang, Y. New stability analysis for neutral type neural networks with discrete and distributed delays using a multiple integral approach. J. Frankl. Inst. 2015, 352, 155–176. [Google Scholar] [CrossRef]
- Yao, L. Global convergence of CNNs with neutral type delays and D operator. Neural Comput. Appl. 2018, 29, 105–109. [Google Scholar] [CrossRef]
- Li, F. Positive periodic solutions for a kind of second-order neutral differential equations with variable coefficient and delay. Mediterr. J. Math. 2018, 15, 134–153. [Google Scholar]
- Xiao, S. Global Exponential Convergence of HCNNs with Neutral Type Proportional Delays and D Operator. Neural Process. Lett. 2019, 49, 347–356. [Google Scholar] [CrossRef]
- Xin, Y.; Cheng, Z.B. Neutral operator with variable parameter and third-order neutral differential equation. Adv. Diff. Equ. 2014, 273, 1–18. [Google Scholar] [CrossRef][Green Version]
- Hadžić, O. Fixed Point Theory in Topological Vector Spaces; Novi Sad, Serbia. 1984. Available online: https://www.kurims.kyoto-u.ac.jp/EMIS/journals/NSJOM/Papers/10/NSJOM_10_023_029.pdf (accessed on 1 March 2024).
- Halanay, A. Differential Equations; Academic Press: New York, NY, USA, 1966. [Google Scholar]
- Halanay, A. Differential equations: Stability, oscillations, time lags. SIAM Rev. 1975, 10, 93–94. [Google Scholar]
- Ou, B.; Jia, B.; Erbe, L. An extended Halanay inequality with unbounded coefficient functions on time scales. J. Inequal. Appl. 2016, 2016, 316. [Google Scholar] [CrossRef]
- Wang, C.; Chen, H.; Lin, R.; Sheng, Y.; Jiao, F. New generalized Halanay inequalities and relative applications to neural networks with variable delays. Bound. Value Probl. 2023, 2023, 95. [Google Scholar] [CrossRef]
- Baker, C. Development and application of Halanay-type theory: Evolutionary differential and difference equations with time lag. J. Comput. Appl. Math. 2010, 234, 2663–2682. [Google Scholar] [CrossRef]
- Ivanov, A.; Liz, E.; Trofimchuk, S. Halanay inequality, Yorke 32 stability criterion, and differential equations with maxima. Tokohu Math. J. 2002, 54, 277–295. [Google Scholar]
- Liu, B.; Lu, W.; Chen, T. Generalized Halanay inequalities and their applications to neural networks with unbounded time-varying delays. IEEE Trans. Neural Netw. 2011, 22, 1508–1513. [Google Scholar] [CrossRef] [PubMed]
- Xu, L. Generalized discrete Halanay inequalities and the asymptotic behavior of nonlinear discrete systems. Bull. Korean Math. Soc. 2013, 50, 1555–1565. [Google Scholar] [CrossRef][Green Version]
- Ruan, D.; Liu, W.; Yang, M.; Huang, Z.; Guo, X. Novel stability results for Halanay inequality and applications to delay neural networks. IEEE Access 2020, 8, 19504–19511. [Google Scholar] [CrossRef]
- Wen, L.; Wang, W.; Yu, Y. Dissipativity and asymptotic stability of nonlinear neutral delay integro-differential equations. Nonlinear Anal. 2010, 72, 1746–1754. [Google Scholar] [CrossRef]
- Jabbar, S. Hardy and Rogers type Contractive condition and common fixed point theorem in Cone 2-metric space for a family of self-maps. Adv. Fuzzy Math. 2022, 17, 165–173. [Google Scholar]
- Niezgoda, M. A companion preorder to G-majorization and a Tarski type fixed-point theorem section: Convex analysis. J. Fixed Point Theory Appl. 2023, 25, 1–5. [Google Scholar] [CrossRef]
- Aydi, H.; Bota, M.; Karapinar, E.; Mitrovic, S. A fixed point theorem for set-valued quasicontractions in b-metric spaces. Fixed Point Theory Appl. 2012, 2012, 88. [Google Scholar] [CrossRef]
- Harandi, A. Fixed point theory for set-valued quasi-contraction maps in metric spaces. Appl. Math. Lett. 2011, 24, 1791–1794. [Google Scholar] [CrossRef]
- Daffer, P.; Kaneko, H. Fixed points of generalized contractive Multi-valued mappings. J. Math. Anal. Appl. 1995, 192, 655–666. [Google Scholar] [CrossRef]
- Singh, S.; Czerwik, S.; Krol, K.; Singh, A. Coincidences and fixed points points of hybrid contractions. Tamsui Oxf. J. Math. Sci. 2008, 24, 401–416. [Google Scholar]
- Ou, B.; Jia, B.; Erbe, L. An extended Halanay inequality of integral type on time scales. Electron. J. Qual. Theory Differ. Equ. 2015, 38, 1–11. [Google Scholar] [CrossRef]
- Wen, L.; Yu, Y.; Wang, W. Generalized Halanay inequalities for dissipativity of Volterra functional differential equations. J. Math. Anal. Appl. 2008, 347, 169–178. [Google Scholar] [CrossRef]
- Ou, B. Halanay inequality on time scales with unbounded coefficient and its applications. Indian J. Pure Appl. Math. 2020, 51, 1023–1038. [Google Scholar] [CrossRef]
- Jia, B.; Erbe, L.; Mert, R. A Halanay-type inequality on time scales in higher dimensional spaces. Math. Inequal. Appl. 2014, 17, 813–821. [Google Scholar] [CrossRef]
- Agarwal, R.; Kim, Y.; Sen, S. New discrete Halanay inequalities: Stability of difference equations. Commun. Appl. Anal. 2008, 12, 83–90. [Google Scholar]
- Adivar, M.; Bohner, E.A. Halanay type inequalities on time scales with applications. Nonlinear Anal. 2011, 74, 7519–7531. [Google Scholar] [CrossRef][Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shu, A.; Li, X.; Du, B. Asymptotic Behavior of Some Differential Inequalities with Mixed Delays and Their Applications. Axioms 2024, 13, 302. https://doi.org/10.3390/axioms13050302
Shu A, Li X, Du B. Asymptotic Behavior of Some Differential Inequalities with Mixed Delays and Their Applications. Axioms. 2024; 13(5):302. https://doi.org/10.3390/axioms13050302
Chicago/Turabian StyleShu, Axiu, Xiaoliang Li, and Bo Du. 2024. "Asymptotic Behavior of Some Differential Inequalities with Mixed Delays and Their Applications" Axioms 13, no. 5: 302. https://doi.org/10.3390/axioms13050302
APA StyleShu, A., Li, X., & Du, B. (2024). Asymptotic Behavior of Some Differential Inequalities with Mixed Delays and Their Applications. Axioms, 13(5), 302. https://doi.org/10.3390/axioms13050302




