Subclasses of Analytic Functions Subordinated to the Four-Leaf Function †
Abstract
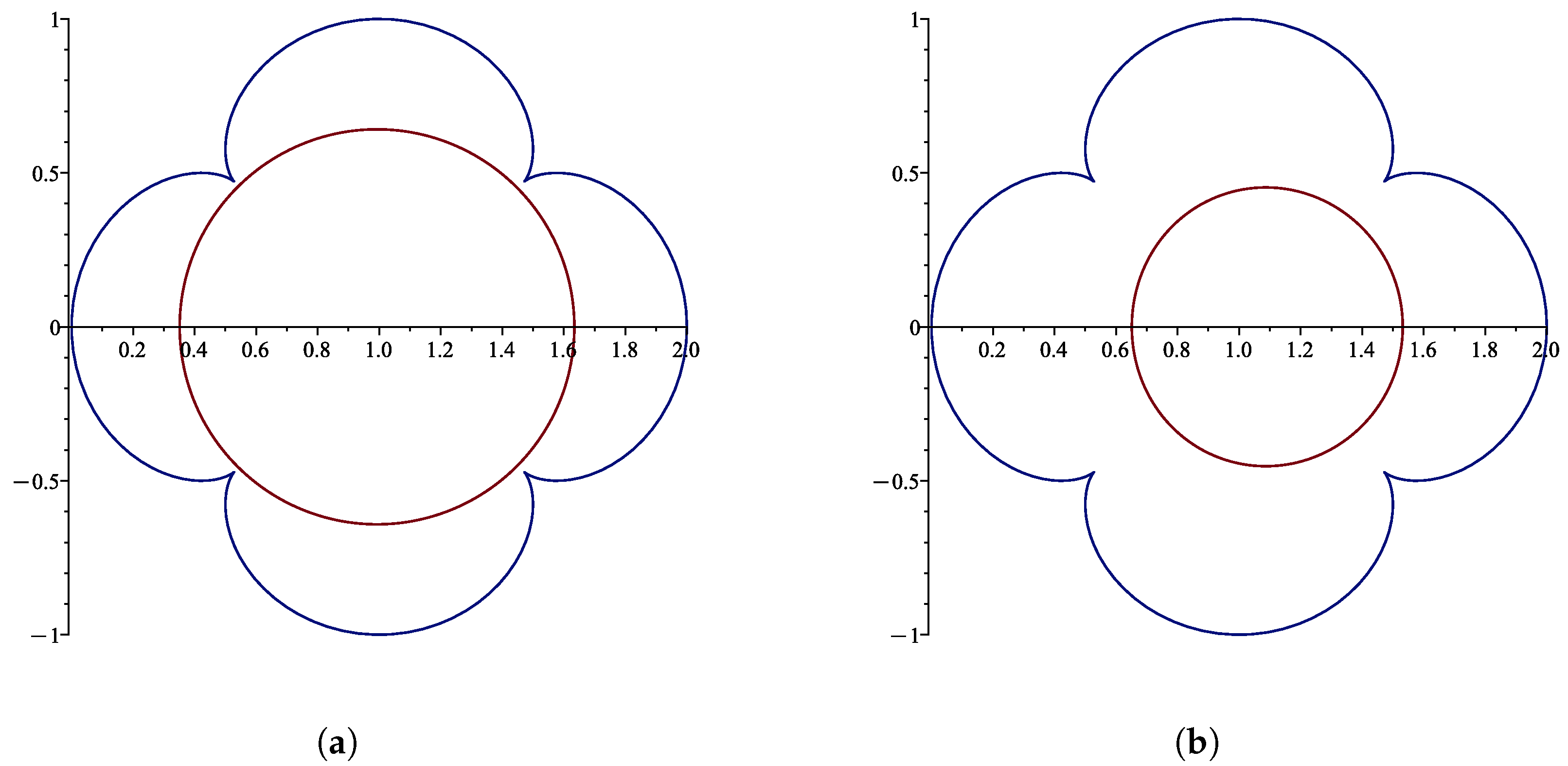
1. Introduction and Preliminaries
2. Initial Coefficient Estimates for Class
3. Krushkal Inequalities for the Class
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goluzin, G.M. Geometric Theory of Functions of a Complex Variable; American Mathematical Soc.: Providence, RI, USA, 1969; Volume 26. [Google Scholar]
- Fekete, M.; Szegő, G. Eine Bemerkung Über ungerade schlichte Funktionen. J. Lond. Math. Soc. 1933, 1, 85–89. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Raza, M.; AbuJarad, E.S.A.; Srivastava, G.; AbuJarad, M.H. Fekete-Szegő inequality for classes of (p, q)-starlike and (p, q)-convex functions. Rev. Real Acad. Cienc. Exactas Fis. Nat. Ser. A-Mat. 2019, 113, 3563–3584. [Google Scholar] [CrossRef]
- Pommerenke, C. On the coefficients and Hankel determinants of univalent functions. J. Lond. Math. Soc. 1966, 1, 111–122. [Google Scholar] [CrossRef]
- Pommerenke, C. On the Hankel determinants of univalent functions. Mathematika 1967, 14, 108–112. [Google Scholar] [CrossRef]
- Hayman, W.K. On the second Hankel determinant of mean univalent functions. Proc. Lond. Math. Soc. 1968, 3, 77–94. [Google Scholar] [CrossRef]
- Obradović, M.; Tuneski, N. Hankel determinants of second and third order for the class S of univalent functions. Math. Slovaca 2021, 71, 649–654. [Google Scholar] [CrossRef]
- Janteng, A.; Halim, S.A.; Darus, M. Coefficient inequality for a function whose derivative has a positive real part. J. Inequal. Pure Appl. Math 2006, 7, 1–5. [Google Scholar]
- Janteng, A.; Halim, S.A.; Darus, M. Hankel determinant for starlike and convex functions. J. Inequal. Pure Appl. Math 2007, 1, 619–625. [Google Scholar]
- Lee, S.K.; Ravichandran, V.; Supramaniam, S. Bounds for the second Hankel determinant of certain univalent functions. J. Inequal. Appl. 2013, 2013, 281. [Google Scholar] [CrossRef]
- Ebadian, A.; Bulboacă, T.; Cho, N.E.; Analouei Adegani, E. Coefficient bounds and differential subordinations for analytic functions associated with starlike functions. Rev. Real Acad. Cienc. Exactas Fis. Nat. Ser. A-Mat. 2020, 114, 128. [Google Scholar] [CrossRef]
- Altınkaya, Ş.; Yalçın, S. Upper bound of second Hankel determinant for bi-Bazilevič functions. Mediterr. J. Math. 2016, 13, 4081–4090. [Google Scholar] [CrossRef]
- Çağlar, M.; Deniz, E.; Srivastava, H.M. Second Hankel determinant for certain subclasses of bi-univalent functions. Turk. J. Math. 2017, 41, 694–706. [Google Scholar] [CrossRef]
- Kanas, S.; Analouei Adegani, A.; Zireh, A. An unified approach to second Hankel determinant of bi-subordinate functions. Mediterr. J. Math. 2017, 14, 233. [Google Scholar] [CrossRef]
- Babalola, K.O. On H3(1) Hankel determinant for some classes of univalent functions. Inequal. Theory Appl. 2010, 6, 1–7. [Google Scholar]
- Altınkaya, Ş.; Yalçın, S. Third Hankel determinant for Bazilevič functions. Adv. Math. Sci. J. 2016, 5, 91–96. [Google Scholar]
- Bansal, D.; Maharana, S.; Prajapat, J.K. Third order Hankel determinant for certain univalent functions. J. Korean Math. Soc. 2015, 52, 1139–1148. [Google Scholar] [CrossRef]
- Krishna, D.V.; Venkateswarlu, B.; RamReddy, T. Third Hankel determinant for bounded turning functions of order alpha. J. Niger. Math. Soc. 2015, 34, 121–127. [Google Scholar] [CrossRef]
- Raza, M.; Malik, S.N. Upper bound of the third Hankel determinant for a class of analytic functions related with lemniscate of Bernoulli. J. Inequal. Appl. 2013, 1, 412. [Google Scholar] [CrossRef]
- Shanmugam, G.; Stephen, B.A.; Babalola, K.O. Third Hankel determinant for α-starlike functions. Gulf J. Math. 2014, 2, 107–113. [Google Scholar] [CrossRef]
- Zaprawa, P. Third Hankel determinants for subclasses of univalent functions. Mediterr. J. Math. 2017, 14, 14–19. [Google Scholar] [CrossRef]
- Kwon, O.S.; Lecko, A.; Sim, Y.J. The bound of the Hankel determinant of the third kind for starlike functions. Bull. Malays. Math. Sci. Soc. 2019, 42, 767–780. [Google Scholar] [CrossRef]
- Zaprawa, P.; Obradović, M.; Tuneski, N. Third Hankel determinant for univalent starlike functions. Rev. Real Acad. Cienc. Exactas Fis. Nat. Ser. A-Mat. 2021, 115, 49. [Google Scholar] [CrossRef]
- Kowalczyk, B.; Lecko, A.; Sim, Y.J. The sharp bound for the Hankel determinant of the third kind for convex functions. Bull. Aust. Math. Soc. 2018, 97, 435–445. [Google Scholar] [CrossRef]
- Lecko, A.; Sim, Y.J.; Śmiarowska, B. The sharp bound of the Hankel determinant of the third kind for starlike functions of order 1/2. Complex Anal. Oper. Theory 2019, 13, 2231–2238. [Google Scholar] [CrossRef]
- Gandhi, S. Radius estimates for three leaf function and convex combination of starlike functions. In Mathematical Analysis I: Approximation Theory, Proceedings of the International Conference on Recent Advances in Pure and Applied Mathematics, New Delhi, India, 23–25 October 2018; Springer: Singapore, 2018; pp. 173–184. [Google Scholar]
- Sunthrayuth, P.; Jawarneh, Y.; Naeem, M.; Iqbal, N.; Kafle, J. Some sharp results on coefficient estimate problems for four-leaf-type bounded turning functions. J. Funct. Spaces 2022, 2022, 8356125. [Google Scholar] [CrossRef]
- Alshehry, A.S.; Shah, R.; Bariq, A. The second Hankel determinant of logarithmic coefficients for starlike and convex functions involving four-leaf-shaped domain. J. Funct. Spaces 2022, 2022, 2621811. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Murugusundaramoorthy, G.; Bulboacă, T. Second Hankel determinant for subclasses of bi-univalent functions associated with a nephroid domain. Rev. Real Acad. Cienc. Exactas Fís. Nat. Ser. A Math. RACSAM 2022, 116, 145. [Google Scholar] [CrossRef]
- Marimuthu, K.; Jayaraman, U.; Bulboacă, T. Coefficient estimates for starlike and convex functions associated with cosine function. Hacet. J. Math. Stat. 2023, 52, 596–618. [Google Scholar]
- Analouei Adegani, E.; Motamednezhad, A.; Jafari, M. Bulboacă, T. Logarithmic coefficients inequality for the family of functions convex in one direction. Mathematics 2023, 11, 2140. [Google Scholar] [CrossRef]
- Marimuthu, K.; Jayaraman, U.; Bulboacă, T. Fekete-Szegő and Zalcman functional estimates for subclasses of alpha-convex functions related to trigonometric functions. Mathematics 2024, 12, 234. [Google Scholar] [CrossRef]
- Pommerenke, C. Univalent Functions; Vandenhoeck and Ruprecht: Göttingen, Germany, 1975. [Google Scholar]
- Carathéodory, C. Über den Variabilitätsbereich der Koeffizienten von Potenzreihen, die gegebene Werte nicht annehmen. Math. Ann. 1907, 64, 95–115. [Google Scholar] [CrossRef]
- Carathéodory, C. Über den Variabilitätsbereich der Fourier’schen Konstanten von positiven harmonischen Funktionen. Rend. Circ. Mat. Palermo (1884–1940) 1911, 32, 193–217. [Google Scholar] [CrossRef]
- Duren, P.L. Univalent Functions; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2001; Volume 259. [Google Scholar]
- Ravichandran, V.; Verma, S. Bound for the fifth coefficient of certain starlike functions. Comptes Rendus Math. 2015, 353, 505–510. [Google Scholar] [CrossRef]
- Livingston, A.E. The coefficients of multivalent close-to-convex functions. Proc. Am. Math. Soc. 1969, 21, 545–552. [Google Scholar] [CrossRef]
- Ali, R.M. Coefficients of the inverse of strongly starlike functions. Bull. Malays. Math. Sci. Soc. 2003, 26, 63–71. [Google Scholar]
- Libera, R.J.; Złotkiewicz, E.J. Early coefficients of the inverse of a regular convex function. Proc. Am. Math. Soc. 1982, 85, 225–230. [Google Scholar] [CrossRef]
- Libera, R.J.; Złotkiewicz, E.J. Bounds for the inverse of a function with derivative in . Proc. Am. Math. Soc. 1983, 87, 251–257. [Google Scholar]
- Krushkal, S.L. A short geometric proof of the Zalcman and Bieberbach conjectures. arXiv 2014, arXiv:1408.1948. [Google Scholar]

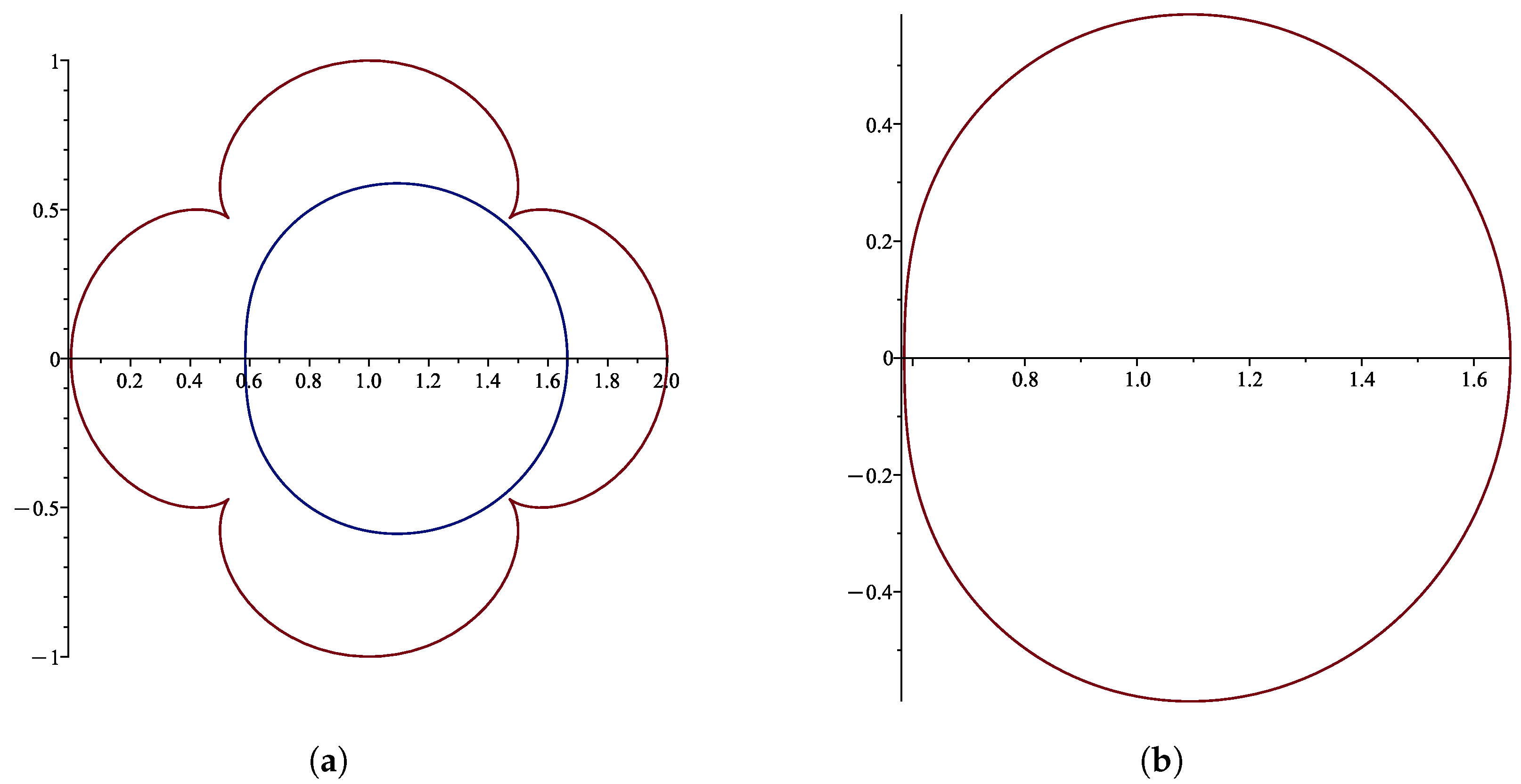

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gunasekar, S.; Sudharsanan, B.; Ibrahim, M.; Bulboacă, T. Subclasses of Analytic Functions Subordinated to the Four-Leaf Function. Axioms 2024, 13, 155. https://doi.org/10.3390/axioms13030155
Gunasekar S, Sudharsanan B, Ibrahim M, Bulboacă T. Subclasses of Analytic Functions Subordinated to the Four-Leaf Function. Axioms. 2024; 13(3):155. https://doi.org/10.3390/axioms13030155
Chicago/Turabian StyleGunasekar, Saravanan, Baskaran Sudharsanan, Musthafa Ibrahim, and Teodor Bulboacă. 2024. "Subclasses of Analytic Functions Subordinated to the Four-Leaf Function" Axioms 13, no. 3: 155. https://doi.org/10.3390/axioms13030155
APA StyleGunasekar, S., Sudharsanan, B., Ibrahim, M., & Bulboacă, T. (2024). Subclasses of Analytic Functions Subordinated to the Four-Leaf Function. Axioms, 13(3), 155. https://doi.org/10.3390/axioms13030155






