Fractal Fractional Derivative Models for Simulating Chemical Degradation in a Bioreactor
Abstract
1. Introduction
2. Preliminaries
3. Analysis of the Model in Classical Sense
4. Analysis of the Model with the Power-Law Kernel
5. Analysis of the Model with the Exponential-Decay Kernel
6. Analysis of the Model with the Mittag–Leffler Kernel
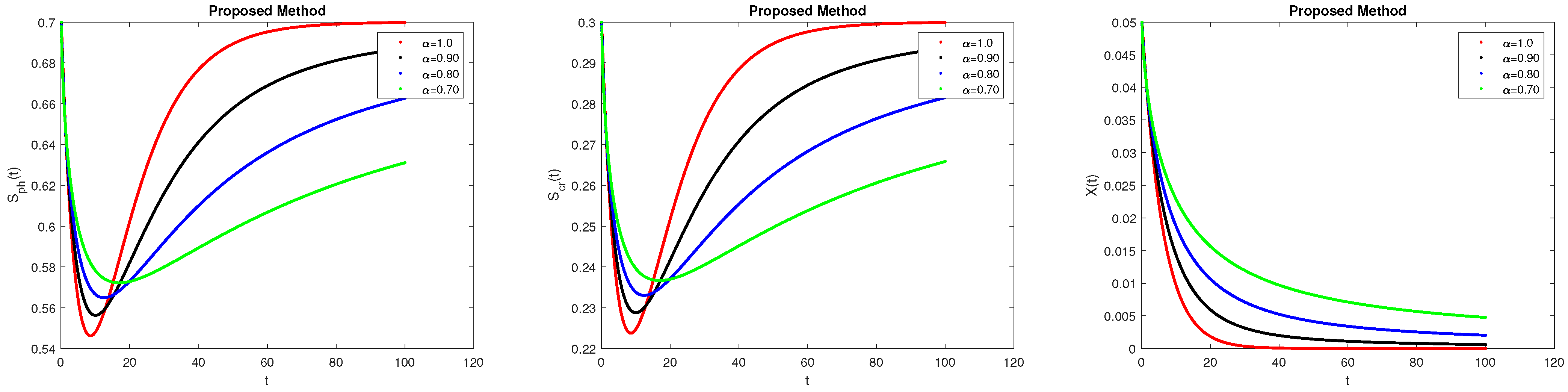
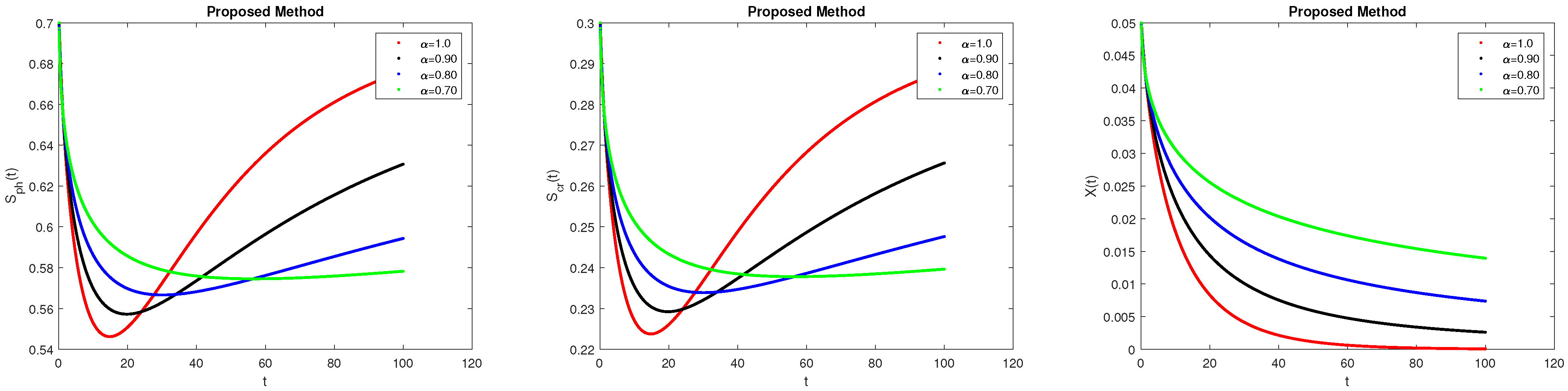
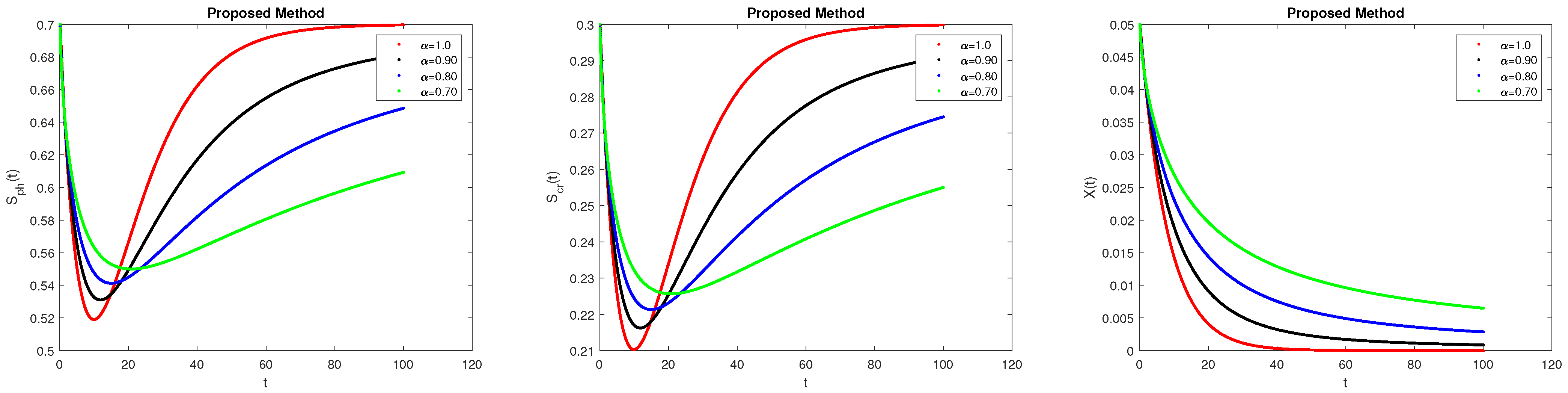
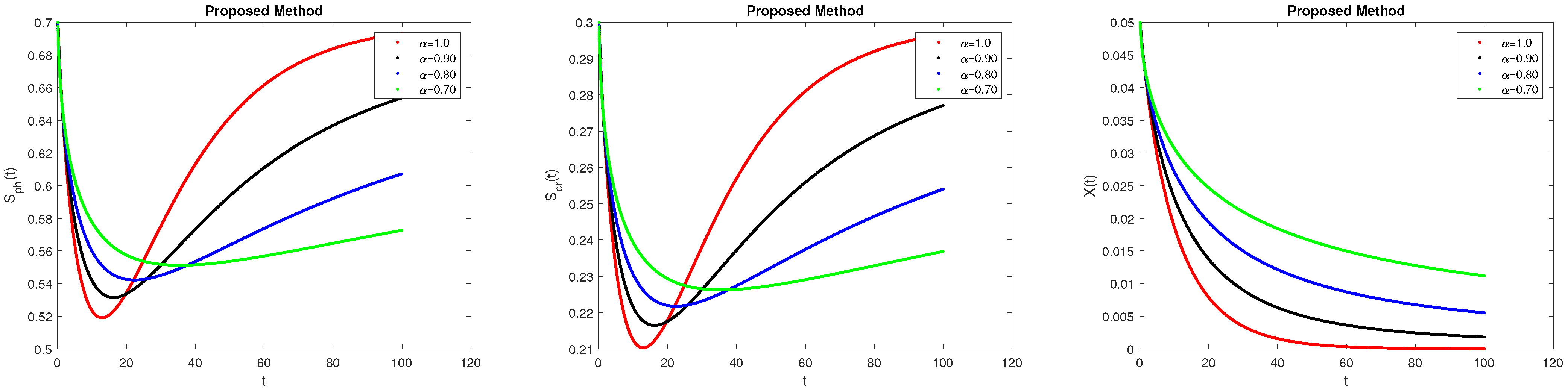
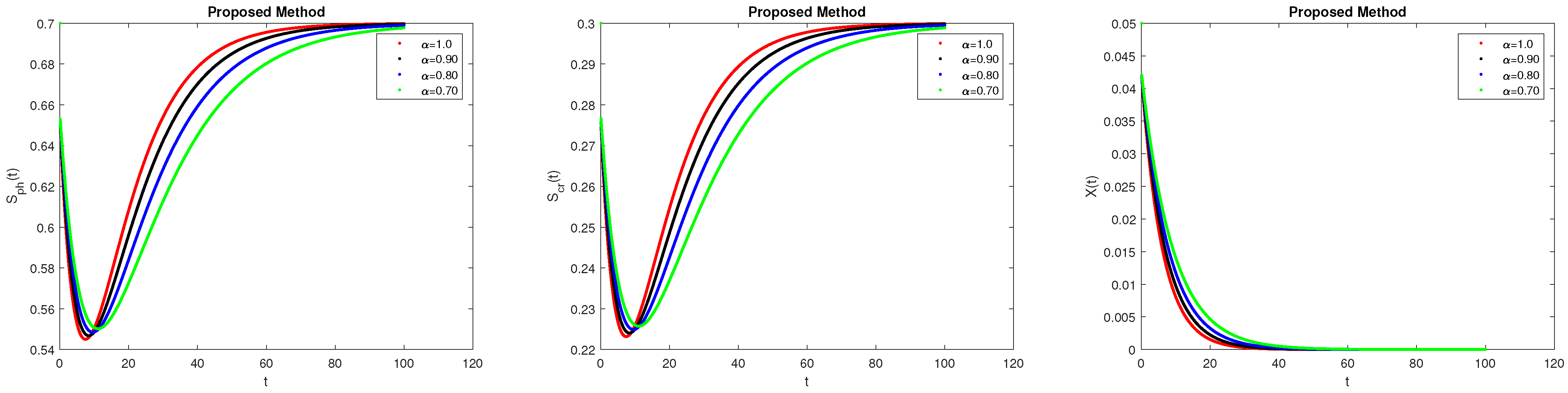
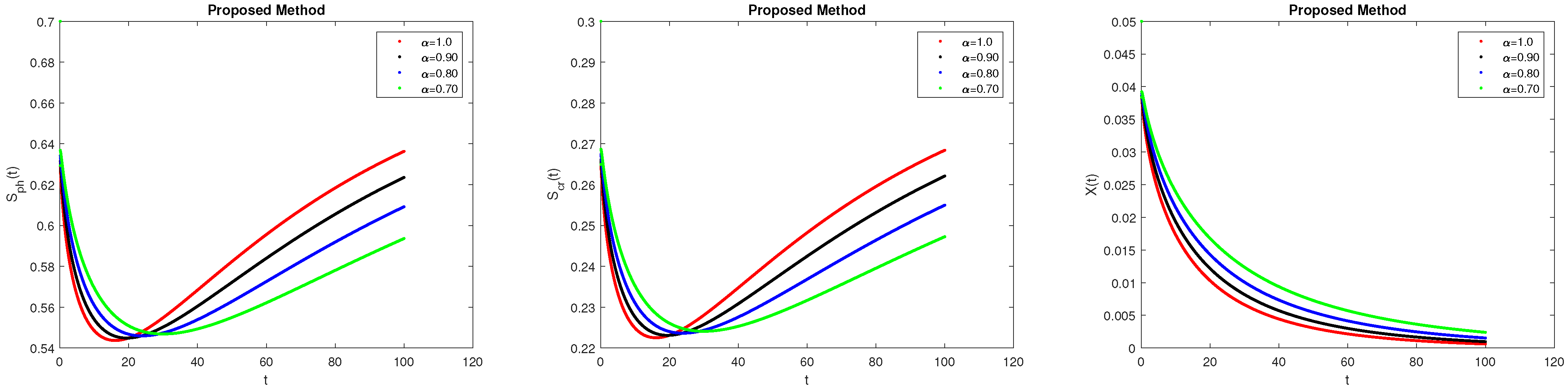
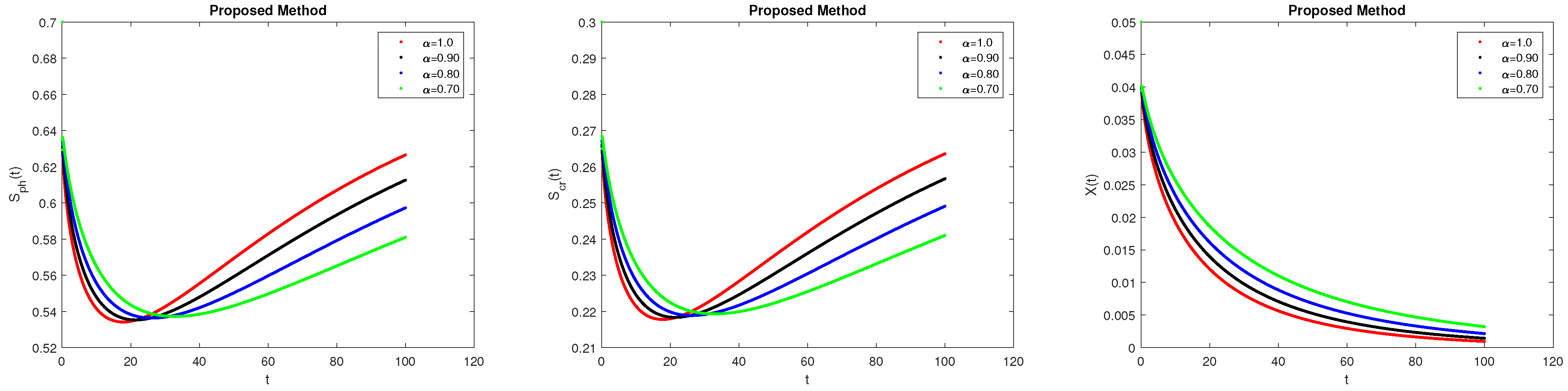
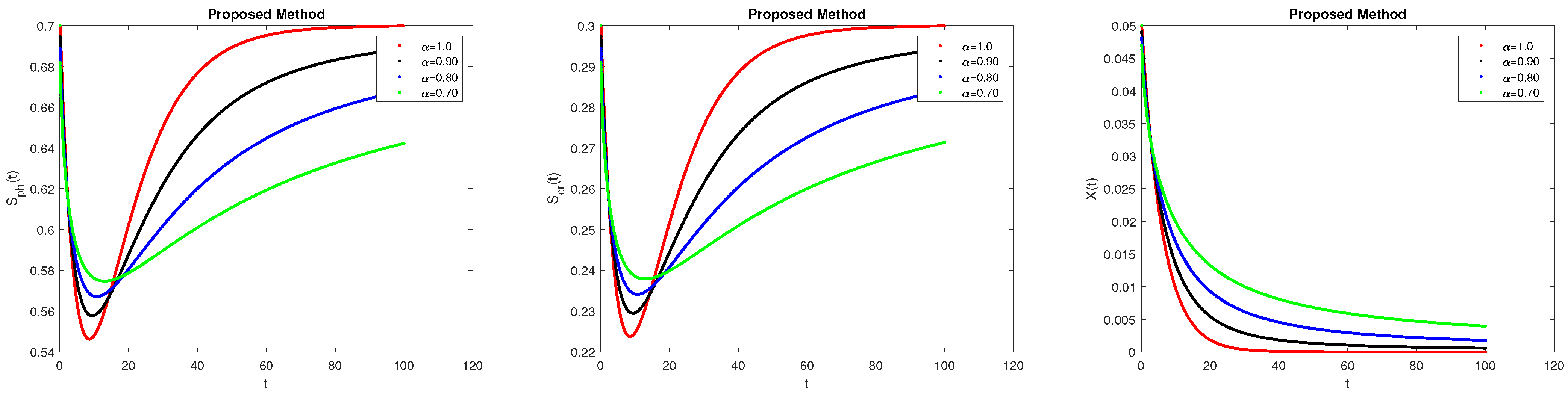
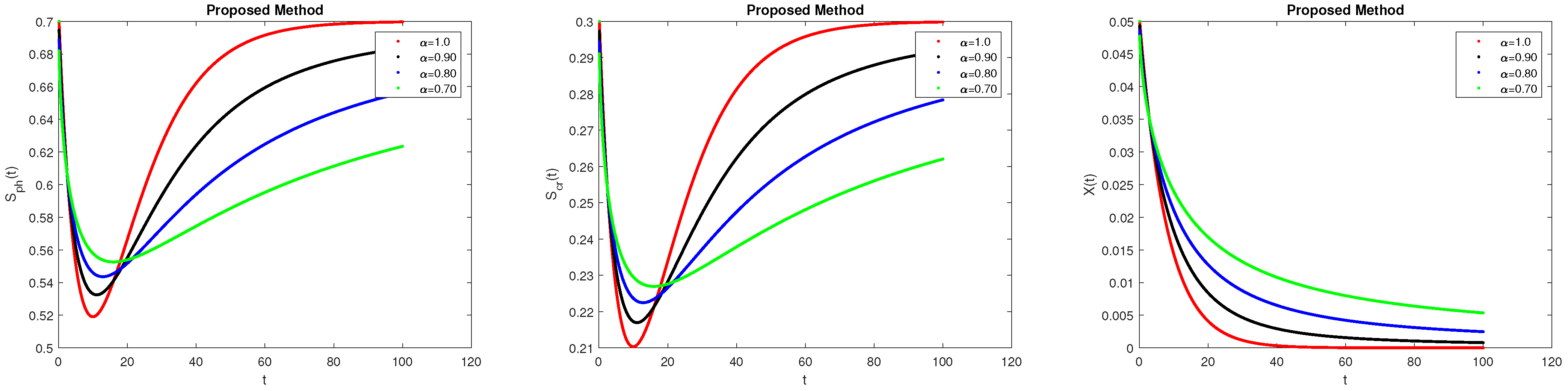
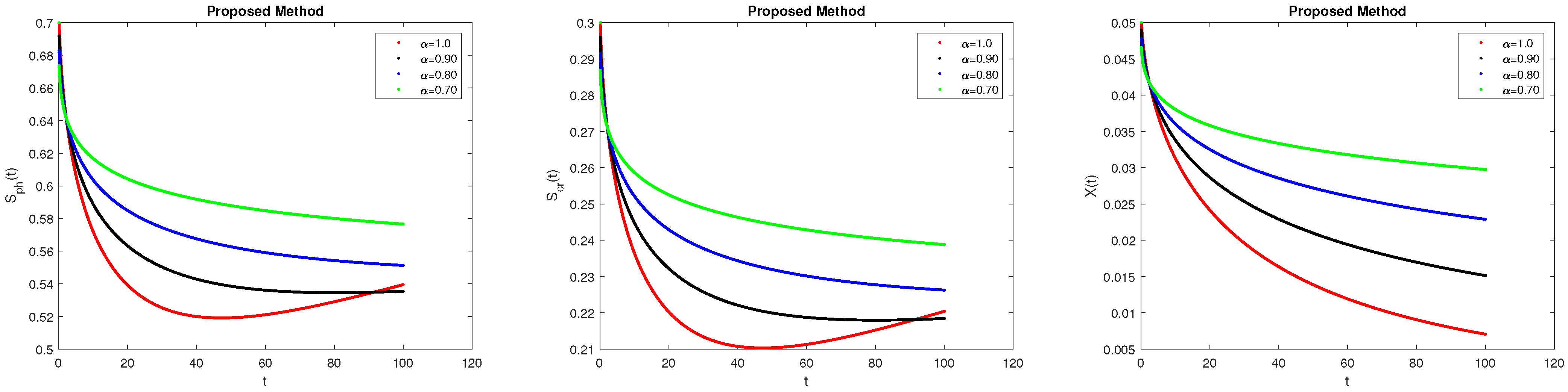
7. Results and Discussions
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dimitrova, N.; Zlateva, P. Global stability analysis of a bioreactor model for phenol and cresol mixture degradation. Processes 2021, 9, 124. [Google Scholar] [CrossRef]
- Seo, J.S.; Keum, Y.S.; Li, Q.X. Bacterial degradation of aromatic compounds. Int. J. Environ. Res. Public Health 2009, 6, 278–309. [Google Scholar] [CrossRef]
- Sharma, N.K.; Philip, L.; Bhallamudi, S.M. Aerobic degradation of phenolics and aromatic hydrocarbons in presence of cyanide. Bioresour. Technol. 2012, 121, 263–273. [Google Scholar] [CrossRef]
- Tomei, M.C.; Annesini, M.C. Biodegradation of phenolic mixtures in a sequencing batch reactor: A kinetic study. Environ. Sci. Pollut. Res. 2008, 15, 188–195. [Google Scholar] [CrossRef]
- Yemendzhiev, H.; Zlateva, P.; Alexieva, Z. Comparison of the biodegradation capacity of two fungal strains toward a mixture of phenol and cresol by mathematical modeling. Biotechnol. Biotechnol. Equip. 2012, 26, 3278–3281. [Google Scholar] [CrossRef][Green Version]
- Kietkwanboot, A.; Chaiprapat, S.; Müller, R.; Suttinun, O. Biodegradation of phenolic compounds present in palm oil mill effluent as single and mixed substrates by Trameteshirsuta AK04. J. Environ. Sci. Health Part A Toxic/Hazard. Subst. Environ. Eng. 2020, 55, 989–1002. [Google Scholar]
- Momani, S. An explicit and numerical solutions of the fractional KdV equation. Math. Comput. Simul. 2005, 70, 110–118. [Google Scholar] [CrossRef]
- Li, C.; Cao, J. A finite difference method for time-fractional telegraph equation. In Proceedings of the IEEE/ASME International Conference on Mechatronics and Embedded Systems and Applications (MESA), Suzhou, China, 8–10 July 2012; pp. 314–318. [Google Scholar]
- Huang, F.; Liu, F. The fundamental solution of the space-time fractional advection-dispersion equation. J. Appl. Math. Comput. 2005, 18, 21–36. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Doha, E.H.; Ezz-Eldien, S.S.; Van Gorder, R.A. A new Jacobi spectral collocation method for solving (1+1)fractional Schrodinger equations and fractional coupled Schrodinger systems. Eur. Phys. J. Plus. 2014, 129, 260. [Google Scholar] [CrossRef]
- Karatay, T.; Bayramoglu, S.R.; Sahin, A. Implicit difference approximation for the time fractional heat equation with the nonlocal condition. Appl. Numer. Math. 2011, 61, 1281–1288. [Google Scholar] [CrossRef]
- Chen, Y.; Yi, M.; Chen, C.; Yu, C. Bernstein polynomials method for fractional convection-diffusion equation with variable coefficients. Comput. Model. Eng. Sci. 2012, 83, 639–653. [Google Scholar]
- Liu, F.; Anh, V.; Turner, I. Numerical solution of space fractional FokkerPlanck equation. J. Comp. Appl. Math. 2004, 166, 209–219. [Google Scholar] [CrossRef]
- Fuente, D.; Lizama, C.; Urchueguía, J.F.; Conejero, J.A. Estimation of the light field inside photosynthetic microorganism cultures through Mittag-Leffler functions at depleted light conditions. J. Quant. Spectrosc. Radiat. Transf. 2018, 204, 23–26. [Google Scholar] [CrossRef]
- Lizama, C.; Murillo-Arcila, M.; Trujillo, M. Fractional Beer-Lambert law in laser heating of biological tissue. AIMS Math. 2022, 14, 14444–14459. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. Comparison between the homotopy perturbation method and the variational iteration method for linear fractional partial differential equations. Comput. Math. Appl. 2007, 54, 910–919. [Google Scholar] [CrossRef]
- El-Sayed, A.M.A.; Gaber, M. The Adomian decomposition method for solving partial differential equations of fractal order in finite domains. Phys. Lett. A 2006, 359, 175–182. [Google Scholar] [CrossRef]
- Ahmad, H.; Khan, M.N.; Ahmad, I.; Omri, M.; Alotaibi, M.F. A meshless method for numerical solutions of linear and nonlinear time-fractional Black-Scholes models. AIMS Math. 2023, 8, 19677–19698. [Google Scholar] [CrossRef]
- Khaliq, S.; Ahmad, S.; Ullah, A.; Ahmad, H.; Saifullah, S.; Nofal, T.A. New waves solutions of the (2 + 1)-dimensional generalized Hirota–Satsuma–Ito equation using a novel expansion method. Res. Phys. 2023, 50, 106450. [Google Scholar] [CrossRef]
- Adel, M.; Khader, M.M.; Ahmad, H.; Assiri, T.A. Approximate analytical solutions for the blood ethanol concentration system and predator-prey equations by using variational iteration method. AIMS Math. 2023, 8, 19083–19096. [Google Scholar] [CrossRef]
- Atangana, A. Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex, system. Chaos Solitons Fractals 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Toufik, M.; Atangana, A. New numerical approximation of fractional derivative with non-local and non-singular kernel: Application to chaotic models. Eur. Phys. J. Plus 132 2017, 10, 444. [Google Scholar] [CrossRef]
- Mohammadi, H.; Kumar, S.; Rezapour, S.; Etemad, S. A theoretical study of the Caputo-Fabrizio fractional modeling for hearing loss due to Mumps virus with optimal control. Chaos Solitons Fractals 2021, 144, 110668. [Google Scholar] [CrossRef]
- Baleanu, D.; Jajarmi, A.; Mohammadi, H.; Rezapour, S. A new study on the mathematical modelling of human liver with Caputo-Fabrizio fractional derivative. Chaos Solitons Fractals 2021, 134, 109705. [Google Scholar] [CrossRef]
- Alzabut, J.; Selvam, A.; Dhineshbabu, R.; Tyagi, S.; Ghaderi, M.; Rezapour, S. A Caputo discrete fractional-order thermostat model with one and two sensors fractional boundary conditions depending on positive parameters by using the Lipschitz-type inequality. J. Inequal. Appl. 2022, 2022, 56. [Google Scholar] [CrossRef]
- Heydarpour, Z.; Izadi, J.; George, R.; Ghaderi, M.; Rezapour, S. On a partial fractional hybrid version of generalized Sturm–Liouville–Langevin equation. Fractal Fract. 2022, 6, 269. [Google Scholar] [CrossRef]
- George, R.; Houas, M.; Ghaderi, M.; Rezapour, S.; Elagan, S.K. On a coupled system of pantograph problem with three sequential fractional derivatives by using positive contraction-type inequalities. Results Phys. 2022, 39, 105687. [Google Scholar] [CrossRef]
- Matar, M.M.; Abbas, M.I.; Alzabut, J.; Kaabar, M.K.A.; Etemad, S.; Rezapour, S. Investigation of the p-Laplacian nonperiodic nonlinear boundary value problem via generalized Caputo fractional derivatives. Adv. Differ. Equ. 2021, 2021, 68. [Google Scholar] [CrossRef]
- Etemad, S.; Avci, I.; Kumar, P.; Baleanu, D.; Rezapour, S. Some novel mathematical analysis on the fractal-fractional model of the AH1N1/09 virus and its generalized Caputo-type version. Chaos Solitons Fractals 2022, 162, 112511. [Google Scholar] [CrossRef]
- Ullah, I.; Ullah, A.; Ahmad, S.; Ahmad, H.; Nofal, T.A. A survey of KdV-CDG equations via nonsingular fractional operators. AIMS Math. 2023, 8, 18964–18981. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204, 523p. [Google Scholar]
- Volterra, V. Sur les équations intégro-différentielles et leurs applications. Acta Math. 1912, 35, 295–356. [Google Scholar] [CrossRef]
- Coimbra, C.F. Mechanics with variable-order differential operators. Ann. Phys. 2003, 12, 11–12. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Valerio, D.; Machado, J.T. Variable order fractional systems. Commun. Nonlinear Sci. Numer. Simul. 2019, 71, 231–243. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akgül, A.; Conejero, J.A. Fractal Fractional Derivative Models for Simulating Chemical Degradation in a Bioreactor. Axioms 2024, 13, 151. https://doi.org/10.3390/axioms13030151
Akgül A, Conejero JA. Fractal Fractional Derivative Models for Simulating Chemical Degradation in a Bioreactor. Axioms. 2024; 13(3):151. https://doi.org/10.3390/axioms13030151
Chicago/Turabian StyleAkgül, Ali, and J. Alberto Conejero. 2024. "Fractal Fractional Derivative Models for Simulating Chemical Degradation in a Bioreactor" Axioms 13, no. 3: 151. https://doi.org/10.3390/axioms13030151
APA StyleAkgül, A., & Conejero, J. A. (2024). Fractal Fractional Derivative Models for Simulating Chemical Degradation in a Bioreactor. Axioms, 13(3), 151. https://doi.org/10.3390/axioms13030151








